
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 21 October 2022
Sec. Fusion Plasma Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1026496
This article is part of the Research TopicLaser-driven Particle Acceleration and Radiation Based on Micro-structured Plasma TargetsView all 9 articles
We propose a new scheme to generate a neutron source with a short duration, and the scheme is validated in two-dimensional radiation hydrodynamic simulations. When a laser beam irradiates a deuterated polystyrene cone with a half-opening angle of
Neutron sources have been utilized across a wide range, such as material probing, nuclear waste treatment, material science [1, 2], and fast neutron imaging [3, 4]. Compared to X-ray radiographs, neutron radiographs are more sensitive to low-Z material and could provide complementary information, allowing robust measurement of interior temperature [5–7]. Although conventional neutron sources, for example, nuclear reactors and accelerator-based spallation, have abilities to provide high-flux neutrons, they are restricted in use due to enormous facilities and expensive costs. The advent of high-intensity lasers, providing a new access to pulsed neutron sources, has the potential to bring a further increase in neutron flux and brightness [8, 9]. When a PW-class intensity laser irradiates a solid target, the ions are accelerated to MeV energy by target normal sheath acceleration [10, 11]. Then the energetic ion beams are dumped into secondary low-Z converter targets to emit directional neutron beams [12–14]. Moreover, the cluster target also creates a dense fusion environment under laser irradiation and produces neutrons by Coulomb explosion [15–18]. The schemes of inertial confinement fusion (ICF) could also produce high-flux neutrons with narrow-band energy distribution, usually achieved by stagnation of ablated plasma [19–21]. However, the arrangement of multiple laser beams and elaborating target fabrication increases the difficulties of experimental operation [22–24].
As a new kind of target structure, the conical target is widely employed in experiments [25–27]. The uniquely converging configuration contributes to generating plasma jets with wide parameter range, which is considered an alternative tool to study astrophysical jets [28, 29]. Based on our previous work about high energy density jets, we propose a scheme of the compact source from the collision of high energy density jets [30]. When a laser beam irradiates the hollow cone which is made of deuterated polystyrene, high energy density plasma jets driven by ablation pressure are produced. Then the collision of counter-propagating jets takes place in a head-on configuration, converts kinetic energy into internal energy efficiently, and induces a significant increase in temperature and density. Eventually, the stagnation layer forms near the middle plane, and plenty of neutrons are released during the confinement period. Two-dimensional simulations show that the neutron yield can reach
The numerical code used is briefly outlined here. FLASH is an open-source radiation hydrodynamic code and has the capabilities to simulate the laser-driven high energy density physics experiments, such as nanosecond laser-plasma interaction, inertial confinement fusion, and laboratory astrophysics [31–33]. In FLASH, Euler’s governing equations are evolved by using a directionally unsplit solver and coupled with laser energy deposition, multigroup radiation transport, and electron thermal conduction. In view of the multi-temperature treatment of plasma, where ion temperature, electron temperature, and radiation temperature are not necessarily equal, the governing equations are given as
where
where
To validate the newly extended thermonuclear reaction module, a two-dimensional radiation hydrodynamic simulation is carried out to simulate the SCPF experiments. According to the experiment setup, the gold spherical hohlraum has an inner diameter of

FIGURE 1. Spatial distribution in simulating the SCPF experiments of mass density distribution with color bar of decimal logarithmic scale at 0.5 ns (A) and 1.5 ns (B). The lower panel (C,D) corresponds to the ion temperature at the same moment.
Based on the extended thermonuclear reaction module, we propose a new scheme of compact neutron sources from the head-on collision of plasma jets. The schematic diagram is depicted in Figure 2. The gray part denotes deuterated polystyrene (CD) cone with a density of
Figure 3 shows the neutron yield (red line) and generation rate (blue line) in our radiation hydrodynamic simulation. Before
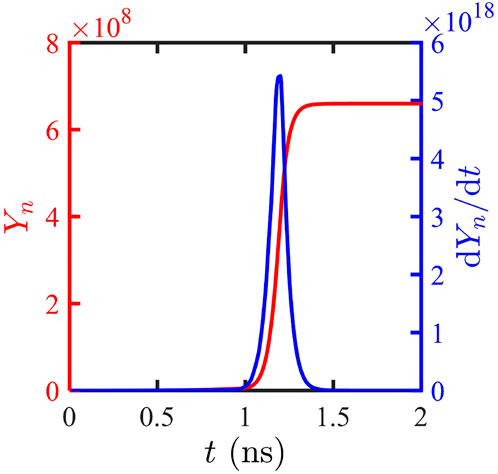
FIGURE 3. Neutron yield (red line) and generation rate integrated over the whole domain (blue line) evolve over time.
If the ion kinetic energy is much larger than the internal energy, they are not in thermal equilibrium with the background plasma. The approximate reactivity is no longer suitable, which means that the beam–target reaction should be employed rather than the thermonuclear reaction. Although the beam–target reaction is not involved in the extended module, we can still analyze the proportion of beam–target neutrons theoretically. There are two channels for D–D thermonuclear reactions with almost the same cross-section
where T, p, and n denote tritium nucleus, protons, and neutrons, respectively [35]. The 2.45 MeV neutrons at a velocity of
The aforementioned parameters are substituted into the Eq. 7, and the ratio is as low as 0.5%.
The formation of plasma jets is of vital importance in our proposed scheme. When a laser normally irradiates the cone, the outer surface vaporizes rapidly to form blow-out corona plasma. The laser energy is only deposited near the critical surface where the laser frequency is equal to the plasma frequency, and then the laser energy is transferred to the electrons by the inverse bremsstrahlung mechanism. Then, the deposited energy is transported inward to the unablated region by the electron thermal conduction. The ablation pressure drives the shock wave, and promotes the cone movement. Figure 4 shows the spatial distribution of plasma mass density and ion temperature at different moments. Benefiting from the converging effect of the cone, the plasma jets are formed due to the collision and extrusion with an average density of
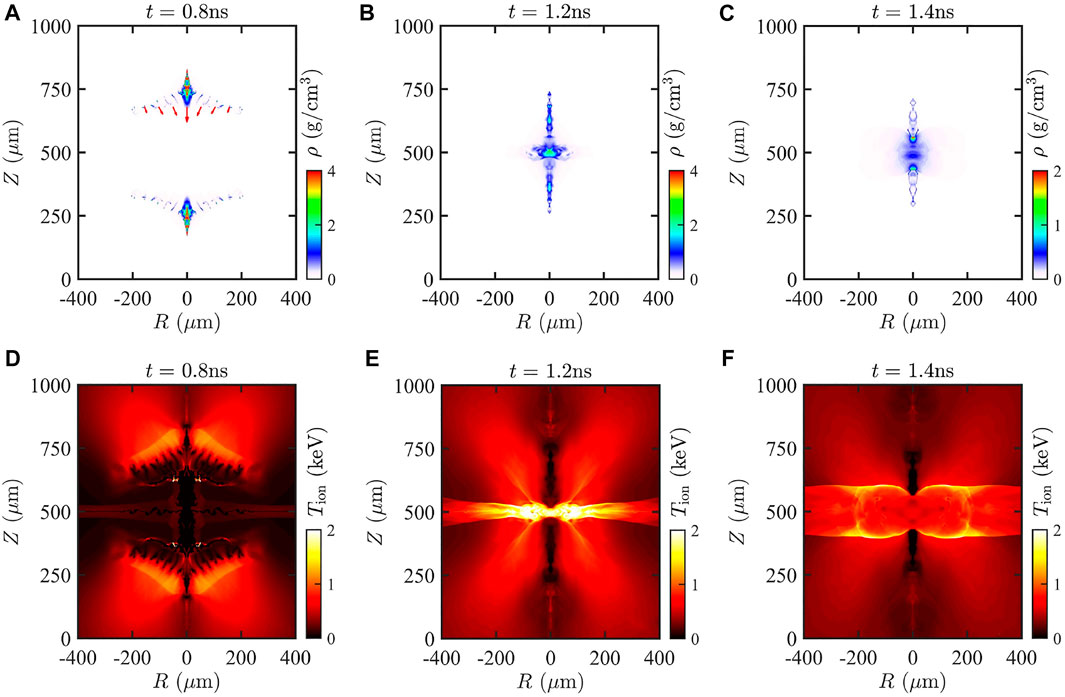
FIGURE 4. Spatial distribution of density at
The velocity is another important characteristic to describe the whole hydrodynamic process from jet formation to collision. Figure 5 shows the velocity distribution near the central axis
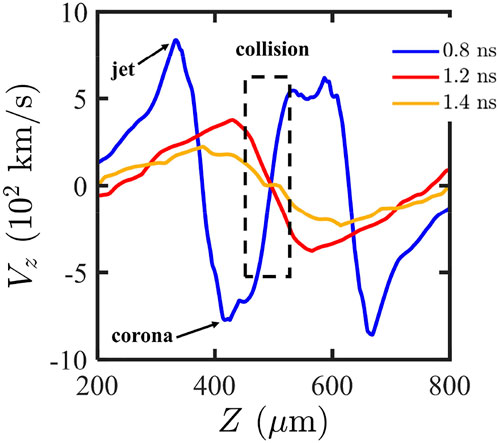
FIGURE 5. Velocity distribution along
As mentioned previously, the confinement time of the hotspot-like plasma is of vital importance to neutron yield. After the head-on collision of plasma jets, the rarefaction wave propagates outward from the center at acoustic speed
The D–D thermonuclear reactions generate not only neutrons but also charged particles. Compared with the internal and kinetic energy density of CD plasma, the deposited energy from newly generated particles could be ignored. Generally, if the areal density is larger than
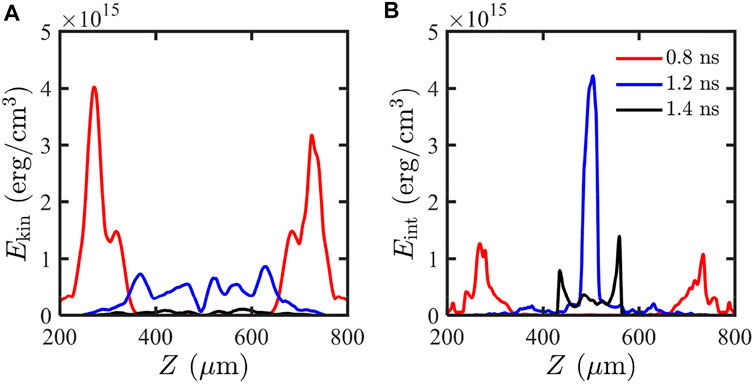
FIGURE 6. Distribution of kinetic energy density (A) and inertial energy density (B) at
Figure 7 shows the ion temperature and maximum density evolve as the half-opening angle
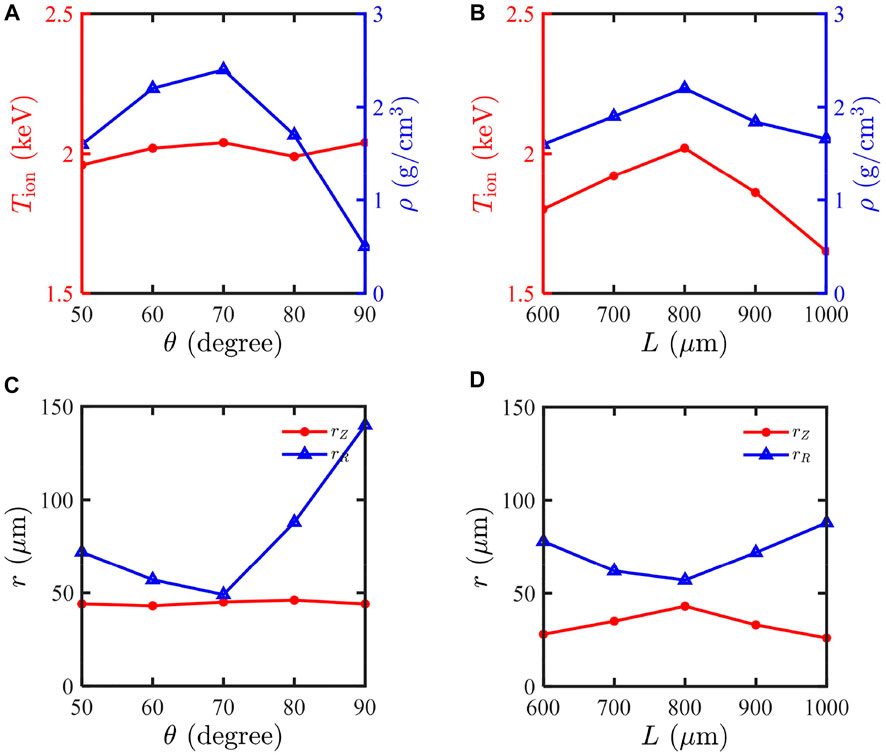
FIGURE 7. Maximum density and ion temperature evolve as the opening angle (A) and the distance of cone tips (B). (C,D) correspond to the hotspot-like plasma along the R-axis and Z-axis under the same condition.
The acceleration distance is mainly related to the distance between cone tips, but not to the opening angle. Notably, the kinetic energy of plasma jets increases as the distance increases. When the distance of cone tips is fixed as
The angle and distance would influence neutron yield. Figure 8 shows the neutron yield and duration evolve as the half-opening angle
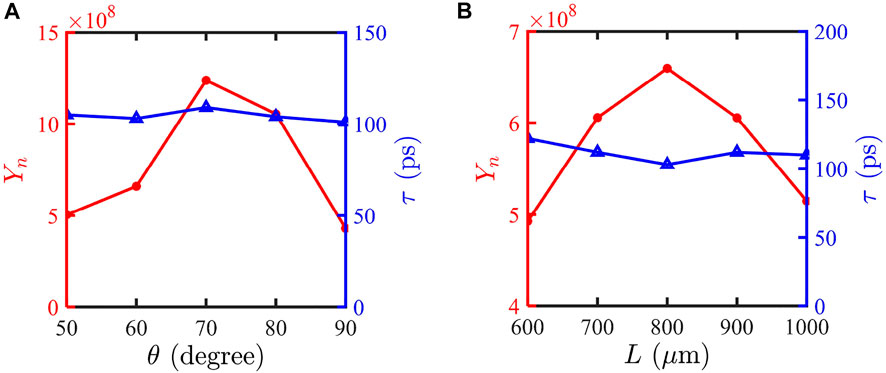
FIGURE 8. Yield (red-circle lines) and duration (blue-triangle lines) evolve as the cone angle (A) and the distance of separate cone tips (B). The distance of cone tips is fixed as
There is no essential difference between the hot but underdense plasma colliding approach and our proposed scheme. They increase neutron production rate and yield in different ways. Generally, higher intensity laser is required to increase plasma temperature. As for the stationary ablation model, the temperature in corona plasma is only in correction with the laser parameters, for example, intensity, energy absorption rate, and wavelength. However, by optimizing the target structure, high density can be achieved although the laser intensity is fixed. A scheme of overdense but cold plasma colliding is easier to implement in experiments.
Table 1 shows the comparison of the laser-driven neutron source. The neutron yield in our scheme is close to the beam–target interaction. Assuming that neutrons are emitted isotropically throughout the whole solid angle, the flux is estimated as
In this study, we propose a new scheme of the compact neutron source. The laser-driven plasma jets are generated due to the convergence effect of the cone target. Under the mirrored geometric structure, two counter-propagating jets collide near the middle plane and form hotspot-like plasma. The conversion from kinetic to internal energy increases the ion temperature, and the D–D thermonuclear reaction is triggered. Plenty of neutrons are released and the neutron yield is as high as
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Y-ZK contributed to the conception and ideas. YC and Y-ZK developed the newly extended thermonuclear module based on the original FLASH code. YC performed the numerical simulations and data analysis. YC completed the writing of the manuscript. X-HY, Y-YM, and F-QS contributed significantly to the analysis and manuscript preparation.
This work was supported by the Strategic Priority Research Program of the Chinese Academy of Science (Grant No. XDA25050200), the National Natural Science Foundation of China (Grant Nos 12175309, 11775305, 11975308, and 12005297), the fund of Science Challenge Project (No. TZ2018001), the State Key Laboratory of Laser Interaction with Matter (No. SKLLIM1908).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Svergun DI, Koch MHJ. Advances in structure analysis using small-angle scattering in solution. Curr Opin Struct Biol (2002) 12(5):654–60. doi:10.1016/s0959-440x(02)00363-9
2. Noguere G, Cserpak F, Ingelbrecht C, Plompen AJM, Quetel CR, Schillebeeckx P. Non-destructive analysis of materials by neutron resonance transmission. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2007) 575(3):476–88. doi:10.1016/j.nima.2007.02.085
3. Strobl M, Manke I, Kardjilov N, Hilger A, Dawson M, Banhart J. Advances in neutron radiography and tomography. J Phys D Appl Phys (2009) 42(24):243001. doi:10.1088/0022-3727/42/24/243001
4. Higginson DP, McNaney JM, Swift DC, Bartal T, Hey DS, Kodama R, et al. Laser generated neutron source for neutron resonance spectroscopy. Phys Plasmas (2010) 17(10):100701. doi:10.1063/1.3484218
5. Yuan VW, Bowman JD, Funk DJ, Morgan GL, Rabie RL, Ragan CE, et al. Shock temperature measurement using neutron resonance spectroscopy. Phys Rev Lett (2005) 94(12):125504. doi:10.1103/physrevlett.94.125504
6. Swift DC, Seifter A, Holtkamp DB, Yuan VW, Bowman D, Clark DA. Explanation of anomalous shock temperatures in shock-loaded Mo samples measured using neutron resonance spectroscopy. Phys Rev B (2008) 77(9):092102. doi:10.1103/physrevb.77.092102
7. Abe Y, Sunahara A, Lee S, Yanagawa T, Zhang Z, Arikawa Y, et al. Production of intense, pulsed, and point-like neutron source from deuterated plastic cavity by mono-directional kilo-joule laser irradiation. Appl Phys Lett (2017) 111(23):233506. doi:10.1063/1.5016531
8. Danson C, Hillier D, Hopps N, Neely D. Petawatt class lasers worldwide. High Pow Laser Sci Eng (2015) 3:e3. doi:10.1017/hpl.2014.52
9. Guler N, Volegov P, Favalli A, Merrill FE, Falk K, Jung D, et al. Neutron imaging with the short-pulse laser driven neutron source at the Trident laser facility. J Appl Phys (2016) 120(15):154901. doi:10.1063/1.4964248
10. Wilks SC, Langdon AB, Cowan TE, Roth M, Singh M, Hatchett S, et al. Energetic proton generation in ultra-intense laser–solid interactions. Phys Plasmas (2001) 8(2):542–9. doi:10.1063/1.1333697
11. Snavely RA, Key MH, Hatchett SP, Cowan TE, Roth M, Phillips TW, et al. Intense high-energy proton beams from petawatt-laser irradiation of solids. Phys Rev Lett (2000) 85(14):2945–8. doi:10.1103/physrevlett.85.2945
12. Higginson DP, McNaney JM, Swift DC, Petrov GM, Davis J, Frenje JA, et al. Production of neutrons up to 18 MeV in high-intensity, short-pulse laser matter interactions. Phys Plasmas (2011) 18(10):100703. doi:10.1063/1.3654040
13. Zhao JR, Zhang XP, Yuan DW, Li YT, Li DZ, Rhee YJ, et al. A novel laser-collider used to produce monoenergetic 13.3 MeV 7Li (d, n) neutrons. Sci Rep (2016) 6(1):27363. doi:10.1038/srep27363
14. Kleinschmidt A, Bagnoud V, Deppert O, Favalli A, Frydrych S, Hornung J, et al. Intense, directed neutron beams from a laser-driven neutron source at PHELIX. Phys Plasmas (2018) 25(5):053101. doi:10.1063/1.5006613
15. Ditmire T, Tisch JWG, Springate E, Mason MB, Hay N, Smith RA, et al. High-energy ions produced in explosions of superheated atomic clusters. Nature (1997) 386(6620):54–6. doi:10.1038/386054a0
16. Ditmire T, Zweiback J, Yanovsky VP, Cowan TE, Hays G, Wharton KB. Nuclear fusion in gases of deuterium clusters heated with a femtosecond laser. Phys Plasmas (2000) 7(5):1993–8. doi:10.1063/1.874020
17. Bang W, Dyer G, Quevedo HJ, Bernstein AC, Gaul E, Rougk J, et al. Optimum laser intensity for the production of energetic deuterium ions from laser-cluster interaction. Phys Plasmas (2013) 20(9):093104. doi:10.1063/1.4821611
18. Ditmire T, Zweiback J, Yanovsky VP, Cowan TE, Hays G, Wharton KB. Nuclear fusion from explosions of femtosecond laser-heated deuterium clusters. Nature (1999) 398(6727):489–92. doi:10.1038/19037
19. He M-Q, Cai H-B, Zhang H, Dong Q-L, Zhou C-T, Wu S-Z, et al. A spherical shell target scheme for laser-driven neutron sources. Phys Plasmas (2015) 22(12):123103. doi:10.1063/1.4936828
20. Zhao JR, Zhang XP, Yuan DW, Chen LM, Li YT, Fu CB, et al. Neutron yield enhancement in laser-induced deuterium-deuterium fusion using a novel shaped target. Rev Scientific Instr (2015) 86(6):063505. doi:10.1063/1.4922912
21. Zhang X, Zhao J, Yuan D, Fu C, Bao J, Chen L, et al. Deuteron-deuteron fusion in laser-driven counter-streaming collisionless plasmas. Phys Rev C (2017) 96(5):055801. doi:10.1103/physrevc.96.055801
22. Craxton RS, Anderson KS, Boehly TR, Goncharov VN, Harding DR, Knauer JP, et al. Direct-drive inertial confinement fusion: A review. Phys Plasmas (2015) 22(11):110501. doi:10.1063/1.4934714
23. Betti R, Hurricane OA. Inertial-confinement fusion with lasers. Nat Phys (2016) 12(5):435–48. doi:10.1038/nphys3736
24. Bose A, Woo KM, Nora R, Betti R. Hydrodynamic scaling of the deceleration-phase Rayleigh–Taylor instability. Phys Plasmas (2015) 22(7):072702. doi:10.1063/1.4923438
25. Hu L-X, Yu T-P, Shao F-Q, Zhu Q-J, Yin Y, Ma Y-Y. Enhanced dense attosecond electron bunch generation by irradiating an intense laser on a cone target. Phys Plasmas (2015) 22(12):033104. doi:10.1063/1.4913984
26. Zhu X-L, Yu T-P, Sheng Z-M, Yin Y, Turcu ICE, Pukhov A. Dense GeV electron–positron pairs generated by lasers in near-critical-density plasmas. Nat Commun (2016) 7(1):13686–8. doi:10.1038/ncomms13686
27. Zhang J, Wang W, Yang XH, Wu D, Ma YY, Jiao J, et al. Double-cone ignition scheme for inertial confinement fusion. Phil Trans R Soc A (2020) 378:20200015. doi:10.1098/rsta.2020.0015
28. Shigemori K, Kodama R, Farley DR, Koase T, Estabrook KG, Remington BA, et al. Experiments on radiative collapse in laser-produced plasmas relevant to astrophysical jets. Phys Rev E (2000) 62(6):8838–41. doi:10.1103/physreve.62.8838
29. Li CK, Tzeferacos P, Lamb D, Gregori G, Norreys PA, Rosenberg MJ, et al. Scaled laboratory experiments explain the kink behaviour of the Crab Nebula jet. Nat Commun (2016) 7(1):13081. doi:10.1038/ncomms13081
30. Ke YZ, Yang XH, Ma YY, Xu BB, Ge ZY, Gan LF, et al. High-energy-density plasma jet generated by laser-cone interaction. Phys Plasmas (2018) 25(4):042706. doi:10.1063/1.5021137
31. Fryxell B, Olson K, Ricker P, Timmes FX, Zingale M, Lamb DQ, et al. Flash: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. Astrophys J Suppl Ser (2000) 131(1):273–334. doi:10.1086/317361
32. Joggerst CC, Nelson A, Woodward P, Lovekin C, Masser T, Fryer CL, et al. Cross-code comparisons of mixing during the implosion of dense cylindrical and spherical shells. J Comput Phys (2014) 275:154–73. doi:10.1016/j.jcp.2014.06.037
33. Derigs D, Winters AR, Gassner GJ, Walch S. A novel high-order, entropy stable, 3D AMR MHD solver with guaranteed positive pressure. J Comput Phys (2016) 317:223–56. doi:10.1016/j.jcp.2016.04.048
34. Orban C, Fatenejad M, Lamb DQ. Code-to-code comparison and validation of the radiation-hydrodynamics capabilities of the FLASH code using a laboratory astrophysical jet. Phys Plasmas (2022) 29(5):053901. doi:10.1063/5.0079493
36. Bosch HS, Hale GM. Improved formulas for fusion cross-sections and thermal reactivities. Nucl Fusion (1992) 32(4):611–31. doi:10.1088/0029-5515/32/4/i07
37. Tumino A, Spitaleri C, Mukhamedzhanov AM, Typel S, Aliotta M, Burjan V, et al. Low-energy d+d fusion reactions via the Trojan Horse Method. Phys Lett B (2011) 700(2):111–5. doi:10.1016/j.physletb.2011.05.001
38. Tumino A, Spartà R, Spitaleri C, Mukhamedzhanov AM, Typel S, Pizzone RG, et al. NEW DETERMINATION OF THE2H(d, p)3H AND2H(d, n)3He REACTION RATES AT ASTROPHYSICAL ENERGIES. Astrophys J (2014) 785(2):96. doi:10.1088/0004-637x/785/2/96
39. Ren G, Yan J, Liu J, Lan K, Chen YH, Huo WY, et al. Neutron generation by laser-driven spherically convergent plasma fusion. Phys Rev Lett (2017) 118(16):165001. doi:10.1103/physrevlett.118.165001
40. More RM, Warren KH, Young DA, Zimmerman GB. A new quotidian equation of state (QEOS) for hot dense matter. Phys Fluids (1994) (1988) 31(10):3059–78. doi:10.1063/1.866963
Keywords: high energy density jets, head-on collision, neutron source, short duration, energy conversion, thermonuclear reaction
Citation: Cui Y, Ke Y-Z, Yang X-H, Ma Y-Y and Shao F-Q (2022) Compact neutron source from head-on collision of high energy density plasma jets. Front. Phys. 10:1026496. doi: 10.3389/fphy.2022.1026496
Received: 24 August 2022; Accepted: 07 October 2022;
Published: 21 October 2022.
Edited by:
Jinqing Yu, Hunan University, ChinaReviewed by:
Marco La Cognata, Laboratori Nazionali del Sud (INFN), ItalyCopyright © 2022 Cui, Ke, Yang, Ma and Shao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yan-Yun Ma, eWFueXVubWFAMTI2LmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.