
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys. , 21 September 2022
Sec. Physical Acoustics and Ultrasonics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1024964
This article is part of the Research Topic Advances in Acoustic/Elastic Wave Sensing for Information Processing View all 6 articles
Acoustic and elastic waves carry a wealth of useful physical information in real world. Sensing acoustic and elastic waves is very important for discovering knowledge in various fields. Conventional wave sensing approaches generally require multiple expensive sensors and complex hardware systems due to the uniform spatial transmission characteristics of physical fields. These limitations prompt the development of wave sensing strategies with high integration degree, lightweight structure, and low hardware cost. Due to their extraordinary physical properties, artificially engineered structures such as metastructures can encode the physical field information by flexibly manipulating the transmission characteristics of acoustic and elastic waves. The fusion of information coding and wave sensing process breaks through the limitations of conventional sensing approaches and reduces the sensing cost. This review aims to introduce the advances in spatial information coding with artificially engineered structures for acoustic and elastic wave sensing. First, we review the enhanced spatial wave sensing with metastructures for weak signal detection and source localization. Second, we introduce computational sensing approaches that combines the spatial transmission coding structures with reconstruction algorithms. Representative progress of computational sensing with metastructures and random scattering media in audio source separation, ultrasonic imaging, and vibration information identification is reviewed. Finally, the open problems, challenges, and research prospects of the spatial information coding structures for acoustic and elastic wave sensing are discussed.
Acoustic and elastic waves carry a wealth of useful physical information in real world. Sensing acoustic and elastic waves is very important for understanding knowledge in various fields [1–3]. However, current wave sensing approaches generally requires multiple expensive sensors and complex hardware systems due to the uniform spatial transmission characteristics of physical field. For example, acoustic camera is an imaging device used to locate sound sources and visualize acoustic fields. It consists a group of microphones, from which signals are simultaneously acquired and processed [4–6]. Limited by the law of spatial sampling, the spatial resolution of acoustic imaging depends on the number of microphones and the array dimension. The requirements for simultaneous data acquisition also lead to complex and very expensive hardware systems. These shortcomings limit the broad applications of acoustic cameras. In medical imaging, structural health monitoring, and the Internet of Things for industry, the same problem arises due to the needs for transducer array and sensor network. Although the sensors can be made smaller and cheaper with the development of manufacturing technologies such as micro-electro-mechanical systems (MEMS) and flexible electronics [7–9], the manufacturing process is usually complicated. Meanwhile, the sensors suffer from problems such as stability, productivity, and longevity. These challenges prompt development of wave sensing strategies with high integration degree, lightweight structure, and low hardware cost.
In homogeneous media, the spatial propagation of acoustic and elastic waves is relatively uniform. Most sensors do not have apparent spatial responses, so they cannot distinguish where the sources come from. On the other hand, directly measuring signals from sources is impossible in most complex cases. Source signals are filtered by the transfer paths and mixed during the propagation. Therefore, it is necessary to fuse the information of multiple sensors and solve inverse problem for wave sensing, that is, to recover the source information by measuring the response of sensing system to external excitations. If we endow the sensors with spatial directionality, or if we know the spatial wave modulation properties of the media, the spatial physical information can be calculated at a lower measurement cost. The latter is the basic idea of computational sensing, where spatial coding structures and devices are used to realize a prior modulation of spatial physical fields. Here, artificially engineered structures play an important role in computational sensing to encode spatial transmission and distribution of wave fields. Structural features can be introduced to spatial information and then merged with computation process. By incorporating computational algorithms, one can recover the source information by using fewer or even a single sensor [10, 11].
One of the representative artificially engineered structures is the metastructure. Metastructures are artificially designed composite structures with unusual mechanical properties that cannot be achieved with natural materials [12–14]. The mechanical properties of metastructures are mainly determined by their microstructures rather than material composition, thereby enabling a flexibly manipulation of wave transmission. The study of metastructures can be traced back to the phononic crystals, a type of wavelength scale periodic structures with bandgaps, and subsequently extended to subwavelength scale structures [15]. Nowadays, the concept of metastructures has been greatly enriched to include a variety of artificially engineered structures that can freely tailor the spatial acoustic and elastic wave fields. Due to their highly designable mechanical properties, spatial transmission can be encoded and then employed to break through the limitations of spatial sampling law and sensor number. By integrating fewer or even a single commercial sensor with metastructure and introducing reconstruction algorithms, we can construct simpler, smaller, and cheaper sensing devices to sense spatial acoustic and elastic waves.
In this review, we introduce the advances in spatial information coding with artificially engineered structures for acoustic and elastic wave sensing. First, we briefly introduce the transmission manipulation of acoustic and elastic waves with metastructures. Next, we review the enhanced spatial wave sensing with metastructures for weak signal detection and source localization. Then, we introduce computational sensing approaches that combines the spatial transmission coding structures with reconstruction algorithms. Representative progresses of computational sensing with metastructures and random scattering media in audio source separation, ultrasonic imaging, and vibration information identification are reviewed. Finally, we discuss the open problems, challenges, and research prospects of the spatial information coding metastructures for acoustic and elastic wave sensing.
In this section, we briefly review the main principles and approaches for manipulating the transmission of acoustic and elastic waves with metastructures. The core idea of the transmission manipulation is to control the macroscopic effective physical properties by designing the microstructures. In 2000, Liu et al. [16] first proposed the concept of locally resonant phononic crystals and achieved acoustic bandgaps with frequencies much lower than that of the Bragg scattering mechanism. The concept of controlling large-wavelength acoustic waves through small structures opened up the research field of acoustic metamaterials [17]. The dipole resonance of local resonators induces the negative effective mass density within the bandgap. The motion of the metallic masses become opposite to the motion of the metamaterial matrices at the first locally resonant frequency. The metamaterial exhibits a negative inertial response to external excitation, thereby suppressing the transmission of acoustic and elastic waves [18–21]. This negative effective mass density can also be observed in membranes with adherent masses [22–26]. With further study, researchers found that a negative effective modulus can be also obtained by generating the monopole resonance with cavity structures [27–29].
Since dipole resonances can give rise to negative effective mass densities and monopole resonances can give rise to negative effective moduli, if it is possible to achieve monopole and dipole resonances at the same time, double negative metamaterials can be then constructed [30–34]. Lee et al. [31] designed a double negative acoustic metamaterial coupling Helmholtz cavity array with thin membranes. Zhu et al. [35] proposed an elastic metamaterial with chiral microstructure made of a single-phase material to experimentally demonstrate negative refraction of elastic waves at the deep-subwavelength scale. The effective mass density and bulk modulus of the proposed metamaterial have simultaneous negative values owing to simultaneous translational and rotational resonances. Metamaterials with such double negative properties have attractive application prospects, such as constructing fluid-like solid structures [36], steering wave beams [37, 38], imaging [39] and cloaking [40].
Metamaterials can also exhibit near-zero equivalent parametric properties. Fleury and Alù [41] proposed the realization of a density near zero acoustic metamaterial, which allows perfect tunneling of sound through very narrow pipes due to the quasi-static nature of propagation. Cselyuszka et al. [42] designed a bulk modulus near zero metamaterial composed of an acoustic duct loaded with a Helmholtz resonator whose dispersive behavior is used to create a compressibility near zero response. Single near-zero metamaterials suffer from low-transmission due to the impedance mismatch with air. Dubois et al. [43] realized an impedance matched double zero metamaterial induced by a Dirac-like cone at the Brillouin zone center. Because both constitutive parameters tend to zero while keeping their ratio (i.e. the impedance) constant, this metamaterial can achieve wave collimation of a point sound source and allow high transmission levels at the same time.
In the past decade, metasurfaces, a type of metastructures with subwavelength thickness capable of providing non-trivial local phase shifts (or amplitude modulation), have received extensive attention [44]. The uniqueness of metasurfaces lies in their ability to freely tailor spatial wave transmissions so that the phase and/or amplitude is fully controlled. Therefore, the wavefront can be flexibly shaped according to the generalized Snell’s law. Fascinating applications based on metasurfaces have been demonstrated such as beam steering and focusing [45–49], holographic imaging [50–52], acoustic levitation [53, 54], perfect absorption [55, 56], acoustic orbital angular momentum [57, 58], and intelligent information processing [59]. Recently, the concept of metasurfaces has been extended from acoustic to elastic waves to achieve unusual wave behaviors, including source illusion [60], ultrathin waveguides [61], and flexural wave absorption [62], that are challenging to realize in conventional solid media.
Metastructures can implement far more functions than those described above. For acoustic and elastic wave sensing, the core idea is to comprehensively use the working mechanisms of metastructures for encoding spatial transmissions of acoustic and elastic waves. The design principles of metastructures need to be closely related to wave sensing in order to achieve desirable performance beyond conventional sensing approaches. It should be pointed out that in addition to metamaterials, some artificially engineered structures such as scattering masks and apertures can also achieve transmission coding in specific scenarios. In Figure 1, we summarize the main principles and structural design strategies of representative artificially engineered structures for coding and sensing spatial acoustic and elastic waves [63–77]. The classification is mainly according to the application scenarios (e.g. source detection and identification) and their applicable frequency range. For low-frequency wave sensing, the mechanisms are mainly based on resonance, while the principles for high-frequency sensing are mainly based on scattering mechanism. The main idea for spatial wave detection is to produce a spatial selective response that enables the source localization. For multiple source identification and imaging, the key solution is to encode spatial transmission for computational sensing. It can be seen that there are knowledge gaps for different types of sensing in the diagram, which can provide a guidance for further studies. In the following sections, we will introduce how artificially engineered structures, including but not limited to metamaterials, can be used to encode spatial information for acoustic and elastic wave sensing in detail.
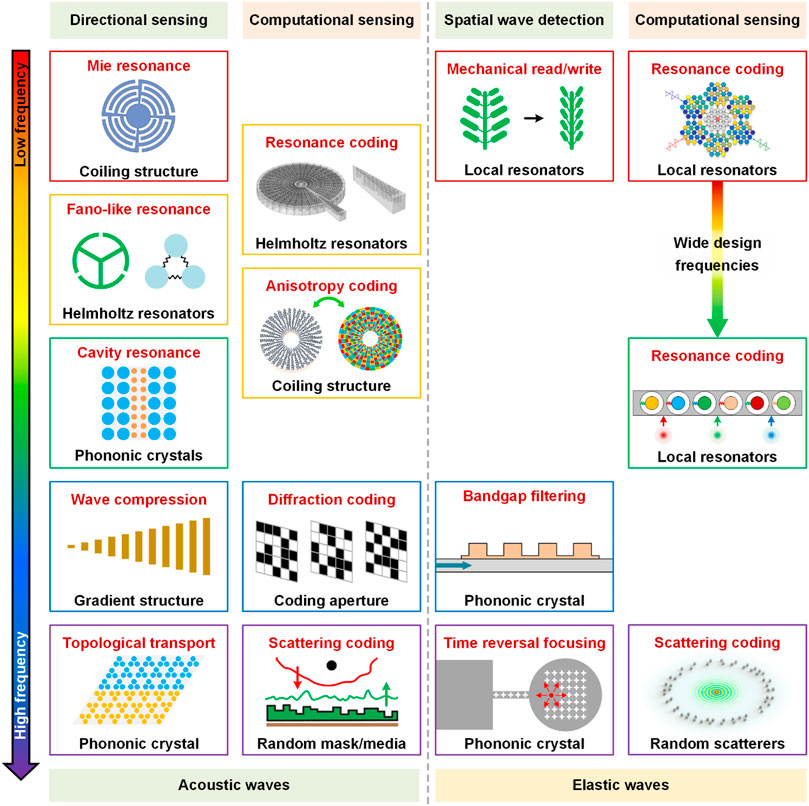
FIGURE 1. The main principles and structural design strategies of artificially engineered structures for coding and sensing spatial acoustic and elastic waves. The illustrated concepts can be found in the literature [63–77].
In acoustic sensing with metastructures, one important research area is overcoming the classical diffraction limit to improve image resolution. Mechanisms such as negative refraction, anisotropy, and resonant tunneling are widely used to manipulate propagative and evanescent waves for subwavelength imaging [47], focusing [78], and edge detection [79]. Differently from the above sensing paradigm, this review mainly focuses on directional acoustic sensing in this section. Metastructures are capable of overcoming the limitation of spatial sampling theorem to achieve directional acoustic source sensing with both high precision and miniaturization. Metastructure-based sound source detection mainly utilizes the selective acoustic responses of metastructures under the excitation of incident acoustic waves in different directions, so as to obtain desirable acoustic directivity characteristics. The studies can be summarized according to the sensing principles as follows.
In 2014, Chen et al. proposed an anisotropic metamaterial with gradient high refractive index [66]. This metamaterial is designed to have strong wave compression effect by increasing the refractive index of medium to allow sound propagation with a large wave vector (Figure 2A). Therefore, a spatial concentration of wave energy and strong pressure enhancement in the metamaterial are induced to achieve an enhanced acoustic sensing. By placing the microphone in different locations of the air gaps in metamaterial, the amplified acoustic signals with different frequencies can be acquired. The signal-to-noise ratio (SNR) achieved in the metamaterial can be enhanced by more than 20 dB, thereby overcoming the conventional acoustic detection limit. Besides the pressure amplification, the metamaterial also exhibits a remarkable directional response. From the directivity patterns of the maximum pressure gain of the metamaterial, it can be clearly seen that the maximum pressure gain is a function of the incident angle of the acoustic waves. It is also evident that at a 0° incident angle, the sound wave can be well coupled into the metamaterial and the highest pressure gain can be obtained, while at 180° incident angle, the pressure gain is minimum due to the serious wave impedance mismatch at the air/metamaterial interface. The strong directional response of the metamaterial can be highly desirable in many acoustic sensing applications and inspire the device design for sound source localizations [80].
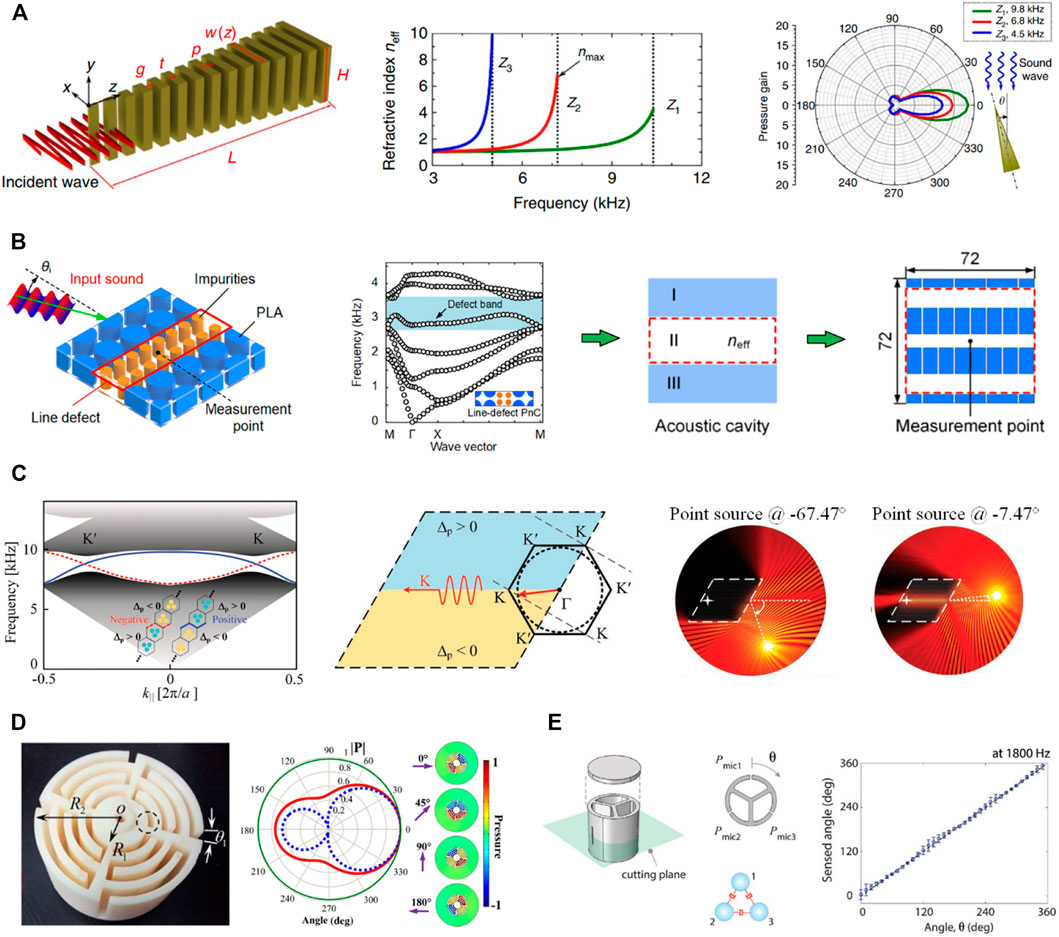
FIGURE 2. Directional acoustic sensing with acoustic metamaterials and phononic crystals. (A) Enhanced acoustic sensing through wave compression and pressure amplification in anisotropic metamaterials [66]. (B) Enhanced directional acoustic sensing with phononic crystal cavity resonance [65]. (C) Directional acoustic antennas based on Valley-Hall topological insulators [67]. (D) Deep-subwavelength-scale directional sensing based on highly localized dipolar Mie resonances [63]. (E)Fano-like acoustic resonance for subwavelength directional sensing with 0–360° measurement [64]. Figure reproduced with permission from: (A), © 2014, Nature Publishing Group; (B), © 2018, AIP Publishing; (C), © 2018, The Authors. Published by WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim; (D), © 2016, American Physical Society; (E), © 2020, Toyota Motor North America. Published by WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim.
The anisotropic effects of acoustic transmission can also be found in phononic crystals to enable directional acoustic sensing. Jiang et al. proposed an enhanced directional acoustic sensing device with phononic crystal cavity resonance [65]. The phononic crystal device is designed with a line defect by replacing a line array with two columns of cylinders (Figure 2B). The line-defect phononic crystal makes a resonant defect band within the perfect phononic crystal band gap range. This means that the line-defect phononic crystal can be equivalent to an acoustic cavity with Fabry-Perot-like resonance. The design enhances the input sound wave at the resonance frequency of the acoustic cavity under the normal incidence, and produces a desirable direction-sensitive response. The sensing frequency can be decreased by enlarging the effective refractive index of the phononic crystal cavity. On the basis of the effective acoustic cavity principle, a simplified structure composed of acoustic gratings with large refractive index is proposed. The device size can be reduced from 2λ of line-defect phononic crystal to 1/1.5 λ of the grating structure, providing a strategy for reducing the device size. Based on the similar principle of phononic crystal defect state, Chen et al. developed a structure that couples phononic crystal point defect with Helmholtz resonators to realize a high energy density acoustic enhancement for directional sensing [81]. Besides the cavity resonance principle, topological acoustic valley transport (Figure 2C) [67] and near-zero index [82] implemented by phononic crystals can also be designed to enable a unique beamforming mechanism that renders a super-directive needle-like sound reception pattern. The phononic crystal direction-finding devices present broad application prospects in weak signal detection and sound source localization.
The gradient index acoustic metamaterials and phononic crystals can realize desirable directional acoustic sensing, but they can hardly be used at low frequencies (<1,000 Hz). By taking advantage of the resonance effect, the working frequency and device size can be significantly reduced at the same time. Zhu et al. design a space-coiling metasurface with highly localized Mie resonances (Figure 2D) [63]. When the frequency of the incident acoustic wave is exactly at the Mie resonance frequency, strong interaction between the core-shell structure and the incident wave excites the dipolar resonant mode of the metasurface. The sound energy can be concentrated into a scale much smaller than the wavelength. The azimuthally dependent pressure field of the Mie resonance provides a key solution to realize directional acoustic sensing at deep-subwavelength scale (1/8 λ).
Although these works can achieve remarkable directivity pattern for directional sensing, active scanning of the devices is needed to obtain the azimuth information of the sound source [83]. Besides, the requirement of the knowledge of the acoustic pressure at the device limits their application in sensing of amplitude-varying acoustic waves. To overcome these problems, Lee et al. proposed a deep-subwavelength-scale (1/8 λ) metamaterial sensor based on Fano-like resonance (Figure 2E) [64]. The metamaterials are designed by coupled Helmholtz resonators interact with each other. Due to the coupling effect between the resonators, the spectral line-shape of resonators show asymmetric characteristic, contriving a Fano-like resonance. By taking the acoustic power ratio of resonators, the incident angle in a range of 0°–360° can be identified without needing to calibrate the acoustic pressure at the device. This work provides a critical understanding of coupled acoustic resonators as well as a viable scheme for directional sensing.
Overall, the above studies achieve directional sensing of sound sources by encoding acoustic transmission through structural anisotropy, providing feasible strategies to break through the spatial sampling theorem and reduce the bulky device size. However, it can be seen that most of the directional acoustic sensing metamaterials have an obvious tradeoff between the directivity resolution and low working frequency. The working bands of the devices are generally narrow. Moreover, the working principle determines that they can hardly be used to identify complex acoustic fields. Therefore, acoustic sensing mechanisms applicable to combine signal processing methods such as computational sensing for acoustic imaging, multiple source separation and identification need to be developed.
For spatial elastic wave detection, metamaterials can also exert their unique advantages. Current studies of metamaterials for elastic wave sensing are mainly focused on amplifying useful physical information and suppressing harmful information carried by elastic waves [73, 84–88]. For example, Jiang et al. proposed an auxetic metamaterial embedded with stretchable strain sensors [86]. The microcracks of the strain sensor are elongated due to the 2D expansion in both directions, thereby significantly improving the sensitivity for recognizing rich medical details from human pulses. Chen et al. proposed a concept of elastic wave sensitivity enhancement by programing the bending stiffness of the metamaterial with an adaptive piezoelectric circuit system [87]. The wavelength of elastic waves can be compressed to achieve over two orders of magnitude amplification for flexural wave signals to overcome the detection limitation. However, the spatial physical information sensing of elastic waves is still not involved.
To extract the spatial physical information contained in elastic waves, Gliozzi et al. [89] and Miniaci et al. [74] used the filtering and focusing characteristics of phononic crystals to select and reflect the high-order harmonics generated by the nonlinear effects of damages (Figure 3A). Combining with the time reversal method, nonlinear elastic source detection can be realized. The proposed devices demonstrate their potential as an efficient, compact, portable, passive apparatus for nonlinear elastic wave sensing and damage detection, but the requirement of scanning elastic wave fields may limit their practical applications. Wave mode splitting and conversion with non-resonant metasurfaces are another attractive approaches to extracting useful spatial physical information from mixed elastic wave modes [90–93]. Moreover, the concepts of self-sensing and actuating metamaterials are developed to achieve fascinating physical characteristics such as nonreciprocal wave propagations [94, 95], showing promising application prospects from vibration protections to ultrasonic sensing and evaluation of engineering structures.
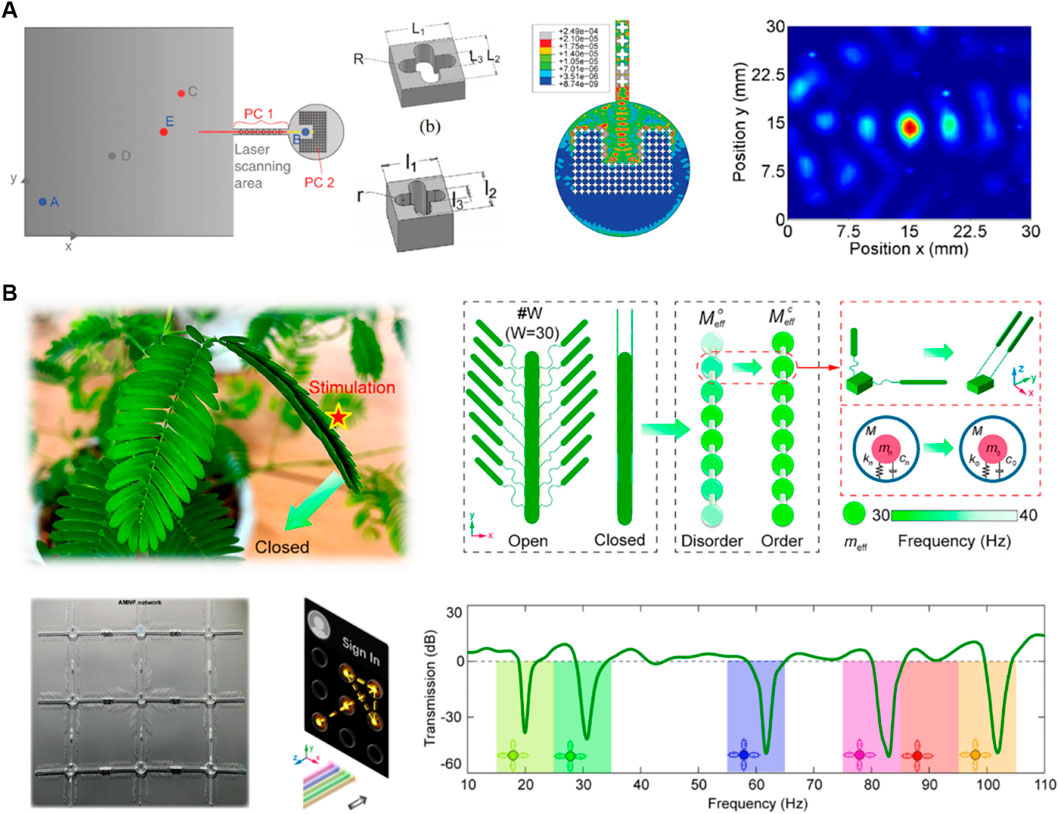
FIGURE 3. Elastic wave detection with metamaterials. (A) Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals [74]. (B) Stimuli-responsive metamaterials with information-driven elastodynamics programming [72]. Figure reproduced with permission form: (A), © 2017, American Physical Society; (B), © 2021, Elsevier Inc.
Driving structural deformations through external stimuli and further recognizing the structural property changes to identify the stimuli information is also an approach for elastic wave information perception. Li et al. proposed a stimuli-responsive programmable metamaterial inspired by Mimosa leaves (Figure 3B) [72]. The metamaterial behaves like an adaptive notch filter to trap the mechanical energy at a specific frequency range by adaptively changing the local resonance state of shape-morphing resonators from disorder to order upon external stimuli. Vibration transmission can thus be encoded to demonstrate a mechanical implementation of write/read operation for information perception and interaction. This work takes a significant step toward the information-driven elastic wave coding, which may release smart devices from complex hardware in scenarios of command input, interactive communication, and robotic operation.
The above studies open up avenues for developing novel metamaterial-based elastic wave information sensing systems. However, they would be stretched when dealing with more complex elastic wave sensing problems, such as elastic wave source identification and multiple object localization. To address this problem, transmission coding of metastructures could associate with the computational algorithms. Research in this area is still in its infancy and has a large improvement space. In the following sections, we will introduce the concept of computational sensing with metastructures and review the representative advances.
In many current examples of sensing systems, the sensing paradigm is typically based on a sequential merger of hardware output and computational analysis applied on this output. For instance, classical optical imaging follows a framework of direct imaging and post-processing. The optical lens focuses the light emitted by the scene on the surface, and the image is acquired by establishing a direct one-to-one correspondence between the detector pixels and the sample. The intensity of the light field is discretely collected by a photodetector and digitally processed by an image processor. The performance of classical optical imaging suffers from expensive lenses and CCDs, low response speed, and diffraction limit. These limitations can be overcome by employing new imaging mode, that is, image formation no longer only depends on optical physical devices, but a joint design of front-end optics and post-detection signal processing. This sensing paradigm is widely known as “computational sensing”. In general, computational sensing organically combines physical field coding and information processing, and provides new avenues and ideas for breaking through many limiting factors in the conventional sensing systems. It should be pointed out that computational sensing is a very broad concept, and it contains many design methods of sensing devices and computational algorithms. Among them, compressive sensing is one powerful mathematical framework that is often leveraged in computational systems. In the following sections, we introduce the studies on acoustic and elastic wave sensing mainly based on the compressive sensing framework.
With the development of information age, the amount of data generated by human society is getting larger. The hardware systems based on traditional Nyquist sampling law face great pressure in high-speed data acquisition, massive data storage, and efficient processing. In 2004, the proposal of compressive sensing theory [96, 97] breaks through the limitations of the traditional Nyquist sampling law by using a smaller number of samples to achieve high-precision signal reconstruction. The basic idea of compressive sensing theory is to use uncorrelated basis functions to sparsely represent the signal, and reconstruct the original signal from undersampled data with high probability by solving the optimization problem. Over the past two decades, compressive sensing has been deeply studied and widely used because it can effectively reduce the sensing cost. One of the most impressive advances in compressive sensing is the design of single-pixel camera [98]. Unlike traditional cameras with CCD or CMOS device, single-pixel camera uses only one photodetector to perform signal measurements that are far fewer than the image pixels. The core device is the digital micro-mirror device (DMD) with different deflection directions, which can perform spatial light modulation by generating multiple random mask patterns as the physical realization of the measurement matrix. The inner product of the target image and the mask pattern is projected onto a single photodetector through a lens. A reconstruction algorithm is used to recover the original image with low measurement cost. This pioneering work has inspired many subsequent works on single-pixel compressive imaging [99–102].
The concept of a general sensing process can be expressed mathematically as
where y is a collection of measurements, H is the measurement matrix, and x is the sampled scene. To enable a unique linear solution for x, the rank of H must equal the dimension of x. In 2006, Candes and Tao [103] proved that when the compressive measurement strategy is pseudo-random, and totally unrelated to the sparse basis, appropriate computational algorithms can recover the correct solution with very high probability from compressive measurements. This pseudo-random coding strategy can be used to construct a desirable measurement matrix H for compressive sensing. The compressive sensing theory allows the reconstruction of underdetermined scenes by solving the minimization problem
where λ is the weighting factor. R(x) expresses the likely composition of the scene, which typically is the l 1-norm of the scene, reflecting the inherent sparsity in natural scenes.
In the last decade, researchers have discovered that metamaterials with novel physical properties can flexibly modulate the spatial wave fields, so they can be used as spatial light modulators (SLMs) to replace the function of DMD to encode the spatial optical fields. In these studies, compressed sensing theory is combined with spatial coding metamaterials to provide new approaches for realizing single-pixel compressed imaging. The metamaterials can be considered as a physical implementation of the measurement matrix in compressive sensing. Hunt et al. [104] pioneered the use of the guided-wave metamaterial aperture to encode the spatial scattering field to perform microwave compressive imaging without lenses, moving parts, or phase shifters (Figure 4A). The proposed metamaterial aperture allows image compression to be performed on the physical hardware layer rather than in the post-processing stage, thus averting the detector, storage, and transmission costs associated with full diffraction-limited sampling of a scene. The metamaterial-based SLMs can also be used for Terahertz imaging [105, 107–109], which is challenging for semiconductor-based imaging due to the large time constants imposed by parasitic inductance and capacitance, and mismatch in energy levels. Watts et al. [105] designed an active metamaterial that functions as a real-time tunable, spectrally sensitive masks for terahertz imaging with only a single-pixel detector (Figure 4B). The modulation can achieve imaging with negative mask values, which is difficult to achieve through intensity-based components. For infrared waves, it is essential to realize a fast and efficient spatial light modulation. Due to the widely tunable electro-optical response of graphene through the entire infrared region, graphene metamaterials [106, 110] are proposed for high speed infrared light modulation and single-pixel imaging (Figure 4C). The metamaterial-based computational imaging systems pave a new path for optical imaging that is distinct from existing focal-plane-array-based cameras. Moreover, they provide inspirations for computational sensing of acoustic and elastic waves.
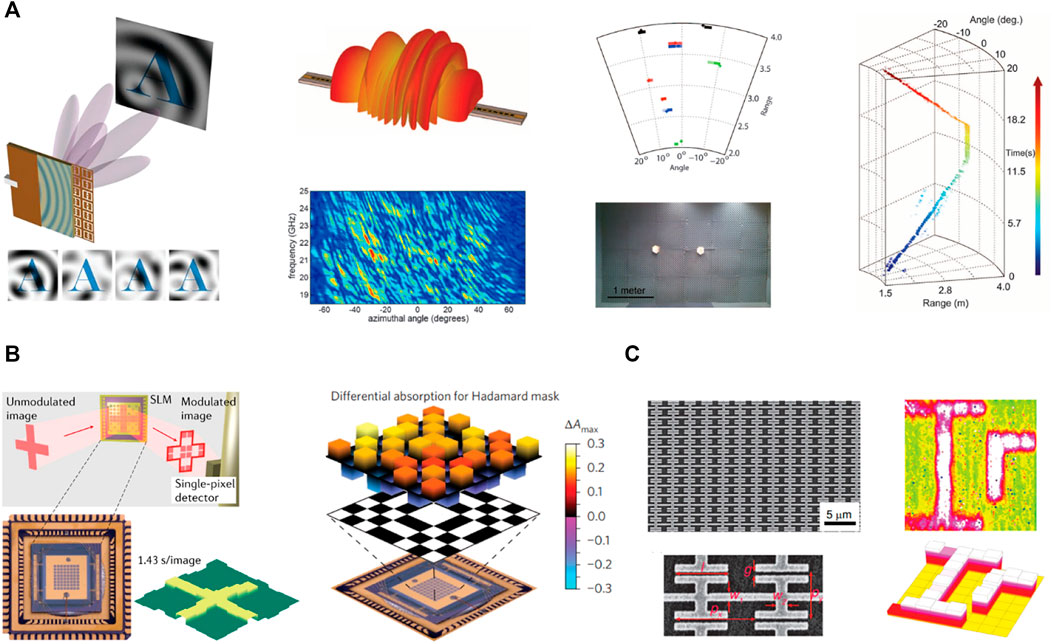
FIGURE 4. Single-pixel imaging with metamaterials. (A) Metamaterial apertures for computational imaging with microwaves [104]. (B) Terahertz compressive imaging with metamaterial spatial light modulators [105]. (C) Graphene metamaterial spatial light modulator for infrared single-pixel imaging [106]. Figure reproduced with permission from: (A), © 2013, American Association for the Advancement of Science; (B), © 2014, Nature Publishing Group; (C), © 2017, Optical Society of America.
Since both electromagnetic and acoustic waves can be described by wave equations, the concept of single-sensor compressive sensing with engineered structures can be extended from electromagnetic waves to acoustic waves. At first, we introduce the concept of coding spatial acoustic fields with random scattering media such as aperture mask and holey cavity [70, 71, 111–114], which are especially suitable for ultrasonic imaging. With the combination of the compressive sensing framework, the requirement for the number of transducers is expected to be reduced to one [115]. In 2017, Kruizinga et al. first proposed a ultrasound imaging device that can perform 3D imaging using a single transducer [71]. The device makes a compressed measurement of the spatial ultrasound field using a randomized aperture mask placed in front of the transducer (Figure 5A). The aperture mask breaks the phase uniformity of the ultrasound transmission and ensures that every pixel in the image is uniquely identifiable in the compressed measurement. By rotating the mask, multiple measurements can be performed and benefit the reconstruction performance. This device can successfully image 3D objects placed in water. This work paves the way for an entirely new method of imaging in which the complexity is shifted away from the hardware and toward computing power [111, 112]. Rogers et al. demonstrated a realization of acoustic source imager, which utilizes a compressive sensing technique coupled to a series of spatially orthogonal acoustic screens to perform source localization in air using a single sensor (Figure 5B) [70]. Here, diffraction effect is considered to account because screen openings comparable to the acoustic wavelength. Later, a holey cavity with diverse frequency modes was proposed for single-transducer 3D ultrasound imaging with physical optimization (Figure 5C) [114]. In this study, a spherical octant is attached to one of the interior corners of the cavity to make the wave pattern asymmetric. By employing the compressive sensing framework to solve the inverse problem, targets such as spheres and letters can be imaged. These studies provide opportunities for cheaper, faster, simpler, and smaller sensing devices and possible new imaging applications.
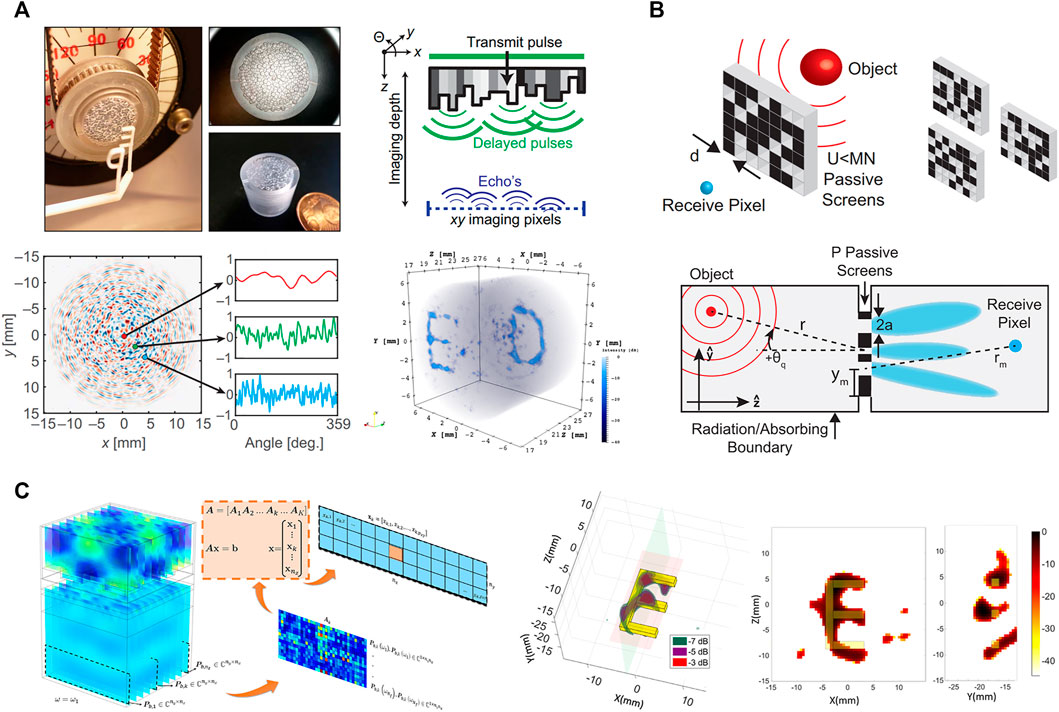
FIGURE 5. Coding spatial acoustic waves with randomized scattering media. (A) Compressive 3D ultrasound imaging using a single sensor [71]. (B) Demonstration of acoustic source localization using single pixel compressive imaging [70]. (C) A holey cavity for single-transducer 3D ultrasound imaging with physical optimization [114]. Figure reproduced with permission from: (A), © 2017, The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science; (B), © 2017, AIP Publishing; (C), © 2020, Elsevier B.V.
Such ideas can also be introduced to the photoacoustic imaging field [116]. In 2017, Yin et al. proposed dynamic focusing of acoustic wave utilizing a randomly scattering lens and a single fixed transducer (Figure 6A) [117]. Benefiting from the high-order multiple scattering in the random scattering lens, the ultrasound emitted by the single transducer can be dynamically focused onto any desired point by manipulating the transmitting waveform. The single channel system can be applied to decode a photoacoustic image from the received ultrasound signal. The proposed system needs neither special materials or delicate structures nor a large number of channels, so it could find broad applications ranging from medical ultrasound imaging to nondestructive detection. Guo et al. proposed single-shot compressed photoacoustic tomographic imaging with a single detector in a scattering medium [118]. The imaged object is illuminated by the speckled field formed through or inside a scattering medium (Figure 6B). The generated photoacoustic signals from spatial positions of an object are recorded by a single ultrasonic transducer after modulation by an acoustic mask. By using the angular-spectrum method and the l 1-minimization algorithms, 3D imaging of objects can be reconstructed. In 2022, Guo et al. further replaced the optical scattering medium with a spatial light modulator to generate a sequence of optical random patterns. Therefore, a dual compressive sensing system is established for fast 3D photoacoustic surface tomography with a high acoustic resolution below λ/10 [119]. The dual-compressed concept, which transforms unobtrusive spatial difference into spatiotemporal detectable information, can be generalized to other imaging modalities to realize efficient, high spatial resolution imaging.
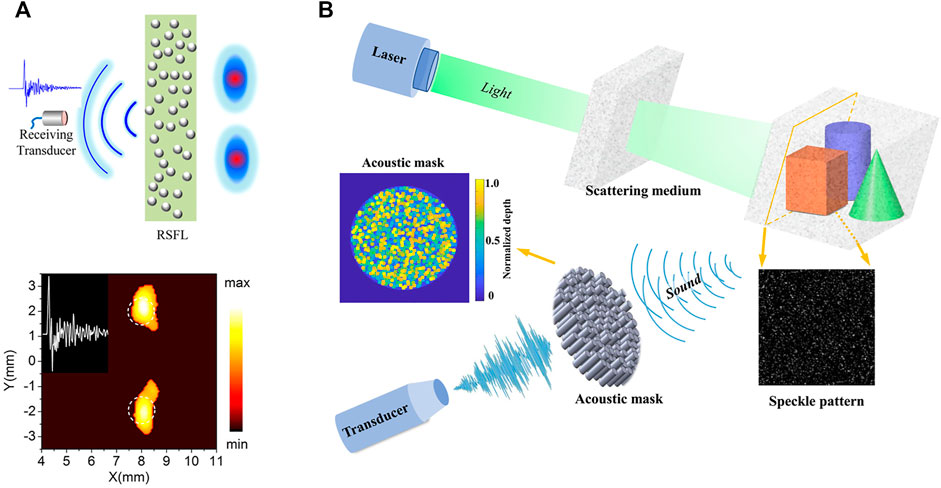
FIGURE 6. Single-detector photoacoustic imaging with scattering media. (A) Dynamic focusing of acoustic wave utilizing a randomly scattering lens and a single fixed transducer [117]. (B) Single-shot compressed photoacoustic tomographic imaging with a single detector in a scattering medium [118]. Figure reproduced with permission from: (A), © 2017, AIP Publishing; (B), © 2020, American Physical Society.
The imaging device based on random scattering media is not suitable for audio acoustic identification because the aperture size of the scattering device is close to the wavelength, resulting in a bulky device size. This problem can be solved using resonant metamaterials. Compared with random scattering media, resonant metamaterials can realize the spatial transmission coding of acoustic waves at the subwavelength scale. In 2015, Xie et al. first designed a single-sensor multi-speaker listening device with acoustic metamaterials to separate simultaneous overlapping sounds from difference sources [68]. The metamaterial consists of randomized Helmholtz resonator arrays to perform diverse frequency modulation (Figure 7A). As a result, it can be useful for encoding independent acoustic signals coming from different spatial locations by creating highly frequency-dependent and spatially complex measurement modes. The frequency responses of incident acoustic waves are highly uncorrelated due to the spatial transmission coding, which actually implements the desirable measurement matrix of compressive sensing in physical layer. Combining with the reconstruction algorithm of compressive sensing, the metamaterial device can achieve the localization and separation of sound sources in different azimuths with only one microphone. This work opens up attractive avenues for novel acoustic imaging paradigms that combine physical layer design and computational sensing algorithms.
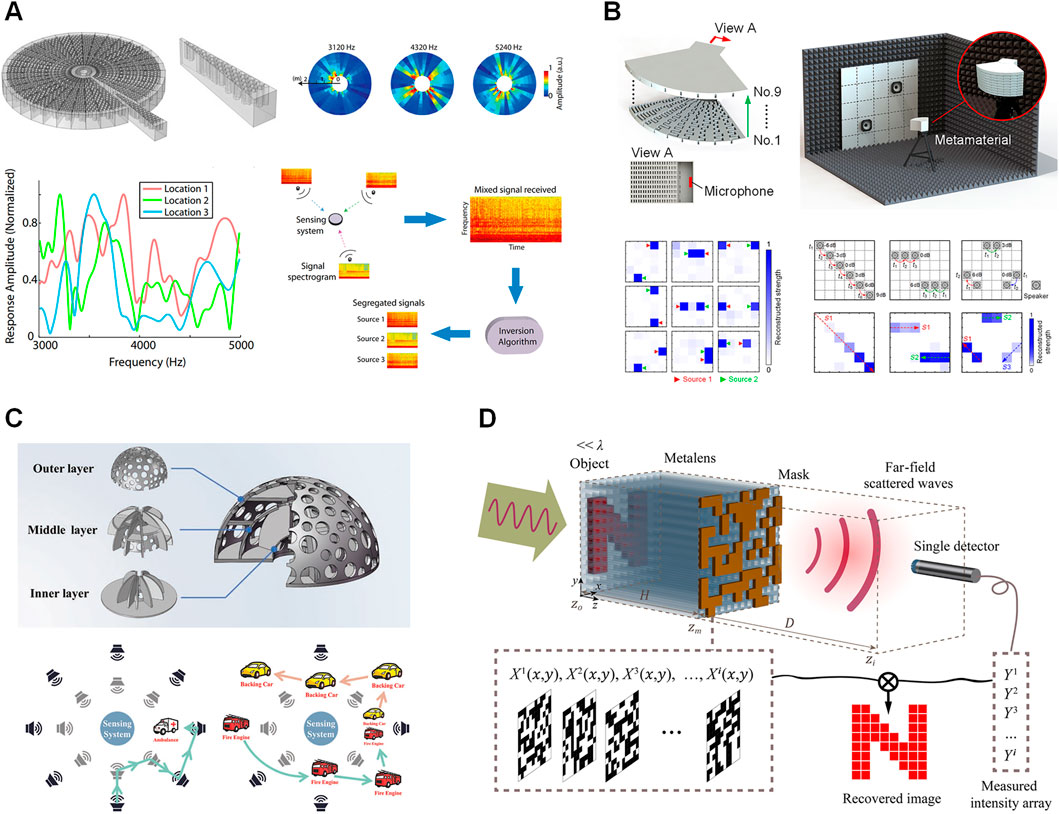
FIGURE 7. Single-sensor computational sensing with metamaterials for audio acoustic waves. (A) Single-sensor multiple speaker listening system with acoustic metamaterials [68]. (B) A prototype of single-detector acoustic camera realized by space-coiling anisotropic metamaterials [69]. (C) A metamaterial enclosure for 3D space sound localization and separation [120]. (D) Far-field subwavelength acoustic computational imaging with a single detector [11]. Figure reproduced with permission from: (A), © 2015, National Academy of Science; (B), © 2019, American Physical Society; (C), © 2019, The Authors. Published by WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim; (D), © 2022, American Physical Society.
The frequency modulation in the above study is determined by the lengths of the Helmholtz resonators, so the device is bulky and not suitable for extension to planar acoustic imaging. In 2019, Jiang et al. propose a prototype of single-sensor acoustic camera with space-coiling metamaterial for spatial planar imaging [69]. The structural randomness of the space-coiling metamaterial makes its effective acoustic parameters highly anisotropic, thereby enabling highly uncorrelated spatial coding of acoustic waves. The metamaterial has a deep-subwavelength scale in height. Therefore, the prototype of single-detector acoustic camera can be realized by stacking different metamaterial modules for planar acoustic imaging (Figure 7B). The reconstruction tasks for imaging and tracking multiple sound sources have been demonstrated. Compared with a conventional acoustic camera based on microphone arrays, the proposed design outperforms the microphone array in terms of dimension, bandwidth, and cost while ensuring the accuracy of the acoustic imaging. In the same year, Sun et al. further extended the dimension of sound source location to 3D space by developing a metamaterial enclosure composed of three-layer hemispherical shells with randomly drilled holes (Figure 7C) [120]. The performance superiority is demonstrated by identifying challenging sound sources in real-life scenarios. In addition to compressive sensing approach, computational ghost imaging can also be used to recover acoustic images by correlating a series of spatially resolved patterns and the corresponding total transmission intensity. Tian et al. proposed a coding metalens to encode the evanescent wave information into the propagating waves due to spatial frequency convolution between the object and masks (Figure 7D) [11]. High-quality images of a subwavelength object can be reconstructed in the far field. These studies provide alternative opportunities beyond traditional techniques in the fields of acoustic sensing such as intelligent scene monitoring, robotic audition, nondestructive evaluation, and medical imaging.
We have reviewed that by appropriately designing metamaterials to spatially encode acoustic fields, multiple source identification with a single sensor can be achieved. However, in practical environments, sometimes it is impossible to extract the inner physical information of structures by simply performing acoustic sensing, because the source signals can be easily overwhelmed by other structural noises. Developing vibration source identification technology can fundamentally determine the sources of noises. The identification of vibration sources mainly depends on solving the dynamical inverse problem, that is, knowing the vibration transfer characteristics and responses of the system, and identifying the vibration excitation. Current vibration source identification methods typically require information fusion from a large number of sensors for two main reasons. One reason is that the vibration transfer characteristics are relatively consistent due to the uniformity of some structures and media. Another reason is the severe aliasing of the excitation signal inside structures during propagation. The vibration source identification accuracy is greatly affected by the layout of sensors. If the vibration transfer characteristics of the structure can be properly designed, it is possible to realize the compressive identification of vibration excitations. Compared with the advances in the acoustic fields, coding spatial vibration transmission and elastic wave fields for single sensor identification is rarely explored. The core issue is how to design an eligible metamaterial with uncorrelated transmissions to encode spatial vibration information.
In 2020, Jiang et al. proposed a randomized resonant metamaterial with randomly coupled local resonators (Figure 8A) for single-sensor identification of elastic vibrations [75]. This metamaterial is designed by using the spiral-based resonators with randomized structural parameters (Figure 8B). Multiple vibration sources are excited at the boundaries of the metamaterial. A single sensor is used to pick up the vibration responses at the center of the metamaterial. The metamaterial is proved to be capable of producing highly uncorrelated transmissions for different spatial vibrations due to the disordered coupling of random effective masses (Figure 8C). Based on encoding spatial vibration information by uncorrelated transmissions, a compressive sensing framework can be used to experimentally identify various vibration events with only a single sensor (Figure 8D). The designed metamaterial is also demonstrated to be a new type of human-machine interface. This study not only is applicable to areas such as smart devices and Internet of Things, but also provides perspectives for designing simpler vibration sensing devices.
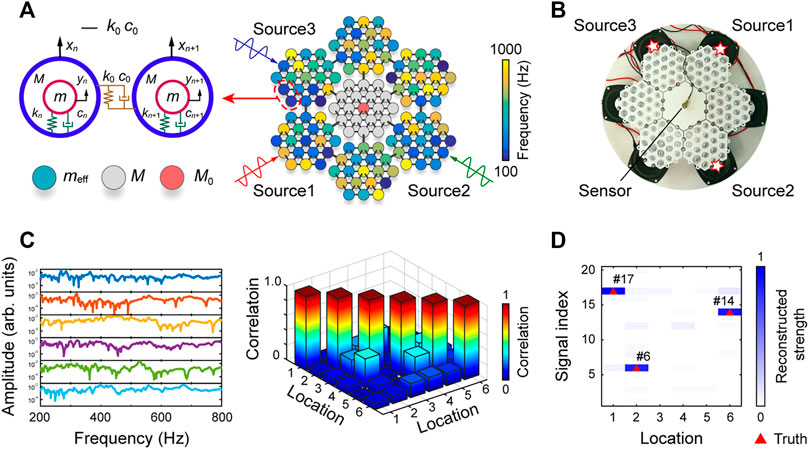
FIGURE 8. Randomized resonant metamaterial for single-sensor vibration identification [75]. (A) The metamaterial with randomly coupled local resonators. (B) The design of the metamaterial. (C) The highly uncorrelated transmission. (D) A reconstruction result with three activated vibration sources.
The advance on vibration transmission coding further motivates the study of on-shaft vibration source identification. It is more challenging for coding vibration transmission on the shaft of rotating machinery because the shaft is generally thin and long, and made of homogeneous materials. In 2021, Li et al. proposed a smart metasurface shaft to realize a single-sensor identification of on-shaft vibration sources (Figure 9A) [76]. The metasurface covering the shaft consists of local resonators with random metallic masses and rubber rings. With this design, the resonance frequencies of local resonators are randomly distributed in the metasurface, leading to the random modulation of on-shaft vibration responses at different locations (Figure 9B). The on-shaft vibration source locations can be reconstructed from the measurement of a single sensor with a high correct recognition ratio (Figure 9C). The smart metasurface shaft shows potential application prospects in rotor dynamics, such as rotating machinery condition monitoring, exciting force identification, and fault diagnosis.
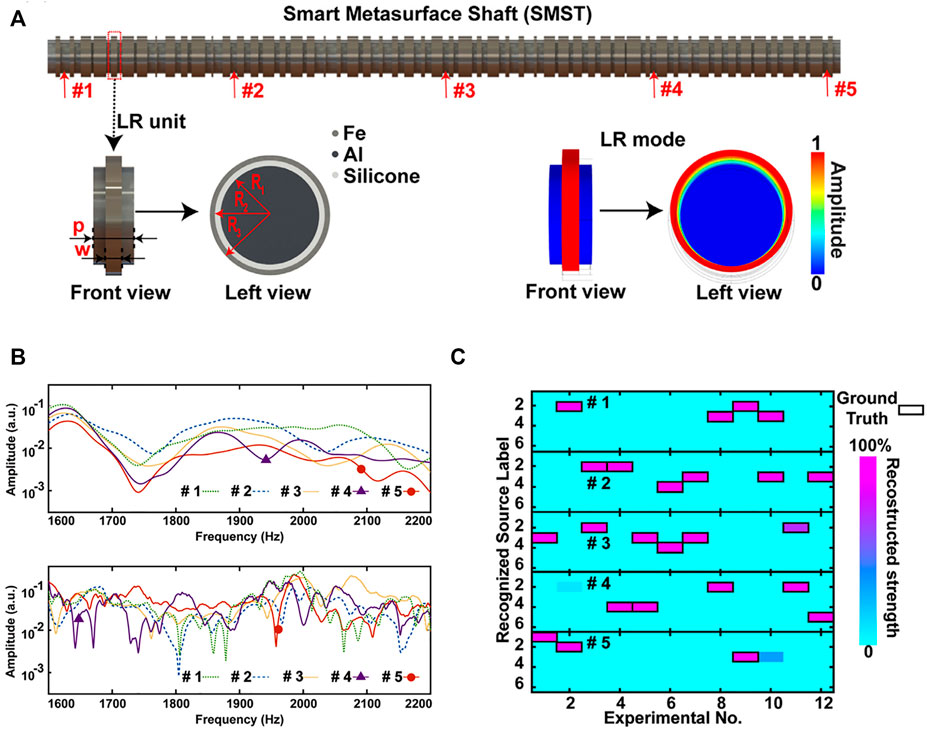
FIGURE 9. Smart metasurfaces shaft for vibration identification with a single sensor [76]. (A) Schematic diagram of the smart metasurface shaft. (B) The measured frequency responses without/with metasurface. (C) The reconstruction results for mechanical fault signals with a high recognition ratio. Figure reproduced with permission from: © 2020, Elsevier Ltd.
Besides the passive elastic wave identification, object localization through active elastic wave is crucial in structural health monitoring and human machine interaction. Compared with the advances in electromagnetic waves for indoor localization [121, 122], active computational sensing with spatial coding is rarely studied in elastic media. A concept of scattering-coded architectured boundary is proposed for computational sensing of Lamb waves (Figure 10A) [77]. The architectured boundary with randomly distributed scatterers achieves multiple scattering of Lamb waves. Complex disturbances are introduced into the scattered field to achieve a highly uncorrelated scattering coding, thereby eliminating the ambiguity of object information. This property ensures that the locations of objects can be uniquely identified with only a single transducer by using the computational sensing framework. By employing Lamb wave excitations with different frequencies, multiple measurements can be performed to improve the imaging performance. Such architectured boundary can be considered as a physical multiplexer. A type of touchscreen with architectured boundary is designed for interactive input as a demonstration (Figure 10B). The input string can be correctly identified for the touchscreen with architectured boundary (Figure 10C). This work opens up avenues for artificially designed boundaries with the capability of information coding and identification, and can provide exciting application perspectives in fields such as structural health monitoring and human-machine interaction.
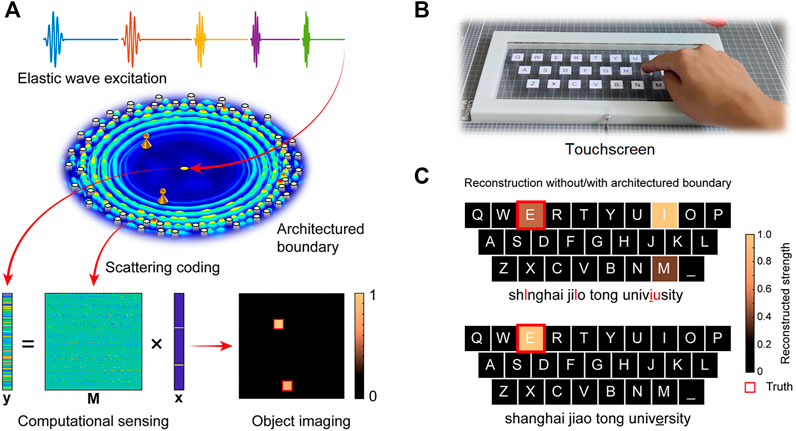
FIGURE 10. Scattering-coded architectured boundary for computational sensing of elastic waves [77]. (A) Concept of computational sensing for object imaging with architectured boundary. (B) The illustration of the designed touchscreen. (C) The reconstruction result of the input string without/with the architectured boundary. All the characters are correctly identified by using the touchscreen with architectured boundary.
We have reviewed the representative advances in spatial acoustic and elastic wave sensing with artificially engineered structures. The studies provide inspirations and promising perspectives for designing novel wave sensing strategies with simpler, cheaper, and smaller devices. In this section, we discuss the open problems, challenges, and research prospects of this field.
Currently, the realization of spatial compressive identification with a single sensor relies on a prior knowledge of the measurement matrix. Most studies use experimental measures to calibrate and construct the measurement matrix, and here are some reasons. Due to the unavoidable manufacturing tolerance and material parameter differences, there is a gap between the actual sample and the theoretically designed one. Besides, the practical test environment is different from the ideal environment. Experimental measurement is the most effective method to obtain spatial transmissions of the artificially engineered structures currently. However, this process is very time consuming, and only a few discrete spatial positions can be calibrated. If we can build a theoretical model to accurately predict the performance of the actual sample, and establish a mapping between the spatial positions and transmission, we can reduce the burden of the calibration process, and overcome the problem that the source information cannot be reconstructed due to the lack of calibration. Theoretical modeling with machine learning and artificial intelligence is one way to address this issue. The mechanical parameters and spatial transmission of metastructures can be learned from simulation and experimental data [123]. Overall, the modeling of artificially engineering structures is an important aspect that needs to be improved.
Another issue is that the source identification is partly dependent on some pre-knowledge of the signals, which is also a reason for pre-experimental calibrations. In some specific scenarios such as object imaging and impact signal identification, this problem has little impact because the wave sensing is mainly determined by the intrinsic properties of the artificial structures. However, for general continuous signals such as speech signals and mechanical vibration noises, it is hard to identify the source localization if we don’t know the pre-knowledge of the unfamiliar signals. This problem limits the application of metastructure-based sensing systems in unfamiliar and complex conditions. Combining the theoretical model mentioned above with machine learning algorithms may be a possible approach to address this issue. Reconstructing the temporal waveforms of multiple source signals is also a challenging but essential research direction. Innovative coding mechanisms, design strategies, and advanced signal processing algorithms need to be further explored.
The optimization of the spatial coding artificially engineered structures is also important. Current studies generally use redundancy design strategies to achieve a desirable transmission coding, which leads to somewhat bulk device sizes. By optimizing the artificial structures, we can reduce the useless microstructures while maintaining the sensing performance. Meanwhile, the miniaturization of the artificial structures is another crucial way to improve the integration degree of systems. Advanced manufacturing technologies such as MEMS and precision 3D printing need to be introduced to make lightweight models, so that the artificially engineered structures can be integrated into various mechanical systems.
In reality, the multi-physics information detection or sensing is desired in coupling systems of acoustic and elastic waves. Here are some perspectives for developing multi-physics sensing devices. One simple way is designing metastructures that can simultaneously handle acoustic and elastic waves in the same frequency range [124, 125] to separately sense the information in different physical domains. For the most common coupling cases, decoupling multi-physics information from one physical field may be a more feasible approach. Matching layers between medium interfaces (e.g. air/water, water/solid, and air/solid interfaces) are required to allow the waves in one physical domain can be efficiently transmitted into another physical domain [126]. The metastructures need to have highly sensitive responses to the excitation waves from other physical domains. The development of decoupling methods and algorithms are also essential to recover the multi-physics information carried by one type of physical waves. With these efforts, the concept of multi-physics sensing with metastructures is hoped to be achieved.
Finally, even though plenty of models and strategies have been proposed, the devices that can be used in the practical environments have not appeared. Although it is challenging to solve practical engineering problems, coding and sensing acoustic and elastic waves with artificially engineered structures is a promising avenue to endow mechanical system with intelligence. We believe that with the development of the above aspects, the artificially engineered structures are expected to be applied in various fields, including but not limited to medical diagnosis, industrial machinery systems, Internet of Things, home automation, and robotic systems.
TJ and QH jointly completed the literature research, analysis, and manuscript writing.
This work was supported by the National Natural Science Foundation of China under Grants No. 11872244, No. 52105112, No. 52275116, No. 12121002, the Program of Shanghai Academic/Technology Research Leader (22XD1421700), the China Postdoctoral Science Foundation under Grants No. 2022T150408, No. 2020M680056, and the National Program for Support of Top-Notch Young Professionals.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Yan W, Noel G, Loke G, Meiklejohn E, Khudiyev T, Marion J, et al. Single fibre enables acoustic fabrics via nanometre-scale vibrations. Nature (2022) 603:616–23. doi:10.1038/s41586-022-04476-9
2. Park B, Shin JH, Ok J, Park S, Jung W, Jeong C, et al. Cuticular pad–inspired selective frequency damper for nearly dynamic noise–free bioelectronics. Science (2022) 376:624–9. doi:10.1126/science.abj9912
3. Yin X, Müller R. Fast-moving bat ears create informative Doppler shifts. Proc Natl Acad Sci U S A (2019) 116:12270–4. doi:10.1073/pnas.1901120116
4. Brooks TF, Humphreys WM. A deconvolution approach for the mapping of acoustic sources (DAMAS) determined from phased microphone arrays. J Sound Vib (2006) 294:856–79. doi:10.1016/j.jsv.2005.12.046
5. Cardenas Cabada E, Leclere Q, Antoni J, Hamzaoui N. Fault detection in rotating machines with beamforming: Spatial visualization of diagnosis features. Mech Syst Signal Process (2017) 97:33–43. doi:10.1016/j.ymssp.2017.04.018
6. Legg M, Bradley S. A combined microphone and camera calibration technique with application to acoustic imaging. IEEE Trans Image Process (2013) 22:4028–39. doi:10.1109/TIP.2013.2268974
7. Xiong W, Zhu C, Guo D, Hou C, Yang Z, Xu Z, et al. Bio-inspired, intelligent flexible sensing skin for multifunctional flying perception. Nano Energy (2021) 90:106550. doi:10.1016/j.nanoen.2021.106550
8. Wang W, Xiao H, Zhang L, Wang Y, Yuan Q, Tan J. Mechanical energy-induced charge separation in intelligent sensing. Cell Rep Phys Sci (2022) 3:100952. doi:10.1016/j.xcrp.2022.100952
9. Wang HS, Hong SK, Han JH, Jung YH, Jeong HK, Im TH, et al. Biomimetic and flexible piezoelectric mobile acoustic sensors with multiresonant ultrathin structures for machine learning biometrics. Sci Adv (2021) 7:eabe5683. doi:10.1126/sciadv.abe5683
10. El Badawy D, Dokmanic I. Direction of arrival with one microphone, a few LEGOs, and non-negative matrix factorization. Ieee/acm Trans Audio Speech Lang Process (2018) 26:2436–46. doi:10.1109/taslp.2018.2867081
11. Tian Y, Ge H, Zhang X-J, Xu X-Y, Lu M-H, Jing Y, et al. Far-field subwavelength Acoustic computational imaging with a single detector. Phys Rev Appl (2022) 18:014046. doi:10.1103/PhysRevApplied.18.014046
12. Ma G, Sheng P. Acoustic metamaterials: From local resonances to broad horizons. Sci Adv (2016) 2:e1501595. doi:10.1126/sciadv.1501595
13. Zangeneh-Nejad F, Fleury R. Active times for acoustic metamaterials. Rev Phys (2019) 4:100031. doi:10.1016/j.revip.2019.100031
14. Wang Y-S, Chen W, Wu B, Wang Y-Z, Wang Y-F. Tunable and active phononic crystals and metamaterials. Appl Mech Rev (2020) 72:040801. doi:10.1115/1.4046222
15. Jin Y, Pennec Y, Bonello B, Honarvar H, Dobrzynski L, Djafari-Rouhani B, et al. Physics of surface vibrational resonances: Pillared phononic crystals, metamaterials, and metasurfaces. Rep Prog Phys (2021) 84:086502. doi:10.1088/1361-6633/abdab8
16. Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, Chan CT, et al. Locally resonant sonic materials. Science (2000) 289:1734–6. doi:10.1126/science.289.5485.1734
17. Ge H, Yang M, Ma C, Lu M-H, Chen Y-F, Fang N, et al. Breaking the barriers: Advances in acoustic functional materials. Natl Sci Rev (2018) 5:159–82. doi:10.1093/nsr/nwx154
18. Jiang T, He Q. Dual-directionally tunable metamaterial for low-frequency vibration isolation. Appl Phys Lett (2017) 110:021907. doi:10.1063/1.4974034
19. Wang P, Casadei F, Shan S, Weaver JC, Bertoldi K. Harnessing buckling to design tunable locally resonant acoustic metamaterials. Phys Rev Lett (2014) 113:014301. doi:10.1103/PhysRevLett.113.014301
20. Li C, Jiang T, He Q, Peng Z. Stiffness-mass-coding metamaterial with broadband tunability for low-frequency vibration isolation. J Sound Vib (2020) 489:115685. doi:10.1016/j.jsv.2020.115685
21. Wang Z, Zhang Q, Zhang K, Hu G. Tunable digital metamaterial for broadband vibration isolation at low frequency. Adv Mater (2016) 28:9857–61. doi:10.1002/adma.201604009
22. Yang Z, Mei J, Yang M, Chan NH, Sheng P. Membrane-type acoustic metamaterial with negative dynamic mass. Phys Rev Lett (2008) 101:204301. doi:10.1103/PhysRevLett.101.204301
23. Mei J, Ma G, Yang M, Yang Z, Wen W, Sheng P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat Commun (2012) 3:756. doi:10.1038/ncomms1758
24. Wang X, Zhao H, Luo X, Huang Z. Membrane-constrained acoustic metamaterials for low frequency sound insulation. Appl Phys Lett (2016) 108:041905. doi:10.1063/1.4940717
25. Yang Z, Dai HM, Chan NH, Ma GC, Sheng P. Acoustic metamaterial panels for sound attenuation in the 50–1000 Hz regime. Appl Phys Lett (2010) 96:041906. doi:10.1063/1.3299007
26. Ma F, Wang C, Liu C, Wu JH. Structural designs, principles, and applications of thin-walled membrane and plate-type acoustic/elastic metamaterials. J Appl Phys (2021) 129:231103. doi:10.1063/5.0042132
27. Fang N, Xi D, Xu J, Ambati M, Srituravanich W, Sun C, et al. Ultrasonic metamaterials with negative modulus. Nat Mater (2006) 5:452–6. doi:10.1038/nmat1644
28. García-Chocano VM, Graciá-Salgado R, Torrent D, Cervera F, Sánchez-Dehesa J. Quasi-two-dimensional acoustic metamaterial with negative bulk modulus. Phys Rev B (2012) 85:184102. doi:10.1103/PhysRevB.85.184102
29.Two-dimensional acoustic metamaterial with negative modulus. J Appl Phys (2010) 108:074911. doi:10.1063/1.3493155
30. Ding Y, Liu Z, Qiu C, Shi J. Metamaterial with simultaneously negative bulk modulus and mass density. Phys Rev Lett (2007) 99:093904. doi:10.1103/PhysRevLett.99.093904
31. Lee SH, Park CM, Seo YM, Wang ZG, Kim CK. Composite acoustic medium with simultaneously negative density and modulus. Phys Rev Lett (2010) 104:054301. doi:10.1103/PhysRevLett.104.054301
32. Liu XN, Hu GK, Huang GL, Sun CT. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl Phys Lett (2011) 98:251907. doi:10.1063/1.3597651
33. Yang M, Ma G, Yang Z, Sheng P. Coupled membranes with doubly negative mass density and bulk modulus. Phys Rev Lett (2013) 110:134301. doi:10.1103/PhysRevLett.110.134301
34. Lee SH, Wright OB. Origin of negative density and modulus in acoustic metamaterials. Phys Rev B (2016) 93:024302. doi:10.1103/PhysRevB.93.024302
35. Zhu R, Liu XN, Hu GK, Sun CT, Huang GL. Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat Commun (2014) 5:5510. doi:10.1038/ncomms6510
36. Lai Y, Wu Y, Sheng P, Zhang ZQ. Hybrid elastic solids. Nat Mater (2011) 10:620–4. doi:10.1038/nmat3043
37. Wu Y, Lai Y, Zhang ZQ. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys Rev Lett (2011) 107:105506. doi:10.1103/PhysRevLett.107.105506
38. Wang W, Bonello B, Djafari-Rouhani B, Pennec Y, Zhao J. Double-negative pillared elastic metamaterial. Phys Rev Appl (2018) 10:064011. doi:10.1103/PhysRevApplied.10.064011
39. Dong H-W, Zhao S-D, Wang Y-S, Zhang C. Topology optimization of anisotropic broadband double-negative elastic metamaterials. J Mech Phys Sol (2017) 105:54–80. doi:10.1016/j.jmps.2017.04.009
40. Shen C, Xu J, Fang NX, Jing Y. Anisotropic complementary acoustic metamaterial for canceling out aberrating layers. Phys Rev X (2014) X4:041033. doi:10.1103/PhysRevX.4.041033
41. Fleury R, Alu A. Extraordinary sound transmission through density-near-zero ultranarrow channels. Phys Rev Lett (2013) 111:055501. doi:10.1103/PhysRevLett.111.055501
42. Cselyuszka N, Sečujski M, Crnojević Bengin V. Compressibility-near-zero acoustic metamaterial. Phys Lett A (2014) 378:1153–6. doi:10.1016/j.physleta.2014.02.022
43. Dubois M, Shi C, Zhu X, Wang Y, Zhang X. Observation of acoustic Dirac-like cone and double zero refractive index. Nat Commun (2017) 8:14871. doi:10.1038/ncomms14871
44. Assouar B, Liang B, Wu Y, Li Y, Cheng J-C, Jing Y. Acoustic metasurfaces. Nat Rev Mater (2018) 3:460–72. doi:10.1038/s41578-018-0061-4
45. Li Y, Jiang X, Li R-q., Liang B, Zou X-y., Yin L-l., et al. Experimental realization of full control of reflected waves with subwavelength Acoustic metasurfaces. Phys Rev Appl (2014) 2:064002. doi:10.1103/PhysRevApplied.2.064002
46. Li Y, Jiang X, Liang B, Cheng J-c., Zhang L. Metascreen-based acoustic passive phased array. Phys Rev Appl (2015) 4:024003. doi:10.1103/PhysRevApplied.4.024003
47. Ma F, Huang Z, Liu C, Wu JH. Acoustic focusing and imaging via phononic crystal and acoustic metamaterials. J Appl Phys (2022) 131:011103. doi:10.1063/5.0074503
48. Zhou H-T, Fu W-X, Wang Y-F, Wang Y-S. High-efficiency ultrathin nonlocal waterborne acoustic metasurface. Phys Rev Appl (2021) 15:044046. doi:10.1103/PhysRevApplied.15.044046
49. Zhu Y, Cao L, Merkel A, Fan SW, Vincent B, Assouar B. Janus acoustic metascreen with nonreciprocal and reconfigurable phase modulations. Nat Commun (2021) 12:7089. doi:10.1038/s41467-021-27403-4
50. Zhu Y, Hu J, Fan X, Yang J, Liang B, Zhu X, et al. Fine manipulation of sound via lossy metamaterials with independent and arbitrary reflection amplitude and phase. Nat Commun (2018) 9:1632. doi:10.1038/s41467-018-04103-0
51. Jiménez-Gambín S, Jiménez N, Benlloch JM, Camarena F. Holograms to focus arbitrary ultrasonic fields through the skull. Phys Rev Appl (2019) 12:014016. doi:10.1103/PhysRevApplied.12.014016
52. Zhu Y, Gerard NJRK, Xia X, Stevenson GC, Cao L, Fan S, et al. Systematic design and experimental demonstration of transmission‐type multiplexed acoustic metaholograms. Adv Funct Mater (2021) 31:2101947. doi:10.1002/adfm.202101947
53. Memoli G, Caleap M, Asakawa M, Sahoo DR, Drinkwater BW, Subramanian S. Metamaterial bricks and quantization of meta-surfaces. Nat Commun (2017) 8:14608. doi:10.1038/ncomms14608
54. Dong H-W, Shen C, Zhao S-D, Qiu W, Zheng H, Zhang C, et al. Achromatic metasurfaces by dispersion customization for ultra-broadband acoustic beam engineering. Natl Sci Rev (2022) nwac030. doi:10.1093/nsr/nwac030/6535631
55. Li Y, Assouar BM. Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl Phys Lett (2016) 108:063502. doi:10.1063/1.4941338
56. Rui Liu C, Hui Wu J, Yang Z, Ma F. Ultra-broadband acoustic absorption of a thin microperforated panel metamaterial with multi-order resonance. Compos Struct (2020) 246:112366. doi:10.1016/j.compstruct.2020.112366
57. Jiang X, Li Y, Liang B, Cheng JC, Zhang L. Convert acoustic resonances to orbital angular momentum. Phys Rev Lett (2016) 117:034301. doi:10.1103/PhysRevLett.117.034301
58. Jiang X, Liang B, Cheng JC, Qiu CW. Twisted acoustics: Metasurface-enabled multiplexing and demultiplexing. Adv Mater (2018) 30:e1800257. doi:10.1002/adma.201800257
59. Weng J, Ding Y, Hu C, Zhu XF, Liang B, Yang J, et al. Meta-neural-network for real-time and passive deep-learning-based object recognition. Nat Commun (2020) 11:6309. doi:10.1038/s41467-020-19693-x
60. Liu Y, Liang Z, Liu F, Diba O, Lamb A, Li J. Source illusion devices for flexural Lamb waves using elastic metasurfaces. Phys Rev Lett (2017) 119:034301. doi:10.1103/PhysRevLett.119.034301
61. Hu Y, Zhang Y, Su G, Zhao M, Li B, Liu Y, et al. Realization of ultrathin waveguides by elastic metagratings. Commun Phys (2022) 5:62. doi:10.1038/s42005-022-00843-0
62. Cao L, Yang Z, Xu Y, Fan S-W, Zhu Y, Chen Z, et al. Flexural wave absorption by lossy gradient elastic metasurface. J Mech Phys Sol (2020) 143:104052. doi:10.1016/j.jmps.2020.104052
63. Zhu X, Liang B, Kan W, Peng Y, Cheng J. Deep-subwavelength-scale directional sensing based on highly localized dipolar Mie resonances. Phys Rev Appl (2016) 5:054015. doi:10.1103/PhysRevApplied.5.054015
64. Lee T, Nomura T, Su X, Iizuka H. Fano-like acoustic resonance for subwavelength directional sensing: 0-360 degree measurement. Adv Sci (Weinh) (2020) 7:1903101. doi:10.1002/advs.201903101
65. Jiang T, He Q, Peng Z-K. Enhanced directional acoustic sensing with phononic crystal cavity resonance. Appl Phys Lett (2018) 112:261902. doi:10.1063/1.5024970
66. Chen Y, Liu H, Reilly M, Bae H, Yu M. Enhanced acoustic sensing through wave compression and pressure amplification in anisotropic metamaterials. Nat Commun (2014) 5:5247. doi:10.1038/ncomms6247
67. Zhang Z, Tian Y, Wang Y, Gao S, Cheng Y, Liu X, et al. Directional acoustic antennas based on Valley-Hall topological insulators. Adv Mater (2018) 30:e1803229. doi:10.1002/adma.201803229
68. Xie Y, Tsai TH, Konneker A, Popa BI, Brady DJ, Cummer SA. Single-sensor multispeaker listening with acoustic metamaterials. Proc Natl Acad Sci U S A (2015) 112:10595–8. doi:10.1073/pnas.1502276112
69. Jiang T, He Q, Peng Z-K. Proposal for the realization of a single-detector acoustic camera using a space-coiling anisotropic metamaterial. Phys Rev Appl (2019) 11:034013. doi:10.1103/PhysRevApplied.11.034013
70. Rogers JS, Rohde CA, Guild MD, Naify CJ, Martin TP, Orris GJ. Demonstration of acoustic source localization in air using single pixel compressive imaging. J. Appl. Phys. (2017) 122:214901. doi:10.1063/1.5003645
71. Kruizinga P, van der Meulen P, Fedjajevs A, Mastik F, Springeling G, de Jong N, et al. Compressive 3D ultrasound imaging using a single sensor. Sci Adv (2017) 3:e1701423. doi:10.1126/sciadv.1701423
72. Li C, Peng Z-K, He Q. Stimuli-responsive metamaterials with information-driven elastodynamics programming. Matter (2022) 5:988–1003. doi:10.1016/j.matt.2021.11.031
73. Shan S, Liu Z, Cheng L, Pan Y. Metamaterial-enhanced coda wave interferometry with customized artificial frequency-space boundaries for the detection of weak structural damage. Mech Syst Signal Process (2022) 174:109131. doi:10.1016/j.ymssp.2022.109131
74. Miniaci M, Gliozzi AS, Morvan B, Krushynska A, Bosia F, Scalerandi M, et al. Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals. Phys Rev Lett (2017) 118:214301. doi:10.1103/PhysRevLett.118.214301
75. Jiang T, Li C, He Q, Peng ZK. Randomized resonant metamaterials for single-sensor identification of elastic vibrations. Nat Commun (2020) 11:2353. doi:10.1038/s41467-020-15950-1
76. Li C, Jiang T, He Q, Peng Z. Smart metasurface shaft for vibration source identification with a single sensor. J Sound Vib (2021) 493:115836. doi:10.1016/j.jsv.2020.115836
77. Jiang T, Liao X, Huang H, Peng Z-K, He Q. Scattering-coded architectured boundary for computational sensing of elastic waves. Cel Rep Phys Sci (2022) 3:100918. doi:10.1016/j.xcrp.2022.100918
78. Ma F, Zhang H, Du P, Wang C, Wu JH. An underwater planar lens for broadband acoustic concentrator. Appl Phys Lett (2022) 120:121701. doi:10.1063/5.0089288
79. Moleron M, Daraio C. Acoustic metamaterial for subwavelength edge detection. Nat Commun (2015) 6:8037. doi:10.1038/ncomms9037
80. Chen T, Li W, Yu D. Broadband and deep subwavelength acoustic antenna based on Fabry-Perot-like acoustic grating resonators. Measurement (2022) 194, 111014. doi:10.1016/j.measurement.2022.111014
81. Chen T, Jiao J, Yu D. Strongly coupled phononic crystals resonator with high energy density for acoustic enhancement and directional sensing. J Sound Vib (2022) 529:116911. doi:10.1016/j.jsv.2022.116911
82. Ma C, Gao S, Cheng Y, Liu X. Acoustic metamaterial antennas for combined highly directive-sensitive detection. Appl Phys Lett (2019) 115:053501. doi:10.1063/1.5107464
83. Esfahlani H, Karkar S, Lissek H, Mosig JR. Exploiting the leaky-wave properties of transmission-line metamaterials for single-microphone direction finding. J Acoust Soc Am (2016) 139:3259–66. doi:10.1121/1.4949544
84. Yan X, Zhu R, Huang G, Yuan F-G. Focusing guided waves using surface bonded elastic metamaterials. Appl Phys Lett (2013) 103:121901. doi:10.1063/1.4821258
85. Danawe H, Okudan G, Ozevin D, Tol S. Conformal gradient-index phononic crystal lens for ultrasonic wave focusing in pipe-like structures. Appl Phys Lett (2020) 117:021906. doi:10.1063/5.0012316
86. Jiang Y, Liu Z, Matsuhisa N, Qi D, Leow WR, Yang H, et al. Auxetic mechanical metamaterials to enhance sensitivity of stretchable strain sensors. Adv Mater (2018) 30:e1706589. doi:10.1002/adma.201706589
87. Chen YY, Zhu R, Barnhart MV, Huang GL. Enhanced flexural wave sensing by adaptive gradient-index metamaterials. Sci Rep (2016) 6:35048. doi:10.1038/srep35048
88. Kurosu M, Hatanaka D, Onomitsu K, Yamaguchi H. On-chip temporal focusing of elastic waves in a phononic crystal waveguide. Nat Commun (2018) 9:1331. doi:10.1038/s41467-018-03726-7
89. Gliozzi AS, Miniaci M, Bosia F, Pugno NM, Scalerandi M. Metamaterials-based sensor to detect and locate nonlinear elastic sources. Appl Phys Lett (2015) 107:161902. doi:10.1063/1.4934493
90. Zheng M, Liu X, Chen Y, Miao H, Zhu R, Hu G. Theory and realization of nonresonant anisotropic singly polarized solids carrying only shear waves. Phys Rev Appl (2019) 12:014027. doi:10.1103/PhysRevApplied.12.014027
91. Zheng M, Park CI, Liu X, Zhu R, Hu G, Kim YY. Non-resonant metasurface for broadband elastic wave mode splitting. Appl Phys Lett (2020) 116:171903. doi:10.1063/5.0005408
92. Li X, Chen Y, Zhang X, Huang G. Shaping elastic wave mode conversion with a piezoelectric-based programmable meta-boundary. Extreme Mech Lett (2020) 39:100837. doi:10.1016/j.eml.2020.100837
93. Wu Q, Zhang X, Shivashankar P, Chen Y, Huang G. Independent flexural wave frequency conversion by a linear active metalayer. Phys Rev Lett (2022) 128:244301. doi:10.1103/PhysRevLett.128.244301
94. Chen Y, Li X, Hu G, Haberman MR, Huang G. An active mechanical Willis meta-layer with asymmetric polarizabilities. Nat Commun (2020) 11:3681. doi:10.1038/s41467-020-17529-2
95. Chen Y, Li X, Scheibner C, Vitelli V, Huang G. Realization of active metamaterials with odd micropolar elasticity. Nat Commun (2021) 12:5935. doi:10.1038/s41467-021-26034-z
96. Candes EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theor (2006) 52:489–509. doi:10.1109/tit.2005.862083
97. Donoho DL. Compressed sensing. IEEE Trans Inf Theor (2006) 52:1289–306. doi:10.1109/tit.2006.871582
98. Duarte MF, Davenport MA, Takhar D, Laska JN, Sun T, Kelly KF, et al. Single-pixel imaging via compressive sampling. IEEE Signal Process Mag (2008) 25:83–91. doi:10.1109/msp.2007.914730
99. Chan WL, Charan K, Takhar D, Kelly KF, Baraniuk RG, Mittleman DM. A single-pixel terahertz imaging system based on compressed sensing. Appl Phys Lett (2008) 93:121105. doi:10.1063/1.2989126
100. Edgar MP, Gibson GM, Padgett MJ. Principles and prospects for single-pixel imaging. Nat Photon (2018) 13:13–20. doi:10.1038/s41566-018-0300-7
101. Shrekenhamer D, Watts CM, Padilla WJ. Terahertz single pixel imaging with an optically controlled dynamic spatial light modulator. Opt Express (2013) 21:12507–18. doi:10.1364/OE.21.012507
102. Phillips DB, Sun MJ, Taylor JM, Edgar MP, Barnett SM, Gibson GM, et al. Adaptive foveated single-pixel imaging with dynamic supersampling. Sci Adv (2017) 3:e1601782. doi:10.1126/sciadv.1601782
103. Candes EJ, Tao T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans Inf Theor (2006) 52:5406–25. doi:10.1109/tit.2006.885507
104. Hunt J, Driscoll T, Mrozack A, Lipworth G, Reynolds M, Brady D, et al. Metamaterial apertures for computational imaging. Science (2013) 339:310–3. doi:10.1126/science.1230054
105. Watts CM, Shrekenhamer D, Montoya J, Lipworth G, Hunt J, Sleasman T, et al. Terahertz compressive imaging with metamaterial spatial light modulators. Nat Photon (2014) 8:605–9. doi:10.1038/nphoton.2014.139
106. Fan K, Suen JY, Padilla WJ. Graphene metamaterial spatial light modulator for infrared single pixel imaging. Opt Express (2017) 25:25318–25. doi:10.1364/OE.25.025318
107. Watts CM, Nadell CC, Montoya J, Krishna S, Padilla WJ. Frequency-division-multiplexed single-pixel imaging with metamaterials. Optica (2016) 3:133. doi:10.1364/optica.3.000133
108. Rout S, Sonkusale SR. A low-voltage high-speed terahertz spatial light modulator using active metamaterial. APL Photon (2016) 1:086102. doi:10.1063/1.4958739
109. Li W, Hu X, Wu J, Fan K, Chen B, Zhang C, et al. Dual-color terahertz spatial light modulator for single-pixel imaging. Light Sci Appl (2022) 11:191. doi:10.1038/s41377-022-00879-5
110. Zeng B, Huang Z, Singh A, Yao Y, Azad AK, Mohite AD, et al. Hybrid graphene metasurfaces for high-speed mid-infrared light modulation and single-pixel imaging. Light Sci Appl (2018) 7:51. doi:10.1038/s41377-018-0055-4
111. van der Meulen P, Kruizinga P, Bosch JG, Leus G. Coding mask design for single sensor ultrasound imaging. IEEE Trans Comput Imaging (2020) 6:358–73. doi:10.1109/tci.2019.2948729
112. Janjic J, Kruizinga P, van der Meulen P, Springeling G, Mastik F, Leus G, et al. Structured ultrasound microscopy. Appl Phys Lett (2018) 112:251901. doi:10.1063/1.5026863
113. Sillanpää T, Longi K, Mäkinen J, Rauhala T, Klami A, Salmi A, et al. Localizing a target inside an enclosed cylinder with a single chaotic cavity transducer augmented with supervised machine learning. AIP Adv (2021) 11:115104. doi:10.1063/5.0068803
114. Ghanbarzadeh-Dagheyan A, Heredia-Juesas J, Liu C, Molaei A, Martinez-Lorenzo JA, Vosoughi Vahdat B, et al. A holey cavity for single-transducer 3D ultrasound imaging with physical optimization. Signal Process. (2021) 179:107826. doi:10.1016/j.sigpro.2020.107826
115. Ghanbarzadeh-Dagheyan A, Liu C, Molaei A, Heredia J, Martinez Lorenzo J. Holey-cavity-based compressive sensing for ultrasound imaging. Sensors (2018) 18:1674. doi:10.3390/s18061674
116. Dean-Ben XL, Ozbek A, Lopez-Schier H, Razansky D. Acoustic scattering mediated single detector optoacoustic tomography. Phys Rev Lett (2019) 123:174301. doi:10.1103/PhysRevLett.123.174301
117. Yin J, Tao C, Liu X. Dynamic focusing of acoustic wave utilizing a randomly scattering lens and a single fixed transducer. J Appl Phys (2017) 121:174901. doi:10.1063/1.4982882
118. Guo Y, Li B, Yin X. Single-shot compressed photoacoustic tomographic imaging with a single detector in a scattering medium. Phys Rev Appl (2020) 13:044009. doi:10.1103/PhysRevApplied.13.044009
119. Guo Y, Li B, Yin X. Dual-compressed photoacoustic single-pixel imaging. Natl Sci Rev (2022). nwac058. doi:10.1093/nsr/nwac058/6554262
120. Sun X, Jia H, Zhang Z, Yang Y, Sun Z, Yang J. Sound localization and separation in 3D space using a single microphone with a metamaterial enclosure. Adv Sci (Weinh) (2020) 7:1902271. doi:10.1002/advs.201902271
121. del Hougne P, Imani MF, Fink M, Smith DR, Lerosey G. Precise localization of multiple noncooperative objects in a disordered cavity by wave front shaping. Phys Rev Lett (2018) 121:063901. doi:10.1103/PhysRevLett.121.063901
122. del Hougne M, Gigan S, del Hougne P. Deeply subwavelength localization with reverberation-coded aperture. Phys Rev Lett (2021) 127:043903. doi:10.1103/PhysRevLett.127.043903
123. Wang S, Luo Z-t., Jing J, Su Z-h., Wu X-k., Ni Z-h., et al. Real-time determination of elastic constants of composites via ultrasonic guided waves and deep learning. Measurement (2022) 200:111680. doi:10.1016/j.measurement.2022.111680
124. Zhu Y, Cao L, Merkel A, Fan S-W, Assouar B. Bifunctional superlens for simultaneous flexural and acoustic wave superfocusing. Appl Phys Lett (2020) 116:253502. doi:10.1063/5.0004428
125. Bilal OR, Ballagi D, Daraio C. Architected lattices for simultaneous broadband Attenuation of airborne sound and mechanical vibrations in all directions. Phys Rev Appl (2018) 10:054060. doi:10.1103/PhysRevApplied.10.054060
Keywords: spatial information coding, artificially engineered structures, acoustic and elastic wave sensing, metastructures, compressive sensing
Citation: Jiang T and He Q (2022) Spatial information coding with artificially engineered structures for acoustic and elastic wave sensing. Front. Phys. 10:1024964. doi: 10.3389/fphy.2022.1024964
Received: 22 August 2022; Accepted: 07 September 2022;
Published: 21 September 2022.
Edited by:
Rui Zhu, Beijing Institute of Technology, ChinaCopyright © 2022 Jiang and He. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qingbo He, cWJoZUBzanR1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.