- 1National Institute of Informatics, Tokyo, Japan
- 2Department of Economic Informatics, Kanazawa Gakuin University, Kanazawa, Japan
We propose a new method to convert individual daily trajectories into token time series by applying the tokenizer “SentencePiece” to a geographic space divided using the Japan regional grid code “JIS X0,410.” Furthermore, we build a highly accurate generator of individual daily trajectories by learning the token time series with the neural language model GPT-2. The model-generated individual daily trajectories reproduce five realistic properties: 1) the distribution of the hourly moving distance of the trajectories has a fat tail that follows a logarithmic function, 2) the autocorrelation function of the moving distance exhibits short-time memory, 3) a positive autocorrelation exists in the direction of moving for one hour in long-distance moving, 4) the final location is often near the initial location in each individual daily trajectory, and 5) the diffusion of people depends on the time scale of their moving.
1 Introduction
Big data on individual daily trajectories is important for addressing issues involving disasters, terrorism, public safety, infectious diseases, spatial segregation, marketing, and traffic congestion. By analyzing big data on human mobility, we can detect the causes of traffic congestion [1] and find efficient traffic control strategies to balance economic activity with infection control [2]; [3]; [4]. We are also able to monitor the evacuation of people in natural disasters and mass protests through telecommunication providers [5]; [6]. By developing models that satisfy the statistical properties of trajectories, we can simulate changes in urban mobility in the presence of new infrastructure, the spread of epidemics, terrorist attacks, and international events such as an Expo [7]; [8]; [9,10]. In addition, generative models are valuable for protecting the geo-privacy of trajectory data [11]; [12]; [13]. While it is difficult to control the trade-off between uncertainty and utility when disclosing real data, synthetic trajectories that preserve statistical properties have the potential to achieve performance comparable to real data on multiple tasks.
The modeling of human mobility can be classified into four types [14]. The first is the Trajectory Generation model that generates realistic individual spatial-temporal trajectories [15]; [16]; [17]; [18]; [19]. The purpose of this model is to generate realistic individual trajectories for ordinary and extraordinary days. This model is also required to reproduce trajectories from home to destination and from destination back to home. The second type is the Flow Generation model that generates realistic Origin-Destination matrices [20]; [21]; [22]. This model is often used to find the relationships between POIs (Points of Interest) and human mobility networks. The third is the Next-Location Prediction model that predicts an individual’s future location [23]; [24]; [25]; [26]; [27]; [28]; [29]; [30]; [31]; [32]; [33]. This type is developed by inputting weather, transportation, and other factors to the model to capture the spatiotemporal patterns that characterize human habits. The fourth type is the Crowd Flow Prediction model that predicts in/out aggregated crowd flows [34]; [35]; [36]; [37]; [38]; [39]; [40]; [41]; [42]; [43]; [44]; [45]; [46]; [47]. This type is used to understand the relationship between external factors such as weather, weekly and daily cycles, and events (e.g., festivals) and the flow network structure. This research is also classified as the first type, i.e., Trajectory Generation modelling, but it also has the ability to predict Next-Location.
Both physics and machine learning approaches have been taken to develop generative models. The physics approach includes the gravity model, the preferential selection model, the Markov chain, and the autoregressive model (e.g., ARIMA) [48]; [49]. While these models are simple and intuitive, they have limitations in generating realistic individual trajectories. On the other hand, machine learning approach includes language models and autoregressive-type neural networks [14]; [50]. This approach generates highly realistic individual trajectories by building complex models with many parameters. In this study, we build a model to generate the individual daily trajectories using GPT-2 [51], one of the Transformer models that is becoming a successful alternative to Recurrent Neural Network in natural language generation. This model inputs the initial locations in the morning (e.g., around the home) and then outputs the individual daily trajectory (e.g., coordinates of the route taken by public transportation to a sightseeing spot, sightseeing and eating, and then returning home).
To apply language models such as GPT-2 to individual trajectories, we need to index the locations as words [14]. We utilize the Japan regional grid code “JIS X0410” for location indexing [52]. This code consists of several subcodes. The first-level subcode represents the absolute location of each grid, where geographic space is divided into squares with a latitude difference of 40 min and a longitude difference of 1 degree. Each grid is divided recursively until the desired resolution is achieved. The second-level and higher subcodes represent relative locations within a divided grid. We do not need a huge number of unique subcodes, even when the geographic space is large and the resolution is high. We can index many locations with subcode combinations. The grid subcodes, codes, and trajectories (i.e., grid code time series) correspond to characters, words, and sentences in natural language.
In language models such as GPT-2, the introduction of subwords between words and letters, such as “un” and “ing”, increases the accuracy of text generation. Words, subwords, and characters are called tokens, and the process of identifying tokens from text is called tokenization. Using tokenizers such as “SentencePiece” [53]; [54], we can find frequent combinations of subcodes from individual daily trajectories expressed by “JIS X0410,” such as major substrings. To apply GPT-2 to individual trajectories, we propose a new method to convert individual daily trajectories into token time series by applying the tokenizer “SentencePiece”.
Trajectory generation requires capturing the temporal and spatial patterns of individual human movements simultaneously. A realistic generative model should reproduce the tendency of individuals to move preferentially within short distances [55]; [56], the heterogeneity of characteristic distances [55]; [56] and their scales [57], the tendency of individuals to split into returners and explorers [58], the routinary and predictable nature of human displacement [59], and the fact that individuals visit a number of locations that are constant in time [60].
Subsequent sections are organized as follows. Section 2 introduces big data on individual daily trajectories for training the model. Section 3 describes the proposed methods: a geospatial tokenizer based on SentencePiece and the GPT-2 individual daily trajectory generator and its comparative models. Section 4 presents the results. We show the statistical spatial-temporal properties that the model-generated individual daily trajectories must satisfy, and we discuss the accuracy of the models for predicting an individual’s future location. Section 5 offers our conclusions.
2 Data
We used the minute-order location data (280 million logs) from a total of 1.7 million smartphones (about 28,000 per day) that passed through the Kyoto Station area (Shimogyo-ku, Kyoto) in November 2021 and January 2022, provided by Agoop Corp [61]. Kyoto is one of the most famous tourist destinations in Japan, and many people from all over Japan visit Kyoto for sightseeing. Location information includes latitude and longitude. GPS accuracy depends on the smartphone model and the communication environment, but it is usually within 20 m. We coarsened each trajectory to a 250-m grid and 30-min order using a sliding 1-min window. This sliding window converts 1.7 million trajectories with a 1-min time resolution to 51 (= 1.7 × 30) million trajectories with a 30-min time resolution. By removing the home grid for each user, we protected geo-privacy and focused only on the trajectory when the user is out of the home. The total number of daily trajectories of individuals who have been out of their homes for over 10 h is 8.4 million time series.
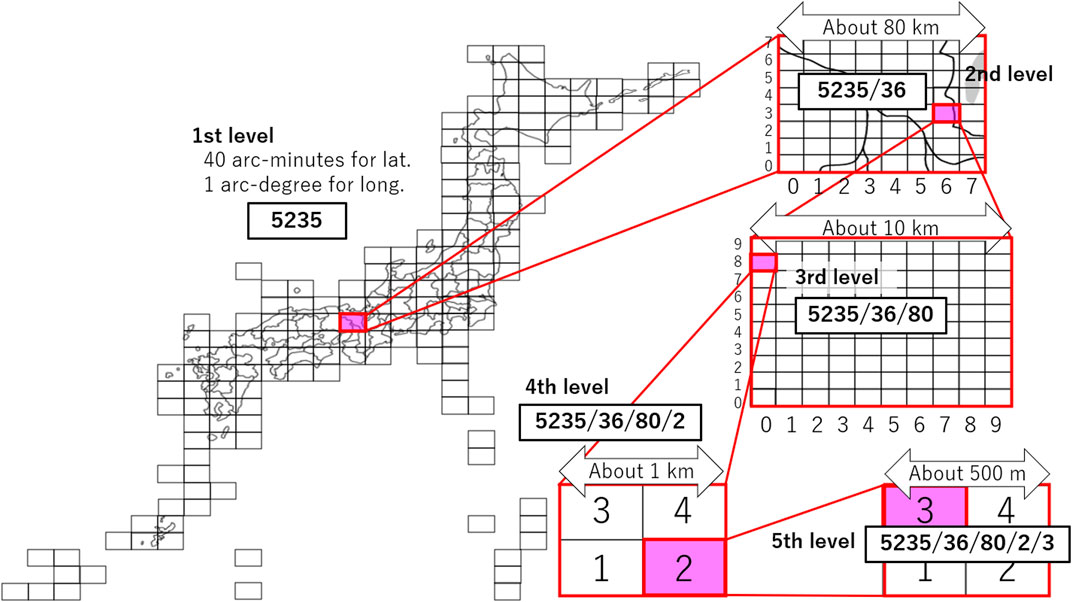
We indexed each location at 250-m grid resolution using the Japan regional grid code “JIS X0410” (see Appendix A for the definition) [52]. The region analysed in this paper is Japan, but if a region outside of Japan were targeted, the extended JIS X0410 [62] would be used. The Japan regional grid is a code given when subdividing Japanese landscape into rectangular subregions by latitude and longitude. A grid code is represented by a combination of five subcodes, such as “5235/36/80/2/3”. The first-level subcode (e.g., 5235) is a four-digit number representing a unique location enclosed by a square with a 40-min difference in latitude and a 1-degree difference in longitude. In Japan, the land areas can be represented by using 176 first-level subcodes, which covers the whole country. The second-level subcode (e.g., 36) is a two-digit number indicating the area created by dividing the first-level grid into eight equal areas in the latitudinal and longitudinal directions. The third-level subcode (e.g., 80) is a two-digit number describing the area obtained by dividing the second-level grid into ten equal areas in the latitudinal and longitudinal directions. The fourth-level subcode (e.g., 2) bisects the third-level grid by latitude and longitude. The fifth-level subcode (e.g., 3) bisects the fourth-level grid by latitude and longitude. The length of one side is about 250 m. In total, about 18 million unique grid codes on land in Japan, at a resolution of 250 m, can be represented by combinations of only 348 subcodes from the first to the fifth level.
Travel from Kyoto station “5235368023” to Kiyomizu Temple “5235369224” can be described in subcode time series, such as “5235/36/80/2/3/_/5235/36/92/2/4/”. We apply the language model GPT-2 to the generation of individual trajectories by corresponding regional grid codes to words, subcodes to characters, and trajectories represented by grid time series to sentences.
3 Methods
First, to apply GPT-2 to individual trajectories, we build a geospatial tokenizer to identify tokens derived from the individual trajectories expressed by grid codes. Next, we introduce four models that generate individual daily trajectories: GPT-2, 2-g, 3-g, and Multi-Output Catboost.
3.1 Geospatial tokenizer
Tokenization is a way of separating a piece of text into smaller units called tokens. Tokens can be either words, characters, or subwords. Tokenization is essential for a language model to efficiently learn the structure of a natural language from a given text. For example, the Oxford English Dictionary contains approximately 600,000 English words. Here, we consider the case in which all tokens are words. Statistically estimating the probability of a word wj occurring after a word wi from the given finite text is difficult because the combinatorial explosion of words occurs. In particular, it is nearly impossible to estimate the probability of rare word combinations. One way to solve this problem is to introduce subwords, which are decomposed words in natural language processing. Words are often composed of subwords, such as “un-relax”, “relax”, “relax-es”, “relax-ed”, “relax-ing”, and “un-relax-ed”. Rare words often consist of a combination of common subwords. By setting the subwords to tokens, we can often statistically estimate the probability that a sentence containing the rare word wj will occur, based on the subword-combination probability.
One of the tokenizers that automatically identifies subwords from a given text is SentencePiece [53]; [54]. In a given text, SentencePiece assumes that a subword of string cicj exists if the joint probability p (ci, cj) of strings ci and cj is statistically significantly higher than the combination probability p (ci)p (cj). This method finds subwords such as “un”, “es”, “ed”, “ing”, etc. Tokens in SentencePiece are subwords and characters, and this tokenizer decomposes text into a minimum number of tokens.
We apply SentencePiece to individual trajectories represented by grid time series. First, as a technical process, we make a “Grid subcode from/to byte-character translation map” by assigning a unique byte character to each subcode. For example, the subcodes 5235/36/36/2/3/are converted to the byte characters
Finally, we add a comma token “,” to a temporary return home and a period token “.” to the last return home each day. This geospatial tokenizer based on SentencePiece transforms the grid code time series into a token time series as follows.
Grid code time series: …_/5235149412/_/5235034923/_/5235030422/…
to
Grid subcode time series: …_/5235/14/94/1/2/_/5235/03/49/2/3/_/5235/03/04/2/2/…
to
Byte-character time series:
to
Token time series:
3.2 Individual daily trajectory generator
We randomly split the 8.4 million individual daily trajectories explained in the Data section into a 4:1 division, under the constraints that the same user is not split. We use 4/5 to build machine learning models and the remaining 1/5 to compare the statistical properties and prediction accuracy between the original and model-generated trajectories. In all models, the split rate is common.
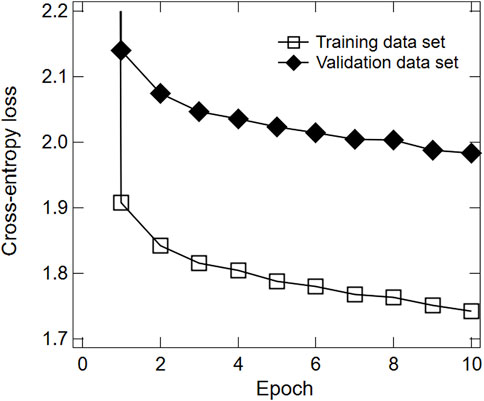
GPT-2 is one of the transformer models of deep neural networks that has multiple Transformer layers consisting of Self-attention and Projection layers. Another well-known transformer model is BERT [63]. By using attention in place of previous recurrence- and convolution-based architectures in natural language generation tasks, the transformer models are becoming successful alternatives to RNNs (Recurrent Neural Networks) and CNNs (Convolutional Neural Networks). GPT-2 is an autoregressive model in neural networks that can sequentially predict the next token from the previous token, i.e., the next location from the past locations, by referring only to the input token sequence prior to the position to be processed in the Transformer layers. Using the geospatial tokenizer, we convert the grid codes obtained from the input location coordinates (or the input grid codes) into byte characters according to the translation map, and then tokenize their byte characters. By inputting these tokens into GPT-2, the GPT-2 recursively generates next tokens. The generated tokens are then reversely converted into grid codes according to the translation map. Through these processes, an individual daily trajectory is generated (See Appendix B for a concrete example). In this paper, we use GPT-2 SMALL proposed by OpenAI, which consists of 12 attention heads and 12 transformer layers as well as 768 dimensions of the embedding and hidden states [51]; [64]. Other hyperparameters are also given with default values. The learning time is about 90 h on one NVIDIA RTX A6000. Figure 1 shows the training and validation losses for each iteration. We used the cross-entropy loss function. Training and validation losses at epoch = 10 are 1.74 and 1.98, respectively.
We introduce three non-neural network models to compare with GPT-2 on the accuracy of generating individual daily trajectories. The first is a 2-g model described by a first-order Markov chain as follows:
where xt is a grid code of the location where a user visited at time t. The second model is a 3-g model described by a second-order Markov chain as follows:
Conditional probabilities in these n-gram models are estimated from combinations of grid codes that occur at least 30 times in the given texts for training.
The third model is Multi-Output Catboost, one of the multi-regression trees with gradient boosting [65]; [66]; [67]. Multi-Output CatBoost is an extension of supervised machine learning with decision trees. In the multi-regression analysis using a decision tree, the multidimensional space of the explanatory variables is divided by the decision trees, and a multi-regression model is constructed to predict representative values such as the average value of the objective variables in each divided area. The learning is performed so that a loss function such as the Multi Root Mean Squared Error (MultiRMSE) of the training data is minimized. In this study, we build a Multi-Output Catboost model that predicts the location vector vt = (longt, latt) defined by latitude and longitude at time t on a given day from t location vectors from time 0 to time t − 1 as follows:
where v* is the location vector predicted by the model. In this study, the unit of time resolution is 30 min, and the maximum of t is 20. Five locations are set for the initial 2.5 h on the initial individual trajectory. That is, the range of t in the prediction is 5 ≤ t ≤ 20. We use 16 (= 20–5 + 1) Multi-Output Catboost models to predict the location vector. We used the official CatBoost Python package [67]. In learning, we used default values for each hyperparameter: MultiRMSE as loss function, maximum number of trees at 1,000, and depth of tree at 6. Other hyperparameters are also given with default values. The final training loss and validation loss for the model predicting the location at t = 5 are 0.2638 and 0.2662, respectively. In the case at t = 20, the losses are 0.222 and 0.219, respectively.
4 Results
First, we plot a typical example of the trajectories generated by each model on a map to intuitively understand the characteristics of those trajectories. Next, we statistically clarify the similarities and differences between the characteristics of the original and model-generated trajectories. Finally, we evaluate the performance of the models in predicting the individual daily trajectories. GPT-2 improves prediction accuracy by fine tuning.
4.1 Typical output examples
Figure 2A shows an example of the input and output locations of the GPT-2 trajectory generator. In this example, sixteen grid codes were output from the generator by inputting the following five grid codes. We manually verified that these grid codes are in the following locations on the OpenStreetMap.
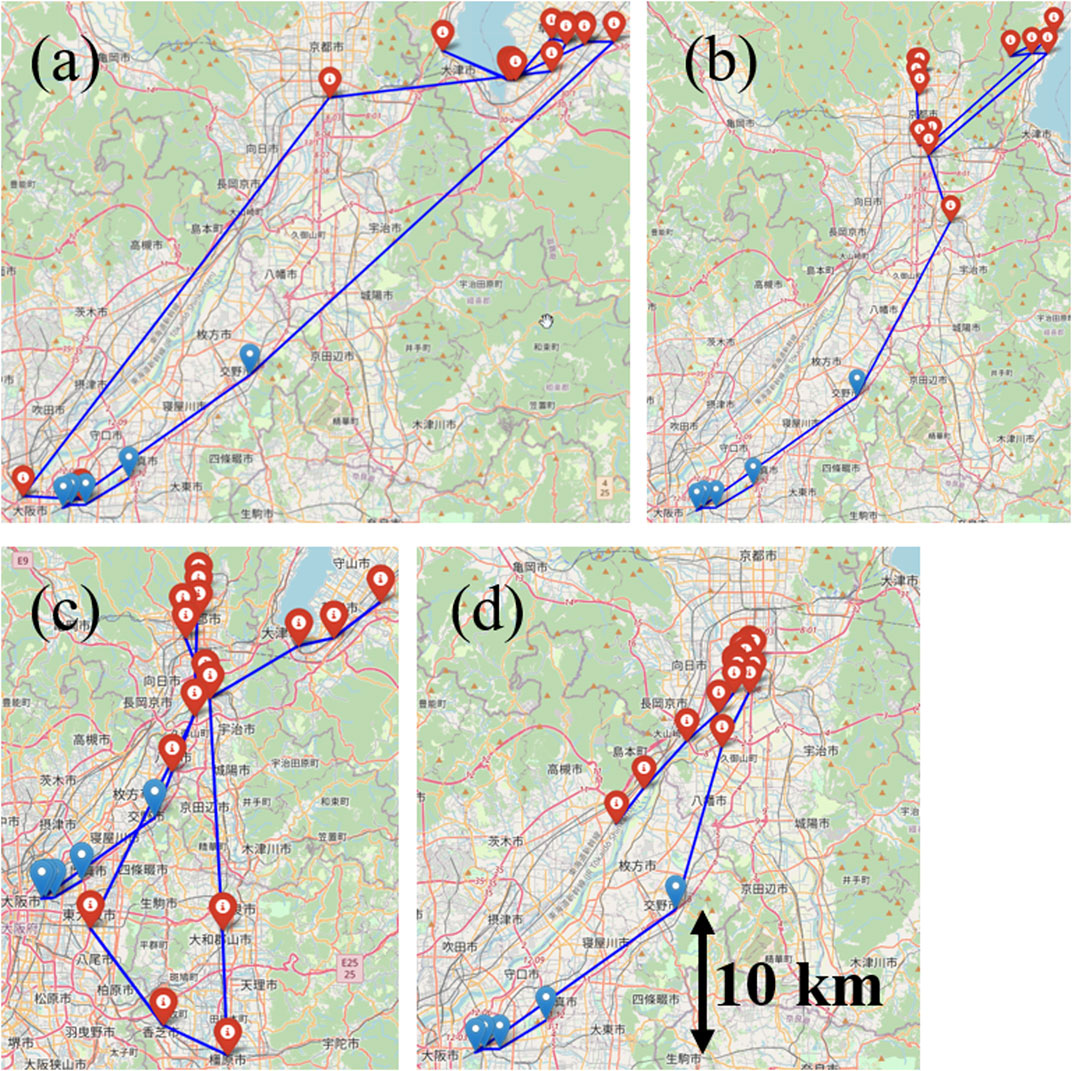
FIGURE 2. Examples of model-generated individual daily trajectories from the same input: (A) GPT-2, (B) 2-g, (C) 3-g, (D) Multi-Output Catboost. Blue and red icons represent inputs and outputs, respectively. The maps were created using OpenStreetMap.
Input: Three locations around Osaka Castle → Daito Tsurumi IC (Kinki Highway) → Katano Kita IC (Daini Keihan Highway)
Output of GPT-2: Ritto IC (Meishin Highway) → five locations in downtown Kusatsu → five locations at the AEON shopping mall in Kusatsu → Otsu City Hall → one location in downtown Kusatsu → Kyoto Station → Osaka Station → one location around Osaka Castle.
The trajectory generated by GPT-2 is very different from a random walk and is human-like. In long-distance moving, expressways and bullet trains are used, and the location coordinates at 30-min intervals are spatially sparse due to the high moving speed. Landmarks and commercial areas are chosen as destinations, where people stay for a long time. They leave in the morning and return in the evening. The same route is likely to be chosen for the outbound and inbound trips.
We input the same five initial grid codes as the GPT-2 trajectory generator into the 2-g, 3-g, and Multi-Output Catboost trajectory generators. Figures 2B,C,D show each of the sixteen outputs generated sequentially by the generators.
Output of 2-g: Fushimi-Momoyama Castle Athletic Park → Kyoto Station → Mt. Hiei Sakamoto Station → Mt. Hiei cable car → Enryakuji Temple on Mt. Hiei → one location around Mt. Hiei Sakamoto Station → two locations around Horikawa Gojo → eight locations around Kitayama Omiya.
Output of 3-g: Kyotanabe TB (Second Keihan Highway) → one location around Fushimi → Nishioji Gojo → Enmachi Station → Horikawa Kitaoji → Kamogawa Junior High School → Nishimarutamachi → Oguraike IC (Second Keihan Highway) → Higashi-Osaka City → Kashiba City → Kashihara City → Yamatokoriyama City → Momoyama → Keihan Ishiyama → two locations around Ritto City.
Output of Multi-Output Catboost: Kugayama → 11 locations around Shimotoba → Yoko-oji → Oyamazaki JCT (Meishin Highway) → Kaminomaki area → southern Takatsuki City.
Typical output examples of these models do not reproduce the return home. In the example of the 2-g model, the generated locations are trapped in a specific area and cannot get out of their area. In n-grams, we cannot statistically estimate the probability of the occurrence of rare trajectories that would escape from the trap because the combinatorial explosion in the number of solutions is unavoidable. In this paper, GPT-2 avoids this problem by using geospatial tokens. In the example of the 3-g model, inefficient moving trajectories are generated, such as multiple trips going back and forth. This phenomenon means that the memory length of past trajectories is not sufficient in 3-g to generate realistic individual trajectories. In GPT-2, we have 1,024 tokens in the default setting, which is a sufficient memory length. Because GPT-2 memorizes the initial location, it can generate trajectories back to that location. In the example of Multi-Output Catboost, the generated location is often far from landmarks and major roads. Catboost adopts a bagging method that averages the predicted coordinates of multiple regression trees. If different regression trees predict different destinations, the output will be their intermediate coordinates. For example, if xi or xj is the destination, Multi-Output Catboost will predict that the intermediate location between them is the destination. In this paper, we do not adopt the bagging method in GPT-2. Instead, we adopt the greedy method to sequentially generate destinations with the highest probability.
4.2 Statistical properties of individual daily trajectories
We investigated the statistical properties of the model-generated individual daily trajectories following five types of statistics: 1) Distribution of moving distance, 2) Auto-correlation of moving distance, 3) Relationship between moving distance and next moving angle, 4) Recurrence probability to initial location, and 5) Diffusion coefficient of people. We measure the distance between two points with the shortest distance on the surface of the Earth’s ellipsoid model WGS84 [68]. The inputs for each model are five locations for the initial 2.5 h in the original trajectory.
For the first type of statistics, the moving distance distribution, Figure 3 shows the cumulative probability distribution of the hourly moving distance in a straight line for the original and model-generated trajectories. Note that the horizontal axis is on a logarithmic scale. The distribution of original trajectory is approximated by a logarithmic function where its R2 is 0.995. Individuals tend to prefer moving within short distances. Half of all moved distances are less than 4 km. Using Jensen-Shannon divergence with the base-2 logarithm, DJS, we measure the similarity of the distance distributions between the original and each model-generated trajectory. For 2-g, 3-g, Catboost, and GPT-2, DJS is 0.0037, 0.0064, 0.030, and 0.049, respectively. DJS ∼ 0 means that these models reproduce the statistical property in which the distribution of the hourly moving distance follows a logarithmic function as in the original trajectories.
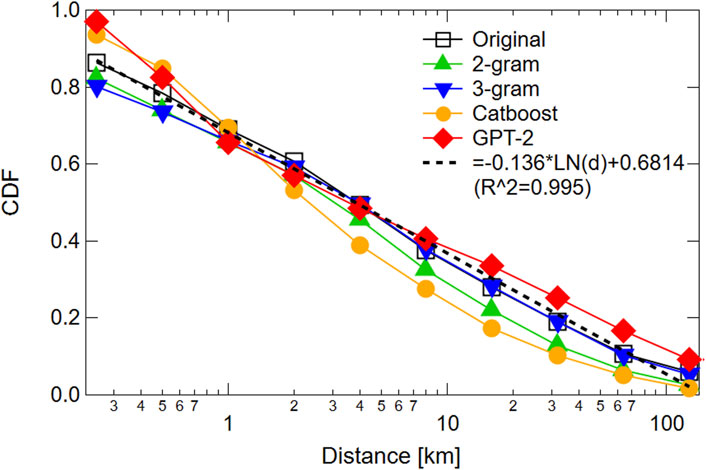
FIGURE 3. Distribution of hourly moving distance in a straight line for (□) original trajectory and trajectories generated by (▴) 2-g, (▾) 3-g, (•) Multi-Output Catboost, and (⧫) GPT-2 models. Dashed line represents the logarithmic function. R2 is 0.995.
The second type is the autocorrelation function of a 30-min moving distance. Note that this minute dimension is not spatial but temporal. As shown in Figure 4, since the original autocorrelation function decays exponentially, the dynamics of the original movement follow a short-term memory process. The 3-g and GPT-2 models reproduce autocorrelations that follow an exponential function. On the other hand, Catboost is less reproducible.
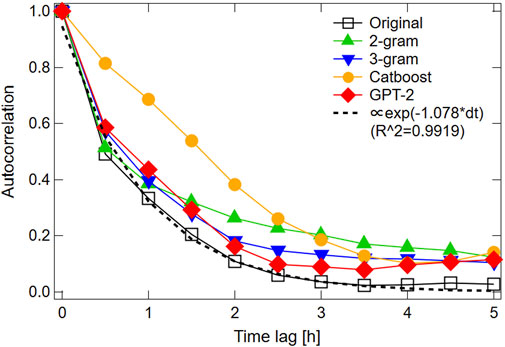
FIGURE 4. Autocorrelation function of 30-minuts moving distance for (□) original trajectory and trajectories generated by (▴) 2-g, (▾) 3-g, (•) Multi-Output Catboost, and (⧫) GPT-2 Models. Dashed line represents the exponential function. R2 is 0.9919.
The third type of trajectory is the relationship between moving distance and next moving angle. Most people move toward their destinations and thus are not random walkers. In Figure 5, we show the relationship between the distance |Xt| of hourly moving vector Xt = (xt − xt−1) and the cosine of the moving vectors as follows:
where xt is a position vector representing location coordinate at time t.
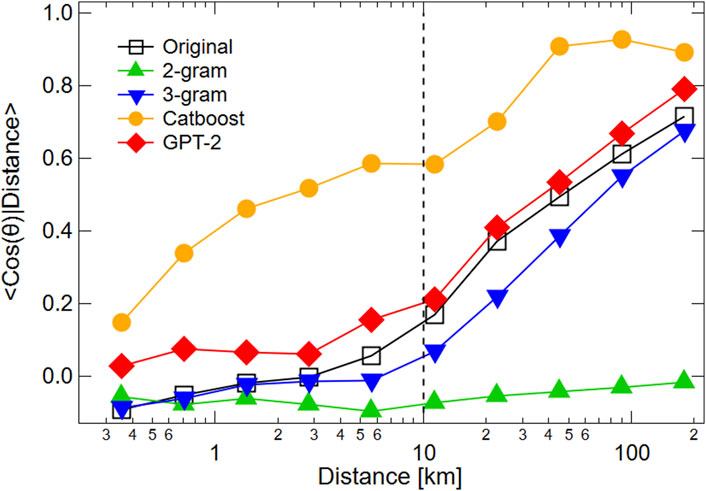
FIGURE 5. Relationship between hourly moving distance and next moving angle for (□) original trajectory and trajectories generated by (▴) 2-g, (▾) 3-g, (•) Multi-Output Catboost, and (⧫) GPT-2 models. Vertical axis is the conditional mean of the cosine between two consecutive one-hour moves. Dashed line represents a moving distance of 10 km.
In the original trajectories, for moving less than 10 km per hour, the conditional mean of next moving angle is ⟨ cos θ||Xt| < 10 km⟩≃ 0. On the other hand, the conditional mean is positive, ⟨ cos θ||Xt|≥ 10 km⟩ > 0, for a moving of more than 10 km per hour. If the distance to the destination is less than 10 km, people can arrive within an hour. On the other hand, if the destination is more than 10 km away, people may not be able to arrive within one hour. In that case, they continue to move toward their destination over the next hour. Figure 5 illustrates these characteristics of human mobility, which can only be reproduced by the GPT-2 and 3-g models.
The Fourth type of statistics is the recurrence probability to the initial location. Most people leave their homes in the morning to go to their destinations and return home after completing their errands at these destinations. In this trajectory dataset, the coordinates are recorded when the smartphones are more than 100 m away from the homes. Therefore, in many cases, the initial coordinate of the daily trajectory is around the home or place of staying. We show in Figure 6 the recurrence probabilities within 3 km of the initial coordinate for the 5 h until the final time (i.e., homecoming time) of the individual daily trajectory. On the original trajectories, the recurrence probability increases from 2 h before the final time. Only GPT-2 reproduces this property.
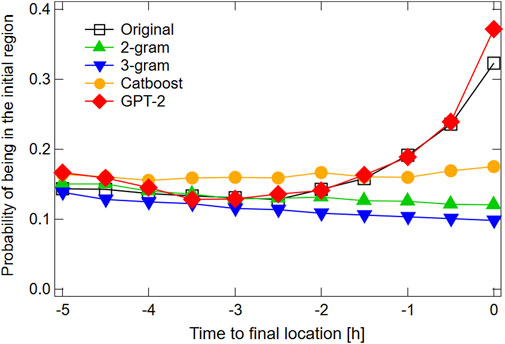
FIGURE 6. Recurrence probability to initial location for the 5 h until the final time (i.e., homecoming time) of the individual daily trajectory: (□), (▴), (▾) original, 2-g, 3-g, (•) Multi-Output Catboost, and (⧫) GPT-2 generated trajectories. Time = 0 represents the final time.
As the fifth type of statistics, we investigated the time-scale dependent properties of trajectories by observing the diffusion coefficients of people. In Figure 7, we plot the elapsed time from the initial time (i.e., time scale) on the horizontal axis and the mean square of the distance from the initial location on the vertical axis. The four plots for the initial 2 h in the left side of the figure are initial values of the models, so they are common to the original and the model-generated trajectories. If the individual trajectory follows a two-dimensional random walk, the mean of squares is proportional to the time scale. If people linearly move away from the initial locations, the mean of squares is proportional to the square of the time scale. The slope of this power-law relationship is the diffusion coefficient of people. The diffusion coefficient of the original trajectories is around 2 until the 4-h time scale and around 1 over the 4-h time scale. These results suggest that the upper limit of moving time from home to destination for Kyoto tourism is about 4 h. The 3-g, Catboost, and GPT-2 models successfully reproduce the properties of people’s diffusion.
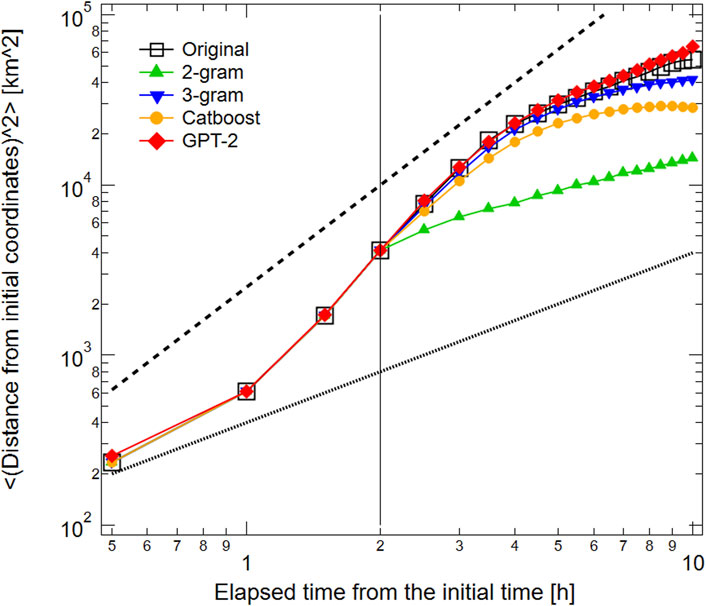
FIGURE 7. People’s diffusion for (□) original trajectory and trajectories generated by (▴) 2-g, (▾) 3-g, (•) Multi-Output Catboost, and (⧫) GPT-2 models. Horizontal axis indicates the elapsed time from the initial time. Vertical axis represents the mean square of the distance from the initial location. The dotted and dashed guidelines show that the mean square of the distance is proportional to the elapsed time and the square of the elapsed time, respectively. The four plots for the initial 2 h on the left side are initial values of the models.
4.3 Prediction accuracy
We confirmed the predictive performance of the GPT-2, N-gram, and Multi-Output Catboost models for individual daily trajectories using test data not used for training. Five initial coordinates for 2.5 h were input to predict the coordinates for the next half hour, one hour, two hours, four hours, and the final time (i.e., homecoming time) of the individual daily trajectory. The probability that the prediction is within 1 km (10 km) of the actual location coordinates is shown in Table 1. For all forecasts, GPT-2 outperforms the other models. Especially for the last location of the day, we could confirm that GPT-2 is eight times more accurate than the other models.

TABLE 1. Probability that the prediction is within 1 km (10 km) of the actual location coordinates for the next half hour, one hour, two hours, four hours, and the final time of the day. We performed 24,247 realizations of each model to estimate the probabilities.
4.4 Fine-tuning GPT-2
Many tourists visit the best places to enjoy viewing the autumn leaves. The autumn leaves season is short in Kyoto, only about two weeks. In 2021, the weekend of November 27 and 28 was the best time to see the autumn leaves. With only two days of modeling targets, it is difficult to collect enough orbital data for the model to learn the characteristics of trajectories from zero. By fine-tuning the GPT-2 parameters learned in the previous section with the trajectories for November 27 and 28, we upgraded GPT-2 to generate the individual daily trajectories for this weekend. Table 2 shows a comparison of the prediction accuracy by the GPT-2 model before and after fine-tuning. To measure this accuracy, we focused on the probability that the prediction is within 1 km (10 km) of the actual location coordinates for the next half hour, one hour, two hours, four hours, and the final time (i.e., homecoming time) of the individual daily trajectories for November 27 and 28. We could significantly improve the accuracy of trajectory prediction on given days by fine tuning the GPT-2 parameters.

TABLE 2. Probability that the prediction is within 1 km (10 km) of the actual location coordinates for the next half hour, one hour, two hours, four hours, and the end of the day for November 27 and 28.
5 Conclusion
We proposed a method to convert individual daily trajectories into token time series by applying the tokenizer SentencePiece to a geographic space divided using the Japan regional grid code JIS X0410. We could build a highly accurate generator of individual daily trajectories by learning the token time series with the neural language model GPT-2. The model-generated individual daily trajectories reproduced the following five realistic properties. The first property is that the cumulative distribution of the hourly moving distance follows a logarithmic function. The second property is that the autocorrelation function of the moving distance exhibits short-time memory. The third property is that there is a positive autocorrelation in the direction of moving for one hour in long-distance trips. The fourth property is that the last location is often near the initial location in each individual daily trajectory. The fifth property is the time-scale dependence of people’s diffusion. On larger time scales, the diffusion is slower. Generators based on n-grams and Catboost, in particular, could not reproduce the recurrence probability to the initial location.
We investigated the prediction accuracy of each model for individual daily trajectories. GPT-2 outperformed the n-gram and Catboost models. Moreover, we showed that fine-tuning the parameters of GPT-2 with a part of the individual trajectories on given days could significantly improve the accuracy of the trajectory prediction for those days.
Aa a final point, we propose three important tasks to be tackled in the future. The first task is to generate trajectories that take into account individual attributes such as gender and age. Since the neural language model can generate text about a given category by training both various texts and their text categories, this method could be applied to the generation of trajectories that depend on individual attributes. As a second challenge, it is constructive to develop the next-location predictor that handles sequences of locations and timestamps. The time resolution used in this paper is fixed at 30 min, so we do not generate the temporal dimension (e.g., Fushimi-Momoyama Castle Athletic Park at 10:00 a.m. → Kyoto Station at 11:15 a.m. → Mt. Hiei Sakamoto Station at 11:20 a.m.). To generate the temporal dimension, it is necessary to develop a model that trains both timestamps and location coordinates. The third task is to generate collective trajectories. In this paper, we introduce models in which individuals do not interact with each other. As part of our future challenges, we plan to develop methods for models to train the interactions. Generating highly accurate synthetic trajectories from models would contribute to fundamental knowledge for such areas as urban planning, what-if analysis, and computational epidemiology.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: Anyone can purchase the data from Agoop-Corp., https://www.agoop.co.jp/.
Author contributions
All authors carried out the conceptualization, methodology, investigation, and validation. TM and SF carried out the formal analysis. TM prepared and wrote the original draft. TM carried out the project administration and funding acquisition. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by Strategic Research Project grant from ROIS (Research Organization of Information and Systems), JST CREST Grant Number JPMJCR20D3 and JSPS KAKENHI Grant Numbers JP19K22852, JP21H01569, and JP21K04557.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Zhu L, Yu FR, Wang Y, Ning B, Tang T. Big data analytics in intelligent transportation systems: A survey. IEEE Trans Intell Transp Syst (2019) 20:383–98. doi:10.1109/tits.2018.2815678
2. Chang S, Pierson E, Koh PW, Gerardin J, Redbird B, Grusky D, et al. Mobility network models of Covid-19 explain inequities and inform reopening. Nature (2021) 589:82–7. doi:10.1038/s41586-020-2923-3
3. Deb P, Furceri D, Ostry JD, Tawk N. The economic effects of Covid-19 containment measures. Open Econ Rev (2022) 33:1–32. doi:10.1007/s11079-021-09638-2
4. Mizuno T, Ohnishi T, Watanabe T. Visualizing social and behavior change due to the outbreak of Covid-19 using mobile phone location data. New Gener Comput (2021) 39:453–68. doi:10.1007/s00354-021-00139-x
5. Sudo A, Kashiyama T, Yabe T, Kanasugi H, Song X, Higuchi T, et al. Particle filter for real-time human mobility prediction following unprecedented disaster. In: SIGSPACIAL ’16: Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems; October 2016 (2016). p. 1–10. vol 5.
6. Rotman A, Shalev M. Using location data from mobile phones to study participation in mass protests. Sociol Methods Res (2020) 51:1357–412. doi:10.1177/0049124120914926
7. Cutter SL, Ahearn JA, Amadei B, Crawford P, Eide EA, Galloway GE, et al. Disaster resilience: A national imperative. Environ Sci Pol Sust Dev (2013) 55:25–9. doi:10.1080/00139157.2013.768076
8.WMO-UNISDR. Disaster risk and resilience. Thematic think piece, UN system task Force on the post-2015 UN development agenda (2012).
9. Yabe T, Tsubouchi K, Sekimoto Y. Cityflowfragility: Measuring the fragility of people flow in cities to disasters using gps data collected from smartphones. Proc ACM Interact Mob Wearable Ubiquitous Technol (2017) 1:1–17. doi:10.1145/3130982
10. Yabe T, Tsubouchi K, Sudo A, Sekimoto Y. A framework for evacuation hotspot detection after large scale disasters using location data from smartphones: Case study of kumamoto earthquake. In: Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (SIGSPACIAL ’16); October 2016 (2016). p. 44.
11. Fiore M, Katsikouli P, Zavou E, Cunche M, Fessant F, Hello DL, et al. Privacy in trajectory micro-data publishing : A survey (2019). arXiv, 1903.12211.
12. Mir DJ, Isaacman S, Caceres R, Martonosi M, Wright RN. Dp-where: Differentially private modeling of human mobility. In: Proceedings of the 2013 IEEE International Conference on Big Data; January 2013 (2013). p. 580–8.
13. Pellungrini R, Pappalardo L, Simini F, Monreale A. Modeling adversarial behavior against mobility data privacy. IEEE Trans Intell Transp Syst (2020) 23:1145–58. doi:10.1109/tits.2020.3021911
14. Luca M, Barlacchi G, Lepri B, Pappalardo L. A survey on deep learning for human mobility. ACM Comput Surv (2023) 55:1–44. doi:10.1145/3485125
15. Wang X, Liu X, Lu Z, Yang H. Large scale gps trajectory generation using map based on two stage gan. J Data Sci (2021) 19:126–41. doi:10.6339/21-jds1004
16. Feng J, Yang Z, Xu F, Yu H, Wang M, Li Y. Learning to simulate human mobility. In: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; August 2020 (2020). p. 3426–33.
17. Yin D, Yang Q. Gans based density distribution privacy-preservation on mobility data. Security Commun Networks (2018) 2018:1–13. doi:10.1155/2018/9203076
18. Kulkarni V, Tagasovska N, Vatter T, Garbinato B. Generative models for simulating mobility trajectories (2018). arXiv , 1811.12801.
19. Huang D, Song X, Fan Z, Jiang R, Shibasaki R, Zhang Y, et al. Autoencoder based generative model of urban human mobility. In: Proceeding of the 2019 IEEE Conference on Multimedia Information Processing and Retrieval (MIPR); March 2019; San Jose, CA, USA. IEEE (2019). p. 425–30.
20. Liu Z, Miranda F, Xiong W, Yang J, Wang Q, Silva C. Learning geo-contextual embeddings for commuting flow prediction. Proc AAAI Conf Artif Intelligence (2020) 34:808–16. doi:10.1609/aaai.v34i01.5425
21. Yao X, Gao Y, Zhu D, Manley E, Wang J, Liu Y. Spatial origin-destination flow imputation using graph convolutional networks. IEEE Trans Intell Transp Syst (2021) 22:7474–84. doi:10.1109/tits.2020.3003310
22. Simini F, Barlacchi G, Luca M, Pappalardo L. Deep gravity: Enhancing mobility flows generation with deep neural networks and geographic information (2020). arXiv , cs.LG/2012.00489.
23. Tang J, Liang J, Yu T, Xiong Y, Zeng G. Trip destination prediction based on a deep integration network by fusing multiple features from taxi trajectories. IET Intell Trans Sys (2021) 15:1131–41. doi:10.1049/itr2.12075
24. Brebisson AD, Simon E, Auvolat A, Vincent P, Bengio Y. Artificial neural networks applied to taxi destination prediction. In: Proceedings of the 2015th International Conference on ECML PKDD Discovery Challenge; September 2015 (2015). p. 40–51.
25. Yao D, Zhang C, Huang J, Bi J. Serm: A recurrent model for next location prediction in semantic trajectories. In: Proceedings of the 2017 ACM on Conference on Information and Knowledge Management; November 2017; Singapore (2017). p. 2411–4.
26. Liu Q, Wu S, Wang L, Tan T. Predicting the next location: A recurrent model with spatial and temporal contexts. In: Thirtieth AAAI conference on artificial intelligence (2016). p. 194–200.
27. Rossi A, Barlacchi G, Bianchini M, Lepri B. Modelling taxi drivers’ behaviour for the next destination prediction. IEEE Trans Intell Transp Syst (2019) 21:2980–9. doi:10.1109/tits.2019.2922002
28. Gao Q, Zhou F, Trajcevski G, Zhang K, Zhong T, Zhang F. Predicting human mobility via variational attention. In: The world wide web conference (2019). p. 2750–6.
29. Kong D, Wu F. Hst-lstm: A hierarchical spatial-temporal long-short term memory network for location prediction. In: Ijcai (2018). p. 2341–7.
30. Chen Y, Long C, Cong G, Li C. Context-aware deep model for joint mobility and time prediction. In: Proceedings of the 13th International Conference on Web Search and Data Mining; Feb 2022; Houston, TX, USA (2022). p. 106–14.
31. Feng J, Li Y, Zhang C, Sun F, Meng F, Guo A, et al. Deepmove: Predicting human mobility with attentional recurrent networks. In: Proceedings of the 2018 world wide web conference; April 2018; New York, NY, USA (2018). p. 1459–68.
32. Bao Y, Huang Z, Li L, Wang Y, Liu Y. A bilstm-cnn model for predicting users’ next locations based on geotagged social media. Int J Geographical Inf Sci (2020) 2020:639–60. doi:10.1080/13658816.2020.1808896
33. Lv J, Li Q, Sun Q, Wang X. T-Conv: A convolutional neural network for multi-scale taxi trajectory prediction. In: Proceedings of the 2018 IEEE international conference on big data and smart computing (bigcomp) (2018). p. 82–9.
34. Dai G, Hu X, Ge Y, Ning Z, Liu Y. Attention based simplified deep residual network for citywide crowd flows prediction. Front Comput Sci (2021) 15:152317–2. doi:10.1007/s11704-020-9194-x
35. Wang S, Cao J, Chen H, Peng H, Huang Z. Seqst-gan: Seq2seq generative adversarial nets for multi-step urban crowd flow prediction. ACM Trans Spat Algorithms Syst (2020) 6:1–24. doi:10.1145/3378889
36. Yang B, Kang Y, Li H, Zhang Y, Yang Y, Zhang L. Spatio-temporal expand-and-squeeze networks for crowd flow prediction in metropolis. IET Intell Trans Sys (2020) 14:313–22. doi:10.1049/iet-its.2019.0377
37. Ren Y, Chen H, Han Y, Cheng T, Zhang Y, Chen G. A hybrid integrated deep learning model for the prediction of citywide spatio-temporal flow volumes. Int J Geographical Inf Sci (2020) 34:802–23. doi:10.1080/13658816.2019.1652303
38. Tian C, Zhu X, Hu Z, Ma J. Deep spatial-temporal networks for crowd flows prediction by dilated convolutions and region-shifting attention mechanism. Appl Intell (Dordr) (2020) 2020:3057–70. doi:10.1007/s10489-020-01698-0
39. Mourad L, Qi H, Shen Y, Yin B. Astir: Spatio-temporal data mining for crowd flow prediction. IEEE Access (2019) 7:175159–65. doi:10.1109/access.2019.2950956
40. Lin Z, Feng J, Lu Z, Li Y, Jin D. Deepstn+: Context-aware spatial-temporal neural network for crowd flow prediction in metropolis. Proc AAAI Conf Artif Intelligence (2019) 33:1020–7. doi:10.1609/aaai.v33i01.33011020
41. Li W, Tao W, Qiu J, Liu X, Zhou X, Pan Z. Densely connected convolutional networks with attention lstm for crowd flows prediction. IEEE Access (2019) 7:140488–98. doi:10.1109/access.2019.2943890
42. Du B, Peng H, Senzhang W, Bhuiyan MZA, Wang L, Gong Q, et al. Deep irregular convolutional residual lstm for urban traffic passenger flows prediction. IEEE Trans Intell Transp Syst (2019) 21:972–85. doi:10.1109/tits.2019.2900481
43. Yao H, Tang X, Wei H, Zheng G, Li Z. Revisiting spatial-temporal similarity: A deep learning framework for traffic prediction. Proc AAAI Conf Artif intelligence (2019) 33:5668–75. doi:10.1609/aaai.v33i01.33015668
44. Zhang J, Zheng Y, Qi D. Deep spatio-temporal residual networks for citywide crowd flows prediction. AAAI’17: Proc Thirty-First AAAI Conf Artif Intelligence (2017) 31:1655–61. doi:10.1609/aaai.v31i1.10735
45. Liu L, Zhen J, Li G, Zhan G, He Z, Du B, et al. Dynamic spatial-temporal representation learning for traffic flow prediction. IEEE Trans Intell Transp Syst (2021) 22:7169–83. doi:10.1109/tits.2020.3002718
46. Ai Y, Li Z, Gan M, Zhang Y, Yu D, Chen W, et al. A deep learning approach on short-term spatiotemporal distribution forecasting of dockless bike-sharing system. Neural Comput Appl (2019) 31:1665–77. doi:10.1007/s00521-018-3470-9
47. Zonoozi A, jae Kim J, Li X-L, Cong G. Periodic-crn: A convolutional recurrent model for crowd density prediction with recurring periodic patterns. In: Ijcai (2018). p. 3732–8.
48. Schlapfer M, Dong L, O’Keeffe K, Santi P, Szell M, Salat H, et al. The universal visitation law of human mobility. Nature (2021) 593:522–7. doi:10.1038/s41586-021-03480-9
49. Song C, Koren T, Wang P, Barabási A-L. Modelling the scaling properties of human mobility. Nat Phys (2010) 6:818–23. doi:10.1038/nphys1760
50. Toch E, Lerner B, Ben-Zion E, Ben-Gal I. Analyzing large-scale human mobility data: A survey of machine learning methods and applications. Knowl Inf Syst (2019) 58:501–23. doi:10.1007/s10115-018-1186-x
51. Radford A, Wu J, Child R, Amodei D, Sutskever I. Language models are unsupervised multitask learners. OpenAI blog (2019) 1:9.
52.Statistics Bureau, Ministry of Internal Affairs and Communications. Overview of grid square statistics (2015). Available at: http://www.stat.go.jp/english/data/mesh/index.htm (Accessed on November 1, 2022).
53. Sennrich R, Haddow B, Birch A. Neural machine translation of rare words with subword units. In: Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics; Berlin, Germany; August 2016. Association for Computational Linguistics (2016). p. 1715–25. vol 1. Available at: https://aclanthology.org/P16-1162/.
54. Kudo T, Richardson J. Sentencepiece: A simple and language independent subword tokenizer and detokenizer for neural text processing. In: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing: System Demonstrations; November 2018; Brussels, Belgium. Association for Computational Linguistics (2018). p. 66–71. Available at: https://aclanthology.org/D18-2012/.
55. Gonzalez MC, Hidalgo CA, Barabasi A-L. Understanding individual human mobility patterns. Nature (2008) 453:779–82. doi:10.1038/nature06958
56. Pappalardo L, Rinzivillo S, Qu Z, Pedreschi D, Giannotti F. Understanding the patterns of car travel. Eur Phys J Spec Top (2013) 215:61–73. doi:10.1140/epjst/e2013-01715-5
57. Alessandretti L, Aslak U, Lehmann S. The scales of human mobility. Nature (2020) 587:402–7. doi:10.1038/s41586-020-2909-1
58. Pappalardo L, Simini F, Rinzivillo S, Pedreschi D, Giannotti F, Barabási A-L. Returners and explorers dichotomy in human mobility. Nat Commun (2015) 6:8166. doi:10.1038/ncomms9166
59. Song C, Qu Z, Blumm N, Barabási A-L. Limits of predictability in human mobility. Science (2010) 327:1018–21. doi:10.1126/science.1177170
60. Alessandretti L, Sapiezynski P, Sekara V, Lehmann S, Baronchelli A. Evidence for a conserved quantity in human mobility. Nat Hum Behav (2018) 2:485–91. doi:10.1038/s41562-018-0364-x
61.Agoop-Corp. Agoop-corp (2022). Available at: https://www.agoop.co.jp/(Accessed on August 7, 2022).
62. Sato A-H, Nishimura S, Tsubaki H. World grid square codes: Definition and an example of world grid square data. In: Proceedings of the 2017 IEEE International Conference on Big Data (Big Data); December 2017 (2017). p. 4238–47.
63. Devlin J, Chang M-W, Lee K, Toutanova K. Bert: Pre-training of deep bidirectional transformers for language understanding (2018). arXiv, 1810.04805.
64.Hugging-Face. Openai gpt2 (2022). Available at: https://huggingface.co/docs/transformers/model_doc/gpt2 (Accessed on August 18, 2022).
65. Dorogush AV, Ershov V, Gulin A. Catboost: Gradient boosting with categorical features support (2018). arXiv, 1810.11363.
66. Hancock JT, Khoshgoftaar TM. Catboost for big data: An interdisciplinary review. J Big Data (2020) 7:94. doi:10.1186/s40537-020-00369-8
67.CatBoost. CatBoost (2022). Available at: https://catboost.ai/en/docs/ (Accessed on August 7, 2022).
Appendix A:
In this paper, we utilize the Japan regional grid code “JIS X0,0410” for location indexing Statistics Bureau, Ministry of Internal Affairs and Communications [52]. This code consists of several subcodes, where the first-level subcode represents the absolute location of each grid, the second-level and higher subcodes represent relative locations within a divided grid.
The first-level subcode (e.g., 5235) is a four-digit number representing a unique location enclosed by a square with a 40-min difference in latitude and a 1-degree difference in longitude, as shown in Figure 8. Throughout Japan, one side-length of this square is about 80 km. All land areas in Japan can be represented using 176 first-level subcodes. The first two digits of the subcode represent latitude (multiplied by 1.5 and rounded down to the nearest integer) and the last two digits represent longitude. The first-level subcode is calculated from the latitude and longitude of the southwest corner of the grid by
The second-level subcode (e.g., 36) is a two-digit number that represents the area created by dividing the first-level grid into eight equal areas in the latitudinal and longitudinal directions. There are 64 second-level subcodes. The length of one side is about 10 km. The first digit of the second-level subcode indicates the direction of latitude and the last digit indicates the direction of longitude. This is connected to the first-level subcode as “5235/36”.
The third-level subcode (e.g., 80) is a two-digit number that represents the area created by dividing the second-level grid into ten equal areas in the latitudinal and longitudinal directions. There are 100 third-level subcodes. The length of one side is about 1 km. The first digit of the third-level subcode indicates the direction of latitude and the last digit indicates the direction of longitude. This is connected to the first-level and second-level subcodes as “5235/36/80”.
The fourth-level subcode (e.g., 2) bisects the third-level grid by latitude and longitude. The length of one side is about 500 m. The southwest area is represented as 1, the southeast as 2, the northwest as 3, and the northeast as 4, as in “5235/36/80/2”.
The fifth-level subcode (e.g., 3) bisects the fourth-level grid by latitude and longitude. The length of one side is about 250 m. The southwest area is represented as 1, the southeast as 2, the northwest as 3, and the northeast as 4, as in “5235/36/80/2/3”.
Appendix B:
We explain how the geospatial tokenizer in section 3.1 and the GPT-2 in section 3.2. Generate a daily trajectory from the input initial coordinates. First, as shown in the following example, we input five initial coordinates (latitude and longitude) that represent the initial 2.5 h moving trajectory into the geospatial tokenizer.
(34.716, 135.586) → (34.696, 135.548) → (34.697, 135.535) → (34.695, 135.529) → (34.788, 135.689)
The initial coordinates are converted into grid codes according to the rules of “JIS X0,410” as follows.
5235045644/_/5235043342/_/5235043242/_/5235043214/_/5235154531/
The grid codes are converted into byte characters according to the translation map in the geospatial tokenizer, and then their byte characters are tokenized as follows.
ßℏ/γ/B/2/_ßℏδB/3/_ßℏλB/3/_ßℏλC/2/_ßμξD/4/
These initial tokens are input into the GPT-2 to generate the next token.
ßℏ/γ/B/2/_ßℏδB/3/_ßℏλB/3/_ßℏλC/2/_ßμξD/4/_ΨηαD/
By recursively inputting the initial and generated tokens into the GPT-2, tokens are generated successively. The GPT-2 stops the recursion process when the end token “.” is generated.
Finally, these tokens are reversely converted into grid codes based on the translation map.
These grid codes are output as a generated daily trajectory. In Figure 2A, we plot the location coordinates of these grit codes. In Section 4.1, we manually show the location names of these grit codes.
Keywords: human mobility, trajectory generation, mobility model, GPT-2, statistical property, nlp
Citation: Mizuno T, Fujimoto S and Ishikawa A (2022) Generation of individual daily trajectories by GPT-2. Front. Phys. 10:1021176. doi: 10.3389/fphy.2022.1021176
Received: 17 August 2022; Accepted: 18 October 2022;
Published: 08 November 2022.
Edited by:
Víctor M. Eguíluz, Institute of Interdisciplinary Physics and Complex Systems (CSIC), SpainReviewed by:
Massimiliano Luca, Bruno Kessler Foundation (FBK), ItalyJorge P. Rodríguez, CSIC-UIB, Spain
Copyright © 2022 Mizuno, Fujimoto and Ishikawa . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Takayuki Mizuno , bWl6dW5vQG5paS5hYy5qcA==
 Takayuki Mizuno
Takayuki Mizuno Shouji Fujimoto
Shouji Fujimoto  Atushi Ishikawa
Atushi Ishikawa