Theoretical studies of high-power laser beam smoothing via stimulated brillouin scattering in plasma

To achieve uniform irradiation, the focal spot from a high-power laser system must be homogeneous; thus, laser beam smoothing is required. In this study, we theoretically demonstrated a novel spatial smoothing method based on stimulated Brillouin scattering (SBS) in a plasma. As SBS is sensitive to pump intensity, the area of higher intensity in the laser beam has a higher reflectivity, leading to a more homogeneous passed beam. From the theoretical simulation, the laser beam modulation significantly decreased in SBS, while the fluence contrast decreased from 15.9% to 9.7%.

Introduction

Inertial confinement fusion requires perfectly controlled laser beams to compress a deuterium-tritium target and achieve nuclear fusion. Laser fusion has extremely high energy requirements. From theoretical analysis, the laser energy deposition must be above 1 MJ, and is spread to dozens of beams. Generally, the energy of a single beam is approximately 10 kJ in high-power laser systems, such as the National Ignition Facility (NIF) [1], Laser MegaJoule [2, 3] and SG-III [4, 5].

The construction of such a system requires specific development of optical techniques. Before the laser energy is deposited at the target, the laser beam undergoes a frequency conversion of the third harmonic (3ω) to 351 nm. After the third harmonic, the UV optical module has the highest risk of damage to the entire system. In actual laser system operation, the laser flux is far below the optical element bulk damage threshold, and most optical damage originates from defects in the subsurface microstructure [6–8]. The laser spatial modulation caused by frequency conversion and beam coherence increases the local laser light intensity, which further increases the optical damage risk.

To reduce the optical damage risk, optical beam smoothing techniques such as liquid crystal spatial light modulators (SLMs) can help improve the near-field beam quality before the main amplifier system [9, 10]. A continuous phase plate (CPP) [11] and smoothing via spectral dispersion [12] have been developed and applied in engineering to realize homogeneous focal spots. However, SLMs have low laser energy transmittance [13]. The smoothing element (e.g., CPP) itself also suffers from damage risk. Moreover, such elements involve complex processing procedures, so any corresponding damage is difficult to repair.

The processing of traditional optical materials has faced bottlenecks: plasma, as an ionized substance, has almost no damage threshold. Accordingly, the plasma density and temperature span are extremely large, which significantly affect interaction of the laser [14–16]. Therefore, making full use of the plasma is crucial to improve laser beam performance [17].

In this study, we developed an optical smoothing method with high energy efficiency based on stimulated Brillouin scattering (SBS) in plasma. SBS, excited by the interaction of the standing wave acoustic field formed by ions, can be applied for beam smoothing. Because SBS has a significant threshold characteristic, scattering is proportional to the square of the injected laser intensity [18–21]. The transmitted light power is restricted to a certain level. Thus, high-frequency modulation of the near-field of the laser can be reduced, and optical smoothing can be achieved.

Theory

During propagation of a 351-nm (3ω) laser with high photon energy, traditional liquid or solid medium are not suitable. For liquid Brillouin medium, the weaker chemical bonds in medium (eg., heavy fluorocarbon) has a greater probability of being directly broken down. For solid Brillouin medium, this pump intensity is easily to cause irreversible damage to components.

The nonlinear effect in the plasma can manifest an “optical limiting” effect, demonstrating beam smoothing. In comparison with the traditional liquid or solid Brillouin medium, the backscattering angle of the SBS in plasma will be larger. The effect of nonlinear scattering further destroys the spatial and temporal coherence of the main laser and enhances the beam smoothing effect.

To theoretically simulate laser beam smoothing in plasma, coupling of the electromagnetic wave equation and the ion acoustic wave equation was realized as follows:

$\left(\frac{{\partial }^2}{\partial t^2}-c^2{\nabla }^2+{\omega }_{pe}^2\right){\overrightarrow{A}}_s=-\frac{4\pi e^2}{m_e}{\stackrel{\sim }{n}}_e{\overrightarrow{A}}_0(1)$

$\left(\frac{{\partial }^2}{\partial t^2}-C_s^2{\nabla }^2\right){\stackrel{\sim }{n}}_e=-\frac{Z{n}_0{e}^2}{m_i{m}_e{c}^2}{\nabla }^2\left({\overrightarrow{A}}_0\cdot {\overrightarrow{A}}_s\right)(2)$

where ${\overrightarrow{A}}_0$and ${\overrightarrow{A}}_S$are the incident and scattered light wavefield vector potentials, respectively; ${\stackrel{\sim }{n}}_0/{\stackrel{\sim }{n}}_e$represents the density disturbance of the plasma; C_s is the ion speed of sound; Z is the ionic charge; m_i is the ion mass; m_e is the electron mass; and ω_pe is the plasma frequency.

At the strong damping limit, the vibration and density perturbation of electrons can be expressed using the same formula for both the electron plasma wave and the ion plasma soundwave as:

${\stackrel{\sim }{n}}_e=-\frac{k^2{e}^2}{m_e^2{c}^2{\omega }_{pe}^2}\frac{{\chi }_e\left(1+{\chi }_i\right)}{\epsilon }{a}_0{a}_s^{*}(3)$

where a₀ and a_s represent the ramping amplitudes of the pump and scattered light, respectively; χ_e and χ_i represent the electron and ion polarizability, respectively; and ε = 1+χ_e+χ_i is the dielectric function of the plasma.

The energy flow is expressed as: $J_0={\omega }_0{v}_{g0}{\left|a_0\right|}^2$, and $J_s={\omega }_s{v}_{gs}{\left|a_s\right|}^2$.

Under one-dimensional (1D) conditions, ignoring the time differential term yields the following equation:

$\frac{\partial \left|J_s\right|}{\partial x}=\frac{k^2{e}^2}{m_e^2{c}^2{\omega }_s{v}_{gs}}\mathrm{I}\mathrm{m}\left[\frac{{\chi }_e\left(1+{\chi }_i\right)}{\epsilon }\right]{\left|a_0\right|}^2(4)$

The above equation was solved to obtain:

$\left|J_S\left(0\right)\right|=\left|J_S\left(L\right)\right|\times \exp \left(\mathrm{G}\right)(5)$

$G=-{\int }_0^L\frac{k^2{e}^2{\left|a_0\right|}^2}{m_e^2{c}^2{\omega }_s{v}_{gs}}\mathrm{I}\mathrm{m}\left[\frac{{\chi }_e\left(1+{\chi }_i\right)}{\epsilon }\right]dx(6)$

$G_{SBS}\approx \frac{1}{8}\frac{{\omega }_0}{c}\frac{n_e}{n_c}\frac{v_0^2}{v_{te}^2}\frac{{\omega }_{IAW}}{v_{IAW}}L(7)$

where n_e/n_c is the electron density normalized to the critical density of the interaction wavelength. The scattering intensity and energy reflectivity of the plasma SBS can be estimated using the gain, and the influence of nonlinear scattering on the light field distribution can be numerically analyzed.

The injected and the scattered light are given by:

$J_0\left(x\right)=J_0\left(0\right)+J_S\left(0\right)-J_S\left(x\right)(8)$

$\frac{\partial \left|{\overline{J}}_S\right|}{\partial x}=-\Gamma \left[1-\left|{\overline{J}}_S\left(0\right)\right|+\left|{\overline{J}}_S\right|\right]\left|{\overline{J}}_S\right|(9)$

$\Gamma =\frac{k^2{e}^2{\left|a_0\right|}^2}{m_e^2{c}^2{\omega }_s{v}_{gs}}\mathrm{I}\mathrm{m}\left[\frac{{\chi }_e\left(1+{\chi }_i\right)}{\epsilon }\right](10)$

Using the above 1D model, SBS of light and the respective properties could be theoretically simulated.

Numerical simulation and analysis

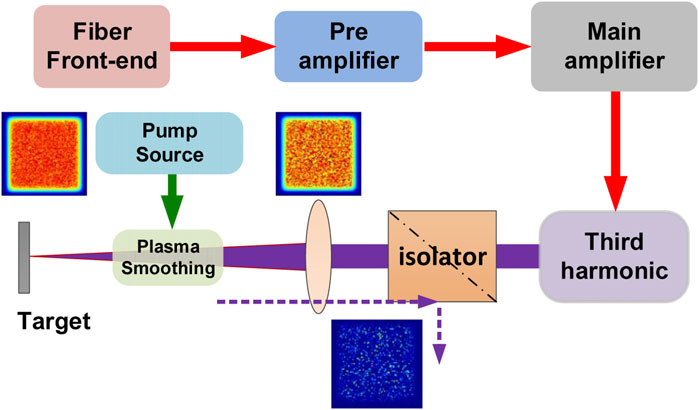
A schematic of plasma SBS beam smoothing is presented in Figure 1. The laser beam was amplified, and the third harmonic was obtained before it was focused on the target. The plasma-smoothing cell was placed in the focused path to realize nonlinear effects in the plasma, which requires a high-power laser, and the plasma was excited using a femtosecond laser. A laser beam with space modulation was introduced into the plasma-smoothing cell. Additionally, an isolator was employed to prevent scattered light. Owing to the threshold properties of the SBS, hotspots in the laser beam exhibited higher reflectivity. The transmitted laser was then smoothed according to this optical limiting property.

FIGURE 1

FIGURE 1. Schematic of simulated Brillouin scattering in plasma for beam smoothing.

For SBS in plasma, the Stokes signal arises from the ion acoustic wave that interacts with the injected laser. Figure 2A presents the theoretically simulated ion acoustic wave (IAW) with SBS at the pump intensity of 10¹⁷ W/cm² and FWHM Gaussian laser pulse of 2 ps. The intensities of the driven waves were plotted as a function of time, and t = 0 refers to the peak of the pump pulse. In theoretical simulation, since the electron mass is much smaller than the ion mass, the temporal evolution of EPWs(electron plasma wave) has a short relaxation time. When the pump laser injection is over, it doesn’t last for a while like IAW, but it decays quickly and fades away. It can be observed that IAWs grow slowly and develop over 3 ps before reaching the saturation area. As the pump pulse falls, IAWs remain in the plasma and dampen slowly. The IAW decay time is much longer than the pump laser falling time, which is comparable to that of Landau damping T_e>>T_i, and no ions move at the phase velocity rate. Thus, in the simulation, the ion movement can be regarded as a steady state.

FIGURE 2

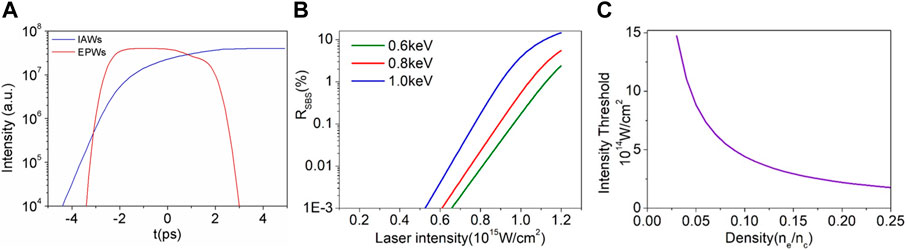
FIGURE 2. Theoretical simulation results of SBS proprieties in plasma. (A) Temporal evolution of scattered intensities of ion acoustic waves (IAWs) and electron plasma wave (EPW) driven by the 2-ps laser pulse. (B) Reflectivity results as a function of laser intensity for T_e of 0.6, 0.8, and 1.0 keV. (C) Intensity at which SBS reaches 1% (intensity threshold) as a function of plasma density.

By numerically solving the electromagnetic wave equation and the ion acoustic wave equation, the SBS reflectivity was found to vary with the injected laser intensity at different temperatures, as detailed in Figure 2. The normalized electron density n_e/n_c was set to 8%. As can be seen in Figure 2B, the SBS threshold decreased with an increase in the plasma temperature. Apparent optical limiting characteristics can be achieved by controlling the laser intensity distribution around 0.5–1.5 × 10¹⁵ GW/cm². Using these simulation results, the pump laser and plasma parameters could be set.

Figure 2C shows that the intensity threshold strongly depends on the plasma density. The electron density was simulated in a 1-mm-long target and varied from 3% to 25%n_c. The plasma temperature was maintained at 1 keV. The SBS reflectivity above was determined as the SBS threshold. This indicates that the SBS threshold decreased quickly before 10%n_c. In the density range of 10%n_c, the thresholds decreased slowly with increasing plasma density. Instantaneous backscatter was determined at the saturation part of the IAWs. It was demonstrated that the increase in scattering was sensitive to the laser intensity and plasma density.

Based on the simulation results in Figure 2, the properties of SBS in plasma depend on the plasma temperature and density. SBS in plasma is driven by the ion acoustic waves. The intensity of ion acoustic waves are affected by the plasma temperature and density and will significantly affect Brillouin gain in plasma. These parameters significantly influence the SBS reflectivity and threshold values [18, 19]. To apply this beam-smoothing method, these parameters must be matched with the intensity of the injected laser to achieve optical limiting and reduce the energy loss of SBS scattering.

As shown in Figure 3, the beam intensity distributions were numerically investigated through the plasma SBS theory. The mean intensity of the injected light was set to 1 × 10¹⁵ GW/cn², the beam size was set to 2 mm × 2 mm, the plasma length was set to 2 mm, the electron density was 8%n_c, and temperature T_e was 1 keV. Figures 3A,D present the 2D and 1D distributions of the pump light, (b) depicts the scattered light, and (c) and (e) show the distributions of the smoothed light. It is clear that the beam distribution was smoothed by transmission through the plasma.

$\text{FOPAI}\left(I_0\right)=\frac{\underset{I_f\left(x_f,y_f\right)\ge I_0\wedge \left(x_f,y_f\right)\in A}{\iint }{I}_f\left(x_f,y_f\right)\mathrm{d}{x}_f\mathrm{d}{y}_f}{\underset{\left(x_f,y_f\right)\in A}{\iint }{I}_f\left(x_f,y_f\right)\mathrm{d}{x}_f\mathrm{d}{y}_f}(11)$

FIGURE 3

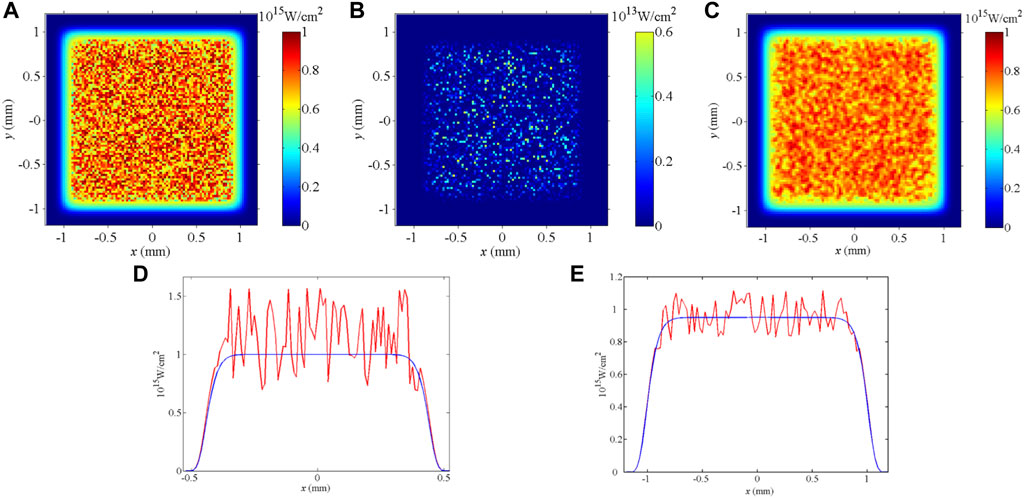
FIGURE 3. Intensity distributions of laser beam: (A) injected laser beam; (B) scattered laser beam; (C) output smoothed laser beam; (D) 1D curve of injected light; (E) 1D curve of output light. To quantitatively analyze the beam smoothing effect, the fractional power above intensity (FOPAI) was evaluated using Eq. 11.

The resulting FOPAI plots for the input and smoothed beams are displayed in Figure 4. In general, if the FOPAI curve is closer to the left side, the proportion of high-intensity laser beams is lower. As shown in Figure 4, the high-intensity hotspot inside the beam was effectively suppressed after beam smoothing via SBS. The initial fluence distribution was relatively dispersed, with the fluence contrast degree of 15.9%. After beam smoothing, the fluence distribution was more centralized with the contrast degree of 9.7%.

FIGURE 4

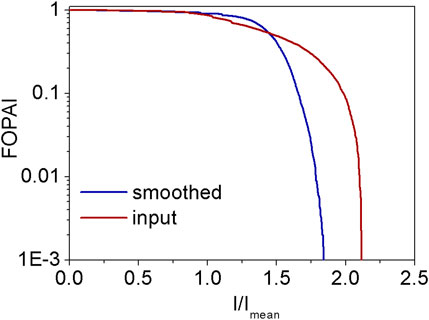
FIGURE 4. Fractional power above intensity (FOPAI) comparisons for the smoothed beam and the input beam.

The potential optical damage strongly correlates with the laser fluence. Beam smoothing elements (such as CPP) in conventional focusing beam paths suffer from a high damage risk. The plasma has virtually no damage threshold, and the passed laser fluence can be extremely high. Thus, this plasma beam smoothing technology will provide new ideas for solving optical element damage.

In high-power laser systems, dozens of optical elements are distributed along the beam path from the front seed to the final target. Each optical element may contain a number of inner defects generated during the material growth process or surface defects generated from component processing. These defects can cause strong local diffraction effects and light intensity enhancement in the laser beam. In addition, inhomogeneity further increases the amplification and frequency conversion, which seriously affects the irradiation uniformity of the subsequent laser. Beam smoothing before the focal spot presents a complicated practical situation. In future research, we will further develop the dynamic control capability of the plasma to achieve dynamic beam smoothing of the focal spot.

Conclusion

In this paper, we present a novel laser beam spatial smoothing method based on SBS in plasma. The key elements of this beam smoothing result from the optical limiting properties of the SBS. Plasma parameters and SBS proprieties are theoretically calculated. Theoretical simulation results show that The SBS reflectivity of the hot spot in the beam is significantly higher than that of the smooth part. High-intensity hotspots were significantly reduced following beam smoothing via SBS. The beam smoothing effect was simulated theoretically, and the results indicate that the fluence contrast decreased from 15.9% to 9.7% after beam smoothing. This approach to spatial beam smoothing is flexible and does not introduce optical damage issues.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HY: Conceptualization, Programming, Acquisition of data, Drafting the manuscript, Funding acquisition JH: Analysis of data, Data Curation ZD: Investigation, Visualization CZ: Writing–Review and Editing YL: Investigation, Validation.

Funding

This work is supported by the National Natural Science Foundation of China No. 61905052.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Haynam CA, Wegner PJ, Auerbach JM, Bowers MW, Dixit SN, Erbert GV, et al. National ignition facility laser performance status. Appl Opt (2007) 46:3276–303. doi:10.1364/ao.46.003276

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fleurot N, Cavailler C, Bourgade JL. The Laser Megajoule (LMJ) Project dedicated to inertial confinement fusion: Development and construction status. FUSION ENGINEERING DESIGN (2005) 74:147–54. doi:10.1016/j.fusengdes.2005.06.251

CrossRef Full Text | Google Scholar

3. Luce J. Beam shaping in the MegaJoule laser project. Proc SPIE (2011) 8130:813002.

CrossRef Full Text | Google Scholar

4. Dai W, Hu D, Zhou W, Zhao J, Jing F, Yang Z, et al. Beam wavefront control of a thermal inertia laser for inertial confinement fusion application. Appl Opt (2009) 48:3691–4. doi:10.1364/ao.48.003691

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Yu H, Jing F, Wei X, Zheng W, Zhang X, Sui Z, et al. Status of prototype of SG-III high-power solid-state laser. Proc SPIE (2009) 7131:713112.

PubMed Abstract | Google Scholar

6. Negres RA, Raman RN, Bude JD, Feit MD, Demos SG. Dynamics of transient absorption in bulk DKDP crystals following laser energy deposition. Opt Express (2012) 20:20447–58. doi:10.1364/oe.20.020447

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Raman RN, Negres RA, Demos SG. Kinetics of ejected particles during breakdown in fused silica by nanosecond laser pulses. Appl Phys Lett (2011) 98:051901. doi:10.1063/1.3549193

CrossRef Full Text | Google Scholar

8. Zheng Y, Ba R, Zhou X, Ding L, Li J, Yuan J, et al. Characteristics of precursors responsible for bulk damage initiation in doubler KDP crystal at different wavelengths. Opt Laser Technol (2017) 96:196–201. doi:10.1016/j.optlastec.2017.05.034

CrossRef Full Text | Google Scholar

9. Ko S-W, Lin T-H, Huang Y-H, Jau H-C, Chu S-C, Chen Y-Y, et al. Electrical control of shape of laser beam using axially symmetric liquid crystal cells. Appl Opt (2012) 51:1540–5. doi:10.1364/ao.51.001540

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Li S, Wang Y, Lu Z, Ding L, Du P, Chen Y, et al. High-quality near-field beam achieved in a high-power laser based on SLM adaptive beam-shaping system. Opt Express (2015) 23:681–9. doi:10.1364/oe.23.000681

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Marozas JA. Fourier transform-based continuous phase-plate design technique: A high-pass phase-plate design as an application for OMEGA and the national ignition facility. J Opt Soc Am A (2007) 24:74–83. doi:10.1364/josaa.24.000074

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Duluc M, Penninckx D, Loiseau P, Riazuelo G, D'Humieres E. Optical smoothing with reduced FM-to-AM conversion in high-power lasers using spectral distribution. Phys Rev Appl (2019) 12:054055. doi:10.1103/physrevapplied.12.054055

CrossRef Full Text | Google Scholar

13. Chen HX, Li DH, Chen ZP. Measuring phase modulation characteristics of LC-SLM by using phase-shift interference. Proc SPIE (2000) 4231:384–6.

CrossRef Full Text | Google Scholar

14. Thaury C, Guillaume E, Döpp A, Lehe R, Lifschitz A, Ta Phuoc K, et al. Demonstration of relativistic electron beam focusing by a laser-plasma lens. Nat Commun (2015) 6:6860. doi:10.1038/ncomms7860

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang HY, Lin C, Sheng ZM, Liu B, Zhao S, Guo ZY, et al. Laser shaping of a relativistic intense, short Gaussian pulse by a plasma lens. Phys Rev Lett (2011) 107:265002. doi:10.1103/physrevlett.107.265002

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wilson R, King M, Gray RJ, Carroll DC, Dance RJ, Armstrong C, et al. Ellipsoidal plasma mirror focusing of high power laser pulses to ultra-high intensities. Phys Plasmas (2016) 23:033106. doi:10.1063/1.4943200

CrossRef Full Text | Google Scholar

17. Weng X, Zhong Z, Li J, Zhang B. Filamentation of spatiotemporal smoothed focal spot in plasma by Beam Smoothing scheme. OPTICS COMMUNICATIONS (2019) 436:216–21. doi:10.1016/j.optcom.2018.12.039

CrossRef Full Text | Google Scholar

18. Lu ZW, Hasi WLJ, Gong HP, Li Q, He WM. Generation of flat-top waveform by double optical limiting based on stimulated Brillouin scattering. Opt Express (2006) 14:5497–501. doi:10.1364/oe.14.005497

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Zhu X, Yang H, Wang G, Wu D, Qiu Y. Optimising of the material and laser parameters for high-power laser spatial beam smoothing based on stimulated Brillouin scattering. Laser Phys (2019) 29:075402. doi:10.1088/1555-6611/ab232a

CrossRef Full Text | Google Scholar

20. Depierreux S, Michel DT, Tassin V, Loiseau P, Stenz C, Labaune C. Effect of the laser wavelength on the saturated level of stimulated Brillouin scattering. Phys Rev Lett (2009) 103:115001. doi:10.1103/physrevlett.103.115001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rousseaux C, Baton SD, Benisti D, Gremillet L, Loupias B, Philippe F, et al. Experimental investigation of stimulated Raman and Brillouin scattering instabilities driven by two successive collinear picosecond laser pulses. Phys Rev E (2016) 93:043209. doi:10.1103/physreve.93.043209

PubMed Abstract | CrossRef Full Text | Google Scholar