Evaluating the connectedness of commodity future markets via the cross-correlation network

Financial markets are widely believed to be complex systems where interdependencies exist among individual entities in the system enabling the risk spillover effect. The detrended cross-correlation analysis (DCCA) has found wide applications in examining the comovement of fluctuations among financial time series. However, to what extent can such cross-correlation represent the spillover effect is still unknown. This article constructs the DCCA network of commodity future markets and explores its proximity to the volatility spillover network. Results show a moderate agreement between the two networks. Centrality measures applied to the DCCA networks are able to identify key commodity futures that are transmitting or receiving risk spillovers. The evolution of the DCCA network reveals a significant change in the network structure during the COVID-19 pandemic in comparison to that of the pre- and post-pandemic periods. The pandemic made the commodity future markets more interconnected leading to a shorter diameter for the network. The intensified connections happen mostly between commodities from different categories. Accordingly, cross-category risk spillovers are more likely to happen during the pandemic. The analysis enriches the applications of the DCCA approach and provides useful insights into understanding the risk dynamics in commodity future markets.

Introduction

Financial markets play a critical role in economic development but have been severely threatened by a wide range of socio-economic events in recent decades, such as the subprime mortgage crisis in 2008, the US–China trade war, and the COVID-19 pandemic [1–3]. Rich and in-depth investigations into these events have demonstrated that the risks not only influence each individual entity in the system but also spread among the entities and evolve into system-wide crises. In other words, the entities in a financial market are interdependent on each other, forming a complex networked system that enables the contagion of risks through the interdependencies [4–6]. Financial systems are thus normally modeled as networks, such as the networks of financial institutions [7, 8], the network of stock indices [9], and the network of commodity futures [10]. The key technique for the construction of a financial network is the quantification of the interdependencies among individual entities. However, for many financial systems (e.g., stock market and future market), such interdependencies between entities (e.g., stock indices and commodity futures) cannot be directly observed. To quantify the pair-wise and system-wise connectedness is accordingly vital to the understanding of the dynamics of risk contagion in financial systems.

In the literature on the volatility spillover effect, connectedness is normally explored as the extent to which a shock in one entity’s time series (e.g., stock price and return) could lead to changes in other entities [11, 12]. Techniques based on vector auto-regression (VAR) are widely applied to study such a problem, and various measures have been accordingly developed. One of the most acknowledged metric frameworks is proposed by Diebold and Yilmaz [13–15]. Instead of studying the spillover effect from one time series to another, they apply variance decomposition to an N-variable VAR. Accordingly, the share of the forecast error variation for a target time series from each of the other time series in the system can be quantified simultaneously. The pair-wise spillover effect is thus directly measured by the results of variance decomposition. Since such a spillover effect is regarded as directional, the ability of an entity to transmit risks can be quantified by totaling the spillover effect from it to all others (out-degree), while the extent of an entity being influenced by others can be quantified by totaling the spillover effect received by the entity (in-degree). Such a method and its variations have been applied to construct and analyze a wide range of financial networks. For example, Yang and Zhou constructed a time-varying volatility spillover network of countries according to the VIX of several major national stock market indices and uncovered the central role of the US market [16]. The spillover effect from the US market to others has intensified since the 2008 global financial crisis. Balcilar et al. investigated the spillover effect among the prices of agricultural futures and crude oil futures and identified two sets of commodity futures to be risk transmitters and risk receivers, respectively [17]. Shen et al. explored the connectedness of different economic sectors in China and found that the sectors such as mechanical equipment act as risk transmitters, while sectors such as banking are the main risk takers [18]. Overall, the variance decomposition framework based on the VAR model has shown effectiveness in representing the volatility spillover effect in financial systems.

Given the nature of financial markets as complex systems, the interdependencies among financial entities have also caught widespread attention in the field of econophysics and complexity science. The detrended cross-correlation analysis (DCCA) [19, 20] has been the most acknowledged and applied technique in the analysis of cross-correlations between financial time series, such as commodity future prices [21, 22] and stock trading volumes or prices [23, 24]. Since there could potentially be cross-correlations between any two financial time series, financial markets can thus be linked into networks [25–27]. The analysis of DCCA networks also has the potential to measure the importance of each individual entity in the whole system. For example, Pereira et al. applied centrality measures of weighted degree and PageRank to the DCCA network of 20 regional stock markets and concluded that European markets play a central role in the world’s financial markets [28]. Mbatha and Alovokpinhou constructed the network of 134 companies from the South African stock market and found that the financial industry plays the most prominent role [29].

When the VAR-based methods characterize the directional relationship that a shock in one time series leads to the volatility change in another time series within a given lag time, the DCCA approach describes the bilateral relationship of co-fluctuation of two time series. In spite of the widespread applications of the DCCA approach in investigating the dynamics of financial networks [8, 27–32], whether, or to what extent, can such an approach represent the volatility spillover effect as indicated by the VAR-based measures is still unclear. The exploration of such a research question is crucial to deepen the understanding of the dynamics of complex financial systems, as well as enrich the application of the DCCA approach.

Focusing on the commodity future market, this article applies both the VAR-based volatility spillover measures and the DCCA coefficient to construct networks of the 19 commodities. Two research questions are thereby explored: 1) to what extent can the DCCA network depict the volatility spillover effect among commodity futures; and 2) how is the DCCA network of commodity futures evolving over time. Centrality measures are applied to the DCCA network, which are found with high effectiveness to identify the key risk takers, while moderate effectiveness to uncover key risk transmitters. Further dynamical analysis of the DCCA network reveals the dramatic impact of COVID-19 on the topology of the DCCA network with intensified cross-category risk spillovers.

Materials and methods

Detrended cross-correlation analysis

The fluctuation of a wide range of real-world time series is found with strong scaling behavior, and the detrended fluctuation analysis (DFA) is proposed to analyze such a phenomenon [33, 34]. Given a time series $x_t,t=\mathit{1},\cdots ,N$, its profile time series is thus $X\left(t\right)={\displaystyle \sum }_{k=\mathit{1}}^t\left(x_k-\overline{x}\right)$, where $\overline{x}$ is the mean value of the original time series. To assess the local trends, the profile time series is further divided into small intervals with an equal size of $s$. Accordingly, this results in $N_s=int\left(N/s\right)$ intervals. The local trend of each interval can be quantified by applying an ordinary least square regression, resulting in a fitted time series $X_f\left(t\right)$. The detrended fluctuations can thus be represented as a new time series by subtracting the local trend from the profile time series, i.e., $X\left(t\right)-X_f\left(t\right)$. The detrended fluctuation of the original time series $x_t$ can be written as a function of the window size $s$, which reads

$F_{DFA}\left(x,s\right)=\sqrt{\frac{\mathrm{1}}{N}{\displaystyle \sum }_{i=\mathrm{1}}^N{\left[X\left(t\right)-X_f\left(t\right)\right]}^{\mathrm{2}}.}(1)$

Normally, the relationship between the detrended fluctuation and the window size follows a power-law, that is, $F_{DFA}\left(x,s\right)\propto s^{\alpha }$. The scaling exponent $\alpha$ is normally used to describe the long-range auto-correlation of the time series.

While DFA deals with the fluctuations of a single time series, the DCCA approach is proposed to investigate the co-fluctuation of two time series [19, 20]. For the scenario of two time series, say, $x_t$ and $y_t$, the same process in DFA can be applied to each of the time series, to obtain the profile time series $X\left(t\right)$ and $Y\left(t\right)$, and the fitted local trends $X_f\left(t\right)$ and $Y_f\left(t\right)$. Instead of the fluctuation of a single time series, the co-fluctuation of the two time series can be accordingly calculated as

$F_{DCCA}^{\mathit{2}}\left(xy,s\right)=\frac{\mathit{1}}{N}{\displaystyle \sum }_{i=\mathrm{1}}^N\left[X\left(t\right)-X_f\left(t\right)\right]\left[Y\left(t\right)-Y_f\left(t\right)\right].(2)$

Similar to DFA, the co-fluctuation of the two time series is also expected to follow a power-law relationship with the window size, i.e., $F_{DCCA}\left(xy,s\right)\propto s^{\alpha }$. If the scaling exponent $\alpha$ takes a nonzero value, a long-range cross-correlation can be concluded between the time series. To obtain a more generalized value to capture the cross-correlation between the time series, the DCCA coefficient can be defined as

${\rho }_{DCCA}\left(xy,s\right)=\frac{F_{DCCA}^{\mathrm{2}}\left(xy,s\right)}{F_{DFA}\left(x,s\right)\cdot F_{DFA}\left(y,s\right)}.(3)$

The DCCA coefficient ${\rho }_{DCCA}$ takes values ranging from -1 to 1, with -1 indicating the perfect anti-cross-correlation, 1 indicating the perfect cross-correlation, and 0 indicating no cross-correlation. When the window size $s$ is a free parameter, we set $s=\mathit{16}$ throughout the following analysis.

Measures for the volatility spillover

While a number of measures have been proposed to characterize the connectedness and volatility spillover effect in financial systems, this article adopts a widely used approach developed by Diebold and Yilmaz [13–15].

Considering a set of $K$ variables (time series) with $V_t={\left(v_{\mathrm{1},t},v_{\mathrm{2},t},\cdots ,v_{K,t}\right)}^{\prime }$ as the vector of variables at a time, each time series is thus $V\left(k\right)=\left\{v_{k,t}\right\},t=\mathrm{1,2},\cdots ,N$. The system can be described by a $K$-variable VAR model as $V_t={\Theta }_{\mathrm{1}}{V}_{t-\mathrm{1}}+{\Theta }_{\mathrm{2}}{V}_{t-\mathrm{2}}+\cdots +{\Theta }_l{V}_{t-l}+{ϵ}_t$, where ${\Theta }_{\mathrm{1}},\cdots {\Theta }_l$ are parameter matrices, ${ϵ}_t$ is the vector of white noise, and $l$ is the time lag. In other words, each variable is modeled as a function of the $l$ lags of its own as well as all the other variables in the system. A moving average representation for the model can be given by

$V_t={\displaystyle \sum }_{i=\mathrm{0}}^{\infty }{A}_i{ϵ}_{t-i},(4)$

where $A_i={\Theta }_{\mathrm{1}}{A}_{i-\mathrm{1}}+{\Theta }_{\mathrm{2}}{A}_{i-\mathrm{2}}+\cdots +{\Theta }_l{A}_{i-l}$ is a $K\times K$ coefficient matrix with $A_{\mathit{0}}$ as an identity matrix and $A_i=\mathrm{0}$ for $i<\mathrm{0}$ . According to the moving average representation, $H$-step-ahead forecast error variance decomposition can be calculated and denoted as ${\Pi }^H=\left[{\pi }_{ij}^H\right]$, where $H=\mathrm{1,2},\cdots$ is the predictive horizon. The element ${\pi }_{ij}^H$ depicts the fraction of time series $V\left(i\right)$’s forecast error variance caused by the shock in time series $V\left(j\right)$ , which can be written as

${\pi }_{ij}^H={\psi }_{jj}^{-\mathrm{1}}\frac{{\displaystyle \sum }_{h=\mathrm{0}}^{H-\mathrm{1}}\left(e_i^{\prime }{A}_h\mathrm{\Psi }{e}_j\right)}{{\displaystyle \sum }_{h=\mathrm{0}}^{H-\mathrm{1}}\left(e_i^{\prime }{A}_h\mathrm{\Psi }{A_h^{\prime }e}_j\right)},(5)$

where $\Psi$ is the covariance matrix for the vector of errors $ϵ$, ${\psi }_{jj}^{-\mathrm{1}}$ is the $j$th diagonal element in matrix $\Psi$, and $e_i$ is a vector with only the $i$th value being 1 while others being 0. The value ${\pi }_{ij}^H$ can thus be used to quantify the spillover effect from a shock in time series $V\left(j\right)$ to time series $V\left(i\right)$, i.e., the directional connectedness from $j$ to $i$. Such a value can be further normalized as

${\stackrel{\sim }{\pi }}_{ij}^H=\frac{{\pi }_{ij}^H}{{\displaystyle \sum }_{k=\mathrm{1}}^K{\pi }_{ik}^H}.(6)$

Accordingly, for each time series $V\left(i\right)$, the summation of the connectedness from other time series equals 1, i.e., ${\displaystyle \sum }_j{\stackrel{\sim }{\pi }}_{ij}^H=\mathrm{1},\forall i$.With the directional connectedness defined, the $K$ time series can be linked as a directed volatility spillover network, where each node is a time series (a financial entity) and each weighted and directed link describes the relative intensity of the spillover effect. Diebold and Yilmaz further defined several measures for node-level connectedness, including to-connectedness and from-connectedness [13–15]. The to-connectedness is defined as

$C_i^{to}={\displaystyle \sum }_{j=\mathrm{1},j\ne i}^K{\stackrel{\sim }{\pi }}_{ij}^H,(7)$

which corresponds to the out-degree of $i$ in the spillover network describing the total spillover effect transmitted by $i$ to others. Similarly, the from-connectedness is defined as

$C_i^{from}={\displaystyle \sum }_{j=\mathrm{1},j\ne i}^K{\stackrel{\sim }{\pi }}_{ji}^H,(8)$

which is basically the in-degree of $i$ in the spillover network describing the total spillovers received by $i$.

Throughout the analysis, we set the predictive horizon to $H=\mathit{5}$, i.e., the volatility spillover effects are calculated based on the $\mathit{5}$-step-ahead forecast error.

Data collection

The future market has been one of the major financial systems that attracted widespread attention in the literature, where strong spillover effects have been frequently uncovered [34, 35]. Meanwhile, the DCCA approach has also found applications in characterizing the cross-correlation among different future markets [21, 22, 36]. The present study thereby adopts the future market as the detailed context to explore the proximity of the DCCA network to the volatility spillover effect and the dynamics of the commodity future network.

Given the purpose of the present analysis, we mainly focus on the commodity contracts in the US market. The various commodities can be divided into five major categories, namely, metals, softs, energy, meats, and grain. While there are normally many commodity futures in each category, here we only consider the commodity futures that are most traded for each category. To be more specific, gold, copper, and silver are selected for metal future contracts; coffee, sugar, orange juice, and cocoa are selected for soft crop future contracts; crude oil, natural gas, heating oil, and gasoline are selected for energy future contracts; live cattle, lean hogs, and feeder cattle are selected for meat future contracts; and rough rice, soybean oil, soybean meal, corn, and oats are selected for grain future contracts. The detailed data were downloaded from Thomson Reuters Datastream, which is a live database for various financial systems. Our data span 9 years, from 1 January 2013 to 31 December 2021. For each trading day, we collect the open, high, low, and close indexes. In other words, the time series to be analyzed are the 9-year-long daily prices of 19 commodity futures.

Results

Static analysis

We first construct and analyze the volatility spillover network and DCCA network using the full 9-year data. Both networks consist of 19 nodes, with each being one commodity future market. The networks are fully connected with different weights on links. The weight of a link in the DCCA network is the absolute value of the cross-correlation coefficient $w_{ij}=\left|{\rho }_{DCCA}\left(ij\right)\right|$ between two commodity futures’ time series of daily close price, $c_t$. In other words, we consider the intensity of the cross-correlation, regardless of its direction. For the volatility spillover network, we first calculate the close-to-close volatility of commodity future price in each week $t$ as ${\sigma }_t=\sqrt{\frac{\mathrm{1}}{T}{\displaystyle \sum }_{i=\mathrm{1}}^T{\left(r_i-\overline{r}\right)}^{\mathrm{2}}}$, where $T$ is the trading days in the week, and $r_i=\log \left(c_i/c_{i-\mathrm{1}}\right)$ is the return of the $i$th day in the week. The variance decomposition is applied to the close-to-close volatility of commodity future prices. The pair-wise connectedness value ${\stackrel{\sim }{\pi }}_{ij}$, as calculated by Eq. 6, is thus regarded as the weight for the link from commodity $i$ to commodity $j$.

As shown in Figure 1, the spillover network and DCCA network of the 19 commodity futures show similar structures, in spite of the fact that the former is directed while the latter is undirected. Energy futures of crude oil, heating oil, and gasoline form a strongly connected triad in both networks. The metal futures of copper, silver, and gold are also closely interconnected. On the other hand, the soft futures, including orange juice, sugar, cocoa, and coffee, are loosely connected to others in either the spillover network or the DCCA network. To get a more generalized quantification of the similarity between the cross-correlation and spillover effect, we calculate the Pearson correlation coefficient between the values of $w_{ij}$ and ${\stackrel{\sim }{\pi }}_{ij}$. The analysis shows that the weights on the matched links from two networks have a correlation of 0.511 ($p=\mathrm{4.107}\times {\mathrm{10}}^{-\mathrm{24}}$), indicating a moderate positive correlation. Thus, the DCCA coefficient between the future prices of two commodities can, to a moderate degree, depict the directed volatility spillover effect. Despite the different underlying logics, the two measures, namely, the DCCA coefficient and volatility spillover, depict the relationship between two time series’ fluctuations. Accordingly, if the volatility of one time series largely influences that of another time series (large value for the spillover), the two time series would tend to co-fluctuate regardless of the time lag, resulting in a strong cross-correlation. However, the volatility spillover is directed and considers not only the two time series but also all the time series in the system. As a consequence, the correlation between the DCCA coefficient and volatility spillover is only moderate but significant.

FIGURE 1

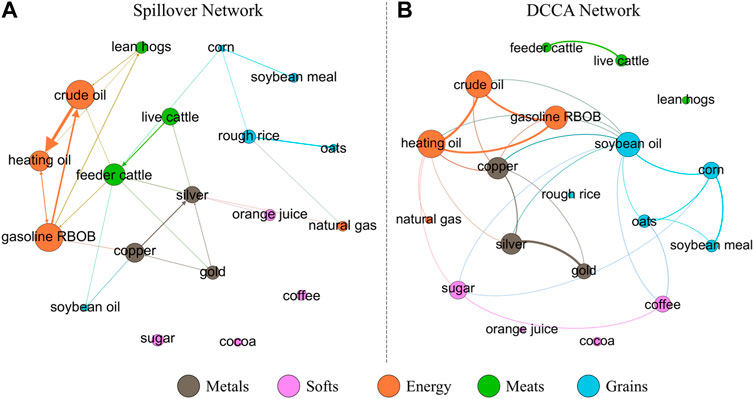
FIGURE 1. Volatility spillover network (A) and DCCA network (B) of 19 commodity futures. The links in the spillover network are directed, and only those with a weight of ${\stackrel{\sim }{\pi }}_{ij}>\mathit{0.15}$ are displayed. The links in the DCCA network are undirected, and all the links with $w_{ij}>\mathit{0.2}$ are displayed. The node size in both networks is proportional to the degree (out-degree for the spillover network).

The volatility spillovers are actually directed, and thus the risk transmitters and risk receivers can be identified by the spillover network via the measures of to-connectedness (out-degree) and from-connectedness (in-degree), respectively. However, the DCCA coefficient is bilateral with no direction. An apparent question is whether the DCCA network of commodities can help to identify the key risk transmitters and risk receivers. Here, we further apply four basic centrality measures to the DCCA network to examine the accuracy of predicting the risk transmitters and risk receivers.

Since the links in the DCCA network are weighted, the degree centrality of a commodity $i$ is thus ${DC}_i={\displaystyle \sum }_{j\ne i}{w}_{ij}$. The eigenvector centrality not only considers the number of neighbors of a node but also evaluates the importance of the neighbors. Thus, the eigenvector centrality of a commodity $i$ can be calculated as the weighted average of the centrality values of its neighbors, i.e., $E{C}_i=\frac{\mathit{1}}{\lambda }{\displaystyle \sum }_{j\ne i}{w}_{ij}\cdot E{C}_j$, where $\lambda$ is the largest eigenvalue of the adjacency matrix $P=\left\{w_{ij}\right\}$. The closeness centrality of a commodity is the average value of its shortest distance to each other commodity. While the DCCA network is weighted, the length of a link is assumed to be the reciprocal of the weight, i.e., $\mathit{1}/w_{ij}$. The distance between two commodities $i$ and $j$, denoted with $d_{ij}$, is thus the summation of length for the shortest path connecting $i$ and $j$, which has the minimal value. Note that, although the network is fully connected, the shortest path is not necessarily the direct link connecting the two commodities. Accordingly, the closeness centrality for $i$ can be calculated as $C{C}_i=\left(K-\mathit{1}\right)/{\displaystyle \sum }_{j\ne i}{d}_{ij}$, where $K$ is the number of commodities in the DCCA network. The PageRank centrality also assumes a node’s importance to be determined by its neighbors. The centrality value can be achieved via an iterative process. At the initial step, each node has a centrality value $P{C}_i\left(t=\mathit{0}\right)=\mathit{1}$. For each following step, the centrality value updates as $P{C}_i\left(t\right)={\displaystyle \sum }_{j\ne i}{w}_{ij}\cdot \frac{P{C}_j\left(t-\mathit{1}\right)}{D{C}_j}$. The eventually stabilized values are then regarded as the PageRank centrality of a commodity node.

We apply the four centrality measures to the constructed DCCA network of commodity future markets to calculate the centralities for each commodity. To test the ability of these centrality measures in identifying the risk transmitters (to-connectedness, as defined in Eq. 7) and risk receivers (from-connectedness, as defined in Eq. 8), we calculate the Pearson correlation coefficients which are reported in Table 1. For the to-connectedness, i.e., the spillovers transmitted by a commodity to others, the centrality measures of degree, eigenvector, and PageRank show moderate accuracies with correlations ranging from 0.479 to 0.549. However, the closeness centrality has a very low correlation of 0.225 to the to-connectedness of commodities. For the from-connectedness, i.e., the spillovers received by a commodity, these centrality measures show higher accuracies. In other words, the centrality measures, including degree, eigenvector, and PageRank, applied to the DCCA network are strongly correlated to the from-connectedness while moderately correlated to the to-connectedness.

TABLE 1

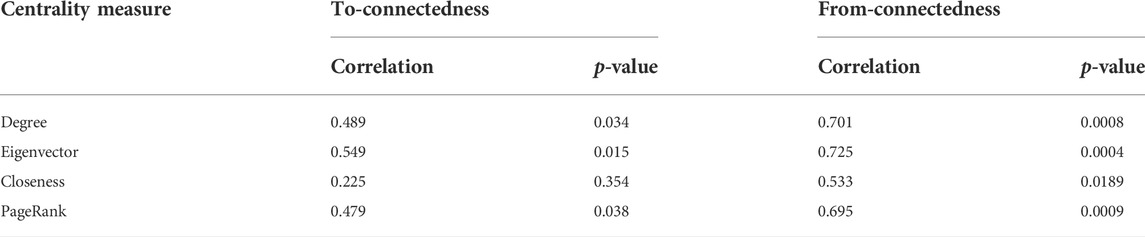
TABLE 1. Pearson correlation coefficients between the centrality measures in the DCCA network and spillover effects, as measured by to-connectedness $C_i^{to}$ and from-connectedness $C_i^{from}$, respectively.

We also compare the most important top five commodities as identified by different measures, as shown in Table 2. According to the volatility spillover effect, the energy futures, including heating oil, crude oil, and gasoline, are the key risk transmitters and at the same time risk receivers. These commodities are also identified by degree centrality, eigenvector centrality, and PageRank centrality as the most influential node in the DCCA network. However, differences between the spillover network and the DCCA network can also be observed. While feeder cattle are also an important risk transmitter and risk receiver, centrality measures in DCCA failed to uncover such an important role. In contrast, soybean oil is evaluated to be an imported commodity in the DCCA network, but it does not transmit nor receive much spillover effect. Despite the different focuses on the two approaches, the DCCA network can be used to identify the key risk transmitters and risk receivers with moderate accuracy.

TABLE 2

TABLE 2. Top five commodity future markets with the highest values for to-connectedness $C_i^{to}$, from-connectedness $C_i^{from}$, degree centrality $D{C}_i$, eigenvector centrality $E{C}_i$, closeness centrality $C{C}_i$, and PageRank centrality $R{C}_i$.

Dynamics of the DCCA network

We further analyze how the DCCA network of commodity future markets has evolved over the past 9 years by constructing a DCCA network for each year. Figure 2 visualizes the DCCA network for 2013, 2017, and 2020, respectively. Intuitively, the cross-correlations among commodities are becoming stronger, and thus the DCCA network gets more connected over the years.

FIGURE 2

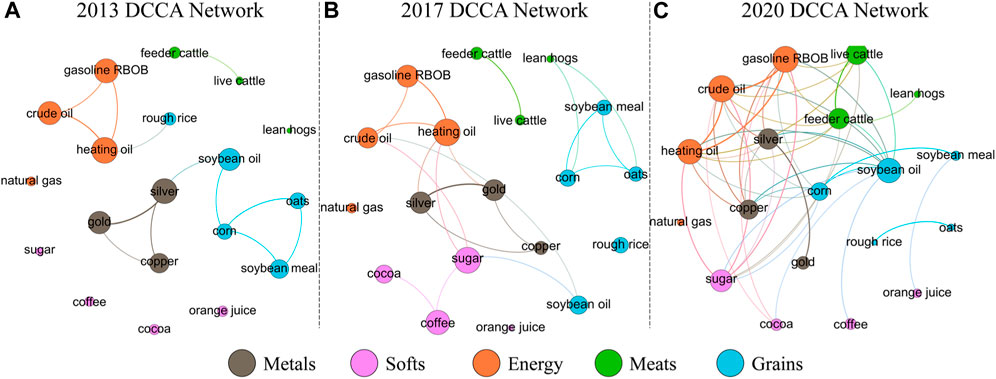
FIGURE 2. DCCA networks of the commodity futures markets in 2013 (A), 2017 (B), and 2020 (C) respectively. Only links with a weight larger than 0.35 are displayed, and the node size is proportional to the degree

To quantitatively explore the dynamics of the network, we focus on four structural features, namely, the average weight, average distance, clustering coefficient, and category modularity. The average weight of the DCCA network is calculated as $W=⟨w_{ij}⟩$, which describes the connectedness of the network. The average distance of the DCCA network is calculated as $D=⟨d_{ij}⟩$, measuring how easy it is for the nodes to reach each other. The clustering coefficient of a node describes how strongly its neighbors are connected to each other. Following the definition proposed by Saramäki et al. [37], the clustering coefficient is calculated as $clusterin{g}_i=\frac{\mathit{1}}{K\left(K-\mathit{1}\right)}{\displaystyle \sum }_{j,k,j\ne k}{\left({\widehat{w}}_{ij}{\widehat{w}}_{ik}{\widehat{w}}_{jk}\right)}^{\mathit{1}/\mathit{3}}$, where ${\widehat{w}}_{ij}=w_{ij}/\max \left(w\right)$. The clustering coefficient of the DCCA network is averaged over that of every node, i.e., $C=⟨clusterin{g}_i⟩$. Since the 19 commodities considered in the present study come from five different categories, we measure the extent to which the links connect commodities within the same category. Following the modularity measure proposed for the community structure in networks [38], we define the category modularity in the commodity network as $Q=\frac{{\displaystyle \sum }_{ij}{a}_{ij}{w}_{ij}}{{\displaystyle \sum }_{ij}{w}_{ij}}$, where $a_{ij}=\mathit{1}$ if the two commodities $i$ and $j$ subject to the same category, and $a_{ij}=\mathit{0}$ otherwise.

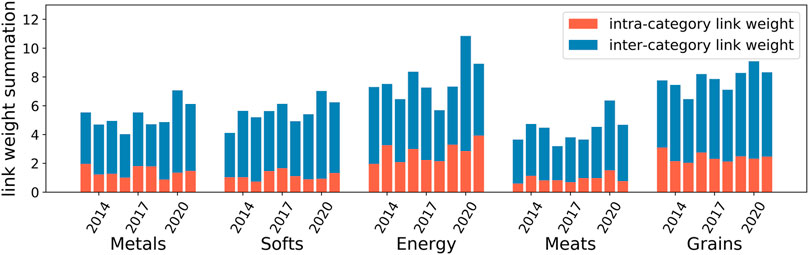
As shown in Figure 3, the connectedness of the DCCA network, i.e., the average weight, has remained at a relatively stable level ranging from 0.15 to 0.18 during the period from 2013 to 2019. However, the connectedness dramatically increased to 0.236 in 2020. Such a result indicates that the COVID pandemic that broke out at the end of 2019 significantly affected the commodity future markets, making them more strongly interconnected. Due to the intensified connections among the commodities, the average distance of the DCCA network decreased, meaning that it becomes easier for risks to spread from one commodity future market to another. Meanwhile, the clustering coefficient largely increased in 2020, indicating that strong triadic cross-correlations are formed under the impact of the pandemic. The overall category modularity saw a dramatic decrease in 2020, that is, the ratio of intra-category links over all links has decreased.

FIGURE 3

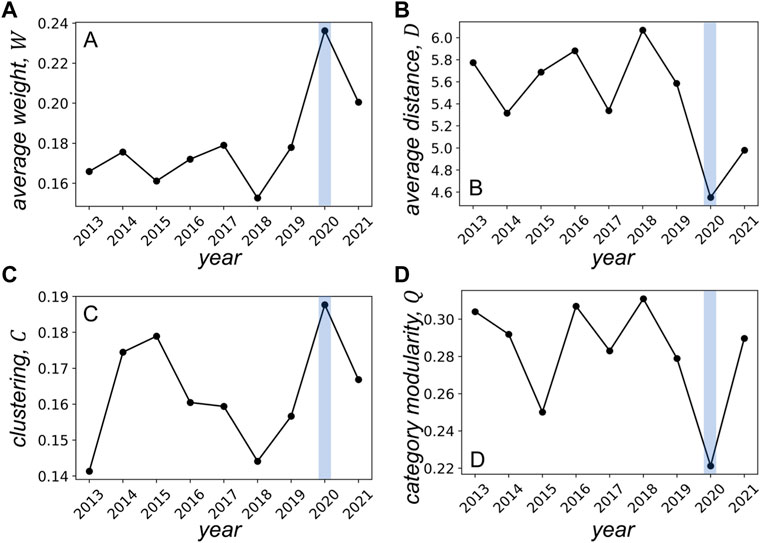
FIGURE 3. Average weight (A), average distance (B), clustering coefficient (C), and category modularity (D) of the yearly DCCA network of commodity future markets.

To have a closer examination of the dynamics of connection patterns in the DCCA network, we investigate how the intra-category links and inter-category links for each category of commodities are evolving. For each category of commodities $c$, we compare the intra-category link weight summation $S_c^{intra}={\displaystyle \sum }_{i\in {\Gamma }_c,j\in {\Gamma }_c,i\ne j}{w}_{ij}$, where ${\Gamma }_c$ is the set of commodities of category $c$ and the inter-category link weight summation $S_c^{inter}={\displaystyle \sum }_{i\in {\Gamma }_c,j\notin {\Gamma }_c}{w}_{ij}$, which are reported in Figure 4. In addition the differences among different categories, the evolutions of intra- and inter-category links also show different patterns. Despite the fluctuations, the intra-category link weight summation $S_c^{intra}$ has remained at a stable level for each category. Even in 2020, there is no significant change in the value of $S_c^{intra}$. On the other hand, the inter-category link weight summation $S_c^{inter}$ increased in 2020, especially for the category of energy and meat. As such, the increase in average cross-correlations, reported in Figure 3A, majorly comes from the inter-category links. This is also the reason for the decrease in category modularity.

FIGURE 4

FIGURE 4. Stacked bar plot for yearly weight summation of intra- and inter-category links.

Despite the dramatic impact the pandemic has made on the connectedness of the DCCA network of commodity future in 2020, such impact does not maintain. As reported in Figure 3, all the network features recovered, to some extent, from the pandemic’s impact in 2021, especially for the clustering (Figure 3C) and category modularity (Figure 3D), the 2021 network shows very similar values as compared to the pre-pandemic networks. The average weight (Figure 3A) and average distance (Figure 3B) of the 2021 network are also not as dramatic as that of 2020. Such recovery of the network structure is partially because of the ease of the pandemic situation in 2021 and also indicates that the extreme external events normally would only make a temporary impact on financial markets.

Conclusion and discussion

Risk spreading in complex financial systems has been widely acknowledged to be central to the understanding of the system dynamics. Different streams of research have developed various approaches to construct networks of financial systems, including the VAR-based approach which measures the extent to which the shock in one financial market influences another with a given time lag, and the DCCA-based approach which measures the comovement of fluctuations between two financial time series. The present article offers a comparison between the networks of commodity future markets constructed by such two streams of approach. The cross-correlation is found with moderate proximity to the spillover network. The centrality measures applied to the DCCA network, including degree, eigenvector, and PageRank, are able to identify risk transmitters and risk receivers. The results indicate the effectiveness of the DCCA network in characterizing the structure of the volatility spillover effect. The cross-correlations among financial time series can thus also serve as an important approach for investors to monitor the risks in financial systems and develop appropriate investment strategies accordingly. However, the DCCA network is not always accurate. For example, soybean oil is identified by the DCCA network as one of the most important commodity future markets, but it is not a key risk transmitter nor a risk receiver. Thus, the difference between the cross-correlation and volatility spillover effect should be considered in the application of DCCA when investigating risk dynamics in financial systems.

The COVID-19 pandemic is revealed to be influential on the connectedness of the commodity future markets. The DCCA network of 2020 is found with stronger average cross-correlations, shorter average distance, and stronger clustering features. In particular, it is found that the cross-correlations between commodities from the same category did not change much, while that between commodities from different categories have become stronger in 2020. Such a result suggests a higher risk of cross-category spillover during the pandemic. This observation is in line with previous findings that financial systems tend to have stronger connectedness during a wide range of extreme external events such as financial crises and pandemics [16, 17]. Thus, investors should be cautious about the intensified risk contagions among commodity future markets during extreme events, especially the cross-category risk spillovers. An interesting observation in this article is that the average degree, average distance, clustering, and category modularity in the 2021 network began to recover to almost the level of pre-pandemic. However, due to the limited time range of the applied data, the present article is unable to track the recovery dynamics of the network of commodity future markets. Future research shall further explore the mechanism and timeliness of the recovery process of financial networks after dramatic structural changes caused by external events.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

Both authors contributed to the study design, data collection, data analysis, and writing.

Funding

The study was partially supported by the Social Science Fund of Jiangsu Province (Grant No. 21TQC005) and the Social Science Foundation of the Jiangsu Higher Education Institutions (Grant No. 2021SJA0164).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Schweitzer F, Fagiolo G, Sornette D, Vega-Redondo F, Vespignani A, White DR. Economic networks: The new challenges. Science (2009) 325(5939):422–5. doi:10.1126/science.1173644

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhang D, Hu M, Ji Q. Financial markets under the global pandemic of COVID-19. Financ Res Lett (2020) 36:101528. doi:10.1016/j.frl.2020.101528

PubMed Abstract | CrossRef Full Text | Google Scholar

3. An J, Mikhaylov A, Richter UH. Trade war effects: Evidence from sectors of energy and resources in Africa. Heliyon (2020) 6(12):e05693. doi:10.1016/j.heliyon.2020.e05693

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Allen F, Gale D. Financial contagion. J Polit Econ (2000) 108(1):1–33. doi:10.1086/262109

CrossRef Full Text | Google Scholar

5. Gai P, Kapadia S. Contagion in financial networks. Proc R Soc A (2010) 466(2120):2401–23. doi:10.1098/rspa.2009.0410

CrossRef Full Text | Google Scholar

6. Jackson MO, Pernoud A. Systemic risk in financial networks: A survey. Annu Rev Econ (2021) 13:171–202. doi:10.1146/annurev-economics-083120-111540

CrossRef Full Text | Google Scholar

7. Elyasiani E, Kalotychou E, Staikouras SK, Zhao G. Return and volatility spillover among banks and insurers: Evidence from pre-crisis and crisis periods. J Financ Serv Res (2015) 48(1):21–52. doi:10.1007/s10693-014-0200-z

CrossRef Full Text | Google Scholar

8. Wang GJ, Yi S, Xie C, Stanley HE. Multilayer information spillover networks: measuring interconnectedness of financial institutions. Quant Finance (2021) 21(7):1163–85. doi:10.1080/14697688.2020.1831047

CrossRef Full Text | Google Scholar

9. Heiberger RH. Stock network stability in times of crisis. Physica A: Stat Mech its Appl (2014) 393:376–81. doi:10.1016/j.physa.2013.08.053

CrossRef Full Text | Google Scholar

10. Xiao B, Yu H, Fang L, Ding S. Estimating the connectedness of commodity futures using a network approach. J Futures Markets (2020) 40(4):598–616. doi:10.1002/fut.22086

CrossRef Full Text | Google Scholar

11. Akkoc U, Civcir I. Dynamic linkages between strategic commodities and stock market in Turkey: Evidence from SVAR-DCC-GARCH model. Resour Pol (2019) 62:231–9. doi:10.1016/j.resourpol.2019.03.017

CrossRef Full Text | Google Scholar

12. Jung RC, Maderitsch R. Structural breaks in volatility spillovers between international financial markets: Contagion or mere interdependence? J Banking Finance (2014) 47:331–42. doi:10.1016/j.jbankfin.2013.12.023

CrossRef Full Text | Google Scholar

13. Diebold FX, Yilmaz K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ J (2009) 119(534):158–71. doi:10.1111/j.1468-0297.2008.02208.x

CrossRef Full Text | Google Scholar

14. Diebold FX, Yilmaz K. Better to give than to receive: predictive directional measurement of volatility spillovers. Int J Forecast (2012) 28(1):57–66. doi:10.1016/j.ijforecast.2011.02.006

CrossRef Full Text | Google Scholar

15. Diebold FX, Yılmaz K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J Econom (2014) 182(1):119–34. doi:10.1016/j.jeconom.2014.04.012

CrossRef Full Text | Google Scholar

16. Yang Z, Zhou Y. Quantitative easing and volatility spillovers across countries and asset classes. Manage Sci (2017) 63(2):333–54. doi:10.1287/mnsc.2015.2305

CrossRef Full Text | Google Scholar

17. Balcilar M, Gabauer D, Umar Z. Crude Oil futures contracts and commodity markets: New evidence from a TVP-VAR extended joint connectedness approach. Resour Pol (2021) 73:102219. doi:10.1016/j.resourpol.2021.102219

CrossRef Full Text | Google Scholar

18. Shen YY, Jiang ZQ, Ma JC, Wang GJ, Zhou WX. Sector connectedness in the Chinese stock markets. Empir Econ (2022) 62(2):825–52. doi:10.1007/s00181-021-02036-0

CrossRef Full Text | Google Scholar

19. Podobnik B, Stanley HE. Detrended cross-correlation analysis: a new method for analyzing two nonstationary time series. Phys Rev Lett (2008) 100(8):084102. doi:10.1103/physrevlett.100.084102

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zebende GF. DCCA cross-correlation coefficient: Quantifying level of cross-correlation. Physica A: Stat Mech its Appl (2011) 390(4):614–8. doi:10.1016/j.physa.2010.10.022

CrossRef Full Text | Google Scholar

21. Liu L. Cross-correlations between crude oil and agricultural commodity markets. Physica A: Stat Mech its Appl (2014) 395:293–302. doi:10.1016/j.physa.2013.10.021

CrossRef Full Text | Google Scholar

22. Wang J, Shao W, Kim J. Analysis of the impact of COVID-19 on the correlations between crude oil and agricultural futures. Chaos Solitons Fractals (2020) 136:109896. doi:10.1016/j.chaos.2020.109896

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Podobnik B, Horvatic D, Petersen AM, Stanley HE. Cross-correlations between volume change and price change. Proc Natl Acad Sci U S A (2009) 106(52):22079–84. doi:10.1073/pnas.0911983106

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Pan Y, Hou L, Pan X. Interplay between stock trading volume, policy, and investor sentiment: A multifractal approach. Physica A: Stat Mech its Appl (2022) 603:127706. doi:10.1016/j.physa.2022.127706

CrossRef Full Text | Google Scholar

25. Adam AM, Kyei K, Moyo S, Gill R, Gyamfi EN. Multifrequency network for SADC exchange rate markets using EEMD-based DCCA. J Econ Finan (2022) 46(1):145–66. doi:10.1007/s12197-021-09560-w

CrossRef Full Text | Google Scholar

26. Li J, Shi Y, Cao G. Topology structure based on detrended cross-correlation coefficient of exchange rate network of the belt and road countries. Physica A: Stat Mech its Appl (2018) 509:1140–51. doi:10.1016/j.physa.2018.06.059

CrossRef Full Text | Google Scholar

27. Ferreira P, Tilfani O, Pereira E, Tavares C, Pereira H, El Boukfaoui MY. Dynamic connectivity in a financial network using time-varying DCCA correlation coefficients. Econometric Res Finance (2021) 6(1):57–75. doi:10.2478/erfin-2021-0004

CrossRef Full Text | Google Scholar

28. Pereira E, Ferreira P, da Silva M, Miranda J, Pereira H. Multiscale network for 20 stock markets using DCCA. Physica A: Stat Mech its Appl (2019) 529:121542. doi:10.1016/j.physa.2019.121542

CrossRef Full Text | Google Scholar

29. Mbatha VM, Alovokpinhou SA. The structure of the South African stock market network during COVID-19 hard lockdown. Physica A: Stat Mech its Appl (2022) 590:126770. doi:10.1016/j.physa.2021.126770

CrossRef Full Text | Google Scholar

30. Wang GJ, Xie C, ChenYJChen S. Statistical properties of the foreign exchange network at different time scales: evidence from detrended cross-correlation coefficient and minimum spanning tree. Entropy (2013) 15(5):1643–62. doi:10.3390/e15051643

CrossRef Full Text | Google Scholar

31. Shin KH, Lim G, Min S. Dynamics of the global stock market networks generated by DCCA methodology. Appl Sci (2020) 10(6):2171. doi:10.3390/app10062171

CrossRef Full Text | Google Scholar

32. Peng CK, Buldyrev SV, Havlin S, Simons M, Stanley HE, Goldberger AL. Mosaic organization of DNA nucleotides. Phys Rev E (1994) 49(2):1685–9. doi:10.1103/physreve.49.1685

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Hu K, Ivanov PC, Chen Z, Carpena P, Stanley HE. Effect of trends on detrended fluctuation analysis. Phys Rev E (2001) 64(1):011114. doi:10.1103/physreve.64.011114

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Kang SH, McIver R, Yoon SM. Dynamic spillover effects among crude oil, precious metal, and agricultural commodity futures markets. Energy Econ (2017) 62:19–32. doi:10.1016/j.eneco.2016.12.011

CrossRef Full Text | Google Scholar

35. Gong X, Liu Y, Wang X. Dynamic volatility spillovers across oil and natural gas futures markets based on a time-varying spillover method. Int Rev Financial Anal (2021) 76:101790. doi:10.1016/j.irfa.2021.101790

CrossRef Full Text | Google Scholar

36. Zhang S, Guo Y, Cheng H, Zhang H. Cross-correlations between price and volume in China's crude oil futures market: A study based on multifractal approaches. Chaos Solitons Fractals (2021) 144:110642. doi:10.1016/j.chaos.2020.110642

CrossRef Full Text | Google Scholar

37. Saramäki J, Kivelä M, Onnela JP, Kaski K, Kertesz J. Generalizations of the clustering coefficient to weighted complex networks. Phys Rev E (2007) 75(2):027105. doi:10.1103/physreve.75.027105

CrossRef Full Text | Google Scholar

38. Newman ME. Modularity and community structure in networks. Proc Natl Acad Sci U S A (2006) 103(23):8577–82. doi:10.1073/pnas.0601602103

PubMed Abstract | CrossRef Full Text | Google Scholar