Multiparticle quantum walk–based error correction algorithm with two-lattice Bose–Hubbard model

When the evolution of discrete time quantum walk is carried out for particles, the ramble state is prone to error due to the influence of system noise. A multiparticle quantum walk error correction algorithm based on the two-lattice Bose–Hubbard model is proposed in this study. First, two point Bose–Hubbard models are constructed according to the local Euclidean generator, and it is proved that the two elements in the model can be replaced arbitrarily. Second, the relationship between the transition intensity and entanglement degree of the particles in the model is obtained by using the Bethe hypothesis method. Third, the position of the quantum lattice is coded and the quantum state exchange gate is constructed. Finally, the state replacement of quantum walk on the lattice point is carried out by switching the walker to the lattice point of quantum error correction code, and the replacement is carried out again. The entanglement of quantum particles in the double-lattice Bose–Hubbard model is simulated numerically. When the ratio of the interaction between particles and the transition intensity of particles is close to 0, the entanglement operation of quantum particles in the model can be realized by using this algorithm. According to the properties of the Bose–Hubbard model, quantum walking error correction can be realized after particle entanglement. This study introduces the popular restnet network as a training model, which increases the decoding speed of the error correction circuit by about 33%. More importantly, the lower threshold limit of the convolutional neural network (CNN) decoder is increased from 0.0058 under the traditional minimum weight perfect matching (MWPM) to 0.0085, which realizes the stable progress of quantum walk with high fault tolerance rate.

1 Introduction

A quantum walk is one of the effective methods to realize quantum computation [1,2]. However, because of the randomness of quantum walk, it is difficult to correct errors when the particles are affected by system noise during particle evolution. The physical system used in this study is a homogeneous system, which extends the two-lattice Bose–Hubbard model to the Bose–Hubbard model, and the arbitrary replacement of two particles does not lead to a new quantum state of the system [3–6].

A quantum walk algorithm can be implemented on many graph structures, and its function is very significant [7–14]. Also, quantum walks have important applications in quantum cryptography and quantum communication [15,16]. Noise research in the quantum walk algorithm is also one of the key points, and general quantum walk calculation based on the Bose–Hubbard model has been proposed [17,18]. On this basis, the multiparticle quantum walk error correction algorithm based on the two-lattice Bose–Hubbard model is further studied. As early as 2003, Shapira et al. used computer simulation to study the influence of unitary noise on one-dimensional quantum walk and showed the variation of probability distribution of quantum walk under the influence of noise [19]. Also, specific noise types are studied, such as the non-Markov continuous time quantum walk algorithm with dynamic noise [20] and the quantum Bernoulli central limit theorem in the quantum walk algorithm [21]. In 2015, Ambainis et al. improved the potential barrier using the Grover algorithm, improved the amplitude of quantum walking coin state, and reduced the impact of noise during particle quantum walking [21,23]. In 2016, Wang et al. proposed to construct time-varying quantum walking with infinite degrees of freedom by using quantum Bernoulli noise [24]. In 2018, Du et al. constructed quantum gates using the quantum walk algorithm under noise, and the algorithm increased the number of addresses on the graph or the ratio of jump strength to potential could improve the coherence time, thus inhibiting the decoherence [25]. In 2019, Claudia et al. address the use of quantum walks as a quantum probe to characterize defects and perturbations occurring in complex, classical, and quantum networks [26]. These algorithms are designed to reduce the influence of noise on particles during the quantum walk.

Similar to the aforementioned algorithm, a multiparticle quantum walk error correction algorithm is proposed to reduce the influence of noise in the quantum walk. The two-lattice Bose–Hubbard model is constructed for the multiparticle quantum ramble, and it is proved that the quantum state does not change after the displacement of any two particles in the model. Using the encoding method of quantum states mentioned in the study in reference [17], entanglement of quantum states in two lattices is generated by controlling the ratio of transition intensity and interaction between particles [27]. Controlling the ratio of model parameters to generate entanglement is easier than other methods [15,28]. The convolutional neural network decoder has been introduced in detail in the study mentioned in reference [29–33]. In this study, the threshold of the quantum walk error correction circuit has been greatly improved by using the convolution operation of the decoder and the improvement of the training speed. The evolution operator of quantum walk is improved and quantum state error correction is realized. Finally, the advantages and disadvantages of the algorithm are analyzed. Figure 1 shows the core idea of the work.

FIGURE 1

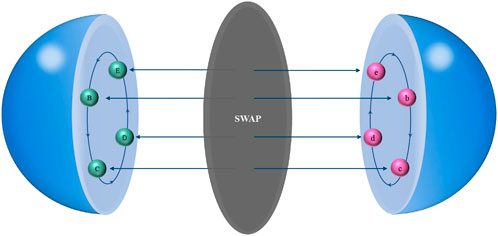
FIGURE 1. In this figure, there are three corresponding layers: the left hemisphere layer is the quantum ramble, right is the error-correcting code, and middle SWAP gate is the exchange gate. The green B → E → B node on the left is the quantum walk process and corresponds to the error correction code of the pink b-e node on the right. When the particles are in a quantum walk, they are swapped through SWAP gate to the lower network to correct errors and then switched back to the original position.

The sections of this article are organized in the following manner. In Section 2, we briefly introduce the background knowledge of discrete quantum walks. In Section 3, the two-lattice Bose–Hubbard model is constructed. In Section 4, the position of the quantum lattice is coded and the quantum state exchange gate is constructed. In Section 5, an analysis of error correction performance is performed, and Section 6concludes the study.

2 Discrete quantum walk

A quantum walk is a quantized model for a classical random walk. The discrete time models discussed here include the walker position state and the “coin” state. The position n of the walker is a vector of infinite dimensional Hilbert space ${\mathcal{H}}_p$, and the basis vector of Hilbert space is {|n⟩: n ∈ Z}, which is called the computational basis for position space.

The evolution of the walk depends on the state of a quantum coin. Suppose the walker is on position |n⟩, after the quantum coin is flipped “heads”, the walker goes to position |n + 1⟩ in the next step. If the coin is flipped “tails”, the walker will go to position |n − 1⟩. Now, the Hilbert space of the whole ramble system is

$\mathcal{H}={\mathcal{H}}_c\otimes {\mathcal{H}}_p,(1)$

where ${\mathcal{H}}_c$ is a two-dimensional Hilbert space of the quantum coin (different walkers have different throwing operators), and the basis vector of Hilbert space is {|0⟩, |1⟩}. The aforementioned ground state is also the computational basis of the quantum coin space, and the computational basis for space $\mathcal{H}$ is {|i⟩|n⟩, i ∈ {0, 1}, n ∈ Z}.

P is the coin operator that determines the direction of the quantum walk. The operator for the walker to move from position |n⟩ to position |n + 1⟩ or position |n − 1⟩ is called the transition operator S.

$\begin{array}{c}S|0\rangle |n\rangle =|0\rangle |n+1\rangle \hfill \\ S|1\rangle |n\rangle =|1\rangle |n-1\rangle \hfill \end{array}.(2)$

We calculated the representation of the transition operator S under the computational basis of Hilbert space $\mathcal{H}$:

$S=|0\rangle \langle 0|\otimes \sum |n+1\rangle \langle n|+|1\rangle \langle 1|\otimes \sum |n-1\rangle \langle n|.(3)$

3 Two-lattice Bose–Hubbard model

It is assumed that the graph structure of quantum walk is G, and the vertices V in the graph represent lattice points and satisfy the local Euclidean symmetry [4]. The two-lattice Bose–Hubbard model is used to describe the discrete time quantum walk in multiparticle interaction on the graph and to correct the error of quantum walk.

To construct the two-lattice Bose–Hubbard model, we first introduce the boson creation (annihilation) operator, $b_j^{†}(b_j)$, where j = 1, 2, …, n, which satisfies the commutation relation:

$\left[{\widehat{b}}_i,{\widehat{b}}_j\right]=0,\left[{\widehat{b}}_i^{†},{\widehat{b}}_j^{†}\right]=0,\left[{\widehat{b}}_i,{\widehat{b}}_j^{†}\right]={\delta }_{ij}.(4)$

Then we get the Hamiltonian of the two-lattice Bose–Hubbard model:

$\widehat{H}=-t\sum _{k=1}^{\propto }\sum _{j_1\cdots j_k}{\tilde{b}}_{j_1}^{†}\cdots {\tilde{b}}_{j_k}^{†}\sum _{j_1^{\prime }\cdots j_k}{\tilde{b}}_{j_1}^{†}\cdots {\tilde{b}}_{j_k^{\prime }}^{†}+\sum _{j}V\left({\widehat{n}}_j\right)+\sum _j{ϵ}_j{\widehat{n}}_j,(5)$

where t is the real parameter to describe the particle jumping intensity (in this work t = 1), ϵ_j is the local potential, and $V({\widehat{n}}_j)$ is the interaction between particles at the lattice point:

$\begin{array}{ll}\hfill V\left({\widehat{n}}_j\right)& =V_2\left({\widehat{n}}_j\right)+V_3\left({\widehat{n}}_j\right)+\cdots \hfill \\ \hfill & =\frac{U_1}{2}{\widehat{n}}_j\left({\widehat{n}}_j-1\right)+\frac{U_2}{6}{\widehat{n}}_j\left({\widehat{n}}_j-1\right)\left({\widehat{n}}_j-2\right)+\cdots ,\hfill \end{array}(6)$

where $V_2({\widehat{n}}_j)$ is the interaction between two particles, $V_3({\widehat{n}}_j)$ is the interaction between three particles, U₁ and U₂ are the strength of the interaction between particles, and ${\widehat{n}}_j={\widehat{b}}_j^{†}{\widehat{b}}_j$.

In Eq. 6, the constraint of the two sets {j₁, j₂, …, j_k} and $\{j_1^{\prime },j_2^{\prime },\dots ,j_k^{\prime }\}$ is that the sum extends over all lattice points, and the two sets are not the same. Also, the operator operation condition is satisfied:

${\tilde{b}}_j=f\left({\widehat{n}}_j\right){\widehat{b}}_j,{\tilde{b}}_j^{†}={\widehat{b}}_j^{†}f\left({\widehat{n}}_j\right),f\left({\widehat{n}}_j\right)=\frac{1}{\sqrt{{\widehat{n}}_j+1}},(7)$

where ${\widehat{n}}_j=b_j^{†}{b}_j$ is the number operator at the lattice point j. Operator $\{{\tilde{b}}_j,{\tilde{b}}_j^{†},{\widehat{n}}_j\}$ satisfy the commutation relation:

$\left[{\widehat{n}}_j,{\tilde{b}}_j\right]=-{\tilde{b}}_j,\left[{\widehat{n}}_j,{\tilde{b}}_j^{†}\right]={\tilde{b}}_j^{†},\left[{\tilde{b}}_j,{\tilde{b}}_j^{†}\right]={\delta }_{n_{j}0}.(8)$

According to the Hamiltonian of the model, the model can make multiple particles transition at the same time without limiting the transition of two adjacent lattice points. In the study mentioned in reference [17], the limit condition of Hilbert space $\mathcal{H}$ of n boson is calculated in the 2ⁿ dimensional computational Hilbert space $\mathcal{C}$, and the location is encoded by subset ${\mathcal{H}}_{\mathcal{C}}\subseteq \mathcal{H}$ and $|{\mathcal{H}}_{\mathcal{C}}|=2^n$, along with an isomorphism $\rho :{\mathcal{H}}_{\mathcal{C}}\to \mathcal{C}$, where $\mathcal{C}$ and ${\mathcal{H}}_{\mathcal{C}}$ are interchangeable. The quantum state $|\mathrm{\Phi }\rangle \in {\mathcal{H}}_{\mathcal{C}}$ in the model system provides a computer state encoding on the n-qubits, $|\mathrm{\Phi }{\rangle }_{\mathcal{C}}=\rho (|\mathrm{\Phi }\rangle )$. A Hamiltonian was obtained by coupling ${\mathcal{H}}_{\mathcal{C}}$ with states space ${\mathcal{H}}_{\tau }$ (${\mathcal{H}}_{\tau }$=$\mathcal{H}\backslash {\mathcal{H}}_{\mathcal{C}}$) outside of the computational space, which generated entanglement in $\mathcal{C}$. It is proved that any initial state can be mapped to $\mathcal{H\_\{C\}}$ and can be returned to $\mathcal{C}$ recoded as a valid computed state.

4 SWAP gate operator construction

Assume two lattices V₀ and V₁ (Figure 2), where V₀ is the location of the quantum walk and V₁ is the error-correcting coded location. The corresponding two lattices in V₀ and V₁ represent a qubit whose calculated ground state is |0⟩ and |1⟩, respectively. The corresponding qubits in the lattice must be entangled, and we show how quantum lattices are encoded and how qubits generate entanglement. Suppose the initial n-qubit state |Φ⟩ satisfies the following condition:

$\sum _{i=0}^1{\left|⟨\mathrm{\Phi }\left|{\tilde{b}}_{j,i}^{†}{\tilde{b}}_{j,i}\right|\mathrm{\Phi }⟩\right|}^2=1.(9)$

FIGURE 2

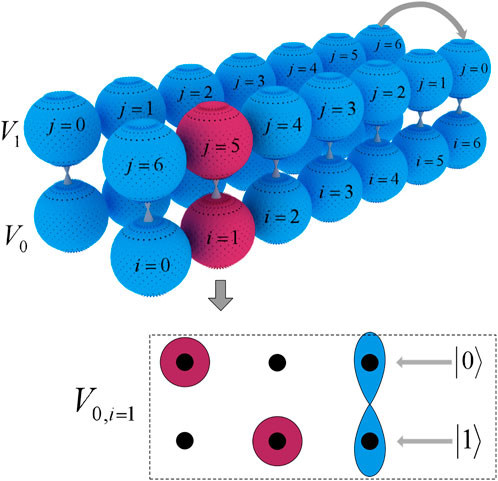
FIGURE 2. Due to the need of quantum walk error correction, two layers of network lattice (V₀ and V₁) are set in the Bose–Hubbard mode. In the 3D figure, the left side represents the original two-dimensional lattice diagram, and the right side represents the lattice encoded by using the Yang diagram method in V₁, where the lattice position in V₀ remains unchanged. The following 2D diagram describes the encoding mode of the particles in the red lattice V_{0, i=1} and V_{0, i=1} = |Φ⟩ = |0⟩ ⊗|1⟩ ⊗| + ⟩ (the particles in the lattice are encoded using the method described in reference [17]).

The function of the four calculated ground-state mapping relations and the creation (annihilation) operators for a 10 dimensional space is

$\begin{array}{cc}\hfill {\tilde{b}}_{j,0}^{†}{\tilde{b}}_{j+\mathrm{1,0}}^{†}|00{\rangle }_i|00{\rangle }_{i+1}& =|10{\rangle }_i|10{\rangle }_{i+1}\leftrightarrow |0{\rangle }_i|0{\rangle }_{i+1},\hfill \\ \hfill {\tilde{b}}_{j,0}^{†}{\tilde{b}}_{j+\mathrm{1,1}}^{†}|00{\rangle }_i|00{\rangle }_{i+1}& =|10{\rangle }_i|10{\rangle }_{i+1}\leftrightarrow |0{\rangle }_i|1{\rangle }_{i+1},\hfill \\ \hfill {\tilde{b}}_{j,1}^{†}{\tilde{b}}_{j+\mathrm{1,0}}^{†}|00{\rangle }_i|00{\rangle }_{i+1}& =|10{\rangle }_i|10{\rangle }_{i+1}\leftrightarrow |1{\rangle }_i|0{\rangle }_{i+1},\hfill \\ \hfill {\tilde{b}}_{j,1}^{†}{\tilde{b}}_{j+\mathrm{1,1}}^{†}|00{\rangle }_i|00{\rangle }_{i+1}& =|10{\rangle }_i|10{\rangle }_{i+1}\leftrightarrow |1{\rangle }_i|1{\rangle }_{i+1},\hfill \end{array}(10)$

The Hamiltonian of the two-lattice Bose–Hubbard model is reduced to

${\widehat{H}}_1=-\sum _{y=1}^N\left(t_{01}^y{b}_{j,0}^{†}{b}_{j,1}+t_{10}^y{b}_{j,1}^{†}{b}_{j,0}\right)+\frac{U}{2}\sum _{j=1}^2\left[{\widehat{n}}_j\left({\widehat{n}}_j-1\right)+{\widehat{n}}_j\left({\widehat{n}}_j-1\right)\right],(11)$

when the interaction of two particles and the local potential ϵ_j are considered only. In Eq.6, N is the particle number, and the subscript j is the lattice position, and the parameter t_ij is

$t_{ij}=t\sqrt{\frac{{\widehat{n}}_i!\left({\widehat{n}}_j-y\right)!}{{\widehat{n}}_j!\left({\widehat{n}}_i-y\right)!}}.(12)$

In the two-lattice Bose–Hubbard model, the six lattice points are coded according to the Yang diagram, so the lattice coding sequence is as follows:

$\begin{array}{c}\hfill |\mathrm{0,6}\rangle |\mathrm{5,1}\rangle |\mathrm{4,2}\rangle |\mathrm{3,3}\rangle |\mathrm{2,4}\rangle |\mathrm{1,5}\rangle |\mathrm{0,6}\rangle \hfill \end{array},(13)$

According to the aforementioned Eqs 11, 12, 13, we can get the energy matrix E₆ by matrix diagonalization. From the energy matrix E₆, the eigenvalues ${\{E_6^{(\iota )}\}}_{\iota =0}^6$ of lattice particles and the ground state of the model can be obtained when determining the values of U/t, which is helpful for the establishment of the two-lattice Bose–Hubbard model. Moreover, the entangled degree calculation system mentioned in the study in reference [4] is used to calculate the entangled degree between the ground-state particles:

$\eta =-\frac{1}{M}\sum _{i=1}^M\mathit{Tr}{\left(\varphi \right)}_{i}lo{g}_{N+1}{\left(\varphi \right)}_i,(14)$

where N is the number of particles, M is the number of lattices, and (ϕ)_i is the reduced density matrix at the ith lattice point. The next step is to find the relationship between the specific value U/t and the degree η of entanglement. The lattice energy matrix of the seven lattice points is shown below.

$E_6=-t\left(\begin{array}{ccccccc}\hfill -\frac{15U}{t}\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill -\frac{10U}{t}\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill -\frac{7U}{t}\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\frac{6U}{t}\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\frac{7U}{t}\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\frac{10U}{t}\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\frac{15U}{t}\hfill \end{array}\right).(15)$

According to the eigenenergy, the Bethe hypothesis method can be obtained, as follows:

$F\left(m,n\right)=E^{\left(\delta \right)}-t-\sum _{j}V\left({\widehat{n}}_j\right)-\sum _{j=1}^M{ϵ}_j{\widehat{n}}_j,(16)$

where − t∑_m,nC(m, n)/F(m, n) = 1, m and n (m ≥ n) are the number in the lattice points, when m = n and C(m, n) = 1 and when m ≠ n and C(m, n) = 2. According to Eq. 16, the calculation formula of entanglement is improved:

$\eta =\sum _{m,n}^N\frac{1}{F{\left(m,n\right)}^2}lo{g}_{N+1}\frac{1}{F{\left(m,n\right)}^2}.(17)$

We can get the degree of entanglement between the two lattice points to 1 at U/t → 0, as shown in Figure 3. The SWAP gate is obtained by limiting [4] to U/t ≈ 0:

$\frac{U}{t}=4\sqrt{\frac{a^2}{{\left(2b+1\right)}^2}-1}\approx 0,a,b\in \mathbf{Z},(18)$

$SWAP=\left(\begin{array}{cccc}\hfill e^{-i\alpha \pi }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{-i\alpha \pi }\hfill \end{array}\right),(19)$

where $\alpha =b+\sqrt{l^2-4a(a+1)-1}$ a and b need to be evaluated according to the degree of entanglement η to ensure the degree of entanglement between two particles.

FIGURE 3

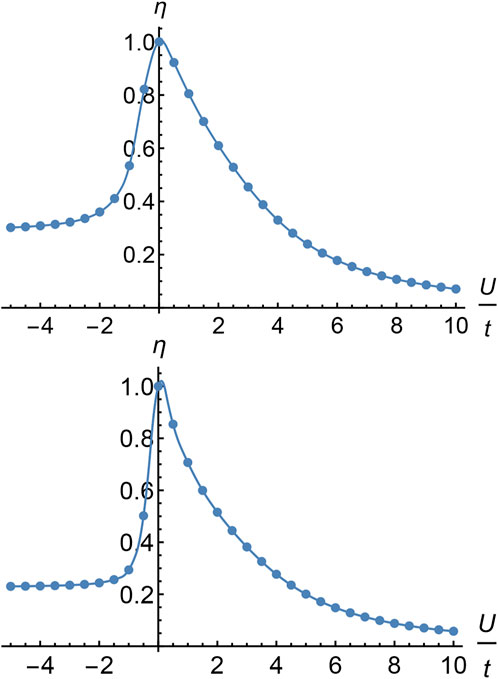
FIGURE 3. According to the Bethe assumption method, the Eq. 17 related to the degree of entanglement can be obtained, which shows the relationship between the degree of entanglement η (vertical axis) and U/t (horizontal axis). The aforementioned two figures are, respectively, the relationship curves of entanglement degree η and U/t when the total number of particles is 10 and 20. It can be seen that the degree of entanglement tends to 1 as U/t → 0, so the two particles in the model can be entangled by controlling the values of parameters U/t.

5 Error correction and analysis

5.1 Quantum walk error correction

Because the generator of local Euclidean symmetry is used to construct the two-lattice Bose–Hubbard model, it is necessary to modify the quantum ramble operator. Assuming that the generator in the model (n lattices) is ${\{{\xi }_i\}}_{i=1}^n$, the modification of quantum walk transfer operator and coin operator is as follows:

$P^{\prime }=\sum _{p,q=0}^1|{\xi }_p\rangle \langle {\xi }_q|,(20)$

$S^{\prime }=|{\xi }_0\rangle \langle {\xi }_0|\otimes \sum _{n=0}^{N-1}|n+1\rangle \langle n|+|{\xi }_1\rangle \langle {\xi }_1|\otimes \sum _{n=1}^N|n-1\rangle \langle n|.(21)$

Because it is currently in a two-dimensional physical system, the aforementioned formula only takes two generative elements to construct the quantum walk evolution operator.

In the previous section, we showed that the quantum states of two corresponding lattice points can be entangled by controlling the ratio of the parameters U/t. Thus, according to the Properties of the Bose–Hubbard model, when particle qubits wander to lattice point α, it can be exchanged with another lattice point α′, which becomes entangled with the particle qubits through the exchange gate and corrects the error.

In the space of N-qubits, a single-bit quantum measurement will appear at each lattice point when the evolution of the particles is in the discrete time quantum walk. The measurement operator is:

$V=\sum _{i=0}^{N-1}\sum _{j=0}^1|v{\rangle }_{i,j}\langle v{|}_{i,j},(22)$

where, |v⟩_i,0 is the encoded quantum state in the first lattice in Figure 2, which is the state of quantum walk; |v⟩_i,1 is the quantum state in the second lattice, which is used to assist quantum error correction. Also, the lattice locations of |v⟩_i,0 and |v⟩_i,1 are entangled in the model. The quantum state |v⟩_i,0 has superposition state in the process of quantum walk:

$|\mathrm{\Psi }\left(t\right)\rangle =\sum _{n=0}^{N-1}{\psi }_{0,n}\left(t\right)|{\xi }_0,n\rangle +{\psi }_{1,n}\left(t\right)|{\xi }_1,n\rangle ,(23)$

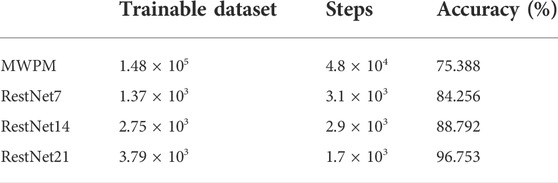
where ψ_0,n and ψ_1,n are the amplitude, |ξ₀⟩ and |ξ₁⟩ are the coin state, and |n⟩ is the position state. In the process of quantum walk, there are mainly two kinds of errors, which are phase inversion and bit inversion. However, the amplitude in Eq. 23 is generated by the superposition state, so the detection and correction of walker errors are mainly aimed at bit inversion errors. The quantum walk error correction circuit is shown in Figure 4. In order to suppress the error generated in the quantum walk, the noise error based on the double-lattice Bose–Hubbard model in the quantum walk is reduced by reducing the circuit gate overhead. Taking depolarization noise as an example, the data map is obtained through the training of the decoder. The decoder uses the convolutional neural network [27–29] in the current hot machine learning algorithm as the dominant algorithm to decode the quantum information in the line. The specific decoding training model is shown in Figure 5. By training with different restnet layers, the accuracy and speed of training are improved; the speed is 1/3 higher than before and the accuracy reaches 99.82%.

FIGURE 4

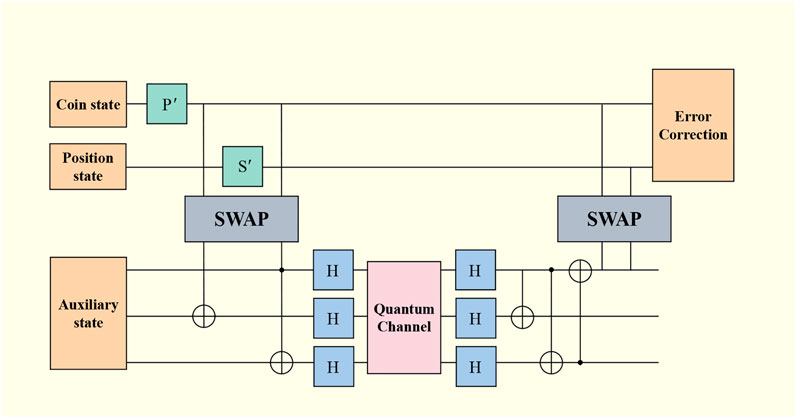
FIGURE 4. Quantum walk error correction circuit diagram. During the quantum walk, the particles are swapped into another lattice via the SWAP gate, which is then swapped into the lattice of quantum walk after correcting the coin state and the initial state by the quantum error-correcting code.

FIGURE 5

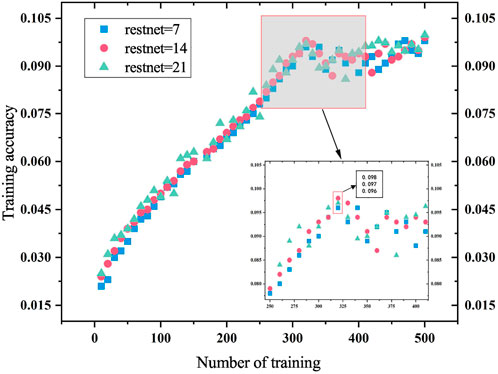
FIGURE 5. Number of training times corresponds to a function of training error rate and training accuracy. The horizontal axis represents the number of training sessions, and the vertical axis represents the training error rate and accuracy rate. Restnet=7, restnet=14, and restnet=21 are marked with blue, red, and green, separately. For intuitive viewing, zoom plots are set up to make it easier to observe the data.

5.2 Algorithm analysis

At present, there are many research achievements in quantum walking. For example, the quantum state operator based on the Bose–Hubbard model is given in the study in reference [17], including single-bit operation, entanglement operation, and permutation operation. This study mainly studies the error correction of system noise during a quantum walk.

The algorithm is based on the two-lattice Bose–Hubbard model, and the evolution of the quantum walk algorithm is carried out. In the first section, it is proved that no new quantum state will be generated after the particles are replaced in the model [17]. Based on the model, this algorithm can correct the quantum walk error by using quantum error correction coding. In the second section, according to the Bethe hypothesis method mentioned in reference [4], we can get the relationship between energy eigenvalues, particle transition intensity, particle interaction, and entanglement (Eq. (17)). Therefore, two lattice points can be entangled by controlling the value of U/t, and the step of generating entanglement can be omitted compared with the study mentioned in reference [17].

5.3 Error correction performance analysis

We extracted non-local regularities from noise and performed transfer learning in various tasks. Applying this advantage to the cost of qubits passing through quantum gates can reduce the cost of qubits. The qubits contain auxiliary qubits in the synthetic measurement process, and the logic overhead is the cost of the auxiliary qubits during the synthetic measurement process. Threshold is an effective way to characterize fault tolerance performance. Specifically, applying quantum error correction for efficient quantum computing can suppress the logical error rate to arbitrarily low levels when the physical error rate of the qubits is below a certain threshold. The CNN used in this study is used for experiments. The number of simulated qubits varies from 3.8 × 10³ to 1.5 × 10⁵ bits. The specific training data quantification is shown in Table 1. Comparing the overhead of MWPM and CNN optimization with thresholds of 0.0058 and 0.0085. Figure 6A shows that with the increase of the number of qubits both the MWPM overhead and the CNN overhead increase, but the increase in CNN-optimized overhead is significantly lower than that of the MWPM overhead. Figure 6B shows that as the number of qubits increases, the optimization overhead of CNN also gets much lower than the original one; although when the number of qubits is 2.0 × 10⁸, the overhead of the optimized CNN is slightly higher than the original one. At the same time, comparing the results under different thresholds in Figure 6, it can be found that the larger threshold, the greater the overhead of quantum circuit gate.

TABLE 1

TABLE 1. Unified quantization of network layers under different decoders.

FIGURE 6

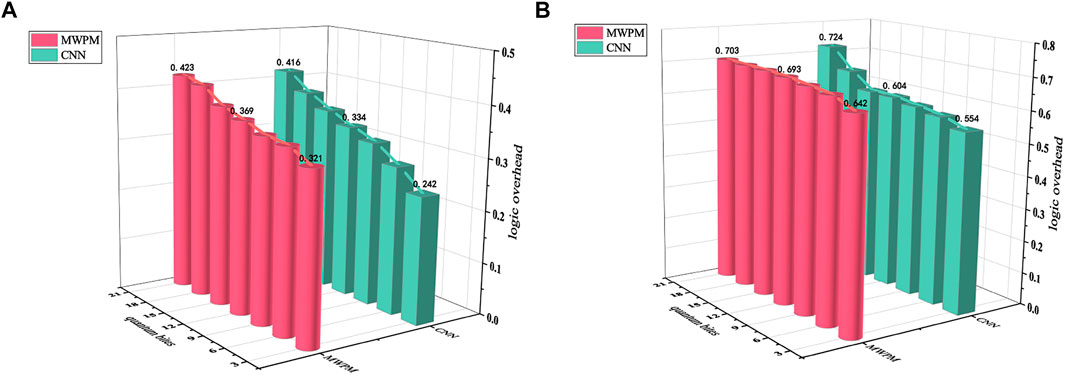
FIGURE 6. Quantum circuit gate overhead data graph. (A) When threshold = 0.005, the cost of MWPM is compared with the optimization cost of CNN network. (B) When threshold = 0.0085, the cost of MWPM is compared with the optimization cost of CNN network. Among them, the abscissa represents the number of qubits, displayed in scientific notation, and the ordinate is the logical cost. The cost of CNN is marked in pink, and the cost of CNN optimization is marked in green.

6 Conclusion

In this study, a multiparticle quantum walk error correction algorithm based on the two-lattice Bose–Hubbard model is proposed. This algorithm controls the proportion of the interaction between particles and the transition intensity of particles to realize the entanglement of quantum state in two lattices and then corrects the quantum walking error by using the invariant property of model particle replacement. Under the condition of the threshold of 0.0085, the restnet network layer is used as a training model, and the error noise of quantum walk is reduced by decoding the error correction circuit model, so as to achieve a more stable walk circuit. Compared with the traditional quantum walk error correction, the threshold limit is increased from 0.0058 under the traditional MWPM to 0.0085, and the speed is increased by a full 1/3. However, when the number of particles or the size of the system exceeds a certain threshold, it is impossible to accurately control the transition strength of particles and the interaction between particles, thus destroying the entanglement operation. The development of quantum convolutional neural network is relatively mature at present, and it is the focus of the next research, in preparation for further improving the fault tolerance performance.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

S-MW: conceptualization, methodology, and software; Y-JQ: data curation and writing—original draft preparation; H-WW: visualization, investigation, and supervision; ZC: writing—reviewing and editing; H-YM: conceptualization, funding acquisition, and resources.

Funding

This project was supported by the National Natural Science Foundation of China (Grant No. 61772295), Natural Science Foundation of Shandong Province, China (Grant Nos. ZR2021MF049, ZR2019YQ01), and Project of Shandong Provincial Natural Science Foundation Joint Fund Application (ZR202108020011).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Aharonov Y, Davidovich L, Zagury N. Quantum random walks. Phys Rev A (Coll Park) (1993) 48:1687–90. doi:10.1103/PhysRevA.48.1687

CrossRef Full Text | Google Scholar

2. Kempe J. Quantum random walks: An introductory overview. Contemp Phys (2003) 44:307–27. doi:10.1080/00107151031000110776

CrossRef Full Text | Google Scholar

3. Anderson MH, Ensher JR, Matthews MR, Wieman CE, Cornell EA. Observation of bose-einstein condensation in a dilute atomic vapor. Science (1995) 269:198–201. doi:10.1126/science.269.5221.198

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Zwierlein MW, Stan CA, Schunck CH, Raupach SM, Gupta S, Hadzibabic Z, et al. Observation of bose-einstein condensation of molecules. Phys Rev Lett (2003) 91:250401. doi:10.1103/PhysRevLett.91.250401

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kennedy CJ, Burton WC, Chung WC, Ketterle W. Observation of bose–einstein condensation in a strong synthetic magnetic field. Nat Phys (2015) 11:859–64. doi:10.1038/nphys3421

CrossRef Full Text | Google Scholar

6. Aveline DC, Williams JR, Elliott ER, Dutenhoffer C, Kellogg JR, Kohel JM, et al. Observation of bose–einstein condensates in an earth-orbiting research lab. Nature (2020) 582:193–7. doi:10.1038/s41586-020-2346-1

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ghosal A, Deb P. Quantum walks over a square lattice. Phys Rev A (Coll Park) (2018) 98:032104. doi:10.1103/PhysRevA.98.032104

CrossRef Full Text | Google Scholar

8. Wong TG. Isolated vertices in continuous-time quantum walks on dynamic graphs. Phys Rev A (2019) 100:062325. doi:10.1103/PhysRevA.100.062325

CrossRef Full Text | Google Scholar

9. Szigeti BE, Homa G, Zimborás Z, Barankai N. Short-time behavior of continuous-time quantum walks on graphs. Phys Rev A (Coll Park) (2019) 100:062320. doi:10.1103/PhysRevA.100.062320

CrossRef Full Text | Google Scholar

10. Cao W, Yang Y, Li D, Dong J, Zhou Y, Shi W. Quantum state transfer on unsymmetrical graphs via discrete-time quantum walk. Mod Phys Lett A (2019) 34:1950317. doi:10.1142/S0217732319503176

CrossRef Full Text | Google Scholar

11. Zhan H. An infinite family of circulant graphs with perfect state transfer in discrete quantum walks. Quan Inf Process (2019) 18:369–26. doi:10.1007/s11128-019-2483-3

CrossRef Full Text | Google Scholar

12. Feng Y, Shi R, Shi J, Zhou J, Guo Y. Arbitrated quantum signature scheme with quantum walk-based teleportation. Quan Inf Process (2019) 18:154–21. doi:10.1007/s11128-019-2270-1

CrossRef Full Text | Google Scholar

13. Rhodes ML, Wong TG. Quantum walk search on the complete bipartite graph. Phys Rev A (Coll Park) (2019) 99:032301. doi:10.1103/PhysRevA.99.032301

CrossRef Full Text | Google Scholar

14. Qiang X, Wang Y, Xue S, Ge R, Chen L, Liu Y, et al. Implementing graph-theoretic quantum algorithms on a silicon photonic quantum walk processor. Sci Adv (2021) 7:eabb8375. doi:10.1126/sciadv.abb8375

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang Y, Lou X, Fan Z, Wang S, Huang G. Verifiable multi-dimensional (t,n) threshold quantum secret sharing based on quantum walk. Int J Theor Phys (2022) 61:1–17. doi:10.1007/s10773-022-05009-w

CrossRef Full Text | Google Scholar

16. Lou X, Wang S, Ren S, Zan H, Xu X. Quantum identity authentication scheme based on quantum walks on graphs with ibm quantum cloud platform. Int J Theor Phys (Dordr) (2022) 61:40–15. doi:10.1007/s10773-022-04986-2

CrossRef Full Text | Google Scholar

17. Underwood MS, Feder DL. Bose-hubbard model for universal quantum-walk-based computation. Phys Rev A (2012) 85:052314. doi:10.1103/PhysRevA.85.052314

CrossRef Full Text | Google Scholar

18. Ye Tian-Yu, Geng Mao-Jie, Xu Tian-Jie, Chen Ying. Efficient semiquantum key distribution based on single photons in both polarization and spatial-mode degrees of freedom. Quantum Information Processing, 2022, 21(4) 123.

CrossRef Full Text | Google Scholar

19. Shapira D, Biham O, Bracken A, Hackett M. One-dimensional quantum walk with unitary noise. Phys Rev A (Coll Park) (2003) 68:062315. doi:10.1103/PhysRevA.68.062315

CrossRef Full Text | Google Scholar

20. Benedetti C, Buscemi F, Bordone P, Paris MG. Dynamics of quantum correlations in colored-noise environments. Phys Rev A (Coll Park) (2013) 87:052328. doi:10.1103/PhysRevA.87.052328

CrossRef Full Text | Google Scholar

21. Wang C, Wang C, Tang Y, Ren S. Quantum walk in terms of quantum Bernoulli noise and quantum central limit theorem for quantum Bernoulli noise. Adv Math Phys (2018) 2018:1–9. doi:10.1155/2018/2507265

CrossRef Full Text | Google Scholar

22. Ambainis A, Wong TG. Correcting for potential barriers in quantum walk search. arXiv preprint (2015). doi:10.48550/arXiv.1505.02035

CrossRef Full Text | Google Scholar

23. Ye Tian-Yu, Li Hong-Kun, Hu Jia-Li. Semi-quantum key distribution with single photons in both polarization and spatial-mode degrees of freedom. International Journal of Theoretical Physics, 2020, 59(9) 2807–2815.

CrossRef Full Text | Google Scholar

24. Wang C, Ye X. Quantum walk in terms of quantum Bernoulli noises. Quan Inf Process (2016) 15:1897–908. doi:10.1007/s11128-016-1259-2

CrossRef Full Text | Google Scholar

25. Du Y, Lu L, Li Y. A rout to protect quantum gates constructed via quantum walks from noises. Sci Rep (2018) 8:7117–1. doi:10.1038/s41598-018-25550-1

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Benedetti C, Rossi MA, Paris MG. Continuous-time quantum walks on dynamical percolation graphs. EPL (Europhysics Letters) (2019) 124:60001. doi:10.1209/0295-5075/124/60001

CrossRef Full Text | Google Scholar

27. Cai W, Ma Y, Wang W, Zou C, Sun L. Bosonic quantum error correction codes in superconducting quantum circuits. Fundam Res (2021) 1:50–67. doi:10.1016/j.fmre.2020.12.006

CrossRef Full Text | Google Scholar

28. Qiu T, Li H, Xie M. Coherent generation and manipulation of stationary light pulses encoded in degrees of freedom of polarization and orbital angular momentum. Phys Rev A (Coll Park) (2019) 100:013844. doi:10.1103/PhysRevA.100.013844

CrossRef Full Text | Google Scholar

29. Chen H, Zhang Y, Kalra MK, Lin F, Chen Y, Liao P, et al. Low-dose ct with a residual encoder-decoder convolutional neural network. IEEE Trans Med Imaging (2017) 36:2524–35. doi:10.1109/TMI.2017.2715284

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Xie T, Grossman JC. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys Rev Lett (2018) 120:145301. doi:10.1103/PhysRevLett.120.145301

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Li J, Zhang H, Chen JZ. Structural prediction and inverse design by a strongly correlated neural network. Phys Rev Lett (2019) 123:108002. doi:10.1103/PhysRevLett.123.108002

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Maskara N, Kubica A, Jochym-O’Connor T. Advantages of versatile neural-network decoding for topological codes. Phys Rev A (Coll Park) (2019) 99:052351. doi:10.1103/PhysRevA.99.052351

CrossRef Full Text | Google Scholar

33. Varona S, Martin-Delgado MA. Determination of the semion code threshold using neural decoders. Phys Rev A (2020) 102:032411. doi:10.1103/PhysRevA.102.032411

CrossRef Full Text | Google Scholar