- Sorbonne Université, CNRS, Institut de Biologie Paris-Seine (IBPS), Laboratoire Jean Perrin (LJP), Paris, France
Cell rearrangements are critical for tissue remodeling during diverse biological processes, such as morphogenesis or cancer progression. They control tissue fluidity and can lead to irreversible shape changes in cohesive tissues. However, the completion of such rearrangements is strongly conditioned by intercellular adhesion, that can prevent their completion or conversely promote them along a given pattern. In this review we explore how intercellular adhesion impacts cell rearrangements at the local scale and how it translates into macroscopic mechanical properties in biological tissues. We first describe general principles obtained from the study of dispersed materials, such as emulsions, in which the mechanical properties and interaction potential between individual particles can be described in a quantitative manner. We then review the effect of varying cell-cell adhesion on rearrangements in vitro model tissues, from cell aggregates to 2D epithelial-like cellular layers. We finally consider developing tissues in which adhesion between the cells is strongly tuned and localized in order to allow for function and shape emergence in the embryo.
1 Introduction
Intercellular adhesion in biological tissues ensures tissue cohesion and controls their mechanical behavior. It is thus central in the regulation of many biological processes such as morphogenesis or cancer progression (see [1–3] for reviews). In particular, epithelial cells adhere together through Adherens Junctions (AJs) that play a central role in tissue morphogenesis (Figure 1A). Indeed, due to their dynamic regulation, they tackle both the role of maintaining tissue architecture and the task of promoting cellular movements during tissue remodelling (see [4, 5] for reviews). In this review we specifically address the impact of adhesion regulation on the mechanics of tissues, with a strong focus on rearrangements at the cellular level. More particularly, we draw analogies with soft matter concepts and report on the role of adhesion in diverse systems, from inert materials to developing tissues.
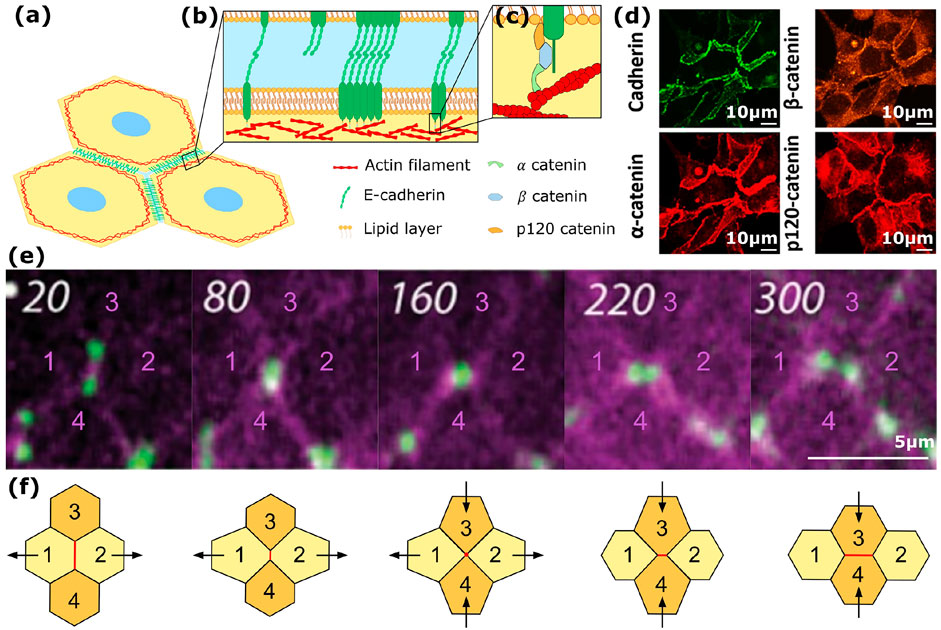
FIGURE 1. Cell-cell adhesion and rearrangements in tissues (A) Schematic representation of cell-cell adhesion in epithelial tissues mediated at adherens junctions by cadherin (green) and actin (red) co-action. (B) Zoom on the cadherin homophilic interactions in the extracellular vicinity of contacting cells: the cadherins interact both through trans adhesions between cadherins of opposing surfaces, and through cis interactions leading to lateral clustering on the cell surface. (C) Schematic representation of the anchorage of the intracellular domains of cadherins to the actin cytoskeleton through β-catenin, α-catenin and p120-catenin. (D) Immunofluorescence microscopy images of α-catenin, β-catenin and p120-catenin in S180 cells expressing GFP-tagged E-cadherin (green). Cadherin and catenin linker proteins appear co-localized at cellular junctions [20]. (E) T1 event observed in a live embryo in which the vertex specific protein sidekick (green) and the DE-cadherin (purple) are labelled. This labelling allows to track the shrinking edge as the vertices come closer, down to the formation 4-way vertex. Eventually a new contact is grown and the new vertices progressively grow apart until the junction is matured [21]. (F) Schematic representation of a rearrangement in the form of a T1 event. First, the adhesive junction between cells 1 and 2 shrinks, all the ways down to a point contact between the 4 cells. Then, cells 1 and 2 finish moving apart and are no longer neighbors, while an adhesive contact between newly neighboring cells 3 and 4 grows.
Transmembrane proteins of the cadherin superfamily are key players of these AJs, ensuring not only cell-cell adhesion but also the mechanical coupling of intracellular structures such as the actin cortex [6] (see Figure 1B): the extracellular domains of cadherins displayed on the surface of contacting cells interact to form cell-cell adhesions through trans interactions [7–9]. These cadherins can also diffuse laterally on the plasma membrane and interact with each other to form 2-dimensional ordered clusters through cis interactions [9, 10]. Cluster formation through such cis interactions is essential to ensure a robust link between the cell-cell junction and the cytoskeleton [11, 12]. Inside the cells, the cadherin intracellular domain interacts with the actin cytoskeleton through linker proteins such as β-catenin, α-catenin and p120-catenin [1, 13–16] (see Figures 1C,D). Moreover, the α-catenins can unfold under mechanical load to interact with vinculin, which results in actin recruitment and provides mechanosensitivity to the AJs [17–19].
This feedback loop between the mechanical constraint applied to a junction and its remodeling make it a very complex structure whose strength cannot be predicted in a straight forward manner. In vitro measurements have therefore been developed to quantify the strength of intercellular interactions and attempt at disentangling the role of all players in these junctions. In particular, pipette assays or microfluidics were used to quantify the separation force between cells that are put in contact together under controlled conditions [12, 20, 22–25]. The separation force between adhering cells was shown to depend on the cadherin concentration on the surface [22, 26], but also on their anchorage to the underlying actin cytoskeleton [24].
However, tissues have to be studied beyond such single cell-cell contacts. Indeed, biological tissues are remodelled at the multicellular scale, for instance when they have to respond to an applied stress, or to drive the emergence of shape and function during development. During these processes, cells undergo shape changes and positional rearrangements to accommodate such tissue remodelling, which are the focus of this review. Different types of cellular rearrangements can take place in tissues. For instance, cell extrusion inherently creates a new neighborhood by accommodating the presence of a new cell in a packing. Likewise, cell division modifies locally the number of cells and hence creates new contacts while deleting others. Finally, rearrangements can occur at a fixed number of cells in the form of coordinated neighbor exchange. A typical rearrangement of this type involves the coordination of 4 cells and is called a T1 event (illustrated in Figures 1E,F). A chain of events needs to occur in order to complete a T1 event: first the existing junction needs to shrink, thus reducing the adhesion area between the cells, then a 4-way junction is transiently formed, and finally a new cell-cell junction has to be formed de novo and grown to its equilibrium size. In this context, vertex-specific proteins, such as sidekick in Drosophila, have been shown to facilitate the completion of T1 events [21]. At the tricellular junctions, sidekick contributes to the anchorage of myosins that in turn transmit the forces necessary to shrink [27] and extend [28] cell-cell junctions during a T1 event. Because adhesions are both ruptured and created in a T1 event, its energetic landscape strongly depends on the adhesion levels between all involved cells. In this review we focus on rearrangements taking place in the form of T1 events and on their dependence on intercellular adhesion.
In order to unravel the processes associated to rearrangements and adhesion regulation in tissues, biomimetic approaches and analogies with elasto-plasticity in soft matter systems are very useful tools. In this article, we therefore review the effects of adhesion on rearrangements with a strong focus on approaches borrowed from materials and soft matter science. In an effort to highlight the link between soft matter and biology we start with the most simple systems, typically inert materials, and progress towards in vivo observations through increasing levels of complexity.
Therefore, we start by considering the structural and mechanical properties of dispersed systems, with a focus on emulsions that are the closest to biological tissues conceptually. We describe the effect of non-specific interparticle interactions on these properties at the microscopic level, i.e. at the scale of individual rearrangements. We then present biomimetic systems (droplets or vesicles) that were developed to tackle the role of specific adhesion between particles. These reductionist approaches allow to uncover precisely the impact of adhesion on the dynamics and topology of rearrangements. Moving into biological systems, we next review in vitro cellular systems in which adhesion can be controlled, leading for instance to cellular sorting in cellular aggregates. These problems have also been studied extensively in silico and theoretical descriptions such as the vertex model implicitly take into account intercellular adhesion and can in turn predict tissue fluidity. Finally, we review some morphogenetic processes in which adhesion modulation directly tunes the rate and location of rearrangements, which in turn controls the emergence of shape and order in the tissue.
2 Interparticle interactions in soft matter systems: From emulsions to foam
2.1 Static structure of adhesive packings
In the absence of attraction or friction between particles, their packing structure under gravity is determined in the framework of the random close packing limit, which corresponds to the jamming point [29]. The Maxwell criterion for mechanical stability determines average properties in these packings such as the coordination number of the particles or their number of neighbors [30]. Emulsions in particular are a great tool to study these properties experimentally as they can be made transparent, which allows to image and quantify their microstructure through confocal microscopy [31]. Interparticle interactions are expected to modify the structural properties of such packings. For instance, attraction between emulsion droplets can be introduced easily through depletion forces. Such interactions have been shown to tune the local and global properties of 3D packings of frictionless droplets: akin to friction in granular systems, attraction stabilizes arches or voids in 3D packings, leading to lower packing fractions [32, 33]. Accordingly, the average number of neighbors and contacts per particle can also be lowered below isostaticity for the highest attraction forces.
2.2 Elastoplasticity of attractive emulsions
The mechanical properties of the above-mentioned packings depend on their local structure and can be understood as a function of their distance to the random close packing limit. Indeed, in the absence of attraction, emulsions under the random close packing fraction (ΦRCP) exhibit a fluid-like behaviour, while they exhibit a solid-like behavior above ΦRCP, i.e., above jamming [34]. However, when attractive interactions are introduced between the particles, these systems can exhibit solid-like properties below ΦRCP [35–37]. Attractive emulsions have also been studied through rheology above ΦRCP, which may be more similar to biological tissues that usually display high packing fractions. These experiments revealed that an additional relaxation process was taking place under shear in the presence of attraction [36]. This suggests that the system undergoes a succession of microscopic events linked to stress release before flowing, but the precise nature of these processes cannot be resolved through bulk rheology approaches.
In order to link bulk properties to microscopic mechanisms, the elastoplastic behavior of emulsions has been widely studied in microfluidic setups that allow to visualize droplet rearrangements and deformations under flow. For instance, using bidisperse compressed emulsions in 2D constrictions revealed a correlation between stress release and T1 events [40]. Introducing attractive interactions between the droplets in such systems is therefore a straight-forward way to understand the microscopic mechanisms, such as T1 events, underlying the effect of attraction on bulk rheological properties of emulsions. In order to impose a large number of tractable rearrangements in these systems, they can be flowed inside constrictions [41, 42] or compressed between parallel plates [38]. These approaches revealed that rearrangements are strongly coordinated in monodisperse emulsions under compression and lead to large predictable fracture events within their crystalline structure [38, 41, 43] (see Figure 2A). This geometric order vanishes as soon as defaults are introduced in the packing structure (by introducing poly- or bidispersity for instance) (Figure 2B), making it deviate from a crystal to a glassy topology. This transition to a glassy system leads to a spread in the occurrence of T1 events, indicating that the energy landscape associated with the compression of attractive emulsions is strongly dependant on the size distribution of the droplets [38]. Similarly, it was shown that depletion attraction could also disturb the positional order of the rearrangements that is normally imposed by geometry [42]. In a microfluidic constriction, attractive forces impair rearrangements and displace them downstream in the constriction (Figure 2C). In turn, these delayed rearrangements induce more deformation of the droplets, i.e., a more elastic response of the emulsion.
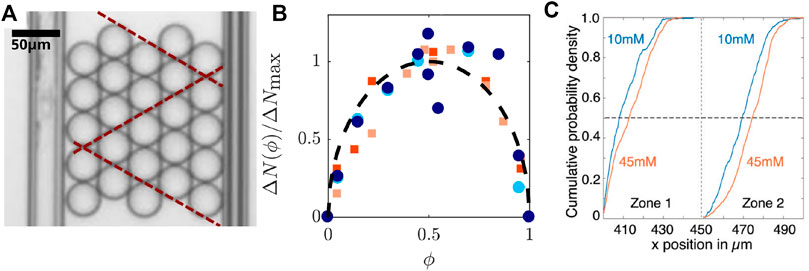
FIGURE 2. Plasticity in attractive emulsions (A) Transmission microscopy image of an oil-in-water emulsion under compression between a force sensor and a pushing plate. Dislocation arrays in the monodisperse emulsions are indicated with the dashed red lines. (B) The forces measured under compression display peaks corresponding to fracture events in monodisperse emulsions or more isolated rearrangements in polydisperse emulsions. The graph in (B) displays the normalized excess number of force peaks during compression with respect to those observed in a monodisperse emulsion, as a function of the fraction of defects Φ introduced through bidispersity, for emulsions with 3 (squares) or 4 (circles) rows in the initial packing. High monodispersity (Φ = 0 or 1) leads to the smallest number of force peaks corresponding to large fracture events. At the highest number of defects, the emulsion is disordered, leading to a higher number of peaks of smaller forces. (A,B) were adapted with permission from [38]. (C) Cumulative distributions of the minimum velocity locations of droplets flowed in a 2D convergent channel with low (10 mM SDS) or high (45 mM SDS) depletion attraction. The velocity minimum is a reporter for the location of rearrangements, before which the droplets stall. This indicated that the rearrangements are impaired by higher attraction forces and appear further down in the constriction. Adapted with permission from [39].
2.3 The case of foams
In foams, the particles at play are air bubbles separated by a liquid film. Their stability and inter-bubble interactions are therefore strongly determined by the nature and amount of surface active molecules introduced in the liquid phase. When foams are subjected to an imposed flow, their bubbles undergo T1 events similarly to emulsions [44, 45]. While the statistics of T1 events was shown to be independent of the aqueous phase viscosity, the choice of the surfactant clearly affects the dynamics of the rearrangements. For instance, the use of proteins or charged surfactants mixed with polymers, instead of pure surfactant, was shown to rigidify the air-water interfaces [44, 46], which subsequently impairs the dynamics of neighbor exchange. However, the direct dependence between the attraction potential between air bubbles and the rearrangements is more elusive. For this reason we do not focus on foams here. Further experimental studies of foam mechanics can be found in previous reviews [47, 48].
3 Biomimetic systems of adhesive tissues
Mimicking cells in vitro through bottom up approaches allows to study specific cellular processes, such as cell-cell adhesion, in a simplified framework. A popular way to reproduce cellular functions artificially relies on the use of model membranes [49]. In particular, giant unilamellar vesicles (or GUVs) share the same size and topology as cells and can be combined with other reconstituted modules to mimic a given cellular function in vitro (See Figures 3A–C). Encapsulation techniques in GUVs have also been developed [50] and allowed to reconstitute biomimetic actin cortices or minimal protein expression solutions in vitro [51, 52]. Alongside the implementation of functional modules inside GUVs, a lot of effort has been provided to introduce specific interactions between them in order to mimic cell-cell adhesion [53–57]. This approach recently led to the production of vesicle aggregates as a model of soft tissues in which cohesion and size can be finely tuned [58]. Despite the fragility of their constitutive elements, these systems will surely provide a great platform to study the elasto-plasticity of minimal adhesive tissues under stress.
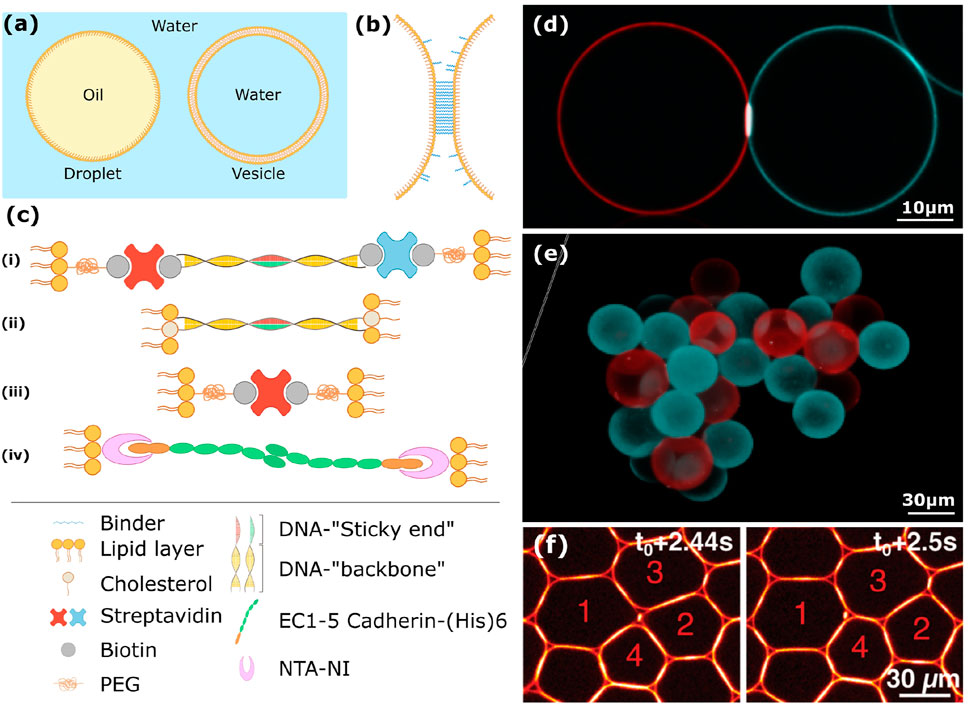
FIGURE 3. Soft matter systems to mimic cell-cell adhesion. (A) Schematic representation of biomimetic droplets stabilized by a monolayer of lipids (left) or biomimetic vesicles (right). (B) General representation of adhesion between the surfaces of droplets or vesicles: binders are attached (or anchored) to the hydrophilic heads of the outer lipid layer and bind to each other upon surface contact. (C) Various type of binders that can ensure specific adhesion, from top to bottom: (i) DNA strands carrying a biotin tag are grafted to a streptavidin which is itself attached biotinylated-PEG groups on the hydrophilic heads of the lipids, or (ii) the DNA strands are directly anchored in the lipid layer through a cholesterol tag. In both cases the DNA sequence usually contains a spacer sequence, made out of a stiff double stranded DNA (represented here in yellow) or a floppy single stranded, followed by a sticky end. The complementary sticky ends of neighboring surfaces interact together to form a complementary double helix upon contact (red/green sequence); (iii) binding through biotin-streptavidin-biotin interactions. The biotinylated lipids on one surface adhere to biotinylated lipids decorated with a streptavidin on a contacting droplet; (iv) adhesion through the extracellular domains of E-cadherin attached to NTA-Ni lipids through a poly-histidin tag. (D) Confocal microscopy of two silicon oil droplets adhering to each other through complementary DNA sticky ends. The color of the droplet codes for the sequence, leading to adhesion patches only at the red/green contacts. (E) Reconstitution of a 3D packing of oil droplets adhering through complementary strands of DNA. (F) Confocal image of silicon oil droplets functionalized with fluorescent streptavidin and adhering through biotin/streptavidin bonds. The droplets undergo a T1 rearrangement as they are flowed in a constriction deforming the emulsion elasto-plastically [39].
Emulsions, and in particular direct oil-in-water emulsions, provide an interesting alternative system to study cell-cell adhesion in vitro. Their stability and versatility allowed to assemble and study the mechanical properties of biomimetic emulsions, which is why we describe in more details their principal characteristics. Indeed, the droplets can be stabilized with phospholipids displaying a functional group on their hydrophilic heads (See Figures 3A,B), which allows to graft a wide range of binders onto those groups (Figure 3C). The most common basis of in vitro adhesion reconstitution is the use of the biotin streptavidin link: streptavidin displays four binding sites for biotin, allowing it to form an adhesive bridge between two biotins located on the fluid surface of the droplets, either by covalent grafting [59, 60] or through the use biotinylated phospholipids to stabilize the oil/water interface [61, 62]. The streptavidin can thus be infused in solution and ensure adhesive bridges between the droplets at the right streptavidin/biotin ratio (see Figure 3F).
Another straight-forward way to mimic intercellular adhesion in vitro is to directly graft the extracellular domains of cadherins onto the fluid surface of oil droplets [63]. 3D packing of such droplets revealed structures containing voids, i.e., signatures of interdroplet attraction, even in the absence of calcium which is classically known to activate interactions between the extracellular domains of cadherins. At higher calcium concentration strong interactions between the surfaces even led to droplet fusion, which was shown to depend strongly on cadherin cis interactions. Therefore, these biomimetic systems are useful tools to get novel insight into the molecular interactions of adhesion molecules.
Finally, an appealing binding strategy relies on the use of complementary strands of DNA [64–66] (Figures 3D,E). In this case, the interaction is highly specific as only two complementary sequences can interact together to form a double helix. Interestingly, the binding energy is also modulated easily through the length of the sequence. The melting temperature above which the double helix is reversibly disassembled is therefore mostly controlled by the size of the sequence and the concentration of salts in solution. The bulk mechanical properties of these systems have been probed through rheology experiments [67]. Similarly to [36], they reveal that below jamming the presence of adhesion between the droplets tends to shift the rheological properties of the system from a viscous to an elastic behavior as the attraction increases by increasing binder concentration. A microscopic mechanism was proposed below jamming: as the bonds are mobile on the fluid droplets surface, the valency of the droplets (i.e., their number of possible adhesive bonds with neighboring droplets, which set by bond concentration) dictates the topology of the droplet clusters that can assemble under strain. Therefore, a valency of 2, i.e., low binder concentration leads to the formation of chains [64, 68], while higher valencies lead to the assembly of higher order clusters percolating throughout the whole sample. Above jamming, increasing the amount of DNA binders delays the onset of plasticity under strain. However, at these densities the link between local rearrangements and macroscopic properties remains elusive.
In order to gain insight into these microscopic mechanisms, the elastoplasticity of adhesive emulsions has been probed through micro-rheology inside microfluidic constrictions [39]. The constriction is used to mimic body axis elongation during development [69] and to impose a large number of rearrangements in the emulsion. The packing fraction in these systems is controlled both by the pressure imposed on the emulsion and by the balance between the adhesion energy between the droplets and the energetic cost associated with their deformation, which sets the size of the observed adhesion patches. Thanks to the 2D geometry, T1 rearrangements can be tracked during the flow and grouped in avalanches [41]. Surprisingly, these experiments revealed that the size of T1 avalanches was not controlled by the level of adhesion between the droplets, indicating that geometry was the only parameter controlling rearrangements. However, individual T1 rearrangements are significantly impaired as the energetic barrier to rupture the existing bond is increased by the presence of an adhesion patch between the droplets. Therefore, the contact between the droplets is maintained longer, inducing a larger deformation of the droplets involved in the T1 (see Figure 3F). According to the above-mentioned energetic considerations, a higher binding energy between the droplets in the constriction is associated with higher deformation levels during T1 rearrangements. This, in turn, deforms all droplets in the emulsion in the axis of elongation, somewhat polarizing the flowing biomimetic tissue. This effect of adhesion could also take place in biological tissues, meaning that a higher adhesion should slow down the dynamics of individual rearrangements and promote elongation of all cells in the axis of the flow. This “in-plane” polarity may be particularly relevant for fast tissue flow in which the active regulations of the cytoskeleton might not have time to respond to the adhesion induced deformation. This could be the case during germband extension in which extrinsic forces drive the first stage of tissue elongation, making elasto-plastic considerations particularly relevant [70]. In particular, this purely mechanical effect may contribute to the propagation of polarity information in cells across different scales in addition to the usual planar cell polarity pathway (see [71] for a review): all droplets are deformed collectively along the same axis through the transmission of forces at their adhesive junctions.
In conclusion, biomimetic models of adhesive tissues are valuable systems to quantitatively shed light on the physical basis of tissue remodeling under force. In order to expand on these results it would be interesting to include other aspects of biological tissues in these synthetic systems. In particular, motility and contractility are key parameters of cellular and tissue mechanics. Conceptually, it is rather straight-forward to imagine an artificial tissue made of vesicles encapsulating active modules of the cytoskeleton, such as contractile acto-myosin networks [72] or active nematics of microtubules [73]. However, the production of large amounts of these objects and the added difficulty of controlling their interactions remain experimentally challenging and have so far prevented their realization. Similarly, various systems of active self-propelled droplets have recently been implemented (see [74] for a review). It is therefore extremely appealing to imagine a new class of biomimetic tissues that could combine the activity of the droplets to the control of interdroplet adhesion. However, the activity of these systems usually depends directly on their local environment, making it difficult to decouple their activity from potential adhesion-based interactions. In addition, the fuel needed for their activity is consumed over time, making the droplets age, which again might impair the adhesive interactions introduced between them.
4 Plasticity control and material properties of in vitro model tissues
4.1 Tuning intercellular adhesion in vitro
Tuning adhesion in synthetic materials is pretty straight forward, but it can also be done in biological materials such as 3D cellular aggregates or 2D cell layers. For instance, the S180 cell line does not constitutively exhibit cell-cell adhesion [77, 78], but can be transfected to obtain cells with various concentrations of E-cadherin expressed on their surfaces [22, 79]. Classical techniques like RNA interference or morpholinos can also be implemented to directly target the activity of one or more proteins involved in the AJs [80–85]. Other approaches rely on the use of cadherin mutants that can independently affect cis and trans interactions in cadherin [9, 86]; or on the use of different calcium concentrations that directly tune cadherin adhesion properties [63, 87–89].
More recently, optochemical tools were also developed to control the link between the cadherins and the actin cytoskeleton through light exposure, thus controlling cell-cell adhesion maturation [90]. Finally, the DNA technologies presented in the previous section were combined with cadherin molecules in order to modulate the association energy between cadherins without affecting their intracellular interactions: to do so, the tip of classical E-cadherins were modified to integrate DNA binders [91] of tunable length, i.e. tunable adhesion energy.
4.2 Self-organization and cellular rearrangements in aggregates
Cell aggregates have been used for decades as an in vitro model system to study the mechanical properties of tissues in a simplified framework [92, 93]. Due to their relative simplicity, these systems offer a great platform to transpose the study of tissue mechanics into a soft matter framework (see [94] for a review). By analogy with viscoelastic materials, an effective viscosity [95] and surface tension can be measured for such tissues [96–100], with a proposed dependence of these properties on the interaction energy between individual cells [79, 101, 102]. These differences in surface tension originating from differences in intercellular adhesion were described as the origin of tissue self-organizing properties in the framework of the differential adhesion hypothesis [103–107]. Following this hypothesis, hierarchy in surface tensions set the equilibrium architecture of tissues displaying a range of intercellular adhesion levels [108], as depicted in Figure 4A. The definition of an effective tissue surface tension has then been refined by taking into account the interplay between cortical tension and intercellular adhesion [104]. Cell motility has also been shown to be a critical parameter when the differential adhesion hypothesis fails to predict the observed tissue organization [109]. In addition, tuning down the adhesion specifically at the interface between distinct cellular populations can allow cells to polarize their mechanical properties or even detach locally, thus promoting the formation of clear boundaries between tissues [110]. This phenomenon, which is critical for tissue boundary establishment during development, has been reconstituted in vitro by using Xenopus embryo explants obtained from different lineages (mesoderm and ectoderm) [111, 112]. Similarly, recent work highlighted the importance of considering the differential adhesion information and morphogen gradients concomitantly, in order to robustly predict pattern emergence during morphogenesis [85], which will be further discussed in Section 6.4.
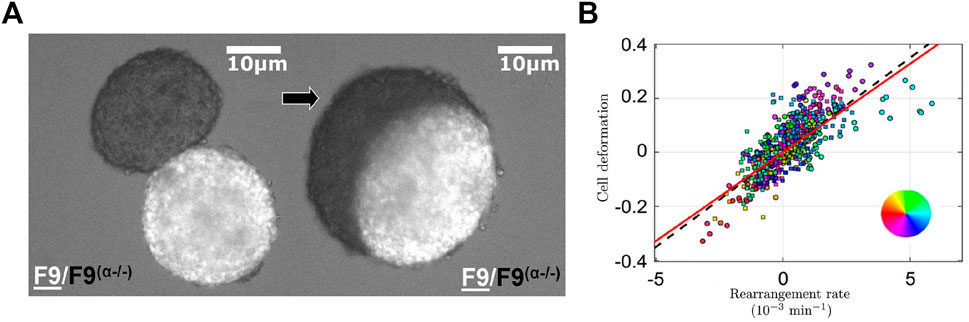
FIGURE 4. Effect of adhesion regulation in vitro cellular systems (A) Merging of two cellular aggregates made from F9 cells (white) and F9 (α−/−) cells in which α-catenin has been knocked out (black), 3 h (left) and 29 h (right) after contact. Due to the reduction of adhesion strength in F9 (α−/−) cells, the black aggregate (lower surface tension) deforms around the more cohesive white aggregate (higher surface tension), in agreement with the differential adhesion hypothesis. Adapted with permission from [75]. (B) Cell deformation as a function of the rearrangement rate in a 2D monolayer of MDCK cells migrating around an obstacle. The correlation between deformation and rearrangement rate is in agreement with a viscoelastic liquid Maxwell model. Adapted with permission from [76].
When such aggregates are submitted to mechanical perturbations, they exhibit an elastoplastic response in which rearrangements take place to relax the applied stress [95]. How these rearrangements are tuned through adhesion modulation remains elusive, but liquid like behaviors and individual cell escapes have been observed when adhesion is impaired, indicating a rise in neighbor exchange [79]. These experiments were also useful to highlight the cross-talk between cell-cell adhesion and cell-matrix adhesion. Indeed, there is a positive feedback loop between cell-substrate adhesion (typically through fibronectin) and cell-cell cadherin-based adhesion [113, 114]. Therefore, on soft substrates, the aggregates are less cohesive and cells can perform rearrangements easily [115, 116], which sheds lights on the importance of adhesion impairment in the context of cancer propagation [117]. Nevertheless, quantitative measurements of cellular rearrangements are difficult in such 3D disordered cellular packings where imaging remains challenging. For this reason, 2D models of cellular tissues in vitro are useful tools to quantitatively relate adhesion regulation to cell-scale events.
4.3 Rearrangements in 2D cellular assemblies
Cellular monolayers can be assembled in order to recapitulate the main features of epithelial sheets such as collective movements, polarization, wound healing, etc … In these systems, the integrity of the extracellular adhesion of E-cadherins has been shown to be essential not only for tissue integrity, but also for efficient wound healing. As a matter of fact, if the E-cadherin extracellular domains are replaced by cadherins of type II, that are associated with weaker slip-bond adhesions in the mesenchyme, closure in wound healing assays is strongly impaired and 2D assemblies fail to maintain epithelial integrity [20].
Intercellular adhesion in various epithelial sheets has also been tuned by depleting cells of E-cadherin through RNA interference [80, 83]. These experiments revealed that the role of E-cadherins was critical for the de novo establishment of intercellular adhesion, rather than the maintenance of existing ones [83]. In fact, the concentration of E-cadherin can be directly correlated to the rate at which tension builds up in epithelial layers [80]. Because the completion of a rearrangement relies on the cells’ ability to grow a new adhesion de novo, this suggest that E-cadherin expression is a controlling parameter for the rate of T1 events in cellular monolayers.
Alternatively, the effect of adhesion has been probed in smaller 2D epithelial cell clusters in which intercellular adhesion has been shown to ensure mechanical coordination over many cellular length scales [118, 119]. Primary mouse keratinocytes assemble in such clusters, in which intercellular adhesion can be tuned through the extracellular calcium concentration [89]. This approach highlighted the role of cadherin-based intercellular adhesion for the transmission of forces to the underlying extracellular matrix, which in turn localizes these traction stresses at the colony periphery. This effect, by targeting the periphery of the cluster, thus also promotes the definition of clear cellular tissue boundaries as described in the previous section. Interestingly, such crosstalk between intercellular and cell-matrix adhesion was also shown to play a role in cell-cell junction dynamics, which should in turn affect T1 rates in these cellular assemblies [120].
All these experiments suggest a link between adhesion strength in epithelial layers and the dynamics of Adherens Junctions assembly and cellular rearrangements. However, to our knowledge, a direct quantitative link between T1 rearrangements frequency and intercellular adhesion levels still remains unclear in these studies that tune E-cadherin expression.
Conversely, experiments from fluid mechanics can be applied to these systems in order to explore explicitly the elasto-plasticity of epithelial sheets. Similarly to experiments performed on emulsions [39], they typically allow to track cellular rearrangements and deformations when the cellular assembly is submitted to a mechanical constraint in 2D. For instance, MDCK (Madin-Darby Canine Kidney) epithelial sheets have been used in channels exhibiting a central obstacle in order to explore the progression of the monolayer around it [76]. The rearrangement rates can then be deduced from coarse-grained analysis by substraction of the cell shape strain rate from the total strain rate of the tissue [121]. This study revealed that deformation and T1 rate fields were strongly correlated (Figure 4B), indicating that the behavior of the 2D cellular sheet could be modelled with a viscoelastic liquid Maxwell model [76, 122]. In particular, these findings highlight the relevance of a timescale associated specifically with intercellular rearrangements for the understanding of the mechanical behavior of these 2D cellular assemblies.
5 Theoretical approaches to tissue plasticity: Influence of adhesion
Biological tissues can be modelled through continuous or discrete descriptions. In the case of continuum models, the tissues are generally described as active gels [123, 124]. For instance, differences in viscosities between the epithelial lung tissues and surrounding mesenchyme could give a physical explanation for its morphogenesis [125–127], therefore proposing the idea of fingering instabilities in tissues [128] by analogy with viscous fingering in liquids [129]. Continuum descriptions also captured the importance of a localized fluidization of the tissues during early morphogenesis [130]. This fluidization was shown to depend on signalling pathways affecting cell-cell adhesion. Such continuum descriptions of tissues have therefore been very useful to characterize mechanical properties at the tissue-scale and shed light on the role of adhesion in the physical principles in morphogenesis [118, 130–134]. However, those approaches are not tailored to specifically study the effect of intercellular adhesion regulation on individual rearrangement dynamics.
In order to take into account rearrangements, one needs to consider cells as discrete elements that can deform and move with respect to each other, and thus use particle based models or vertex models. In particular, deformable particle models are useful to describe static packing properties with [135] or without adhesion [136, 137] (Figures 5A,B). This approach has also been used to study the flow of monodisperse and polydisperse particles with a range of attraction strength and deformability (akin to surface tension) [39]. The results of these simulations showed that avalanche statistics for T1 events were conserved independently of adhesion for a given polydispersity and deformability.
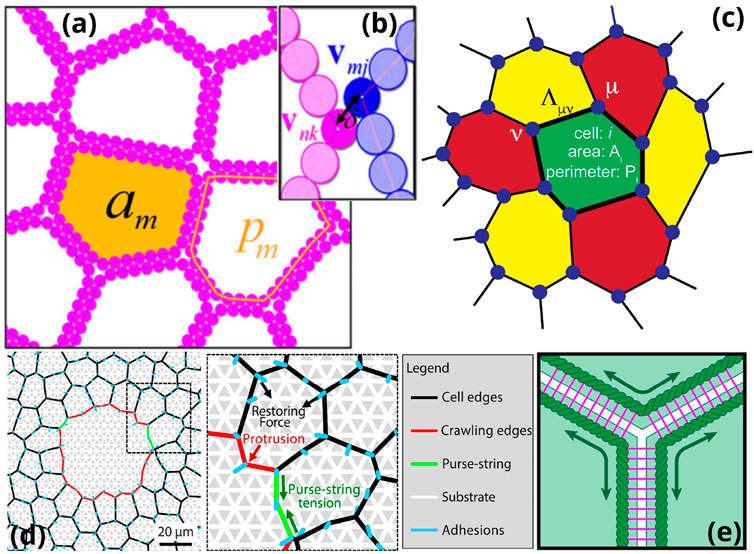
FIGURE 5. Theoretical descriptions of biological tissues (A,B) Deformable polygons or deformable particles model: each polygon is defined by its area a and perimeter p. The perimeter is divided in N = 34 vertices whose positions are determined by different energetic contributions: one that takes into accounts springs between each vertex on a polygon, a compressibility term, a line tension term, a bending energy term for the contour of the polygon, and a repulsive term preventing overlaps between adjacent polygons [136]. (C) Schematic representation of the vertex model in which each cell i of the space tiling is defined by a target area Ai and perimeter Pi of reference. Three (or more) edges of neighboring cells meet at vertices and each junction between two vertices has a line tension [138]. (D) Application of an active vertex model to wound healing. Protrusive forces and adhesion to the substrate are added to the vertex model for wound closure [139]. (E) Apposed-cortex adhesion model: in this extension of the vertex model the cortices of neighboring cells (dark green) are explicitly coupled through adhesion molecules (pink), allowing for continuous rearrangements in the tissue through slippage [140].
In this context, approaches such as the vertex [104, 141–149] or cellular potts models [150–155] are relevant to study the relationship between intercellular adhesion, rearrangements and tissues properties (see [156] for a review). In the cellular potts model each cell is modeled as an assembly of positions and energetic states in a grid and there is an explicit coupling between the state of each cell. Conversely, in the vertex model the tissue is modelled geometrically by a network of vertices connected by edges (Figure 5C). The energy of the cells in the tissue is calculated by taking into account a bulk elasticity of the cell, the contractility of the cortex underlying its surface and the cost of deformation due to the interfacial tension. The sign of this interfacial tension depends on the balance between intercellular adhesion and cortical tension.
In that framework, one can define a shape parameter p0 for individual cells as
Alternatively, the dynamics of cellular positions have been modeled through self-propelled particles descriptions. Akin to motility induced transition approaches, the tissues undergo rigidity transitions as a function of cell dynamics and density [158]. However, these models do not focus on intercellular adhesion regulation, which is at the center of this review. Various models have been proposed to introduce an active term in the vertex model [159] (see [160] for a review). For instance, one straightforward way to do this is to combine the self-propelled particle and the vertex models to account for topology as well as activity of the cells in the tissue [138, 161, 162]. This model is commonly referred to as the self-propelled Voronoi or SPV model. In particular, this model was used to predict jamming transitions in real tissues. In this context, the critical shape parameter
A recent implementation of these models also takes into account the intercellular spaces (like in the DP model) and focuses on cortical tension fluctuations [165]. Interestingly, this model distinguishes two modes of neighborhood changes: for confluent tissues at high cell-cell adhesion levels, rearrangements are mostly in the form of T1 events and their frequency vanishes when contractility decreases, which is a signature of structural arrest; for non-confluent tissues at low adhesion levels, the neighborhood of a cell changes mostly due to creation or loss of cell-cell contacts. It also indicates that there is a threshold tension fluctuation value over which the tissue will always be fluid independently of the level of adhesion. Below this value the tissue fluidity depends directly on cell-cell adhesion. Whether a tissue would modulate tension fluctuation or adhesion strength between the cells remains an interesting question.
At the molecular level, the physical presence of adhesion proteins at the cell-cell junctions can be considered through approaches such as the newly developed apposed-cortex adhesion model [140] (Figure 5E). With this model, the physical properties of the elements that constitute a junction, among which the adhesion molecules between neighboring cells, are explicitly influencing the process of neighbor exchange. For instance, the presence of adhesion molecules between sliding cell surfaces induces a viscous friction that opposes rearrangements [166]. A fast turnover of adhesion molecules therefore relaxes this opposing force and enables neighbor exchanges. This adhesion molecules turnover in biological tissues will be discussed in Section 6.1.
6 Role of adhesion modulation in the control of morphogenesis
Just like in soft matter models, rearrangements in tissues can be coordinated to yield global shape changes and are a local source of stress relaxation upon applied forces [164, 167, 168]. The general mechanics of tissues therefore depends strongly on the details of these rearrangements (see [169, 170] for reviews). In particular, tissue elongation during morphogenesis, also known as convergent extension [171], has been extensively studied in the spectrum of cell rearrangements [70, 170, 172–174]. For instance, the process of tissue elongation during the first fast stage of germ-band extension in Drosophila has been described as the passive response of an adhesive assembly of deformable cells under an applied extrinsic force [70]. In other words, a balance between cell deformations and cell rearrangements leads to overall tissue extension under external forces: an impaired plasticity therefore leads to more intense cellular deformations, just like in synthetic systems [39]. It is clear through this particular example that adhesion is crucial for morphogenetic processes (see [5, 175] for reviews). Among the immense literature discussing the role of classical cadherins in Adherens Junctions (AJs) for tissue remodelling, we will narrow down our reports on some experimental studies that focus on adhesion regulation in developing tissues, and its direct impact on cell rearrangements.
6.1 Modulation of adhesion strength in vivo
There are several ways in which a tissue can modulate intercellular adhesion, at different scales in time and space [176, 177]. At long timescales (hours) and large lengthscales (hundreds of microns), adhesion can be regulated under the influence of a morphogen that will tune the expression of the components of the AJs [85, 178, 179]. Adhesion can also be regulated on such timescales through the expression of Eph/ephrin repulsive signalling: when the complementary Eph receptors and ephrin ligands bind to each other, they trigger the cleavage of E-cadherins by the protease ADAM10 [180], as well as an increase of actomyosin cortical contractility [181], resulting in a downregulation of cell-cell adhesion.
Conversely, trafficking of transmembrane proteins ensures the regulation of adhesion molecules on the timescale of minutes [177, 182, 183]. Multiple factors have indeed been shown to regulate E-cadherin trafficking and control AJ dynamics. For instance, Rab5A [184], Nemo [185] or Rab5C [186] can promote E-cadherin endocytosis at AJs independently of acto-myosin contractility. The link between such adhesion regulation processes and the control of cellular rearrangements has been shown in multiple morphogenetic instances [183, 187, 188].
Mechanical signals can also contribute to the dynamical regulation of adhesion. For instance, AJs under tension are usually less likely to undergo endocytosis, which could be in part due to membrane tension preventing the invagination of the membrane [189, 190]. However, the opposite effect if observed during Drosophila wing extension: the p120 catenin is detached from E-cadherins under high tension, causing an increase in the endocytosis of E-cadherins [191] and AJs destabilization.
6.2 Control of tissue shape during morphogenesis
At the beginning of its development, the embryo has a spherical shape. The first significant change of shape is the transition from the cell-filled spherical morula to the blastula, in which cells form a spherical capsule around a fluid center. In mammals, this fluid-filled cavity is formed by the successive fusion of micro-lumens [192]: the hydraulic pressure of the fluid pumped by the cells can break cell-cell adhesions [193] and form small cavities that subsequently fuse into an unique compartment. The pressure-mediated breaking of cell-cell adhesions therefore rearranges the cells in the tissue around this central cavity. When the strength of adhesion is not homogeneously distributed, the fluid cavity forms preferentially in the low adhesion area where the energetic cost of cell rearrangements is the lowest [192].
During gastrulation, the tissues then start changing their shape drastically to form a tubular shape in which different cell layers can be distinguished. For instance, at the onset of epiboly in the zebrafish, specific layers of cells start spreading onto the yolk. This process has been shown to depend on E-cadherin mediated adhesion [194, 195]. In particular, the selective disassembly of cadherin junctions at the center of this tissue [130], and not at its borders, leads to a decrease in cell-cell connectivity and a rapid fluidization - through intercalation - of the tissue [84]. This local modulation of adhesion during epiboly has been shown to depend on E-cadherin trafficking regulation [196]. Therefore, the spatio-temporal modulation of adhesion directly controls the connectivity at the cell scale and thus tunes the viscosity at the tissue scale, eventually controlling its morphogenesis.
After gastrulation, during germband extension, the increased endocytosis of cadherins at the AJs along the dorso-ventral axis decreases their strength [187, 197, 198]. As a result, the weakened junctions undergo parallel T1 events, leading to a coordinated elongation of the tissue along the antero-posterior axis. This process is also regulated by the mechanosensitivity of the AJs. Indeed, efficient cell intercalation, that is necessary for germband extension, requires the mechanosensitive binding of vinculin to α-catenin. Therefore, embryos in which the α-catenin domains allowing binding to vinculin are disrupted are shorter, indicating an impaired convergent extension [199].
In all these morphogenetic stages, the spatial pattern of adhesion modulation sets a localized fluidization through facilitated rearrangements, or a preferred axis for the rearrangements, leading eventually to layering, folding or extension processes.
6.3 Control of epithelial packing topology
Many tissues require precise cellular packings in order to ensure their biological function. For instance the precise packing of cells in the eye is necessary to control the optical properties of the tissue. Another well-studied system is the precise arrangement of hair in the Drosophila wing, which is essential for the control of air flow [200]. To ensure such a precise control of cellular packing in the plane of the tissue, modulation of AJ stability is necessary to fluidify the tissue locally so that the cells can rearrange in a directed manner and reach a specific packing topology. In particular, during Drosophila wing development, the tissue undergoes two phases of oriented rearrangements that ensure elongation along the antero-posterior axis, and then along the proximal-distal axis [201]. After these successive events associated to extensive cellular rearrangements, the cells need to reach a precise hexagonal packing in order to ensure proper hair position in the wing. Such ordering of the cellular position results from a spatial regulation of E-cadherin endocytosis, which in turn controls the direction of the cellular rearrangements [202]. This spatial control of junction regulations is performed under the regulation of planar polarity pathways [183]. Therefore, biological tissues can be locally and asymmetrically fluidized to drive the emergence of a given packing topology.
6.4 Sorting and patterning during morphogenesis
Cellular sorting was mostly described in the context of the differential adhesion hypothesis in vitro cellular aggregates. However, differences in adhesion proteins expression have also been demonstrated to play a role in a wide range of morphogenetic processes requiring cell sorting (see [203] for a review). In fact, during development, cells are continuously mixed through rearrangements and morphogen gradients are not always sufficient to ensure precise patterning. In some situations, processes that are driven by differential adhesion are therefore necessary, in addition to morphogen signaling, to maintain positional information against rearrangement-induced mixing.
In particular, in the zebrafish embryo, the 3 types of neural progenitors of the spinal chord each express a unique combination of 3 adhesion proteins, in response to morphogen gradients: each cell type adheres preferentially to cells of the same type. During the convergent extension stage of the spinal chord morphogenesis, this adhesion pattern drives cellular sorting and its combination with a morphogen gradient ensures the maintenance of sharp boundaries between the 3 cell types, despite the extensive rearrangements occurring during this elongation process [85]. Similarly, in the Drosophila abdominal epidermis, expression of the cell-cell adhesion protein Toll-1 at the boundaries of histoblasts helps maintain a straight frontier between compartments during development [179]. With a different mechanism, the expression of a complementary pattern of Eph and ephrins in mesoderm and ectoderm cells of the Xenopus embryo tunes down the cadherin adhesion at the boundary between the two tissues. In the absence of this signalling pathway, cells of the two lineages mix in the embryo, leading to a loss of spatial organization [111].
6.5 Collective migration during morphogenesis
During some developmental processes, groups or clusters of cells need to maintain their cohesiveness while also moving collectively within the surrounding tissue. In this case, a rigid-like cluster of cells has to co-exist within a fluid-like surrounding tissue, highlighting the necessity of precise adhesion regulation in these processes. These subtle links between adhesion, rearrangements and collective migration, are also central for the study of tumor progression and metastasis. We here review a few examples of such processes in which adhesion regulation is key to control cell-cell intercalation inside and outside of moving cellular clusters.
During gastrulation, the newly defined mesendoderm internalizes in a collective motion to form a layered 3-dimensional tissue. Yet, it must preserve the positional order of the cells that were previously exposed to a gradient of the morphogen Nodal. It was shown recently that this orderly collective motion is ensured by a preferential adhesion set by the Nodal gradient: each cell adheres best to the cells that have received a similar dose of morphogen [178]. Cells exposed to the highest concentrations act as leader cells with an increased protrusive activity, inducing a local unjamming. At the same time, the differential adhesion ensures that the cells move sequentially by following only the neighbors with the same initial position. This process reveals how the mechanism described in the previous section can be combined with motility in order to yield a collective motion preserving the positional order set by gradients of morphogens.
In later stages of development, some groups of cells need to migrate long distances to reach their final destination. To migrate as a collective assembly, and yet not be stuck or jammed, they need to regulate precisely their level of cell-cell adhesion. For instance, the eye morphogenesis in Drosophila strongly depends on the chiral rotation of cellular ommatidial clusters [204]. It was shown that this process is controlled directly by factors that regulate E-cadherin trafficking and AJs dynamics in the different tissues [185]: Nemo upregulation leads to increased E-cadherin endocytosis, which leads to a fluid-like transition of the tissue between ommatidial clusters, allowing for their rotation. Conversely, Nemo loss of function leads to reduced E-cad endocytosis, which in turn leads to higher levels at the junctions of such cells and tissue rigidification.
Similarly, the collective migration of neural crest cells has been studied in Xenopus. After the formation of the neural tube, neural crest cells undergo an epithelial to mesenchymal transition, delaminate from the neural tube by down-regulating their cadherin expression and start migrating in the body. The transition may be partial and neural crest cells then migrate as small cohesive clusters of cells. In these clusters, adhesion levels are finely tuned through N-cadherin endocytosis, so that the cluster remains cohesive while cells are still able to rearrange in order to migrate through narrow gaps [205]. When N-cadherin is over-expressed, the clusters become solid-like as rearrangements become too costly. Conversely, when N-cadherin expression is too low, the clusters lose their cohesion.
It is also important to note that cell rearrangements continue to play a major role in tissue plasticity even after development, and in particular during wound healing [164]. For instance, repulsive signalling by Eph/ephrins, already shown to promote cell rearrangements via adhesion downregulation [111, 112, 180], is also necessary in vivo to rearrange the epithelium during wound closure [206].
6.6 Modification of rearrangements dynamics through the regulation of vertex-specific proteins
Unlike emulsions or foams, epithelial tissues often maintain their packing fraction at values close to 100% in order to ensure the impermeability of the monolayer. Therefore, there is an additional set of specialized proteins that close the gaps at the vertices where three or more cells meet (see [207, 208] for reviews). The Drosophila sidekick has been identified as a protein of such tricellular adhesion complexes [21, 27, 28, 209]. Like cadherins, these proteins are regulated by the levels of tension at the junction. During a T1 transition, the sidekick aggregates present at vertices fuse on the shrinking contact, then separate into new vertices as the T1 resolves. Therefore, the critical role of sidekick has been underlined in processes involving intense epithelial remodelling, such as germband extension [21] or tracheal morphogenesis [27]. During these processes, the absence of sidekick proteins slows down the T1 transitions, which then fail to resolve as the cells remain at the 4-way vertex intermediary stage, leading to defects in the remodeling tissue. Therefore, the action of these specific adhesion proteins actually promotes the completion of rearrangements. Likewise, during the Drosophila male genital development, sidekick and E-cadherin were seen to exclude each other [28]: the accumulation of sidekick in shrinking junctions favors the disassembly of the adhesive contact by excluding E-cadherin. Conversely, its localization at the newly formed vertices favors cadherin-mediated adhesion at the growing edge and the formation of a new AJ.
7 Conclusion and perspectives: Adhesion in the jamming phase diagram for biological tissues
In this review we presented the effect of adhesion on rearrangements in a wide range of systems, ranging from particles and biomimetic systems, to tissue remodelling during morphogenesis. Synthetic approaches did allow to gain quantitative insight into the processes controlling rearrangements in adhesive assemblies of particles. For instance, it was evidenced that the topology of rearrangements in the presence of non-specific adhesion depends on the size of the particles, yielding large predictable avalanches in monodisperse packings, and smaller disordered ones in polydisperse assemblies. It was also shown that specific adhesion was responsible for the oriented deformation of the droplets undergoing rearrangements, similarly to processes observed in vivo during germband extension. Conversely, it is difficult to disentangle the different cellular processes at stake during rearrangements in biological tissues, because of the feedback loop between intercellular adhesion and cellular mechanics through mechanotransduction. However, we reported here on some developmental stages depending on cellular rearrangements that are directly regulated through intercellular adhesion, leading to tissue shape changes, self-organization, fluidization or cellular packing modifications.
An appealing strategy to unify all these out-of-equilibrium processes is to describe them in the framework of a jamming phase diagram [210]. Indeed, by analogy with granular systems, biological tissues have been increasingly described in the framework of the jamming transition (see [210, 211] for reviews). During such a transition, the tissue undergoes structural arrest, i.e. its cells are caged by each other and stop moving [212–217]. Conversely, increased cellular fluctuations and motility can drive uncaging and therefore unjamming in a tissue [184, 218, 219].
Based on these analogies and on experimental observations, phase diagrams for jamming phenomena in biological tissues have been proposed recently, revolving typically along three axes. The first axis concerns the fluctuations provided by contractility (shape fluctuations [95]) or motility, i.e., positional fluctuations). The higher the fluctuations the less jammed the tissue. The second one, in direct analogy with inert materials, is taken as the inverse of the tissue packing fraction, simply meaning that cellular crowding is a jamming factor. While this parameter is not explicitly dependant on cell-cell adhesion, it has been shown that down-regulating adhesion in developing tissues leads to a decrease in tissue packing fraction [213]. The third axis is described as geometric incompatibility in [210], which translates the idea that deviations from a preferred cell shape is sufficient to induce rigidity transitions in an otherwise constant network of contacts [157].
While adhesion is not explicitly an axis of these phase diagrams, it has been shown to play a role on tissue packing fraction and neighbor rate exchange in developing zebrafish embryos [213], which are both critical parameters for tissue rigidity. Moreover, the network of adhesive contacts in tissues can also control their mechanical properties. An analogy can be drawn with rigidity percolation theories in soft matter: if the network of intercellular adhesive contacts is percolating, the mechanical stability of the network provides the tissue with increased viscosity [84]. Effects of percolation have also been observed on the deformation of biomimetic droplets in static 2D packings [220]. The study of adhesion networks in tissues could therefore be a key parameter to study mechanical properties from the individual cell scale to the tissue level in a unified framework. In particular, it would be interesting to couple the idea of percolation theory to a measurement of the adhesion strength in the contact network. For instance, if the adhesion energy between 2 cells is low enough, the contact between these cells could be considered as a weak link and not participate in the adhesion network. While a continuum of adhesion energy might be difficult to include in that framework, a first step towards this idea could consist in setting a threshold value of adhesion strength below which a contact between cells would be removed from the contact network. Studying how the rigidity of such networks evolves as a function of this threshold value could give insight into the link between the energetics of individual rearrangements and the mechanical properties of the whole tissue.
Author contributions
L-LP, LM, and QG wrote the original draft and edited it.
Acknowledgments
The authors thank Thibault Bertrand, Silvia Grigolon, Elie Wandersman and Alexis Prevost for fruitful discussions. L-LP acknowledges financial support from Agence Nationale de la Recherche (BOAT, ANR-17-CE30-0001) and from Emergence(s) Ville de Paris.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Gumbiner BM. Regulation of cadherin-mediated adhesion in morphogenesis. Nat Rev Mol Cel Biol (2005) 6:622–34. doi:10.1038/nrm1699
2. Borghi N, James Nelson W. Intercellular adhesion in morphogenesis: Molecular and biophysical considerations. Curr Top Dev Biol (2009) 89:1–32. Elsevier Inc. doi:10.1016/S0070-2153(09)89001-7
3. Janiszewska M, Primi MC, Izard T. Cell adhesion in cancer: Beyond the migration of single cells. J Biol Chem (2020) 295:2495–505. doi:10.1074/JBC.REV119.007759
4. Harris TJ, Tepass U. Adherens junctions: From molecules to morphogenesis. Nat Rev Mol Cel Biol (2010) 11:502–14. doi:10.1038/nrm2927
5. Takeichi M. Dynamic contacts: rearranging adherens junctions to drive epithelial remodelling. Nat Rev Mol Cel Biol (2014) 15:397–410. doi:10.1038/nrm3802
6. Ladoux B, Nelson WJ, Yan J, Mège RM. The mechanotransduction machinery at work at adherens junctions. Integr Biol : quantitative Biosciences nano macro (2015) 7:1109–19. doi:10.1039/C5IB00070J
7. Boggon TJ, Murray J, Chappuis-Flament S, Wong E, Gumbiner BM, Lawrence S. C-cadherin ectodomain structure and implications for cell adhesion mechanisms. Science (2002) 296:1308–13. doi:10.1126/science.1071559
8. Kudo S, Caaveiro JM, Tsumoto K. Adhesive dimerization of human P-cadherin catalyzed by a chaperone-like mechanism. Structure (2016) 24:1523–36. doi:10.1016/j.str.2016.07.002
9. Harrison OJ, Jin X, Hong S, Bahna F, Ahlsen G, Brasch J, et al. The extracellular architecture of adherens junctions revealed by crystal structures of type i cadherins. Structure (2011) 19:244–56. doi:10.1016/j.str.2010.11.016
10. Wu Y, Kanchanawong P, Zaidel-Bar R. Actin-delimited adhesion-independent clustering of E-cadherin forms the nanoscale building blocks of adherens junctions. Dev Cel (2015) 32:139–54. doi:10.1016/j.devcel.2014.12.003
11. Strale PO, Duchesne L, Peyret G, Montel L, Nguyen T, Png E, et al. The formation of ordered nanoclusters controls cadherin anchoring to actin and cell–cell contact fluidity. J Cel Biol (2015) 210:333–46. doi:10.1083/jcb.201410111
12. Engl W, Arasi B, Yap LL, Thiery JP, Viasnoff V. Actin dynamics modulate mechanosensitive immobilization of E-cadherin at adherens junctions. Nat Cel Biol (2014) 16:584–91. doi:10.1038/ncb2973
13. Koslov ER, Maupin P, Pradhan D, Morrow JS, Rimm DL. α-Catenin can form asymmetric homodimeric complexes and/or heterodimeric complexes with ॆ-Catenin. J Biol Chem (1997) 272:27301–6. doi:10.1074/JBC.272.43.27301
14. Yap aS, Brieher WM, Pruschy M, Gumbiner BM. Lateral clustering of the adhesive ectodomain: A fundamental determinant of cadherin function. Curr Biol (1997) 7:308–15. doi:10.1016/s0960-9822(06)00154-0
15. Aberle H, Butz S, Stappert J, Weissig H, Kemler R, Hoschuetzky H. Assembly of the cadherin-catenin complex in vitro with recombinant proteins. J Cel Sci (1994) 107:3655–63. doi:10.1242/JCS.107.12.3655
16. Drees F, Pokutta S, Yamada S, Nelson WJ, Weis WI. α-Catenin is a molecular switch that binds E-cadherin-β-catenin and regulates actin-filament assembly. Cell (2005) 123:903–15. doi:10.1016/J.CELL.2005.09.021
17. Yonemura S, Wada Y, Watanabe T, Nagafuchi A, Shibata M. α-Catenin as a tension transducer that induces adherens junction development. Nat Cel Biol (2010) 12:533–42. doi:10.1038/ncb2055
18. Yao M, Goult BT, Chen H, Cong P, Sheetz MP, Yan J. Mechanical activation of vinculin binding to talin locks talin in an unfolded conformation. Sci Rep (2014) 4:4610–7. doi:10.1038/srep04610
19. Seddiki R, Narayana GHNS, Strale PO, Balcioglu HE, Peyret G, Yao M, et al. Force-dependent α -catenin regulates cell–cell contact stability and collective cell behavior. Mol Biol Cel (2018) 29:380–8. doi:10.1091/MBC.E17-04-0231
20. Aladin DMK, Chu YS, Shen S, Robinson RC, Dufour S, Viasnoff V, et al. Extracellular domains of E-cadherin determine key mechanical phenotypes of an epithelium through cell- and non-cell-autonomous outside-in signaling. PLOS ONE (2021) 16:e0260593. doi:10.1371/JOURNAL.PONE.0260593
21. Finegan TM, Hervieux N, Nestor-Bergmann A, Fletcher AG, Blanchard GB, Sanson B. The tricellular vertex-specific adhesion molecule Sidekick facilitates polarised cell intercalation during Drosophila axis extension. Plos Biol (2019) 17:e3000522. doi:10.1371/JOURNAL.PBIO.3000522
22. Chu YS, Thomas WA, Eder O, Pincet F, Perez E, Thiery JP, et al. Force measurements in E-cadherin-mediated cell doublets reveal rapid adhesion strengthened by actin cytoskeleton remodeling through Rac and Cdc42. J Cel Biol (2004) 167:1183–94. doi:10.1083/jcb.200403043
23. Chu YS, Dufour S, Thiery JP, Perez E, Pincet F. Johnson-kendall-roberts theory applied to living cells. Phys Rev Let American Physical Society (2005). doi:10.1103/PhysRevLett.94.028102
24. Maître JL, Berthoumieux H, Krens SFG, Salbreux G, Jülicher F, Paluch E, et al. Adhesion functions in cell sorting by mechanically coupling the cortices of adhering cells. Science (2012) 338:253–6. doi:10.1126/science.1225399
25. Slováková J, Sikora M, Arslan FN, Caballero-Mancebo S, Krens SF, Kaufmann WA, et al. Tension-dependent stabilization of E-cadherin limits cell-cell contact expansion in zebrafish germ-layer progenitor cells. Proc Natl Acad Sci U S A (2022) 119:e2122030119. doi:10.1073/PNAS.2122030119
26. Krieg M, Arboleda-Estudillo Y, Puech PH, Käfer J, Graner F, Müller DJ, et al. Tensile forces govern germ-layer organization in zebrafish. Nat Cel Biol (2008) 10:429–36. doi:10.1038/ncb1705
27. Letizia A, He D, Astigarraga S, Colombelli J, Hatini V, Llimargas M, et al. Sidekick is a key component of tricellular adherens junctions that acts to resolve cell rearrangements. Dev Cel (2019) 50:313–26.e5. doi:10.1016/j.devcel.2019.07.007
28. Uechi H, Kuranaga E. The tricellular junction protein sidekick regulates vertex dynamics to promote bicellular junction extension. Dev Cel (2019) 50:327–38.e5. doi:10.1016/j.devcel.2019.06.017
30. Clusel M, Corwin EI, Siemens AON, Brujić J. A ‘granocentric’model for random packing of jammed emulsions. Nature (2009) 460:611–5. doi:10.1038/nature08158
31. Brujić J, Song C, Wang P, Briscoe C, Marty G, Makse HA. Measuring the coordination number and entropy of a 3D jammed emulsion packing by confocal microscopy. Phys Rev Lett (2007) 98:248001. doi:10.1103/PhysRevLett.98.248001
32. Jorjadze I, Pontani LL, Newhall KA, Brujic J. Attractive emulsion droplets probe the phase diagram of jammed granular matter. Proc Natl Acad Sci U S A (2011) 108:4286–91. doi:10.1073/pnas.1017716108
33. Koeze DJ, Tighe BP. Sticky matters: Jamming and rigid cluster statistics with attractive particle interactions. Phys Rev Lett (2018) 121:188002. doi:10.1103/PhysRevLett.121.188002
34. Mason TG, Bibette J, Weitz DA. Elasticity of compressed emulsions. Phys Rev Lett (1995) 75:2051–4. doi:10.1103/PhysRevLett.75.2051
35. Jorjadze I, Pontani LL, Brujic J. Microscopic approach to the nonlinear elasticity of compressed emulsions. Phys Rev Lett (2013) 110:048302. doi:10.1103/PhysRevLett.110.048302
36. Datta SS, Gerrard DD, Rhodes TS, Mason TG, Weitz DA. Rheology of attractive emulsions. Phys Rev E (2011) 84:041404. doi:10.1103/PhysRevE.84.041404
37. Koeze DJ, Hong L, Kumar A, Tighe BP. Elasticity of jammed packings of sticky disks. Phys Rev Res (2020) 2:032047. doi:10.1103/physrevresearch.2.032047
38. Ono-Dit-Biot JC, Soulard P, Barkley S, Weeks ER, Salez T, Raphaël E, et al. Rearrangement of two dimensional aggregates of droplets under compression: Signatures of the energy landscape from crystal to glass. Phys Rev Res (2020) 2:023070. doi:10.1103/PhysRevResearch.2.023070
39. Golovkova I, Montel L, Pan F, Wandersman E, Prevost AM, Bertrand T, et al. Adhesion as a trigger of droplet polarization in flowing emulsions. Soft Matter (2021) 17:3820–8. doi:10.1039/D1SM00097G
40. Chen D, Desmond KW, Weeks ER. Topological rearrangements and stress fluctuations in quasi-two-dimensional hopper flow of emulsions. Soft Matter (2012) 8:10486–92. doi:10.1039/C2SM26023A
41. Gai Y, Leong CM, Cai W, Tang SKY. Spatiotemporal periodicity of dislocation dynamics in a two-dimensional microfluidic crystal flowing in a tapered channel. Proc Natl Acad Sci U S A (2016) 113:12082–7. doi:10.1073/pnas.1606601113
42. Golovkova I, Montel L, Wandersman E, Bertrand T, Prevost AM, Pontani LL. Depletion attraction impairs the plasticity of emulsions flowing in a constriction. Soft Matter (2020) 16:3294–302. doi:10.1039/c9sm02343g
43. McDermott D, Reichhardt CJ, Reichhardt C. Avalanches, plasticity, and ordering in colloidal crystals under compression. Phys Rev E (2016) 93:062607. doi:10.1103/physreve.93.062607
44. Durand M, Stone HA. Relaxation time of the TopologicalT1Process in a two-dimensional foam. Phys Rev Lett (2006) 97:226101. doi:10.1103/physrevlett.97.226101
45. Dollet B, Bocher C. Flow of foam through a convergent channel. Eur Phys J E (2015) 38:123–11. doi:10.1140/epje/i2015-15123-3
46. Bergeron V, Langevin D, Asnacios A. Thin-film forces in foam films containing anionic polyelectrolyte and charged surfactants. Langmuir (1996) 12:1550–6. doi:10.1021/la950654z
47. Cohen-Addad S, Höhler R, Pitois O. Flow in foams and flowing foams. Annu Rev Fluid Mech (2013) 45:241–67. doi:10.1146/annurev-fluid-011212-140634
48. Dollet B, Raufaste C. Rheology of aqueous foams. Comptes Rendus Phys (2014) 15:731–47. doi:10.1016/j.crhy.2014.09.008
49. Fenz SF, Sengupta K. Giant vesicles as cell models. In: Integrative biology quantitative biosciences from nano to macro (2012). doi:10.1039/c2ib00188h
50. Pautot S, Frisken BJ, Weitz DA. Production of unilamellar vesicles using an inverted emulsion. Langmuir (2003) 19:2870–9. doi:10.1021/la026100v
51. Pontani LL, Van Der Gucht J, Salbreux G, Heuvingh J, Joanny JF, Sykes C. Reconstitution of an actin cortex inside a liposome. Biophysical J (2009) 96:192–8. doi:10.1016/j.bpj.2008.09.029
52. Noireaux V, Libchaber A. A vesicle bioreactor as a step toward an artificial cell assembly. Proc Natl Acad Sci U S A (2004) 101:17669–74. doi:10.1073/pnas.0408236101
53. Smith AS, Sackmann E. Progress in mimetic studies of cell adhesion and the mechanosensing. ChemPhysChem (2009) 10:66–78. doi:10.1002/cphc.200800683
54. Bachmann SJ, Kotar J, Parolini L, Šarić A, Cicuta P, Di Michele L, et al. Melting transition in lipid vesicles functionalised by mobile DNA linkers. Soft Matter (2016) 12:7804–17. doi:10.1039/c6sm01515h
55. Hadorn M, Hotz PE. DNA-mediated self-assembly of artificial vesicles. PLOS ONE (2010) 5:e9886. doi:10.1371/JOURNAL.PONE.0009886
56. Chiruvolu S, Walker S, Israelachvili J, Schmitt FJ, Leckband D, Zasadzinski JA. Higher order self-assembly of vesicles by site-specific binding. Science (New York, N.Y.) (1994) 264:1753–6. doi:10.1126/SCIENCE.8209255
57. Parolini L, Kotar J, Di Michele L, Mognetti BM. Controlling self-assembly kinetics of DNA-functionalized liposomes using toehold exchange mechanism. ACS Nano (2016) 10:2392–8. doi:10.1021/acsnano.5b07201
58. Casas-Ferrer L, Brisson A, Massiera G, Casanellas L. Design of vesicle prototissues as a model for cellular tissues. Soft Matter (2021) 17:5061–72. doi:10.1039/d1sm00336d
59. Fattaccioli J, Baudry J, Henry N, Brochard-Wyart F, Bibette J. Specific wetting probed with biomimetic emulsion droplets. Soft Matter (2008) 4:2434. doi:10.1039/b806635c
60. Bourouina N, Husson J, Waharte F, Pansu RB, Henry N, Purdy PW, et al. Formation of specific receptor–ligand bonds between liquid interfaces. Soft Matter (2011) 7:9130. doi:10.1039/c1sm05659j
61. Pontani LL, Jorjadze I, Viasnoff V, Brujic J. Biomimetic emulsions reveal the effect of mechanical forces on cell–cell adhesion. Proc Natl Acad Sci U S A (2012) 109:9839–44. doi:10.1073/pnas.1201499109
62. Campàs O, Mammoto T, Hasso S, Sperling RA, O’Connell D, Bischof AG, et al. Quantifying cell-generated mechanical forces within living embryonic tissues. Nat Methods (2014) 11:183–9. doi:10.1038/nmeth.2761
63. Pontani LL, Jorjadze I, Brujic J. Cis and trans cooperativity of E-cadherin mediates adhesion in biomimetic lipid droplets. Biophysical J (2016) 110:391–9. doi:10.1016/j.bpj.2015.11.3514
64. Feng L, Pontani LL, Dreyfus R, Chaikin P, Brujic J. Specificity, flexibility and valence of dna bonds guide emulsion architecture. Soft Matter (2013) 9:9816. doi:10.1039/c3sm51586a
65. Hadorn M, Boenzli E, Sorensen KT, Fellermann H, Eggenberger Hotz P, Hanczyc MM. Specific and reversible DNA-directed self-assembly of oil-in-water emulsion droplets. Proc Natl Acad Sci U S A (2012) 109:20320–5. doi:10.1073/pnas.1214386109
66. Zhang Y, McMullen A, Pontani LL, He X, Sha R, Seeman NC, et al. Sequential self-assembly of DNA functionalized droplets. Nat Commun (2017) 8:21. doi:10.1038/s41467-017-00070-0
67. Stoev ID, Caciagli A, Mukhopadhyay A, Ness C, Eiser E. Bulk rheology of sticky DNA-functionalized emulsions. Phys Rev E (2021) 104:054602. doi:10.1103/PHYSREVE.104.054602
68. McMullen A, Hilgenfeldt S, Brujic J. DNA self-organization controls valence in programmable colloid design. Proc Natl Acad Sci U S A (2021) 118:e2112604118. doi:10.1073/PNAS.2112604118
69. Keller R. Mechanisms of elongation in embryogenesis. Development (Cambridge, England) (2006) 133:2291–302. doi:10.1242/DEV.02406
70. Butler LC, Blanchard GB, Kabla AJ, Lawrence NJ, Welchman DP, Mahadevan L, et al. Cell shape changes indicate a role for extrinsic tensile forces in Drosophila germ-band extension. Nat Cel Biol (2009) 11:859–64. doi:10.1038/NCB1894
71. Zallen JA. Planar polarity and tissue morphogenesis. Cell (2007) 129:1051–63. doi:10.1016/J.CELL.2007.05.050
72. Tsai FC, Stuhrmann B, Koenderink GH. Encapsulation of active cytoskeletal protein networks in cell-sized liposomes. Langmuir (2011) 27:10061–71. doi:10.1021/la201604z
73. Sanchez T, Chen DT, Decamp SJ, Heymann M, Dogic Z. Spontaneous motion in hierarchically assembled active matter. Nature (2012) 491:431–4. doi:10.1038/nature11591
74. Dwivedi P, Pillai D, Mangal R. Self-propelled swimming droplets. Curr Opin Colloid Interf Sci (2022) 101614. doi:10.1016/J.COCIS.2022.101614
75. Stirbat TV, Mgharbel A, Bodennec S, Ferri K, Mertani HC, Rieu JP, et al. Fine tuning of tissues’ viscosity and surface tension through contractility suggests a new role for α-. PLoS ONE (2013) 8:52554. doi:10.1371/journal.pone.0052554
76. Tlili S, Durande M, Gay C, Ladoux B, Graner F, Delanoë-Ayari H. Migrating epithelial monolayer flows like a Maxwell viscoelastic liquid. Phys Rev Lett (2020) 125:088102. doi:10.1103/physrevlett.125.088102
77. Friedlander DR, Mege RM, Cunningham BA, Edelman GM. Cell sorting-out is modulated by both the specificity and amount of different cell adhesion molecules (CAMs) expressed on cell surfaces. Proc Natl Acad Sci U S A (1989) 86:7043–7. doi:10.1073/PNAS.86.18.7043
78. Dufour S, Beauvais-Jouneau A, Delouvée A, Thiery JP. Differential function of N-cadherin and cadherin-7 in the control of embryonic cell motility. J Cel Biol (1999) 146:501–16. doi:10.1083/JCB.146.2.501
79. Douezan S, Guevorkian K, Naouar R, Dufour S, Cuvelier D, Brochard-Wyart F. Spreading dynamics and wetting transition of cellular aggregates. Proc Natl Acad Sci U S A (2011) 108:7315–20. doi:10.1073/pnas.1018057108
80. Bazellières E, Conte V, Elosegui-Artola A, Serra-Picamal X, Bintanel-Morcillo M, Roca-Cusachs P, et al. Control of cell–cell forces and collective cell dynamics by the intercellular adhesome. Nat Cel Biol (2015) 17:409–20. doi:10.1038/ncb3135
81. Martin AC, Gelbart M, Fernandez-Gonzalez R, Kaschube M, Wieschaus EF. Integration of contractile forces during tissue invagination. J Cel Biol (2010) 188:735–49. doi:10.1083/jcb.200910099
82. Montero JA, Carvalho L, Wilsch-Bräuninger M, Kilian B, Mustafa C, Heisenberg CP. Shield formation at the onset of zebrafish gastrulation. Development (2005) 132:1187–98. doi:10.1242/dev.01667
83. Capaldo CT, Macara IG. Depletion of E-cadherin disrupts establishment but not maintenance of cell junctions in madin-darby canine Kidney epithelial cells. Mol Biol Cel (2007) 18:189–200. doi:10.1091/MBC.E06-05-0471
84. Petridou NI, Corominas-Murtra B, Heisenberg CP, Hannezo E. Rigidity percolation uncovers a structural basis for embryonic tissue phase transitions. Cell (2021) 184:1914–28.e19. doi:10.1016/j.cell.2021.02.017
85. Tsai TY, Sikora M, Xia P, Colak-Champollion T, Knaut H, Heisenberg CP, et al. An adhesion code ensures robust pattern formation during tissue morphogenesis. Science (2020) 370:113–6. doi:10.1126/science.aba6637
86. Handschuh G, Candidus S, Luber B, Reich U, Schott C, Oswald S, et al. Tumour-associated E-cadherin mutations alter cellular morphology, decrease cellular adhesion and increase cellular motility. Oncogene (1999) 18:4301–12. doi:10.1038/sj.onc.1202790
87. Nagar B, Overduin M, Ikura M, Rini JM. Structural basis of calcium-induced E-cadherin rigidification and dimerization. Nature (1996) 380:360–4. doi:10.1038/380360A0
88. Kim SA, Tai CY, Mok LP, Mosser EA, Schuman EM. Calcium-dependent dynamics of cadherin interactions at cell-cell junctions. Proc Natl Acad Sci U S A (2011) 108:9857–62. doi:10.1073/pnas.1019003108
89. Mertz AF, Che Y, Banerjee S, Goldstein JM, Rosowski KA, Revilla SF, et al. Cadherin-based intercellular adhesions organize epithelial cell-matrix traction forces. Proc Natl Acad Sci U S A (2013) 110:842–7. doi:10.1073/pnas.1217279110
90. Ollech D, Pflästerer T, Shellard A, Zambarda C, Spatz JP, Marcq P, et al. An optochemical tool for light-induced dissociation of adherens junctions to control mechanical coupling between cells. Nat Commun (2020) 11:472–13. doi:10.1038/s41467-020-14390-1
91. Schoenit A, Lo Giudice C, Hahnen N, Ollech D, Jahnke K, Göpfrich K, et al. Tuning epithelial cell-cell adhesion and collective dynamics with functional DNA-E-cadherin hybrid linkers. Nano Lett (2022) 22:302–10. doi:10.1021/acs.nanolett.1c03780
92. Steinberg MS. Reconstruction of tissues by dissociated cells. Science (1963) 141:401–8. doi:10.1126/science.141.3579.401
93. Vasilica Stirbat T, Tlili S, Houver T, Rieu JP, Barentin C, Delanoë-Ayari H. Multicellular aggregates: A model system for tissue rheology. Eur Phys J E (2013) 36:84. doi:10.1140/EPJE/I2013-13084-1
94. Gonzalez-Rodriguez D, Guevorkian K, Douezan S, Brochard-Wyart F. Soft matter models of developing tissues and tumors. Science (New York, N.Y.) (2012) 338:910–7. doi:10.1126/science.1226418
95. Marmottant P, Mgharbel A, Käfer J, Audren B, Rieu JP, Vial JC, et al. The role of fluctuations and stress on the effective viscosity of cell aggregates. Proc Natl Acad Sci U S A (2009) 106:17271–5. doi:10.1073/pnas.0902085106
96. Foty RA, Forgacs G, Pfleger CM, Steinberg MS. Liquid properties of embryonic tissues: Measurement of interfacial tensions. Phys Rev Lett (1994) 72:2298–301. doi:10.1103/PHYSREVLETT.72.2298
97. Forgacs G, Foty RA, Shafrir Y, Steinberg MS. Viscoelastic properties of living embryonic tissues: A quantitative study. Biophysical J (1998) 74:2227–34. doi:10.1016/S0006-3495(98)77932-9
98. Mgharbel A, Delanoë-Ayari H, Rieu JP. Measuring accurately liquid and tissue surface tension with a compression plate tensiometer. HFSP J (2009) 3:213–21. doi:10.2976/1.3116822
99. Norotte C, Marga F, Neagu A, Kosztin I, Forgacs G. Experimental evaluation of apparent tissue surface tension based on the exact solution of the Laplace equation. Europhys Lett (2008) 81:46003. doi:10.1209/0295-5075/81/46003
100. Guevorkian K, Colbert MJ, Durth M, Dufour S, Brochard-Wyart F. Aspiration of biological viscoelastic drops. Phys Rev Lett (2010) 104:218101. doi:10.1103/PhysRevLett.104.218101
101. Foty RA, Steinberg MS. The differential adhesion hypothesis: A direct evaluation. Dev Biol (2005) 278:255–63. doi:10.1016/J.YDBIO.2004.11.012
102. Steinberg MS, Takeichi M. Experimental specification of cell sorting, tissue spreading, and specific spatial patterning by quantitative differences in cadherin expression. Proc Natl Acad Sci U S A (1994) 91:206–9. doi:10.1073/pnas.91.1.206
103. Foty RA, Pfleger CM, Forgacs G, Steinberg MS. Surface tensions of embryonic tissues predict their mutual envelopment behavior. Development (Cambridge, England) (1996) 122:1611–20. doi:10.1242/dev.122.5.1611
104. Manning ML, Foty RA, Steinberg MS, Schoetz EM. Coaction of intercellular adhesion and cortical tension specifies tissue surface tension. In: Proceedings of the National Academy of Sciences of the United States of America (2010). doi:10.1073/pnas.1003743107
105. Armstrong PB. Cell sorting out: The self-assembly of tissues in vitro. Crit Rev Biochem Mol Biol (1989) 24:119–49. doi:10.3109/10409238909086396
106. Holtfreter J. A study of the mechanics of gastrulation. J Exp Zool (1944) 95:171–212. doi:10.1002/JEZ.1400950203
107. Steinberg MS. Adhesion in development: An historical overview. Dev Biol (1996) 180:377–88. doi:10.1006/DBIO.1996.0312
108. Davis GS, Phillips HM, Steinberg MS. Germ-layer surface tensions and “tissue affinities” inRana pipiensGastrulae: Quantitative measurements. Dev Biol (1997) 192:630–44. doi:10.1006/DBIO.1997.8741
109. Pawlizak S, Fritsch AW, Grosser S, Ahrens D, Thalheim T, Riedel S, et al. Testing the differential adhesion hypothesis across the epithelial-mesenchymal transition. New J Phys (2015) 17:083049. doi:10.1088/1367-2630/17/8/083049
110. Amack JD, Manning ML. Knowing the boundaries: Extending the differential adhesion hypothesis in embryonic cell sorting. Science (New York, N.Y.) (2012) 338:212–5. doi:10.1126/SCIENCE.1223953
111. Rohani N, Parmeggiani A, Winklbauer R, Fagotto F. Variable combinations of specific ephrin ligand/eph receptor pairs control embryonic tissue separation. Plos Biol (2014) 12:e1001955. doi:10.1371/journal.pbio.1001955
112. Rohani N, Canty L, Luu O, Fagotto F, Winklbauer R. EphrinB/EphB signaling controls embryonic germ layer separation by contact-induced cell detachment. Plos Biol (2011) 9:e1000597. doi:10.1371/journal.pbio.1000597
113. Jasaitis A, Estevez M, Heysch J, Ladoux B, Dufour S. E-Cadherin-Dependent stimulation of traction force at focal adhesions via the src and PI3K signaling pathways. Biophysical J (2012) 103:175–84. doi:10.1016/J.BPJ.2012.06.009
114. Alessandri K, Sarangi BR, Gurchenkov VV, Sinha B, Kießling TR, Fetler L, et al. Cellular capsules as a tool for multicellular spheroid production and for investigating the mechanics of tumor progression in vitro. Proc Natl Acad Sci U S A (2013) 110:14843–8. doi:10.1073/pnas.1309482110
115. Beaune G, Stirbat TV, Khalifat N, Cochet-Escartin O, Garcia S, Gurchenkov VV, et al. How cells flow in the spreading of cellular aggregates. Proc Natl Acad Sci U S A (2014) 111:8055–60. doi:10.1073/pnas.1323788111
116. Gory Beaune G, Duclos G, Khalifat N, Tomita A, Stirbat V, Matic D, et al. Reentrant wetting transition in the spreading of cellular aggregates. Soft Matter (2017) 13:8474–82. doi:10.1039/c7sm00768j
117. Fidler IJ. The pathogenesis of cancer metastasis: The ’seed and soil’ hypothesis revisited. Nat Rev Cancer (2003) 3:453–8. doi:10.1038/NRC1098
118. Mertz AF, Banerjee S, Che Y, German GK, Xu Y, Hyland C, et al. Scaling of traction forces with the size of cohesive cell colonies. Phys Rev Lett (2012) 108:198101. doi:10.1103/PHYSREVLETT.108.198101
119. Tambe DT, Hardin CC, Angelini TE, Rajendran K, Park CY, Serra-Picamal X, et al. Collective cell guidance by cooperative intercellular forces. Nat Mater (2011) 10:469–75. doi:10.1038/nmat3025
120. Liu Z, Tan JL, Cohen DM, Yang MT, Sniadecki NJ, Ruiz SA, et al. Mechanical tugging force regulates the size of cell-cell junctions. Proc Natl Acad Sci U S A (2010) 107:9944–9. doi:10.1073/pnas.0914547107
121. Blanchard GB, Kabla AJ, Schultz NL, Butler LC, Sanson B, Gorfinkiel N, et al. Tissue tectonics: Morphogenetic strain rates, cell shape change and intercalation. Nat Methods (2009) 6:458–64. doi:10.1038/nmeth.1327
122. Lee P, Wolgemuth CW. Crawling cells can close wounds without purse strings or signaling. Plos Comput Biol (2011) 7:e1002007. doi:10.1371/JOURNAL.PCBI.1002007
123. Prost J, Jülicher F, Joanny JF. Active gel physics. Nat Phys (2015) 11:111–7. doi:10.1038/nphys3224
124. Banerjee S, Marchetti MC. Continuum models of collective cell migration. Adv Exp Med Biol (2019) 1146:45–66. doi:10.1007/978-3-030-17593-1_4
125. Lubkin SR, Murray JD. A mechanism for early branching in lung morphogenesis. J Math Biol (1995) 34:77–94. doi:10.1007/BF00180137
126. Lubkin SR, Li Z. Force and deformation on branching rudiments: cleaving between hypotheses. Biomech Model Mechanobiol (2002) 1:5–16. doi:10.1007/S10237-002-0001-4
127. Varner VD, Nelson CM. Computational models of airway branching morphogenesis. Semin Cel Dev Biol (2017) 67:170–6. doi:10.1016/J.SEMCDB.2016.06.003
128. Alert R, Blanch-Mercader C, Casademunt J. Active fingering instability in tissue spreading. Phys Rev Lett (2019) 122:088104. doi:10.1103/physrevlett.122.088104
129. Saffman PG, Taylor G. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc R Soc Lond Ser A. Math Phys Sci (1958) 245:312–29. doi:10.1098/RSPA.1958.0085
130. Petridou NI, Grigolon S, Salbreux G, Hannezo E, Heisenberg CP. Fluidization-mediated tissue spreading by mitotic cell rounding and non-canonical wnt signalling. Nat Cel Biol (2019) 21:169–78. doi:10.1038/s41556-018-0247-4
131. Popović M, Nandi A, Merkel M, Etournay R, Eaton S, Jülicher F, et al. Active dynamics of tissue shear flow. New J Phys (2017) 19:033006. doi:10.1088/1367-2630/AA5756
132. Pérez-González C, Alert R, Blanch-Mercader C, Gómez-González M, Kolodziej T, Bazellieres E, et al. Active wetting of epithelial tissues. Nat Phys (2018) 15:79–88. doi:10.1038/s41567-018-0279-5
133. Duclut C, Sarkar N, Prost J, Jülicher F. Fluid pumping and active flexoelectricity can promote lumen nucleation in cell assemblies. Proc Natl Acad Sci U S A (2019) 116:19264–73. doi:10.1073/PNAS.1908481116
134. Duclut C, Prost J, Jülicher F. Hydraulic and electric control of cell spheroids. Proc Natl Acad Sci U S A (2021) 118:e2021972118. doi:10.1073/pnas.2021972118
135. Teomy E, Kessler DA, Levine H. Confluent and nonconfluent phases in a model of cell tissue. Phys Rev E (2018) 98:042418. doi:10.1103/PhysRevE.98.042418
136. Boromand A, Signoriello A, Ye F, O’Hern CS, Shattuck MD. Jamming of deformable polygons. Phys Rev Lett (2018) 121:248003. doi:10.1103/PhysRevLett.121.248003
137. Boromand A, Signoriello A, Lowensohn J, Orellana CS, Weeks ER, Ye F, et al. The role of deformability in determining the structural and mechanical properties of bubbles and emulsions. Soft Matter (2019) 15:5854–65. doi:10.1039/c9sm00775j
138. Barton DL, Henkes S, Weijer CJ, Sknepnek R. Active Vertex Model for cell-resolution description of epithelial tissue mechanics. Plos Comput Biol (2017) 13:e1005569. doi:10.1371/journal.pcbi.1005569
139. Staddon MF, Bi D, Tabatabai AP, Ajeti V, Murrell MP, Banerjee S. Cooperation of dual modes of cell motility promotes epithelial stress relaxation to accelerate wound healing. Plos Comput Biol (2018) 14:e1006502. doi:10.1371/journal.pcbi.1006502
140. Nestor-Bergmann A, Blanchard GB, Hervieux N, Fletcher AG, Étienne J, Sanson B. Adhesion-regulated junction slippage controls cell intercalation dynamics in an Apposed-Cortex Adhesion Model. Plos Comput Biol (2022) 18:e1009812. doi:10.1371/JOURNAL.PCBI.1009812
141. Merkel M, Etournay R, Popović M, Salbreux G, Eaton S, Jülicher F. Triangles bridge the scales: Quantifying cellular contributions to tissue deformation. Phys Rev E (2017) 95:032401. doi:10.1103/physreve.95.032401
142. Murisic N, Hakim V, Kevrekidis IG, Shvartsman SY, Audoly B. From discrete to continuum models of three-dimensional deformations in epithelial sheets. Biophysical J (2015) 109:154–63. doi:10.1016/J.BPJ.2015.05.019
143. Fletcher AG, Osterfield M, Baker RE, Shvartsman SY. Vertex models of epithelial morphogenesis. Biophys J (2014) 106:2291–304. doi:10.1016/J.BPJ.2013.11.4498
144. Hannezo E, Prost J, Joanny JF. Theory of epithelial sheet morphology in three dimensions. Proc Natl Acad Sci U S A (2014) 111:27–32. doi:10.1073/pnas.1312076111
145. Salbreux G, Barthel LK, Raymond PA, Lubensky DK. Coupling mechanical deformations and planar cell polarity to create regular patterns in the zebrafish retina. Plos Comput Biol (2012) 8. doi:10.1371/JOURNAL.PCBI.1002618
146. Hilgenfeldt S, Erisken S, Carthew RW. Physical modeling of cell geometric order in an epithelial tissue. Proc Natl Acad Sci U S A (2008) 105:907–11. doi:10.1073/PNAS.0711077105
147. Farhadifar R, Röper JC, Aigouy B, Eaton S, Jülicher F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr Biol (2007) 17:2095–104. doi:10.1016/J.CUB.2007.11.049
148. Hufnagel L, Teleman AA, Rouault H, Cohen SM, Shraiman BI. On the mechanism of wing size determination in fly development. Proc Natl Acad Sci U S A (2007) 104:3835–40. doi:10.1073/PNAS.0607134104
149. Honda H, Tanemura M, Nagai T. A three-dimensional vertex dynamics cell model of space-filling polyhedra simulating cell behavior in a cell aggregate. J Theor Biol (2004) 226:439–53. doi:10.1016/J.JTBI.2003.10.001
150. Graner F, Glazier JA. Simulation of biological cell sorting using a two-dimensional extended Potts model. Phys Rev Lett (1992) 69:2013–6. doi:10.1103/PhysRevLett.69.2013
151. Glazier JA, Graner F. Simulation of the differential adhesion driven rearrangement of biological cells. Phys Rev E (1993) 47:2128–54. doi:10.1103/PHYSREVE.47.2128
152. Hogeweg P. Evolving mechanisms of morphogenesis: on the interplay between differential adhesion and cell differentiation. J Theor Biol (2000) 203:317–33. doi:10.1006/JTBI.2000.1087
153. Ouchi NB, Glazier JA, Rieu JP, Upadhyaya A, Sawada Y. Improving the realism of the cellular Potts model in simulations of biological cells. Physica A: Stat Mech its Appl (2003) 329:451–8. doi:10.1016/S0378-4371(03)00574-0
154. Szabó A, Ünnep R, Méhes E, Twal WO, Argraves WS, Cao Y, et al. Collective cell motion in endothelial monolayers. Phys Biol (2010) 7:046007. doi:10.1088/1478-3975/7/4/046007
155. Kabla AJ. Collective cell migration: Leadership, invasion and segregation. J R Soc Interf (2012) 9:3268–78. doi:10.1098/RSIF.2012.0448
156. Alt S, Ganguly P, Salbreux G. Vertex models: From cell mechanics to tissue morphogenesis. Phil Trans R Soc B (2017) 372:20150520. doi:10.1098/RSTB.2015.0520
157. Bi D, Lopez JH, Schwarz JM, Manning ML. A density-independent rigidity transition in biological tissues. Nat Phys (2015) 11:1074–9. doi:10.1038/nphys3471
158. Henkes S, Fily Y, Marchetti MC. Active jamming: Self-propelled soft particles at high density. Phys Rev E (2011) 84:040301. doi:10.1103/PhysRevE.84.040301
159. Sato K, Umetsu D. A novel cell vertex model formulation that distinguishes the strength of contraction forces and adhesion at cell boundaries. Front Phys (2021) 9:406. doi:10.3389/fphy.2021.704878
160. Merkel M, Manning ML. Using cell deformation and motion to predict forces and collective behavior in morphogenesis. Semin Cel Dev Biol (2017) 67:161–9. Elsevier
161. Bi D, Yang X, Marchetti MC, Manning ML. Motility-driven glass and jamming transitions in biological tissues. Phys Rev X (2016) 6:021011. doi:10.1103/PhysRevX.6.021011
162. Yang X, Bi D, Czajkowski M, Merkel M, Manning ML, Marchetti MC. Correlating cell shape and cellular stress in motile confluent tissues. Proc Natl Acad Sci U S A (2017) 114:12663–8. doi:10.1073/pnas.1705921114
163. Ranft J, Basan M, Elgeti J, Joanny JF, Prost J, Jülicher F. Fluidization of tissues by cell division and apoptosis. Proc Natl Acad Sci U S A (2010) 107:20863–8. doi:10.1073/pnas.1011086107
164. Tetley RJ, Staddon MF, Heller D, Hoppe A, Banerjee S, Mao Y. Tissue fluidity promotes epithelial wound healing. Nat Phys (2019) 15:1195–203. doi:10.1038/s41567-019-0618-1
165. Kim S, Pochitaloff M, Stooke-Vaughan GA, Campàs O. Embryonic tissues as active foams. Nat Phys (2021) 17:859–66. doi:10.1038/s41567-021-01215-1
166. Reboux S, Richardson G, Jensen OE. Bond tilting and sliding friction in a model of cell adhesion. Proc R Soc A (2007) 464:447–67. doi:10.1098/RSPA.2007.0210
167. Staple DB, Farhadifar R, Röper JC, Aigouy B, Eaton S, Jülicher F. Mechanics and remodelling of cell packings in epithelia. Eur Phys J E (2010) 33:117–27. doi:10.1140/EPJE/I2010-10677-0
168. Clément R, Dehapiot B, Collinet C, Lecuit T, Lenne PF. Viscoelastic dissipation stabilizes cell shape changes during tissue morphogenesis. Curr Biol (2017) 27:3132–42.e4. doi:10.1016/J.CUB.2017.09.005
169. Guirao B, Bellaïche Y. Biomechanics of cell rearrangements in Drosophila. Curr Opin Cel Biol (2017) 48:113–24. doi:10.1016/J.CEB.2017.06.004
170. Shindo A. Models of convergent extension during morphogenesis. Wiley Interdiscip Rev Dev Biol (2018) 7:e293. doi:10.1002/WDEV.293
171. Wieschaus E, Sweeton D, Costa M. Convergence and extension during germband elongation in Drosophila embryos. Gastrulation (1991) 213–23. doi:10.1007/978-1-4684-6027-8_13
172. Aigouy B, Farhadifar R, Staple DB, Sagner A, Röper JC, Jülicher F, et al. Cell flow reorients the axis of planar polarity in the wing epithelium of Drosophila. Cell (2010) 142:773–86. doi:10.1016/j.cell.2010.07.042
173. Huebner RJ, Wallingford JB. Coming to consensus: A unifying model emerges for convergent extension. Dev Cel (2018) 46:389–96. doi:10.1016/J.DEVCEL.2018.08.003
174. Tada M, Heisenberg CP. Convergent extension: using collective cell migration and cell intercalation to shape embryos. Development (Cambridge, England) (2012) 139:3897–904. doi:10.1242/DEV.073007
175. Papusheva E, Heisenberg CP. Spatial organization of adhesion: Force-dependent regulation and function in tissue morphogenesis. EMBO J (2010) 29:2753–68. doi:10.1038/emboj.2010.182
176. Fagotto F, Winklbauer R, Rohani N. Ephrin-Eph signaling in embryonic tissue separation. Cell Adh Migr (2014) 8:308–26. doi:10.4161/19336918.2014.970028
177. Katsuno-Kambe H, Yap AS. Endocytosis, cadherins and tissue dynamics. Traffic (2020) 21:268–73. doi:10.1111/tra.12721
178. Pinheiro D, Kardos R, Hannezo É, Heisenberg CP. Morphogen gradient orchestrates pattern-preserving tissue morphogenesis via motility-driven (un)jamming. bioRxiv (2022). doi:10.1101/2022.05.16.492018
179. Iijima N, Sato K, Kuranaga E, Umetsu D. Differential cell adhesion implemented by Drosophila Toll corrects local distortions of the anterior-posterior compartment boundary. Nat Commun (2020) 11:6320. doi:10.1038/s41467-020-20118-y
180. Solanas G, Cortina C, Sevillano M, Batlle E. Cleavage of E-cadherin by ADAM10 mediates epithelial cell sorting downstream of EphB signalling. Nat Cel Biol (2011) 13:1100–7. doi:10.1038/ncb2298
181. Kindberg AA, Srivastava V, Muncie JM, Weaver VM, Gartner ZJ, Bush JO. EPH/EPHRIN regulates cellular organization by actomyosin contractility effects on cell contacts. J Cel Biol (2021) 220:e202005216. doi:10.1083/jcb.202005216
182. West JJ, Harris TJC. Cadherin trafficking for tissue morphogenesis: Control and consequences. Traffic (2016) 17:1233–43. doi:10.1111/tra.12407
183. Xie Y, Miao H, Blankenship JT. Membrane trafficking in morphogenesis and planar polarity. Traffic (2018) 19:679–89. doi:10.1111/tra.12580
184. Malinverno C, Corallino S, Giavazzi F, Bergert M, Li Q, Leoni M, et al. Endocytic reawakening of motility in jammed epithelia. Nat Mater (2017) 16:587–96. doi:10.1038/NMAT4848
185. Founounou N, Farhadifar R, Collu GM, Weber U, Shelley MJ, Mlodzik M. Tissue fluidity mediated by adherens junction dynamics promotes planar cell polarity-driven ommatidial rotation. Nat Commun (2021) 12:6974. doi:10.1038/s41467-021-27253-0
186. Ulrich F, Krieg M, Schötz EM, Link V, Castanon I, Schnabel V, et al. Wnt11 functions in gastrulation by controlling cell cohesion through Rab5c and E-cadherin. Dev Cel (2005) 9:555–64. doi:10.1016/J.DEVCEL.2005.08.011
187. Levayer R, Pelissier-Monier A, Lecuit T. Spatial regulation of Dia and Myosin-II by RhoGEF2 controls initiation of E-cadherin endocytosis during epithelial morphogenesis. Nat Cel Biol (2011) 13:529–40. doi:10.1038/ncb2224
188. Jewett CE, Vanderleest TE, Miao H, Xie Y, Madhu R, Loerke D, et al. Planar polarized rab35 functions as an oscillatory ratchet during cell intercalation in the drosophila epithelium. Nat Commun (2017) 8:476–16. doi:10.1038/s41467-017-00553-0
189. Gauthier NC, Masters TA, Sheetz MP. Mechanical feedback between membrane tension and dynamics. Trends Cel Biol (2012) 22:527–35. doi:10.1016/j.tcb.2012.07.005
190. Weng M, Wieschaus E. Myosin-dependent remodeling of adherens junctions protects junctions from Snail-dependent disassembly. J Cel Biol (2016) 212:219–29. doi:10.1083/jcb.201508056
191. Iyer KV, Piscitello-Gómez R, Paijmans J, Jülicher F, Eaton S. Epithelial viscoelasticity is regulated by mechanosensitive E-cadherin turnover. Curr Biol (2019) 29:578–91.e5. doi:10.1016/j.cub.2019.01.021
192. Dumortier JG, Le Verge-Serandour M, Tortorelli AF, Mielke A, de Plater L, Turlier H, et al. Hydraulic fracturing and active coarsening position the lumen of the mouse blastocyst. Science (2019) 365:465–8. doi:10.1126/science.aaw7709
193. Casares L, Vincent R, Zalvidea D, Campillo N, Navajas D, Arroyo M, et al. Hydraulic fracture during epithelial stretching. Nat Mater (2015) 14:343–51. doi:10.1038/nmat4206
194. Kane DA, McFarland KN, Warga RM. Mutations in half baked/e-cadherin block cell behaviors that are necessary for teleost epiboly. Development The company of Biologists (2005).
195. Shimizu T, Yabe T, Muraoka O, Yonemura S, Aramaki S, Hatta K, et al. E-cadherin is required for gastrulation cell movements in zebrafish. Mech Dev (2005) 122:747–63. doi:10.1016/j.mod.2005.03.008
196. Song S, Eckerle S, Onichtchouk D, Marrs JA, Nitschke R, Driever W. Pou5f1-dependent egf expression controls e-cadherin endocytosis, cell adhesion, and zebrafish epiboly movements. Dev Cel (2013) 24:486–501. doi:10.1016/j.devcel.2013.01.016
197. Rauzi M, Lenne PF, Lecuit T. Planar polarized actomyosin contractile flows control epithelial junction remodelling. Nature (2010) 468:1110–4. doi:10.1038/nature09566
198. Levayer R, Lecuit T. Oscillation and polarity of E-cadherin asymmetries control actomyosin flow patterns during morphogenesis. Dev Cel (2013) 26:162–75. doi:10.1016/j.devcel.2013.06.020
199. Han MKL, Hoijman E, Nöel E, Garric L, Bakkers J, de Rooij J. αE-catenin-dependent mechanotransduction is essential for proper convergent extension in zebrafish. Biol Open (2016) 5:1461–72. doi:10.1242/bio.021378
200. Wootton RJ. Functional morphology of insect wings. Annu Rev Entomol (1992) 37:113–40. doi:10.1146/annurev.en.37.010192.000553
201. Etournay R, Popović M, Merkel M, Nandi A, Blasse C, Aigouy B, et al. Interplay of cell dynamics and epithelial tension during morphogenesis of the Drosophila pupal wing. eLife (2015) 4:e07090. doi:10.7554/eLife.07090
202. Classen AK, Anderson KI, Marois E, Eaton S. Hexagonal packing of Drosophila wing epithelial cells by the planar cell polarity pathway. Dev Cel (2005) 9:805–17. doi:10.1016/j.devcel.2005.10.016
203. Tsai TYC, Garner RM, Megason SG. Adhesion-based self-organization in tissue patterning. Annu Rev Cel Dev Biol (2022). doi:10.1146/ANNUREV-CELLBIO-120420-100215
204. Jenny A. Planar cell polarity signaling in the Drosophila eye. Curr Top Dev Biol (2010) 93:189–227. doi:10.1016/B978-0-12-385044-7.00007-2
205. Kuriyama S, Theveneau E, Benedetto A, Parsons M, Tanaka M, Charras G, et al. In vivo collective cell migration requires an LPAR2-dependent increase in tissue fluidity. J Cel Biol (2014) 206:113–27. doi:10.1083/jcb.201402093
206. Nunan R, Campbell J, Mori R, Pitulescu ME, Jiang WG, Harding KG, et al. Ephrin-bs drive junctional downregulation and actin stress fiber disassembly to enable wound Re-epithelialization. Cel Rep (2015) 13:1380–95. doi:10.1016/j.celrep.2015.09.085
207. Bosveld F, Wang Z, Bellaïche Y. Tricellular junctions: A hot corner of epithelial biology. Curr Opin Cel Biol (2018) 54:80–8. doi:10.1016/j.ceb.2018.05.002
208. Bosveld F, Bellaïche Y. Tricellular junctions. Curr Biol (2020) 30:R249–51. doi:10.1016/j.cub.2020.01.029
209. Salomon J, Gaston C, Magescas J, Duvauchelle B, Canioni D, Sengmanivong L, et al. Contractile forces at tricellular contacts modulate epithelial organization and monolayer integrity. Nat Commun (2017) 8:13998. doi:10.1038/ncomms13998
210. Lawson-Keister E, Manning ML. Jamming and arrest of cell motion in biological tissues. Curr Opin Cel Biol (2021) 72:146–55. doi:10.1016/J.CEB.2021.07.011
211. Blauth E, Kubitschke H, Gottheil P, Grosser S, Käs JA. Jamming in embryogenesis and cancer progression. Front Phys (2021) 9:445. doi:10.3389/fphy.2021.666709
212. Angelini TE, Hannezo E, Trepat X, Marquez M, Fredberg JJ, Weitz DA. Glass-like dynamics of collective cell migration. Proc Natl Acad Sci U S A (2011) 108:4714–9. doi:10.1073/pnas.1010059108
213. Mongera A, Rowghanian P, Gustafson HJ, Shelton E, Kealhofer DA, Carn EK, et al. A fluid-to-solid jamming transition underlies vertebrate body axis elongation. Nature (2018) 561:401–5. doi:10.1038/s41586-018-0479-2
214. Haeger A, Krause M, Wolf K, Friedl P. Cell jamming: Collective invasion of mesenchymal tumor cells imposed by tissue confinement. Biochim Biophys Acta (Bba) - Gen Subj (2014) 1840:2386–95. doi:10.1016/J.BBAGEN.2014.03.020
215. Sadati M, Taheri Qazvini N, Krishnan R, Park CY, Fredberg JJ. Collective migration and cell jamming. Differentiation (2013) 86:121–5. doi:10.1016/j.diff.2013.02.005
216. Czajkowski M, Sussman DM, Marchetti MC, Manning ML. Glassy dynamics in models of confluent tissue with mitosis and apoptosis. Soft Matter (2019) 15:9133–49. doi:10.1039/C9SM00916G
217. Schoetz EM, Lanio M, Talbot JA, Manning ML. Glassy dynamics in three-dimensional embryonic tissues. J R Soc Interf (2013) 10:20130726. doi:10.1098/rsif.2013.0726
218. Park JA, Kim JH, Bi D, Mitchel JA, Qazvini NT, Tantisira K, et al. Unjamming and cell shape in the asthmatic airway epithelium. Nat Mater (2015) 14:1040–8. doi:10.1038/nmat4357
219. Kim S, Pochitaloff M, Stooke-Vaughan GA, Campàs O. Embryonic tissues as active foams. Nat Phys. (2021) 17:859–866. doi:10.1038/s41567-021-01215-1
Keywords: adhesion, biological tissues, deformation, rearrangements, plasticity, intercellular adhesion, biomimetic tissues, emulsions
Citation: Montel L, Guigue Q and Pontani L-L (2022) Adhesion regulation and the control of cellular rearrangements: From emulsions to developing tissues. Front. Phys. 10:1014428. doi: 10.3389/fphy.2022.1014428
Received: 08 August 2022; Accepted: 05 September 2022;
Published: 26 September 2022.
Edited by:
Changjin Huang, Nanyang Technological University, SingaporeReviewed by:
Massimo Pica Ciamarra, Nanyang Technological University, SingaporeWylie Ahmed, California State University, Fullerton, United States
Copyright © 2022 Montel, Guigue and Pontani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lea-Laetitia Pontani, bGVhLWxhZXRpdGlhLnBvbnRhbmlAc29yYm9ubmUtdW5pdmVyc2l0ZS5mcg==
 Lorraine Montel
Lorraine Montel Quentin Guigue
Quentin Guigue Lea-Laetitia Pontani
Lea-Laetitia Pontani