
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys. , 11 October 2022
Sec. Optics and Photonics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1010053
This article is part of the Research Topic Women in Science: Optics and Photonics View all 5 articles
Optical microscopes allow us to study highly dynamic events from the molecular scale up to the whole animal level. However, conventional three-dimensional microscopy architectures face an inherent tradeoff between spatial resolution, imaging volume, light exposure and time required to record a single frame. Many biological processes, such as calcium signalling in the brain or transient enzymatic events, occur in temporal and spatial dimensions that cannot be captured by the iterative scanning of multiple focal planes. Snapshot volumetric imaging maintains the spatio-temporal context of such processes during image acquisition by mapping axial information to one or multiple cameras. This review introduces major methods of camera-based single frame volumetric imaging: so-called multiplane, multifocus, and light field microscopy. For each method, we discuss, amongst other topics, the theoretical framework; tendency towards optical aberrations; light efficiency; applicable wavelength range; robustness/complexity of hardware and analysis; and compatibility with different imaging modalities, and provide an overview of applications in biological research.
Biological specimens like cells, tissue and whole animals are inherently three-dimensional structures, and many dynamic processes occur throughout their volume on various timescales. Traditional camera-based microscopes used to investigate these processes usually capture two-dimensional in-focus images from one sample plane on the imaging sensor. The arguably simplest mechanism to obtain 3D information is to sequentially move the sample and focus plane of the system with respect to each other. This requires the movement of relatively large objects, e.g. the sample, objective lens, or camera, along the optical axis (z), which makes the process comparably slow. Fast adaptive elements in the detection path, such as tunable acoustic gradient index of refraction (TAG) lenses [1] or adaptive optics [2] can circumvent this macroscopic scanning and adjust the focus optically via remote focusing [3]. A more traditional implementation of remote focusing uses a second objective and a small scanning mirror, and avoids aberrations by optical design [4, 5]. As long as telecentricity (uniform magnification along z) is ensured, these implementations can reduce the axial sampling time to the millisecond regime and are already more suitable than conventional axial scanning for imaging biological processes in 3D as they avoid physical sample movement. However, although the field of view and the distance between the scanned focal planes can be adjusted, the volumetric imaging speed is nonetheless limited by the need for sequential acquisition. Furthermore, axial scanning alone does not prevent the detection of blurred background signal from out-of-focus structures by the camera. Therefore, a plethora of light sheet microscopy or selective plane illumination techniques [6] have been developed to limit the excitation to the current focal plane.
The volumetric imaging speed, as illustrated in Figure 1, depends on the volumetric imaging method, the labelling density and emission properties of the fluorophores [7] that are used, and the detection efficiency and readout rate of the detector [8]. This is most relevant for fluorescence imaging, in particular for single-molecule and super-resolution (SR) microscopy techniques. Thus, fast volumetric imaging with the appropriate method is not just an end in itself, but a means to free up the parameter space for imaging optimization. In particular, the methods for instantaneous snapshot volumetric imaging that we are reporting in this review, can reduce the light dose per fluorophore, and make imaging with less photostable dyes feasible while acquiring high resolution live-cell data at framerates ultimately limited by the camera readout speed [9–13].
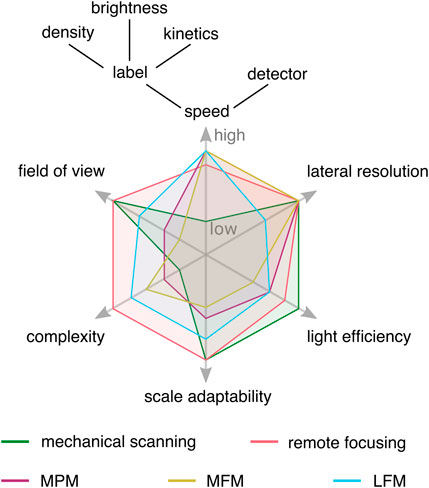
FIGURE 1. Conceptual experimental tradeoffs of selected volumetric imaging methods. Imaging speed is limited by the slowest component in the experiment, which can be the volumetric imaging method, labeling characteristics, or detector readout speed. Lateral resolution refers to conventional microscopy, and the light efficiency is mainly influenced by the transmission efficiency of optical components. Snapshot volumetric imaging techniques reduce constraints on imaging speed, opening the experimental design space, but come with their own trade-offs. MPM: multiplane microscopy, MFM: multifocus microscopy, LFM: light field microscopy.
Besides sacrificing temporal resolution for axial information in scanning methods, one can also make other trade-offs to achieve 3D imaging. For example, point spread function (PSF) engineering encodes axial information into the shape of the PSF, i.e. so that the 2D image of a point emitter changes as a function of the z-position. Commonly used engineered PSFs are axially dependent astigmatism [14], the double helix [15], and the tetrapod PSF [16]. This approach only works when sparse point-like objects are imaged, e.g. in particle tracking or 3D single-molecule localization microscopy, and leads to reduced lateral localization precision. The system’s PSF is also used to reconstruct 3D volumes from single exposures in focus sweep or extended-depth-of-field (EDOF) and lensless volumetric imaging. In EDOF, a quasi-3D single frame imaging is achieved by axially scanning the focal plane of the system through the specimen within a single camera exposure. An image with increased depth of field (DOF, see paragraph 5.1) can be recovered by deconvolving with the response function of the imaging system [17]. This becomes increasingly difficult with larger EDOF ranges because the out-of-focus background increases. Lensless imaging systems replace the lens with encoding elements to map a point to multiple points on the sensor [18, 19]. This does not produce a traditional image, but requires solving a 3D inverse problem to recover the spatial information [20].
Many of these drawbacks can be overcome using snapshot volumetric microscopy. Three generally applicable implementations of snapshot volumetric microscopy are so-called multiplane (MPM, Figure 2B) [10, 11, 21, 22], multifocus (MFM, Figure 2C) [21] or light field microscopy (LFM, Figure 2D) [24]. The former two enable the simultaneous volumetric imaging of distinct focal planes in the sample, and the latter computationally reconstructs 3D volumes from multiple perspective views. All three methods can be implemented as add-ons to conventional camera-based microscopes and are compatible with a range of different imaging modalities. As these three implementations are all camera-based instantaneous volumetric imaging techniques, we recommend a recent article by Mertz [25] for readers interested in an overview of scanning techniques.
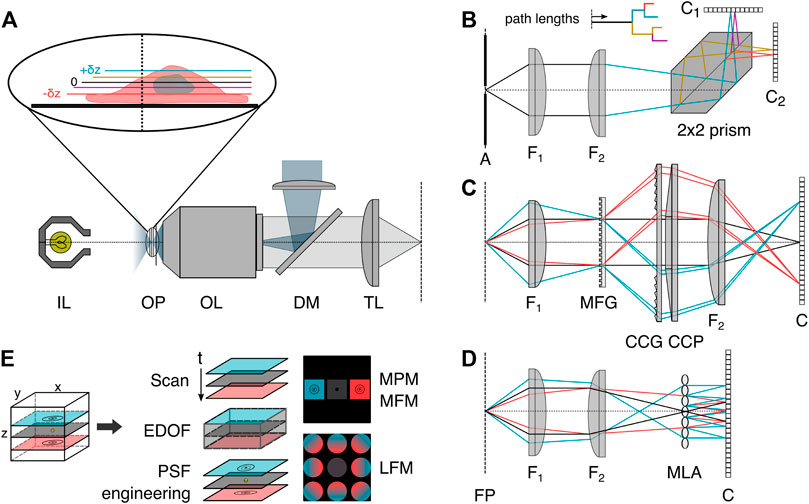
FIGURE 2. Volumetric image splitting. (A) Conventional fluorescence epi-illumination and white light microscope with focal plane indicated as 0, and relative axial position changes ±δz indicated in color blue (+) and red (−). (B) In a variant of MPM, a refractive image splitting prism [10] separates the convergent detection beam onto two cameras, via total internal reflection and a beam-splitting interface on the main diagonal. Inset: indication of the different path lengths corresponding to different axial object-side positions. (C) In MFM, a multifocus grating (MFG) splits the incident light into several diffraction orders associated with different degrees of defocus, which are subsequently chromatically corrected by a blazed grating (CCG) and prism (CCP) and focused with lateral displacement on the detector [21]. (D) In light field microscopy, a microlens array (MLA) is placed at the intermediate image plane, and a sensor is positioned behind it. Each microlens records a perspective view of the object. (E) Schematics of selected volumetric imaging methods discussed in the introduction. EDOF: extended-depth-of-field, PSF: point spread function, MPM: multiplane microscopy, MFM: multifocus microscopy, LFM: light field microscopy, OP: object focal plane, OL: objective lens, IL: white light source, DM: dichroic mirror, TL: tube lens, A: aperture field stop, FP: Fourier plane, F1: Fourier lens, F2: focusing lens, Ci: camera, 2 × 2 prism: refractive image splitter.
We first introduce MPM, MFM and LFM and describe in detail the methods used to achieve spatial separation of axial information on a single or several detectors, namely image splitting based on refractive elements, diffractive elements, and light field acquisition. For each 3D technique, we then discuss various implementations, possibilities for combination with imaging modalities, and their use in biological investigations. We then elaborate on general characteristics one needs to consider when imaging in 3D. A brief summary in regard to practical aspects and a selection of implementations concludes our review.
Simultaneous recording of multiple focal planes can be achieved by splitting the detection path using refractive elements and encoding axial information in optical path length differences. The resulting images then correspond to a small z-stack in object space. In the simplest form of MPM, multiple non-polarizing 50:50 beamsplitters (BS) can be used in combination with different camera positions offset from the nominal focal plane (as depicted in Figure 3B) or tube lenses with different focal lengths can be used [22, 26–32]. To decrease the spatial footprint of this configuration, mirrors can be interspaced (Figure 3C) with the BS [12, 22]. This allows for the adjustment of the interplane distance independent of the choice of the pixel size, making it a very adaptive configuration with variable lateral and axial sampling that can be optimized for the particular experiment. Every component introduced into the system, however, makes the configuration more susceptible to drift and misalignment, impeding the long term data acquisition needed for super-resolution imaging or necessitating drift correction in post-processing. This motivates the design of robust and easy-to-implement image splitters in a single glass prism based entity, as depicted in Figure 3E.
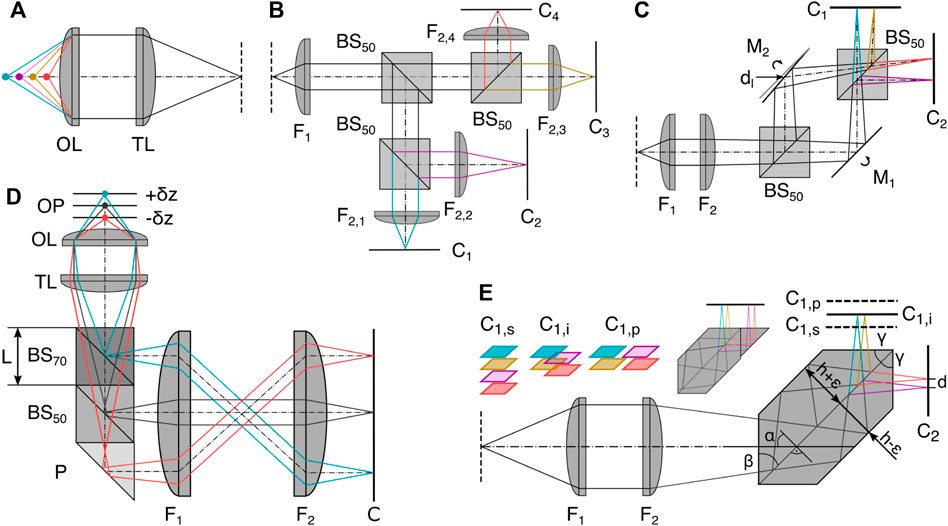
FIGURE 3. Refractive image splitting. (A) Definition of axial position with respect to the objective lens OL and tube lens TL. (B) 50:50 beam splitter BS50 and different focal length lens implementations (F2,i [22]. (C) Beamsplitter BS50 and mirror Mi combination whereby M2 is displaced horizontally by d and rotated out of the symmetric position. Dual camera Ci positioning allows interleaved, sequential, or high-speed configuration depending on relative axial positioning [23]. (D) Multiplane image splitter consisting of a 30R:70T BS cube, a 50R:50T BS cube and a right-angle prism (P) all cemented together using optical adhesive [11]. (E) The single entity prism in the 2 × 2 configuration as a more robust iteration of (C) [10]. Axial displacement of one camera C1 leads to sequential (s), interleaved (i) and parallel (p) plane configurations; the same camera positions are also possible in (C). Insert: a potential single camera configuration. F1: Fourier lens, F2: focusing lens.
The prisms split the detected light into multiple paths and introduce lateral displacements and different axial path lengths to focus several images side-by-side on two cameras. The depicted 4-plane prism consists of two isosceles trapezoidal prisms joined along their base; the connecting surface is coated to serve as a 50:50 BS, and total internal reflection at the interface of the glass prism with the surrounding air replaces the mirrors. The majority of design considerations take place before manufacturing, making it an easy-to-implement and mechanically stable configuration with almost no chromatic aberration over the visible spectral range, enabling diffraction-limited imaging [3, 10, 33, 34]. The assembly of a compact image splitter is also possible by gluing together different off-the-shelf components, such as BS cubes and right angle prisms [11], see Figure 3D. This enables a large variety of configurations, but has not yet been shown to be compatible with single-molecule or super-resolution imaging.
The distribution of several whole fields-of-view (FOV) images across one or two camera sensors needs to take into account the dimensions of the sensor area. For both compact image splitter implementations, the lateral displacement is coupled to the axial path length difference (see for details below). The dimensions of the assembled prisms are fixed, and thus so is the image-side interplane distance Δz.The object-side interplane distance δz and projected pixel size pxy can only be varied by a shared parameter, the magnification of the microscope. Most of the presented configurations can be used at different magnifications, enabling easy imaging across scales by varying the objectives or other lenses in the imaging path.
Multiplane imaging is versatile and can be combined with fluorescence or white-light excitation for imaging on a wide range of spatial and temporal scales (see Table 1). This is supported by the high transmission efficiencies of the deployed refractive elements (e.g. >90% across wavelengths for the 2 × 2 prism). The first implementations focused on fluorescence single-particle tracking of beads and small organelles, as well as single receptor proteins [22, 35, 36]. Later, different super-resolution microscopy modalities were realized (localization microscopy [29], (live-cell) super-resolution optical fluctuation imaging [10, 22, 37], and live-cell structured illumination imaging [33]). The systems can be adapted for single-cell and whole organism imaging, e.g. by changing the objective to lower magnifications [11, 12], and combined with phase imaging [11, 34, 38], laser speckle contrast [47], and dark-field microscopy [11, 12] for imaging fast flagellar beating of bacteria and sperm, or to track whole C. elegans. Even simultaneous multicolor acquisition is possible, e.g. using a single prism [34].
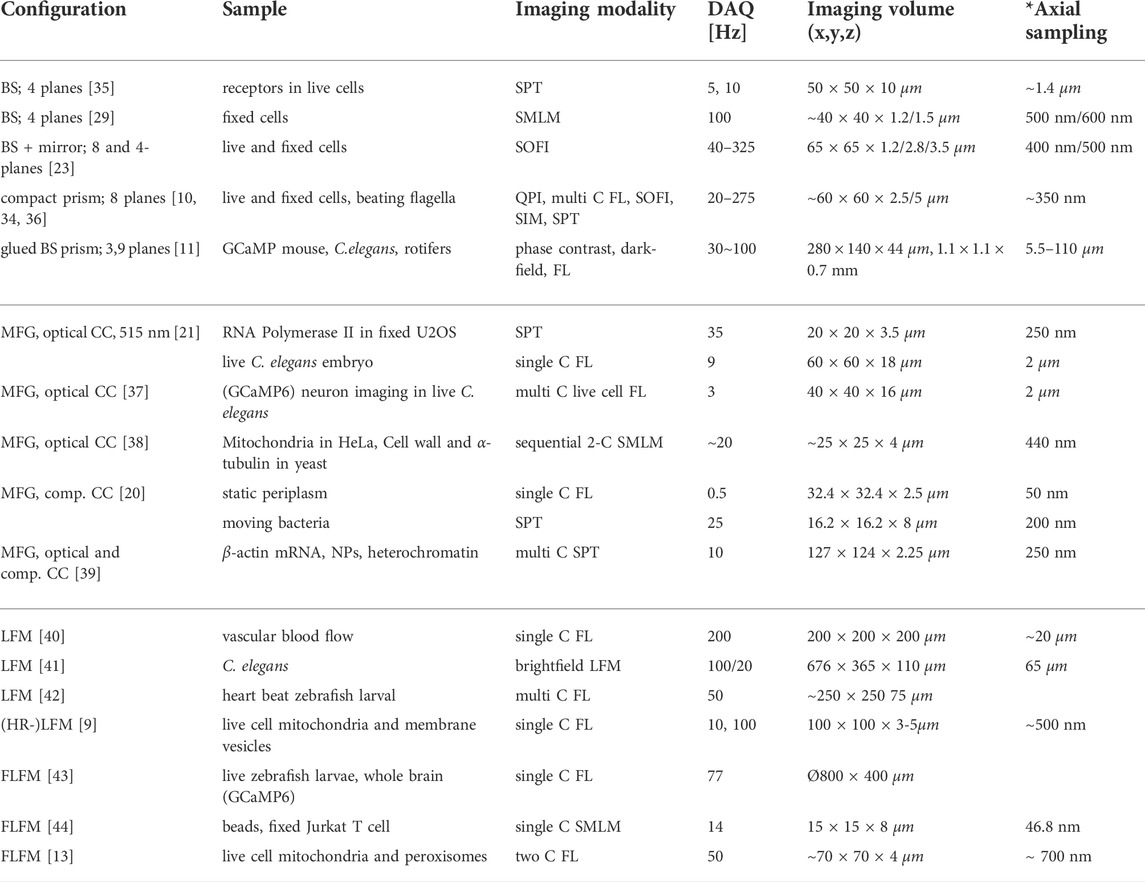
TABLE 1. Representative selection of volumetric imaging configurations. BS: beamsplitter, C: color, DAQ: data acquisition, FL: fluorescence, NP: nuclear pore, SPT: single particle tracking, SMLM: single molecule localization microscopy, SOFI: super-resolution optical fluctuation imaging, SIM: structured illumination microscopy, QPI: quantitative phase imaging. * Axial sampling in LFM is reported as smallest rendering unit, if applicable.
In the following, we will discuss the different implementations of compact image splitters using refractive elements in detail.
Recently, a concept was introduced for custom-designed image splitting prisms for robust multimodal multiplane microscopy ([10]) and realized in 8-plane and a 4-plane splitter variants. Here, we explain the principle behind the 2 × 2 = 4-plane prism (see Figure 3E) in detail. Two cemented plane parallel prisms with side cuts α = 45 are assembled into a single element, and the coated interface formed by the two bases serves as a non-polarizing 50:50 beam splitter. The prisms have a height h ±ϵ with a difference
where np is the refractive index of the prism. Therefore, the axial separation between object planes in the sample amounts to an object-side interplane distance of:
with axial magnification
whereby d has an upper limit determined by the sensor size W, e.g. d < (W/2) for the 2 × 2 prism.
The separation in object space can be directly manipulated via the lateral magnification Ml, the prism refractive index n and the height difference between the two prism halves. As mentioned above, only the microscope’s magnification can be changed after the image splitter is assembled, which also changes the projected pixel size
A ray-tracing analysis showed that the detection path and image splitting prisms introduce no significant aberrations up to third order and allow diffraction limited performance across the spectral range from 500–700 nm [10]. The remaining aberrations in the prism configuration are dominated by axial color, which incidentally compensates most of the axial chromatic aberration introduced by the achromatic lenses used in the ray-tracing analysis. More specifically, the theoretically calculated ∼220 nm axial displacement between color channels in the MPM system (see supporting information [10]) is small and closely matches with the measured color-dependent differences (520–685 nm) in interplanar distance that accumulate over the full axial depth range of ∼ 2.5 μm in the 8-plane prism [34], reaching maximally 140 nm. Both the 8- and 4-plane prisms are commercially available through Scoptonic imaging technologies.
To simplify the manufacturing of robust MPM implementations, an approach using off-the-shelf beamsplitter components has been realized [11] (see Figure 3D). As an example, we discuss a sequential three-plane prism consisting of two differently transmissive BS cubes and a right-angle prism. These components can be bought in a limited range of transmission:reflection ratios and with certain side lengths depending on the supplier. The parts need to be carefully assembled and connected by an optical adhesive. Transmission rates through the BS cubes (30:70 and 50:50) are chosen to ensure approximately equal light power output from the final surfaces of each component prior to the camera.
Assuming a glass BS cube with side length L and refractive index nBS, the optical path length difference associated with each output beam thus increases by nBSL. From that result, non-overlapping lateral FOVs on the sensor are defined by
For a sample with refractive index ns, this leads to an axial object-side separation of focal planes, i.e. object side interplanar distance δz:
To date, configurations from three to nine focal planes in grid or linearized arrangements have been realized [11, 38, 39].
In multifocus microscopy (MFM), the simultaneous recording of multiple focal planes is achieved by a diffractive optical element that has the key role of splitting the incident light into different diffraction orders [20, 40]. This so-called multifocus grating (MFG) performs two main functions. First, it splits the fluorescent light emitted from the sample into separate paths that are laterally distributed onto a camera plane, as illustrated in Figure 4A. Second, it refocuses the separated light paths so that a series of images are formed that correspond to different focal planes in the sample with constant interplanar separation. Each focal plane that the MFG produces is a traditional wide-field image, containing in-focus information as well as an out-of-focus blur (see Figure 4B).
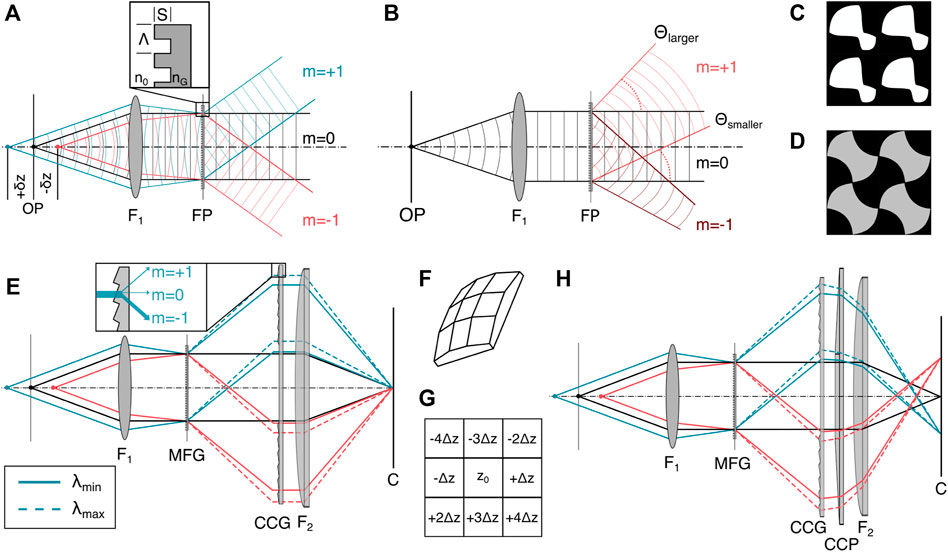
FIGURE 4. Diffractive image splitting. (A) The binary MFG with etch depth S, motif period Λ and refractive index nG splits the incident light from the sample into a set of diffraction orders. (B) Each sub-image produced by the MFG is a traditional wide-field image containing both in-focus information and as an out-of-focus-blur. The diffraction angle θ depends on diffractive order m, wavelength λ and motif spacing Λ according to Eq. 6. (C) Binary 2D motif for a 3 × 3 order grating with phase step ∈ [0, π] [21]. (D) Binary 2D motif for a 3 × 3 order grating with phase step ∈ [0, 0.84π] [49]. (E) The MFG diffracts light with an outward smear that depends on the incident wavelength. A blazed chromatic correction diffractive grating (CCG) directs most of the light into the m = −1 diffractive order, with dispersion opposite that of the MFG. (F) 3D schematic of the correction prism (CCP). (G) Distribution of axially displaced image planes of the same lateral FOV on an image sensor for a 9-plane prism. (H) The CCP is placed behind the CCG to laterally separate the images on the sensor. Figures inspired by [21]. F1: objective lens, FP: Fourier plane, MFG: multi-focus grating, C: camera.
The grating itself introduces chromatic dispersion, which deteriorates the imaging performance. To correct for dispersion, the MFG can be combined with a blazed transmission grating that is typically referred to as chromatic correction grating (CCG, Figure 4E) [21]. On its own, the CCG unfortunately also reverses the lateral displacement of the diffraction orders and needs to be combined with a refractive prism (Figure 4F) to maintain the lateral displacement of the positions of the different focal planes on the camera chip, as depicted in Figure 4H.
Gratings are thin components with spatially periodic transparency and are commonly deployed as diffractive elements [37]. Multifocus gratings, as spearheaded by Abrahmsson et al., are often fabricated with photolithography masks and etched silica wafers [37]. In the following, we describe the design considerations relevant to gratings that can be used in MFM. The periodic transparency can affect either the complex phase or the real component of the amplitude of the electromagnetic wave, leading to so-called phase or amplitude gratings. Both transmissive and reflective grating designs, which transmit the dispersed light or diffract it back into the plane of incidence, respectively, exist and can achieve similar characteristics for the outgoing wavefronts. Most MFM implementations use transmission phase gratings due to their superior light transmission efficiency and achievable diffractive order count compared to transmission amplitude gratings. Transmission phase gratings’ transmission efficiency is higher because they do not rely on partial amplitude attenuation of the incident beam as amplitude gratings do, and more orders contribute to the final 3D image formation. To optimize light efficiency in MFM, one should aim to optimize the fluorescent light emission from the sample with maximum efficiency into the orders one chooses to image. Furthermore, light should be distributed evenly between these orders, both to ensure that a minimal exposure time can be used to record each multi-focus image while still getting sufficient signal in each plane, and to obtain an even signal throughout the 3D image.
The shape and pitch Λ of the grating pattern (motif) and its etch depth S constitute the grating function, Eq. 6, and determine the energy distribution between diffractive orders [21]. A geometrical distortion of the otherwise regular motif across the MFG area introduce a different phase shift per diffractive order m, leading to a focus shift that defines distinct planes of the multifocus image. The transmitted wavefront focus shift and the diffraction angle θ depend on the order m, the wavelength λ and the grating pitch Λ according to the grating equation Eq. 6.
When refocusing deep into a thick sample, which can be the case for some focal planes created with the MFG, the microscope objective is used far away from its designed focal distance. This can give rise to depth-induced spherical aberration, which can be calculated and compensated for in the MFG at the same time. This ensures that supposed out-of-focus planes, like the in-focus plane, exit the MFG with a flat wavefront and can be focused on the camera with diffraction limited performance.
The interplane distance, i.e., sample-side axial defocus shift, between consecutive individual planes is tied to the out-of-focus phase error of the wavefront of a point source. This can in turn be manipulated through the motif pitch Λ, wavelength λ, immersion medium refractive index n, and focal length of the objective FOL (for the derivation see [21]).
Most of the modern phase grating designs for MFG use etching depths with discrete phase steps of
As mentioned above, the grating functions of all diffractive image splitting techniques have a chromatic dependence [50]. After a MFG, each diffractive order has a lateral dispersion of δλ/Λ where Λ is the average grating period of the MFG motif and δλ is the wavelength bandwidth in the image. Even within a single-fluorophore emission spectrum of a few tens of nanometers, this will cause substantial lateral dispersion, worsening the possible resolution. This chromatic aberration can only be corrected over a narrow wavelength range by the combination of a blazed chromatic correction grating (CCG) and prism (CCP). This necessitates a fluorophore-optimized grating design with individual separate optical arms for different color channels [37]. However, this chromatic dependency can also be exploited to facilitate multiplexed multifocus imaging [51].
Varying material dispersion, and thus intensity loss in the CCG across diffraction orders, also needs to be accounted for to preserve uniform intensity across subimages. On one hand, this is primarily achieved by including a material-cost term in the optimization of the MFG. On the other hand, the use of multiple optimizable elements offer the flexibility to correct for other aberrations, including those induced by depth or sample refractive index mismatch.
There is a three-fold strain on the photon-budget: First, due to the small bandwidth necessary for chromatic dispersion correction, only a fraction of the total emission spectrum of a fluorophore is collected. Second, the theoretical maximum transmission efficiencies of MFGs rarely exceed 78%, and the CCG and CCP each transmit ≈95% [20, 41]. Finally, the detected signal is split into n individual planes, as in MPM, leading to an inherently lower SNR compared to 2D imaging [20].
MFM requires the complex design and manufacturing of an application-specific micro-optical phase grating, a chromatic aberration correction grating and a refractive prism. To our knowledge, there is no commercially available MFG or MFM module, which would still require an adaption to the individual imaging system and detection wavelengths. The optical assembly of the three components in the detection path requires careful alignment, which is critical for achieving optimal performance and might have contributed to the limited use of MFM as a volumetric imaging method. To circumvent the grating manufacturing process, the grating can be replaced with a spatial light modulator. The use of a spatial light modulator as a diffractive element has the potential to allow the phase mask to adapt to multiple wavelengths or object plane separation requirements, although at the cost of additional polarization dependence [46, 52].
In recent years, MFM has already been applied to a variety of different applications. Abberation-corrected implementations allowed, e.g. diffraction-limited single-particle tracking of RNA polymerase or insulin granules in live cells [47, 21] as well as combination with fluorescence super-resolution imaging (localization microscopy [38] or structured illumination imaging [55]). Multicolor imaging requires careful 3D co-alignment of the color channels, and has also been used to analyze the spatial distribution of fluorescently labeled mRNA in relation to nuclear pore complexes and chromatin [39]. Functional imaging of whole animals has been realized, e.g. by recording calcium transients in C. elegans sensory neurons. In addition, a MFG has been combined with polarized illumination to enable high speed live-cell 3D polarization imaging for both birefringence and fluorescence anisotropy measurements [56].
In a conventional single-plane microscope, all light rays emitted from a point source that lie within the acceptance cone of the objective lens (determined by its numerical aperture) are focused to a common point on the camera sensor, and angular information is lost. In light field microscopy (LFM), this angular information is recorded, which enables the computational reconstruction of the full 3D volume of the sample from a single camera frame. It thereby encodes axial information via angular representation, in contrast to MPM and MFM, wherein distinct focal planes are mapped to separate locations on the detector. The concept of LFM dates back to Lippmann’s 1908 description of integral photography and subsequent early holography developments in the 20th century [57]. It was pioneered by a 2006 prototype, where a microlens array (MLA) was placed in the native image plane (NIP) of a conventional microscope with a camera at the focal plane of the MLA [58]. MLAs are a periodic arrangement of highly transmissive lenslets in a non-transmissive chrome mask. Every lens in the MLA produces a view of a separate, laterally shifted observer with respect to the object. This allows the system to “look around corners”up to the angular limit of the rays that are captured. A raw LFM image is thus a 4D dataset that contains information about the radiance of light coming from the object as a function of both spatial location in the sample and propagation direction, and consists of an array of circular subimages. Each subimage represents a different location in the sample, and each pixel within a subimage corresponds to light emanating from that location in a particular direction [59]. Taking the same pixel from each circular subimage gives a view of the object from that specific direction [54, 58]. Summing the pixels within each microlens subimage results in a conventional image of the object focused at the NIP.
More formally, light fields are a parametrization of light rays in the framework of the plenoptic function [58]. This function describes how, from a geometrical optics perspective, all polychromatic light rays of wavelengths λi can be sampled at every point in 3D space in any direction (via angle θ and ϕ) at any moment in time t [57], yielding a 5D spatial function. A simplified representation of the plenoptic function defines rays of a single wavelength and in a single timeframe by their intersection with two planes at arbitrary positions with coordinate systems u, v and s, t. An oriented ray L(s, t, u, v) is thus defined between points on each of the respective planes, within a so-called light slab [24]. These planes can be the NIP and the camera plane, as depicted in Figure 5A.
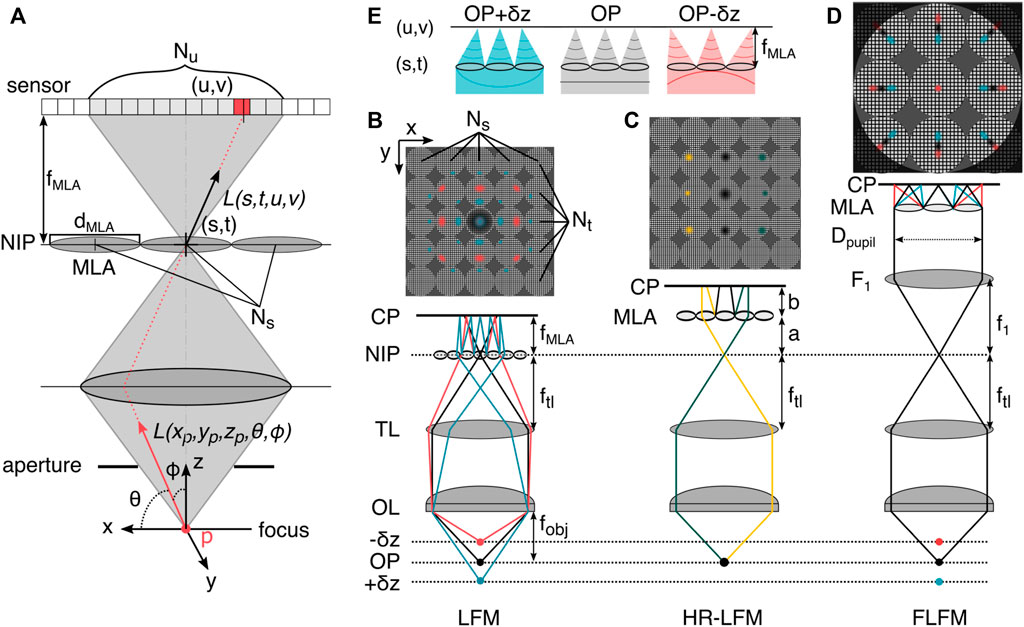
FIGURE 5. The plenoptic function and light field microscopy. (A) In three-dimensional space, the plenoptic function is five-dimensional. Its rays can be parametrized by three spatial coordinates and two angles. In the absence of occluders, the function becomes four-dimensional. Shown is the light slab parametrization by pairs of intersections between two planes, here at a microlens in the NIP (s,t) and in the sensor plane with pixels (u,v). (B) LFM prototype configuration [58], the microlens array (MLA) is placed in the native image plane (NIP), and the sensor is placed at the camera plane (CP) behind this, positioned so that each microlens records an in-focus image of the objective (rays not shown). The MLA consists of Ns × Nt lenses with diameter dMLA/2. On the sensor, Nu × Nv pixels are mapped to the lenses. (C) High-resolution light field microscopy (HR-LFM) configuration [9] with the MLA positioned to form a defocused image, with its location defined by the distances a (to the NIP) and b (to the CP). As in other LFM methods, rays propagating in different directions (green and yellow) are mapped onto to different camera pixels, allowing the reconstruction of perspective views of the object. (D) Fourier light field microscopy (FLFM) configuration [56, 60]. The objective lens (OL) and tube lens (TL) form an image at the NIP. The Fourier lens (F1) transforms the image at the NIP to the back focal plane of the FL, where the MLA is situated. The light-field information is recorded by the camera at the back focal plane of the MLA. Identification of the emitter in multiple subimages and subsequent axial information recovery from the radial position in the subimages enables volumetric single-molecule imaging. (E) The microlens array in FLFM (D) samples spatial and angular information from the wavefront, indicated by a colored line below the MLA, which exhibits asymmetric curvature about the primary image plane. Hence, z-displaced emitters are mapped to different positions in the perspective view. OP: object plane, f: focal length.
Varying the MLA location in the detection path changes the sampling rates of the spatial and angular ray coordinates. Relevant positions are the conjugate image plane which results in regular LFM (Figure 5B) and the Fourier plane, which results in so-called Fourier light field microscopy (FLFM, Figure 5D), and a defocused relationship between MLA, NIP and camera plane (HR-LFM as illustrated in Figure 5C).
In conventional LFM, the MLA samples the spatial domain, with each lenslet recording a perspective view of the scene observed from that position on the array. This resampling of spatial information partitions the sensor into individual lens representations and results in an increase in pixelsize and loss of spatial resolution, due to an axially dependent partition of the photon budget [61]. A further loss in spatial resolution is due to the inherent trade-off between preservation of angular information and spatial resolution, tied to the amount of resolvable angular spots per microlens [58]. The fillfactor of an MLA describes the relative area that the lenslets occupy in relation to the non-transmissive mask and governs its transmission efficiency (typically in the range 65%–90%), which can place additional burden on the resolution of the associated LFM. For a more elaborate MLA design guide, the paper about the original LFM prototype is highly recommended [58].
Conventional LFM results in uneven axial sampling, which limits its applicability. Especially near the NIP, this leads to reconstruction artifacts caused by an aliased signal at the back focal plane of the MLA [62]. Existing LFM techniques mainly circumvent the problem by imaging on only one side of the focal plane [59, 61], reducing the angular sampling by reducing the MLA pitch and thereby the depth of field (DOF) [59], or imaging via two MLAs on separate detectors with slightly displaced axial position in the volume [64], which compromises either the imaging depth or lateral resolution [9].
To overcome the limiting non-uniform resolution across depth of conventional LFM, Li et al. [9] proposed a configuration for so-called high-resolution LFM (HR-LFM) with lateral and axial resolutions of ∼ 300 nm and 600 nm, at several microns sample depth. In the configuration depicted in Figure 5C, the MLA is positioned to form a defocused image with
where a denotes the distance to the NIP, b the distance to the camera sensor, and fMLA describes the focal length of the MLA.
This design contrasts with conventional LFM, where a = 0 and b = fMLA, as depicted in Figure 5D, and improves spatial resolution in two main ways. First, a displaces the artifact region away from the DOF by
Fourier light field microscopy (FLFM) records the 4D light field not in the spatial, but the Fourier domain. This is achieved by placing a relay lens (F1, see 5D) in a 4f configuration with the tube lens TL, which images the Fourier plane onto the MLA. The camera is again placed in the focal plane of the MLA. This alters the imaging in two ways. First, it encodes the spatial and angular information of the incident light in a non-redundant manner (similar to HR-LFM), thereby reducing potential artifacts. Second, it reduces the computational cost because signals in the Fourier domain are processed in parallel fashion, allowing for a description of the image formation with a unified 3D PSF [60]. Both factors result in more homogeneous resolution and signal-to-noise (SNR) than in traditional LFM configurations, although at the cost of lateral FOV size and DOF. The decrease in lateral resolution of FLFM compared with conventional LFM is directly related to the relative aperture division of the MLA, with an aperture partition coefficient pA = Dpupil/dMLA leading to a factor of a pA times worse resolution [61, 60].
Sampling at the conjugate pupil plane of the objective lens derives spatial and angular information from the wavefront, which exhibits asymmetric curvature about the primary image plane (see Figure 5C). An individual microlens locally partitions the wavefront and focuses onto the camera, proportionally displacing it in the direction of the average gradient of the masked wavefront (see Figure 5E). This tilt appears as a radial smear of the PSF (as a function of the average wavefront) on the camera plane, shifting radially outward with increasing distance of the emitter from the objective, as depicted in Figure 5E. Based on the displacement of individual emitter positions from the locations of the foci in each subpartitioned image, the 3D emitter positions can be reconstructed, allowing for robust 3D single molecule localization [44].
FLFM has seen a variety of promising applications (see Table 1) from single molecule localization [44], to subcellular multicolor live-cell imaging [13], super-resolution optical fluctuation microscopy [65], and improved optical sectioning [66]. It can further be deployed as a Shack-Hartmann wavefront sensor in an adaptive optical microscope [67] because of its configuration. The moderate spatial resolution and high DOF of LFM have made it a versatile and fast technique for deep volumetric neuroimaging in combination with genetically-encoded calcium imaging [65, 68]. It has been shown to be a robust tool for 3D behavioral phenotyping of C. elegans [41] in bright field imaging, overcoming the limits of non-physiological 2D posture studies; and for 3D particle velocimetry experiments to measure fluid flows [70].
Considering the wavelength dependence of the plenoptic function, one can already imagine that chromatic aberrations introduced by the MLA make multicolor applications cumbersome. To address this, approaches that extend spatial, angular and color sampling to the excitation side [71] or deploy sequential chromatic excitation and multicolor phase-space deconvolution have been proposed [42]. Concerning spatial resolution, the low image-side NA of the MLA results in blurred PSFs and hence lower signal intensity, increasing susceptibility to background shot noise. This has motivated reconstruction methods (compressive LFM [72] and sparse decomposition LFM [73]) that exploit the sparse spatial signal and high temporal resolution in LFM and FLFM recordings of neuronal activity. In these methods, active, sparse signal was localized within a passive background, thereby improving the effective spatial resolution and signal-to-noise ratio (SNR). This review can only serve as a primer on this vast technique for the interested reader, so we would like to recommend some more dedicated light-field imaging literature [64, 72–76].
Considering the photoelectrons measured per pixel as a line integrals through the object (reporting either attenuation or emission, depending on the imaging modality), creates two dominant frameworks for 3D structure reconstruction from the 4D light field [75, 58]. One approach synthetically refocuses the light field iteratively and subsequently deconvolves the 3D focal stack with an experimentally determined or simulated PSF to retrieve optically sectioned 3D volume data [9, 59]. Virtual refocusing is achieved by shifting and summing subaperture images by rebinning pixels [78]. Although the original algorithm could reconstruct a 3D volume quickly, it was hindered by the limited axial sampling, which is tied to the microlens pitch [79]. Through the years, improvements like a waveoptics based model and Richardson-Lucy deconvolution [61] have increased the axial sampling density and image quality [79]. In a recent reconstruction method termed quantitative LFM, compatible with various kinds of LFM, an incoherent multiscale scattering model was proposed to computationally improve optical sectioning in densely labeled or scattering samples [80].
The second approach relies on a direct tomographic reconstruction of the 3D volume data [64]. In this case, some assumptions need to be satisfied, most notably the absence of scattering and a spatially coherent illumination [58, 80]. Recently, novel deep learning frameworks for volumetric light field reconstruction have been implemented, with promising results [82, 83].
The ability to recover axial information is supplemented by an increased DOF in LFM compared to the underlying 2D microscope. This extension is related to a geometrical optics term of the MLA itself but is restricted by the amount of angular information available per microlens, resulting in Eq. 8 [84, 58]. Here, the NA describes the numerical aperture of the objective lens and Nu × Nu the number of pixels behind a single microlens, which is the limiting factor in defining angular resolution.
The snapshot volumetric imaging methods for camera-based systems presented here aim to map multiple 2D planes from the object plane magnified onto the 2D plane of the camera sensor (MPM and MFM) or to reconstruct a 3D volume from 2D images (LFM). As these methods are purely detection-side extensions to conventional widefield microscopy, certain characteristics of the design of volumetric sampling are shared and discussed on in the following section.
An image does not represent an infinitesimally thin plane in a sample, but is rather a projection of a small volume in the sample that is considered “in focus”, corresponding to the depth of focus on the detection side of the imaging system. Thus, when considering the required axial dimensions of a volumetric imaging system to obtain a continuous volume, one should account for the axial resolution of the 2D imaging plane to avoid under- or oversampling of the specimen, in particular when the distance between focal planes is non-linear across the volume as, e.g., in conventional LFM. Other factors, such as post-processing by deconvolution or image processing for fluorescence super-resolution reconstructions, impose additional demands on axial and lateral point spread function pixel sampling.
The depth of field DOFM, or axial resolution, of an imaging system, as defined in Eq. 9, is the distance between the closest and farthest planes in object space parallel to the optical axis that are still considered to be in focus. It is governed by a wave term accounting for the spatial extent of the focused light (especially relevant in microscopy) and a geometrical optics term that dominates at low numerical apertures (NA) [86]. The DOF depends inversely on the NA and lateral magnification (Ml) and scales with n, the refractive index of the light-carrying medium at wavelength λ and the smallest resolvable distance in the image plane, e (usually the pixel spacing).
Each of the presented methods, MPM, MFM, and LFM, employs different optical components to encode axial information in the image plane, and as such induces specific aberrations. Imaging of planes far from the nominal working distance of the objective is known to introduce wavefront aberrations, most notably spherical aberration [4]. This influence is aggravated by stronger mismatches between refractive index of the immersion liquid and the sample medium (commonly aqueous) and by deeper imaging depth. An index-matched objective (e.g. silicone or water immersion) can alleviate some of these effects [23]. Further distortions might arise from imperfect alignment or drift of optical components, leading to non-telecentricity and slightly tilted image formation [34]. Lateral registration of the respective subimages in post-processing can compensate for rigid distortions of the individual subimages [39]. A careful choice of all optical components can minimize the total wavefront errors, e.g. by allowing diffraction-limited imaging with the high-magnification multiplane prism implementations detailed above. Multifocus implementations using diffractive elements always require aberration correction [37, 50]. Light field imaging is inherently affected by spherical aberrations introduced by the microlenses, which can be accounted for in the reconstruction PSF [56, 58].
Multiple factors can affect the SNR in volumetric imaging, some of which are specific to the 3D implementation choice. Imaging multiple planes simultaneously requires photons from separate planes to divided among different locations on the camera sensor. Hence, the individual signal in a focal plane “looses”photons compared to a 2D acquisition (if sampled within the original DOF), while exhibiting equal readout noise levels and shot-noise effects; this leads to a lower SNR. At the same time, the simultaneous recording of the different planes can reduce photobleaching compared to slower sequential imaging with epi-illumination, since volumetric imaging may offer more depth information than from the recorded planes alone. For example, for super-resolution imaging [23] the depth sampling can be computationally increased, while sequential imaging would need to sample more planes, which would require longer exposure of the sample to light, resulting in more photobleaching. In addition, optical elements that are introduced to split the light have themselves varying degrees of transmission or reflection efficiencies, decreasing the signal reaching the sensor. This varies with implementation, but MPM generally reaches efficiencies of ∼ 90%, while MFM and LFM reach 65%–90%, with additional loss at the CCG and CCP. The low image-side NA in LFM can additionally result in blurred PSFs, making it more susceptible to background shot noise than MPM and MFM.
When epi-illumination images are split into individual axial planes via refractive or diffractive optical elements or perspective views in LFM, the diminished SNR and lack of optical sectioning require denoising and out-of-focus background removal methods. Smoothing by, e.g., Gaussian filtering can alleviate sparse noise common in low SNR conditions, but also blurs the detected structures. More sophisticated deterministic approaches [87] such as non-local means [88] or wavelet filtering [89] can reduce shot- and readout noise using dedicated noise models. In recent years, deep learning (DL) has emerged as a successful and versatile tool to remove this noise while retaining useful signal [90, 91].
Most of the volumetric imaging methods presented in this review rely on simple widefield illumination, and hence lack optical sectioning. However, some imaging modalities, in particular in the super-resolution regime (e.g. SMLM, SOFI, SIM), inherently provide optical sectioning, often in combination with deconvolution. Deconvolution itself can increase the contrast and resolution of images. Often, an experimentally determined or theoretically proposed PSF is used in conjunction with the iterative Richardson-Lucy algorithm [93] to reconstruct the underlying information. More sophisticated algorithms, e.g., ones accounting for the 3D information [11], or using novel deep learning-based frameworks [95] can be applied.
Advanced illumination strategies such as multiphoton or selective-plane excitation [76] provide additional improvements, including optical sectioning, to the imaging performance. Stroehl et al. [97] recently presented scanned oblique light-sheet instant-volume sectioning (SOLIS), where an oblique light-sheet illuminates the sample axially and is laterally scanned within a single camera exposure with synchronized rolling shutter readout. SOLIS realizes optical sectioning within a single frame while exploiting simultaneous multiplane detection. Confocal LFM, a configuration in which images formed by the MLA are spatially filtered by a confocal mask attached to glass slides of varying thickness, has also been combined with vertical scanning light sheet excitation. This enabled optically sectioned, high SNR, deep tissue imaging at single cell resolution, albeit at the cost of decreased imaging speed and increased system complexity [98].
Multiplane, multifocus, and light field microscopy enable the simultaneous acquisition of different focal planes or whole 3D volumes within a sample. This eliminates the need for scanning methods and allows the robust observation of faster dynamics, ultimately limited only by the camera acquisition speed. As a secondary benefit, photobleaching of markers can be mitigated or delayed. This in turn opens the optimization space for 3D imaging experiments, enabling the usage of different markers for multicolor fluorescence imaging, robust 3D single-molecule particle tracking, and combinations with a variety of different imaging modalities. For example, a non-iterative tomographic phase reconstruction method that allows quantitative label-free imaging and fluorescence super-resolution imaging within the same imaging instrument was recently introduced [10]. This phase recovery only requires a 3D brightfield image stack as input; it is in principle adaptable to all the detection-side multiplane modalities presented here, turning any existing microscope into an ultrafast 3D quantitative phase imaging system with slight modifications.
The combination of the presented detection-side volumetric methods with excitation-side optical sectioning or structured illumination further expands the design space for more advanced dynamic investigations in vitro, on the intracellular or multicellular level, or even in whole animals. The appropriate choice of snapshot volumetric imaging method is thereby imperative and can be specific to the experimental requirements and expertise of the lab.
Refractive configurations are arguably the easiest to implement and align using commercially available components with high light efficiency. Diffractive components require considerable design and manufacturing effort upfront, in addition to a demanding alignment. LFM imaging can be conducted with commercially available MLAs, but might require optimized designs and computational knowledge in the group, as reconstructions are non-trivial.
Reduced lateral resolution is the largest trade-off one has to consider when choosing LFM for volumetric imaging, while both image-splitting techniques can achieve similar lateral resolution to mechanical axial scanning in conventional microscopy. Despite this constraint, sub-diffraction limited imaging via SOFI and SMLM is compatible with FLFM. 3D image reconstruction from the light field has advanced beyond the artifact-proneness of early LFM implementations, but still requires significant expertise.
In conventional single-color fluorescence microscopy, in medium-to-bright light conditions, the differences between MPM and MFM can be marginal and relate more to the expertise of the user. The relevant trade-off for almost all implementations of the two image-splitting techniques, is the field of view, because multiple images need to be placed on the same camera. The earliest MPM implementations used individual cameras for each axial plane, alleviating the FOV restriction at the cost of an increased spatial footprint and associated factors. Most prism-based MPM configurations split the FOV across two detectors, enabling slightly larger FOVs and easy adjustment of the DOF via the axial camera positioning (sequential, interleaved and parallel). In MFM, the subimages are usually distributed on a single detector and hence further restrict the potential FOV. In LFM, increasing the magnification and hence sacrificing FOV can make up for the decreased spatial resolution to a certain extent, while in FLFM the FOV is restricted to the focal length and size of an individual lenslet.
Light transmission efficiency over the visible wavelength range is high in all optimized implementations (⩾ 90%), but drops considerably in binary MFM grating designs (∼ 67%) and coarse, non-flush split MLAs (∼ 70%). The chromatic dependency of MFM can further decrease transmission efficiency at wavelengths other than the grating’s design wavelength. MPM implementations are mostly wavelength-agnostic across the visible range in terms of light efficiency, but can suffer from minor chromatic aberrations, which are usually compensated in MFM by the design of CCG. Simultaneous multicolor fluorescence applications in LFM are still challenging, while existing MPM configurations can usually be extended with dichroic mirrors, splitting according to the wavelength orthogonal to the axial information on the sensor.
The different volumetric imaging methods vary drastically in their ability to image across different magnifications within a single instrument. MFM gratings are commonly designed for a specific magnification; changing the magnification would require a simultaneous change of the grating and its position relative to the objective. With careful MLA and objective lens selection, similar adaptions can be partially avoided in LFM, while in MPM prism implementations may require realignment but no additional design changes.
For all three volumetric imaging methods, we have compiled a selection of biological applications and representative 3D hardware implementations in Table 1 to serve as a primer for the interested microscopist.
The code for tomographic phase recovery for Koehler illuminated multiplane stacks mentioned in the summary of this study can be found in the TPR4Py repository of the Grussmayer Lab [https://github.com/GrussmayerLab/TPR4Py].
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
We thank the Department of Bionanoscience and Delft University of Technology for funding. We want to thank Dirk-Peter Herten and Ran Huo for their critical reading of the manuscript and Kaley McCluskey for proofreading of the revised version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Martínez-Corral M, Hsieh PY, Doblas A, Sánchez-Ortiga E, Saavedra G, Huang YP. Fast axial-scanning widefield microscopy with constant magnification and resolution. J Display Technol (2015) 11:913–20. doi:10.1109/JDT.2015.2404347
2. Ji N. Adaptive optical fluorescence microscopy. Nat Methods (2017) 14:374–80. doi:10.1038/nmeth.4218
3. Navikas V, Descloux AC, Grussmayer KS, Marion S, Radenovic A. Adaptive optics enables multimode 3d super-resolution microscopy via remote focusing. Nanophotonics (2021) 10:2451–8. doi:10.1515/nanoph-2021-0108
4. Botcherby EJ, Juskaitis R, Booth MJ, Wilson T. Aberration-free optical refocusing in high numerical aperture microscopy. Opt Lett (2007) 32. doi:10.1364/ol.32.002007
5. Botcherby EJ, Juškaitis R, Booth MJ, Wilson T. An optical technique for remote focusing in microscopy. Opt Commun (2008) 281:880–7. doi:10.1016/j.optcom.2007.10.007
6. Stelzer EH, Strobl F, Chang BJ, Preusser F, Preibisch S, McDole K, et al. Light sheet fluorescence microscopy. Nat Rev Methods Primers (2021) 1:73–25. doi:10.1038/s43586-021-00069-4
7. Grimm JB, Lavis LD. Caveat fluorophore: An insiders’ guide to small-molecule fluorescent labels. Nat Methods (2022) 19:149–58. doi:10.1038/s41592-021-01338-6
8. Schermelleh L, Heintzmann R, Leonhardt H. A guide to super-resolution fluorescence microscopy. J Cel Biol (2010) 190:165–75. doi:10.1083/jcb.201002018
9. Li H, Guo C, Kim-Holzapfel D, Li W, Altshuller Y, Schroeder B, et al. Fast, volumetric live-cell imaging using high-resolution light-field microscopy. Biomed Opt Express (2019) 10:29–49. doi:10.1364/BOE.10.000029
10. Descloux A, Grußmayer KS, Bostan E, Lukes T, Bouwens A, Sharipov A, et al. Combined multi-plane phase retrieval and super-resolution optical fluctuation imaging for 4d cell microscopy. Nat Photon (2018) 12:165–72. doi:10.1038/s41566-018-0109-4
11. Xiao S, Gritton H, Tseng HA, Zemel D, Han X, Han X, et al. High-contrast multifocus microscopy with a single camera and z-splitter prism. Optica (2020) 7(11):14771477–1486 71486. doi:10.1364/OPTICA.404678
12. Hansen JN, Gong A, Wachten D, Pascal R, Turpin A, Jikeli JF, et al. Multifocal imaging for precise, label-free tracking of fast biological processes in 3d. Nat Commun (2021) 12:4574. doi:10.1038/S41467-021-24768-4
13. Hua X, Liu W, Jia S. High-resolution Fourier light-field microscopy for volumetric multi-color live-cell imaging. Optica (2021) 8:614–20. doi:10.1364/OPTICA.419236
14. Huang B, Wang W, Bates M, Zhuang X. Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy. Science (2008) 319:810–3. doi:10.1126/science.1153529
15. Thompson MA, Lew MD, Badieirostami M, Moerner W. Localizing and tracking single nanoscale emitters in three dimensions with high spatiotemporal resolution using a double-helix point spread function. Nano Lett (2010) 10:211–8. doi:10.1021/nl903295p
16. Weiss LE, Shalev Ezra Y, Goldberg S, Ferdman B, Adir O, Schroeder A, et al. Three-dimensional localization microscopy in live flowing cells. Nat Nanotechnol (2020) 15:500–6. doi:10.1038/s41565-020-0662-0
17. Liu S, Hua H. Extended depth-of-field microscopic imaging with a variable focus microscope objective. Opt Express (2011) 19:353–62. doi:10.1364/OE.19.000353
18. Adams JK, Boominathan V, Avants BW, Vercosa DG, Ye F, Baraniuk RG, et al. Single-frame 3d fluorescence microscopy with ultraminiature lensless flatscope. Sci Adv (2017) 3:e1701548. doi:10.1126/sciadv.1701548
19. Antipa N, Kuo G, Heckel R, Mildenhall B, Bostan E, Ng R, et al. Diffusercam: Lensless single-exposure 3d imaging. Optica (2018) 5:1–9. doi:10.1364/OPTICA.5.000001
20. He K, Wang Z, Huang X, Wang X, Yoo S, Ruiz P, et al. Computational multifocal microscopy. Biomed Opt Express (2018) 9:6477. doi:10.1364/boe.9.006477
21. Abrahamsson S, Chen J, Hajj B, Stallinga S, Katsov AY, Wisniewski J, et al. Fast multicolor 3d imaging using aberration-corrected multifocus microscopy. Nat Methods (2013) 10:60–3. doi:10.1038/nmeth.2277
22. Prabhat P, Ram S, Ward ES, Ober RJ. Simultaneous imaging of different focal planes in fluorescence microscopy for the study of cellular dynamics in three dimensions. IEEE Trans Nanobioscience (2004) 3:237–42. doi:10.1109/TNB.2004.837899
23. Geissbuehler S, Sharipov A, Godinat A, Bocchio NL, Sandoz PA, Huss A, et al. Live-cell multiplane three-dimensional super-resolution optical fluctuation imaging. Nat Commun (2014) 5:5830. doi:10.1038/NCOMMS6830
24. Levoy M, Hanrahan P. Light field rendering. In: Proceedings of the 23rd annual conference on Computer graphics and interactive techniques (1996). p. 31–42.
25. Mertz J. Strategies for volumetric imaging with a fluorescence microscope. Optica (2019) 6:1261. doi:10.1364/OPTICA.6.001261
26. Ram S, Prabhat P, Chao J, Ward ES, Ober RJ. High accuracy 3d quantum dot tracking with multifocal plane microscopy for the study of fast intracellular dynamics in live cells. Biophysical J (2008) 95:6025–43. doi:10.1529/biophysj.108.140392
27. Gan Z, Ram S, Ober RJ, Ward ES. Using multifocal plane microscopy to reveal novel trafficking processes in the recycling pathway. J Cel Sci (2013) 126:1176–88. doi:10.1242/jcs.116327
28. Itano MS, Bleck M, Johnson DS, Simon SM. Readily accessible multiplane microscopy: 3d tracking the hiv-1 genome in living cells. Traffic (Copenhagen, Denmark) (2016) 17:179–86. doi:10.1111/TRA.12347
29. Babcock HP. Multiplane and spectrally-resolved single molecule localization microscopy with industrial grade cmos cameras. Sci Rep (2018) 8:1726. doi:10.1038/S41598-018-19981-Z
30. Walker BJ, Wheeler RJ. High-speed multifocal plane fluorescence microscopy for three-dimensional visualisation of beating flagella. J Cel Sci (2019) 132:jcs231795. doi:10.1242/JCS.231795
31. Johnson KA, Noble D, Machado R, Hagen GM. Flexible multiplane structured illumination microscope with a four-camera detector. bioRxiv (2020). doi:10.1101/2020.12.03.410886
32. Sacconi L, Silvestri L, Rodríguez EC, Armstrong GA, Pavone FS, Shrier A, et al. Khz-rate volumetric voltage imaging of the whole zebrafish heart. Biophysical Rep (2022) 2:100046. doi:10.1016/j.bpr.2022.100046
33. Descloux A, Müller M, Navikas V, Markwirth A, Eynde RVD, Lukes T, et al. High-speed multiplane structured illumination microscopy of living cells using an image-splitting prism. Nanophotonics (2020) 9:143–8. doi:10.1515/NANOPH-2019-0346
34. Gregor I, Butkevich E, Enderlein J, Mojiri S. Instant three-color multiplane fluorescence microscopy. Biophysical Rep (2021) 1:100001. doi:10.1016/J.BPR.2021.100001
35. Ram S, Kim D, Ober R, Ward E. 3d single molecule tracking with multifocal plane microscopy reveals rapid intercellular transferrin transport at epithelial cell barriers. Biophysical J (2012) 103:1594–603. doi:10.1016/j.bpj.2012.08.054
36. Louis B, Camacho R, Bresolí-Obach R, Abakumov S, Vandaele J, Kudo T, et al. Fast-tracking of single emitters in large volumes with nanometer precision. Opt Express (2020) 28:28656–71. doi:10.1364/OE.401557
37. Abrahamsson S, Ilic R, Wisniewski J, Mehl B, Yu L, Chen L, et al. Multifocus microscopy with precise color multi-phase diffractive optics applied in functional neuronal imaging. Biomed Opt Express (2016) 7:855. doi:10.1364/boe.7.000855
38. Hajj B, Wisniewski J, El Beheiry M, Chen J, Revyakin A, Wu C, et al. Whole-cell, multicolor superresolution imaging using volumetric multifocus microscopy. Proc Natl Acad Sci U S A (2014) 111:17480–5. doi:10.1073/pnas.1412396111
39. Smith CS, Preibisch S, Joseph A, Abrahamsson S, Rieger B, Myers E, et al. Nuclear accessibility of β-actin mRNA is measured by 3D single-molecule real-time tracking. J Cel Biol (2015) 209:609–19. doi:10.1083/jcb.201411032
40. Wagner N, Norlin N, Gierten J, de Medeiros G, Balázs B, Wittbrodt J, et al. Instantaneous isotropic volumetric imaging of fast biological processes. Nat Methods (2019) 16:497–500. doi:10.1038/s41592-019-0393-z
41. Shaw M, Zhan H, Elmi M, Pawar V, Essmann C, Srinivasan MA. Three-dimensional behavioural phenotyping of freely moving c. elegans using quantitative light field microscopy. PLOS ONE (2018) 13:e0200108–15. doi:10.1371/journal.pone.0200108
42. Lu Z, Zhang Y, Zhu T, Yan T, Wu J, Dai Q. High-speed 3d observation with multi-color light field microscopy. In: Biophotonics congress: Biomedical optics 2020 (translational, microscopy, OCT, OTS, BRAIN). Washington, DC, USA: Optica Publishing Group (2020). MM2A.6. doi:10.1364/MICROSCOPY.2020.MM2A.6
43. Cong L, Wang Z, Chai Y, Hang W, Shang C, Yang W, et al. Rapid whole brain imaging of neural activity in freely behaving larval zebrafish (Danio rerio). eLife (2017) 6:e28158. doi:10.7554/eLife.28158
44. Sims RR, Sims RR, Rehman SA, Lenz MO, Benaissa SI, Bruggeman E, et al. Single molecule light field microscopy. Optica (2020) 7(9):1065–72. doi:10.1364/OPTICA.397172
45. Grußmayer K, Lukes T, Lasser T, Radenovic A. Self-blinking dyes unlock high-order and multiplane super-resolution optical fluctuation imaging. ACS Nano (2020) 14:9156–65. doi:10.1021/acsnano.0c04602
46. Mertz J, Xiao S, Zheng S. High-speed multifocus phase imaging in thick tissue. Biomed Opt Express (2021) 12(9):5782–92. doi:10.1364/BOE.436247
47. Cruz-Martín A, Mertz J, Kretsge L, Xiao S, Zheng S. Depth resolution in multifocus laser speckle contrast imaging. Opt Lett (2021) 46(19):5059–62. doi:10.1364/OL.436334
48. Blanchard PM, Greenaway AH. Simultaneous multiplane imaging with a distorted diffraction grating. Appl Opt (1999) 38:6692–9. doi:10.1364/AO.38.006692
49. Hajj B, Oudjedi L, Fiche JB, Dahan M, Nollmann M. Highly efficient multicolor multifocus microscopy by optimal design of diffraction binary gratings. Sci Rep (2017) 7:5284. doi:10.1038/s41598-017-05531-6
50. Amin MJ, Petry S, Shaevitz JW, Yang H. Localization precision in chromatic multifocal imaging. J Opt Soc Am B (2021) 38:2792–8. doi:10.1364/JOSAB.430594
51. Jesacher A, Roider C, Ritsch-Marte M. Enhancing diffractive multi-plane microscopy using colored illumination. Opt Express (2013) 21:11150. doi:10.1364/oe.21.011150
52. Amin MJ, Petry S, Yang H, Shaevitz JW. Uniform intensity in multifocal microscopy using a spatial light modulator. PloS one (2020) 15:e0230217. doi:10.1371/journal.pone.0230217
53. Maurer C, Khan S, Fassl S, Bernet S, Ritsch-Marte M. Depth of field multiplexing in microscopy. Opt Express (2010) 18:3023–34. doi:10.1364/OE.18.003023
54. Wang X, Yi H, Gdor I, Hereld M, Scherer NF. Nanoscale resolution 3d snapshot particle tracking by multifocal microscopy. Nano Lett (2019) 19:6781–7. doi:10.1021/acs.nanolett.9b01734
55. Abrahamsson S, Blom H, Agostinho A, Jans DC, Jost A, Müller M, et al. Multifocus structured illumination microscopy for fast volumetric super-resolution imaging. Biomed Opt Express (2017) 8:4135–40. doi:10.1364/BOE.8.004135
56. Abrahamsson S, McQuilken M, Mehta SB, Verma A, Larsch J, Ilic R, et al. Multifocus polarization microscope (mf-polscope) for 3d polarization imaging of up to 25 focal planes simultaneously. Opt Express (2015) 23:7734–54. doi:10.1364/OE.23.007734
57. Adelson EH, Wang JY. Single lens stereo with a plenoptic camera. IEEE Trans Pattern Anal Mach Intell (1992) 14:99–106. doi:10.1109/34.121783
58. Levoy M. Light fields and computational imaging. Computer (2006) 39:46–55. doi:10.1109/mc.2006.270
59. Sims R, O’holleran K, Shaw M. Light field microscopy: Principles and applications principles of light field microscopy. infocus (2019) 53. doi:10.1109/34.121783
60. Guo C, Liu W, Hua X, Li H, Jia S. Fourier light-field microscopy. Opt Express (2019) 27:25573–94. doi:10.1364/OE.27.025573
61. Broxton M, Grosenick L, Yang S, Cohen N, Andalman A, Deisseroth K, et al. Wave optics theory and 3-d deconvolution for the light field microscope. Opt Express (2013) 21:25418–39. doi:10.1364/OE.21.025418
62. Levoy M, Zhang Z, McDowall I. Recording and controlling the 4d light field in a microscope using microlens arrays. J Microsc (2009) 235:144–62. doi:10.1111/j.1365-2818.2009.03195.x
63. Prevedel R, Yoon YG, Hoffmann M, Pak N, Wetzstein G, Kato S, et al. Simultaneous whole-animal 3d-imaging of neuronal activity using light-field microscopy. Nat Methods (2014) 11:727–30. doi:10.1038/NMETH.2964
64. Andalman A, Deisseroth K, Grosenick L, Levoy M, Broxton M, Cohen N, et al. Wave optics theory and 3-d deconvolution for the light field microscope. Opt Express (2013) 21(21):25418–39. doi:10.1364/OE.21.025418
65.[Dataset] Huang H, Qiu H, Wu H, Ji Y, Li H, Yu B, et al. Sofflfm: Super-resolution optical fluctuation fourier light-field microscopy (2022). doi:10.48550/ARXIV.2208.12599
66. Sanchez-Ortiga E, Scrofani G, Saavedra G, Martínez-Corral M. Optical sectioning microscopy through single-shot lightfield protocol. IEEE Access (2020) 8:14944–52. doi:10.1109/access.2020.2966323
67. Yoon GY, Jitsuno T, Nakatsuka M, Nakai S. Shack hartmann wave-front measurement with a large f-number plastic microlens array. Appl Opt (1996) 35:188–92. doi:10.1364/AO.35.000188
68. Perez CC, Lauri A, Symvoulidis P, Cappetta M, Erdmann A, Westmeyer GG. Calcium neuroimaging in behaving zebrafish larvae using a turn-key light field camera. J Biomed Opt (2015) 20:096009–5. doi:10.1117/1.JBO.20.9.096009
69. Wang D, Zhu Z, Xu Z, Zhang D. Neuroimaging with light field microscopy: A mini review of imaging systems. Eur Phys J Spec Top (2022) 231:749–61. doi:10.1140/epjs/s11734-021-00367-8
70. Truscott TT, Belden J, Ni R, Pendlebury J, McEwen B. Three-dimensional microscopic light field particle image velocimetry. Exp Fluids (2017) 58:16–4. doi:10.1007/s00348-016-2297-3
71. Yao M, Cai Z, Qiu X, Li S, Peng J, Zhong J. Full-color light-field microscopy via single-pixel imaging. Opt Express (2020) 28:6521–36. doi:10.1364/OE.387423
72. Pégard NC, Liu HY, Antipa N, Gerlock M, Adesnik H, Waller L. Compressive light-field microscopy for 3d neural activity recording. Optica (2016) 3:517–24. doi:10.1364/optica.3.000517
73. Yoon YG, Wang Z, Pak N, Park D, Dai P, Kang JS, et al. Sparse decomposition light-field microscopy for high speed imaging of neuronal activity. Optica (2020) 7:1457–68. doi:10.1364/optica.392805
74. Javidi B, Martínez-Corral M. Fundamentals of 3d imaging and displays: A tutorial on integral imaging, light-field, and plenoptic systems. Adv Opt Photon (2018) 10(3):512–66. doi:10.1364/AOP.10.000512
75. Bimber O, Schedl DC. Light-field microscopy: A review. J Neurol Neuromedicine (2019) 4:1–6. doi:10.29245/2572.942x/2019/1.1237
76. Zhang Z, Cong L, Bai L, Wang K. Light-field microscopy for fast volumetric brain imaging. J Neurosci Methods (2021) 352:109083. doi:10.1016/j.jneumeth.2021.109083
77. Kim K. Single-shot light-field microscopy: An emerging tool for 3d biomedical imaging. Biochip J (2022) 1–12. doi:10.1007/s13206-022-00077-w
78. Cui Q, Park J, Ma Y, Gao L. Snapshot hyperspectral light field tomography. Optica (2021) 8:1552–8. doi:10.1364/OPTICA.440074
79. Verinaz-Jadan H, Song P, Howe CL, Foust AJ, Dragotti PL. Volume reconstruction for light field microscopy. In: ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Barcelona, Spain: IEEE (2020). p. 1459–63.
80. Zhang Y, Lu Z, Wu J, Lin X, Jiang D, Cai Y, et al. Computational optical sectioning with an incoherent multiscale scattering model for light-field microscopy. Nat Commun (2021) 12:6391–11. doi:10.1038/s41467-021-26730-w
81. Tian L, Waller L. 3d intensity and phase imaging from light field measurements in an led array microscope. Optica (2015) 2:104. doi:10.1364/optica.2.000104
82. Li X, Qiao H, Wu J, Lu Z, Yan T, Zhang R, et al. Deeplfm: Deep learning-based 3d reconstruction for light field microscopy. In: Biophotonics congress: Optics in the life sciences congress 2019 (BODA,BRAIN,NTM,OMA,OMP). Washington, DC, USA: Optica Publishing Group (2019). NM3C.2. doi:10.1364/NTM.2019.NM3C.2
83. Wang Z, Zhu L, Zhang H, Li G, Yi C, Li Y, et al. Real-time volumetric reconstruction of biological dynamics with light-field microscopy and deep learning. Nat Methods (2021) 18:551–6. doi:10.1038/s41592-021-01058-x
84. Wagner N, Beuttenmueller F, Norlin N, Gierten J, Boffi JC, Wittbrodt J, et al. Deep learning-enhanced light-field imaging with continuous validation. Nat Methods (2021) 18:557–63. doi:10.1038/s41592-021-01136-0
87. Meiniel W, Olivo-Marin JC, Angelini ED, Member S. Denoising of microscopy images: A review of the state-of-the-art, and a new sparsity-based method. IEEE Trans Image Process (2018) 27:3842–56. doi:10.1109/TIP.2018.2819821
88. Buades A, Coll B, Morel JM. A non-local algorithm for image denoising. In: 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05). San Diego, CA, USA: IEEE (2005). p. 60–5. vol. 2. doi:10.1109/CVPR.2005.38
89. Luisier F, Vonesch C, Blu T, Unser M. Fast interscale wavelet denoising of Poisson-corrupted images. Signal Process. (2010) 90:415–27. doi:10.1016/j.sigpro.2009.07.009
90. Weigert M, Schmidt U, Boothe T, Müller A, Dibrov A, Jain A, et al. Content-aware image restoration: Pushing the limits of fluorescence microscopy. Nat Methods (2018) 12:151090–7. doi:10.1038/s41592-018-0216-7
91. Krull A, Buchholz TO, Jug F. Noise2void-learning denoising from single noisy images. Proc IEEE/CVF Conf Comput Vis pattern recognition (2019) 2129–37.
92. Laine RF, Jacquemet G, Krull A. Imaging in focus: An introduction to denoising bioimages in the era of deep learning. Int J Biochem Cel Biol (2021) 140:106077. doi:10.1016/j.biocel.2021.106077
93. Richardson WH. Bayesian-based iterative method of image restoration*. J Opt Soc Am (1972) 62:55–9. doi:10.1364/JOSA.62.000055
94. Lucy LB. An iterative technique for the rectification of observed distributions. Astron J (1974) 79:745. doi:10.1086/111605
95. Krishnan AP, Belthangady C, Nyby C, Lange M, Yang B, Royer LA. Optical aberration correction via phase diversity and deep learning. bioRxiv (2020). doi:10.1101/2020.04.05.026567
96. Yanny K, Monakhova K, Shuai RW, Waller L. Deep learning for fast spatially varying deconvolution. Optica (2022) 9:96–9. doi:10.1364/OPTICA.442438
97.[Dataset] Ströhl F, Hansen DH, Grifo MN, Birgisdottir AB. Multifocus microscopy with optically sectioned axial superresolution (2022). doi:10.48550/ARXIV.2206.01257
Keywords: multiplane microscopy, multifocus microscopy, light field microscopy, image splitting, volumetric imaging, 3D imaging, PRISM
Citation: Engelhardt M and Grußmayer K (2022) Mapping volumes to planes: Camera-based strategies for snapshot volumetric microscopy. Front. Phys. 10:1010053. doi: 10.3389/fphy.2022.1010053
Received: 02 August 2022; Accepted: 26 September 2022;
Published: 11 October 2022.
Edited by:
Petra Granitzer, University of Graz, AustriaReviewed by:
Mario Feingold, Ben-Gurion University of the Negev, IsraelCopyright © 2022 Engelhardt and Grußmayer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Moritz Engelhardt, TS5MLksuRW5nZWxoYXJkdEB0dWRlbGZ0Lm5s; Kristin Grußmayer, Sy5TLkdydXNzbWF5ZXJAdHVkZWxmdC5ubA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.