Scheme for implementing nonlocal high-fidelity quantum controlled-not gates on quantum-dot-confined electron spins using optical microcavities and photonic hyperentanglement

Quantum information networks can transmit quantum states and perform quantum operations between different quantum network nodes, which are essential for various applications of quantum information technology in the future. In this paper, a potentially practical scheme for implementing nonlocal quantum controlled-not (CNOT) gate operations on quantum-dot-confined electron spins between two quantum network nodes is presented. The scheme can realize parallel teleportation of two nonlocal quantum CNOT gates simultaneously by employing hyperentangled photon pairs to establish quantum channel, which can effectively improve the channel capacity and operational speed. The core of the scheme are two kinds of photon-spin hybrid quantum CNOT gate working in a failure-heralded and fidelity-robust fashion. With the heralded mechanism, the nonlocal CNOT gates can be implementated with unity fidelities in principle, even if the particularly ideal conditions commonly used in other schemes are not satisfied strictly. Our analysis and calculations indicate that the scheme can be demonstrated efficiently (with efficiency exceeding 99%) with current or near-future technologies. Moreover, the utilized photon-spin hybrid quantum gates can be regarded as universal modules for many other quantum information processing (QIP) tasks. Therefore, the scheme is potential for constructing elementary quantum networks, and realizing nolocal QIP with high channel capacities, high fidelities, and high efficiencies.

1 Introduction

Quantum information technology, which aims to develop new theories and methods for processing information based on the laws of quantum mechanics, has developed very rapidly during the past decades. The main branches of this field, i.e., quantum communication [1], quantum computation [2–4], and quantum metrology [5, 6], have been established and become the focus of research. One of the ultimate directions for the development and integration of quantum information technology in the future is to construct quantum information networks [7–9], which are considered as spatially separated quantum network nodes connected by quantum communication channels. The fundamental characteristic of quantum networks lies in the capability to nonlocally transmit not only quantum states but also quantum operations between different quantum nodes, which makes it essential for various applications such as quantum secure direct communication [10–15] and secure multi-party quantum computation [16–21]. The quantum network can therefore significantly improve the power of quantum information processing (QIP) compared with individual QIP systems.

For the physical implementation of quantum networks, photon is the best carrier for fast and reliable communication over long distance, which plays the central role in the realization of nonlocal interactions between spatially distant quantum network nodes [22–24]. In particular, some interesting schemes for implementing nonlocal quantum operations between two different nodes have been proposed based on the sharing of entangled photon pairs, which act as the quantum channel for the teleportation of quantum gates [25–29]. In contrast to other schemes which rely on the transmission of a single photon through an optical channel to transmit interaction between two separate nodes, an attractive advantage of teleportation-based architectures is that the environmental noise and photon loss could be well overcome via entanglement purification together with quantum repeaters [30–36]. Moreover, photon possesses multiple degrees of freedom (DOFs) for encoding, such as polarization, spatial mode, frequency, time bin, and orbit angular momentum. Photon hyperentanglement [37–39], which refers to entanglements simultaneously existing in multiple DOFs of photons, has been demonstrated and proven useful in high-performance quantum communications [40–45], and hence represents a valuable quantum resource for quantum networks.

Solid-state spin systems such as electron or hole spins confined in semiconductor quantum dots (QDs) are ideal candidates for stationary qubits due to their good properties such as spin coherence and potential scalability [46–50]. Fast initialization, manipulation, and measurement of electron spins in charged QDs have been well-investigated [51–54]. Spin echo and dynamical decoupling techniques can be used to preserve the electron-spin coherence [55, 56]. With the help of optical microcavities or nanocavities, effective coupling between photons and singly charged QDs can be realized in coupled QD-cavity systems, which is crucial for realizing various quantum interfaces between single photons and spins [57–60]. With the photon-spin quantum interfaces, many QIP schemes such as universal quantum logic gates [61–67], quantum entanglement generation and analysis [68–73], and quantum entanglement purification and concentration [74–77] have been proposed. The QD-cavity systems supply ideal platforms for implementing quantum networks by constituting the quantum nodes and providing photon-spin interfaces [78, 79]. Significant progress has been achieved towards the practical demonstration of the photon-spin interfaces. For example, photon sorter [80], photon switch [81], Faraday rotation induced by a single electron or hole spin [82, 83] have been explored in experiments. These experiments were performed in the weakly-coupled cavity quantum electrodynamics (QED) regime.

In this work, we present a potentially practical scheme for implementing nonlocal quantum controlled-not (CNOT) gate operations on QD-confined electron spins between two quantum network nodes, by exploiting optical microcavities, hyperentangled photon pairs, and linear-optical elements. The scheme can realize parallel teleportation of two nonlocal quantum CNOT gates simultaneously by employing hyperentangled photon pairs to establish quantum channel, which can effectively improve the channel capacity and operational speed of the quantum network. The core units of the scheme are two kinds of photon-spin hybrid quantum CNOT gate constructed based on the interaction between an input photon and a singly charged QD mediated by a single-sided optical microcavity, which work in a failure-heralded and fidelity-robust fashion. With the help of the heralded mechanism, the nonlocal CNOT gates can be implemented with unity fidelities in principle, even if the particularly ideal conditions commonly used in other schemes are not satisfied strictly. Our analysis and calculations indicate that the scheme can be demonstrated efficiently with current or near-future technologies. Moreover, the photon-spin hybrid quantum gates used in this scheme can be regarded as universal modules, and can be used in many other QIP tasks. Therefore, the scheme has potential application prospects in constructing elementary quantum networks and realizing nonlocal QIP tasks with high channel capacities, high fidelities, and high efficiencies.

2 Interaction between an input photon and a singly charged QD mediated by a single-sided optical microcavity

As shown in Figure 1A, we consider a singly charged semiconductor QD [e.g., a self-assembled In(Ga)As QD or a GaAs interface QD] with an excess electron embedded in a single-sided optical micropillar cavity constructed by two GaAs/Al(Ga)As distributed Bragg reflectors (DBRs) and with a circular cross-section. The bottom DBR is 100% reflective and the top DBR is partially reflective so that the single-sided cavity hypothesis is valid. When we consider an input single photon interacting with the singly charged QD mediated by the single-sided optical microcavity, it has been proven that the optical property of the singly charged QD is dominated by the spin-dependent optical transitions of a negatively charged exciton (X⁻). The X⁻ is composed of two electrons bound to one hole, and the optical transition rule is based on the Pauli exclusion principle and the conservation of total spin angular momentum. The related energy levels and the optical transition rule of X⁻ transitions is shown in Figure 1B. The left-circularly polarized photon |L⟩ and the right-circularly polarized photon |R⟩ drive the transitions |↑⟩ → |↑↓⇑⟩ and |↓⟩ → |↓↑⇓⟩, respectively. Here, we use ∣ ↑⟩ and ∣ ↓⟩ to represent the excess-electron spin states with spins $J_z=\frac{1}{2}$ and $-\frac{1}{2}$, respectively. ∣ ⇑⟩ and ∣ ⇓⟩ represent the heavy-hole spin states with spins $J_z=\frac{3}{2}$ and $-\frac{3}{2}$, respectively. The spin-quantization axis (z-axis) is along the normal direction of the cavity.

FIGURE 1

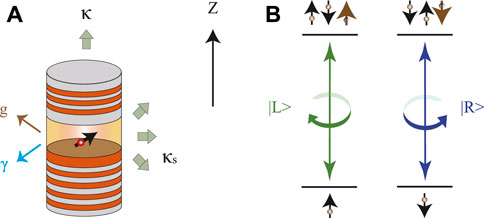
FIGURE 1. (A) Schematic diagram of a singly charged QD inside a single-sided optical micropillar cavity with two DBRs and circular cross section. g is the QD-microcavity coupling strength. γ is the exciton decay rate. κ and κ_s are the cavity-mode decay rates into the input-output mode and the leaky mode (side leakage), respectively. (B) The energy levels and the optical transition rule of exciton transitions. |L⟩ and |R⟩ represent the photonic left-circularly and right-circularly polarized states, respectively. The left-circularly polarized photon |L⟩ and the right-circularly polarized photon |R⟩ drive the transitions |↑⟩ → |↑↓⇑⟩ and |↓⟩ → |↓↑⇓⟩, respectively. z axis is the spin-quantization axis.

By solving the Heisenberg-Langevin equations of the cavity mode operator $\widehat{a}$ and the X⁻ dipole operator ${\widehat{\sigma }}_{-}$ in the interaction picture, we can calculate the optical reflection coefficient of the QD-cavity system [57]. Including losses in both the cavity and QD, as well as cavity excitation, we can attain the Heisenberg–Langevin equations as

$\begin{array}{ll}\hfill \frac{d\widehat{a}}{dt}& =-\left[i\left({\omega }_c-\omega \right)+\frac{\kappa }{2}+\frac{{\kappa }_s}{2}\right]\widehat{a}-g{\widehat{\sigma }}_{-}-\sqrt{\kappa }{\widehat{a}}_{in}+\widehat{H},\hfill \\ \hfill \frac{d{\widehat{\sigma }}_{-}}{dt}& =-\left[i\left({\omega }_{X^{-}}-\omega \right)+\frac{\gamma }{2}\right]{\widehat{\sigma }}_{-}-g{\widehat{\sigma }}_z\widehat{a}+\widehat{G}.\hfill \end{array}(1)$

Here, ω_c, ω, and ${\omega }_{X^{-}}$ represent frequencies of the cavity mode, the incident photon, and the X⁻ transition, respectively. κ and κ_s are the input-output decay rate and the leakage rate of the cavity field mode. g is the coupling strength between X⁻ and the cavity mode. γ is the X⁻ dipole decay rate. ${\widehat{\sigma }}_z$ is the population operator. ${\widehat{a}}_{in}$ is the input field operator, which connects to the output field operator ${\widehat{a}}_{\mathit{out}}$ through the standard cavity input-output relation ${\widehat{a}}_{\mathit{out}}={\widehat{a}}_{in}+\sqrt{\kappa }\widehat{a}$. $\widehat{H}$ and $\widehat{G}$ are the noise operators related to reservoirs. In the approximation of weak excitation, we take $⟨{\widehat{\sigma }}_z⟩=-1$ and the reflection coefficient of the QD-cavity system can be described by

$r\left(\mathrm{\Delta },g\right)=\frac{\left(i\mathrm{\Delta }+\frac{\gamma }{2}\right)\left(i\mathrm{\Delta }-\frac{\kappa }{2}+\frac{{\kappa }_s}{2}\right)+g^2}{\left(i\mathrm{\Delta }+\frac{\gamma }{2}\right)\left(i\mathrm{\Delta }+\frac{\kappa }{2}+\frac{{\kappa }_s}{2}\right)+g^2}.(2)$

Here we set ${\omega }_c={\omega }_{X^{-}}$, and $\mathrm{\Delta }={\omega }_{X^{-}}-\omega ={\omega }_c-\omega$ is the frequency detuning between the input photon and the cavity mode. When the photon does not couple to the QD (g = 0), the reflection coefficient is

$r\left(\mathrm{\Delta },0\right)=\frac{i\mathrm{\Delta }-\frac{\kappa }{2}+\frac{{\kappa }_s}{2}}{i\mathrm{\Delta }+\frac{\kappa }{2}+\frac{{\kappa }_s}{2}}.(3)$

When the excess electron is in the spin state ∣ ↑⟩(∣ ↓⟩), only the |L⟩(|R⟩) state photon can couple to the transition |↑⟩↔|↑↓⇑⟩(|↓⟩↔|↓↑⇓⟩) and obtain the reflection coefficient r (Δ, g), while the |R⟩(|L⟩) photon would feel an empty cavity and obtain the reflection coefficient r (Δ, 0). This is due to the optical transition rule and the cavity-QED effect. The reflection coefficients of coupled case r (Δ, g) and uncoupled case r (Δ, 0) can be significantly different, which is the so called giant circular birefringence effect [57]. As the single-photon input-output process is coherent, this description holds for superposition states as well. Therefore, when a horizontal polarized photon $|H\rangle =(|R\rangle +|L\rangle )/\sqrt{2}$ or a vertical polarized photon $|V\rangle =-i(|R\rangle -|L\rangle )/\sqrt{2}$ interacts with a QD-cavity system with the excess electron spin being prepared in the state $|\pm \rangle =(\mid \uparrow \rangle \pm \mid \downarrow \rangle )/\sqrt{2}$ initially, the photon-spin hybrid system evolves according to the following rules

$\begin{array}{ll}\hfill |H\rangle |& \pm \rangle \to \left[r_{+}\left(\mathrm{\Delta }\right)|H\rangle |\pm \rangle +i{r}_{-}\left(\mathrm{\Delta }\right)|V\rangle |\mp \rangle \right]/\sqrt{p_1},\hfill \\ \hfill |V\rangle |& \pm \rangle \to \left[i{r}_{+}\left(\mathrm{\Delta }\right)|V\rangle |\pm \rangle +r_{-}\left(\mathrm{\Delta }\right)|H\rangle |\mp \rangle \right]/\sqrt{p_1}.\hfill \end{array}(4)$

Here, r_±(Δ) = [r (Δ, 0)±r (Δ, g)]/2, p₁ = [|r (Δ, 0)|² + |r (Δ, g)|²]/2 is the probability of the photon being reflected by the QD-cavity system. That is, after the photon interacts with the QD-cavity system, the photon-spin system evolves into an orthogonally entangled state with two components: 1) due to the imperfect photon scattering process in reality, both the photon and electron spin remain unchanged with the probability of |r₊(Δ)|²/p₁; 2) both the photon and electron spin are flipped with the probability of |r₋(Δ)|²/p₁, which is the valid interaction we use to construct the quantum gates between a single photon and an electron spin. We note that the evolution rule is general and does not depend on the particularly ideal conditions [κ_s → 0, g > (κ, γ), |Δ|≪ g] usually used in other schemes.

3 Heralded photon-spin hybrid quantum CNOT gates with theoretically unity fidelities

Now we present two hybrid quantum CNOT gates, which are represented by ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ and ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ operation units, respectively. In the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ gate, the spatial-mode state of an incident photon encodes the control qubit, while the electron spin confined in QD encodes the target qubit. In the ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ gate, the polarization state of an incident photon encodes the control qubit, while the QD spin encodes the target qubit. The quantum circuits for ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ and ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ are shown in Figure 2. Hereinafter, VBS represents an adjustable beam splitter with transmission coefficient r₋(Δ) and reflection coefficient $\sqrt{1-|r_{-}(\mathrm{\Delta }){|}^2}$. D_i (i = 1, 2, 3, 4) represents a single-photon detector. DL is the delay line, which makes the photon components in spatial modes s₁ and s₂ arrive the output port simultaneously without affecting the quantum state. PBS_j (j = 1, 2, … , 6) is a polarization beam splitter, which transmits the photonic horizontal polarization component |H⟩ and reflects the vertical polarization component |V⟩. $P_{\theta }=|H\rangle \langle H|+e^{-\frac{\pi }{2}i}|V\rangle \langle V|$ is a quantum phase gate on the polarization of the photon. X_t (t = 1, 2, 3) is a half-wave plate which performs a polarization bit-flip operation ${\sigma }_X^P=|H\rangle \langle V|+|V\rangle \langle H|$. R_f (f = 1, 2) completes the polarization rotation $|H\rangle \to r_{-}(\mathrm{\Delta })|H\rangle +\sqrt{1-|r_{-}(\mathrm{\Delta }){|}^2}|V\rangle$ u and d are to distinguish two different spatial modes in the quantum circuits. The red dots denote the optical switches.

FIGURE 2

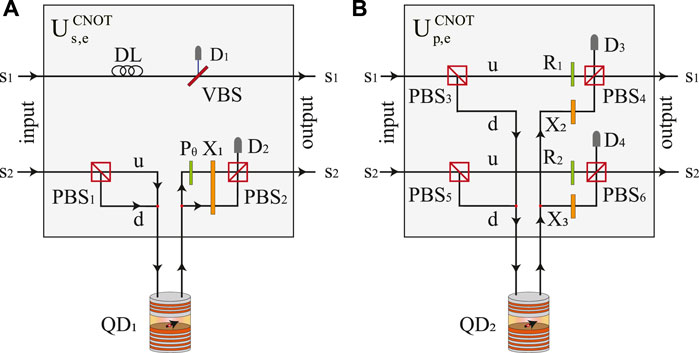
FIGURE 2. Schematics of the heralded photon-spin hybrid CNOT gates. (A) The spatial mode of the photon is the control qubit, and the QD-confined electron spin is the target qubit. (B) The polarization of the photon is the control qubit, and the QD-confined electron spin is the target qubit. All the functions of the optical elements are presented in the text.

As shown in Figure 2A, suppose the initial states of the input photon and the electron spin confined in QD are |ψ_p⟩ = (k|H⟩ + l|V⟩) (m|s₁⟩ + n|s₂⟩) and |ψ_e⟩ = μ| + ⟩ + ν| − ⟩, respectively. Before the photon enters the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ unit, the state of the photon-spin hybrid system is

$|{\psi }_0\rangle =|{\psi }_p\rangle \otimes |{\psi }_e\rangle =\left(k|H\rangle +l|V\rangle \right)\left(m|s_1\rangle +n|s_2\rangle \right)\otimes \left(\mu |+\rangle +\nu |-\rangle \right).(5)$

Here, s₁ and s₂ are two spatial modes of the photon, respectively. When the photon enters the unit from the input port, the photon component in spatial mode s₁ passes through the delay line DL with state unchanged. The photon component in spatial mode s₂ passes PBS₁, and the |H⟩(|V⟩) photon component interacts with the QD-cavity system via spatial mode u(d) as described by Eq. 4. Then the photon component in spatial mode u passes P_θ and X₁, the photon component in spatial mode d passes X₁. After which, the state of the photon-spin system becomes

$\begin{array}{ll}\hfill |{\psi }_1\rangle & =m|s_1\rangle \left(k|H\rangle +l|V\rangle \right)\left(\mu |+\rangle +\nu |-\rangle \right)\hfill \\ \hfill & +n\left[r_{-}\left(\mathrm{\Delta }\right)\left(k|{H\rangle }_u+l|{V\rangle }_d\right)\left(\mu |-\rangle +\nu |+\rangle \right)\right.\hfill \\ \hfill & +\left.r_{+}\left(\mathrm{\Delta }\right)\left(k|{V\rangle }_u+il|{H\rangle }_d\right)\left(\mu |+\rangle +\nu |-\rangle \right)\right],\hfill \end{array}(6)$

where the subscripts u and d are used to distinguish the spatial modes. Then, the photon components pass through VBS and PBS₂, respectively. When neither of the photon detectors D₁ and D₂ click, we call this a valid state evolution, and we get the state

$|{\psi }_2\rangle =r_{-}\left(\mathrm{\Delta }\right)\left(k|H\rangle +l|V\rangle \right)\left[m|s_1\rangle \left(\mu |+\rangle +\nu |-\rangle \right)+n|s_2\rangle \left(\mu |-\rangle +\nu |+\rangle \right)\right].(7)$

Then the heralded photon-spin hybrid CNOT gate is completed, where the spatial mode of the incident photon is the control qubit and the electron spin confined in the QD is the target qubit. The polarization state of the photon does not change after this process.

On the contrary, if the photon detector D₁ or D₂ clicks, these two cases mean that errors occur in the state evolution. Any detector response means photon loss, and we get an invalid quantum state evolution result. This failure-herald mechanism guarantees the fidelity of the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ unit by filtering out the errors. The QD-spin state does not change when an error occurs, and we can let a new photon enter the circuit to repeat the operation until success.

The ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ operation unit is shown in Figure 2B. Suppose the initial state of the photon-spin hybrid system is still |ψ₀⟩. Similar to the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ gate, if no photon detector responds, the photon leaves the output port and the state of the photon-spin system changes from |ψ₀⟩ to

$|{\psi }_3\rangle =r_{-}\left(\mathrm{\Delta }\right)\left[k|H\rangle \left(\mu |+\rangle +\nu |-\rangle \right)+l|V\rangle \left(\mu |-\rangle +\nu |+\rangle \right)\right]\left(m|s_1\rangle +n|s_2\rangle \right).(8)$

The hybrid CNOT gate ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ is completed, in which the polarization of the incident single photon controls the electron spin confined in the QD. The spatial-mode state of the photon does not change. If the photon detector D₁ or D₂ clicks, the operation failed, and the spin state does not change. We can repeat the operation until success.

These two hybrid CNOT gates ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ and ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ have some characteristics for building quantum circuits. First, the CNOT gates can work when the particularly ideal conditions usually used in other schemes cannot be satisfied. Second, the failure of the operations can be announced by the single-photon detectors, so we can know whether the operation succeeded or not. Third, the fidelities of the CNOT gates can reach unity in principle. As modular functional units, the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ and ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ operation units can not only be used in the proposed scheme but also in many other QIP tasks.

4 Nonlocal high-fidelity quantum controlled-not gates on QD-confined electron spins between quantum network nodes

In this section, we propose the scheme for nonlocal high-fidelity quantum CNOT gates between two remote quantum network nodes Alice and Bob, resorting to single-sided QD-cavity systems, hyperentangled photon pairs, and linear optical elements. As shown in Figure 3, the quantum network node consists of two electron spins confined in QD-cavity systems. We assume the QD-cavity systems in the scheme are identical. Network node Alice holds the electron spins AA′ and the initial state is |Ψ_AA′⟩ = (α| +⟩ +β|−⟩)_A (α′| +⟩ +β′|−⟩)_A′. Network node Bob holds the electron spins BB′ and the initial state is |Ψ_BB′⟩ = (γ| +⟩ +ξ|−⟩)_B (γ′| +⟩ +ξ′|−⟩)_B′. The subscripts A, A′, B, and B′ are used to distinguish the four electron spins. The coefficients satisfy the relation |α|² + |β|² = 1, |α′|² + |β′|² = 1, |γ|² + |ξ|² = 1, and |γ′|² + |ξ′|² = 1. The electron spin A (A′) of Alice is the control qubit, while the electron spin B(B′) of Bob is the target qubit. The hyperentangled photon pair a and b are used to build the quantum channel and encoded in two DOFs, i.e., the polarization and the spatial mode. Photons a and b are initially prepared in the state $|{\mathrm{\Psi }}_{ab}\rangle =\frac{1}{2}{(|HH\rangle +|VV\rangle )}_{ab}(|a_1{b}_1\rangle +|a_2{b}_2\rangle )$, where the subscripts a and b are used to distinguish two photons. |a₁⟩(|b₁⟩) and |a₂⟩(|b₂⟩) are the two spatial modes of photon a(b), respectively. The scheme is detailed as follows.

FIGURE 3

FIGURE 3. Schematic of nonlocal high-fidelity quantum CNOT gates between remote quantum network nodes. The electron spin A (A′) of Alice is the control qubit, while the electron spin B(B′) of Bob is the target qubit. a and b are hyperentangled photon pair. BS_i (i = 1, 2, 3) is a 50:50 beam splitter used to perform a Hadamard operation on the spatial mode DOF of a photon, which completes the following transformation: $|s_1\rangle \to (|s_1\rangle +|s_2\rangle )/\sqrt{2}$ and $|s_2\rangle \to (|s_1\rangle -|s_2\rangle )/\sqrt{2}(s=a,b)$. H_j (j = 1, 2, … , 6) represents a half-wave plate to perform a Hadamard operation on the polarization of a photon, which completes the following transformation: $|H\rangle \to (|H\rangle +|V\rangle )/\sqrt{2}$ and $|V\rangle \to (|H\rangle -|V\rangle )/\sqrt{2}$. Alice and Bob holds four local single-photon detectors, respectively. i.e., D₁-D₄ and D₅-D₈. The other elements have the same function as that in Figure 2.

Before the photons enter the circuits, the state of the system composed of photon a, photon b, electron spin AA′ and BB′ is

$\begin{array}{ll}\hfill |{\mathrm{\Psi }\rangle }_0& =|{\mathrm{\Psi }}_{ab}\rangle \otimes |{\mathrm{\Psi }}_{A{A}^{\prime }}\rangle \otimes |{\mathrm{\Psi }}_{B{B}^{\prime }}\rangle \hfill \\ \hfill & =\frac{1}{2}{\left(|HH\rangle +|VV\rangle \right)}_{ab}\left(|a_1{b}_1\rangle +|a_2{b}_2\rangle \right)\otimes {\left(\alpha |+\rangle +\beta |-\rangle \right)}_A\hfill \\ \hfill & \times {\left({\alpha }^{\prime }|+\rangle +{\beta }^{\prime }|-\rangle \right)}_{A^{\prime }}\otimes {\left(\gamma |+\rangle +\xi |-\rangle \right)}_B{\left({\gamma }^{\prime }|+\rangle +{\xi }^{\prime }|-\rangle \right)}_{B^{\prime }}.\hfill \end{array}(9)$

After the hyperentangled photon pair a and b are prepared, photon a is sent to Alice, while photon b is sent to Bob simultaneously. Photon a enters the node Alice and sequentially passes through H₁, H₂, ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$, H₃, H₄, BS₁, ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$, BS₂ in both spatial modes a₁ and a₂. If none of the photon detectors in the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ and ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ units clicks, the state of the photon-spin system is changed from |Ψ⟩₀ to |Ψ⟩₁ in unnormalized form

$\begin{array}{ll}\hfill |{\mathrm{\Psi }\rangle }_1& =\frac{r_{-}^2\left(\mathrm{\Delta }\right)}{2}\left[\alpha |{+\rangle }_A\left(|a_1{b}_1\rangle +|a_2{b}_2\rangle \right)+\beta |{-\rangle }_A\left(|a_2{b}_1\rangle +|a_1{b}_2\rangle \right)\right]\hfill \\ \hfill & \otimes \left[{\alpha }^{\prime }|{+\rangle }_{A^{\prime }}{\left(|HH\rangle +|VV\rangle \right)}_{ab}+{\beta }^{\prime }|{-\rangle }_{A^{\prime }}{\left(|VH\rangle +|HV\rangle \right)}_{ab}\right].\hfill \end{array}(10)$

At the same time, photon b enters the node Bob and sequentially passes through ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$, ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ in both spatial modes b₁ and b₂. If no detector in the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ and ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ units clicks, the state of the system evolves into

$\begin{array}{ll}\hfill |{\mathrm{\Psi }\rangle }_2& =\frac{r_{-}^4\left(\mathrm{\Delta }\right)}{2}\left\{\alpha |{+\rangle }_A\left[|a_1{b}_1\rangle {\left(\gamma |+\rangle +\xi |-\rangle \right)}_B+|a_2{b}_2\rangle {\left(\gamma |-\rangle +\xi |+\rangle \right)}_B\right]\right.\hfill \\ \hfill & +\left.\beta |{-\rangle }_A\left[|a_2{b}_1\rangle {\left(\gamma |+\rangle +\xi |-\rangle \right)}_B+|a_1{b}_2\rangle {\left(\gamma |-\rangle +\xi |+\rangle \right)}_B\right]\right\}\hfill \\ \hfill & \otimes \left\{{\alpha }^{\prime }|{+\rangle }_{A^{\prime }}\left[\left(|H{H\rangle }_{ab}{\left({\gamma }^{\prime }|+\rangle +{\xi }^{\prime }|-\rangle \right)}_{B^{\prime }}+|V{V\rangle }_{ab}{\left({\gamma }^{\prime }|-\rangle +{\xi }^{\prime }|+\rangle \right)}_{B^{\prime }}\right]\right.\right.\hfill \\ \hfill & +\left.\left.{\beta }^{\prime }|{-\rangle }_{A^{\prime }}\left[|V{H\rangle }_{ab}{\left({\gamma }^{\prime }|+\rangle +{\xi }^{\prime }|-\rangle \right)}_{B^{\prime }}+|H{V\rangle }_{ab}{\left({\gamma }^{\prime }|-\rangle +{\xi }^{\prime }|+\rangle \right)}_{B^{\prime }}\right)\right]\right\}.\hfill \end{array}(11)$

Then, Hadamard operations are performed on photon b in both the polarization and the spatial mode via H₅, H₆, and BS₃. Before photon b gets the photon detectors D₅-D₈, the state of the system is

$\begin{array}{ll}\hfill |{\mathrm{\Psi }\rangle }_3& =\frac{r_{-}^4\left(\mathrm{\Delta }\right)}{4}\left\{\alpha |{+\rangle }_A\left[|a_1\rangle \left(|b_1\rangle +|b_2\rangle \right){\left(\gamma |+\rangle +\xi |-\rangle \right)}_B+|a_2\rangle \left(|b_1\rangle \right.\right.\right.\hfill \\ \hfill & -\left.\left.|b_2\rangle \right){\left(\gamma |-\rangle +\xi |+\rangle \right)}_B\right]+\beta |{-\rangle }_A\left[|a_2\rangle \left(|b_1\rangle +|b_2\rangle \right)\left(\gamma |+\rangle \right.\right.\hfill \\ \hfill & +\left.\left.{\left.\xi |-\rangle \right)}_B+|a_1\rangle \left(|b_1\rangle -|b_2\rangle \right){\left(\gamma |-\rangle +\xi |+\rangle \right)}_B\right]\right\}\hfill \\ \hfill & \otimes \left\{{\alpha }^{\prime }|{+\rangle }_{A^{\prime }}\left[|{H\rangle }_a{\left(|H\rangle +|V\rangle \right)}_b{\left({\gamma }^{\prime }|+\rangle +{\xi }^{\prime }|-\rangle \right)}_{B^{\prime }}+|{V\rangle }_a\left(|H\rangle \right.\right.\right.\hfill \\ \hfill & -\left.{\left.|V\rangle \right)}_b{\left({\gamma }^{\prime }|-\rangle +{\xi }^{\prime }|+\rangle \right)}_{B^{\prime }}\right]+{\beta }^{\prime }|{-\rangle }_{A^{\prime }}\left[|{V\rangle }_a{\left(|H\rangle +|V\rangle \right)}_b\left({\gamma }^{\prime }|+\rangle \right.\right.\hfill \\ \hfill & +\left.\left.{\left.{\xi }^{\prime }|-\rangle \right)}_{B^{\prime }}+|{H\rangle }_a{\left(|H\rangle -|V\rangle \right)}_b{\left({\gamma }^{\prime }|-\rangle +{\xi }^{\prime }|+\rangle \right)}_{B^{\prime }}\left.\right)\right]\right\}.\hfill \end{array}(12)$

Finally, the photons a and b pass the PBSs and get the local photon detectors D₁-D₄ and D₅-D₈, respectively. Alice and Bob communicate their measurement results through a classical communication channel. According to the results, Alice and Bob choose the corresponding single-qubit rotation operations on electron spins according to Table 1. For example, if the photon pair ab are finally detected in the state |a₁b₁H_aH_b⟩, the state of the four-spin system AA′BB′ is

$\begin{array}{ll}\hfill |{\mathrm{\Psi }}_{A{A}^{\prime }B{B}^{\prime }}\rangle & =\frac{r_{-}^4\left(\mathrm{\Delta }\right)}{4}\left[\alpha |{+\rangle }_A{\left(\gamma |+\rangle +\xi |-\rangle \right)}_B+\beta |{-\rangle }_A{\left(\gamma |-\rangle +\xi |+\rangle \right)}_B\right]\hfill \\ \hfill & \otimes \left[{\alpha }^{\prime }|{+\rangle }_{A^{\prime }}{\left({\gamma }^{\prime }|+\rangle +{\xi }^{\prime }|-\rangle \right)}_{B^{\prime }}+{\beta }^{\prime }|{-\rangle }_{A^{\prime }}{\left({\gamma }^{\prime }|-\rangle +{\xi }^{\prime }|+\rangle \right)}_{B^{\prime }}\right],\hfill \end{array}(13)$

TABLE 1

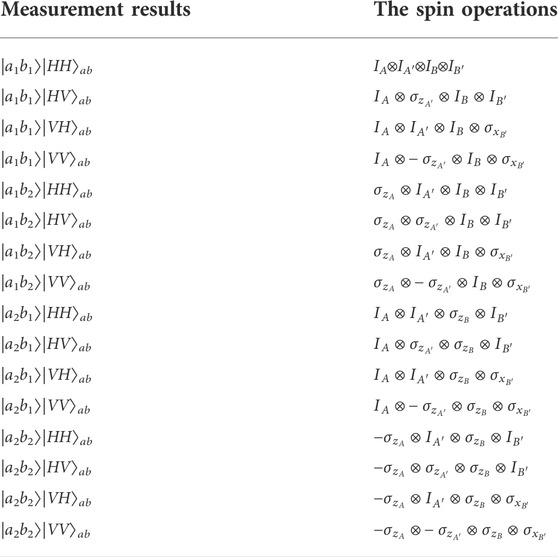
TABLE 1. The measurement results of the photons and the corresponding single-qubit gate rotation operations required on the electron spins.

which means two CNOT gates between the spins AA′ of Alice and the spins BB′ of Bob have been implemented. If the photons are detected in the state |a₁b₂V_aV_b⟩, Alice should perform a σ_z operation on the electron spin A and a − σ_z operation on the spin A′, and Bob should perform a σ_x operation on the spin B′. After the operations above, the state |Ψ_AA′BB′⟩ can be obtained. Other situations can be seen in Table 1. Moreover, if any photon detector in the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ or ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ unit clicks, it declares a failed operation, and we can restart the process just via launching a new pair of hyperentangled photons.

So far, we have described the teleportation of two nonlocal CNOT gates operations on spin qubits between two quantum network nodes in parallel assisted by single-sided QD-cavity systems. Electron spin A (A′) of Alice is the control qubit, while the electron spin B(B′) of Bob is the target qubit. Two CNOT gates are achieved simultaneously. The modular functional units make the circuit more flexible and extensible. For instance, if we let the electron spin A (A′) of Alice control B′(B) of Bob, we only need to let photon b pass through a linear optical ${\mathrm{U}}_{s,p}^{\mathit{SWAP}}$ unit shown in Figure 4 before the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$, which swaps the spatial mode and polarization states of the incident photon.

FIGURE 4

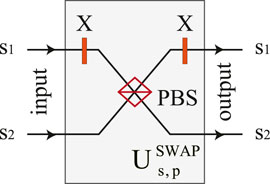
FIGURE 4. Schematic of the ${\mathrm{U}}_{s,p}^{\mathit{SWAP}}$ unit, which swaps the polarization and spatial mode states of the incident photon. The elements have the same function as that in Figure 2.

5 Discussion and summary

In this section, we discuss the performance of the scheme, which can be characterized by fidelity and efficiency. We define the fidelity as F = |⟨Ψ_r|Ψ_i⟩|², where |Ψ_r⟩ is the final state of the system composed of four electron spins hold by two network nodes Alice and Bob in reality, and |Ψ_i⟩ is the final state of the system in ideal conditions, which should be

$\begin{array}{ll}\hfill |{\mathrm{\Psi }}_i\rangle & =\frac{1}{4}\left[\alpha |{+\rangle }_A{\left(\gamma |+\rangle +\xi |-\rangle \right)}_B+\beta |{-\rangle }_A{\left(\gamma |-\rangle +\xi |+\rangle \right)}_B\right]\hfill \\ \hfill & \otimes \left[{\alpha }^{\prime }|{+\rangle }_{A^{\prime }}{\left({\gamma }^{\prime }|+\rangle +{\xi }^{\prime }|-\rangle \right)}_{B^{\prime }}+{\beta }^{\prime }|{-\rangle }_{A^{\prime }}{\left({\gamma }^{\prime }|-\rangle +{\xi }^{\prime }|+\rangle \right)}_{B^{\prime }}\right].\hfill \end{array}(14)$

Consider the cavity QED parameters (g, κ, κ_s, γ), the final state of the system in unnormalized form is

$\begin{array}{ll}\hfill |{\mathrm{\Psi }}_r\rangle & =|{\mathrm{\Psi }}_{A{A}^{\prime }B{B}^{\prime }}\rangle \hfill \\ \hfill & =\frac{r_{-}^4\left(\mathrm{\Delta }\right)}{4}\left[\alpha |{+\rangle }_A{\left(\gamma |+\rangle +\xi |-\rangle \right)}_B+\beta |{-\rangle }_A{\left(\gamma |-\rangle +\xi |+\rangle \right)}_B\right]\hfill \\ \hfill & \otimes \left[{\alpha }^{\prime }|{+\rangle }_{A^{\prime }}{\left({\gamma }^{\prime }|+\rangle +{\xi }^{\prime }|-\rangle \right)}_{B^{\prime }}+{\beta }^{\prime }|{-\rangle }_{A^{\prime }}{\left({\gamma }^{\prime }|-\rangle +{\xi }^{\prime }|+\rangle \right)}_{B^{\prime }}\right].\hfill \end{array}(15)$

The average fidelity of the scheme is

$\begin{array}{ll}\hfill \bar{F}& =\overline{|\langle {\mathrm{\Psi }}_r|{\mathrm{\Psi }}_i\rangle {|}^2}\hfill \\ \hfill & =\frac{1}{4{\pi }^4}{\int }_0^{2\pi }d{\theta }_A{\int }_0^{2\pi }d{\theta }_{A^{\prime }}{\int }_0^{2\pi }d{\varphi }_B{\int }_0^{2\pi }d{\varphi }_{B^{\prime }}\frac{|\langle {\mathrm{\Psi }}_r|{\mathrm{\Psi }}_i\rangle {|}^2}{\langle {\mathrm{\Psi }}_r|{\mathrm{\Psi }}_r\rangle }=1,\hfill \end{array}(16)$

where cos θ_A = α, sin θ_A = β, cos θ_A′ = α′, sin θ_A′ = β′, cos ϕ_B = γ, sin ϕ_B = ξ, cos ϕ_B′ = γ′, and sin ϕ_B′ = ξ′. The fidelity of the scheme is unity in principle. The herald mechanism of the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ and ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ operation units filters out the errors and announces them via single-photon detectors, which guarantees high fidelity. We can conclude that the fidelity is robust to the cavity QED parameters (g, κ, κ_s, γ) and photon loss.

The efficiency of the scheme is defined as the probability that the hyperentangled photon pair are detected by the local single-photon detectors of Alice and Bob. In other words, the efficiency is the probability that none of the single-photon detectors of ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ or ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ operation units clicks, and the network nodes Alice and Bob each have a local single-photon detector click. The efficiency can be described as

$\begin{array}{ll}\hfill \eta & ={\left|r_{-}{\left(\mathrm{\Delta }\right)}^4\right|}^2={\left|\frac{r\left(\mathrm{\Delta },0\right)-r\left(\mathrm{\Delta },g\right)}{2}\right|}^8\hfill \\ \hfill & ={\left|\frac{-4g^2/{\kappa }^2}{\left(2i\mathrm{\Delta }/\kappa +1+{\kappa }_s/\kappa \right)\left[\left(2i\mathrm{\Delta }/\kappa +\gamma /\kappa \right)\left(2i\mathrm{\Delta }/\kappa +1+{\kappa }_s/\kappa \right)+4g^2/{\kappa }^2\right]}\right|}^8,\hfill \end{array}(17)$

which depends on cavity-QED parameters. The relation between the absolute amplitude of r₋(Δ), the cavity-QED parameters (g, κ, κ_s, γ), and the frequency detuning Δ is depicted in Figure 5, where we take γ = 0.01κ. As shown in Figure 5, we take the slices g/κ = 0.5, g/κ = 1, g/κ = 2.4, κ_s/κ = 0, κ_s/κ = 0.05, and κ_s/κ = 0.1 for examples. We can conclude that |r₋(Δ)| can get relevant high values not only around the resonant frequency Δ = 0 but also at some other frequency detuning such as Δ = ±g. The cavity side leakage and loss rate κ_s/κ decrease |r₋(Δ)| slightly.

FIGURE 5

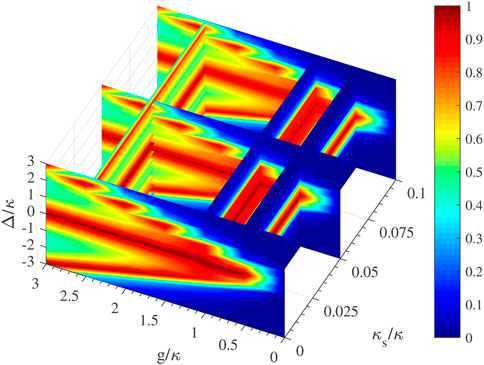
FIGURE 5. The absolute amplitude |r₋(Δ)| of r₋(Δ) vs. the cavity QED parameters (g, κ, κ_s, γ) and the frequency detuning Δ. The slices shown are g/κ = 0.5, g/κ = 1, g/κ = 2.4, κ_s/κ = 0, κ_s/κ = 0.05, and κ_s/κ = 0.1. γ = 0.01κ.

When the system works under the resonance frequency (Δ = 0), the efficiency η is the function of the coupling strength g/κ and the cavity decay rate κ_s/κ under given γ. The relation between η and the cavity QED parameters (g, κ, κ_s, γ) under the resonant frequency Δ = 0 is shown in Figure 6. When the side leakage is negligible, the efficiency is 92.35% at g = 0.5κ, 98.021% at g = κ, and 99.65% at g = 2.4κ. The scheme has high efficiency without the strict requirement of the strong-coupling condition. When κ_s = 0.05κ, the efficiency is 62.26% at g = 0.5κ, 66.28% at g = κ, and 67.44% at g = 2.4κ. The scheme still works when the side leakage is taken into account. To obtain high efficiency, the side leakage and the cavity loss rate κ_s/κ should be controlled as small as possible. The side leakage κ_s can be reduced by engineering the fabrication and adjusting the material, structure and size of the cavity.

FIGURE 6

FIGURE 6. The efficiency η vs. g/κ and κ_s/κ at the resonant frequency Δ = 0. γ = 0.01κ.

The hyperentangled photon pairs can be generated by combinations of the techniques used for creating entanglement in a single DOF [37, 38], such as with the assistance of an optical cavity [84, 85] or spontaneous four-wave mixing [86]. The bandwidth of the hyperentangled pules should be narrow than the linewidth of the cavity mode. The superposition state of an electron spin can be prepared assisted by nanosecond ESR pulses or picosecond optical pulses [53]. The fast single-qubit rotation operations on the electron spin can be achieved by ultrafast optical pulses or optically controlled geometric phases [54]. The dark counts of photon detectors may lead to false-positive responses that affect the efficiency slightly. Other factors such as the imperfect hyperentangled sources and the linear elements would affect the performance of the scheme, and can be improved by the manufacturing process.

In summary, assisted by single-sided QD-cavity systems, we presented two robust photon-spin hybrid CNOT gates with a herald mechanism, i.e., the ${\mathrm{U}}_{s,e}^{\mathit{CNOT}}$ and ${\mathrm{U}}_{p,e}^{\mathit{CNOT}}$ operation units. The units can work without the strict requirement of strong coupling. Single-photon detectors can herald the failure of the operation. The fidelities of the units can get unity in principle. Utilizing the units, we propose a parallel teleportation scheme of two nonlocal quantum CNOT gates between two remote quantum network nodes, Alice and Bob. Electron spins A and A′ of Alice simultaneously control electron spins B and B′ of Bob, respectively. The scheme has some characteristics. First, we use hyperentangled photon pairs to build the quantum channel for nonlocal operations, which can effectively improve the channel capacity. Second, with the herald mechanism, the fidelities of the nonlocal CNOT gates can be raised to unity in principle. Third, teleporting two CNOT gates in parallel can save quantum resources and accelerate computing speed. Fourth, the scheme with the modular design has good flexibility. The advantages above make the scheme feasible with current technology, which may open promising possibilities for nonlocal quantum computation and quantum information networks. To construct a practical multi-node quantum network, a series of cascade cavities with coupled quantum memories or registers are required. Although our scheme could weaken the requirements for coupling strength and cavity leakage to some extent, it is still a technical challenge to connect multiple different cavities while keeping all cavities in the required coupling conditions. Therefore, we have great expectations for the optimization of microcavity parameters design and the improvement of the microfabrication process.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The project was supported by Fund of State Key Laboratory of Information Photonics and Optical Communications (Beijing University of Posts and Telecommunications) (No. IPOC2022ZT07), P. R. China. This work was also supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 61701035 and 61671085.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Gisin N, Thew R. Quantum communication. Nat Photon (2007) 1:165–71. doi:10.1038/nphoton.2007.22

CrossRef Full Text | Google Scholar

2. Ekert A, Jozsa R. Quantum computation and shor’s factoring algorithm. Rev Mod Phys (1996) 68:733–53. doi:10.1103/revmodphys.68.733

CrossRef Full Text | Google Scholar

3. Grover LK. Quantum mechanics helps in searching for a needle in a haystack. Phys Rev Lett (1997) 79:325–8. doi:10.1103/physrevlett.79.325

CrossRef Full Text | Google Scholar

4. Long GL. Grover algorithm with zero theoretical failure rate. Phys Rev A (Coll Park) (2001) 64:022307. doi:10.1103/physreva.64.022307

CrossRef Full Text | Google Scholar

5. Giovannetti V, Lloyd S, Maccone L. Quantum metrology. Phys Rev Lett (2006) 96:010401. doi:10.1103/physrevlett.96.010401

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Giovannetti V, Lloyd S, Maccone L. Advances in quantum metrology. Nat Photon (2011) 5:222–9. doi:10.1038/nphoton.2011.35

CrossRef Full Text | Google Scholar

7. Wehner S, Elkouss D, Hanson R. Quantum internet: A vision for the road ahead. Science (2018) 362:eaam9288. doi:10.1126/science.aam9288

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Awschalom D, Berggren KK, Bernien H, Bhave S, Carr LD, Davids P, et al. Development of quantum interconnects (quics) for next-generation information technologies. PRX Quan (2021) 2:017002. doi:10.1103/prxquantum.2.017002

CrossRef Full Text | Google Scholar

9. Long GL, Pan D, Sheng YB, Xue Q, Lu J, Hanzo L. An evolutionary pathway for the quantum internet relying on secure classical repeaters. (2022) arXiv preprint arXiv:2202.03619.

CrossRef Full Text | Google Scholar

10. Long GL, Liu XS. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys Rev A (Coll Park) (2002) 65:032302. doi:10.1103/physreva.65.032302

CrossRef Full Text | Google Scholar

11. Deng FG, Long GL, Liu XS. Two-step quantum direct communication protocol using the einstein-podolsky-rosen pair block. Phys Rev A (Coll Park) (2003) 68:042317. doi:10.1103/physreva.68.042317

CrossRef Full Text | Google Scholar

12. Deng FG, Long GL. Secure direct communication with a quantum one-time pad. Phys Rev A (Coll Park) (2004) 69:052319. doi:10.1103/physreva.69.052319

CrossRef Full Text | Google Scholar

13. Niu PH, Zhou ZR, Lin ZS, Sheng YB, Yin LG, Long GL. Measurement-device-independent quantum communication without encryption. Sci Bull (2018) 63:1345–50. doi:10.1016/j.scib.2018.09.009

CrossRef Full Text | Google Scholar

14. Zhou Z, Sheng Y, Niu P, Yin L, Long G, Hanzo L. Measurement-device-independent quantum secure direct communication. Sci China Phys Mech Astron (2020) 63:230362. doi:10.1007/s11433-019-1450-8

CrossRef Full Text | Google Scholar

15. Yang YF, Duan LZ, Qiu TR, Xie XM. Controlled quantum secure direct communication based on four-qubit cluster states and quantum search algorithm. Front Phys (2022) 10:875441. doi:10.3389/fphy.2022.875441

CrossRef Full Text | Google Scholar

16. Crépeau C, Gottesman D, Smith A. Secure multi-party quantum computation. In: Proceedings of the thiry-fourth annual ACM symposium on Theory of computing (2002). p. 643–52.

Google Scholar

17. Clementi M, Pappa A, Eckstein A, Walmsley IA, Kashefi E, Barz S. Classical multiparty computation using quantum resources. Phys Rev A (Coll Park) (2017) 96:062317. doi:10.1103/physreva.96.062317

CrossRef Full Text | Google Scholar

18. Yang HY, Ye TY. Secure multi-party quantum summation based on quantum Fourier transform. Quan Inf Process (2018) 17:129. doi:10.1007/s11128-018-1890-1

CrossRef Full Text | Google Scholar

19. Fan L, Cao C. A synchronous quantum blind signature scheme with entanglement swapping. Int J Quan Inform (2019) 17:1950007. doi:10.1142/s0219749919500072

CrossRef Full Text | Google Scholar

20. Yi X, Cao C, Fan L, Zhang R. Quantum secure multi-party summation protocol based on blind matrix and quantum Fourier transform. Quan Inf Process (2021) 20:249. doi:10.1007/s11128-021-03183-0

CrossRef Full Text | Google Scholar

21. Gao LZ, Zhang X, Lin S, Wang N, Guo GD. Authenticated multiparty quantum key agreement for optical-ring quantum communication networks. Front Phys (2022) 10:962781. doi:10.3389/fphy.2022.962781

CrossRef Full Text | Google Scholar

22. Cirac JI, Zoller P, Kimble HJ, Mabuchi H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys Rev Lett (1997) 78:3221–4. doi:10.1103/physrevlett.78.3221

CrossRef Full Text | Google Scholar

23. Ritter S, Nölleke C, Hahn C, Reiserer A, Neuzner A, Uphoff M, et al. An elementary quantum network of single atoms in optical cavities. Nature (2012) 484:195–200. doi:10.1038/nature11023

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Reiserer A, Rempe G. Cavity-based quantum networks with single atoms and optical photons. Rev Mod Phys (2015) 87:1379–418. doi:10.1103/revmodphys.87.1379

CrossRef Full Text | Google Scholar

25. Zhou XF, Zhang YS, Guo GC. Nonlocal gate of quantum network via cavity quantum electrodynamics. Phys Rev A (Coll Park) (2005) 71:064302. doi:10.1103/physreva.71.064302

CrossRef Full Text | Google Scholar

26. Wang HF, Zhu AD, Zhang S, Yeon KH. Optically controlled phase gate and teleportation of a controlled-not gate for spin qubits in a quantum-dot-microcavity coupled system. Phys Rev A (Coll Park) (2013) 87:062337. doi:10.1103/physreva.87.062337

CrossRef Full Text | Google Scholar

27. Wang TJ, Wang C. Parallel quantum computing teleportation for spin qubits in quantum dot and microcavity coupled system. IEEE J Sel Top Quan Electron (2014) 21:91–7. doi:10.1109/jstqe.2014.2321523

CrossRef Full Text | Google Scholar

28. Liu AP, Cheng LY, Guo Q, Su SL, Wang HF, Zhang S. Heralded teleportation of a controlled-not gate for nitrogen-vacancy centers coupled to a microtoroid resonator. Laser Phys (2019) 29:025205. doi:10.1088/1555-6611/aaf90c

CrossRef Full Text | Google Scholar

29. Wan Y, Kienzler D, Erickson SD, Mayer KH, Tan TR, Wu JJ, et al. Quantum gate teleportation between separated qubits in a trapped-ion processor. Science (2019) 364:875–8. doi:10.1126/science.aaw9415

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Briegel HJ, Dür W, Cirac JI, Zoller P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys Rev Lett (1998) 81:5932–5. doi:10.1103/physrevlett.81.5932

CrossRef Full Text | Google Scholar

31. Dür W, Briegel HJ, Cirac JI, Zoller P. Quantum repeaters based on entanglement purification. Phys Rev A (Coll Park) (1999) 59:169–81. doi:10.1103/physreva.59.169

CrossRef Full Text | Google Scholar

32. Sheng YB, Deng FG, Zhou HY. Efficient polarization-entanglement purification based on parametric down-conversion sources with cross-kerr nonlinearity. Phys Rev A (Coll Park) (2008) 77:042308. doi:10.1103/physreva.77.042308

CrossRef Full Text | Google Scholar

33. Cao C, Wang C, Ly H, Zhang R. Atomic entanglement purification and concentration using coherent state input-output process in low-q cavity qed regime. Opt Express (2013) 21:4093–105. doi:10.1364/oe.21.004093

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Cao C, Chen X, Duan Y, Fan L, Zhang R, Wang T, et al. Concentrating partially entangled w-class states on nonlocal atoms using low-q optical cavity and linear optical elements. Sci China Phys Mech Astron (2016) 59:100315. doi:10.1007/s11433-016-0253-x

CrossRef Full Text | Google Scholar

35. Hu XM, Huang CX, Sheng YB, Zhou L, Liu BH, Guo Y, et al. Long-distance entanglement purification for quantum communication. Phys Rev Lett (2021) 126:010503. doi:10.1103/physrevlett.126.010503

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Huang CX, Hu XM, Liu BH, Zhou L, Sheng YB, Li CF, et al. Experimental one-step deterministic polarization entanglement purification. Sci Bull (2022) 67:593–7. doi:10.1016/j.scib.2021.12.018

CrossRef Full Text | Google Scholar

37. Kwiat PG. Hyper-entangled states. J Mod Opt (1997) 44:2173–84. doi:10.1080/09500349708231877

CrossRef Full Text | Google Scholar

38. Deng FG, Ren BC, Li XH. Quantum hyperentanglement and its applications in quantum information processing. Sci Bull (2017) 62:46–68. doi:10.1016/j.scib.2016.11.007

CrossRef Full Text | Google Scholar

39. Xu W, Wang T, Cao C, Wang C. High dimensional quantum logic gates and quantum information processing. Chin Sci Bull (2019) 64:1691–701. doi:10.1360/n972019-00252

CrossRef Full Text | Google Scholar

40. Simon DS, Sergienko AV. High-capacity quantum key distribution via hyperentangled degrees of freedom. New J Phys (2014) 16:063052. doi:10.1088/1367-2630/16/6/063052

CrossRef Full Text | Google Scholar

41. Wang XL, Cai XD, Su ZE, Chen MC, Wu D, Li L, et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature (2015) 518:516–9. doi:10.1038/nature14246

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Cao C, Wang TJ, Mi SC, Zhang R, Wang C. Nonlocal hyperconcentration on entangled photons using photonic module system. Ann Phys (2016) 369:128–38. doi:10.1016/j.aop.2016.03.003

CrossRef Full Text | Google Scholar

43. Williams BP, Sadlier RJ, Humble TS. Superdense coding over optical fiber links with complete bell-state measurements. Phys Rev Lett (2017) 118:050501. doi:10.1103/physrevlett.118.050501

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Sheng YB, Zhou L, Long GL. One-step quantum secure direct communication. Sci Bull (2022) 67:367–74. doi:10.1016/j.scib.2021.11.002

CrossRef Full Text | Google Scholar

45. Zhou L, Sheng YB. One-step device-independent quantum secure direct communication. Sci China Phys Mech Astron (2022) 65:250311. doi:10.1007/s11433-021-1863-9

CrossRef Full Text | Google Scholar

46. Loss D, DiVincenzo DP. Quantum computation with quantum dots. Phys Rev A (Coll Park) (1998) 57:120–6. doi:10.1103/physreva.57.120

CrossRef Full Text | Google Scholar

47. Imamog A, Awschalom DD, Burkard G, DiVincenzo DP, Loss D, Sherwin M, et al. Quantum information processing using quantum dot spins and cavity qed. Phys Rev Lett (1999) 83:4204–7. doi:10.1103/physrevlett.83.4204

CrossRef Full Text | Google Scholar

48. Delteil A, Sun Z, Gao W, Togan E, Faelt S, Imamoğlu A. Generation of heralded entanglement between distant hole spins. Nat Phys (2016) 12:218–23. doi:10.1038/nphys3605

CrossRef Full Text | Google Scholar

49. Prechtel JH, Kuhlmann AV, Houel J, Ludwig A, Valentin SR, Wieck AD, et al. Decoupling a hole spin qubit from the nuclear spins. Nat Mater (2016) 15:981–6. doi:10.1038/nmat4704

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Wang K, Xu G, Gao F, Liu H, Ma RL, Zhang X, et al. Ultrafast coherent control of a hole spin qubit in a germanium quantum dot. Nat Commun (2022) 13:206. doi:10.1038/s41467-021-27880-7

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Atature M, Dreiser J, Badolato A, Hogele A, Karrai K, Imamoglu A. Quantum-dot spin-state preparation with near-unity fidelity. Science (2006) 312:551–3. doi:10.1126/science.1126074

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Berezovsky J, Mikkelsen M, Gywat O, Stoltz N, Coldren L, Awschalom D. Nondestructive optical measurements of a single electron spin in a quantum dot. Science (2006) 314:1916–20. doi:10.1126/science.1133862

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Press D, Ladd TD, Zhang B, Yamamoto Y. Complete quantum control of a single quantum dot spin using ultrafast optical pulses. Nature (2008) 456:218–21. doi:10.1038/nature07530

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Kim ED, Truex K, Xu X, Sun B, Steel D, Bracker A, et al. Fast spin rotations by optically controlled geometric phases in a charge-tunable inas quantum dot. Phys Rev Lett (2010) 104:167401. doi:10.1103/physrevlett.104.167401

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Press D, De Greve K, McMahon PL, Ladd TD, Friess B, Schneider C, et al. Ultrafast optical spin echo in a single quantum dot. Nat Photon (2010) 4:367–70. doi:10.1038/nphoton.2010.83

CrossRef Full Text | Google Scholar

56. West JR, Lidar DA, Fong BH, Gyure MF. High fidelity quantum gates via dynamical decoupling. Phys Rev Lett (2010) 105:230503. doi:10.1103/physrevlett.105.230503

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Hu C, Young A, O’brien J, Munro W, Rarity J. Giant optical faraday rotation induced by a single-electron spin in a quantum dot: applications to entangling remote spins via a single photon. Phys Rev B (2008) 78:085307. doi:10.1103/physrevb.78.085307

CrossRef Full Text | Google Scholar

58. Hu C, Munro W, O’Brien J, Rarity J. Proposed entanglement beam splitter using a quantum-dot spin in a double-sided optical microcavity. Phys Rev B (2009) 80:205326. doi:10.1103/physrevb.80.205326

CrossRef Full Text | Google Scholar

59. Cao C, Duan YW, Chen X, Zhang R, Wang TJ, Wang C. Implementation of single-photon quantum routing and decoupling using a nitrogen-vacancy center and a whispering-gallery-mode resonator-waveguide system. Opt Express (2017) 25:16931–46. doi:10.1364/oe.25.016931

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Wang K, Gao YP, Jiao R, Wang C. Recent progress on optomagnetic coupling and optical manipulation based on cavity-optomagnonics. Front Phys (Beijing) (2022) 17:42201. doi:10.1007/s11467-022-1165-2

CrossRef Full Text | Google Scholar

61. Bonato C, Haupt F, Oemrawsingh SS, Gudat J, Ding D, van Exter MP, et al. Cnot and bell-state analysis in the weak-coupling cavity qed regime. Phys Rev Lett (2010) 104:160503. doi:10.1103/physrevlett.104.160503

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Wei HR, Deng FG. Universal quantum gates for hybrid systems assisted by quantum dots inside double-sided optical microcavities. Phys Rev A (Coll Park) (2013) 87:022305. doi:10.1103/physreva.87.022305

CrossRef Full Text | Google Scholar

63. Luo MX, Wang X. Parallel photonic quantum computation assisted by quantum dots in one-side optical microcavities. Sci Rep (2014) 4:5732. doi:10.1038/srep05732

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Li T, Deng FG. Error-rejecting quantum computing with solid-state spins assisted by low-Qoptical microcavities. Phys Rev A (Coll Park) (2016) 94:062310. doi:10.1103/physreva.94.062310

CrossRef Full Text | Google Scholar

65. Xia BY, Cao C, Han YH, Zhang R. Universal photonic three-qubit quantum gates with two degrees of freedom assisted by charged quantum dots inside single-sided optical microcavities. Laser Phys (2018) 28:095201. doi:10.1088/1555-6611/aac904

CrossRef Full Text | Google Scholar

66. Cao C, Han YH, Zhang L, Fan L, Duan YW, Zhang R. High-fidelity universal quantum controlled gates on electron-spin qubits in quantum dots inside single-sided optical microcavities. Adv Quan Technol (2019) 2:1900081. doi:10.1002/qute.201900081

CrossRef Full Text | Google Scholar

67. Han YH, Cao C, Fan L, Zhang R. Heralded high-fidelity quantum hyper-cnot gates assisted by charged quantum dots inside single-sided optical microcavities. Opt Express (2021) 29:20045–62. doi:10.1364/oe.426325

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Wang TJ, Lu Y, Long GL. Generation and complete analysis of the hyperentangled bell state for photons assisted by quantum-dot spins in optical microcavities. Phys Rev A (Coll Park) (2012) 86:042337. doi:10.1103/physreva.86.042337

CrossRef Full Text | Google Scholar

69. Ren BC, Wei HR, Hua M, Li T, Deng FG. Complete hyperentangled-bell-state analysis for photon systems assisted by quantum-dot spins in optical microcavities. Opt Express (2012) 20:24664–77. doi:10.1364/oe.20.024664

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Wang GY, Ai Q, Ren BC, Li T, Deng FG. Error-detected generation and complete analysis of hyperentangled bell states for photons assisted by quantum-dot spins in double-sided optical microcavities. Opt Express (2016) 24:28444–58. doi:10.1364/oe.24.028444

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Zheng Y, Liang L, Zhang M. Error-heralded generation and self-assisted complete analysis of two-photon hyperentangled bell states through single-sided quantum-dot-cavity systems. Sci China Phys Mech Astron (2019) 62:970312. doi:10.1007/s11433-018-9338-8

CrossRef Full Text | Google Scholar

72. Cao C, Zhang L, Han YH, Yin PP, Fan L, Duan YW, et al. Complete and faithful hyperentangled-bell-state analysis of photon systems using a failure-heralded and fidelity-robust quantum gate. Opt Express (2020) 28:2857–72. doi:10.1364/oe.384360

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Fan L, Cao C. Deterministic cnot gate and complete bell-state analyzer on quantum-dot-confined electron spins based on faithful quantum nondemolition parity detection. J Opt Soc Am B (2021) 38:1593–603. doi:10.1364/josab.415321

CrossRef Full Text | Google Scholar

74. Wang C, Zhang Y, Jin G. Entanglement purification and concentration of electron-spin entangled states using quantum-dot spins in optical microcavities. Phys Rev A (Coll Park) (2011) 84:032307. doi:10.1103/physreva.84.032307

CrossRef Full Text | Google Scholar

75. Wang C. Efficient entanglement concentration for partially entangled electrons using a quantum-dot and microcavity coupled system. Phys Rev A (Coll Park) (2012) 86:012323. doi:10.1103/physreva.86.012323

CrossRef Full Text | Google Scholar

76. Cao C, Fan L, Chen X, Duan YW, Wang TJ, Zhang R, et al. Efficient entanglement concentration of arbitrary unknown less-entangled three-atom w states via photonic faraday rotation in cavity qed. Quan Inf Process (2017) 16:98. doi:10.1007/s11128-017-1549-3

CrossRef Full Text | Google Scholar

77. Liu YT, Wu YM, Du FF. Self-error-rejecting multipartite entanglement purification for electron systems assisted by quantum-dot spins in optical microcavities. Chin Phys B (2022) 31:050303. doi:10.1088/1674-1056/ac4489

CrossRef Full Text | Google Scholar

78. Lodahl P. Quantum-dot based photonic quantum networks. Quan Sci Technol (2017) 3:013001. doi:10.1088/2058-9565/aa91bb

CrossRef Full Text | Google Scholar

79. Borregaard J, Sørensen AS, Lodahl P. Quantum networks with deterministic spin–photon interfaces. Adv Quan Technol (2019) 2:1800091. doi:10.1002/qute.201800091

CrossRef Full Text | Google Scholar

80. Bennett A, Lee J, Ellis D, Farrer I, Ritchie D, Shields A. A semiconductor photon-sorter. Nat Nanotechnol (2016) 11:857–60. doi:10.1038/nnano.2016.113

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Sun S, Kim H, Solomon GS, Waks E. A quantum phase switch between a single solid-state spin and a photon. Nat Nanotechnol (2016) 11:539–44. doi:10.1038/nnano.2015.334

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Arnold C, Demory J, Loo V, Lemaître A, Sagnes I, Glazov M, et al. Macroscopic rotation of photon polarization induced by a single spin. Nat Commun (2015) 6:6236. doi:10.1038/ncomms7236

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Androvitsaneas P, Young AB, Schneider C, Maier S, Kamp M, Höfling S, et al. Charged quantum dot micropillar system for deterministic light-matter interactions. Phys Rev B (2016) 93:241409. doi:10.1103/physrevb.93.241409

CrossRef Full Text | Google Scholar

84. Barreiro JT, Langford NK, Peters NA, Kwiat PG. Generation of hyperentangled photon pairs. Phys Rev Lett (2005) 95:260501. doi:10.1103/physrevlett.95.260501

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Suo J, Dong S, Zhang W, Huang Y, Peng J. Generation of hyper-entanglement on polarization and energy-time based on a silicon micro-ring cavity. Opt Express (2015) 23:3985–95. doi:10.1364/oe.23.003985

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Zhao TM, Ihn YS, Kim YH. Direct generation of narrow-band hyperentangled photons. Phys Rev Lett (2019) 122:123607. doi:10.1103/physrevlett.122.123607

PubMed Abstract | CrossRef Full Text | Google Scholar