Precision frequency transfer with fiber frequency combs

We review methods for precision transfer of frequencies across broad optical wavelength ranges. Single-branch supercontinuum generation allows for a frequency transfer stability of < 1 × 10⁻¹⁷ in 1 s across an octave. With supercontinuum stitching, highly coherent supercontinuum spectra spanning across more than two octaves are generated. With noise cancellation techniques a relative frequency transfer stability of ≈ 2 × 10⁻¹⁸ in 1 s can be achieved. Highly stable frequency transfer along with a maximization of power per mode at multiple freely selectable frequency bands is further enabled via pulse shaping techniques. We also include a brief review of general fiber combs and research aimed at frequency extension of frequency combs covering the whole spectral range from the XUV to the mid IR, power scaling of frequency combs as well as low noise microwave and mmwave technology enabled with frequency combs.

Introduction

Within the realm of optical fiber technology, broadband frequency combs can be constructed from modelocked fiber lasers [1], a cw laser in conjunction with an electro-optic modulator generating sidebands, commonly referred to as EO combs [2], or can be generated via four-wave mixing (FWM) of two frequency tones in several stages comprising highly nonlinear fiber [3]. Here we will review only the first method, excellent reviews of EO combs can be found in Ref. [4] and details of FWM combs are discussed in Ref. [5].

The output of a mode-locked laser consists of an ultrafast pulse train with pulses equally spaced by the round trip time in the oscillator. The corresponding optical frequency spectrum is a frequency comb of equally spaced spectral narrow lines that can be described by [6].

$f_n=n{f}_{rep}+f_{ceo}(1)$

where $n$ is a large integer (often called the mode number), $f_{rep}=1/T$ is the pulse repetition rate, where $T$ is the pulse spacing (or cavity round trip time), and $f_{ceo}$ is the offset frequency between the whole comb spectrum and the frequency f = 0. The carrier envelope offset frequency is governed by the difference in group ${\mathrm{v}}_{\mathrm{g}}$ and phase velocity ${\mathrm{v}}_{\mathrm{p}}$ in a mode-locked oscillator, which results in a phase advance (or phase slip) of $\delta {\varphi }_c=\left(1/{\mathrm{v}}_{\mathrm{p}}–1/{\mathrm{v}}_{\mathrm{g}}\right){\omega }_0\mathrm{L}$ of the carrier frequency ${\omega }_0$ per round trip, where L is the cavity length. The carrier envelope offset frequency is given by [7]

$f_{ceo}=\left(\delta {\varphi }_c\mathrm{mod}2\pi \right)f_{rep}/2\pi (2)$

Since mode-locked lasers have a comb spectrum in the frequency domain, they are sometimes also referred to as frequency combs. It is more common to describe mode-locked lasers as frequency combs when they are frequency stabilized, or when the comb structure is critical for a particular application.

Due to a variety of noise sources inside the cavity, $f_{rep}$ and $f_{ceo}$ drift and the pulse envelope as well as the pulse phase are subject to statistical fluctuations, which broaden the individual comb lines. However, once $f_{rep}$ and $f_{ceo}$ from Eq. 1 are controlled in a mode-locked oscillator, the temporal evolution of the electromagnetic field corresponding to an optical pulse oscillating in the fiber laser cavity is completely characterized. Moreover, the frequency spectrum can now contain in excess of 10⁶ perfectly characterized individual comb lines. Additional noise arises from fiber amplifiers, nonlinear fibers and even simple fiber leads and free-space sections downstream of the oscillator. How to handle these additional noise sources is the subject of frequency transfer technology. Methods for control of ${\mathrm{f}}_{\mathrm{r}\mathrm{e}\mathrm{p}}$ and ${\mathrm{f}}_{\mathrm{c}\mathrm{e}\mathrm{o}}$ and a review of early work on modelocked fiber lasers and frequency combs can be found in ref. 8.

Er fiber frequency combs

Because of their relative simplicity of construction, compatibility with standard highly reliable optical components from the optical telecommunications field and ultra-high stability, Er fiber frequency combs have been used in many applications, comprising for example optical clock construction, LIDAR and precision frequency spectroscopy. A typical set-up of an ultra-stable fiber frequency comb based on a nonlinear amplifying loop mirror (NALM) [9] is shown in Figure 1, as adapted from ref. 10.

FIGURE 1

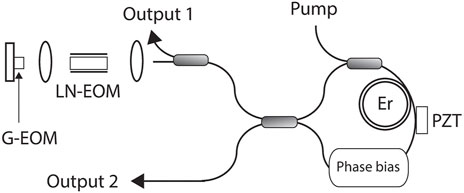
FIGURE 1. Schematic of an all-PM NALM Er-doped modelocked fiber laser with fast graphene electro-optic modulator (G-EOM) and lithium niobate electro-optic modulator (LN-EOM) for f_ceo and f_rep control, respectively, adapted from ref. 10.

Advanced high-performance Er-doped fiber frequency combs use modulators with large modulation bandwidths for control of fceo and frep. Those are for example lithium niobate-based electro-optic modulators (LN-EOM) for $f_{rep}$ [11] and graphene-based EOMs (G-EOM) for $f_{ceo}$ [12]. The modulation bandwidth can be as large as 1 MHz. The frequency comb shown in Figure 1 incorporates such high bandwidth modulators. The oscillator is based on an all PM fiber laser incorporating a NALM [9] as developed for the generation of sub 100 fs pulses from passively modelocked fiber lasers operating near zero dispersion [13]. The NALM incorporates a phase bias element in the loop as discussed in refs. 9 and 13. Here the LN-EOM is used in transmission and the G-EOM is used in reflection. The refractive index of LN is changed by an applied voltage, producing a modulation of the cavity length. Since the modulation range of an LN-EOM is very small, a PZT is also installed to induce larger cavity-length changes. The G-EOM also uses the electro-optic effect. Any applied field changes the Fermi level of graphene, thus modulating its absorption, which produces a cavity-loss change. Because the G-EOM modulates the cavity loss instead of the gain, f_ceo modulation induced by the G-EOM is not limited by the relaxation time of Er, but rather by the photon lifetime in the cavity, which can be much faster [12]. For the construction of a frequency comb, generally an optical amplifier is included down-stream of the oscillator, which in conjunction with nonlinear amplification allows for the generation of ≈30 fs pulses with a pulse energy between 2 – 4 nJ. The short pulses are subsequently injected into a highly nonlinear fiber for octave spanning supercontinuum generation and the detection of fceo via an f-2f interferometer [8, 10]

Because of the large-bandwidth modulators and the intrinsically low phase noise provided by an all-polarization maintaining (PM) NALM design, ultra-low phase noise is obtained, with a phase noise (Φ) of $f_{ceo}$ or $f_{beat}$ below 50 mrad integrated over offset frequencies from 100 Hz to 2 MHz with η = 99.9% fractional RMS power in the coherent carrier, where η = exp (−Φ²). The typical RF spectra of a phase locked fceo signal and a beat signal (fbeat) between a comb line and an external cw laser of a NALM based fiber comb system in shown in Figure 2.

FIGURE 2

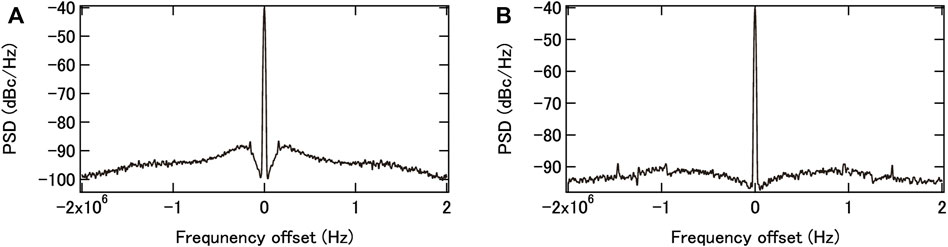
FIGURE 2. RF spectra of phase-locked (A) f_ceo and (B) f_beat in an ultra-low-noise all-PM Er-doped fiber comb using a NALM (from ref. 9). PSD = phase noise spectral density.

For phase locking of $f_{rep}$ in the RF domain, the pulse train can be directly photo-detected. The ultimate frequency comb stability is then determined by the RF reference used. Although phase locking of $f_{rep}$ in the RF domain is sufficient for many applications, phase locking of $f_{rep}$ can be used in the optical domain to utilize the world’s best frequency references, which operate in the optical domain. The frequency stability of available precision RF and optical references is ≈ 10⁻¹⁴ and ≈10⁻¹⁷ at 10 s, respectively [14].

Yb fiber frequency combs

As an alternative to fiber frequency combs, Yb fiber frequency combs have also been used in many applications, since they are directly compatible with high power Yb fiber amplifiers [15, 16] and can generate a supercontinuum spectrum from 600—1,600 nm [17], spanning across most clock wavelengths used in precision metrology as well as the important 1,550 nm spectral range that is typically used for the construction of reference cavities. Yb fiber frequency combs have allowed the demonstration of sub mHz relative linewidths relative to a Ti:sapphire laser based frequency comb [18], revealing essentially perfect relative comb coherence. One disadvantage of Yb fiber vs. Er fiber frequency combs is typically the need for bulk dispersion compensating elements for system construction. Therefore it is sometimes preferable to implement frequency shifting of Er fiber combs to the Yb spectral range [19] rather than to use Yb fiber frequency combs in Yb comb applications.

Yb fiber frequency comb oscillators can in general operate with similar phase noise compared to Er fiber combs and allow for the generation of very stable and very narrow linewidth (<10 kHz) free running fceo signals, as already demonstrated in ref. 18 and more recently confirmed in Li et al [20] and a very detailed investigation by Meyer et al [21]. Both Li et al and Meyer et al [20, 21] implemented NALMs in the comb oscillator construction. The achievable phase noise for the fbeat signal in an Yb fiber comb is around 120 mrad, which after filtering with an enhancement cavity can be reduced to around 20 mrad [22].

Because of the high power capabilities of Yb fiber amplifiers, Yb fiber frequency combs have been used as pump sources for high power optical parametric oscillators operating in the mid IR spectral range [23] as well as high power XUV sources based on high harmonic generation in enhancement cavities [15, 24]. More recently cavity-enhanced Yb fiber frequency combs are also being considered as excitation or reference sources for nuclear spectroscopy [22], which can potentially expand optical clock technology to nuclear transitions, opening many opportunities for further great advances in precision metrology.

Tm fiber frequency combs

Tm fiber frequency combs [12, 25, 26] are of interest since they produce direct access to the mid IR spectral range. Tm fibers can be relatively highly doped compared to Er and Yb fibers and allow for operation at repetition rates > 500 MHz [27], about a factor of two higher than typical with Er and Yb fiber combs. Moreover, just as Er fiber combs, Tm fiber combs can be perfectly integrated. Tm fiber amplifiers can also be operated at average powers > 100 W and have been used for the demonstration of 100 W level Tm fiber combs; in conjunction with nonlinear spectral broadening techniques Watt-level powers in the whole mid IR spectral range can be demonstrated [28]. High power mid IR frequency generation is one of the most important applications for Tm frequency combs [29] and is highly relevant for precision spectroscopy [30].

Ultra-high stability frequency transfer

One of the most popular applications for fully stabilized frequency combs can be found in the construction of optical clocks. Optical clocks are prime candidates for the future redefinition of the world-wide time standard, aimed at providing a higher accuracy than supplied by the current definition of the standard second with cesium clocks. While cesium clocks use a microwave frequency (∼9.2 GHz) as the clock transition, optical clocks use a frequency in the optical domain, e.g., 429 THz for the popular strontium lattice clock. Prior to the availability of optical frequency combs, counting (i.e., measuring) optical-clock wavelengths was extremely difficult and required highly complex frequency chains [31]. Such frequency chains are now obsolete since optical frequency combs are used as a frequency gear, in which optical frequency combs directly convert frequencies from the optical to the microwave domains [31]. In a typical optical-clock system, an $f_{ceo}$-stabilized comb is for example phase locked to a cw laser referenced to an optical cavity, which is in turn used for interrogation of an optical-clock transition via generation of a beat signal f_beat between the cw laser and one of the comb lines. The transition frequency of the optical clock is then fully determined by $f_{ceo}$, $f_{rep}$, and $f_{beat}$, which can all be measured in the microwave domain with the use of frequency counters. The optical-clock frequency can then be calculated once the mode number is known, which can for example be determined with the use of a wavemeter.

For the future definition of the standard second, because of redundancy requirements, several optical clocks need to be functional simultaneously, hence an accurate comparison of the clock frequencies between different optical clocks, as shown in Figure 3, is required. For this application, a first comb mode is locked to a first CW laser, which interrogates the first optical clock. Similarly, a second clock is interrogated with a second CW laser. The second clock is then compared to the first clock by using the second CW laser to generate a beat signal with a second comb mode. Counting of the beat signal between the second comb mode and the second CW laser then produces a measurement of the relative frequency stability between the two clocks. The concept is extendable to the comparison of multiple clocks.

FIGURE 3

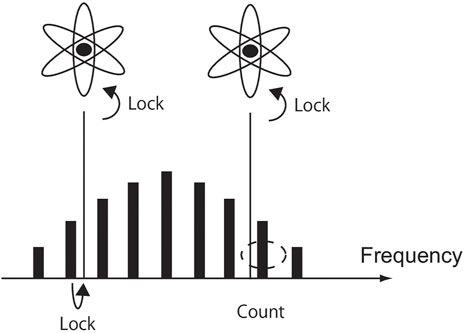
FIGURE 3. Concept for optical clock comparison via frequency combs. The frequency comb is locked to a first optical clock, and compared with another optical clock via the use of frequency counters to measure the stability of the beat frequencies.

Most clock wavelengths are in the visible, e.g., at 698 nm for Sr lattice clocks and at 578 nm for Yb lattice clocks. Hence to utilize supercontinuum generation from Er-doped fiber frequency combs, the frequency of cw lasers operating in the infrared is typically frequency doubled, such that the fundamental infrared wavelength from the cw laser can be interfered with the supercontinuum generated with an Er-doped fiber frequency comb and the frequency doubled light can be interrogated by optical clocks.

Multi-branch versus single branch comb systems

Early fiber comb systems as used for optical clock comparison were based on multi-branch designs, where the Er-doped fiber frequency comb oscillator is branched out to feed several independent fiber amplifiers and supercontinuum stages. Each of the independent amplifier branches is then used for interrogation of only one clock wavelength via generation of ${\mathrm{f}}_{\mathrm{b}\mathrm{e}\mathrm{a}\mathrm{t}}$ between the clock and a selected comb line. Each of the amplifier branches is further carefully constructed to maximize the signal/noise ratio (SN) of ${\mathrm{f}}_{\mathrm{b}\mathrm{e}\mathrm{a}\mathrm{t}}$ for the various clock wavelengths. Such multi-branch Er-doped fiber frequency combs exhibit a relative frequency instability of 10⁻¹⁶ at 1 s, which was sufficient in the early days of optical clock research.

However, recent progress in optical reference cavities and optical clocks requires more sophisticated Er-doped fiber frequency combs, such as for example single branch designs, where only one Er amplifier and supercontinuum generation stage is used to eliminate inter-branch noise. An example of a single branch ultra-stable Er-doped fiber frequency comb system is shown in Figure 4. In this system, all fibers and fiber components are polarization maintaining, so the system is very robust [32]. Moreover, the generated supercontinuum (Figure 4B) is used not only for optical beat detection between the CW lasers and the frequency comb, but also for $f_{ceo}$ detection. Compared with a multi-branch system, where the Er-doped fiber frequency comb is branched out to feed several independent fiber amplifiers and supercontinuum stages, the single-branch system exhibits about 10 times better stability, as shown in Figure 4C, where a relative frequency stability better than 10⁻¹⁷ in 1 s was reached. Here the frequency stability is shown in terms of modified Allan deviation as a function of averaging time τ, which corresponds to the square root of the variance of M successive frequency measurements in that time interval τ.

FIGURE 4

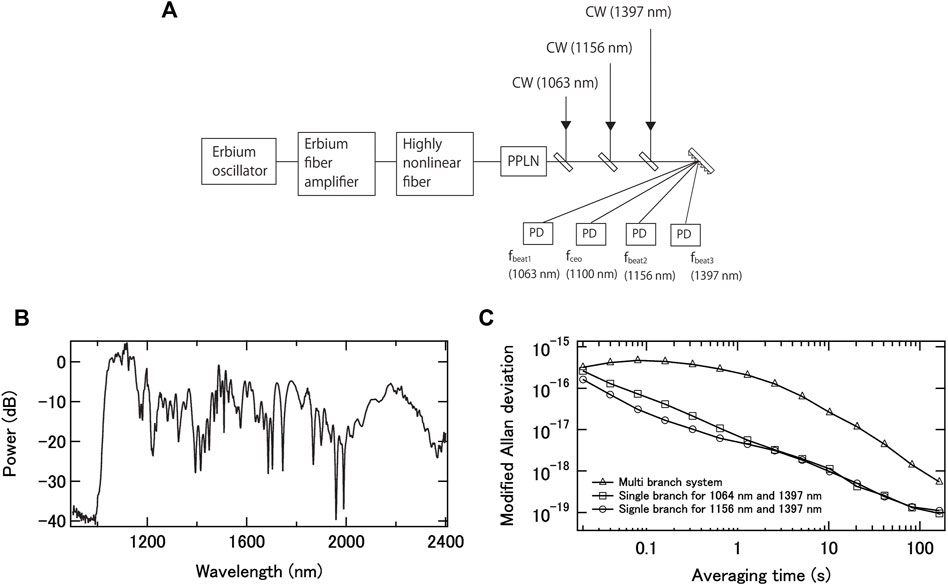
FIGURE 4. (A) Experimental set up for a single-branch frequency-comb system as used for optical-clock comparison adapted from ref. 32; PPLN = periodically poled lithium niobate; PD = photodiode. (B) Optical spectrum of supercontinuum generation from an Er-doped fiber optical frequency comb. (C) Frequency transfer stability of single-branch and multi-branch Er-doped fiber frequency combs.

In subsequent work, the relative frequency instability across two frequencies was reduced further to around <3 × 10⁻¹⁸ in 1 s [33], limited by the relative frequency noise imparted by free space optical sections within the comb system.

Ultrabroadband supercontinua via supercontinuum stitching

Instead of frequency doubling the CW laser to interrogate optical clock transitions, the short pulses generated from the Er-doped fiber frequency comb and amplified in an Er-doped fiber amplifier can also be frequency doubled and a highly coherent visible supercontinuum centered near 780 nm can be generated via coupling of the ultra-short frequency-doubled pulses into a photonic crystal fiber. Via coherent stitching of an IR supercontinuum generated with another Er-doped fiber amplifier, a highly coherent supercontinuum spanning the whole range from around 500 nm to 2,400 nm can be generated, where a frequency stability better than 10⁻¹⁸ in 1 s is potentially achievable [34]. The coherently stitched spectrum and the measured frequency stability between 1,560 and 780 nm are shown in Figures 5A,B respectively.

FIGURE 5

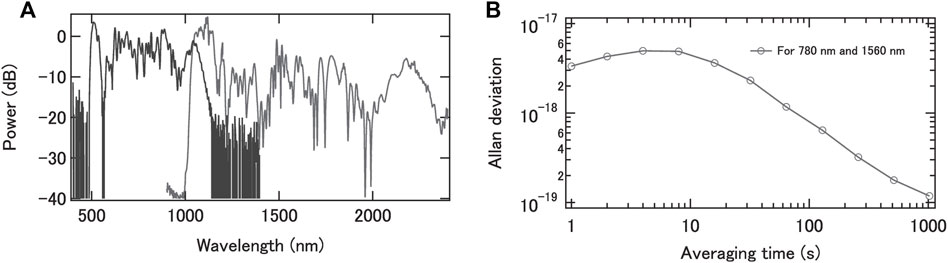
FIGURE 5. (A) Ultra-broadband coherently stitched supercontinuum generated with an Er-doped fiber comb and a frequency-doubled Er-doped fiber comb. (B) Frequency instability of the two-octave frequency comb measured for 780 nm and 1,560 nm. (from ref. 34).

Noise cancellation with reference lasers

Typical optical clocks require the simultaneous presence of well-defined optical frequencies for their operation, a constraint that is proportionally more difficult to satisfy when clock comparison among a multitude of optical clocks is concerned. To overcome these issues Kashiwagi et al [35] have suggested the use of multi-branch frequency combs with inter-branch noise cancellation which goes beyond the limitations of single-branch combs. Kashiwagi et al [35] demonstrated a reduction of noise between the non-common amplifier branches using the beats of the generated supercontinua with a common external cw laser reference for branch length stabilization, based on actual physical fiber length stabilization of the various amplifier branches. Giunta et al [36] improved on these results by implementing a software solution to the noise cancellation problem, relying on the Doppler property of the phase noise $\phi \left({\omega }_{\mathrm{m}}\right)$ imparted by a fiber of length L, namely its direct scaling with optical frequency. Just as in Kashiwagi et al [35], for proper frequency comparison across a multi-branch system a common external reference laser is required, which provides a measurement of the inter-branch noise $\phi \left({\omega }_{\mathrm{m}}\right)$ at frequency ${\omega }_{\mathrm{m}}$. More recently, a hardware-based technique for real-time noise cancellation without any post processing [37] was demonstrated. For a selected amplifier branch, the corrected phase noise $\phi \left({\omega }_{\mathrm{x}}\right)$ at a frequency ω_x can be obtained from $\phi \left({\omega }_{\mathrm{x}}\right)=\left({\omega }_{\mathrm{x}}/{\omega }_{\mathrm{m}}\right)\times \phi \left({\omega }_{\mathrm{m}}\right)$, where ${\omega }_{\mathrm{x}}/{\omega }_{\mathrm{m}}$ is the frequency ratio between the test laser at frequency ω_x and the noise transfer laser at ${\omega }_{\mathrm{m}}$. To enable noise cancellation in hardware, a first amplifier branch can be used for phase locking to a primary frequency reference at ω_r as well as for fceo locking. The first amplifier branch then is also used to lock the noise transfer laser at ω_m to the frequency comb. The second branch then needs to contain spectral output near both a frequency ω_m and a secondary frequency reference at ω_x, for which noise cancellation is to be implemented. This allows for the generation of two beat signals ⁿf_bm and ⁿf_bx, which both contain the inter-branch noise; to elucidate that these two signals contain interbranch noise we added the superscript ⁿ as a pre-fix, resulting in ⁿf_bm and ⁿf_bx. To cancel the inter-branch noise, these two beat signals can be mixed with a dual balanced mixer with appropriate scaling of ⁿf_bm, providing a noise cancelled beat signal ^cf_bx, where ^c stands for noise cancelled,

${{}^{\mathrm{c}}\mathrm{f}}_{\mathrm{b}\mathrm{x}}{=}^{\mathrm{n}}{\mathrm{f}}_{\mathrm{b}\mathrm{x}}–{\left({\omega }_{\mathrm{x}}/{\omega }_{\mathrm{m}}\right)}^{\mathrm{n}}{\mathrm{f}}_{\mathrm{b}\mathrm{m}}.(3)$

More than two amplifier branches can be added and the same principle can be applied. Hence for each amplifier one needs to optimize only the SN ratios of two beat signals related to the noise transfer laser ⁿf_bm on the one hand and another frequency reference at (f_x1, f_x2,…f_xn) on the other hand. In clock comparison applications the implementation of the frequency mixer produces a frequency offset, which can however be easily accounted for when calculating the difference frequencies of actual clock signals.

The amount of noise cancellation obtainable with a dual branch frequency comb system is shown in Figure 6. The Allan deviation and modified Allan deviation of the beat signal from the second branch supercontinuum output with a cw 1,064 nm reference laser before and after noise cancellation is shown, where the 1,064 nm was used both as the primary and secondary reference. Noise cancellation can reduce the interbranch noise by a factor of around 30–100, depending on averaging times. At 1 s an Allan deviation before noise cancellation of 5*10⁻¹⁷ is obtained and after noise cancellation $\approx 2\times {10}^{-18}$. At 10,000 s the Allan deviation reduces to 2.7 × 10⁻¹⁹ before and 4.4 × 10⁻²¹ after noise cancellation.

FIGURE 6

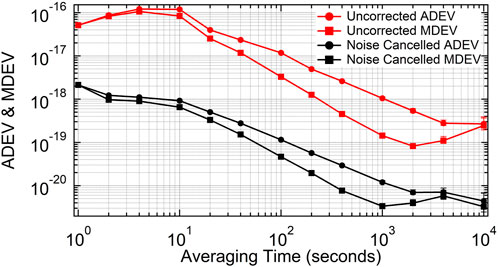
FIGURE 6. Red dot and square: Allan deviation and modified Allan deviation of uncorrected f_beat signal at 1,064 nm. Black dot and square: Allan deviation and modified Allan deviation of noise cancelled f_beat signal at 1,064 nm.

Supercontinuum manipulation via pulse shaping

When generating supercontinuum from a given pulse in nonlinear fiber, the main controls available are the laser power and fiber lengths. Optimizing one or two wavelengths is straight-forward, but the optimization of multiple wavelengths simultaneously is not always possible. To overcome this limitation a pulse shaper can be used that modulates the pulse injected into the supercontinuum generating highly nonlinear fiber. With appropriate control one can indeed focus the supercontinuum power into desired wavelength channels while still preserving an octave spanning spectral width [38]. Moreover, a fully integrated pulse shaper based on spectral phase shaping in a chirped fiber Bragg grating can be implemented, allowing for a compact experimental set up.

The experimental set-up for such an integrated spectral phase shaper is shown in Figure 7, adapted from ref. 38. To enable spectral phase shaping, a pair of chirped fiber Bragg gratings reflectively stretch and compress the seed pulse, illustrated in the top branch of Figure 7. The gratings have the same specified group delay dispersion but are inserted in opposite directions, nominally resulting in no additional dispersion. The seed pulse is spectrally phase shaped by mounting the compressor grating on an array of computer controlled heaters. Typically one heater element can increase the group delay by up to about 1 ps through the temperature dependence of the refractive index by changing the wavelength that reflects at that position.

FIGURE 7

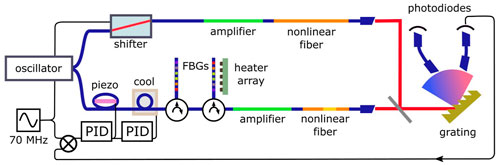
FIGURE 7. Illustration of shaped supercontinuum fiber laser (lower branch); unshaped reference supercontinuum with frequency shift (upper branch); and interference and narrow band spectral filtering in free space for relative stability tests.

The Allan deviations of the beat signals obtained after supercontinuum shaping at various popular clock frequencies as well as at the frequencies used for f_ceo locking (i.e., at 2,100 and 1,050 nm) are shown in Figure 8. The Allan deviation at 1 s is below 6 × 10^–17 for all three clock wavelengths (1,147, 1,314, and 1,397 nm), comparable to the best optical clocks [14]. Here the relative frequency transfer stability was limited by the environmental control in the fiber Bragg grating stretcher and compressor, which are temperature sensitive. With better environmental control another improvement in transfer stability by an order of magnitude or more can be envisaged.

FIGURE 8

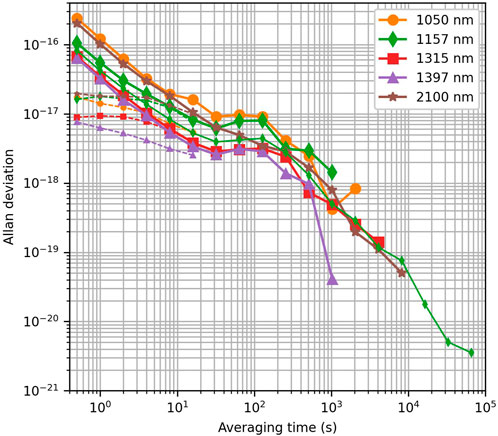
FIGURE 8. Allan deviations of the optical frequency of the shaped supercontinuum at various clock wavelengths relative to an unshaped supercontinuum. Dashed lines use averaged phase values over 0.5 s to remove white noise. Deviations at 1 s are at the 10⁻¹⁷ level, which is already comparable to the best optical clocks.

Power and frequency extension

Er fiber combs in conjunction with supercontinuum generation dominate in realm of optical clock research. For many other applications in nonlinear optics and spectroscopy higher power levels than obtainable with standard Er fiber combs and wavelengths covering the whole spectral range from the XUV to the mid IR are required. A review of research on power scaling and frequency shifting can be found in Ref. [39]. As already mentioned, power scaling of fiber frequency combs can be enabled by the use of Yb fibers as power amplifiers [15, 16], where an optical seed near 1,050 nm can be readily provided via Yb fiber combs [15] or appropriate frequency shifting of Er fiber lasers [19], allowing for example full access to the stabilization techniques developed for Er fiber combs. With Yb fiber frequency combs amplified to the 100 W level, frequency combs in the XUV spectral range can be demonstrated via for example high harmonic generation in an enhancement cavity [22, 24].

Similar frequency shifting techniques can also be implemented to use Er fiber frequency combs to seed high power Tm fiber amplifiers providing for several Watts of power near 1900 nm [26, 28]. In conjunction with supercontinuum generation, single-cycle pulse generation (centered around 1900 nm) with a spectral bandwidth from 700–3,000 nm can be obtained [40]. Single cycle pulses can also be generated with high power Yb fiber lasers in conjunction with pulse compression in gas-filled hollow core fibers [41]. Recently, amplification of Er fiber frequency combs to power levels > 10 W and pulse energies > 100 nJ via the implementation of large mode fiber amplifiers and spectral phase shaping techniques [42] has also been demonstrated. The fbeat and fceo phase noise of these high power Er fiber combs can be below 400 mrad as required for coherent frequency transfer, thus such systems will open new avenues for high field research.

High power fiber frequency combs can themselves produce power levels in the mid IR spectral range of several Watts via frequency shifting for example via nonlinear optical parametric oscillators [29, 30], difference frequency generation (DFG) [28, 43] or optical parametric amplification (OPA) [44], where in principle all generated frequencies can be referenced to optical clocks via high power Er fiber amplifiers. The set-up for a high power DFG system comprising both a high power Er fiber frequency comb pump, which is further frequency shifted and amplified in a Tm fiber amplifer to provide a high power signal, is shown in Figure 9 below, adapted from ref. 43. Here a power level in the 6–11 µm range > 50 mW was obtained at a repetition rate of 100 MHz, where the Er pump provided around 2 W of pump power. With the recently available 10 W Er fiber frequency combs, much higher power levels in the mid IR spectral range can be expected. In a recent experiment a power level of 6.7 W was demonstrated at a wavelength of 3 µm via DFG/OPA between a high power Yb fiber and an Er fiber comb [44].

FIGURE 9

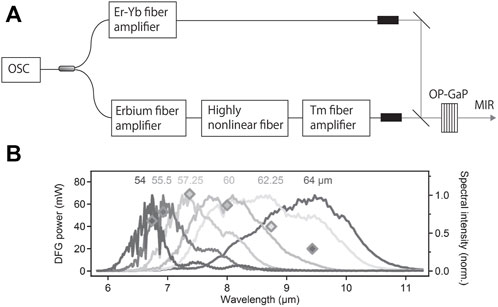
FIGURE 9. Schematic of setup for DFG based on a dual-branch comb configuration. (B) Optical mid IR spectra generated via DFG. OSC = oscillator, OPGaP = orientation-patterned gallium phosphide, MIR = mid-infrared output.

Ultra-low phase noise microwave and mmwave generation

The stability benefits of frequency comb technology cannot only be utilized in the optical domain, but can also be transferred to the microwave and mmwave domain, enabling ultra-low phase noise and ultra-high stability microwave and mmwave generation, as for example highly relevant for signal processing and precision radar. Photo-detection of the mode-locked pulse train can be implemented for direct optical to microwave conversion. Pulse interleaving is typically implemented to increase the repetition rate of modelocked fiber lasers to the few GHz range [45], which in turn increases the average power of the generated microwaves and reduces the shot noise level in the microwave domain. In a state-of-the-art demonstration [46], the repetition rate of the pulse train from a modelocked Er fiber laser was multiplied by a factor of 16 with four interleavers, i.e., from 250 MHz to 4 GHz. At the photo-detector, a microwave signal with an ultra-low phase noise at a frequency of 12 GHz was generated, which was derived from the third harmonic of the multiplied pulse train. At carrier offset frequencies in the range from 10 to 100 kHz, a single-sideband phase noise of −170 dBc/Hz was obtained, which is highly competitive with classical low-noise microwave oscillators.

Although free-running mode-locked lasers can produce low microwave phase noise at offset frequencies greater than 10 kHz, to fully utilize precision optical frequency references the frequency comb needs to be locked in the optical domain, i.e., to a cw laser locked to an optical cavity. Optical-domain locking enables conversion of the phase noise from the optical domain to the microwave domain through so-called optical frequency division; assuming the optical reference is at a frequency υ_n and the generated microwave frequency is at a frequency of Ω = nf_rep, the reduction in phase noise from the optical to the microwave domain is governed by the ratio R = (υ_n/Ω)² in power. For a typical optical frequency of 200 THz and Ω = 10 GHz, R = 86 dB. Hence very low phase noise can be obtained close to the carrier with reference cavities with a Hz-level linewidth. Such reference cavities are still relatively complicated and bulky, though research is underway to make reference cw lasers more compact [47].

The measurement of stability transfer from the optical to microwave domain does not necessarily require ultra-high stability reference cavities. For example a transfer stability < 2 × 10⁻¹⁶ in 1 s from the optical to the microwave domain (at 192 THz and 10 GHz respectively) can be demonstrated with correlation—based phase noise measurements [48], where two combs are both locked to a common optical reference (such as a RIO laser) and the generated 10 GHz signals are simultaneously down-converted to 10 MHz via a common 10 GHz synthesizer, before phase comparison in a phase meter. An example of such a measurement system is shown in Figure 10 [49]. An even higher frequency transfer stability to the microwave domain can be measured with an ultra-high stability optical reference and a carrier-suppressed correlation based measurement technique, where a relative stability for optical to microwave conversion of < 2 × 10⁻¹⁷ in 1 s can be obtained [50].

FIGURE 10

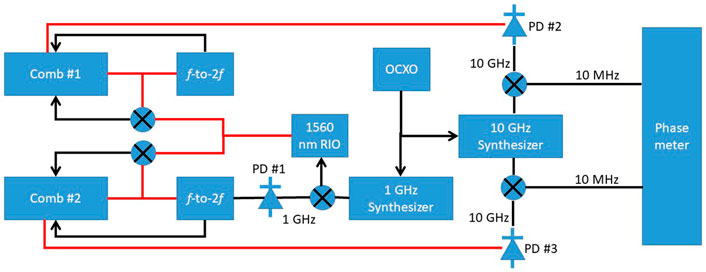
FIGURE 10. Correlation based phase noise measurement system for evaluation of frequency transfer from the optical to microwave domain. Here two frequency combs are locked to a common frequency reference such as a RIO laser. The repetition rate of both combs is further locked to a low noise 1 GHz frequency synthesizer, disciplined to a low noise 10 MHz reference such as an oven crystal oscillator (OCXO). The relative stability of the two 10 GHz microwave tones is analyzed with a phase meter. PD = photo-detector.

Finally, frequency combs can also be used for the generation of ultra-high stability signals in the mmwave or THz frequency range. To generate mmwave signals low noise 10 GHz microwave signal as generated from a fiber comb can for example be optically multiplied with the help of EO comb generation and an optical etalon [51]. The etalon can then select individual frequency nodes separated by 100 GHz or more, where beating those frequency nodes on a high bandwidth uni-travelling carrier (UTC) photodiode generates the low noise signal in the mmwave domain. However, for THz frequency range generation the use of microcombs [52] is generally more straight-forward as microcombs themselves can be constructed with repetition rates that can be as high as 1 THz. Moreover, one can then use frequency division rather than frequency multiplication in order to generate low phase noise and high stability mmwave signals. With this scheme a frequency stability at 300 GHz of around $2\times {10}^{-11}$ at 1 s was demonstrated [53], limited by the optical frequency reference implemented.

Conclusion

With recent advances in fiber frequency comb technology, precision frequency transfer at the 10⁻²¹ relative stability level is now possible, while the fundamental benefits of fiber based frequency comb technology, namely highly integrated, all-fiber construction, robust and long-term stable operation does not need to be compromised. As such, fiber frequency combs support frequency measurements for even the most advanced optical clocks and are bound to be an essential apparatus for the actual realization of a future ultra-high precision time standard. Moreover, fiber frequency combs have now become standard operational tools in many research labs and are increasingly being also used in actual applications in the field. The research and application potential for high power frequency combs operating at the 10–100 W level and in the single cycle regime has not even been scratched and many exciting new applications can be expected. Further broadening of the comb application potential can be expected with the implementation of microcombs. Most of the frequency comb systems discussed here are commercially available, from companies such as IMRA America Inc. https://www.imra.com/products/imra-scientific, providing a great, easily accessible resource for serving new research.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

Authors MF, KL, PL, AR, and JJ were employed by company IMRA America Inc.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Fermann ME, Hofer M, Haberl F, Craig Ryan SP. Femtosecond fibre laser. Electron Lett (1990) 26:1737–8. doi:10.1049/el:19901109

CrossRef Full Text | Google Scholar

2. Wu R, Torres-Company V, Leaird DE, Weiner AM. Supercontinuum-based 10-GHz flat-topped optical frequency comb generation. Opt Express (2013) 21:6045–52. doi:10.1364/oe.21.006045

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Myslivets E, Kuo BPP, Alic N, Radic S. Generation of wideband frequency combs by continuous-wave seeding of multistage mixers with synthesized dispersion. Opt Express (2012) 20:3331–44. doi:10.1364/oe.20.003331

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Torres-Company V, Weiner AM. Optical frequency comb technology for ultra-broadband radio-frequency photonics. Laser Photon Rev (2014) 8:368–93. doi:10.1002/lpor.201300126

CrossRef Full Text | Google Scholar

5. Tong Z, Radic S. Low-noise optical amplification and signal processing in parametric devices. Adv Opt Photon (2013) 5:318–84. doi:10.1364/aop.5.000318

CrossRef Full Text | Google Scholar

6. Udem T, Reichert J, Holzwarth R, Hänsch TW. Absolute optical frequency measurement of the Cesium D₁ line with a mode-locked laser. Phys Rev Lett (1999) 82:3568–71. doi:10.1103/physrevlett.82.3568

CrossRef Full Text | Google Scholar

7. Jones DJ, Diddams SA, Ranka JK, Stentz A, Windeler RS, Hall JL, et al. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science (2000) 288:635–9. doi:10.1126/science.288.5466.635

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Fermann ME, Kuse N. Mode-locked fiber lasers. In: MJ Digonnet, editor. Rare earth doped fiber lasers and amplifiers. 3rd ed. chapter 11 (“in press”).

Google Scholar

9. Fermann ME, Haberl F, Hofer M, Hochreiter H. Nonlinear amplifying loop mirror. Opt Lett (1990) 15:752–4. doi:10.1364/ol.15.000752

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kuse N, Jiang J, Lee CC, Schibli TR, Fermann ME. All polarization-maintaining Er fiber-based optical frequency combs with nonlinear amplifying loop mirror. Opt Express (2016) 24:3095–102. doi:10.1364/oe.24.003095

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hudson DD, Holman KW, Jones RJ, Cundiff ST, Ye J, Jones DJ. Mode-locked fiber laser frequency-controlled with an intracavity electro-optic modulator. Opt Lett (2005) 30:2948–50. doi:10.1364/ol.30.002948

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lee CC, Mohr C, Bethge J, Suzuki S, Fermann ME, Hartl I, et al. Frequency comb stabilization with bandwidth beyond the limit of gain lifetime by an intracavity graphene electro-optic modulator. Opt Lett (2012) 37:3084–6. doi:10.1364/ol.37.003084

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Fermann ME, Hofer M, Haberl F, Ober MH, Schmidt AJ. Additive-pulse-compression mode locking of a neodymium fiber laser. Opt Lett (1991) 16:244–6. doi:10.1364/ol.16.000244

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Nakamura T, Davila-Rodriguez J, Leopardi H, Sherman JA, Fortier TM, Xie X, et al. Coherent optical clock down-conversion for microwave frequencies with 10⁻¹⁸ instability. Science (2020) 368:889–92. doi:10.1126/science.abb2473

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Hartl I, Schibli TR, Marcinkevicius A, Yost DC, Hudson DD, Fermann ME, et al. Cavity-enhanced similariton Yb-fiber laser frequency comb: 3×10¹⁴ W/cm² peak intensity at 136 MHz. Opt Lett (2007) 32:2870–2. doi:10.1364/ol.32.002870

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ruehl A, Marcinkevicius A, Fermann ME, Hartl I. 80 W, 120 fs Yb-fiber frequency comb. Opt Lett (2010) 35:3015–7. doi:10.1364/ol.35.003015

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ruehl A, Martin MJ, Cossel KC, Chen L, McKay H, Thomas B, et al. Ultra-broadband coherent supercontinuum frequency comb. Phys Rev A (Coll Park) (2011) 84:011806. doi:10.1103/physreva.84.011806

CrossRef Full Text | Google Scholar

18. Schibli TR, Hartl I, Yost DC, Martin MJ, Marcinkevicius A, Fermann ME, et al. Optical frequency comb with submillihertz linewidth and more than 10 W average power. Nat Photon (2008) 2:355–9. doi:10.1038/nphoton.2008.79

CrossRef Full Text | Google Scholar

19. Fermann ME, Galvanauskas A, Stock ML, Wong KK, Harter D, Goldberg L. Ultrawide tunable Er soliton fiber laser amplified in Yb-doped fiber. Opt Lett (1999) 24:1428–30. doi:10.1364/ol.24.001428

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Li Y, Kuse N, Rolland A, Stepanenko Y, Radzewicz C, Fermann ME. Low noise, self-referenced all polarization maintaining Ytterbium fiber laser frequency comb. Opt Express (2017) 25:18017–23. doi:10.1364/oe.25.018017

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Mayer AS, Grosinger W, Fellinger J, Winkler G, Perner LW, Droste S, et al. Flexible all-PM NALM Yb:fiber laser design for frequency comb applications: Operation regimes and their noise properties. Opt Express (2020) 28:18946–68. doi:10.1364/oe.394543

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhang C, Li P, Jiang J, von der Wense L, Fermann ME, Ye J. A tunable VUV frequency comb for ^229mTh nuclear spectroscopy. In: Proceedings of the 2021 Conference on Lasers and Electro-Optics (CLEO); 09-14 May 2021; San Jose, CA, USA (2021). in press.

Google Scholar

23. Adler F, Cossel KC, Thorpe MJ, Hartl I, Fermann ME, Ye J. Phase-stabilized, 1.5 W frequency comb at 2.8 – 4.8 μm. Opt Lett (2009) 34:1330–2. doi:10.1364/ol.34.001330

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Cingöz A, Yost DC, Allison TK, Rühl A, Fermann ME, Hartl I, et al. Direct frequency comb spectroscopy in the extreme ultraviolet. Nature (2012) 482:68–71. doi:10.1038/nature10711

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Bethge J, Jiang J, Mohr C, Fermann ME, Hartl I. Optically referenced Tm-Fiber-Laser frequency comb. In: Proceedings of the Conf. on Advanced Solid State Lasers, OSA Technical Digest (CD) San Diego, United States Jan/Feb, 2012 (2012). (Optica Publishing Group) paper AT5A.3.

CrossRef Full Text | Google Scholar

26. Adler F, Diddams SA. High-power, hybrid Er:fiber/Tm:fiber frequency comb source in the 2 μm wavelength region. Opt Lett (2012) 37:1400–2. doi:10.1364/ol.37.001400

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Jiang J, Mohr C, Bethge J, Mills A, Mefford W, Hartl I, et al. 500 MHz, 58fs highly coherent Tm fiber soliton laser. In: Proceedings of the Conf. on Lasers and Electro-Optics (CLEO); 06-11 May 2012; San Jose, CA, USA (2012). OSA Technical Digest (online) (Optica Publishing Group, paper CTh5D.7.

CrossRef Full Text | Google Scholar

28. Butler TP, Lilienfein N, Xu J, Nagl N, Hofer C, Gerz D, et al. Multi-octave spanning, Watt-level ultrafast mid-infrared source. J Phys Photon (2019) 1:044006. doi:10.1088/2515-7647/ab4976

CrossRef Full Text | Google Scholar

29. Leindecker N, Marandi A, Byer RL, Vodopyanov KL, Jiang J, Hartl I, et al. Octave-spanning ultrafast OPO with 2.6 – 6.1 µm instantaneous bandwidth pumped by femtosecond Tm-fiber laser. Opt Express (2012) 20:7046–53. doi:10.1364/oe.20.007046

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Muraviev AV, Smolski VO, Loparo ZE, Vodopyanov KL. Massively parallel sensing of trace molecules and their isotopologues with broadband subharmonic mid-infrared frequency combs. Nat Photon (2018) 12:209–14. doi:10.1038/s41566-018-0135-2

CrossRef Full Text | Google Scholar

31. Diddams SA. The evolving optical frequency comb [Invited]. J Opt Soc Am B (2010) 27:B51–B62. doi:10.1364/josab.27.000b51

CrossRef Full Text | Google Scholar

32. Ohmae N, Kuse N, Fermann ME, Katori H. All polarization-maintaining, single-port Er:fiber comb for high-stability comparison of optical lattice clocks. Appl Phys Express (2017) 10:062503_4. doi:10.7567/apex.10.062503

CrossRef Full Text | Google Scholar

33. Leopardi H, Davila-Rodriguez J, Quinlan F, Olson J, Sherman JA, Diddams SA, et al. Single-branch Er:fiber frequency comb for precision optical metrology with 10⁻¹⁸ fractional instability. Optica (2017) 4:879–85. doi:10.1364/optica.4.000879

CrossRef Full Text | Google Scholar

34. Rolland A, Li P, Kuse N, Jiang J, Cassinerio M, Langrock C, et al. Ultra-broadband dual-branch optical frequency comb with 10^-18 instability. Optica (2018) 5:1070–7. doi:10.1364/optica.5.001070

CrossRef Full Text | Google Scholar

35. Kashiwagi K, Nakajima Y, Wada M, Okubo S, Inaba H. Multi-branch fiber comb with relative frequency uncertainty at 10⁻²⁰ using fiber noise difference cancellation. Opt Express (2018) 26:8831–40. doi:10.1364/oe.26.008831

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Giunta M, Hänsel W, Fischer M, Lezius M, Udem T, Holzwarth R. Real-time phase tracking for wide-band optical frequency measurements at the 20th decimal place. Nat Photon (2020) 14:44–9. doi:10.1038/s41566-019-0520-5

CrossRef Full Text | Google Scholar

37. Li P, Rolland A, Jiang J, Fermann ME. Coherent frequency transfer at < 5*10^-21 relative stability via a multi-branch comb with noise cancellation. Opt Express (2022) 30:22957–62. doi:10.1364/oe.461440

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Lee KF, Rolland A, Li P, Jiang J, Fermann ME. Coherent supercontinuum shaping for multiple wavelength optimization over an octave. Opt Express (2022) 30:427–35. doi:10.1364/oe.445586

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Fermann ME, Hartl I. Ultrafast fibre lasers. Nat Photon (2013) 7:868–74. doi:10.1038/nphoton.2013.280

CrossRef Full Text | Google Scholar

40. Xing S, Lesko DM, Umeki T, Lind AJ, Hoghooghi N, Wu TH, et al. Single-cycle all-fiber frequency comb. APL Photon (2021) 6:086110-1–086110-9. doi:10.1063/5.0055534

CrossRef Full Text | Google Scholar

41. Tani F, Lampen J, Butryn M, Frosz MH, Jiang J, Fermann ME, Russell PS. Temporal self-compression and self-frequency shift of sub-µJ pulses at 8 MHz repetition rate. In: Proceedings of the 2022 Conference on Lasers and Electro-Optics (CLEO); 15-20 May 2022; San Jose CA, USA (2022). p. 11538. arXiv.2207.

Google Scholar

42. Lee KF, Zhou G, Yun Y, Jiang J, Winful HG, Fermann ME. Surpassing soliton compression limits in anomalous dispersion high-power erbium fiber comb. Optica (2021) 8:846–53. doi:10.1364/optica.427977

CrossRef Full Text | Google Scholar

43. Lee KF, Hensley CJ, Schunemann PG, Fermann ME. Midinfrared frequency comb by difference frequency of erbium and thulium fiber lasers in orientation-patterned gallium phosphide. Opt Express (2017) 25:17411–6. doi:10.1364/oe.25.017411

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Catanese A, Rutledge J, Silfies MC, Li X, Timmers H, Kowligy AS, et al. Mid-infrared frequency comb with 6.7 W average power based on difference frequency generation. Opt Lett (2020) 45:1248–51. doi:10.1364/ol.385294

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Haboucha A, Zhang W, Li T, Lours M, Luiten AN, Le Coq Y, et al. Optical-fiber pulse rate multiplier for ultralow phase-noise signal generation. Opt Lett (2011) 36:3654. doi:10.1364/ol.36.003654

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Xie X, Bouchand R, Nicolodi D, Giunta M, Hänsel W, Lezius M, et al. Photonic microwave signals with zeptosecond-level absolute timing noise. Nat Photon (2017) 11:44–7. doi:10.1038/nphoton.2016.215

CrossRef Full Text | Google Scholar

47. Guo J, McLemore CA, Xiang C, Lee D, Wu L, Jin W, et al. Chip-based laser with 1 hertz integrated linewidth, Priprint arXiv:2203.16739v1 (2022).

Google Scholar

48. Rubiola E, Giordano V. Correlation-based phase noise measurements. Rev Sci Instrum (2000) 71:3085–91. doi:10.1063/1.1304871

CrossRef Full Text | Google Scholar

49.IMRA America Inc. Unpublished data. Ann Arbor, Michigan: IMRA America Inc.

50. Baynes FN, Quinlan F, Fortier TM, Zhou Q, Beling A, Campbell JC, et al. Attosecond timing in optical-to-electrical conversion. Optica (2015) 2:141–6. doi:10.1364/optica.2.000141

CrossRef Full Text | Google Scholar

51. Fortier TM, Rolland A, Quinlan F, Baynes FN, Metcalf AJ, Hati A, et al. Optically referenced broadband electronic synthesizer with 15 digits of resolution. Laser Photon Rev (2016) 10:780–90. doi:10.1002/lpor.201500307

CrossRef Full Text | Google Scholar

52. Herr T, Brasch V, Jost JD, Wang CY, Kondratiev NM, Gorodetsky ML, et al. Temporal solitons in optical microresonators. Nat Photon (2014) 8:145–52. doi:10.1038/nphoton.2013.343

CrossRef Full Text | Google Scholar

53. Tetsumoto T, Nagatsuma T, Fermann ME, Navickaite G, Geiselmann M, Rolland A. Optically referenced 300 GHz millimetre-wave oscillator. Nat Photon (2021) 15:516–22. doi:10.1038/s41566-021-00790-2

CrossRef Full Text | Google Scholar