Aerodynamics simulations of three-dimensional inviscid flow using curvilinear discontinuous Galerkin method on unstructured meshes

Over the last decades, the discontinuous Galerkin (DG) method has demonstrated its excellence in accurate, higher-order numerical simulations for a wide range of applications in aerodynamics simulations. However, the development of practical, computationally accurate flow solvers for industrial applications is still in the focus of active research, and applicable boundary conditions and fluxes are also very important parts. Based on curvilinear DG method, we have developed a flow solver that can be used for solving the three-dimensional subsonic, transonic and hypersonic inviscid flows on unstructured meshes. The development covers the geometrical transformation from the real curved element to the rectilinear reference element with the hierarchical basis functions and their gradient operation in reference coordinates up to full third order. The implementation of solid wall boundary conditions is derived by the contravariant velocities, and an enhanced algorithms of Harten-Lax-van Leer with contact (HLLC) flux based on curved element is suggested. These new techniques do not require a complex geometric boundary information and are easy to implement. The simulation of subsonic, transonic and hypersonic flows shows that the linear treatment can limit the accuracy at high order and demonstrates how the boundary treatment involving curved element overcomes this restriction. In addition, such a flow solver is stable on a reasonably coarse meshes and finer ones, and has good robustness for three-dimensional flows with various geometries and velocities. For engineering practice, a reasonable accuracy can be obtained at reasonably coarse unstructured meshes.

1 Introduction

Computational Fluid Dynamics (CFD) has become a very important and useful design tool in aerodynamics [1, 2]. The theoretical basis of CFD includes fluid mechanics, numerical analysis, computer technology and other fields. Based on the various calculation method [3–8], the approximate solution of the fluid governing equation is obtained by using the powerful computing capability of computer. In the past decades, due to the increasing demand for complex fluid flow simulations, great effort has been done by the CFD community in order to increase the accuracy and reduce the calculation costs [9–15]. It is now well understood that numerical errors play a key role in the accuracy of CFD results [10, 12]. In recent years, there has been an increasing interest in the application of high-order discretization methods with curved meshes, which can reduce the numerical errors to aerodynamic flows [16]. Curved meshes are commonly employed to provide a satisfactory representation of the domain boundary with only a moderate number of mesh elements, so that the polynomial degree can be increased while keeping the global number of degrees of freedom (DOFs). The role that curved meshes play in obtaining accurate solutions when combined with high-order numerical discretization methods has been demonstrated, such as [16–20]. Therefore, numerical discretization methods with curved meshes supporting arbitrary approximation orders have received an increasing amount of attention.

Initially developed for advection problems, the discontinuous Galerkin (DG) method has recently been applied in the field of CFD with great success [21–24]. The DG method combine two advantageous features commonly associated with finite element and finite volume methods [25]. As in classical finite element methods, accuracy is obtained by means of high-order polynomial approximation within an element rather than by wide stencils as in the case of finite volume methods. Conservation is, similarly to finite volume methods, enforced through the use of a flux at element boundaries, where a Riemann problem is solved [17]. Furthermore, the discretization lends itself to local mesh adaptation and efficient parallelization on modern distributed memory computer architectures. The implementation of efficient DG method on curved meshes is an open field of research and crucial for developing accurate numerical schemes. In the framework of the steady-state compressible inviscid flow, the necessity of a higher-order treatment of curved wall boundaries was put in evidence by Bassy and Rebay, and is now generally accepted [26, 27]. The curved meshes method via an isoparametric parametric approximation to curve boundary is rather convenient to use for DG schemes [22, 26]. A low-storage curvilinear DG method was proposed and analyzed in [28], where the geometric factors were included in both solution and test function spaces with a provable convergence under a mild condition on the mesh. Recent works by Chan et al. [29, 30] rely on reference frame polynomial spaces introducing weight-adjusted L²-inner products in order to recover high-order accuracy. In [20], a simple boundary treatment, which can be implemented as a modified DG scheme defined on triangles adjacent to boundary, was proposed. Even though integration along the curve is still necessary, integrals over any curved element are avoided. Blended isogeometric DG method formulated on elements that exactly preserve the CAD geometry have also been recently proposed in [31].

However, three-dimensional flows with curved meshes are rarely studied and the way to impose solid wall boundary conditions in curved meshes is not mentioned. Proper boundary treatment is critical in CFD. Its importance is obvious because it is the boundary conditions that determine the flow characteristics once the governing equations are given, at least for steady flow problems [32]. Even though the boundary conditions via a correct representation of the normal to the geometry is rather convenient to use for DG schemes [17, 27], the acquisition of normal is not very easy and needs to provide geometric information, which is not provided by the general mesh generator, especially when the boundary geometry is three-dimensional. Therefore, it is difficult to extend this curved meshes method to engineering applications. A highly adaptable numerical flux format is needed in aerodynamic simulations to accommodate a wide variety of flow velocities, including subsonic flow, transonic flow, supersonic flow and hypersonic flow, and so on. However, the implementation of numerical fluxes generally depends on Lax-Friedrichs scheme and Roe flux in the curved meshes. Although there are references to other (Godunov flux) format numerical fluxes, but display expression is not given. The Harten-Lax-van Leer with contact (HLLC) has gathered interest because of their accuracy, mathematical simplicity, inherent entropy satisfying property, positivity, lack of demand for knowledge of complete eigenstructure of flux Jacobians, ability to satisfactorily handle shocks and expansion fans and their easy extensibility to various hyperbolic systems of governing equations [33–35]. The HLLC scheme is one of the simplest known Riemann solver that can resolve both linearly degenerate and genuinely nonlinear wavefields accurately. Therefore, it is very significant for researchers to find a display expression for HLLC flux on curved meshes.

In recent years, open source solvers have also become very popular. Such as famous open source libraries libMesh [36] and deal.II [37]are both excellent, which have brought inspiration and convenience to many researchers. However, Local Lax-Friedrichs (LLF) flux was used in deal.II [37, 38]. LLF has a larger numerical viscosity, which is not as applicable as HLLC in practical engineering such as supersonic and transonic. In [39], Qiu also point out that the HLLC fluxes might be good choices as fluxes for the RKDG method when all factors such as the cost of CPU time, numerical errors and resolution of discontinuities in the solution are considered. The libMesh is more of a software framework than a complete solver. In practical problems, libMesh has almost no complete functional modules that can be directly applied, and researchers need to do secondary development according to the specific problems. Therefore, the development of three-dimensional solver of aerodynamics simulation is very meaningful work.

In the present work, for aerodynamics simulation, a simulation tool based on curvilinear DG method will be provided to include both three-dimensional solid walls boundary conditions on curved meshes and HLLC flux on curved meshes. First, we present the relevant closed form expressions for a widely used set of hierarchical basis functions up to full high order for a reference element, as well as the necessary expressions for the Jacobian for a high order polynomial geometrical transformation. Given these results, implementation is then straightforward. The derived expressions are used to implement the curved meshes, which are then applied to integration along curved element and curved face for complex geometries. Second, we present the implementation process of HLLC flux in the curved element. Third, the implementation of solid wall boundary conditions depends on contravariant velocities which include the Jacobian of the transformation function of the map from each curved element to a rectilinear reference element. Based on the above three points, we have developed a simulation tool that can be used for solving the three-dimensional subsonic, transonic and hypersonic inviscid flows. Academic problem of subsonic flow past a sphere is used to show how the linear treatment of wall boundaries limits the accuracy, and demonstrate how the boundary treatment involving curved element overcomes this restriction. The results suggest that such a scheme is stable on a reasonably coarse meshes and finer ones. Engineering problems of transonic flow past an ONERA M6 wing, hypersonic flow past a blunt cone, and hypersonic flow past a HB-2 ballistic model are used to demonstrate the ability of this method for engineering practice. Numerical tests suggest that the curvilinear DG method has great robustness for three-dimensional inviscid flows with various geometries and velocities on unstructured meshes.

The paper is organized as follows: we first discuss the main idea of curvilinear DG method in Section 2 for three-dimensional inviscid flows. We present an implementation process of HLLC flux with curved element in Section 3. As a demonstration, we discuss the boundary treatment in Section 4. Numerical tests are shown in Section 5. Section 6 consists of concluding remarks.

2 Discontinuous Galerkin discretization

2.1 Three-dimensional compressible Euler equations

The governing equations for the three-dimensional inviscid flow can be written as follows:

$\frac{\partial \mathbf{u}}{\partial t}+\nabla \cdot \mathbf{F}\left(\mathbf{u}\right)=\mathbf{0},(1)$

which is defined on a boundary domain $\Omega$ with appropriate well-posed boundary data prescribed on $\partial \Omega$. The conservation variables $\mathbf{u}$ and the Cartesian components $\mathbf{f}\left(\mathbf{u}\right)$, $\mathbf{g}\left(\mathbf{u}\right)$, and $\mathbf{h}\left(\mathbf{u}\right)$ of the flux function $\mathbf{F}\left(\mathbf{u}\right)$ are given by

$\mathbf{u}=\left\{\begin{array}{c}\rho \\ \rho u\\ \rho v\\ \rho w\\ \rho e\end{array}\right\},\mathbf{f}\left(\mathbf{u}\right)=\left\{\begin{array}{c}\rho u\\ \rho uu+p\\ \rho uv\\ \rho uw\\ \rho hu\end{array}\right\},\mathbf{g}\left(\mathbf{u}\right)=\left\{\begin{array}{c}\rho v\\ \rho vu\\ \rho vv+p\\ \rho vw\\ \rho hv\end{array}\right\},\mathbf{h}\left(\mathbf{u}\right)=\left\{\begin{array}{c}\rho w\\ \rho wu\\ \rho wv\\ \rho ww+p\\ \rho hw\end{array}\right\}.(2)$

As is customary, $\rho$ is the density of the fluid, $u$, $v$, and $w$ are components of the velocity vector $\overrightarrow{v}$, $p$ is the pressure, and $e$ is the total internal energy per unit mass. The total enthalpy per unit mass is defined as $h=e+p/\rho$. We assume that the fluid is perfect gas satisfying the equation of state

$p=\left(\gamma -1\right)\rho \left(e-{\Vert \overrightarrow{v}\Vert }^2/2\right),(3)$

where $\gamma$ indicates the ratio between the specific heats of the fluid, which is set to 1.4 for the numerical experiments.

2.2 Discretization

The governing equation Eq. 1 is discretized using a DG finite element formulation which originally proposed in reference [40]. Here we provide a brief synopsis of the numerical scheme. For numerical discretization, we divide the problem domain $\Omega$ into a collection of non-overlapping elements

$\mathrm{\Omega }=\underset{h=1}{\overset{N_h}{{\displaystyle \cup }}}{\mathrm{\Omega }}_h.(4)$

Then, approximate solution ${\mathbf{u}}_h$ is introduced on element ${\Omega }_h$ and we construct a Galerkin problem by multiplying Eq. 1 with a test function ${\upsilon }_h$, integrating over the domain ${\Omega }_h$, and using an integration by parts to obtain

${\int }_{{\mathrm{\Omega }}_h}{\upsilon }_h\frac{\partial {\mathbf{u}}_h}{\partial t}dV+{\int }_{\partial {\mathrm{\Omega }}_h}{\upsilon }_h\mathbf{F}\left({\mathbf{u}}_h\right)\cdot \overrightarrow{n}dS-{\int }_{{\mathrm{\Omega }}_h}\nabla {\upsilon }_h\cdot \mathbf{F}\left({\mathbf{u}}_h\right)dV=\mathbf{0},(5)$

where $\overrightarrow{n}$ is the outward unit normal vector to the boundary $\partial {\Omega }_h$. The solution ${\mathbf{u}}_h$ is approximated by the combination of $N_m$ shape functions,

${\mathbf{u}}_h={\displaystyle \sum }_{i=1}^{N_m}{\mathbf{U}}_i\left(\mathrm{t}\right){\varphi }_i^m\left(x,y,z\right),(6)$

where ${\varphi }_i^m\left(x,y,z\right)$ is the shape function of the polynomial of degree $m$ and $N_m=\left(m+1\right)\left(m+2\right)/2$. Then the Eq. 5 becomes the following system of $N_m$ equations

${\displaystyle \sum }_{i=1}^{N_m}\frac{\partial {\mathbf{U}}_i}{\partial t}{\int }_{{\mathrm{\Omega }}_h}{\varphi }_i^m{\varphi }_j^{m}dV+{\int }_{\partial {\mathrm{\Omega }}_h}{\varphi }_j^m\mathbf{F}\left({\mathbf{u}}_h\right)\cdot \overrightarrow{n}dS-{\int }_{{\mathrm{\Omega }}_h}\nabla {\varphi }_j^m\cdot \mathbf{F}\left({\mathbf{u}}_h\right)dV=\mathbf{0},1\le j\le N_m.(7)$

Due to the discontinuous nature of the numerical solution, the normal flux ${\mathbf{F}}_n=\mathbf{F}\left({\mathbf{u}}_h\right)\cdot \overrightarrow{n}$ is not defined on $\partial {\Omega }_h$. The usual strategy is to define it in terms of a numerical flux ${\mathbf{F}}_n\left({\mathbf{u}}_h,{\mathbf{u}}_k\right)$ that depends on the solution ${\mathbf{u}}_h$ on $\partial {\Omega }_h$ and ${\mathbf{u}}_k$ on the neighboring element $\partial {\Omega }_k$ sharing the portion of the boundary $\partial {\Omega }_{hk}$ common to both elements. In our experiments, we use the HLLC flux which is necessary to consider the property of curved element discussed in Section 3. In Eq. 7, the method of calculating the integral of the volume and surface will be introduced in the following sections.

By assembling all the elemental contributions together, the system of ordinary differential equations which govern the evolution in time of the discrete solution can be written as

$\mathbf{M}\frac{d\mathbf{U}}{dt}=\mathbf{R}\left(\mathbf{U}\right),(8)$

where $\mathbf{M}$ denotes the mass matrix and $\mathbf{R}\left(\mathbf{U}\right)$ denotes the residual vector. The above system of ordinary differential equations is discretized in time by a three-stage TVD Runge-Kutta method [40].

$\begin{array}{c}{\mathbf{U}}^{\left(1\right)}={\mathbf{U}}^n+∆t{\mathbf{M}}^{-1}\mathbf{R}\left({\mathbf{U}}^n\right)\\ {\mathbf{U}}^{\left(2\right)}=\frac{3}{4}{\mathbf{U}}^n+\frac{1}{4}\left[{\mathbf{U}}^{\left(1\right)}+∆t{\mathbf{M}}^{-1}\mathbf{R}\left({\mathbf{U}}^{\left(1\right)}\right)\right]\\ {\mathbf{U}}^{n+1}=\frac{1}{3}{\mathbf{U}}^n+\frac{2}{3}\left[{\mathbf{U}}^{\left(2\right)}+∆t{\mathbf{M}}^{-1}\mathbf{R}\left({\mathbf{U}}^{\left(2\right)}\right)\right]\end{array}.(9)$

2.3 Geometric mapping of curved element

In order to improve the representation of curved wall boundaries, elements with second-order shape can be used in the vicinity of the geometry. The geometric transformation of the real curved element in $\left(x,y,z\right)$ space to a rectilinear reference element in $\left(\xi ,\eta ,\zeta \right)$ space, shown in Figure 1, is defined (via the Jacobian) in terms of second order Lagrangian interpolation functions. Figure 1B is a standard reference element and the lengths of the tetrahedron edges along the $\xi$, $\eta$ and $\zeta$ axes are unitary. Hence, it is apparent to define three of simplex coordinates ${\lambda }_2=\xi$, ${\lambda }_3=\eta$, ${\lambda }_4=\zeta$ on this tetrahedron [41, 42], and the last is then ${\lambda }_1=1-\xi -\eta -\zeta$. The second order Lagrangian interpolation functions are constructed by ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$ and identical to those used as nodal basis functions in finite elements. For the ten node tetrahedron, these transformation functions are defined by

$\begin{array}{c}{L}_1\left(\xi ,\eta ,\zeta \right)=2\left({\lambda }_1-1\right){\lambda }_1=\left[2\left(1-\xi -\eta -\zeta \right)\left(1-\xi -\eta -\zeta \right)\right]\\ L_2\left(\xi ,\eta ,\zeta \right)=2\left({\lambda }_2-1\right){\lambda }_2=\left(2\xi -1\right)\xi \\ L_3\left(\xi ,\eta ,\zeta \right)=2\left({\lambda }_3-1\right){\lambda }_3=\left(2\eta -1\right)\eta \\ L_4\left(\xi ,\eta ,\zeta \right)=2\left({\lambda }_4-1\right){\lambda }_4=\left(2\zeta -1\right)\zeta \\ L_5\left(\xi ,\eta ,\zeta \right)=4{\lambda }_1{\lambda }_2=4\left(1-\xi -\eta -\zeta \right)\xi \\ L_6\left(\xi ,\eta ,\zeta \right)=4{\lambda }_1{\lambda }_3=4\left(1-\xi -\eta -\zeta \right)\eta \\ L_7\left(\xi ,\eta ,\zeta \right)=4{\lambda }_1{\lambda }_4=4\left(1-\xi -\eta -\zeta \right)\zeta \\ L_8\left(\xi ,\eta ,\zeta \right)=4{\lambda }_2{\lambda }_3=4\xi \eta \\ L_9\left(\xi ,\eta ,\zeta \right)=4{\lambda }_2{\lambda }_4=4\xi \zeta \\ L_{10}\left(\xi ,\eta ,\zeta \right)=4{\lambda }_3{\lambda }_4=4\eta \zeta \end{array}.(10)$

FIGURE 1

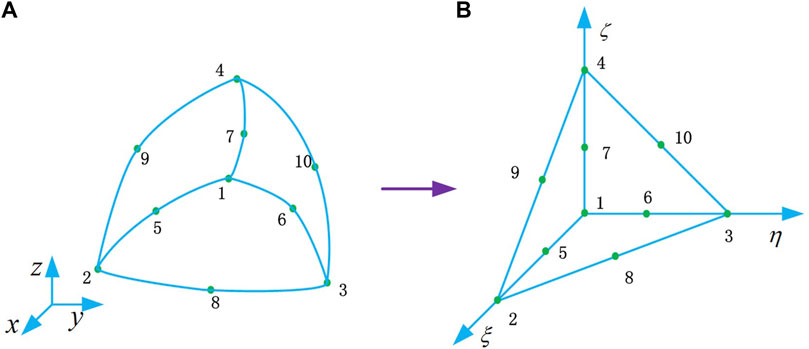
FIGURE 1. Curved element of global coordinates and rectilinear reference element of local coordinates, (A) is curved element, (B) is rectilinear reference element.

The transformation from reference to real coordinates is then accomplished by

$\begin{array}{c}x={\displaystyle \sum }_{i=1}^{10}{L}_i\left(\xi ,\eta ,\zeta \right)x_i\\ y={\displaystyle \sum }_{i=1}^{10}{L}_i\left(\xi ,\eta ,\zeta \right)y_i\\ z={\displaystyle \sum }_{i=1}^{10}{L}_i\left(\xi ,\eta ,\zeta \right)z_i\end{array},(11)$

where $\left(x_i,y_i,z_i\right)$ are the nodal coordinates in real space.

In order to define and manipulate vector quantities within a curved element, the unitary base vectors (co-variant) are introduced

$\begin{array}{c}{\overrightarrow{g}}_1=\frac{\partial x}{\partial \xi }{\overrightarrow{e}}_x+\frac{\partial y}{\partial \xi }{\overrightarrow{e}}_y+\frac{\partial z}{\partial \xi }{\overrightarrow{e}}_z\\ {\overrightarrow{g}}_2=\frac{\partial x}{\partial \eta }{\overrightarrow{e}}_x+\frac{\partial y}{\partial \eta }{\overrightarrow{e}}_y+\frac{\partial z}{\partial \eta }{\overrightarrow{e}}_z\\ {\overrightarrow{g}}_3=\frac{\partial x}{\partial \zeta }{\overrightarrow{e}}_x+\frac{\partial y}{\partial \zeta }{\overrightarrow{e}}_y+\frac{\partial z}{\partial \zeta }{\overrightarrow{e}}_z\end{array},(12)$

and the reciprocal base vectors are

${\overrightarrow{g}}^1=\nabla \xi ,{\overrightarrow{g}}^2=\nabla \eta ,{\overrightarrow{g}}^3=\nabla \zeta .(13)$

Then, a vector can be represented by both its covariant components and the reciprocal base vectors

$\overrightarrow{B}=\left(\overrightarrow{B}\cdot {\overrightarrow{g}}_1\right){\overrightarrow{g}}^1+\left(\overrightarrow{B}\cdot {\overrightarrow{g}}_2\right){\overrightarrow{g}}^2+\left(\overrightarrow{B}\cdot {\overrightarrow{g}}_3\right){\overrightarrow{g}}^3.(14)$

Differentiation in the reference coordinate system is connected to that in the real coordinate system as follows [22, 41]:

$\left[\begin{array}{c}\frac{\partial }{\partial \xi }\\ \frac{\partial }{\partial \eta }\\ \frac{\partial }{\partial \zeta }\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial x}{\partial \xi }& \frac{\partial y}{\partial \xi }& \frac{\partial z}{\partial \xi }\\ \frac{\partial x}{\partial \eta }& \frac{\partial y}{\partial \eta }& \frac{\partial z}{\partial \eta }\\ \frac{\partial x}{\partial \zeta }& \frac{\partial y}{\partial \zeta }& \frac{\partial z}{\partial \zeta }\end{array}\right]\left[\begin{array}{c}\frac{\partial }{\partial x}\\ \frac{\partial }{\partial y}\\ \frac{\partial }{\partial z}\end{array}\right]=\left[J\right]\left[\begin{array}{c}\frac{\partial }{\partial x}\\ \frac{\partial }{\partial y}\\ \frac{\partial }{\partial z}\end{array}\right],(15)$

where $\left[J\right]$ is the Jacobian of the transformation function and the inverse of the Jacobian can be written as

${\left[J\right]}^{-1}=\left[\begin{array}{ccc}\frac{\partial \xi }{\partial x}& \frac{\partial \eta }{\partial x}& \frac{\partial \zeta }{\partial x}\\ \frac{\partial \xi }{\partial y}& \frac{\partial \eta }{\partial y}& \frac{\partial \zeta }{\partial y}\\ \frac{\partial \xi }{\partial z}& \frac{\partial \eta }{\partial z}& \frac{\partial \zeta }{\partial z}\end{array}\right].(16)$

Then, Eq. 14 can be written as

$\left[\begin{array}{c}{B}_x\\ B_y\\ B_z\end{array}\right]={\left[J\right]}^{-1}\left[\begin{array}{c}{B}_{\xi }\\ B_{\eta }\\ B_{\zeta }\end{array}\right],(17)$

where $B_{\xi }$, $B_{\eta }$, and $B_{\zeta }$ are the covariant components in the reference cell. Finally, the function Eqs 10, 11 are differentiated to obtain the Jacobian, which is shown in Table 1.

TABLE 1

TABLE 1. Functions required for the Jacobian: second order curved element.

Although the expression is given, it is worth pointing out that the Jacobian is position-dependent within the element, and must be computed at each quadrature point when computing the integral of the volume and surface in the next subsection. It should be noted that the second order polynomial geometric transformation used here does not exactly model curved. More accurate geometrical modeling can be obtained by either increasing the order of the polynomial mapping or using tetrahedral rational Bezier volumes as shown in [43]. Although there are still some geometrical approximation errors, the fit is far better than that achieved using rectilinear elements.

2.4 Gradient operation of basis functions in reference coordinates

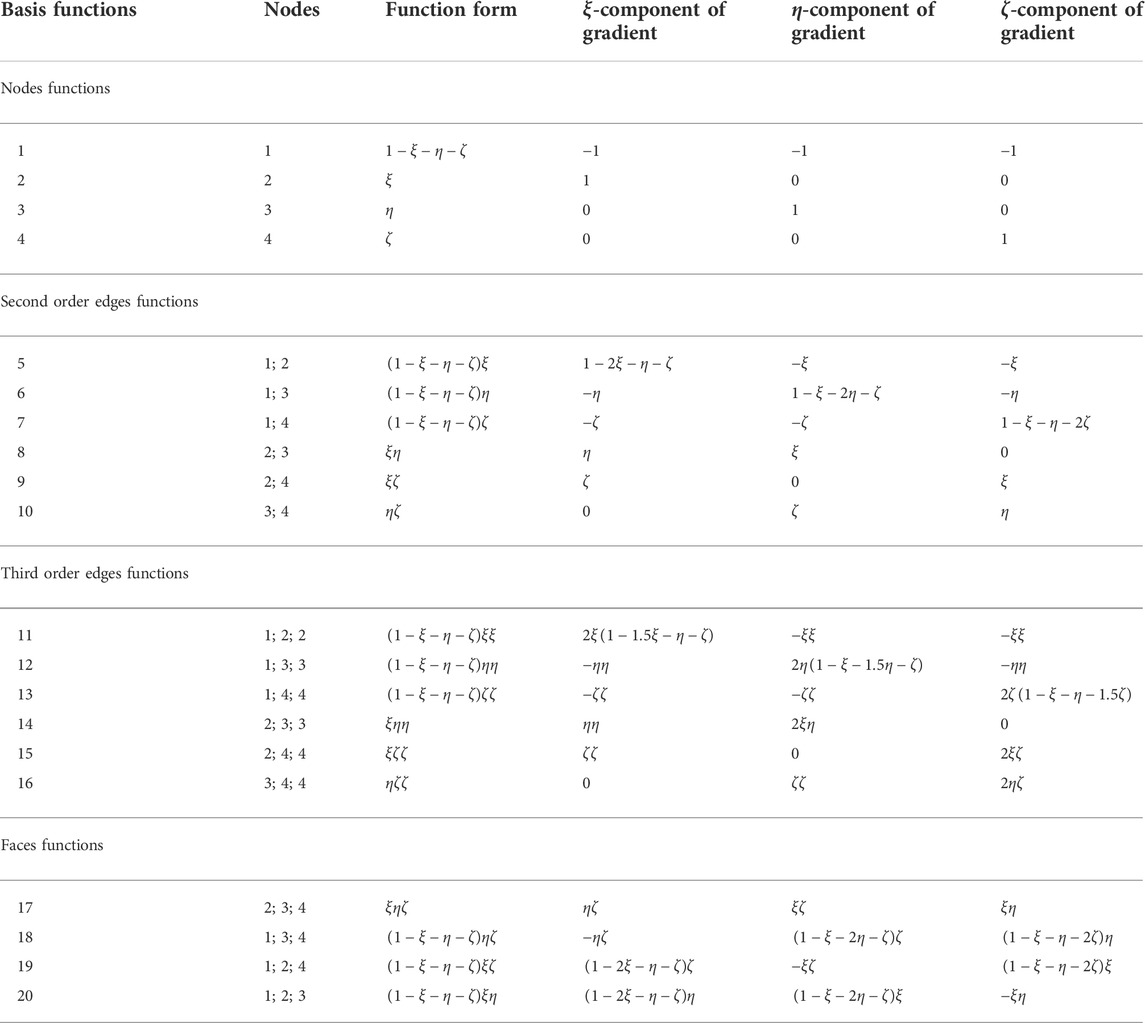
The basis functions and their gradient operation are derived for the parent element in terms of simplex coordinates. The actual set of basis functions used is the hierarchical type [44]. The hierarchical basis functions mean that the low order basis functions are maintained as a subset of the next higher-order basis functions. In order to derive the gradient on the reference element, the following associations are again made:

$\begin{array}{c}{\lambda }_1=1-\xi -\eta -\zeta \\ {\lambda }_2=\xi \\ {\lambda }_3=\eta \\ {\lambda }_4=\zeta \end{array}.(18)$

In the reference coordinates, $\nabla \xi$, the reciprocal base vector, is simply ${\overrightarrow{e}}_{\xi }$, and similarly $\nabla \eta ={\overrightarrow{e}}_{\eta }$ and $\nabla \zeta ={\overrightarrow{e}}_{\zeta }$. The hierarchical basis functions and their gradient operation complete to full third order are presented in Table 2.

TABLE 2

TABLE 2. Hierarchical basis functions and their gradient operation in reference coordinates.

2.5 Computation of integral of the volume and surface

The above subsections discussed geometric mapping of curved element. The real curved element (in the global $\left(x,y,z\right)$ coordinate system) is mapped to a rectilinear parent element (in the local $\left(\xi ,\eta ,\zeta \right)$) coordinate system. Therefore, the integral of the volume and surface is changed, which should take into account the factors of the curved element.

In Eq. 8, the mass matrix elements are computed as

$M_{ij}={\int }_{{\mathrm{\Omega }}^{\prime }}{\varphi }_i^m{\varphi }_j^m\left|\mathrm{d}\mathrm{e}\mathrm{t}\left[J\right]\right|d\xi d\eta d\zeta ,(19)$

and the residual vector elements are separated into the following two parts

${\mathbf{R}}_j={\mathbf{R}}_j^1+{\mathbf{R}}_j^2,(20)$

${\mathbf{R}}_j^1={\int }_{\mathrm{\Omega }}\nabla {\varphi }_j^m\cdot \mathbf{F}\left({\mathbf{u}}_l\right)dV,(21)$

${\mathbf{R}}_j^2=-{\int }_{\partial \mathrm{\Omega }}{\varphi }_j^m{\mathbf{F}}_n\left({\mathbf{u}}_l,{\mathbf{u}}_r\right)dS,(22)$

where $l$ indicates the element, and $r$ indicates the neighboring element. In the reference coordinate system, considering Eqs 17, 21 becomes

${\mathbf{R}}_j^1={\int }_{{\mathrm{\Omega }}^{\prime }}\left({\left[J\right]}^{-1}\nabla {\varphi }_j^m\right)\cdot \mathbf{F}\left({\mathbf{u}}_l\right)\left|\mathrm{d}\mathrm{e}\mathrm{t}\left[J\right]\right|d\xi d\eta d\zeta .(23)$

In Eq. 22, ${\mathbf{F}}_n\left({\mathbf{u}}_l,{\mathbf{u}}_r\right)$ is a HLLC schemes numerical flux which will be discussed in the next section. Considering Eq. 17, the calculation of ${\mathbf{R}}_j^2$ has the following four situations.

In the case where $S_L>0$, the Eq. 22 becomes

${\mathbf{R}}_j^2=-{\int }_{\partial {\mathrm{\Omega }}^{\prime }}{\varphi }_j^m\mathbf{F}\left({\mathbf{u}}_l\right)\cdot \left({\left[J\right]}_S^{-1}\left[\begin{array}{c}{n}_{\xi }\\ n_{\eta }\\ n_{\zeta }\end{array}\right]\right)\left|\mathrm{d}\mathrm{e}\mathrm{t}{\left[J\right]}_S\right|d\xi d\eta ,(24)$

in the case where $S_L\le 0<S_M$, the Eq. 22 becomes

${\mathbf{R}}_j^2=-{\int }_{\partial {\mathrm{\Omega }}^{\prime }}{\varphi }_j^m\mathbf{F}\left({\mathbf{u}}_l\right)\cdot \left({\left[J\right]}_S^{-1}\left[\begin{array}{c}{n}_{\xi }\\ n_{\eta }\\ n_{\zeta }\end{array}\right]\right)\left|\mathrm{d}\mathrm{e}\mathrm{t}{\left[J\right]}_S\right|d\xi d\eta -{\int }_{\partial {\mathrm{\Omega }}^{\prime }}{\varphi }_j^m{S}_L\left({\mathbf{U}}_l^{\ast }-{\mathbf{U}}_l\right)\left|\mathrm{d}\mathrm{e}\mathrm{t}{\left[J\right]}_S\right|d\xi d\eta ,(25)$

in the case where $S_M\le 0\le S_R$, the Eq. 22 becomes

${\mathbf{R}}_j^2=-{\int }_{\partial {\mathrm{\Omega }}^{\prime }}{\varphi }_j^m\mathbf{F}\left({\mathbf{u}}_r\right)\cdot \left({\left[J\right]}_S^{-1}\left[\begin{array}{c}{n}_{\xi }\\ n_{\eta }\\ n_{\zeta }\end{array}\right]\right)\left|\mathrm{d}\mathrm{e}\mathrm{t}{\left[J\right]}_S\right|d\xi d\eta -{\int }_{\partial {\mathrm{\Omega }}^{\prime }}{\varphi }_j^m{S}_R\left({\mathbf{U}}_r^{\ast }-{\mathbf{U}}_r\right)\left|\mathrm{d}\mathrm{e}\mathrm{t}{\left[J\right]}_S\right|d\xi d\eta ,(26)$

and in the case where $S_R<0$, the Eq. 22 becomes

${\mathbf{R}}_j^2=-{\int }_{\partial {\mathrm{\Omega }}^{\prime }}{\varphi }_j^m\mathbf{F}\left({\mathbf{u}}_r\right)\cdot \left({\left[J\right]}_S^{-1}\left[\begin{array}{c}{n}_{\xi }\\ n_{\eta }\\ n_{\zeta }\end{array}\right]\right)\left|\mathrm{d}\mathrm{e}\mathrm{t}{\left[J\right]}_S\right|d\xi d\eta ,(27)$

where ${\left[J\right]}_S$ is the Jacobian matrix of face, the superscript ${\left(\right)}^{\prime }$ indicates the parameter in the reference element, $S_L\left({\mathbf{U}}_l^{*}-{\mathbf{U}}_l\right)$ and $S_R\left({\mathbf{U}}_r^{*}-{\mathbf{U}}_r\right)$ expressions will be discussed in the next section.

The integral of the volume and surface cannot be evaluated analytically and must be computed numerically using quadrature techniques [45]. The use of high order quadrature rules results in increased computational cost when using curvilinear as opposed to rectilinear elements. Therefore, it is advisable that curved elements only be used along the curved boundaries of the domain.

3 The implementation process of Harten-Lax-van Leer with contact flux in curved element

Amongst various approximate Riemann solvers that exist in the literature, the HLLC schemes have gained popularity because of their simplicity and accuracy. In this work, we intend to closely study the numerical schemes of HLLC flux in curved element. The original Harten-Lax-van Leer (HLL) scheme was devised by Harten, Lax and van Leer [46]. It assumes a wave structure consisting of two waves that separates three constant states. Although quite accurate in resolution of nonlinear waves, a major drawback of the HLL scheme is its inability to exactly resolve the contact and shear waves. The loss of accuracy on these waves occurs because of the assumption of constant average state between the two wave structure [34]. The inability of HLL solver to resolve contact and shear waves was mitigated through the development of the HLLC Riemann solver (C for Contact) by Toro et al. [47]. This improvement was achieved by considering two averaged intermediate states, separated by adding a contact wave with speed $S_M$ to the pre-existing two wave HLL structure.

The two-state approximate Riemann solution is defined as [46]

${\mathbf{U}}_{HLLC}=\{\begin{array}{c}{\mathbf{U}}_{l}if{S}_L>0\\ {\mathbf{U}}_l^{\ast }if{S}_L\le 0<S_M\\ {\mathbf{U}}_r^{\ast }if{S}_M\le 0\le S_R\\ {\mathbf{U}}_{r}if{S}_R<0\end{array},(28)$

The corresponding interface flux, denoted ${\mathbf{F}}_n\left({\mathbf{u}}_l,{\mathbf{u}}_r\right)={\mathbf{F}}_{HLLC}$, is defined as

${\mathbf{F}}_{HLLC}=\{\begin{array}{c}{\mathbf{F}}_{l}if{S}_L>0\\ {\mathbf{F}}_l^{\ast }if{S}_L\le 0<S_M\\ {\mathbf{F}}_r^{\ast }if{S}_M\le 0\le S_R\\ {\mathbf{F}}_{r}if{S}_R<0\end{array},(29)$

where ${\mathbf{F}}_l=\mathbf{F}\left({\mathbf{u}}_l\right)\cdot \overrightarrow{n}$, ${\mathbf{F}}_r=\mathbf{F}\left({\mathbf{u}}_r\right)\cdot \overrightarrow{n}$; $S_L$ and $S_R$ are numerical approximations to the speeds of the left most and right most running characteristics that emerge as the solution of the Riemann problem at an interface.

In the rectilinear reference element, through Eq. 17, the unit normal vector $\overrightarrow{n}$ is represented as

$\begin{array}{c}{n}_x={\xi }_x{n}_{\xi }+{\eta }_x{n}_{\eta }+{\zeta }_x{n}_{\zeta }\\ n_y={\xi }_y{n}_{\xi }+{\eta }_y{n}_{\eta }+{\zeta }_y{n}_{\zeta }\\ n_z={\xi }_z{n}_{\xi }+{\eta }_z{n}_{\eta }+{\zeta }_z{n}_{\zeta }\end{array},(30)$

where $n_{\xi }$, $n_{\eta }$ and $n_{\zeta }$ are the component of the unit normal vector of the interface in rectilinear reference element. Therefore, the directed velocity, $q=u{n}_x+v{n}_y+z{n}_z$ in real curved element, can be rewritten as follow

$Q=U{n}_{\xi }+V{n}_{\eta }+W{n}_{\zeta },(31)$

where $U$, $V$ and $W$ are contravariant velocities, which can be defined as

$\begin{array}{c}U={\xi }_{x}u+{\xi }_{y}v+{\xi }_{z}w\\ V={\eta }_{x}u+{\eta }_{y}v+{\eta }_{z}w\\ W={\zeta }_{x}u+{\zeta }_{y}v+{\zeta }_{z}w\end{array}.(32)$

The choice of wavespeeds are given as [33]

$\begin{array}{c}{S}_L=\min \left(Q_l-c_l\left(\left|\nabla \xi \right|+\left|\nabla \eta \right|+\left|\nabla \zeta \right|\right)/3,\stackrel{\sim }{Q}-\stackrel{\sim }{c}\left(\left|\nabla \xi \right|+\left|\nabla \eta \right|+\left|\nabla \zeta \right|\right)/3\right)\\ S_R=\max \left(Q_r+c_r\left(\left|\nabla \xi \right|+\left|\nabla \eta \right|+\left|\nabla \zeta \right|\right)/3,\stackrel{\sim }{Q}+\stackrel{\sim }{c}\left(\left|\nabla \xi \right|+\left|\nabla \eta \right|+\left|\nabla \zeta \right|\right)/3\right)\end{array},(33)$

where $\left|\nabla \xi \right|=\sqrt{{\xi }_x^2+{\xi }_y^2+{\xi }_z^2}$, $\left|\nabla \eta \right|=\sqrt{{\eta }_x^2+{\eta }_y^2+{\eta }_z^2}$, $\left|\nabla \zeta \right|=\sqrt{{\zeta }_x^2+{\zeta }_y^2+{\zeta }_z^2}$; $Q_l$ and $Q_r$ are the normal velocities across an interface; $c_l$ and $c_r$ are the respective sonic speeds; superscript “∼” indicates the standard Roe averaged quantities at the interface [48]. Applying the Rankine-Hugoniot conditions across the $S_L$ wave gives [33]

${\mathbf{F}}_l^{\ast }={\mathbf{F}}_l+S_L\left({\mathbf{U}}_l^{\ast }-{\mathbf{U}}_l\right).(34)$

Similarly, the jump relations across the $S_R$ wave gives

${\mathbf{F}}_r^{\ast }={\mathbf{F}}_r+S_R\left({\mathbf{U}}_r^{\ast }-{\mathbf{U}}_r\right).(35)$

For three-dimensional Euler equations with states ${\mathbf{U}}_l$ and ${\mathbf{U}}_r$ separated by an interface with unit normal vector $\overrightarrow{n}$, Eq. 34 becomes [33]

$S_L\left[\begin{array}{c}{\rho }_l^{\ast }\\ {\rho }_l^{\ast }{u}_l^{\ast }\\ {\rho }_l^{\ast }{v}_l^{\ast }\\ {\rho }_l^{\ast }{w}_l^{\ast }\\ {\rho }_l^{\ast }{e}_l^{\ast }\end{array}\right]-\left[\begin{array}{c}{\rho }_l^{\ast }{Q}_l^{\ast }\\ {\rho }_l^{\ast }{u}_l^{\ast }{Q}_l^{\ast }+p^{\ast }\left({\xi }_x{n}_{\xi }+{\eta }_x{n}_{\eta }+{\zeta }_x{n}_{\zeta }\right)\\ {\rho }_l^{\ast }{v}_l^{\ast }{Q}_l^{\ast }+p^{\ast }\left({\xi }_y{n}_{\xi }+{\eta }_y{n}_{\eta }+{\zeta }_y{n}_{\zeta }\right)\\ {\rho }_l^{\ast }{w}_l^{\ast }{Q}_l^{\ast }+p^{\ast }\left({\xi }_z{n}_{\xi }+{\eta }_z{n}_{\eta }+{\zeta }_z{n}_{\zeta }\right)\\ \left({\rho }_l^{\ast }{e}_l^{\ast }+p^{\ast }\right)Q_l^{\ast }\end{array}\right]=S_L\left[\begin{array}{c}{\rho }_l\\ {\rho }_l{u}_l\\ {\rho }_l{v}_l\\ {\rho }_l{w}_l\\ {\rho }_l{e}_l\end{array}\right]-\left[\begin{array}{c}{\rho }_l{Q}_l\\ {\rho }_l{u}_l{Q}_l+p_l\left({\xi }_x{n}_{\xi }+{\eta }_x{n}_{\eta }+{\zeta }_x{n}_{\zeta }\right)\\ {\rho }_l{v}_l{Q}_l+p_l\left({\xi }_y{n}_{\xi }+{\eta }_y{n}_{\eta }+{\zeta }_y{n}_{\zeta }\right)\\ {\rho }_l{w}_l{Q}_l+p_l\left({\xi }_z{n}_{\xi }+{\eta }_z{n}_{\eta }+{\zeta }_z{n}_{\zeta }\right)\\ \left({\rho }_l{e}_l+p_l\right)Q_l\end{array}\right].(36)$

Similarly, Eq. 35 becomes

$S_R\left[\begin{array}{c}{\rho }_r^{\ast }\\ {\rho }_r^{\ast }{u}_r^{\ast }\\ {\rho }_r^{\ast }{v}_r^{\ast }\\ {\rho }_r^{\ast }{w}_r^{\ast }\\ {\rho }_r^{\ast }{e}_r^{\ast }\end{array}\right]-\left[\begin{array}{c}{\rho }_r^{\ast }{Q}_r^{\ast }\\ {\rho }_r^{\ast }{u}_r^{\ast }{Q}_r^{\ast }+p^{\ast }\left({\xi }_x{n}_{\xi }+{\eta }_x{n}_{\eta }+{\zeta }_x{n}_{\zeta }\right)\\ {\rho }_r^{\ast }{v}_r^{\ast }{Q}_r^{\ast }+p^{\ast }\left({\xi }_y{n}_{\xi }+{\eta }_y{n}_{\eta }+{\zeta }_y{n}_{\zeta }\right)\\ {\rho }_r^{\ast }{w}_r^{\ast }{Q}_r^{\ast }+p^{\ast }\left({\xi }_z{n}_{\xi }+{\eta }_z{n}_{\eta }+{\zeta }_z{n}_{\zeta }\right)\\ \left({\rho }_r^{*}{e}_r^{*}+p^{*}\right)Q_r^{*}\end{array}\right]=S_R\left[\begin{array}{c}{\rho }_r\\ {\rho }_r{u}_r\\ {\rho }_r{v}_r\\ {\rho }_r{w}_r\\ {\rho }_r{e}_r\end{array}\right]-\left[\begin{array}{c}{\rho }_r{Q}_r\\ {\rho }_r{u}_r{Q}_r+p_r\left({\xi }_x{n}_{\xi }+{\eta }_x{n}_{\eta }+{\zeta }_x{n}_{\zeta }\right)\\ {\rho }_r{v}_r{Q}_r+p_r\left({\xi }_y{n}_{\xi }+{\eta }_y{n}_{\eta }+{\zeta }_y{n}_{\zeta }\right)\\ {\rho }_r{w}_r{Q}_r+p_r\left({\xi }_z{n}_{\xi }+{\eta }_z{n}_{\eta }+{\zeta }_z{n}_{\zeta }\right)\\ \left({\rho }_r{e}_r+p_r\right)Q_r\end{array}\right].(37)$

To determine ${\mathbf{U}}_l^{*}$, ${\mathbf{U}}_r^{*}$ (and hence ${\mathbf{F}}_l^{*}$, ${\mathbf{F}}_r^{*}$), Batten et al. [33] made the assumption that

$S_M=Q_l^{\ast }=Q_r^{\ast }=Q^{\ast },(38)$

where $Q^{*}$ is the average directed velocity between the two acoustic waves. Multiplying the second, third, and fourth equations of Eq. 36 by $n_x$, $n_y$ and $n_z$ respectively, and summing minus multiplying the second, third, and fourth equations of Eq. 37 by $n_x$, $n_y$ and $n_z$ respectively, and summing, a closed form expression for the contact wavespeed, $S_M$, can be written as

$S_M=\frac{{\rho }_r{Q}_r\left(S_R-Q_r\right)-{\rho }_l{Q}_l\left(S_L-Q_l\right)+P_l-P_r}{{\rho }_r\left(S_R-Q_r\right)-{\rho }_l\left(S_L-Q_l\right)},(39)$

where

$\begin{array}{c}{P}_l=p_l\left[{\left({\xi }_x{n}_{\xi }+{\eta }_x{n}_{\eta }+{\zeta }_x{n}_{\zeta }\right)}^2+{\left({\xi }_y{n}_{\xi }+{\eta }_y{n}_{\eta }+{\zeta }_y{n}_{\zeta }\right)}^2+{\left({\xi }_z{n}_{\xi }+{\eta }_z{n}_{\eta }+{\zeta }_z{n}_{\zeta }\right)}^2\right]=p_{l}N\\ P_r=p_r\left[{\left({\xi }_x{n}_{\xi }+{\eta }_x{n}_{\eta }+{\zeta }_x{n}_{\zeta }\right)}^2+{\left({\xi }_y{n}_{\xi }+{\eta }_y{n}_{\eta }+{\zeta }_y{n}_{\zeta }\right)}^2+{\left({\xi }_z{n}_{\xi }+{\eta }_z{n}_{\eta }+{\zeta }_z{n}_{\zeta }\right)}^2\right]=p_{r}N\end{array}.(40)$

Once $S_M$ is obtained, Eq. 36 can be manipulated to find all remaining components of ${\mathbf{U}}_l^{*}$. Using Eq. 38, the first equation in Eq. 36 gives

${\rho }_l^{\ast }={\rho }_l\frac{\left(S_L-Q_l\right)}{\left(S_L-S_M\right)}.(41)$

Multiplying the second, third, and fourth equations of Eq. 36 by $n_x$, $n_y$ and $n_z$ respectively, and summing gives

$S_L{\rho }_l^{\ast }{S}_M-{\rho }_l^{\ast }{S}_M^2-P^{\ast }=S_L{\rho }_l{Q}_l-{\rho }_l{Q}_l^2-P_l.(42)$

Using Eq. 41 this simplifies to give

$p^{\ast }={\rho }_l\left(Q_l-S_L\right)\left(Q_l-S_M\right)/N+p_l.(43)$

With ${\rho }_l^{\ast }$ and $p^{\ast }$ specified, ${\left(\rho u\right)}_l^{\ast }$, ${\left(\rho v\right)}_l^{\ast }$, ${\left(\rho w\right)}_l^{\ast }$ and ${\left(\rho e\right)}_l^{\ast }$ may be obtained from Eq. 36 as

${\left(\rho u\right)}_l^{\ast }=\frac{\left(S_L-Q_l\right){\rho }_l{u}_l+\left(p^{\ast }-p_l\right)\left({\xi }_x{n}_{\xi }+{\eta }_x{n}_{\eta }+{\zeta }_x{n}_{\zeta }\right)}{S_L-S_M},(44)$

${\left(\rho v\right)}_l^{\ast }=\frac{\left(S_L-Q_l\right){\rho }_l{v}_l+\left(p^{\ast }-p_l\right)\left({\xi }_y{n}_{\xi }+{\eta }_y{n}_{\eta }+{\zeta }_y{n}_{\zeta }\right)}{S_L-S_M},(45)$

${\left(\rho w\right)}_l^{\ast }=\frac{\left(S_L-Q_l\right){\rho }_l{w}_l+\left(p^{\ast }-p_l\right)\left({\xi }_z{n}_{\xi }+{\eta }_z{n}_{\eta }+{\zeta }_z{n}_{\zeta }\right)}{S_L-S_M},(46)$

${\left(\rho e\right)}_l^{\ast }=\frac{\left(S_L-Q_l\right){\rho }_l{e}_l-p_l{Q}_l+p^{\ast }{S}_M}{S_L-S_M}.(47)$

From Eqs 41–47, the flux vector ${\mathbf{F}}_l^{*}$ may be obtained directly from Eq. 36. In the case where $S_M\le 0\le S_R$, the equations for ${\mathbf{F}}_r^{*}$ follow by simply changing the $l$ or $L$ subscripts to $r$ and $R$, respectively.

4 Boundary conditions with curved element

4.1 Mesh generation

When exploiting the ability of higher-order discretization methods to generate accurate approximations on coarse meshes, a crucial point is to provide a proper representation of curved wall boundaries [23]. Using a finer mesh to fit the boundary is a common method. However, inserting additional elements close to a boundary with the sole purpose of resolving the geometry impedes the aims of higher-order methods.

A more adequate approach we pursue within the proposed method is to represent the boundary by Simmetrix’ Modeling Suite [49], which is able to cope with high-order meshes. We gain detailed information on the geometry via additional point data included in the mesh.

The curved mesh generation process is briefly illustrated by an example in Figure 2. Firstly, solver read the model and mesh parameters, then call the mesh generation module, and use a certain method (such as Delaunay triangulation) to generate the first-order meshes, as shown in Figures 2A,D. According to geometry information, second-order meshes are then produced by projecting the mid-point of boundary edges on the geometry, resulting in curved elements on the boundary, as shown in Figures 2B and Figure 2E.

FIGURE 2

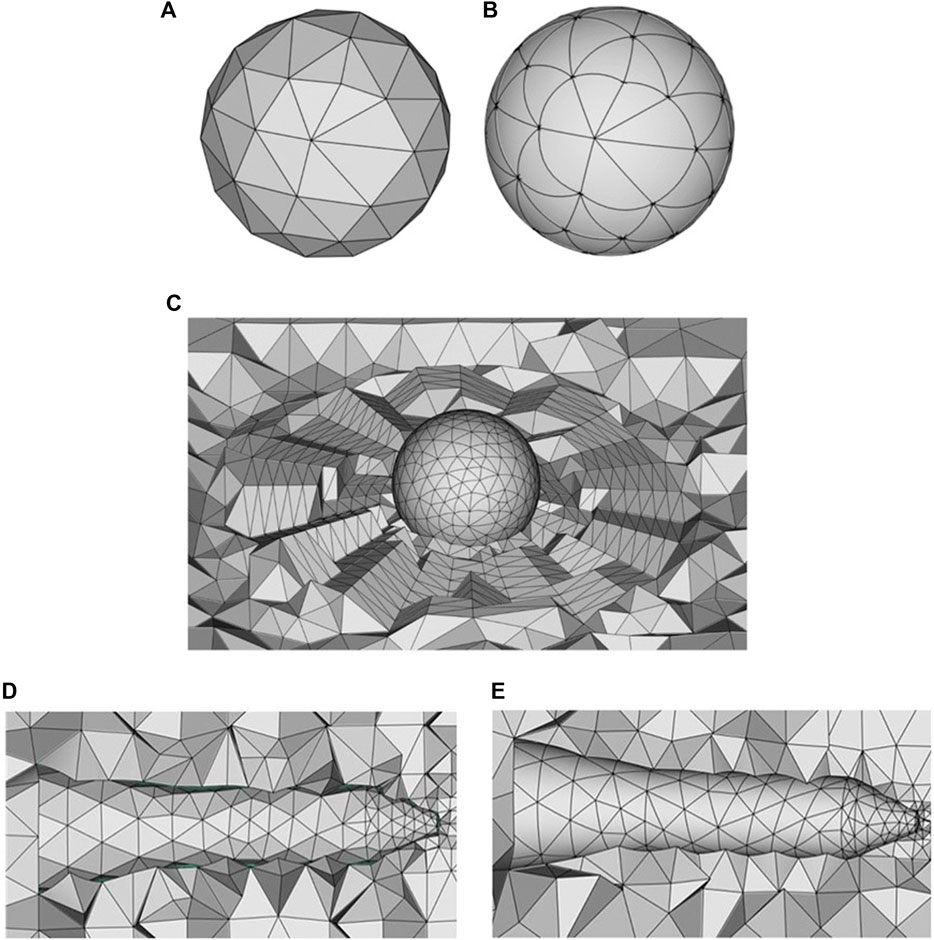
FIGURE 2. Detail of mesh generation process of sphere. (A) is first-order meshes of sphere, (B) is second-order meshes of sphere. (C) is computational domain meshes of sphere. (D) first-order meshes of HB-2, (E) second-order meshes of HB-2.

4.2 Boundary conditions

When the boundary face of an element belongs to $\partial \Omega$, the normal flux function ${\mathbf{F}}_n\left({\mathbf{u}}_l,{\mathbf{u}}_r\right)$ must be consistent with the boundary condition to be imposed on $\partial \Omega$ and will be denoted by ${\mathbf{F}}_n\left({\mathbf{u}}_l,{\mathbf{u}}_{bc}\right)$, where ${\mathbf{u}}_l$ is the internal boundary state at the current time level and ${\mathbf{u}}_{bc}$ is chosen according to the conditions that must be satisfied on the boundary. At inflow and outflow boundaries, the state is computed by means of a local one-dimensional characteristic analysis in a direction normal to the boundary by imposing the available data and the Riemann invariants associated to outgoing characteristics [26]. The most popular way to impose boundary conditions at solid wall is the reflection technique, where an extra row (rows) of ghost cells is added behind the wall. All interior solution components are reflected symmetrically to ghost states except for the normal velocity which is negated [27].

The reflecting boundary conditions state that no flow penetrates a solid wall, i.e., the normal velocity at the wall is zero. Depending on the numerical scheme, a ghost state or cell is created on the part of the numerical boundary $\partial {\Omega }^W$ corresponding to the solid wall. With the DG methods, a ghost state is created at every integration point on $\partial {\Omega }^W$, where all components of the ghost solution are set equal to the corresponding interior values at the same point except for the normal velocity, which is negated. Then, the interior and ghost states are passed to a Riemann solver. Due to the symmetry of the reflection, the solution of the Riemann problem at integration point ${\mathbf{x}}_k\in \partial {\Omega }^W$ satisfies [27]

$\overrightarrow{v}\left({\mathbf{x}}_k\right)\cdot \overrightarrow{n}=0,(48)$

where $\overrightarrow{v}$ is velocity vector, $\overrightarrow{n}$ is the inward unit normal vector to the boundary face of an element $H$ belongs to $\partial {\Omega }^W$ which is shown in Figure 3A. The geometric description of Eq. 48 is shown in Figure 3C.

FIGURE 3

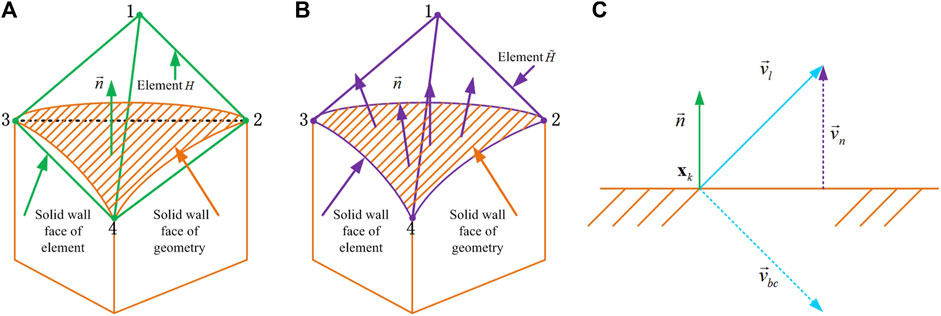
FIGURE 3. Solid wall boundary and geometric description of boundary conditions. (A) is rectilinear boundary element, (B) is curved boundary element, (C) is geometric description of boundary conditions.

A general process for implementing boundary conditions is shown below. A ghost state ${\overrightarrow{v}}_{bc}$ is created at each boundary integration point ${\mathbf{x}}_k$. Via Figure 3C, by the addition of vectors, the ${\overrightarrow{v}}_{bc}$ relative to the element $H$ at the ghost state is given by

${\overrightarrow{v}}_{bc}={\overrightarrow{v}}_l-2{\overrightarrow{v}}_n,(49)$

where ${\overrightarrow{v}}_l$ is the interior state, and ${\overrightarrow{v}}_n$ is the normal velocity. The ${\overrightarrow{v}}_n$ is defined as

${\overrightarrow{v}}_n=\left({\overrightarrow{v}}_l\cdot \overrightarrow{n}\right)\overrightarrow{n},(50)$

while the density and pressure are copied exactly from the interior values at the same point. We obtain the ghost state vector as

$\begin{array}{c}{\rho }_{bc}={\rho }_l\\ u_{bc}=u_l-2\left(u_l{n}_x+v_l{n}_y+w_l{n}_z\right)n_x\\ v_{bc}=v_l-2\left(u_l{n}_x+v_l{n}_y+w_l{n}_z\right)n_y\\ w_{bc}=w_l-2\left(u_l{n}_x+v_l{n}_y+w_l{n}_z\right)n_z\\ p_{bc}=p_l\end{array}.(51)$

Finally, the Riemann problem ${\mathbf{F}}_n\left({\mathbf{u}}_l,{\mathbf{u}}_{bc}\right)$ is solved. From Eq. 51 we found that the ghost state vector at each integration point of the boundary face of an element $H$ belongs to $\partial {\Omega }^W$ is the same.

This approach works well for straight-sided bodies. However, results are inferior when a physical geometry is more complex [27]. Even more, the DG method is highly sensitive to the error due to approximation of a curved geometry by a straight-sided element meshes. This error may dominate the discretization error of the scheme and lead to a wrong solution. We seek to impose boundary conditions which would take this into consideration and model flow more accurately. When considering the factors of the curved element, we proceed as follow.

In Section 4.1, we know that the solid wall boundary region is discretized by curved elements. When the boundary face of a curved element $\stackrel{\sim }{H}$ belongs to $\partial {\Omega }^W$, the normalized inward unit normal vector $\overrightarrow{n}$ at each quadrature point is different which is shown in Figure 3B. Therefore, the solid wall boundary conditions, Eq. 51, cannot be directly applied. Even though the boundary conditions via a correct representation of the normal to the geometry is rather convenient to use for Eq. 51 [17, 27], the acquisition of normal is not very easy and needs to provide geometric information. Here, we show a direct method to implement solid wall boundary conditions which only requires some variables of rectilinear reference element.

Using the variables of rectilinear reference element, the normalized inward unit normal vector $\overrightarrow{n}$ can be written as

$\begin{array}{c}{n}_x={\overline{\xi }}_x{n}_{\xi }+{\overline{\eta }}_x{n}_{\eta }+{\overline{\zeta }}_x{n}_{\zeta }\\ n_y={\overline{\xi }}_y{n}_{\xi }+{\overline{\eta }}_y{n}_{\eta }+{\overline{\zeta }}_y{n}_{\zeta }\\ n_z={\overline{\xi }}_z{n}_{\xi }+{\overline{\eta }}_z{n}_{\eta }+{\overline{\zeta }}_z{n}_{\zeta }\end{array},(52)$

where

$\begin{array}{c}{\overline{\xi }}_x={\xi }_x/\left|\nabla \xi \right|,{\overline{\xi }}_y={\xi }_y/\left|\nabla \xi \right|,{\overline{\xi }}_z={\xi }_z/\left|\nabla \xi \right|\\ {\overline{\eta }}_x={\eta }_x/\left|\nabla \eta \right|,{\overline{\eta }}_y={\eta }_y/\left|\nabla \eta \right|,{\overline{\eta }}_z={\eta }_z/\left|\nabla \eta \right|\\ {\overline{\zeta }}_x={\zeta }_x/\left|\nabla \zeta \right|,{\overline{\zeta }}_y={\zeta }_y/\left|\nabla \zeta \right|,{\overline{\zeta }}_z={\zeta }_z/\left|\nabla \zeta \right|\end{array}.(53)$

Using Eqs 52, 50 becomes

$\begin{array}{c}{\left({\overrightarrow{v}}_n\right)}_x=\left(\overline{U}{n}_{\xi }+\overline{V}{n}_{\eta }+\overline{W}{n}_{\zeta }\right)\left({\overline{\xi }}_x{n}_{\xi }+{\overline{\eta }}_x{n}_{\eta }+{\overline{\zeta }}_x{n}_{\zeta }\right)\\ {\left({\overrightarrow{v}}_n\right)}_y=\left(\overline{U}{n}_{\xi }+\overline{V}{n}_{\eta }+\overline{W}{n}_{\zeta }\right)\left({\overline{\xi }}_y{n}_{\xi }+{\overline{\eta }}_y{n}_{\eta }+{\overline{\zeta }}_y{n}_{\zeta }\right)\\ {\left({\overrightarrow{v}}_n\right)}_z=\left(\overline{U}{n}_{\xi }+\overline{V}{n}_{\eta }+\overline{W}{n}_{\zeta }\right)\left({\overline{\xi }}_z{n}_{\xi }+{\overline{\eta }}_z{n}_{\eta }+{\overline{\zeta }}_z{n}_{\zeta }\right)\end{array},(54)$

where

$\begin{array}{c}\overline{U}={\overline{\xi }}_x{u}_l+{\overline{\xi }}_y{v}_l+{\overline{\xi }}_z{w}_l\\ \overline{V}={\overline{\eta }}_x{u}_l+{\overline{\eta }}_y{v}_l+{\overline{\eta }}_z{w}_l\\ \overline{W}={\overline{\zeta }}_x{u}_l+{\overline{\zeta }}_y{v}_l+{\overline{\zeta }}_z{w}_l\end{array}.(55)$

From Eq. 49 we obtain the ghost state vector as

$\begin{array}{c}{\rho }_{bc}={\rho }_l\\ u_{bc}=u_l-2\left(\overline{U}{n}_{\xi }+\overline{V}{n}_{\eta }+\overline{W}{n}_{\zeta }\right)\left({\overline{\xi }}_x{n}_{\xi }+{\overline{\eta }}_x{n}_{\eta }+{\overline{\zeta }}_x{n}_{\zeta }\right)\\ v_{bc}=v_l-2\left(\overline{U}{n}_{\xi }+\overline{V}{n}_{\eta }+\overline{W}{n}_{\zeta }\right)\left({\overline{\xi }}_y{n}_{\xi }+{\overline{\eta }}_y{n}_{\eta }+{\overline{\zeta }}_y{n}_{\zeta }\right)\\ w_{bc}=w_l-2\left(\overline{U}{n}_{\xi }+\overline{V}{n}_{\eta }+\overline{W}{n}_{\zeta }\right)\left({\overline{\xi }}_z{n}_{\xi }+{\overline{\eta }}_z{n}_{\eta }+{\overline{\zeta }}_z{n}_{\zeta }\right)\\ p_{bc}=p_l\end{array}.(56)$

Since ${\left[J\right]}^{-1}$ has a different value at each integration point, the ghost state vector at each quadrature point of the boundary face of an element $\stackrel{\sim }{H}$ belongs to $\partial {\Omega }^W$ is different.

5 Numerical examples

In order to demonstrate the performance of the proposed flow solver, we present several examples. All simulations were carried out on a Windows 10 64-bit Intel Core E5-2697 2.3-GHz and 256-GB RAM small workstation. For transonic flow and supersonic flow, the HWENO limiter in reference [50] is applied to the proposed flow solver. All computations were performed until solution coefficients reached a steady state, defined as the residual in reference [27].

5.1 Subsonic flow

We consider a subsonic flow at March number $M_{\infty }=0.38$ on four meshes having 10,670, 13,944, 271,327, 901,175 elements (the average spherical surface mesh sizes are 0.4, 0.2, 0.1, 0.05, defined as the ratio to the radius of the sphere). In order to check the accuracy and the convergence properties of the flow solver we have performed various computations using different combinations of interpolation functions for the unknowns and for the geometric mapping. Different elements are denoted by $P_k{Q}_m$, where $k$ indicates the order of the complete polynomials used to approximate the unknowns and $m$ indicates the order of the complete polynomials used for the geometric mapping [26].

First, we solve the problem on the sequence of meshes with $P_1{Q}_1$ element and plot Mach distribution in Figure 4A. These solutions are very inaccurate, as put in evidence by the nonphysical boundary which develops along the solid wall and by the associated wake in the downstream region of the sphere. Notice that the solution obtained on the finest mesh is asymmetric and has a visible wake.

FIGURE 4

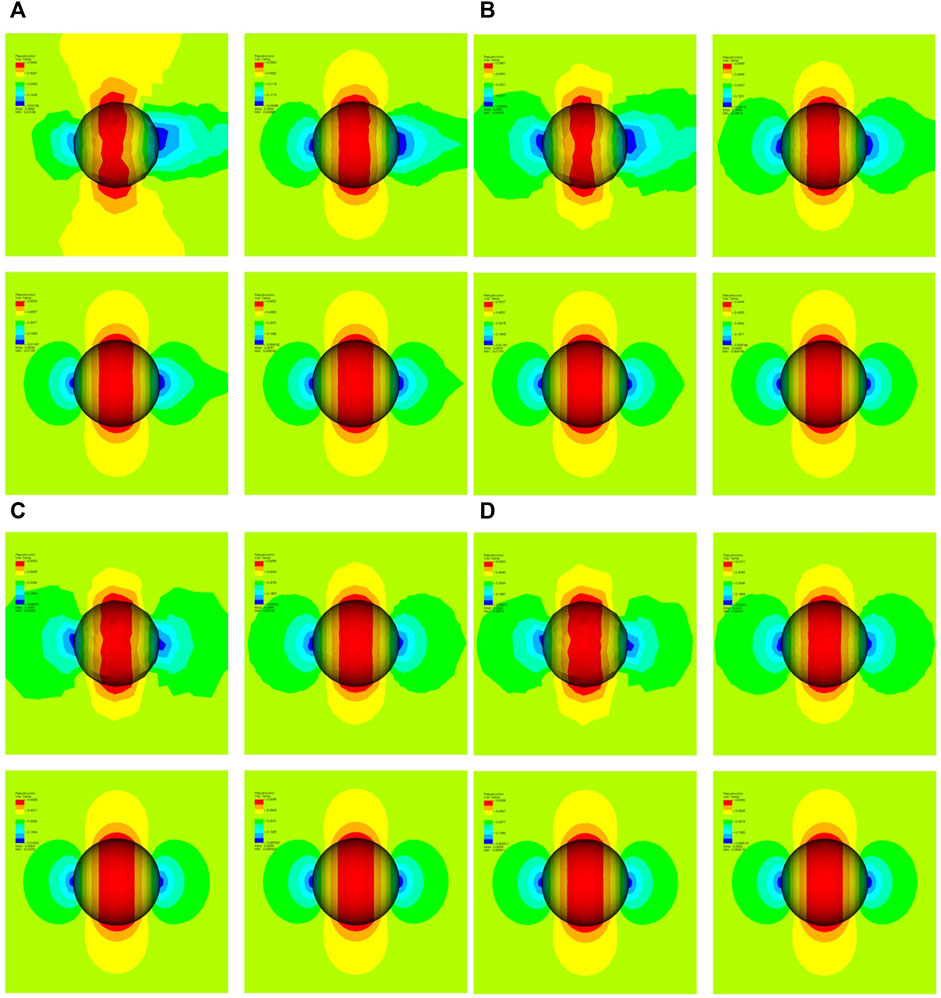
FIGURE 4. (A) Mach distribution with $P_1{Q}_1$ element on 0.4, 0.2, 0.1 and 0.05 mesh size form left to right and from top to bottom. (B) Mach distribution with $P_1{Q}_2$ element on 0.4, 0.2, 0.1 and 0.05 mesh size form left to right and from top to bottom. (C) Mach distribution with $P_2{Q}_2$ element on 0.4, 0.2, 0.1 and 0.05 mesh size form left to right and from top to bottom. (D) Mach distribution with $P_3{Q}_2$ element on 0.4, 0.2, 0.1 and 0.05 mesh size form left to right and from top to bottom.

The picture changes completely when using $P_1{Q}_2$, $P_2{Q}_2$ and $P_3{Q}_2$ elements, as reported in Figures 4B–D, which shows the Mach distribution computed on the four successively refined meshes. The quality of the solution clearly improves as $P$ and $Q$ increases, which is asymmetric in the upstream-downstream direction. The solution corresponding to $P_3{Q}_2$ element on the coarsest mesh is similar to one obtained on the finest mesh with $P_1{Q}_1$.

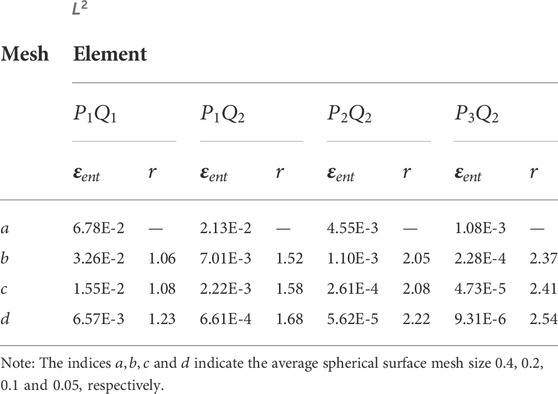
To quantify our findings, we measure $L^2$ errors in entropy ${\epsilon }_{ent}$ defined as

${\epsilon }_{ent}={\frac{P}{P_{\infty }}/\left(\frac{\rho }{{\rho }_{\infty }}\right)}^{\gamma }-1,(57)$

where $P_{\infty }$ and ${\rho }_{\infty }$ are pressure and density of the free stream, respectively. Table 3 reports the entropy error and the order of accuracy for the $P_1{Q}_1$, $P_1{Q}_2$, $P_2{Q}_2$ and $P_3{Q}_2$ computations. The convergence rate $r$ obtained by comparing the solutions of mesh $\alpha$ and of mesh $\beta$ is computed as

$r=\frac{\log \left({\left({\epsilon }_{ent}\right)}_{\alpha }/{\left({\epsilon }_{ent}\right)}_{\beta }\right)}{\log \left(h_{\alpha }/h_{\beta }\right)},(58)$

where $h$ is the mesh size. These computations allow us to appreciate the potentialities offered by second-order accurate elements in the numerical solutions of the three-dimensional Euler equations on unstructured mesh.

TABLE 3

TABLE 3. $L^2$ errors in entropy and convergence rates for the sphere.

Further, we present two aerodynamic quantities: the pressure coefficient $C_p$

$C_p=\frac{P-P_{\infty }}{0.5{\rho }_{\infty }{\Vert {\overrightarrow{v}}_{\infty }\Vert }^2},(59)$

and the total pressure loss coefficient defined as a ratio of the total pressure $P_t$

$P_t=P{\left(1+\frac{\gamma -1}{2}{M}^2\right)}^{\gamma /\left(\gamma -1\right)}(60)$

at a point to the pressure of the free stream. The accuracy of the method is also evidenced by two aerodynamic quantities. The distribution of the pressure coefficient around the surface for four different meshes are shown in Figures 5A–D. The distribution of the total pressure loss coefficient around the surface for various meshes are shown in Figures 5E–H. We specify that mesh one to four refer to the coarse mesh to the fine mesh.

FIGURE 5

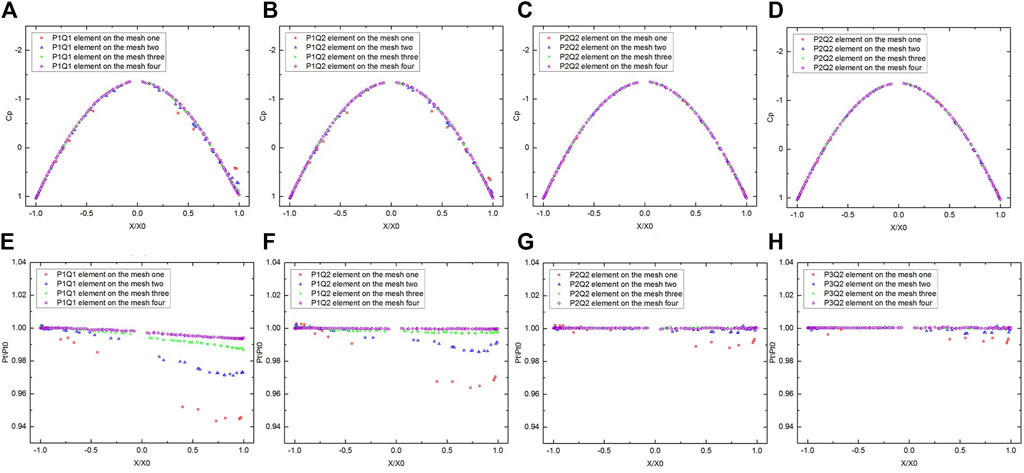
FIGURE 5. (A) Pressure coefficient distribution around a circle of sphere surface with $P_1{Q}_1$ element. (B) Pressure coefficient distribution around a circle of sphere surface with $P_1{Q}_2$ element. (C) Pressure coefficient distribution around a circle of sphere surface with $P_2{Q}_2$ element. (D) Pressure coefficient distribution around a circle of sphere surface with $P_3{Q}_2$ element. (E) Total pressure loss coefficient distribution around a circle of sphere surface with $P_1{Q}_1$ element. (F) Total pressure loss coefficient distribution around a circle of sphere surface with $P_1{Q}_2$ element. (G) Total pressure loss coefficient distribution around a circle of sphere surface with $P_2{Q}_2$ element. (H) Total pressure loss coefficient distribution around a circle of sphere surface with $P_3{Q}_2$ element.

5.2 Transonic flow past ONERA M6 wing

A transonic flow over the ONERA M6 wing at a Mach number of $M_{\infty }=0.8395$ and an attack angle of $\alpha =3.06°$ is considered in this example [51, 52]. This test case is chosen to demonstrate that the proposed flow solver with curvilinear DG method is able to enhance the accuracy of the underlying (rectilinear) methods for solving transonic flow problems and engineering problems. The mesh used in this computation consists of 682,726 elements, 122,679 points. As with the first example, $P_1{Q}_1$ indicates that the order of polynomials used to approximate the unknowns is one, and the order of the complete polynomials used for the geometric mapping is one too. The definition of $P_2{Q}_2$ is similar. In other words, $P_1{Q}_1$ is rectilinear element, and $P_2{Q}_2$ is curved element. The computed pressure distribution obtained by the DG solution on the wing surface are shown in Figure 6. In Figure 7 compares the pressure coefficient distributions at six span-wise locations (Figures 7A–F) on the wing surface between the numerical results and the experimental data. Under the same number of meshes, the pressure coefficient calculated by the curvilinear DG method is closer to the experimental value than the rectilinear DG method.

FIGURE 6

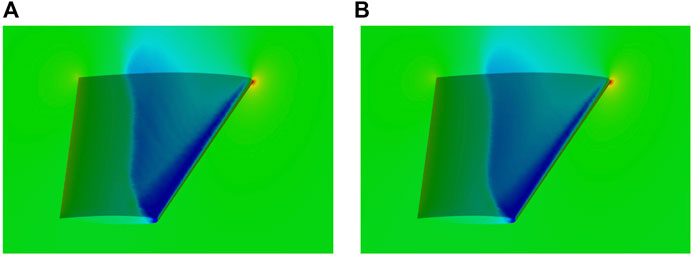
FIGURE 6. (A) The computed pressure distribution on the surface of ONERA M6 with $P_1{Q}_1$ element. (B) The computed pressure distribution on the surface of ONERA M6 with $P_2{Q}_2$ element.

FIGURE 7

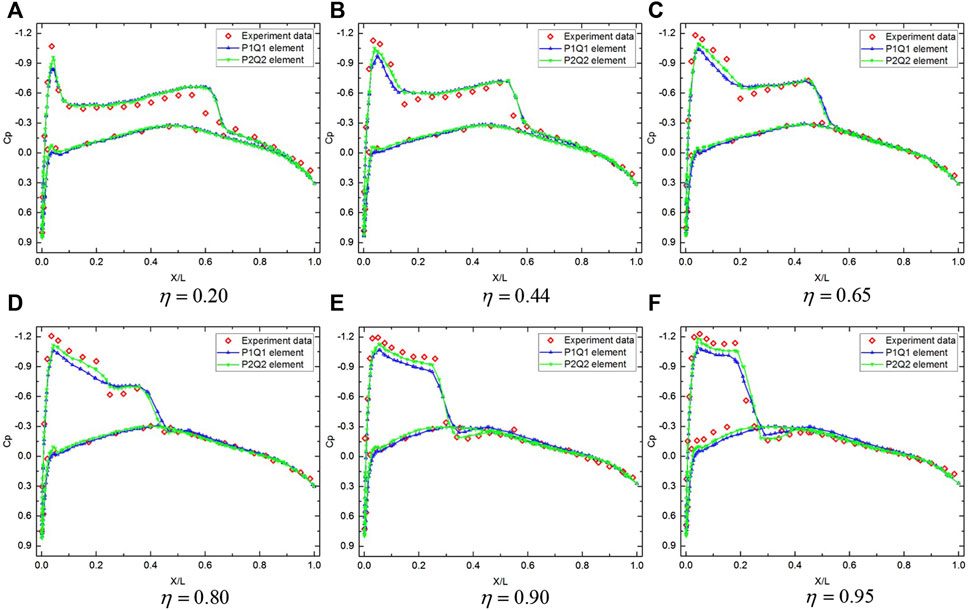
FIGURE 7. Comparison of the pressure coefficient distributions with experimental data for ONERA M6 wing at six span-wise locations. (A) $\eta =0.20$. (B) $\eta =0.44$. (C) $\eta =0.65$. (D) $\eta =0.80$. (E) $\eta =0.90$. (F) $\eta =0.95$.

5.3 Hypersonic flow past blunt cone

This test case is selected to demonstrate that the proposed flow solver is able to solve hypersonic flow problems. The computation are performed for a high Mach number flow past the blunt cone model [53] using curvilinear and rectilinear DG method. The free stream Mach number, attack, pressure and temperature [53] for the blunt cone model correspond to $Ma=7.99$, $\alpha =0°$, $p=413Pa$ and $T=110.33K$.

A three-dimensional axi-symmetric simulation is considered with the left and right boundaries defined as supersonic inflow and outflow boundaries respectively. The wall is modeled as a slip surface. The mesh used in this computation consists of 2,039,128 elements, 357,006 points. As with the previous definition, $P_1{Q}_1$ is rectilinear element, and $P_2{Q}_2$ is curved element. The computed density and pressure distribution near the blunted cone for the blunt cone model with $Ma=7.99$ is shown in Figure 8. The strong bow shock upstream of the body that is characteristic for this type of flow is well captured from our computations. The predicted wall pressure distribution non-dimensionalized with respect to the computed free stream pressure $P_{\infty }$ is compared with experimental data and shown in Figure 9. The computed pressure profile is slightly below predicted for a small region behind blunt cone, but in general the predicted pressure distribution is in good agreement with the experimental results. In Figure 9, we found that the results obtained by the curvilinear DG method are smoother, although the trends of wall pressure of curvilinear and rectilinear DG method are consistent.

FIGURE 8

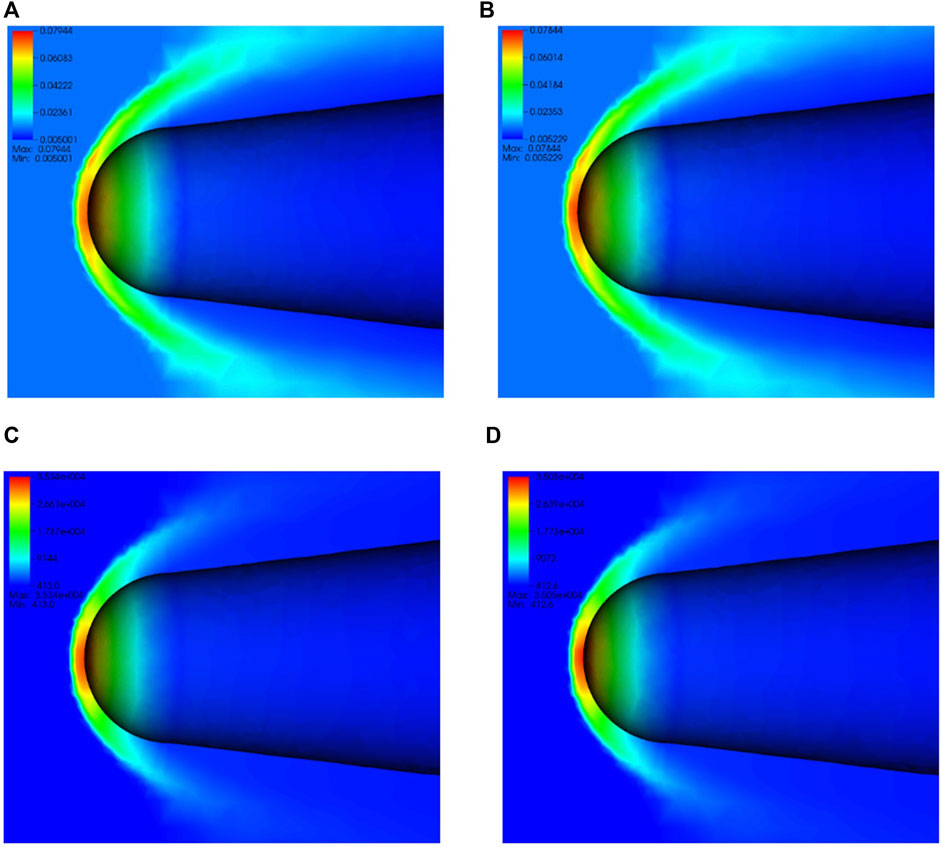
FIGURE 8. Computed flow distribution of (A) density with $P_1{Q}_1$ element, (B) density with $P_2{Q}_2$ element, (C) pressure with $P_1{Q}_1$ element and (D) pressure with $P_2{Q}_2$ element for the blunt cone model.

FIGURE 9

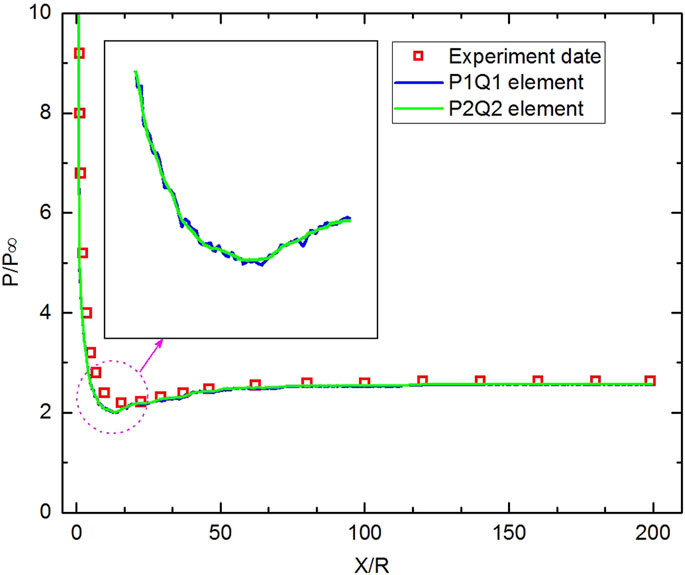
FIGURE 9. Comparison of the normalized pressure coefficient distributions with experimental data on the surface of blunt cone model.

5.4 Hypersonic flow past HB-2 ballistic model

Hypersonic flow past a HB-2 ballistic model is studied in this subsection. We carry out simulations at the flow conditions for which experimental setup details are available in the literature [54]. The free stream Mach number, attack, pressure and temperature [55, 56] for the HB-2 ballistic mode are $Ma=7.5$, $\alpha =0°$, $p=362.942Pa$ and $T=138.9K$.

A three-dimensional axi-symmetric simulation is considered with the left and right boundaries defined as supersonic inflow and outflow boundaries respectively. The wall is modeled as a slip surface. The mesh used in this computation consists of 1,489,139 elements, 259,493 points. As with the previous definition, $P_1{Q}_1$ is rectilinear element, and $P_2{Q}_2$ is curved element. The computed density on the full computational domain as well as the pressure distribution near the blunted cone for the HB-2 ballistic mode with $Ma=7.5$ is shown in Figure 10. The strong bow shock upstream of the body as well as a weaker shock over the cylinder–cone juncture that is characteristic for this type of flow is well captured from our computations. The predicted wall pressure distribution non-dimensionalized with respect to the computed stagnation point pressure $P_0$ is compared with experimental data and shown in Figure 11. The computed pressure profile is slightly below predicted for a small region over the cylinder, but in general the predicted pressure distribution is in good agreement with the experimental results.

FIGURE 10

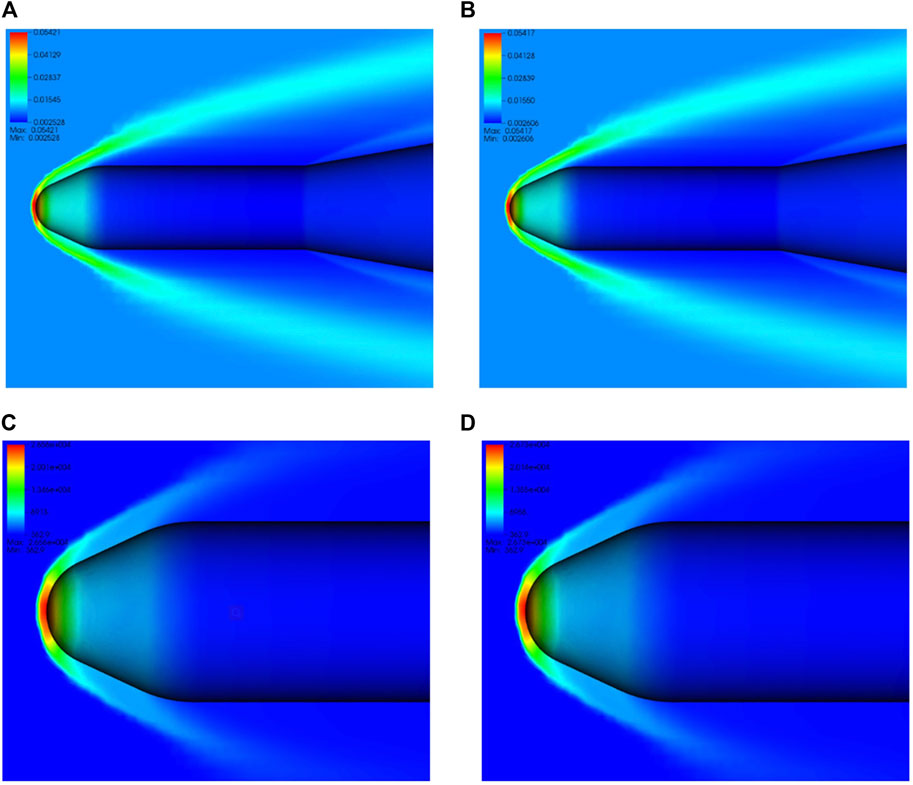
FIGURE 10. Computed flow distribution of (A) density with $P_1{Q}_1$ element, (B) density with $P_2{Q}_2$ element, (C) pressure with $P_1{Q}_1$ element and (D) pressure with $P_2{Q}_2$ element for the HB-2 ballistic model.

FIGURE 11

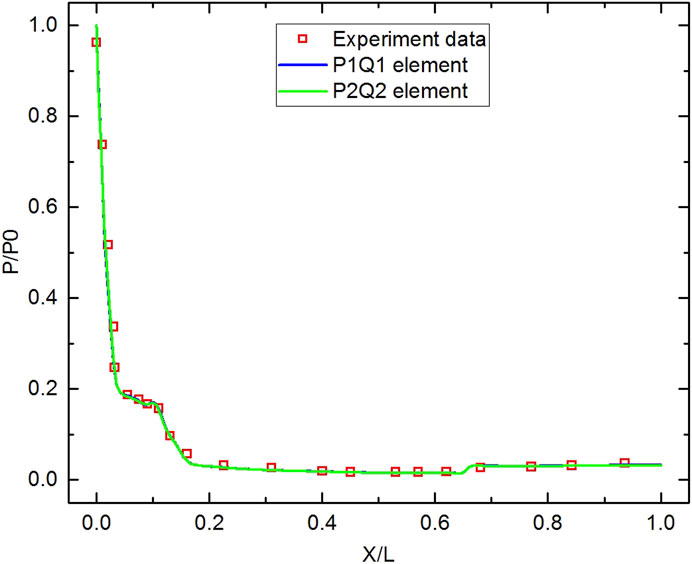
FIGURE 11. Comparison of the normalized pressure coefficient distributions with experimental data on the surface of HB-2 ballistic model.

6 Conclusion

A flow solver based on curvilinear DG method has been presented for solving the three-dimensional subsonic, transonic and hypersonic inviscid flows on curved meshes. The method aims to present the relevant closed form expressions for a widely used set of hierarchical basis functions up to full high order for a reference element, as well as the necessary expressions for the Jacobian for a high order polynomial geometrical transformation. Given these results, the implementation of solid walls boundary conditions is very simple because it is based on the contravariant velocities and does not require a complex geometric boundary information. Based on covariant vectors, an improved algorithm of HLLC flux for solving the subsonic, transonic and hypersonic flows is suggested. A number of numerical experiments for a variety of flow conditions have been conducted to demonstrate the superior performance of this flow solver (curvilinear) over the underlying method (rectilinear). The solution of subsonic flow past a sphere indicates that such a flow solver is stable on a reasonably coarse mesh and finer ones, and can get accurate results at reasonably coarse tetrahedral mesh. The solution of transonic flow past an ONERA M6 wing, hypersonic flow past a blunt cone and hypersonic flow past a HB-2 ballistic model verify that our flow solver has engineering practice value. The simulation of subsonic, transonic and hypersonic flows show that the flow solver has great robustness for three-dimensional fluids with various geometries and velocities. In future work, the developed method will be applied to more complicated geometries, and extended to viscosity flows with curve boundary layer.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author contributions

SH: methodology and theoretical derivation, preprocess part and DGM coding, data curation and formal analysis, original draft writing and revising. JY: conceptualization, theoretical derivation, flux part coding, article review and editing, funding acquisition, project administration. LX: theoretical guidance, supervision and funding acquisition. BL: theoretical guidance, supervision. All authors discussed the results and contributed to manuscript revision. And all authors have read and agreed to the published version of the manuscript.

Funding

The author would like to acknowledge the financial support provided by the National Natural Science Foundation of China under Grant 12102087, 62071102, and 61921002.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Oktay E, Alemdaroğlu N, Tarhan E, Champigny P, Espiney P. Unstructured euler solutions for missile aerodynamics. Aerosp Sci Technol (2000) 4(7):453–61. doi:10.1016/s1270-9638(00)01072-5

CrossRef Full Text | Google Scholar

2. Pan J, Liu F. Wing flutter prediction by a small-disturbance euler method on body-fitted curvilinear grids. AIAA J (2019) 57(11):4873–84. doi:10.2514/1.j058120

CrossRef Full Text | Google Scholar

3. Beghami W, Maayah B, Bushnaq S, Arqub OA. The laplace optimized decomposition method for solving systems of partial differential equations of fractional order. Int J Appl Comput Math (2022) 8(2):52–18. doi:10.1007/s40819-022-01256-x

CrossRef Full Text | Google Scholar

4. Arqub OA, Hayat T, Alhodaly M. Analysis of lie symmetry, explicit series solutions, and conservation laws for the nonlinear time-fractional phi-four equation in two-dimensional space. Int J Appl Comput Math (2022) 8:145. doi:10.1007/s40819-022-01334-0

CrossRef Full Text | Google Scholar

5. Srivastava HM, Iqbal J, Arif M, Khan A, Gasimov YS, Chinram R. A new application of gauss quadrature method for solving systems of nonlinear equations. Symmetry (2021) 13(3):432. doi:10.3390/sym13030432

CrossRef Full Text | Google Scholar

6. Pourghanbar S, Manafian J, Ranjbar M, Aliyeva A, Gasimov YS. An efficient alternating direction explicit method for solving a nonlinear partial differential equation. Math Probl Eng (2020) 2020:1–12. doi:10.1155/2020/9647416

CrossRef Full Text | Google Scholar

7. Arqub OA. Numerical simulation of time-fractional partial differential equations arising in fluid flows via reproducing kernel method. Int J Numer Methods Heat Fluid Flow (2019) 30:4711–33. doi:10.1108/hff-10-2017-0394

CrossRef Full Text | Google Scholar

8. Arqub OA. Reproducing kernel algorithm for the analytical-numerical solutions of nonlinear systems of singular periodic boundary value problems. Math Probl Eng (2015) 2015:518406–13. doi:10.1155/2015/518406

CrossRef Full Text | Google Scholar

9. Mascarenhas BS, Helenbrook BT, Atkins HL. Application of P-multigrid to discontinuous Galerkin formulations of the euler equations. AIAA J (2009) 47(5):1200–8. doi:10.2514/1.39765

CrossRef Full Text | Google Scholar

10. Abbas A, Vicente JD, Valero E. Aerodynamic technologies to improve aircraft performance. Aerosp Sci Technol (2013) 28(1):100–32. doi:10.1016/j.ast.2012.10.008

CrossRef Full Text | Google Scholar

11. Kouhi M, Onate E, Mavriplis D. Adjoint-based adaptive finite element method for the compressible euler equations using finite calculus. Aerosp Sci Technol (2015) 46:422–35. doi:10.1016/j.ast.2015.08.008

CrossRef Full Text | Google Scholar

12. Ponsin J, Fraysse F, Gomez M, Cordero-Gracia M. An adjoint-truncation error based approach for goal-oriented mesh adaptation. Aerosp Sci Technol (2015) 41:229–40. doi:10.1016/j.ast.2014.10.021

CrossRef Full Text | Google Scholar

13. Deng X, Xie B, Xiao F. Multimoment finite volume solver for euler equations on unstructured grids. AIAA J (2017) 55(8):2617–29. doi:10.2514/1.j055581

CrossRef Full Text | Google Scholar

14. Pagliuca G, Timme S. Model reduction for flight Dynamics simulations using computational fluid Dynamics. Aerosp Sci Technol (2017) 69:15–26. doi:10.1016/j.ast.2017.06.013

CrossRef Full Text | Google Scholar

15. Liu Y, Zhang W, Kou J. Mode multigrid-a novel convergence acceleration method. Aerosp Sci Technol (2019) 92:605–19. doi:10.1016/j.ast.2019.06.001

CrossRef Full Text | Google Scholar

16. Botti L, Pietro DAD. Assessment of hybrid high-order methods on curved meshes and Comparison with discontinuous Galerkin methods. J Comput Phys (2018) 370:58–84. doi:10.1016/j.jcp.2018.05.017

CrossRef Full Text | Google Scholar

17. Toulorge T, Desmet W. Curved boundary treatments for the discontinuous Galerkin method applied to aeroacoustic propagation. AIAA J (2010) 48(2):479–89. doi:10.2514/1.45353

CrossRef Full Text | Google Scholar

18. Bassi F, Botti L, Colombo A, Rebay S. Agglomeration based discontinuous Galerkin discretization of the euler and Navier-Stokes equations. Comput Fluids (2012) 61:77–85. doi:10.1016/j.compfluid.2011.11.002

CrossRef Full Text | Google Scholar

19. Zhang X, Tan S. A simple and accurate discontinuous Galerkin scheme for modeling scalar-wave propagation in media with curved interfaces. Geophysics (2015) 80(2):T83–T9. doi:10.1190/geo2014-0164.1

CrossRef Full Text | Google Scholar

20. Zhang X. A curved boundary treatment for discontinuous Galerkin schemes solving time dependent problems. J Comput Phys (2016) 308:153–70. doi:10.1016/j.jcp.2015.12.036

CrossRef Full Text | Google Scholar

21. Cockburn B, Karniadakis GE, Shu CW. Discontinuous Galerkin methods: Theory, computation and applications. New York: Springer Science & Business Media (2012).

Google Scholar

22. Hesthaven JS, Warburton T. Nodal discontinuous Galerkin methods: Algorithms, analysis, and applications. New York: Springer Science & Business Media (2007).

Google Scholar

23. Hartmann R, Held J, Leicht T, Prill F. Discontinuous Galerkin methods for computational aerodynamics-3d adaptive flow simulation with the dlr padge code. Aerosp Sci Technol (2010) 14(7):512–9. doi:10.1016/j.ast.2010.04.002

CrossRef Full Text | Google Scholar

24. Antonietti PF, Cangiani A, Collis J, Dong Z, Georgoulis EH, Giani S, et al. Review of discontinuous Galerkin finite element methods for partial differential equations on complicated domains. Cham: Springe (2016).

Google Scholar

25. Luo H, Xia Y, Spiegel S, Nourgaliev R, Jiang Z. A reconstructed discontinuous Galerkin method based on a hierarchical weno reconstruction for compressible flows on tetrahedral grids. J Comput Phys (2013) 236:477–92. doi:10.1016/j.jcp.2012.11.026

CrossRef Full Text | Google Scholar

26. Bassi F, Rebay S. High-order accurate discontinuous finite element solution of the 2d euler equations. J Comput Phys (1997) 138(2):251–85. doi:10.1006/jcph.1997.5454

CrossRef Full Text | Google Scholar

27. Krivodonova L, Berger M. High-order accurate implementation of solid wall boundary conditions in curved geometries. J Comput Phys (2006) 211(2):492–512. doi:10.1016/j.jcp.2005.05.029

CrossRef Full Text | Google Scholar

28. Warburton T. A low-storage curvilinear discontinuous Galerkin method for wave problems. SIAM J Sci Comput (2013) 35(4):A1987–A2012. doi:10.1137/120899662

CrossRef Full Text | Google Scholar

29. Chan J, Hewett RJ, Warburton T. Weight-adjusted discontinuous Galerkin methods: Curvilinear meshes. SIAM J Sci Comput (2017) 39(6):A2395–A421. doi:10.1137/16m1089198

CrossRef Full Text | Google Scholar

30. Chan J, Wilcox LC. On discretely entropy stable weight-adjusted discontinuous Galerkin methods: Curvilinear meshes. J Comput Phys (2019) 378:366–93. doi:10.1016/j.jcp.2018.11.010

CrossRef Full Text | Google Scholar

31. Michoski C, Chan J, Engvall L, Evans JA. Foundations of the blended isogeometric discontinuous Galerkin (bidg) method. Comput Methods Appl Mech Eng (2016) 305:658–81. doi:10.1016/j.cma.2016.02.015

CrossRef Full Text | Google Scholar

32. Wang ZJ, Sun Y. Curvature-based wall boundary condition for the euler equations on unstructured grids. AIAA J (2003) 41(1):27–33. doi:10.2514/2.1931

CrossRef Full Text | Google Scholar

33. Batten P, Clarke N, Lambert C, Causon DM. On the choice of wavespeeds for the hllc Riemann solver. SIAM J Sci Comput (1997) 18(6):1553–70. doi:10.1137/s1064827593260140

CrossRef Full Text | Google Scholar

34. Simon S, Mandal JC. A cure for numerical shock instability in hllc Riemann solver using antidiffusion control. Comput Fluids (2018) 174:144–66. doi:10.1016/j.compfluid.2018.07.001

CrossRef Full Text | Google Scholar

35. Simon S, Mandal JC. A simple cure for numerical shock instability in the hllc Riemann solver. J Comput Phys (2019) 378:477–96. doi:10.1016/j.jcp.2018.11.022

CrossRef Full Text | Google Scholar

36. Kirk BS, Peterson JW, Stogner RH, Carey GF. Libmesh : A C++ library for parallel adaptive mesh refinement/coarsening simulations. Eng Comput (2006) 22(3-4):237–54. doi:10.1007/s00366-006-0049-3

CrossRef Full Text | Google Scholar

37. Bangerth W. Deal.Ii (2021). Available from https://www.dealii.org/ (Accessed August 16, 2022).

Google Scholar

38. Bangerth W. Deal.Ii the step-67 tutorial program (2021). Available from https://www.dealii.org/current/doxygen/deal.II/step_67.html (Accessed August 17, 2022).

Google Scholar

39. Qiu J, Khoo B, Shu CW. A numerical study for the performance of the Runge-Kutta discontinuous Galerkin method based on different numerical fluxes. J Comput Phys (2006) 212(2):540–565. doi:10.1016/j.jcp.2005.07.011

CrossRef Full Text | Google Scholar

40. Cockburn B, Shu CW. The Runge–Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. J Comput Phys (1998) 141(2):199–224. doi:10.1006/jcph.1998.5892

CrossRef Full Text | Google Scholar

41. Swartz JP, Davidson DB. Curvilinear vector finite elements using a set of hierarchical basis functions. IEEE Trans Antennas Propag (2007) 55(2):440–6. doi:10.1109/tap.2006.888448

CrossRef Full Text | Google Scholar

42. Fahs H. Improving accuracy of high-order discontinuous Galerkin method for time-domain electromagnetics on curvilinear domains. Int J Comput Math (2011) 88(10):2124–53. doi:10.1080/00207160.2010.527960

CrossRef Full Text | Google Scholar

43. Martini E, Pelosi G, Selleri S. A hybrid finite-element-modal-expansion method with a new type of curvilinear mapping for the analysis of microwave passive devices. IEEE Trans Microw Theor Tech (2003) 51(6):1712–7. doi:10.1109/tmtt.2003.812571

CrossRef Full Text | Google Scholar

44. Yin JH, Xu L, Wang H, Xie P, Huang SC, Liu HX, et al. Accurate and fast three-dimensional free vibration analysis of large complex structures using the finite element method. Comput Struct (2019) 221:142–56. doi:10.1016/j.compstruc.2019.06.002

CrossRef Full Text | Google Scholar

45. Zhang L, Cui T, Liu H. A set of symmetric quadrature rules on triangles and tetrahedra. J Comput Math (2009) 27(1):89–96.

Google Scholar

46. Harten A, Lax PD, Leer BV. On upstream differencing and godunov-type schemes for hyperbolic conservation laws. SIAM Rev (1983) 25(1):35–61. doi:10.1137/1025002

CrossRef Full Text | Google Scholar

47. Toro EF, Spruce M, Speares W. Restoration of the contact surface in the hll-riemann solver. Shock Waves (1994) 4(1):25–34. doi:10.1007/bf01414629

CrossRef Full Text | Google Scholar

48. Roe PL. Approximate Riemann solvers, parameter vectors, and difference schemes. J Comput Phys (1981) 43(2):357–72. doi:10.1016/0021-9991(81)90128-5

CrossRef Full Text | Google Scholar

49. Simmetrix I. Simmetrix’ modeling suite (2013). Available from http://www.simmetrix.com (Accessed August 6, 2021).

Google Scholar

50. Luo H, Baum JD, Löhner R. A hermite weno-based limiter for discontinuous Galerkin method on unstructured grids. J Comput Phys (2007) 225(1):686–713. doi:10.1016/j.jcp.2006.12.017

CrossRef Full Text | Google Scholar

51. Schmitt V, Charpin F. Pressure distributions on the Onera-M6-Wing at transonic mach numbers. Exp Data base Comput Program Assess. Report of the Fluid Dynamics Panel Working Group 04, AGARD AR 138 (1979). Available from http://www.ttctech.com/samples/onera_m6_wing_multiblock/onera_mb.htm.

Google Scholar

52. Batina JT. Accuracy of an unstructured-grid upwind-euler algorithm for the onera M6 wing. J Aircr (1991) 28(6):397–402. doi:10.2514/3.46040

CrossRef Full Text | Google Scholar

53. Zhong X, Ma Y. Boundary-layer receptivity of Mach 7.99 flow over a blunt cone to free-stream acoustic waves. J Fluid Mech (2006) 556:55–103. doi:10.1017/s0022112006009293

CrossRef Full Text | Google Scholar

54. Damljanović D, Rašuo B, Đ V, Mandić S, Isaković J. Hypervelocity ballistic reference models as experimental supersonic test cases. Aerosp Sci Technol (2016) 52:189–97. doi:10.1016/j.ast.2016.02.035

CrossRef Full Text | Google Scholar

55. Tissera S. Assessment of high-resolution methods in hypersonic real-gas flows. Cranfield: Cranfield University (2010).

Google Scholar

56. John B, Emerson DR, Gu XJ. Parallel Navier-Stokes simulations for high speed compressible flow past arbitrary geometries using flash. Comput Fluids (2015) 110:27–35. doi:10.1016/j.compfluid.2014.12.008

CrossRef Full Text | Google Scholar