A Robust Checkerboard Corner Detection Method for Camera Calibration Based on Improved YOLOX

Camera calibration plays an important role in various optical measurement and computer vision applications. Accurate calibration parameters of a camera can give a better performance. The key step to camera calibration is to robustly detect feature points (typically in the form of checkerboard corners) in the images captured by the camera. This paper proposes a robust checkerboard corner detection method for camera calibration based on improved YOLOX deep learning network and Harris algorithm. To get high checkerboard corner detection robustness against the images with poor quality (i.e., degradation, including focal blur, heavy noise, extreme poses, and large lens distortions), we first detect the corner candidate areas through the improved YOLOX network which attention mechanism is added. Then, the Harris algorithm is performed on these areas to detect sub-pixel corner points. The proposed method is not only more accurate than the existing methods, but also robust against the types of degradation. The experimental results on different datasets demonstrate its superior robustness, accuracy, and wide effectiveness.

1 Introduction

Camera calibration plays an important role in various optical measurement and computer vision applications. Accurate calibration parameters of cameras can perform better in scene reconstruction, stereo matching, and other aspects in the field of computer vision and optical measurement. The most important process in camera calibration is to find out the mapping relationship between the two-dimensional coordinates in the images captured by the camera and the three-dimensional coordinates in the real world. The relationship can be represented by feature points, such as checkerboard corners, circular array, and so on.

As a conventional feature extraction template, checkerboard corners detection is widely applied in most research. Accurate mathematical definition in corner points has not yet been proposed currently. Conventionally, the following points are usually called corner points: the junction point of two straight line edges [1], the point with sharp brightness changes in all directions of images, and the extreme point of maximum curvature of the edge curve in images [2]. Research in corner detection is mainly divided into three methods according to the definition of corners: intensity-based, contour-based, and binary-based methods [3]. Within these methods, the binary-based method is not popular in actual engineering applications.

For intensity-based methods in corner detection, the Moravec corner detection algorithm can find out the correlation between the patch combined with the neighborhood around a pixel and other surrounding patches by detecting each pixel of images [4]. This correlation was calculated by the sum of squared differences between the two patches, the smaller the value, the higher the similarity. Although the Moravec algorithm can recognize corners quickly, it is too sensitive for image edges and noise. In addition, it has limitations in direction. Activated by Moravec, Harris and Stephens [5] proposed the Harris algorithm which improved the Moravec corner detection algorithm. They calculated the autocorrelation function for each pixel in the image and defined the response function. Compared with the Moravec corner detection algorithm, the Harris algorithm possesses the rotation invariance but its threshold must be set manually. Smith and Brady [6] proposed a new method named SUSAN (Same Univalue Segment Assimilating Nucleus), which detected corners by a circular template belonging to surrounding pixels. Although the algorithm has fast speed, high location accuracy, high repeatability, and translation and rotation invariance, many detected features are located at the edges instead of real corners. In addition, it is sensitive for noise so that it performs poorly while detecting blurred images. Rosten and Drummond [7] proposed a faster corner detection algorithm which utilized machine learning to accelerate the process of corner detection.

Compared with intensity-based detection methods, contour-based detectors detect the edge contour before the corner detection, which detect corners in the contours instead of in total images, so it possesses extremely low detection error. Rachmawati et al. [8] proposed a polygon approximation technology combined with high-speed corner detection methods with the Freeman chain code. Mokhtarian and Suomela [9] proposed the corner detection method named Curvature Scale-Space (CSS). Zhong and Liao [10] proposed Direct Curvature Scale Space (DCSS). Hossain and Tushar [11] proposed Chord-to-Point Distance Accumulation (CPDA) and improved it with Chord Angle Deviation using Tangent (CADT). However, the localization of corners using the above methods may be poor if the detection is achieved on a large scale. Besides, these methods usually require complex and expensive mathematical operations.

In recent years, with great advances in deep learning for computer vision tasks, many attempts explored the possibility to use neural networks for camera calibration. The FAST (Features from Accelerated Segment Test) algorithm in the image corner detector is based on machine learning [7], and FAST-ER (FAST-Enhanced Repeatability) is its development [12, 13]. Song et al. [14] proposed a fully convolutional network (FCN)-based approach to detect building corners in aerial images. Raza et al. [15] presented a technique that uses trained convolutional neural network (CNN) to extract corners. Chen et al. [16] proposed a model based on FCN to detect corners to get a corner score on each pixel. Moreover, maximum response, non-maximum suppression (NMS), and clustering techniques are used to obtain the final pixel level corners.

In the field of object detection, deep learning performs best. There are various classical detection network structures such as R-CNN (Regions with CNN features) [17], Fast R-CNN [18], Faster R-CNN [19], SSD (Single Shot MultiBox Detector) [20], and YOLO (You Only Look Once) [21]. YOLO, as a one-stage algorithm, models object detection as a regression problem and directly predicts multiple bounding boxes from the input image. Aiming at the problem of YOLOv1 which only supports input of the same resolution image as the training image, YOLOv2 [22] improved the network in the network structure and the location prediction method, which can make the model adapt to multi-scale input. YOLOv3 [23] simply implemented independent logistic classifiers to achieve multilabel classification. However, it is not good at detecting small objects. Most recently, Bochkovskiy et al. heavily improved YOLOv3 and as a result they built YOLOv4 [24], which gives an efficient and powerful object detection model that can perfectly detect small objects. Ge et al. [25] presented some experienced improvements to the YOLO series and proposed a new high-performance detector - YOLOX. Zhang et al. [26] adopted YOLOX to obtain the detection boxes and associate them with the proposed method called BYTE. Sun et al. [27] used the YOLOX detector to perform object detection on the DanceTrack0027 video and to conduct different object association algorithms following that. Compared to the existing networks, YOLOX has been proven to be powerful for object detection.

Since all the traditional methods not only are affected by complex background, but also their threshold needs to be set manually, the above methods are difficult to detect corners on the large lens distortions checkerboard acquired from a fisheye lens or omnidirectional lens. Besides, some methods based on CNN can obtain great performance but only get pixel level corner points. In this paper, we propose a robust checkerboard corner detection method for camera calibration based on improved YOLOX deep learning network and the Harris algorithm. The improved YOLOX network is trained on a huge number of checkerboard images acquired from multiple scenarios. The corner candidate areas are first extracted by improved YOLOX and are then imported into the Harris algorithm to obtain the final sub-pixel corner points.

Our proposed method has the main advantages as follows:

(1)Recognize all checkerboard corners in such a particularly large angle between the camera’s optical axis and the checkerboard plane;

(2)Recognize corners in the cases of focal blur and heavy noise when the camera is overexposed;

(3)Detect the corners in the case of severe lens distortions.

2 Materials and Methods

2.1 Dataset and Environment Setup

Our original dataset is captured by a mobile phone (iPhone XR) and an industrial camera. The dataset consists of 141 images. Since deep learning requires sufficient data to complete the training process, the corner detection model should be robust to the types of degradation including focal blur, heavy noise, extreme poses, and large lens distortions. Therefore, the original dataset is mainly enhanced by the following four approaches: 1) rotating images (the angles include $90°$, $180°$, and $270°$); 2) blurring images; 3) noising images; and 4) images with inverted gray value. One or more of these approaches is applied to each image. Finally, 2810 images are obtained for models training. The examples of our dataset are shown in Figure 1.

FIGURE 1

FIGURE 1. The examples of our dataset. (A) Original image, (B) rotating image, (C) blurring image, (D) noising image, and (E) inverted image.

In addition to the dataset we created, the images for testing the generalization performance of the proposed method are from another three datasets: the uEye and GoPro datasets from ROCHADE [28], and the fisheye dataset [29]. The uEye dataset captured by IDS UI-1241LE camera has a slight distortion; the GoPro dataset is used to illustrate the robustness against large lens distortions. The fisheye dataset is captured by using a fisheye camera with $220°$ FOV that exhibits heavy lens distortions. Image examples of the three datasets used in our experiments are shown in Figure 2.

FIGURE 2

FIGURE 2. The examples of three other datasets. (A) uEye dataset [28], (B) GoPro dataset [28], and (C) fisheye dataset [29].

The training of the model is done using Python 3.6 with Pytorch 1.2.0 library on a Personal Computer (PC). The entire experiments are run on an Intel Core i5-9600KF CPU (3.70 GHz) and an NVIDIA RTX 2080Ti GPU with 11 G RAM.

2.2 Proposed Method

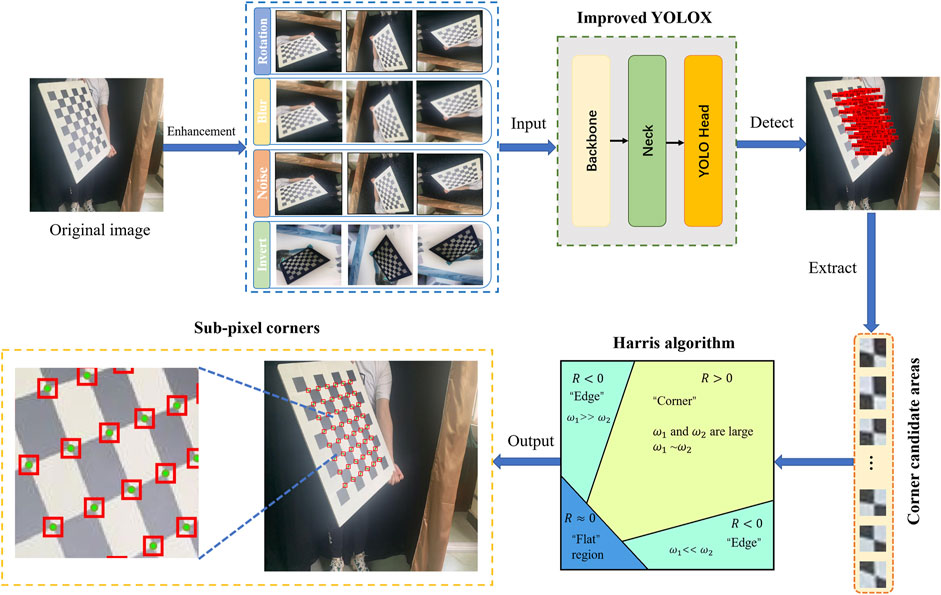
The traditional corner detection methods are difficult to avoid the influence of the image background. Once the background is complicated, the traditional methods may inevitably generate pseudo corner points that possibly lead to further complexity. Furthermore, it is difficult to detect sub-pixel corners on the large lens distortions checkerboard acquired from the fisheye lens or the omnidirectional lens. To solve the shortcomings of traditional corner detection methods, we propose a robust corner detection method based on the improved YOLOX deep learning network and the Harris algorithm. In this method, we first detect the target and obtain the candidate areas through improved YOLOX. In the case of large lens distortions, this can accurately capture the candidate corner areas. The main work can be divided into four steps. The first step is to take the 2810 images after enhancement containing the corner areas for model training. The second step is to detect the candidate corner areas and obtain the coordinates of the areas through trained YOLOX. The third step is to extract the candidate corner areas and separate false areas by clustering algorithm. The last step is to detect the sub-pixel checkerboard corners with the Harris algorithm on these areas. The overview of the proposed method is depicted in Figure 3.

FIGURE 3

FIGURE 3. The overview of our proposed method.

2.2.1 Improved YOLOX

YOLOX is an improved version of the YOLO series, which combines the advantages of each YOLO deep learning network [25]. The archor-free mechanism is implemented in this model, which significantly reduces the number of design parameters. Meanwhile, to solve the Optimal Transport (OT) problem and simplify it to get an approximate solution, SimOTA is used. YOLOX has different model structures, such as YOLOX-s, YOLOX-m, YOLOX-l, YOLOX-x, and so on. Since the features of a corner point are easier to recognize and do not require a complex detection network, the YOLOX-s model is chosen to detect the corner candidate areas in this study. The parameters and floating-point operations per second (FLOPs) of YOLOX-s are only 9 M and 26.8 G, respectively.

The overall model of YOLOX mainly consists of three key parts, which are Backbone, Neck, and YOLO Head. The Backbone is the backbone feature extraction network of the entire model. The three feature layers are obtained in the Backbone. Then three feature layers will be performed in the feature fusion in the Neck part. The YOLO Head is divided into a classifier and a regressor, which mainly makes judgements on feature points and determines whether there are objects corresponding to them. Especially, we add the squeeze-and-excitation (SE) attention mechanism [30] to capture position information after the Spatial Pyramid Pooling (SPP) module to improve the YOLOX-s model, which can also help the model to locate and recognize regions of interest more precisely. The structure of the improved YOLOX-s network is shown in Figure 4.

FIGURE 4

FIGURE 4. The structure of improved YOLOX-s.

The basic components of the corner candidate areas of extraction network based on YOLOX-s are as follows:

(1) The Focus module. The input images are sliced to expand the feature dimension while retaining the complete image information in this module.

(2) The CBS (Convolution, Batch Normalization, and SiLU) module. The three subcomponents of the module are the convolution layer, batch normalization layer, and SiLU activation function.

(3) The CSP (Center and Scale Prediction) module. There are two CSP network structures used in YOLOX-s. CSP1_n is consisted of the CBS module, n residual units, and a concat function. CSP2_n is formed by the CBS module and a concat function. The functions of the two structures are to enhance the learning ability and feature integration ability of the network, respectively.

(4) The SPP module. To fuse multiscale features, the maximum pooling approach is used in this module.

The prediction process of the YOLOX network is similar to the YOLO series [31]. It also first resizes the input images so that all images have the same fixed size (640 × 640). Next, the input images are divided into grids with the size S × S. Each grid will use B bounding boxes to detect an object. Thus, for an input image, S × S × B bounding boxes will be generated. If the center of an object falls in a certain grid, the bounding boxes in this grid will predict the object. In the prediction process, confidence threshold is proposed to reduce the redundancy of bounding boxes. If the confidence score of the bounding box is higher than the confidence threshold, the bounding box will be kept; else the bounding box will be deleted. The confidence score of the bounding box can be obtained in the following:

$C_i^j=P_{i,j}\ast IO{U}_{pred}^{truth}(1)$

where $C_i^j$ is the confidence score of the j th bounding box in the i th grid. $P_{i,j}$ is merely a function of the object. If the object is in the j th box of the i grid, the value of $P_{i,j}$ will be 1; otherwise $P_{i,j}=0$. The $IO{U}_{pred}^{truth}$ represents the intersection over union between the predicted box and the ground truth box. The larger the abjectness score, the closer the predicted box is to the ground truth box. The loss function of YOLOX is composed of three parts. It can be expressed as follows:

$Loss=los{s}_{Reg}+los{s}_{Obj}+los{s}_{Cls}(2)$

where $\mathit{los}{\mathit{s}}_{\mathit{Reg}}$, $\mathit{los}{\mathit{s}}_{\mathit{Obj}}$, and $\mathit{los}{\mathit{s}}_{\mathit{Cls}}$ are bounding box regression loss function, confidence loss function, and classification loss function, respectively [31].

2.2.2 Harris Algorithm

The Harris algorithm was proposed in the 1990s, and was used to image registration [5]. The algorithm analyzes the correlation between the pixel points in an image and the surrounding pixel points to detect the edge domains and corners of the image. The detection of a corner is usually judged by the gray level changing on the image in all directions. Therefore, assume that there is a small window on the image that can be moved in all directions. If the area of the small windows passed does not have gray level changed, then there is no corner in the area. If the windows move in a certain direction, the gray level changes greatly; but there is no gray level change in the other direction, which may be a straight line in this area. When the gray level of the pixel in the area shows a large change in all directions, the pixel at that location is defined as a corner. The schematic diagram is shown in Figure 5.

FIGURE 5

FIGURE 5. The schematic diagram of the Harris algorithm. (A) “Flat” region. (B) “Edge.” (C) “Corner.”

The autocorrelation function for the area near the corner is as follows:

$Z\left(u,v\right)={\displaystyle \sum }_{x,y}w\left(x,y\right){\left[I\left(x+u,y+v\right)-I\left(x,y\right)\right]}^2(3)$

where $u,v$ is the offset in the x, y direction; $I\left(x+u,y+v\right)$ is the gray level value of the offset pixel; $I(x,y)$ is the gray level value before offset; $w\left(x,y\right)$ is a window function, which can be either a constant or a Gaussian-shaped function.

Taylor’s formula of the autocorrelation function $Z\left(u,v\right)$ is

$T\left(u,v\right)\approx \left[u,v\right]\ast {\displaystyle \sum }_{xy}w\left(x,y\right)\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right](4)$

where $I_x$, $I_y$ are gradients of pixels in the $x$, $y$ directions, respectively. The eigenvalues of the matrix ${\displaystyle \sum }_{x,y}w\left(x,y\right)\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]$ are ${\omega }_1$, ${\omega }_2$, which represents the image characteristics of the pixels. Based on the above principles, we will get the response function:

$R={\omega }_1{\omega }_2-k{\left({\omega }_1+{\omega }_2\right)}^2(5)$

where $k$ is an empirical constant. If $R\approx 0$, which represents the two eigenvalues are all small, there is a flat region; if $R<0$, the window area is an edge; if $R>0$ and greater than a certain threshold, there is a corner in the area.

3 Experiments and Discussion

3.1 Model Training

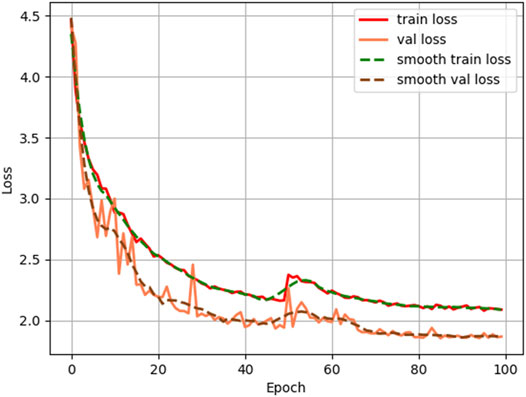
The adaptive moment estimation (Adam) method is used as the optimizer. During the network training, the Mosaic data augmentation is used to learn how to identify objects that are smaller than normal, and it also encourages the model to locate different types of images in various parts of the network framework. The process of training is divided into two parts, which are freezing epoch with a batch size of 8 and unfreezing epoch with a batch size of 4, respectively. Figure 6 shows the relationship between loss and epochs. The model training process proceeds for 100 epochs with 50 epochs for freezing and 50 epochs for unfreezing on the problem of detecting the corner candidate areas. The loss function converges rapidly at the beginning of training, and then decreases gradually in the subsequent training. After 50 epochs, the backbone of the model starts the training and gradually smoothes out as the epoch increases.

FIGURE 6

FIGURE 6. Loss curves during training.

3.2 Evaluation Criteria

The evaluation criteria used in this paper are accuracy, the missed corner rate, the double detection rate, and the number of false positives on the test datasets. If the average distance between the detected corners and the ground truth corners of all images is less than five pixels, this is counted as a true positive. The missed corner rate denotes how many ground truths are detected as non-corners. The double detection rate shows how many ground truths have several detections. False positives show how many non-corner locations are detected as the corners on the whole dataset.

3.3 Experimental Results

3.3.1 Experimental Results on Our Dataset

The first experiment is focused on the robustness of our proposed method for the images (blur, noise, and extreme poses). The test results for an example image with extreme poses under blur and noise are shown in Figures 7A,B, respectively. The proposed method successfully detects checkerboard corners of extreme poses and maintains effective performance in the presence of blur and noise interference. From Figure 7C, the proposed method is almost not affected by the selected range of image noise and slightly influenced by the selected range of image blur. The accuracy defined by the average distance between the detected corners and the ground truth corners of all images is only 0.1639 at the strongest 3-pixel blur level, which is about four times as much as original images (0-pixel blur level). Therefore, our proposed method has a great accuracy and robustness of checkerboard corner detection.

FIGURE 7

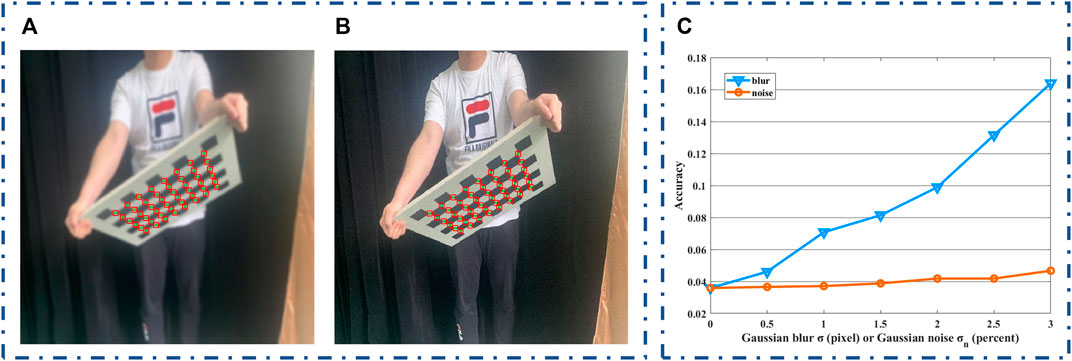
FIGURE 7. The results of our proposed method. (A) Blur test, (B) noise test, and (C) the influence of blur and noise on the accuracy.

In the experiments, the proposed method can effectively avoid double detections due to NMS structure of YOLOX. Besides, there are no false positives in our test images because of using the cluster algorithm. It can be demonstrated that the trained YOLOX model can accurately detect the corner candidate areas and the Harris algorithm can detect the sub-pixel corner points in the areas in different types of degradation.

3.3.2 Experimental Results on uEye and GoPro Datasets

To evaluate the performance of the proposed method, we conduct comparative experiments on the uEye dataset and GoPro dataset, which vary widely in resolution and lens distortions, from 1280 × 1024 images in uEye to 4000 × 3000 images with strong lens distortions in the GoPro. We borrow the published results using the methods CCDN, MATE, ChESS, ROCHADE, and OCamCalib in [16]. The examples of these two datasets detection results using the proposed method are illustrated in Figure 8.

FIGURE 8

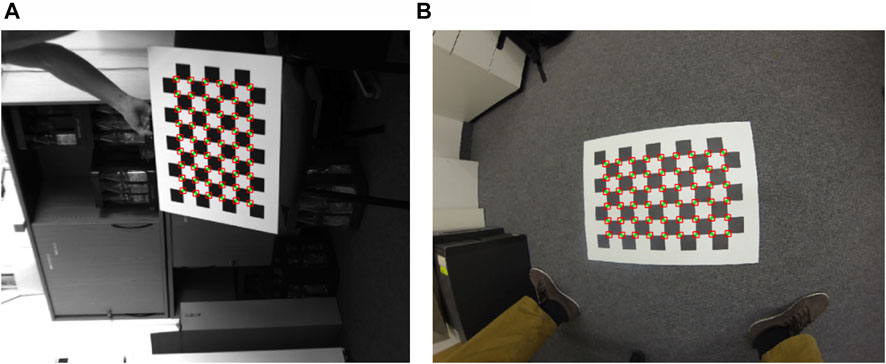
FIGURE 8. The examples of the two datasets and detection results when using our proposed method. (A) uEye dataset and (B) GoPro dataset.

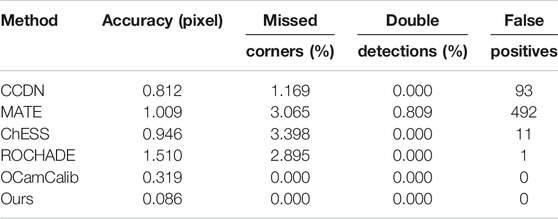
The results summarized in Tables 1 and 2 show that the proposed method outperforms other methods on the two datasets. Different than CCDN, the proposed method can achieve sub-pixel level corner detection, which also performs best in terms of accuracy. It can be found that OCamCalib does not have any false positives and double detections because it requires the number of squares in a checkerboard pattern in advance. Evaluations on the different datasets show the superior robustness and accuracy of our proposed method.

TABLE 1

TABLE 1. Results on the uEye dataset.

TABLE 2

TABLE 2. Results on the GoPro dataset.

3.3.3 Experimental Results on Fisheye Dataset

In the third group of experiments, we perform several quantitative comparisons on the fisheye lens dataset (large lens distortions) using the corner detection methods of ours, CCDN, and MATLAB. As for the fisheye dataset containing images with resolution of 1600 × 1200, we calculate the rate of missed corners, double detections, and false positives for the three methods. The corners representative of one of the test images by the three methods are shown in Figure 9. From Figure 9A, CCDN finds 44 of the 88 corners. As illustrated in Figure 9B, MATLAB only detects 24 corners, in addition to 2 false positives which are shown in a red box. With the proposed method, all corners of the checkerboard are detected accurately and can be used for calibration, which is illustrated in Figure 9C.

FIGURE 9

FIGURE 9. The example of the fisheye dataset and detection results when using the three methods. (A) CCDN, (B) MATLAB, and (C) ours.

The results listed in Table 3 show that the proposed method outperforms other methods on large lens distortion images. The trained YOLOX model can effectively extract the corner candidate areas so that false positives can be avoided. Meanwhile, the rate of missed corners using our method is only 3.582%. CCDN detects only 34 false positives, but the rate of missed corners is relatively high (up to 36.825%). MATLAB detects many false positives and has a high missed corner rate, which are 4516 and 62.558%, respectively. Besides, in terms of detect speed per image, our method requires less computation time of 0.0474 s. The detect time of MATLAB is 8 times longer than that of the proposed method, which reaches 0.329 s per image. The time required for CCDN to detect an image is 0.0688 s. It can be proven that MATLAB has inferior performance on the images of large lens distortions. The above results show that the proposed method is quite robust and fast for large lens distortions.

TABLE 3

TABLE 3. Results on the fisheye dataset.

4 Conclusion

In our work, a new checkerboard corner detection method based on the improved YOLOX and the Harris algorithm is presented. We use the improved YOLOX to detect the corner candidate areas and input them into the Harris algorithm to obtain the final sub-pixel corners. Theoretical analysis and experimental results show that the proposed method can be robust against the types of degradation (focal blur, heavy noise, extreme poses, and large lens distortions). Compared to traditional corner detection methods, the proposed method can detect not only corners against complex background, but also sub-pixel level corners. Thus, it can be seen as a specific checkerboard detector that is accurate, robust, and suitable for automatic detection and camera calibration. Our current work only discusses simple checkerboard corner detection. However, the related work of other types of calibration patterns such as deltille grids (regular triangular tiling) still needs further analysis and research. In future work, we will focus on the feature points detection model that is applicable to more types of calibration patterns.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors contributed to the research work. GW and HZ proposed the approach and designed the experiments; HZ and XZ performed the experiments; GW, HZ, and XZ analyzed the data and wrote the manuscript.

Funding

This research is funded by President’s Fund of Xi’an Technological University (Grant No. XGPY200216) and Comprehensive Reform Research and Practice Project of Graduate Education in Shaanxi Province (Grant No. YJSZG2020074).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The work is partly done during the first author’s visit at Nanyang Technological University, Singapore, with support from Kemao Qian. We gratefully acknowledge Dr. Kemao Qian for his valuable help. We would also like to thank the reviewers for the valuable and constructive comments that helped us improve the presentation.

References

1. Mehrotra R, Nishan S, Ranganathan N. Corner Detection. Pattern Recognition (1990) 23:1223–33. doi:10.1016/0031-3203(90)90118-5

CrossRef Full Text | Google Scholar

2. Dutta A, Kar A, Chatterji BN. Coner Detection Algorithms for Digital Images in Last Three Decades. IETE Tech Rev (2008) 25:123–33. doi:10.4103/02564602.2008.10876651

CrossRef Full Text | Google Scholar

3. Wang J, Zhang W. A Survey of Corner Detection Methods. In: Proceedings of the 2018 2nd International Conference on Electrical Engineering and Automation; March 25-26, 2018; Chengdu (2018). 214–9. doi:10.2991/iceea-18.2018.47

CrossRef Full Text | Google Scholar

4. Moravec HP. Techniques towards Automatic Visual Obstacle Avoidance. In: Proceedings of the 5th International Joint Conference on Artificial Intelligence (1977). 584.

Google Scholar

5. Harris C, Stephens M. A Combined Corner and Edge Detector. In: Proceedings of the British Machine Vision Conference (1988). 147–52. doi:10.5244/C.2.23

CrossRef Full Text | Google Scholar

6. Smith SM, Brady JM. SUSAN—A New Approach to Low Level Image Processing. Int J Comput Vis (1997) 23:45–78. doi:10.1023/A:1007963824710

CrossRef Full Text | Google Scholar

7. Rosten E, Drummond T. Machine Learning for High-Speed Corner Detection. In: Proceedings of the 9th European Conference on Computer Vision (2006). 430–43. doi:10.1007/11744023_34

CrossRef Full Text | Google Scholar

8. Rachmawati E, Supriana I, Khodra ML. FAST Corner Detection in Polygonal Approximation of Shape. In: Proceedings of the 3rd International Conference on Science in Information Technology (2017). 166–70. doi:10.1109/ICSITech.2017.8257104

CrossRef Full Text | Google Scholar

9. Mokhtarian F, Suomela R. Robust Image Corner Detection through Curvature Scale Space. IEEE Trans Pattern Anal Machine Intell (1998) 20:1376–81. doi:10.1109/34.735812

CrossRef Full Text | Google Scholar

10. Zhong B, Liao W. Direct Curvature Scale Space in Corner Detection. In: Proceedings of the Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition and Structural and Syntactic Pattern Recognition (2006). 235–42. doi:10.1007/11815921_25

CrossRef Full Text | Google Scholar

11. Hossain MA, Tushar AK. Chord Angle Deviation Using tangent (CADT), an Efficient and Robust Contour-Based Corner Detector. In: Proceedings of the 2017 IEEE International Conference on Imaging Vision Pattern Recognition (2017). 1–6. doi:10.1109/ICIVPR.2017.7890857

CrossRef Full Text | Google Scholar

12. Rosten E, Porter R, Drummond T. Faster and Better: A Machine Learning Approach to Corner Detection. IEEE Trans Pattern Anal Machine Intell (2010) 32:105–19. doi:10.1109/TPAMI.2008.275

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Donné S, De Vylder J, Goossens B, Philips W. MATE: Machine Learning for Adaptive Calibration Template Detection. Sensors (2016) 16:1858. doi:10.3390/s16111858

CrossRef Full Text | Google Scholar

14. Song W, Zhong B, Sun X. Building Corner Detection in Aerial Images with Fully Convolutional Networks. Sensors (2019) 19:1915. doi:10.3390/s19081915

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Raza SN, Raza ur Rehman H, Lee SG, Sang Choi G. Artificial Intelligence Based Camera Calibration. In: Proceedings of the 15th International Wireless Communications Mobile Computing Conference (2019). 1564–9. doi:10.1109/IWCMC.2019.8766666

CrossRef Full Text | Google Scholar

16. Chen B, Xiong C, Zhang Q. CCDN: Checkerboard Corner Detection Network for Robust Camera Calibration. In: Proceedings of the International Conference on Intelligent Robotics and Applications (2018). 324–34. doi:10.1007/978-3-319-97589-4_27

CrossRef Full Text | Google Scholar

17. Girshick R, Donahue J, Darrell T, Malik J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In: Proceeding of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (2014). 580–7. doi:10.1109/CVPR.2014.81

CrossRef Full Text | Google Scholar

18. Girshick R. Fast R-CNN. In: Proceedings of the 2015 IEEE International Conference on Computer Vision (2015). 1440–8. doi:10.1109/ICCV.2015.169

CrossRef Full Text | Google Scholar

19. Ren S, He K, Girshick R, Sun J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans Pattern Anal Mach Intell (2017) 39:1137–49. doi:10.1109/tpami.2016.2577031

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liu W, Anguelov D, Erhan D, Szegedy C, Reed S, Fu C-Y, et al. SSD: Single Shot Multibox Detector. In: Proceedings of the European Conference on Computer Vision (2016). 21–37. doi:10.1007/978-3-319-46448-0_2

CrossRef Full Text | Google Scholar

21. Redmon J, Divvala S, Girshick R, Farhadi A. You Only Look once: Unified, Real-Time Object Detection. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2016). 779–88. doi:10.1109/CVPR.2016.91

CrossRef Full Text | Google Scholar

22. Redmon J, Farhadi A. YOLO9000: Better, Faster, Stronger. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (2017). 6517–25. doi:10.1109/CVPR.2017.690

CrossRef Full Text | Google Scholar

23. Redmon J, Farhadi A. YOLOv3: An Incremental Improvement. arXiv [Preprint] (2018). Available at: https://arxiv.org/abs/1804.02767.

Google Scholar

24. Bochkovskiy A, Wang CY, Liao HYM. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv [Preprint] (2020). Available at: https://arxiv.org/abs/2004.10934.

Google Scholar

25. Ge Z, Liu S, Wang F, Li Z, Sun J. YOLOX: Exceeding YOLO Series in 2021. arXiv [Preprint] (2021). Available at: https://arxiv.org/abs/2107.08430.

Google Scholar

26. Zhang Y, Sun P, Jiang Y, Yu D, Yuan Z, Luo P, et al. ByteTrack: Multi-Object Tracking by Associating Every Detection Box. arXiv [Preprint] (2021). Available at: https://arxiv.org/abs/2110.06864.

Google Scholar

27. Sun P, Cao J, Jiang Y, Yuan Z, Bai S, Kitani K, et al. DanceTrack: Multi-Object Tracking in Uniform Appearance and Diverse Motion. arXiv [Preprint] (2021). Available at: https://arxiv.org/abs/2111.14690.

Google Scholar

28. Placht S, Fürsattel P, Mengue EA, Hofmann H, Schaller C, Balda M, et al. ROCHADE: Robust Checkerboard Advanced Detection for Camera Calibration. In: Proceedings of the European Conference on Computer Vision (2014). 766–79. doi:10.1007/978-3-319-10593-2_50

CrossRef Full Text | Google Scholar

29. Ha H, Perdoch M, Alismail H, Kweon IS, Sheikh Y. Deltille Grids for Geometric Camera Calibration. In: Proceedings of the 2017 IEEE International Conference on Computer Vision (2017). 5344–52. doi:10.1109/ICCV.2017.571

CrossRef Full Text | Google Scholar

30. Hu J, Shen L, Sun G. Squeeze-and-excitation Networks. In: Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (2018). 7132–41. doi:10.1109/CVPR.2018.00745

CrossRef Full Text | Google Scholar

31. Jiang Z, Zhao L, Li S, Jia Y. Real-time Object Detection Based on Improved YOLOv4-Tiny. arXiv [Preprint] (2020). Available at: https://arxiv.org/abs/2011.04244.

Google Scholar