3D Reconstruction of Non-Lambertian Surfaces by Perspective Shape-From-Shading With Fast Viscosity Solution

Shape-from-shading (SFS) is an important method to reconstruct three-dimensional (3D) shape of a surface in photometry and computer vision. Lambertian surface reflectance and orthographic camera projection are two fundamental assumptions which generally result in undesirable reconstructed results since inaccurate imaging model is adopted. In this paper, we propose a new fast 3D shape reconstruction approach via the SFS method relaxing the two assumptions. To this end, the Oren-Nayar reflectance and perspective projection models are used to establish an image irradiance equation which depicts the relationship between the 3D shape of non-Lambertian surfaces and its corresponding two-dimensional (2D) shading image. Considering the light attenuation of the near point source, the image irradiance equation is transformed into a static Hamilton-Jacobi partial differential equation (PDE) by solving a quadratic equation. The viscosity solution of the resultant Hamilton-Jacobi PDE is approximated by using optimal control theory and iterative fast marching method starting from a viscosity supersolution. The performance of the proposed approach is evaluated on both synthetic and real-world images and the experimental results demonstrate that the proposed approach is accurate and fast.

Introduction

Shape-from-shading (SFS) is an important method to reconstruct three-dimensional (3D) surfaces in the field of photometry and computer vision. The work has been initiated by Horn [1, 2] who established an image irradiance equation depicting the relationship between the 3D shape of a surface and its corresponding two-dimensional (2D) shading image. Inspired by his work, a lot of different SFS methods are extensively studied (for surveys, see [3, 4]). In these methods, Lambertian surface reflectance and orthographic camera projection are two fundamental assumptions. Even for the diffuse surfaces, however, the Lambertian model has been proved to be inaccurate expression of the reflectance property [5–7]. Furthermore, the image can be seen as formed through a so-called pin-hole camera which should be modeled by perspective projection. Since these methods do not adopt accurate physical and/or optical imaging model, the reconstructed results lack accuracy.

Recently, Tankus et al. [8] changed the classical orthographic projection assumption to a perspective one and formulated the image irradiance equation. They suggested the orthographic fast marching method of Kimmel and Sethian [9] as the initial solution and then approximated the perspective image irradiance equation using an iterative fast marching method. Another perspective SFS was addressed by Courteille et al. [10] who considered the “pseudo-Eikonal equation” and solved it with a prior knowledge. Yuen et al. [11] proposed an alternative perspective SFS which is also based on the fast marching method of Kimmel and Sethian [9]. Their method, however, does not require the iterative process. It is well worth mentioning that Prados and his colleagues [12, 13] had made a great contribution to the SFS field. They presented a more realistic imaging model for SFS problem, where the orthographic camera projection is substituted by the perspective projection and the light source is assumed to be placed at the optical center of the camera. Moreover, a light attenuation term 1/d² (d defines the distance between the 3D surface point and the position of the light source) has been considered. They generalized the SFS problem and related the derived image irradiance equation with a Hamiltonian and approximated its viscosity solution using optimal control strategy. With their work, Ahmed and Farag [6, 7] replaced Lambertian reflectance by a more advanced Oren-Nayar reflectance and proposed a non-Lambertian SFS method. In addition, they used the Lax-Friedrichs sweeping scheme [14] to solve the explicit partial differential irradiance equation and got a promising reconstructed result. Although [6, 7] worked well on the non- Lambertian surfaces, they still need the exact values on the boundary. Moreover, it is difficult to find a good estimate for the artificial viscosity term and it would take too much time to reach the stopping criterion. To avoid these problems, Vogel and Cristiani [15] used the Upwind scheme to get a more efficient solution with less convergence time. Ju et al. [16] extended the work of Galliani et al. [17]. They used spherical surface parameterization to Oren-Nayar reflectance model and thus could deal with an arbitrary position of the light source. Compared with the method of [6, 7, 15], this work can obtain a very compact and elegant image irradiance equation. Unfortunately, the solving process need transform the fast marching method described in Cartesian coordinates [18] into spherical coordinates. Tozza and Falcone [19, 20] presented another non-Lambertian SFS method using a semi-Lagrangian approximation scheme and proved a convergence result. However, their work still assumes an orthographic camera projection and a distant light source. More recently, some SFS approaches have been proposed by deep learning techniques [21–23]. Yang and Deng [21] addressed the SFS problem by training deep networks with only synthetic images which can not be rendered by any external shape dataset. Henderson and Ferrari [22] presented a unified framework for both reconstruction and generation of 3D shapes, which was trained to model 3D meshes using only 2D supervision. Tokieda et al. [23] proposed a high-frequency shape recovery from shading method using CNN which the U-Net structure was employed. The approaches [21–23] can achieve state-of-the-art performance. However, they need sufficient amount of data for training.

In the current study, based on our previous work [24–27], we propose a new fast perspective SFS approach for non-Lambertian surface reconstruction. The Oren-Nayar reflectance model is also adopted to approximate the surface reflectance property. Then, with a point light source close to the projection center of the camera which performs perspective projection, we formulate the image irradiance equation that can be transformed into a quadratic equation. The main contribution of our work is that we establish a static Hamilton-Jacobi partial differential equation (PDE) by solving the quadratic image irradiance equation that contains the 3D shape, after which we attempt to get the viscosity solution of the resultant PDE by using optimal control theory and iterative fast marching method. It is worth mentioning that the light attenuation term 1/d² has also been employed to remove the ambiguity which leads SFS to be an ill-posed problem. Compared with other existing SFS approach, the proposed approach is more accurate and faster.

The remainder of the paper is structured as follows. In section 2, we give the SFS imaging model of non-Lambertian surfaces to derive the image irradiance equation that serves as the basis for our approach. Section 3 presents a new method to approximate the viscosity solution of the image irradiance equation using optimal control theory and iterative fast marching method. Experimental results on both synthetic and real-world images are performed and discussed in section 4. Finally, we conclude our approach in section 5.

Image Irradiance Equation

SFS Imaging Model of Non-Lambertian Surfaces

To derive the image irradiance equation of non-Lambertian SFS, we firstly make a brief review of the imaging process for the SFS problem which describes the relationship between the 3D shape of a surface and its corresponding 2D shading image. It is well-known that the following relationship between the image irradiance and the surface reflected radiance [1, 25] is modeled as:

$E_i=L_s\frac{\pi }{4}{\left(\frac{D}{F}\right)}^2{\cos }^4\chi ,(1)$

where $E_i$ is image irradiance, which is usually considered to be proportional to the image brightness $I$. $L_s$ defines the surface reflected radiance along the direction of the camera. The camera lens focuses light from the surface on the imaging sensor (i.e., the image plane) and $D,F$ are its diameter and focal length, respectively. $\chi$ is the angle between optical axis and the line of sight to a 3D surface point of a corresponding 2D image point. The term ${\cos }^4\chi$ implies non-uniform image irradiance even for uniform radiance, but the actual optical system of the camera is generally designed to correct it. Consequently, we may consider the image irradiance $E_i$ to be proportional to the surface reflected radiance $L_s$, i.e., $E_i=\eta L_s$.

For an ideal diffuse surface and a distant point light source, the surface has a Lambertian reflectance and the reflected radiance can be expressed as [1]:

$L_s\left({\theta }_i\right)=\frac{\rho }{\pi }{I}_0\cos {\theta }_i,(2)$

where $\rho$ is the diffuse albedo and $I_0$ is the intensity of the point light source. The term $\cos {\theta }_i$ is the scalar product between the surface normal vector $\mathbf{n}$ and the light source vector $\mathbf{L}$.

However, the Lambertian model has been proved to be inaccurate expression of the reflectance property for the real-world diffuse surfaces [5–7]. In order to eliminate the inaccuracy resulting from the assumption of the Lambertian surface reflectance, Oren and Nayar [5] developed an advanced reflectance model for rough diffuse surfaces. Assuming that the surface is composed of extended symmetric V-shaped cavities and each V-cavity has two planar facets following the Lambert’s law, they applied the roughness model that the surface roughness is specified using a probability function for the facet orientations to obtain the expression for the surface reflected radiance. For a Gaussian distribution, with reflection geometry shown in Figure 1A, $L_s$ is formulated as:

$L_s\left({\theta }_i,{\phi }_i;{\theta }_r,{\phi }_r;\sigma \right)=\frac{\rho }{\pi }{I}_0\cos {\theta }_i\left(A+B\max \left[0,\cos \left({\phi }_r-{\phi }_i\right)\right]\sin \alpha \tan \beta \right),(3)$

where ${\theta }_i,{\phi }_i$ and ${\theta }_r,{\phi }_r$ are the slant, tilt angles of $\mathbf{L}$ and the camera vector $\mathbf{V}$, respectively,

$A=1-0.5\frac{{\sigma }^2}{{\sigma }^2+0.33},B=0.45\frac{{\sigma }^2}{{\sigma }^2+0.09},(4)$

$\alpha =\max \left[{\theta }_i,{\theta }_r\right]$ and $\beta =\min \left[{\theta }_i,{\theta }_r\right]$. The parameter $\sigma$ denotes the standard deviation of the Gaussian distribution and is employed as a measure of the surface roughness.

FIGURE 1

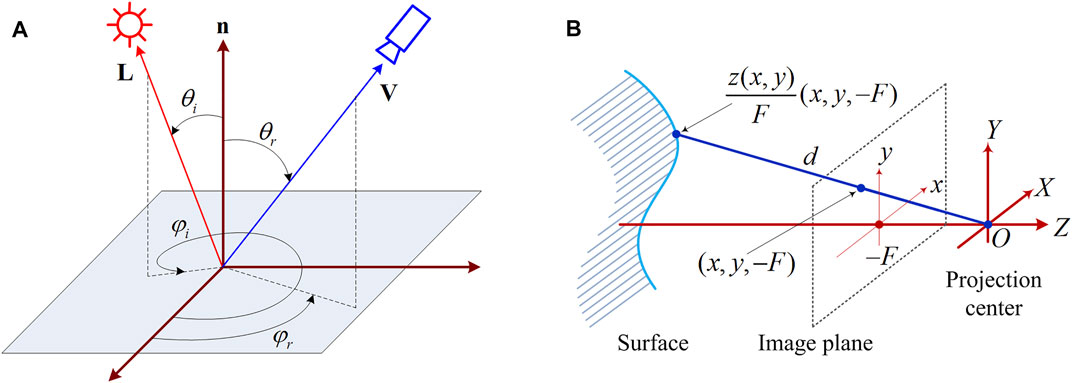
FIGURE 1. Imaging model for perspective SFS. (A) Reflection geometry model of a surface and (B) Perspective projection model of a camera.

Taking Eq. 3 into Eq. 1, the image irradiance equation of non-Lambertian SFS is now:

$E_i\left({\theta }_i,{\phi }_i;{\theta }_r,{\phi }_r\right)=\eta \frac{\rho }{\pi }{I}_0\cos {\theta }_i\left(A+B\max \left[0,\cos \left({\phi }_r-{\phi }_i\right)\right]\sin \alpha \tan \beta \right).(5)$

Since the image irradiance is usually considered to be proportional to the image brightness, we denote $I=\pi E_i/\eta \rho I_0$ and the image irradiance Eq. 5 is rewritten as:

$I\left({\theta }_i,{\phi }_i;{\theta }_r,{\phi }_r\right)=\cos {\theta }_i\left(A+B\max \left[0,\cos \left({\phi }_r-{\phi }_i\right)\right]\sin \alpha \tan \beta \right).(6)$

Image Irradiance Equation of Perspective SFS

As shown in Figure 1B, for a perspective camera projection whose center is $O$, $S\left(X,Y,Z\right)$ represents the 3D shape of interested surface for a certain image domain $\Omega$, and can be parameterized by

$S\left(X,Y,Z\right)=\frac{z\left(x,y\right)}{F}\left(x,y,-F\right),\left(x,y\right)\in \Omega ,(7)$

where $F>0$ and $z\left(x,y\right)>0$ is the distance between the surface point $\left(X,Y,Z\right)$ and $O-XY$ plane. To get a surface normal vector, we calculate the tangent vectors in both $x$ and $y$ directions, respectively and compute their cross product. Then the normal vector $\mathbf{n}\left(x,y\right)$ at the point $\left(X,Y,Z\right)$ is formulated as:

$\mathbf{n}(x,y)=\left(F\frac{\partial z}{\partial x},F\frac{\partial z}{\partial y},z+x\frac{\partial z}{\partial x}+y\frac{\partial z}{\partial y}\right).(8)$

With the point light source whose attenuation term 1/d² has been considered to remove the ambiguity which leads SFS to be an ill-posed problem is located near the projection center $O$, the light source vector $\mathbf{L}\left(x,y\right)$ at the point $(X,Y,Z)$ is given by

$\mathbf{L}\left(x,y\right)=\left(-x,-y,F\right)(9)$

and the parameters in Oren-Nayar reflectance model satisfy

${\theta }_i={\theta }_r=\alpha =\beta ,{\phi }_i={\phi }_r.(10)$

Therefore, the image irradiance Eq. 6 is simplified to

$I\left({\theta }_i\right)=\frac{1}{d^2}\left(A\cos {\theta }_i+B{\sin }^2{\theta }_i\right).(11)$

Since the term $\cos {\theta }_i$ is the scalar product between $\mathbf{n}\left(x,y\right)$ and $\mathbf{L}\left(x,y\right)$, substituting Eqs 8, 9 into Eq. 11, we can obtain the image irradiance equation of perspective SFS:

$I\left(x,y\right)=\frac{1}{d^2}\left(A\frac{Q\left(x,y\right)}{V\left(x,y,\nabla u\right)}+B\frac{V{(x,y,\nabla u)}^2-Q{\left(x,y\right)}^2}{V{\left(x,y,\nabla u\right)}^2}\right),(12)$

where $u=\ln z\left(x,y\right)$, $V\left(x,y,\nabla u\right)=\sqrt{{\left(F\partial u/\partial x\right)}^2+{\left(F\partial u/\partial y\right)}^2+{\left(x\partial u/\partial x+y\partial u/\partial y+1\right)}^2}$, $Q\left(x,y\right)={F/\left(x^2+y^2+F^2\right)}^{1/2}$, $d=z\left(x,y\right)/Q\left(x,y\right)=e^u/Q\left(x,y\right)$.

Method of Solving the Image Irradiance Equation

Obviously, the image irradiance Eq. 12 can be described by a quadratic equation with respect to the variable $V\left(x,y,\nabla u\right)$. Then the equation is transformed into

$\left(I(x,y)e^{2u}Q{\left(x,y\right)}^{-2}-B\right)V{\left(x,y,\nabla u\right)}^2-AQ\left(x,y\right)V\left(x,y,\nabla u\right)+BQ{\left(x,y\right)}^2=0.(13)$

Solving the quadratic Eq. 13 and satisfying $V\left(x,y,\nabla u\right)>0$, we have

$V\left(x,y,\nabla u\right)=\frac{A+\sqrt{A^2-4\left(I\left(x,y\right)e^{2u}Q{\left(x,y\right)}^{-2}-B\right)B}}{2\left(I\left(x,y\right)e^{2u}Q{\left(x,y\right)}^{-2}-B\right)}Q\left(x,y\right).(14)$

Now, we can obtain a novel image irradiance equation

$\begin{array}{l}-\frac{1}{A-\sqrt{A^2-4\left(I\left(x,y\right)e^{2u}Q{\left(x,y\right)}^{-2}-B\right)B}}\\ +\frac{1}{2BQ\left(x,y\right)}\sqrt{{\left(F\frac{\partial u}{\partial x}\right)}^2+{\left(F\frac{\partial u}{\partial y}\right)}^2+{\left(x\frac{\partial u}{\partial x}+y\frac{\partial u}{\partial y}+1\right)}^2}=0.\end{array}(15)$

It is easy to see that Eq. 15 does not have classical solutions since it is a first-order non-linear PDE. Thus one can appeal to the notion of viscosity solution [28, 29] that is a solution in the weak sense. For the PDE (15), to ensure the uniqueness of the viscosity solution, Dirichlet boundary conditions usually need to be imposed, and therefore a static Hamilton-Jacobi PDE could be got

$\{\begin{array}{c}H\left(x,y,u,\mathbf{g}\right)=0,\forall \left(x,y\right)\in \Omega ,\\ u\left(x,y\right)=\chi \left(x,y\right),\forall \left(x,y\right)\in \partial \Omega ,\end{array}(16)$

where $\chi \left(x,y\right)$ is a real function which is defined on $\partial \Omega$ and

$H\left(x,y,u,\mathbf{g}\right)=-{\left(A-\sqrt{A^2-4\left(I\left(x,y\right)e^{2u}Q{\left(x,y\right)}^{-2}-B\right)B}\right)}^{-1}+W\left(x,y\right)\sqrt{F^2\left|\right|\mathbf{g}|{|}^2+{\left(\left(x,y\right)\cdot \mathbf{g}+1\right)}^2}(17)$

is the associated Hamiltonian, where $W\left(x,y\right)={\left(2BQ\left(x,y\right)\right)}^{-1}$ and $\mathbf{g}=\left(\partial u/\partial x,\partial u/\partial y\right)$. According to [12, 29] and our previous work [24], using viscosity solution and optimal control theories, the Hamiltonian (17) can be addressed as a control-type formulation

$H\left(x,y,u,\mathbf{g}\right)=-{\left(A-\sqrt{A^2-4\left(I\left(x,y\right)e^{2u}Q{\left(x,y\right)}^{-2}-B\right)B}\right)}^{-1}+\underset{\mathrm{a}\in B_2\left(\mathrm{0,1}\right)}{\sup }\left\{-l_c\left(x,y,\mathbf{a}\right)-{\mathbf{f}}_c\left(x,y,\mathbf{a}\right)\cdot \mathbf{g}\right\},(18)$

where $B_2\left(\mathrm{0,1}\right)$ is the unit ball of center $0$ in ${ℝ}^2$, ${\mathbf{f}}_c\left(x,y,\mathbf{a}\right)=-W\left(x,y\right){\mathbf{R}}^T\left(x,y\right)\mathbf{D}\left(x,y\right)\mathbf{R}\left(x,y\right)\mathbf{a}$ and $l_c\left(x,y,\mathbf{a}\right)=-\sqrt{1-\left|\right|\mathbf{a}|{|}^2}/2B-W\left(x,y\right){\mathbf{R}}^T\left(x,y\right)\mathrm{v}\left(x,y\right)\cdot \mathbf{a}$ with

$\mathbf{R}(x,y)=\{\begin{array}{cc}\left(\begin{array}{cc}x{\left(x^2+y^2\right)}^{-1/2}& y{\left(x^2+y^2\right)}^{-1/2}\\ -y{\left(x^2+y^2\right)}^{-1/2}& x{\left(x^2+y^2\right)}^{-1/2}\end{array}\right),& x^2+y^2\ne 0,\\ \left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),& x^2+y^2=0,\end{array}(19)$

$\mathbf{D}\left(x,y\right)=\left(\begin{array}{cc}\sqrt{x^2+y^2+F^2}& 0\\ 0& F\end{array}\right),\mathbf{v}\left(x,y\right)=\left(\begin{array}{c}\sqrt{\left(x^2+y^2\right){\left(x^2+y^2+F^2\right)}^{-1}}\\ 0\end{array}\right).(20)$

We approximate $H\left(x,y,u,\mathbf{g}\right)$ by

$H\left(x,y,\mathbf{g}\right)\approx -{\left(A-\sqrt{A^2-4\left(I\left(x,y\right)e^{2u}Q{\left(x,y\right)}^{-2}-B\right)B}\right)}^{-1}+\underset{\mathrm{a}\in B_2\left(\mathrm{0,1}\right)}{\sup }\{-l_c\left(x,y,\mathbf{a}\right)+\min \left[-f_1\left(x,y,\mathbf{a}\right),0\right]g_1^{+}+\max \left[-f_1\left(x,y,\mathbf{a}\right),0\right]g_1^{-}+\min \left[-f_2\left(x,y,\mathbf{a}\right),0\right]g_2^{+}+\max \left[-f_2\left(x,y,\mathbf{a}\right),0\right]g_2^{-}\},(21)$

where $f_k\left(x,y,\mathbf{a}\right)$ is the $k$ th component of ${\mathbf{f}}_c\left(x,y,\mathbf{a}\right)$ and $g_k^{+}$, $g_k^{-}$ stand for the corresponding forward and backward difference approximations of the $k$ th component of $\mathrm{g}$ respectively. Obviously, for the approximation method (21), it is necessary to solve the optimum problem and we can use optimal control theory and our proposed approach in [24] to get it.

The explicit time marching scheme for the Hamilton-Jacobi PDE (16) applying the forward Euler as the time discretization could be described in the form:

$u^{n+1}=u^n-\Delta tH\left(x,y,\mathbf{g}\right),(22)$

where $\Delta t$ is a time step. In order to accelerate the convergence speed of scheme (22), our proposed iterative fast marching strategy in [24] is adopted.

The method to approximate the viscosity solution of the resultant Hamilton-Jacobi PDE (16) is organized as follows:

1) Initialization (iteration $n=0$). Set $u^0=u_0\left(x_i,y_j\right)$, where $\left(x_i,y_j\right)$ is the discretization of $\left(x,y\right)$ at grid point $(i,j)$ and $u_0$ is a viscosity supersolution. In this paper, $u_0\left(x_i,y_j\right)=0.5\ln \left(A\right)-0.5\ln \left(I\left(x_i,y_j\right)Q{\left(x_i,y_j\right)}^{-2}\right)$.

2) Iterative Marching (iteration $n+1$).

(1) Definitions. Each grid point $\left(i,j\right)$ is assigned to one of three sets, known, front, unknown, in the following:

• Known is the set of the initial grid points corresponding to the extremums of $u$. Known points are the seeded points whose values will not be recalculated.

• Front is the set of the neighbours of known points, not in known. In our method, front points are the four nearest neighbours of known points and their values will be recalculated later.

• Unknown is the rest of the grid points, where there is not yet a calculation for $u$.

(2) Marching.

• Let $\left(i_{\min },j_{\min }\right)$ be the point among all front points that has the smallest $u$ value.

• Remove the point $\left(i_{\min },j_{\min }\right)$ from front and add it to known.

• Label as neighbours any points $\left(i_{\min },j_{\min }+1\right)$, $\left(i_{\min }+1,j_{\min }\right)$, $\left(i_{\min },j_{\min }-1\right)$, $\left(i_{\min }-1,j_{\min }\right)$ which are either in front or unknown. If the neighbour belongs to unknown, add it to front and remove it from unknown.

• Recalculate the value of $u$ at the four nearest neighbours of $\left(i_{\min },j_{\min }\right)$ that are in front by applying the scheme (22).

• If all grid points are known then exit, otherwise return to top of marching.

(3) Convergence test. If ${\Vert u^{n+1}-u^n\Vert }_{L^1}\le \delta$, where $\delta$ is a given stopping strategy, the method converges and stops; otherwise returns to 2). In this paper, $\delta ={10}^{-5}$.

Experimental Results and Discussion

Several experiments on two synthetic Vase and Mozart and one real-world shading images have been carried out in order to evaluate the performance of the proposed approach. We compare our proposed approach with Vogel and Cristiani’s approach [15] because it has a better performance than Ahmed and Farag’s approach [6, 7]. We implement the two approaches in Matlab, using C mex functions. All the experiments are conducted on a computer with a Xeon E5-1650 processor and 16 GB of DDR3 memory. The unit in the experiments is pixel.

Experimental Results on Synthetic Images

Figure 2 illustrates the experimental results on Vase and Mozart surfaces. Figure 2A shows the ground truth surfaces which are benchmark Dataset given by Zhang et al. [3]. Figure 2B illustrates the synthetic shading images of Vase and Mozart surfaces with the surface roughness $\sigma =0.2$ and image domain $\Omega =128\times 128$. Figures 2C,D show the reconstructed surfaces and errors by Vogel and Cristiani’s approach respectively. Figures 2E,F show the reconstructed surfaces and errors by our proposed approach respectively. Figure 2G illustrates the central cross section of ground truth and reconstructed surfaces of Vase and Mozart surfaces.

FIGURE 2

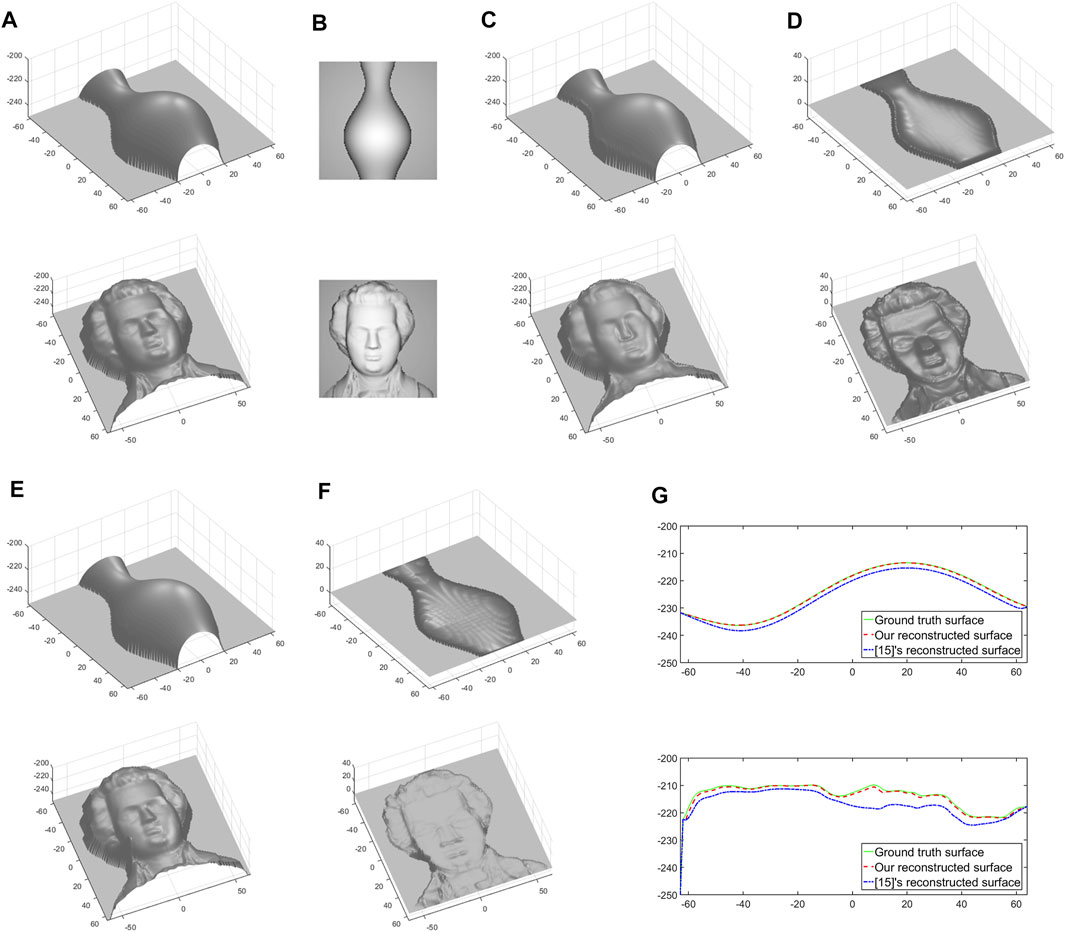
FIGURE 2. Experimental results on Vase and Mozart surfaces. (A) Ground truth surfaces, (B) Synthetic shading images, (C) Reconstructed surfaces by Vogel and Cristiani’s approach, (D) Surface errors between (C) and (A), (E) Reconstructed surface by our proposed approach, (F) Surface errors between (E) and (A), and (G) Central cross section of ground truth and reconstructed surfaces.

It is seen from Figures 2C–G that both Vogel and Cristiani’s and our approaches can give satisfactory surface reconstruction. Furthermore, we can see that our proposed approach produces reconstruction results with smaller errors and exhibits better than Vogel and Cristiani’s approach. The performance of Vogel and Cristiani’s approach and our proposed approach is further quantitatively described by the mean absolute (MA) error, root mean square (RMS) error and running time. The MA and RMS errors defines as:

$\mathrm{MA}=\frac{1}{m\times n}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n\left|z_{ij}-{\tilde{z}}_{ij}\right|}},(23)$

$\mathrm{RMS}=\sqrt{\frac{1}{m\times n}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\left|z_{ij}-{\tilde{z}}_{ij}\right|}^2}}},(24)$

where $m\times n$ denotes the size of the image domain $\Omega$ and $z_{ij}$, ${\tilde{z}}_{ij}$ denote the reconstructed surface and the ground truth surface respectively.

Table 1 demonstrates the quantitative comparisons of approaches for Vase and Mozart surfaces. It can be observed obviously that our proposed approach has much more superiority both in the MA and RMS errors. The MA and RMS errors of our proposed approach are about one-fifth and one-fourth of Vogel and Cristiani’s approach for the Vase, and about one-fifth and one-third for the Mozart, respectively because our image irradiance equation is approximated by using control-type Hamiltonian and iterative fast marching method while Vogel and Cristiani’s is approximated by Upwind scheme. In addition, it is also seen that our approach is much faster than Vogel and Cristiani’s approach as the same reason above.

TABLE 1

TABLE 1. Comparisons of approaches for Vase and Mozart surfaces.

Experimental Results on Real-World Image

Figure 3 illustrates the experiments on the real-world shading of a paper cylinder which is shown in Figure 3A. Figures 3B,C demonstrate the reconstructed surfaces by Vogel and Cristiani’s approach and our proposed approach respectively. Figure 3D shows the special case of our proposed approach with Lambertian reflectance, that is, the surface roughness $\sigma =0$. From the experimental results illustrated in Figures 3B,C, it is also seen that both Vogel and Cristiani’s and our approaches can give satisfactory surface reconstruction for the real-world shading. Furthermore, our approach also exhibits a slightly better performance that is more vivid than Vogel and Cristiani’s approach. It is well worth noting that Figure 3D shows a worse performance since it uses the Lambertian model which is inaccurate expression of the reflection property.

FIGURE 3

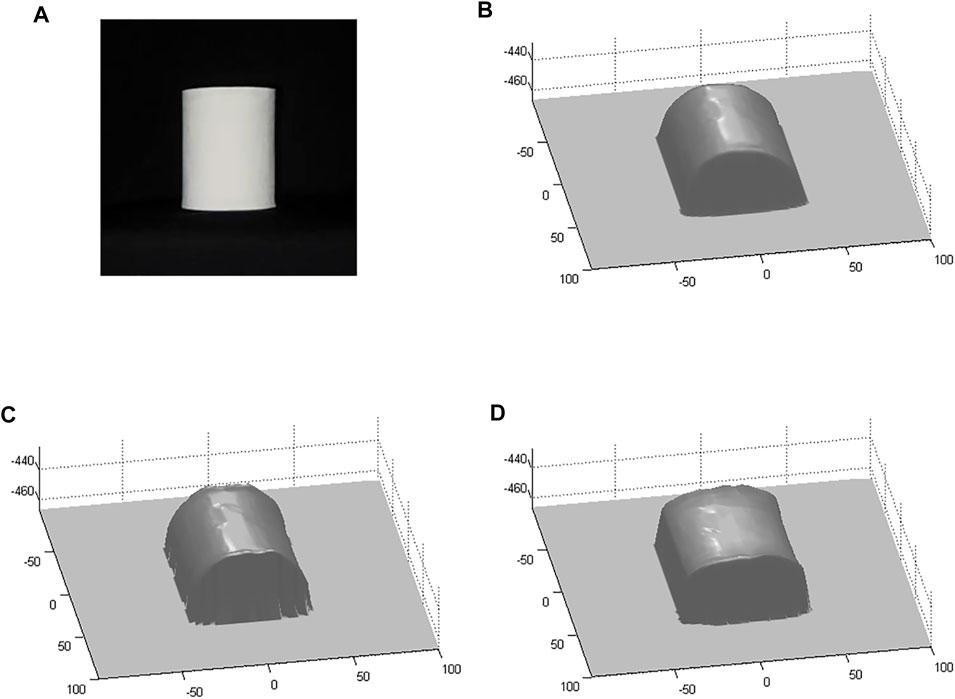
FIGURE 3. Real-world shading image and reconstructed surface. (A) Shading image, (B) Reconstructed surface by Vogel and Cristiani’s approach, (C) Reconstructed surface by our proposed approach, and (D) Reconstructed surface by our proposed approach with Lambertian reflectance.

Conclusion

We have proposed a fast 3D shape reconstruction approach for non-Lambertian surfaces via perspective SFS and viscosity solution. We first formulated the image irradiance equation as a quadratic equation with respect to the variable that contains the 3D shape of the surface and thus a static Hamilton-Jacobi PDE was derived by solving the quadratic equation. We employed an optimal control scheme and an iterative fast marching strategy to compute the viscosity solution of the resultant PDE. Finally, the experimental results verified that our proposed approach can provide satisfactory surface reconstruction with a higher accuracy in less running time. Further study of non-Lambertian SFS includes faster approximated methods and the more accurate imaging models.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Both authors contributed to the research work. GW proposed the approach; GW and HZ performed the experiments and analyzed the data; GW wrote the manuscript.

Funding

This research is funded by President’s Fund of Xi’an Technological University (Grant No. XGPY200216) and National Natural Science Foundation of China (Grant No. 61102144).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The work is partly done during the first author’s visit at Nanyang Technological University, Singapore, with a support by Kemao Qian; We gratefully acknowledge Kemao Qian for his very valuable help. We would also like to thank the reviewers for the valuable and constructive comments that helped us improve the presentation.

References

1. Horn BKP. Shape from Shading: A Method for Obtaining the Shape of a Smooth Opaque Object from One View. PhD dissertation. Cambridge (MA): Massachusetts Institute of Technology (1970).

Google Scholar

2. Horn BKP, Brooks MJ. The Variational Approach to Shape from Shading. Computer Vis Graphics, Image Process (1986) 33:174–208. doi:10.1016/0734-189X(86)90114-3

CrossRef Full Text | Google Scholar

3. Zhang R, Tsai PS, Cryer JE, Shah M. Shape-From-Shading: A Survey. IEEE Trans Pattern Anal Machine Intell (1999) 21:690–706. doi:10.1109/34.784284

CrossRef Full Text | Google Scholar

4. Durou JD, Falcone M, Sagona M. Numerical Methods for Shape-From-Shading: A New Survey with Benchmarks. Computer Vis Image Understanding (2008) 109:22–43. doi:10.1016/j.cviu.2007.09.003

CrossRef Full Text | Google Scholar

5. Oren M, Nayar SK. Generalization of the Lambertian Model and Implications for Machine Vision. Int J Comput Vis (1995) 14:227–51. doi:10.1007/bf01679684

CrossRef Full Text | Google Scholar

6. Ahmed AH, Farag AA. A New Formulation for Shape from Shading for Non-lambertian Surfaces. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2006) 1817–24. doi:10.1109/cvpr.2006.35

CrossRef Full Text | Google Scholar

7. Ahmed AH. Shape from Shading Under Various Imaging Conditions. PhD dissertation. Louisville (KY): University of Louisville (2008).

Google Scholar

8. Tankus A, Sochen N, Yeshurun Y. Shape-From-Shading Under Perspective Projection. Int J Comput Vis (2005) 63:21–43. doi:10.1007/s11263-005-4945-6

CrossRef Full Text | Google Scholar

9. Kimmel R, Sethian JA. Optimal Algorithm for Shape From Shading and Path Planning. J Math Imaging Vis (2001) 14:237–44. doi:10.1023/A:1011234012449

CrossRef Full Text | Google Scholar

10. Courteille F, Crouzil A, Durou JD, Gurdjos P. Shape from Shading for the Digitization of Curved Documents. Machine Vis Appl (2007) 18:301–16. doi:10.1007/s00138-006-0062-y

CrossRef Full Text | Google Scholar

11. Yuen SY, Tsui YY, Chow CK. A Fast Marching Formulation of Perspective Shape From Shading Under Frontal Illumination. Pattern Recognition Lett (2007) 28:806–24. doi:10.1016/j.patrec.2006.11.008

CrossRef Full Text | Google Scholar

12. Prados E. Application of the Theory of the Viscosity Solutions to the Shape from Shading Problem. PhD dissertation. Nice (France): University of Nice-Sophia Antipolis (2004).

Google Scholar

13. Prados E, Camilli F, Faugeras O. A Unifying and Rigorous Shape from Shading Method Adapted to Realistic Data and Applications. J Math Imaging Vis (2006) 25:307–28. doi:10.1007/s10851-006-6899-x

CrossRef Full Text | Google Scholar

14. Kao CY, Osher S, Qian J. Lax-Friedrichs Sweeping Scheme for Static Hamilton-Jacobi Equations. J Comput Phys (2004) 196:367–91. doi:10.1016/j.jcp.2003.11.007

CrossRef Full Text | Google Scholar

15. Vogel O, Cristiani E. Numerical Schemes for Advanced Reflectance Models for Shape from Shading. In: Proceedings of the 18th IEEE International Conference on Image Processing (2011) 5–8. doi:10.1109/ICIP.2011.6116621

CrossRef Full Text | Google Scholar

16. Ju YC, Tozza S, Breuss M, Bruhn A, Kleefeld A. Generalised Perspective Shape from Shading with Oren-Nayar Reflectance. In: Proceedings of the 24th British Machine Vision Conference (2013). doi:10.5244/C.27.42

CrossRef Full Text | Google Scholar

17. Galliani S, Ju YC, Breuß M, Bruhn A. Generalised Perspective Shape from Shading in Spherical Coordinates. In: Proceedings of the International Conference on Scale Space and Variational Methods in Computer Vision (2013) 222–33. doi:10.1007/978-3-642-38267-3_19

CrossRef Full Text | Google Scholar

18. Sethian JA. Fast Marching Methods. SIAM Rev (1999) 41:199–235. doi:10.1137/S0036144598347059

CrossRef Full Text | Google Scholar

19. Tozza S, Falcone M. Analysis and Approximation of Some Shape-From-Shading Models for Non-lambertian Surfaces. J Math Imaging Vis (2016) 55:153–78. doi:10.1007/s10851-016-0636-x

CrossRef Full Text | Google Scholar

20. Tozza S, Falcone M. A Comparison of Non-lambertian Models for the Shape-From-Shading Problem. In: M Breuß, A Bruckstein, P Maragos, and S Wuhrer, editors. Perspectives in Shape Analysis. Cham, Switzerland: Springer International Publishing AG (2016) 15–42. doi:10.1007/978-3-319-24726-7_2

CrossRef Full Text | Google Scholar

21. Yang D, Deng J. Shape from Shading through Shape Evolution. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (2018) 3781–90. doi:10.1109/CVPR.2018.00398

CrossRef Full Text | Google Scholar

22. Henderson P, Ferrari V. Learning Single-Image 3D Reconstruction by Generative Modelling of Shape, Pose and Shading. Int J Comput Vis (2020) 128:835–54. doi:10.1007/s11263-019-01219-8

CrossRef Full Text | Google Scholar

23. Tokieda K, Iwaguchi T, Kawasaki H. High-frequency Shape Recovery from Shading by CNN and Domain Adaptation. In: Proceedings of the IEEE International Conference on Image Processing (2021) 3672–6. doi:10.1109/ICIP42928.2021.9506450

CrossRef Full Text | Google Scholar

24. Wang G, Han J, Zhang X. Three-dimensional Reconstruction of Endoscope Images by a Fast Shape from Shading Method. Meas Sci Technol (2009) 20:125801. doi:10.1088/0957-0233/20/12/125801

CrossRef Full Text | Google Scholar

25. Wang G, Cheng J. Three-Dimensional Reconstruction of Hybrid Surfaces Using Perspective Shape from Shading. Optik (2016) 127:7740–51. doi:10.1016/j.ijleo.2016.05.120

CrossRef Full Text | Google Scholar

26. Wang G, Zhang X, Cheng J. A Unified Shape-From-Shading Approach for 3D Surface Reconstruction Using Fast Eikonal Solvers. Int J Opt (2020) 2020:6156058. doi:10.1155/2020/6156058

CrossRef Full Text | Google Scholar

27. Wang G, Zhang X. Fast Shape-From-Shading Algorithm for 3D Reconstruction of Hybrid Surfaces Under Perspective Projection. Acta Optica Sinica (2021) 41:1215003. doi:10.3788/AOS202141.1215003

CrossRef Full Text | Google Scholar

28. Crandall MG, Lions PL. Viscosity Solutions of Hamilton-Jacobi Equations. Trans Amer Math Soc (1983) 277:1–42. doi:10.1090/S0002-9947-1983-0690039-8

CrossRef Full Text | Google Scholar

29. Bardi M, Capuzzo-Dolcetta I. Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations. Boston, MA: Birkhäuser Press (1997).

Google Scholar