Effects of Measurement Configurations on the Sensitivity of Morpho Butterfly Scales Based Chemical Biosensor

The Morpho butterfly wing with tree-shaped alternating multilayer is an effective chemical biosensor to distinguish between ambient medium, and its detection sensitivity is inextricably linked to the measurement configuration including incident angle, azimuthal angle, and so on. In order to reveal the effects and the selection of measurement configuration. In this work, the model of the Morpho butterfly wing is built using the rigorous coupled-wave analysis method by considering its profile is a rectangular-groove grating. On basis of the above model, the reflectivity of different diffraction orders at a different incident angle and azimuthal angle is calculated, and the influence of incident angle and azimuthal angle on performance of Morpho butterfly scales-based biosensor is analyzed. The optimal incident angle at each azimuthal angle is given according to the proposed choice rule, then the azimuthal angle and the corresponding incident angle can be selected further.

Introduction

In recent years, the Morpho butterfly wings are widely studied for their selective absorption and reflection of electromagnetic waves with different wavelengths [1–6]. The structural color—Morpho blue is the main color of the Morpho butterfly wing in connection with various optical phenomena such as scattering, interference, and diffraction [7, 8]. Several optical modeling methods such as finite-difference time-domain (FDTD) [7, 9, 10] and rigorous coupled-wave analysis (RCWA) [11–13] have been introduced to analyze the optical properties of the Morpho blue. The analysis has shown that the tree-like microstructure existed in the wing scales is the major cause of Morpho blue formation [11]. According to their conclusion, many applications of the tree-like microstructure have been proposed, including the establishment of color selection ability by fabricating the tree-like structure [10, 14–16], distinguishing between different vapors [2, 17, 18] and different ambient liquids [13, 19, 20] with butterfly wing.

In a famous application proposed by Potyrailo [18] which is using the butterfly wing as a biosensor to distinguish vapors, they showed that the iridescent scales of the Morpho sulkowskyi butterfly have different optical responses when it acts on different individual vapors, and this optical response dramatically outperforms the existing nano-engineered photonic sensors. By further expanding the application range of butterfly wing-based biosensors, Yang et al. [13] also found that the color and the brightness of the butterfly wings change significantly when the surrounding medium of the butterfly wing was altered. Namely, they demonstrated that the reflectance peak shift (RPS) is proportionate to the refractive index of the ambient medium. However, the simulations and experiments were inclined to conduct at normal incidence with an azimuthal angle of 0° under TM mode. This leads us to consider several questions:

1) Does the measurement configuration which is the combination of normal incidence and zero-degree azimuthal angle is the only one that can ensure the RPS is proportional to the refractive index of ambient medium?

2) Does the law that the RPS is proportional to the refractive index of the ambient medium still fulfilled if the measurement configuration varies?

3) Can we select an optimal measurement configuration to maximize the RPS for an ambient medium?

To answer these questions, we simulated the reflectance for the tree-like structure under different ambient media at different incident angles and azimuthal angles.

Modeling Based on RCWA Methods

One essential feature in the Morpho butterfly wing scale which is widely studied is the tree-shaped alternating multilayer as shown in Figure 1A. According to the previous work [7], the multilayer interference phenomenon and grating diffraction phenomenon are the two main reasons that cause the structural colours of the Morpho butterfly wing. This sliced structure is suitable for calculating in RCWA, here we choose to emphasize the grating diffraction phenomenon using RCWA. The complex refractive indexes of region 1 and region 2 are n₁ and n₂ respectively. In the rectangular coordinate system, incident angle and azimuthal angle are respectively $\theta$ and $\phi$, the intersection angle between incident electric vector E_inc and incident wave vector k₁ is polarizing angle $\psi$. The tree-shaped alternating multilayer model is an ordered array of ridges with lamellae running nearly parallel to the substrate of the scale and periodically staggered on both sides of each ridge, which can be characterized by the following parameters: the thickness of the lamellae H_r; the thickness of the air gap H_g; the offset ΔH between the left lamellae and the corresponding right lamellae along the Z-axis; the width of the bottom lamellae W_r; the width of the trunk W_t; the height between the top surface of the substrate and the bottom surface of the longest lamellae H_o; the thickness of the substrate H_s; the height of the trunk H_t; and the period $\mathit{\Lambda }$. As shown on the right-hand side of Figure 1B, the tree-shaped structure is easy to be sliced into 33 layers, and layer l can be regarded as a rectangular grating with width and height of W_l and H_l respectively. For the sliced structure, it is obvious that it’s a typical multiple overlay model.

FIGURE 1

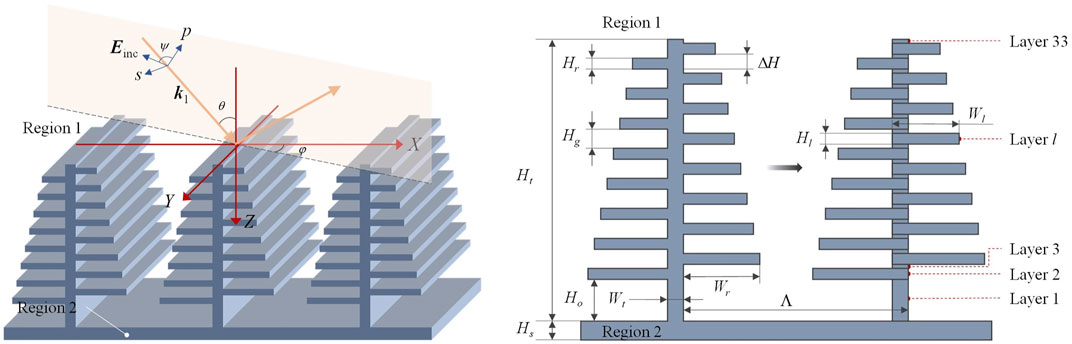
FIGURE 1. (A) Geometry of the Morpho butterfly wing scale; (B) layers division for inverse modeling based on RCWA.

In the grating region, the periodic relative permittivity of layer l is expandable in the forms of Fourier series [21, 22]:

${\epsilon }_l\left(x\right)={\displaystyle \sum _n{\epsilon }_{l,n}\exp \left(\text{j}\frac{2\pi n}{\mathit{\Lambda }}\right)}$(2-1)

where ${\epsilon }_{l,n}$ is the nth component of the Fourier series of layer l.

The electrical component of the incident plane wave defined as an incident normalized electrical field is given by:

${\mathit{E}}_{\text{inc}}=\mathit{u}\exp \left(-\text{j}{\mathit{k}}_1\cdot \mathit{r}\right)$(2-2)

Where u is the normalized electrical component, r is the position vector of an arbitrary point on the wave plane.

According to the Rayleigh expansion, the normalized solutions in region 1 (Z < 0) and region 2 (Z > H_t) are expressed as [23, 24]:

${\mathit{E}}_1={\mathit{E}}_{\text{inc}}+{\displaystyle \sum _i{\mathit{R}}_i\exp \left[-\text{j}\left(k_{xi}x+k_{y}y-k_{1,zi}z\right)\right]}$(2-3)

${\mathit{E}}_2={\displaystyle \sum _i{\mathit{T}}_i\exp \left\{-\text{j}\left[k_{xi}x+k_{y}y+k_{2,zi}\left(z-d\right)\right]\right\}}$(2-4)

Where R_i and T_i are amplitude vectors of ith incident wave and reflected wave. k_xi, k_y, and k_m,zi (m = 1,2) are the X, Y, and Z components of the ith diffraction wave vector, respectively. The mathematic expressions of k_xi, k_y and k_m,zi are given by:

$k_{xi}=k_0\left(n_1\sin \theta \cos \phi -i\lambda /\Lambda \right)$(2-5)

$k_y=k_0{n}_1\sin \theta \sin \phi$(2-6)

$k_{m,zi}=\{\begin{array}{c}+\sqrt{{\left(k_0{n}_m\right)}^2-k_{xi}^2-k_y^2},{\left(k_0{n}_m\right)}^2\ge k_{xi}^2+k_y^2\\ -\text{j}\sqrt{k_{xi}^2+k_y^2-{\left(k_0{n}_m\right)}^2},{\left(k_0{n}_m\right)}^2<k_{xi}^2+k_y^2\end{array},m=\mathrm{1,2}$(2-7)

In the grating region (0 < Z < D), the electrical field and magnetic field of layer l can be expressed by the Fourier expansion of the harmonic waves in space as follows [22]:

${\mathit{E}}_{l,g}={\displaystyle \sum _i\left[S_{l,xi}\left(z\right)\widehat{\mathit{x}}+S_{l,yi}\left(z\right)\widehat{\mathit{y}}+S_{l,zi}\left(z\right)\widehat{\mathit{z}}\right]}\exp \left[-\text{j}\left(k_{xi}x+k_{y}y\right)\right]$(2-8)

${\mathit{H}}_{l,g}=-\text{j}\sqrt{\frac{{\epsilon }_0}{{\mu }_0}}{\displaystyle \sum _i\left[U_{l,xi}\left(z\right)\widehat{\mathit{x}}+U_{l,yi}\left(z\right)\widehat{\mathit{y}}+U_{l,zi}\left(z\right)\widehat{\mathit{z}}\right]}\exp \left[-\text{j}\left(k_{xi}x+k_{y}y\right)\right]$(2-9)

where ${\mathit{S}}_{l,i}\left(z\right)=S_{l,xi}\left(z\right)\widehat{\mathit{x}}+S_{l,yi}\left(z\right)\widehat{\mathit{y}}+S_{l,zi}\left(z\right)\widehat{\mathit{z}}$ and ${\mathit{U}}_{l,i}\left(z\right)=U_{l,xi}\left(z\right)\widehat{\mathit{x}}+U_{l,yi}\left(z\right)\widehat{\mathit{y}}+U_{l,zi}\left(z\right)\widehat{\mathit{z}}$ related to W_l and H_l are the electrical and magnetic components of the ith space harmonic vector in layer l, respectively. And E_l,g and H_l,g satisfy Maxwell’s equation in the grating region:

$\nabla \times {\mathit{E}}_{l,g}=-\text{j}\omega {\mu }_0{\mathit{H}}_{l,g}$(2-10)

$\nabla \times {\mathit{H}}_{l,g}=\text{j}\omega {\epsilon }_0{\epsilon }_l\left(x,y\right){\mathit{E}}_{l,g}$(2-11)

Where ${\epsilon }_0$ and ${\mu }_0$ are permittivity and permeability in free space.

By substituting (2-8), (2-9) into (2-10), (2-11) and eliminating E_l,gz and H_l,gz (the Z components of E_l,g and H_l,g), and applying the inverse rule [25], the coupled-wave equations under TE mode can be obtained:

$\left[{\partial }^2{\mathbf{S}}_{l,y}/\partial {\left(z^{\prime }\right)}^2\right]=\left[{\mathbf{A}}_l\right]\left[{\mathbf{S}}_{l,y}\right]$(2-12)

Where, ${\mathit{S}}_{l,y}$ is the Y component of ${\displaystyle \sum {\mathit{S}}_{l,i}\left(z\right)}$, ${\mathit{A}}_l={\mathit{K}}_x-{\mathit{E}}_l$ and ${\mathit{K}}_x$ is an N-dimensional diagonal matrix (N is the number of Fourier series) whose diagonal elements are defined by k_xi/k₀, E_l is an N-dimensional Toeplitz matrix composed of ${\epsilon }_{l,g}$, whose element of the pth row and the qth column is ${\epsilon }_{l,p-q}$.

Likewise, the coupled-wave equations under TM mode can be obtained:

$\left[{\partial }^2{\mathbf{U}}_{l,\mathrm{y}}/\partial {\left(z^{\prime }\right)}^2\right]={\left[{\mathbf{F}}_l\right]}^{-1}\left[{\mathbf{B}}_l\right]\left[{\mathbf{U}}_{l,\mathrm{y}}\right]$(2-13)

Where, ${\mathit{U}}_{l,y}$ is the Y component of ${\displaystyle \sum {\mathit{S}}_{l,i}\left(z\right)}$, ${\mathit{F}}_l$ is an N-dimensional Toeplitz matrix composed of ${\left(\frac{1}{\epsilon }\right)}_{l,g}$, whose element of the pth row and the qth column is ${\left(\frac{1}{\epsilon }\right)}_{l,p-q}.{\mathbf{B}}_{\mathit{l}}$ is expressed by ${\mathit{B}}_l={\mathit{K}}_x{\mathit{E}}_l^{-1}{\mathit{K}}_x-\mathit{I}$.

Then the ${\mathit{S}}_{l,i}\left(z\right)$ and ${\mathit{U}}_{l,i}\left(z\right)$ can be obtained by solving the coupled-wave equations (2-12) and (2-13).

Finally, to get the electric field component R_s under TE mode ($\psi =90°$) and magnetic field component R_p under TM mode ($\psi =\text{0}°$) of the reflected wave, the continuous conditions should be considered on the boundaries of every layer and at interfaces of the adjacent region.

Simulations and Discussions

In simulations, the tree-shaped structure has the same complex refractive index 1.56 + 0.06i [26] as the substrate, and the complex refractive index is constant in the wavelength range [27], which is from 193 to 1,000 nm with a wavelength step of 5 nm. The difference between adjacent lamellae on both sides of the trunk is a constant of 20 nm. The tree-shaped alternating multilayer is periodic along the X-axis with a pitch $\mathit{\Lambda }$ of 700 nm. The values of other structural parameters shown in Figure 1 are set in Table 1. The modeling and parameters solution is carried out with the program we have written in MATLAB.

TABLE 1

TABLE 1. The values of structural parameters.

Before studying the impact of measurement configurations on the sensitivity of Morpho butterfly scales-based chemical biosensor, we take account of a special condition in Zhu’s study [7]. In which case a diffraction grating consists of alternating multilayers was illuminated by a beam at normal incidence with a specified wavelength under TM polarization. Then the reflectivity under different diffraction orders was calculated. The results showed that only the first-order diffraction is mainly responsible for the reflectivity peak that causes the structural colour with waveband of visible light. Likewise, we simulated the reflectivity at normal incidence under zeroth and first-order diffraction for the structure in Figure 1 with visible light. Since an arbitrarily polarized light can be transformed into a linear combination of TE and TM polarized light, we focus on the simulations for TE and TM polarization. In the simulations, the surrounding mediums of the structure are air, carbinol, and ethanol, respectively.

The results shown in Figure 2 indicate that the reflectivity under first-order diffraction is indeed mainly responsible for the peak of total reflectivity in the three cases, while the reflectivity under zeroth-order diffraction is suppressed owing to the destructive interference of the multilayer in the visible waves. However, the effects of reflectivity caused by different incident angles and azimuthal angles are rarely considered. For a diffraction grating, different measurement configurations differ in their sensitivity grades [28–30]. Once the optimal measurement configuration is obtained, the optimal measurement does become available.

FIGURE 2

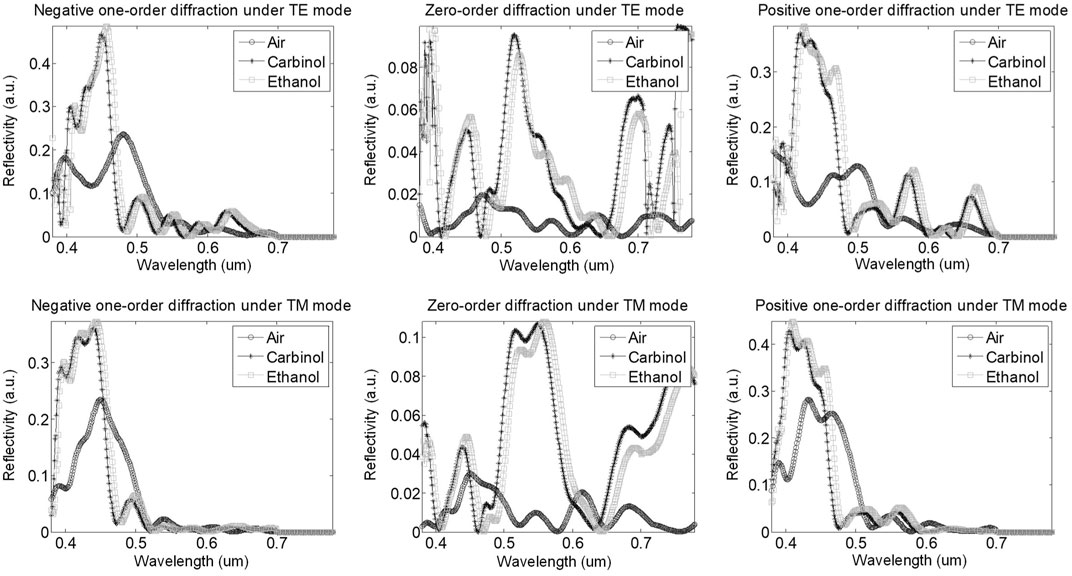
FIGURE 2. Simulated results of the reflectivity of zeroth and first-order diffraction under TE and TM mode.

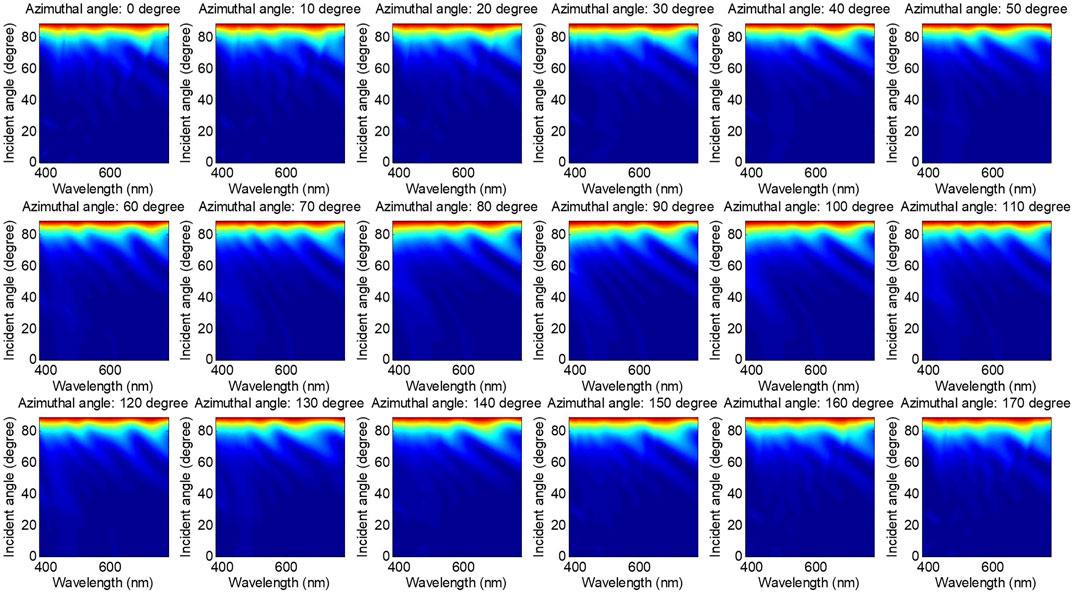
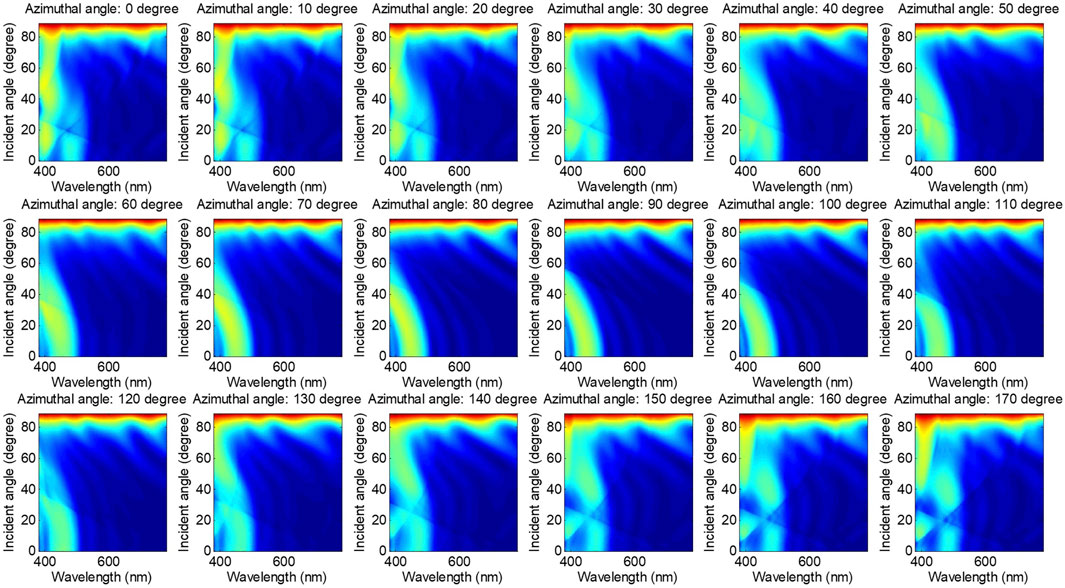
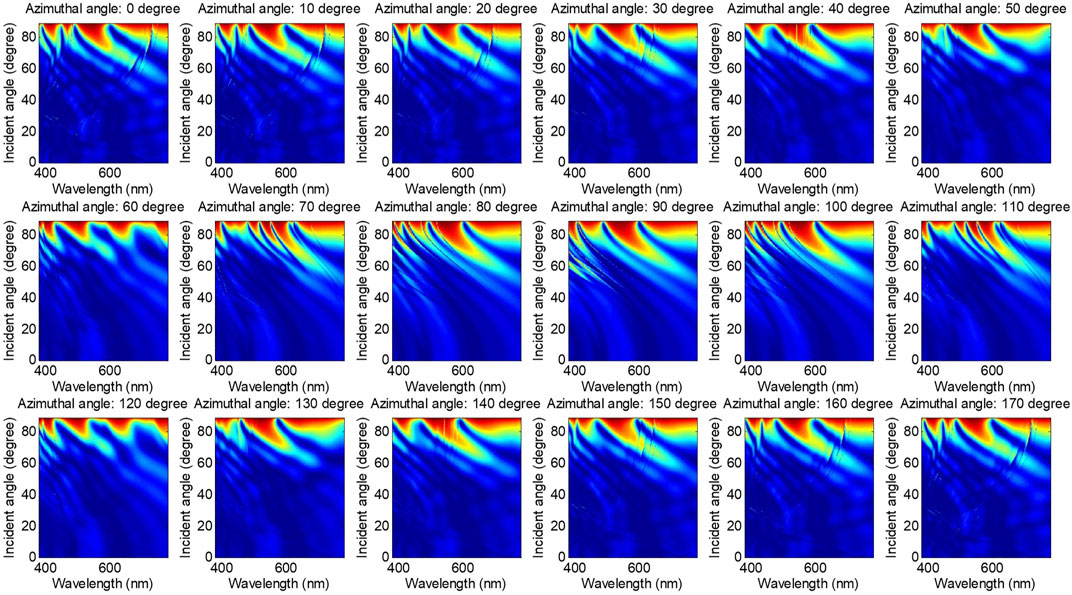
For the Morpho butterfly scales-based chemical biosensor, the refractive index of ambient gas or liquid is characterized through the colour of the Morpho butterfly’s wing. Therefore, to find the optimal measurement configuration and enhance the colour change more markedly. We simulated the reflectivity of the structure in Figure 1 at different incident angles and azimuthal angles (the range of the incident angle was set from 0 to 89° with an increment of 0.05°, and the range of the azimuthal angle was set from 0 to 170° with an increment of 10°) using visible light under the TE mode. Since the difference between carbinol and ethanol is only the refractive index, we do not simulate both. In the following simulations which are from Figures 3 to 6, the ambient materials are air (refractive index equals 1) and ethanol (refractive index equals 1.36), respectively.

FIGURE 3

FIGURE 3. Simulated results of zeroth-order diffraction reflectivity of air under TE mode.

FIGURE 4

FIGURE 4. Simulated results of total diffraction orders reflectivity of air under TE mode.

FIGURE 5

FIGURE 5. Simulated results of zeroth-order diffraction reflectivity of alcohol under TE mode.

FIGURE 6

FIGURE 6. Simulated results of total diffraction orders reflectivity of alcohol under TE mode.

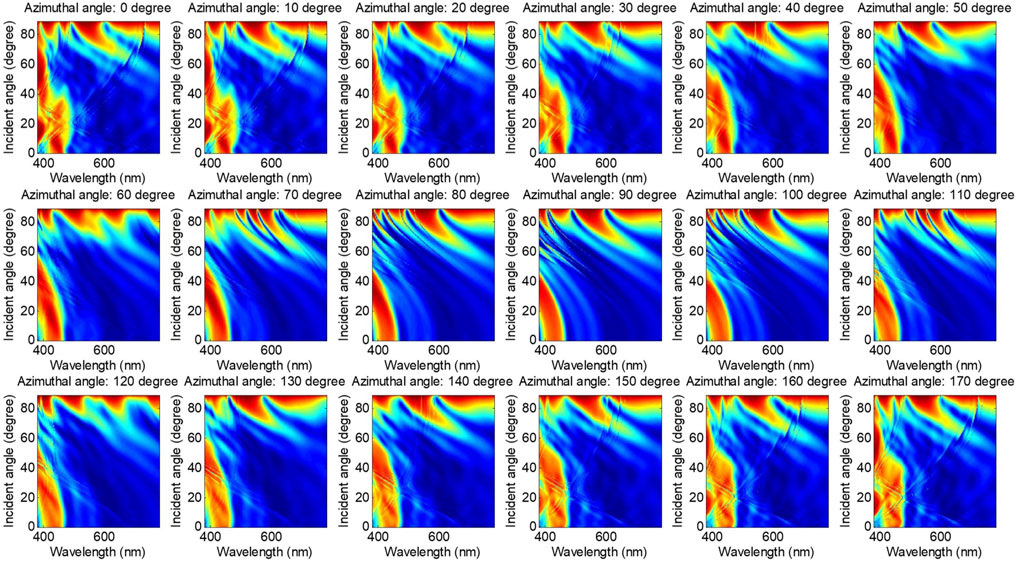
In Figure 4, the reflectivity of the total diffraction orders was simulated for the Morpho butterfly’s wing with the ambient air. When compared to Figure 3 apples-to-apples, we find that the sum of the reflectivity aside from zeroth-order diffraction is mainly responsible for the left part of each subfigure. Namely, it is the chief cause of structural colour. And the left part of each subfigure varies with the azimuthal angle, which means the sum of the reflectivity of the diffraction orders other than the zeroth order is sensitive to the azimuthal angle. These phenomena show that if we want to characterize the structural parameters or the optical parameters of the butterfly wing using the Optical Critical Dimension (OCD) liked method, the zeroth-order should not be used. In addition, visually, we can find that the structural colour of the Morpho butterfly is not always blue under some specified incident angle and azimuthal angle—The simulation is carried out under the condition of 110° azimuthal angle for example. The total reflectivity of the butterfly wing is low in the incident angle region which is from 42 to 70 under the 110° azimuthal angle, in which case the colour of the Morpho butterfly will look a lit bit like black to the naked eye. Then we have carried out other simulations for the butterfly wing which is surrounded by the liquid of ethanol, the simulations are shown in Figures 5, 6.

When doing the apples-to-apples comparison with Figures 3, 5 shows the same characteristic, the reflectivity of zeroth-order diffraction is insensitivity to the azimuthal angle, and there is an upper threshold of incident angle below which the reflectivity is quite low under all the wavelengths. The direct difference between Figures 3, 5 is that the reflectivity obtained above the incident angle of 80° is more regular in Figure 3. In contrast, there are many peaks and valleys on the top of each subfigure in Figures (4–6) share similar characteristics that result from the sum of the total diffraction orders except for the zeroth-order. Also, the sum of the non-zeroth diffraction orders is sensitive to the azimuthal angle when the butterfly wing is surrounded by the liquid of ethanol.

In Yang’s study [13], they showed that the reflectance peak migrates from 475 to 565nm and 570 nm when the surrounding medium change from air to carbinol and ethanol, respectively. Moreover, the law that the wavelength of the reflectivity peak of total orders increases with the refractive index of ambient medium can be discovered. It must be stressed that the simulation and experiment were conducted in the conditions of normal incidence and the azimuthal angle of 0°. But when we adjust the incident angle and azimuthal angle in the simulation, the law introduced above no longer obtain in some cases. The simulation results are shown as follows:

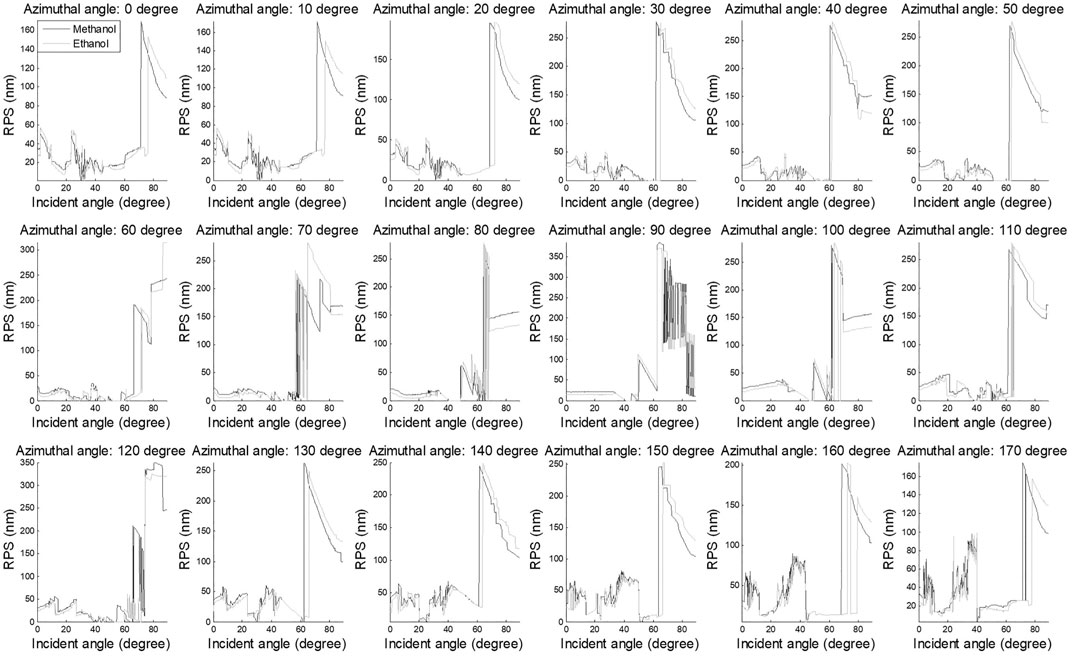
We can detect that the two curves which denote the RPS of carbinol and ethanol under total diffraction orders have some intersections. These appearances show that the RPS of the carbinol is bigger than that of ethanol under some specified incident angles and azimuthal angles. Take the case of the sub-figure in the top-left corner of Figure 7, we can see that the RPS of the carbinol is smaller than that of the ethanol with incident angle range of 60–75°, it quite coheres with the conclusion in Yang’s paper [13]. However, the RPS of the carbinol is bigger than that of the ethanol between the incident angle of 75 and 85°. Thus, if the RPS should be used for distinguishing between ambient media of the butterfly wing scale-based biosensor, the measurement configuration must be selected carefully to ensure that the RPS is proportional or inversely proportional to the refractive index of ambient medium.

FIGURE 7

FIGURE 7. Simulated results of RPS of total diffraction orders.

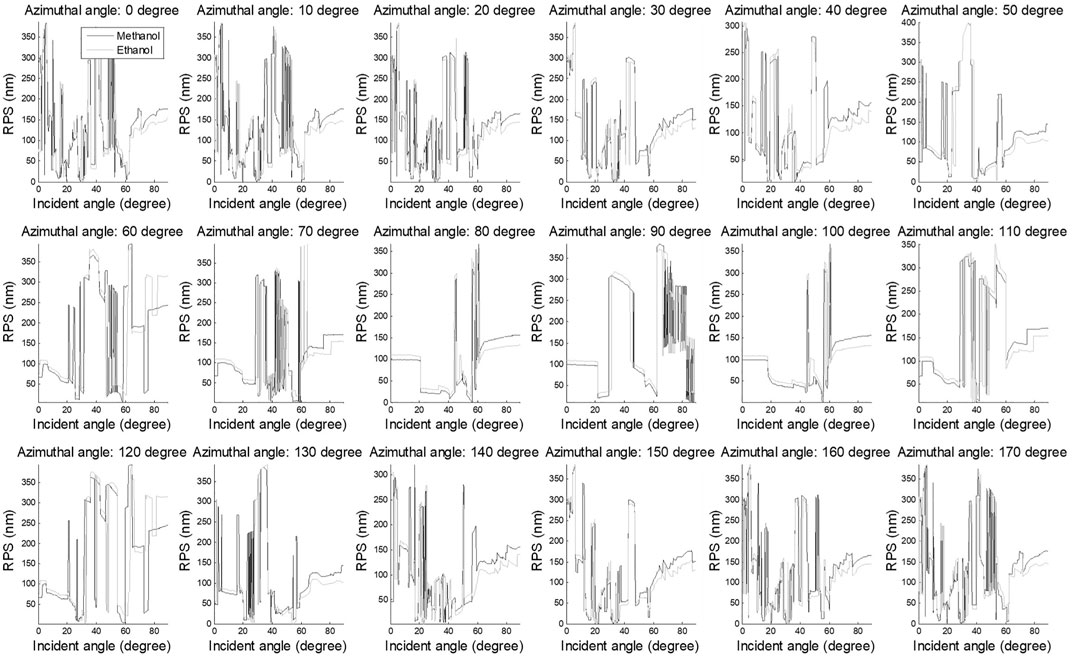
In most researches of nano/micro-structures, zeroth-order diffraction is the highest priority. Hence, we also simulate the RPS under zeroth-order diffraction for the ambient medium of carbinol and ethanol, respectively. The simulation result is shown in Figure 8.

FIGURE 8

FIGURE 8. Simulated results of RPS of zeroth-order diffraction.

It is obvious that the curves in Figure 8 show more volatility compared with the curves in Figure 7, and we can hardly determine whether one is higher between two curves. In other words, the zeroth-order diffraction is not a very appropriate observation parameter to distinguish two ambient media with similar refractive index. Even so, we can find that when the azimuthal angle is set as 80, 90, and 100°, the number of oscillations is much less than the other sub-figures, and the curve has longer smooth parts.

Since the RPS is used to represent and characterize different ambient media in the Morpho butterfly wing-based biosensor, the difference between the RPSs should be maximized for ambient medium with a similar refractive index. Furthermore, not all measurement configurations can guarantee that the RPS is proportional to the refractive index of ambient medium in the simulations discussed above, and given the uncertainty (including random noise, system noise, the uncertainty of tool’s incident angle, and azimuthal angle, etc.) in the practical measurement, those continuously increased incident angles under a specified azimuthal angle should be select to guarantee a trend that the relative bigger refractive index corresponds to a bigger RPS. Hence, the measurement configuration such as the incident angle and azimuthal angle should be set prudentially. We have extracted those measurement configurations that can satisfy the relationship of direct proportion between the RPS and refractive index for both zeroth-order diffraction and total diffraction orders beforehand. The statistical result is shown in Figure 9 (the range of incident angle in the above simulations is from 0 to 89° with an increment of 0.25°, which means the number of incident angles is 357):

FIGURE 9

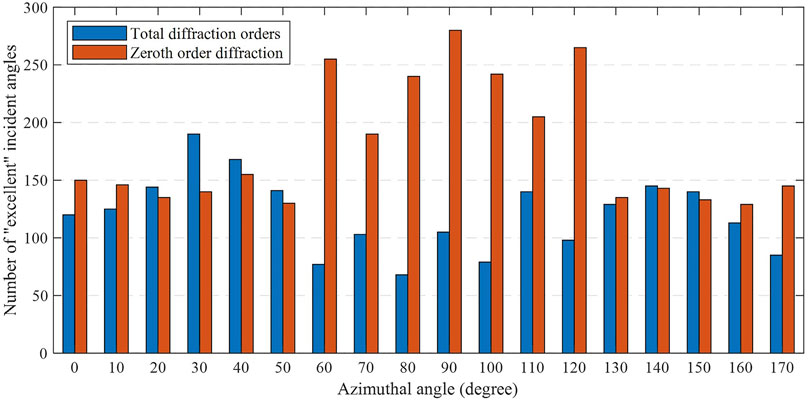
FIGURE 9. The number of “excellent” incident angles of total diffraction orders and zero-order diffraction.

In Figure 9, the “excellent” incident angles mean that if the measurement is conducted under these incident angles, the RPS is proportional to the refractive index of ambient medium. From the two sub-figures, we can observe that the number of “excellent” incident angles under zeroth-order diffraction is bigger than that of the total diffraction orders for most of the azimuthal angles. One issue is that the difference of RPS for ambient medium should be maximized to ensure good sensitivity of the biosensor. Hence, the incident angle that can maximize the difference should be picked up from those “excellent” incident angles under a specified azimuthal angle. The other issue is that the continuous sub-range of incident angle that contains our picks should strive to be longer, because of the uncertainty of tool’s incident angle, etc. in the practical measurement. Based on this strategy, the well-chosen incident angles which we called optimal incident angles are shown in Figure 10B.

FIGURE 10

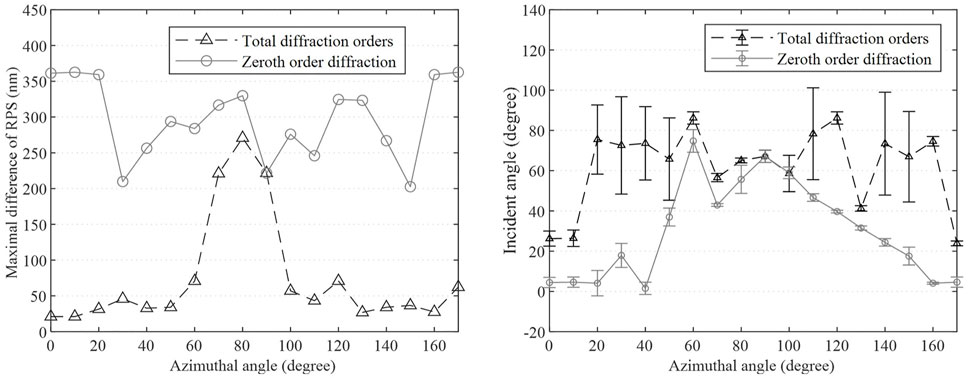
FIGURE 10. (A) The maximal RPS difference and (B) continuous incident angle range of total diffraction orders and zeroth-order diffraction at each azimuthal angle.

In Figure 10A, the maximal difference of RPS between ambient carbinol and ethanol under total diffraction orders is 275 nm at the azimuthal angle of 80°, and the corresponding optimal incident angle is 68°. However, for the zeroth-order diffraction, the RPS is over 200 nm under all the azimuthal angles. In Figure 10B, the continuous ranges not only contain the optimal incident angle but also ensure the RPS is proportional to the refractive index of the ambient medium. For the azimuthal angle of 80°, the continuous range of corresponding incident angle is too short, it will lead to the criterion of direct proportion may not be valid at larger uncertainty in practical measurement. Compared with the total diffraction orders, the zeroth-order diffraction can provide a bigger difference of RPS between the carbinol and ethanol under a few incident angles and azimuthal angles. However, the continuous ranges of incident angles have shorter lengths for most of the azimuthal angles. Thus, if we want to distinguish two different ambient media accurately, a perfect tradeoff should be gained among the RPS and the continuous range before measuring.

Conclusion

In this paper, the impact of incident angle and azimuthal angle on Morpho butterfly scales-based biosensors has been investigated. According to the simulation result of reflectivity under zeroth-order diffraction and non-zeroth order diffraction, we can conclude that the reflectivity of zeroth-order diffraction is less sensitive to the azimuthal angle than of non-zeroth order diffraction, and the non-zeroth order diffraction is a major contributor to structural color for most incident angles. Thus, we suggest that zeroth-order diffraction should not be used to characterize the structural parameters or the optical parameters of the butterfly wing by the method parallel to OCD. Furthermore, we have calculated the RPS of carbinol and ethanol relative to the air, the law obtained at normal incidence and zero-degree azimuthal angle is no longer active in some cases. The appropriate incident angle and azimuthal angle must be reconsidered. On the one hand, we hope the RPS is proportional to refractive index, and have obvious difference among ambient media with similar reflectivity index. On the other hand, we also expect the incident angle that satisfies previous point to have a wider contiguous range. Therefore, a compromise between above two points can be made, according to the maximal RPS difference and the continuous range of optimal incident angles at each azimuthal angle we have given. Theoretically, the selected configuration can provide better robustness and accuracy especially if exist in larger uncertainty of measurement. In the future work, we will carry out experiments for further verification of this beneficial effect.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

HZ, ST, and CL performed the simulations under the guidance of ZD and LN, ZD, HZ, and XW wrote the manuscript with contributions from all.

Funding

National Natural Science Foundation of China (Grant No. 51975191).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Li Q, Zeng Q, Shi L, Zhang X, Zhang KQ. Bio-Inspired Sensors Based on Photonic Structures of Morpho Butterfly Wings: A Review. J Mater Chem C (2016) 4(9):1752–63. doi:10.1039/C5TC04029A

CrossRef Full Text | Google Scholar

2. He J., Villa NS., Luo Z., An S., Shen Q., Tao P., et al. Integrating Plasmonic Nanostructures with Natural Photonic Architectures in Pd-Modified Morpho Butterfly Wings for Sensitive Hydrogen Gas Sensing. RSC Adv (2018) 8(57):32395–400. doi:10.1039/C8RA05046E

CrossRef Full Text | Google Scholar

3. De Bellis I, Ni B, Martella D, Parmeggiani C, Keller P, Wiersma DS., et al. Color Modulation in Morpho Butterfly Wings Using Liquid Crystalline Elastomers. Adv Intell Syst (2020) 2(9):2000035. doi:10.1002/aisy.202000035

CrossRef Full Text | Google Scholar

4. Luo Z., Weng Z., Shen Q., An S., He J., Fu B., et al. Vapor Detection through Dynamic Process of Molecule Desorption from Butterfly Wings. Pure Appl Chem (2020) 92(2):223–32. doi:10.1515/pac-2019-0118

CrossRef Full Text | Google Scholar

5. Yamashita K, Kunitsu K, Hattori T, Kuwahara Y, Saito A. Demonstration of a Diffraction-Based Optical Diffuser Inspired by the Morpho Butterfly. Opt Express (2021) 29(19):30927–36. doi:10.1364/OE.436193

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Song B, Johansen VE, Sigmund O, Shin JH. Reproducing the Hierarchy of Disorder for Morpho-Inspired, Broad-Angle Color Reflection. Sci Rep (2017) 7(1):1–8. doi:10.1038/srep46023

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhu D, Kinoshita S, Cai D, Cole JB. Investigation of Structural Colors inMorphobutterflies Using the Nonstandard-Finite-Difference Time-Domain Method: Effects of Alternately Stacked Shelves and ridge Density. Phys Rev E (2009) 80(5):051924. doi:10.1103/PhysRevE.80.051924

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Giraldo MA, Stavenga DG. Brilliant Iridescence of Morpho Butterfly wing Scales Is Due to Both a Thin Film Lower Lamina and a Multilayered Upper Lamina. J Comp Physiol A (2016) 202(5):381–8. doi:10.1007/s00359-016-1084-1

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhang S, Chen Y. Nanofabrication and Coloration Study of Artificial Morpho Butterfly Wings with Aligned Lamellae Layers. Sci Rep (2015) 5(1):1–10. doi:10.1038/srep16637

CrossRef Full Text | Google Scholar

10. Rodríguez RE., Agarwal SP., An S., Kazyak E., Das D., Shang W., et al. Biotemplated Morpho Butterfly Wings for Tunable Structurally Colored Photocatalysts. ACS Appl Mater Inter (2018) 10(5):4614–21. doi:10.1021/acsami.7b14383

CrossRef Full Text | Google Scholar

11. Butt H, Yetisen AK, Mistry D, Khan SA, Hassan MU, Yun SH. MorphoButterfly-Inspired Nanostructures. Adv Opt Mater (2016) 4(4):497–504. doi:10.1002/adom.201500658

CrossRef Full Text | Google Scholar

12. Kim HM, Kim SH, Lee GJ, Kim K, Song YM. Parametric Studies on ArtificialMorphoButterfly Wing Scales for Optical Device Applications. J Nanomater (2015) 16(1):1–7. doi:10.1155/2015/451834

CrossRef Full Text | Google Scholar

13. Yang X, Peng Z, Zuo H, Shi T, Liao G. Using Hierarchy Architecture of Morpho Butterfly Scales for Chemical Sensing: Experiment and Modeling. Sensors Actuators A: Phys (2011) 167(2):367–73. doi:10.1016/j.sna.2011.03.035

CrossRef Full Text | Google Scholar

14. Zhang S, Chen Y, Lu B, Liu J, Shao J, Xu C. Lithographically-generated 3D Lamella Layers and Their Structural Color. Nanoscale (2016) 8(17):9118–27. doi:10.1039/C6NR00936K

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Watanabe K, Hoshino T, Kanda K, Haruyama Y, Kaito T, Matsui S. Optical Measurement and Fabrication from a Morpho-Butterfly-Scale Quasistructure by Focused Ion Beam Chemical Vapor Deposition. J Vac Sci Technol B (2005) 23(2):570–4. doi:10.1116/1.1868697

CrossRef Full Text | Google Scholar

16. Kang SH, Tai TY, Fang TH. Replication of Butterfly wing Microstructures Using Molding Lithography. Curr Appl Phys (2010) 10(2):625–30. doi:10.1016/j.cap.2009.08.007

CrossRef Full Text | Google Scholar

17. Poncelet O., Tallier G., Mouchet SR., Crahay A., Rasson J., Kotipalli R., et al. Vapour Sensitivity of an ALD Hierarchical Photonic Structure Inspired by Morpho. Bioinspir Biomim (2016) 11(3):036011. doi:10.1088/1748-3190/11/3/036011

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Potyrailo RA, Ghiradella H, Vertiatchikh A, Dovidenko K, Cournoyer JR, Olson E. Morpho Butterfly wing Scales Demonstrate Highly Selective Vapour Response. Nat Photon (2007) 1(2):123–8. doi:10.1038/nphoton.2007.2

CrossRef Full Text | Google Scholar

19. Han Z., Yang M., Li B., Mu Z., Niu S., Zhang J., et al. Excellent Color Sensitivity of Butterfly wing Scales to Liquid Mediums. J Bionic Eng (2016) 13(3):355–63. doi:10.1016/S1672-6529(16)60308-6

CrossRef Full Text | Google Scholar

20. Xue H., Liu D., Chi D., Xu C., Niu S., Han Z., et al. Toward the Burgeoning Optical Sensors with Ultra‐Precision Hierarchical Structures Inspired by Butterflies. Adv Mater Inter (2021) 8(15):2100142. doi:10.1002/admi.202100142

CrossRef Full Text | Google Scholar

21. Moharam MG, Gaylord TK, Pommet DA, Grann EB. Stable Implementation of the Rigorous Coupled-Wave Analysis for Surface-Relief Gratings: Enhanced Transmittance Matrix Approach. J Opt Soc Am A (1995) 12(5):1077–86. doi:10.1364/JOSAA.12.001077

CrossRef Full Text | Google Scholar

22. Moharam MG, Gaylord TK, Grann EB, Pommet DA. Formulation for Stable and Efficient Implementation of the Rigorous Coupled-Wave Analysis of Binary Gratings. J Opt Soc Am A (1995) 12(5):1068–76. doi:10.1364/JOSAA.12.001068

CrossRef Full Text | Google Scholar

23. Moharam MG, Gaylord TK. Coupled-Wave Analysis of Reflection Gratings. Appl Opt (1981) 20(2):240–4. doi:10.1364/AO.20.000240

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Gaylord TK, Moharam MG. Analysis and Applications of Optical Diffraction by Gratings. Proc IEEE (1985) 73(5):894–937. doi:10.1109/PROC.1985.13220

CrossRef Full Text | Google Scholar

25. Li L. Use of Fourier Series in the Analysis of Discontinuous Periodic Structures. J Opt Soc Am A (1996) 13(9):1870–6. doi:10.1364/JOSAA.13.001870

CrossRef Full Text | Google Scholar

26. Vukusic P, Sambles JR, Lawrence CR, Wootton RJ. Quantified Interference and Diffraction in Single Morpho Butterfly Scales. Proc R Soc Lond B (1999) 266(1427):1403–11. doi:10.1098/rspb.1999.0794

CrossRef Full Text | Google Scholar

27. Wu W, Liao G, Shi T, Malik R, Zeng C. The Relationship of Selective Surrounding Response and the Nanophotonic Structures of Morpho Butterfly Scales. Microelectronic Eng (2012) 95:42–8. doi:10.1016/j.mee.2011.12.017

CrossRef Full Text | Google Scholar

28. Foldyna M., De Martino A., Garcia-Caurel E., Ossikovski R., Licitra C., Bertin F., et al. Critical Dimension of Biperiodic Gratings Determined by Spectral Ellipsometry and Mueller Matrix Polarimetry. Eur Phys J Appl Phys (2008) 42(3):351–9. doi:10.1051/epjap:2008089

CrossRef Full Text | Google Scholar

29. Novikova T, De Martino A, Hatit SB, Drévillon B. Application of Mueller Polarimetry in Conical Diffraction for Critical Dimension Measurements in Microelectronics. Appl Opt (2006) 45(16):3688–97. doi:10.1364/AO.45.003688

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Vagos P, Hu J, Liu Z, Rabello S. Uncertainty and Sensitivity Analysis and its Applications in OCD Measurements. Metrology, Inspection, and Process Control for Microlithography XXIII. Int Soc Opt Photon (2009) 7272: 543–551. doi:10.1117/12.814363

CrossRef Full Text | Google Scholar