- 1Department of Mathematics and Physics, Xinjiang Institute of Engineering, Urumqi, China
- 2College of Mathematics and System Sciences, Xinjiang University, Urumqi, China
In this article, the convergence speed and robustness of the consensus for several dual-layered star-composed multi-agent networks are studied through the method of graph spectra. The consensus-related indices, which can measure the performance of the coordination systems, refer to the algebraic connectivity of the graph and the network coherence. In particular, graph operations are introduced to construct several novel two-layered networks, the methods of graph spectra are applied to derive the network coherence for the multi-agent networks, and we find that the adherence of star topologies will make the first-order coherence of the dual-layered systems increase some constants in the sense of limit computations. In the second-order case, asymptotic properties also exist when the index is divided by the number of leaf nodes. Finally, the consensus-related indices of the duplex networks with the same number of nodes but non-isomorphic structures have been compared and simulated, and it is found that both the first-order coherence and second-order coherence of the network
1 Introduction
Consensus is a class of distributed coordination problems of multi-agent systems, and the essence of the problem is that all agents are required to achieve a common state value under some given control strategies. In the networked system, the agents are required to communicate with each other based on the graph of the network so that they can cooperate effectively to accomplish the predetermined goals.
As a valuable interdisciplinary research field, consensus problems have received more and more attention from scholars and engineers in recent years, and there exist many potential applications in several aspects related to consensus such as sensor networks, formation control, and decision making. Researchers have done many good research works on consensus from various perspectives [1–18] and factors including the dynamics order (first/second order [1–15] or higher order), communication ways (continuous or discontinuous [4, 6], the types of topologies (fixed or switching [5]), convergence time (finite time or fixed time [16, 17]), and control methods (intermittent control [6], adaptive control [7], impulsive control, etc.).
To solve the consensus problems, the linking structure among agents is always interpreted by the communication graph of the system, and the performance indices of consensus models, such as convergence speed [1, 8] and network coherence [10–14], can be characterized by the Laplacian eigenvalues of the graph. Synchronization problems, which share similar control strategies and have the same essence as consensus problems, are always connected with the network structure [19–24] and are studied from the angle of graph theory.
There exist a great many valuable articles on coordination problems with the application of Laplacian eigenvalues [1, 5–15, 20]. This enlightening research [1] has shown that the Fiedler eigenvalue λ2 of an undirected (or directed) graph can characterize the convergence speed of consensus problems.
In [9], the authors have investigated how the robustness depends on the properties of the Laplacian eigenvalues of graphs and give a derivation for the convergence speed and the H2 norms of several classic graphs.
In [10, 11], the notion of network coherence has been proposed, and it had been proved that the network coherence can be quantified by nonzero Laplacian eigenvalues. Ref. [13] studies the noisy consensus dynamics on windmill-type graphs, and it is found that graph parameters and the number of leaders have a profound impact on the studied consensus algorithms. In [14], the authors found that 5-rose networks with small size have high network coherence and can be considered to be more robust to noise than networks with low coherence.
Lately, multilayer network is a frontier research branch of network science, and the multilayered structure has many examples in reality, for instance, the interactions between power grid and Internet, friendship and family relations, or transportation and aviation networks. Multiplex networks are coupled multilayer networks where each layer consists of the same node set but possibly different graph structures and layers interact with each other only via counterpart nodes of different layers [24, 25].
Considering that many real-world systems have multilayered structures, it is necessary to extend the consensus theory related to the Laplacian spectrum to multilayered graph structures. From the perspective of the application, the star graph is one of the most classic computer network structures. Star-related topologies are widely considered in many fields including coordination control problems [9, 15, 21, 22, 26, 27].
Based on the above analysis, this paper considers some dual-layered networks with certain meaningful topologies constructed by the graph operations, and each of the layers contains star subgraphs. It is familiar that the star network can be viewed as a point-to-multipoint communication system, and the dual-layered networks with star subgraphs can be comprehended as adding communication links among the counterpart nodes of different layers of the networks.
This paper makes further efforts to use the theory of graph spectra for studying the consensus indices related to robustness and convergence speed. In this research, some scale-free networks with symmetric structures and star subgraphs are considered.
Based on the chosen undirected graphs, we mainly study the network coherence of consensus to communication noise with an application of the theory of graph spectra. Specifically, the main contributions of this paper are listed as follows:
1. Several novel duplex star-composed networks with different linking structures but the same number of nodes have been constructed by graph operations, and the similar structure is the basis for comparative optimization.
2. Methods of graph spectra are applied to derive the Laplacian spectrum. Several new results on the asymptotic behavior of the consensus indices have been acquired.
3. The results that the first-order robustness will increase by a certain value depending on the number of leaf nodes have been found.
The main aim of this research is to investigate the consensus indices of the dynamical system with additive stochastic disturbances, which are described as network coherence and derived through the Laplacian spectrum.
The paper is organized as follows. In Section 2, some notations on graph theory are summarized, and the relations between performance and Laplacian eigenvalues are explained. In Section 3, the constructions of two-layered systems and main results are given. In Section 4, combined with the theorem of algebraic graph theory, the simulation results are compared and analyzed in Section 3.
2 Preliminaries
2.1 Graph Theory and Notations
A complete graph of n vertices is denoted by Kn, and a star graph with k leaves is denoted by Sk, where the leaf refers to the vertex of degree 1.
To construct the novel dual-layered networks, the following graph operations are needed.
Definition 1. [29] (The corona of two graphs) Let G1 and G2 be two graphs on disjoint sets of n and k vertices, respectively. The corona G1◦G2 of G1 and G2 is defined as the graph obtained by taking one copy of G1 and n copies of G2 and then joining the ith vertex of G1 to every vertex in the ith copy of G2.
Definition 2. [30, 31] (The Cartesian product of two graphs) For two graphs G1 = (V1, E1) and G2 = (V2, E2), the Cartesian product graph G = G1 × G2 is the graph with vertex set V1 × V2, and there is an edge from the vertex (x1, y1) to the vertex (x2, y2) if and only if either x1 = x2 and y1, y2 ∈ E2 or y1 = y2 and x1, x2 ∈ E1.
Lemma 1. [32] The eigenvalues of a circulant matrix
where
Lemma 2. [29] Let G1 be any graph with n1 vertices and m1 edges and G2 be any graph with n2 vertices and m2 edges. Suppose that
i) Two multiplicity one eigenvalues
ii) δj + 1 ∈ spec (L (G1◦G2)) with multiplicity n1 for every eigenvalue δj (j = 2, …, n2) of S (L (G2)).
Lemma 3. [28] Let G be a graph of order n, and let
2.2 Relations Between Consensus Index and Laplacian Spectrum
The main objective of this work is to investigate the robustness of the two-layered systems when the dynamics have external disturbances and to accurately quantify the relations between the consensus indices and Laplacian eigenvalues. The robustness of the systems with noise can be described by the network coherence; in addition, the convergence speed, which can be characterized by λ2 (algebraic connectivity), is discussed.
i) The first-order system with noise is described by
with x ∈ RN and where ξ(t) ∈ RN is a vector of delta-correlated noise, and L(G) is the Laplacian matrix.
Definition 3. [10, 11] The first-order network coherence is defined as the mean steady-state variance of the deviation from the average of all node values:
It has been proved that [10, 11] the first-order coherence Hf is completely determined by the spectrum of L. Let the eigenvalues of L be 0 = λ1 < λ2 ≤ …, ≤ λN, and then the first-order network coherence is given by
ii) In the second-order system like the vehicle formation problem, there are N vehicles, each with a position and a velocity. The states in the system have a position vector x ∈ RN and a velocity vector v ∈ RN. The system can be described by
where ϱ is a 2N-vector of zero mean white noise processes. I is the identity matrix.The second-order coherence can be also determined by the eigenvalues of Laplacian matrix, that is,
The notion of network coherence implies the ability of maintaining its convergence trend under the effect of stochastic disturbances. The characterization of this consensus index has some similarity with the Kirhoff index [33, 34].
3 Main Results
As we mentioned in the Introduction part, the layered star-like networks of this paper are a kind of network in which all nodes have identical dynamics, and they have the topology composed by linking the center nodes among the basic star topologies. All the star-composed structures in this article are undirected and connected; therefore, the networks considered in this paper can achieve consensus. The following subsections are given to define the three classes of networks and to derive the coherence.
It should be noticed that in the case of
3.1 The consensus Indices for Network Topology
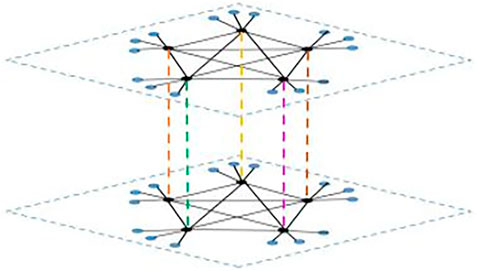
In this subsection, a sort of duplex star-like graph with symmetric structure based on
As shown in Figure 1, let each node in
The Laplacian matrix of
therefore, by the corresponding characteristic polynomial, one has
i) 0 and
ii)
iii)
iv)
v)
Therefore, it can be acquired that
then if the number of nodes k is fixed, let n → ∞, and then one has
The second-order coherence of the network can be calculated as follows:
when k is fixed, let n → ∞, and one has
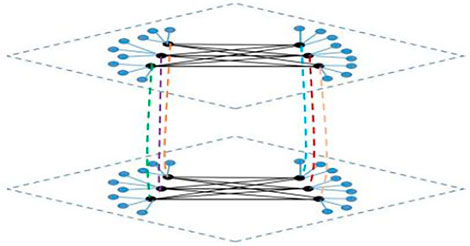
3.2 The Consensus Indices for Network Topology
As shown in Figure 2, let each node in
Since
where
and then one has
where the circulant matrices
Therefore, the asymptotic properties of coherence for
Therefore, by Lemma 2, the Laplacian spectrum of
1) p + 1 and
2)
3)
4)
5)
6)
7)
Therefore, the convergence speed has the description
Suppose that p is fixed, and then the first-order coherence of network
If p is fixed, then we have
and when n is fixed,
Remark 1. From the above derivation, it can be acquired that if the layered network has been added star topologies with each node, then H(1) will increase
If n is fixed, one has
If p is fixed, one has
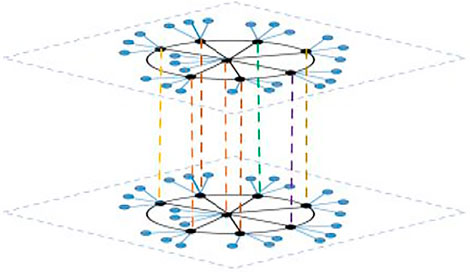
3.3 The Consensus Indices for Network Topology
In this subsection, based on the idea that the leaf nodes might have communications with each other, fan-graph structures are added on the original layered dual-star topology, i.e.,
where
Then it can be derived that
therefore, to network
1) 0 and
2)
3)
4)
5)
6)
7)
Therefore, the first-order coherence of
Therefore, 1) when m is fixed, n → ∞, one has
Hence,
Then, one has
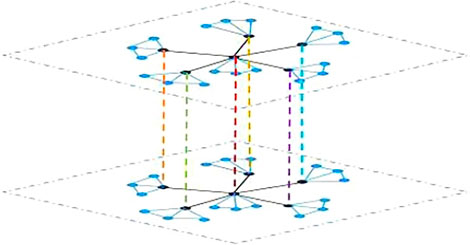
3.4 The Consensus Indices for Network Topology
In this subsection, the two layered star-composed multi-agent network
Through the similar methods of former subsection, it can be derived that
and then we have
To the case with network structure
1) 0 and
2)
3)
4)
5)
6)
7)
Then the coherence for
when the number of leaves, i.e., k is fixed, and m → ∞, then
If the number of leaf nodes k is fixed, then one has
Remark 2. To the dual-layered star-composed networks
Remark 3. A limitation of the framework in this article is that the graph is undirected, and one may consider some reasonable directed cases in future research. In addition, another worthy research direction may be focused on extending the two-layered case into multilayered ones.
4 Simulation and Comparison
In this section, the comparisons of performance for these two-layered multi-star networks are made. One can see from Section 3 that the convergence speed of
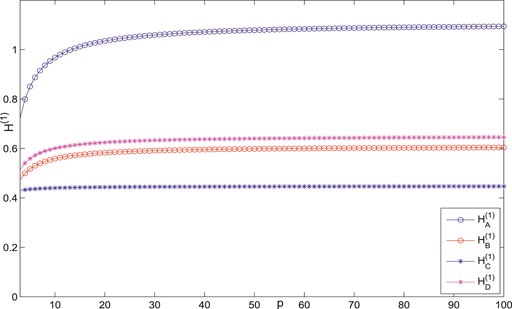
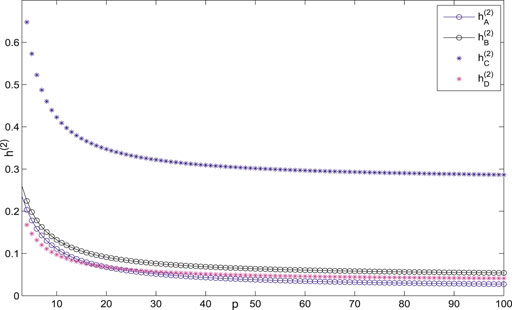
To the network coherence for the duplex networks and the two-layered multi-star ones, two perspective comparisons are made; that is, vertically,
Horizontally,
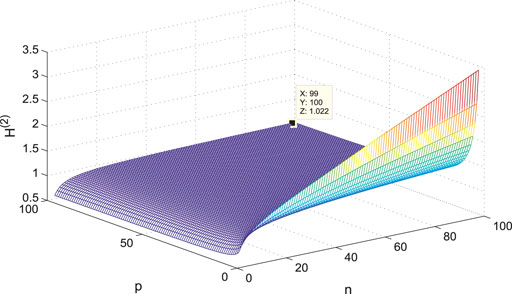
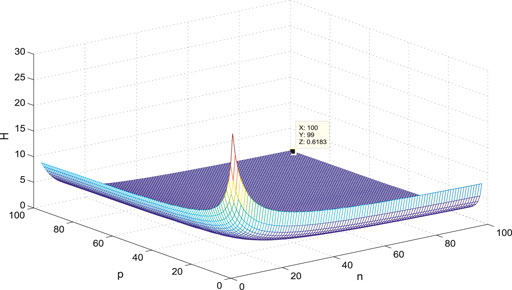
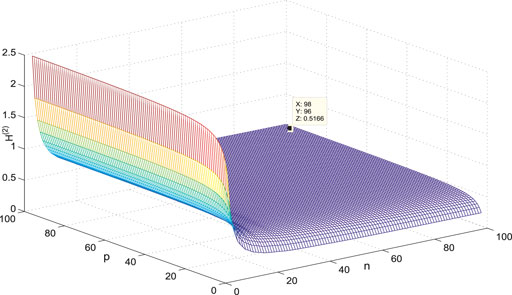
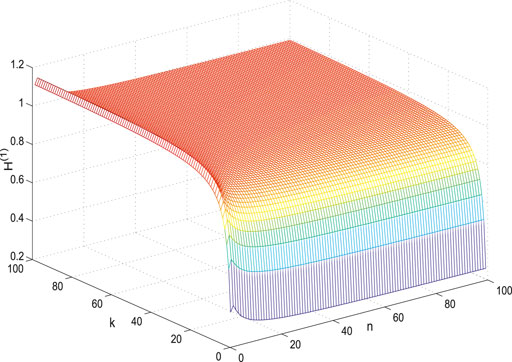
The variance of the first- and second-order coherence for
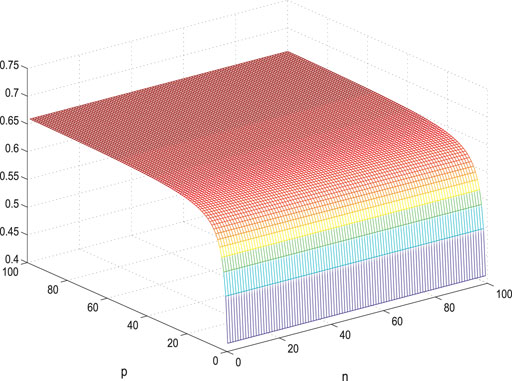
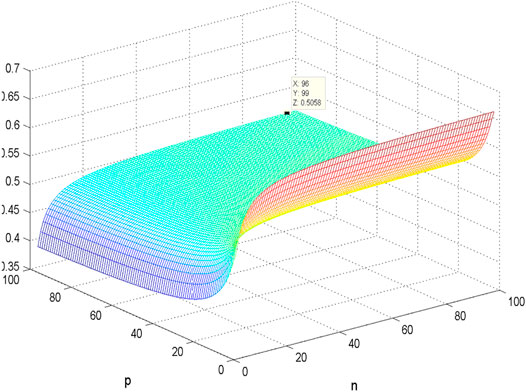
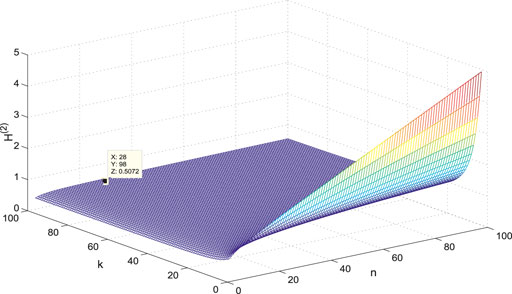
Figures 7–14 show the change of the first- and second-order coherence of the four networks with respect to the two parameters n and p (n, p ∈ [3, 100]). It can be seen that the simulation verifies the results well.
Conclusion
In this research, the convergence speed and robustness of the consensus for several dual-layered multi-agent systems, which can be measured by the algebraic connectivity and the network coherence, are studied. In particular, the methods of graph spectra are applied to analyze the graph structure and derive the network coherence for the multi-agent networks, and it is found that there exist some asymptotic properties for the indices. When the number of leaf and center node p, n is large enough, the operation of adding star topologies will make the first-order coherence of
Finally, the consensus-related indices of the duplex networks with the same number of nodes but non-isomorphic structures have been compared and simulated, and it is found that
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Author Contributions
DH and HJ: methodology. ZY and DH: software. DH and JB: validation. DH and JB: formal analysis. DH: writing—original draft preparation. DH and JB: writing—review and editing. HJ and ZY: supervision. DH: project administration.
Funding
This work was supported by the Natural Science Foundation of Xinjiang (NSFXJ) (No. 2019D01B10), National Natural Science Foundation of the People’s Republic of China (NSFC) (Grant No. 62003289), and Research Fund for the Doctoral Program of Xinjiang Institute of Engineering (2020xgy012302).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We express our sincere gratitude to the people who gave us valuable comments.
References
1. Olfati-Saber R, Murray RM. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans Automat Contr (2004) 49(9):1520–33. doi:10.1109/tac.2004.834113
2. Ren W. On Consensus Algorithms for Double-Integrator Dynamics. IEEE Trans Automat Contr (2008) 53:1503–9. doi:10.1109/tac.2008.924961
3. Wenwu Yu W, Guanrong Chen G, Ming Cao M, Kurths J. Second-order Consensus for Multiagent Systems with Directed Topologies and Nonlinear Dynamics. IEEE Trans Syst Man Cybern B (2010) 40:881–91. doi:10.1109/tsmcb.2009.2031624
4. Wen G, Duan Z, Yu W, Chen G. Consensus of Second-Order Multi-Agent Systems with Delayed Nonlinear Dynamics and Intermittent Communications. Int J Control (2013) 86:322–31. doi:10.1080/00207179.2012.727473
5. Yu Z, Jiang H, Huang D, Hu C. Consensus of Nonlinear Multi-Agent Systems with Directed Switching Graphs: A Directed Spanning Tree Based Error System Approach. Nonlinear Anal Hybrid Syst (2018) 28:123–40. doi:10.1016/j.nahs.2017.12.001
6. Huang D, Jiang H, Yu Z, Hu C, Fan X. Cluster-delay Consensus in MASs with Layered Intermittent Communication: a Multi-Tracking Approach. Nonlinear Dyn (2019) 95:1713–30. doi:10.1007/s11071-018-4604-4
7. Yu Z, Huang D, Jiang H, Hu C. Consensus of Second-Order Multi-Agent Systems with Nonlinear Dynamics via Edge-Based Distributed Adaptive Protocols. J Franklin Inst (2016) 353:4821–44. doi:10.1016/j.jfranklin.2016.09.015
8. Sun Y, Li W, Zhao D. Convergence Time and Speed of Multi-Agent Systems in Noisy Environments. Chaos (2012) 22:043126. doi:10.1063/1.4768663
9. Young G, Scardovi L, Leonard N. Robustness of Noisy Consensus Dynamics with Directed Communication. In: Proceedings of the American Control Conference; 30 June-2 2010; Baltimore, MD (2010). p. 6312–7. doi:10.1109/acc.2010.5531506
10. Bamieh B, Jovanovic MR, Mitra P, Patterson S. Coherence in Large-Scale Networks: Dimension-dependent Limitations of Local Feedback. IEEE Trans Automat Contr (2012) 57:2235–49. doi:10.1109/tac.2012.2202052
11. Patterson S, Bamieh B. Consensus and Coherence in Fractal Networks. IEEE Trans Control Netw Syst (2014) 1(4):338–48. doi:10.1109/tcns.2014.2357552
12. Yi Y, Zhang Z, Shan L, Chen G. Robustness of First-And Second-Order Consensus Algorithms for a Noisy Scale-free Small-World Koch Network. IEEE Trans Control Syst Technology (2016) 25(1):342–50.
13. Sun W, Li Y, Liu S. Noisy Consensus Dynamics in Windmill-type Graphs. Chaos (2020) 30:123131. doi:10.1063/5.0020696
14. Wang X, Xu H, Dai M. First-order Network Coherence in 5-rose Graphs. Physica A: Stat Mech its Appl (2019) 527:121129. doi:10.1016/j.physa.2019.121129
15. Wan Y, Namuduri K, Akula S, Varanasi M. The Impact of Multi-Group Multi-Layer Network Structure on the Performance of Distributed Consensus Building Strategies. Int J Robust Nonlinear Control (2013) 23(6):653–62. doi:10.1002/rnc.2783
16. Shang Y. Finite-time Consensus for Multi-Agent Systems with Fixed Topologies. Int J Syst Sci (2012) 43(3):499–506. doi:10.1080/00207721.2010.517857
17. Shang Y. Fixed-time Group Consensus for Multi-Agent Systems with Nonlinear Dynamics and Uncertainties. IET Control Theor Appl (2015) 12(3):395–404.
18. Shang Y. Consensus and Clustering of Expressed and Private Opinions in Dynamical Networks against Attacks. IEEE Syst J (2020) 14(2):2078–84. doi:10.1109/jsyst.2019.2956116
19. Li H-L, Cao J, Jiang H, Alsaedi A. Graph Theory-Based Finite-Time Synchronization of Fractional-Order Complex Dynamical Networks. J Franklin Inst (2018) 355:5771–89. doi:10.1016/j.jfranklin.2018.05.039
20. Drauschke F, Sawicki J, Berner R, Omelchenko IE, Schöll E. Effect of Topology upon Relay Synchronization in Triplex Neuronal Networks. Chaos (2020) 30:051104. doi:10.1063/5.0008341
21. Gu Y-Q, Shao C, Fu X-C. Complete Synchronization and Stability of star-shaped Complex Networks. Chaos, Solitons & Fractals (2006) 28:480–8. doi:10.1016/j.chaos.2005.07.002
22. Xu Ming-Ming MM, Lu Jun-An JA, Zhou Jin J. Synchronizability and Eigenvalues of Two-Layer star Networks. Acta Physica Sinica (2016) 65:028902. doi:10.7498/aps.65.028902
23. He W, Chen G, Han Q-L, Du W, Cao J, Qian F. Multiagent Systems on Multilayer Networks: Synchronization Analysis and Network Design. IEEE Trans Syst Man Cybern, Syst (2017) 47:1655–67. doi:10.1109/tsmc.2017.2659759
24. Kivela M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer Networks. J Complex Networks (2014) 2:203–71. doi:10.1093/comnet/cnu016
25. Wang Z, Xia C, Chen Z, Chen G. Epidemic Propagation with Positive and Negative Preventive Information in Multiplex Networks. IEEE Trans Cybern (2021) 51:1454–62. doi:10.1109/tcyb.2019.2960605
26. Kamal A. Star Local Area Networks: A Performance Study. IEEE Trans Comput (1987) C-36(4):483–99. doi:10.1109/tc.1987.1676930
27. Rescigno AA. Optimally Balanced Spanning Tree of the star Network. IEEE Trans Comput (2001) 50(1):88–91. doi:10.1109/12.902755
28. Cvetkovic D, Rowlinson P, Simic S. An Introduction to the Theory of Graph Spectra. New York: Cambridge University Press (2010).
29. Barik S, Pati S, Sarma BK. The Spectrum of the Corona of Two Graphs. SIAM J Discrete Math (2007) 21(1):47–56. doi:10.1137/050624029
31. Huang D, Zhang Z. On Cyclic Vertex-Connectivity of Cartesian Product Digraphs. J Comb Optim (2012) 24:379–88. doi:10.1007/s10878-011-9395-1
32. Good IJ. On the Inversion of Circulant Matrices. Biometrika (1950) 37:185–6. doi:10.1093/biomet/37.1-2.185
33. Zhang H, Yang Y, Li C. Kirchhoff index of Composite Graphs. Discrete Appl Mathematics (2009) 157:2918–27. doi:10.1016/j.dam.2009.03.007
Keywords: consensus, coherence, Cartesian product, convergence speed, robustness, Laplacian spectrum
Citation: Huang D, Bian J, Jiang H and Yu Z (2021) Consensus Indices of Two-Layered Multi-Star Networks: An Application of Laplacian Spectrum. Front. Phys. 9:803941. doi: 10.3389/fphy.2021.803941
Received: 28 October 2021; Accepted: 15 November 2021;
Published: 22 December 2021.
Edited by:
Nuno A. M. Araújo, University of Lisbon, PortugalReviewed by:
Yilun Shang, Northumbria University, United KingdomQing Yun Wang, Beihang University, China
Copyright © 2021 Huang, Bian, Jiang and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Da Huang, eGlhb2RhODZvcEAxNjMuY29t
 Da Huang
Da Huang Jicheng Bian1
Jicheng Bian1