Massively Multidimensional Diffusion-Relaxation Correlation MRI

Diverse approaches such as oscillating gradients, tensor-valued encoding, and diffusion-relaxation correlation have been used to study microstructure and heterogeneity in healthy and pathological biological tissues. Recently, acquisition schemes with free gradient waveforms exploring both the frequency-dependent and tensorial aspects of the encoding spectrum b(ω) have enabled estimation of nonparametric distributions of frequency-dependent diffusion tensors. These “D(ω)-distributions” allow investigation of restricted diffusion for each distinct component resolved in the diffusion tensor trace, anisotropy, and orientation dimensions. Likewise, multidimensional methods combining longitudinal and transverse relaxation rates, R₁ and R_2, with (ω-independent) D-distributions capitalize on the component resolution offered by the diffusion dimensions to investigate subtle differences in relaxation properties of sub-voxel water populations in the living human brain, for instance nerve fiber bundles with different orientations. By measurements on an ex vivo rat brain, we here demonstrate a “massively multidimensional” diffusion-relaxation correlation protocol joining all the approaches mentioned above. Images acquired as a function of the magnitude, normalized anisotropy, orientation, and frequency content of b(ω), as well as the repetition time and echo time, yield nonparametric D(ω)-R₁-R₂-distributions via a Monte Carlo data inversion algorithm. The obtained per-voxel distributions are converted to parameter maps commonly associated with conventional lower-dimensional methods as well as unique statistical descriptors reporting on the correlations between restriction, anisotropy, and relaxation.

Introduction

Magnetic resonance imaging (MRI) allows non-invasive characterization of microstructure and local chemical composition in healthy and pathological biological tissues by monitoring the self-diffusion and nuclear magnetic relaxation properties of water molecules [1–4]. While the apparent diffusion coefficient D reports on cell density and membrane permeability [5], longitudinal and transverse relaxation rates, R₁ and R₂^(*), are sensitive to chemical exchange of protons between water and hydroxyl and amine groups on metabolites and macromolecules [6, 7], molecular exchange between compartments [8], magnetization transfer/cross relaxation between exchangeable and non-exchangeable protons [9], and paramagnetic relaxation from iron or added contrast agents [8, 10]. Especially for studies of the nervous system, the diffusion is often expressed in terms of a diffusion tensor D related to cell shapes and orientations [11]. White matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) all have characteristic diffusion [12] and relaxation [13, 14] properties that determine how the MRI signal varies as a function of acquisition variables such as b-value [15, 16], repetition time τ_R, and echo time τ_E.

A major challenge of studying brain tissue microstructure lies in the prevalence of intra-voxel heterogeneity in terms of not only the proportions of WM, GM, and CSF, but also the distribution of cell types, sizes, densities, orientations, membrane permeabilities, and chemical compositions. This heterogeneity gives rise to corresponding distributions of water populations with varying diffusion and relaxation properties that contribute to the total signal response from a given voxel. Comprehensive exploration of the multidimensional space defined by the acquisition variables in the MRI measurements is essential for disentangling the contributions from the distinct water populations [17]. Along these lines, methods such as diffusion-relaxation correlation [18] and tensor-valued encoding [19] have been used to address intra-voxel heterogeneity, whereas oscillating gradients [20] have enabled studies of microstructural length-scales via the frequency-dependence of the diffusion properties. A brief overview of these approaches is presented below to highlight their relevance and benefits that each provide to study the tissue microstructure.

Diffusion-relaxation correlation nuclear magnetic resonance (NMR) has for decades been widely applied to heterogeneous porous media [21–23] and has more recently been integrated with MRI [24, 25], giving spatially resolved nonparametric distributions [26] of various combinations of D, R₁, and R₂^(*). Recent MRI examples include 2D D-R₂ of ex vivo mouse spinal cord [27], 2D D-R₂^* of in vivo human placenta [28], 2D D-R₂ of ex vivo human prostate [29], and combined 2D D-R₁, 2D D-R₂, and 2D R₁-R₂ of ex vivo ferret spinal cord [30] and ex vivo human brain [31]. All these studies were limited to analysis in terms of scalar D, merging diverse properties such as short-time diffusivity, restriction, anisotropy, orientation, and flow into a single metric which is appropriate for quantifying diffusion in isotropic liquids but lacks specificity for anisotropic biological tissues with structural features on the micrometer length-scale [32].

Multidimensional diffusion MRI [33] builds on selective signal encoding strategies from multidimensional solid-state NMR spectroscopy [34] to separate and correlate the diverse aspects of translational motion. In particular, diffusion versions of the classical solid-state NMR techniques magic-angle spinning [35], magic-angle hopping [36], and variable-angle spinning [37] yield separation [38, 39] and correlation [40] of the isotropic and anisotropic contributions to the observed diffusivities. Independently of the exact details of the diffusion-encoding gradients, the relevant acquisition variables are summarized in the well-known b-matrix [11] or b-tensor [41] b, often assumed to be axisymmetric and parameterized with its trace b, normalized anisotropy b_Δ, and orientation (Θ,Φ) [39]. When combined with the likewise well-known concept of D-distributions [42, 43], tensor-valued encoding enables model-free characterization of the voxel content in terms of nonparametric 4D D-distributions with the dimensions of isotropic diffusivity D_iso, squared normalized anisotropy D_Δ², and orientation (θ,ϕ) [44]. The distribution means E[D_iso] and E[D_Δ²] carry similar microstructural information as conventional mean diffusivity [11] and microscopic anisotropy measures [45–49]. For in vivo mouse brain, the distinct (D_iso,D_Δ²)-coordinates of components assigned to WM, GM, and CSF can be utilized to define “bins” in the 2D D_iso-D_Δ² projection for calculating nominally tissue-specific signal fractions and diffusion metrics [50] analogously to earlier binning of 1D R₂-distributions to estimate myelin water fractions [39] and 2D “spectral regions of interest” capturing diverse tissue types in various 2D correlation experiments [27–31]. Augmenting conventional diffusion-relaxation correlation with tensor-valued encoding gives signal in a 6D acquisition space b-τ_R-τ_E which upon inversion yields nonparametric 6D D-R₁-R₂ distributions [51]. Recent examples of the approach include 5D D-R₁ [52], 5D D-R₂ [53, 54], and 6D D-R₁-R₂ [55] of in vivo human brain where subtle differences in R₁ or R₂ can be detected provided the components are resolved in the 2D D_iso-D_Δ² or θ-ϕ projections, the latter being utilized for model-free estimation of bundle-specific R₁ or R₂ in areas with crossing fibers [52, 54].

Advanced diffusion encoding schemes such as oscillating gradients give access to the diffusion spectrum D(ω) [56, 57] for investigating diffusion at the length-scales of subcellular structures [20]. The time/frequency-dependence has been studied in porous media with NMR [57–59] as well as in rodent [60–62] and in vivo human brain [63, 64] with MRI. Particularly, oscillating gradients measurements provide a distinctive increased image contrast in mouse brain in the cerebellum, dentate gyrus, and hippocampus, which correlates with the nuclear volume fractions in regions containing densely packed cells [61]. Studies of WM and GM in in vivo mouse and human brain have shown the potential of using the frequency-dependence to characterize biological tissues at cellular to sub-cellular scales [62–64]. Recently, modulated gradient waveforms combining elements of both oscillating gradients and variable-angle spinning [65] have enabled convenient exploration of both the frequency-dependent and tensorial aspect of the tensor-valued encoding spectrum b(ω) [66], making it possible to study the frequency-dependence of each distinct component resolved in a nonparametric D(ω)-distribution [67].

Here we merge all approaches mentioned above into “massively multidimensional” diffusion-relaxation correlation MRI with signal acquired in an effectively 7D space b(ω)-τ_R-τ_E and data inversion into nonparametric D(ω)-R₁-R₂ distributions giving the benefits of the lower-dimensional methods in a joint acquisition and analysis framework. Measurements on ex vivo rat brain are used to illustrate the vast amount of per-voxel information available for detailed description of brain tissue microstructure and heterogeneity.

Theory

Combining our recent nonparametric D(ω)-distributions [67] with previous (ω-independent) D-R₁-R₂-distributions [51], we here approximate the b(ω)-τ_R-τ_E encoded signal S as a sum of contributions from components i characterized by their statistical weight w_i, tensor-valued diffusion spectra D_i(ω), and longitudinal and transverse relaxation rates R_1,i and R_2,i according to

$S\left[\mathbf{b}\left(\omega \right),{\tau }_{\mathbf{R}},{\tau }_{\mathrm{E}}\right]={\displaystyle \sum }_i{w}_i\mathrm{e}\mathrm{x}\mathrm{p}\left(-\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\mathbf{b}\left(\omega \right):{\mathbf{D}}_i\left(\omega \right)\mathrm{d}\omega \right)\left[1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\tau }_{\mathbf{R}}{R}_{1,i}\right)\right]\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\tau }_{\mathrm{E}}{R}_{2,i}\right),(1)$

where the colon denotes a generalized scalar product [68] and the sum of w_i yields the non-weighted signal S₀, nominally proportional to the proton density, via

$S_0={\displaystyle \sum }_i{w}_i.(2)$

As described in detail in Ref. [67], inversion of Eq. 1 is rendered tractable by approximating D_i(ω) as axisymmetric Lorentzians parameterized by the zero-frequency axial and radial diffusivities D_A,i and D_R,i, orientation (θ_i,ϕ_i), high-frequency isotropic diffusivity D_0,i, and axial and radial transition frequencies Γ_A,i and Γ_R,i, giving

${\mathbf{D}}_i\left(\omega \right)=\mathbf{R}\left({\theta }_i,{\varphi }_i\right)\left(\begin{array}{ccc}{D}_{\text{R},i}\left(\omega \right)& 0& 0\\ 0& D_{\text{R},i}\left(\omega \right)& 0\\ 0& 0& D_{\text{A},i}\left(\omega \right)\end{array}\right){\mathbf{R}}^{-1}\left({\theta }_i,{\varphi }_i\right),(3)$

where R(θ_i,ϕ_i) is a rotation matrix, and

$D_{\mathbf{A},i/\mathbf{R},i}\left(\omega \right)=D_{0,i}-\frac{D_{0,i}-D_{\text{A},i/\mathbf{R},i}}{1+{\omega }^2/{\mathrm{\Gamma }}_{\mathbf{A},i/\mathbf{R},i}^2}.(4)$

Although the data inversion yields a set of components described with the parameter set [D_A,i,D_R,i,θ_i,ϕ_i,D_0,i,Γ_A,i,Γ_R,i,R_1,i,R_2,i], it is convenient to express the diffusion dimensions in terms of the ω-dependent isotropic diffusivity D_iso,i(ω) and normalized diffusion anisotropy [69] D_Δ,i(ω) via

$D_{\mathbf{iso},i}\left(\omega \right)=\frac{D_{\text{A},i}\left(\omega \right)+2D_{\mathbf{R},i}\left(\omega \right)}{3}(5)$

and

$D_{\text{Δ},i}\left(\omega \right)=\frac{D_{\text{A},i}\left(\omega \right)-D_{\mathbf{R},i}\left(\omega \right)}{3D_{\mathbf{iso},i}\left(\omega \right)},(6)$

where D_A,i(ω) and D_R,i(ω) are given by Eq. 4.

The diffusion-encoding magnetic field gradient g(t) with duration τ gives b(ω) via

$\mathbf{q}\left(\omega \right)=\mathit{\gamma }\underset{0}{\overset{\tau }{{\displaystyle \int }}}\underset{0}{\overset{t}{{\displaystyle \int }}}\mathbf{g}\left(t\prime \right)\mathrm{d}{t}^{\prime }\exp \left(\mathrm{i}\omega t\right)\mathrm{d}t,(7)$

where γ is the gyromagnetic ratio, and

$\mathbf{b}\left(\omega \right)=\frac{1}{2\mathrm{\pi }}\mathbf{q}\left(\omega \right)\mathbf{q}{\left(-\omega \right)}^{\text{T}}.(8)$

While the full tensorial and ω-dependent form of b(ω) is used in our data processing based on Eq. 1, it is instructive to extract some more familiar metrics to characterize the properties of the diffusion encoding. The conventional b-matrix [70] b and dephasing power spectrum [56] b(ω) are obtained from b(ω) through

$\mathbf{b}=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\mathbf{b}\left(\omega \right)\mathrm{d}\omega (9)$

and

$b\left(\omega \right)=\mathrm{trace}\left\{\mathbf{b}\left(\omega \right)\right\}.(10)$

These give the b-value via

$b=\mathrm{trace}\left\{\mathbf{b}\right\}(11)$

or

$b=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}b\left(\omega \right)\mathrm{d}\omega .(12)$

The average spectral content of the diffusion encoding is captured by the centroid frequency [71] ω_cent written as

${\omega }_{\mathbf{cent}}=\frac{{{\displaystyle \int }}_{-\infty }^{\infty }\left|\omega \right|b\left(\omega \right)\mathrm{d}\omega }{{{\displaystyle \int }}_{-\infty }^{\infty }b\left(\omega \right)\mathrm{d}\omega }.(13)$

The “shape” of the b-matrix may be reported in terms of the normalized anisotropy b_Δ given by [39]

$b_{\text{Δ}}=\frac{1}{b}\left(b_{ZZ}-\frac{b_{YY}+b_{XX}}{2}\right),(14)$

where b_XX, b_YY, and b_ZZ are the eigenvalues of b ordered according to the convention |b_ZZ–b/3| > |b_XX–b/3| > |b_YY–b/3|. The polar and azimuthal angles Θ and Φ give the lab-frame orientation of the eigenvector corresponding to the b_ZZ eigenvalue. The key properties of the diffusion encoding spectrum b(ω) may thus be summarized with the parameters b, Θ, and Φ, which are identical to the b-value and b-vector in conventional DTI, as well as the centroid frequency ω_cent and normalized anisotropy b_Δ from oscillating gradient [20] and tensor-valued [19] encoding.

Materials and Methods

Tissue Preparation and Light Microscopy

A healthy adult rat Sprague-Dawley (Harlan Netherlands B.V.) was intracardially perfused with 0.9% saline followed by 4% paraformaldehyde (PFA). The brain was carefully extracted from the skull and stored in 4% PFA solution at 4°C. The procedure was approved by the Animal Committee of the Provincial Government of Southern Finland in accordance with the guidelines established by the European Union Directives 2010/63/EU. Before imaging, the brain was sagittally sectioned by the midline in left and right hemispheres and placed in 0.1 M phosphate buffer saline (PBS) solution containing 50 µl/10 ml of gadoteric acid (Dotarem 0.5 M; Guerbet, and France) 24 h before scanning. MRI was performed on the right hemisphere immersed in perfluoropolyether (Galden; TMC Industries, United States) in a 10 mm NMR tube at 20°C room temperature.

For comparison between histology and MRI data, representative sections from a healthy adult rat were stained with gold chloride and Nissl [72]. High resolution photomicrographs were taken using a light microscope (Zeiss Axio Imager2) equipped with a motorized stage and a digital camera (Zeiss Axiocam color 506).

MRI Acquisition and Reconstruction

The multidimensional diffusion-relaxation data set was acquired on a Bruker Avance-III HD 11.7 T spectrometer equipped with a MIC-5 probe giving 3 T/m maximum gradient amplitude on-axis. The images have an in-plane spatial resolution of 80 × 80 μm² and 250 µm slice thickness with a 119 × 119 × 1 matrix size localized approximately at −3.3 mm from bregma. The data set was obtained using Bruker’s multi-slice multi-echo (MSME) sequence customized for diffusion encoding with general gradient waveforms. The diffusion gradients are derived from the variable-angle modification of magic-angle spinning of the q-vector [73] using two symmetric self-refocusing gradient waveforms with 8 ms duration on each side of the refocusing radiofrequency pulse. Images were acquired at varying b-value (0.037–5.4.10⁹ sm⁻²), centroid frequency ω_cent/2π (50–150 Hz), normalized anisotropy b_Δ (−0.5–1), orientation (Θ,Φ), repetition time τ_R (80–600 ms), and echo time τ_E (9–38 ms) according to the scheme in Figure 1. The calculation of b(ω) with Eqs 7 and 8 included the dedicated diffusion gradients as well as the read and slice gradients from the center of the excitation pulse to the time point of the spin echo. The shortest values of τ_E were reached by omitting the diffusion gradients. The values of b, ω_cent, b_Δ, Θ, and Φ shown in Figure 1 were obtained from the calculated b(ω) via Eqs 9–14. Acquisition of 809 images, each of which requiring 119 separate excitations to traverse k-space, resulted in a total measurement time of 20 h. After image reconstruction in Bruker’s ParaVision 6.0.1, the data was preprocessed with MRtrix3 [74] software for denoising based on random matrix theory [75] and Matlab (Natick, Massachusetts: The MathWorks Inc.) was used for further analysis with the md-dmri Matlab toolbox [76]. Blender 2.92 (Amsterdam, Netherlands: Blender Foundation) was used for the ODF visualization.

FIGURE 1

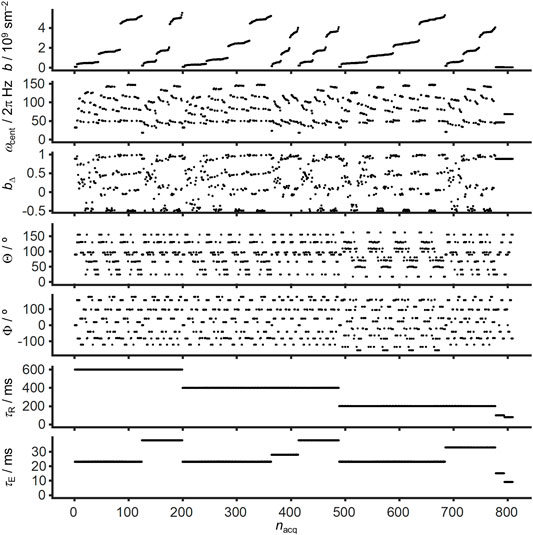
FIGURE 1. Example acquisition scheme for massively multidimensional diffusion-relaxation correlation MRI. Free gradient waveforms combining elements of conventional DTI with oscillating gradient and tensor-valued encoding are used to explore the effectively 5D acquisition space spanned by the trace b, orientation (Θ,Φ), centroid frequency ω_cent, and normalized anisotropy b_Δ of the tensor-valued encoding spectrum b(ω). Variation of the repetition time τ_R and echo time τ_E gives access to two additional dimensions, resulting in a 7D acquisition. The acquisition point index n_acq is sorted according to decreasing τ_R, increasing τ_E, and increasing b.

Estimation and Visualization of Nonparametric D(ω)-R₁-R₂-Distributions

The D(ω)-R₁-R₂ distributions, expressed in the space of [D_A,D_R,θ,ϕ,D₀,Γ_A,Γ_R,R₁,R₂], were obtained by Monte Carlo inversion [77] as described in detail in Ref. [51]. The inversion algorithm has previously been applied to various diffusion and relaxation correlation measurements including [D_A,D_R] [40], [D_A,D_R,θ,ϕ] [44, 50], [D_A,D_R,θ,ϕ,R₁] [52], [D_A,D_R,θ,ϕ,R₂] [53, 54], [D_A,D_R,θ,ϕ,R₁,R₂] [51], and [D_A,D_R,θ,ϕ,D₀,Γ_A,Γ_R] [67]. Here, the inversion was performed with the limits 5⋅10⁻¹² m²s⁻¹ < D_0/A/R < 5⋅10⁻⁹ m²s⁻¹, 0.1 s⁻¹ < Γ_A/R < 10⁵ s⁻¹, 0.2 s⁻¹ < R₁ < 20 s⁻¹, and 2 s⁻¹ < R₂ < 200 s⁻¹, as well as 20 steps of proliferation, 20 steps of mutation/extinction, 200 input components per step of proliferation and mutation/extinction, 10 output components, and bootstrapping by 100 repetitions using random sampling with replacement. The ranges of D_0/A/R, R₁, and R₂ were selected to be consistent with the values of b, τ_R, and τ_E in the acquisition protocol, while the range of Γ_A/R was deliberately chosen to extend far beyond the range of ω_cent in order to allow for components without ω-dependence within the investigated frequency window. For every voxel, the Monte Carlo inversion outputs an ensemble of 100 independent solutions, each of which comprising weights w and coordinates [D_A,D_R,θ,ϕ,D₀,Γ_A,Γ_R,R₁,R₂] for 10 components within the pseudo-randomly sampled analysis space. As opposed to most nonparametric inversion methods in diffusion and relaxation MRI, the coordinates are only constrained by the outer boundaries of the analysis space, but not to a pre-defined multidimensional grid within this space. Likewise, the Monte Carlo inversion algorithm does not include penalty terms aiming to promote smoothness in the analysis or image spaces. Data inversion for 100 repetitions of 8,000 voxels required in total 25 h of processing time on a 3.6 GHz 8-core CPU, corresponding to on average 0.9 s per voxel, repetition, and core. All metrics described below were calculated for each of the 100 solutions per voxel, and the values displayed in maps, projections, and ODFs were obtained as medians over the individual solutions.

With inspiration from the recent concept of “dynamics detectors” to extract model-independent information about rotational diffusion from NMR relaxation dispersion data [78], the diffusion dimensions of the D(ω)-R₁-R₂ distributions in the primary analysis space [D_A,D_R,θ,ϕ,D₀,Γ_A,Γ_R,R₁,R₂] were evaluated with Eq. 4 at selected values of ω within the narrow 50–150 Hz window actually probed by the gradient waveforms, giving a set of ω-dependent distribution in the [D_A(ω),D_R(ω),θ,ϕ,R₁,R₂] space. For each value of ω, these results can be visualized as previous ω-independent distributions [44, 50, 52–54] by projecting D_A(ω) and D_R(ω) to the dimensions of isotropic diffusivity D_iso(ω) and squared normalized anisotropy D_Δ²(ω), via Eqs 5 and 6, as well as the lab-frame diagonal elements D_xx(ω), D_yy(ω), and D_zz(ω), and subsequently converting to means E[x], variances V[x], and covariances C[x,y] over relevant dimensions and sub-divisions (“bins”) of the distribution space. The diagonal elements and the maximum eigenvalue D₃₃ were used to generate the directionally-encoded color map. Following conventions often used to display results from oscillating gradient encoding [20, 61, 71, 79–81], the effects of restricted diffusion were quantified by a finite difference approximation of the rate of change of the diffusivity metrics with frequency within the investigated window, for instance

${\text{Δ}}_{\omega /2\text{π}}\mathrm{E}\left[D_{\mathbf{iso}}\right]=\frac{\mathrm{E}\left[D_{\mathbf{iso}}\left({\omega }_{\mathbf{max}}\right)\right]-\mathrm{E}\left[D_{\mathbf{iso}}\left({\omega }_{\mathbf{min}}\right)\right]}{\left({\omega }_{\mathbf{max}}-{\omega }_{\mathbf{min}}\right)/2\mathrm{\pi }}.(15)$

As in previous in vivo studies [50], results for voxels known from anatomy to contain pure WM, GM, or PBS were used to define three bins in the 2D D_iso-D_Δ² plane. Here we used the following bin limits: bin1, D_iso < 1·10⁻⁹ m²s⁻¹ and D_Δ² > 0.25; bin2, D_iso < 1·10⁻⁹ m²s⁻¹ and D_Δ² < 0.25; and bin3, D_iso > 1·10⁻⁹ m²s⁻¹ as illustrated in Figure 2D. On account of the effects of low temperature and tissue fixation, the D_iso border between bin1/bin2 and bin3 was set to 1·10⁻⁹ m²s⁻¹ rather than the value 2.5 10⁻⁹ m²s⁻¹ often used in vivo [50]. While the selected bins are mainly related to WM, GM, and CSF/PBS for healthy brain, the binning is less straightforward in the presence of various pathologies such as tumors or edema [82] and we prefer to use the noncommittal labels bin1, bin2, and bin3 rather than potentially misleading anatomical terms. The per-bin signal fractions (f_bin1,f_bin2,f_bin3) were calculated and visualized with RGB color coding (Figure 2D).

FIGURE 2

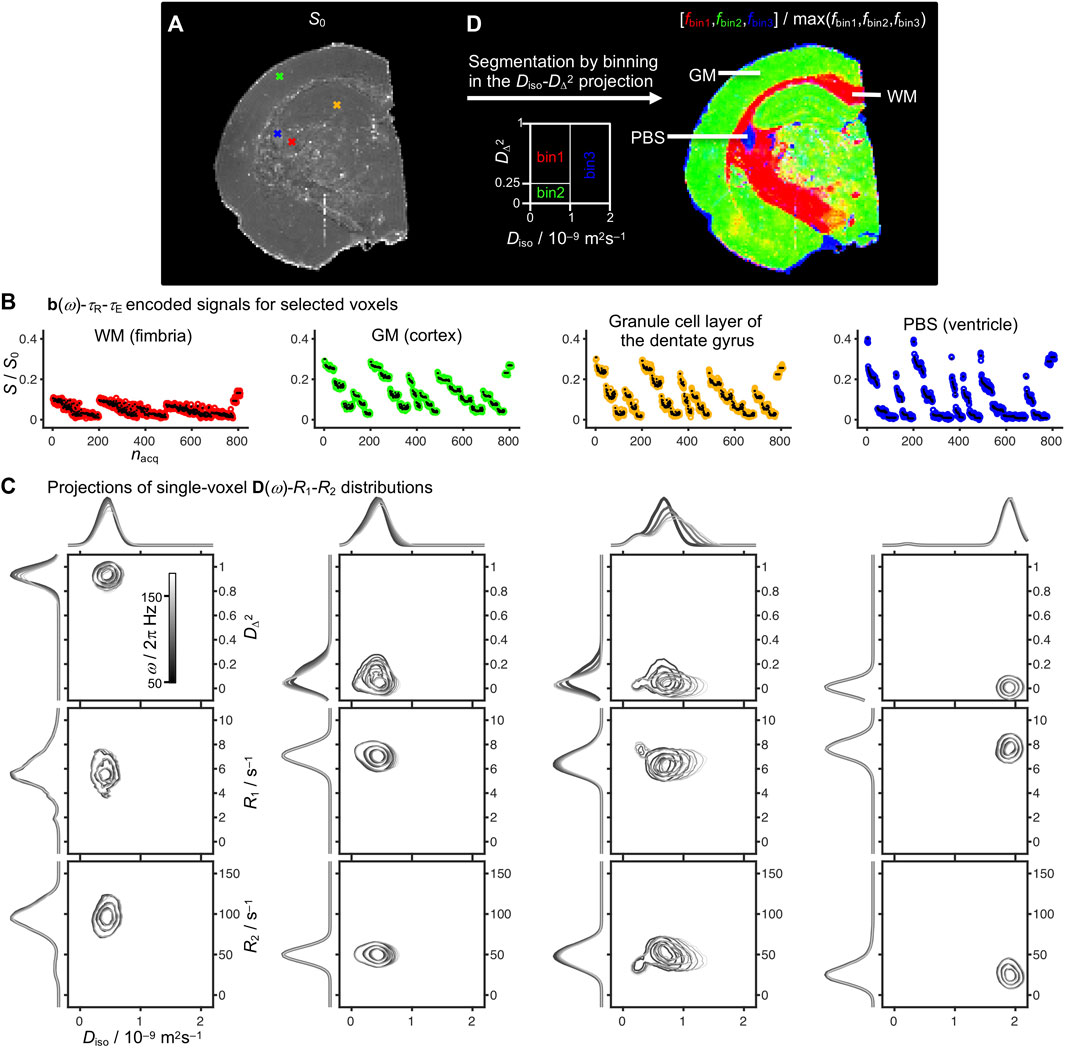
FIGURE 2. Experimental results for representative voxels in an ex vivo rat brain and tissue segmentation by binning. (A) S₀ map with crosses indicating single voxels representative for white matter (WM) in the fimbria (red), gray matter (GM) in the cortex (green), the granule cell layer of the dentate gyrus (orange), and phosphate buffer saline (PBS) in the ventricle (blue). (B) Single-voxel signals S as a function of acquisition index n_acq according to the 7D b(ω)-τ_R-τ_E scheme in Figure 1 (colored circles: experimental; black dots: back-calculated from the distributions). The values of S₀ correspond to the signals extrapolated to b = 0, τ_R = ∞, and τ_E = 0. (C) D(ω)-R₁-R₂ distributions for each of the selected voxels projected onto the 2D D_iso-D_Δ², D_iso-R₁, and D_iso-R₂ planes for five frequencies in the range ω/2π = 50–150 Hz as indicated with the linear gray scale of the contour lines. (D) Tissue segmentation by binning in the 2D D_iso-D_Δ² projection at the frequency ω/2π = 50 Hz, resulting in per-bin signal fractions f_bin1 (red), f_bin2 (green), and f_bin3 (blue) aiming to capture the spatial distributions of WM, GM, and PBS.

Single-voxel D(ω)-R₁-R₂ distributions were visualized by projecting and mapping the weights of the discrete components onto 64 × 64 meshes in the 2D D_iso-D_Δ², D_iso-R₁, and D_iso-R₂ planes using 3 × 3 grid points Gaussian kernel for five linearly spaced values of ω/2π in the 50–150 Hz range. Correspondingly, orientation distribution functions (ODFs) were generated by projecting the weights and metrics of the bin1 components onto a 1,000 points spherical mesh with a 10° spherical Gaussian kernel [83, 84]. 3D models of the ODF projections were exported in “.wrl” format and processed in Blender (Figure 6C).

Results

Figure 2 displays signal responses S[b(ω)-τ_R-τ_E] and the corresponding nonparametric D(ω)-R₁-R₂ distributions for representative voxels containing WM (fimbria), GM (cortex), and PBS (ventricle), as well as a voxel in the granule cell layer of the dentate gyrus, which structurally is a region with compact cell bodies [62]. The S₀ map in Figure 2A is obtained from the component weights w_i by Eq. 2 and corresponds to the signal S extrapolated to b = 0, τ_R = ∞, and τ_E = 0, and thus shows lower anatomical contrast than conventional S₀ maps from DTI which also includes R₁- and R₂-weighting. The quality of the fits can be discerned from the plots in Figure 2B of the measured signals (circles) and the corresponding signals (black dots) back-calculated from the distributions, giving standard deviations of the fit error (S_measured–S_fit)/S₀ between 0.5 and 1% for the four voxels. These numbers can be translated to the rather modest signal-to-noise ratios of approximately 20 for WM and 40 for PBS for the maximum measured signals at finite τ_R and τ_E.

The per-voxel D(ω)-R₁-R₂ distributions are visualized in Figure 2C as projections onto the 2D D_iso-D_Δ², D_iso-R₁, and D_iso-R₂ planes for five frequencies ω/2π between 50 and 150 Hz. The well-known differences in tissue microstructure are most clearly manifested in the 2D D_iso-D_Δ² projections, showing low D_iso and high D_Δ² in WM; low values of both D_iso and D_Δ² in GM; intermediate D_iso and low D_Δ² in the granule cell layer; and high D_iso and low D_Δ² in PBS. Additionally, the granule cell layer features the most pronounced ω-dependence. The values of R₁ increase slightly in the sequence WM < GM < PBS, presumably reflecting the accessibility to the added contrast agent rather than any intrinsic tissue property. Conversely, the values of R₂ increase markedly in the order PBS < GM < WM more in line with in vivo observations. The addition of contrast agents in ex vivo diffusion MRI studies is a common practice to enable reduction of τ_R, and thus increase the number of acquisitions while minimizing the total scanning time and experimental costs. Particularly, the contrast agent used in this study is not expected to penetrate intact cell membranes [85].

Although the WM, GM, and PBS give distinct signatures in both the 2D D_iso-D_Δ² and D_iso-R₂ projections, we here for convenience choose the former representation to define three bins for tissue segmentation as illustrated in Figure 2D. The per-bin signal fractions, f_bin1, f_bin2, and f_bin3, evaluated at ω/2π = 50 Hz effectively distinguishes between WM (red), GM (green), and PBS (blue). The color scale of the bin fractions is continuous; hence voxels with contributions of multiple tissue types or PBS are displayed as mixed colors, e.g., WM + GM (yellow), WM + PBS (purple), and GM + PBS (turquoise).

Figure 3 shows a collection of parameter maps derived from the per-voxel D(ω)-R₁-R₂ distributions. While each parameter has been explained in detail in previous lower-dimensional studies [52, 53, 67], we here summarize them briefly to illustrate the vast amount of information that can be extracted for each voxel and provide an intuitive and simple interpretation of the maps. For completeness, Figure 3A repeats the S₀ and fractions maps from Figure 2. The maps in Figure 3B display the per-voxel means E[x], variances V[x], and covariances C[x,y] for D_iso, D_Δ², R₁, and R₂ evaluated at ω/2π = 50 Hz. The means E[D_iso], E[R₁], and E[R₂] correspond to conventional mean diffusivity [11] and quantitative R₁ = 1/T₁ and R₂ = 1/T₂ [4], while E[D_Δ²] is analogous to earlier metrics quantifying microscopic diffusion anisotropy [45–49]. The E[D_iso] map highlights regions with free water, such as PBS in the ventricle, while providing limited contrast between WM and GM. Conversely, the E[D_Δ²] map reveals WM while just barely distinguishing between the low values of GM and PBS. In the E[R₁] and E[R₂] maps of this specimen with high concentration of added contrast agent, GM and PBS show higher E[R₁] and lower E[R₂] than WM in agreement with the single-voxel distributions in Figure 2C.

FIGURE 3

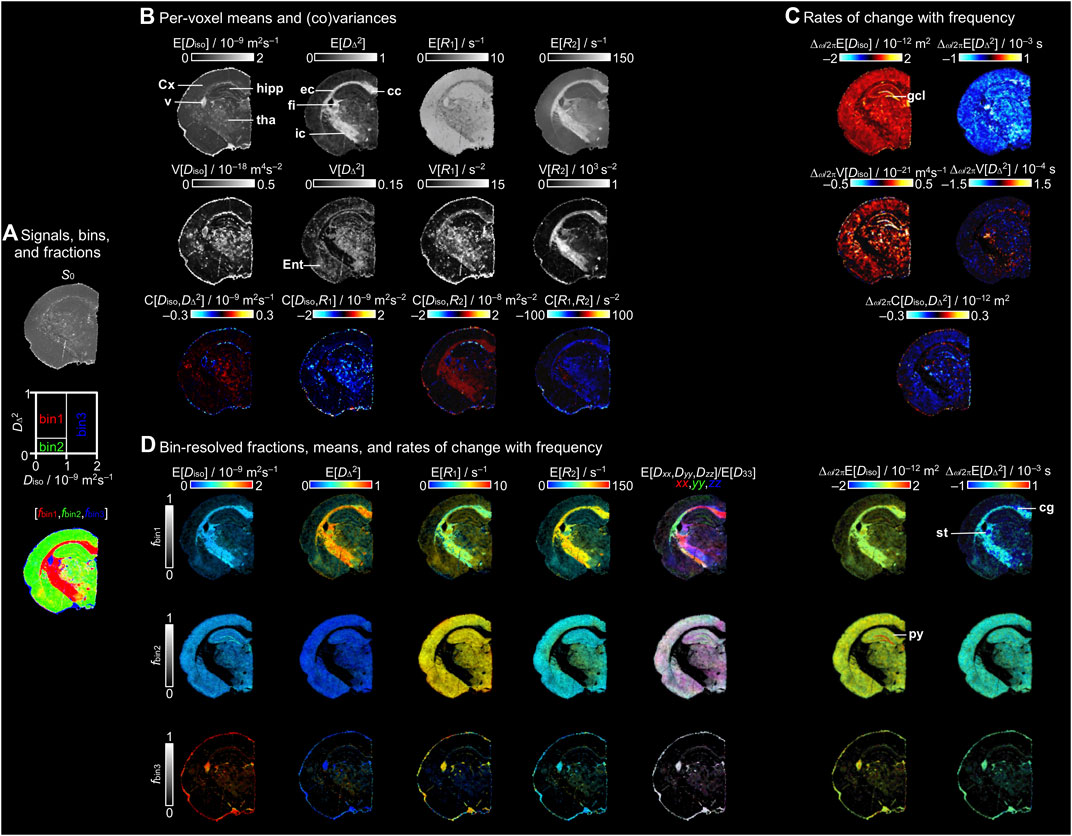
FIGURE 3. Parameter maps derived from the per-voxel D(ω)-R₁-R₂ distributions. (A) S₀ map displayed in gray scale, diagram with the division of the 2D D_iso-D_Δ² projection into three bins (bin1,bin2,bin3), and the resulting signal fractions (f_bin1,f_bin2,f_bin3) coded into RGB color. (B) Per-voxel means E[x], variances V[x], and covariances C[x,y] for the D_iso, D_Δ², R₁, and R₂ dimensions at a selected encoding frequency ω/2π = 50 Hz. (C) Parameter maps of the rate of change with frequency Δ_ω/2π of the per-voxel means, variances, and covariance of D_iso and D_Δ². (D) Bin-resolved maps of E[x] and Δ_ω/2πE[x]. The brightness and color scales represent, respectively, the signal fractions and the values of each parameter. Directionally-encoded color (DEC) maps are obtained from the lab-frame diagonal values [D_xx,D_yy,D_zz] normalized by the maximum eigenvalue D₃₃. Labeled lines indicate selected anatomical structures mentioned in the text. Abbreviations: cc, corpus callosum; cg, cingulum; Cx, cortex; ec, external capsule; Ent, entorhinal cortex; fi, fimbria; gcl, granule cell layer; hipp, hippocampus; ic, internal capsule; py, pyramidal cell layer; st, stria terminalis; tha, thalamus; and v, ventricle.

The variance V[x] and covariance C[x,y] maps in Figure 3B report on various aspects of intravoxel heterogeneity and highlight voxels comprising multiple water populations with different diffusion and/or relaxation properties. In previous studies, the V[D_iso] parameter has shown elevated values for voxels containing intra- and extracellular water populations separated by the unusually impermeable cell membranes found in the commercial strain of baker’s yeast [47], and has been correlated with cell density heterogeneity in brain tumors [86]. In healthy human brain, the values are high primarily in voxels containing both CSF (high D_iso) and WM or GM (both having low D_iso) [52, 53]. The V[D_Δ²] parameter yields high values in voxels with multiple water populations having distinctly different anisotropy, for instance free water and liquid crystal [44] or CSF and WM [52, 53]. Similarly to V[D_iso], in healthy human brain V[R₁] and V[R₂] are highest in voxels with both CSF (low R₁ and R₂) and WM or GM (high R₁ and R₂) [52, 53]. In Figure 3B non-zero values of V[D_iso] are found in particular for voxels comprising both PBS and WM or GM, but also in the thalamus and ventricle. The V[D_Δ²] values were high in regions with contributions of multiple tissue types, such as in the thalamus or entorhinal cortex and voxels with equal amounts of WM and PBS or GM, while the main WM tracts, such as the corpus callosum, fimbria, and internal capsule, display values close to zero. The WM, thalamus, and ventricle exhibit high values of V[R₁] compared to cortex and hippocampus, while high V[R₂] is mainly found for WM. Non-zero covariance C[x,y] requires that both variances V[x] and V[y] are non-zero and the values of x and y are correlated, for instance in voxels containing partial volumes of both WM (low D_iso and high D_Δ²) and CSF (high D_iso and low D_Δ²) [53]. In Figure 3B, positive C[D_iso,R₂] and negative C[R₁,R₂] are observed for WM.

The frequency-dependence is reported in Figure 3C in terms of the rate of change with frequency within the investigated window 50–150 Hz for the per-voxel means, variances, and covariance of D_iso and D_Δ². In the Δ_ω/2πE[D_iso] map, the highest positive values are found as a distinct band following the granule cell layer of the dentate gyrus, while smaller positive values are mainly distributed along GM, and values close to zero are observed for WM. These findings are consistent with the qualitative observations in the selected representative voxels of the ω-dependent distributions in Figure 2C. Conversely, Δ_ω/2πE[D_Δ²] shows negative values throughout the GM. Similarly to Δ_ω/2πE[D_iso], the values of Δ_ω/2πV[D_iso] are positive along the GM and the highest values are found in the granule cell layer. The values of Δ_ω/2πC[D_iso,D_Δ²] are negative in the GM and the lowest values occur in the granule cell layer.

Figure 3D shows bin-resolved maps with the means of the relevant properties. Each map combines two orthogonal scales: the brightness intensity shows the relative signal fraction and the color scale represents the value of the property of interest. In the bin-resolved E[D_iso] maps, we observe that in bin1 (WM) and bin2 (GM) the values are characteristically low. Conversely, bin3 that corresponds to PBS shows high E[D_iso] due to free diffusion. Regarding the bin1 E[D_Δ²] map, the main WM tracts, such as the corpus callosum, fimbria, or external capsule, display values approaching the theoretical maximum of 1. Besides major WM tracts, other brain regions, such as the thalamus, hippocampus, or entorhinal cortex, present values between ∼0.25 and ∼0.5. These intermediate values may correspond to the existence of myelinated axons and bundles that contribute to the anisotropy. For bin2 and bin3, showing the contributions of GM in regions such as the cortex or hippocampus and PBS inside the ventricle, the E[D_Δ²] values are close to zero corresponding to isotropic diffusion. In the per-bin relaxation rates, we observe higher values of E[R₁] in GM and PBS, ∼7 s⁻¹, than in WM with values of ∼6 s⁻¹; however, in E[R₂], we find that the main WM tracts show higher values than GM and PBS. As discussed above in relation to Figure 2C, the values of E[R₁] in this study are probably dominated by the paramagnetic relaxation from the added contrast agent. With the information about orientation (θ,ϕ) expressed in terms of E[D_xx,D_yy,D_zz]/E[D₃₃], we calculated the per-voxel principal orientation of the tensors and displayed as directionally-encoded color (DEC) maps for each of the bins. For bin1, the corpus callosum shows a medio-lateral main orientation while the external capsule fibers follow the characteristic dorso-ventral orientation. The last two columns of Figure 3D shows the bin-resolved values of Δ_ω/2πE[D_iso] and Δ_ω/2πE[D_Δ²], which provide a more precise assignment of the tissue type contributing to the per-voxel values. For bin1, the major WM tracts display Δ_ω/2πE[D_iso] and Δ_ω/2πE[D_Δ²] values near zero with slightly elevated Δ_ω/2πE[D_iso] and negative Δ_ω/2πE[D_Δ²] in the stria terminalis and cingulum. For bin2, the granule cell layer of the dentate gyrus shows the highest values of Δ_ω/2πE[D_iso]. Also for the pyramidal cell layer the values are slightly elevated compared to the ones for the cortex.

The histograms in Figure 4 summarize the numerical values of selected parameters from the maps in Figure 3 and highlight representative values for WM, GM, PBS, and some additional anatomical structures. In general, the peaks of the bin-resolved histograms coincide with the dominant values for WM, GM, and PBS as obtained by direct inspection of the maps. However, for both bin1 and bin3 secondary features appear, in particular for E[R₁] and E[R₂], as a result of low but non-zero values of f_bin1 and f_bin3 in large volumes of GM. Conversely, the granule cell layer and stria terminalis have unique values of Δ_ω/2πE[D_iso] and Δ_ω/2πE[D_Δ²] that are readily visible in the maps but occur only in a few voxels and thus do not show up in the histograms.

FIGURE 4

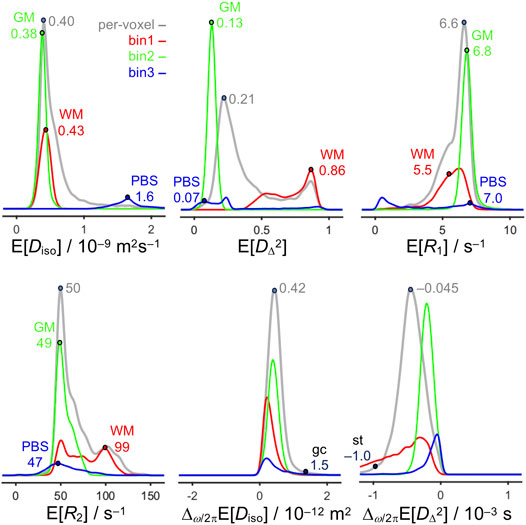
FIGURE 4. Histograms of quantitative parameters across all voxels in the image. The histograms are obtained from the per-voxel (gray) and bin-resolved (red, green, and blue) maps of E[D_iso], E[D_Δ²], E[R₁], E[R₂], Δ_ω/2πE[D_iso], and Δ_ω/2πE[D_Δ²] in Figure 3 and include weighting by S₀, f_bin1, f_bin2, and f_bin3. The abscissas cover the same ranges as the scale bars in Figure 3. Labeled points highlight representative values for WM in the corpus callosum, external capsule, and fimbria, GM in the cortex, and PBS in the ventricle, as well as the granule cell layer (gcl), and stria terminalis (st).

In Figure 5A, bin1-resolved E[R₂], E[D_Δ²], and E[D_xx,D_yy,D_zz]/E[D₃₃] maps are compared with a histological section stained with gold chloride for myelin. As observed in the closer view of the histological section, the fimbria, external capsule, and internal capsule have the highest staining due the high density of myelinated axons, while the cortex gives low staining. With the histological comparison, we demonstrate that f_bin1 adequately corresponds with the major contrast in the myelin-stained section. As mentioned in Figure 3D the highest values of E[D_Δ²] and E[R₂] are found in the main WM tracts. In the closer view of the myelin staining (Figure 5A), most of the fibers in the external capsule follow a dorso-ventral orientation and other fibers continue towards the external capsule. These orientations are observed in the E[D_xx,D_yy,D_zz]/E[D₃₃] map, where in green are the external capsule dorso-ventral fibers and in yellow/red the dorso-ventral/medio-lateral fibers towards the internal capsule.

FIGURE 5

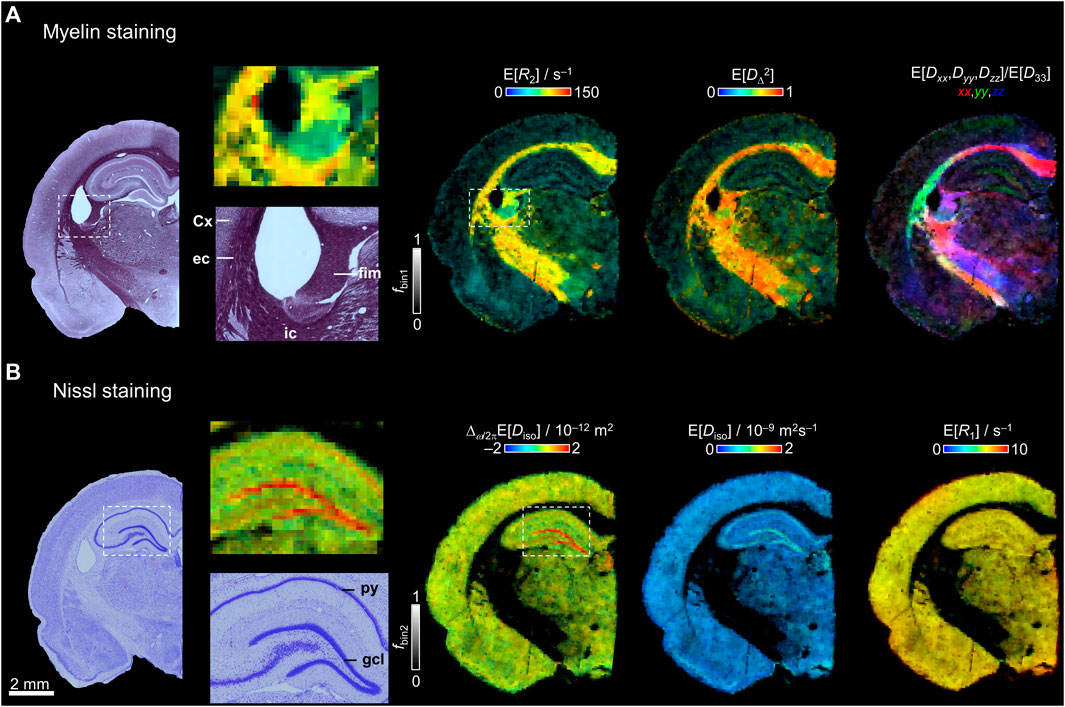
FIGURE 5. Comparison between histology and selected parameter maps. (A) Myelin-stained section and bin1-resolved E[R₂], E[D_Δ²], and E[D_xx,D_yy,D_zz]/ E[D₃₃] maps with brightness and color-coding as in Figure 3D. The darker intensities in the myelin staining correspond to the main white matter tracts and the lighter regions have lower density of myelin. A closer view to the myelin staining and E[R₂] is displayed showing the fimbria (fim), cortex (Cx), external capsule (ec), and internal capsule (ic). (B) Nissl-stained section and bin2-resolved Δ_ω/2πE[D_iso], E[D_iso], and E[R₁] maps. A closer view of the hippocampus and dentate gyrus in the Nissl staining and the Δ_ω/2πE[D_iso] map displays the granule cell layer (gcl) and pyramidal cell layer (py).

The bin2-resolved maps are compared with a Nissl-stained section to assess the cytoarchitecture of the brain tissue in Figure 5B. The closer view of the hippocampal proper reveal the high cell density in the granule and pyramidal cell layers. The restriction map Δ_ω/2πE[D_iso] follows the same contrast as the histological section where the highest values are in the granule and pyramidal cell layers. The Nissl-stained section displays the presence of cells along the whole brain and correlates with f_bin2 as can be observed with the example maps E[D_iso] and E[R₁].

Considering the relevance of extracting per-bundle information within a voxel in WM, we generated nonparametric ODFs from the bin1 components. The resulting ODF lobes correspond to orientation histograms as in Ref. [87]. Figure 6A displays ODFs color-coded for the E[D_Δ²] parameter overlaid on a synthetized R₂-weighted image at τ_E = 20 ms for anatomical reference. The largest lobes correspond to the major WM tracts and a closer look in the joint of the external capsule with the internal capsule shows a crossing fibers region. ODFs color-coded for the E[D_iso], E[R₁], E[R₂], E[D_xx,D_yy,D_zz]/E[D₃₃], Δ_ω/2πE[D_iso], and Δ_ω/2πE[D_Δ²] parameters were also calculated and are displayed in Figure 6B. In the conventional DEC ODFs, the fiber population that follow a dorso-ventral orientation (external capsule) can be observed in green and a second population that contains rostro-caudal fibers with mixed trajectory of the medio-lateral orientations (towards internal capsule) is displayed in a mixture of red and blue colors. The magnifications of the crossing fibers ODFs reveal that in this case the parameter values are nearly identical for the two fiber populations. Corresponding in vivo human brain measurements with lower-dimensional methods have shown that for crossing fibers with distinctly different properties, the rich information in the nonparametric distributions allows quantification of not only per-bin, but also per-bundle values of E[R₁] [52] and E[R₂] [54].

FIGURE 6

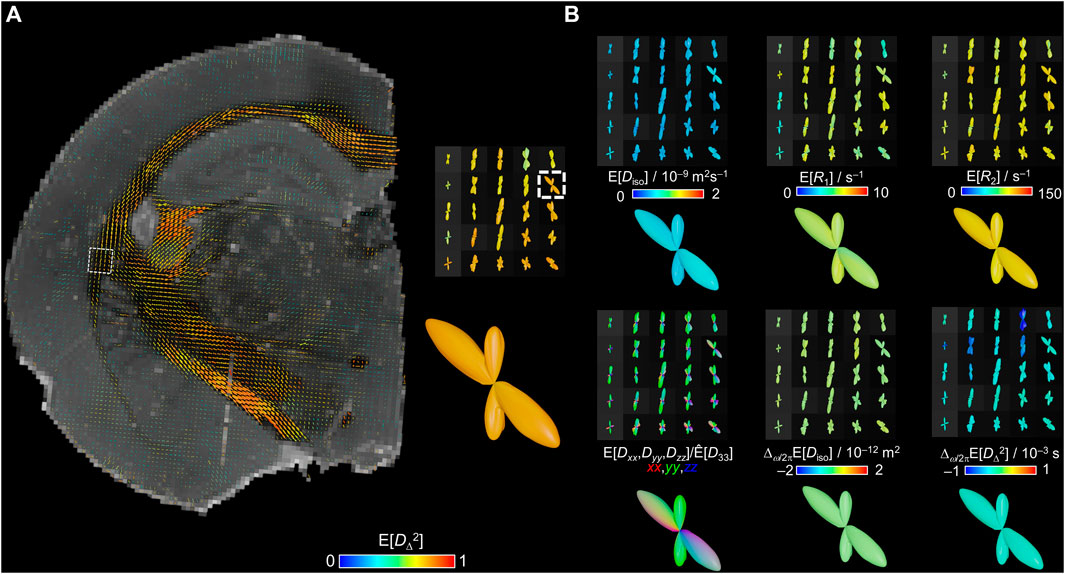
FIGURE 6. Per-voxel ODFs of the bin1 fraction. The ODFs are obtained from the per-voxel D(ω)-R₁-R₂ distributions by mapping the bin1-component weights w, orientations (θ,ϕ), and parameters D_iso, D_Δ², R₁, R₂, D_xx, D_yy, and D_zz onto a spherical mesh using a 10° spherical Gaussian convolution kernel for two frequencies ω/2π = 50 and 150 Hz. ODF radii are given by the orientation-resolved mean weights while the colors derive from the orientation-resolved mean parameters using the same color scheme as in the Figure 3D. (A) E[D_Δ²]-colored ODFs displayed over a synthetized R₂-weighted image calculated from the per-voxel D(ω)-R₁-R₂ distributions with Eq. 1 using b = 0, τ_R = ∞, and τ_E = 20 ms. A closer view on one voxel reveals two distinct fiber populations with similar values of E[D_Δ²]. (B) ODFs colored by E[D_iso], E[R₁], E[R₂], E[D_xx,D_yy,D_zz]/[D₃₃], Δ_ω/2πE[D_iso], and Δ_ω/2πE[D_Δ²] from the same region as the closer view of (A).

Discussion

The projections, parameter maps, and ODFs presented from Figure 2 to Figure 6 illustrate the abundance of information contained within the nonparametric D(ω)-R₁-R₂-distributions estimated via Monte Carlo inversion of the signal acquired in the b(ω)-τ_R-τ_E space. In this study, the distributions were obtained from 809 images which is comparable to a recent 6D D-R₁-R₂ in vivo human brain study with acquisition of 633 image volumes in 25 min measurement time [55], thus indicating potential for translation of our method to clinical research. In previous lower-dimensional studies, each of the obtained parameters have been related to some underlying microstructural properties, local chemical composition, or heterogeneity of the tissue of interest. While most of our parameters have already been introduced in the literature under different names, we here choose to consistently use the means E[x], variances V[x], and covariances C[x,y] convention [44] to emphasize that the parameters all report on some specific aspect of the same D(ω)-R₁-R₂-distribution. The most prominent examples are the equivalences between E[D_iso], apparent diffusion coefficient (ADC) [16], and mean diffusivity (MD) [11]; E[D_Δ²] and microscopic fractional anisotropy (µFA) [47, 49]; E[R₁] and E[R₂] and quantitative R₁ = 1/T₁ and R₂ = 1/T₂ [4]; V[D_iso], isotropic variance (${\mu }_2^{\text{iso}}$) [47], and isotropic mean kurtosis (MK_I) [86]; and Δ_ω/2πE[D_iso] and rate of change of the apparent diffusion coefficient with frequency (Δ_fADC) [61]. Consequently, the insights from the extensive literature on the relations between, for instance, MD and cell density [5], µFA and cell shape [88], T₁ and myelination or iron concentration [14], MK_I and cell density heterogeneity [86], and Δ_fADC and axon diameter [81], can be directly translated to our equivalent metrics.

Unlike lower-dimensional studies where the given metrics are averaged over all the components within a voxel, our multidimensional correlation method allows resolving, for instance, E[R₁], E[R₂], and Δ_ω/2πE[D_iso] for each bin defined in the 2D D_iso-D_Δ² plane and, for anisotropic components, each direction in the 2D θ-ϕ projection. Our version of directionally-encoded color (DEC) based on bin1-resolved E[D_xx,D_yy,D_zz]/E[D₃₃] gives similar results as the more conventional DEC fractional anisotropy (FA) typically used to visualize the main directions of the WM tracts as estimated with DTI. The increase in level of detail when going from DEC-FA to DEC-ODF obtained by constrained spherical deconvolution of HARDI data [89] is mirrored in our step from bin- to orientation-resolved metrics [52, 54]—with the major difference that color-coding of maps and ODFs is not limited to orientation but can be based on any of the obtained parameters. The 2D D_iso-D_Δ² binning corresponds to the 2D MD-FA binning to separate WM, GM, and CSF voxels introduced by Pierpaoli et al. already in 1996 [12], and does here not take advantage of the additional dimensions that could be utilized to tease apart distinct water populations or tissue types. As examples, binning in the 3D D_iso-D_Δ²-R₂ volume has been shown to also differentiate between deep and cortical GM [53] and binning in the 4D D_iso-D_Δ²-θ-ϕ space allows estimation of specific E [R₁] or E [R₂] for a few distinct fiber bundles within the same voxel [52, 54]. Speculating based on the maps in Figure 3, binning in a dimension related to ω-dependence could be utilized to isolate components similar to the granule cell layer or the stria terminalis. Manual binning becomes increasingly challenging in even higher-dimensional spaces and should preferably be implemented as some automatic data-driven approach incorporating information from multiple voxels, for instance building on the recent works in Refs. [90–92].

Even without binning, the spread and correlations between the dimensions are captured with the per-voxel (co)variance metrics V[x] and C[x,y] which may be more generally applicable than the bin-resolved ones for pathologies where the distinction between clusters of components is less clear-cut than in the current example with WM, GM, and PBS. The single-tissue voxels in Figure 2C give low but finite (co)variances that may be challenging to distinguish from the distribution widths originating from the measurement noise and inversion uncertainty [44]. Although comparison between independently processed neighboring voxels and uncertainty estimation by bootstrapping give an indication of the precision of the estimated parameters, they may still suffer from bias that is difficult to correct for [93]. In particular for the larger voxel sizes used for in vivo human measurements, partial volume effects give rise to larger (co)variances, the magnitudes and signs of which may be predicted from single-tissue results. As examples, the representative values of D_iso, R₁, and R₂ of WM and GM reported in Figure 4 would give negative C[D_iso,R₁], positive C[D_iso,R₂], and negative C[R₁,R₂] for a voxel comprising comparable fractions of the two tissue types.

Parameter maps such as E[D_iso] and E[D_Δ²] show similar trends as in previous in vivo mouse and human brain studies [50, 52, 53]. A direct quantitative comparison of conventional ADC and E[D_iso] must consider that the results of our method is in effect extrapolated to the limit b = 0, τ_R = ∞, and τ_E = 0 unlike conventional ADC, which is obtained at the finite values of τ_R and τ_E given by the pulse sequence timings. Our E[D_iso] results showing locally higher values in the granule and pyramidal cell layers, which according to histology have higher cell densities than the neighboring tissues, and seemingly contradicts the simplified interpretation of low ADC or E[D_iso] corresponding to high cellularity. Additional factors contributing to the ADC values are cell membrane permeability, allowing molecular exchange between the intra- and extracellular spaces, and between adjacent cells [94], the relative fraction of the extracellular space [5], and tissue architecture. In the rodent brain, the granule and pyramidal cell layers are mostly tightly packed cells with a regular geometry [62] in contrast with other brain areas (e.g., cortex, thalamus) where the cells are more scattered and share space with an array of neuropil in multiple orientations. Hence, the observation of elevated E[D_iso] in the granule cell layer results from the combined effects of the cell density, nuclear volume fractions, geometry, and molecular exchange [5, 95–98].

For in vivo human brain, WM showed higher values of both E[R₁] and E[R₂] than GM [52, 53, 55], which is consistent with our E[R₂] results. Conversely, we found that E[R₁] in WM is slightly lower than in GM, which on the other hand agrees with in vivo rat model-based diffusion-relaxation correlation [99]. However, besides the obvious futility of trying to compare quantitative relaxation measures from previous in vivo studies with our data on an ex vivo specimen at rather extreme levels of added contrast agent to reduce the scanning time, there are some more fundamental issues with attempting to compare quantitative R₁ from different studies or different pulse sequences as recently elucidated in detail by Manning et al. [8]. The value of R₁ observed by varying some relaxation delay in the pulse sequence does not report on just the properties of the water molecules giving rise to signal intensity in the actually detected images, but instead results from a complex interplay between partial excitation by the radiofrequency pulses, relaxation, and exchange of molecules, protons, or magnetization between numerous proton pools, for instance intra/extracellular water, myelin water, non-aqueous myelin, and non-aqueous non-myelin protons, all having have their distinct NMR properties in terms of R₁, R₂, and linewidth. This latter property determines how the proton pool is affected by radiofrequency pulses with limited bandwidth as invariably used on clinical MRI hardware and also on pre-clinical scanners for slice selection. Taken together, quantitative R₁ will in general not be the same if measured with different pulse sequences and may even depend on the detailed acquisition settings such as slice thickness or the bandwidth of the radiofrequency pulses. Consequently, our values of E[R₁] and E[R₂] should not be compared in too much detail with other results obtained under different conditions.

In the per-voxel and bin-resolved frequency-dependence maps in Figure 3, Δω_/2πE[D_iso] is equivalent to Δ_fADC measured with oscillating gradients in earlier studies [61, 62, 96, 100]. Applying a model of spherical confinement [101] to a liquid with bulk diffusivity 1.6·10⁻⁹ m²s⁻¹ (corresponding to PBS in Figure 4) and a frequency range of 50–150 Hz yields elevated values of Δ_ω/2πE[D_iso] in the approximate diameter range of 4–12 μm with a maximum at 7 μm. In Figure 5, the highest values of Δ_ω/2πE[D_iso] are observed in the granule cell layer of the dentate gyrus which according to histology comprises densely packed granule cells of approximately 15–18 μm length and 10 μm width [102, 103], the latter being within the window giving elevated Δ_ω/2πE[D_iso]. The other highlighted region in Δ_ω/2πE[D_iso] is the pyramidal cell layer of the hippocampus, which comprises just two rows of cells unlike the granule cells in dentate gyrus with eight rows. Compared to previous studies with oscillating gradients, our values were less elevated in the pyramidal cell layer. The difference could be related to the 50–150 Hz frequency range in our study which was somewhat lower and narrower than the 60–180 Hz range in previous rat brain studies. Thus, it is desirable to optimize the gradient waveforms to cover a wider frequency range [100]. Another reason for inconsistent values of Δ_fADC across studies could be relaxation bias resulting from the specific values τ_R and τ_E determined by the hardware and imaging parameters. The Δ_ω/2πE[D_Δ²] map showed negative values in the stria terminalis which in histology corresponds to an area of less myelinated axons than major white matter tracts. The time/frequency-dependence of μFA, similar to our Δ_ω/2πE[D_Δ²] map, has been less studied; however, it has been seen that it could provide complementary information in regions of heterogenous microstructure [104]. The frequency-dependence of FA has been inconsistent across studies unlike the diffusivity, which has been constantly observed to increase with frequency [63, 96, 104].

Conclusion and Outlook

Massively multidimensional diffusion-relaxation correlation MRI joins diffusion-relaxation correlation, time/frequency-dependent (“restricted”) diffusion, and tensor-valued encoding into a common data acquisition and analysis framework, giving per-voxel nonparametric D(ω)-R₁-R₂-distributions which can be projected to the parameter spaces of all the constituent lower-dimensional methods. The unprecedented level of detail opens new opportunities to provide a more specific description of the contribution of cell types, local chemical composition, axonal density, restriction, and orientations within a voxel by a single set of measurements. This method adds the possibility of disentangling bundle-specific metrics within a WM voxel with multiple fiber orientations. As diffusion-relaxation correlation [52], oscillating gradients [105, 106], and tensor-valued encoding [107] with spin echo-prepared EPI read-out are all increasingly used for in vivo human studies on high-end conventional clinical scanners, our massively multidimensional acquisition and analysis approach has potential for translation to clinical research studies using only moderately longer scanning times than each of the individual lower-dimensional methods. Further studies are needed where all the quantitative information from the obtained distributions and maps is integrated with phantoms validation [108], as well as with advanced histological validation [109] of healthy and pathological tissues.

Data Availability Statement

Data and code supporting the conclusion of this article will be made available at https://github.com/daniel-topgaard.

Ethics Statement

The animal study was reviewed and approved by the Animal Committee of the Provincial Government of Southern Finland.

Author Contributions

ON: preparation of rat brain; acquisition and interpretation of MRI and histology data; drafting the manuscript. LS: analysis, implementation and visualization of ODFs. MY: development of ParaVision data acquisition code and Matlab conversion code. AS: preparation of rat brain; acquisition and interpretation of MRI and histology data; revising the manuscript. DT: development of theory; Matlab and Python data inversion code; revising the manuscript. All authors contributed to the final version of the manuscript.

Funding

This work was financially supported the Swedish Foundation for Strategic Research (ITM17-0267) and Swedish Research Council (2018-03697), Academy of Finland (#323385), and Erkko Foundation.

Conflict of Interest

DT owns shares in Random Walk Imaging AB (Lund, Sweden, and http://www.rwi.se/), holding patents related to the described methods.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Maarit Pulkkinen for her assistance in animal and tissue handling and histology.

Abbreviations

ADC, apparent diffusion coefficient; corpus callosum; cg, cingulum; Cx, cortex; dMRI, diffusion magnetic resonance imaging, DTD, diffusion tensor distributions; DTI, diffusion tensor imaging; ec, external capsule; Ent, entorhinal cortex; fi, fimbria; Gd, gadolinium; GM, gray matter; gcl, granule cell layer; hipp, hippocampus; ic, internal capsule; MRI, magnetic resonance imaging; MD, mean diffusivity; NMR, nuclear magnetic resonance; ODF, orientation distribution function; PBS, phosphate buffer saline; py, pyramidal cell layer; st, stria terminalis; tha, thalamus; v, ventricle; WM, white matter.

References

1. Callaghan PT. Translational Dynamics and Magnetic Resonance. Oxford, UK: Oxford University Press (2011). doi:10.1093/acprof:oso/9780199556984.001.0001

CrossRef Full Text | Google Scholar

2. Price WS. NMR Studies of Translational Motion. Cambridge, UK: Cambridge University Press (2009). doi:10.1017/CBO9780511770487

CrossRef Full Text | Google Scholar

3. Halle B. Molecular Theory of Field-dependent Proton Spin-Lattice Relaxation in Tissue. Magn Reson Med (2006) 56:60–72. doi:10.1002/mrm.20919

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Weiskopf N, Edwards LJ, Helms G, Mohammadi S, Kirilina E. Quantitative Magnetic Resonance Imaging of Brain Anatomy and In Vivo Histology. Nat Rev Phys (2021) 3:570–88. doi:10.1038/s42254-021-00326-1

CrossRef Full Text | Google Scholar

5. Padhani AR, Liu G, Mu-Koh D, Chenevert TL, Thoeny HC, Takahara T, et al. Diffusion-weighted Magnetic Resonance Imaging as a Cancer Biomarker: Consensus and Recommendations. Neoplasia (2009) 11:102–25. doi:10.1593/neo.81328

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Hills BP, Wright KM, Belton PS. Proton N.M.R. Studies of Chemical and Diffusive Exchange in Carbohydrate Systems. Mol Phys (1989) 67:1309–26. doi:10.1080/00268978900101831

CrossRef Full Text | Google Scholar

7. Hills BP, Cano C, Belton PS. Proton NMR Relaxation Studies of Aqueous Polysaccharide Systems. Macromolecules (1991) 24:2944–50. doi:10.1021/ma00010a047

CrossRef Full Text | Google Scholar

8. Manning AP, MacKay AL, Michal CA. Understanding Aqueous and Non-aqueous Proton T1 Relaxation in Brain. J Magn Reson (2021) 323:106909. doi:10.1016/j.jmr.2020.106909

CrossRef Full Text | Google Scholar

9. Edzes HT, Samulski ET. The Measurement of Cross-Relaxation Effects in the Proton NMR Spin-Lattice Relaxation of Water in Biological Systems: Hydrated Collagen and Muscle. J Magn Reson (1978) 31:207–29. doi:10.1016/0022-2364(78)90185-3

CrossRef Full Text | Google Scholar

10. Does MD. Inferring Brain Tissue Composition and Microstructure via MR Relaxometry. Neuroimage (2018) 182:136–48. doi:10.1016/j.neuroimage.2017.12.087

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Basser PJ, Mattiello J, LeBihan D. MR Diffusion Tensor Spectroscopy and Imaging. Biophysical J (1994) 66:259–67. doi:10.1016/S0006-3495(94)80775-1

CrossRef Full Text | Google Scholar

12. Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G. Diffusion Tensor MR Imaging of the Human Brain. Radiology (1996) 201:637–48. doi:10.1148/radiology.201.3.8939209

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Gelman N, Ewing JR, Gorell JM, Spickler EM, Solomon EG. Interregional Variation of Longitudinal Relaxation Rates in Human Brain at 3.0 T: Relation to Estimated Iron and Water Contents. Magn Reson Med (2001) 45:71–9. doi:10.1002/1522-2594(200101)45:1<71:aid-mrm1011>3.0.co;2-2

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Stüber C, Morawski M, Schäfer A, Labadie C, Wähnert M, Leuze C, et al. Myelin and Iron Concentration in the Human Brain: A Quantitative Study of MRI Contrast. Neuroimage (2014) 93:95–106. doi:10.1016/j.neuroimage.2014.02.026

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time‐Dependent Field Gradient. J Chem Phys (1965) 42:288–92. doi:10.1063/1.1695690

CrossRef Full Text | Google Scholar

16. Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR Imaging of Intravoxel Incoherent Motions: Application to Diffusion and Perfusion in Neurologic Disorders. Radiology (1986) 161:401–7. doi:10.1148/radiology.161.2.3763909

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Slator PJ, Palombo M, Miller KL, Westin CF, Laun F, Kim D, et al. Combined Diffusion‐relaxometry Microstructure Imaging: Current Status and Future Prospects. Magn Reson Med (2021) 86:2987–3011. doi:10.1002/mrm.28963

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Tax CMW. Chapter 7. Estimating Chemical and Microstructural Heterogeneity by Correlating Relaxation and Diffusion. In: D Topgaard, editor. Advanced Diffusion Encoding Methods in MRI. Cambridge, UK: Royal Society of Chemistry (2020). p. 186–227. doi:10.1039/9781788019910-00186

CrossRef Full Text | Google Scholar

19. Reymbaut A. Chapter 3. Diffusion Anisotropy and Tensor-Valued Encoding. In: D Topgaard, editor. Advanced Diffusion Encoding Methods In MRI. Cambridge, UK: Royal Society of Chemistry (2020). p. 68–102. doi:10.1039/9781788019910-00068

CrossRef Full Text | Google Scholar

20. Aggarwal M. Chapter 4. Restricted Diffusion and Spectral Content of the Gradient Waveforms. In: D Topgaard, editor. Advanced Diffusion Encoding Methods In MRI. Cambridge, UK: Royal Society of Chemistry (2020). p. 103–22. doi:10.1039/9781788019910-00103

CrossRef Full Text | Google Scholar

21. Galvosas P, Callaghan PT. Multi-dimensional Inverse Laplace Spectroscopy in the NMR of Porous media. Comptes Rendus Physique (2010) 11:172–80. doi:10.1016/j.crhy.2010.06.014

CrossRef Full Text | Google Scholar

22. Bernin D, Topgaard D. NMR Diffusion and Relaxation Correlation Methods: New Insights in Heterogeneous Materials. Curr Opin Colloid Interf Sci (2013) 18:166–72. doi:10.1016/j.cocis.2013.03.007

CrossRef Full Text | Google Scholar

23. Song YQ, Venkataramanan L, Kausik R, Heaton N. Chapter 4. Two-Dimensional NMR of Diffusion and Relaxation. In: R Valiullin, editor. Diffusion NMR of Confined Systems. Cambridge, UK: Royal Society of Chemistry (2016). p. 111–55. doi:10.1039/9781782623779-00111

CrossRef Full Text | Google Scholar

24. Zhang Y, Blümich B. Spatially Resolved D-T2 Correlation NMR of Porous media. J Magn Reson (2014) 242:41–8. doi:10.1016/j.jmr.2014.01.017

CrossRef Full Text | Google Scholar

25. Benjamini D, Basser PJ. Multidimensional Correlation MRI. NMR Biomed (2020) 33:33. doi:10.1002/nbm.4226

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Benjamini D. Chapter 10. Nonparametric Inversion of Relaxation and Diffusion Correlation Data. In: D Topgaard, editor. Advanced Diffusion Encoding Methods In MRI. Cambridge, UK: Royal Society of Chemistry (2020). p. 278–316. doi:10.1039/9781788019910-00278

CrossRef Full Text | Google Scholar

27. Kim D, Doyle EK, Wisnowski JL, Kim JH, Haldar JP. Diffusion‐relaxation Correlation Spectroscopic Imaging: A Multidimensional Approach for Probing Microstructure. Magn Reson Med (2017) 78:2236–49. doi:10.1002/mrm.26629

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Slator PJ, Hutter J, Palombo M, Jackson LH, Ho A, Panagiotaki E, et al. Combined Diffusion‐relaxometry MRI to Identify Dysfunction in the Human Placenta. Magn Reson Med (2019) 82:95–106. doi:10.1002/mrm.27733

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Zhang Z, Wu HH, Priester A, Magyar C, Afshari Mirak S, Shakeri S, et al. Prostate Microstructure in Prostate Cancer Using 3-T MRI with Diffusion-Relaxation Correlation Spectrum Imaging: Validation with Whole-Mount Digital Histopathology. Radiology (2020) 296:348–55. doi:10.1148/radiol.2020192330

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Benjamini D, Basser PJ. Magnetic Resonance Microdynamic Imaging Reveals Distinct Tissue Microenvironments. Neuroimage (2017) 163:183–96. doi:10.1016/j.neuroimage.2017.09.033

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Benjamini D, Iacono D, Komlosh ME, Perl DP, Brody DL, Basser PJ. Diffuse Axonal Injury Has a Characteristic Multidimensional MRI Signature in the Human Brain. Brain (2021) 144:800–16. doi:10.1093/brain/awaa447

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Topgaard D. Multiple Dimensions for Random Walks. J Magn Reson (2019) 306:150–4. doi:10.1016/j.jmr.2019.07.024

CrossRef Full Text | Google Scholar

33. Topgaard D. Multidimensional Diffusion MRI. J Magn Reson (2017) 275:98–113. doi:10.1016/j.jmr.2016.12.007

CrossRef Full Text | Google Scholar

34. Schmidt-Rohr K, Spiess HW. Multidimensional Solid-State NMR and Polymers. San Diego: Academic Press (1994).

Google Scholar

35. Andrew ER, Bradbury A, Eades RG. Removal of Dipolar Broadening of Nuclear Magnetic Resonance Spectra of Solids by Specimen Rotation. Nature (1959) 183:1802–3. doi:10.1038/1831802a0

CrossRef Full Text | Google Scholar

36. Szeverenyi NM, Bax A, Maciel GE. Magic-angle Hopping as an Alternative to Magic-Angle Spinning for Solid State NMR. J Magn Reson (1985) 61:440–7. doi:10.1016/0022-2364(85)90184-2

CrossRef Full Text | Google Scholar

37. Frydman L, Chingas GC, Lee YK, Grandinetti PJ, Eastman MA, Barrall GA, et al. Variable‐angle Correlation Spectroscopy in Solid‐state Nuclear Magnetic Resonance. J Chem Phys (1992) 97:4800–8. doi:10.1063/1.463860

CrossRef Full Text | Google Scholar

38. Eriksson S, Lasič S, Topgaard D. Isotropic Diffusion Weighting in PGSE NMR by Magic-Angle Spinning of the Q-Vector. J Magn Reson (2013) 226:13–8. doi:10.1016/j.jmr.2012.10.015

CrossRef Full Text | Google Scholar

39. Eriksson S, Lasič S, Nilsson M, Westin C-F, Topgaard D. NMR Diffusion-Encoding with Axial Symmetry and Variable Anisotropy: Distinguishing between Prolate and Oblate Microscopic Diffusion Tensors with Unknown Orientation Distribution. J Chem Phys (2015) 142:104201. doi:10.1063/1.4913502

CrossRef Full Text | Google Scholar

40. de Almeida Martins JP, Topgaard D. Two-dimensional Correlation of Isotropic and Directional Diffusion Using NMR. Phys Rev Lett (2016) 116:087601. doi:10.1103/PhysRevLett.116.087601

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Westin C-F, Szczepankiewicz F, Pasternak O, Özarslan E, Topgaard D, Knutsson H, et al. Measurement Tensors in Diffusion MRI: Generalizing the Concept of Diffusion Encoding. Med Image Comput Comput Assist Interv (2014) 17:209–16. doi:10.1007/978-3-319-10443-0_27

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Basser PJ, Pajevic S. A Normal Distribution for Tensor-Valued Random Variables: Applications to Diffusion Tensor MRI. IEEE Trans Med Imaging (2003) 22:785–94. doi:10.1109/TMI.2003.815059

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Jian B, Vemuri BC, Özarslan E, Carney PR, Mareci TH. A Novel Tensor Distribution Model for the Diffusion-Weighted MR Signal. Neuroimage (2007) 37:164–76. doi:10.1016/j.neuroimage.2007.03.074

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Topgaard D. Diffusion Tensor Distribution Imaging. NMR Biomed (2019) 32:e4066–12. doi:10.1002/nbm.4066

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Lawrenz M, Koch MA, Finsterbusch J. A Tensor Model and Measures of Microscopic Anisotropy for Double-Wave-Vector Diffusion-Weighting Experiments with Long Mixing Times. J Magn Reson (2010) 202:43–56. doi:10.1016/j.jmr.2009.09.015

CrossRef Full Text | Google Scholar

46. Jespersen SN, Lundell H, Sønderby CK, Dyrby TB. Orientationally Invariant Metrics of Apparent Compartment Eccentricity from Double Pulsed Field Gradient Diffusion Experiments. NMR Biomed (2013) 26:1647–62. doi:10.1002/nbm.2999

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Lasič S, Szczepankiewicz F, Eriksson S, Nilsson M, Topgaard D. Microanisotropy Imaging: Quantification of Microscopic Diffusion Anisotropy and Orientational Order Parameter by Diffusion MRI with Magic-Angle Spinning of the Q-Vector. Front Phys (2014) 2:1–11. doi:10.3389/fphy.2014.00011

CrossRef Full Text | Google Scholar

48. Topgaard D. Chapter 7. NMR Methods for Studying Microscopic Diffusion Anisotropy. In: R Valiullin, editor. Diffusion NMR of Confined Systems: Fluid Transport In Porous Solids And Heterogeneous Materials. Cambridge, UK: Royal Society of Chemistry (2016). p. 226–59. doi:10.1039/9781782623779-00226

CrossRef Full Text | Google Scholar

49. Shemesh N, Jespersen SN, Alexander DC, Cohen Y, Drobnjak I, Dyrby TB, et al. Conventions and Nomenclature for Double Diffusion Encoding NMR and MRI. Magn Reson Med (2016) 75:82–7. doi:10.1002/mrm.25901

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Yon M, de Almeida Martins JP, Bao Q, Budde MD, Frydman L, Topgaard D, et al. Diffusion Tensor Distribution Imaging of an In Vivo Mouse Brain at Ultrahigh Magnetic Field by Spatiotemporal Encoding. NMR Biomed (2020) 33:1–14. doi:10.1002/nbm.4355

CrossRef Full Text | Google Scholar

51. de Almeida Martins JP, Topgaard D. Multidimensional Correlation of Nuclear Relaxation Rates and Diffusion Tensors for Model-free Investigations of Heterogeneous Anisotropic Porous Materials. Sci Rep (2018) 8:1–12. doi:10.1038/s41598-018-19826-9

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Reymbaut A, Critchley J, Durighel G, Sprenger T, Sughrue M, Bryskhe K, et al. Toward Nonparametric Diffusion‐ Characterization of Crossing Fibers in the Human Brain. Magn Reson Med (2021) 85:2815–27. doi:10.1002/mrm.28604

PubMed Abstract | CrossRef Full Text | Google Scholar

53. de Almeida Martins JP, Tax CMW, Szczepankiewicz F, Jones DK, Westin C-F, Topgaard D. Transferring Principles of Solid-State and Laplace NMR to the Field of In Vivo Brain MRI. Magn Reson (2020) 1:27–43. doi:10.5194/mr-1-27-2020

CrossRef Full Text | Google Scholar

54. de Almeida Martins JP, Tax CMW, Reymbaut A, Szczepankiewicz F, Chamberland M, Jones DK, et al. Computing and Visualising Intra‐voxel Orientation‐specific Relaxation-Diffusion Features in the Human Brain. Hum Brain Mapp (2021) 42:310–28. doi:10.1002/hbm.25224

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Martin J, Reymbaut A, Schmidt M, Doerfler A, Uder M, Laun FB, Topgaard D. Nonparametric D-R₁-R₂ Distribution MRI of the Living Human Brain. Neuroimage (2021) 245:118753. doi:10.1016/j.neuroimage.2021.118753

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Stepišnik J. Analysis of NMR Self-Diffusion Measurements by a Density Matrix Calculation. Phys B (1981) 104:350–64. doi:10.1016/0378-4363(81)90182-0

CrossRef Full Text | Google Scholar

57. Callaghan PT, Stepišnik J. Frequency-domain Analysis of Spin Motion Using Modulated-Gradient NMR. J Magn Reson Ser A (1995) 117:118–22. doi:10.1006/jmra.1995.9959

CrossRef Full Text | Google Scholar

58. Topgaard D, Malmborg C, Söderman O. Restricted Self-Diffusion of Water in a Highly Concentrated W/o Emulsion Studied Using Modulated Gradient Spin-echo NMR. J Magn Reson (2002) 156:195–201. doi:10.1006/jmre.2002.2556

CrossRef Full Text | Google Scholar

59. Stepišnik J, Lasič S, Mohorič A, Serša I, Sepe A. Spectral Characterization of Diffusion in Porous media by the Modulated Gradient Spin echo with CPMG Sequence. J Magn Reson (2006) 182:195–9. doi:10.1016/j.jmr.2006.06.023

CrossRef Full Text | Google Scholar

60. Wu D, Martin LJ, Northington FJ, Zhang J. Oscillating Gradient Diffusion MRI Reveals Unique Microstructural Information in normal and Hypoxia-Ischemia Injured Mouse Brains. Magn Reson Med (2014) 72:1366–74. doi:10.1002/mrm.25441

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Aggarwal M, Jones MV, Calabresi PA, Mori S, Zhang J. Probing Mouse Brain Microstructure Using Oscillating Gradient Diffusion MRI. Magn Reson Med (2012) 67:98–109. doi:10.1002/mrm.22981

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Aggarwal M, Burnsed J, Martin LJ, Northington FJ, Zhang J. Imaging Neurodegeneration in the Mouse hippocampus after Neonatal Hypoxia-Ischemia Using Oscillating Gradient Diffusion MRI. Magn Reson Med (2014) 72:829–40. doi:10.1002/mrm.24956

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Baron CA, Beaulieu C. Oscillating Gradient Spin-echo (OGSE) Diffusion Tensor Imaging of the Human Brain. Magn Reson Med (2014) 72:726–36. doi:10.1002/mrm.24987

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Van AT, Holdsworth SJ, Bammer R. In Vivo investigation of Restricted Diffusion in the Human Brain with Optimized Oscillating Diffusion Gradient Encoding. Magn Reson Med (2014) 71:83–94. doi:10.1002/mrm.24632

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Jiang H, Topgaard D. Gradient Waveforms for Comprehensive Sampling of the Frequency and “Shape” Dimensions in b(ω)-Encoded Diffusion MRI. In: Proceedings of the International Society for Magnetic Resonance in Medicine; 2021 May 15–20 (2021):2458.

Google Scholar

66. Lundell H, Nilsson M, Dyrby TB, Parker GJM, Cristinacce PLH, Zhou F-L, et al. Multidimensional Diffusion MRI with Spectrally Modulated Gradients Reveals Unprecedented Microstructural Detail. Sci Rep (2019) 9:1–12. doi:10.1038/s41598-019-45235-7

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Narvaez O, Yon M, Jiang H, Bernin D, Forssell-Aronsson E, Sierra A, et al. Model-free Approach to the Interpretation of Restricted and Anisotropic Self-Diffusion in Magnetic Resonance of Biological Tissues. arXiv [Preprint] (2021). Available from: https://arxiv.org/abs/2111.07827.

Google Scholar

68. Kingsley PB. Introduction to Diffusion Tensor Imaging Mathematics: Part II. Anisotropy, Diffusion-Weighting Factors, and Gradient Encoding Schemes. Concepts Magn Reson (2006) 28A:123–54. doi:10.1002/cmr.a.20049

CrossRef Full Text | Google Scholar

69. Conturo TE, McKinstry RC, Akbudak E, Robinson BH. Encoding of Anisotropic Diffusion with Tetrahedral Gradients: A General Mathematical Diffusion Formalism and Experimental Results. Magn Reson Med (1996) 35:399–412. doi:10.1002/mrm.1910350319

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Mattiello J, Basser PJ, Lebihan D. Analytical Expressions for the B Matrix in NMR Diffusion Imaging and Spectroscopy. J Magn Reson Ser A (1994) 108:131–41. doi:10.1006/jmra.1994.1103

CrossRef Full Text | Google Scholar

71. Arbabi A, Kai J, Khan AR, Baron CA. Diffusion Dispersion Imaging: Mapping Oscillating Gradient Spin‐echo Frequency Dependence in the Human Brain. Magn Reson Med (2020) 83:2197–208. doi:10.1002/mrm.28083

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Laitinen T, Sierra A, Bolkvadze T, Pitkänen A, Gröhn O. Diffusion Tensor Imaging Detects Chronic Microstructural Changes in white and gray Matter after Traumatic Brain Injury in Rat. Front Neurosci (2015) 9:9. doi:10.3389/fnins.2015.00128

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Topgaard D. Director Orientations in Lyotropic Liquid Crystals: Diffusion MRI Mapping of the Saupe Order Tensor. Phys Chem Chem Phys (2016) 18:8545–53. doi:10.1039/C5CP07251D

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Tournier J-D, Smith R, Raffelt D, Tabbara R, Dhollander T, Pietsch M, et al. MRtrix3: A Fast, Flexible and Open Software Framework for Medical Image Processing and Visualisation. Neuroimage (2019) 202:116137. doi:10.1016/j.neuroimage.2019.116137

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Cordero-Grande L, Christiaens D, Hutter J, Price AN, Hajnal JV. Complex Diffusion-Weighted Image Estimation via Matrix Recovery under General Noise Models. Neuroimage (2019) 200:391–404. doi:10.1016/j.neuroimage.2019.06.039

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Nilsson M, Szczepankiewicz F, Lampinen B, Ahlgren A, de Almeida Martins JP, Lasič S, et al. An Open-Source Framework for Analysis of Multidimensional Diffusion MRI Data Implemented in MATLAB. In: Proceedings International Society Of Magnetic Resonance In Medicine; 2018 Jun 16–21; Paris, France (2018).

Google Scholar

77. Prange M, Song YQ. Quantifying Uncertainty in NMR Spectra Using Monte Carlo Inversion. J Magn Reson (2009) 196:54–60. doi:10.1016/j.jmr.2008.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Smith AA, Ernst M, Meier BH. Because the Light Is Better Here: Correlation-Time Analysis by NMR Spectroscopy. Angew Chem Int Ed (2017) 56:13590–5. doi:10.1002/anie.201707316

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Xu J, Li H, Li K, Harkins KD, Jiang X, Xie J, et al. Fast and Simplified Mapping of Mean Axon Diameter Using Temporal Diffusion Spectroscopy. NMR Biomed (2016) 29:400–10. doi:10.1002/nbm.3484

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Aggarwal M, Smith MD, Calabresi PA. Diffusion‐time Dependence of Diffusional Kurtosis in the Mouse Brain. Magn Reson Med (2020) 84:1564–78. doi:10.1002/mrm.28189

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Harkins KD, Beaulieu C, Xu J, Gore JC, Does MD. A Simple Estimate of Axon Size with Diffusion MRI. Neuroimage (2021) 227:117619. doi:10.1016/j.neuroimage.2020.117619

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Reymbaut A, Zheng Y, Li S, Sun W, Xu H, Daimiel Naranjo I, et al. Chapter 14. Clinical Research with Advanced Diffusion Encoding Methods in MRI. In: D Topgaard, editor. Advanced Diffusion Encoding Methods In MRI. Cambridge, UK: Royal Society of Chemistry (2020). p. 406–29. doi:10.1039/9781788019910-00406

CrossRef Full Text | Google Scholar

83. Watson GS. Equatorial Distributions on a Sphere. Biometrika (1965) 52:193. doi:10.2307/2333824

CrossRef Full Text | Google Scholar

84. Mardia K, Jupp P. Directional Statistics; Wiley Series in Probability and Statistics. Chichester, UK: Wiley (2009).

Google Scholar

85. Sakol N, Egawa A, Fujiwara T. Gadolinium Complexes as Contrast Agent for Cellular NMR Spectroscopy. Ijms (2020) 21:4042. doi:10.3390/ijms21114042

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Szczepankiewicz F, van Westen D, Englund E, Westin C-F, Ståhlberg F, Lätt J, et al. The Link between Diffusion MRI and Tumor Heterogeneity: Mapping Cell Eccentricity and Density by Diffusional Variance Decomposition (DIVIDE). Neuroimage (2016) 142:522–32. doi:10.1016/j.neuroimage.2016.07.038

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Salo RA, Belevich I, Jokitalo E, Gröhn O, Sierra A. Assessment of the Structural Complexity of Diffusion MRI Voxels Using 3D Electron Microscopy in the Rat Brain. Neuroimage (2021) 225:117529. doi:10.1016/j.neuroimage.2020.117529

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Szczepankiewicz F, Lasič S, van Westen D, Sundgren PC, Englund E, Westin C-F, et al. Quantification of Microscopic Diffusion Anisotropy Disentangles Effects of Orientation Dispersion from Microstructure: Applications in Healthy Volunteers and in Brain Tumors. Neuroimage (2015) 104:241–52. doi:10.1016/j.neuroimage.2014.09.057

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Tournier JD. Diffusion MRI in the Brain - Theory and Concepts. Prog Nucl Magn Reson Spectrosc (2019) 112-113:1–16. doi:10.1016/j.pnmrs.2019.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Molina‐Romero M, Gómez PA, Sperl JI, Czisch M, Sämann PG, Jones DK, et al. A Diffusion Model‐free Framework with echo Time Dependence for Free‐water Elimination and Brain Tissue Microstructure Characterization. Magn Reson Med (2018) 80:2155–72. doi:10.1002/mrm.27181

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Pas K, Komlosh ME, Perl DP, Basser PJ, Benjamini D. Retaining Information from Multidimensional Correlation MRI Using a Spectral Regions of Interest Generator. Sci Rep (2020) 10:3246. doi:10.1038/s41598-020-60092-5

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Slator PJ, Hutter J, Marinescu RV, Palombo M, Jackson LH, Ho A, et al. Data-Driven Multi-Contrast Spectral Microstructure Imaging with InSpect: INtegrated SPECTral Component Estimation and Mapping. Med Image Anal (2021) 71:102045. doi:10.1016/j.media.2021.102045

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Prange M, Song YQ. Understanding NMR Spectral Uncertainty. J Magn Reson (2010) 204:118–23. doi:10.1016/j.jmr.2010.02.010

CrossRef Full Text | Google Scholar

94. Stanisz GJ, Wright GA, Henkelman RM, Szafer A. An Analytical Model of Restricted Diffusion in Bovine Optic Nerve. Magn Reson Med (1997) 37:103–11. doi:10.1002/mrm.1910370115

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Topgaard D. Chapter 1. Translational Motion of Water in Biological Tissues - A Brief Primer. In: Advanced Diffusion Encoding Methods In MRI. Cambridge, UK: Royal Society of Chemistry (2020). p. 1–11. doi:10.1039/9781788019910-00001

CrossRef Full Text | Google Scholar

96. Kershaw J, Leuze C, Aoki I, Obata T, Kanno I, Ito H, et al. Systematic Changes to the Apparent Diffusion Tensor of In Vivo Rat Brain Measured with an Oscillating-Gradient Spin-echo Sequence. Neuroimage (2013) 70:10–20. doi:10.1016/j.neuroimage.2012.12.036

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Stanisz GJ. Diffusion MR in Biological Systems: Tissue Compartments and Exchange. Isr J Chem (2010) 43:33–44. doi:10.1560/e0wu-7ffh-31m6-vlyt

CrossRef Full Text | Google Scholar

98. Buizza G, Paganelli C, Ballati F, Sacco S, Preda L, Iannalfi A, et al. Improving the Characterization of Meningioma Microstructure in Proton Therapy from Conventional Apparent Diffusion Coefficient Measurements Using Monte Carlo Simulations of Diffusion MRI. Med Phys (2021) 48:1250–61. doi:10.1002/mp.14689

PubMed Abstract | CrossRef Full Text | Google Scholar

99. De Santis S, Barazany D, Jones DK, Assaf Y. Resolving Relaxometry and Diffusion Properties within the Same Voxel in the Presence of Crossing Fibres by Combining Inversion Recovery and Diffusion-Weighted Acquisitions. Magn Reson Med (2016) 75:372–80. doi:10.1002/mrm.25644

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Portnoy S, Flint JJ, Blackband SJ, Stanisz GJ. Oscillating and Pulsed Gradient Diffusion Magnetic Resonance Microscopy over an Extended B -value Range: Implications for the Characterization of Tissue Microstructure. Magn Reson Med (2013) 69:1131–45. doi:10.1002/mrm.24325

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Stepišnik J. Time-dependent Self-Diffusion by NMR Spin-echo. Phys B (1993) 183:343–50. doi:10.1016/0921-4526(93)90124-O

CrossRef Full Text | Google Scholar

102. Claiborne BJ, Amaral DG, Cowan WM. Quantitative, Three-Dimensional Analysis of Granule Cell Dendrites in the Rat Dentate Gyrus. J Comp Neurol (1990) 302:206–19. doi:10.1002/cne.903020203

CrossRef Full Text | Google Scholar

103. Nielsen J, Sierra A, Belevich I, Jokitalo E, Aggarwal M. Exploring the Epileptic Rat Hippocampus Using Oscillating Gradients, 3D Electron Microscopy and Monte Carlo Simulations. In: Proceedings International Society Of Magnetic Resonance In Medicine; 2021 May 15–20 (2021).

Google Scholar

104. Ianuş A, Jespersen SN, Serradas Duarte T, Alexander DC, Drobnjak I, Shemesh N. Accurate Estimation of Microscopic Diffusion Anisotropy and its Time Dependence in the Mouse Brain. Neuroimage (2018) 183:934–49. doi:10.1016/j.neuroimage.2018.08.034

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Baron CA, Kate M, Gioia L, Butcher K, Emery D, Budde M, et al. Reduction of Diffusion-Weighted Imaging Contrast of Acute Ischemic Stroke at Short Diffusion Times. Stroke (2015) 46:2136–41. doi:10.1161/STROKEAHA.115.008815

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Xu J, Jiang X, Li H, Arlinghaus LR, McKinley ET, Devan SP, et al. Magnetic Resonance Imaging of Mean Cell Size in Human Breast Tumors. Magn Reson Med (2020) 83:2002–14. doi:10.1002/mrm.28056

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Lampinen B, Zampeli A, Björkman‐Burtscher IM, Szczepankiewicz F, Källén K, Compagno Strandberg M, et al. Tensor‐valued Diffusion MRI Differentiates Cortex and white Matter in Malformations of Cortical Development Associated with Epilepsy. Epilepsia (2020) 61:1701–13. doi:10.1111/epi.16605

PubMed Abstract | CrossRef Full Text | Google Scholar

108. McHugh DJ, Hubbard Cristinacce PL. Chapter 12. Phantoms for Validating Advanced Diffusion Sequences. In: D Topgaard, editor. Advanced Diffusion Encoding Methods In MRI. Cambridge, UK: Royal Society of Chemistry (2020). p. 349–76. doi:10.1039/9781788019910-00349

CrossRef Full Text | Google Scholar

109. Sierra A. Chapter 13. Advanced Histology for Validation of Advanced Diffusion MRI. In: D Topgaard, editor. Advanced Diffusion Encoding Methods In MRI. Cambridge, UK: Royal Society of Chemistry (2020). p. 377–405. doi:10.1039/9781788019910-00377

CrossRef Full Text | Google Scholar