Tunable Topological Surface States of Three-Dimensional Acoustic Crystals

Topological design for band structures of artificial materials such as acoustic crystals provides a powerful tool to manipulate wave propagating in a robust and symmetry-protected way. In this paper, based on the band folding and breaking mechanism by building blocks with acoustic atoms, we construct a three-dimensional topological acoustic crystal with a large complete bandgap. At a mirror-symmetry domain wall, two gapped symmetry and anti-symmetry surface states can be found in the bandgap, originated from two opposite Su-Schrieffer-Heeger chains. Remarkably, by enforcing a glide symmetry on the domain wall, we can tune the original gapped surface states in a gapless fashion at the boundaries of surface Brillouin zone, acting as omnidirectional acoustic quantum spin Hall effect. Our tunable yet straightforward acoustic crystals offer promising potentials in realizing future topological acoustic devices.

Introduction

In the past decades, the cross-disciplinary science of topology in mathematics and solid-state material in physics has led to a prosperous research field, i.e., topological physics [1, 2]. The well-known cases are the family of quantum Hall effect [1, 3] and topological insulators [4, 5]. One of the most intriguing characters is the topologically robust boundary states protected by their bulk topology [6]. In 2008, Haldane and Raghu made a crucial claim that topology is an intrinsic feature of periodic Bloch waves independent of the statistical difference between fermions and bosons [7, 8], extending the scope of topological physics from electronic to classical-wave systems, such as photonic crystal and acoustic crystal (AC). The advantages of classical-wave systems in studying topological behaviors come from their flexible structures, less complicated samples, and more accessible measurements [9–12]. Since then, there have been enormous works focusing on the classical-wave analogs of topological phases, ranging from one-dimensional (1D) to three-dimensional (3D) and even higher synthetic dimensions [13–22]. These topological models provide unprecedented ways to manipulate waves with robust and symmetry-protected manners. For example, the localized zero-dimensional (0D) bound states in 1D Su-Schrieffer-Heeger (SSH) chains can support extremely enhanced field intensity [13], and the 1D chiral edge states in two-dimensional (2D) Chern insulators can support backscattering-immune one-way boundary transport [20]. Compared to 1D and 2D topological phases, 3D topological phases can efficiently manipulate waves in multiple dimensions [23–27]. Nevertheless, despite many works on 3D acoustic semimetals [28–38], the studies on 3D acoustic topological insulators are insufficient [39, 40].

In general, the topology of band structure space originates from its nontrivial geometry phase, e.g., Zak phase in 1D [41] or Berry phase in 2D [2], which is ill-defined at the degenerated point. In other words, the degenerated point of band structure might be the phase transition point between trivial phase and some topological phase. An excellent way to realize topological insulators is to lift band degeneracy by breaking symmetries. One can lift the linear or quartic band degenerated point by either breaking time-reversal symmetry to obtain 2D quantum Hall effect [42], or breaking spatial symmetry to 2D topological valley [43] and quantum spin Hall effect [44]. Regarding the construction of degeneracy by building symmetries, there are mainly three approaches. The first one is to resort to group theory, creating a high symmetric structure with 2D irreducible representation such as E in C_3v [43] or C_4v [45] lattices. This kind of band degeneracy requires careful lattice optimization to obtain favorite dispersion and eliminate the influence of other bands. The second one is to construct accidental band degeneracy relying on elaborately designed parameters [46]. Last but not least, the band folding mechanism increases symmetries by enlarging the primitive unit cell. For example, with in-plane 2D folding, four-fold degeneracy can be constructed using a triple unit cell three times larger than the primitive one [44, 47]. Likewise, with out-of-plane 1D folding, two two-fold Weyl points can reshape into one four-fold Dirac degeneracy [40, 48]. Thus, extending the band folding and breaking mechanism to a 3D Brillouin zone (BZ) would bring us a convenient way to realize topological insulators in 3D ACs.

In this paper, we propose a 3D AC with tunable topological surface states based on the 3D band folding and breaking mechanism. We start from one simplest 3D AC structure with a simple cubic lattice by building blocks. By doubling the unit cell in real space, the first isolated band of AC is folded in a 3D BZ, forming two-fold band degeneracy with a nodal plane. Then, we break the band degeneracy with a NaCl-like AC structure to get a large 3D complete bandgap. We can also obtain tunable topological surface states in the bandgap upon different symmetries of domain walls, e.g., mirror or glide symmetry. Our model shows the controllable and reconfigurable abilities of topological sound transport on a 2D plane.

Band Folding and Breaking in a 3D AC

To begin with, we try to construct an AC by building blocks, using two acoustic cavity-tube structures as shown in Figure 1A. The structure parameters are h = 0.4a, l = h′ = 0.2a, where a is the lattice constant. These two cavities having different resonant frequencies act as two different acoustic atoms, represented by b and o. The connecting tubes act as the hopping of neighboring atoms. Thus, as shown in Figures 1B–D, a simple cubic lattice AC can be built using identical b-type acoustic atoms, where the primitive unit cell only contains one atom. Using band folding and breaking mechanism, we can double the primitive unit cell in real space with two atoms to create band degeneracy. Then, we break such degeneracy by replacing the nearest neighbors to be o-type acoustic atoms with a NaCl-like structure. Accordingly, their band structures will experience a folding and breaking process to open a 3D complete bulk bandgap (Figures 1E–G). Here, we only focus and operate on the first band of such AC. In Figure 1C, the unit cell is chosen to be rhombic dodecahedral geometry which is twice large as that of a simple cubic case, associating with a half volume of bulk BZ in Figure 1F. The band degeneracy originates from additional symmetries in this non-primitive unit cell. In other words, the cubic BZ is folded into a truncated octahedral BZ in 3D.

FIGURE 1

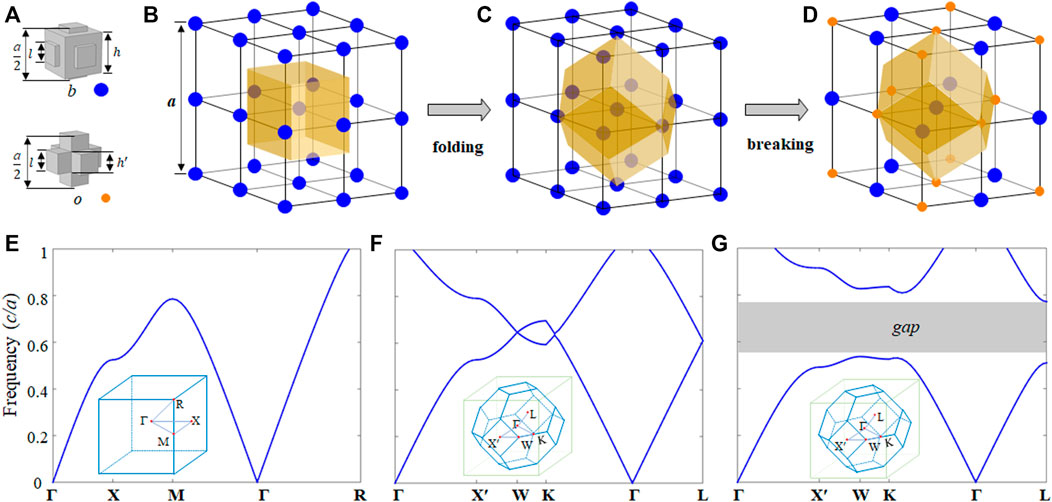
FIGURE 1. Band folding and breaking in a 3D AC. (A) Two different acoustic atoms b (blue ball) and o (orange ball) with air cavity-tube structures. The structure parameters are h = 0.4a, l = h′ = 0.2a (B) Simple cubic structure with identical b atoms, where the primitive unit cell is cubic structure denoted by yellow area (C) Doubling case with the unit cell enlarged to a rhombic dodecahedral shape (D) Breaking the a/2 spatial translation symmetry by replacing the nearest neighbors with o atoms. (E–G) Bulk band structures corresponding to (B–D), where the insets show the first BZs.

We resort to the tight-binding approximation (TBA) method to further illustrate the degeneracy created by band folding. The TBA model can well describe our cavity-tube structure with definite local resonance and hopping effect. Considering two acoustic atoms (b and o) in a rhombic dodecahedral unit cell, the Bloch Hamiltonian on the basis of sublattices is:

$\mathit{H}\left(\mathit{k}\right)=\left(\begin{array}{cc}{\mathit{m}}_1& {\mathit{H}}_{\mathit{AB}}\\ {\mathit{H}}_{\mathit{AB}}^{\mathit{*}}& {\mathit{m}}_2\end{array}\right)$

where $H_{AB}=2t[\cos \left(a{k}_x/2\right)+\cos \left(a{k}_y/2\right)+\cos \left(a{k}_z/2\right)]$, Bloch wavevector $\mathit{k}=(k_x,k_y,k_z)$, a represents the lattice constant, t represents the nearest-neighbor hopping, and $m_1$ ($m_2$) represents the onsite energy of the sublattice b (o). The results are shown in Figures 2A,C. In identical atoms case ($m_1=m_2=1$), the band structure possesses a two-fold degenerated nodal plane in the first 3D BZ, which is similar to the Fermi surface of copper (Cu). Then, we can lift the nodal plane to open a 3D complete bulk bandgap by changing $m_2=2$, corresponding to the broken half-lattice symmetry with a NaCl-like AC in Figure 1D.

FIGURE 2

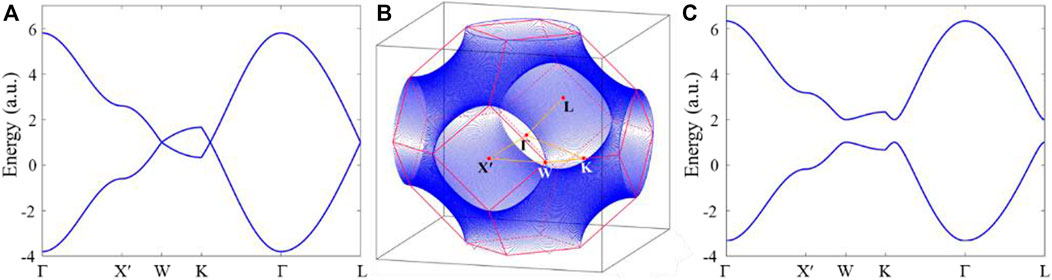
FIGURE 2. Bulk band structures via TBA. (A) Band structures with $m_1=m_2=1$, t = 0.8 (B) A 3D view of nodal plane in the 3D BZ. (C) Complete bandgap case of the NaCl-like AC when $m_2=2$.

In our model, the moderate structure parameters already ensure a large complete bandgap with a relative bandwidth of 36%, which facilities the propagation and manipulation of acoustic surface states. Increasing the contrast ratio of two acoustic atoms will bring a broader bandgap. The nodal plane in Figure 2B resembles a sphere with a nearly identical amplitude of Bloch vectors. It implies that the broken half-lattice symmetry would have almost the same effect on the band degeneracy along all directions, which minimizes the directional bandgap overlap to guarantee a large 3D complete bandgap. In this work, the numerical results are calculated using a finite element method software package (COMSOL Multiphysics). The density and velocity are chosen to be 1.25 kg/m³ and 343 m/s, respectively.

Tunable Topological Surface States on Different Domain Walls

Then, we focus on the surface states on the (001) surface, the same as those on (100) or (010) surfaces. Figure 3A is a supercell configuration without a domain wall along the z-direction. A periodical segment is denoted by T. Figure 3B shows the surface BZ. A typical domain wall can be introduced by adding a mirror symmetry at the interface with a T-T’ configuration, where segment T’ is the mirror counterpart of T (Figure 3C). Due to the equivalence of each principal axis in a cubic lattice, T and T’ also possess a relative a/2 shift along x- or y-direction. Figure 3D is the projected band structure without the domain wall, where the 3D complete bandgap agrees with Figure 1G. For the case of the mirror-symmetry domain wall, two gapped surface states in the bulk bandgap can be found (Figure 3E).

FIGURE 3

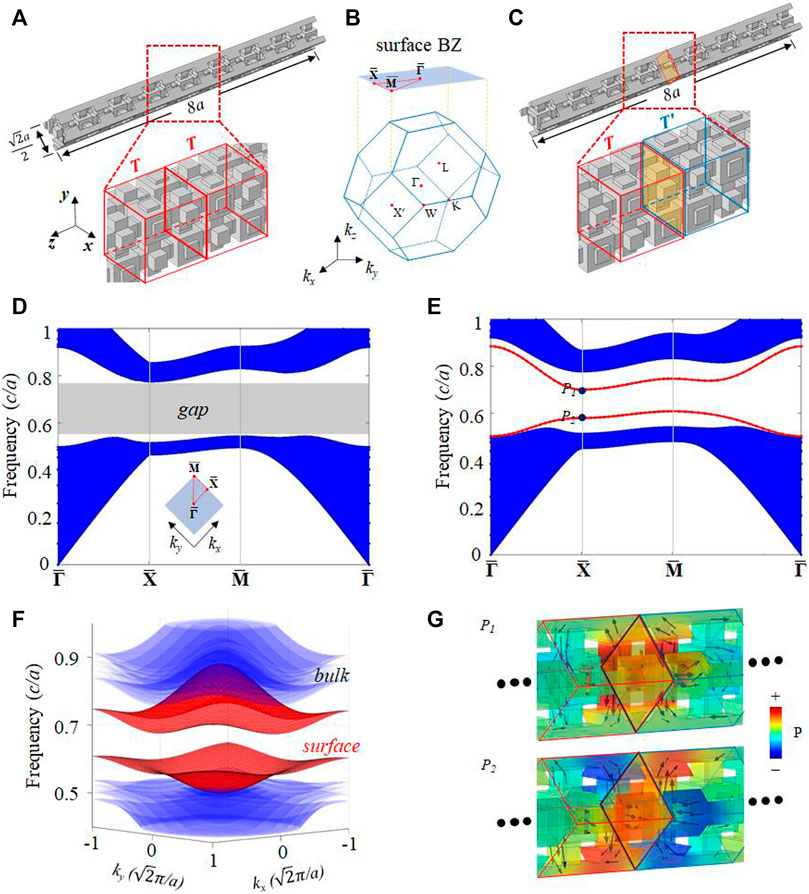
FIGURE 3. Surfaces states on the mirror-symmetry domain wall. (A) Supercell configuration without domain wall. (B) The bulk BZ and (001) surface BZ. (C) Supercell configuration with a mirror-symmetry domain wall. (D-E) Projected band structures on (001) surface corresponding to (A) and (C), respectively. (F) 3D view of surface states in (E). (G) Acoustic field distributions at points P₁ and P₂ in (E), where black arrows represent the directions of energy flow.

These two surface states on the mirror-symmetry domain wall can be taken as an extension of two bound states of two z-direction SSH chains in the k_xy plane. Here, we can exchange the onsite and hopping terms and denote the original connecting tube as u. Then, the cuboid supercell is composed of a pair of SSH chains, as ($\cdots \frac{u}{2}\stackrel{o}{\leftrightarrow }u\stackrel{b}{\leftrightarrow }\frac{u}{2}$)-($\frac{u}{2}\stackrel{b}{\leftrightarrow }u\stackrel{o}{\leftrightarrow }\frac{u}{2}\cdots$) and ($\cdots \frac{u}{2}\stackrel{b}{\leftrightarrow }u\stackrel{o}{\leftrightarrow }\frac{u}{2}$)-($\frac{u}{2}\stackrel{o}{\leftrightarrow }u\stackrel{b}{\leftrightarrow }\frac{u}{2}\cdots$) along the z-axis. Each chain gives one bound state at the domain wall according to 1D SSH with different Zak phases on each side of the interface [41, 49]. In a 3D case, these two 0D bound states extend to two 2D surface states with dispersion under the coupling of two chains in the k_xy plane. Along the boundaries of surface BZ, the in-plane (k_xy plane) coupling is missing. Therefore, two surface states are separated. As in-plane coupling increases from BZ boundary to center, these two surface states will gradually merge into bulk bands in opposite directions, forming two inverted bowl shapes (Figure 3F). Due to the mirror symmetry $M_z:\left(x,y,z\right)\to (x,y,-z)$ relative to the interface, two surface states can also be classified into symmetry and anti-symmetry modes. Moreover, the interface is an anti-phase boundary formed by shifting a portion of the crystal lattice as well, which can support pseudospin-momentum locking [50, 51]. The acoustic pseudospin can be defined by the rotating direction of the energy flow [52–55]. The acoustic field distributions of anti-symmetry surface mode P₁ and symmetry mode P₂ at $\overline{\text{X}}$ point, with counter-rotation of energy flow (black arrows), are presented in Figure 3G.

Besides the mirror-symmetry domain wall, our model can possess a glide-symmetry domain wall as well. Here, we consider an additional air layer (O) with a thickness of t_xa/2 added on both mirror-symmetry and glide-symmetry domain walls (Figures 4A,B). As the thickness parameter (t_x) increases from 0.1 to 1, for the mirror-symmetry case (T-O-T’ configuration), the anti-symmetry mode gradually emerges into bulk bands, and the symmetry one has a blue shift connecting the upper bulk band (Figure 4C). On the other hand, for the glide-symmetry case (T-O-T configuration), the surface states are always two-fold degenerated at the boundaries of surface BZ (Figure 4D). Such band degeneracy is the consequence of glide symmetries [56–58], i.e., $G_x:\left(x,y,z\right)\to G(-x,y+a/2,z)$ and $G_y:\left(x,y,z\right)\to G(x+a/2,-y,z)$. The 3D views of surface states with t_x = 1 are plotted in Figures 4E,F.

FIGURE 4

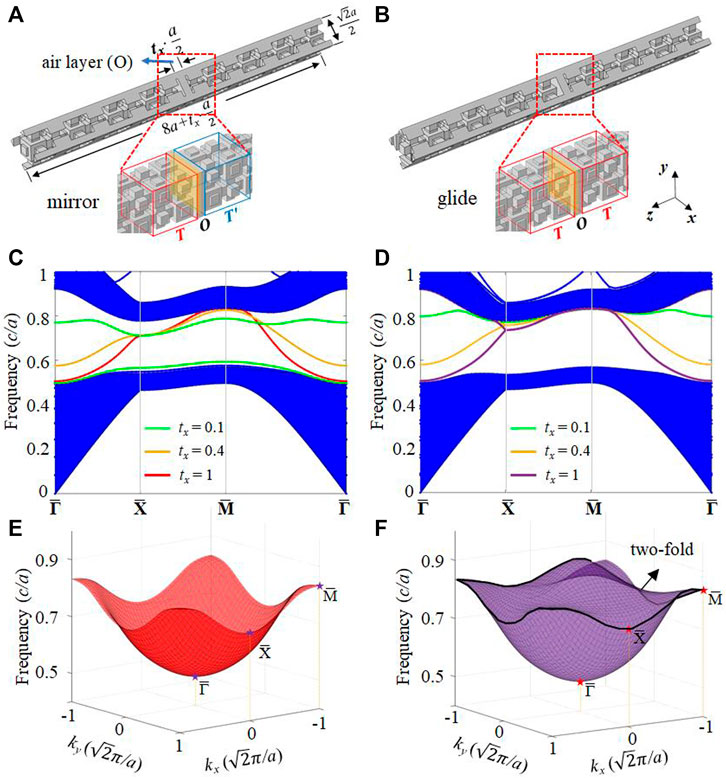
FIGURE 4. Tunable surfaces states on different symmetries of domain walls. (A) Mirror-symmetry domain wall with a t_xa/2-thickness air layer at the interface (T-O-T’ configuration). (B) Glide-symmetry case (T-O-T configuration). (C-D) Projected band structures under various thicknesses of air layers corresponding to (A–B). The green, orange, and red lines represent t_x = 0.1, 0.4, and 1, respectively (E-F) 3D views of surface states in (C–D) when t_x = 1.

These flexible and tunable surface states can be used to realize reconfigurable directional acoustic filters. For example, the surface states have directional surface bandgap along $\overline{Г}\overline{\text{X}}$ direction in the mirror-symmetry case, which is different from the glide-symmetry case with gapless surface states. Their transmission spectra are shown in Figures 5A,B. In a wide frequency window from 0.58 to 0.76 c/a, $\overline{Г}\overline{\text{M}}$ transmission spectra maintain a high valve for both two cases. However, $\overline{Г}\overline{\text{X}}$ transmission is forbidden for the mirror-symmetry case in the frequency window from 0.70 to 0.76 c/a, but allowed for the glide-symmetry case. The acoustic field distributions at a frequency of 0.74 c/a in Figures 5C–F match well with projected band structures and transmission spectra. It should be noticed that T and T’ are the same structures, only possessing a relative a/2 shift along the x- or y-direction. That means we can efficiently turn on/off sound transport by simply tuning the relative displacement between left-side and right-side ACs in the experiment.

FIGURE 5

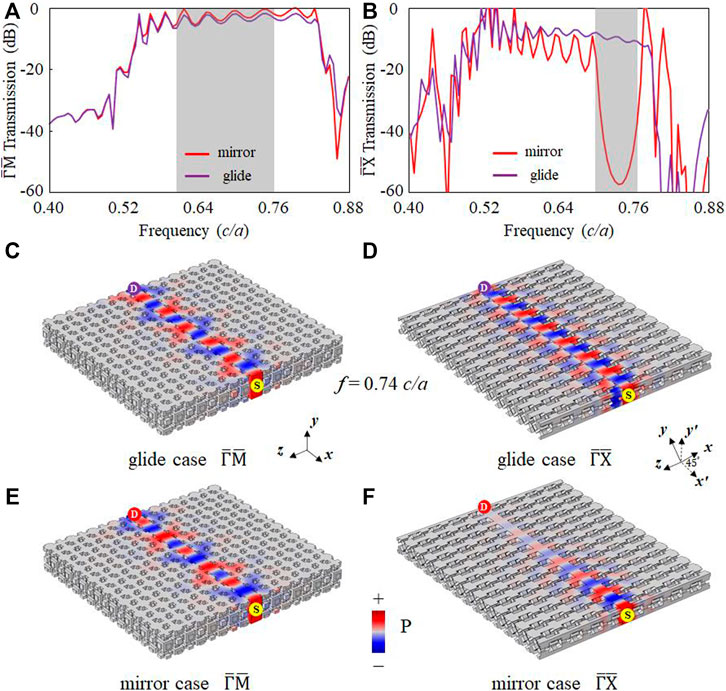
FIGURE 5. Acoustic transmission spectra. (A) $\text{Γ}¯\text{M}$-direction transmission spectra on mirror- and glide-symmetry domain walls. The shadow area represents the complete bulk bandgap. (B) $\overline{\text{Γ}}¯\text{X}$-direction transmission spectra, where the shadow area represents the directional surface bandgap of the mirror case. (C-F) Acoustic field distributions at a frequency of 0.74 c/a.

Omnidirectional Acoustic Quantum Spin Hall Effect

In addition to the directional surface bandgap, we can also construct a complete surface bandgap by modifying the interface. In Figure 6A, we elaborately tune the aforementioned air-interface layer to another modified interface layer C with a/2 thickness composed of uniform o-type acoustic atoms. The mirror symmetry and glide symmetries still sustain in T-C-T’ and T-C-T configuration, respectively. The projected band structures are shown in Figure 6B. A complete surface bandgap is constructed for the mirror-symmetry case, forbidding surface sound transport in all directions. For the glide-symmetry case, the surface states at the boundaries of the surface BZ are still degenerated but with flat dispersion.

FIGURE 6

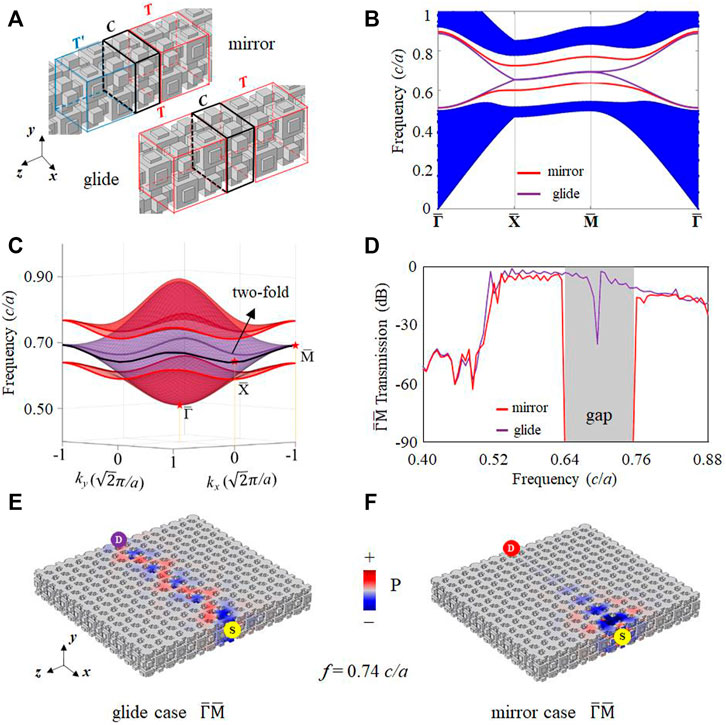
FIGURE 6. Tunable surface states with modified interface layer. (A) Supercells of mirror and glide cases. The interface with uniform o-type acoustic atoms (denoted as C). (B) Projected band structure. The red (purple) line represents the mirror (glide) case (C) A 3D view of surface states. (D) $\text{Γ}¯\text{M}$-direction transmission spectra. The shadow area represents the surface bandgap of the mirror case (E-F) Acoustic field distributions at a frequency of 0.74 c/a.

In the glide-symmetry case, two SSH chains can be described as modified ($\cdots \frac{o}{2}\stackrel{u}{\leftrightarrow }b\stackrel{u}{\leftrightarrow }\frac{o}{2}$)-($\frac{b}{2}\stackrel{u}{\leftrightarrow }o\stackrel{u}{\leftrightarrow }\frac{b}{2}\cdots$) and ($\cdots \frac{b}{2}\stackrel{u}{\leftrightarrow }o\stackrel{u}{\leftrightarrow }\frac{b}{2}$)-($\frac{o}{2}\stackrel{u}{\leftrightarrow }b\stackrel{u}{\leftrightarrow }\frac{o}{2}\cdots$) along the z-axis. The interface is chosen to be identical o-type acoustic atoms. Like two unmodified chains in the mirror-symmetry case (T-T’ configuration), each modified chain also gives one bound state. Around the surface BZ center with strong in-plane (k_xy plane) coupling, these two bound states lift in both cases. However, the situation is different at the surface BZ boundaries without in-plane coupling. The additional glide symmetry (T-C-T configuration) guarantees two-fold degeneracy, forming two buckled bowl-shaped fashion (Figure 6C). In each k_y (or k_x) slice, these two degenerate surface states turn into a pair of helical edge states, which implies that such glide-symmetry domain wall can act as an omnidirectional acoustic quantum spin Hall layer on a 2D plane [46, 59].

The simulated transmission spectra for both mirror-symmetry and glide-symmetry cases are shown in Figure 6D, consisting of their gapped and gapless surface states. The corresponding acoustic field distributions at a frequency of 0.74 c/a are shown in Figures 6E,F. Note that there is a slight dip at a frequency of 0.70 c/a due to the linear degeneracy, resembling the ballistic transport of sound at the surface Dirac point [60, 61].

Conclusion

To conclude, we construct a sizeable topological bandgap in an AC by building blocks based on a 3D band folding and breaking mechanism. By adjusting the interface symmetries of domain walls, we realize various kinds of topological surface states to turn on/off sound transport efficiently. The omnidirectional acoustic quantum spin Hall layer can be achieved under a glide-symmetry domain wall as well. Compared to 1D edge states in 2D models, these tunable surface states show great potentials in manipulating acoustic signals in multiple directions. Our simple yet flexible 3D AC may provide a route of realizing tunable acoustic devices such as acoustic filters on a 2D plane.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

CH and Y-FC conceived the idea and supervised the project. H-SL, Y-LX, and BH performed the numerical simulations. H-SL and X-CS did the theoretical analysis. H-SL wrote the article.

Funding

The work was jointly supported by the National Key R&D Program of China (Grant No. 2017YFA0305100) and the National Natural Science Foundation of China (Grant Nos. 52022038, 11874196, 11890700, and 51721001).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Klitzing Kv., Dorda G, Pepper M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys Rev Lett (1980) 45:494–7. doi:10.1103/PhysRevLett.45.494

CrossRef Full Text | Google Scholar

2. Berry MV. Quantal phase factors accompanying adiabatic changes. Proc R Soc Lond A (1984) 392:45–57. doi:10.1098/rspa.1984.0023

CrossRef Full Text | Google Scholar

3. Bernevig BA, Hughes TL, Zhang S-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science (2006) 314:1757–61. doi:10.1126/science.1133734

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Hatsugai Y. Chern number and edge states in the integer quantum Hall effect. Phys Rev Lett (1993) 71:3697–700. doi:10.1103/PhysRevLett.71.3697

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kane CL, Mele EJ. Quantum spin Hall effect in graphene. Phys Rev Lett (2005) 95:226801. doi:10.1103/PhysRevLett.95.226801

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Thouless DJ, Kohmoto M, Nightingale MP, den Nijs M. Quantized Hall conductance in a two-dimensional periodic potential. Phys Rev Lett (1982) 49:405–8. doi:10.1103/PhysRevLett.49.405

CrossRef Full Text | Google Scholar

7. Haldane FDM, Raghu S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys Rev Lett (2008) 100:013904. doi:10.1103/PhysRevLett.100.013904

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Raghu S, Haldane FDM. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys Rev A (2008) 78:033834. doi:10.1103/PhysRevA.78.033834

CrossRef Full Text | Google Scholar

9. Huber SD. Topological mechanics. Nat Phys (2016) 12:621–3. doi:10.1038/nphys3801

CrossRef Full Text | Google Scholar

10. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. Topological photonics. Rev Mod Phys (2019) 91:015006. doi:10.1103/RevModPhys.91.015006

CrossRef Full Text | Google Scholar

11. Lu L, Joannopoulos JD, Soljačić M. Topological states in photonic systems. Nat Phys (2016) 12:626–9. doi:10.1038/nphys3796

CrossRef Full Text | Google Scholar

12. Ma G, Xiao M, Chan CT. Topological phases in acoustic and mechanical systems. Nat Rev Phys (2019) 1:281–94. doi:10.1038/s42254-019-0030-x

CrossRef Full Text | Google Scholar

13. Xiao M, Ma G, Yang Z, Sheng P, Zhang ZQ, Chan CT. Geometric phase and band inversion in periodic acoustic systems. Nat Phys (2015) 11:240–4. doi:10.1038/nphys3228

CrossRef Full Text | Google Scholar

14. Yang Z, Gao F, Shi X, Lin X, Gao Z, Chong Y, et al. Topological acoustics. Phys Rev Lett (2015) 114:114301. doi:10.1103/PhysRevLett.114.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Xiao M, Chen W-J, He W-Y, Chan CT. Synthetic gauge flux and Weyl points in acoustic systems. Nat Phys (2015) 11:920–4. doi:10.1038/nphys3458

CrossRef Full Text | Google Scholar

16. Deng W, Huang X, Lu J, Peri V, Li F, Huber SD, et al. Acoustic spin-Chern insulator induced by synthetic spin-orbit coupling with spin conservation breaking. Nat Commun (2020) 11:3227. doi:10.1038/s41467-020-17039-1

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Deng Y, Oudich M, Gerard NJ, Ji J, Lu M, Jing Y. Magic-angle bilayer phononic graphene. Phys Rev B (2020) 102:180304. doi:10.1103/PhysRevB.102.180304

CrossRef Full Text | Google Scholar

18. Yang Y, Lu J, Yan M, Huang X, Deng W, Liu Z. Hybrid-Order Topological Insulators in a Phononic Crystal. Phys Rev Lett (2021) 126:156801. doi:10.1103/PhysRevLett.126.156801

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chen Z-G, Zhu W, Tan Y, Wang L, Ma G. Acoustic Realization of a Four-Dimensional Higher-Order Chern Insulator and Boundary-Modes Engineering. Phys Rev X (2021) X11:011016. doi:10.1103/PhysRevX.11.011016

CrossRef Full Text | Google Scholar

20. Wang Z, Chong Y, Joannopoulos JD, Soljačić M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature (2009) 461:772–5. doi:10.1038/nature08293

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Khanikaev AB, Fleury R, Mousavi SH, Alù A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat Commun (2015) 6:8260. doi:10.1038/ncomms9260

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Xu C, Chu H, Luo J, Hang ZH, Wu Y, Lai Y. Three-Dimensional Electromagnetic Void Space. Phys Rev Lett (2021) 127:123902. doi:10.1103/PhysRevLett.127.123902

PubMed Abstract | CrossRef Full Text | Google Scholar

23. He H, Qiu C, Ye L, Cai X, Fan X, Ke M, et al. Topological negative refraction of surface acoustic waves in a Weyl phononic crystal. Nature (2018) 560:61–4. doi:10.1038/s41586-018-0367-9

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Xu C, Chen Z-G, Zhang G, Ma G, Wu Y. Multi-dimensional wave steering with higher-order topological phononic crystal. Sci Bull (2021) 66:1740–5. doi:10.1016/j.scib.2021.05.013

CrossRef Full Text | Google Scholar

25. Lu J, Huang X, Yan M, Li F, Deng W, Liu Z. Nodal-Chain Semimetal States and Topological Focusing in Phononic Crystals. Phys Rev Appl (2020) 13:054080. doi:10.1103/PhysRevApplied.13.054080

CrossRef Full Text | Google Scholar

26. Zhang X, Xie B-Y, Wang H-F, Xu X, Tian Y, Jiang J-H, et al. Dimensional hierarchy of higher-order topology in three-dimensional sonic crystals. Nat Commun (2019) 10:5331. doi:10.1038/s41467-019-13333-9

PubMed Abstract | CrossRef Full Text | Google Scholar

27. He C, Yu S-Y, Wang H, Ge H, Ruan J, Zhang H, et al. Hybrid acoustic topological insulator in three dimensions. Phys Rev Lett (2019) 123:195503. doi:10.1103/PhysRevLett.123.195503

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Li F, Huang X, Lu J, Ma J, Liu Z. Weyl points and Fermi arcs in a chiral phononic crystal. Nat Phys (2017) 14:30–4. doi:10.1038/nphys4275

CrossRef Full Text | Google Scholar

29. Ge H, Ni X, Tian Y, Gupta SK, Lu M-H, Lin X, et al. Experimental Observation of Acoustic Weyl Points and Topological Surface States. Phys Rev Appl (2018) 10:014017. doi:10.1103/PhysRevApplied.10.014017

CrossRef Full Text | Google Scholar

30. Xie B, Liu H, Cheng H, Liu Z, Tian J, Chen S. Dirac points and the transition towards Weyl points in three-dimensional sonic crystals. Light Sci Appl (2020) 9:201. doi:10.1038/s41377-020-00416-2

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Yang Y, Sun H-x., Xia J-p., Xue H, Gao Z, Ge Y, et al. Topological triply degenerate point with double Fermi arcs. Nat Phys (2019) 15:645–9. doi:10.1038/s41567-019-0502-z

CrossRef Full Text | Google Scholar

32. Luo L, Wang H-X, Lin Z-K, Jiang B, Wu Y, Li F, et al. Observation of a phononic higher-order Weyl semimetal. Nat Mater (2021) 20:794–9. doi:10.1038/s41563-021-00985-6

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wei Q, Zhang X, Deng W, Lu J, Huang X, Yan M, et al. Higher-order topological semimetal in acoustic crystals. Nat Mater (2021) 20:812–7. doi:10.1038/s41563-021-00933-4

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Cheng H, Sha Y, Liu R, Fang C, Lu L. Discovering Topological Surface States of Dirac Points. Phys Rev Lett (2020) 124:104301. doi:10.1103/PhysRevLett.124.104301

PubMed Abstract | CrossRef Full Text | Google Scholar

35. He H, Qiu C, Cai X, Xiao M, Ke M, Zhang F, et al. Observation of quadratic Weyl points and double-helicoid arcs. Nat Commun (2020) 11:1820. doi:10.1038/s41467-020-15825-5

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yang Y, Xia J-p., Sun H-x., Ge Y, Jia D, Yuan S-q., et al. Observation of a topological nodal surface and its surface-state arcs in an artificial acoustic crystal. Nat Commun (2019) 10:5185. doi:10.1038/s41467-019-13258-3

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Huang X, Deng W, Li F, Lu J, Liu Z. Ideal Type-II Weyl Phase and Topological Transition in Phononic Crystals. Phys Rev Lett (2020) 124:206802. doi:10.1103/PhysRevLett.124.206802

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Deng W, Huang X, Lu J, Li F, Ma J, Chen S, et al. Acoustic spin-1 Weyl semimetal. Sci China Phys Mech Astron (2020) 63:287032. doi:10.1007/s11433-020-1558-8

CrossRef Full Text | Google Scholar

39. He C, Yu S-Y, Ge H, Wang H, Tian Y, Zhang H, et al. Three-dimensional topological acoustic crystals with pseudospin-valley coupled saddle surface states. Nat Commun (2018) 9:4555. doi:10.1038/s41467-018-07030-2

PubMed Abstract | CrossRef Full Text | Google Scholar

40. He C, Lai H-S, He B, Yu S-Y, Xu X, Lu M-H, et al. Acoustic analogues of three-dimensional topological insulators. Nat Commun (2020) 11:2318. doi:10.1038/s41467-020-16131-w

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Zak J. Berry's phase for energy bands in solids. Phys Rev Lett (1989) 62:2747–50. doi:10.1103/PhysRevLett.62.2747

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Wang Z, Chong YD, Joannopoulos JD, Soljačić M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys Rev Lett (2008) 100:013905. doi:10.1103/PhysRevLett.100.013905

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Lu J, Qiu C, Ye L, Fan X, Ke M, Zhang F, et al. Observation of topological valley transport of sound in sonic crystals. Nat Phys (2017) 13:369–74. doi:10.1038/nphys3999

CrossRef Full Text | Google Scholar

44. Wu L-H, Hu X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys Rev Lett (2015) 114:223901. doi:10.1103/PhysRevLett.114.223901

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Peri V, Song Z-D, Serra-Garcia M, Engeler P, Queiroz R, Huang X, et al. Experimental characterization of fragile topology in an acoustic metamaterial. Science (2020) 367:797–800. doi:10.1126/science.aaz7654

PubMed Abstract | CrossRef Full Text | Google Scholar

46. He C, Ni X, Ge H, Sun X-C, Chen Y-B, Lu M-H, et al. Acoustic topological insulator and robust one-way sound transport. Nat Phys (2016) 12:1124–9. doi:10.1038/nphys3867

CrossRef Full Text | Google Scholar

47. Du L, Liu Y, Li M, Ren H, Song K, Zhao X. Non-Trivial Transport Interface in a Hybrid Topological Material with Hexagonal Lattice Arrangement. Front Phys (2020) 8:595621. doi:10.3389/fphy.2020.595621

CrossRef Full Text | Google Scholar

48. Lu L, Gao H, Wang Z. Topological one-way fiber of second Chern number. Nat Commun (2018) 9:5384. doi:10.1038/s41467-018-07817-3

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Xiao M, Zhang ZQ, Chan CT. Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems. Phys Rev X (2014) X4:021017. doi:10.1103/PhysRevX.4.021017

CrossRef Full Text | Google Scholar

50. Kong X, Zhou Y, Xiao G, Sievenpiper DF. Spin-momentum locked modes on anti-phase boundaries in photonic crystals. Opt Express (2020) 28:2070. doi:10.1364/OE.379672

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Ahn KH, Lookman T, Saxena A, Bishop AR. Electronic properties of structural twin and antiphase boundaries in materials with strong electron-lattice couplings. Phys Rev B (2005) 71:212102. doi:10.1103/PhysRevB.71.212102

CrossRef Full Text | Google Scholar

52. Long Y, Ren J, Chen H. Intrinsic spin of elastic waves. Proc Natl Acad Sci USA (2018) 115:9951–5. doi:10.1073/pnas.1808534115

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Shi C, Zhao R, Long Y, Yang S, Wang Y, Chen H, et al. Observation of acoustic spin. Natl Sci Rev (2019) 6:707–12. doi:10.1093/nsr/nwz059

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Long Y, Zhang D, Yang C, Ge J, Chen H, Ren J. Realization of acoustic spin transport in metasurface waveguides. Nat Commun (2020) 11:4716. doi:10.1038/s41467-020-18599-y

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Long Y, Ge H, Zhang D, Xu X, Ren J, Lu M-H, et al. Symmetry selective directionality in near-field acoustics. Natl Sci Rev (2020) 7:1024–35. doi:10.1093/nsr/nwaa040

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Liu C-X, Zhang R-X, VanLeeuwen BK. Topological nonsymmorphic crystalline insulators. Phys Rev B (2014) 90:085304. doi:10.1103/PhysRevB.90.085304

CrossRef Full Text | Google Scholar

57. Zhang P. Symmetry and degeneracy of phonon modes for periodic structures with glide symmetry. J Mech Phys Sol (2019) 122:244–61. doi:10.1016/j.jmps.2018.09.016

CrossRef Full Text | Google Scholar

58. Xia Y, Cai X, Li G. Multitype Dirac fermions protected by orthogonal glide symmetries in a noncentrosymmetric system. Phys Rev B (2020) 102:041201. doi:10.1103/PhysRevB.102.041201

CrossRef Full Text | Google Scholar

59. Tong S, Ren C. Directional acoustic emission via topological insulators based on cavity-channel networks. Appl Phys Lett (2020) 117:093504. doi:10.1063/5.0015591

CrossRef Full Text | Google Scholar

60. Zhang X, Liu Z. Extremal Transmission and Beating Effect of Acoustic Waves in Two-Dimensional Sonic Crystals. Phys Rev Lett (2008) 101:264303. doi:10.1103/PhysRevLett.101.264303

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Yu S-Y, Sun X-C, Ni X, Wang Q, Yan X-J, He C, et al. Surface phononic graphene. Nat Mater (2016) 15:1243–7. doi:10.1038/nmat4743

PubMed Abstract | CrossRef Full Text | Google Scholar