
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys. , 06 December 2021
Sec. Optics and Photonics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.786028
This article is part of the Research Topic Recent Developments in Si-based Materials and Devices View all 8 articles
Silicon Photonics, the technology where optical devices are fabricated by the mainstream microelectronic processing technology, was proposed almost 30 years ago. I joined this research field at its start. Initially, I concentrated on the main issue of the lack of a silicon laser. Room temperature visible emission from porous silicon first, and from silicon nanocrystals then, showed that optical gain is possible in low-dimensional silicon, but it is severely counterbalanced by nonlinear losses due to free carriers. Then, most of my research focus was on systems where photons show novel features such as Zener tunneling or Anderson localization. Here, the game was to engineer suitable dielectric environments (e.g., one-dimensional photonic crystals or waveguide-based microring resonators) to control photon propagation. Applications of low-dimensional silicon raised up in sensing (e.g., gas-sensing or bio-sensing) and photovoltaics. Interestingly, microring resonators emerged as the fundamental device for integrated photonic circuit since they allow studying the hermitian and non-hermitian physics of light propagation as well as demonstrating on-chip heavily integrated optical networks for reconfigurable switching applications or neural networks for optical signal processing. Finally, I witnessed the emergence of quantum photonic devices, where linear and nonlinear optical effects generate quantum states of light. Here, quantum random number generators or heralded single-photon sources are enabled by silicon photonics. All these developments are discussed in this review by following my own research path.
Silicon is the material on which microelectronics industry has been built. At the end of the eighties, the semiconductor industry was betting on III-V materials for the development of optoelectronic devices and high-speed electronics. III-V semiconductors were called the semiconductor of the future. However, a young British scientist demonstrated that quantum confinement in silicon allows getting visible room-temperature luminescence with high quantum efficiency [1]. This result pushed a large international effort toward light-emitting silicon [2] in an effort to make silicon an active optoelectronic material and, thus, to replace III-V semiconductors. At that time, I was working toward my PhD on GaAs and Al1−xGaxAs alloys in an effort to get relevant information about the physics of doping and of the defects by using photoluminescence [3]. It was therefore easy for me to start working in this new field and try to contribute with my own intuitions. The field evolved rapidly (see Figure 1). Big motivations for the emerging field of silicon photonics were to take pace with the Moore’s law and to apply to optics the same successful paradigm of microelectronics: improve device performances by integration while reducing the device cost with economy of scale thanks to high-volume manufacturing. I have contributed to silicon photonics with my own work here and reviewed and followed the field by editing few books [4–9] and handbooks [10, 11]. Since this review of silicon photonics is quite a personal history and a story of my contributions to the field, almost all the cited works refer to my own papers. The interested reader can find relevant literature in the original papers or in other recent reviews [12–24]. At the end of each subsection, I cite few references where recent contributions to the related field are reported.
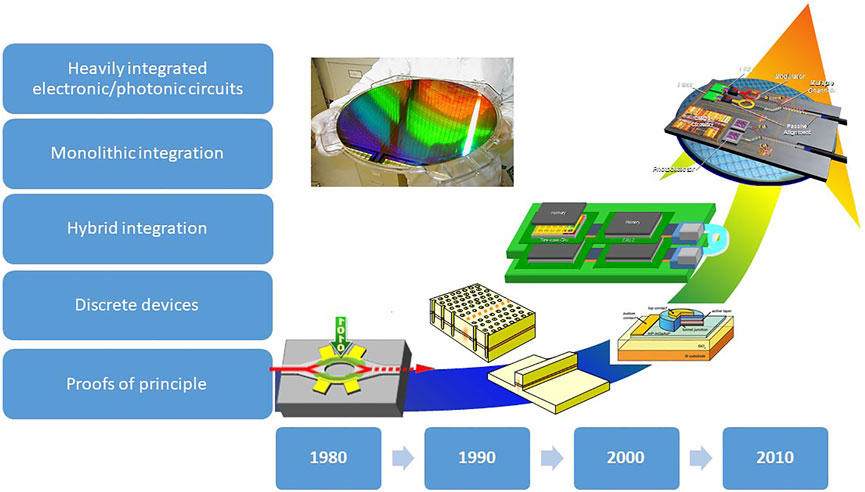
FIGURE 1. A schematics of the evolution of silicon photonics along the years. From [25].
This review is organized in eight sections, which mostly follow the temporal evolution of the field. Section 1 introduces the review. Section 2 deals with porous silicon (PS) and the analogies between electrons and photons: photon Anderson localization, photonic crystals, Bloch oscillations, and Zener tunneling. Section 3 treats low-dimensional Silicon: the observation of optical gain, the development of light-emitting diodes (LED), the use of Er doping for all-optical light amplification, the application in photovoltaics. Section 4 presents one of the most potentially disruptive applications of silicon photonics: sensing. I discuss PS multiparameter sensors, through membrane sensors, luminescence sensors, and integrated optical sensors. Section 5 reviews microresonators and their application in heavily integrated photonic chips: first, the hermitian and non-hermitian physics of microresonators, then the behavior of sequence of microresonators and their application in routing and switching. Here, the discussion of a complex on-chip network shows the high electronic-photonic integration achieved. Finally, the use of microrings to develop neural network as a hardware platform for artificial intelligence is presented. Section 6 reports the recent achievement in nonlinear silicon photonics: the use of nanocrystals for high-speed all-optical switches and for nonlinear optical bistability, the use of strain to induce second-order nonlinearities in silicon, the exploitation of the third-order silicon nonlinearity for efficient discrete broad-band spectral translation, and the physics of four wave mixing in photonic molecule. Section 7 presents experiments toward integrated quantum photonics: the use of spontaneous emission as a source of entropy for random number generation based on quantum physics, the single-particle entanglement as a resource for quantum information, and the development of heralded single-photon sources for mid-infrared or ultra-pure quantum light sources. Section 8 concludes the review with a discussion on the perspectives of silicon photonics.
In the early nineties, a new form of silicon emerged as a suitable platform for photonics. This material is porous silicon which can be easily produced by silicon through an anodic electrochemical etching [26]. Remarkably, the resulting partial silicon dissolution leaves a crystalline silicon skeleton that has one-dimensional (quantum wires) or zero-dimensional (quantum dots or nanocrystals, Si-NC) nano-structures [2]. This low-dimensional silicon beats the main limitations of silicon (see Figure 2) by quantum confinement and spatial carrier localization [1, 27]. In fact, bulk silicon is characterized by a long radiative lifetime (few ms) due to its indirect band-gap. Therefore, fast nonradiative processes (few hundreds of ns) represent the preferred recombination paths for photoexcited electron-hole (e-h) pairs. This yields a negligible internal quantum efficiency. In Si-NC, on one side, quantum confinement enlarges the band-gap and increases the overlap in the momentum space between the electron and hole (e-h) wavefunctions, causing a reduced e-h radiative lifetime (few μs). On the other side, spatial confinement reduces the e-h encounter probability with recombination centers (defects) which lengthens the e-h nonradiative lifetime. As a result visible room temperature luminescence is routinely observed in PS and Si-NC. Surface treatments improve the quantum yields by surface passivation [28] up to values of almost 100% at low temperatures [29].
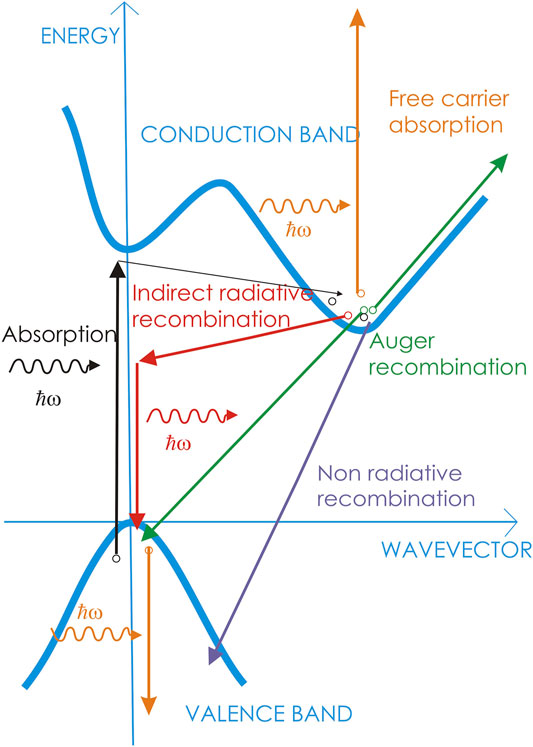
FIGURE 2. Energy diagram of silicon. The various arrows indicate the recombination paths for an excited electron. Black arrows: absorption by a phonon-mediated process. Red arrows: radiative recombination by a phonon-assisted process. Violet arrow: nonradiative recombination. Green arrows: Auger recombination. Orange arrows: free-carrier absorption. From Ref. [25].
Time-resolved luminescence of excitons in PS is characterized by a stretched exponential lineshape with μs time constants [31]. Analogies with electronic transport in random media allow interpreting the stretched exponential decay of the luminescence as due to the disordered distribution of nanocrystals and of inter-nanocrystal distances, as well as due to the random energy-confining potentials that result from surface passivation. Monte Carlo modeling shows further analogies between the recombination dynamics in PS and diffusion of particles in complex systems: critical scale emerges for cluster percolation and Anderson-like carrier localization [32]. The trap-controlled hopping mechanism of dispersive motion of excitons in a random spatial arrangement of interconnected quantum dots is able to account for the experiments [33]. Recent works point out the relevant role of surface groups in determining PS luminescence [34] and of the excitation conditions in determining the luminescence decay lineshapes [35].
The interplay between the silicon skeleton and the pores is reflected in a porosity dependence of the refractive index (n). An accurate control of the etching parameters (current and duration) allows modulating the effective n of the etched layer and, therefore, the production of PS multilayers (Figure 3A) [36]. In this way, PS microcavities where the emission rate is strongly influenced by the dielectric environment were fabricated [37]. In addition, also free standing dielectric multilayers structures can be fabricated which show in transmission the typical variation in the density of photonic states characteristics of one-dimensional photonic crystals [38]. These developments lead to the engineering of the phase dispersion to form photonic bands with fine features associated with the presence of photonic Bloch modes confined in the finite structure [39]. The group velocity displays wide variations, including peculiar features such as photon slowing down at the band edge and superluminal behavior within the photonic band-gap [40]. Recent progresses show that, by using electrochemical etching and photoacoustic, high-quality multilayers are feasible [41].
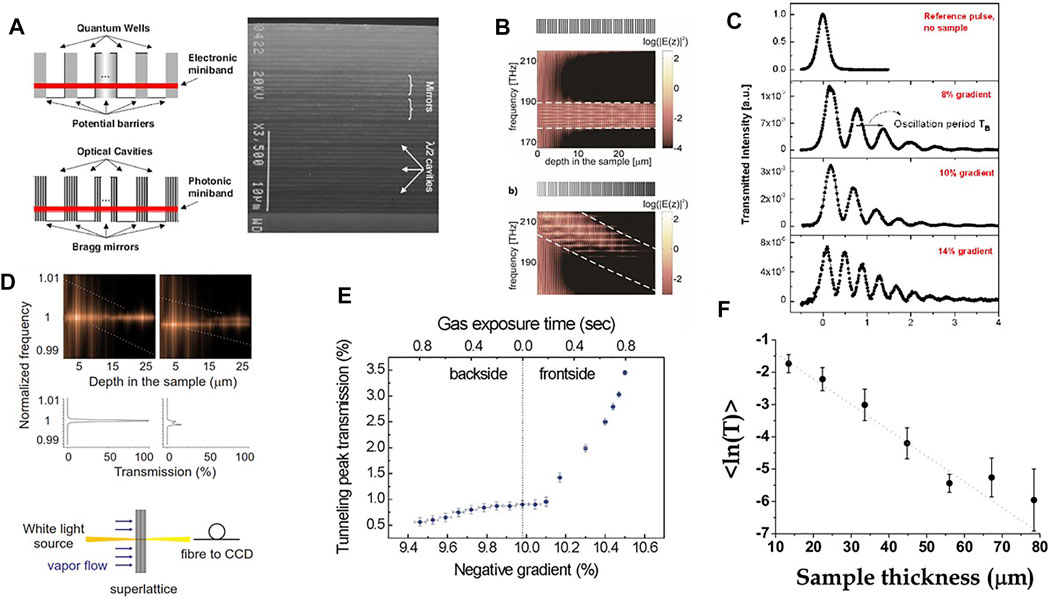
FIGURE 3. (A) In analogy to the electronic coupling of separate quantum wells in a semiconductor superlattice (top), an optical superlattice can be realized when optical cavities are brought together (bottom) resulting in the formation of a miniband of extended photonic states. On the right there is a SEM micrograph of a 1D optical superlattice formed by a PS multilayer. (B) Scattering state calculation of the distribution of the energy spectrum inside the multilayer. Top: flat band situation. Bottom: tilted band situation obtained by a gradient in the optical path (n times the layer thickness). The dashed lines indicate the theoretical tilting of the miniband. Above each panel, the coupled microcavity structure is schematically shown; the gray scale refers to the n variation along the depth in the sample (the darker the larger n). (C) Temporal response of the system for various values of the optical path gradient, i.e., photonic band tilting. The top panel shows the undisturbed probe pulse without sample. (D) The calculated light intensity distribution inside the optical superlattice. The frequency is normalized with respect to the Zener tunneling frequency. In the middle, there are the corresponding transmission spectra for two cases of resonantly coupled (left panels) and decoupled Wannier-Stark states (right panels). Below, sketch of the experimental setup. (E) Resonant Zener breakdown of the optical superlattice. With an increased optical path gradient along the sample, the light transmission shows a threshold-like behavior, in a close analogy to the tunneling current of electrons in a reverse-biased solid-state diode. (F) Spectral average of the logarithm of the measured transmission versus sample thickness. The error bars are obtained by measurements in various spots on the sample and, therefore, reflect lateral sample inhomogeneities. Compiled from Ref. [30].
Still the use of the analogies between photons and electrons shows that the two are governed by functionally similar equations which reflect their wave-nature. In the one-dimensional case, the electron dynamics is governed by the following Schrödinger equation:
while photons (i.e., the electric field associated with the photon mode) by the following Helmholtz equations:
Therefore, the control of n(x) in a dielectric multilayer allows introducing an effective potential (Veff(x)) for photons (Figure 3B) and, thus, inducing photon propagation dynamics similar to the ones of electrons. Indeed, by using this analogy we were able to demonstrate photonic Bloch oscillations (Figure 3C) [42], Zener tunneling of photons (Figure 3D) [43], rectification of the transmission though a photonic diode (Figure 3E) [44], and, even, new phenomena such as optical bistability due to capillary condensation [45]. On the other hand, Bloch oscillations and Zener tunneling are not only observed in electronic or photonic systems. Interestingly, similar phenomenologies are observed also in quantum gasses [46], spin waves [47], coupled LC circuits [48], elastic waves [49], etc., which further proves the wave nature origin of the associated physics [50].
Disorder can be also a resource, e.g., in random lasing or in surface enhanced Raman spectroscopy [51]. Interestingly, dielectric multi-layers can be realized as a-periodic one-dimensional quasi-crystals, of the Fibonacci type, to show anomalous photon diffusion behavior. Near the band edges, critically localized states appear which decay weaker than exponentially [52]. On the other hand, purely random one-dimensional structures show exponential decay which reflects the same physics as electronic Anderson localization in amorphous materials (Figure 3E). In addition, interference phenomena in these structures show the building-up of coherent necklace states, observed as modes with a characteristic multiresonance time response and relatively fast decay [53]. The balance between localization and delocalization found in the necklace states can be placed on a more solid ground by modeling the stochastic dissipation in non-hermitian Anderson systems [54, 55]. This effect can also be engineered and exploited in devices such as the “pearl” spectrometer [56].
Si-NCs were initially developed to be used in floating gate memories and to achieve a better control on the surface passivation than with PS [10]. They are usually formed either by thermal phase separation of silicon and silica in silicon-rich silicon oxide (SRSO) film or by direct chemical precipitation of Si-NC in colloidal suspension. To enter the quantum regime, Si-NC sizes need to be in the few nanometers range. Their surface is almost perfectly passivated by a nm thick silicon-rich oxide (SRO) layer [57]. Nowadays, the properties and fabrication methods are consolidated [58, 59] and, even, there are companies that provide them for a variety of applications.
A first striking optical property of Si-NCs is that, under very specific excitation conditions, they show optical gain (Figure 4) [61]. Since direct electrical excitation of Si-NCs is difficult, the used method was based on the amplified spontaneous emission (ASE) (Figure 4A) [62]. The initial observations were reproduced by using Si-NC formed in different dielectric matrices [63] by CW pump-probe transmission experiments (Figure 4E) and by time-resolved ASE experiments (Figure 4B) [64]. Since a large Stoke shift between absorption and emission is observed, and the gain is spectrally on the high-energy side of the emission (Figures 4A,D) a four-level system was suggested to explain the gain (Figure 4C) [64]. The gain is attributed to the population inversion of interface states (Si-O double bonds) formed at the surface of the Si-NC (Figure 4F) [57]. A very delicate balance between Auger recombination and confined carrier absorption, on one side, and stimulated emission and waveguide losses, on the other side, determines whether loss or gain prevails [65]. This could explain the few late observations of gain [66–68]. Eventhough, claims for lasing in distributed feedback structures appeared [69], the use of Si-NC as an active laser medium seems improbable. Therefore, alternative approaches are now dominating the research and development of a silicon photonic laser, where either quantum dots and other materials are cointegrated in the silicon chip [70–73], or hereogeneous integration and chip bonding of III-V semiconductors are used to make a hybrid III-V laser on silicon [74, 75, 75, 76], or, finally, nonlinear effects are exploited [77].
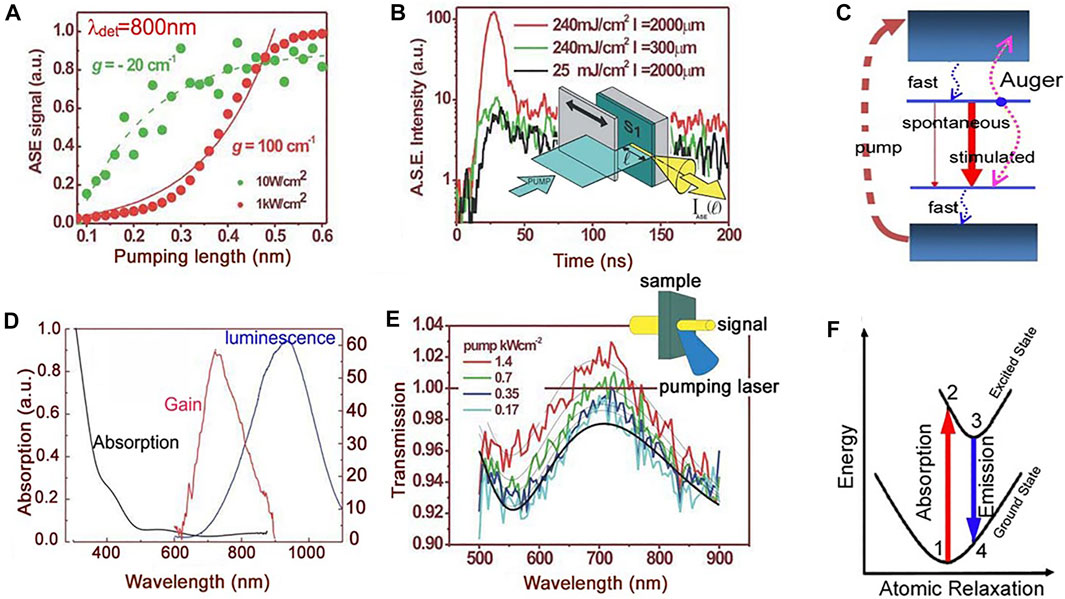
FIGURE 4. (A) Optical gain in Si-NC observed by the variable length stripe (VLS) technique. On increasing the pumped volume at high pumping rates, the amplified spontaneous emission (ASE) intensity—collected from the edge of a waveguide containing Si-NC—grows exponentially. In the figure, the ASE is reported as a function of the pumping length for two pump powers. The dots are experimental data while the lines are fit with the VLS model. (B) Time-resolved measurements at various pumping rates and excited stripe lengths. The inset shows the VLS method. (C) The four-level model to describe the population inversion in Si-NC. The large red arrow shows the lasing transition due to interface states. (D) The optical spectra of Si-NC where absorption, gain, and luminescence are reported for the same sample. (E) The transmission spectra of a weak probe beam for different large pump powers. The inset shows the experimental method. (F) A configuration coordinate diagram that links the four-level model to the Si=O interface state configuration. From Ref. [60].
Having observed luminescence and gain by optical excitation of Si-NC, a strong research effort was paid to get emission from the Si-NC by electrical injection, i.e. to make LEDs. Here, the problem is associated with the fact that the Si-NC are formed in a dielectric matrix (e.g., SRO) which is an insulating material. Therefore, the only chance to get electroluminescence is by tunneling. Two types of tunneling mechanisms are possible, depending on the oxide thickness and on the energy barrier height (Figure 5A):
• Fowler-Nordheim (F-N) tunneling where the carriers are injected in the Si-NCs through a triangular potential barrier caused by the voltage drop across the oxide. In this case, the energetic carrier excites by an inverse Auger process an e-h pair that in turn recombines by emitting a photon. The process is highly inefficient, has an onset at high voltages, and is prone to oxide damage and device failure;
• direct tunneling into the Si-NC. This happens when the oxide thickness is thinner than 2 nm. In this case to get electroluminescence, a concurrent tunneling of the other kind of carrier into the same Si-NC is needed (bipolar tunneling).
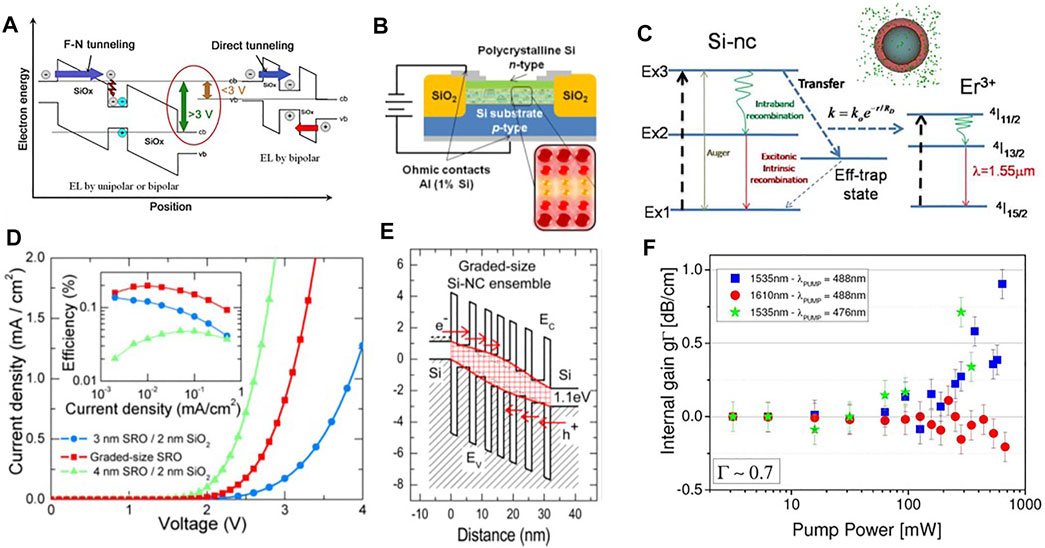
FIGURE 5. (A) Schematic view of the process of generation of e-h pairs in Si-NCs by Fowler-Nordheim (F–N) tunneling and impact excitation or direct tunneling. cb or vb refer to the conduction or valence band edges. From Ref. [25]. (B) Cross section of the Si-NC multilayer (ML) LED with graded size Si-NC. From Ref. [78]. (C) Scheme of the levels of the Er ions/Si-NC system. Arrows refer to the various radiative and nonradiative transitions involved in the energy transfer mechanism. This last is mediated by interface states and shows a rate (k) which depends on the distance between the Si-NC and the Er ion. From Ref. [79]. The inset shows a Si-NC embedded in an Er (green dots) doped SRO matrix. (D) J–V characteristics of two periodic ML LEDs with Si-NC size of 3 and 4 nm and of the graded-size Si-NC ML LED. The inset shows the related power efficiencies as a function of the current density. From Ref. [80]. (E) Energy band diagram for a graded Si-NC ML LED. EC and EV refer to the bottom of the conduction and the top of the valence bands, respectively. Notice an even alignment of the (electron and hole) ground states of Si-NC near the electrodes and a wider band gap in the middle of the active region. From Ref. [78]. (F) Internal gain (gΓ, where Γ is the optical mode confinement factor) measured in an Er/Si-NC codoped waveguide with pump and probe technique. Results for probe wavelengths tuned with the Er3+ emission peak (1,535 nm) and almost outside the gain spectrum (1,610 nm) and for different excitation pump wavelengths (resonant with the Er absorption lines 488 nm or not-resonant 476 nm) are compared. From Ref. [79].
Engineering of the active layer of the LED (Figure 5B) leads to the demonstration of bipolar tunneling [81]. In addition, grading the Si-NC sizes by using large Si-NC near the electrodes, which facilitates injection, and smaller Si-NC in the center of the device, which increases the radiative efficiency (Figure 5E), allows reaching high external quantum efficiency (Figure 5D) [78]. Still record quantum efficiencies in Si-NC LED are achieved by using chemically synthesized or surface-modified Si-NC [82], with record efficiencies of ≃ 10% [83] and luminance of 2060 cd/m2 [84].
Erbium-doped fiber amplifiers have permitted the development of long-haul optical communication. Therefore, an effort was paid to develop Er-doped waveguide amplifiers to enable on-chip light amplification and, possibly, laser emission [2]. With this respect, the codoping with Er of Si-NCs allows, on one side, to put Er in an environment similar to the one in silica fiber and, on the other side, to exploit the sensitization action of the Er emission by the Si-NC. Sensitization means that the Er ions are indirectly excited by energy transfer from the Si-NC (Figure 5C), which increases by several orders of magnitude the Er excitation efficiency [85]. Er-doped Si-NC waveguide indeed shows signal enhancement but no net amplification of the propagating light (Figure 5F) [86]. Here, careful experimental studies and modeling allow identifying the main limitations to this approach: a low excitable Er fraction through the Si-NC due to the distance-dependent transfer rate [87], cooperative upconversion among the Er ions and confined carrier absorption in the Si-NC [88, 89]. Therefore, most of the introduced Er ions are not contributing to the amplification but provides significant absorption losses that prevent reaching net-optical gain [90]. Time-resolved experiments confirm these observations and elucidate the important role played by Auger recombination in the Si-NC which allows recycling a fraction of the excitons to contribute to the energy transfer [85]. Still, the system can be integrated in complex circuits to realize on-chip electrically pumped optical waveguides that emit at 1,540 nm [91]. Recently, the use of a deep cooling technique to prevent Er clustering has made it possible to achieve high brigthness Er-doped Si LED with superluminescent (stimulated) emission [92]. Alternatively, Er silicate nanocrystals codeposited with Si-NC allow reaching efficient electroluminescence at 1,540 nm in MOS devices [93].
Silicon solar cells have reached records in efficiency and endurance. Still, there are margins of improvement by making a better use of the solar energy. Among other approaches, one enabled by Si-NCs is solar spectrum reshaping [96]. This is based on the modification of the light spectrum, which reaches the active part of the solar cell, to enhance the power conversion efficiency (PCE). There are specifically two regions on which one can act: the low-energy infrared region where silicon does not absorb and the high-energy region where photo-excited e-h pairs suffer by surface recombination. As shown in Figure 6A, solar light from these spectral regions can be moved to the visible either by upconversion (infrared photons are absorbed and e-h pairs recombine emitting higher energy photons [97]) or by down conversion (otherwise named quantum cutting, photons are absorbed at high energy by generating two e-h pairs that recombine at low energy) or by down-shifting (high-energy photons are absorbed, the generated e-h pair thermalizes and recombines by emitting a low-energy photon). Si-NCs allow photoluminescence downshifting [94]. We designed solar cells that are coated by an optimal layer of Si-NCs. In our modeling [98], we considered both the effect of the change of the surface reflectance due to the different effective n of the coating layer as well as the combined action of Si-NCs absorption and emission (Figure 6B). Results show a sizeable increase in the photoresponsivity (Figure 6C). Based on this, state-of-the-art interdigitated back contact (IBC) silicon solar cells were covered by optimized layers of Si-NCs. Experiments show a % increase of the power efficiency mostly due to the increased short circuit current (Figures 6D,E) [95]. Remarkably, the effect was even enhanced when the dielectric environment of the Si-NC was tuned to force the emission to the bulk of the cell with a suitable interposer layer that maximizes the Purcell effect (Figure 6F) [95]. An update review on the use of nanocrystals for downshiting can be found in [99]. On the other hand, Si-NC can be also used in the active layer of a solar cell. Engineering the system allows demonstrating Si/Si-NC tandem cell with 32% PCE [100] or indoor Si-NC hybrid cells with 9.7% PCE [101]. In a different approach, Si-NC are used in luminescent solar concentrators integrated in semi-transparent photovoltaic windows [102].
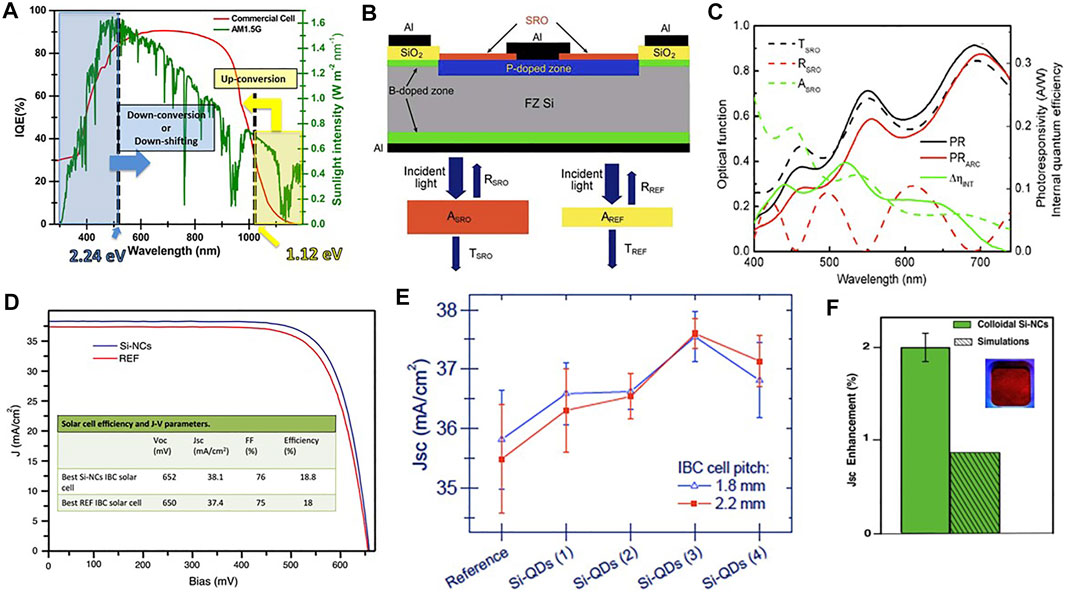
FIGURE 6. (A) Spectrum of the incident solar radiation (green line) with the mechanisms of down-conversion or down-shifting (blue arrow) and up-conversion (yellow arrow). The relative activation thresholds for a silicon solar cell are 2.24 eV (equivalent to two times the silicon band gap) and 1.12 eV (equivalent to the silicon band gap). The red line represents the internal quantum efficiency of a commercial Si solar cell. From Ref. [94] (B) Cross-section of a solar cell covered by a SRO layer (red). (Bottom panel) The optical functions for the SRO layer (left) and for a usual passivating SiO2 layer (right). From Ref. [94] (C) Optical functions (transmittance, black dashed line, reflectance, red dashed line, absorbance, green dashed line), measured photoresponsivity (PR, black line), modeled photoresponsivity without emission from the Si-NC layer (PRARC, red line), and increment in the internal quantum efficiency of the cell (ΔηINT, green line) for a Si-NC-coated solar cell. From Ref. [94]. (D) J–V characteristics of a 18.8%-efficient Si-NC IBC cell (blue line) and of the best reference solar cell (red line) coated by industry-standard SiNx layer under AM1.5G illumination. The inset summarizes the solar cell efficiencies and the J–V parameters (VOC open circuit voltage, JSC short circuit current density, FF filling factor). From Ref. [95]. (E) JSC for different coated Si-NC and reference IBC solar cells. (F) JSC enhancement. The inset shows the visible emission of the Si-NC. From Ref. [95].
In optical sensors, the analyte changes the optical properties of the sensing materials. Therefore, the presence of the analyte is transduced into a variation of an optical signal which is then monitored by the read-out system. This represents an emerging market for silicon photonics where lab-on-the-chip systems, point-of-care applications, and wearable electronic devices represent an enormous market potential. The specific analyte can be a gas, a liquid, a molecule, or a particle. A recent review of the field can be found in [103].
PS due to its large specific internal surface offers many reaction sites to bind analytes and, thus, PS is a suitable material for a sensor [26]. In addition, different PS properties are influenced by the pore content such as its photoluminescence, refractive index, and conductivity. Specifically, highly luminescent PS microcavities (see Section 2.2), when infiltrated by an organic liquid, show both a refractive index dependence of the microcavity peak position and a low-frequency dielectric constant dependence of the luminescence intensity (Figure 7A). Therefore, PS microcavity sensors have a response that depends on two different analyte properties that allow the discrimination between different organic liquids [104]. Furthermore, PS electrical conductivity is also affected by the ambient. Indeed, a conductometric sensor can be realized by measuring the current flowing through a mesoporous silicon layer. A high sensitivity to the NO2 pollutant gas at room temperature with limit of detection (LOD) of 12 ppb in dry air and 50 ppb in humid air is observed (Figure 7C) [106]. More interestingly, three independent quantities can be measured in PS, i.e., the electrical conductance, the photoluminescence intensity, and the wavelength of the optical resonance [109]. By monitoring the change of these three parameters as a function of the NO2 content (0.5–5 ppm), ethanol (300–15,000 ppm), and relative humidity (0–100%), we demonstrated that the analytes affect the measured parameters in a different way (Figure 7B) [109]. In this way, it is possible to distinguish between a pollutant like NO2 and interfering gases like humidity and ethanol [105]. Despite the semplicity of the PS sensor, its performances are still state-of-the-art. Indeed, typical limit of detection in integrated silicon optical gas sensors is in the few ppb range [110]. Recent progresses in the use of PS as a biosensor are reviewed in [111]. A critical assesment of these is provided by [112].
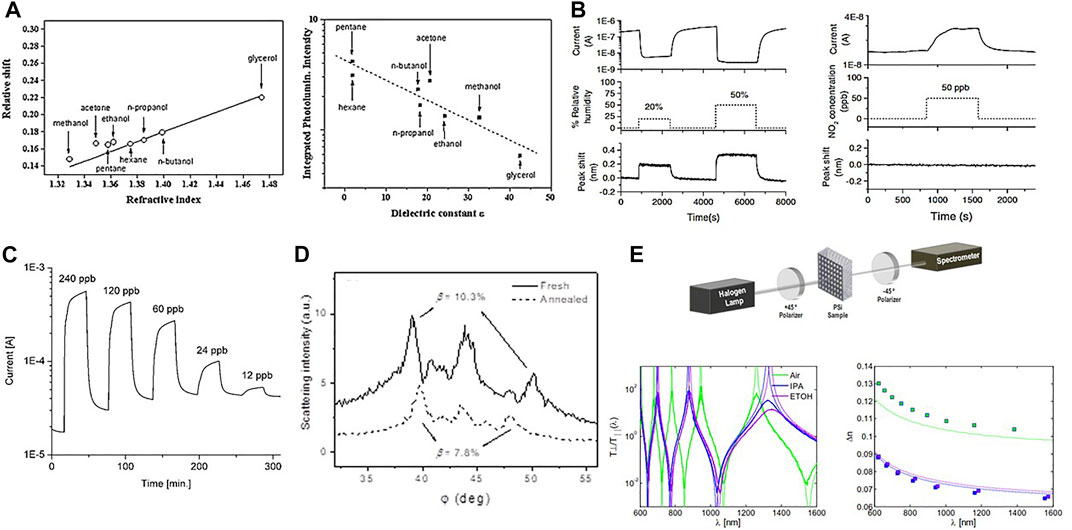
FIGURE 7. (A) Relative peak shift for total filling vs n and integrated relative intensity ≃ 550–850 nm as a function of the low-frequency dielectric constant of the solvent for a PS microcavity initially centered at 570 nm. From Ref. [104]. (B) Simultaneous measurement of the optical and the electrical response to humidity and NO2. Left plot: response to two different humidity values in the absence of NO2. Right plot: response to 50 ppb of NO2 in presence of 20% humid air. From Ref. [105] (C) Dynamic response of the sensor to different concentrations of NO2 in dry air. From Ref. [106]. (D) Scattering ring pattern of a fresh PS layer (solid line) and the same after thermal annealing (dashed line) under unpolarized illumination. β is the birefringence parameter. From Ref. [107]. (E) Scheme of the setup used for the optical characterization of PS membranes. Transmission spectra for empty pores (black line), and pores completely filled with isopropanol (green line) and ethanol (blue line). Birefringence data from the measured spectra (dots) and simulated curves using the Bruggeman model (dashed lines) for isopropanol (green) and ethanol (blue). From Ref. [108].
PS can be also used as a birefringence sensor. Birefringence is the degree of optical anisotropy of a material and depends on the geometrical material parameters as well as on the material properties. Owing to the porous structure of PS, which results from differently oriented and branched pores, its optical anisotropy can be influenced by the etching process and by the pore filling. Therefore, two methods to exploit PS as birefringence sensor have been investigated. In the first, light scattering from a PS layer is used because of the formation of scattering rings whose angles depend on its optical anisotropy [107]. In fact, multiple scattering from a random arrangement of vertical cylinders (the pore walls) generates a scattering cone from an oblique incident beam [113]. The cone aperture depends on the anisotropy of the PS. In the second, we used polarized light transmission through a free standing PS membrane [108]. In particular, heavily doped PS presents very high values of birefringence, as the pore shape is much less branched than in lightly doped PS. This special geometry also produces ring-shaped scattering of light, whose angular maxima are connected to the optical anisotropy of the layer. Filling the pores with different liquids or oxidizing the inner pore structures causes a change to the birefringence which can be measured by the angular position of the scattering rings (Figure 7D) [107]. On the other hand, by etching PS in (110)-oriented silicon wafer, pores grow along the [100] and (010) directions. Therefore, normal incidence light sees a different effective composition, i.e., a different effective n, depending on its polarization. This allows us to use the polarimetric setup of Figure 7E to measure the degree of birefringence of the layer. Filling the pores with different substances allows detecting their presence by measuring the spectral birefringence, as shown in the figure [108]. Recently, it has been demonstrated that this kind of sensors can achieve sensitivity of few ppm when ethanol is probed [114].
PS optical microcavities show a resonance frequency that depends on the composition of the fluid filling the pore. A similar effect is observed with optical microring resonator (MR) (see Section 5.1). Briefly, MR are formed by a waveguide closed on itself in a loop (of radius R and effective index neff) which is side coupled to another waveguide [119]. Measuring the transmission intensity from this side waveguide, transmission dips are observed whenever the light is coupled to the MR. The resonance wavelengths of these transmission dips are mλm = 2π neffR, where m is an integer. Therefore, if neff changes also λm changes which allows measuring n eff: a simple refractometric optical sensor is formed. We have engineered the MR based sensor by studying the delicate balance between the resonance quality factor (Q-factor) and the evanescent field overlap with the surrounding environment [120]. Based on the design, MR were fabricated with SiON as core materials and their bulk sensitivity S = Δλm/Δneff measured (Figure 8A) [115]. Here, we use the term bulk sensitivity to indicate the sensor response to a bulk change of the cladding material. This differs with respect to the surface sensitivity that refers to a change of neff caused by the chemical binding of the analyte on the MR surface. In this case, the surface of the sensor should be functionalized by the formation of active chemical bonds able to capture the specific molecula which one wants to detect. In our case, we were interested to detect low concentration of a toxin in milk because of the danger of its ingestion by humans. Milk is a complex fluid and many biosensors have been developed to detect its different allergens that are based, e.g., on nanoparticles or electrochemical methods [121]. We were specifically targeting the aflatoxyn M1 (AFM1) toxyn that is cancerous if assumed even in small quantities. We developed a specific functionalization protocol based on small strands of DNA (aptamers) or on antibodies (Fab’) (Figure 8E) [116]. Example of the resonance shift due to the flow of a buffer with different concentrations of AFM1 (the sample) is shown in Figure 8B [116]. Notably, the sensorgram (the time response of the sensor) shows the different phases of the arrival of the sample (the initial rapid large shift), the progressive chemical bonding of the analyte on the MR surface (the following slow shift), and the regeneration of the sensor by glicyne flow which recovers the initial resonance position. Measuring the response for different AFM1 concentrations allows determining the sensor sensitivity, while measuring the sensor response to different toxins allows determining the sensor specificity to AFM1 (Figure 8C). In this example, the response of the sensor to Ocratoxin (OTA) is negligible, while it is still responding to as low as a few nM of AFM1 [116]. The proposed sensor is competitive with immune-detection strip in terms of response time (minutes vs hours), while it lacks behind in terms of sensitivity (ppb vs ppt) [122]. However, this example shows the potential interest of silicon photonics sensors that, indeed, have been widely used for various specific targets. Reviews can be found in [20, 123–125].
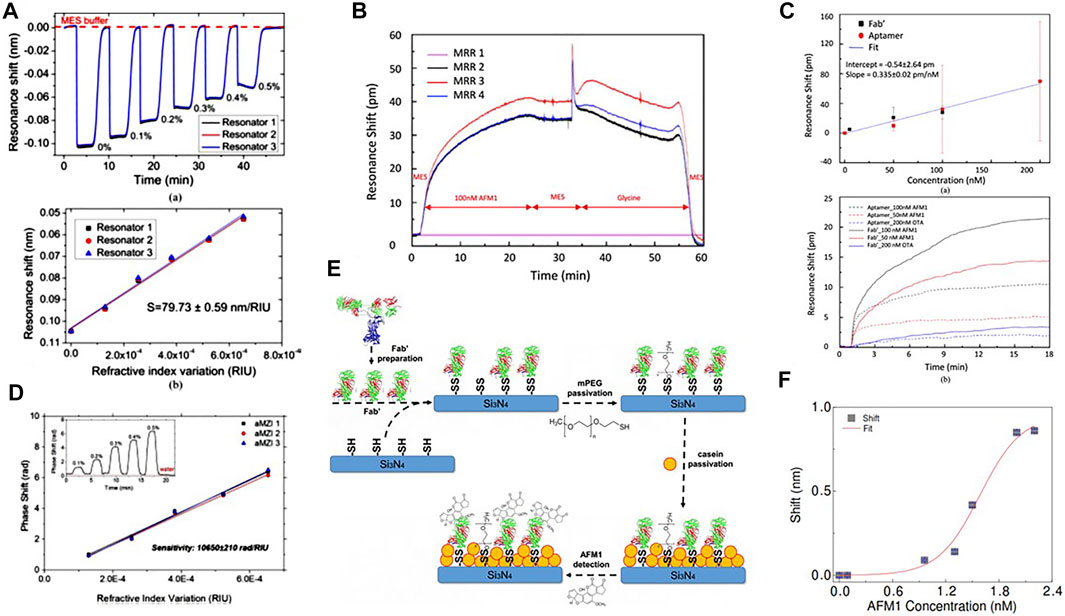
FIGURE 8. (A) Bulk sensitivity measurements on three equal MRs for transverse electric (TE) polarization. Top, temporal evolution of the resonance wavelength upon subsequent injections of water-glucose solutions at different concentrations. Bottom, the corresponding resonance wavelength shifts as a function of the n variation. From Ref. [115]. (B) Sensorgram of a complete measurement cycle for a MR functionalized with Fab’ and for a 100 nM AFM1 solution. At t = 0, MES buffer is flowing through the sensors. The toxin is injected at t = 2 min and at t = 25 min the toxin flow is stopped and the MES buffer is injected again. After 30 min a glycine solution is injected to restore the sensor to its virgin state. At t = 55 min MES buffer was injected again. From Ref. [116]. (C) Top: the resonance shift for different concentrations of AFM1 detected with Fab’ (black squares) and aptamers (red circles) based functionalization. Bottom: the corresponding sensorgrams. Sensing measurements of 50 and 100 nM pure AFM1 and 200 nM OTA diluted in MES performed on sensors functionalized with both aptamer (dash lines) and Fab’ (straight lines). The flowing buffer is MES. From Ref. [116]. (D) Volume sensitivity measurements for three equal asymmetric MZIs. Inset: phase shift curve for one of the aMZI sensors during the injection of the water-glucose solutions (glucose concentration in %w/w labeled on the plot). From Ref. [117]. (E) Schematics of the surface functionalization principle. Note that the molecule sizes are not scaled and are not corresponding to the real proportions. From Ref. [118]. (F) Aflatoxin M1 (AFM1) detection in milk sample: calibration function for MZI-based sensor. A logistic fit of the shift values is shown. From Ref. [118].
As the chemical bonding of the analyte to the sensor surface changes neff of a waveguide, other interferometer geometries can be used to realize optical sensors. In particular, the work-horse of integrated photonic interferometer is the Mach-Zehnder interferometer (MZI). It has been widely used to realize optical modulators (see the bottom left device in Figure 1) [11]. The MZI transmission T is determined by the interference between the light that propagates along its two arms
Almost in the same period when Gordon Moore announced its famous empiric law about the evolution of the semiconductor industry (1964), Stewart E. Miller on the Technical Journal of the Bell Company proposed that integrated optics could be developed to form photonic circuitry with economical and performance advantages (1969) [128]. The microelectronic industry evolved following the Moore’s law, while the photonic industry was not able to take pace with large-scale integration and only recently heavily integrated photonic circuits have been developed [9]. Photonic circuits are made possible by the optical confinement of light in sub-micron regions due to the refractive index contrast between the core and the cladding materials. This confinement follows the classical law of electromagnetism. In particular, in this section, we deal with silicon photonic devices that are based on classical electromagnetism even though novel physics is explored and new functionalities are demonstrated.
Si-NC emitters coupled to optical cavities show modified optical properties. In particular, by using optical lithography and etching it is possible to define optical active thin microdisk rich of Si-NC and standing on a pedestal (Figure 9A) [133]. Their emission spectrum is strongly different with respect to the broad emission band of Si-NC. In fact, narrow directional emission lines are observed in the plane parallel to the microdisk (Figure 9A, middle panels). These lines are due to the change in the photonic density of states caused by the optical cavity where whispering gallery modes (WGM) form in a way similar to what Sir. Rayleigh observed for sound waves in the Saint Paul cathedral. WGM spectral positions reflect the disk geometry that can be tuned by using a stressing layer which upward bends the disk in a micro-kylix shape affecting the WGM dispersion and the optical cavity Q-factor [129]. More interestingly, the coupling of the Si-NC with the modified density of photonic modes observed in the WGM microdisk is also reflected in a variation of the Si-NC radiative lifetime. In fact, the radiative lifetime of an emitter is described by the Fermi golden rule that linearly depends on the density of photon modes. Where the photon modal density is large, the radiative lifetime is short and vice versa. This effect named Purcell effect is clearly observed in the Si-NC emission in a microdisk resonator (Figure 9D) [132]. A sizeable reduction of the radiative lifetime is observed whenever the emission wavelength matches a WGM.
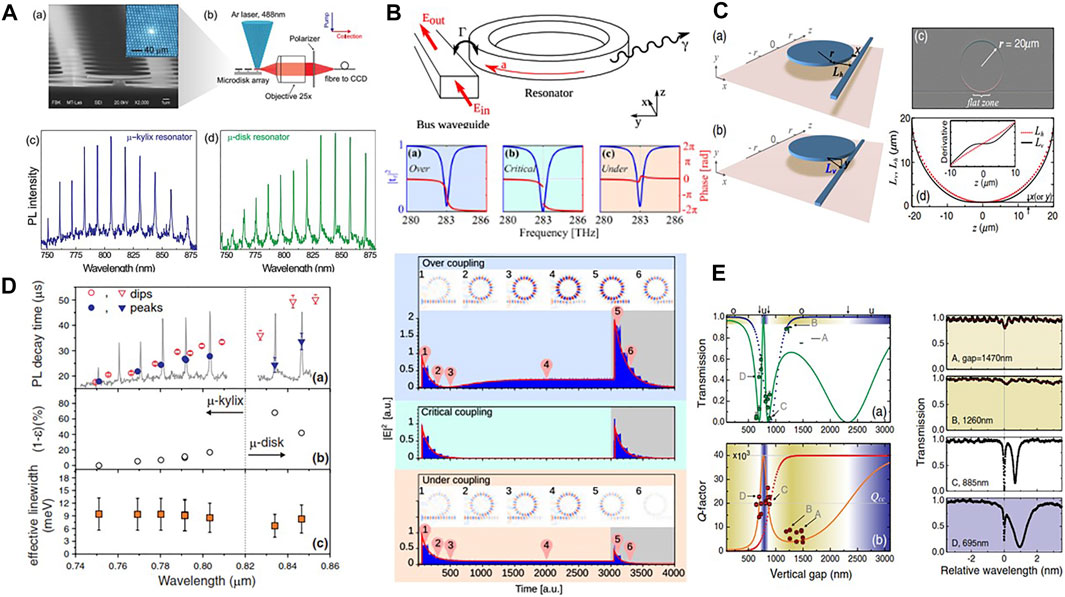
FIGURE 9. (A) WGM emission from microkylix and microdisk resonators. (a) SEM image of the microkylix array with a cross-sectioned microkylix resonator on the sample edge. The inset shows the bright spot corresponding to the Si-NC emission from a single device. (b) Micro-photoluminescence (PL) setup. (c) Emission spectrum of the microkylix resonator. (d) Emission spectrum of the microdisk resonator. From Ref. [129]. (B) Sketch of a resonator coupled to a bus waveguide. Panels (a), (b), and (c) display the over-, critical-, and under-coupling regime. Bottom: FDTD simulations of a microring coupled to a bus waveguide excited with a resonant CW source. The source is turned on at t = 0 and stopped at t = 3,000 a. u. which is represented by the gray background. The plots show the squared electric field at the output of the waveguide as a function of the time. The images show the electric field z-component. From Ref. [130]. (C) Sketches of the in-plane and the vertical resonator-waveguide coupling geometries. (c) Digitally processed optical image of the vertically coupled resonator showing the wide parallel coupling zone. (d) Plot of the resonator-waveguide separation as a function of the z coordinate along the waveguide axis in the in-plane (Lh(z), red dotted line] and vertical geometries (Lv(z), solid line]. The presence of the flat zone in Lv(z) is highlighted in the inset, where the first derivative of Lv(z) is plotted. From Ref. [131]. (D) Measured PL lifetimes for the peaks (filled symbols) and dips (empty symbols) of the WGM spectrum. Calculated lifetime shortening and the estimated Si-NC effective line-width at room temperature. From Ref. [132]. (E) Vertical gap dependence of the resonant transmission Tdip (a) and the resonance Q-factor (b) for the mode of the wavelength closest to 1.58 μm. Experimental points are compared to the theoretical predictions (solid line). For comparison, the T and Q trends for the point coupling model are reported as dotted lines. The background colors underline the regions where under-coupling (blue), critical coupling (white), and over-coupling (yellow) are expected. The right panels show the experimental spectra around λ = 1.58 μm for a few specific values of the gap as indicated in the left panels by the A, B, C, and D labels: the x-axis zero is set to the center of the resonance dip. From Ref. [131].
Despite this interesting physics, pedestal standing microdisks are difficult photonic components. Careful coupling with nearby tapered fibers or optical objectives are needed to study their properties. A preferred system, which allows also to be inserted into complex photonic circuits, is the one provided by MR coupled to a side waveguide (Figure 9B). The light from the side waveguide (also called bus waveguide) couples with the microresonator due to the overlap between the waveguide mode and the resonator mode which occurs in the coupling region. Here, the physics can be simply described by an optical mode equation based on the temporal coupled mode theory (TCMT) [130]:
where α is the electric field amplitude (optical mode) in the resonator, ω0 is the resonant angular frequency of the resonator, Ein is the input electric field amplitude, Eout is the output electric field amplitude, and Γ (γ) is the extrinsic (intrinsic) damping rate which are positive real values. Let us note that γ describes the losses in the resonator which are due to intrinsic factors (material absorption, scattering, bending, etc.), while Γ is related to the coupling with the bus waveguide (extrinsic factor). Indeed, a fraction
From this solution, the resonator Q-factor is easily derived as
In Figure 9B, both the transmission intensity |tr(ω)|2 and its phase (arg (tr)) are reported for different values of the damping rates, corresponding to the over-coupling (Γ > γ), critical coupling (Γ = γ), and under-coupling (Γ < γ) regimes. Typical Lorentzian lineshapes are observed for these coupling regimes, with a vanishing transmission dip for the critical coupling case. Also the phase shows a characteristic behavior with a π delay for the over-coupling regime and a zero delay for the under-coupling regime. The reason for these different behaviors can be understood by looking at Eq. 4, which shows that the output electric field results from the interference between the input field and the resonator optical mode. The temporal solution to Eq. 3 allows computing the output electric field as a function of time (Figure 9B, bottom). It is observed that a destructive interference occurs between the optical mode in the resonator and the input electric field in critical coupling conditions, once the resonator is loaded [130].
What we have described applies to a microresonator side coupled to a bus waveguide by a point coupling geometry (Figure 9C). Another coupling geometry, where a buried waveguide is vertically coupled to the MR, is possible. This vertical coupling has several interesting properties: 1) the two optical components can have different composition and cross-section, 2) the relative position of the bus waveguide allows exciting high order radial modes in a microdisk resonator, 3) the distance between the resonator and the bus waveguide can be controlled at the nm-scale without the need of high-resolution lithography [134]. In addition to these, the vertical coupling shows a new physics associated with the observed oscillatory coupling (Figure 9E) [131]. This last is caused by an extended effective coupling region (named flat zone in Figure 9C). Therefore, the vertical coupling can be modeled as two coupled waveguides of an effective coupling length given by the flat zone. Since oscillation in the power transfer occurs as a function of the effective coupling length, also the transmission oscillates as a function of the vertical distance between the bus waveguide and the resonator. This can be readily measured in experiments (Figure 9E). Further investigations allowed to fully understand the physics of the couplings which leads to an optimization of the system geometry [135].
Let us now consider a MR with clockwise αCW and counterclockwise αCCW propagating optical modes (Figure 10A). TCMT shows that
where β12 and β21 are the complex coupling coefficient between the two modes. These coupled equations show that a continuous energy exchange between the two modes occurs when a mechanism couples them. A possible mechanism is back-reflections due to surface roughness [136]. Equations 7, 8 are written for a forward (F) excitation (i.e. light is input from the left). Extension to a reverse (R) excitation (light input from the right) is straightforward. Solutions to Eqs. 7, 8 for the transmission (tF and tR) and reflection (rF and rR) coefficients are:
where Δω = ωinc − ω0 is the detuning frequency. If
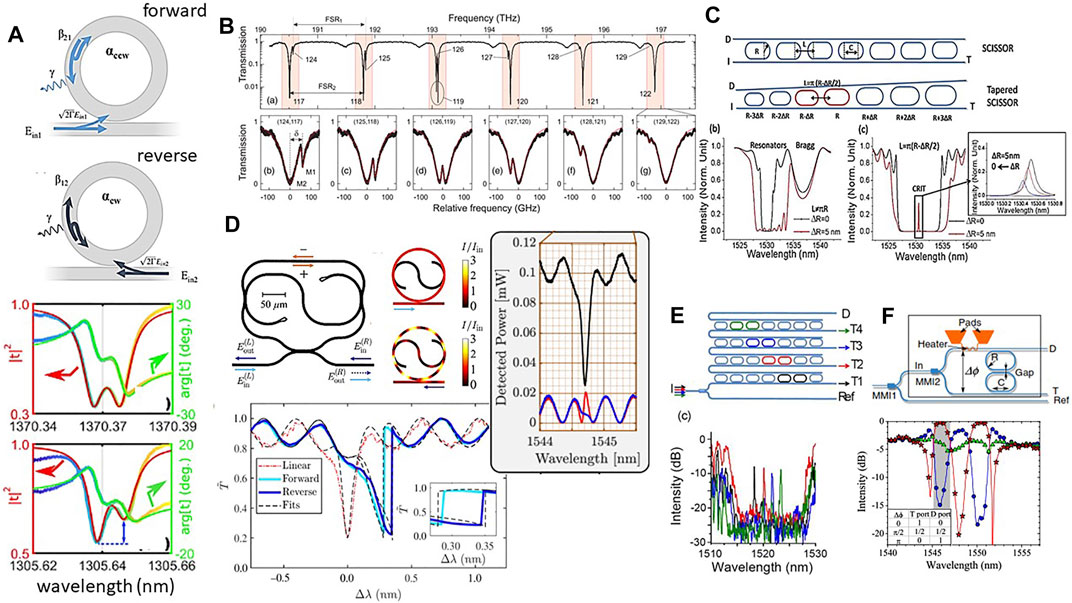
FIGURE 10. (A) Sketch of the fields in the forward and the reverse excitation configurations. (Bottom) Experimental spectra of the transmitted intensity and phase for a microresonator showing a balanced and an unbalanced doublet. From Ref. [136]. (B) Measured transmission spectrum of a vertically coupled 40-μm-diameter microdisk. Two radial modal families with different free spectral ranges FSR1 and FSR2 are observed. Bottom: blow-ups of the light red regions. From Ref. [137]. (C) A SCISSOR device. I refers to the input port, T to the through port, and D to the drop port. Racetrack resonators are used instead of ring resonators because of a larger coupling for TE-polarized light. Each racetrack resonator is characterized by a radius R and a coupling section C. L defines the resonator separation. Bottom: a tapered SCISSOR where each racetrack resonator has a radius that differs by ΔR from its neighbor. Simulations of the T port transmission in a SCISSOR (black line) and in a tapered SCISSOR (red line) for nondegenerate resonator and Bragg resonances. Simulation parameters: R = 3.250 μm, C = 7 μm, L = 5.105 μm, gap = 200 nm. (c) Simulations for a SCISSOR (black line) and for a tapered SCISSOR (red line) when the resonator and Bragg resonances overlap. The inset shows the dependence of the CRIT resonance on ΔR. Simulation parameters: R = 3.250 μm, C = 7 μm, L = 10.210 μm (black line) 10.200 μm (red line), gap = 160 nm. From Ref. [138]. (D) A taiji resonator coupled to a bus waveguide. In the forward configuration (light blue arrows) light enters the sample from the left; in the reverse configuration (dark blue arrows) light is injected from the right. Simulated intensity I (in units of the input intensity Iin) inside the resonator operating in the forward (up) and reverse (down) configurations. Normalized transmittance T̃ = T/Tmax as a function of the detuning Δλ = λ − λ0 from the linear resonance wavelength. The red dotted line is the experimental transmittance in the linear regime for an input power P = 0.01 W. The light and dark blue solid lines are the experimental transmittance in the forward and reverse configurations at a fixed input power P = 0.21 W. The inset gives a magnified view of the region of the strongest nonreciprocal behavior. From Ref. [139]. On the right, normalized transmission (black lines) and reflection spectra (blue line for the forward and red line for the reverse configuration) in the linear regime. From Ref. [140]. (E) Sketch of the 1 × 4 mux/demux composed by 4 tapered SCISSOR cascaded via the drop waveguide. Experimental transmission spectra for the Through ports: T1 black, T2 red, T3 blue, and T4 green. From Ref. [138]. (F) The reconfigurable interleaver. Waveguides are in blue, metallic wires are in orange. Transmission spectra of the D port for several powers dissipated by the heater corresponding to a Δϕ, respectively, of 0 (circles), π/2 (triangles), and π (stars). The inset is the table of routing for the band highlighted by the gray area. From Ref. [141].
Non-Hermitian physics can be observed in high-Q factor MR due to the excitation of the counter-propagating mode caused by back-scattering of the propagating mode due to the random sidewall roughness [136]. Or it can be observed as a consequence of the coupling between different radial modes in a vertically coupled microdisk through the buried waveguide [137]. In this case, the spatial overlap between the different radial modes governs the interaction and introduces a complex or reactive inter-mode coupling that is manifested by a self-shift of the resonant frequencies. We have described this phenomenon as an analogy to the electronic Lamb-shift term [137]. Notably, the coupling between the narrow first-order mode and the broad second-order mode of the microdisk causes a characteristic Fano lineshape that is characterized by a sharp asymmetry in the response spectrum (Figure 10B, bottom panel). Tuning of the coupling and of the Fano lineshape asymmetry is possible by using nonlinear effects [142]. Clearly, these are only few observations of the phenomena associated to non-Hermitian photonic systems, more studies have been reported in the literature, see e.g., [143–146].
Inspired by the work on coupled miroresonators geometries [147, 148], we have proposed a special resonator geometry where an S-shaped waveguide provides nonreciprocal losses inside the cavity (Figure 10D). Owing to its geometry, we named this resonator a taiji resonator [149]. The taiji MR is a non-Hermitian system and shows direction-dependent properties. Notably in the forward excitation direction, light does not propagate in the S-shaped waveguide and the CW mode is not excited. On the contrary in the reverse excitation direction, light couples to the S-shapes waveguide and the CCW is excited. Therefore, the taiji MR is a prototype system for non-Hermitian physics with, in the ideal case, β12 = 0 and β21 ≠ 0. Consequently, the taiji MR behaves as a unidirectional reflector. Note that another consequence of the taiji geometry is a larger power storage in the MR for the reverse configuration than for the forward one. The asymmetric coupling to the S-shaped waveguide allows recirculating the light coupled to it in the reverse case, while it is radiated away in the forward case. This causes a different resonator heating that affects the neff and, in turn, causes a nonlinear shift of the transmission resonance [150]. For the same input power, the shift is different for the F and R excitation configuration. In fact, a different transmission is observed (Figure 10D) [139], which means that Lorentz reciprocity is broken in this simple passive and nonmagnetic device. The model here described has to be carefully considered when taiji resonators are arranged in complex topology because interference with other photonic components can alter this simple picture [140]. Taiji MR are used for unidirectional [151] or topological lasers [152, 153] or as building blocks for topological photonic systems [154, 155].
Isolated single MRs show a rich physics that can be used in functional device systems (see e.g., Section 5.4). Coupled MRs show even more interesting properties. Sequence of MR can be coupled side by side in what is called a CROW (coupled resonator optical waveguides) or coupled through side waveguides in what is called a SCISSOR (side-coupled integrated sequences of optical resonators) (Figure 10C). In this last case, in addition to the resonances due to the single resonators (mRλR = 2πneffR), the periodicity of the sequence causes the formation of other resonance bands due to a Bragg-like effect (mBλB = 2neffLC, where LC is the distance between the center of two adjacent rings). In fact, the light dropped by the single optical resonators for specific wavelengths and resonator separation (sequence periods) can interfere constructively in the side waveguide in a way similar to what happens in dielectric Bragg reflectors (DBR). These two resonant conditions are visible as two transmission dips at λR and λB in the through port (T-port) of the SCISSOR (Figure 10Cb). If λB = λR, i.e. LC = πR, then the two resonances spectrally overlap and a coherent feedback occurs. When the two bands are in close spectral proximity and the single resonators have slightly different resonances, then a new sharp resonance peak appears in the T-port transmission (Figure 10Cc). This is due to the coherent coupling of two resonators and, therefore, is named CRIT (coupled resonator induced transparency) [156]. This represents the optical analog of the electromagnetically induced transparency (EIT). The CRIT condition can be engineered in a new SCISSOR geometry which we called tapered SCISSOR since it is made by resonators with slightly increasing radii along the sequence where only two are separated by the positive interference Bragg condition (LC = πR) and all the other are spaced by a distance LC ≃ 3/2πR which causes a destructive interference (Figure 10C) [157]. A router device based on a sequence of tapered SCISSOR can therefore be fabricated where the routing wavelength is determined by the CRIT condition (Figure 10E) [138]. Since this is a stringent requirement, the CRIT router is robust with respect to geometrical imperfections and can be easily reconfigured by changing either the single-resonator resonance or the coupling Bragg conditions [158].
Also CROW can be used as routers. In Figure 10F, we show a design of a reconfigurable interleaver or band router which is based on a two-resonator CROW. Here the idea is to use the CROW as an element of an interferometer where the phase difference (Δϕ) between the CROW inputs is controlled by the power dissipated in a metallic heater [141]. The device shows three output states: through, drop and a 50/50 split state that divides the input equally among the two outputs. Experimental data collected on a four-resonator CROW show that the interferometric switch works as expected (Figure 10F, bottom).
Here, we discussed two devices enabled by coherently coupling MR, actually the related physics is much richer [163, 164]. Other applications are possible such as synchronization of comb frequencies [165] or cavity quantum electrodynamics with trapped atoms [166] or perfect absorption [146].
It is well known that most of the data traffic occurs within data centers. Here one of the most imperative requirements is to handle high bandwidth with low power consumption and data latency. Therefore, reconfigurable optical switches are looked for as the solution for data transport in data centers [8]. The usual MEMS (micro electro-mechanical system) based switches used in telecom networks show limitation due to long switching time, cost, sizes, and resources optimization. Silicon photonics, with electro-optic integration, is currently the most viable alternative. A transponder aggregator (TPA), which distributes selected wavelengths received from the optical node to transponders (devices that convert the electric data flow into optical data flow at a given wavelength, thus connecting the users to the optical network) without any limitation in terms of wavelengths and directions or, in the opposite direction, which combines any wavelengths from transponders to the optical node, is the function of the IRIS (Integrated Reconfigurable sIlicon photonic Switch) optical switch [160].
The concept of the IRIS device is shown in Figure 11A [160]. A matrix of thermally controlled ring resonators are used to switch selected wavelengths. From the 4 network ports (NP) a set of 6 wavelengths are coupled to the IRIS-TPA by using grating couplers (SPGC). Interleavers (INT) separate the even and the odd wavelengths to increase the channel spacing. Then, demultiplexers based on array waveguide grating (AWG) devices [161] separate the different wavelengths along different waveguides that form the various rows of the 48 × 16 switching matrix. Along the rows there are nodes (switching elements (SE) shown as colored dots in Figure 11A) where ring resonators in the add-drop configurations are thermally moved into resonance or out of resonance with respect to the given wavelength. In case the wavelength has to be dropped, a given ring is moved in resonance with this wavelength in such a way that the light is coupled to the ring and dropped to waveguides which form the matrix column. At the end of each column, an interleaver combines the odd and even channels and a grating outputs the wavelength to the selected 8 local ports (LP). The IRIS switch can be also used in the other direction, i.e. a wavelength can be added to the IRIS switch by a specific local port and sent to the desired network port. To this end, the light is coupled to the photonic chip by a grating, then it is routed to the even or odd channel columns and, based to which network port it has to be routed, the switch element at the proper node of the matrix is brought into resonance with this wavelength so that the light is dropped from the column to the row. Then, the wavelengths on the various rows are multiplexed by AWG, the odd and even channels are recombined by the interleaver and via a grating the wavelength is routed to the proper network port. The switch elements are made by two coupled ring resonators (Figure 11G) to get a large channel isolation and a flat top transfer function (Figure 11B). On the top of each ring, a metal heater is fabricated to locally heat the ring and to change the resonance wavelength by controlling the neff via the thermo-optic effect. Owing to the small size of the ring, a shift by a free spectral range is achieved within few μs and with few mW which implies order of magnitude improvement with respect to MEMS optical switches. Interleavers and AWG have been designed and fabricated by using novel designs [160]. Specifically, whiskered AWG, where the star coupler surface is designed to trap the reflected light [167], have been used since they are robust to phase errors and show the required performances (Figure 11D) [161]. The various optical components are integrated in a silicon photonic chip that is bonded through metal bumps to a specifically designed ASIC chip (Figure 11H [160]). Electrical currents are flowing between the two chips for setting the desired resonator wavelength (Figure 11F) or to monitor the light signal in the photonic chip by reading integrated photodetectors (PD) [162]. The resulting electric/photonic integrated system has the cross section shown in Figure 11E. Remarkably, a fiber array is also pigtailed to the photonic chip to input and output the optical data (Figure 11H) [159]. In the final packaged device (Figure 11H), 1,398 photonic components controlled by more than 2000 electronic components are integrated in a 65 mm2 area. The photonic chip, with a switching matrix of 768 SE, was fabricated with a 193 nm deep-UV lithography in a fully CMOS-compatible process on 8-inch SOI (Silicon on Insulator) wafers, while the electronic chip by the STMicroelectronics’ BCD 0.16 μm technology. The IRIS switch needs to be calibrated before operation since the suitable currents to be injected in the metallic heaters to trim the interleavers or the switch elements have to be determined. This process (Figure 11G) is automatically performed by a purposely designed genetic algorithm [168]. After this, the switch can be operated and the desired wavelength addressed to the desired port (Figure 11C). Remarkably, the presence of on-chip monitor photodiodes allows us to trace the optical signal in different points of the switching matrix and to assess the related device losses. Despite that the switch is able to operate at 25 Gbps without adding extra power penality due to interferring signals and a total power consumption of about 1W, the overall power loss due to the matrix of 22 dB is still too high. By using higher resolution lithography and by integration of semiconductor optical amplifiers (SOA), better performances are achievable [9]. Indeed, these have been demonstrated in a 32 × 32 switch matrix that had only 10 dB of fiber-to-fiber loss and MZIs as switching nodes [169], while improvements due to on-chip SOA are discussed in [170]. A discussion of the state-of-the-art of reconfigurable photonic circuits with an emphasis on the power consumption is reported in [171].
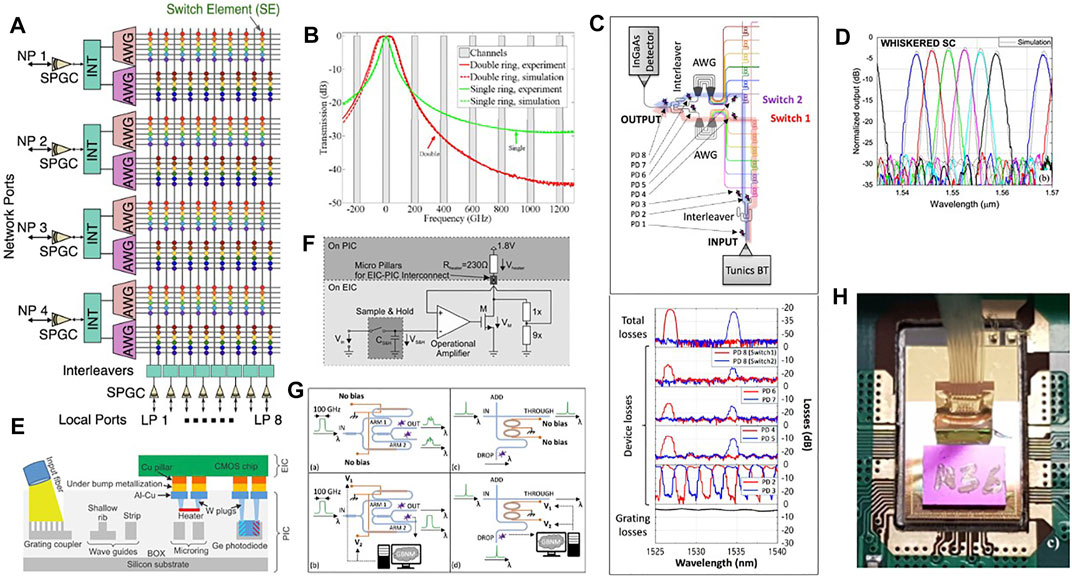
FIGURE 11. (A) IRIS switch architecture. From Ref. [159]. (B) Transmission spectra of single (red) and double micro-ring switching node (green). Solid lines represent the experiment, dashed lines the simulation. The 200 GHz-spaced channel positions are indicated with gray rectangles. Zero frequency corresponds to approximately 1,552 nm. From Ref. [160]. (C) Optical paths of the switch matrix set in the add configuration, with measured spectra acquired at different points in- and off-chip. From Ref. [159]. (D) Measured spectrum of the whiskered-shaped star coupler AWG. From Ref. [161]. (E) Schematic cross section of the electric-photonic integrated chip (not to scale). From Ref. [162]. (F) Block diagram of one heater control circuit. From Ref. [160]. (G) Schematics of the automatic optimization of the interleaver (left panels) and of the MR switch node (right panels). From Ref. [159]. (H) Photograph of the electric-photonic integrated IRIS switch wire bonded to the module board and pigtailed with a fiber array. From Ref. [159].
The MR resonance wavelength is determined by its geometrical parameters as well as by neff. When the input power is increased, nonlinear effects set-in which change neff. Specifically, in the CW case, the high input power induces two-photon absorption (TPA) which generates excess free carriers (with a density ΔN) at a rate (gTPA) in the conduction and valence band of silicon waveguide. These free carriers both cause free carrier absorption (with an associated loss ηFCA) and free carrier dispersion (FCD) as well as they thermalize with a typical free carrier lifetime (τFC) self-heating the material. The resulting increased temperature (ΔT) affects neff via the thermo-optic effects [175]. All these are related to the input pump power. Therefore, the linear Eq. 3 is modified by a system of coupled equations of α, ΔN and ΔT [172, 175]:
Equation (14) is the Newton’s law, where Pabs is the absorbed power by the material that causes heating, m indicates the mass of the ring, cp is the silicon-specific heat, and τth indicates the thermal decay time due to the heat dissipation with the surrounding medium. The nonlinear effects are given by the change of the resonance frequency ω0(t) = ω0 + δωnl(t), where ω0 is the MR resonance frequency in the absence of the pump light (cold MR frequency) and
Self-pulsing is particularly relevant since it transforms a CW input signal in a periodic oscillating output signal. Being simple the description of an isolated MR [175], the physics gets much more interesting in a SCISSOR [172]. Figure 12A shows the different temporal responses of a SCISSOR in the nonlinear regime. By measuring with an IR camera the scattered light from the SCISSOR (which is linearly proportional to |α|2) we can trace the number of rings that are excited by the input light. We note that if two rings are excited a periodic behavior in the T-port output signal is observed (Figure 12A, orange box). If three rings are excited, an a-periodic behavior is observed (Figure 12A, green box). If more rings are excited, a chaotic behavior is observed (Figure 12A, red box). Chaos is demonstrated by showing that the output is extremely sensible to negligible variations of the input [172].
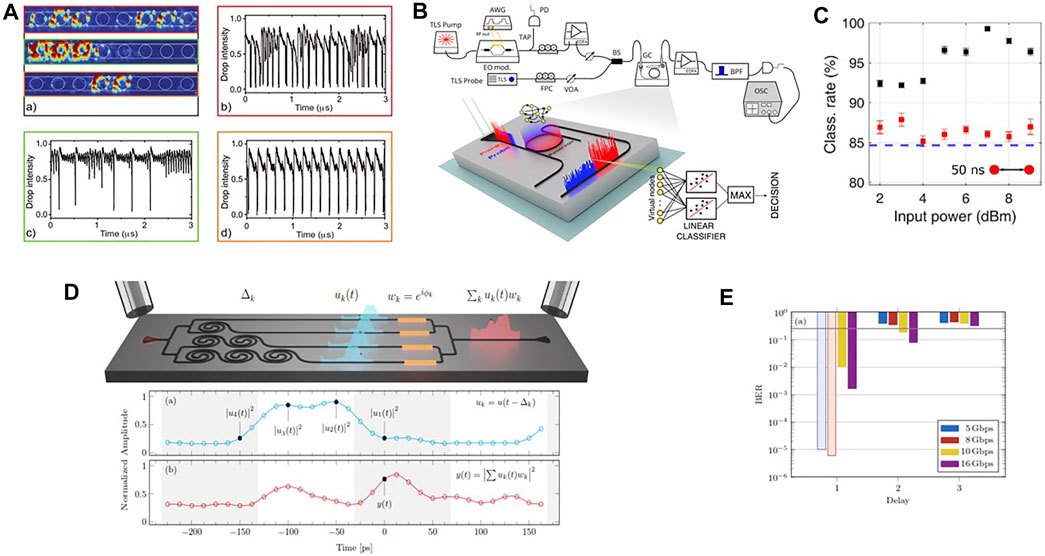
FIGURE 12. (A) Top scattered light from the SCISSOR associated with the three waveforms shown in the other panels, respectively. A schematic of the device geometry (white line on the scattering images) illustrates the position of the rings in the chain. Drop signal waveforms at different input powers (Pin, coupled in the waveguide) and wavelength (λp) combinations (b) Pin = 20mW λp = 1,543.225 nm, (c) Pin = 13mW λp = 1,543.170 nm, (d) Pin = 14.5mW λp = 1,543.990 nm—showing six (b), three (c), and two (d) hot resonators. From Ref. [172]. (B) Sketch of the experimental setup. TLS = Tunable Laser Source, AWG = Arbitrary Waveform Generator, EO mod. = Electro Optic modulator, FPC = Fiber Polarization Controller, VOA = Variable Optical Attenuator, PD = Photodiode, EDFA = Erbium Doped Fiber Amplifier, BS = Beam Splitter, GC = Grating Coupler, BPF = BandPass Filter, OSC = Oscilloscope. An enlarged view of the device layout and the main logical steps that describe how the information is processed are shown in the bottom part of the figure. From Ref. [173]. (C) Classification rate as a function of the average input pump power for Nv = 50 and bitrates of 20 Mbps. Black scatters use virtual nodes sampled from the output probe while red scatters from the input pump. The dashed blue line is the lower bound in the classification rate obtained by feeding the input samples into a linear classifier, without electro-optic conversion. From Ref. [173]. (D) Sketch of the integrated photonic circuit which performs as a complex perceptron. (Bottom) (a) Input signal versus time. The black circles show the sampling of the input signal done by the four delay lines. (b) Perceptron output at the photodetector versus time. This signal is the one that results after the photodetector. The dot shows the time at which the complex sum is performed. From Ref. [174]. (E) BER for the several bit rates indicated in the inset and XOR bit delay. The BER is indicated with transparent bars when the statistical limit is achieved, i.e., the operation is error-free. The black line refers to the nonlinear separability threshold. From Ref. [174].
Chaos in MR can be beneficial in many applications, such as achieving two-octave spanning frequency combs [176] or to suppress lasing instabilities [177]. Here, it leads us to consider MR as nonlinear nodes for photonic neural networks (see chap. 10 in [9]). We started from a very simple network, physically realized by a single nonlinear MR [173]. We implemented a reservoir computing scheme by using the nonlinearity of a MR and time multiplexing (Figure 12B). In this type of neural network, the input data are processed by a reservoir whose nodes are interconnected and the strengths of the connections are randomly chosen. In this way, the input is projected in a multidimensional space and the nonlinear dynamics of the reservoir guarantees the network separability. Only the reservoir outputs are trained by varying the weights in a linear combination of the output states of the reservoir. In our implementation, we encoded the input signal in time bins of different light intensity, which are input in the device. This sequence defines the virtual nodes (of number Nv) of the reservoir. The time bin duration is set of the same order of the nonlinear MR dynamics, which triggers a transient state in the free carrier population. The carrier dynamics defines the connections between the virtual nodes, i.e. the network memory. Specifically, we used a pump-probe technique (Figure 12B): the intensity modulated pump (red) and the CW probe (blue) are injected into the MR. An incoherent transfer of information from the pump to the probe occurs due to FCA and FCD within the resonator, where the different virtual nodes (yellow dots in Figure 12B) interact and process the input data. The probe exits from the D-port of the MR, carrying the result of the computation, and is detected by a fast PD. Virtual nodes are sampled and sent into a linear classifier, trained to perform a specific task. As an example, we classified the different species of the IRIS flower achieving state-of-the-art performances (Figure 12C) [173]. Note that the increase of the input power yields better classification rate up to a power level where self-pulsing is induced.
In [173], the linear combination of the reservoir outputs (perceptron) is done off the chip. Actually, this is also possible in the chip by properly designing the photonic circuit (Figure 12D). Here, it is shown a simple time delay network that integrates a complex perceptron [174]. Gratings are used to couple the light in and out of the chip. A 1 × 4 splitter distributes the input signal (u(t)) to four delay lines, realized by spirals (each spiral adds a delay of Δt). Then, thermal phase modulators allow controlling the relative phases
More advanced structures have been shown in the literature where both photonic accelerators (devices specialized to perform a single function and which are interfaced with electronic computer) [178, 179] or photonic integrated neural networks [180–183] with extremely high capacity and speed [184, 185] are demonstrated.
Up to now we have mostly discussed linear photonic devices. Still many other devices are enabled by the rich phenomenology of nonlinear optics. Silicon and silicon-based materials are widely used with this respect despite that the silicon nonlinearities are not as large as the one of other semiconductor materials. The polarization vector P and the applied optical field E are related by [150].
where ɛ0 is the vacuum permittivity, χ(1) the first-order susceptibility, χ(2) and χ(3) are the second- and third-order susceptibilities. Higher order susceptibility terms are smaller and smaller and they are effective only for large field intensities. Silicon optical nonlinearities are mostly dominated by the third-order effects since the second-order nonlinearity is vanished by its centrosimmetric lattice.
Si-NCs have a crystalline core of silicon which shows a Kerr-type nonlinearity (χ(3)) that competes with FCD and TO effects. In Si-NC, the variation of the refractive index (Δn) as a function of a pulsed high-field intensity can be modeled by Δn = n2be|E|2 − σFCDΔN, where n2be is the contribution due to the fast polarization of the electronic clouds while the second term is due to the excess free carriers generated by TPA [194]. Overall, n2be in Si-NC is one order of magnitude larger than that of bulk Si and three orders of magnitude larger than that of silica [194]. The large value is explained by the cumulative effects of quantum confinement and of the dielectric mismatch between the Si-NC and the dielectric matrix which enhances the field intensity in the high dielectric regions. The high n2be can be used in MR to achieve all optical switching [186]. In fact, when a Si-NC-based MR is pumped with a high power laser, the resonance frequency of the MR is shifted (Figure 13A). This effect can be used to realize an all-optical switch where a CW probe beam is switched on or off by a pulsed (1ps long pulse, 10 GHz repetition rate) high power beam (Figure 13D). Similarly, the slow TO effects can induce an optical bistable behavior in a MR [191]. Here, an integrated microdisk with embedded Si-NC is vertically coupled to a SiON waveguide. The transmission is recorded as a function of the input power, and depending on the power sweep directions an hysteresis loop is formed (Figure 13G). Optical bistability is only observed when the pump wavelength is on the long wavelength side (red-detuning) of the cold resonance wavelength so that a positive feedback can take place (power is absorbed which increases the temperature which increases neff which red-shifts the resonance which increases the absorbed power which ⋯). As a result, above a power threshold the resonance wavelength locks to the pump wavelength (see the spectra in Figure 13G at point 3). The power threshold is different (which explains the hysteresis) if the sweep is performed starting from low or high pump power. Thus, for the same input power in the hysteresis loop, the MR transmission shows two states (points 2 and 4 in Figure 13G). Other applications of Si-NC optical nonlinearities have been reported in [195].
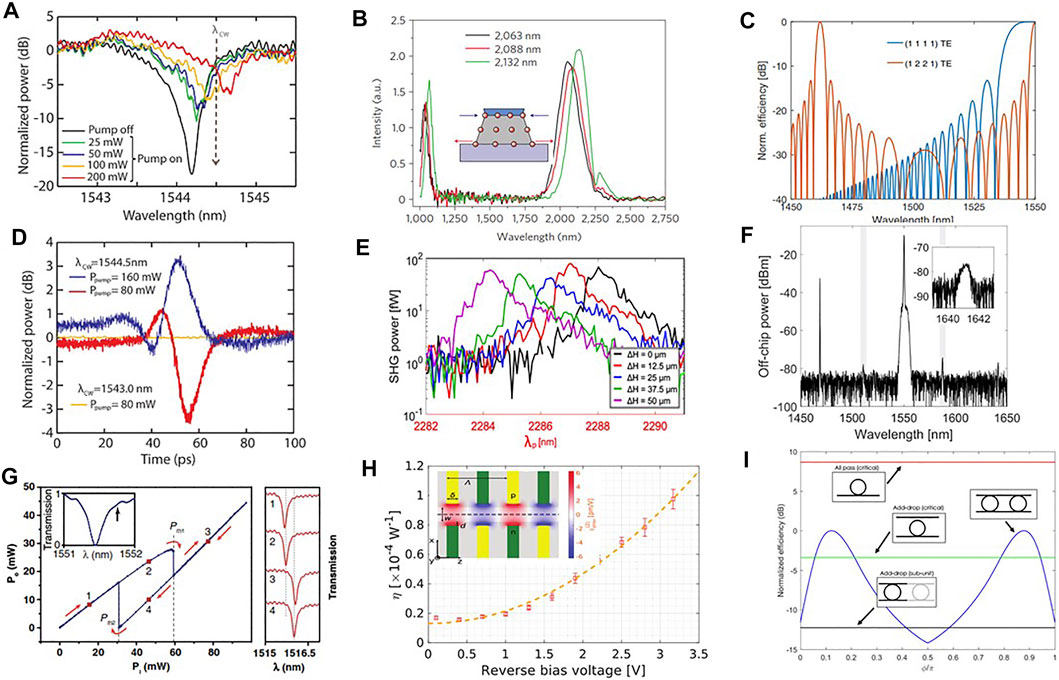
FIGURE 13. (A) Transmission spectra of a MR resonance for different pump powers, resonant with an adjacent resonance (λP = 1,557.5 nm). From Ref. [186]. (B) 10.7-μm-wide strained silicon waveguide transmission spectra of a fs pump with a peak power of 30 kW. The inset shows the lattice deformation of the waveguide due to the stressing layer (blue layer). The arrows show the kind of tensile/compressive strain observed. From Ref. [187]. (C) Spectral dependence of the idler generation efficiency for the (1111) intramodal FWM and for the (1221) intermodal FWM. All waves have TE polarization. A silicon waveguide with a cross Section 3.5 μm × 243 nm was used in the calculation. Each efficiency is normalized to its maximum. From Ref. [188]. (D) Time evolution of the probe signal for various pump powers. The probe wavelength is shown as a vertical dashed arrow in (A). Note that for the red line the resonance shift due to the pump power is not enough to overcome the probe, hence the negative dip. For the blue line the pump power is large enough to shift the resonance at wavelength longer than the probe, hence the positive peak. Yellow line corresponds to a probe wavelength out of resonance. From Ref. [186]. (E) SHG power as a function of the pump wavelength for different values of the waveguide deformation (ΔH) given in the inset. From Ref. [189]. (F) Stimulated inter-modal FWM for the 1221 TE combination. The waveguide width is 4 μm. Spectrum measured at the signal port. The idler CW seed is at 1.468.5 nm. The signal is generated at 1,641.1 nm. The gray boxes highlight spurious peaks. In the inset we show the generated signal spectrum. From Ref. [190]. (G) Optical bistability of the transmitted pump power as a function of the input power. Inset: cold resonance spectrum. The arrow indicates the pump laser position. On the right, transmission for various pump powers across another resonance at the two stable transmission states (1,2) and (3,4), corresponding to the red markers on the bistability curve. From Ref. [191]. (H) SHG efficiency η, as a function of the reverse bias voltage for an interdigitated configuration with w = 0.79 μm, Λ = 2.56 μm, and L ≃ 15.7 mm. A peak pump power of 0.1 W and a wavelength of λp = 2.34 μm were used. In the inset we show the top view of the waveguide for the interdigitated configuration. The yellow and green regions on the sides are the p- and n-type doped regions, respectively. In the figure, the electric field map for a bias of 3.5 V is reported. From Ref. [192]. (I) The FWM conversion efficiency of the photonic molecule (blue curve), as a function of the phase ϕ, is compared to the one of the critically coupled All-Pass (red curve) and Add-Drop (green curve) resonators, and to the one of the Add-Drop resonators which form the molecule (black curve). The maximum of the conversion efficiency of the photonic molecule has been set to 0 dB, and all the curves are referred to this level. From Ref. [193].
Despite that the second-order nonlinearity is negligible in Si, the need of fast electro-optic modulators in silicon photonics motivated a strong research effort to induce second-order nonlinearities in silicon. A simple idea was to break the silicon centrosymmetry by using a stressing layer (see the inset to Figure 13B), i.e. to strain silicon. Therefore, strained silicon waveguides cladded by SiN stressing layers were tested for second harmonic generation (SHG) [187]. Encouraging results were obtained where a significant peak at the double of the pump wavelength was observed (Figure 13B). Micro-Raman measurements revealed the large in-homogeneous strain induced in the silicon waveguide by the stressing layer [196]. Even other geometries were tested with different degrees of stress and chemical composition of the cladding layer [197]. However, some puzzling results were reported. First, no relation between the degree of strain induced by the stressing layer and the SHG efficiency was observed [197]. Second, the electrooptic effects due to the second-order nonlinearity in strained silicon MZI vanish for driving frequency larger than the inverse of τFC [198]. Finally, an experiment where strained silicon waveguides are mechanically deformed to increase the strain does not show any influence of the strain on the SHG (Figure 13E) [189]. All these data are explained by the electric field induced second harmonic (EFISH) effect [197]. Charged defects form at the interface between the core silicon waveguide and the stressing layer. These charges induce a static electric field EDC across the waveguide core. An effective χ(2) is then induced by the combined action of χ(3) and E DC:
The parametric nonlinear process mostly used in silicon is four wave mixing (FWM) which is based on χ(3) nonlinearities [150]. In FWM, two pump beams mix with a pair of weak beams, called signal and idler beams. The signal is typically the shorter wavelength beam and the idler the longer wavelength beam. FWM fulfills energy conservation and momentum conservation. The former is written as
with ωj (j = p1, p2, s, i) the frequencies of the pumps, signal, and idler beams. The momentum conservation, also known as phase matching condition, is given by
with kj = neff (ωj)ωj/c (j = p1, p2, s, i) the wavevectors of the pumps, signal, and idler photons. neff is different for each optical mode. The FWM generation efficiency η is given by [150].
where L is the length of the waveguide and f,j,q,l,m the overlap integral between the involved modes. Therefore, to get large generation efficiencies, Δk should be almost zero.
For brevity, let us assume degenerate pump beams (ωp1 = ωp2 = ωp). Neglecting other nonlinear effects (e.g., cross phase modulation, self phase modulation, etc.) [150],
Δk = 0 is achieved when all the frequencies and effective indexes involved in the process are almost equal, i.e. the four beams propagate on the same waveguide mode (Figure 13C, blue line). Another condition is found in multimodal waveguides [188]. In this case, the four beams could propagate on different modes with different dispersion relations. Thus, the frequency difference between the various beams is compensated by the different neff of the various modes and the phase matching condition can be obtained at signal and idler frequencies different from the pump frequencies (inter-modal phase matching) [188]. In a simple picture, by expanding the propagation constants of the different modes around the pump frequency, it is possible to write [202]:
where Δk0 is the phase mismatch at the pump frequency and k1,j = ∂kj/∂ω is related to the group velocity of the j mode. The basic idea of the inter-modal phase-matching technique is then to balance the Δk0 parameter by means of the difference between the signal and idler group velocities. The resulting η is shown in Figure 13C for a modal combination by which the pumps are in the 1 and 2 order modes, while the signal and the idler are on the 2 and 1 order modes. Intermodal FWM is characterized by a large spectral translation between the beams, very narrow generation bands, and a large flexibility in the mode selections. A photonic circuit was designed and tested to demonstrate the concept and a large spectral translation of 800 nm between the idler and signal beams was achieved [190]. As an example, Figure 13F shows a stimulated FWM (sFWM) spectrum where an idler beam is spectrally translated into a signal beam. Intermodal FWM has been lately used to generate supercontinuum in multimode fibers [203] or in multimode waveguides [204, 205] which allows facing the challenge to obtain a coherent and broadband source with nonlinear integrated optics [206].
Let us consider Eqs. 7, 8. Here, the two equations described the time evolution of two propagating modes in a single MR. The same can be also used to describe the evolution of the modes in two coupled MR, where now the coupling coefficients β12 = β21 = 2Γ exp (−iϕ) and ϕ = ω/c neffL where L is the distance between the two resonators. Quite interestingly, coupled MRs can be described as a photonic molecule since a supermode can form between the two when they have the same resonance wavelength [207]. In addition, the coherent control of the coupling and of the MR resonances allow us to fine tune the efficiency of FWM which can be enhanced, left unchanged, or completely suppressed with respect to the one of a single isolated MR (Figure 13I) [193]. Experimentally, the FWM control is achieved by thermal heaters that change neff, i.e. either ϕ or the resonance detuning. The FWM efficiency increase is due to a sharp raise of the internal field of one of the MR, due to the presence of the other because of the excitation of a sub-radiant mode of the photonic molecule. The FWM suppression arises from the coherent destructive interference between the signal waves generated in the 2 MR and, then, coupled into the common side waveguide where they do negatively interfere. This research is within the growing field of optical molecules which was recently reviewed in [208].
We are on the dawn of the next quantum technological revolution due to the advances in quantum information. In this technology, photons are suitable qubits and a strong effort to push integrated photonics as a platform to enable quantum information is played (see chapter 2 in [7] and chapter 11 in [9]). There concepts such as single photons, superposition, entanglement, contestuality are all relevant and play a crucial role.
As a first technological development, here we consider the application of quantum technology for security. Specifically, we aim to exploit the inherent probabilistic nature of quantum physics to develop photonic systems able to generate sequence of unpredictable bits to be used as seed for cryptography applications. These are called random number generator with the specification that they are based on a quantum effect, i.e. quantum random number generator (QRNG). Reviews of QRNG can be found in [214–216]. State-of-the-art results of a silicon photonics integrated QRNG are reported in [217]. In the following, we review a simple, low-cost, and CMOS-compatible system. The first concept we used is the probabilistic nature of spontaneous emission, by which a light source emits randomly photons whose time of arrival on single-photon detectors (single-photon avalanche photodiode, SPAD) is used to generate random bits (Figure 14A) [209]. To use an all silicon approach, the photon source was a Si-NC LED where, with our setup, we measured a Poisson distribution of the emitted photons [218]. With a poissonian distribution, given a photon flux λ, if we use a time-bin tw = ln (2)/λ we have an equal probability to detect one photon and no photon. Therefore, we can use the SPAD clicks to generate the random bit sequence. This idea works for short sequences, but fails for long sequences due to unwanted ambient fluctuations that affect the LED emission rate. Thus, we have developed another procedure to generate the random bits which is robust to ambient fluctuations. It is based on a random bit extraction implemented on a dedicated field programmable gate array (FPGA) without any postprocessing of the data. Briefly, the Poisson statistics has the property that if there is only one single arrival in a time interval (0, T), the distribution of the arrival times is uniform throughout the interval. We have therefore built an interval and attributed different hexadecimal symbols to 16 subintervals. In addition, we used non-symbol generating intervals to take into account the dead time and the afterpulsing of the SPAD, and we used cyclic permutations of the symbols to consider for electronic artifacts. The final scheme is shown in Figure 14D. Each time a photon is detected in a subinterval a symbol is generated whose binary code represents the random bits. This procedure turns out to be extremely robust to any external factor that influences the system (see, e.g. Figure 14B where large temperature variations that impact the photon flux generation do not influence the probability to generate bit 1 or 0) [210]. Then, we interfaced Si-NC LEDs and a matrix of SPAD in the silicon photomultiplier (PM) configuration with still high quality random number generation [219]. Finally, we moved to a single-chip QRNG, where the light source is provided by a reverse biased pn junction operating in the avalanche regime within a Si PM interfaced to a SPAD (Figure 14E) [209]. A compact board implements the bit extraction methodology, enables easy of operation, and shows the potential compactness of the QRNG which passes all the different statistical tests for randomness of the generated bit sequence without postprocessing [220].
FIGURE 14. (A) Schema of the photonic QRNG: a source of photons (NPh) is coupled with a single-photon detector (NPD), followed by a digital processing unit to extract the sequence of random bits (NRb). From Ref. [209]. (B) The electroluminescence (EL) variation at different temperatures (black line) and the probability of ones (blue line) for different temperatures. From Ref. [210]. (C) Setup used to generate random numbers from SPE photons with the generation (red box), the rotation (orange box), and the detection (blue box) stages. GTP, Glan-Thompson polarizer; BS, beam splitter; MR, mirror; DL, delay line; PBS, polarized beam splitter; PR, polarization rotator (half-wave plate); SPAD, single-photon avalanche diode. Table: generated raw random number sequence coding the event “which SPAD detected the photon,” given a certain couple of states. From Ref. [211]. (D) Schematic of (a) a conventional interval with 16 hexadecimal symbols, (b) the “double length” interval with the first half of no number symbol (N) and the second half with N subintervals between symbols, and (c) the super interval containing 16 “double length” intervals as in (b) with a consecutive one-rotation of symbols. From Ref. [210]. (E) Cross section of the QRNG realized with integrated emitter (mini SiPM) and two detectors (SPADs). On the top the cross-section, indicating secondary photon emission toward the SPAD. On the bottom, the biasing scheme and the read-out circuit of the QRNG chip, with emitters and one SPAD detector. In the inset a photo of the testing board with the QRNG chip. From Ref. [209]. (F) An example of the actual recorded traces. The blue line refers to the emitter bias Ve and the red line to the detector signal. From Ref. [212]. (G) Bell inequality measurement for a filtered (1 nm bandwidth) LED. Data points are experimental results while lines are theoretical curves. From Ref. [213]. (H) Minimum entropy Hmin as a function of the mean number of emitted photons μh based on a different estimate of the photon losses k. From Ref. [212]. (I) Min-entropy
One of the main advantages of QRNG is the fact that they are based on simple physical principles and do not rely on complex stochastic models to estimate the randomness (entropy) they generate. However, for the QRNG we discussed so far we had to trust the working of the device, i.e., the fact that the random numbers are generated according to the quantum process and not to some other source, such as classical noise. This has raised the issue of the certification of the quantum nature of the process. To this end, we developed a self-testing QRNG based on the chip in Figure 14E [212]. The objective is to model the QRNG with minimal assumption on the devices and compute the expected amount of minimal quantum entropy (Hmin) which can be extracted. The methodology is based on a prepare-and-measure approach, where the light source is the preparation stage and the SPAD the measurement one. In other word, we assume to know the source and the properties of the emitted states and we leave completely uncharacterized the detector. Randomness is then generated by an unambiguous state discrimination strategy. When the source generates a state (e.g. one photon or no photon, state x) the SPAD can click or not (Figure 14F). This means that the measurement is not able to discriminate whether a photon was emitted or not. These inconclusive events have a random occurrence (the clicks generate the random bits b). From this, we can compute the conditional probability P (b|x) that allows estimating Hmin (Figure 14H). Hmin can be as large as 5% (i.e. 5 % of the bits in the random sequence are certified as due to a quantum process) [212].
One of the most intriguing characteristics of quantum mechanics is the fact that two particles might show one degree of freedom quantum correlated (entangled) even at large distances (nonlocality). More intriguing is the fact that the results of the measurement of a state depend on the measurement (contextuality). Entanglement of two degrees of freedom of a same particle (single-particle entanglement, SPE) does not rely on the nonlocality but relates to the non-contextuality nature of quantum physics [221]. We have worked on the use of SPE as a resource for quantum information due to the fact that this kind of entanglement is easy to be produced and is robust to decoherence. In addition, SPE is not shared nonlocally by two space-like separated photons which means that there is no need of time correlation between different particles. Finally, generation of SPE needs less resources because it relays on single photons generated by any light sources (either an attenuated laser, a LED, or a lamp) [213]. We considered two degrees of freedom (momentum, i.e. direction, and polarization) of a photon. Given a photon with a given direction and polarization (state
The usual method to test the entanglement is to verify whether the state violates the Bell inequality. To this aim, we projected the SPE state on all the different combinations of the momentum and polarization (Figure 14C, rotation by angles ϕ, ϕ′, θ, θ′) and detected the different occurrence probabilities (Figure 14C, measurement) from which the correlation coefficients and the violation can be measured. In particular, we test the Clauser, Horne, Shimony, and Holt (CHSH) inequality |S (ϕ, ϕ′, θ, θ′) ≤ 2| and found a significant violation with all the different light sources used (Figure 14G) [213]. We finally implemented this source of SPE as a self-testing QRNG. In fact, the specific SPAD that clicks for a set of rotation angles in the CHSH inequality maximum violation condition is a random variable as a function of time (Figure 14C, bottom table). Careful analysis of the experimental setup and of the generation protocol [222] allows us to estimate Hmin with different degrees of trust on the experiment. Values that span from 2.5% up to 30.1% are observed for different levels of description of the setup (Figure 14I) [211]. Moreover, it has been reported that SPE is a resource for other kind of quantum information applications, for example quantum key distribution [223, 224], quantum teleportation [225], state swapping [226], entanglement concentration [227], and single-photon steering [228, 229].
In photonic quantum computing and quantum measurements, single photons are a relevant resource. Ideal single-photon sources emit deterministically only one photon at a time with unit probability. Quantum dots or localized color centers are used to produce such sources with limited performances in terms of indistinguishability. An alternative, which is probabilistic in nature, is to use heralded single-photon sources [202]. Here, a source of time-correlated photons is used where one photon of the pair is detected to herald the other photon. To generate the pair, nonlinear optics is used. Figure 15A shows an example of a heralded single-photon source based on the spontaneous intermodal FWM process (SFWM) [230]. A pulsed pump laser is coupled into a monomode silicon waveguide. Then, a directional coupler (DC) splits the pump beam equally. One part enters a multimode waveguide (MMWG) and excites its fundamental mode, while the other part is coupled to the multimode waveguide by using an asymmetrical direction coupler (ADC) engineered to excite the second-order mode of the MMWG. The MMWG is engineered so that an intermodal phase-matching of the 1221 configuration is achieved. In this way, the pump photons in the TE0 and TE1 modes spontaneously generate idler photons on TE0 and signal photons on the TE1 mode of the MMWG. Then, another ADC is used to couple the signal photon to the TE0 mode of the output waveguide. The chip thus generates pairs of correlated photons at different wavelengths that are output by different waveguides. Detecting the idler photon heralds the signal photons. To verify that the source is indeed a single-photon source, a triggered Hanbury–Brown and Twiss (HBT) interferometer is used which allows us to measure the antibunching characteristics of the signal photons [202]. In fact, single photons are never detected contemporaneously at the two output ports of the BS (coincidence measurements between the two detectors yield 0 for zero time delay). To this end, a BS is placed on the signal path and a three-photon coincidence measurement is performed [230] to measure the heralded second-order coincidence function
FIGURE 15. (A) Heralded single-photon setup. A pump (green) pulsed laser at 1,550.3 nm (40 ps pulse width, 80 MHz repetition rate) is coupled to the chip. On the chip, after a 3-dB directional coupler (DC), half of the pump remains on the TE0, while the other half is converted to the TE1 via an asymmetric directional coupler (ADC1) (92% efficiency). In the multimode waveguide MMWG, the inter-modal SFWM process generates the idler (blue) and signal (red) photons in the TE0 and TE1 modes, respectively. The signal is then converted to the TE0 via ADC2. Idler and signal are then out-coupled from the chip. Pump residual and Raman noise are rejected from the idler beam by a short pass filter (SP). The idler is then detected via an InGaAs SPAD, triggered by the pump. The signal is polarization rotated through a free space half-wave plate (λ/2) and upconverted to the visible through an upconverter system (UC). Then, the signal photons are analyzed by means of a Hanbury Brown and Twiss (HBT) interferometer, which is composed by a 50/50 beam splitter (BS) and two silicon SPAD. A time tagging unit is used to monitor individual singles and coincidences between the three detectors. Inset: profiles of the TE0 and TE1 modes. From Ref. [230]. (B) Heralded second-order coincidence function
Another important property of intermodal SFWM is the narrow, spectrally displaced, and discrete generation bands (Figure 13C). This is important to achieve heralded single-photon sources of high purity [202]. In fact, in single-mode waveguides photon pairs are generated by SFWM broadly about the pump with a high degree of spectral anticorrelation which should be removed by using narrow band-pass filters to increase the single-photon purity at the expense of the heralding efficiency. Alternatively, by engineering intermodal SFWM in spiralled MMWG, it is possible to generate photons in discrete pump sidebands with a width that matches the pump pulse bandwidth. In addition, to take into account residual correlations due to the spatial wake-off of the two pump photons, a temporal delay can be added as illustrated in Figure 15G [232]. The chip allows also separating the signal and idler photons in two spatial modes via mode converters. Figure 15E reports the measured biphoton joint spectral intensity that shows no correlation between the idler and signal photons (purity of 0.9904 ± 0.0006) when a delay of 1.46 ps is used. Another important property of the source is the fact that it is integrated in silicon photonics, which means that more sources can be easily fabbricated in the very same chip. In this case, it is important that the generated single pure photons are indistinguishable and that the system does not add unwanted multiphoton noise. The performed experiment is an on-chip 4-photon heralded Hong-Ou-Mandel interference experiment (see the inset of Figure 15F) by which the idler photons generated by two sources herald the quantum interfering signal photons. The measured visibility was as high as 0.96 (2) (Figure 15F) which is a consequence of almost perfect mutual indistinguishability of 0.987(2) [232]. These results pave the way for a massive scaling of photonic quantum information processing [239–241] or for chip-based quantum communications [242], enabled by nonlinear integrated quantum sources [243].
After more than 30 years of development, silicon photonics is now a mature technological platform. Millions of silicon photonic transceivers operating at data rates equal to or larger than 100 Gbps are annually sold [244]. Co-packaged optics, where both the silicon-photonic transceivers and the silicon electronic switches are packaged in a single board for networking data centers [22], have demonstrated aggregated data rate of 25 Tbps and higher [245].
New commercial opportunities opened in consumer electronics where, e.g., digital health solutions based on spectophotometer-on-a-chip sensing modules are integrated in popular smartwatches [246] or diagnosis systems based on silicon photonic chips for immunoassays are used for point-of-care applications [247]. Other physical sensing technologies are also enabled by silicon photonics, such as Fiber Optical Gyroscopes (FOG) [248] and LiDAR (Light Detection And Ranging) [249], and could impact the automotive or the autonomous vehicle markets.
More long-term applications are found in the use of silicon photonics as the platform for advanced computational systems such as the coherent Ising machine [250], the neuromorphic computer [184], or the quantum computer (based on squeezed states [251] or on fusion gates [252]). Even, programmable photonic circuits that can be reconfigured using a software have been demonstrated [253], which moves photonics along the similar path from ASIC (application-specific integrated circuits) to FPGA of electronics. From a basic science perspective, research on topological systems (see Chapter 8 in [9]), non-hermitian systems (see Chapter 7 in [9]), and devices based on exceptional point physics [146] provides many new phenomena and device concepts [254]. Thus, at the end of this 30-year-long journey, I belive that photonics made with complex silicon circuitry has yet to unveil new physics from which new understanding and new applications can emerge.
LP wrote this paper which is based on a collaborative work with his PhD students, coworkers and collaborators along the years. These valuable coworkers are properly cited in the references.
This research is presently supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreements No 788793, BACKUP, and No 963463, ALPI), from the European Union’s Horizon 2020 research and innovation programme under grant agreements No 820405 (QRANGE) and No 899368 (EPIQUS), and from the MUR under the project PRIN PELM (20177 PSCKT). This research is also supported by Q@TN, the joint lab between University of Trento, FBK-Fondazione Bruno Kessler, INFN-National Institute for Nuclear Physics, and CNR-National Research Council.
The author declares that the following patents have been filed and are based on some of the work here described: WO2008117249A1 Integrated optical waveguide amplifier or laser with rare earth ions and sensitizer elements co-doped core and related optical pumping method, WO2005064394A1 Method for producing an integrated fabry-perot microcavity device with silicon technology, US2002163003A1 Laser device based on silicon nanostructures, WO2016016741A1 True random number generator, WO2018073802A1 Improved random number generator, in particular improved true random number generator, WO2021/186292A1 An apparatus for producing a multiciplity of photons comprising quantum-entangled single photon states, IT102021000011357 Modulo Ottico Di Tasmissione-Ricezione con Rete Neurale, GB2005827.7 Optical apparatus. Apart from these patents, there are no other commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The research here described is the results of the hard work of all the people who were or are at the Nanoscience Laboratory of the University of Trento. They can be recognized as the authors of the papers listed in the references. I am honored and blessed to have had the chance to work with them over these years.
1. Canham LT. Silicon Quantum Wire Array Fabrication by Electrochemical and Chemical Dissolution of Wafers. Appl Phys Lett (1990) 57:1046–8. doi:10.1063/1.103561
2. Ossicini S, Pavesi L, Priolo F. Light Emitting Silicon for Microphotonics, 194. Berlin: Springer Science & Business Media (2003).
3. Pavesi L, Guzzi M. Photoluminescence of AlxGa1−xAs Alloys. J Appl Phys (1994) 75:4779–842. doi:10.1063/1.355769
4. Lockwood DJ, Pavesi L. Silicon Photonics. In: Topics in Applied Physics, 94. Berlin: Springer (2004).
5. Pavesi L, Guillot G. Optical Interconnects, 119. Berlin: Springer series in optical sciences (2006).
6. Lockwood DJ, Pavesi L. Silicon Photonics II: Components And Integration. In: Topics in Applied Physics, 119. Berlin: Springer (2010).
7. Pavesi L, Lockwood DJ. Silicon Photonics III: Systems And Applications. In: Topics in Applied Physics, 122. Berlin: Springer (2016).
9. Lockwood DJ, Pavesi L. Silicon Photonics IV: Innovative Frontiers. In: Topics in Applied Physics, 139. Berlin: Springer (2021).
10. Pavesi L, Turan R. Silicon Nanocrystals: Fundamentals, Synthesis and Applications. Weinheim, Germany: John Wiley & Sons (2010).
12. Doerr CR. Silicon Photonic Integration in Telecommunications. Front Phys (2015) 3:37. doi:10.3389/fphy.2015.00037
13. Li Y, Zhang Y, Zhang L, Poon AW. Silicon and Hybrid Silicon Photonic Devices for Intra-datacenter Applications: State of the Art and Perspectives. Photon Res (2015) 3:B10–B27. doi:10.1364/prj.3.000b10
14. García-Meca C, Lechago S, Brimont A, Griol A, Mas S, Sánchez L, On-chip Wireless Silicon Photonics: from Reconfigurable Interconnects to Lab-On-Chip Devices. Light: Sci Appl 6 (2017) e17053. doi:10.1038/lsa.2017.53
15. Cheng Q, Bahadori M, Glick M, Rumley S, Bergman K. Recent Advances in Optical Technologies for Data Centers: a Review. Optica (2018) 5:1354–70. doi:10.1364/optica.5.001354
16. Chen X, Milosevic MM, Stanković S, Reynolds S, Bucio TD, Li K, et al. The Emergence of Silicon Photonics as a Flexible Technology Platform. Proc IEEE (2018) 106:2101–16. doi:10.1109/jproc.2018.2854372
17. Blumenthal DJ, Heideman R, Geuzebroek D, Leinse A, Roeloffzen C. Silicon Nitride in Silicon Photonics. Proc IEEE (2018) 106:2209–31. doi:10.1109/jproc.2018.2861576
18. Rahim A, Spuesens T, Baets R, Bogaerts W. Open-access Silicon Photonics: Current Status and Emerging Initiatives. Proc IEEE (2018) 106:2313–30. doi:10.1109/jproc.2018.2878686
19. Li C, Liu D, Dai D. Multimode Silicon Photonics. Nanophotonics (2019) 8:227–47. doi:10.1515/nanoph-2018-0161
20. Wang H, Chai H, Lv Z, Zhang Z, Meng L, Yang X, et al. Silicon Photonic Transceivers for Application in Data Centers. J Semiconductors (2020) 41:101301. doi:10.1088/1674-4926/41/10/101301
21. Shekhar S. Silicon Photonics: A Brief Tutorial. IEEE Solid-State Circuits Mag (2021) 13:22–32. doi:10.1109/mssc.2021.3088966
22. Minkenberg C, Krishnaswamy R, Zilkie A, Nelson D. Co-packaged Datacenter Optics: Opportunities and Challenges. IET Optoelectronics (2021) 15:77–91. doi:10.1049/ote2.12020
23. Siew SY, Li B, Gao F, Zheng HY, Zhang W, Guo P, et al. Review of Silicon Photonics Technology and Platform Development. J Lightwave Technol (2021) 39:4374–4389. doi:10.1109/jlt.2021.3066203
24. Margalit N, Xiang C, Bowers SM, Bjorlin A, Blum R, Bowers JE. Perspective on the Future of Silicon Photonics and Electronics. Appl Phys Lett (2021) 118:220501. doi:10.1063/5.0050117
25. Daldosso N, Pavesi L. Nanosilicon Photonics. Laser Photon Rev (2009) 3:508–34. doi:10.1002/lpor.200810045
26. Bisi O, Ossicini S, Pavesi L. Porous Silicon: a Quantum Sponge Structure for Silicon Based Optoelectronics. Surf Sci Rep (2000) 38:1–126. doi:10.1016/s0167-5729(99)00012-6
27. Canham L. Introductory Lecture: Origins and Applications of Efficient Visible Photoluminescence from Silicon-Based Nanostructures. Faraday Discuss (2020) 222:10–81. doi:10.1039/d0fd00018c
28. Gelloz B, Juangsa FB, Nozaki T, Asaka K, Koshida N, Jin L. Si/sio2 Core/shell Luminescent Silicon Nanocrystals and Porous Silicon Powders with High Quantum Yield, Long Lifetime, and Good Stability. Front Phys (2019) 7:47. doi:10.3389/fphy.2019.00047
29. Valenta J, Greben M, Dyakov S, Gippius N, Hiller D, Gutsch S, et al. Nearly perfect near-infrared luminescence efficiency of si nanocrystals: A comprehensive quantum yield study employing the purcell effect. Scientific Rep (2019) 9:1–9. doi:10.1038/s41598-019-47825-x
30. Ghulinyan M, Pavesi L. Porous Multilayers as a Dielectric Host for Photons Manipulation. ECS Trans (2008) 16:307. doi:10.1149/1.2982570
31. Pavesi L, Ceschini M. Stretched-exponential Decay of the Luminescence in Porous Silicon. Phys Rev B (1993) 48:17625. doi:10.1103/physrevb.48.17625
32. Roman HE, Pavesi L. Monte Carlo Simulations of the Recombination Dynamics in Porous Silicon. J Phys Condensed Matter (1996) 8:5161. doi:10.1088/0953-8984/8/28/003
33. Pavesi L. Influence of Dispersive Exciton Motion on the Recombination Dynamics in Porous Silicon. J Appl Phys (1996) 80:216–25. doi:10.1063/1.362807
34. Sinelnikov R, Dasog M, Beamish J, Meldrum A, Veinot JG. Revisiting an Ongoing Debate: What Role Do Surface Groups Play in Silicon Nanocrystal Photoluminescence? ACS Photon (2017) 4:1920–9. doi:10.1021/acsphotonics.7b00102
35. Greben M, Valenta J. Power-dependent Photoluminescence Decay Kinetics of Silicon Nanocrystals under Continuous and Pulsed Excitation. Faraday Discuss (2020) 222:274–93. doi:10.1039/c9fd00100j
37. Pellegrini V, Tredicucci A, Mazzoleni C, Pavesi L. Enhanced Optical Properties in Porous Silicon Microcavities. Phys Rev B (1995) 52:R14328. doi:10.1103/physrevb.52.r14328
38. Ghulinyan M, Oton C, Bonetti G, Gaburro Z, Pavesi L. Free-standing Porous Silicon Single and Multiple Optical Cavities. J Appl Phys (2003) 93:9724–9. doi:10.1063/1.1578170
39. Galli M, Bajoni D, Marabelli F, Andreani L, Pavesi L, Pucker G. Photonic bands and group-velocity dispersion in si/sio 2 photonic crystals from white-light interferometry. Phys Rev B (2004) 69:115107. doi:10.1103/physrevb.69.115107
40. Ghulinyan M, Galli M, Toninelli C, Bertolotti J, Gottardo S, Marabelli F, et al. Wide-band Transmission of Nondistorted Slow Waves in One-Dimensional Optical Superlattices. Appl Phys Lett (2006) 88:241103. doi:10.1063/1.2209716
41. Ramirez-Gutierrez CF, Martinez-Hernandez HD, Lujan-Cabrera IA, Rodriguez-García ME. Design, Fabrication, and Optical Characterization of One-Dimensional Photonic Crystals Based on Porous Silicon Assisted by In-Situ Photoacoustics. Scientific Rep (2019) 9:1–15. doi:10.1038/s41598-019-51200-1
42. Sapienza R, Costantino P, Wiersma D, Ghulinyan M, Oton CJ, Pavesi L. Optical Analogue of Electronic Bloch Oscillations. Phys Rev Lett (2003) 91:263902. doi:10.1103/physrevlett.91.263902
43. Ghulinyan M, Oton CJ, Gaburro Z, Pavesi L, Toninelli C, Wiersma DS. Zener Tunneling of Light Waves in an Optical Superlattice. Phys Rev Lett (2005) 94:127401. doi:10.1103/physrevlett.94.127401
44. Ghulinyan M, Gaburro Z, Wiersma DS, Pavesi L. Tuning of Resonant Zener Tunneling by Vapor Diffusion and Condensation in Porous Optical Superlattices. Phys Rev B (2006) 74:045118. doi:10.1103/physrevb.74.045118
45. Barthelemy P, Ghulinyan M, Gaburro Z, Toninelli C, Pavesi L, Wiersma DS. Optical Switching by Capillary Condensation. Nat Photon (2007) 1:172–5. doi:10.1038/nphoton.2007.24
46. Masi L, Petrucciani T, Ferioli G, Semeghini G, Modugno G, Inguscio M, et al. Spatial Bloch Oscillations of a Quantum Gas in a” Beat-Note” Superlattice. Phys Rev Lett (2021) 127:020601. doi:10.1103/physrevlett.127.020601
47. Laurenson A, Bertolotti J, Kruglyak V. Bloch Oscillations of Backward Volume Magnetostatic Spin Waves. Phys Rev B (2020) 102:054416. doi:10.1103/physrevb.102.054416
48. Bahmani S, Askarpour AN. Bloch Oscillations and Wannier-Stark Ladder in the Coupled Lc Circuits. Phys Lett A (2020) 384:126596. doi:10.1016/j.physleta.2020.126596
49. Kim H, Shi X, Kim E, Yang J. Bloch Oscillation of Elastic Waves in the Graded Lattice of 3d-Printed Hollow Elliptical Cylinders. Appl Phys Lett (2019) 114:101905. doi:10.1063/1.5089508
50. Pagel Z, Zhong W, Parker RH, Olund CT, Yao NY, Müller H. Symmetric Bloch Oscillations of Matter Waves. Phys Rev A (2020) 102:053312. doi:10.1103/physreva.102.053312
51. Ghulinyan M, Pavesi L. Light Localisation and Lasing: Random and Pseudo-random Photonic Structures. Cambridge: Cambridge University Press (2015).
52. Dal Negro L, Oton CJ, Gaburro Z, Pavesi L, Johnson P, Lagendijk A, et al. Light Transport through the Band-Edge States of Fibonacci Quasicrystals. Phys Rev Lett (2003) 90:055501. doi:10.1103/PhysRevLett.90.055501
53. Bertolotti J, Gottardo S, Wiersma DS, Ghulinyan M, Pavesi L. Optical Necklace States in anderson Localized 1d Systems. Phys Rev Lett (2005) 94:113903. doi:10.1103/physrevlett.94.113903
54. Balasubrahmaniyam M, Mondal S, Mujumdar S. Necklace-state-mediated Anomalous Enhancement of Transport in anderson-localized Non-hermitian Hybrid Systems. Phys Rev Lett (2020) 124:123901. doi:10.1103/physrevlett.124.123901
55. Weidemann S, Kremer M, Longhi S, Szameit A. Coexistence of Dynamical Delocalization and Spectral Localization through Stochastic Dissipation. Nat Photon (15) 576–581. doi:10.1038/s41566-021-00823-w
56. Kwak Y, Park SM, Ku Z, Urbas A, Kim YL. A Pearl Spectrometer. Nano Lett (2020) 21:921–30. doi:10.1021/acs.nanolett.0c03618
57. Daldosso N, Luppi M, Ossicini S, Degoli E, Magri R, Dalba G, et al. Role of the Interface Region on the Optoelectronic Properties of Silicon Nanocrystals Embedded in Sio 2. Phys Rev B (2003) 68:085327. doi:10.1103/physrevb.68.085327
58. Liang J, Huang C, Gong X. Silicon Nanocrystals and Their Composites: Syntheses, Fluorescence Mechanisms, and Biological Applications. ACS Sustain Chem Eng (2019) 7:18213–27. doi:10.1021/acssuschemeng.9b04359
59. Milliken S, Thiessen AN, Cheong IT, O’Connor K, Li Z, Hooper RW, et al. “turning the Dials”: Controlling Synthesis, Structure, Composition, and Surface Chemistry to Tailor Silicon Nanoparticle Properties. Nanoscale (2021). doi:10.1039/d1nr04701a
60. Pavesi L. Silicon Light Emitters and Amplifiers: State of the Art. In: JA Kubby, and GT Reed, editors. Proc. of SPIE, San Jose, CA, 6125. International Society for Optics and Photonics (2006). p. 612508. Silicon Photonics.
61. Pavesi L, Dal Negro L, Mazzoleni C, Franzo G, Priolo F. Optical Gain in Silicon Nanocrystals. Nature (2000) 408:440–4. doi:10.1038/35044012
62. Dal Negro L, Bettotti P, Cazzanelli M, Pacifici D, Pavesi L. Applicability Conditions and Experimental Analysis of the Variable Stripe Length Method for Gain Measurements. Opt Commun (2004) 229:337–48. doi:10.1016/j.optcom.2003.10.051
63. Ruan J, Fauchet P, Dal Negro L, Cazzanelli M, Pavesi L. Stimulated Emission in Nanocrystalline Silicon Superlattices. Appl Phys Lett (2003) 83:5479–81. doi:10.1063/1.1637720
64. Dal Negro L, Cazzanelli M, Danese B, Pavesi L, Iacona F, Franzo G, et al. Light Amplification in Silicon Nanocrystals by Pump and Probe Transmission Measurements. J Appl Phys (2004) 96:5747–55. doi:10.1063/1.1803613
65. Dal Negro L, Cazzanelli M, Pavesi L, Ossicini S, Pacifici D, Franzò G, et al. Dynamics of Stimulated Emission in Silicon Nanocrystals. Appl Phys Lett (2003) 82:4636–8. doi:10.1063/1.1586779
66. Lian CW, Lin GR. Amplified Spontaneous Emission and Optical Gain Coefficient of Siox Based Planar Waveguide with Buried Silicon Nanocrystals on Silicon Substrate. In: Conference on Lasers and Electro-Optics, San Jose, CA, May 4-9, 2008. Optical Society of America (2008). p. CMK4.
67. Žídek K, Pelant I, Trojánek F, Malỳ P, Gilliot P, Hönerlage B, et al. Ultrafast Stimulated Emission Due to Quasidirect Transitions in Silicon Nanocrystals. Phys Rev B (2011) 84:085321. doi:10.1103/PhysRevB.84.085321
68. Monroy B, Crégut O, Gallart M, Hönerlage B, Gilliot P. Optical Gain Observation on Silicon Nanocrystals Embedded in Silicon Nitride under Femtosecond Pumping. Appl Phys Lett (2011) 98:261108. doi:10.1063/1.3607276
69. Zeng P, Wang F, Zhang Y, Zhou W, Guo Z, Wu X, et al. Edge-emitting Silicon Nanocrystal Distributed Feedback Laser with Extremely Low Exciton Threshold. ACS Photon (2021) 8:1353–63. doi:10.1021/acsphotonics.0c01846
70. Liu AY, Srinivasan S, Norman J, Gossard AC, Bowers JE. Quantum Dot Lasers for Silicon Photonics. Photon Res (2015) 3:B1–B9. doi:10.1364/prj.3.0000b1
71. Zhou Z, Yin B, Michel J. On-chip Light Sources for Silicon Photonics. Light: Sci Appl (2015) 4:e358. doi:10.1038/lsa.2015.131
72. Grillot F, Norman JC, Duan J, Zhang Z, Dong B, Huang H, et al. Physics and Applications of Quantum Dot Lasers for Silicon Photonics. Nanophotonics (2020) 9:1271–86. doi:10.1515/nanoph-2019-0570
73. Liu DS, Wu J, Xu H, Wang Z. Emerging Light-Emitting Materials for Photonic Integration. Adv Mater (2021) 33:2003733. doi:10.1002/adma.202003733
74. Liang D, Bowers JE. Recent Progress in Lasers on Silicon. Nat Photon (2010) 4:511–7. doi:10.1038/nphoton.2010.167
75. Tang M, Park JS, Wang Z, Chen S, Jurczak P, Seeds A, et al. Integration of iii-v lasers on si for si photonics. Prog Quan Electron (2019) 66:1–18. doi:10.1016/j.pquantelec.2019.05.002
76. Park SW, Kim MW, Park KT, Ku JH, No YS. On-chip Transferrable Microdisk Lasers. ACS Photon (2020) 7:3313–20. doi:10.1021/acsphotonics.0c01330
77. Otterstrom NT, Behunin RO, Kittlaus EA, Wang Z, Rakich PT. A Silicon Brillouin Laser. Science (2018) 360:1113–6. doi:10.1126/science.aar6113
78. Anopchenko A, Marconi A, Wang M, Pucker G, Bellutti P, Pavesi L. Graded-size si quantum dot ensembles for efficient light-emitting diodes. Appl Phys Lett (2011) 99:181108. doi:10.1063/1.3658625
79. Navarro-Urrios D, Jambois O, Lupi FF, Pellegrino P, Garrido B, Pitanti A, et al. Si Nanoclusters Coupled to Er3+ Ions in a Sio2 Matrix for Optical Amplifiers. Opt Mater (2011) 33:1086–90. doi:10.1016/j.optmat.2010.12.003
80. Anopchenko A, Marconi A, Sgrignuoli F, Cattoni L, Tengattini A, Pucker G, et al. Electroluminescent Devices Based on Nanosilicon Multilayer Structures. physica status solidi (a) (2013) 210:1525–31. doi:10.1002/pssa.201200957
81. Marconi A, Anopchenko A, Wang M, Pucker G, Bellutti P, Pavesi L. High Power Efficiency in Si-Nc/sio 2 Multilayer Light Emitting Devices by Bipolar Direct Tunneling. Appl Phys Lett (2009) 94:221110. doi:10.1063/1.3147164
82. Morozova S, Alikina M, Vinogradov A, Pagliaro M. Silicon Quantum Dots: Synthesis, Encapsulation, and Application in Light-Emitting Diodes. Front Chem (2020) 8:191. doi:10.3389/fchem.2020.00191
83. Cheng KY, Anthony R, Kortshagen UR, Holmes RJ. High-efficiency Silicon Nanocrystal Light-Emitting Devices. Nano Lett (2011) 11:1952–6. doi:10.1021/nl2001692
84. Zhang YC, Yu ZY, Xue XY, Wang FL, Li S, Dai XY, et al. High Brightness Silicon Nanocrystal white Light-Emitting Diode with Luminance of 2060 Cd/m 2. Opt Express (2021) 29:34126–34. doi:10.1364/oe.437737
85. Pitanti A, Navarro-Urrios D, Prtljaga N, Daldosso N, Gourbilleau F, Rizk R, et al. Energy Transfer Mechanism and Auger Effect in Er 3+ Coupled Silicon Nanoparticle Samples. J Appl Phys (2010) 108:053518. doi:10.1063/1.3476286
86. Daldosso N, Navarro-Urrios D, Melchiorri M, Pavesi L, Gourbilleau F, Carrada M, et al. Absorption cross section and signal enhancement in er-doped si nanocluster rib-loaded waveguides. Appl Phys Lett (2005) 86:261103. doi:10.1063/1.1957112
87. Navarro-Urrios D, Pitanti A, Daldosso N, Gourbilleau F, Rizk R, Garrido B, et al. Energy transfer between amorphous si nanoclusters and er 3+ ions in a sio 2 matrix. Phys Rev B (2009) 79:193312. doi:10.1103/physrevb.79.193312
88. Navarro-Urrios D, Daldosso N, Garcia C, Pellegrino P, Garrido B, Gourbilleau F, et al. Signal enhancement and limiting factors in waveguides containing si nanoclusters and er3+ ions. Jpn J Appl Phys (2007) 46:6626. doi:10.1143/jjap.46.6626
89. Navarro-Urrios D, Pitanti A, Daldosso N, Gourbilleau F, Rizk R, Pucker G, et al. Quantification of the Carrier Absorption Losses in Si-Nanocrystal Rich Rib Waveguides at 1.54 μ M. Appl Phys Lett (2008) 92:051101. doi:10.1063/1.2840181
90. Navarro-Urrios D, Ferrarese Lupi F, Prtljaga N, Pitanti A, Jambois O, Ramírez J, et al. Copropagating Pump and Probe Experiments on Si-Nc in Sio2 Rib Waveguides Doped with Er: The Optical Role of Non-emitting Ions. Appl Phys Lett (2011) 99:231114. doi:10.1063/1.3665950
91. Tengattini A, Gandolfi D, Prtljaga N, Anopchenko A, Ramírez J, Lupi FF, et al. Toward a 1.54μm Electrically Driven Erbium-Doped Silicon Slot Waveguide and Optical Amplifier. J Lightwave Technol (2012) 31:391–7. doi:10.1109/JLT.2012.2231050
92. Hong J, Wen H, He J, Liu J, Dan Y, Tomm JW, et al. Stimulated Emission at 1.54 μm from Erbium/oxygen-Doped Silicon-Based Light-Emitting Diodes. Photon Res (2021) 9:714–21. doi:10.1364/prj.417090
93. He M, Yang D, Li D. Electroluminescence from Metal–Oxide–Semiconductor Devices Based on Erbium Silicate Nanocrystals and Silicon Nanocrystals Co-embedded in Silicon Oxide Thin Films. J Mater Sci Mater Electron (2021) 32:20659–67. doi:10.1007/s10854-021-06579-x
94. Yuan Z, Pucker G, Marconi A, Sgrignuoli F, Anopchenko A, Jestin Y, et al. Silicon Nanocrystals as a Photoluminescence Down Shifter for Solar Cells. Solar Energ Mater Solar Cell (2011) 95:1224–7. doi:10.1016/j.solmat.2010.10.035
95. Sgrignuoli F, Ingenhoven P, Pucker G, Mihailetchi V, Froner E, Jestin Y, et al. Purcell Effect and Luminescent Downshifting in Silicon Nanocrystals Coated Back-Contact Solar Cells. Solar Energ Mater Solar Cell (2015) 132:267–74. doi:10.1016/j.solmat.2014.09.007
96. Yuan Z, Anopchenko A, Pavesi L. Innovative Quantum Effects in Silicon for Photovoltaic Applications. Advanced Silicon Materials for Photovoltaic Applications (2012). doi:10.1002/9781118312193.ch10
97. Hossain S, Anopchenko A, Prezioso S, Ferraioli L, Pavesi L, Pucker G, et al. Subband gap Photoresponse of Nanocrystalline Silicon in a Metal-Oxide-Semiconductor Device. J Appl Phys (2008) 104:074917. doi:10.1063/1.2999561
98. Sgrignuoli F, Paternoster G, Marconi A, Ingenhoven P, Anopchenko A, Pucker G, et al. Modeling of Silicon Nanocrystals Based Down-Shifter for Enhanced Silicon Solar Cell Performance. J Appl Phys (2012) 111:034303. doi:10.1063/1.3679140
99. Meng L, Wu XG, Ma S, Shi L, Zhang M, Wang L, et al. Improving the Efficiency of Silicon Solar Cells Using In Situ Fabricated Perovskite Quantum Dots as Luminescence Downshifting Materials. Nanophotonics (2020) 9:93–100. doi:10.1515/nanoph-2019-0320
100. Jia X, Puthen-Veettil B, Xia H, Yang TCJ, Lin Z, Zhang T, et al. All-silicon Tandem Solar Cells: Practical Limits for Energy Conversion and Possible Routes for Improvement. J Appl Phys (2016) 119:233102. doi:10.1063/1.4954003
101. Otsuka M, Kurokawa Y, Ding Y, Juangsa FB, Shibata S, Kato T, et al. Silicon Nanocrystal Hybrid Photovoltaic Devices for Indoor Light Energy Harvesting. RSC Adv (2020) 10:12611–8. doi:10.1039/d0ra00804d
102. Meinardi F, Ehrenberg S, Dhamo L, Carulli F, Mauri M, Bruni F, et al. Highly Efficient Luminescent Solar Concentrators Based on Earth-Abundant Indirect-Bandgap Silicon Quantum Dots. Nat Photon (2017) 11:177–85. doi:10.1038/nphoton.2017.5
103. Tsarev A. Overview of Integrated Optical Sensors Based on Silicon: Forecasts and Results of the Decade [invited Article]. Optoelectronics, Instrumentation Data Process (2020) 56:412–30. doi:10.3103/s8756699020040123
104. Mulloni V, Pavesi L. Porous Silicon Microcavities as Optical Chemical Sensors. Appl Phys Lett (2000) 76:2523–5. doi:10.1063/1.126396
105. Oton C, Pancheri L, Gaburro Z, Pavesi L, Baratto C, Faglia G, et al. Multiparametric Porous Silicon Gas Sensors with Improved Quality and Sensitivity. physica status solidi (a) (2003) 197:523–7. doi:10.1002/pssa.200306557
106. Pancheri L, Oton C, Gaburro Z, Soncini G, Pavesi L. Very Sensitive Porous Silicon No2 Sensor. Sens Act B: Chem (2003) 89:237–9. doi:10.1016/s0925-4005(02)00471-9
107. Oton CJ, Ghulinyan M, Gaburro Z, Bettotti P, Pavesi L, Pancheri L, et al. Scattering Rings as a Tool for Birefringence Measurements in Porous Silicon. J Appl Phys (2003) 94:6334–40. doi:10.1063/1.1611632
108. Álvarez J, Bettotti P, Suárez I, Kumar N, Hill D, Chirvony V, et al. Birefringent Porous Silicon Membranes for Optical Sensing. Opt Express (2011) 19:26106–16. doi:10.1364/oe.19.026106
109. Baratto C, Faglia G, Sberveglieri G, Gaburro Z, Pancheri L, Oton C, et al. Multiparametric Porous Silicon Sensors. Sensors (2002) 2:121–6. doi:10.3390/s20300121
110. Hänsel A, Heck MJ. Opportunities for Photonic Integrated Circuits in Optical Gas Sensors. J Phys Photon (2020) 2:012002. doi:10.1088/2515-7647/ab6742
111. Arshavsky-Graham S, Massad-Ivanir N, Segal E, Weiss S. Porous Silicon-Based Photonic Biosensors: Current Status and Emerging Applications. Anal Chem (2018) 91:441–67. doi:10.1021/acs.analchem.8b05028
112. De Stefano L. Porous Silicon Optical Biosensors: Still a Promise or a Failure? Sensors (2019) 19:4776. doi:10.3390/s19214776
113. Oton C, Gaburro Z, Ghulinyan M, Pancheri L, Bettotti P, Negro LD, et al. Scattering Rings in Optically Anisotropic Porous Silicon. Appl Phys Lett (2002) 81:4919–21. doi:10.1063/1.1531834
114. Hakshur K, Trajtenberg-Mills S, Ruschin S. Gas Sensing through Mixed Polarization in Birefringent Porous Silicon Thin Film. IEEE Sensors Lett (2019) 3:1–4. doi:10.1109/lsens.2019.2910162
115. Samusenko A, Gandolfi D, Pucker G, Chalyan T, Guider R, Ghulinyan M, et al. A Sion Microring Resonator-Based Platform for Biosensing at 850 Nm. J Lightwave Technol (2016) 34:969–77. doi:10.1109/jlt.2016.2516758
116. Chalyan T, Pasquardini L, Gandolfi D, Guider R, Samusenko A, Zanetti M, et al. Aptamer-and Fab’-Functionalized Microring Resonators for Aflatoxin M1 Detection. IEEE J Sel Top Quan Electron (2017) 23:350–7. doi:10.1109/jstqe.2016.2609100
117. Chalyan T, Guider R, Pasquardini L, Zanetti M, Falke F, Schreuder E, et al. Asymmetric Mach–Zehnder Interferometer Based Biosensors for Aflatoxin M1 Detection. Biosensors (2016) 6:1. doi:10.3390/bios6010001
118. Chalyan T, Potrich C, Schreuder E, Falke F, Pasquardini L, Pederzolli C, et al. Afm1 detection in milk by fab’functionalized si3n4 asymmetric mach–zehnder interferometric biosensors. Toxins (2019) 11:409. doi:10.3390/toxins11070409
119. Ramiro-Manzano F, Biasi S, Bernard M, Mancinelli M, Chalyan T, Turri F, et al. Microring Resonators and Silicon Photonics. MRS Adv (2016) 1:3281–93. doi:10.1557/adv.2016.393
120. Gandolfi D, Ramiro-Manzano F, Aparicio Rebollo FJ, Ghulinyan M, Pucker G, Pavesi L. Role of Edge Inclination in an Optical Microdisk Resonator for Label-free Sensing. Sensors (2015) 15:4796–809. doi:10.3390/s150304796
121. Nehra M, Lettieri M, Dilbaghi N, Kumar S, Marrazza G. Nano-biosensing Platforms for Detection of Cow’s Milk Allergens: An Overview. Sensors (2020) 20:32. doi:10.3390/s20010032
122. Di Giovanni S, Zambrini V, Varriale A, D’Auria S. Sweet Sensor for the Detection of Aflatoxin M1 in Whole Milk. ACS omega (2019) 4:12803–7. doi:10.1021/acsomega.9b01300
123. Luan E, Shoman H, Ratner DM, Cheung KC, Chrostowski L. Silicon Photonic Biosensors Using Label-free Detection. Sensors (2018) 18:3519. doi:10.3390/s18103519
124. Steglich P, Hülsemann M, Dietzel B, Mai A. Optical Biosensors Based on Silicon-On-Insulator Ring Resonators: A Review. Molecules (2019) 24:519. doi:10.3390/molecules24030519
125. Gauglitz G. Critical Assessment of Relevant Methods in the Field of Biosensors with Direct Optical Detection Based on Fibers and Waveguides Using Plasmonic, Resonance, and Interference Effects. Anal Bioanal Chem (2020) 412:3317–49. doi:10.1007/s00216-020-02581-0
126. Leuermann J, Fernández-Gavela A, Torres-Cubillo A, Postigo S, Sánchez-Postigo A, Lechuga LM, et al. Optimizing the Limit of Detection of Waveguide-Based Interferometric Biosensor Devices. Sensors (2019) 19:3671. doi:10.3390/s19173671
127. Ma X, Wu J, Jiang L, Wang M, Deng G, Qu S, et al. On-chip Integration of a Metal–Organic Framework Nanomaterial on a Sio 2 Waveguide for Sensitive Voc Sensing. Lab A Chip (2021) 21:3298–306. doi:10.1039/d1lc00503k
128. Miller SE. Integrated Optics: An Introduction. Bell Syst Tech J (1969) 48:2059–69. doi:10.1002/j.1538-7305.1969.tb01165.x
129. Ghulinyan M, Pitanti A, Pucker G, Pavesi L. Whispering-gallery Mode Micro-kylix Resonators. Opt Express (2009) 17:9434–41. doi:10.1364/oe.17.009434
130. Biasi S, Guillemé P, Volpini A, Fontana G, Pavesi L. Time Response of a Microring Resonator to a Rectangular Pulse in Different Coupling Regimes. J Lightwave Technol (2019) 37:5091–9. doi:10.1109/jlt.2019.2928640
131. Ghulinyan M, Ramiro-Manzano F, Prtljaga N, Guider R, Carusotto I, Pitanti A, et al. Oscillatory Vertical Coupling between a Whispering-Gallery Resonator and a Bus Waveguide. Phys Rev Lett (2013) 110:163901. doi:10.1103/physrevlett.110.163901
132. Pitanti A, Ghulinyan M, Navarro-Urrios D, Pucker G, Pavesi L. Probing the Spontaneous Emission Dynamics in Si-Nanocrystals-Based Microdisk Resonators. Phys Rev Lett (2010) 104:103901. doi:10.1103/physrevlett.104.103901
133. Ghulinyan M, Navarro-Urrios D, Pitanti A, Lui A, Pucker G, Pavesi L. Whispering-gallery Modes and Light Emission from a Si-Nanocrystal-Based Single Microdisk Resonator. Opt express (2008) 16:13218–24. doi:10.1364/oe.16.013218
134. Ramiro-Manzano F, Prtljaga N, Pavesi L, Pucker G, Ghulinyan M. A Fully Integrated High-Q Whispering-Gallery Wedge Resonator. Opt express (2012) 20:22934–42. doi:10.1364/oe.20.022934
135. Pfeiffer MH, Liu J, Geiselmann M, Kippenberg TJ. Coupling Ideality of Integrated Planar High-Q Microresonators. Phys Rev Appl (2017) 7:024026. doi:10.1103/physrevapplied.7.024026
136. Biasi S, Ramiro-Manzano F, Turri F, Larre PE, Ghulinyan M, Carusotto I, et al. Hermitian and Non-hermitian Mode Coupling in a Microdisk Resonator Due to Stochastic Surface Roughness Scattering. IEEE Photon J (2019) 11:6101114. doi:10.1109/jphot.2018.2880281
137. Ghulinyan M, Manzano FR, Prtljaga N, Bernard M, Pavesi L, Pucker G, et al. Intermode Reactive Coupling Induced by Waveguide-Resonator Interaction. Phys Rev A (2014) 90:053811. doi:10.1103/physreva.90.053811
138. Mancinelli M, Bettotti P, Fedeli J, Pavesi L. Reconfigurable Optical Routers Based on Coupled Resonator Induced Transparency Resonances. Opt express (2012) 20:23856–64. doi:10.1364/oe.20.023856
139. de las Heras AM, Franchi R, Biasi S, Ghulinyan M, Pavesi L, Carusotto I. Nonlinearity-induced Reciprocity Breaking in a Single Nonmagnetic Taiji Resonator. Phys Rev Appl (2021) 15:054044. doi:10.1103/physrevapplied.15.054044
140. Franchi R, Biasi S, Heras AM, Ghulinyan M, Carusotto I, Pavesi L. Influence of the Bus Waveguide on the Linear and Nonlinear Response of a Taiji Microresonator. Opt Express (2021) 29:29615–30. doi:10.1364/oe.434239
141. Mancinelli M, Bettotti P, Fedeli JM, Pavesi L. Interferometric Switching in Coupled Resonator Optical Waveguides-Based Reconfigurable Optical Device. Opt Lett (2013) 38:217–9. doi:10.1364/ol.38.000217
142. Bernard M, Manzano FR, Pavesi L, Pucker G, Carusotto I, Ghulinyan M. Complete Crossing of Fano Resonances in an Optical Microcavity via Nonlinear Tuning. Photon Res (2017) 5:168–75. doi:10.1364/prj.5.000168
143. Hafezi M, Mittal S, Fan J, Migdall A, Taylor J. Imaging Topological Edge States in Silicon Photonics. Nat Photon (2013) 7:1001–5. doi:10.1038/nphoton.2013.274
144. Midya B, Zhao H, Feng L. Non-Hermitian Photonics Promises Exceptional Topology of Light. Nat Commun (2018) 9:1–4. doi:10.1038/s41467-018-05175-8
145. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. Topological Photonics. Rev Mod Phys (2019) 91:015006. doi:10.1103/revmodphys.91.015006
146. Wang C, Sweeney WR, Stone AD, Yang L. Coherent Perfect Absorption at an Exceptional point. Science (2021) 373:1261–5. doi:10.1126/science.abj1028
147. Chang L, Jiang X, Hua S, Yang C, Wen J, Jiang L, et al. Parity–time Symmetry and Variable Optical Isolation in Active–Passive-Coupled Microresonators. Nat Photon (2014) 8:524–9. doi:10.1038/nphoton.2014.133
148. Peng B, Özdemir ŞK, Lei F, Monifi F, Gianfreda M, Long GL, et al. Parity–Time-symmetric Whispering-Gallery Microcavities. Nat Phys (2014) 10:394–8. doi:10.1038/nphys2927
149. Calabrese A, Ramiro-Manzano F, Price H, Biasi S, Bernard M, Ghulinyan M, et al. Unidirectional Reflection from an Integrated “Taiji” Microresonator. Photon Res (2020) 8:1333–41. doi:10.1364/prj.393070
150. Borghi M, Castellan C, Signorini S, Trenti A, Pavesi L. Nonlinear Silicon Photonics. J Opt (2017) 19:093002. doi:10.1088/2040-8986/aa7a6d
151. de las Heras AM, Carusotto I. Unidirectional Lasing in Nonlinear Taiji Microring Resonators. Phys Rev A (2021) 104:043501. doi:10.1103/physreva.104.043501
152. Harari G, Bandres MA, Lumer Y, Rechtsman MC, Chong YD, Khajavikhan M, et al. Topological Insulator Laser: Theory. Science (2018) 359: eaar4003. doi:10.1126/science.aar4003
153. Bandres MA, Wittek S, Harari G, Parto M, Ren J, Segev M, et al. Topological Insulator Laser: Experiments. Science (2018) 359: eaar4005. doi:10.1126/science.aar4005
154. Ota Y, Takata K, Ozawa T, Amo A, Jia Z, Kante B, et al. Active Topological Photonics. Nanophotonics (2020) 9:547–67. doi:10.1515/nanoph-2019-0376
155. Liu YG, Hemmatyar O, Hassan AU, Jung PS, Choi JH, Christodoulides DN, et al. Engineering Interaction Dynamics in Active Resonant Photonic Structures. APL Photon (2021) 6:050804. doi:10.1063/5.0045228
156. Mancinelli M, Guider R, Masi M, Bettotti P, Vanacharla MR, Fedeli JM, et al. Optical Characterization of a Scissor Device. Opt Express (2011) 19:13664–74. doi:10.1364/oe.19.013664
157. Mancinelli M, Guider R, Bettotti P, Masi M, Vanacharla MR, Pavesi L. Coupled-resonator-induced-transparency Concept for Wavelength Routing Applications. Opt express (2011) 19:12227–40. doi:10.1364/oe.19.012227
158. Bettotti P, Mancinelli M, Guider R, Masi M, Vanacharla MR, Pavesi L. Robust Design of an Optical Router Based on a Tapered Side-Coupled Integrated Spaced Sequence of Optical Resonators. Opt Lett (2011) 36:1473–5. doi:10.1364/ol.36.001473
159. Testa F, Tondini S, Gambini F, Velha P, Bianchi A, Kopp C, et al. Integrated Reconfigurable Silicon Photonics Switch Matrix in Iris Project: Technological Achievements and Experimental Results. J Lightwave Technol (2018) 37:345–55.
160. Testa F, Oton CJ, Kopp C, Lee JM, Ortuno R, Enne R, et al. Design and Implementation of an Integrated Reconfigurable Silicon Photonics Switch Matrix in Iris Project. IEEE J Sel Top Quan Electron (2016) 22:155–68. doi:10.1109/jstqe.2016.2547322
161. Tondini S, Castellan C, Mancinelli M, Kopp C, Pavesi L. Methods for Low Crosstalk and Wavelength Tunability in Arrayed-Waveguide Grating for On-Silicon Optical Network. J Lightwave Technol (2017) 35:5134–41. doi:10.1109/jlt.2017.2768161
162. Zečević N, Hofbauer M, Goll B, Zimmermann H, Tondini S, Chalyan A, et al. A 3d Photonic-Electronic Integrated Transponder Aggregator with 48×16 Heater Control Cells. IEEE Photon Technol Lett (2018) 30:681–4. doi:10.1109/lpt.2018.2811464
163. Gu L, Fang H, Li J, Fang L, Chua SJ, Zhao J, et al. A Compact Structure for Realizing Lorentzian, Fano, and Electromagnetically Induced Transparency Resonance Lineshapes in a Microring Resonator. Nanophotonics (2019) 8:841–8. doi:10.1515/nanoph-2018-0229
164. Naweed A. Evolution of All-Optical Electromagnetically Induced Absorption and Induced Transparency in Triple-Microcavity-Based One-Dimensional Photonic Crystals. OSA Continuum (2021) 4:1358–71. doi:10.1364/osac.423150
165. Jang JK, Klenner A, Ji X, Okawachi Y, Lipson M, Gaeta AL. Synchronization of Coupled Optical Microresonators. Nat Photon (2018) 12:688–93. doi:10.1038/s41566-018-0261-x
166. Chang TH, Zhou X, Zhu M, Fields BM, Hung CL. Efficiently Coupled Microring Circuit for On-Chip Cavity Qed with Trapped Atoms. Appl Phys Lett (2020) 117:174001. doi:10.1063/5.0023464
167. Castellan C, Tondini S, Mancinelli M, Kopp C, Pavesi L. Reflectance Reduction in a Whiskered Soi star Coupler. IEEE Photon Technol Lett (2016) 28:1870–3. doi:10.1109/lpt.2016.2574364
168. Tondini S, Castellan C, Medina MA, Pavesi L. Automatic Initialization Methods for Photonic Components on a Silicon-Based Optical Switch. Appl Sci (2019) 9:1843. doi:10.3390/app9091843
169. Ikeda K, Suzuki K, Konoike R, Namiki S, Kawashima H. Large-scale Silicon Photonics Switch Based on 45-nm Cmos Technology. Opt Commun (2020) 466:125677. doi:10.1016/j.optcom.2020.125677
170. Goki PN, Imran M, Fresi F, Cavaliere F, Potì L. Lossless Roadm by Exploiting Low Gain Soas in Fronthaul Network. In: 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan. IEEE (2019). p. 1–3. doi:10.23919/ps.2019.8817763
171. Xie Y, Shi Y, Liu L, Wang J, Priti R, Zhang G, et al. Thermally-reconfigurable Silicon Photonic Devices and Circuits. IEEE J Sel Top Quan Electron (2020) 26:1–20. doi:10.1109/jstqe.2020.3002758
172. Mancinelli M, Borghi M, Ramiro-Manzano F, Fedeli J, Pavesi L. Chaotic Dynamics in Coupled Resonator Sequences. Opt express (2014) 22:14505–16. doi:10.1364/oe.22.014505
173. Borghi M, Biasi S, Pavesi L. Reservoir Computing Based on a Silicon Microring and Time Multiplexing for Binary and Analog Operations. Sci Rep (2021) 11:15642. doi:10.1038/s41598-021-94952-5
174. Mancinelli M, Bazzanella D, Bettotti P, Pavesi L. A Photonic Complex Perceptron for Ultrafast Data Processing (2021). arXiv preprint arXiv:2106.11050.
175. Borghi M, Bazzanella D, Mancinelli M, Pavesi L. On the Modeling of thermal and Free Carrier Nonlinearities in Silicon-On-Insulator Microring Resonators. Opt Express (2021) 29:4363–77. doi:10.1364/oe.413572
176. Chen HJ, Ji QX, Wang H, Yang QF, Cao QT, Gong Q, et al. Chaos-assisted Two-Octave-Spanning Microcombs. Nat Commun (2020) 11:1–6. doi:10.1038/s41467-020-15914-5
177. Bittner S, Guazzotti S, Zeng Y, Hu X, Yılmaz H, Kim K, et al. Suppressing Spatiotemporal Lasing Instabilities with Wave-Chaotic Microcavities. Science (2018) 361:1225–31. doi:10.1126/science.aas9437
178. Kitayama K, Notomi M, Naruse M, Inoue K, Kawakami S, Uchida A. Novel Frontier of Photonics for Data Processing—Photonic Accelerator. APL Photon (2019) 4:090901. doi:10.1063/1.5108912
179. Miscuglio M, Sorger VJ. Photonic Tensor Cores for Machine Learning. Appl Phys Rev (2020) 7:031404. doi:10.1063/5.0001942
180. Marković D, Mizrahi A, Querlioz D, Grollier J. Physics for Neuromorphic Computing. Nat Rev Phys (2020) 2:499–510. doi:10.1038/s42254-020-0208-2
181. Sunny FP, Taheri E, Nikdast M, Pasricha S. A Survey on Silicon Photonics for Deep Learning. J Emerg Technol Comput Syst (2021) 17:61. doi:10.1145/3459009
182. Brunner D, Psaltis D. Competitive Photonic Neural Networks. Nat Photon (2021) 15:323–4. doi:10.1038/s41566-021-00803-0
183. Shastri BJ, Tait AN, de Lima TF, Pernice WH, Bhaskaran H, Wright CD, et al. Photonics for Artificial Intelligence and Neuromorphic Computing. Nat Photon (2021) 15:102–14. doi:10.1038/s41566-020-00754-y
184. Xu X, Tan M, Corcoran B, Wu J, Boes A, Nguyen TG, et al. 11 Tops Photonic Convolutional Accelerator for Optical Neural Networks. Nature (2021) 589:44–51. doi:10.1038/s41586-020-03063-0
185. Feldmann J, Youngblood N, Karpov M, Gehring H, Li X, Stappers M, et al. Parallel Convolutional Processing Using an Integrated Photonic Tensor Core. Nature (2021) 589:52–8. doi:10.1038/s41586-020-03070-1
186. Martínez A, Blasco J, Sanchis P, Galán JV, García-Rupérez J, Jordana E, et al. Ultrafast All-Optical Switching in a Silicon-Nanocrystal-Based Silicon Slot Waveguide at Telecom Wavelengths. Nano Lett (2010) 10:1506–11. doi:10.1021/nl9041017
187. Cazzanelli M, Bianco F, Borga E, Pucker G, Ghulinyan M, Degoli E, et al. Second-harmonic Generation in Silicon Waveguides Strained by Silicon Nitride. Nat Mater (2012) 11:148–54. doi:10.1038/nmat3200
188. Signorini S, Mancinelli M, Borghi M, Bernard M, Ghulinyan M, Pucker G, et al. Intermodal Four-Wave Mixing in Silicon Waveguides. Photon Res (2018) 6:805–14. doi:10.1364/prj.6.000805
189. Castellan C, Trenti A, Vecchi C, Marchesini A, Mancinelli M, Ghulinyan M, et al. On the Origin of Second Harmonic Generation in Silicon Waveguides with Silicon Nitride Cladding. Sci Rep (2019) 9:1–12. doi:10.1038/s41598-018-37660-x
190. Signorini S, Finazzer M, Bernard M, Ghulinyan M, Pucker G, Pavesi L. Silicon Photonics Chip for Inter-Modal Four Wave Mixing on a Broad Wavelength Range. Front Phys (2019) 7:128. doi:10.3389/fphy.2019.00128
191. Ramiro-Manzano F, Prtljaga N, Pavesi L, Pucker G, Ghulinyan M. Thermo-Optical bistability with si nanocrystals in a whispering gallery mode resonator. Opt Lett (2013) 38:3562–5. doi:10.1364/ol.38.003562
192. Franchi R, Castellan C, Ghulinyan M, Pavesi L. Second-Harmonic Generation in Periodically Poled Silicon Waveguides with Lateral Pin Junctions. Opt Lett (2020) 45:3188–91. doi:10.1364/ol.391988
193. Borghi M, Trenti A, Pavesi L. Four Wave Mixing Control in a Photonic Molecule Made by Silicon Microring Resonators. Sci Rep (2019) 9:1–14. doi:10.1038/s41598-018-36694-5
194. Spano R, Daldosso N, Cazzanelli M, Ferraioli L, Tartara L, Yu J, et al. Bound Electronic and Free Carrier Nonlinearities in Silicon Nanocrystals at 1550nm. Opt express (2009) 17:3941–50. doi:10.1364/oe.17.003941
195. Lacava C, Strain M, Minzioni P, Cristiani I, Sorel M. Integrated Nonlinear Mach Zehnder for 40 Gbit/s All-Optical Switching. Opt express (2013) 21:21587–95. doi:10.1364/oe.21.021587
196. Bianco F, Fedus K, Enrichi F, Pierobon R, Cazzanelli M, Ghulinyan M, et al. Two-dimensional Micro-raman Mapping of Stress and Strain Distributions in Strained Silicon Waveguides. Semicond Sci Technol (2012) 27:085009. doi:10.1088/0268-1242/27/8/085009
197. Schriever C, Bianco F, Cazzanelli M, Ghulinyan M, Eisenschmidt C, de Boor J, et al. Second-order Optical Nonlinearity in Silicon Waveguides: Inhomogeneous Stress and Interfaces. Adv Opt Mater (2015) 3:129–36. doi:10.1002/adom.201400370
198. Borghi M, Mancinelli M, Merget F, Witzens J, Bernard M, Ghulinyan M, et al. High-frequency Electro-Optic Measurement of Strained Silicon Racetrack Resonators. Opt Lett (2015) 40:5287–90. doi:10.1364/ol.40.005287
199. Timurdogan E, Poulton CV, Byrd M, Watts M. Electric Field-Induced Second-Order Nonlinear Optical Effects in Silicon Waveguides. Nat Photon (2017) 11:200–6. doi:10.1038/nphoton.2017.14
200. Janjan B, Ahmadi V, Fathi D. Low-voltage Electrically-Induced Second Harmonic Generation in a Silicon Waveguide Based on Modal Phase Matching. J Lightwave Technol (2020) 38:6272–9. doi:10.1109/jlt.2020.3010624
201. Singh N, Raval M, Ruocco A, Watts MR. Broadband 200-nm Second-Harmonic Generation in Silicon in the Telecom Band. Light: Sci Appl (2020) 9:1–7. doi:10.1038/s41377-020-0254-7
202. Signorini S, Pavesi L. On-chip Heralded Single Photon Sources. AVS Quan Sci (2020) 2:041701. doi:10.1116/5.0018594
203. Perret S, Fanjoux G, Bigot L, Fatome J, Millot G, Dudley JM, et al. Supercontinuum Generation by Intermodal Four-Wave Mixing in a Step-index Few-Mode Fibre. Apl Photon (2018) 4:022905. doi:10.1063/1.5045645
204. Zhang J, Alonso-Ramos C, Vivien L, He S, Cassan E. Self-adaptive Waveguide Boundary for Inter-mode Four-Wave Mixing. IEEE J Sel Top Quan Electron (2019) 26:1–8. doi:10.1109/JSTQE.2019.2929700
205. Franz Y, Haines J, Lacava C, Guasoni M. Strategies for Wideband Light Generation in Nonlinear Multimode Integrated Waveguides. Phys Rev A (2021) 103:013511. doi:10.1103/physreva.103.013511
206. Kang Z, Mei C, Zhang L, Zhang Z, Evans J, Cheng Y, et al. Advanced Progress on X (3) Nonlinearity in Chip-Scale Photonic Platforms (Invited Review). Prog Electromagn. Res (2021) 170:17–62. doi:10.2528/pier20122108
207. Qian B, Chen K, Chen S, Li W, Zhang X, Xu J, et al. On-chip Silicon-Based Active Photonic Molecules by Complete Photonic Bandgap Light Confinement. Appl Phys Lett (2011) 99:034105. doi:10.1063/1.3614548
208. Liao K, Hu X, Gan T, Liu Q, Wu Z, Fan C, et al. Photonic Molecule Quantum Optics. Adv Opt Photon (2020) 12:60–134. doi:10.1364/aop.376739
209. Acerbi F, Massari N, Gasparini L, Tomasi A, Zorzi N, Fontana G, et al. Structures and Methods for Fully-Integrated Quantum Random Number Generators. IEEE J Sel Top Quan Electron (2020) 26:1–8. doi:10.1109/jstqe.2020.2990216
210. Bisadi Z, Fontana G, Moser E, Pucker G, Pavesi L. Robust Quantum Random Number Generation with Silicon Nanocrystals Light Source. J Lightwave Technol (2017) 35:1588–94. doi:10.1109/jlt.2017.2656866
211. Leone N, Azzini S, Mazzucchi S, Moretti V, Pavesi L. Certified Quantum Random Number Generator Based on Single-Photon Entanglement. arXiv preprint arXiv:2104.04452 (2021).
212. Leone N, Rusca D, Azzini S, Fontana G, Acerbi F, Gola A, et al. An Optical Chip for Self-Testing Quantum Random Number Generation. APL Photon (2020) 5:101301. doi:10.1063/5.0022526
213. Pasini M, Leone N, Mazzucchi S, Moretti V, Pastorello D, Pavesi L. Bell-inequality Violation by Entangled Single-Photon States Generated from a Laser, an Led, or a Halogen Lamp. Phys Rev A (2020) 102:063708. doi:10.1103/physreva.102.063708
214. Ma X, Yuan X, Cao Z, Qi B, Zhang Z. Quantum Random Number Generation. npj Quan Inf (2016) 2:1–9. doi:10.1038/npjqi.2016.21
215. Herrero-Collantes M, Garcia-Escartin JC. Quantum Random Number Generators. Rev Mod Phys (2017) 89:015004. doi:10.1103/revmodphys.89.015004
217. Bai B, Huang J, Qiao GR, Nie YQ, Tang W, Chu T, et al. 18.8 Gbps Real-Time Quantum Random Number Generator with a Photonic Integrated Chip. Appl Phys Lett (2021) 118:264001. doi:10.1063/5.0056027
218. Bisadi Z, Meneghetti A, Tomasi A, Tengattini A, Fontana G, Pucker G, et al. Generation of High Quality Random Numbers via an All-Silicon-Based Approach. phys status solidi (a) (2016) 213:3186–93. doi:10.1002/pssa.201600298
219. Bisadi Z, Acerbi F, Fontana G, Zorzi N, Piemonte C, Pucker G, et al. Compact Quantum Random Number Generator with Silicon Nanocrystals Light Emitting Device Coupled to a Silicon Photomultiplier. Front Phys (2018) 6:9. doi:10.3389/fphy.2018.00009
220. Acerbi F, Bisadi Z, Fontana G, Zorzi N, Piemonte C, Pavesi L. A Robust Quantum Random Number Generator Based on an Integrated Emitter-Photodetector Structure. IEEE J Sel Top Quan Electron (2018) 24:1–7. doi:10.1109/jstqe.2018.2814787
221. Azzini S, Mazzucchi S, Moretti V, Pastorello D, Pavesi L. Single-particle Entanglement. Adv Quan Tech (2020) 3:2000014. doi:10.1002/qute.202000014
222. Mazzucchi S, Leone N, Azzini S, Pavesi L, Moretti V. Entropy Certification of a Realistic Quantum Random-Number Generator Based on Single-Particle Entanglement. Phys Rev A (2021) 104:022416. doi:10.1103/physreva.104.022416
223. Adhikari S, Home D, Majumdar AS, Pan AK, Shenoy A, Srikanth R. Toward Secure Communication Using Intra-particle Entanglement. Quan Inf Process (2015) 14:1451–68. doi:10.1007/s11128-015-0941-0
224. Li W, Wang L, Zhao S. Phase Matching Quantum Key Distribution Based on Single-Photon Entanglement. Scientific Rep (2019) 9:1–12. doi:10.1038/s41598-019-51848-9
225. Jino H, Chang-Ho H, Jong-In L, Hyung-Jin Y. Bidirectional Quantum Teleportation of Unknown Photons Using Path-Polarization Intra-particle Hybrid Entanglement and Controlled-Unitary gates via Cross-Kerr Nonlinearity. Chin Phys B (2015) 24:050304. doi:10.1088/1674-1056/24/5/050304
226. Adhikari S, Majumdar A, Home D, Pan A. Swapping Path-Spin Intraparticle Entanglement onto Spin-Spin Interparticle Entanglement. EPL (Europhys Lett) (2010) 89:10005. doi:10.1209/0295-5075/89/10005
227. Cheng LY, Shao XQ, Zhang S. Entanglement Concentration Using a Path–Spin Hybrid-Entangled State. Phys Scripta (2011) 83:025004. doi:10.1088/0031-8949/83/02/025004
228. Guerreiro T, Monteiro F, Martin A, Brask J, Vértesi T, Korzh B, et al. Demonstration of Einstein-Podolsky-Rosen Steering Using Single-Photon Path Entanglement and Displacement-Based Detection. Phys Rev Lett (2016) 117:070404. doi:10.1103/PhysRevLett.117.070404
229. Aguilar LA. Nonlocal Single Particle Steering Generated through Single Particle Entanglement. Sci Rep (2021) 11:1–11. doi:10.1038/s41598-021-85508-8
230. Signorini S, Sanna M, Piccione S, Ghulinyan M, Tidemand-Lichtenberg P, Pedersen C, et al. A Silicon Source of Heralded Single Photons at 2μ M (2021). arXiv preprint arXiv:2108.01031.
231. Mancinelli M, Trenti A, Piccione S, Fontana G, Dam JS, Tidemand-Lichtenberg P, et al. Mid-infrared Coincidence Measurements on Twin Photons at Room Temperature. Nat Commun (2017) 8:1–8. doi:10.1038/ncomms15184
232. Paesani S, Borghi M, Signorini S, Maïnos A, Pavesi L, Laing A. Near-ideal Spontaneous Photon Sources in Silicon Quantum Photonics. Nat Commun (2020) 11:1–6. doi:10.1364/fio.2020.fm4a.1
233. Gilaberte Basset M, Setzpfandt F, Steinlechner F, Beckert E, Pertsch T, Gräfe M. Perspectives for Applications of Quantum Imaging. Laser Photon Rev (2019) 13:1900097. doi:10.1002/lpor.201900097
234. Degen CL, Reinhard F, Cappellaro P. Quantum Sensing. Rev Mod Phys (2017) 89:035002. doi:10.1103/revmodphys.89.035002
235. Sidhu JS, Joshi SK, Gundogan M, Brougham T, Lowndes D, Mazzarella L, et al. Advances in Space Quantum Communications. IET Quantum Commun (2021). doi:10.1049/qtc2.12015
236. Rosenfeld LM, Sulway DA, Sinclair GF, Anant V, Thompson MG, Rarity JG, et al. Mid-infrared Quantum Optics in Silicon. Opt Express (2020) 28:37092–102. doi:10.1364/oe.386615
237. Prabhakar S, Shields T, Dada AC, Ebrahim M, Taylor GG, Morozov D, et al. Two-photon Quantum Interference and Entanglement at 2.1 μm. Sci Adv (2020) 6:eaay5195. doi:10.1126/sciadv.aay5195
238. Verma V, Korzh B, Walter A, Lita A, Briggs R, Colangelo M, et al. Single-photon Detection in the Mid-infrared up to 10 μ M Wavelength Using Tungsten Silicide Superconducting Nanowire Detectors. APL Photon (2021) 6:056101. doi:10.1063/5.0048049
239. Moody G, Chang L, Steiner TJ, Bowers JE. Chip-scale Nonlinear Photonics for Quantum Light Generation. AVS Quan Sci (2020) 2:041702. doi:10.1116/5.0020684
240. Adcock JC, Bao J, Chi Y, Chen X, Bacco D, Gong Q, et al. Advances in Silicon Quantum Photonics. IEEE J Sel Top Quan Electron (2020) 27:1–24. doi:10.1109/JSTQE.2020.3025737
241. Vigliar C, Paesani S, Ding Y, Adcock JC, Wang J, Morley-Short S, et al. Error-protected Qubits in a Silicon Photonic Chip. Nat Phys (2021) 1–7. doi:10.1038/s41567-021-01333-w
242. Wang Q, Zheng Y, Zhai C, Li X, Gong Q, Wang J. Chip-based Quantum Communications. J Semiconductors (2021) 42:091901. doi:10.1088/1674-4926/42/9/091901
243. Wang Y, Jöns KD, Sun Z. Integrated Photon-Pair Sources with Nonlinear Optics. Appl Phys Rev (2021) 8:011314. doi:10.1063/5.0030258
244. Kennedy P. Hands-on with the Intel Co-packaged Optics and Silicon Photonics Switch (2020). Available at: https://www.servethehome.com/hands-on-with-the-intel-co-packaged-optics-and-silicon-photonics-switch/ [Dataset].
245.Intel. Intel Demonstrates Industry-First Co-packaged Optics Ethernet Switch (2020). Available at: https://newsroom.intel.com/news/intel-demonstrates-industry-first-co-packaged-optics-ethernet-switch/#gs.byzc4j [Dataset].
246.Businesswire. Rockley Photonics Unveils End-To-End Digital Health Monitoring Solution Based on Spectrophotometer-On-A-Chip Sensing Module (2021). Available at: https://rockleyphotonics.com/rockley-unveils-end-to-end-digital-health-monitoring-solution [Dataset].
247.Genalyte. Genalyte Announces Oversubscribed 50 Million Financing Round to Expand Testing Menu and Deploy Platform (2021). Available at: https://www.genalyte.com/2021/01/11/genalyte-announces-oversubscribed-50-million-financing-round-to-expand-testing-menu-and-deploy-platform/ [Dataset].
248. Connors J. KVH Introduces P-Series Imus with Pic Technology and New Accelerometers (2021). Available at: https://www.kvh.com/press-room/press-releases/2021/210427-kvh-introduces-p-series-imus-with-pic-technology-and-new-accelerometers [Dataset].
249. Chung S, Nakai M, Idres S, Ni Y, Hashemi H. 19.1 Optical Phased-Array Fmcw Lidar with On-Chip Calibration. In: 2021 IEEE International Solid-State Circuits Conference (ISSCC), 64. IEEE (2021). p. 286–8.
250. Tezak N, Van Vaerenbergh T, Pelc JS, Mendoza GJ, Kielpinski D, Mabuchi H, et al. Integrated Coherent Ising Machines Based on Self-phase Modulation in Microring Resonators. IEEE J Sel Top Quan Electron (2019) 26:1–15.
251. Arrazola J, Bergholm V, Brádler K, Bromley T, Collins M, Dhand I, et al. Quantum Circuits with many Photons on a Programmable Nanophotonic Chip. Nature (2021) 591:54–60. doi:10.1038/s41586-021-03202-1
253. Bogaerts W, Pérez D, Capmany J, Miller DA, Poon J, Englund D, et al. Programmable Photonic Circuits. Nature (2020) 586:207–16. doi:10.1038/s41586-020-2764-0
Keywords: silicon, porous silicon, silicon nanocrystals, nonlinear optics, neuromorphic photonics, microresonators, quantum photonics, silicon photonics
Citation: Pavesi L (2021) Thirty Years in Silicon Photonics: A Personal View. Front. Phys. 9:786028. doi: 10.3389/fphy.2021.786028
Received: 29 September 2021; Accepted: 09 November 2021;
Published: 06 December 2021.
Edited by:
Olivier J.F. Martin, Swiss Federal Institute of Technology Lausanne, SwitzerlandReviewed by:
Nicolas Le Thomas, Ghent University, BelgiumCopyright © 2021 Pavesi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lorenzo Pavesi, bG9yZW56by5wYXZlc2lAdW5pdG4uaXQ=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.