Stability of Hybrid SDEs Driven by fBm

In this paper, the exponential stability of stochastic differential equations driven by multiplicative fractional Brownian motion (fBm) with Markovian switching is investigated. The quasi-linear cases with the Hurst parameter H ∈ (1/2, 1) and linear cases with H ∈ (0, 1/2) and H ∈ (1/2, 1) are all studied in this work. An example is presented as a demonstration.

1 Introduction

In the natural world, it is a common phenomena that many practical systems may face random abrupt changes in their structures and parameters, such as environmental variance, changing of subsystem interconnections and so on. To deal with these abrupt changes, Markovian switching systems, a particular class of hybrid systems, are investigated and widely used [1, 2]. Especially in signal processing, financial engineering, queueing networks, wireless communications and so on (see, e.g. [1, 3]).

In recent years, much attention has been paid to the stability of stochastic hybrid systems. For example, Mao [4] considers the exponential stability of general nonlinear stochastic hybrid systems. In [5], the criteria of moment exponential stability are obtained for stochastic hybrid delayed systems with Lévy noise in mean square. Zhou [6] investigates the pth moment exponential stability of the same systems. Some sufficient conditions for asymptotic stability in distribution of SDEs with Markovian switching are reported in [7]. See also [8, 9] for more results about Markovian switching.

On the other hand, it is generally known that if H ∈ (0, 1/2) and H ∈ (1/2, 1), ${\left\{B_t^H\right\}}_{t\ge 0}$ has a long range dependence, which means if we put

$r(n)=\mathrm{c}\mathrm{o}\mathrm{v}(B_1^H,(B_{n+1}^H-B_n^H)),$

then ${\sum }_{n=1}^{\infty }r(n)=\infty$. Besides, the process ${\left\{B_t^H\right\}}_{t\ge 0}$ is also self-similar for any H ∈ (0, 1). Since the pioneering work of Hurst [10, 11] and Mandelbrot [12], the fractional Brownian motion has been suggested as a useful tool in many fields such as mathematical finance [13, 14] and weather derivatives [15]. Even though fractional Brownian motion is not a semimartingale, more and more financial models have been extended to fBm (see, e.g. [16, 17]). Therefore, in this paper, the risk assets are described by hybrid stochastic systems driven by multiplicative fBm. Then it is a natural and interesting question that under what conditions, this stochastic systems have some exponential stability. For the sake of clarity, we only consider the one dimensional cases. For more details about fractional noise, we refer the reader to [18–21].

The main purpose of this paper is to discuss the exponential stability of a risky asset, with price dynamics:

$\left\{\begin{array}{c}\text{d}{X}_t=f(X_t,t,r_t)\text{d}t+g(X_t,t,r_t)\text{d}{B}_t^H,\hfill \\ X_0=x_0>0,\hfill \end{array}\right.(1)$

where g(X_t, t, r_t) = σ(t, r_t)X_t, ${\{r_t\}}_{t\ge 0}$ is a Markov chain taking values in $\mathbb{S}=\{\mathrm{1,2},\dots ,N\}$, ${\left\{B_t^H\right\}}_{t\ge 0}$ is a standard fractional Brownian motion. Moreover, $f(x,t,r_t):\mathbb{R}\times {\mathbb{R}}_{+}\times \mathbb{S}\to \mathbb{R}$ and $\sigma (t,r_t):{\mathbb{R}}_{+}\times \mathbb{S}\to \mathbb{R}$. In this paper, the initial value x₀ is assumed to be deterministic, otherwise more calculations about Wick product are required.

Equation 1 can be regarded as the result of the following N fractional stochastic differential equations:

$\left\{\begin{array}{c}\text{d}{X}_t=f(X_t,t,i)\text{d}t+g(X_t,t,i)\text{d}{B}_t^H,1\le i\le N,\hfill \\ X_0=x_0>0,\hfill \end{array}\right.$

switching from one to another according to the movement of ${\{r_t\}}_{t\ge 0}$.

Throughout this paper, unless otherwise specified, we let C denote a general constant and p denote a non-negative constant. Let $C^{\mathrm{2,1}}(\mathbb{R}\times {\mathbb{R}}_{+}\times \mathbb{S};\mathbb{R})$ denote the family of all real value functions on $\mathbb{R}\times {\mathbb{R}}_{+}\times \mathbb{S}$ which are continuously twice differentiable with respect to the first variables and once differentiable with respect to the second variables.

This paper is organized as follows. For the convenience of the reader, we briefly recall some of the basic results in Section 2. In Section 3, we investigate the solution and an extended Itô’s Formula for the general hybrid fractional stochastic differential Equation 1. Section 3 is devoted to the linear cases. In this section the moment exponential stability and almost sure exponential stability are discussed respectively. In Section 4, some useful criteria for the exponential stability with respect to quasi-linear cases are presented. Finally, a numerical example and graphical illustration are presented in Section 6.

2 Preliminaries

2.1 Markov Chain

Let ${\{r_t\}}_{t\ge 0}$ be a right-continuous Markov chain taking values in a finite state space $\mathbb{S}=\{\mathrm{1,2},\dots ,N\}$. The generator $Q={(q_{ij})}_{N\times N}$ is given by

$\mathbb{P}\{r_{t+△}=j\mid r_t=i\}=\left\{\begin{array}{c}{q}_{ij}△+o(△),\text{if}i\ne j,\hfill \\ 1+q_{ij}△+o(△),\text{if}i=j,\hfill \end{array}\right.$

where △ > 0.

Here q_ij is the transition rate from i to j if i ≠ j. According to [22, 23], a continuous-time Markov chain ${\{r_t\}}_{t\ge 0}$ with generator $Q={(q_{ij})}_{N\times N}$ can be represented as a stochastic integral with respect to a Poisson random measure. Then we have

$\mathrm{d}{r}_t={\int }_{\mathbb{R}}h(r_{t-},y)\nu (\mathrm{d}t\times \mathrm{d}y),$

with initial condition r₀ = i₀, where ν(dt × dy) is a Poisson random measure with intensity dt × m(dy). Here m(⋅) is the Lebesgue measure on $\mathbb{R}$.

Throughout this paper, unless otherwise specified, the Markov chain ${\{r_t\}}_{t\ge 0}$ has the invariant probability measure $\mu ={({\mu }_i)}_{i\in \mathbb{S}}$ and is assumed to be independent of ${\left\{B_t^H\right\}}_{t\ge 0}$. Almost every sample path of the Markov chain ${\{r_t\}}_{t\ge 0}$ is assumed to be a right-continuous step function with a finite number of simple jumps in any finite time interval [0, T]. The generator $Q={(q_{ij})}_{N\times N}$ is assumed to be irreducible and conservative, i.e., q_i≔ − q_ii = ∑_i≠j q_ij < ∞. For more details about Markovian switching we further refer the reader to [24–26].

2.2 Fractional Brownian Motion and Wick Product

We recall some of the basic results of fBm briefly, which will be needed throughout this paper. For more details about fBm we refer the reader to [16, 17, 27, 28]. If H ∈ (0, 1/2) ∪ (1/2, 1), then the (standard) fractional Brownian motion with Hurst parameter H is a continuous centered Gaussian process ${\left\{B_t^H\right\}}_{t\ge 0}$ with $\mathbb{E}(B_t^H)=0$ and covariance function:

${\mathbb{R}}^H(s,t)=\mathbb{E}(B_s^H{B}_t^H)=\frac{1}{2}(|s{|}^{2H}+|t{|}^{2H}-|s-t{|}^{2H}),s,t\ge 0.$

To simplify the representation, it is always assumed that $B_0^H=0$.

Besides, ${\left\{B_t^H\right\}}_{t\ge 0}$ has the following Wiener integral representation:

$B_t^H={\int }_0^t{K}^H(t,s)\mathrm{d}{W}_s,$

where ${\{W_t\}}_{t\ge 0}$ is a Wiener process and K^H(t, s) is the kernel function defined by

$K_H(t,s)=c_H{s}^{\frac{1}{2}-H}{\int }_0^t{(u-s)}^{H-\frac{3}{2}}{u}^{H-\frac{1}{2}}\mathrm{d}u,$

in which $c_H={\left(\frac{H(2H-1)}{B(2-2H,H-\frac{1}{2})}\right)}^{\frac{1}{2}}$, where B(⋅, ⋅) is the Beta function, and s < t. In this paper, ${\left\{B_t^H\right\}}_{t\ge 0}$ generates a filtration $\{{\mathcal{F}}_t,t\ge 0\}$ with ${\mathcal{F}}_t=\sigma \{B_s^H,t\ge 0\}$. Denote $(\mathrm{\Omega },\mathcal{F},P,{\mathcal{F}}_t)$ the complete probability space, with the filtration described above.

Let $\mathcal{I}$ be the set of all finite multi-indices α = (α₁, …, α_n) for some n ≥ 1 of non-negative integers. Denote |α| = α₁ + ⋯ + α_n, and α! = α₁!⋯α_n!.

Define the Hermite polynomials:

$h_n(x)={(-1)}^n{e}^{x^2}\frac{d^n}{d{x}^n}(e^{-x^2}),n\ge 0,$

and Hermite functions:

${\tilde{h}}_n(x)={\pi }^{-\frac{1}{4}}{(n!)}^{-\frac{1}{2}}{h}_n(x)e^{-\frac{x^2}{4}},n\ge 0.$

Let $S(\mathbb{R})$ denote the Schwartz space of rapidly decreasing infinitely differentiable $\mathbb{R}$-valued functions. Denote the dual space of $S(\mathbb{R})$ by $S^{\prime }(\mathbb{R})$. Define

${\mathcal{H}}_{\alpha }(\omega )=\prod _{i=1}^n{h}_{{\alpha }_i}(⟨{\tilde{h}}_i(x),\omega ⟩),$

the product of Hermite polynomials. Consider a square integrable random variable

$F=F(\omega )\in L^2(S^{\prime }(\mathbb{R}),\mathcal{F},P).$

According to [17, 29], every F(ω) has a unique representation:

$F(\omega )=\sum _{\alpha \in \mathcal{I}}{c}_{\alpha }{\mathcal{H}}_{\alpha }(\omega ),$

besides,

$\Vert F{\Vert }_{L^2(\omega )}^2=\sum _{\alpha \in \mathcal{I}}\alpha !c_{\alpha }^2<\infty .$

Definition 2.1. (Wick Product) For $F,G\in L^2(S^{\prime }(\mathbb{R}),\mathcal{F},P)$, set $F(\omega )={\sum }_{\alpha \in \mathcal{I}}{c}_{\alpha }{\mathcal{H}}_{\alpha }(\omega )$ and $G(\omega )={\sum }_{\beta \in \mathcal{I}}{d}_{\beta }{\mathcal{H}}_{\beta }(\omega )$. Their Wick product is defined by

$\begin{array}{cc}\hfill F\diamond G(\omega )& =\sum _{\alpha ,\beta \in \mathcal{I}}{a}_{\alpha }{b}_{\beta }{\mathcal{H}}_{\alpha +\beta }(\omega )\hfill \\ \hfill & =\sum _{\gamma \in \mathcal{I}}\left(\sum _{\alpha +\beta =\gamma }{a}_{\alpha }{b}_{\beta }\right){\mathcal{H}}_{\gamma }(\omega ).\hfill \end{array}$

2.3 Malliavin Derivative

Let $L^p≔L^p(\mathrm{\Omega },\mathcal{F},P)$ be the space of all random variables $\mathrm{\Omega }\to \mathbb{R}$, such that

$\Vert F{\Vert }_p=\mathbb{E}{(|F{|}^p)}^{1/p}<\infty ,$

and let

$\begin{array}{c}\hfill L_{\varphi }^2({\mathbb{R}}_{+})=\{f|f:{\mathbb{R}}_{+}\to \mathbb{R},|f{|}_{\varphi }^2≔{\int }_0^{\infty }{\int }_0^{\infty }f(s)f(t)\varphi (s,t)\mathrm{d}s\mathrm{d}t<\infty \},\end{array}$

where ϕ(s, t) = H(2H − 1)|s − t|^2H−2.

Definition 2.2. The ϕ-derivative of F ∈ L^p in the direction of Φ_g is defined by

$D_{{\mathrm{\Phi }}_g}F(\omega )=\underset{\delta \to 0}{\lim }\frac{1}{\delta }\left\{F\left(\omega +\delta {\int }_0^{\cdot }({\mathrm{\Phi }}_g)(u)\mathrm{d}u\right)-F(\omega )\right\},$

if the limit exists in L^p. Moreover if there exists a process $(D_s^{\varphi }{F}_s,s\ge 0)$ such that

$D_{{\mathrm{\Phi }}_g}F={\int }_0^{\infty }{D}_s^{\varphi }{F}_s{g}_s\mathrm{d}sa.s.,$

for all $g\in L_{\varphi }^2$, then F is said to be ϕ-differentiable.According to [16, 30], let $\mathcal{A}(0,T)$ be the family of stochastic process on [0, T] such that $F\in \mathcal{A}(0,T)$ if $\mathbb{E}|F{|}_{\varphi }^2<\infty$ and F is ϕ-differentiable, the trace of $(D_s^{\varphi }{F}_t,0\le s\le T,0\le t\le T)$ exists and $\mathbb{E}{\int }_0^T{(D_s^{\varphi }{F}_s)}^{2}ds<\infty$, and for each sequence of partitions ${\pi }_n,n\in \mathbb{N}$ such that |π_n| → 0, as n → ∞. Moreover

$\sum _{i=0}^{n-1}\mathbb{E}{\left\{{\int }_{t_i^{(n)}}^{t_{i+1}^{(n)}}|D_s^{\varphi }{F}_{t_i^{(n)}}^{\pi }-D_s^{\varphi }{F}_s|\mathrm{d}s\right\}}^2\to 0,$

and

$\mathbb{E}|F^{\pi }-F{|}_{\varphi }^2\to 0,$

as n → ∞. Here ${\pi }_n:0=t_0^{(n)}<t_1^{(n)}<\dots <t_n^{(n)}=T$, and $|{\pi }_n|={\max }_{i\in \{\mathrm{0,1},\dots ,n-1\}}\{t_{i+1}^{(n)}-t_i^{(n)}\}$.Now we define the $B_t^H$-integral considered in [16].

Definition 2.3. Let ${\{F_t\}}_{t\ge 0}$ be a stochastic process such that $F\in \mathcal{A}(0,T)$. Define ${\int }_0^T{F}_s\mathrm{d}{B}_s^H$ by

${\int }_0^T{F}_s\mathrm{d}{B}_s^H=\underset{|\pi |\to 0}{\lim }\sum _{i=0}^{n-1}{F}_{t_i}^{\pi }\diamond (B_{t_{i+1}}^H-B_{t_i}^H),$

where |π| =  max_{i∈{0,1,…,n−1}}{t_i+1 − t_i}.

Remark 2.1.: According to Theorem 3.6.1 in [16], if $F_s\in \mathcal{A}(0,T)$, then the stochastic integral satisfies $\mathbb{E}{\int }_0^T{F}_s\mathrm{d}{B}_s^H=0$, and

$\mathbb{E}{\left|{\int }_0^T{F}_s\mathrm{d}{B}_s^H\right|}^2=\mathbb{E}\left[{\left({\int }_0^T{D}_s^{\varphi }{F}_s\mathrm{d}s\right)}^2+\mid 1_{[0,T]}F{\mid }_{\varphi }^2\right]$

What’s more, according to Definition 3.4.1 in [16], the stochastic integral can be extended by

${\int }_{\mathbb{R}}{F}_t\mathrm{d}{B}_t^H≔{\int }_{\mathbb{R}}{F}_t\diamond W^H(t)dt,$

where $F:\mathbb{R}\to {(\mathcal{S})}_H^{*}$ is a given function such that F_t ⋄ W^H(t) is dṭ − integrable in ${(\mathcal{S})}_H^{*}$. Here ${(\mathcal{S})}_H^{*}$ is the fractional Hida distribution space defined by Definition 3.1.11 in [16]. In particular, the integral on [0, T] can be defined by

${\int }_0^T{F}_t\mathrm{d}{B}_t^H={\int }_{\mathbb{R}}{F}_t{I}_{[0,T]}(t)\mathrm{d}{B}_t^H.$

3 Hybrid Fractional Systems

In this section, firstly, we consider the existence and uniqueness of solution for Eq. 1. Then, an extended Itô’s Formula is presented.

3.1 Existence and Uniqueness

To ensure the existence and uniqueness, we impose the following assumptions.

Assumption 3.1. Let $f=f(x,t,i):\mathbb{R}\times {\mathbb{R}}_{+}\times \mathbb{S}\to \mathbb{R}$ satisfy the hypothesises:

1) For each fixed $i\in \mathbb{S}$, f(x, t, i) is measurable in all the arguments.

2) For each fixed $i\in \mathbb{S}$, there exists a constant C > 0, such that $|f(x,t,i)-f(y,t,i)|\le C|x-y|,\forall x,y\in \mathbb{R},\forall t\in {\mathbb{R}}_{+}$.

3) For each fixed $i\in \mathbb{S}$, there exists a constant C > 0, such that

$|f(x,t,i)|\le C(1+|x|),\forall (x,t)\in \mathbb{R}\times {\mathbb{R}}_{+}.$

Assumption 3.2. Let $\sigma =\sigma (t,i):{\mathbb{R}}_{+}\times \mathbb{S}\to \mathbb{R}$ satisfy the hypothesises:

1) For each fixed $i\in \mathbb{S}$, σ(t, i) is nonrandom;

2) For each fixed $i\in \mathbb{S}$, $\sigma (t,i)\in L^{\frac{1}{H}}({\mathbb{R}}_{+})$.

Lemma 3.1.: Let Assumptions 3.1, 3.2 hold. Then Eq. 1 has a unique solution.

Proof: The existence and uniqueness can be proved similar to that for Theorem 2.6 in [31], so we omit it here.

3.2 The Itô Formula

Next, we first review the results in [16, 30] on the Itô formula with respect to fBm. Then we extend it to SDEs driven by fBm with Markovian switching.

Lemma 3.2. [16] (The Itô Formula) Let (F_u, 0 ≤ u ≤ T) be a stochastic process in $\mathcal{A}(0,T)$. Assume that there exists an α > 1 − H and C > 0 such that

$\mathbb{E}|F_u-F_v{|}^2\le C|u-v{|}^{2\alpha },$

where |u − v| ≤ δ for some δ > 0 and

$\underset{0\le u,v\le t,|u-v|\to 0}{\lim }\mathbb{E}|D_u^{\varphi }(F_u-F_v){|}^2=0.$

Let sup_0≤s≤T|G_s| < ∞ and $\tilde{g}=\tilde{g}(x,t)\in C^{\mathrm{2,1}}(\mathbb{R}\times {\mathbb{R}}_{+};\mathbb{R})$ with bounded derivatives. Moreover, for ${\eta }_t={\int }_0^t{F}_u\mathrm{d}{B}_u^H$, it is assumed that $\mathbb{E}{\int }_0^T|F_s{D}_s^{\varphi }{\eta }_s|\mathrm{d}s<\infty$ and $(\frac{\partial \tilde{g}}{\partial x}(s,{\eta }_s)F_s,s\in [0,T])$ is in $\mathcal{A}(0,T)$. Denote $x_t=x_0+{\int }_0^t{G}_u\mathrm{d}u+{\int }_0^t{F}_u\mathrm{d}{B}_u^H$, $x_0\in \mathbb{R}$ for t ∈ [0, T]. Let $(\frac{\partial \tilde{g}}{\partial x}(x_s,s)F_s,s\in [0,T])\in \mathcal{A}(0,T)$, $\mathbb{E}\left[{\sup }_{0\le s\le t}|G_s|\right]<\infty$. Then for t ∈ [0, T],

$\begin{array}{cc}\hfill \tilde{g}(x_t,t)& =\tilde{g}(x_0,0)+{\int }_0^t\frac{\partial \tilde{g}}{\partial s}(x_s,s)\mathrm{d}s+{\int }_0^t\frac{\partial \tilde{g}}{\partial x}(x_s,s)G_s\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t\frac{\partial \tilde{g}}{\partial x}(x_s,s)F_s\mathrm{d}{B}_s^H+{\int }_0^t\frac{{\partial }^2\tilde{g}}{\partial x^2}(x_s,s)F_s{D}_s^{\varphi }{x}_s\mathrm{d}s.\hfill \end{array}$

Here $D_s^{\varphi }{x}_s$ is the Malliavin derivative defined in Definition 2.2.In particular, for the process $X_t^{(i)}=X_0^{(i)}+{\int }_0^{t}f(X_s^{(i)},s,i)\mathrm{d}s+{\int }_0^{t}g(X_s^{(i)},s,i)\mathrm{d}{B}_s^H$, with each fixed $i\in \mathbb{S}$, we have that

$\begin{array}{cc}\hfill F(X_t^{(i)},t,i)& =F(X_0^{(i)},0,i)+{\int }_0^t\frac{\partial F}{\partial s}(X_s^{(i)},s,i)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t\frac{\partial F}{\partial x}(X_s^{(i)},s,i)f(X_s^{(i)},s,i)\mathrm{d}s+{\int }_0^t\frac{\partial F}{\partial x}(X_s^{(i)},s,i)g(X_s^{(i)},s,i)\mathrm{d}{B}_s^H\hfill \\ \hfill & +{\int }_0^t\frac{{\partial }^{2}F}{\partial x^2}(X_s^{(i)},s,i)g(X_s^{(i)},s,i)D_s^{\varphi }{X}_s^{(i)}\mathrm{d}s,\hfill \end{array}(2)$

Formally,

$\begin{array}{c}\hfill \mathrm{d}F(X_t^{(i)},t,i)=F_t(X_t^{(i)},t,i)\mathrm{d}t+F_{xx}(X_t^{(i)},t,i)g(X_t^{(i)},t,i)D_s^{\varphi }{X}_s^{(i)}\mathrm{d}t\\ +F_x(X_t^{(i)},t,i)f(X_t^{(i)},t,i)\mathrm{d}t+F_x(X_t^{(i)},t,i)g(X_t^{(i)},t,i)\mathrm{d}{B}_t^H,\hfill \end{array}$

Let

$\begin{array}{cc}\hfill {\mathcal{L}}^{(i)}F(X_t^{(i)},t,i)& =F_t(X_t^{(i)},t,i)+F_x(X_t^{(i)},t,i)f(X_t^{(i)},t,i)\hfill \\ \hfill & +F_{xx}(X_t^{(i)},t,i)g(X_t^{(i)},t,i)D_s^{\varphi }{X}_s.\hfill \end{array}(3)$

Substituting Eq. 3 into Eq. 2, we get

$\begin{array}{cc}\hfill F(X_t^{(i)},t,i)& =F(X_0^{(i)},0,i)+{\int }_0^t{\mathcal{L}}^{(i)}F(X_s^{(i)},s,i)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{F}_x(X_s^{(i)},s,i)g(X_s^{(i)},s,i)\mathrm{d}{B}_s^H.\hfill \end{array}(4)$

In the sequel of this paper, unless otherwise specified, we let the coefficients of Eq. 1 satisfy the conditions in Lemma 3.2, for each fixed $i\in \mathbb{S}$. Set $V(X_t,t,r_t)\in C^{\mathrm{2,1}}(\mathbb{R}\times {\mathbb{R}}_{+}\times \mathbb{S};{\mathbb{R}}_{+})$. Next we consider the Itô formula which reveals how V maps (X_t, t, r_t) into a new process V(X_t, t, r_t), where ${\{X_t\}}_{t\ge 0}$ is a stochastic process with the stochastic differential Eq. 1.

Lemma 3.3. If $V(X_t,t,r_t)\in C^{\mathrm{2,1}}(\mathbb{R}\times {\mathbb{R}}_{+}\times \mathbb{S};{\mathbb{R}}_{+})$, then for any 0 ≤ s < t,

$\begin{array}{cc}\hfill \mathbb{E}V(X_t,t,r_t)& =\mathbb{E}V(X_s,s,r_s)+\mathbb{E}{\int }_s^t\mathcal{A}V(X_u,u,r_u)\mathrm{d}u\hfill \\ \hfill & +\mathbb{E}{\int }_s^t{V}_x(X_u,u,r_u)g(X_u,u,r_u)\mathrm{d}{B}_u^H\hfill \end{array}(5)$

where $\mathcal{A}V$ is defined by

$\mathcal{A}V(x,t,i)={\mathcal{L}}^{(i)}V(x,t,i)+\sum _{j=1}^N{\gamma }_{ij}V(x,t,j).$

Proof: This result can be obtained similarly to that in [31] and we therefore omit it. For further details we also refer to [2, 23].

4 Linear Hybrid Fractional Systems

There are many models for financial markets with fBm (see, e.g. [16]). The simplest nontrivial type of market is the fBm version of the classical Black Scholes market, in which linear fractional SDEs is used. Thus, we would like to give some new criteria for switching linear fractional SDEs with $H\in (0,\frac{1}{2})$ or $H\in (\frac{1}{2},1)$. At first, we present a definition and a useful lemma.

Definition 4.1. Let H ∈ (0, 1). The operator M is defined on functions $f\in S(\mathbb{R})$ by

$Mf(x)=-\frac{d}{dx}\frac{C_H}{(H-1/2)}{\int }_{\mathbb{R}}(t-s)|t-x{|}^{H-\frac{3}{2}}f(t)\mathrm{d}t(6)$

where

$\begin{array}{ccc}\hfill C_H={\left\{2\mathrm{\Gamma }\left(H-\frac{1}{2}\right)\cos \left[\frac{\pi }{2}\left(H-\frac{1}{2}\right)\right]\right\}}^{-1}& \hfill & \hfill \\ \hfill {\left[\mathrm{\Gamma }(2H+1)\sin (\pi H)\right]}^{\frac{1}{2}}.& \hfill & \hfill \end{array}$

Here Γ(⋅) denotes the classical Gamma function.According to [16], Eq. 6 can be restated as follows.For H ∈ (0, 1/2), we have

$Mf(x)=C_H{\int }_{\mathbb{R}}\frac{f(x-t)-f(x)}{|t{|}^{3/2-H}}\mathrm{d}t.$

For H = 1/2, we have

$Mf(x)=f(x).$

For H ∈ (1/2, 1), we have

$Mf(x)=C_H{\int }_{\mathbb{R}}\frac{f(t)}{|t-x{|}^{3/2-H}}\mathrm{d}t.$

Lemma 4.1. Let ${\{r_t\}}_{t\ge 0}$ be a right-continuous Markov chain which takes values in a finite state space $\mathbb{S}=\{\mathrm{1,2},\dots ,N\}$. Assume that it is irreducible and positive recurrent with invarient measure μ. If $\alpha (\cdot ):\mathbb{S}\to \mathbb{R}$ is a function verifying

$\alpha ≔\sum _{i\in \mathbb{S}}\mu (i)\alpha (i)>0.$

Then there exists constants C, c > 0 such that:

$c{e}^{-\alpha t}\le \mathbb{E}\left[e^{-{\int }_0^t\alpha (r_s)\mathrm{d}s}\right]\le C{e}^{-\alpha t},$

for any initial condition r₀ and every t ≥ 0.

Proof: It is a consequence of Perron-Frobenius theorem and the study of eigenvalues. See Proposition 4.1 in [25], Proposition 4.2 in [25], and Lemma 2.7 in [26], for further details.In Eq. 1, let us consider the case g(x, t, r_t) = σ(t, r_t)x = t^hb(r_t)x, f(x, t, r_t) = α(r_t)x, where α(i) and b(i) are constants for each $i\in \mathbb{S}$. This means that we are considering the following linear equation:

$\left\{\begin{array}{c}\mathrm{d}{X}_t=\alpha (r_t)X_t\mathrm{d}t+\sigma (t,r_t)X_t\mathrm{d}{B}_t^H,\hfill \\ X_0=x_0.\hfill \end{array}\right.(7)$

Set $\bar{b}=\max \{|b(i)|,i\in \mathbb{S}\}$ and $\underline{b}=\min \{|b(i)|,i\in \mathbb{S}\}$. x₀ is the deterministic initial value. For the sake of clarity, we firstly set h = 1/2 − H.

4.1 pth Moment Exponential Stability

Theorem 4.1. Let ${\{X_t\}}_{t\ge 0}$ be the solution of Eq. 7 with H ∈ (1/2, 1), h = 1/2 − H.

1) If ${\sum }_{i\in S}{\mu }_i\alpha (i)-\frac{(1-p){\underline{b}}^2}{2}<0$, then $\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log (\mathbb{E}|X_t{|}^p)<0$.

2) If ${\sum }_{i\in \mathbb{S}}{\mu }_i\alpha (i)-\frac{(1-p){\bar{b}}^2}{2}>0$, then $\underset{t\to \infty }{\lim }\mathbb{E}|X_t{|}^p=\infty$.

Proof. According to [16], without too many calculations, we obtain that ${\{X_t\}}_{t\ge 0}$ has the following form:

$X_t=x_0\exp \left[{\int }_0^t\sigma (r_s)\mathrm{d}{B}_s^H+{\int }_0^t\alpha (r_s)\mathrm{d}s-\frac{1}{2}{\int }_{\mathbb{R}}{(M_s(\sigma (t,r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\right],(8)$

where M_s is the operator M acting on the variable s. Let x₀ ≠ 0. It follows from Eq. 8 that

$\begin{array}{cc}\hfill & \mathbb{E}|X_t{|}^p\hfill \\ \hfill =& \mathbb{E}{\left(|x_0|\exp \left[{\int }_0^t\sigma (t,r_s)\mathrm{d}{B}_s^H+{\int }_0^t\alpha (r_s)\mathrm{d}s-\frac{1}{2}{\int }_{\mathbb{R}}{(M_s(\sigma (t,r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\right]\right)}^p\hfill \end{array}(9)$

We then see from Eq. 9 that

$\mathbb{E}|X_t{|}^p=\mathbb{E}\left(\exp \left(p\left[{\int }_0^t\alpha (r_s)\mathrm{d}s-\frac{1-p}{2}{\int }_{\mathbb{R}}{(M_s(\sigma (t,r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\right]\right){\zeta }_t\right),(10)$

where

$\begin{array}{ccc}\hfill {\zeta }_t=|x_0{|}^p\exp \left[\right.{\int }_0^{t}p\sigma (s,r_s)\mathrm{d}{B}_s^H-\frac{p^2}{2}& \hfill & \hfill \\ \hfill {\int }_{\mathbb{R}}{(M_s(\sigma (t,r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\left.\right].& \hfill & \hfill \end{array}$

Noting that ζ_t is the solution to the equation

$\mathrm{d}{\zeta }_t=p\sigma (t,r_t){\zeta }_t\mathrm{d}{B}_t^H,$

with initial value ζ₀ = |x₀|^p. Thus

${\zeta }_t=|x_0{|}^p+{\int }_0^{t}p\sigma (t,r_s)\mathrm{d}{B}_s^H,$

which yields

$\mathbb{E}{\zeta }_t=\mathbb{E}\left[|x_0{|}^p+{\int }_0^{t}p\sigma (t,r_s)\mathrm{d}{B}_s^H\right]=|x_0{|}^p.(11)$

Substituting Eq. 11 into Eq. 10 gives

$\mathbb{E}|X_t{|}^p=\mathbb{E}\exp \left(p\left[{\int }_0^t\alpha (r_s)\mathrm{d}s-\frac{1-p}{2}{\int }_{\mathbb{R}}{(M_s(\sigma (r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\right]\right)|x_0{|}^p.(12)$

Note that

$\begin{array}{ccc}\hfill {\int }_{\mathbb{R}}{(M_s(\underline{b}{s}^h{I}_{[0,t]}(s)))}^2\mathrm{d}s\le {\int }_{\mathbb{R}}{(M_s(\sigma (t,r_s)I_{[0,t]}(s)))}^2& \hfill & \hfill \\ \hfill \mathrm{d}s\le {\int }_{\mathbb{R}}{(M_s(\bar{b}{s}^h{I}_{[0,t]}(s)))}^2\mathrm{d}s.& \hfill & \hfill \end{array}$

Consequently, by Definition 4.1 and [16], one has

${\underline{b}}^{2}t\le {\int }_{\mathbb{R}}{(M_s(\sigma (r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\le {\bar{b}}^{2}t.(13)$

Making use of Eqs 12, 13, we obtain that

$\begin{array}{cc}\hfill & \mathbb{E}\exp \left(p\left[{\int }_0^t\alpha (r_s)\mathrm{d}s-\frac{1-p}{2}{\bar{b}}^{2}t\right)\right]|x_0{|}^p\le \mathbb{E}|X_t{|}^p\hfill \\ \hfill & \le \mathbb{E}\exp \left(p\left[{\int }_0^t\alpha (r_s)\mathrm{d}s-\frac{1-p}{2}{\underline{b}}^{2}t\right)\right]|x_0{|}^p.\hfill \end{array}$

Therefore, by Lemma 4.1 and Eq. 12, the required assertions follow. The proof is complete.

Theorem 4.2. Let ${\{X_t\}}_{t\ge 0}$ be the solution of Eq. 7 with H ∈ (0, 1/2), h = 1/2 − H.

1) If ${\sum }_{i\in S}{\mu }_i\alpha (i)<\frac{(1-p){\underline{b}}^2}{2}$, then $\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log (\mathbb{E}|X_t{|}^p)<0$.

2) If ${\sum }_{i\in \mathbb{S}}{\mu }_i\alpha (i)>\frac{(1-p){\bar{b}}^2}{2}$, then $\underset{t\to \infty }{\lim }\mathbb{E}|X_t{|}^p=\infty$.

Proof: Similar to Theorem 4.1, we write the solution as follows.

$\mathbb{E}|X_t{|}^p=\mathbb{E}\exp \left(p\left[{\int }_0^t\alpha (r_s)\mathrm{d}s+\frac{p-1}{2}{\int }_{\mathbb{R}}{(M_s(\sigma (r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\right]\right)|x_0{|}^p.(14)$

Note that M_s is the operator M acting on the variable s, where

$Mf(x)=C_H{\int }_{\mathbb{R}}\frac{f(x-t)-f(x)}{|t{|}^{3/2-H}}\mathrm{d}t.$

According to [16], we also have that

${\underline{b}}^{2}t\le {\int }_{\mathbb{R}}{(M_s(\sigma (t,r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\le {\bar{b}}^{2}t.(15)$

Consequently, by Lemma 4.1, the result follows. The proof is complete.

Remark 4.1. In the above Theorems 4.1, 4.2, the parameter h is supposed to be H − 1/2. Noting that by Eqs 13, 15 and together with the Definition 4.1, the stability of solution for Eq. 7 with h < 1/2 − H or h > 1/2 − H can be deduced respectively without too many difficulties.

Remark 4.2. Take H = 1/2. It’s easy to show that if ${\sum }_{i\in S}{\mu }_i\alpha (i)=\alpha <\frac{(1-p){\underline{\sigma }}^2}{2}$, then $\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log (\mathbb{E}|X_t{|}^p)<0$, and if ${\sum }_{i\in \mathbb{S}}{\mu }_i\alpha (i)=\alpha >\frac{(1-p){\bar{\sigma }}^2}{2}$, then $\underset{t\to \infty }{\lim }\mathbb{E}|X_t{|}^p=\infty$, which coincide with the results of SDEs driven by Brownian motion in [4, 32].

4.2 Almost Sure Exponential Stability

To proceed, we need to introduce the definition of almost sure stability and a useful lemma.

Definition 4.2. The equilibrium point x = 0 is said to be almost surely exponential stable if

$\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log |X_t|<0a.s.$

for any $x_0\in \mathbb{R}$.

Lemma 4.2. (Law of the iterated logarithm) For a standard fBm ${\left\{B_t^H\right\}}_{t\ge 0}$, we have that

$\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{B_t^H}{t^H\sqrt{\log \log t}}=C_H,(16)$

where C_H > 0 is a suitable constant.

Proof: By [33], we have

$\underset{t\to 0^{+}}{\mathrm{lim\; sup}}\frac{B_t^H}{t^H\sqrt{\log \log t^{-1}}}=c_H,$

where c_H is a suitable constant. Then the thesis follows by the self-similarity of fBm and a change of variable t → 1/t.For the sake of clarity, we firstly set h = 0. Namely, let us consider

$\left\{\begin{array}{c}d{X}_t=\alpha (r_t)X_t\mathrm{d}t+b(r_t)X_t\mathrm{d}{B}_t^H,\hfill \\ X_0=x_0.\hfill \end{array}\right.(17)$

Noting that Eq. 17 is exactly the geometry fBm with Markovian Switching. We proceed to discuss the almost sure exponential stability about it.

Theorem 4.3. 1) If 0 < H < 1/2, the equilibrium point x = 0 of the system Eq. 17 is almost surely exponential stable when ${\sum }_{i\in \mathbb{S}}{\mu }_i\alpha (i)<0$, but unstable when ${\sum }_{i\in \mathbb{S}}{\mu }_i\alpha (i)>0$; 2) If H = 1/2, the equilibrium point x = 0 of the system Eq. 17 is almost surely exponential stable when ${\sum }_{i\in \mathbb{S}}{\mu }_i\alpha (i)<\frac{1}{2}{\underline{b}}^2$, but unstable when ${\sum }_{i\in \mathbb{S}}{\mu }_i\alpha (i)>\frac{1}{2}{\bar{b}}^2$; 3) If 1/2 < H < 1, the equilibrium point x = 0 of the system Eq. 17 is almost surely exponential stable for all parameters α(i) and σ(i), $i\in \mathbb{S}$.

Proof: Define

$\lambda =\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log |X_t|.$

From Eqs 8, 16, we have

$\begin{array}{c}\hfill \lambda =\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log |X_t|\\ =\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log |x_0\exp [{\int }_0^t\sigma (r_s)\mathrm{d}{B}_s^H+{\int }_0^t\alpha (r_s)\mathrm{d}s-\frac{1}{2}{\int }_{\mathbb{R}}{(M_s(\sigma (r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\left]\right|\hfill \\ =\underset{t\to \infty }{\lim }\left(\sum _{i\in \mathbb{S}}{\mu }_i\alpha (i)-\frac{1}{2t}{\int }_{\mathbb{R}}{(M_s(\sigma (r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\right).\hfill \end{array}$

By Definition 4.1 and [16], one has

${\underline{b}}^2{t}^{2H}\le {\int }_{\mathbb{R}}{(M_s(b(r_s)I_{[0,t]}(s)))}^2\mathrm{d}s\le {\bar{b}}^2{t}^{2H}.(18)$

Making use of Eq. 18, we get

$\lambda =\left\{\begin{array}{c}\sum _{i\in \mathbb{S}}{\mu }_i\alpha (i),0<H<1/2;\hfill \\ -\infty ,1/2<H<1.\hfill \end{array}\right.$

Especially, when H = 1/2, we have that

$\sum _{i\in \mathbb{S}}{\mu }_i\alpha (i)-\frac{1}{2}{\bar{b}}^2\le \lambda \le \sum _{i\in \mathbb{S}}{\mu }_i\alpha (i)-\frac{1}{2}{\underline{b}}^2.$

Therefore, the required results follows. The proof is complete.

Remark 4.3. Making use of Eq. 18, one can discuss the almost sure exponential stability for Eq. 7 with h ≠ 0. The proofs are similar to Theorem 4.3 and are omitted.

5 Quasi-Linear Hybrid Fractional Systems

We now apply the extended Itô Formula in Section 3 to discuss the stability for quasi-linear fractional SDEs with Markovian switching.

Theorem 5.1.: Let Assumptions 3.1, 3.2 hold. If there exists a function $V\in C^{\mathrm{2,1}}(\mathbb{R}\times {\mathbb{R}}_{+}\times \mathbb{S};{\mathbb{R}}_{+})$ and positive constants a₁, a₂, b and p ≥ 1, such that

$a_1|X_t{|}^p\le |V(X_t,t,i)|\le a_2|X_t{|}^p,(19)$

${\mathcal{L}}^{(i)}V(X_t,t,i)\le -b|X_t{|}^p,(20)$

for all $X_t\in \mathbb{R}$, t ≥ t₀, $i\in \mathbb{S}$.Then the solution of Eq. 1 is pth moment exponential stable. More precisely,

$\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log (\mathbb{E}|X_t{|}^p)<0.$

Proof: According to Lemma 3.1, Eq. 1 has a unique solution. Denote it ${\{X_t\}}_{t\ge 0}$. Set

$U(X_t,t,i)=e^{\lambda t}V(X_t,t,i),$

where $\lambda \in (\eta ,\frac{b}{a_2})$, η > 0. Making use of Definition 2.3 and Lemma 3.2, one has $\mathcal{A}U=e^{\lambda t}(\lambda V+\mathcal{A}V)$ and $(U_{x}g,s\in [0,T])\in \mathcal{A}(0,T)$.Applying the conditions Eq. 19, 20, together with the generalized ItôEq. 5 and Remark 2.1, we obtain that for any t ∈ [0, T]

$\begin{array}{cc}\hfill & a_1{e}^{\eta t}\mathbb{E}|X_t{|}^p\le \mathbb{E}U(X_t,t,i)\hfill \\ \hfill & =\mathbb{E}V(X_0,0,r_0)+\mathbb{E}{\int }_0^t\mathcal{A}U\mathrm{d}s+\mathbb{E}{\int }_0^t{U}_{x}g{Ḅ}_s^H\hfill \\ \hfill & =\mathbb{E}V(X_0,0,r_0)+\mathbb{E}{\int }_0^t{\mathcal{L}}^{(r_s)}U\mathrm{d}s=\mathbb{E}V(X_0,0,r_0)+\hfill \\ \hfill \mathbb{E}{\int }_0^t{e}^{\lambda s}(\lambda V+\mathcal{A}V)\mathrm{d}s\\ \hfill & \le \mathbb{E}V(X_0,0,r_0)+\mathbb{E}{\int }_0^t{e}^{\lambda s}(\lambda a_2-b)|X_t{|}^p\mathrm{d}s.\hfill \end{array}$

Thus we obtain that

$a_1{e}^{\eta t}\mathbb{E}|X_t{|}^p\le \mathbb{E}V(X_0,0,r_0)+\mathbb{E}{\int }_0^t{e}^{\lambda s}(\lambda a_2-b)|X_t{|}^p\mathrm{d}s.(21)$

Dividing both sides of Eq. 21 by a₁e^ηt, noting that λa₂ − b < 0, we get

$\begin{array}{cc}\hfill \mathbb{E}|X_t{|}^p& \le \frac{e^{-\eta t}}{a_1}\mathbb{E}V(X_0,0,r_0)+\frac{e^{-\eta t}}{a_1}\mathbb{E}{\int }_0^t{e}^{\lambda s}(\lambda a_2-b)|X_t{|}^p\mathrm{d}s\hfill \\ \hfill & \le \frac{e^{-\eta t}}{a_1}\mathbb{E}V(X_0,0,r_0).\hfill \end{array}$

Consequently,

$\underset{t\in [0,T]}{\sup }{a}_1{e}^{\eta t}\mathbb{E}|X_t{|}^p\le \mathbb{E}V(X_0,0,r_0).$

Letting T → ∞ gives

$\underset{t\ge 0}{\sup }\mathbb{E}|X_t{|}^p\le \frac{e^{-\eta t}}{a_1}\mathbb{E}V(X_0,0,r_0),$

and the required assertion follows. The proof is complete.In the sequel of this section, we give another useful criterion and prove it briefly.

Theorem 5.2. Assume that Eq. 1 has a unique solution and there exist a function $V\in C^{\mathrm{2,1}}(\mathbb{R}\times {\mathbb{R}}_{+}\times \mathbb{S};{\mathbb{R}}_{+})$ and positive constants b₁, b₂, p ≥ 1 and ${\beta }_i\in \mathbb{R}$ such that for all $x\in \mathbb{R}$, t ≥ t₀, $i\in \mathbb{S}$,

$b_1|x{|}^p\le |V(x,t,i)|\le b_2|x{|}^p,$

${\mathcal{L}}^{(i)}V(x,t,i)\le {\beta }_{i}V(x,t,i),$

and

$\sum _{i\in \mathbb{S}}{\mu }_i{\beta }_i<0$

Then Eq. 1 is pth moment exponential stable.

Proof: Set ${\bar{\beta }}_i=\frac{1}{\theta }{\beta }_i$, where θ ∈ (0, 1). Let $\delta =-{\sum }_{i\in \mathbb{S}}{\mu }_i{\bar{\beta }}_i=-\mu \bar{\beta }$. Let $\mathbb{1}$ denote the vector which all elements are 1. Then,

$\mu (\bar{\beta }+\delta \mathbb{1})=\mu \bar{\beta }+\delta =-\delta +\delta =0.(22)$

By [1], Eq. 22 implies the Poisson equation:

$Qc=\bar{\beta }+\delta \mathbb{1}.(23)$

Note that Eq. 23 has the solution $c={(c_1,\dots ,c_N)}^T$. Hence,

$-\delta ={\bar{\beta }}_i-\sum _{j=1}^N{q}_{ij}{c}_j,i\in \mathbb{S}.(24)$

For each $i\in \mathbb{S}$, set U(x, t, i) = (1 − θc_i)V(x, t, i), where θ ∈ (0, 1) is already defined and sufficiently small satisfying 1 − θc_i > 0.Then, for any t ∈ [0, T] we get

$\begin{array}{cc}\hfill \mathcal{A}U(x,t,i)& =(1-\theta c_i){\mathcal{L}}^{(i)}V(x,t,i)+\sum _{i\ne j}{q}_{ij}(U(x,t,j)-U(x,t,i))\hfill \\ \hfill & =(1-\theta c_i){\mathcal{L}}^{(i)}V(x,t,i)-\theta V(x,t,i)\sum _{i\ne j}{q}_{ij}(c_j-c_i)\hfill \\ \hfill & \le (1-\theta c_i)\theta V(x,t,i)\left[{\bar{\beta }}_i-\sum _{i\ne j}{q}_{ij}\frac{c_j-c_i}{(1-\theta c_i)}\right].\hfill \end{array}(25)$

According to [1, 31], one has

$\begin{array}{cc}\hfill & \sum _{i\ne j}{q}_{ij}\frac{c_j-c_i}{(1-\theta c_i)}=\sum _{i\ne j}{q}_{ij}{c}_j+\sum _{i\ne j}{q}_{ij}\frac{\theta c_i{c}_j-c_i}{1-\theta c_i}\hfill \\ \hfill =& \sum _{j=1}^N{q}_{ij}{c}_j+\sum _{i\ne j}{q}_{ij}\frac{c_i(c_j-c_i)}{1-\theta c_i}\theta =\sum _{j=1}^N{q}_{ij}{c}_j+o(\theta ).\hfill \end{array}(26)$

Making use of Eqs 25, 26, we obtain that

$\mathcal{A}U(x,t,i)\le (1-\theta c_i)\theta V(x,t,i)\left[{\bar{\beta }}_i-\sum _{j=1}^N{q}_{ij}{c}_j+o(\theta )\right].(27)$

Substituting Eq. 24 into Eq. 27, we get

$\mathcal{A}U(x,t,i)\le (1-\theta c_i)\theta V(x,t,i)[o(\theta )-\delta ]=\kappa U(x,t,i),$

where κ < 0. Making use of Theorem 5.1, the desired criterion follows.On the other hand, we can prove it in another way. Set η > 0 and λ ∈ (η, − κ). Define

$\bar{U}(X_t,t,i)=\frac{e^{\lambda t}}{1-\theta c_i}U(X_t,t,i).$

Compute

$\begin{array}{cc}\hfill & b_1{e}^{\eta t}\mathbb{E}|X_t{|}^p\le \mathbb{E}\bar{U}(X_t,t,i)=\mathbb{E}U(X_0,0,i_0)+\mathbb{E}{\int }_0^t\mathcal{A}\bar{U}\mathrm{d}s+\mathbb{E}{\int }_0^t{\bar{U}}_{x}g\mathrm{d}{B}_s^H\hfill \\ \hfill & =\mathbb{E}U(X_0,0,i_0)+\mathbb{E}{\int }_0^t{e}^{\lambda s}(\lambda U+\mathcal{A}U)\mathrm{d}s\le \mathbb{E}U(X_0,0,i_0)+\mathbb{E}{\int }_0^t{e}^{\lambda s}(\lambda +\kappa )U\mathrm{d}s\hfill \\ \hfill & =\mathbb{E}V(x_0,0,i_0)+\mathbb{E}{\int }_0^t{e}^{\lambda s}(\lambda +\kappa )V\mathrm{d}s\hfill \\ \hfill & \le \mathbb{E}V(x_0,0,i_0)+\mathbb{E}{\int }_0^t{e}^{\lambda s}(\lambda +\kappa )b_2|X_t{|}^p\mathrm{d}s.\hfill \end{array}$

Thus we obtain that

$b_1{e}^{\eta t}\mathbb{E}|X_t{|}^p\le V(x_0,0,i_0)+\mathbb{E}{\int }_0^t{e}^{\lambda s}{b}_2(\lambda +\kappa )|X_t{|}^p\mathrm{d}s,(28)$

Dividing both sides of Eq. 28 by b₁e^ηt, noting that b₂(λ + κ) < 0, we get

$\begin{array}{cc}\hfill \mathbb{E}|X_t{|}^p& \le \frac{e^{-\eta t}}{b_1}\mathbb{E}V(X_0,0,r_0)+\frac{e^{-\eta t}}{b_1}\mathbb{E}{\int }_0^t{e}^{\lambda s}{b}_2(\lambda +\kappa )|X_t{|}^p\mathrm{d}s\hfill \\ \hfill & \le \frac{e^{-\eta t}}{b_1}\mathbb{E}V(X_0,0,r_0).\hfill \end{array}$

Therefore, we obtain the required assertion

$\underset{t\to \infty }{\mathrm{lim\; sup}}\frac{1}{t}\log (\mathbb{E}|X_t{|}^p)<0.$

The proof is complete.

6 Example

In this section we give a numerical example to illustrate our results.

Example 1. Let ${\{r_t\}}_{t\ge 0}$ be a right-continuous Markov chain taking values in $\mathbb{S}=\{\mathrm{1,2}\}$ with invariant probability measure ${\mu }_1={\mu }_2=\frac{1}{2}$.Consider a risky asset, with the price dynamics:

$\left\{\begin{array}{c}\mathrm{d}{X}_t=f(X_t,t,r_r)\mathrm{d}t+\sigma (t,r_t)X_t\mathrm{d}{B}_t^H,\hfill \\ X_0=1,\hfill \end{array}\right.(29)$

on t ≥ 0. Here we take H = 0.7 and

$\left\{\begin{array}{c}f(x,t,i)=-4x,\sigma (t,i)=\frac{1}{t+1},\text{if\hspace{0.17em}}i=1,\hfill \\ f(x,t,i)=[2-\sin (x)]x,\sigma (t,i)=e^{-t},\text{if\hspace{0.17em}}i=2.\hfill \end{array}\right.$

Note that for all $i\in \mathbb{S}$, $\mathrm{d}{X}_t=f(X_t,t,i)\mathrm{d}t+\sigma (t,i)X_t\mathrm{d}{B}_t^H$ satisfy the hypothesises (i)-(v). Then, by Lemma 3.1, it is easy to show that Eq. 29 has a unique solution ${\{X_t\}}_{t\ge 0}$ as well. Set V(x, t, i) = x², for i = 1, 2.Noting that for some t₀ > 0 sufficiently large and all t > t₀, we have

$\begin{array}{cc}\hfill {\mathcal{L}}^{(1)}V(x,t,1)& =V_x(x,t,1)f(X_t,t,1)+V_{xx}(x,t,1)\frac{1}{t+1}x{D}_s^{\varphi }x\hfill \\ \hfill & \le -8x^2+2\frac{1}{t+1}x\left[xH{t}^{2H-1}\right]\hfill \\ \hfill & =-8x^2+o(1)x^2≔{\beta }_1{x}^2,\hfill \end{array}$

and

$\begin{array}{cc}\hfill {\mathcal{L}}^{(2)}V(x,t,2)& =V_x(x,t,2)f(X_t,t,2)+V_{xx}(x,t,2)e^{-t}x{D}_s^{\varphi }x\hfill \\ \hfill & =2x^2[2-\sin (x)]+o(1)x^2\hfill \\ \hfill & \le 6x^2+o(1)x^2≔{\beta }_2{x}^2.\hfill \end{array}$

Compute

$\sum _{i\in \mathbb{S}}{\mu }_i{\beta }_i=\frac{1}{2}(-8+6)+o(1)<0.$

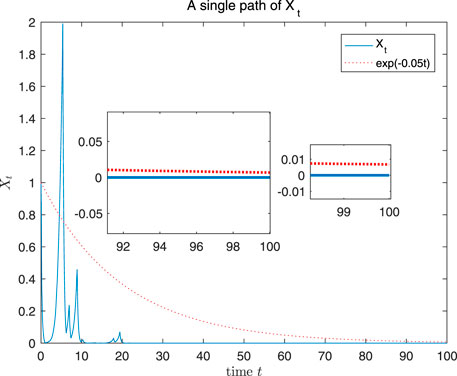
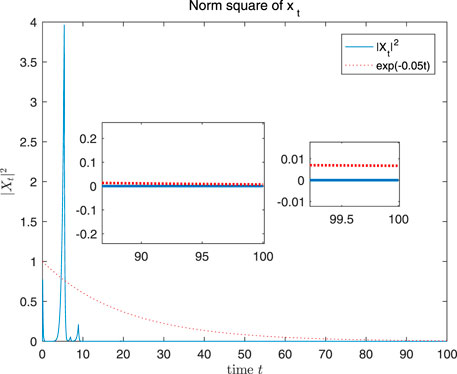
By Theorem 5.2, it’s clear that the solution of Eq. 29 is second moment exponential stable. Figures 1, 2 show a single path of the solution and the solution’s norm square, respectively.

FIGURE 1

FIGURE 1. A single path of solution.

FIGURE 2

FIGURE 2. Norm square trajectory.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

WP contributed to conception and design of the study. WP wrote the first draft of the manuscript. ZZ and WP wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The research of WP was supported by the Characteristic and Preponderant Discipline of Key Construction Universities in Zhejiang Province (Zhejiang Gongshang University-Statistics).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to thank the reviewers for careful reading of the paper and for helpful comments that led to improvement of the first version of this paper.

References

1. Yin GG, Zhu C. Hybrid switching diffusions: Properties and applications, Stoch. Model. Appl. Probab. New York: Springer (2010).

Google Scholar

2. Mao XR, Yuan CG. Stochastic differential equations with Markovian switching. South Kensington: Imperial College Process (2006).

Google Scholar

3. Hamilton JD. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica (1989) 57:357–84. doi:10.2307/1912559

CrossRef Full Text | Google Scholar

4. Mao X. Stability of stochastic differential equations with Markovian switching. Stochastic Process their Appl (1999) 79:45–67. doi:10.1016/s0304-4149(98)00070-2

CrossRef Full Text | Google Scholar

5. Yuan C, Mao X. Stability of stochastic delay hybrid systems with jumps. Eur J Control (2010) 16:595–608. doi:10.3166/ejc.16.595-608

CrossRef Full Text | Google Scholar

6. Zhou W, Yang J, Yang X, Dai A, Liu H, Fang JA. pth Moment exponential stability of stochastic delayed hybrid systems with Lévy noise. Appl Math Model (2015) 39:5650–8. doi:10.1016/j.apm.2015.01.025

CrossRef Full Text | Google Scholar

7. Yuan C, Mao X. Asymptotic stability in distribution of stochastic differential equations with Markovian switching. Stochastic Process their Appl (2003) 103:277–91. doi:10.1016/s0304-4149(02)00230-2

CrossRef Full Text | Google Scholar

8. Li X, Mao X. A note on almost sure asymptotic stability of neutral stochastic delay differential equations with Markovian switching. Automatica (2012) 48:2329–34. doi:10.1016/j.automatica.2012.06.045

CrossRef Full Text | Google Scholar

9. Wu H, Sun J. p-Moment stability of stochastic differential equations with impulsive jump and Markovian switching. Automatica (2006) 42:1753–9. doi:10.1016/j.automatica.2006.05.009

CrossRef Full Text | Google Scholar

10. Hurst HE. Long-term storage capacity in reservoirs. Trans Amer Soc Civil Eng (1951) 116:400–10. doi:10.1061/taceat.0006518

CrossRef Full Text | Google Scholar

11. Hurst HE. Methods of using long-term storage in reservoirs. Proc Inst Civil Eng (1956) 5:519–43. doi:10.1680/iicep.1956.11503

CrossRef Full Text | Google Scholar

12. Mandelbrot BB. The Fractal Geometry of Nature. San Francisco, CA: Freeman (1983).

Google Scholar

13. Mandelbrot BB. Fractals and Scaling in Finance: Discontinuity, Concentration, Risk. Berlin: Springer-Verlag (1997).

Google Scholar

14. Hu Y, Øksendal B. Fractional white noise calculus and applications to finance. Infin Dimens Anal Quan Probab. Relat. Top. (2003) 06:1–32. doi:10.1142/s0219025703001110

CrossRef Full Text | Google Scholar

15. Brody DC, Syroka J, Zervos M. Dynamical pricing of weather derivatives. Quantitative Finance (2002) 2:189–98. doi:10.1088/1469-7688/2/3/302

CrossRef Full Text | Google Scholar

16. Biagini F, Hu YZ, Øksendal B, Zhang TS. Stochastic calculus for fractional Brownian motion and applications. London: Springer-Verlag (2008).

Google Scholar

17. Mishura YS. Stochastic calculus for Fractional Brownian Motion and related process. Berlin: Springer-Verlag (2008).

Google Scholar

18. Li M. Modified multifractional Gaussian noise and its application. Phys Scr (2021) 96:125002. doi:10.1088/1402-4896/ac1cf6

CrossRef Full Text | Google Scholar

19. Li M. Generalized fractional Gaussian noise and its application to traffic modeling. Physica A (2021) 579:1236137. doi:10.1016/j.physa.2021.126138

CrossRef Full Text | Google Scholar

20. Li M. Multi-fractional generalized Cauchy process and its application to teletraffic. Physica A: Stat Mech its Appl (2020) 550:123982. doi:10.1016/j.physa.2019.123982

CrossRef Full Text | Google Scholar

21. Li M. Fractal time series a tutorial review. Math Probl Eng (2010) 2010:157264. doi:10.1155/2010/157264

CrossRef Full Text | Google Scholar

22. Ghosh MK, Arapostathis A, Marcus SI. Ergodic control of switching diffusions. SIAM J Control Optim (1997) 35:1952–88. doi:10.1137/s0363012996299302

CrossRef Full Text | Google Scholar

23. Skorohod AV. Asymptotic Methods in the Theory of Stochastic Differential Equations. US: American Mathematical Society (1989).

Google Scholar

24. Anderson WJ. Continuous-time Markov chain. New York: Springer (1991).

Google Scholar

25. Bardet JB, Gurin H, Malrieu F. Long time behavior of diffusions with Markov switching. ALEA Lat Am J Probab Math Stat (2010) 7:151–70.

Google Scholar

26. Cloez B, Hairer M. Exponential ergodicity for Markov processes with random switching. Bernoulli (2015) 21:505–36. doi:10.3150/13-bej577

CrossRef Full Text | Google Scholar

27. Alos E, Mazet O, Nualart D. Stochastic calculus with respect to Gaussian processes. Ann Probab (1999) 29:766–801.

Google Scholar

28. Nualart D, Răşcanu A. Differential equations driven by fractional Brownian motion. Collect Math (2000) 53:55–81.

Google Scholar

29. Holdeb H, Øksendal B, Ubøe J, Zhang T. Stochastic partial differential equations. Boston: Birkhäuser (1996).

Google Scholar

30. Duncan TE, Hu Y, Pasik-Duncan B. Stochastic Calculus for Fractional Brownian Motion I. Theory. SIAM J Control Optim (2000) 38:582–612. doi:10.1137/s036301299834171x

CrossRef Full Text | Google Scholar

31. Yan L, Pei WY, Pei W, Zhang Z. Exponential stability of SDEs driven by fBm with Markovian switching. Discrete Cont Dyn-a (2019) 39:6467–83. doi:10.3934/dcds.2019280

CrossRef Full Text | Google Scholar

32. Mao XR. Stochastic differential equations and applications. New York: Horwood (1997).

Google Scholar

33. Arcones MA. On the law of the iterated logarithm for gaussian processes. J Theor Probab (1995) 8:877–903. doi:10.1007/bf02410116

CrossRef Full Text | Google Scholar