Current-Driven Domain Wall Motion in Curved Ferrimagnetic Strips Above and Below the Angular Momentum Compensation

Current driven domain wall motion in curved Heavy Metal/Ferrimagnetic/Oxide multilayer strips is investigated using systematic micromagnetic simulations which account for spin-orbit coupling phenomena. Domain wall velocity and characteristic relaxation times are studied as functions of the geometry, curvature and width of the strip, at and out of the angular momentum compensation. Results show that domain walls can propagate faster and without a significant distortion in such strips in contrast to their ferromagnetic counterparts. Using an artificial system based on a straight strip with an equivalent current density distribution, we can discern its influence on the wall terminal velocity, as part of a more general geometrical influence due to the curved shape. Curved and narrow ferrimagnetic strips are promising candidates for designing high speed and fast response spintronic circuitry based on current-driven domain wall motion.

1 Introduction

A magnetic domain wall (DW) is the transition region that separates two uniformly magnetized domains [1]. These magnetic configurations are interesting due to fundamental physics, but also due to potential technological applications [2, 3]. In fact, during the last decades DWs have been at the core of theoretical and experimental studies which have provided with a deep understanding of different spin-orbit coupling phenomena [4–8]. For instance, straight stacks where an ultra-thin ferromagnetic (FM) layer is sandwiched between a heavy metal (HM) and an oxide (Ox), present perpendicular magnetic anisotropy (PMA) and therefore, the domains are magnetized along the out-of-plane direction of the stacks: up $(+{\vec{u}}_z)$ or down $(-{\vec{u}}_z)$. DWs in these HM/FM/Ox stacks adopt an homochiral configuration due to the Dzyaloshinskii-Moriya interaction (DMI) [5, 7, 9]. Adjacent DWs have internal magnetic moments along the longitudinal direction $({\vec{m}}_{DW}=\pm {\vec{u}}_x)$, and the sense is imposed by the sign of the DMI, which in turns depends on the HM [5]. For left-handed stacks such as Pt/Co/AlO, up-down (UD) and down-up (DU) DWs have internal moments with ${\vec{m}}_{DW}=-{\vec{u}}_x$ and ${\vec{m}}_{DW}=+{\vec{u}}_x$, respectively [5]. These DWs are driven with high efficiency by injecting electrical currents along the longitudinal direction of the HM/FM/Ox stack [4]. Due to the spin-Hall effect [5], the electrical current in the HM generates a spin polarized current which exerts spin-orbit torques (SOTs) on the magnetization of the FM layer, and drives series of homochiral DWs which are displaced along the longitudinal direction (x-axis). DW velocities of V_DW ∼ 500 m/s have been reported upon injection of current densities of J_HM ∼ 1 TA/m² in Pt/Co/AlO [4]. Consequently, these stacks have been proposed to develop highly-packed magnetic recording devices, where the information coded in the domains between DWs can be efficiently driven by pure electrical means. Both UD and DU DWs move with the same velocity along straight stacks, but some implementations of these memory or logic devices would require to design 2D circuits, where straight parts of HM/FM/Ox stack are connected each other with curved or semi-rings sections. However, recent experimental observations [10] and theoretical studies [11] have pointed out that adjacent UD and DU DWs move with different velocity along curved HM/FM/Ox stacks, which is detrimental for applications because the size of the domain between adjacent DWs changes during the motion, with the perturbation of the information coded therein. Therefore, other systems must be proposed in order to design reliable 2D circuits for DW-based memory and logic devices.

Other stacks with materials and/or layers with antiferromagnetic coupling, such as synthetic antiferromagnets (SAF) and ferrimagnetic (FiM), have proven to outperform FM in terms of current-driven DW dynamics [11–15]. Ultrafast magnetization dynamics in the THz regime, marginal stray field effects and insensitivity to external magnetic fields are other significant advantages of materials with antiferromagnetic coupling with respect to their FM counterparts. As conventional antiferromagnets (AFs), FiM alloys are also constituted by two specimens, typically a rare earth (RE) and transition metal (TM), that form two ferromagnetic sublattices antiferromagnetically coupled to each other. GdFeCo, GdFe, or TbCo are archetypal FiM alloys, with the RE being Gd or Tb and the TM being FeCo or Co. In contrast to AFs with zero net magnetization, the magnetic properties of FiMs, such as magnetization and coercivity, are largely influenced by the relative RE and TM composition (or equivalently, temperature). This fact offers additional degrees of freedom to control the current-driven DW velocity. The spontaneous magnetization of each sublattice M_S,_i can be tuned by changing the composition of the FiM and/or the temperature of the ambient (T) [13, 14]. For a given composition of the FiM (RE_xTM_1−x), there are two relevant temperatures below the Curie threshold. One is the magnetization compensation temperature (T_M) at which the saturation magnetization of the two sublattices are equal $(M_{s1}\left(T_M\right)=M_{s2}(T_M))$, so the FiM behaves as a perfect antiferromagnetic material, with zero net magnetization and diverging coercive field. The other is the temperature at which the angular momentum compensates, T_A, at which $M_{s1}\left(T_A\right)/{\gamma }_1=M_{s2}(T_A)/{\gamma }_2$, where γ_i is the gyromagnetic ratio of each sublattice (i:1,2 for 1:TM and 2:RE). As the gyromagnetic ratio depends on the Landé factors (g_i) which are different for each sublattice, the angular compensation temperature T_A is in general different from the magnetization compensation temperature (T_M). Consequently, the FiM have a net magnetization at T_A, so conventional techniques used for FMs can be also adopted to detect the magnetic state of FiM samples [16]. Moreover, recent experimental observations have evidenced that the current-driven DW velocity along straight HM/FiM stacks can be significantly optimized at the angular momentum compensation temperature (T = T_A), with velocities reaching V_DW ∼ 2000 m/s for typical injected density current of J_HM ∼ 1 TA/m² along the HM underneath [14]. The DW velocity drops either below (T < T_A) and above (T > T_A) angular momentum compensation. Note that alternatively to tuning the temperature for a fixed composition x of the FiM alloy RE_xTM_1−x, even working at room temperature (T = 300 K) the DW velocity peaks at a given composition where angular momentum compensates [13]. Therefore, both studies, either fixing the composition (x) and changing temperature of the ambient (T), or fixing the ambient temperature and modifying the FiM composition are equivalent for our purposes of DW dynamic. Although the current-driven DW motion (CDDWM) along HM/FiM stacks suggests their potential for memory and logic applications, previous studies have been mainly focused on straight FiM strips [13–15]. The further develop of novel DW-based devices also requires to analyze the dynamics of DWs along HM/FiM with curved parts which would connect straight paths to design any 2D circuit. Such investigation of the dynamics along curved is still missing, and it is the aim of the present study.

Here we theoretically explore the CDDWM along curved HM/FiM stacks by means of micromagnetic (μm) simulations. Our modeling allows us to account for the magnetization dynamics in the two sublattices independently. We explore the CDDWM below, at and above the angular momentum compensation (AMC) for different curved samples, with different widths and curvatures, and considering the realistic spatial distribution of the injected current along the HM. In particular, we will infer and isolate the relevance of different aspects governing such dynamics, as the role of the non-uniform current and other purely geometrical aspects of the curved shape. This work completes previous studies on straight samples [11, 13–15], and will be practical for designing more compact and efficient DW-based devices. The rest of the paper is organized as follows. In Section 2 we describe the numerical details of the micromagnetic model along with the material parameters and the geometrical details of the evaluated samples. Section 3 presents the micromagnetic results of the CDDWM in different scenarios. Firstly, exploring the role of the FiM sample width (w) for a fixed the curvature (ρ, given by the inverse of the average radius, ρ = 1/r_e), and secondly fixing the width and varying the curvature. After that, we present results which allow us to infer the role of non-uniform current and geometrical aspect (w, ρ) comparing curved and straight samples. The main conclusions are summarized in Section 4.

2 Materials and Methods

CDDWM is numerically studied here along curved HM/FiM stacks as schematically shown in Figure 1, where r_i and r_o are the inner and outer radius r_o respectively, and r_e = (r_o + r_i)/2 is the mean effective radius. w and t_FiM are the width and the thickness of the FiM respectively. The relaxed magnetization configuration of the sublattice i = 1, shown in Figure 1 (opposite configuration in sublattice i = 2), serves as the initial state to study the CDDWM upon of current injection along the HM underneath. The temporal evolution of the magnetization of each sublattice is given by the Landau-Lifshitz-Gilbert equation (LLG) [17],

$\begin{array}{l}\hfill \frac{d{\vec{m}}_i(t)}{dt}=-{\gamma }_{0,i}{\vec{m}}_i(t)\times {\vec{H}}_{e\mathit{ff},i}+{\alpha }_i{\vec{m}}_i\times \frac{d{\vec{m}}_i(t)}{dt}+{\vec{\tau }}_{SOT,i},\end{array}(1)$

where here the sub-index i stands for i: 1 and 2 sublattices respectively. γ_i = g_iμ_B/ℏ and α_i are the gyromagnetic ratios and the Gilbert damping constants, respectively. g_i is the Landé factor of each layer, and ${\vec{m}}_i\left(\vec{r},t\right)={\vec{M}}_i/M_{s,i}$ is the normalized local magnetization to its saturation value (M_s,_i), defined differently for each sublattice: M_s,_i(i: 1, 2). In our micromagnetic model the FiM strip is formed by computational elementary cells, and within each cell we have two magnetic moments, one for each component of the FiM. The respective effective field $({\vec{H}}_{e\mathit{ff},i})$ acts on the local magnetization of each sublattice $({\vec{m}}_i\left(\vec{r},t\right))$, and it is the sum of the magnetostatic, the anisotropy (PMA), the DMI and the exchange fields [11, 15]. The magnetostatic field on each local moment in the sublattice is numerically computed from the average magnetization of each elementary cell using similar numerical techniques as for the single FM case (see [11, 15]). We checked that the demagnetising field has a marginal influence in the simulation results compared to other contributions to the effective field. For the PMA field, the easy axis is along the out-of-plane direction (z-axis), and the anisotropy constants for each sublattice are K_u,_i (PMA constant). D_i is the DMI parameter for each sublattice i: 1, 2 [11, 15]. The exchange field of each sublattice includes the interaction with itself (intra-lattice exchange interaction, ${\vec{H}}_{exch,i}$) and with the other sublattice (inter-lattice exchange interaction, ${\vec{H}}_{exch,12}$). The inter-lattice exchange effective field is computed as for a single FM sample, $H_{exch,i}=\frac{2A_i}{{\mu }_0{M}_{s,i}}{\nabla }^2{\vec{m}}_i$, where A_i is the intralattice exchange parameter. The inter-lattice exchange contribution ${\vec{H}}_{exch,12}$ to the effective field ${\vec{H}}_{e\mathit{ff},i}$, acting on each sublattice is computed from the corresponding energy density, ${\omega }_{exch,i}=-B_{ij}{\vec{m}}_i\cdot {\vec{m}}_j$, where B_ij [in (J m⁻³)] is a parameter describing the inter-lattice exchange coupling between sublattices (here, we used the notation i: 1 and j: 2).

FIGURE 1

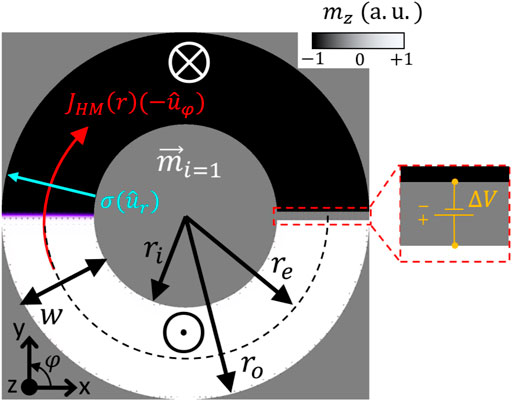
FIGURE 1. Scheme showing the relaxed states of spins in sub-lattice i = 1, in the positive z-direction (white domain), in the negative z-direction (black domain) and in the plane of the strip for an “Up to Down” (UD) domain wall (purple) according to the current direction, for an exemplary curved strip. The direction of the applied electric current (red arrow) in the Heavy Metal beneath the magnetic strip, generated from a potential difference ΔV (see inset), is shown as well as the geometrical parameters of the strip.

In Eq. 1, ${\vec{\tau }}_{SOT,i}$ are the SOTs acting on each sublattice, which are related to the electrical current along the HM $({\vec{J}}_{HM})$. Based on preliminary studies [18], here we assume that ${\vec{\tau }}_{SOT,i}$ is dominated by the spin Hall effect (SHE), so ${\vec{\tau }}_{SOT,i}=-{\gamma }_0{H}_{SL}{\vec{m}}_i\times \left({\vec{m}}_i\times \vec{\sigma }\right)$ where $H_{SL}=\frac{\hslash {\theta }_{SH,i}{J}_{HM}}{2\left|e\right|{\mu }_0{M}_s{t}_{FiM}}$ [19]. ℏ is the Planck constant, and θ_SH,_i is the spin Hall angle, which determines the ratio between the electric current and the spin current (J_s = θ_SHJ_HM) for each sublattice. $\vec{\sigma }={\vec{u}}_J\times {\vec{u}}_z$ is the unit vector along the polarization direction of the spin current generated by the SHE in the HM, being orthogonal to both the direction of the electric current ${\vec{u}}_J$ and the vector ${\vec{u}}_z$ standing for the normal to the HM/FiM interface. For a longitudinal current $({\vec{u}}_J={\vec{u}}_x)$, the spin current is polarized along the transverse direction, $\vec{\sigma }=-{\vec{u}}_y$. For curved samples where the current density ${\vec{J}}_{HM}=J_{HM}\left(r\right){\vec{u}}_J$ has azimuthal direction $({\vec{u}}_J={-\vec{u}}_{\varphi })$, the direction of the polarization is radial, $\vec{\sigma }={\vec{u}}_J\times {\vec{u}}_z={\vec{u}}_r$, as shown in Figure 1. A potential difference is applied between the ends of the curved track to inject current in the right circulation. Therefore, a gap of 25 nm is also modelled, leading to a split ring shape for the strip (see inset in Figure 1). The spatial distribution of current as a function of the radial coordinate (r_i < r < r_o) is taken from [11, 20], and it depends on the width (w) and the radial distance (r) as $J_{HM}\left(r\right)=J_{0}w/(r\log \left(1+w/r_i\right))$, where J₀ is the nominal, uniform current density, in an equivalent straight strip of same cross-section (w × t_HM, where t_HM is the thickness of the HM strip).

In order to illustrate the current-driven DW dynamics along curved HM/FiM stacks we fix t_FiM = 6 nm, and samples with different widths (w) and radii (r_e) were evaluated. The following common material parameters were adopted for the two sublattices i: 1, 2: A_i = 70 pJ/m, K_u,_i = 1.4 × 10⁶ J/m³, α_i = 0.02, D_i = 0.12 J/m², θ_SH,_i = 0.155. The strength of the antiferromagnetic coupling between the sublattices was fixed to B_ij ≡ B₁₂ = − 0.9 × 10⁷ J/m³. The gyromagnetic ratios (γ_i = g_iμ_B/ℏ) are different due to the different Landé factor: g₁ = 2.05 and g₂ = 2.0. The saturation magnetization of each sublattice M_s,_i can be tuned with the composition of the FiM and/or with the temperature of the ambient (T). Here, we assume the following temperature dependences for each sublattice: $M_{s,i}\left(T\right)=M_{s,i}(0){\left(1-\frac{T}{T_C}\right)}^{a_i}$, where T_C = 450 K is the Curie temperature of the FiM, $M_{s,1}\left(0\right)=1.4\times {10}^6$ A/m and $M_{s,2}\left(0\right)=1.71\times {10}^6$ A/m are the saturation magnetization at zero temperature, and a₁ = 0.5 and a₂ = 0.76 are the exponents describing the temperature dependence of the saturation magnetization of each sublattice. The temperature at which the net saturation magnetization vanishes [M_s,₁(T_M) = M_s,₂(T_M)] is T_M = 241.5 K, and the angular momentum compensation temperature corresponding to M_s,₁(T_A)/g₁ = M_s,₂(T_A)/g₂, is T_A = 260 K. We evaluate the CDDWM below, at and above the angular momentum compensation adopting three representative temperatures: T = 220 K $<T_A$, T = 260 K = T_A and T = 300 K $>T_A$. Samples were discretized using a 2D finite difference scheme using computational cells with Δx = Δy = 0.2 nm and Δz = t_FiM. Several tests were carried to certify that the presented results are free of discretization errors.

3 Micromagnetic Results

Due to the several combination of parameters to consider in our study, we divided this section in three sub-sections: (A) The study on the influence of the strip width (w); (B) the study on curvature $(\rho =r_e^{-1})$; and (C) same studies for a straight strip with identical material parameters, to explore by comparison the effects of curvature on the DW dynamics. In parts (A) and (B), scenarios for three different temperatures, T₁ = 220 K, T₂ = 260 K, T₃ = 300 K are considered, to study the DW motion below the AMC (T₁), at the AMC (T₂) and above the AMC (T₃). We also define and refer to T₃ = 300 K as for “room temperature” in our study. Note that a change in temperature only affects M_S in our model, therefore it has equivalent effects to changing material composition [13]. In addition to DW velocity, we also characterize the inertial motion of the DW as a function of current density. As an example, Figure 2 shows typical results of the DW position and its velocity in a ring-like strip (w = 256 nm and r_e = 384 nm) under a density current J_HM = 2 TA/m² and at T = 260 K. Qualitatively similar results are obtained at T = 220 K and T = 300 K (not shown). Insets show the (clockwise) DW displacement as a function of time for one sublattice (i = 1).

FIGURE 2

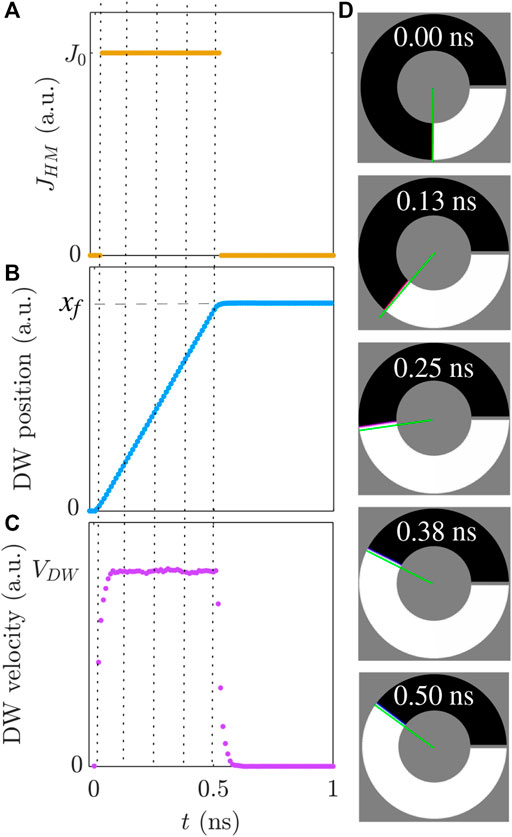
FIGURE 2. Micromagnetic results of applying a uniform J_HM = J₀ = 2 TA/m² (A) showing the relative and final position x_f (B) and velocity V_DW (C), as a function of time t, of an UD DW in a curved strip (w = 256 nm and r_e = 384 nm), at T = 260 K. Insets (D) are snapshots of the magnetic configuration in sublattice i = 1 at different times [highlighted by the vertical dotted lines in (A–C)]. Green solid lines are for guiding the eye and are co-parallel with the strip radius.

3.1 Influence of Width for a Fixed Curvature

In this study, the curvature is fixed (r_e = 384 nm) and width (w) is varied from 56 to 296 nm in steps of 40 nm. Figure 3 shows the results for the terminal DW velocity (|V_DW,_i|) as a function of the nominal density current J_HM = j₀, equivalent to the homogeneous density current in a straight strip with the same cross-section. In the next sections, we use the notation J_HM = J for simplicity. Figure 3 shows that temperature has a noticeable effect on the terminal velocity on the DW type equally, Up to Down domain (UD) or Down to Up domain (DU). As it was expected from previous work on straight FiM strips [11, 13], at T_A the DW velocities are greater. Also, the DW velocities increase for narrower strips (red symbols). In fact, the observed trend is very similar to straight strips: the terminal velocity is maximum at the temperature of AMC, T_A = 260 K and significantly increased, exceeding 2000 m/s for the narrowest strip as compared to ∼1800 m/s for the widest. These results also suggest that the DWs velocities are equal for both types of DWs (UD and DU), which would lead to no distortion of the size of a domain between two adjacent DWs travelling along the curved strip. This result is significantly different from FM systems [11].

FIGURE 3

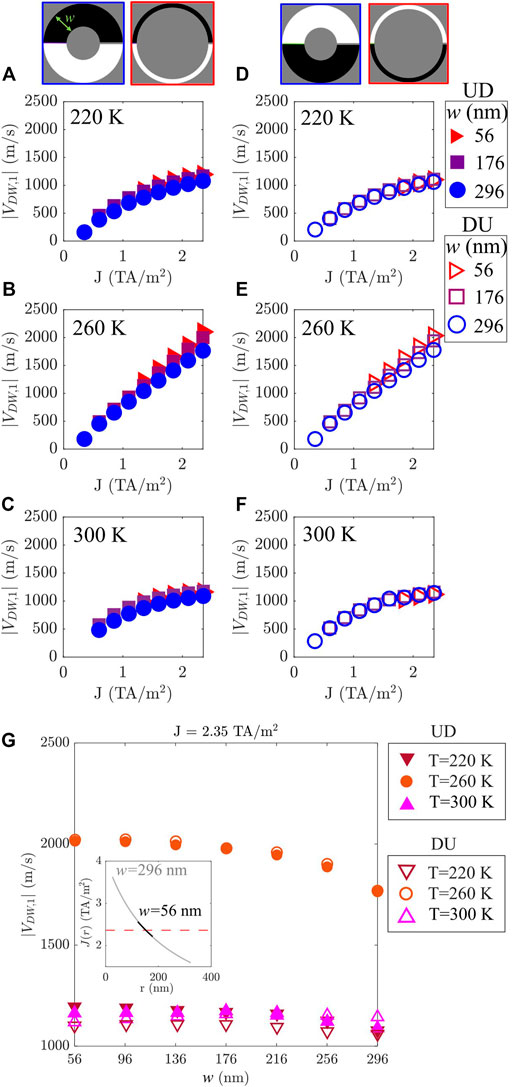
FIGURE 3. Terminal velocities as a function of J for a UD (A–C) and a DU (D–F) DW obtained for sub-lattice i = 1 and for three different temperatures: below, above and at the AMC temperature (220, 300, and 260 K, respectively). Strips for the two limiting cases are shown in the red and blue contour insets at the top. (G) Terminal velocities as a function of w for a UD (full symbols) and a DU (open symbols) type wall for J = 2.35 TA/m² and the three chosen temperatures. Inset in (G) shows J(r) for two values of w. Red dashed line indicates J = 2.35 TA/m².

At T ≠ T_A, the DW velocity is reduced either increasing or reducing temperature with respect to T_A, leading to velocities around 1100 m/s, generally regardless of the width and DW type. For a given J value, as the strip gets wider, however, the velocity is slightly smaller but these differences are negligible (see Figures 3A,C,D,F). This result contrasts with that of a FM strip, where a greater difference of velocities between a DU and a UD along a curved strip was shown [11].

To characterize the inertial motion of the DW, we evaluate the temporal evolution of the DW velocity [V(t), computed from the spatial averaging of m₁,_z(t)] as a function of time (or instant velocity) under a current square pulse of duration 0.1 ns and start at t = 0. The μm results can be fitted to the following exponentials: $V_{\infty }(1-e^{-t/{\tau }_r})$ during the duration of the pulse (t ≤ 0.1 ns), and $V_{\infty }{e}^{-t/{\tau }_f}$, after the pulse ends (t > 0.1 ns), where V_∞ is the DW terminal velocity (see Figures 2A–F). The characteristic relaxation times τ_r (or rising time) and τ_f (or fall time) represent the duration of such transients and characterize the inertial motion of the DW. These parameters can be extracted by fitting the μm results to the exponentials (see solid curves in Figure 4A).

FIGURE 4

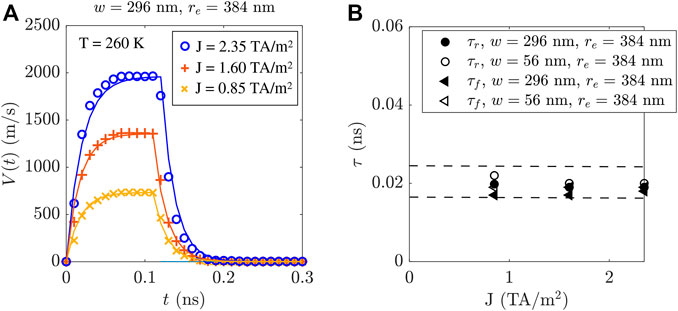
FIGURE 4. Instantaneous DW velocities V(t) for three values of J and for a curved strip of r_e = 384 nm and w = 296 nm at T = T_A (A). Symbols are the μm data, from which τ (rise and fall times) are extracted for the narrowest and widest strips (B). Dashed lines in (B) are the upper and lower bounds of a 95% confidence interval.

Although simulations were performed for both types of DWs, note that we only present here results for the DU type wall, for sake of simplicity. Identical results (not shown) were obtained for the UD DW. Figure 4A show the “instantaneous” DW velocity V(t) and the relaxation times τ for three selected values of J (see solid symbols) at T = T_A for the widest strip (w = 296 nm). Solid lines are the exponential curves to which the obtained simulated data is fit. For each current, the minimal τ is expected for T = T_A = 260 K. Figure 4B shows that τ_r and τ_f for the two limiting cases (w = 56 nm and w = 296 nm) are quantitatively similar, in the order of 0.02 ns, since they fall within the 95% confidence interval, set by the largest error bars obtained for τ from the fitted results, among all J. Also, all values are similar in order to the step-size used in simulations, 0.01 ns (see Figure 4D).

Similar values of τ were obtained for strips of other widths. Relaxation times are not noticeably influenced by temperature, and they generally remain within the range of 0.01 ∼0.03 ns for T = 200 K and T = 300 K. This is more than one order of magnitude smaller than in FM strips, the latter being about $\sim 1$ ns according to Ref. [21]. Besides, the relaxation times of current-driven DWs in curved strips found here are in good agreement with those from field-driven or thermally driven DWs in antiferromagnetic straight strips, in the order of picoseconds [22, 23].

3.2 Influence of Curvature for a Fixed Width

In this study, the strip width is fixed to w = 256 nm and the curvature parameter ρ is varied. In other words, the equivalent radii r_e (r_e = ρ⁻¹) is varied from 134 to 534 nm in steps of 50 nm. Figure 5 shows the results for the terminal velocity (|V_DW,₁|) of DU and UD DWs, for several values of r_e in nanometers, where the red (blue) curve corresponds to the smaller (greater) values, for three different temperatures.

FIGURE 5

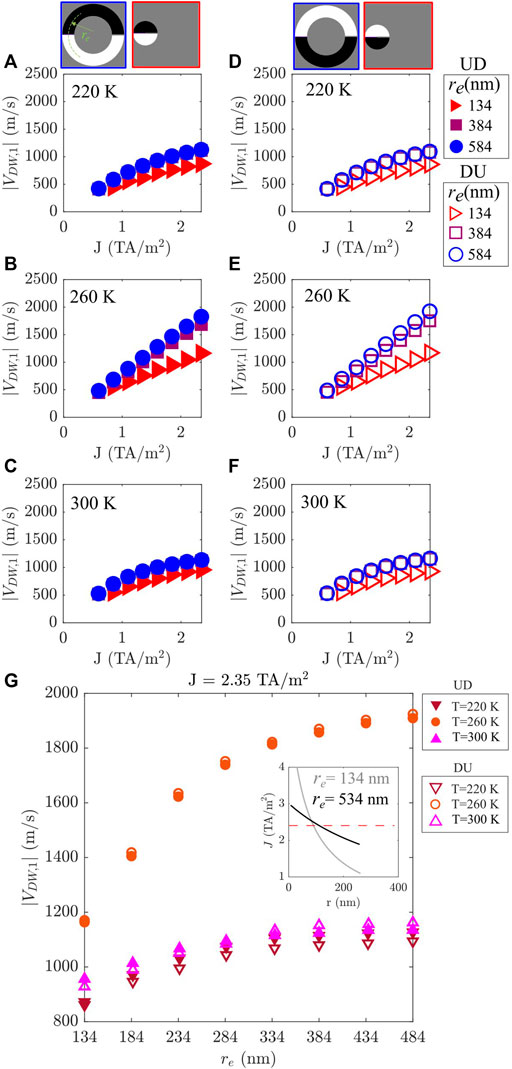
FIGURE 5. Terminal velocities as a function of J for a UD (A–C) and a DU (D–F) DW in the curved strip obtained for sub-lattice i = 1 and for three different temperatures: below, above and at the AMC temperature (220, 300, and 260 K, respectively). Strips for the two limiting cases are shown in the red and blue contour insets at the top. (G) Terminal velocities as a function of r_e for a UD (full symbols) and a DU (open symbols) type wall for J = 2.35 TA/m² and the three chosen temperatures. Inset in (G) shows J(r) for two values of r_e. Red dashed line indicates J = 2.35 TA/m².

Figures 5A–F shows that, at T = T_A and for a given curvature, the DW velocities of DU and UD types are very similar for the whole range of currents explored. DW velocity reduces as the curvature increases (see Figure 5G). It is worth noting that the latter cannot be a consequence of only a nonuniform J(r) as defined in [11]. In fact, for curved-most strips (r_e = 134 nm), the spatial-dependent density current J(r) varies with r similarly as it does for changing w (see inset in Figures 3G, 5G), which would suggest similar variations to DW velocities as those found in Figure 3G. In other words, the impact of the non-uniform J(r) is not so relevant to be the only source of the big differences between the DW velocities for large and small curvatures (orange symbols in Figure 5G for r_e = 134 nm and r_e = 484 nm, respectively). Figure 5G also shows that as the strip curvature is reduced, DW velocity converges to the straight strip case (r_e → ∞).

For T ≠ T_A, the dependence of the DW velocity with temperature is minimal regardless of the DW type. As the strip curvature increases there is a prominent change in the maximal terminal DW velocity for both DW types. However, the relative difference of velocities is almost negligible. Therefore, results suggest that the strip curvature affects in a similar way to width, and equally, to both DWs. In other words, the terminal velocity is significantly reduced as curvature (or width) increases, while the differences between DWs remain negligible (see Figure 5G). This behavior is even more pronounced at T = T_A. As discussed in Section 3. A, the latter would imply that the robustness of a transmitted bit, encoded in a domain between two DWs, can be optimised in such curved-most strips and reaches larger velocities in the strip.

Figure 6A show the DW velocity as a function of time and for three selected values of J for an effective radius of r_e = 534 nm (least curved strip) and intermediate width w = 256 nm, at T = T_A. Results look quantitatively similar to those shown in Figure 4A, where r_e was fixed to an intermediate value of 384 nm.

FIGURE 6

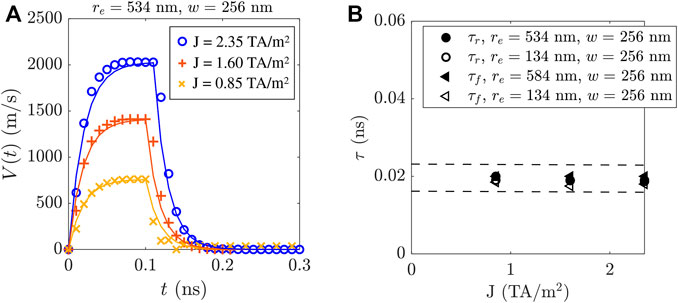
FIGURE 6. Instantaneous DW velocities V(t) for three values of J and for a curved strip of r_e = 584 nm and w = 256 nm at T = T_A (A). Symbols are the μm data, from which τ (rise and fall times) are extracted for the narrowest and widest strips (B). Dashed lines in (B) are the upper and lower bounds of a 95% confidence interval.

As in Figures 4B, 6B shows that τ_r and τ_f for the two limiting cases (r_e = 134 nm and r_e = 534 nm) are quantitatively similar, in the order of 0.02 ns. For all the FiM curved strips explored at, above and below AMC, τ_r and τ_f remain within the range of 0.01 ∼0.03 ns, approximately one order of magnitude less than their FM counterparts. This is in good agreement with results presented in the previous section and other work in straight strips [8], which further supports the negligible inertia of DWs in such FiM systems.

3.3 Discussion on the Effective Influence of a Curved Shape on the Wall Velocity

A non-uniform current distribution is expected to influence the terminal velocity of the DW for a given curvature, specially for wide curved strips [11]. In this section, to explore further the degree of influence of the non-uniform current, equivalent studies on w and ρ on a straight strip with an artificially implemented non-uniform J(r = y) at T = T_A are performed. A straight strip is a bounding case for a curved strip that shows no effective curvature (r_e → ∞, ρ → 0) and an homogeneous density current J = J₀. Therefore, we explore whether “curvature (ρ) effects” are mainly dominated by the intrinsic inhomogenous current, or whether they can also arise from the curved shape itself [24]. We aim to discern the actual influence of an inhomogeneous current, as part of an more global effect due to the curved shape. For the following study, and since the straight shape must be retained, r_e (or equivalently ρ) is artificially modified in the non-uniform current distribution expression: $\vec{\text{J}}(y,w,r_e)$ [11] in the x-direction, as if the strip was curved. Note that ρ represents the inverse of the averaged or effective curvature radius of the strip $(\rho =r_e^{-1})$ and not the cylindrical radial coordinate (r) in the system.

Figures 7A,B show the velocity of an UD wall in the straight strip for J = J₀ = 2.35 TA/m² (black crosses) and for an inhomogeneous J(y) (blue circles), varying r_e in J(y, r_e) (see insets) for a fixed width w = 256 nm, and varying width (w) for a fixed r_e, J(y, r_e = 384). While it is expected that an inhomogeneous J(y, w, r_e) will influence the DW velocity [especially for curved-most strips, see r_e = 134 nm in (a)], the differences with the case of J = J₀ are almost negligible. Figures 7C,D show results for curved strips. For these cases, w and r_e are naturally varied in J(r, w, r_e) by modifying the shape itself. From the standpoint of the applied current, this is expected to be equivalent to doing it by changing the shape itself. Results from an inhomogeneous current (blue circles, reproduced from Figures 3G, 5G) consistently tend to converge to the straight strip as ρ is reduced. The strip is straight when ρ = 0 (r_e → ∞).

FIGURE 7

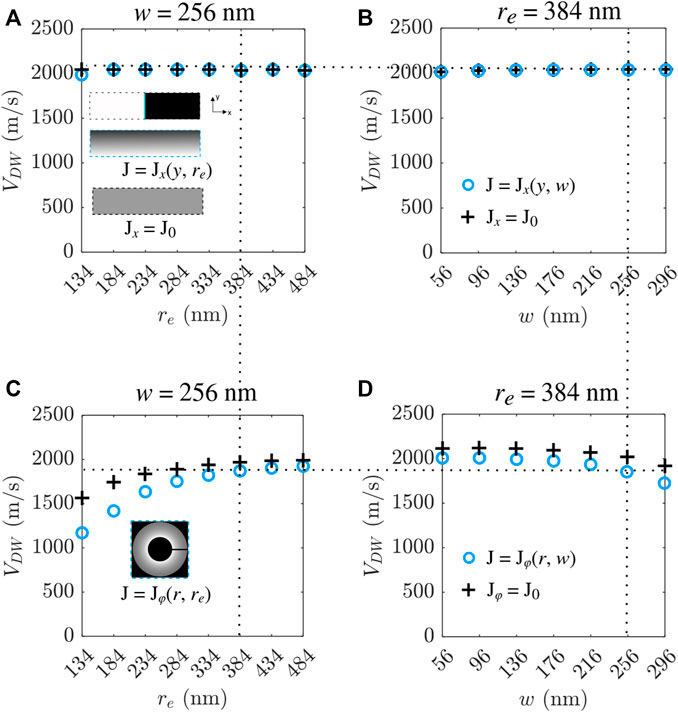
FIGURE 7. DW terminal velocities in a straight strip for an inhomogeneous J(y, w, r_e) (blue circles) and for a uniform J₀ (black crosses) as a function of radius r_e (A) and width w (B) at same temperature (T = 260 K). Insets in (A) show the magnetic configuration of sublattice i = 1 at t = 0 and schematics of the current spatial distribution in the strips as examples. (B) DW terminal velocities in a curved strips with the same parameters as a function of radius r_e (C) and width w (D). As an example, inset in (C) shows the radial dependence of an inhomogenous current distribution in such a strip. Dotted lines highlight the cases where the two geometrical parameters (w and r_e) are coincident among all the studies.

When the strip is either straight (a-b) or curved (c-d), for both studies (fixing w and varying r_e or vice-versa), the DW velocity is found to be the same when the geometrical parameters are coincident, i.e., w = 256 nm and r_e = 384 nm, as expected [see horizontal dotted lines in (a-b) or (c-d)]. However, when the shape is different, even in the cases when w and r_e are coincident (and therefore, J(w, r_e) is expected to also be the same), different DW velocities are obtained [see vertical dotted lines in (a-c) and (b-d)] below and slightly above 2000 m/s, respectively. Moreover, by modifying either r_e or w in the curved strip by directly changing its shape [see (c-d) and previous sections], there is a clear larger impact on DW velocity, than by artificially (but equivalently) modifying r_e or w in the straight strip [see (a-c)]. In the curved strips, the trend when varying r_e or w is qualitatively similar regardless to the homogeneity of the applied J [see black crosses and blue circles in either (c) or (d)]. Since J(r) is modeled in an equivalent way in all studies by simply changing J(r) = J(y) for the straight strip, marked differences between the wall velocity in (a-b) (straight strip) and (c-d) (curved strip), specially for very curved strips, suggest that not only the non-uniform J(r) is influencing the UD DW motion.

Our results suggest that the curved shape may have an intrinsic influence on the wall velocity, manifested as a more marked dependence with w and r_e, regardless of the inhomogeneity of the current density [see Fig. (c–d)], as the shape becomes more curved. An influence due to the inhomogeneous current, still appears naturally in the curved strip, but may have a lesser impact compared to other geometrical factors (see differences between black crosses and blue circles).

4 Discussion and Summary

We have provided a study on DW motion in curved FiM strips, particularised to one of the two strongly coupled sub-lattices, for three different temperatures, and as a function of geometrical parameters for a HM/FiM/Ox multilayer structure. We observe an absence of tilting of the DW and domain distortion at different temperatures, 40 K above and below the angular momentum compensation temperature.

Width and curvature effects on the DW velocity are discussed. Besides contributions from a non-uniform J(r), there is an overall significant influence from the shape of the strip itself on DW velocity. This implies that, for a fixed temperature (or composition), DW velocity can be optimised by optimising the geometrical parameters of the curved strip. The relative differences between a DU and a UD walls are marginal in general. In other words, geometrical factors affect them almost equally, which is positive for a robust transmission of a bit encoded in an Up or Down domain between two adjacent DWs. With reducing current, differences in velocities between curved and straight strips are still minimised at the expense of slower DWs. Similar effect is observed as width or curvature is increased. This is beneficial for designing intricate 2D circuit tracks combining curved and straight sections, while preserving DW velocities still larger than those found in their FM counterparts. Also, DWs in a curved FiM strip show a negligible inertia in contrast to their FM counterparts (τ_FiM ≪ τ_FM) for all the explored scenarios. The DWs start to move and stop almost immediately (τ_FiM ∼ 0.02 ns) after the application or removal of current.

Considering the obtained results altogether and assuming T ≠ T_A, which will be most of the experimental cases at room temperature (T = 300 K), our study allows us to conclude that narrow enough FiM strips are ideal candidates for designing curved tracks for 2D spintronic circuits of an arbitrary shape based on CDDWM, where bits are encoded in domains separated by walls. This is due to very fast rise and fall times (τ_r ∼ τ_f ≪ 0.1 ns), high velocities (V_DW > 1000 m/s) and negligible distortion of the two types of DWs (UD and DU) in all the scenarios explored in this work. Greater DW terminal velocities and smaller time responses in curved FiM strips than those in their FM counterparts are obtained. These results can help in the further research, development and improvement of FiM-based spintronic circuitry that may require compactness and high-speed functionality with high robustness to DW (and/or domain) distortion.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

DOR performed the micromagnetic simulations, designed the numerical experiments, performed the analysis of data and wrote the manuscript. VR provided with the micromagnetic code, OA and EM provided with the idea for the research and EM also contributed to the writing of the manuscript.

Funding

This work was supported by the project SA114P20 from Junta de Castilla y Leon (JCyL), and partially supported by the projects SA299P18 from JCyL, MAT2017-87072-C4-1-P and PID2020-117024GB-C41 from the Ministry of Economy, Spanish government, and MAGNEFI, from the European Commission (European Union). All data created during this research are openly available from the University of Salamanca’s institutional repository at https://gredos.usal.es/handle/10366/138189.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hubert A, Schäfer R. Magnetic Domains: The Analysis of Magnetic Microstructures. New York, NY, United States. Springer-Verlag Berlin Heidelberg (1998).

Google Scholar

2. Parkin SSP. Shiftable Magnetic Shift Register and Method of Using the Same. US6834005B1 (2004).

Google Scholar

3. Parkin S, Yang S-H. Memory on the Racetrack. Nat Nanotech (2015) 10:195–8. doi:10.1038/nnano.2015.41

CrossRef Full Text | Google Scholar

4. Miron IM, Moore T, Szambolics H, Buda-Prejbeanu LD, Auffret S, Rodmacq B, et al. Fast Current-Induced Domain-wall Motion Controlled by the Rashba Effect. Nat Mater (2011) 10:419–23. doi:10.1038/nmat3020

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Emori S, Bauer U, Ahn S-M, Martinez E, Beach GSD. Current-driven Dynamics of Chiral Ferromagnetic Domain walls. Nat Mater (2013) 12:611–6. doi:10.1038/nmat3675

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Haazen PPJ, Murè E, Franken JH, Lavrijsen R, Swagten HJM, Koopmans B. Domain wall Depinning Governed by the Spin Hall Effect. Nat Mater (2013) 12:299–303. doi:10.1038/nmat3553

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ryu K-S, Thomas L, Yang S-H, Parkin S. Chiral Spin Torque at Magnetic Domain walls. Nat Nanotech (2013) 8:527–33. doi:10.1038/nnano.2013.102

CrossRef Full Text | Google Scholar

8. Torrejon J, Martinez E, Hayashi M. Tunable Inertia of Chiral Magnetic Domain walls. Nat Commun (2016) 7:13533. doi:10.1038/ncomms13533

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Dzyaloshinsky I. A Thermodynamic Theory of "weak" Ferromagnetism of Antiferromagnetics. J Phys Chem Sol (1958) 4:241–55. doi:10.1016/0022-3697(58)90076-3

CrossRef Full Text | Google Scholar

10. Garg C, Yang S-H, Phung T, Pushp A, Parkin S. Dramatic Influence of Curvature of Nanowire on Chiral Domain wall Velocity. Sci Adv (2017) 3:e1602804. doi:10.1126/sciadv.1602804

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Alejos O, Raposo V, Martínez E. Domain wall Motion in Magnetic Nanostrips. In: Materials Science and Technology. Berlin, Germany. American Cancer Society (2020). p. 1–49. doi:10.1002/9783527603978.mst0459

CrossRef Full Text | Google Scholar

12. Yang S-H, Ryu K-S, Parkin S. Domain-wall Velocities of up to 750 M S−1 Driven by Exchange-Coupling Torque in Synthetic Antiferromagnets. Nat Nanotech (2015) 10:221–6. doi:10.1038/nnano.2014.324

CrossRef Full Text | Google Scholar

13. Siddiqui SA, Han J, Finley JT, Ross CA, Liu L. Current-Induced Domain Wall Motion in a Compensated Ferrimagnet. Phys Rev Lett (2018) 121:057701. doi:10.1103/physrevlett.121.057701

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Caretta L, Mann M, Büttner F, Ueda K, Pfau B, Günther CM, et al. Fast Current-Driven Domain walls and Small Skyrmions in a Compensated Ferrimagnet. Nat Nanotech (2018) 13:1154–60. doi:10.1038/s41565-018-0255-3

CrossRef Full Text | Google Scholar

15. Martínez E, Raposo V, Alejos Ó. Current-driven Domain wall Dynamics in Ferrimagnets: Micromagnetic Approach and Collective Coordinates Model. J Magnet Magn Mater (2019) 491:165545. doi:10.1016/j.jmmm.2019.165545

CrossRef Full Text | Google Scholar

16. Arpaci S, Lopez-Dominguez V, Shi J, Sánchez-Tejerina L, Garesci F, Wang C, et al. Observation of Current-Induced Switching in Non-collinear Antiferromagnetic IrMn3 by Differential Voltage Measurements. Nat Commun (2021) 12:3828. doi:10.1038/s41467-021-24237-y

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Landau L, Lifshitz E. On the Theory of the Dispersion of Magnetic Permeability in Ferromagnetic Bodies. Phys Zeitsch der Sow (1935) 8:153–69.

Google Scholar

18. Martinez E, Emori S, Perez N, Torres L, Beach GSD. Current-driven Dynamics of Dzyaloshinskii Domain walls in the Presence of In-Plane fields: Full Micromagnetic and One-Dimensional Analysis. J Appl Phys (2014) 115:213909. doi:10.1063/1.4881778

CrossRef Full Text | Google Scholar

19. Slonczewski JC. Current-driven Excitation of Magnetic Multilayers. J Magnet Magn Mater (1996) 159:L1–L7. doi:10.1016/0304-8853(96)00062-5

CrossRef Full Text | Google Scholar

20. Alejos O, Raposo V, Sanchez-Tejerina L, Tomasello R, Finocchio G, Martinez E. Current-driven Domain wall Dynamics in Ferromagnetic Layers Synthetically Exchange-Coupled by a Spacer: A Micromagnetic Study. J Appl Phys (2018) 123:013901. doi:10.1063/1.5009739

CrossRef Full Text | Google Scholar

21. Thiaville A, Nakatani Y, Piéchon F, Miltat J, Ono T. Transient Domain wall Displacement under Spin-Polarized Current Pulses. Eur Phys J B (2007) 60:15–27. doi:10.1140/epjb/e2007-00320-3

CrossRef Full Text | Google Scholar

22. Gomonay O, Jungwirth T, Sinova J. High Antiferromagnetic Domain Wall Velocity Induced by Néel Spin-Orbit Torques. Phys Rev Lett (2016) 117:017202. doi:10.1103/physrevlett.117.017202

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Selzer S, Atxitia U, Ritzmann U, Hinzke D, Nowak U. Inertia-Free Thermally Driven Domain-Wall Motion in Antiferromagnets. Phys Rev Lett (2016) 117:107201. doi:10.1103/physrevlett.117.107201

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Yang L. Pinning Effect on Current-Induced Domain Wall Motion in Nanostrip. East Asian J Appl Math (2017) 7:837–51. doi:10.4208/eajam.181016.300517d

CrossRef Full Text | Google Scholar