Observation of the Rotational Doppler Effect With Structured Beams in Atomic Vapor

A vector beam with the spatial variation polarization has attracted keen interest and is progressively applied in quantum information, quantum communication, precision measurement, and so on. In this letter, the spectrum observation of the rotational Doppler effect based on the coherent interaction between atoms and structured light in an atomic vapor is realized. The geometric phase and polarization of the structured beam are generated and manipulated by using a flexible and efficacious combination optical elements, converting an initial linearly polarized Gaussian beam into a phase vortex beam or an asymmetric or symmetric vector beam. These three representative types of structured beam independently interact with atoms under a longitudinal magnetic field to explore the rotational Doppler shift associated with the topological charge. We find that the rotational Doppler broadening increases obviously with the topological charge of the asymmetric and symmetric vector beam. There is no rotational Doppler broadening observed from the spectrum of the phase vortex beam, although the topological charge, and spatial profile of the beam change. This study can be applied to estimate the rotational velocity of the atom-level or molecule-level objects, measure the intensity of magnetic fields and study the quantum coherence in atomic ensembles.

1 Introduction

The quantum coherent interaction of light with an atomic system results in various fascinating phenomena. For instance, Hanle effect [1], coherent population trapping (CPT) [2], electromagnetically induced transparency (EIT) [3]and electromagnetically induced absorption (EIA) [4]. In particular, coherent effects arise strong interest based on Hanle-effect configuration for only needing a single light field such as Hanle-CPT, Hanle-EIT, and Hanle-EIA [5–7], which have been utilized in sensitive atomic magnetometer and light storage [8–10].

In recent years, an optical field known as vector beam (VB) has materially enriched the study of structured light interacting with atoms [11]. A VB with the spatial variation of polarization state can be decomposed into two orthogonal circularly polarized components with different orbital angular momentum (OAM) [12]. And then, it has been applied in a variety of realms over the last decades, such as high-resolution imaging [13–15], optical communication [16, 17], optical manipulation [18] and quantum application [19–21]. Generally, there are two methods for generating the VB. The first one is the intra-cavity generation technique, which provides an efficient way to generate the VB directly from the laser source [22]. The second method is the extra-cavity technique, including using phase-dependent optical elements [23] or an interferometer associated with the spatial light modulator [24, 25]. Thus, benefiting from the mature technology for generating the VB allows us to explore vectorial light-matter interaction thoroughly. Recently, some researches show that employing the VB in atomic medium can realize manipulating spatial anisotropy [26–28], spatially dependent EIT [29, 30], quantum memory [31, 32], and non-linear optical propagation [33]. One of the most exciting works is using symmetric beams to observe the rotational Doppler effect (RDE) of atoms [34]. In their study, an interferometer combined with the spiral phase plates (SPP) is applied to generate experimental beams containing two phase vortex beams (OAM beams) with equal but opposite of topological charge (ℓ₁ = − ℓ₂). Nevertheless, the disadvantage of this superposition approach to generating the VB is that the alignment of two arms is an extremely difficult challenge, especially utilizing OAM beams with different $\left|\ell \right|$, since a tiny misalignment can lead to undesired Doppler broadening in atomic medium. For instance, a small angle β between the two beams results in broadening the order of βΔ_Dopp (Δ_Dopp ≃ 500 MHz) and also decrease the EIT peak transmission. Hence, in order to accurately study the RDE with atoms, an approach to generating VBs in a more stable and convenient way is imperative.

In this letter, instead of the interferometer configuration, a more convenient procedure to generate the symmetric and asymmetric VB is presented. The symmetric VB is that the OAM topological charges of two orthogonal circularly polarized components of VB are equivalent $(\left|{\ell }_1\right|=\left|{\ell }_2\right|)$, and the asymmetric VB is unequal $(\left|{\ell }_1\right|\ne \left|{\ell }_2\right|)$. By using a combination of spiral phase plate and vortex retarder plate (VRP), the geometric phase of initial linearly polarized beams are manipulated and converted into VB in the experiment. The advantage of our method is that generated VBs with varied OAM topological charges ($\left|{\ell }_1\right|=\left|{\ell }_2\right|$ or $\left|{\ell }_1\right|\ne \left|{\ell }_2\right|$) are directly produced without considering the misalignment or mismatching when interacting with atoms. Furthermore, asymmetric VBs, symmetric VBs and phase vortex beams (OAM beams) are utilized to detect the RDE in atoms, respectively. The experimental results show that RDE does not have an impact on the resonance linewidths of single linearly polarized OAM beams. However, the spectrum with rotational Doppler broadening is increasingly apparent as the difference $(\left|{\ell }_1-{\ell }_2\right|)$ of both asymmetric and symmetric VBs increases. One thing should be noted is that any decoherent effects (or noise effects) will dramatically decrease the peak transmission and large width of the EIT signal [35, 36], same as other coherent processions [37–39]. Thus, the broadened signal associated with the RDE will be drowned in the background noise and become too weak to be observed. However, we only change the topological charge combination of vector beams and set other parameters appropriately in the experiment, which make linewidth narrow enough to study the influence of RED.

2 Experimental Setup

The experimental setup is shown in Figure 1. The output of a 795 nm external cavity diode laser is split into two parts. One part is sent to a saturated absorption spectroscopy setup to lock laser frequency. The other part passes through a single-mode fiber (SMF) to improve the mode quality of the laser beam. After the fiber, the beam is adjusted by a half-wave plate and a polarizing beam splitter (PBS) to control the intensity and also fix it with horizontal polarization state. A telescope is applied to expand the beam size and the achieved high-quality Gaussian beam’s waist is 4 mm. The VB is generated by sending the linearly polarized beam through a setup composed of an SPP and a VRP. SPP is an optical element with a helical surface where the optical thickness of the component increases with azimuthal position according to ℓλθ/2π(n − 1), where n is the refractive index of the medium [40]. Moreover, VRP is a liquid-crystal-based retardation wave plate with an inhomogeneous optical axis that displays an azimuthal topological charge [23]. The laser frequency is locked to the $5{\mathrm{S}}_{1/2},F=2\to 5P_{1/2},F^{\prime }=1$ transition of the ⁸⁷Rb D₁-line. The Rb cell has a length of 50 mm. A three-layer μ-metal magnetic shield is used to isolate the atoms from the environmental magnetic fields. A solenoid coil inside the inner layer offers a uniform longitudinal magnetic field whose direction is parallel to the light propagation direction, k. The temperature of the cell is set at 40°C with a temperature controller. A neutral density filter is used to control the power of the incident laser beam. In the experiment, the beam intensity at the cell is approximately 17.98 μW/cm². After the beam transmits through the cell, the total intensity as a function of the applied longitudinal magnetic field is recorded by a photodiode.

FIGURE 1

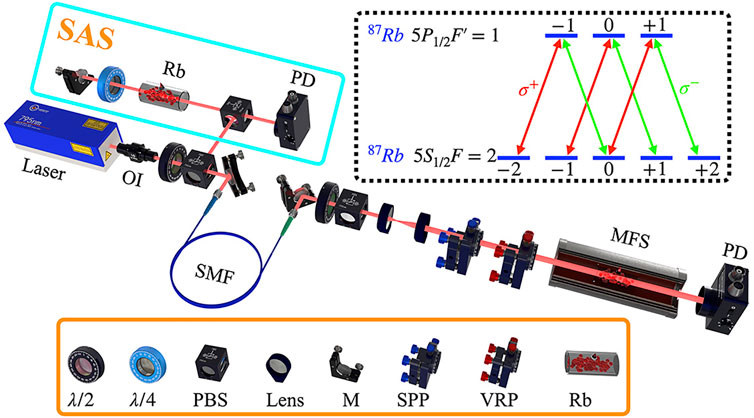
FIGURE 1. Schematic of the experimental setup and atomic energy levels. HWP: half-wave plate; QWP: quarter-wave plate; PBS: polarization beam splitter; M: mirror; SPP: spiral phase plate; VRP: vortex retarder plate; OI: optics isolator; SMF: single-mode fiber; MFS: magnetic field shielding; PD: photo-detector; Rb: rubidium vapor; SAS: saturated absorption spectroscopy.

Next, we briefly present the process of generating the light field we needed. It is known that a linear polarization Gaussian beam can be represented by a superposition of right- (|R⟩) and left-circular (|L⟩) polarized beams as

$|{\mathrm{\Phi }\rangle }_0=\frac{1}{\sqrt{2}}(|\mathrm{L}\rangle +|\mathrm{R}\rangle )(1)$

A SPP can transform the linear polarization Gaussian beam |Φ⟩₀ into an OAM mode with linear polarization state and an azimuthal phase component e^iℓθ, where ℓ is the OAM topological charge and θ is the azimuthal angle, resulting in the beam carrying the orbital angular momentum (ℓℏ). Then the beam can be expressed as:

$|{\mathrm{\Phi }\rangle }_1=\frac{1}{\sqrt{2}}(|\ell ,\mathrm{L}\rangle +|\ell ,\mathrm{R}\rangle )(2)$

To convert a linear polarization OAM beam |Φ⟩₁ into an asymmetric VB, a VRP is used, which couples OAM with spin angular momentum. After passing through the VRP, the beam |Φ⟩₁ is transformed into an asymmetric vector beam |Φ⟩₂ that has polarization variations along the azimuthal direction. Then the asymmetric VB can be written as

$|{\mathrm{\Phi }\rangle }_2=\frac{1}{\sqrt{2}}(|\ell +\mathrm{m},\mathrm{L}\rangle +|\ell -\mathrm{m},\mathrm{R}\rangle )(3)$

where m is the azimuthal charge induced by the VRP. As shown in Eq. 3, the |Φ⟩₂ beam is turned into a superposition state with different OAM (|ℓ + m, L⟩, |ℓ − m, R⟩).

For the generation of a symmetric VB, an initial linearly polarized Gaussian beam directly runs through a VRP. Thereby, the symmetric VB |Φ⟩₃ also has polarization variations as the azimuth varies and can be expressed:

$|{\mathrm{\Phi }\rangle }_3=\frac{1}{\sqrt{2}}(|\mathrm{m},\mathrm{L}\rangle +|-\mathrm{m},\mathrm{R}\rangle )(4)$

It’s seen that the symmetric VB |Φ⟩₃ possesses two OAMs with equal absolute value but different sign ± m.

3 Experimental Results and Discussion

As is known, in addition to the usual axial Doppler and radial shifts, moving atoms interacting with light beams carrying OAM also experience an azimuthal frequency shift under the resonant frequency. Thus, the total frequecy shift of an OAM beam is given by [41, 42].

${\delta }_{\text{OAM}}^{\ell }={\kappa }_{\text{z}}{\mathrm{V}}_{\text{z}}+{\kappa }_{\text{r}}{\mathrm{V}}_{\text{r}}+\kappa \varphi {\mathrm{V}}_{\varphi }(5)$

where ${\kappa }_{\text{z}}=-{\mathrm{k}+\mathrm{k}\mathrm{r}}^2/2(z^2+z_R^2)[2z^2/(z^2+z_R^2)-1]-(\left|\ell \right|+1){\mathrm{z}}_R/(z^2+z_R^2),$ ${\kappa }_{\text{r}}=-\mathrm{k}\mathrm{r}/\bar{\mathrm{z}}$, κ_ϕ = − ℓ/r, and (r, z, ϕ) represents the position in cylindrical coordinates. V_z, V_r, and V_ϕ are the axial, radial and azimuthal velocity components of the atom. ${\mathrm{z}}_{\text{R}}=\pi {\omega }_0^2/\lambda$ is the Rayleigh range and ω₀ is the beam waist and $\bar{\mathrm{z}}=(z_R^2+z^2)/z$.

The axial Doppler shift, corresponding to the usual Doppler shift, is the first term of Eq. 5, associated with motion (V_z) along the beam vector k directed along z. The second term of Eq. 5 is the radial Doppler shift induced by the wave front curvature and proportional to the radial velocity V_r. The only OAM related influence is the last term in Eq. 5 corresponding to the azimutal Doppler shift, also known as rotational Doppler effect (RDE). The RDE is directly proportional to the OAM quantum number ℓ as $(-\frac{\ell }{\mathrm{r}}){\mathrm{V}}_{\varphi }$. The only problem is that this term is too small to be directly detected. However, based on Hanle-EIT, the RDE can be easily observed through the spectroscopy of atoms associated with two light beams carrying OAM without being influenced by other unnecessary Doppler shifts [34].

The Hanle-EIT, a well-known phenomenon, is that light beams stimulate the atomic transitions between Zeeman sublevels of two hyper-fine states (ground state and exited state) to reach the condition of two-photon resonance. Thus, the coherence between atomic energy levels (Figure 1) allows the absorption of the light significantly reduced, leading to a transparent peak when scanning the longitudinal magnetic field B around zero and along the beam propagation direction k [1]. However, when two orthogonally circular polarized beams (σ⁺ and σ⁻) with different OAM (ℓ₁ and ℓ₂) simultaneously couple transitions satisfying the selection rule Δm_F = ±1, the frequency shift will occur due to the Doppler effect, leading to broadening of the transparent peak. In the condition of the moving atom, the two-photon resonance condition is:

${\bar{\delta }}_{\text{OAM}}-\delta =0(6)$

where $\delta =\Delta m_F{g}_F{\mu }_{B}B\left(\right.{\mathrm{g}}_{\text{F}}$ is the gyromagnetic factor of the ground state, μ_B is the Bohr magneton) is the Zeeman shift caused by the magnetic field B and

${\bar{\delta }}_{\text{OAM}}={\delta }_{\text{OAM}}^{{\ell }_1}-{\delta }_{\text{OAM}}^{{\ell }_2}(7)$

Combined with Eqs 5, 7, the axial and radial Doppler shift are eliminated, and the remaining shift only relates to the RDE as:

${\bar{\delta }}_{\text{OAM}}=\left(\frac{{\ell }_1-{\ell }_2}{\mathrm{r}}\right){\mathrm{V}}_{\varphi }(8)$

When the magnetic field is modulated around zero value, the azimutal Doppler broadening will not happen in the Hanle-EIT spectroscopic with the situation of ℓ₁ = ℓ₂. Under the condition of ℓ₁ ≠ ℓ₂, there is a fascinating phenomenon that the Hanle resonance spectroscopic presents the Doppler broadening induced by the RDE.

Now we turn our attention to the experimental phenomena of different light beams interacting with atoms. A horizontally polarized Gaussian beam passes through a SPP or a VRP or both two to produce a series of structured beams, as shown in Figure 2. The beam transmission is recorded by a photodiode as a function of applied longitude magnetic field modulated parallel to the direction of the beam.

FIGURE 2

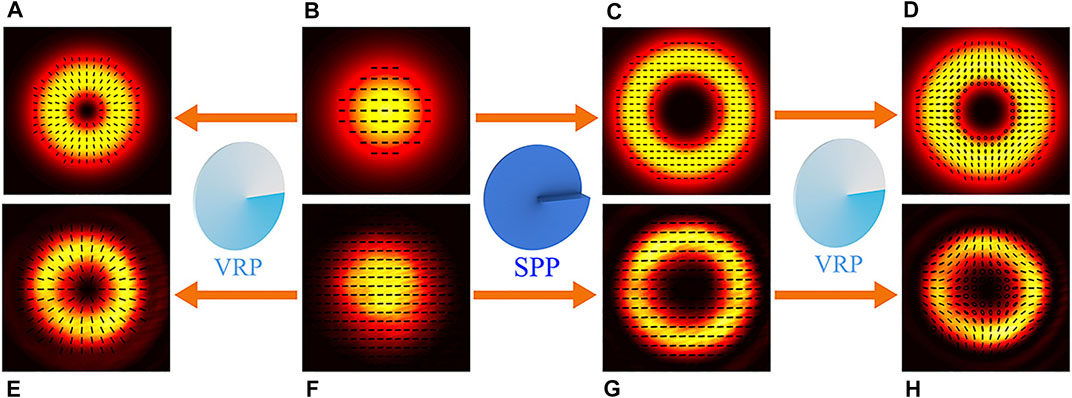
FIGURE 2. Schematic of generating the experimental light beams. SPP: spiral phase plate; VRP: retardation wave plate. (B, F) the theoretical and experimental Gaussian beam, respectively. (A, C, D) the generation of OAM beams, symmetric and asymmetric VBs in theory. (E, G, H) the generation of OAM beams, symmetric and asymmetric vector beams in experiment. Linearly polarized Gaussian beam (F) directly passes through a VRP (or SPP) to generate a symmetric vector beam (E) [or a linearly polarized OAM beam (G)]. For the generation of an asymmetric vector beam (H), the linearly polarized OAM beam (G) continues to run through a VRP.

Firstly, asymmetric VBs generated by the combination of SPPs and VRPs go through the vapor to interact with atoms. As shown in Figures 2F–H, a horizontally polarized beam (Figure 2F) first passes through the SPP to generate an OAM beam (Figure 2G). After that, the beam runs through a VRP and transforms into an asymmetric VB (Figure 2H). An asymmetric VB can be considered as a superposition of two orthogonal circularly polarized beams with different OAM absolute values $\left|\ell \right|$, i.e., $\left|{\ell }_1,R\right.⟩+\left|{\ell }_2,R\right.⟩$. After passing through the vapor, the transmission spectroscopy of the beam presents a Hanle resonance curve with the magnetic field scanning. As shown in Figure 3A, the resonance linewidth of the vector beam (VB_−1∩1) with m = 1 is wider than that of the Gaussian beam, since the linearly polarized Gaussian beam can be considered as two circular polarization beams without OAM. However, the basis of VB_−1∩1 carries different topological charge ℓ₁ = − 1 and ℓ₂ = 1, respectively. Thereby, the resonance linewidth of the VB_−1∩1 is broaden by the RDE. Figure 3B shows the Hanle resonance curve contains the RDE of asymmetric VB (ASVB_7∩9) with two circularly polarized orthogonal basis possessing different topological charge ℓ₁ = 7 and ℓ₂ = 9, respectively. Compared Figure 3B with Figure 3A, the resonance linewidth of ASVB_7∩9 is about equal to the VB_−1∩1 due to the equivalent value of $\left|{\ell }_1-{\ell }_2\right|=2$. In the case, two circularly polarized orthogonal basis of different asymmetric VBs $\left|{\ell }_1,\mathrm{R}\right.⟩$ and $\left|{\ell }_2,\mathrm{L}\right.⟩$ has the same nonzero-difference $\left|{\ell }_1-{\ell }_2\right|$, so the Hanle resonance linewidths have the similar broadening with each other induced by the RDE. The equivalent of linewidth FWHM (full width at half maximum) of the different asymmetric VBs with the equal difference $\left|{\ell }_1-{\ell }_2\right|=2$ is seen in Figure 3C.

FIGURE 3

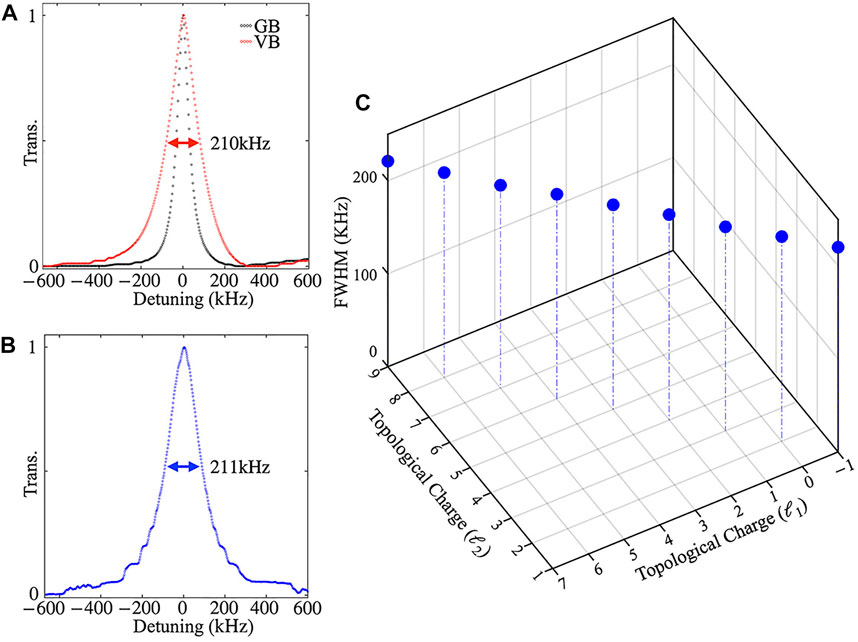
FIGURE 3. FWHM depending on topological charge as a function of the total Zeeman shift $\delta =2\mathrm{g}{\mu }_{\text{B}}\left|\mathbf{B}\right|$. (A) The transmission spectrum of Gaussian beam (GB) and vector beam (VB) with ℓ₁ = − 1 and ℓ₂ = 1; (B) The transmission spectrum of vector beam with ℓ₁ = 7 and ℓ₂ = 9; (C) FWHM of different asymmetric VB. One asymmetric VB brings two OAMs with unequal quantum number absolute value $\left|{\ell }_1\right|\ne \left|{\ell }_2\right|$. And the difference $(\left|{\ell }_2-{\ell }_1\right|)$ of these asymmetric VBs are equal, namely $\left|{\ell }_2-{\ell }_1\right|=2$.

Secondly, in order to observe the increase of Doppler broadening due to the RDE along with the topological charge m, symmetric VBs with different m generated by the VRP are used to interact with atoms (Figure 2E). As shown in Figure 4, an interesting phenomenon is that the Hanle resonance linewidths are gradually broadened with m increasing. It should be noted that in the case of m = 0, there is no RDE due to the beam without carrying the OAM. As a result, the resonance linewidth of m = 0 beam exhibits the normal Hanle resonance linewidth without the RDE related broadening. For normal Hanle resonance, the linewidth is determined by few factors, such as the beam intensity, the decay rate between ground states, the laser linewidth itself and other decoherence effects. In the case of m ≠ 0, ${\bar{\delta }}_{\text{OAM}}=\left[({\ell }_1-{\ell }_2)/\mathrm{r}\right]{\mathrm{V}}_{\varphi }=(\mathrm{2}\mathrm{m}/\mathrm{r}){\mathrm{V}}_{\varphi }$, the transmission signal broadens with m increasing and is broader than that of the case of m = 0 induced by the RDE. Moreover, Figure 5A shows that the spectral FWHM increases with the VB topological charge m.

FIGURE 4

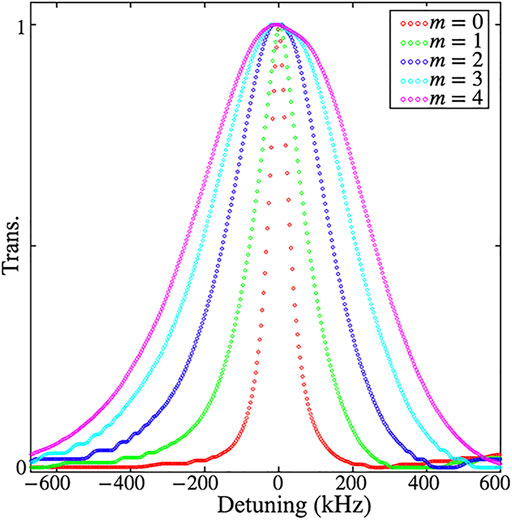
FIGURE 4. The Hanle resonance signals of symmetric VBs as a function of the total Zeeman shift $\delta =2\mathrm{g}{\mu }_{\text{B}}\left|\mathbf{B}\right|$. m = 0 is the linearly polarized Gaussian beam.

FIGURE 5

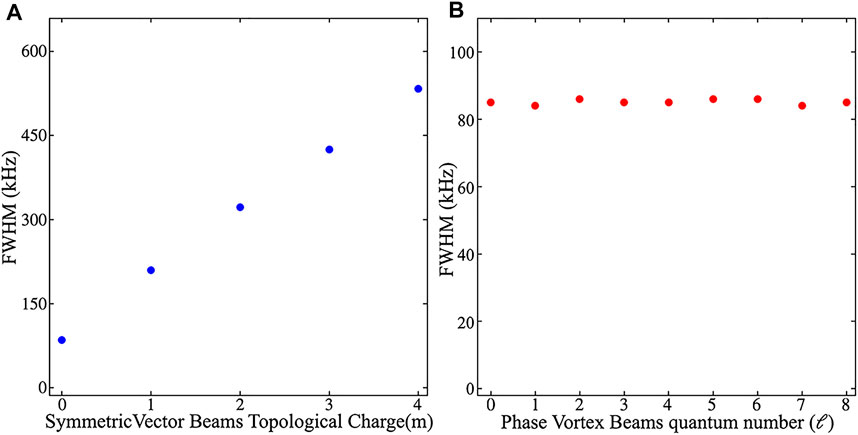
FIGURE 5. Linewidths depend on the topological charge of the symmetric vector beam and the phase vortex beam. (A) FWHMs depend on the symmetric vector beam topological charge m; (B) FWHMs depend on the phase vortex beam topological charge ℓ.

Furthermore, a series of OAM beams (Figure 2G) are produced by the SPP with different topological charges ℓ to measure the Hanle resonance signal. A linearly polarized OAM beam can be decomposed into a couple of orthogonal circularly polarized beams with the same ℓ as |ℓ, R⟩+|ℓ, L⟩. In this case, the resonance linewidth of any OAM beams coincides with each other and is the same as that of the Gaussian beam with no RDE as ${\bar{\delta }}_{\text{OAM}}=\left[({\ell }_1-{\ell }_2)/\mathrm{r}\right]{\mathrm{V}}_{\varphi }=\left[(\ell -\ell )/\mathrm{r}\right]{\mathrm{V}}_{\varphi }=0$. As shown in Figure 5B, the FWHM of ℓ from 0 to 8 are about equal.

4 Conclusion

In conclusion, we invest a simple and efficient procedure for the generation of the asymmetric and symmetric VB. A flexible and efficacious combination of SPP and VRP is used to manipulate the geometric phase of initial linearly polarized beams and convert initial beams into VBs. Furthermore, asymmetric VBs, symmetric VBs, and phase vortex beams interact with atoms under the longitudinal magnetic field to observe the rotational Doppler effect, respectively. We find that the rotational Doppler broadening is increasingly obvious as the difference $(\left|{\ell }_1-{\ell }_2\right|)$ of VB increase. The Hanle resonance of phase vortex beams are no rotational Doppler broadening. These results may have applications in estimating the rotational velocity of the atom-level or molecule-level objects, measuring the intensity of magnetic fields and studying the quantum coherence in atomic ensembles. Furthermore, recent research also showed that the Doppler effect induced nonreciprocity in coherent media [43, 44], which opens up new possibilities for our system.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

SQ, MC and HG contributed to conception and design of the study. JW organized the database. XY performed the statistical analysis. SQ wrote the first draft of the manuscript. JW, XY, SZ and FL wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (92050103, 11774286, 11534008, 11604257, and 11574247) and the Fundamental Research Funds for the Central Universities of China.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Renzoni F, Maichen W, Windholz L, Arimondo E. Coherent Population Trapping with Losses Observed on the Hanle Effect of theD1sodium Line. Phys Rev A (1997) 55:3710–8. doi:10.1103/PhysRevA.55.3710

CrossRef Full Text | Google Scholar

2. Stähler M, Wynands R, Knappe S, Kitching J, Hollberg L, Taichenachev A, et al. Coherent Population Trapping Resonances in thermal ^85Rb Vapor: D_1 versus D_2 Line Excitation. Opt Lett (2002) 27:1472–4. doi:10.1364/OL.27.001472

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Fleischhauer M, Imamoglu A, Marangos JP. Electromagnetically Induced Transparency: Optics in Coherent media. Rev Mod Phys (2005) 77:633–73. doi:10.1103/RevModPhys.77.633

CrossRef Full Text | Google Scholar

4. Lezama A, Barreiro S, Akulshin AM. Electromagnetically Induced Absorption. Phys Rev A (1999) 59:4732–5. doi:10.1103/PhysRevA.59.4732

CrossRef Full Text | Google Scholar

5. Valente P, Failache H, Lezama A. Comparative Study of the Transient Evolution of Hanle Electromagnetically Induced Transparency and Absorption Resonances. Phys Rev A (2002) 65(8):023814. doi:10.1103/PhysRevA.65.023814

CrossRef Full Text | Google Scholar

6. Alzetta G, Gozzini S, Lucchesini A, Cartaleva S, Karaulanov T, Marinelli C, et al. Complete Electromagnetically Induced Transparency in Sodium Atoms Excited by a Multimode Dye Laser. Phys Rev A (2004) 69(9):063815. doi:10.1103/PhysRevA.69.063815

CrossRef Full Text | Google Scholar

7. Anupriya J, Ram N, Pattabiraman M. Hanle Electromagnetically Induced Transparency and Absorption Resonances with a Laguerre Gaussian Beam. Phys Rev A (2010) 81(6):043804. doi:10.1103/PhysRevA.81.043804

CrossRef Full Text | Google Scholar

8. Kastler A. The Hanle Effect and its Use for the Measurements of Very Small Magnetic fields. Nucl Instr Methods (1973) 110:259–65. doi:10.1016/0029-554X(73)90698-8

CrossRef Full Text | Google Scholar

9. Phillips DF, Fleischhauer A, Mair A, Walsworth RL, Lukin MD. Storage of Light in Atomic Vapor. Phys Rev Lett (2001) 86:783–6. doi:10.1103/PhysRevLett.86.783

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gao H, Rosenberry M, Batelaan H. Light Storage with Light of Arbitrary Polarization. Phys Rev A (2003) 67(4):053807. doi:10.1103/PhysRevA.67.053807

CrossRef Full Text | Google Scholar

11. Wang J, Castellucci F, Franke-Arnold S. Vectorial Light-Matter Interaction: Exploring Spatially Structured Complex Light fields. AVS Quan Sci. (2020) 2(12):031702. doi:10.1116/5.0016007

CrossRef Full Text | Google Scholar

12. Milione G, Sztul HI, Nolan DA, Alfano RR. Higher-Order Poincaré Sphere, Stokes Parameters, and the Angular Momentum of Light. Phys Rev Lett (1999) 107(4):053601. doi:10.1103/PhysRevLett.107.053601

CrossRef Full Text | Google Scholar

13. Dorn R, Quabis S, Leuchs G. Sharper Focus for a Radially Polarized Light Beam. Phys Rev Lett (1999) 91(4):233901. doi:10.1103/PhysRevLett.91.233901

CrossRef Full Text | Google Scholar

14. Moh KJ, Yuan X-C, Bu J, Zhu SW, Gao BZ. Surface Plasmon Resonance Imaging of Cell-Substrate Contacts with Radially Polarized Beams. Opt Express (2008) 16:20734–41. doi:10.1364/OE.16.020734

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Xie X, Chen Y, Yang K, Zhou J. Harnessing the point-spread Function for High-Resolution Far-Field Optical Microscopy. Phys Rev Lett (2014) 113(5):263901. doi:10.1103/PhysRevLett.113.263901

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Milione G, Nguyen TA, Leach J, Nolan DA, Alfano RR. Using the Nonseparability of Vector Beams to Encode Information for Optical Communication. Opt Lett (2015) 40:4887–90. doi:10.1364/OL.40.004887

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhao Y, Wang J. High-base Vector Beam Encoding/decoding for Visible-Light Communications. Opt Lett (2015) 40:4843–6. doi:10.1364/OL.40.004843

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Otte E, Denz C. Optical Trapping Gets Structure: Structured Light for Advanced Optical Manipulation. Appl Phys Rev (2020) 7(22):041308. doi:10.1063/5.0013276

CrossRef Full Text | Google Scholar

19. Erhard M, Fickler R, Krenn M, Zeilinger A. Twisted Photons: New Quantum Perspectives in High Dimensions. Light Sci Appl (2018) 7(11):17146. doi:10.1038/lsa.2017.146

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Cozzolino D, Da Lio B, Bacco D, Oxenløwe LK. High‐Dimensional Quantum Communication: Benefits, Progress, and Future Challenges. Adv Quan Tech (2019) 2:1900038. doi:10.1002/qute.201900038

CrossRef Full Text | Google Scholar

21. Ndagano B, Nape I, Cox MA, Rosales-Guzman C, Forbes A. Creation and Detection of Vector Vortex Modes for Classical and Quantum Communication. J Lightwave Technol (2018) 36:292–301. doi:10.1109/JLT.2017.2766760

CrossRef Full Text | Google Scholar

22. Forbes A. Structured Light from Lasers. Laser Photon Rev (2019) 13:1900140. doi:10.1002/lpor.201900140

CrossRef Full Text | Google Scholar

23. Marrucci L, Manzo C, Paparo D. Optical Spin-To-Orbital Angular Momentum Conversion in Inhomogeneous Anisotropic media. Phys Rev Lett (2006) 96:163905. doi:10.1103/PhysRevLett.96.163905

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Forbes A, Dudley A, McLaren M. Creation and Detection of Optical Modes with Spatial Light Modulators. Adv Opt Photon (2016) 8:200–27. doi:10.1364/AOP.8.000200

CrossRef Full Text | Google Scholar

25. Scholes S, Kara R, Pinnell J, Rodríguez-Fajardo V, Forbes A. Structured Light with Digital Micromirror Devices: a Guide to Best Practice. Opt Eng (2019) 59:1. doi:10.1117/1.OE.59.4.041202

CrossRef Full Text | Google Scholar

26. Fatemi FK. Cylindrical Vector Beams for Rapid Polarization-dependent Measurements in Atomic Systems. Opt Express (2011) 19:25143–50. doi:10.1364/OE.19.025143

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wang J, Yang X, Li Y, Chen Y, Cao M, Wei D, et al. Optically Spatial Information Selection with Hybridly Polarized Beam in Atomic Vapor. Photon Res (2018) 6:451–6. doi:10.1364/PRJ.6.000451

CrossRef Full Text | Google Scholar

28. Wang J, Yang X, Dou Z, Qiu S, Liu J, Chen Y, et al. Directly Extracting the Authentic Basis of Cylindrical Vector Beams by a Pump-Probe Technique in an Atomic Vapor. Appl Phys Lett (2019) 115:221101. doi:10.1063/1.5125988

CrossRef Full Text | Google Scholar

29. Radwell N, Clark TW, Piccirillo B, Barnett SM, Franke-Arnold S. Spatially Dependent Electromagnetically Induced Transparency. Phys Rev Lett (2015) 114:123603. doi:10.1103/PhysRevLett.114.123603

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yang X, Chen Y, Wang J, Dou Z, Cao M, Wei D, et al. Observing Quantum Coherence Induced Transparency of Hybrid Vector Beams in Atomic Vapor. Opt Lett (2019) 44:2911–4. doi:10.1364/OL.44.002911

CrossRef Full Text | Google Scholar

31. Parigi V, D’Ambrosio V, Arnold C, Marrucci L, Sciarrino F, Laurat J. Storage and Retrieval of Vector Beams of Light in a Multiple-Degree-Of-freedom Quantum Memory. Nat Commun (2015) 6:7706. doi:10.1038/ncomms8706

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Ye Y-H, Dong M-X, Yu Y-C, Ding D-S, Shi B-S. Experimental Realization of Optical Storage of Vector Beams of Light in Warm Atomic Vapor. Opt Lett (2019) 44:1528–31. doi:10.1364/OL.44.001528

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Bouchard F, Larocque H, Yao AM, Travis C, De Leon I, Rubano A, et al. Polarization Shaping for Control of Nonlinear Propagation. Phys Rev Lett (2016) 117:233903. doi:10.1103/PhysRevLett.117.233903

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Barreiro S, Tabosa JWR, Failache H, Lezama A. Spectroscopic Observation of the Rotational Doppler Effect. Phys Rev Lett (2006) 97:113601. doi:10.1103/PhysRevLett.97.113601

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Figueroa E, Vewinger F, Appel J, Lvovsky AI. Decoherence of Electromagnetically Induced Transparency in Atomic Vapor. Opt Lett (2006) 31:2625–7. doi:10.1364/OL.31.002625

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Shuker M, Firstenberg O, Pugatch R, Ben-Kish A, Ron A, Davidson N. Angular Dependence of Dicke-Narrowed Electromagnetically Induced Transparency Resonances. Phys Rev A (2007) 76:023813. doi:10.1103/PhysRevA.76.023813

CrossRef Full Text | Google Scholar

37. Ishizaki A, Fleming GR. On the Adequacy of the redfield Equation and Related Approaches to the Study of Quantum Dynamics in Electronic Energy Transfer. J Chem Phys (2009) 130:234110. doi:10.1063/1.3155214

CrossRef Full Text | Google Scholar

38. Ishizaki A, Fleming GR. Unified Treatment of Quantum Coherent and Incoherent Hopping Dynamics in Electronic Energy Transfer: Reduced Hierarchy Equation Approach. J Chem Phys (2009) 130:234111. doi:10.1063/1.3155372

CrossRef Full Text | Google Scholar

39. Wang B-X, Tao M-J, Ai Q, Xin T, Lambert N, Ruan D, et al. Efficient Quantum Simulation of Photosynthetic Light Harvesting. Npj Quan Inf (2018) 4:52. doi:10.1038/s41534-018-0102-2

CrossRef Full Text | Google Scholar

40. Yao AM, Padgett MJ. Orbital Angular Momentum: Origins, Behavior and Applications. Adv Opt Photon (2011) 3:161–204. doi:10.1364/AOP.3.000161

CrossRef Full Text | Google Scholar

41. Allen L, Babiker M, Power WL. Azimuthal Doppler Shift in Light Beams with Orbital Angular Momentum. Opt Commun (1994) 112:141–4. doi:10.1016/0030-4018(94)00484-6

CrossRef Full Text | Google Scholar

42. Power WL, Allen L, Babiker M, Lembessis VE. Atomic Motion in Light Beams Possessing Orbital Angular Momentum. Phys Rev A (1995) 52:479–88. doi:10.1103/PhysRevA.52.479

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Zhang S, Hu Y, Lin G, Niu Y, Xia K, Gong J, et al. Thermal-motion-induced Non-reciprocal Quantum Optical System. Nat Photon (2018) 12:744–8. doi:10.1038/s41566-018-0269-2

CrossRef Full Text | Google Scholar

44. Huang HB, Lin JJ, Yao YX, Xia KY, Yin ZQ, Ai Q. Optical Nonreciprocity in Rotating diamond with Nitrogen-Vacancy center. arXiv preprint arXiv:2109.03588 (2021). Available at: https://arxiv.org/abs/2109.03588#:∼:text=Optical%20nonreciprocity%20in%20rotating%20diamond%20with%20nitrogen%2Dvacancy%20center,-Hong%2DBo%20Huang&text=When%20the%20control%20and%20probe,two%20fields%20are%20the%20same.

Google Scholar