
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 26 October 2021
Sec. Optics and Photonics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.770589
This article is part of the Research Topic Topological Photonics View all 15 articles
Recent developments of band topology have revealed a variety of higher-order topological insulators (HOTIs). These HOTIs are characterized by a variety of different topological invariants, making them different at a fundamental level. However, despite such differences, the fact that they all sustain higher-order topological boundary modes poses a challenge to phenomenologically tell them apart. This work presents experimental measurements of the coupling effects of topological corner modes (TCMs) existing in two different types of two-dimensional acoustic HOTIs. Although both HOTIs have a similar four-site square lattice, the difference in magnetic flux per unit cell dictates that they belong to different types of topologically nontrivial phases—one lattice possesses quantized dipole moments, but the other is characterized by quantized quadrupole moment. A link between the topological invariants and the response line shape of the coupled TCMs is theoretically established and experimentally confirmed. Our results offer a pathway to distinguish HOTIs experimentally.
The recent development of topological band theory has revealed the existence of higher-order topological insulators (HOTIs) [1–5]. An important hallmark of such HOTIs is the existence of
For HOTIs with two real-space dimensions, the higher-order topological boundary modes are zero-dimensional modes localized at the corners of the lattice. These topological corner modes (TCMs) can be protected by a variety of topological invariants, such as quantized dipole moments [9, 10, 22], quantized quadrupole moments [1, 23, 24], combinations of first Chern numbers [17], etc. However, although their topological protection can be revealed by theoretical computation of the topological invariants, it is difficult to distinguish them from an observational point of view.
A previous theoretical study has analyzed the finite-size effect on neighboring TCMs in a 2D HOTI [25]. By comparing two different types of topologically nontrivial square-lattice HOTIs—a topological dipole insulator (TDI) wherein the dipole moments are quantized and a topological quadrupole insulator (TQI) with a quantized quadrupole moment, it was shown that the TCMs’ spectral responses split, and the line shapes are associated with the topological characteristics of the HOTI. As such, the spectral responses of the coupled TCMs are an observable effect, by which the underlying topological nature can be phenomenologically revealed.
For the sake of completeness, we first briefly summarize the important theoretical background. A complete theoretical analysis can be found in Ref. [25]. Here, the TDIs and TQIs are both based on the extensions of the 1D Su-Schrieffer-Heeger (SSH) model, and we show the unit-cell structures for the 2D TDI and TQI in Figure 1A,B, respectively. The strengths of the staggered nearest couplings along x and y directions are denoted as intracell
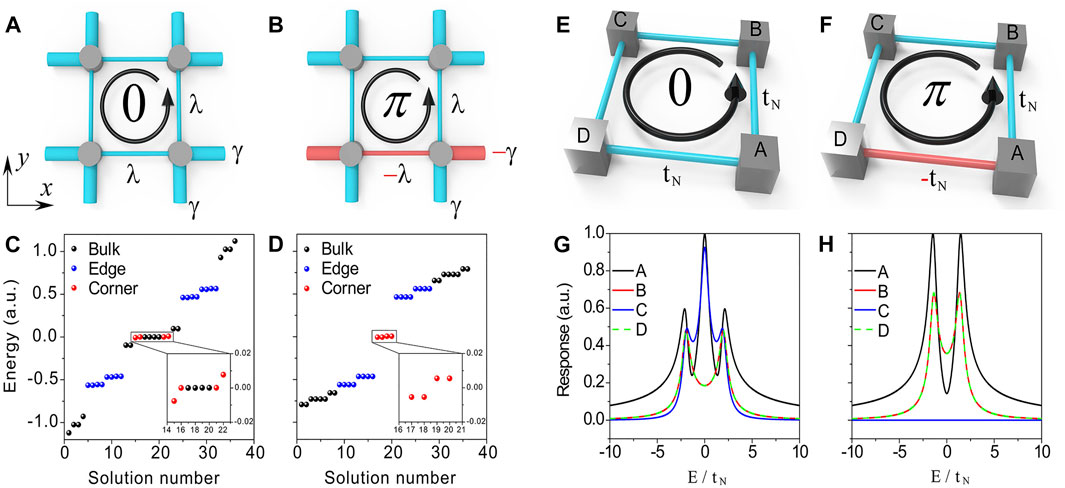
FIGURE 1. The unit cell of the TDI (A) and TQI (B), where the thin and thick tubes denote the intracell (
For a
with
where
where
We plot the eigenvalues of Eq. 1, 3 in Figures 1C,D, respectively. The parameters are set as
for the TDI, and
for the TQI. Here,
where
We next present the designs of phononic crystals to realize both the TDI and TQI. The unit cells are shown in Figures 2A,B, respectively. The gray blocks denote the acoustic cavities, whose first-order resonance fulfills the role of the on-site orbital. The cavities have a height of
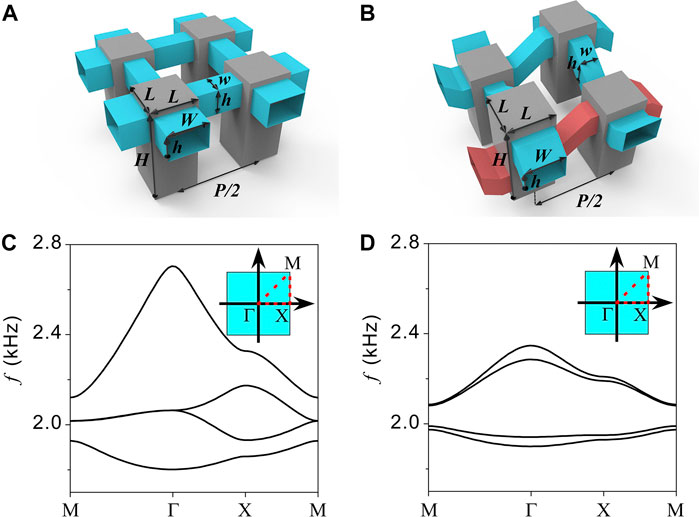
FIGURE 2. (A–B) The designs of phononic crystal unit cells of the TDI (A) and TQI (B). (C–D) The band structures of the TDI (C) and TQI (D). The inset in each plot denotes the first Brillouin zone.
Based on these two designs, we have fabricated the phononic crystals. The cavities are machined from aluminum alloy and the coupling tubes are 3D printed using photosensitive resin. The photographs of the TDI and TQI configurations are shown in Figure 3A, 4A, respectively. Both lattices are
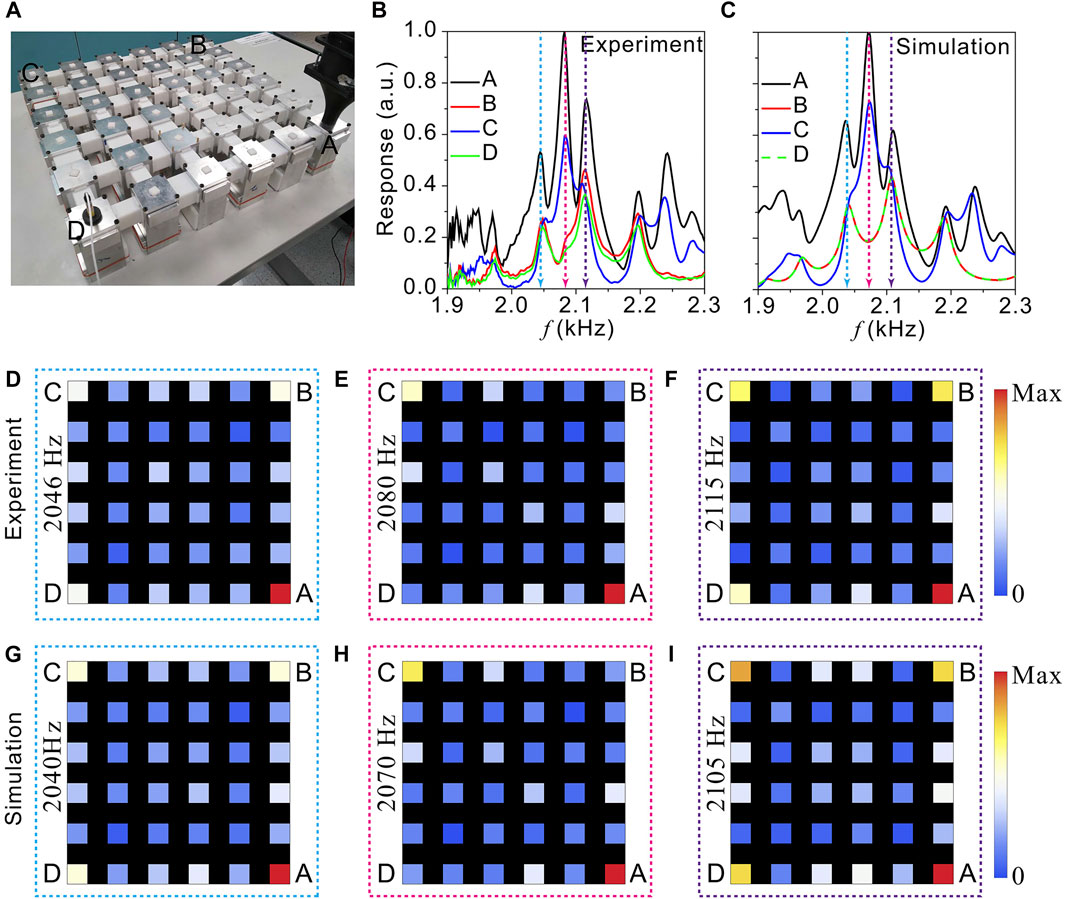
FIGURE 3. (A) A photograph showing the fabricated TDI phononic crystal. (B–C) Measured (B) and simulated (C) corner responses. (D–F) Measured responses at the frequencies corner-mode resonant peaks: (D) 2046Hz, (E) 2080Hz, (F) 2115 Hz. (G–I) Simulated responses at the frequencies corner-mode resonant peaks: (G) 2040Hz, (H) 2070Hz, (I) 2105 Hz.
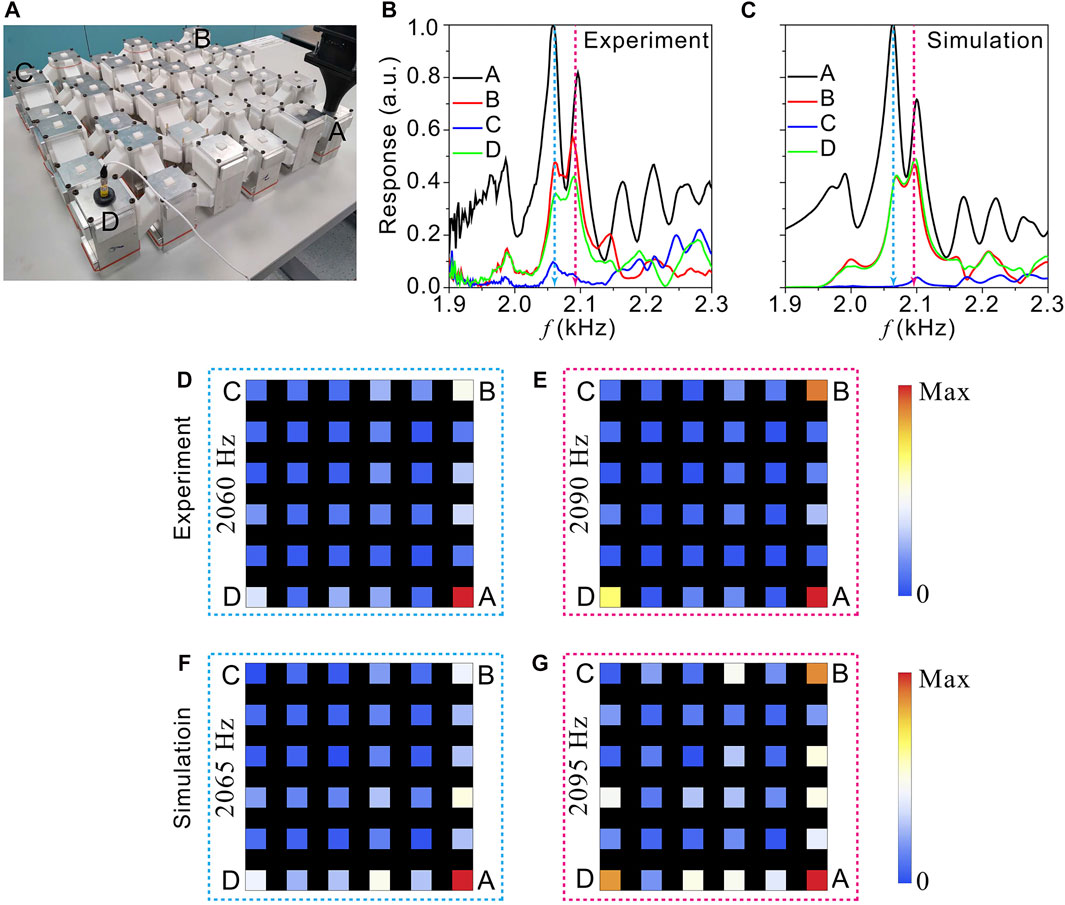
FIGURE 4. (A) A photograph showing the fabricated TQI phononic crystal. (B–C) Measured (B) and simulated (C) corner responses. (D–E) Measured responses at the frequencies corner-mode resonant peaks: (D) 2060Hz, (E) 2090 Hz. (F–G) Simulated responses at the frequencies corner-mode resonant peaks: (F) 2065Hz, (G) 2095 Hz.
Similar experiments were performed for the TQI lattice. In Figure 4B, two response peaks are identified in the bulk gap (2,000–2,150 Hz) for the spectra measured at corners A, B, D. Also, the response at corner C is significantly weaker. These observations again align with the prediction (Figures 1D,H) and simulations (Figure 4C). We further confirm in the measured (Figures 4D,E) and simulated (Figures 4F,G) spatial maps that the response peaks are indeed due to the TCMs.
In summary, we have experimentally observed the coupling effects of TCMs in two different types of acoustic HOTIs. The measured line shapes of the corner responses agree excellently with a previous theoretical study, which confirms that the topological properties of the HOTIs can indeed influence the coupling effects of TCMs. Therefore, the corner responses can serve as an experimental hallmark to separate HOTIs of different classes. It is interesting to further the study by investigating the coupling effects in other types of HOTIs such as a Kagome lattice [4], honeycomb lattice [20], etc. On the other hand, the coupled higher-order topological modes can be a useful starting point for higher-order non-Hermitian physics [27, 28]. They may also find applications such as topological wave and light confinement [13, 29] and topological lasing [30, 31].
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
XL and SW performed numerical simulations and designed the experiment. XL, SW, GZ carried out the measurements. All authors analyzed and discussed the results. XL and GM wrote the manuscript with inputs from others. GM initiated and supervised the research.
This work was supported by Hong Kong Research Grants Council (12302420, 12300419, 22302718, and C6013-18G), National Natural Science Foundation of China (11922416, 11802256), and Hong Kong Baptist University (RC-SGT2/18-19/SCI/006).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The authors thank Weiwei Zhu for the discussions.
1. Benalcazar WA, Bernevig BA, Hughes TL. Quantized Electric Multipole Insulators. Science (2017) 357:61–6. doi:10.1126/science.aah6442
2. Benalcazar WA, Bernevig BA, Hughes TL. Electric Multipole Moments, Topological Multipole Moment Pumping, and Chiral Hinge States in Crystalline Insulators. Phys Rev B (2017) 96:245115. doi:10.1103/physrevb.96.245115
3. Schindler F, Cook AM, Vergniory MG, Wang Z, Parkin SSP, Bernevig BA, et al. Higher-order Topological Insulators. Sci Adv (2018) 4:eaat0346. doi:10.1126/sciadv.aat0346
4. Ezawa M. Higher-Order Topological Insulators and Semimetals on the Breathing Kagome and Pyrochlore Lattices. Phys Rev Lett (2018) 120:026801. doi:10.1103/PhysRevLett.120.026801
5. Xie B, Wang HX, Zhang X, Zhan P, Jiang JH, Lu M, et al. Higher-order Band Topology. Nat Rev Phys (2021) 1-13. doi:10.1038/s42254-021-00323-4
6. Peterson CW, Benalcazar WA, Hughes TL, Bahl G. A Quantized Microwave Quadrupole Insulator with Topologically Protected Corner States. Nature (2018) 555:346–50. doi:10.1038/nature25777
7. Mittal S, Orre VV, Zhu G, Gorlach MA, Poddubny A, Hafezi M. Photonic Quadrupole Topological Phases. Nat Photon (2019) 13:692–6. doi:10.1038/s41566-019-0452-0
8. Noh J, Benalcazar WA, Huang S, Collins MJ, Chen KP, Hughes TL, et al. Topological protection of Photonic Mid-gap Defect Modes. Nat Photon (2018) 12:408–15. doi:10.1038/s41566-018-0179-3
9. Chen X-D, Deng W-M, Shi F-L, Zhao F-L, Chen M, Dong J-W. Direct Observation of Corner States in Second-Order Topological Photonic Crystal Slabs. Phys Rev Lett (2019) 122:233902. doi:10.1103/physrevlett.122.233902
10. Xie B-Y, Su G-X, Wang H-F, Su H, Shen X-P, Zhan P, et al. Visualization of Higher-Order Topological Insulating Phases in Two-Dimensional Dielectric Photonic Crystals. Phys Rev Lett (2019) 122:233903. doi:10.1103/physrevlett.122.233903
11. El Hassan A, Kunst FK, Moritz A, Andler G, Bergholtz EJ, Bourennane M. Corner States of Light in Photonic Waveguides. Nat Photon (2019) 13:697–700. doi:10.1038/s41566-019-0519-y
12. Zhang L, Yang Y, Lin ZK, Qin P, Chen Q, Gao F, et al. Higher-Order Topological States in Surface-Wave Photonic Crystals. Adv Sci (Weinh) (2020) 7:1902724. doi:10.1002/advs.201902724
13. Xu C, Chen Z-G, Zhang G, Ma G, Wu Y. Multi-Dimensional Wave Steering with Higher-Order Topological Phononic Crystal. Sci Bull (2021) 66:1740–5. doi:10.1016/j.scib.2021.05.013
14. Xue H, Yang Y, Gao F, Chong Y, Zhang B. Acoustic Higher-Order Topological Insulator on a Kagome Lattice. Nat Mater (2019) 18:108–12. doi:10.1038/s41563-018-0251-x
15. Ni X, Weiner M, Alù A, Khanikaev AB. Observation of Higher-Order Topological Acoustic States Protected by Generalized Chiral Symmetry. Nat Mater (2019) 18:113–20. doi:10.1038/s41563-018-0252-9
16. Zhang X, Wang H-X, Lin Z-K, Tian Y, Xie B, Lu M-H, et al. Second-order Topology and Multidimensional Topological Transitions in Sonic Crystals. Nat Phys (2019) 15:582–8. doi:10.1038/s41567-019-0472-1
17. Chen ZG, Zhu W, Tan Y, Wang L, Ma G. Acoustic Realization of a Four-Dimensional Higher-Order Chern Insulator and Boundary-Modes Engineering. Phys Rev X (2021) 11(1):011016. doi:10.1103/physrevx.11.011016
18. Chen ZG, Wang L, Zhang G, Ma G. Chiral Symmetry Breaking of Tight-Binding Models in Coupled Acoustic-Cavity Systems. Phys Rev Appl (2020) 14(2):024023. doi:10.1103/physrevapplied.14.024023
19. Serra-Garcia M, Peri V, Süsstrunk R, Bilal OR, Larsen T, Villanueva LG, et al. Observation of a Phononic Quadrupole Topological Insulator. Nature (2018) 555:342–5. doi:10.1038/nature25156
20. Fan H, Xia B, Tong L, Zheng S, Yu D. Elastic Higher-Order Topological Insulator with Topologically Protected Corner States. Phys Rev Lett (2019) 122(20):204301. doi:10.1103/physrevlett.122.204301
21. Wu Q, Chen H, Li X, Huang G. In-plane Second-Order Topologically Protected States in Elastic Kagome Lattices. Phys Rev Appl (2020) 14(1):014084. doi:10.1103/physrevapplied.14.014084
22. Xie B-Y, Wang H-F, Wang H-X, Zhu X-Y, Jiang J-H, Lu M-H, et al. Second-order Photonic Topological Insulator with Corner States. Phys Rev B (2018) 98(20):205147. doi:10.1103/physrevb.98.205147
23. Qi Y, Qiu C, Xiao M, He H, Ke M, Liu Z. Acoustic Realization of Quadrupole Topological Insulators. Phys Rev Lett (2020) 124(20):206601. doi:10.1103/physrevlett.124.206601
24. Xue H, Ge Y, Sun H-X, Wang Q, Jia D, Guan Y-J, et al. Observation of an Acoustic Octupole Topological Insulator. Nat Commun (2020) 11:2442. doi:10.1038/s41467-020-16350-1
25. Zhu W, Ma G. Distinguishing Topological Corner Modes in Higher-Order Topological Insulators of Finite Size. Phys Rev B (2020) 101(R):161301. doi:10.1103/physrevb.101.161301
26. Zhao YX, Huang Y-X, Yang SA. Z2 -projective Translational Symmetry Protected Topological Phases. Phys Rev B (2020) 102:161117. doi:10.1103/physrevb.102.161117
27. Ding K, Ma G, Xiao M, Zhang ZQ, Chan CT. Emergence, Coalescence, and Topological Properties of Multiple Exceptional Points and Their Experimental Realization. Phys Rev X (2016) 6:021007. doi:10.1103/physrevx.6.021007
28. Tang W, Jiang X, Ding K, Xiao Y-X, Zhang Z-Q, Chan CT, et al. Exceptional Nexus with a Hybrid Topological Invariant. Science (2020) 370:1077–80. doi:10.1126/science.abd8872
29. Ota Y, Liu F, Katsumi R, Watanabe K, Wakabayashi K, Arakawa Y, et al. Photonic crystal Nanocavity Based on a Topological Corner State. Optica (2019) 6:786. doi:10.1364/optica.6.000786
30. Kim H-R, Hwang M-S, Smirnova D, Jeong K-Y, Kivshar Y, Park H-G. Multipolar Lasing Modes from Topological Corner States. Nat Commun (2020) 11:5758. doi:10.1038/s41467-020-19609-9
Keywords: topological corner modes, higher-order topological insulators, phononic crystals, tightbinding model, green’s function
Citation: Li X, Wu S, Zhang G, Cai W, Ng J and Ma G (2021) Measurement of Corner-Mode Coupling in Acoustic Higher-Order Topological Insulators. Front. Phys. 9:770589. doi: 10.3389/fphy.2021.770589
Received: 04 September 2021; Accepted: 07 October 2021;
Published: 26 October 2021.
Edited by:
Yiqi Zhang, Xi’an Jiaotong University, ChinaReviewed by:
Haoran Xue, Nanyang Technological University, SingaporeCopyright © 2021 Li, Wu, Zhang, Cai, Ng and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guancong Ma, cGhnY21hQGhrYnUuZWR1Lmhr
†Present address: Shiqiao Wu, School of Physical Science and Technology, Soochow University, Suzhou, China
‡These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.