A Generalised Plastic Model for Gravelly Soils Considering Evolution of Void Ratio and Particle Breakage

Gravelly soils exhibit complicated mechanical behaviours closely related to particle breakage and relative density state. To better capture the mechanical responses of gravelly soils, a generalised plastic model considering evolution of void ratio and particle breakage was developed within the framework of critical state soil mechanics. In the model, particle breakage effect was described by incorporating breakage index to deviate the critical state line off the ideal position. A differential equation relating increment of void ratio to variation of volumetric strain was used to depict the evolution of current void ratio. It indirectly reflected the relative density state of gravelly soils. The model was applied to conducting numerical simulations for a series of triaxial tests on four types of gravelly soils. Comparisons between the test data and the modelling results indicated that considerations of void ratio evolution and particle breakage could better simulate the stress-dependent dilatation/contraction behaviours of gravelly soils.

1 Introduction

Gravelly soils (including coarse-grained aggregates, rockfill materials and railway basalts) are widely used as construction materials in the various geotechnical projects (e.g. roadbeds and dams). Over the past several decades, researchers have made efforts to investigate the mechanical properties of gravelly soils [1]. Experimental studies have indicated that particle breakage greatly affects the mechanical behaviours of gravelly soils [2,3]. In a microstructure view, particle breakage changed the grain distributions. Then, the mechanical responses of gravelly soils have changed remarkably with the reconfiguration of particle grading [3].

Based on the fundamental observations, particle breakage has been generally taken into account to build the constitutive models for gravelly soils [3–6]. In the constitutive descriptions, effect of particle breakage was described using a variable of breakage index. Particle grading evolution was often used to define the breakage index [2,3]. Investigations have indicated that particle breakage index is correlated to plastic-dissipation energy and formulated as a hyperbolic function of plastic work [5].

Besides the constitutive frameworks of traditional elastoplasticity [7], generalised plasticity [8] and critical state soil mechanics [9] have been often combined to construct the constitutive models of gravelly soils. In this group of models, as an important state parameter, particle breakage index has been incorporated into the equation of critical state line [3,5,6]. Such mathematical treatments can describe the translation effects of particle breakage on the critical state line of gravelly soils [5]. On the other hand, generalised plasticity is a type of simple constitutive framework, due to without consideration on the complex failure surfaces of geomaterials [8]. Thus, a number of generalised plastic models have been developed for gravelly soils based on the critical state concept [5,10–12]. These models considering particle breakage could well capture the main mechanical behaviours of gravelly soils, including stress-dependent volumetric dilatancy and nonlinear strength and deformation.

However, most of these models have not made clear expositions on the variations of void ratio during volume changing process. As we all know, current void ratio of a soil mass closely relates to and evolves with the volume deformation. By identifying the current, maximum and minimum void ratio values, the relative density state of soil mass could be estimated. As for gravelly soils, relative density state (dense or loose sates relative to critical state) decides whether they exhibit volume dilatation or contraction behaviours [12]. Considering the relationship between void ratio and relative density state, the evolution of void ratio should be included in the constitutive descriptions. In this way, the changing process of relative density state synchronous with the variation of volume deformation can be captured precisely. Therefore, besides particle breakage, it is reasonable to take the evolution of void ratio into account to build the constitutive models for gravelly soils. In this respect, there are some research attempts of considering evolution of void ratio in the constitutive models of granular soils [6,13].

In this study, an evolution equation of void ratio was incorporated into a generalised plastic model that was established within the framework of critical state soil mechanics. In the model, current void ratio and particle breakage index were regard as two state-dependent variables updating with the variation of volumetric strain and shifting the critical state line, respectively. The model was used to simulate the mechanical responses of four types of gravelly soils during triaxial tests. By analysing the simulation results, constitutive modelling effectiveness of considering evolution of void ratio and particle breakage was evaluated.

2 Constitutive Modelling Description

2.1 Generalised Plasticity Framework

In this study, generalised plasticity framework firstly proposed by Pastor and Zienkiewicz [8] was used to build the constitutive model for gravelly soils. In a generalised plasticity model, incremental stress-strain relationship is expressed as follows:

$d\mathbf{\sigma }={\mathbf{D}}^{ep}d\mathbf{\epsilon }(1)$

where $d\mathbf{\sigma }$ and $d\epsilon$ represent the increments of stress $\mathbf{\sigma }$ and strain $\mathbf{\epsilon }$, respectively. ${\mathbf{D}}^{\mathrm{e}\mathrm{p}}$ is the elastoplastic stiffness matrix, explicitly expressed as follows:

${\mathbf{D}}^{\mathrm{e}\mathrm{p}}={\mathbf{D}}^{\mathrm{e}}-\frac{{\mathbf{D}}^{\mathrm{e}}\mathbf{g}{\mathbf{f}}^{\mathrm{T}}{\mathbf{D}}^{\mathrm{e}}}{{\mathbf{f}}^{\mathrm{T}}{\mathbf{D}}^{\mathrm{e}}\mathrm{g}+H}(2)$

where ${\mathbf{D}}^{\mathrm{e}}$ is the elastic constitutive stiffness matrix. $\mathbf{g}$ and $\mathbf{f}$ are the normalised plastic flow and plastic loading direction, respectively. $H$ denotes the plastic modulus.

2.2 Elastic Behaviour

Nakai [14] provided the following Eqs 3, 4 to describe the elastic and plastic volumetric strains of sands under isotropic consolidation.

${\epsilon }_{\mathrm{v}}^{\mathrm{e}}=c_e\left[{\left(\frac{p}{p_a}\right)}^m-{\left(\frac{p_0}{p_a}\right)}^m\right](3)$

${\epsilon }_{\mathrm{v}}^{\mathrm{p}}=\left(c_t-c_e\right)\left[{\left(\frac{p}{p_a}\right)}^m-{\left(\frac{p_0}{p_a}\right)}^m\right](4)$

where $p=\left({\sigma }_{11}+{\sigma }_{22}+{\sigma }_{33}\right)/3$ is the mean stress. ${\epsilon }_v={\epsilon }_{11}+{\epsilon }_{22}+{\epsilon }_{33}$ denotes the volumetric strain. $c_t$ and $c_e$ are the compression and resilience indexes. $m$ is a material constant. $p_0$ represents the initial value of mean stress. $p_a=0.098\text{MPa}$ denotes the engineering atmosphere pressure.

Using Eq. 3 and Poisson’s ratio $\nu$, the elastic bulk modulus $K$ and shear modulus $G$ can be defined as follows:

$\begin{array}{l}K=\frac{p_a^m}{m{c}_e{p}^{m-1}},\\ G=\frac{3\left(1-2\nu \right)}{2\left(1+\nu \right)}K\end{array}(5)$

2.3 Critical State Considering Particle Breakage

As for gravelly soils, particle breakage remarkably changes the critical void state. This phenomenon was observed in triaxial tests [15,16]. In this study, a sigmoid function suggested by Liu et al. [3] was adopted to define the critical state line (CSL) influenced by particle breakage. That is:

$e_c=e_{\min }+\left(e_{\max }-e_{\min }\right)\sqrt{1-B_r}\exp \left[-\lambda {\left(p/p_a\right)}^{\xi }\right](6)$

where $e_c$ means the critical-state void ratio, $e_{\max }$ and $e_{\min }$ are the maximum and minimum critical state void ratios of a gravelly soil mass, respectively. $\lambda$ and $\xi$ are the material constants. $B_r$ is the particle breakage index. In this study, a function proposed by Lade et al. [17] is adopted to link particle breakage index $B_r$ to plastic dissipated energy $w^p$. That is:

$B_{\mathrm{r}}=\frac{w^{\mathrm{p}}}{a+b{w}^{\mathrm{p}}}(7)$

where $a$ and $b$ are both the material constants. $w^{\mathrm{p}}$ denotes the plastic dissipated energy that is calculated using:

$w^{\mathrm{p}}={\displaystyle \int {\mathbf{\sigma }}^{\mathrm{T}}d\mathbf{\epsilon }}(8)$

2.4 Evolution of Void Ratio

In soil mechanics, it is always assumed that the volume of solid phase $V_s$ is constant during loading and volume change is only related to the void phase $V_v$. Assuming $V_s=1$, void phase volume $V_v$ is equal to void ratio $e$. Thus, the change of void ratio causes an increment of volumetric strain. This relationship is formulated with:

$d{\epsilon }_v=\frac{d{V}_v}{V_s+V_v}=\frac{de}{1+e}\to de=d{\epsilon }_v\left(1+e\right)(9)$

The second formula in Eq. 9 is a differential equation. It has a solution expressed as follows:

$e=A\exp \left({\epsilon }_v\right)-1(10)$

In Eq. 10, the parameter $A$ can be determined using the initial condition. That is ${\epsilon }_v=0$, $e=e_0\Rightarrow A=1+e_0$.

The current void ratio $e$, however, is not always just onto the CSL, but usually above or below the CSL. To identify the relative density state of soils, Been and Jefferies [18] proposed the following state parameter $\psi$:

$\psi =e-e_c(11)$

where the state variable $\psi$ describes the evolution of dilatation curve from contraction line towards the critical state line. $\psi <0$ indicates that the relative density state of a gravelly soil is denser than the critical state. The gravelly soil may undergo a volume-dilatation behaviour. $\psi >0$ means the gravelly soil is in the looser state than the critical state. The gravelly soil may exhibit a volume-contraction behaviour.

2.5 Nonlinear Strength and Dilatancy Behaviours

Gravelly soils generally exhibit significant nonlinear strength behaviours. A power function is widely used to describe the nonlinear strength behaviours of geomaterials [3,19]:

$q=M_{c0}g\left(\theta \right)p_a{\left(\frac{p}{p_a}\right)}^{n_f}(12)$

where $q=\sqrt{3\left({\sigma }_{ij}-p{\delta }_{ij}\right)\left({\sigma }_{ij}-p{\delta }_{ij}\right)/2}$ is the deviatoric stress. Correspondingly, ${\sigma }_{ij}$ is the second-order stress tensor. ${\delta }_{ij}$ is the Kronecker tensor, with $i=j$, ${\delta }_{ij}=1$; $i\ne j$, ${\delta }_{ij}=\text{0}$. $g\left(\theta \right)$ is a shape function of the failure criterion on the deviatoric plane. For simplification, $g\left(\theta \right)=1$ is used in this study.

In Eq. 12, $M_{c0}$ and $n_f$ are both material constants. Using Eq. 12, the critical stress state ratio $M_c$ is defined as the tangent slope of the strength envelope, that is:

$M_c=\frac{dq}{dp}=n_f{M}_{c0}{\left(\frac{p}{p_a}\right)}^{n_f-1}(13)$

The dilatation stress ratio $M_d=q_d/p_d$ is used to describe the stress state of transition phase point, which locates the stress threshold for the onset of volume-dilatation behaviour. Following the studies of Dafalias and Manzari [20], the dilatation stress ratio $M_d$ in this work is defined as a function of the state variable $\psi$:

$M_d=M_c\exp \left(\kappa \psi \right)(14)$

where $\kappa$ is a material constant for describing dilatation behaviour.

The dilatation coefficient $d_g$ is related to the shear stress ratio $\eta =q/p$ and the dilatation stress ratio $M_d$ using the following equation [11]:

$d_g=\frac{d{\epsilon }_{\mathrm{v}}^{\mathrm{p}}}{d{\overline{\gamma }}^{\mathrm{p}}}=\alpha \left(M_d-\eta \right)\exp \left(\eta /M_d\right)(15)$

where ${\overline{\gamma }}^{\mathrm{p}}$ is the plastic component of the equivalent shear strain $\overline{\gamma }=\sqrt{2\left({\epsilon }_{ij}-{\epsilon }_{\mathrm{v}}{\delta }_{ij}/3\right)\left({\epsilon }_{ij}-{\epsilon }_{\mathrm{v}}{\delta }_{ij}/3\right)/3}$.

2.6 Plastic Flow and Loading Direction

In the $p-q$ stress plane, the plastic flow $\mathbf{g}$ is given by Pastor et al. [8]:

$\mathbf{g}=\frac{1}{\sqrt{d_g^2+1}}\left\{\begin{array}{c}{d}_g\\ 1\end{array}\right\}(16)$

As the nonassociated flow rule is assumed, the plastic loading direction $\mathbf{f}$ is different with the plastic flow $\mathbf{g}$. For simplification, $\mathbf{f}$ can be expressed in a formula similar to $\mathbf{g}$, as follows:

$\mathbf{f}=\frac{1}{\sqrt{d_f^2+1}}\left\{\begin{array}{c}{d}_f\\ 1\end{array}\right\}(17)$

where $d_{\text{f}}$ is defined as the loading direction factor, which is a state variable related to critical state. Similar to $d_{\text{g}}$, $d_{\text{f}}$ is defined as:

$d_f=\alpha \left(M_c-\eta \right)\exp \left(\eta /M_c\right)(18)$

2.7 Plastic Modulus

Under the isotropic compression condition, there is $q=0$ and $dq=0$. The incremental relationship between plastic volumetric strain and mean stress can be simply expressed as follows:

$d{\epsilon }_{\mathrm{v}}^{\mathrm{p}}=\frac{dp}{H}(19)$

Additionally, the plastic volumetric strain increment can be determined by differentiating Eq. 4, that is:

$d{\epsilon }_{\mathrm{v}}^{\mathrm{p}}=m\left(c_t-c_e\right)p_a^{-m}{p}^{m-1}dp(20)$

Combination Eqs 19, 20 leads to the formula of plastic modulus $H$:

$H=\frac{p_a^m{p}^{1-m}}{m\left(c_t-c_e\right)}(21)$

Eq. 21 is only suitable for the isotropic compression condition. Inspired by Chen et al. [10], a formulation of plastic modulus $H$, suitable for more general cases, was developed. That is expressed as follows:

$H=\frac{M_c-\eta }{M_c}\cdot \frac{1+{\left(1+\eta /M_d\right)}^2}{1+{\left(1-\eta /M_d\right)}^2}\cdot \frac{p_a^m{p}^{1-m}}{m\left(c_t-c_e\right)}(22)$

3 Model Calibration and Simulations

This constitutive model has 15 material constants and can be classified into six groups. They can be determined using triaxial compression tests.

3.1 Calibration of Model Constants

3.1.1 Compression and Elastic Constants

Material constants $c_t$, $c_e$ and $m$ can be determined using loading/unloading ${\epsilon }_{\mathrm{v}}\sim p$ curves under various isotropic compression stress states. In particular, by analysing the unloading curves, ${\epsilon }_{\mathrm{v}}^{\mathrm{e}}$ and ${\epsilon }_{\mathrm{v}}^{\mathrm{p}}$ can be accurately distinguished from ${\epsilon }_v$. Then, using Eqs 3, 4 to fit the test data pairs $\left(\mathrm{p},{\epsilon }_{\mathrm{v}}^e\right)$ and $\left(p,{\epsilon }_{\text{v}}^{\text{p}}\right)$, respectively, the values of $c_t$, $c_e$ and $m$ can be determined.

Additionally, using the elastic constants: $c_t$, $c_e$ and $m$, the value of $K$ can be determined. Then, using $K$ and Poisson’s ratio $\nu$, the value of $G$ can be calculated.

3.1.2 Initial void Ratio

Initial void ratio $e_0$ can be determined using the following formula:

$e_0=\frac{G_s\left(1+\omega \right){\rho }_w}{{\rho }_0}-1(23)$

where $G_s$ is the specific weight of soil particles. $\omega$ and ${\rho }_0$ are the water content and density of soil mass, respectively. ${\rho }_w$ denotes the water density.

3.1.3 Critical state Constants

The critical state constants $e_{\max }$, $e_{\min }$, $\lambda$ and $\xi$ are determined from the triaxial tests under small confining pressures, which no obvious particle breakage occurred. Eq. 6 (with $B_r\approx 0$) is used to fit a number of data pairs $\left(e_c,p\right)$. Then, the values of $e_{\max }$, $e_{\min }$, $\lambda$ and $\xi$ can be determined.

3.1.4 Strength constants

The strength constants: $M_{c0}$ and $n_f$ can be determined by fitting the strength data $\left(p,q\right)$ at the failure states using the strength criterion in Eq. 12. Because of nonlinearity of Eq. 12, at least three triaxial compression tests under different confining pressures are needed.

3.1.5 Dilatation constants

Using the test data of plastic volumetric and shear strains, $d_g$ can be calculated by $d_g=d{\epsilon }_{\mathrm{v}}^{\mathrm{p}}/d{\overline{\gamma }}^{\mathrm{p}}$. Certainly, it is difficult to depart the plastic strain increment $d{\epsilon }^{\mathrm{p}}$ from the total strain increment $d\epsilon$. For simplification, it is assumed that $d_g\approx d{\epsilon }_v/d\overline{\gamma }$. By relating $d_g$ and $\eta =q/p$, then using Eq. 15, $\alpha$ can be determined.

Using the test data at the dilatation point, the dilatation stress ratio $M_d$ can be calculated. With the value of initial void ratio $e_0$, Eq. 10 is used to compute the current void ratio $e$. Then, using Eqs 6, 11, the state variable $\psi$ can be determined. In this way, the dilatation constant $\kappa$ can be determined using the formula $\ln \left(M_d/M_c\right)=\kappa \psi$ to fit the test data pairs $\left[\ln \left(M_d/M_c\right),\psi \right]$.

3.1.6 Particle breakage Parameters

Using Eq. 8, the plastic dissipated energy $w^p$ can be calculated. By comparing the particle size gradation before and after the tests, particle breakage index $B_r$ can be estimated [2,3]. Then, using Eq. 7, the particle breakage parameters $a$ and $b$ can be determined.

If $B_r$ cannot be explicitly estimated, an available method is combining Eqs 6, 7 to fit a number of test data pairs $\left(e_{\text{c}},p,w^{\text{p}}\right)$ on the CSL to indirectly determine the values of $a$ and $b$.

3.2 Performance of the Proposed Model

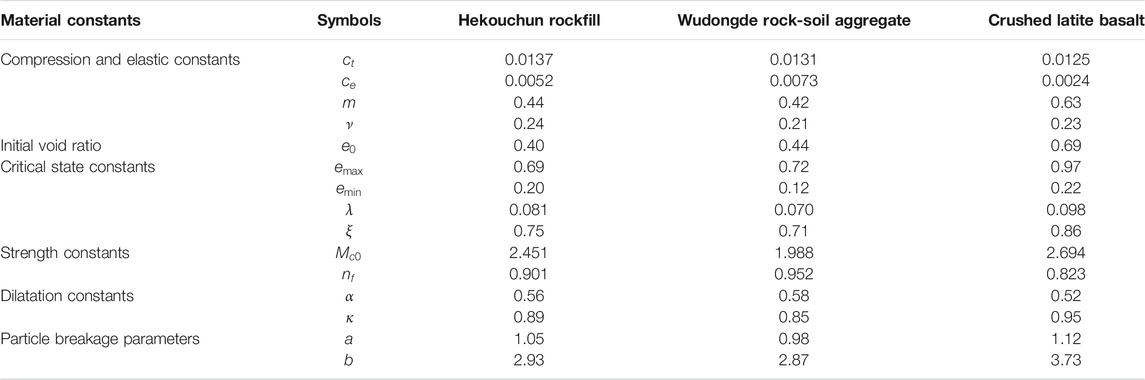
The proposed model was used to simulate the mechanical behaviours of four gravelly soils: Hekouchun rockfill [21], Wudongde rock-soil aggregate [22] and crushed latite basalt [23]. The material constants of the gravelly soils are given in Table 1. The test data and simulation results are shown in Figures 1–3. In these figures, the scatter symbols and curves represent the test data and modelling results, respectively.

TABLE 1

TABLE 1. Material constants of the gravelly soils simulated in this study.

FIGURE 1

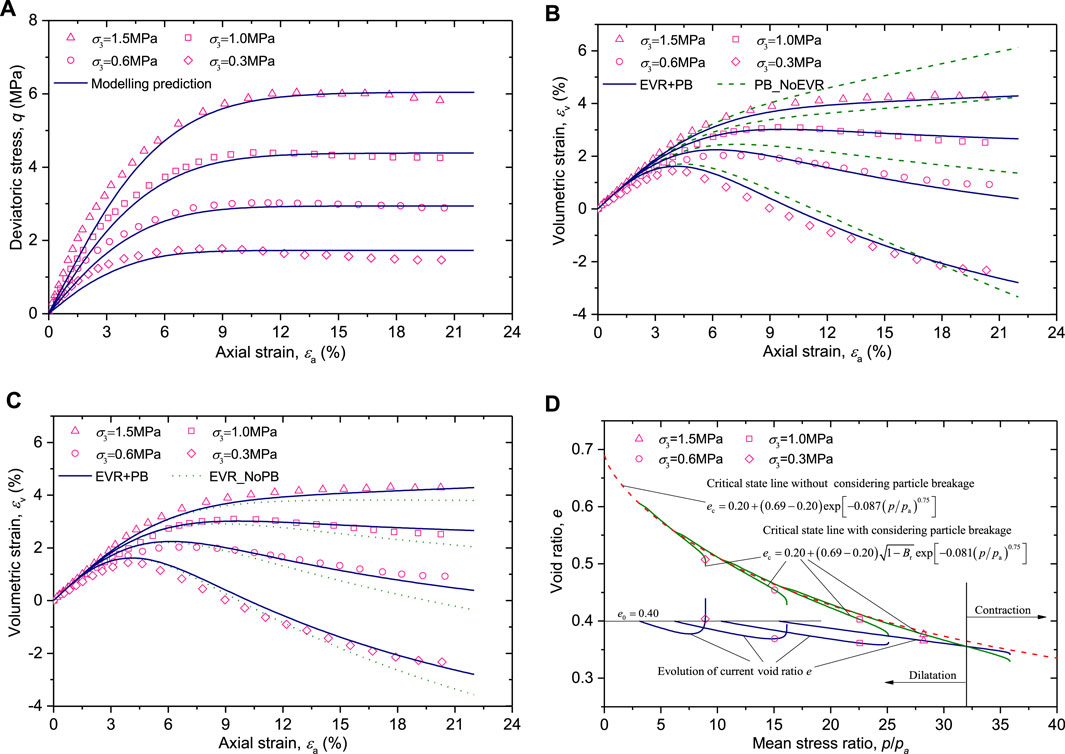
FIGURE 1. Model predations and experimental results of the Hekouchun rockfill (test data were from [21]).

FIGURE 2

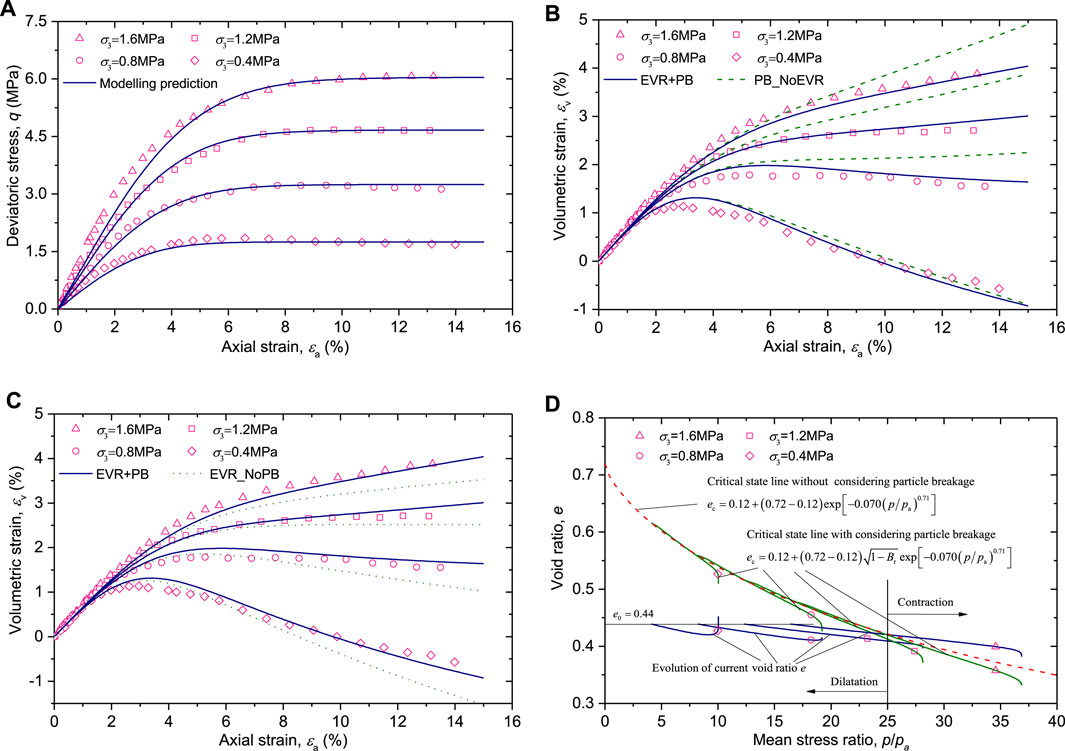
FIGURE 2. Model predations and experimental results of the Wudongde rock-soil aggregate (test data were from [22]).

FIGURE 3

FIGURE 3. Model predations and experimental results of the crushed basalt (test data were from [23]).

Two factors: particle breakage and evolution of void ratio were taken into account to formulate the constitutive model. To observe their influences on the modelling effectiveness, three computing conditions were comparatively analysed. They are termed as:

A “EVR + PB”, which represent that the modelling predictions consider the compound effects of evolution of void ratio and particle breakage.

B “PB_NoEVR”, which represent that the modelling predictions only consider the effect of particle breakage.

C “EVR_NoPB”, which represent that the modelling predictions only consider the evolution of void ratio.

In the model, the shapes of numerical modelling $q\sim {\epsilon }_a$ curves are mainly controlled by the material constants: $c_t$, $c_e$, $m$, $\nu$, $M_{c0}$ and $n_f$. Thus, EVR + PB, PB_NoEVR and EVR_NoPB obtain almost the same modelling predictions of $q\sim {\epsilon }_a$ curves.

3.2.1 Hekouchun rockfill

Hekouchun rockfill material was a type of dolomitic limestone, which would be adopted to construct the Hekouchun reservoir dam. Cai et al. [21] conducted a series of large-scale consolidated and drained triaxial shear tests on Hekouchun rockfill material with an initial relative density $D_r=60\%$. The model parameters of the Hekouchun rockfill material are summarised in Table 1. The test data and modelling results are shown in Figure 1.

As seen from Figure 1 in both stress-strain and volume deformation responses, there is a good agreement between the test data and modelling predictions. Figure 1A shows that the model is capable of capturing the deformation and strength behaviours of Hekouchun rockfill material over a range of confining pressures from 0.3 to 1.5 MPa. Figures 1B,C show the testing volumetric strains and modelling results predicted by EVR + PB, PB_NoEVR and EVR_NoPB. It is found that, on the whole, EVR + PB achieves better simulations, but PB_NoEVR and EVR_NoPB overestimates and under-predicts the volumetric contraction strains, respectively.

The evolution curves of current and critical-state void ratios modelled by EVR + PB are shown in Figure 1D. The ideal CSL without considering particle breakage is plotted using a red dash curve. It is found that the realistic CSLs are influenced by particle breakage and gradually depart from the ideal CSL with the increase of mean stress. When the confining pressure increases, the volume-contraction behaviour of Hekouchun rockfill material becomes more prominent. The evolution rule of current void ratio is consistent with the volume changing rules.

3.2.2 Wudongde rock-Soil Aggregate

Wudongde rock-soil aggregate was a type of natural gravelly soil, sampled from an ancient landslide mass, which was located downstream of the Wudongde Hydropower Dam on the Jinsha River, southwest China. Huang et al. [22] conducted large-scale triaxial tests on the Wudongde rock-soil aggregate under the confining pressures of 0.4, 0.8, 1.2, and 1.6 MPa. The material constants are listed in Table 1 and the modelling results are compared with test data in Figure 2.

Figure 2A shows that the modelling stress-strain relations exhibit good agreements in accordance with the test data. Figures 2B,C show that EVR + PB provides more accurate modelling predictions. PB_NoEVR overestimates volume contraction strains. EVR_NoPB tends to over-predict the volume-dilatation behaviour. In Figure 2D, it is found that EVR + PB modelling curves of current and critical-state void ratios have an intersection point at $p/p_a=25$. This indicates that, at this mean stress state, the volume deformation transits from dilatation to contraction. Therefore, it is reasonable to deduce that, under the confining pressure of 1.6 MPa, Wudongde rock-soil aggregate undergoes a phase change from relative dense to loose state.

3.2.3 Crushed latite Basalt

Salim and Indraratna [23] used a series of confining pressures: 0.05, 0.1, 0.2, and 0.3 MPa to conduct large-scale triaxial tests on a type of crushed latite basalt. Although the confining pressures were relatively lower, the volumetric strains had still undergone a transition from dilatation to contraction. Table 1 lists the material constants of the crushed latite basalt. Figure 3 shows the test data and modelling predictions.

Figure 3A indicates that the model is capable of reproducing the stress-strain relations of the crushed latite basalt. The testing and modelling volumetric strains are compared in Figures 3B,C. Under the confining pressures of 0.05 and 0.1 MPa, EVR + PB, PB_NoEVR and EVR_NoPB achieve relatively better simulations for the volume-dilatation behaviour. With an increase of confining pressure, PB_NoEVR predicts larger volumetric contraction strains. This phenomenon may be related to that PB_NoEVR overestimates the gap between the current void ratio and the CSL. Figure 3D shows the EVR + PB modelling curves of current and critical-state void ratios. Upward-bending evolutions of current void ratios indicates that volume-dilatation responses occur under the confining pressures of 0.05, 0.1, and 0.2 MPa. Under the confining pressure of 0.3 MPa, when the mean stress ratio $p/p_a>7.9$, volume deformation of the crushed latite basalt transits from dilatation to contraction.

4 Conclusions

In this study, a generalised plastic model considering evolution of void ratio and particle breakage was developed for gravelly soils. The model was used to simulate the mechanical behaviours of four gravelly soils. By comparing three computing conditions: EVR + PB, PB_NoEVR, and EVR_NoPB, the effects of void ratio evolution and particle breakage on the modelling predictions were analysed. Following conclusions can be summarised:

1. Because the evolution of void ratio and particle breakage are not considered in the constitutive descriptions of stiffness and strength behaviours, the three computing conditions: EVR + PB, PB_NoEVR, and EVR_NoPB predict almost the same relations between deviatoric stress and axial strain.

2. Under the PB_NoEVR computing condition, current void ratio is constant. In this condition, the proposed model overestimates the volume-contraction strains. The higher the confining pressure, PB_NoEVR will more greatly overestimate the volume-contraction strains.

3. Under the EVR_NoPB computing condition, the ideal CSL is used and current void ratio evolves with the variation of volumetric strain. Overall, EVR_NoPB underestimates the volume-contraction strains and overestimates volume-dilatation strains.

4. In general, the model considering EVR + PB achieves relatively better simulation results for the volume dilatation/contraction responses of gravelly soils. It is reasonable for us to believe that the constitutive model considering EVR + PB could better reflect the volume deformation and failure mechanism of gravelly soils.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conception and design of study was mainly contributed by RW. Numerical simulations was mainly contributed by JZ, YL. Drafting the manuscript was mainly contributed by JZ.

Funding

The work presented in this paper were financially supported by Open Funds at the Key Laboratory of Geological Hazards on Three Gorges Reservoir Area (China Three Gorges University), Ministry of Education (Grant Nos. 2015KDZ16 and 2015KDZ15).

Conflict of Interest

YL is employed by Sinosteel Ma’anshan Institute of Mining Research Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Xiao Y, Liu H, Zhang W, Liu H, Yin F, Wang Y. Testing and Modeling of Rockfill Materials: A Review. J Rock Mech Geotechnical Eng (2016) 8:415–22. doi:10.1016/j.jrmge.2015.09.009

CrossRef Full Text | Google Scholar

2. Hardin BO. Crushing of Soil Particles. J Geotechnical Eng (1985) 111:1177–92. doi:10.1061/(asce)0733-9410(1985)111:10(1177)

CrossRef Full Text | Google Scholar

3. Liu M, Zhang Y, Zhu H. 3D Elastoplastic Model for Crushable Soils with Explicit Formulation of Particle Crushing. J Eng Mech (2017) 143:04017140. doi:10.1061/(asce)em.1943-7889.0001361

CrossRef Full Text | Google Scholar

4. Christophe D. A Constitutive Model for Granular Materials Considering Grain Breakage. Sci China Technol Sci (2011) 54:2188–96.

Google Scholar

5. Liu H, Zou D. Associated Generalized Plasticity Framework for Modeling Gravelly Soils Considering Particle Breakage. J Eng Mech (2013) 139:606–15. doi:10.1061/(asce)em.1943-7889.0000513

CrossRef Full Text | Google Scholar

6. Saberi M, Annan C-D, Konrad J-M. Constitutive Modeling of Gravelly Soil-Structure Interface Considering Particle Breakage. J Eng Mech (2017) 143:04017044. doi:10.1061/(asce)em.1943-7889.0001246

CrossRef Full Text | Google Scholar

7. Sukkarak R, Pramthawee P, Jongpradist P. A Modified Elasto-Plastic Model with Double Yield Surfaces and Considering Particle Breakage for the Settlement Analysis of High Rockfill Dams. KSCE J Civil Eng (2017) 21:1–12. doi:10.1007/s12205-016-0867-9

CrossRef Full Text | Google Scholar

8. Pastor M, Zienkiewicz OC, Chan AHC. Generalized Plasticity and the Modelling of Soil Behaviour. Int J Numer Anal Methods Geomech (1990) 14:151–90. doi:10.1002/nag.1610140302

CrossRef Full Text | Google Scholar

9. Roscoe KH, Schofield AN, Wroth CP. On the Yielding of Soils. Géotechnique (2008) 8:22–53. doi:10.1680/geot.1958.8.1.22

CrossRef Full Text | Google Scholar

10. Chen S-s., Fu Z-z., Han H-q., Peng C. An Elastoplastic Model for Rockfill Materials Considering Particle Breakage. Chin J Geotechnical Eng (2011) 33:1489–95.

Google Scholar

11. Guo W-l., Zhu J-g., Peng W-m. Study on Dilatancy Equation and Generalized Plastic Constitutive Model for Coarse-Grained Soil. Chin J Geotechnical Eng (2017) 32:1–7.

Google Scholar

12. Liu MC, Gao YF. Constitutive Modeling of Coarse-Grained Materials Incorporating the Effect of Particle Breakage on Critical State Behavior in a Framework of Generalized Plasticity. Int J Geomechanics (2016) 17:04016113. doi:10.1061/(ASCE)GM.1943-5622.0000759

CrossRef Full Text | Google Scholar

13. Bauer E, Fu Z, Liu S. Hypoplastic Constitutive Modeling of Wetting Deformation of Weathered Rockfill Materials. Front Archit Civ Eng China (2010) 4:78–91. doi:10.1007/s11709-010-0011-8

CrossRef Full Text | Google Scholar

14. Nakai T. An Isotropic Hardening Elastoplastic Model for Sand Considering the Stress Path Dependency in Three-Dimensional Stresses. Soils and Foundations (1989) 29:119–37. doi:10.3208/sandf1972.29.119

CrossRef Full Text | Google Scholar

15. Bandini V, Coop MR. The Influence of Particle Breakage on the Location of the Critical State Line of Sands. Soils and Foundations (2011) 51:591–600. doi:10.3208/sandf.51.591

CrossRef Full Text | Google Scholar

16. Ghafghazi M, Shuttle DA, Dejong JT. Particle Breakage and the Critical State of Sand. Soils and Foundations (2014) 54:451–61. doi:10.1016/j.sandf.2014.04.016

CrossRef Full Text | Google Scholar

17. Lade PV, Yamamuro JA, Bopp PA. Significance of Particle Crushing in Granular Materials. J Geotechnical Eng (1996) 122:309–16. doi:10.1061/(asce)0733-9410(1996)122:4(309)

CrossRef Full Text | Google Scholar

18. Been K, Jefferies MG. A State Parameter for Sands. Géotechnique (1985) 35:99–112. doi:10.1680/geot.1985.35.2.99

CrossRef Full Text | Google Scholar

19. Yao Y-P, Yamamoto H, Wang N-D. Constitutive Model Considering Sand Crushing. Soils and Foundations (2008) 48:603–8. doi:10.3208/sandf.48.603

CrossRef Full Text | Google Scholar

20. Dafalias YF, Manzari MT. Simple Plasticity Sand Model Accounting for Fabric Change Effects. J Eng Mech (2004) 130:622–34. doi:10.1061/(asce)0733-9399(2004)130:6(622)

CrossRef Full Text | Google Scholar

21. Cai Z-y., Li X-m., Han L, Guan Y-f. Critical State of Rockfill Materials Considering Particle Gradation and Breakage. Chin J Geotechnical Eng (2016) 38:1357–64.

Google Scholar

22. Huang S, Ding X, Zhang Y, Cheng W. Triaxial Test and Mechanical Analysis of Rock-Soil Aggregate Sampled from Natural Sliding Mass. Adv Mater Sci Eng (20152015) 2015:1–14. doi:10.1155/2015/238095

CrossRef Full Text | Google Scholar

23. Salim W, Indraratna B. A New Elastoplastic Constitutive Model for Coarse Granular Aggregates Incorporating Particle Breakage. Can Geotech J (2004) 41:657–71. doi:10.1139/t04-025

CrossRef Full Text | Google Scholar