- 1Department of Chemistry, New York University, New York, NY, United States
- 2Department of Chemical Engineering, University of New Hampshire, Durham, NH, United States
We report simulation studies on the self-assembly of a binary mixture of snowman and dumbbell shaped lobed particles. Depending on the lobe size and temperature, different types of self-assembled structures (random aggregates, spherical aggregates, liquid droplets, amorphous wire-like structures, amorphous ring structures, crystalline structures) are observed. At lower temperatures, heterogeneous structures are formed for lobed particles of both shapes. At higher temperatures, homogeneous self-assembled structures are formed mainly by the dumbbell shaped particles, while the snowman shaped particles remain in a dissociated state. We also investigated the porosities of self-assembled structures. The pore diameters in self-assemblies increased with an increase in temperature for a given lobe size. The particles having smaller lobes produced structures with larger pores than the particles having larger lobes. We further investigated the effect of σ, a parameter in the surface-shifted Lennard-Jones potential, on the self-assembled morphologies and their porosities. The self-assembled structures formed at a higher σ value are found to produce larger pores than those at a lower σ.
1 Introduction
The spherical colloidal particles usually self-assemble into close-packed structures driven by their isotropic interactions [1]. On the contrary, colloidal particles with patches, the patchy particles, can self-assemble into diverse structures due to anisotropic interactions [2]. Therefore, the synthesis and the self-assembly behavior of patchy particles are being increasingly investigated in the materials science research [3–19], because these particles provide a way to fabricate unique morphologies on a nanometer to micrometer scale for various technological and biomedical applications [20–25].
Although several methods have been developed to produce spherical or non-spherical patchy particles, producing a homogeneous mixture of a single type of particles remains challenging [26–29]. As a result, studies are needed to probe the self-assembly behavior of mixtures of different types of particles. In our earlier studies [30–33], we reported on self-assembled morphologies obtained from different types of lobed patchy particles where the patches around a central seed sphere appear as protrusions or lobes. Specifically, we showed that unique porous self-assembled morphologies can be produced depending on the number and the location of lobes. We reported that the dumbbell shaped particles, having two lobes at two opposite poles, can produce larger pores than the particles with higher number of lobes [31]. In addition, our earlier study on the effect of the lobe size and temperature on the self-assembly showed that the single-lobed snowman shaped particles self-assemble into only sheets or micelle like structures, whereas the dumbbell shaped particles can self-assemble into different non-crystalline and crystalline structures at different lobe sizes and temperatures. Moreover, the dumbbell shaped particles self-assemble at a wider range of temperature and lobe size, but the snowman shaped particles self-assemble only at higher lobe sizes and lower temperatures. In the present work, we aim to study the self-assembled morphologies and porosities obtained from a binary mixture of these two types of particles. A binary mixture of these lobed particles, that have only fewer number of lobes, is expected to enrich the spectrum of the morphologies. For example, an earlier theoretical study showed that a large part of the phase space of the self-assembled structures formed by a binary mixture of patchy particles having very fewer number of patches are occupied by empty liquids [34].
Among experimental methods to produce patchy particles, Park et al. [35] developed a method of producing monodispersed snowman shaped particles (in their work, they refer the particles having two spheres as dumbbell-shaped particles) on the micrometer scale using seeded-emulsion polymerization technique. The dumbbell shaped particles, that they produced at different diameter ratios of two spheres, self-assembled into thin two-dimensional layers. Using the same seeded-emulsion polymerization method, Peng et al. [36] synthesized monodisperse snowman and dumbbell shaped particles. Wang et al. [5] developed a method of making non-spherical particles having not only one or two lobes, but more than two lobes. At first, by making the clusters of different shapes using polystyrene beads, and then using a two-stage swelling and polymerization technique, they produced particles of seven different shapes. They showed that a binary mixture of snowman and dumbbell shaped particles, where the lobes of each kind of particles are functionalized with complementary DNA strands, self-assemble into small linear chains at smaller lobe sizes. When the lobes are smaller and the amount of single-lobed snowman shaped particles is less, they form cis-trans-like isomers. When the amount of snowman shaped particles is increased, they form ethylene like molecules where a dumbbell shaped particle using its two lobes remains attached with four snowman shaped particles.
In our work, we studied the self-assembled morphologies produced by a mixture of the snowman and dumbbell shaped particles at different lobe sizes. An earlier study [5] showed that the mixtures of these two types of particles self-assemble into different small clusters at different conditions. Andre et al. [29] showed that the dumbbell and snowman-shaped soft patchy particles at nanometer scale range can co-assemble into colloidal polymers of several micrometers. However, the larger clusters, that can be obtained from the co-assembly of the snowman and dumbbell shaped hard particles, have not been reported yet but such structures would find practical technological or biological applications [37, 38]. To probe these questions, we studied a binary mixture of the snowman and dumbbell shaped lobed particles where we have varied several parameters including the lobe size, temperature, and the σ in the shifted Lennard-Jones potential, and observed their effect on self-assembled morphologies and their functional properties such as porosities.
2 Models and Methods
We studied the self-assembly of a mixture of snowman and dumbbell shaped particles. To model these particles, we followed the approach reported in our previous work [31]. For each dumbbell shaped particle, we placed two spherical beads (Supplementary Figure S1) each with a diameter (σB) of 1.0 (in all of our simulations, σB is the unit of distance) at a distance of 1.0 σB, that is equal to the sum of their radius (1.0 σB), meaning that two spherical beads touch each other. We then placed another spherical bead (the diameter of which is denoted by σS) at the center of mass of these two spherical beads. Therefore, the distance between the central bead and any of the terminal beads is 0.5σB. Following our previous work [31], we refer to the central bead as a seed. After inserting the seed, the exposed parts of the terminal beads, act as lobes. For the snowman-shaped particles, we first placed two spherical beads at a 0.5 σB distance apart. One of these two spherical beads acts as the seed and the exposed part of another bead acts as the lobe. For both types of particles, we gradually changed the seed diameter (σS) from 1.0 σB to 2.0 σB to vary the lobe size, and fixed the diameter of the beads which act as lobes. The higher the diameter of the seed, lower is the lobe size (Supplementary Figures S1B–G). We quantify the lobe size by a parameter termed qL which is the ratio of σB to σS (qL = σB/σS). As we increase the seed diameter (σS), qL decreases from 1.0 to 0.50 (qL = 1.0, 0.83, 0.71, 0.63, 0.56, 0.50). The opening angle (δ) of the lobes (Supplementary Figure S1H), which is defined by the equation (39)
We performed coarse grained Langevin dynamics simulations in constant volume and temperature ensemble using the HOOMD-Blue software [40, 41]. We studied the self-assembly of the mixture at three different number ratios (rN = NS/ND; where NS and ND is the number of the snowman and dumbbell shaped particles, respectively) of the lobed particles (rN = 0.5, 1.0, and 2.0). When rN is equal to 1.0, the simulation domain contains 8,000 lobed particles of each type, thereby totaling 16,000 particles. At rN = 0.5 or 2.0, the number of particles of one type is doubled keeping the number of particles of the other type fixed at 8,000. Therefore, the total number of the particles at rN = 0.5 and 2.0 is 24,000. In all of our simulations, the length of the simulation domain is 140 σB in each direction.
The size of a seed and a lobe is same for each particle present in the simulation domain. In Figure 1, we show a snowman and a dumbbell shaped particle of σS = 1.2 and an initial simulation domain of the binary mixture where the lobed particles are in a dissociated state. We studied the self-assembly at six different seed diameters, and for each seed diameter, we varied the temperature (kBT) from 0.1 to 0.5 (kBT = 0.1, 0.2, 0.3, 0.4, 0.5). For each simulation, we first obtained a randomized initial configuration by performing Langevin dynamics simulation for 105 steps at a higher temperature (kBT = 1.5). We used the randomized initial configuration of each system to study the self-assembly at a desired temperature. The lobe in each snowman shaped particle and the two lobes in each dumbbell shaped particle are connected to the central seed by harmonic bonds. The force constants were stiff enough to maintain the stability of lobes during all simulations. The non-bonded interactions between every pair of particles were modeled by a surface-shifted Lennard-Jones (SSLJ) potential. The functional form of the SSLJ potential between particle i and particle j at a distance r is given by
where ϵij is the depth of the potential well and Δ = (σi + σj)/2–1, where σi and σj are the diameters of the particle i and particle j, respectively. Here, σ measures how close two non-bonded particles can come in an equilibrated self-assembled structure. In all of our simulations, ϵij was set to 1.0 for every type (seed-seed, lobe-lobe, seed-seed) of pair in particles. The interactions in a lobe-lobe pair are attractive, and between a seed-seed or seed-lobe pair are repulsive. The cut-off distance for the pairs of lobes was set to 3.0 and the cut-off distances for the seed-seed and seed-lobe pairs were set to 21/6σ. For each set of seed diameter (except σS = 1.0) and temperature, we carried out two simulations; in one σ was set to 1.0 and in another one σ was set to equal to the seed diameter, σS. In Supplementary Figure S2, we show a trace of VSSLJ vs. r at two different σ for σS = 1.4. At a higher σ, the location of the potential well shifts to the right side.
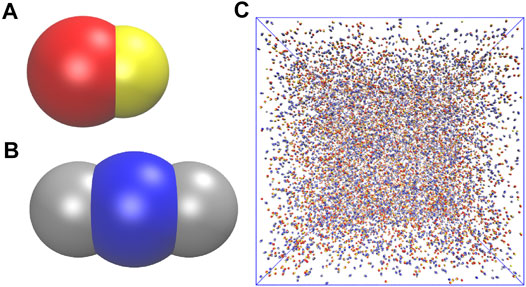
FIGURE 1. (A) A snowman shaped and (B) a dumbbell shaped particle. The seed and the lobe of the snowman shaped particle are represented in red and yellow color respectively. The seed and the lobes of the dumbbell shaped particle are represented in blue and gray color respectively. (C) A representation of the simulation domain showing a disassembled mixture of snowman and dumbbell shaped particles.
We performed a total of 165 simulations (55 simulations for each of the three rN values; 30 simulations at σ = 1.0 and 25 simulations at higher σ values). Each simulation was carried out for 108 steps using a time step of 0.005. We present the potential energy per particle vs. time for all systems in Supplementary Figure S3 which show a convergence of the potential energy with time. To examine the robustness of the self-assembled morphologies, we performed many additional simulations starting from different initial configurations. We observed that the self-assembled structures generated at a particular set of parameters is invariable among different starting configurations. We estimated the radial distribution (RDF) functions for the seed pairs to understand the morphologies of the self-assembled structures (see details in the supporting information).
To examine the homogeneity of the self-assembled structures, we defined a parameter Φ which is given by [42].
where N is the total number of particles present in the system. ⟨…⟩ denotes the time average, and Φi is defined as
3 Results and Discussion
In this section, we describe the self-assembled morphologies and porosities obtained from the mixtures of snowman and dumbbell shaped particles at different seed diameters (σS) and temperatures (kBT). At first, we discuss the morphologies obtained at σ = 1.0 (the SSLJ parameter) and rN = 1.0. We show a state diagram in Figure 2. Then we describe the results obtained at higher σ values and at the other number ratios of the lobed particles.
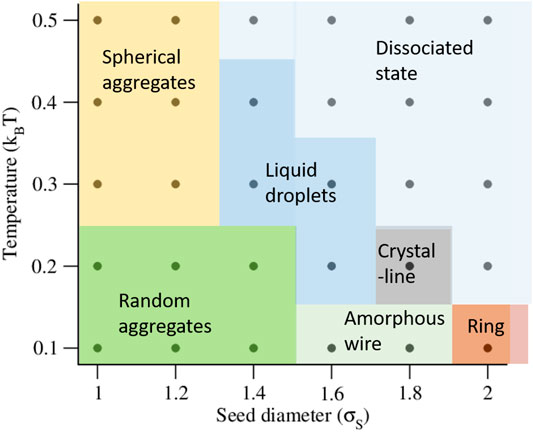
FIGURE 2. A phase diagram of all self-assembled morphologies observed at different seed diameters and temperatures for σ = 1.0 (the SSLJ parameter) and rN = 1.0.
Random Aggregates of Different Shapes at Lower σS
At σS = 1.0 (qL = 1.0), the self-assembly occurs at all five temperatures (kBT = 0.1, 0.2, 0.3, 0.4, 0.5) studied in this work. The RDFs shown in Figure 3A reveal that the self-assembled structures formed at σS = 1.0 are mainly random aggregates. At lower temperatures, the lobes are sticky due to stronger interactions between them. As a result, when the smaller aggregates generated at the initial stages in simulations merge to form larger aggregates, the lobed particles cannot rearrange their positions inside these aggregates, thereby leading to different shapes. The aggregates formed at lower temperatures are composed of both snowman and dumbbell shaped particles (Figure 3B). However, at higher temperatures, the lobes are not so sticky as the interactions between them are moderate, and the lobed particles can rearrange their positions to reduce the interfacial tension and finally appear in a spherical shape (Figure 2 and Figures 3D,F). The spherical aggregates formed at higher temperatures are homogeneous, as revealed by the parameter Φ at different temperatures (Figure 4A; black curve). The cross sectional views of the random aggregates shown in Figures 3C,E reveal that the cores of the random aggregates are formed mainly by the dumbbell shaped particles and the outer most shell is covered by a single layer of snowman shaped particles. This is partly driven by the excluded volume effect and partly driven by the energy. As the volume of the dumbbell shaped particles are higher than the snowman shaped particles, the formation of the central cores of the self-assembled structure only by the dumbbell shaped particles reduces more excluded volume, which makes it favorable to form these morphologies. In addition, the dumbbell shaped particles, when they are at the cores of the self-assembled structures, utilize their two lobes to interact with the other particles, and lower the energy of the system. And the snowman shaped particles due to having one lobe interact with the other particles from one direction only, and form the outer surfaces of the self-assembled structures, making the process partly energy driven. We suggest that the self-assembled monolayers formed at lower temperatures by the snowman shaped particles can stabilize, and control several properties like wetting, adhesion, and chemical resistance of the inner self-assembled structures formed by the dumbbell shaped particles [43, 44].
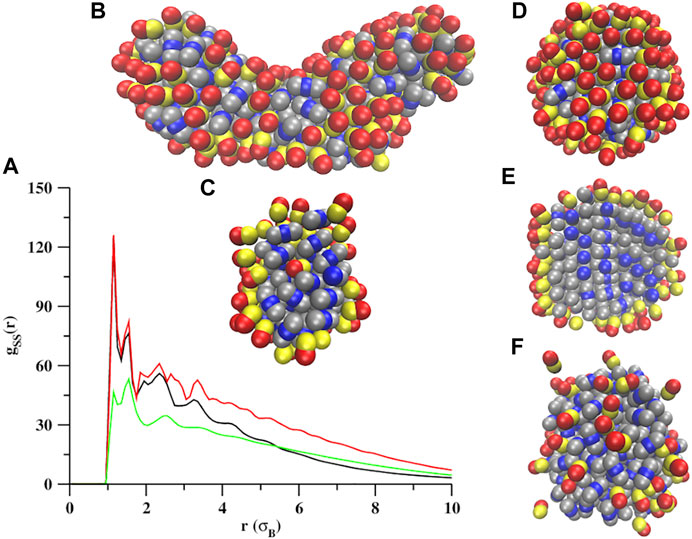
FIGURE 3. Self-assembly of a mixture of snowman and dumbbell shaped particles at σS = 1.0. The RDFs computed for the seed pairs at kBT = 0.1 (black trace), kBT = 0.3 (red trace), and kBT = 0.5 (green trace). Shown are the zoomed views of the random aggregates formed at (B) kBT = 0.1, (D) 0.3, and (F) 0.5. The cross-sectional views (panels C and E) of aggregates given in B and D are also shown.
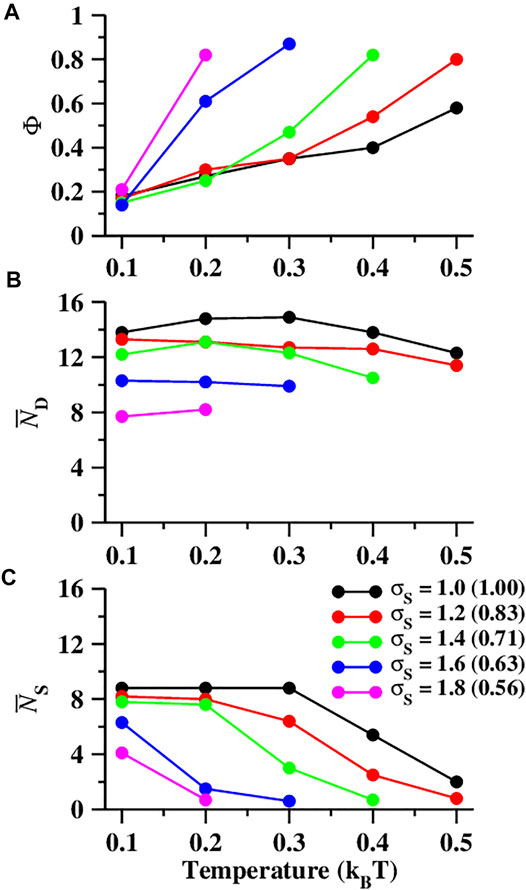
FIGURE 4. (A) The change in the parameter Φ (defined by Eq. 2) with an increase in temperature (kBT) at different seed diameters (σS) for the SSLJ parameter σ = 1. At each seed diameter, the values of Φ increases with an increase in temperature, revealing the formation of homogeneous self-assembled structures at higher temperatures. (B and C) The average number of particles in the first coordination shell of (B) dumbbell shaped particles (
We also estimated the average number of particles present in the first coordination shells of dumbbell shaped (
At σS = 1.2 (qL = 0.83), we observed a very similar kind of self-assembly phenomenon that we observed at σS = 1.0 (Supplementary Figure S4). At lower temperatures (kBT = 0.1, 0.2), random aggregates of different shapes are formed (Supplementary Figures S4A,D), and at higher temperatures (kBT = 0.3, 0.4, 0.5), these aggregates become spherical (Supplementary Figures. S4B,C, E–G). With an increase in temperature, the aggregates become homogeneous (Figure 4A; red curve), formed mainly by the dumbbell shaped particles. The variations in
A Transition from Random Aggregates to Liquid Droplets at Moderate σS
At σS = 1.4 (qL = 0.71) and σS = 1.6 (qL = 0.63), we observed a transition from random aggregates to a liquid droplet state with an increase in temperature. At σS = 1.4, the self-assembly occurs at kBT = 0.1 to 0.4. At kBT = 0.1 and 0.2, heterogeneous random aggregates form (Supplementary Figures S5A,C,E, and F). At higher temperatures (kBT > 0.2), the self-assembled structures become homogeneous, formed predominantly by the dumbbell shaped particles (Figure 4A; green curve). At higher temperatures, the self-assembled structures formed by the dumbbell shaped particles attain a liquid droplet state (Supplementary Figures S5B,D,G), and the snowman shaped particles remain in a dissociated state.
At σS = 1.6, the self-assembly occurs from kBT = 0.1 to 0.3 (Figure 5 and Supplementary Figure S6). At a lower temperature, kBT = 0.1, we observed wire-like structures, that are amorphous and heterogeneous in nature, formed by both types (dumbbell and snowman shaped) of particles (Figure 5B and Supplementary Figure S6B). At kBT = 0.2, most of the snowman shaped particles disassemble (Figure 4C, blue curve) and the dumbbell shaped particles self-assemble into amorphous three-dimensional aggregates (Figure 5C and Supplementary Figure S6C). At both kBT = 0.1 and 0.2, the dumbbell shaped particles form the cores of the self-assembled structures and the snowman shaped particles are found in the outer shell (Figures 5B,C). At both temperatures, the average number of particles present in the first coordination shells of the dumbbell shaped particles (
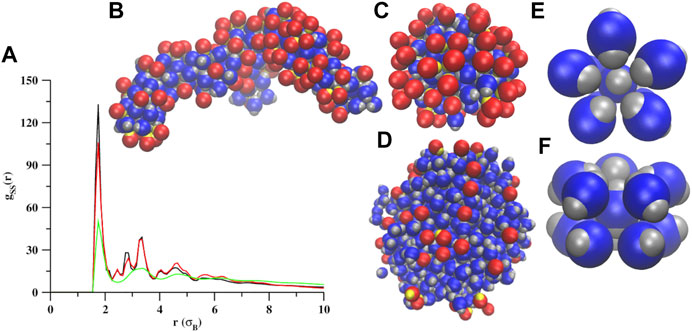
FIGURE 5. Self-assembly of a mixture of snowman and dumbbell shaped particles at σS = 1.6. (A) The RDFs computed for the seed pairs at kBT = 0.1 (black trace), kBT = 0.2 (red trace), and kBT = 0.3 (green trace). Shown also are the enlarged views of a wire-like cluster formed at kBT = 0.1 (B), a three-dimensional amorphous cluster (C), and a liquid droplet (D). In all of these structures, the snowman shaped particles are found at the surfaces only. The first coordination shells of the dumbbell shaped particles look similar at kBT = 0.1 and kBT = 0.2. The top and side views of the first coordination shell are shown in panels (E,F).
For σS ≥ 1.6, we observed a rapid phase separation with an increase in temperature. For an increase in temperature (kBT) from 0.1 to 0.2 at σS = 1.6, the values of Φ were observed to significantly increase from 0.14 to 0.61 (Figure 4A; blue curve). The values of
Amorphous Wire and Ring like Structures and Crystalline Structures at higher σS
At σS = 1.8, the self-assembly occurs only at lower temperatures (kBT = 0.1 and 0.2), and a transition from a wire-like structure (Figure 6B and Supplementary Figure S7B) to a crystalline structure (Figure 6D and Supplementary Figure S7C) is observed with an increase in temperature. At kBT = 0.1, the heterogeneous wire-like structures (Figure 6B and Supplementary Figure S7B) are formed by both types (snowman and dumbbell shaped) of particles. The lobed particles were observed to self-assemble into tetrahedral or octahedral clusters (Figure 6C) before forming an extended wire-like structure. The dumbbell shaped particles contribute to form the central cores of the wires, thereby helping in lengthening the wires via two lobes at the opposite poles. The snowman shaped particles are mainly found at the surfaces of wires, which prevents the growth of wires orthogonal to the axes of the wires. At higher seed diameters, the volumes of the snowman and the dumbbell shaped particles are almost equal. Therefore, the excluded volume effect almost diminishes at this condition. So, the formation of the central cores of the self-assembled structures by the dumbbell shaped particles and the outer surface by the snowman shaped particles is mainly energy driven.
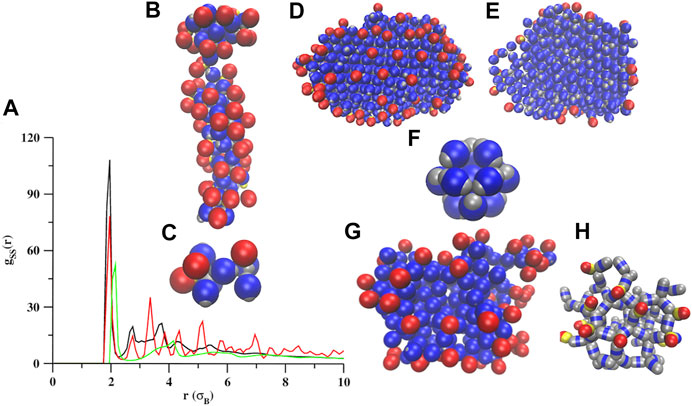
FIGURE 6. Self-assembly of a mixture of snowman and dumbbell shaped particles at different seed diameters and temperatures. (A) The RDFs computed for the seed pairs at σS = 1.8 and kBT = 0.1 (black trace), σS = 1.8 and kBT = 0.2 (red trace), and σS = 2.0 and kBT = 0.1 (green trace). (B) The wire like structures and (C) a small cluster showing an octahedral and a tetrahedral arrangement of particles at two ends of a dumbbell shaped particle at σS = 1.8 and kBT = 0.1. (D,E) A cluster and its cross sectional view, and (F) a face centered cubic unit cell formed at σS = 1.8 and kBT = 0.2. (G) A cluster formed at σS = 2.0 and kBT = 0.1 and (H) a smaller part of it (shown in a stick representation). The particles present in the cluster (G and H) are observed to self-assemble into tetrahedral arrangements before forming large ring-like structures.
At higher temperatures, the snowman shaped particles separate from the assembly leaving only homogeneous self-assembled structures formed by the dumbbell shaped particles. We observed a large increase in the Φ value from 0.21 to 0.82 (Figure 4A; the magenta curve) with a small increment in the temperature from 0.1 to 0.2, revealing a rapid transition from the heterogeneous to homogeneous structures. The variations in
At σS = 2.0, the self-assembly occurs only at kBT = 0.1, predominantly by the dumbbell shaped particles (Figure 6G). The self-assembled structures are amorphous and made up of ring like structures (Figure 6H). We did not observe any long-range order between the particles (Figure 6A; the green curve) but a short-range order is observed where the first coordination shell possesses a trigonal prismatic geometry. The lobed particles were observed to self-assemble into a tetrahedral geometry before forming a ring like structure (Figure 6G). The dumbbell shaped particles form the bulk of the clusters, and the snowman shaped particles are observed only at the surfaces of the clusters (Figure 6G).
Heterogeneous Wire-like Structures to Homogeneous Liquid Droplets at σS = 1.4 and σ = 1.4
The self-assembled morphologies, that we have described so far, were obtained at the SSLJ parameter σ = 1.0. Now we will describe the self-assembled morphologies obtained at higher σ. For the seed diameters (σS) equal to 1.2, 1.4, 1.6, 1.8, and 2.0, we carried out a second set of simulations where the values of σ were set equal to their respective σS values. At these higher σ values, we observed the self-assembly only at σS = 1.2 and 1.4. At σS = 1.2, we observed self-assembly at four different temperatures (kBT = 0.1, 0.2, 0.3, and 0.4). At lower temperatures, heterogeneous random aggregates are formed, and at higher temperatures, homogeneous liquid droplets primarily formed by the dumbbell shaped particles are observed (Supplementary Figure S8). At σS = 1.4, we observed the self-assembly at two different temperatures (kBT = 0.1 and 0.2). At kBT = 0.1, the heterogeneous wire-like structures (Figure 7A), that are amorphous in nature, are formed. The lobed particles self-assemble into octahedral clusters (Figures 7B,C) before forming the extended wire-like structures. At kBT = 0.2, homogeneous liquid droplets are formed mainly by the dumbbell shaped particles, and the snowman shaped particles are found in a dissociated state (Figure 7D).
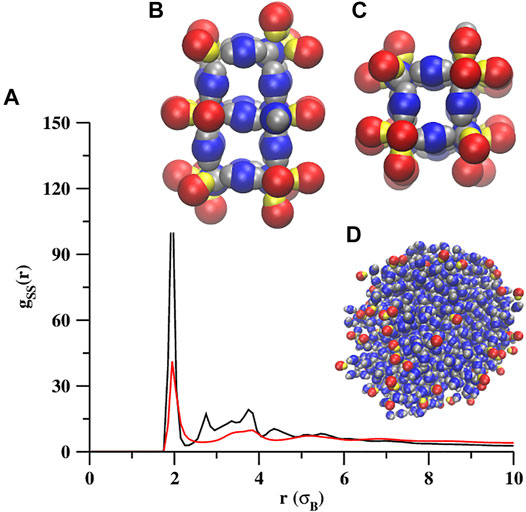
FIGURE 7. Self-assembly of a binary mixture of snowman and dumbbell shaped particles at σS = 1.4 and σ = 1.4. Shown are the RDFs for the wire like structures (black trace) formed at kBT = 0.1 and liquid droplets (red trace) formed at kBT = 0.2. The top and side views of a part of wire-like structures (B,C) and a liquid droplet (D) are also shown.
At any seed diameter and temperature, the self-assembled morphologies remain same at different number ratios (rN) of the lobed particles. At any combination of the seed diameter (σS), temperature (kBT), and the SSLJ parameter, σ, the morphologies of the self-assembled structures formed at two other number ratios (rN = 0.5 and 2.0) of the lobed particles are similar to the structures formed at rN = 1.0 (Supplementary Figures S9, S10). At any seed diameters, homogeneous structures are formed at lower temperatures, and heterogeneous structures are formed at higher temperatures (Supplementary Figure S11). The variations in
Porosities of Self-Assembled Structures
At the SSLJ patameter σ = 1.0, the largest pores are found at σS = 2.0 and kBT = 0.1. We estimated pore diameters for those structures that are three dimensional, and not extended wire-like. At any seed diameter, the three-dimensional structures usually form at higher temperatures, and the extended wire-like structures or narrow random aggregates form at lower temperatures. Therefore we estimated the pore size distributions, which are shown in Figure 8, Supplementary Figures S13, S14, for the higher temperature structures only. For three-dimensional self-assembled structures, we extracted large cuboids, and then used the Zeo++ software [45, 46] to estimate the pore size distributions, as carried out in our previous work [30, 31]. For each seed diameter, the pore diameters were observed to increase with an increase in the temperature. The lobed particles having larger seeds or smaller lobes were observed to produce bigger pores than the particles having smaller seeds. At σ = 1.0, the largest pores were found for σS = 2.0 at kBT = 0.1 (Supplementary Figure S13F). We obtained a broader pore size distribution because of the amorphous ring structures formed at this condition. The pore diameters were found to vary between ∼ 1.5σB and ∼ 3.5σB.
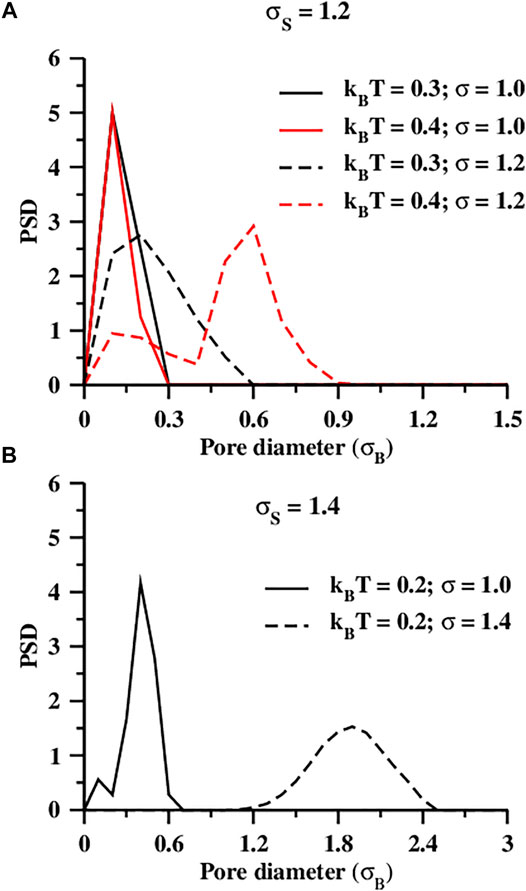
FIGURE 8. Pore size distributions (PSDs) at different temperatures and at different values of the SSLJ parameter, σ for the seed diameter, σS = 1.2 (A) and 1.4 (B). For comparison, we present the PSDs only at those temperatures, where three-dimensional self-assembled structures are formed for both the σ values.
Self-Assembled Structure Formed at a Higher σ Value Produce Larger Pores than the Corresponding Structure Formed at a Lower Sigma Value
The self-assembled structures formed at higher σ values are observed to form larger pores than the corresponding structures formed at lower σ values (Figure 8). Among the self-assembled structures formed at higher σ values, the structures self-assembled at σS = 1.4 and σ = 1.4 were found to possess the largest pores at kBT = 0.2 (Figure 8B, Supplementary Figure S14B). At this condition, the pore diameter varies between ∼ 1.0σB and ∼ 2.5σB. The structures self-assembled at the same seed diameter and temperature (σS = 1.4 and kBT = 0.2) but at a lower σ value (σ = 1.0) produce very small pores (∼ 0.2σB to ∼ 0.7σB), revealing the effect of the Lennard-Jones parameters σ on the porosities of the self-assembled structures. The central seeds, at a higher σ value, become more repulsive and therefore remain further from each other compared to a lower σ, which is why the pore diameters at a higher σ are much larger than at a lower σ.
As all the simulation domains in our work contain a mixture of snowman and dumbbell shaped particles, the self-assembly phenomenon is observed mainly at lower temperatures. For example, in our earlier study [31], we observed that the highest temperature at which the dumbbell shaped particles of σS = 1.6 self-assemble is 0.4, and at that condition the pore diameters vary between 0.1σB and 2.3σB [31]. But in the presence of snowman shaped particles, the highest temperature at which the self-assembly occurs at σS = 1.6 is 0.3. Although the self-assembled structures formed at kBT = 0.3 in the present work are almost similar to the structures formed at kBT = 0.4 in our previous study (in both cases liquid droplets are formed by the dumbbell shaped particles), the pore diameters found in the present work (Supplementary Figure S13D, red curve) are relatively smaller (0.1σB to 1.2σB) than the previous work due to the difference in the temperature. As pore diameters increase with the temperature, and the presence of the snowman shaped particles inhibits the self-assembly at higher temperatures, we recommend the usage of only dumbbell shaped particles for better porous self-assembled structures. Moreover, as the snowman shaped particles remain only at surfaces of the self-assembled structures and the bulk of the self-assembled structures are formed mainly by the dumbbell shaped particles at any seed diameter and temperature, the snowman shaped particles do not have a significant impact on the porosities of the self-assembled structures.
4 Conclusion
We have reported studies on self-assembled structures obtained from a mixture of the snowman and dumbbell shaped particles at different lobe sizes and temperatures. We also investigated the effect of the SSLJ parameter σ on the self-assembled morphologies and porosites. At lower temperatures, heterogeneous self-assembled structures are formed by both the dumbbell and snowman shaped particles. The dumbbell shaped particles form the cores of self-assembled structures, and the snowman shaped particles are self-assembled in a single layer at the surfaces of the self-assembled structures. With an increase in temperature, homogeneous self-assembled structures formed predominantly by the dumbbell shaped particles are observed, and the snowman shaped particles are found in a dissociated state. The difference in the number of lobes between these two types of particles is the reason for the self-assembly of snowman particles only at lower temperatures, while those of the dumbbell shaped particles at higher temperatures too. At larger seed diameters, the transition from the heterogeneous to homogeneous structures occurs faster than at smaller seed diameters. Depending on the seed diameter and temperature, we found different types of self-assembled structures (random aggregates, wire-like structures, liquid droplets, crystalline, and ring structures). The self-assembled morphologies are invariant with respect to the number ratios of the constituent lobed particles in the mixture. At higher σ values, the self-assembly occurs only at lower seed diameters (σS = 1.2 and 1.4). Our work suggests that the repulsive interactions between the seed particles play a major role in producing porous self-assembled structures, as suggested by the results at various σ values. Our work also shows that the simpler particle shapes like snowman and dumbbell shaped lobed particles, having very small number of lobes that are easier to synthesize, can produce a variety of structures when they are mixed and when the interactions between them are tuned.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
HV: conceptualization, supervision, and funding acquisition. SP: modeling, simulation, analysis. SP and HV: writing, draft preparation. All authors contributed to the article and approved the submitted version.
Funding
We are grateful for financial support provided by the National Science Foundation (award No. OIA-1757371; HV). We acknowledge computational support through the following resources: Premise, a central shared HPC cluster at UNH supported by the Research Computing Center; and BioMade, a heterogeneous CPU/GPU cluster supported by the NSF EPSCoR award (OIA-1757371; HV).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.767623/full#supplementary-material
References
1. Manoharan VN. Colloidal matter: Packing, geometry, and entropy. Science (2015) 349:1253751. doi:10.1126/science.1253751
2. Zhang Z, Glotzer SC. Self-assembly of patchy particles. Nano Lett (2004) 4:1407–13. doi:10.1021/nl0493500
3. Chen Q, Bae SC, Granick S. Directed self-assembly of a colloidal kagome lattice. Nature (2011) 469:381–4. doi:10.1038/nature09713
4. Kraft DJ, Ni R, Smallenburg F, Hermes M, Yoon K, Weitz DA, et al. Surface roughness directed self-assembly of patchy particles into colloidal micelles. Proc Natl Acad Sci (2012) 109:10787–92. doi:10.1073/pnas.1116820109
5. Wang Y, Wang Y, Breed DR, Manoharan VN, Feng L, Hollingsworth AD, et al. Colloids with valence and specific directional bonding. Nature (2012) 491:51–5. doi:10.1038/nature11564
6. Ku KH, Kim Y, Yi G-R, Jung YS, Kim BJ. Soft patchy particles of block copolymers from interface-engineered emulsions. ACS Nano (2015) 9:11333–41. doi:10.1021/acsnano.5b05058
7. Diaz A. JA, Oh JS, Yi G-R, Pine DJ. Photo-printing of faceted dna patchy particles. Proc Natl Acad Sci U.S.A (2020) 117:10645–53. doi:10.1073/pnas.1918504117
8. Pons-Siepermann IC, Glotzer SC. Design of patchy particles using quaternary self-assembled monolayers. ACS Nano (2012) 6:3919–24. doi:10.1021/nn300059x
9. Long AW, Ferguson AL. Rational design of patchy colloidsvialandscape engineering. Mol Syst Des Eng (2018) 3:49–65. doi:10.1039/c7me00077d
10. Long AW, Ferguson AL. Nonlinear machine learning of patchy colloid self-assembly pathways and mechanisms. J Phys Chem B (2014) 118:4228–44. doi:10.1021/jp500350b
11. Morphew D, Shaw J, Avins C, Chakrabarti D. Programming hierarchical self-assembly of patchy particles into colloidal crystals via colloidal molecules. ACS Nano (2018) 12:2355–64. doi:10.1021/acsnano.7b07633
12. Tsyrenova A, Miller K, Yan J, Olson E, Anthony SM, Jiang S. Surfactant-mediated assembly of amphiphilic janus spheres. Langmuir (2019) 35:6106–11. doi:10.1021/acs.langmuir.9b00500
13. Kraft DJ, Vlug WS, van Kats CM, van Blaaderen A, Imhof A, Kegel WK. Self-assembly of colloids with liquid protrusions. J Am Chem Soc (2009) 131:1182–6. doi:10.1021/ja8079803
14. Hong L, Cacciuto A, Luijten E, Granick S. Clusters of amphiphilic colloidal spheres. Langmuir (2008) 24:621–5. doi:10.1021/la7030818
15. Bharti B, Rutkowski D, Han K, Kumar AU, Hall CK, Velev OD. Capillary bridging as a tool for assembling discrete clusters of patchy particles. J Am Chem Soc (2016) 138:14948–53. doi:10.1021/jacs.6b08017
16. Sato M. Effect of patch area and interaction length on clusters and structures formed by one-patch particles in thin systems. ACS Omega (2020) 5:28812–22. doi:10.1021/acsomega.0c04159
17. Sato M. Effect of the interaction length on clusters formed by spherical one-patch particles on flat planes. Langmuir (2021) 37:4213–21. doi:10.1021/acs.langmuir.1c00102
18. Harper ES, van Anders G, Glotzer SC. The entropic bond in colloidal crystals. Proc Natl Acad Sci USA (2019) 116:16703–10. doi:10.1073/pnas.1822092116
19. van Anders G, Klotsa D, Ahmed NK, Engel M, Glotzer SC. Understanding shape entropy through local dense packing. Proc Natl Acad Sci USA (2014) 111:E4812–E4821. –E4821 doi:10.1073/pnas.1418159111
20. Ravaine S, Duguet E. Synthesis and assembly of patchy particles: Recent progress and future prospects. Curr Opin Colloid Interf Sci (2017) 30:45–53. doi:10.1016/j.cocis.2017.05.002
21. Li F, Josephson DP, Stein A. Colloidal assembly: The road from particles to colloidal molecules and crystals. Angew Chem Int Ed (2011) 50:360–88. doi:10.1002/anie.201001451
22. Glotzer SC, Solomon MJ, Kotov NA. Self-assembly: From nanoscale to microscale colloids. Aiche J (2004) 50:2978–85. doi:10.1002/aic.10413
23. Xia Y, Gates B, Li Z-Y. Self-assembly approaches to three-dimensional photonic crystals. Adv Mater (2001) 13:409–13. doi:10.1002/1521-4095(200103)13:6<409:aid-adma409>3.0.co;2-c
24. Pawar AB, Kretzschmar I. Fabrication, assembly, and application of patchy particles. Macromol Rapid Commun (2010) 31:150–68. doi:10.1002/marc.200900614
25. Boncheva M, Whitesides GM. Biomimetic Approaches to the Design of Functional, Self-Assembling Systems. 1st ed. edn, vol. 1. New York, NY: Marcel Dekker (2004). p. 287–94. 873.
26. Bao H, Bihr T, Smith A-S, Klupp Taylor RN. Facile colloidal coating of polystyrene nanospheres with tunable gold dendritic patches. Nanoscale (2014) 6:3954–66. doi:10.1039/c3nr04016j
27. Meester V, Verweij RW, van der Wel C, Kraft DJ. Colloidal recycling: Reconfiguration of random aggregates into patchy particles. ACS Nano (2016) 10:4322–9. doi:10.1021/acsnano.5b07901
28. van Ravensteijn BGP, Kamp M, van Blaaderen A, Kegel WK. General route toward chemically anisotropic colloids. Chem Mater (2013) 25:4348–53. doi:10.1021/cm4025606
29. Gröschel AH, Walther A, Löbling TI, Schacher FH, Schmalz H, Müller AHE. Guided hierarchical co-assembly of soft patchy nanoparticles. Nature (2013) 503:247–51. doi:10.1038/nature12610
30. Paul S, Vashisth H. Self-assembly of lobed particles into amorphous and crystalline porous structures. Soft Matter (2020) 16:1142–7. doi:10.1039/c9sm01878f
31. Paul S, Vashisth H. Self-assembly behavior of experimentally realizable lobed patchy particles. Soft Matter (2020) 16:8101–7. doi:10.1039/d0sm00954g
32. Rocha BC, Paul S, Vashisth H. Enhanced porosity in self-assembled morphologies mediated by charged lobes on patchy particles. J Phys Chem B (2021) 125:3208–15. doi:10.1021/acs.jpcb.0c11096
33. Gorai B, Rocha BC, Vashisth H. Design of functionalized lobed particles for porous self-assemblies. JOM (2021) 73:2413–22. doi:10.1007/s11837-021-04715-w
34. Rovigatti L, de las Heras D, Tavares JM, Telo da Gama MM, Sciortino F. Computing the phase diagram of binary mixtures: A patchy particle case study. J Chem Phys (2013) 138:164904. doi:10.1063/1.4802026
35. Park J-G, Forster JD, Dufresne ER. High-yield synthesis of monodisperse dumbbell-shaped polymer nanoparticles. J Am Chem Soc (2010) 132:5960–1. doi:10.1021/ja101760q
36. Peng B, Vutukuri HR, van Blaaderen A, Imhof A. Synthesis of fluorescent monodisperse non-spherical dumbbell-like model colloids. J Mater Chem (2012) 22:21893–900. doi:10.1039/c2jm35229j
37. Matson JB, Zha RH, Stupp SI. Peptide self-assembly for crafting functional biological materials. Curr Opin Solid State Mater Sci (2011) 15:225–35. doi:10.1016/j.cossms.2011.08.001
38. Loh QL, Choong C. Three-dimensional scaffolds for tissue engineering applications: Role of porosity and pore size. Tissue Eng B: Rev (2013) 19:485–502. doi:10.1089/ten.teb.2012.0437
39. Avvisati G, Vissers T, Dijkstra M. Self-assembly of patchy colloidal dumbbells. J Chem Phys (2015) 142:084905. doi:10.1063/1.4913369
40. Anderson JA, Lorenz CD, Travesset A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J Comput Phys (2008) 227:5342–59. doi:10.1016/j.jcp.2008.01.047
41. Glaser J, Nguyen TD, Anderson JA, Lui P, Spiga F, Millan JA, et al. Strong scaling of general-purpose molecular dynamics simulations on gpus. Comp Phys Commun (2015) 192:97–107. doi:10.1016/j.cpc.2015.02.028
42. Goyal A, Hall CK, Velev OD. Self-assembly in binary mixtures of dipolar colloids: Molecular dynamics simulations. J Chem Phys (2010) 133:064511. doi:10.1063/1.3477985
43. Laibinis PE, Whitesides GM, Allara DL, Tao YT, Parikh AN, Nuzzo RG. Comparison of the structures and wetting properties of self-assembled monolayers of n-alkanethiols on the coinage metal surfaces, copper, silver, and gold. J Am Chem Soc (1991) 113:7152–67. doi:10.1021/ja00019a011
44. Love JC, Estroff LA, Kriebel JK, Nuzzo RG, Whitesides GM. Self-assembled monolayers of thiolates on metals as a form of nanotechnology. Chem Rev (2005) 105:1103–70. doi:10.1021/cr0300789
45. Pinheiro M, Martin RL, Rycroft CH, Haranczyk M. High accuracy geometric analysis of crystalline porous materials. CrystEngComm (2013) 15:7531–8. doi:10.1039/c3ce41057a
Keywords: lobed particles, self-assembly, porous structures, particle mixtures, Langevin dynamics
Citation: Paul S and Vashisth H (2021) Self-Assembly of Porous Structures From a Binary Mixture of Lobed Patchy Particles. Front. Phys. 9:767623. doi: 10.3389/fphy.2021.767623
Received: 31 August 2021; Accepted: 30 September 2021;
Published: 19 October 2021.
Edited by:
Ramon Castañeda-Priego, University of Guanajuato, MexicoReviewed by:
Gerardo Odriozola, Autonomous Metropolitan University, MexicoJose Antonio Moreno-Razo, Autonomous Metropolitan University, Mexico
Copyright © 2021 Paul and Vashisth. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Harish Vashisth, aGFyaXNoLnZhc2hpc3RoQHVuaC5lZHU=
 Sanjib Paul
Sanjib Paul Harish Vashisth
Harish Vashisth