
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 28 January 2022
Sec. High-Energy and Astroparticle Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.765960
In this work, we explicate a new approach for eliminating renormalization scale and scheme (RSS) dependence in observables. We develop this approach by matching RSS-dependent observables (such as cross-sections and decay rates) to a theory which is independent of both these forms of dependencies. We term the fundamental basis behind this approach as the principle of observable effective matching (POEM), which entails matching of a scale- and scheme-dependent observable with the fully physical scale (PS) and dynamical scale-dependent theory at loop orders at which RSS independence is guaranteed. This is aimed toward achieving so-called “effective” RSS-independent expressions as the resulting dynamical dependence is derived from a particular order in RSS-dependent perturbation theory. With this matching at a PS at which the coupling (and masses) is experimentally determined at this scale, we obtain an “effective theoretical observable (ETO)”, a finite-order RSS-independent version of the RSS-dependent observable. We illustrate our approach with a study of the cross-section ratio
In perturbative quantum field theory (QFT), singularities are encountered in theoretical expressions of physical observables which require renormalization techniques. Rendering finiteness to such quantities, such as physical cross-sections and decay rates, introduces renormalization scale and scheme (RSS) dependencies. These dependencies ultimately lead to theoretical uncertainties in predictions. This is especially problematic in the case of perturbative quantum chromodynamics (pQCD), wherein the strong coupling constant is large and RSS dependencies can lead to higher theoretical uncertainties. Hence, the main motivation of this work is the elimination of the RSS dependencies, which is aimed to lead to theoretical predictions with higher accuracy. This is demonstrated in the case of the QCD cross-section ratio
The issue of RSS ambiguities is treated via the principle of minimal sensitivity (PMS) [1–4]. Other approaches to reducing and/or eliminating scheme dependence include the approaches of effective charge [5, 6], Brodsky–Lepage–Mackenzie (BLM) [7–9], renormalization group (RG) summation [10], RG summation with RS invariants [11–14], complete renormalization group improvement (CORGI) [15–17], the principle of maximal confomality (PMC) [18–23], and sequential extended BLM (seBLM) [24]. In this work, we detail a new and alternate approach toward achieving RSS independence, inspired by effective field theory (EFT) techniques of matching. Our work is also surmised on the observation that at increasing order in the expansion of a small expansion parameter, along with convergence, such dependencies would be reduced and the penultimate expression would have full dependence only on dynamical and physical scales. As such, it is based on what we conceptualize as the “principle of observable effective matching” (POEM). Since this principle is applicable for achieving RSS independence only up to a fixed order in perturbation theory, we use the term “effective” for the observable having only physical scale (PS) and dynamical scale dependence, which is also the scale at which matching occurs. We term the derived perturbative expression as an “effective theoretical observable (ETO)”, which implies these caveats. The study is outlined as follows: we introduce POEM next and then work out the RSS-independent quantum chromodynamics (QCD) cross-section ratio
Physical observables computed to all orders in perturbative QFT within various RSS approaches are expected to result in scale and scheme independence if results at all orders are computed and hence must be the same in this limit. This is the starting point for POEM which can be expressed as follows:
Here, O denotes perturbative contributions to a physical observable such as in a decay rate or a cross-section computed in two schemes denoted by superscripts i and j at some loop orders n and l, respectively, while a and m denote the coupling and mass, respectively, tied to the respective renormalization scales μi and μj. Q and M denote dynamical PS. Eq. 1 can be further generalized by including multiple couplings and masses as well as factorization scales and momentum fractions. This equation nevertheless implies that if O is computed at a certain large limit of perturbation theory, this results in an RSS-independent result with dependence only on Q and M. While it is rather challenging to find expressions to all orders in perturbation theory, we consider such to be an RSS-independent theory or full theory whereby all implicit and explicit renormalization scales within any scheme cancel, and the equalization across in Eq. 1 implies an overall RSS independence, leading to an independent observable termed as Ofull dependent only on a scale-independent coupling and mass, as well as physical scales, Q and M.
While in Eq. 1, RSS independence is achieved for an observable computed at all orders in perturbation theory, for practical purposes, and as criteria to derive an effective version of such an all-order observable, RSS independence holds true trivially at the tree level (when no quantum corrections exist), and this is also valid at the some r-loop level at a physical scale (typically, this is at one- and two-loop levels). With these properties in mind, we propose the POEM condition which can be applied to achieve an effective RSS independence at an order-by-order basis for truncated expressions of a physical observable as follows:
Here, Oeff is conceptualized in a finite-order perturbative physical representation termed as the ETO which is truncated at the r-loop order in order to be consistent with RSS independence and is dependent only on dynamical scales and PSs. Equation 2 denotes a general RSS independence requirement whereby matching is done at a PS Q* at the r-loop, via an effective RSS-independent dynamical coupling and mass depending on a PS, which are denoted as aeff and meff, respectively, in both equations, although in the RSS-dependent expression, these are computed via a truncated order, n, thereby denoting the effective nature of these RSS independence conditions. Scale independence is achieved via matching at a physical point Q*, whereby the couplings and masses are referenced to observed values, which ultimately renders the ETOs free from unphysical scale ambiguity. Since POEM is based on the EFT matching approach and focused directly on the observable itself, it must also be noted that in this approach, the PS or reference matching scale Q* is not arbitrary but is rather based on the physical observable, the relevant physical process, and the relevant and valid EFT describing the physics process with relevant degrees of freedom. The value of the coupling (and masses) must be experimentally determined at this physical scale, and the range of applicability cannot exceed beyond the relevant physical degrees of freedom or go beyond the perturbative cutoff of the theory. Moreover, the resummation that happens due to POEM, in analogy, “integrates out” the unphysical RSS dependencies from the observable to an independent ETO. In regard to the arbitrary renormalization scale μ dependence, by matching and referencing the EFT at a physical scale Q* at which the coupling (and masses) is determined via experiments, POEM leads to scale independence in the observable as the observable is now fully renormalized to the dynamical scale Q. As such, with POEM, we also perform an “effective dynamical renormalization” (EDR) of the RSS-dependent physical observable via matching (and resulting resummation) which renders it completely dynamical, with the ETO tied to the physical relevance of the scale of matching with applicability to the underlying theory while preserving physical degrees of freedom.
Scheme independence in aeff and meff and ultimately the ETO is simultaneously achieved using matching, whereby explicit dependence is absorbed into these running parameters and implicit dependence is eliminated by restricting their running to r-loops; hence, we use truncated RG functions at this order. In Equation 2, the k subscript denotes a particular scheme for a truncated observable O at a loop order n (for example, the
Typically, EFT techniques are applied at the level of operators instead of observables and deal with physical degrees of freedom, dealing with RSS dependence as auxiliary variables. Therefore, broadly speaking, our approach via POEM is to bridge conventional renormalization techniques with EFT techniques, with a first focus on observables in this work. Since POEM and the matching of observables to achieve RSS independence are unprecedented, we demonstrate its efficacy in this approach first and we will explicate the construction of ETOs from the RSS-independent Lagrangian of the underlying EFT in a separate work1. The advantage of using our approach over using fixed-order perturbation theory is that both explicit dependence and implicit dependence on the renormalization scale and scheme are eliminated at an order-by-order basis via the POEM matching process, and the derived ETOs are resummed expressions that are referenced at a physically relevant matching scale.
Overall, Eq. 2 allows for a practical realization of Eq. 1 at a finite order of perturbation theory for our proposed implementation of the POEM approach and implies RSS independence in the ETO to hold both at the matching scale Q* and for dynamical degrees of freedom, Q and M, which can be explicitly stated as follows:
where μ is the renormalization scale, while ci are renormalization scheme-dependent RG coefficients.
We remark here that Eq. 3 is due to the application of POEM and the resulting resummed expressions, or ETOs,
For the case of the cross-section ratio
It follows that if there is a different matching scale chosen based on the initial physical matching reference scale such that
Then, the dynamical scale must also rescale by the same constant k as follows:
This is consistent with Eq. (4), or in other words, this is consistent with the reference physical scale of Q∗ (and the underlying measurement of couplings and masses at this scale). While renormalization group (RG) functions can be used to evolve the coupling and masses using Q∗ to another matching scale,
Finally, it is interesting to note that since RSS independence is guaranteed trivially at the tree level so that via Eq. 2, we also can express this particular case as follows:
In this relationship, we introduce a dynamical scheme-independent cutoff scale at renormalization μ = Λeff for the observable which denotes the point at which no quantum corrections occur in the matching RSS-independent theory at the tree level. As it is dependent only on dynamical scales, this RSS-independent cutoff scale is indeed distinct from typical renormalization coupling and mass cutoffs, which are scheme-dependent (see [25] for analysis on RS dependence of the strong coupling constant and its cutoff ΛQCD). As such, Eq. 6 is a particular case of the general POEM condition, which has interesting new implications, while holding no bearing in deriving ETOs which necessarily contain perturbative quantum corrections.
The relation of the cross-section ratio
with
The explicit dependence of R on the renormalization scale parameter μ is compensated for by implicit dependence of the “running coupling” a(μ2) on μ,
where a ≡ αs(μ2)/π, while αs is the QCD strong coupling constant.
The cross-section ratio
where the choice of the number of flavors is based on the center of mass energies Q (for which the ETO will be derived) which are for those above the b-quark mass.
In the
where the values of b and c are the same in any mass-independent renormalization scheme, while the values of c2 and c3 in Eq. 11 are particular to the
At the Z-pole mass (MZ = 91.1876 GeV), we have [33] in the
Utilizing Eq. 2, we therefore find the following POEM-based relationship:
With Equation 14, which is matching done at the one-loop level, we choose the matching point Q∗ = MZ = 91.1876GeV and also subtract the only explicit scheme-dependent term, appearing in the expression for T31, which is 2c2 in the
The choice of Q∗ = MZ and the number of quarks, nf = 5, is predicted on deriving the ETO for center of mass energies Q above the b-quark mass (and also below the t-quark threshold mass).
Since for the ETO we absorb higher-order loop contributions from an RSS-dependent scheme at the one-loop order for RSS independence,
where
is a one-loop beta-function solution in the dynamical ETO, with an initial value set at
Since we are at the one-loop matching, we find the one-loop solution to aeff(Q) which leads to the prediction of
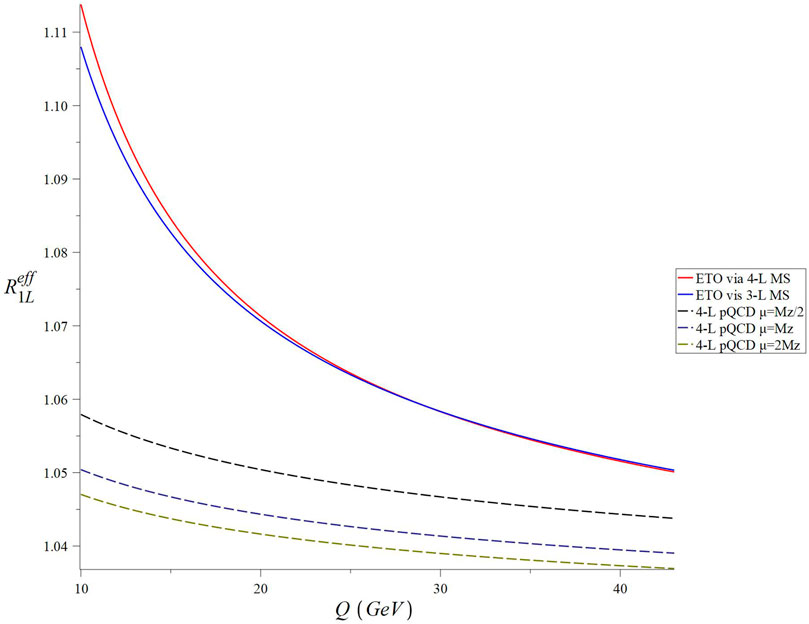
FIGURE 1. Q dependence of RSS-independent Reff at one loop matched with three- and four-loop
As in the previous section, we choose Q∗ = MZ, eliminate the scheme-dependent term, and find
Here,
where
and
while
Equations 21–23 represent an exact closed form solution of the two-loop beta-function for the ETO, which is expressed as a Lambert-W function, whereby W−1(ζ) denotes the applicable branch of the function for relevant values of ζ > 1. We utilize the initial value set at aeff(μ0 = Q∗) = aeff(Q∗, Q), which in our case is given by the positive root of Eq. 20. At the two-loop ETO matching, we find that the prediction is nearly the same as the one-loop ETO, which is
We plot the Q dependence of the ETO Reff at two-loop matching with three- and four-loop
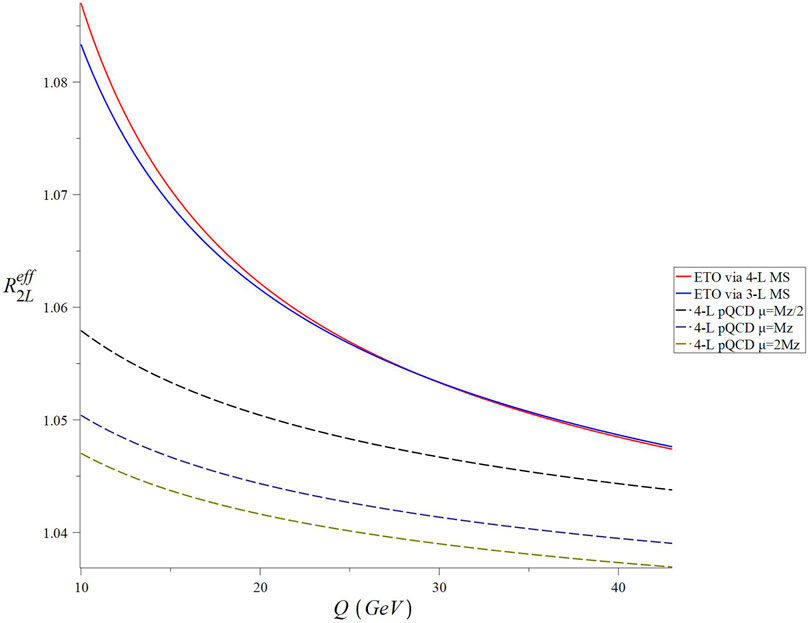
FIGURE 2. Q dependence of RSS-independent Reff at two loops matched with three- and four-loop MS and compared to four-loop perturbative QCD in the
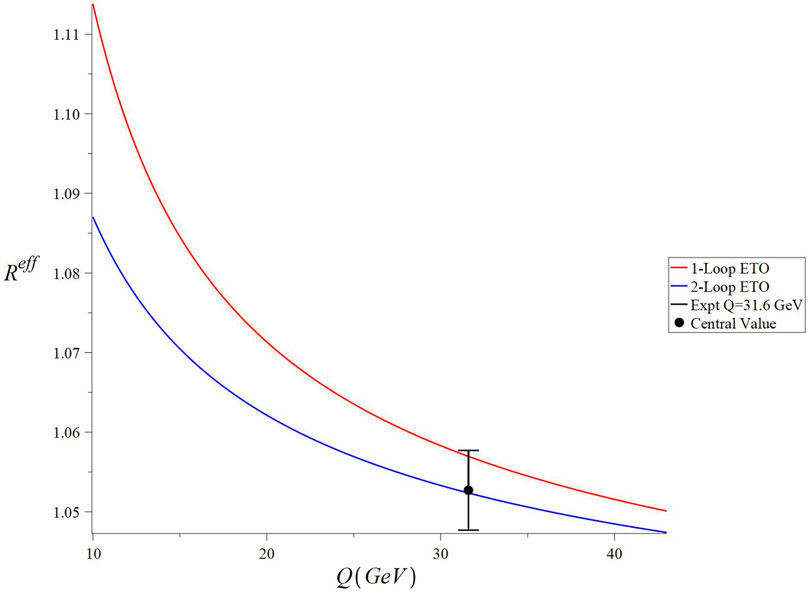
FIGURE 4. Q dependence of RSS-independent
With respect to considerations of higher-order perturbative corrections, we find that both the one- and two-loop ETOs yield results which are nearly identical for both three- and four-loop
In comparison with our findings, Akrami and Mirjalili [37] present perturbative QCD, RG summation and RS invariants, and CORGI approach estimates of R at Q = 31.6GeV to be
In this work, we have introduced a new approach for achieving RSS independence via a principle termed as POEM, which is based on equivalence of physical observables across both physical scale and scheme dependencies in their perturbative content under certain limits. Inspired by EFT techniques, which involve matching at a physical scale, this integrated renormalization approach, via EDR, provides results as RSS-independent ETOs, which contain only physical scales at a fixed order of perturbation theory. We demonstrate that POEM provides excellent results for the QCD cross-section ratio
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
The author confirms being the sole contributor of this work and has approved it for publication.
Author FC was employed by the company Spatial Informatics Group, LLC.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
The author thanks Gerry McKeon and Thomas G. Steele for helpful discussions and comments on the initial drafts of this work.
1Farrukh A. Chishtie, in preparation.
2Farrukh A. Chishtie, in preparation.
3Farrukh A. Chishtie, in preparation.
1. Stevenson PM. Optimized Perturbation Theory. Phys Rev D (1981) 23:2916–44. doi:10.1103/physrevd.23.2916
2. Stevenson PM. Explicit Formula for the Renormalization-Scheme Invariants of Perturbation Theory. Phys Rev D (1986) 33:3130–1. doi:10.1103/physrevd.33.3130
3. McKeon G. Renormalization Scheme Dependency and Decoupling in the Mass Independent Renormalization Scheme. Can J Phys (1983) 61:564–70. doi:10.1139/p83-071
4. McKeon G. On the Mass-independent Renormalization Scheme. Can J Phys (1981) 59:1327–33. doi:10.1139/p81-173
5. Grunberg G. Renormalization Group Improved Perturbative QCD. Phys Lett B (1980) 95:70–4. doi:10.1016/0370-2693(80)90402-5
6. Grunberg G. Renormalization-Scheme-Invariant QCD and QED: The Method of Effective Charges. Phys Rev D (1984) 29:2315. doi:10.1103/PhysRevD.29.2315
7. Brodsky SJ, Lepage GP, Mackenzie PB. On the Elimination of Scale Ambiguities in Perturbative Quantum Chromodynamics. Phys Rev D (1983) D28:228–35. doi:10.1103/physrevd.28.228
8. Melić B, Nižić B, and Passek K. Brodsky-Lepage-Mackenzie Scale for the Pion Transition Form Factor. Phys Rev D (2002) 65:053020. doi:10.1103/PhysRevD.65.053020
9. Caporale F, Ivanov D, Murdaca B, Papa A. Brodsky-Lepage-Mackenzie Optimal Renormalization Scale Setting for Semihard Processes. Phys Rev D (2015) 91:114009. doi:10.1103/PhysRevD.91.114009
10. Ahmady MR, Chishtie FA, Elias V, Fariborz AH, Fattahi N, McKeon DGC, et al. Closed-Form Summation of Renormalization-Group-Accessible Logarithmic Contributions to Semileptonic B Decays and Other Perturbative Processes. Phys Rev D (2002) 66:014010. doi:10.1103/PhysRevD.66.014010
11. McKeon DGC. Renormalization Scheme Dependence With Renormalization Group Summation. Phys Rev D (2015) 92:045031. doi:10.1103/PhysRevD.92.045031
12. Chishtie FA, McKeon DGC, Sherry TN. Renormalization Scheme Dependence in a QCD Cross Section. Phys Rev D (2016) 94:054031. doi:10.1103/PhysRevD.94.054031
13. Chishtie FA, McKeon DGC. Renormalization Scheme Dependence and Renormalization Group Summation. Can J Phys (2017) 96:233. doi:10.1139/cjp-2016-0780
14. Chishtie FA, McKeon DGC. Renormalization Scheme Dependence and the Renormalization Group Beta Function. Phys Rev D (2017) 95:116013. doi:10.1103/physrevd.95.116013
15. Maxwell CJ. Complete Renormalization Group Improvement- Avoiding Scale Dependence in QCD Predictions. Nucl Phys B - Proc Supplements (2000) 86:74–7. doi:10.1016/s0920-5632(00)00545-4
16. Brooks PM, Maxwell CJ. Improved Analysis of Moments of in Neutrino-Nucleon Scattering Using the Bernstein Polynomial Method. Nucl Phys B (2007) 780:76–103. doi:10.1016/j.nuclphysb.2007.05.011
17. Maxwell CJ, Mirjalili A. Complete Renormalization Group Improvement - Avoiding Factorization and Renormalization Scale Dependence in QCD Predictions. Nucl Phys B (2000) 577:209–20. doi:10.1016/s0550-3213(00)00184-x
18. Brodsky SJ, Wu XG. Scale Setting Using the Extended Renormalization Group and the Principle of Maximum Conformality: The QCD Coupling Constant at Four Loops. Phys Rev D (2012) 85:034038. doi:10.1103/PhysRevD.85.034038
19. Brodsky SJ, Di Giustino L. Setting the Renormalization Scale in QCD: The Principle of Maximum Conformality. Phys Rev D (2012) 86:085026. doi:10.1103/PhysRevD.86.085026
20. Brodsky SJ, Wu XG. Eliminating the Renormalization Scale Ambiguity for Top-Pair Production Using the Principle of Maximum Conformality. Phys Rev Lett (2012) 109:042002. doi:10.1103/physrevlett.109.042002
21. Mojaza M, Brodsky SJ, Wu X-G. Systematic All-Orders Method to Eliminate Renormalization-Scale and Scheme Ambiguities in Perturbative QCD. Phys Rev Lett (2013) 110:192001. doi:10.1103/physrevlett.110.192001
22. Brodsky SJ, Mojaza M, Wu XG. Systematic Scale-Setting to All Orders: The Principle of Maximum Conformality and Commensurate Scale Relations. Phys Rev D (2014) 89:014027. doi:10.1103/PhysRevD.89.014027
23. Ma Y, Wang SQ, Fu HB, Ma HH, Brodsky SJ, Mojaza M. Renormalization Group Invariance and Optimal QCD Renormalization Scale-Setting: A Key Issues Review. Rep Phys (2015) 78:126201. doi:10.1088/0034-4885/78/12/126201
24. Kataev AL, Mikhailov SV. Generalization of the Brodsky-Lepage-Mackenzie Optimization Within the {β}-Expansion and the Principle of Maximal Conformality. Phys Rev D (2015) 91:014007. doi:10.1103/PhysRevD.91.014007
25. Celmaster W, Gonsalves RJ. Renormalization-prescription Dependence of the Quantum-Chromodynamic Coupling Constant. Phys Rev D (1979) 20:1420–34. doi:10.1103/physrevd.20.1420
26. Brodsky SJ, Lu HJ. Commensurate Scale Relations in Quantum Chromodynamics. Phys Rev D (1995) 51:3652–68. doi:10.1103/physrevd.51.3652
27. Brodsky SJ, Gabadadze GT, Kataev AL, Lu HJ. The Generalized Crewther Relation in QCD and its Experimental Consequences. Phys Lett B (1996) 372:133–40. doi:10.1016/0370-2693(96)00057-3
28. ’t Hooft G. In: A Zichichi, editor. The Whys of Subnuclear Physics, Erice 1977. New York: Plenum Press N.Y. (1979).
30. van Ritbergen T, Vermaseren JAM, Larin SA. The Four-Loop β-function in Quantum Chromodynamics. Phys Lett B (1997) 400:379–84. doi:10.1016/s0370-2693(97)00370-5
31. Chetyrkin KG, Kühn JH, Kwiatkowski A. QCD corrections to the e+e− cross-section and the Z boson decay rate: concepts and results. Phys Rep (1996) 277:189–281. doi:10.1016/s0370-1573(96)00012-9
32. Baikov PA, Chetyrkin KG, Kuhn JH, Rittinger J. Vector Correlator in Massless QCD at Order O(αs4) and the QED β-Function at Five Loop. J High Energ Phys. (2012) 07:017. doi:10.1007/JHEP07(2012)017
33. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, et al. Particle Data Group. Phys Rev D (2018) 98:030001. doi:10.1103/PhysRevD.98.030001
34. Achard P, Adriani O, Aguilar-Benitez M, Alcaraz J, Alemanni G, Allaby J, et al. Measurement of hadron and lepton-pair production in e+e- collisions at √s=192−208GeV at LEP. Eur Phys J (2006) C47:1. doi:10.1140/epjc/s2006-02539-1
35. Adeva B, Becker U, Becker-Szendy R, Berdugo J, Boehm A, Branson JG, et al. Measurement of Strong-Coupling Constant αs to Second Order for 22<√s<46.78 GeV. Phys Rev Lett (1985) 54:1750. doi:10.1103/PhysRevLett.54.1750
36. Abe K, Amako K, Arai Y, Asano Y, Chiba M, Chiba Y, et al. VENUS Measurement of R and search for new quark flavors decaying into multi-jet final states in e+e− collisions between 54.0 and 61.4 GeV CM energies. Phys Lett B (1990) B234:382.
37. Akrami M, Mirjalili A. Comparing Optimized Renormalization Schemes for QCD Observables. Phys Rev D (2020) 101:034007. doi:10.1103/PhysRevD.101.034007
38. Di Giustino L, Brodsky SJ, Wang SQ, Wu XG. Infinite-Order Scale-Setting Using the Principle of Maximum Conformality: A Remarkably Efficient Method for Eliminating Renormalization Scale Ambiguities for Perturbative QCD. Phys Rev D (2020) 102:014015. doi:10.1103/PhysRevD.102.014015
Keywords: perturbation theory, resummation methods, perturbative QCD, quantum field theory (QFT), quantum chromodynamics (QCD)
Citation: Chishtie FA (2022) Achieving Effective Renormalization Scale and Scheme Independence via the Principle of Observable Effective Matching. Front. Phys. 9:765960. doi: 10.3389/fphy.2021.765960
Received: 27 August 2021; Accepted: 28 September 2021;
Published: 28 January 2022.
Edited by:
Mariana Frank, Concordia University, CanadaCopyright © 2022 Chishtie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Farrukh A. Chishtie, ZmFjaGlzaHRAdXdvLmNh
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.