Salt-Mediated Stiffening, Destruction, and Resculpting of Actomyosin Network

Cells dynamically change their viscoelastic properties by restructuring networks of actin filaments in the cytoskeleton, enabling diverse mechanical processes such as mobility and apoptosis. This restructuring is modulated, in part, by actin-binding proteins, such as myosin II, as well as counterions such as Mg²⁺ and K⁺. While high concentrations of Mg²⁺ can induce bundling and crosslinking of actin filaments, high concentrations of K⁺ destabilize myosin II minifilaments necessary to crosslink actin filaments. Here, we elucidate how the mechanics and structure of actomyosin networks evolve under competing effects of varying Mg²⁺ and K⁺ concentrations. Specifically, we couple microfluidics with optical tweezers microrheology to measure the time-varying linear viscoelastic moduli of actin networks crosslinked via myosin II as we cycle between low and high Mg²⁺ and K⁺ concentrations. Our complementary confocal imaging experiments correlate the time-varying viscoelastic properties with salt-mediated structural evolution. We find that the elastic modulus displays an intriguing non-monotonic time dependence in high-salt conditions, that correlates with structural changes, and that this process is irreversible, with the network evolving to a new steady-state as Mg²⁺ and K⁺ decrease back to their initial concentrations.

1 Introduction

Diverse networks of semiflexible actin filaments, key components of the cell cytoskeleton, play important mechanical and structural roles in myriad cellular processes ranging from motility and division to shape change and metastasis [1–5]. To enable such diverse processes, a wide variety of actin-binding proteins (ABPs) crosslink, bundle, sever, and pull on actin filaments [6–8]. The size, shape, binding affinity and concentration of the ABP determines the resulting mechanical and structural network properties [7,9–11,11–20].

Myosin II, one of the most widely-studied ABPs [21–27], is best known for its ATP-driven restructuring of actin networks by polymerizing into minifilaments that actively push and pull on actin filaments [28–32]. However, at low ATP concentrations (≲1 mM), myosin II minifilaments function as passive transient crosslinkers that can also bundle actin filaments [24–27]. Microrheological measurements of actomyosin networks carried out in this limit [26,31] have shown that myosin crosslinking leads to an increased plateau modulus and reduced stress dissipation [26].

Further, due to the polyelectrolyte nature of actin filaments, high concentrations of multivalent counterions, such as Mg²⁺, can also crosslink and bundle actin filaments by forming counterion crossbridges [2,13,33–37]. Several studies have investigated this effect, focusing on the structural properties of actin networks formed under varying multivalent salt conditions [33,38–42]. Further, we previously showed that the plateau modulus, nonlinear stiffness, and relaxation timescales of entangled actin networks were all higher when polymerized in the presence of higher Mg²⁺ concentrations (ranging from 2 to 52 mM) [34].

On the other hand, increasing the concentration of K⁺ in actomyosin networks, can destabilize myosin minifilaments [43]. At K⁺ concentrations of ∼600 mM, myosin remains in dimeric form, but upon lowering to $<$150 mM, myosin dimers assemble into minifilaments that can crosslink and bundle actin filaments and generate forces at high enough ATP concentration [30,43,44].

Here, we use time-resolved optical tweezers microrheology coupled with microfluidics to probe the time-varying viscoelasticity of steady-state actomyosin networks subject to in situ modulation of [K⁺] and [Mg²⁺] (Figure 1). Our complementary confocal microscopy experiments shed light on the structural evolution that gives rise to the non-equilibrium viscoelasticity. We find that networks exhibit first an increase then a decrease in elastic modulus with increasing [Mg²⁺] and [K⁺], and that this non-monotonic dependence is irreversible, with the networks transitioning to a new steady-state as the environment returns to the initial ionic conditions. We postulate that this intriguing behavior arises from a competition between salt-mediated actin bundling, which increases the modulus, and myosin minifilament depolymerization, which destroys the network connectivity and thus elasticity. While minifilament disassembly is reversible, filament bundling is not; so the network that reforms at low salt is in a new bundled state.

FIGURE 1

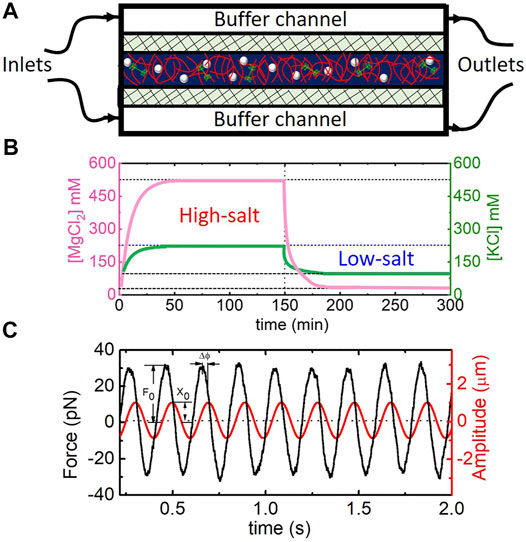
FIGURE 1. Experimental approach to measuring the time-varying microrheological response of actomyosin networks subject to in situ salt modulation. (A) Schematic of microfluidic device containing a central chamber that holds the sample of actin (red), myosin II (green), and microspheres (white); flanking Buffer channels used to pull in new buffer (through the Inlet) and remove existing buffer (via the Outlet), and two semipermeable membranes (crosshatches) to allow for buffer exchange via passive diffusion. Cartoon is not drawn to scale. (B) Plot depicting the concentrations of Mg²⁺ and K⁺ in the sample chamber as a function of time, enabled by in situ buffer exchange via the microfluidic device. Initial [Mg²⁺] and [K⁺] of 1 and 50 mM, respectively, and are increased to 500 and 200 mM over ∼10 min. After 150 min, [Mg²⁺] and [K⁺] are reduced back to initial concentrations for the remaining 150 min. Curves shown are those expected based on concentration measurements from Ricketts et al. [33]. (C) Sample data trace from optical tweezers microrheology experiment showing measured stage position (red) and force exerted on the microsphere (black) over the course of the 2 min acquisition time. The amplitude of the force F₀ and position x₀, as well as the phase shift Δϕ between the two oscillations, are used to determine viscoelastic moduli G′ and G^″. Data shown is for a frequency of ω = 32 rad s⁻¹.

2 Materials and Methods

Sample Preparation: Rabbit skeletal actin (Cytoskeleton, Inc. AKL99) and Alexa-568 labeled actin (Thermo Fisher Scientific, A12373) are stored at −80°C in G-buffer (2 mM Tris pH 8.0, 0.5 mM DTT, 0.1 mM CaCl₂, 0.2 mM ATP). Chicken skeletal myosin II, a gift from the Kovar lab at University of Chicago, is stored at −80°C in (600 mM KCl, 25 mM KPO4, 10 mM EDTA, 1 mM DTT). Before experiments, myosin is dialyzed against 300 mM KCl in a 96-well 10 KDa MWCO microdialysis plate (ThermoFisher) for 4 h, changing the buffer once after 2 h, and stored on ice.

To polymerize actin and myosin and assemble actomyosin networks, 0.23 μM myosin II dimers and 11.6 μM actin monomers (at a molar ratio of 1:10 of Alexa-568-labeled and unlabeled actin monomers) are mixed and incubated in F-buffer (10 mM Imidazole pH 7.0, 50 mM KCl, 1 mM MgCl₂, 1 mM EGTA, 0.2 mM ATP) for 1 h at room temperature. For reference, the nominal mesh size of an actin network with concentration c_a = 0.5 mg/ml (11.6 μM) is ξ ≃ 0.3/$\sqrt{c_a}\simeq$ 0.42 μm [45]. Note that the initial Mg²⁺ and K⁺ concentrations are 1 and 50 mM, respectively, and the ATP level is low enough to prevent noticeable myosin II ATPase activity. A trace amount of Alexa Fluor 488-BSA-coated polystyrene microspheres (Polysciences Inc.), with radius a = 2.25 μm, is added for microrheology measurements. The microsphere diameter was chosen to be ∼5 times larger than the network mesh size, such that our microrheology measurements described below are reporting the properties of the full network [46–48].

Microfluidics: The microfluidic device shown in Figure 1 is assembled as previously described [33,49,50]. Briefly, a coverslip (no. 0, 22 × 22 mm) and glass slide are washed thoroughly with acetone, isopropanol, and deionized water (DI), then plasma cleaned. A parafilm spacer is placed between the slip and slide and the resulting chamber is fused together using a soldering iron. To form two semipermeable membranes in the chamber, a 50:1 mixture of poly (ethylene glycol) diacrylate (PEG-DA) and a photoinitiator (2-hydroxy-2-methylpropiophenone) diluted to 20% (v/v) in DI, are flowed into the chamber. The chamber is then exposed to UV through a custom photomask to form two cross-linked PEG-DA membranes, and flushed with DI to remove the PEG-DA solution. This process results in a central chamber for holding the sample separated by semipermeable membranes from two flanking channels that enable buffer exchange via diffusion (Figure 1A).

For experiments, the actomyosin solution is pipetted into the central chamber, and the flanking buffer channels are filled with F-buffer. Buffer channels are then connected to capillary tubes at both ends. Both tubes from one end are connected to Tygon tubing I, which is connected to a syringe pump, while the tubes at the other end are connected to two separate Tygon tubing II which are inserted into a buffer reservoir to enable buffer exchange. All channels are then sealed with epoxy. Using the syringe pump, the existing buffer is pulled from the buffer channels at a flow rate of 5 μl/min as new buffer from the reservoir is pulled in, thereby enabling diffusion-controlled buffer exchange into the central chamber. To vary the buffer conditions between “low-salt” (1 mM MgCl₂ and 50 mM KCl) and “high-salt” (500 mM MgCl₂ and 200 mM KCl), the F-buffer in the reservoir is replaced with F-buffer containing the “high” concentrations of MgCl₂ and KCl at the beginning of the 300 min experiment (Figure 1B). After 150 min, the buffer in the reservoir is replaced with the initial “low-salt” F-buffer. Complete buffer exchange in each cycle is achieved in ∼10 min. Note that the concentrations of all other buffer components remain constant throughout the experiment.

Microrheology: The optical trap used in microrheology measurements was built by outfitting an Olympus IX71 fluorescence microscope with a 1064 nm ND:YAG fiber laser (Manlight) focused with a 60x 1.4 NA objective, as previously thoroughly described [51–53]. The trap stiffness was calibrated via Stokes drag in water [54,55] and passive equipartition methods [56], as previously described and validated [52,53]. For each measurement, a probe embedded in the sample is trapped and oscillated sinusoidally relative to the sample at an amplitude of x₀ = 1.0 μm at five frequencies from ω = 0.5 to 107 rad/s by using a piezoelectric nanopositioning stage (Mad City Laboratories) to oscillate the sample while keeping the trap fixed. A position-sensing detector (First Sensor) measures the laser deflection, which is proportional to the force F exerted on the probe by the surrounding network. We analyze the stage position and laser deflection for each trial to ensure that the stage completes full amplitude oscillations and the bead remains trapped for the duration of the measurement. The stage position and force data are both fit to sine curves using the least-squares method, from which the frequency-dependent elastic modulus G′ and viscous modulus G^″ are computed via G′ = |F_o| cos(Δϕ)/6πa|X_o| and G^″ = |F_o| sin(Δϕ)/6πa|X_o|, where F_o and Δϕ are the amplitude of measured force F and the phase shift between the force and the stage oscillations. Measurements are performed every 5 min over the course of 300 min where t = 0 is immediately before exchange from low-to high-salt buffer is initiated, and t = 150 min is immediately before exchange from high-salt back to low-salt buffer begins. G′ and G^″ data shown in Figure 2 are averaged over all frequencies for two replicates and error bars are the standard error of these values. As shown in Supplementary Figure S1, while there is modest frequency dependence of G′ and G^″, this dependence does not depend on the measurement time, so averaging over frequency does not impact the time-dependence shown in Figure 2. Further, due to the dynamic nature of the network, there is inherent noise in the measurement due to network fluctuations, such that averaging over a range of frequencies results in more robust measured trends.

FIGURE 2

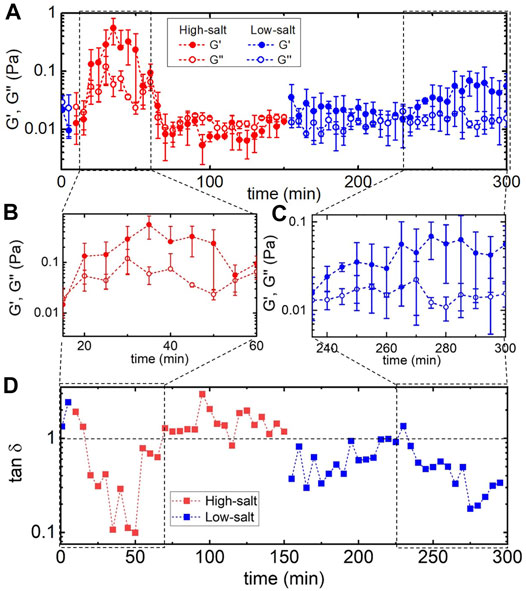
FIGURE 2. Actomyosin networks display non-monotonic and irreversible changes in viscoelastic properties during in situ cycling of [Mg²⁺] and [K⁺]. (A) Linear elastic and viscous moduli, G′ (filled) and G^″ (open), of actomyosin networks during a complete cycle of salt modulation - starting (t = 0) in “low-salt” conditions (1 mM MgCl₂, 50 mM KCl) (blue), switching to “high-salt” (500 mM MgCl₂, 200 mM KCl) until t = 150 min (red), then returning to “low-salt” (1 mM MgCl₂, 50 mM KCl) conditions (blue) for the remaining duration of the 300 min measurement. Each data point is an average over five frequencies across two replicates and error bars are standard error. Boxed-in regions highlight times in which G′ increases substantially. Zoom-ins of these regions are shown in (B) and (C). Switching from low-salt to high-salt conditions leads to a nearly ∼100x increase in G′ followed by rapid drop. Upon reintroducing the initial low-salt conditions G′ slowly increases to values well above the starting values. (D) Loss tangent, tan δ, versus time for the full time course of the experiment, highlighting the complex variation in the elastic storage of the network during salt modulation. Dashed horizontal line indicates G′ = G^″. For data points below this line, elastic storage dominates the response over viscous dissipation, with smaller tan d values indicating more elastic-like behavior.

Microscopy: To gain insight into the salt-mediated structural reorganization of actomyosin networks during exchanging between low-salt and high-salt conditions, the same buffer exchange program described above is performed while imaging the Alexa-568-labeled actin comprising the actomyosin networks using a Nikon A1R laser scanning confocal microscope with 60x 1.4 NA objective and 561 nm laser line. Single 512 × 512 pixel images are collected every minute for a total of 300 min. To quantify the network structure at various time-points during the experiment, a custom-written python script was used to perform spatial image autocorrelation (SIA) analysis on each image [57]. SIA measures the correlation g(r) in intensity I(r) of two pixels in an image as a function of separation distance r. We generate each autocorrelation curve by taking the fast Fourier transform of an image, multiplying by its complex conjugate, applying an inverse Fourier transform, and then normalizing by the intensity squared: g(r) = F⁻¹(|F(I(r))|²)/[I(r)]² where F and F⁻¹ represent fast Fourier and inverse Fourier transforms, respectively. The corresponding correlation length ξ is obtained by curve-fitting autocorrelation curves to g(r) = g_o  exp(−r/ξ). This approach is based on previous studies that have applied SIA to confocal images of cytoskeleton networks to determine correlation lengthscales [58,59]. Because many of the curves exhibit non-exponential tails at large distances due to flat-field noise, as in these prior studies, we restrict curve-fitting to $g\left(r\le 2\mu \right.$m).

3 Results and Discussion

To determine the effect of combined increases in Mg²⁺ and K⁺ on the mechanics and structure of actomyosin networks, we use microfluidic perfusion chambers to modulate the counterion concentration without inducing flow or disrupting the network. Importantly, we keep the ATP concentration low such that the enzymatic activity of the myosin motors is suppressed [26]. We form networks in the standard “low-salt” buffer (containing 1 mM MgCl₂ and 50 mM KCl) in the microfluidic chamber. At the start of our measurements (either microrheology or confocal imaging), we immediately switch to the “high-salt” buffer (with 500 mM MgCl₂ and 200 mM KCl), and after 150 min we exchange the buffer again to return to the initial “low-salt” buffer. The low-salt conditions have been shown to result in homogeneous entangled networks of individual actin filaments [7,13,14,18–20,55,60] and the formation of myosin-II minifilaments that crosslink actin [43,61]. Mg²⁺ concentrations above ∼20 mM have been shown to induce substantial bundling of actin filaments [33,34], while [K⁺] greater than ∼150 mM depolymerizes myosin-II minifilaments [43,44].

We perform time-resolved optical tweezers microrheology measurements during the course of the 300-min cycle of salt modulation to determine how the mechanical properties of the network vary in response to changing salt concentrations. We complement these measurements with corresponding confocal imaging experiments to link the changing viscoelastic properties of the network to the structure.

Figure 2 displays the results of our microrheology measurements, which reveal non-monotonic and irreversible changes to the viscoelastic moduli of actomyosin networks upon introduction of high-salt conditions. Specifically, G′ and G^″ both increase as high-salt buffer is introduced, reaching a maximum at ∼35 min, before dropping to values below their starting values, which remain constant for the duration of the high-salt period. Upon returning to low-salt conditions at 150 min there is modest increase in the elastic modulus that remains constant until ∼240 min at which point G′ steadily increases for ∼30 min before reaching a steady value that is nearly an order of magnitude larger than the value at t = 0. Both periods of increased G′ values (in high-salt and low-salt conditions) display elastic behavior with G′ significantly larger than G^″, as shown in Figures 2B,C. To better quantify the time-varying elastic storage of the network we compute the loss tangent, tan δ = G^″/G′, which is a measure of the viscous dissipation in the system (Figure 2D). tan δ > 1 indicates largely viscous behavior while tan δ < 1 indicates elastic-like behavior with lower values indicating increased elastic storage. As shown, the elasticity increases dramatically at the beginning of the high-salt phase and then abruptly drops to a viscous-dominated regime. Substantial elasticity is not recovered until near the end of the subsequent low-salt phase.

Two features of the described time-varying mechanical properties that are surprising and notable are: 1) the abrupt drop in tan δ after the initial increase, and 2) the increase in tan δ at the end of the low-salt phase. To understand feature (1), we recall that high Mg²⁺ concentrations induce actin bundling and crosslinking via counterion crossbridges [26,27,31], which we expect to result in increased elasticity [50], as we see in the first ∼30 min of the experiment. However, the unexpected subsequent drop to a viscous-dominated regime suggests disruption of myosin-crosslinks, as seen in previous studies on steady-state actomyosin networks [25–27]. We postulate that this effect is due to the high [K⁺] conditions depolymerizing myosin II minifilaments, as described in the Introduction [43,50], and thus destroying the crosslinks they form between actin filaments. In the following section, we shed further light on the structural evolution that competing effects of actin bundling and myosin minifilament disassembly give rise to. Feature (2) is counterintuitive as one would expect that returning the system to its initial buffer conditions would cause the system to return to a state similar to its initial state. Namely, we would expect actin filaments to de-bundle and myosin II minifilaments to reform and re-connect actin filaments, such that G′ and G^″ at t = 0 and t = 300 min would be similar. Instead we find that the network exhibits substantially more elasticity at the end of the experiment than at the beginning - suggestive of more bundling or connectivity. This effect implies that there are irreversible processes at play and that the network is encoding information about its previous state (i.e., mechano-memory). We investigate this phenomenon further below.

We note that the error bars shown in Figure 2, which represent the standard error (SE), are indeed larger than is typical in steady-state microrheology measurements [34], with corresponding percent error (PE = SE/mean) values that average to $<PE>$ = 31% and 38% for G′ and G^″, respectively. This spread is a result of: 1) averaging over all frequencies, as there is a modest frequency dependence of G′ and G^″ (which does not depend on time, see Supplementary Figure S1); and 2) the dynamic nature of the system (i.e., its rheological and structural properties are changing over time), such that there are larger fluctuations than for a steady-state system. As such, to demonstrate the statistical significance of our measured trends, we compare $<PE>$ to the percent variation in G′(t) and G^″(t) over the course of the experimental time t. Specifically, we average over all G′ and G^″ values over the course of the experiment ($<{G>}_t$), and determine the corresponding percent error (PE_t), which has values of PE_t = 111% and 64% for G′ and G^″ respectively, both significantly larger than the corresponding $<PE>$ values.

To shed light on the structural changes that give rise to the salt-mediated variation in the viscoelastic response of the network, we turn to our confocal imaging experiments performed under the exact conditions as the microrheology measurements (Figure 2, Supplementary Movie S1). Figure 3 shows images of the fluorescent-labeled actin filaments comprising the network at different time points during the salt modulation. The top row shows the structural evolution in high-salt conditions (t < 150 min) while the bottom row shows the low-salt phase (t > 150 min). As shown, the network formed under low-salt conditions (t = 0 min) is homogeneous and comprised of thin fibers. The minimal thermal noise in the images indicates substantial crosslinking via myosin minifilaments [26,50]. However, upon introduction of high-salt buffer, the fibers become darker and thicker, indicating bundling. The mesh size appears to increase accordingly as the network transitions to one composed of fewer, thicker bundles. Surprisingly, after ∼30 min, the network rapidly dissolves, with no signs of fibers for the remaining duration of the high-salt period (until t = 150 min). Fragments of disconnected fibers would appear as thermal noise so the absence of any clear structure suggests that the bundles are no longer connected and are thus rapidly diffusing. This destruction is likely the result of the crosslinking myosin II minifilaments depolymerizing due to the increased [K⁺], thereby disrupting actin network connectivity. Further, reintroducing the initial low-salt buffer leads to the re-emergence of stable actin networks. However, these networks are markedly different than the initial network, despite the fact that the buffer conditions are identical. Specifically, the reformed networks are comprised of much thicker and apparently stiffer (i.e., less bent by thermal fluctuations) fibers that are more sparsely connected. This irreversibility suggests that while myosin minifilaments can reform as [K⁺] is lowered, salt-induced actin bundling is not reversible, likely due to entropic depletion interactions [44,50,62].

FIGURE 3

FIGURE 3. Laser scanning confocal microscopy images of fluorescent-labeled actin filaments comprising actomyosin networks subject to in situ cycling of [Mg²⁺] and [K⁺]. The buffer exchange program is identical to that done for microrheology measurements. Times are listed in minutes in the top right corner of each image. Scale bars shown for t = 0 apply to all images and are 40 μm for main images and 10 μm for the zoomed-in insets. Colors around each image indicate the buffer conditions as in Figure 2 [blue = low-salt (1 mM MgCl₂, 50 mM KCl), red = high-salt (500 mM MgCl₂, 200 mM KCl)]. At t = 0 the network is homogeneous and comprised of thin fibers. Switching to “high-salt” leads to thickening (i.e., bundling) of fibers (t = 10, 20, and 30) followed by network destruction (t = 60, 90, and 150). Re-introducing “low-salt” buffer leads to slow re-emergence of networks that are substantially more bundled that the initial low-salt network (t = 200, 240, 280, and 300). Each 512 × 512 inverted greyscale image is captured using an A1R laser scanning fluorescence confocal microscope with 60x 1.4 NA objective and 561 nm laser line.

We note that in Figure 3, the network appears to reach maximum bundling at ∼25 min (see Supplementary Movie S1) rather than at ∼30–35 min, where we measure a minimum in tan δ in Figure 2. Nevertheless, we maintain that maximal bundling coincides with maximal G′ values (and minima in tan δ), and that this ∼5–10 min difference, which equates to ≲ 3% of the total measurement time, is due to sample-to-sample variation. Specifically, confocal experiments were performed on different samples than microrheology experiments, so we expect there to be slight differences in the time at which peak bundling and network elasticity occur. These variations are also evident in the different microrheology trials we conducted and add to the spread in the microrheology data shown in Figure 2.

To quantify the structural changes depicted in Figure 3, we compute the spatial image autocorrelation function g(r) as a function of distance r between pixels for each image shown in Figures 4A,B. Faster decay of g(r) with r indicates smaller network features and a higher initial value indicates brighter features and higher signal-to-noise (resulting from filament bundling or clustering). As shown, autocorrelation curves increase in magnitude and decay more slowly as t increases from 0 to ∼30 min (the time period at which we observe substantial bundling), after which g(0) is reduced and g(r) decays more quickly until ∼200 min (the time over which the network is destroyed), at which point g(0) increases once again and the decay becomes more broad as the network reforms.

FIGURE 4

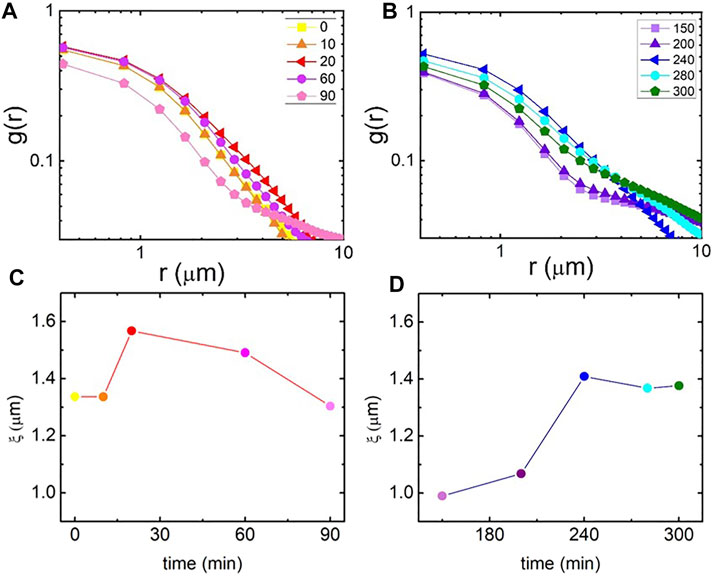
FIGURE 4. Spatial image autocorrelation analysis quantifies the salt-mediated structural changes to actomyosin networks that give rise to the time-varying viscoelastic properties. (A, B) Spatial image autocorrelation functions g(r) versus distance r computed from confocal images shown in Figure 3. Plots are divided into “high-salt” (A) and “low-salt” (B) conditions with the experimental time (in min) of each image listed in the legend. (C, D) Structural correlation lengths ξ determined from fitting each g(r) shown in (A) and (B) to an exponential decay function g(r) ∼ e^−r/ξ. ξ, which indicates the average size of structural features, shows bundling (increasing ξ) and subsequent destruction (drop in ξ) during the high-salt period (C), followed by re-assembly into highly-bundled networks during the low-salt period [(D), increase in ξ to value larger than t = 0 value].

Because all curves exhibit exponential decay for distances up to ∼2 μm, we fit this portion of each curve to g(r) = g₀ exp(−r/ξ) to extract a characteristic correlation length ξ for the network as a function of time. This correlation length, which is proportional to the mesh size for an isotropic polymer network, displays noticeable changes that track with the rheological changes we present in Figure 2. Specifically, ξ displays a non-monotonic dependence on time during the high-salt phase, peaking at a similar time at which the loss tangent exhibits a minimum, indicating that the highly bundled network retains the most elastic storage, in line with previous experiments [34]. During the low-salt re-introduction ξ steadily rises starting at ∼200 min, when we observe network reformation and a decrease in tan δ. ξ continues to increase until ∼240 min when the network appears to stabilize and tan δ reaches a new minimum. As ξ is a measure of the average size of the features of the network, this lengthscale could be reporting the mesh size or the bundle size. However, because the formation of bundles leads to larger mesh sizes, as the network becomes composed of fewer, but more rigid, fibers, the bundling lengthscale and mesh size should scale together. Further, the time dependence of both of these feature sizes should track with tan δ, as we see in Figures 2, 4.

We note that these findings differ from those previously reported for entangled composites of DNA and actin in which actin bundling led to a decrease in network elasticity [63]. In this previous work, the loss of elasticity was due to bundling destroying the percolation of the actin network. As the actin filaments bundled together, the mesh size grew (as in our system), eventually surpassing a critical point at which percolation was destroyed and thus the network was no longer predominantly elastic. In our current work, we do not reach this critical point, as evidenced by the confocal images that show that bundles remain connected. These connections are likely further facilitated by the myosin crosslinkers which were not present in the DNA-actin composites.

Finally, it is informative to contrast our results with those expected in the absence of either [Mg²⁺] or [K⁺] modulation. Previous studies [33] examined the bulk conformational changes of actin networks subject to increasing and decreasing [Mg²⁺]. These experiments showed that actin networks bundle and contract as [Mg²⁺] increases, as we see here, but actually continue to bundle when [Mg²⁺] is subsequently lowered, albeit at a slower rate. There is no observed network dissolution in these studies. As such, we expect that under Mg²⁺ modulation only, we would observe continued bundling over the course of the experiment; however, upon cycling back to low [Mg²⁺] conditions, the network would slow bundling significantly but remain in a bundled state rather than returning to its starting structure (a network of individual filaments). Based on the reported effect of [KCl] on myosin polymerization and stability [64], as we discuss above, as well as the evidence that monovalent salt does not effectively bundle actin filaments [64,65], we expect that networks subject to [K⁺] modulation only would show minimal bundling, and would instead exhibit elastic weakening as [K⁺] increases due to the crosslinking myosin minifilaments falling apart. Upon decreasing [K⁺] again the network would reconnect and rigidify, likely returning to a crosslinked state similar to its initial state.

4 Conclusion

Here, we elucidate the effects of simultaneous cycling of Mg²⁺ and K⁺ concentrations on the mechanics and structure of actin networks crosslinked via myosin II minifilaments. We find that while increasing [Mg²⁺] serves to bundle actin filaments, increasing network strength and elasticity, increasing [K⁺] destabilizes crosslinking myosin II minifilaments, thereby compromising the connectivity and integrity of the network.

Specifically, we couple time-resolved optical tweezers microrheology and confocal fluorescence imaging with microfluidic perfusion chambers to characterize the time-varying viscoelastic and structural properties of actomyosin networks as we cycle the buffer conditions from low-salt (1 mM MgCl₂ and 50 mM KCl) to high-salt (500 mM MgCl₂ and 200 mM KCl), then back to low-salt. Our results reveal a surprising non-monotonic time-dependence of the network elasticity under high-salt conditions, which mirrors the time course of actin bundling and subsequent network destruction. Namely, we observe a dramatic rise in the elastic modulus, coupled to increased actin bundling, followed by an abrupt drop to a viscous-dominated regime and apparent destruction of a connected network. We postulate that this complex time-dependence arises from the increased [Mg²⁺] driving actin bundling via charge-screening, followed by slower [K⁺]-triggered depolymerization of myosin II minifilaments that disconnect and disrupt the network of bundles. Upon lowering [Mg²⁺] and [K⁺] back to their initial concentrations, a connected network slowly re-emerges but with features that are distinct from the initial networks formed in the same ionic conditions. Namely, the network exhibits increased elasticity and more bundled features, suggesting that while connectivity can be restored as myosin II minifilaments re-polymerize, actin bundling cannot be as easily reversed.

Our robust experimental approach can be applied to wide-ranging soft and active materials to explore how varying environmental conditions alter the mechanics and structure of the system in real-time. Further, our results shed important light on the various mechanisms that the cytoskeleton can use to alter its mechanical and structural features. More generally, our results demonstrate that the mechanical response of biopolymer networks can encode information regarding their previous state, which may be exploited in the design of next-generation biosensors, memory storage devices, and other smart materials applications. In future work, we will explore how varying the concentrations of actin and myosin, as well as the types and concentrations of salts, can be used to tune the mechanical and structural response of cytoskeleton networks.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

BG conducted experiments, analyzed and interpreted data, and wrote the manuscript. RR-A designed and guided experiments, analyzed and interpreted data, and wrote the manuscript. MR, MD, and JR advised on experimental design and results.

Funding

This research was funded by an NSF CAREER Award (No. 1255446) to RR-A and a W. M. Keck Foundation Research Grant to RR-A, MR, MD, and JR.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Prof David Kovar and Caitlin Anderson for providing us with myosin II along with corresponding handling protocols and guidance. We thank Shea Ricketts for assistance with microfluidic device assembly and confocal imaging.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.760340/full#supplementary-material

References

1. Insall R Actin in 2021. Curr Biol (2021) 31:R496–R498. doi:10.1016/j.cub.2021.04.013

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Gardel ML, Kasza KE, Brangwynne CP, Liu J, Weitz DA Chapter 19 Mechanical Response of Cytoskeletal Networks. Methods Cel Biol (2008) 89:487–519. doi:10.1016/s0091-679x(08)00619-5

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Blanchoin L, Boujemaa-Paterski R, Sykes C, Plastino J Actin Dynamics, Architecture, and Mechanics in Cell Motility. Physiol Rev (2014) 94:235–63. doi:10.1152/physrev.00018.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Svitkina T The Actin Cytoskeleton and Actin-Based Motility. Cold Spring Harb Perspect Biol (2018) 10:a018267. doi:10.1101/cshperspect.a018267

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cooper GM Structure and Organization of Actin Filaments. In: The Cell: A Molecular Approach 2 (2000).

Google Scholar

6. Bausch AR, Kroy K A Bottom-Up Approach to Cell Mechanics. Nat Phys (2006) 2:231–8. doi:10.1038/nphys260

CrossRef Full Text | Google Scholar

7. Schmoller KM, Lieleg O, Bausch AR Structural and Viscoelastic Properties of Actin/filamin Networks: Cross-Linked versus Bundled Networks. Biophysical J (2009) 97:83–9. doi:10.1016/j.bpj.2009.04.040

CrossRef Full Text | Google Scholar

8. Castaneda N, Park J, Kang EH Regulation of Actin Bundle Mechanics and Structure by Intracellular Environmental Factors. Front Phys (2021) 9:227. doi:10.3389/fphy.2021.675885

CrossRef Full Text | Google Scholar

9. Lieleg O, Schmoller KM, Cyron CJ, Luan Y, Wall WA, Bausch AR Structural Polymorphism in Heterogeneous Cytoskeletal Networks. Soft Matter (2009) 5:1796–803. doi:10.1039/b814555p

CrossRef Full Text | Google Scholar

10. Tharmann R, Claessens MM, Bausch AR. Viscoelasticity of Isotropically Cross-Linked Actin Networks. Phys Rev Lett (2007) 98:088103. doi:10.1103/PhysRevLett.98.088103

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Shin JH, Mahadevan L, So PT, Matsudaira P Bending Stiffness of a Crystalline Actin Bundle. J Mol Biol (2004) 337:255–61. doi:10.1016/j.jmb.2004.01.028

CrossRef Full Text | Google Scholar

12. Lieleg O, Claessens MM, Heussinger C, Frey E, Bausch AR. Mechanics of Bundled Semiflexible Polymer Networks. Phys Rev Lett (2007) 99:088102. doi:10.1103/PhysRevLett.99.088102

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Stricker J, Falzone T, Gardel ML Mechanics of the F-Actin Cytoskeleton. J Biomech (2010) 43:9–14. doi:10.1016/j.jbiomech.2009.09.003

CrossRef Full Text | Google Scholar

14. Janmey PA, Hvidt S, Käs J, Lerche D, Maggs A, Sackmann E, et al. The Mechanical Properties of Actin Gels. Elastic Modulus and Filament Motions. J Biol Chem (1994) 269:32503–13. doi:10.1016/s0021-9258(18)31663-6

CrossRef Full Text | Google Scholar

15. Käs J, Strey H, Tang JX, Finger D, Ezzell R, Sackmann E, et al. F-actin, a Model Polymer for Semiflexible Chains in Dilute, Semidilute, and Liquid Crystalline Solutions. Biophysical J (1996) 70:609–25. doi:10.1016/s0006-3495(96)79630-3

CrossRef Full Text | Google Scholar

16. Koenderink GH, Atakhorrami M, MacKintosh FC, Schmidt CF High-frequency Stress Relaxation in Semiflexible Polymer Solutions and Networks. Phys Rev Lett (2006) 96:138307. doi:10.1103/physrevlett.96.138307

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Liu J, Koenderink GH, Kasza KE, MacKintosh FC, Weitz DA Visualizing the Strain Field in Semiflexible Polymer Networks: Strain Fluctuations and Nonlinear Rheology ofF-Actin Gels. Phys Rev Lett (2007) 98:198304. doi:10.1103/physrevlett.98.198304

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Broedersz CP, Kasza KE, Jawerth LM, Münster S, Weitz DA, MacKintosh FC Measurement of Nonlinear Rheology of Cross-Linked Biopolymer Gels. Soft Matter (2010) 6:4120–7. doi:10.1039/c0sm00285b

CrossRef Full Text | Google Scholar

19. Claessens MMAE, Bathe M, Frey E, Bausch AR Actin-binding Proteins Sensitively Mediate F-Actin Bundle Stiffness. Nat Mater (2006) 5:748–53. doi:10.1038/nmat1718

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lieleg O, Kayser J, Brambilla G, Cipelletti L, Bausch AR Slow Dynamics and Internal Stress Relaxation in Bundled Cytoskeletal Networks. Nat Mater (2011) 10:236–42. doi:10.1038/nmat2939

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ideses Y, Sonn-Segev A, Roichman Y, Bernheim-Groswasser A Myosin Ii Does it All: Assembly, Remodeling, and Disassembly of Actin Networks Are Governed by Myosin Ii Activity. Soft Matter (2013) 9:7127–37. doi:10.1039/c3sm50309g

CrossRef Full Text | Google Scholar

22. Betapudi V Life without Double-Headed Non-muscle Myosin Ii Motor Proteins. Front Chem (2014) 2:45. doi:10.3389/fchem.2014.00045

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Soares e Silva MMS, Stuhrmann B, Betz T, Koenderink GH Time-resolved Microrheology of Actively Remodeling Actomyosin Networks. New J Phys (2014) 16:075010. doi:10.1088/1367-2630/16/7/075010

CrossRef Full Text | Google Scholar

24. Laevsky G, Knecht DA Cross-linking of Actin Filaments by Myosin Ii Is a Major Contributor to Cortical Integrity and Cell Motility in Restrictive Environments. J Cel Sci (2003) 116:3761–70. doi:10.1242/jcs.00684

CrossRef Full Text | Google Scholar

25. Wachsstock DH, Schwarz WH, Pollard TD Cross-linker Dynamics Determine the Mechanical Properties of Actin Gels. Biophysical J (1994) 66:801–9. doi:10.1016/s0006-3495(94)80856-2

CrossRef Full Text | Google Scholar

26. Humphrey D, Duggan C, Saha D, Smith D, Käs J Active Fluidization of Polymer Networks through Molecular Motors. Nature (2002) 416:413–6. doi:10.1038/416413a

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Koenderink GH, Dogic Z, Nakamura F, Bendix PM, MacKintosh FC, Hartwig JH, et al. An Active Biopolymer Network Controlled by Molecular Motors. Proc Natl Acad Sci (2009) 106:15192–7. doi:10.1073/pnas.0903974106

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Reichl EM, Ren Y, Morphew MK, Delannoy M, Effler JC, Girard KD, et al. Interactions between Myosin and Actin Crosslinkers Control Cytokinesis Contractility Dynamics and Mechanics. Curr Biol (2008) 18:471–80. doi:10.1016/j.cub.2008.02.056

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Martens JC, Radmacher M Softening of the Actin Cytoskeleton by Inhibition of Myosin Ii. Pflugers Arch - Eur J Physiol (2008) 456:95–100. doi:10.1007/s00424-007-0419-8

CrossRef Full Text | Google Scholar

30. Rauzi M, Lenne P-F Cortical Forces in Cell Shape Changes and Tissue Morphogenesis. In: M Labouesse, editor. Forces and Tension in Development, 95. Academic Pressof Current Topics in Developmental Biology (2011). p. 93–144. 93 – 144. doi:10.1016/B978-0-12-385065-2.00004-9

CrossRef Full Text | Google Scholar

31. Mizuno D, Tardin C, Schmidt CF, MacKintosh FC Nonequilibrium Mechanics of Active Cytoskeletal Networks. Science (2007) 315:370–3. doi:10.1126/science.1134404

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Huxley HE Fifty Years of Muscle and the Sliding Filament Hypothesis. Eur J Biochem (2004) 271:1403–15. doi:10.1111/j.1432-1033.2004.04044.x

CrossRef Full Text | Google Scholar

33. Ricketts SN, Khanal P, Rust MJ, Das M, Ross JL, Robertson-Anderson RM Triggering Cation-Induced Contraction of Cytoskeleton Networks via Microfluidics. Front Phys (2020) 8:596699. doi:10.3389/fphy10.3389/fphy.2020.596699

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Gurmessa B, Francis M, Rust MJ, Das M, Ross JL, Robertson-Anderson RM Counterion Crossbridges Enable Robust Multiscale Elasticity in Actin Networks. Phys Rev Res (2019) 1:013016. doi:10.1103/physrevresearch.1.013016

CrossRef Full Text | Google Scholar

35. MacKintosh FC, Schmidt CF Active Cellular Materials. Curr Opin Cel Biol (2010) 22:29–35. doi:10.1016/j.ceb.2010.01.002

CrossRef Full Text | Google Scholar

36. Wen Q, Janmey PA Polymer Physics of the Cytoskeleton. Curr Opin Solid State Mater Sci (2011) 15:177–82. doi:10.1016/j.cossms.2011.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Cooper GM, Ganem D The Cell: A Molecular Approach. Nat Med (1997) 3:1042.

Google Scholar

38. Deshpande S, Pfohl T Real-time Dynamics of Emerging Actin Networks in Cell-Mimicking Compartments. PloS one (2015) 10:e0116521. doi:10.1371/journal.pone.0116521

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Huber F, Strehle D, Käs J Counterion-induced Formation of Regular Actin Bundle Networks. Soft Matter (2012) 8:931–6. doi:10.1039/c1sm06019h

CrossRef Full Text | Google Scholar

40. Huber F, Strehle D, Schnauß J, Käs J Formation of Regularly Spaced Networks as a General Feature of Actin Bundle Condensation by Entropic Forces. New J Phys (2015) 17:043029. doi:10.1088/1367-2630/17/4/043029

CrossRef Full Text | Google Scholar

41. Castaneda N, Zheng T, Rivera-Jacquez HJ, Lee H-J, Hyun J, Balaeff A, et al. Cations Modulate Actin Bundle Mechanics, Assembly Dynamics, and Structure. J Phys Chem B (2018) 122:3826–35. doi:10.1021/acs.jpcb.8b00663

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Strehle D, Schnauß J, Heussinger C, Alvarado J, Bathe M, Käs J, et al. Transiently Crosslinked F-Actin Bundles. Eur Biophys J (2011) 40:93–101. doi:10.1007/s00249-010-0621-z

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kaminer B, Bell AL Myosin Filamentogenesis: Effects of Ph and Ionic Concentration. J Mol Biol (1966) 20:391–401. doi:10.1016/0022-2836(66)90070-2

CrossRef Full Text | Google Scholar

44. Matsuda K, Kobayashi T, Sugawa M, Koiso Y, Toyoshima YY, Yajima J Myosin-driven Fragmentation of Actin Filaments Triggers Contraction of a Disordered Actin Network. bioRxiv (2018) 332684.

Google Scholar

45. Isambert H, Maggs AC Dynamics and Rheology of Actin Solutions. Macromolecules (1996) 29:1036–40. doi:10.1021/ma946418x

CrossRef Full Text | Google Scholar

46. Weigand WJ, Messmore A, Tu J, Morales-Sanz A, Blair DL, Deheyn DD, et al. Active Microrheology Determines Scale-dependent Material Properties of Chaetopterus Mucus. PloS one (2017) 12:e0176732. doi:10.1371/journal.pone.0176732

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Chapman CD, Lee K, Henze D, Smith DE, Robertson-Anderson RM Onset of Non-continuum Effects in Microrheology of Entangled Polymer Solutions. Macromolecules (2014) 47:1181–6. doi:10.1021/ma401615m

CrossRef Full Text | Google Scholar

48. Francis ML, Ricketts SN, Farhadi L, Rust MJ, Das M, Ross JL, et al. Non-monotonic Dependence of Stiffness on Actin Crosslinking in Cytoskeleton Composites. Soft Matter (2019) 15:9056–65. doi:10.1039/c9sm01550g

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Park C-Y, Jacobson DR, Nguyen DT, Willardson S, Saleh OA A Thin Permeable-Membrane Device for Single-Molecule Manipulation. Rev Scientific Instr (2016) 87:014301. doi:10.1063/1.4939197

CrossRef Full Text | Google Scholar

50. Gurmessa BJ, Bitten N, Nguyen DT, Saleh OA, Ross JL, Das M, et al. Triggered Disassembly and Reassembly of Actin Networks Induces Rigidity Phase Transitions. Soft matter (2019) 15:1335–44. doi:10.1039/c8sm01912f

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Robertson-Anderson RM Optical Tweezers Microrheology: From the Basics to Advanced Techniques and Applications (2018). Dataset.

Google Scholar

52. Gurmessa B, Ricketts S, Robertson-Anderson RM Nonlinear Actin Deformations lead to Network Stiffening, Yielding, and Nonuniform Stress Propagation. Biophysical J (2017) 113(7):1540–50. doi:10.1016/j.bpj.2017.01.012

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Falzone TT, Blair S, Robertson-Anderson RM Entangled F-Actin Displays a Unique Crossover to Microscale Nonlinearity Dominated by Entanglement Segment Dynamics. Soft matter (2015) 11:4418–23. doi:10.1039/c5sm00155b

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Falzone TT, Robertson-Anderson RM Active Entanglement-Tracking Microrheology Directly Couples Macromolecular Deformations to Nonlinear Microscale Force Response of Entangled Actin. ACS Macro Lett (2015) 4:1194–9. doi:10.1021/acsmacrolett.5b00673

CrossRef Full Text | Google Scholar

55. Gurmessa B, Fitzpatrick R, Falzone TT, Robertson-Anderson RM Entanglement Density Tunes Microscale Nonlinear Response of Entangled Actin. Macromolecules (2016) 49:3948–55. doi:10.1021/acs.macromol.5b02802

CrossRef Full Text | Google Scholar

56. Brau RR, Ferrer JM, Lee H, Castro CE, Tam BK, Tarsa PB, et al. Passive and Active Microrheology with Optical Tweezers. J Opt A: Pure Appl Opt (2007) 9:S103–S112. doi:10.1088/1464-4258/9/8/s01

CrossRef Full Text | Google Scholar

57. Robertson C, George SC Theory and Practical Recommendations for Autocorrelation-Based Image Correlation Spectroscopy. J Biomed Opt (2012) 17:080801. doi:10.1117/1.jbo.17.8.080801

CrossRef Full Text | Google Scholar

58. Lee G, Leech G, Rust MJ, Das M, McGorty RJ, Ross JL, et al. Myosin-driven Actin-Microtubule Networks Exhibit Self-Organized Contractile Dynamics. Sci Adv (2021) 7:eabe4334. doi:10.1126/sciadv.abe4334

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Sheung JY, Achiriloaie DH, Currie C, Peddireddy K, Xie A, Simon-Parker J, et al. Motor-driven Restructuring of Cytoskeleton Composites Leads to Tunable Time-Varying Elasticity. ACS Macro Lett (2021) 10:1151–8. doi:10.1021/acsmacrolett.1c00500

CrossRef Full Text | Google Scholar

60. Schmidt FG, Hinner B, Sackmann E Microrheometry Underestimates the Values of the Viscoelastic Moduli in Measurements onF-Actin Solutions Compared to Macrorheometry. Phys Rev E (2000) 61:5646–53. doi:10.1103/physreve.61.5646

CrossRef Full Text | Google Scholar

61. Davis JS Assembly Processes in Vertebrate Skeletal Thick Filament Formation. Annu Rev Biophys Biophys Chem (1988) 17:217–39. doi:10.1146/annurev.bb.17.060188.001245

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Fisher CI, Kuo SC Filament Rigidity Causes F-Actin Depletion from Nonbinding Surfaces. Proc Natl Acad Sci (2009) 106:133–8. doi:10.1073/pnas.0804991106

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Fitzpatrick R, Michieletto D, Peddireddy KR, Hauer C, Kyrillos C, Gurmessa BJ, et al. Synergistic Interactions between Dna and Actin Trigger Emergent Viscoelastic Behavior. Phys Rev Lett (2018) 121:257801. doi:10.1103/physrevlett.121.257801

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Tang JX, Janmey PA The Polyelectrolyte Nature of F-Actin and the Mechanism of Actin Bundle Formation. J Biol Chem (1996) 271:8556–63. doi:10.1074/jbc.271.15.8556

CrossRef Full Text | Google Scholar

65. Yu X, Carlsson AE Multiscale Study of Counterion-Induced Attraction and Bundle Formation of F-Actin Using an Ising-like Mean-Field Model. Biophysical J (2003) 85:3532–43. doi:10.1016/s0006-3495(03)74773-0

CrossRef Full Text | Google Scholar