Memristive Computation-Oriented Chaos and Dynamics Control

A variable boostable chaotic system and the Hindmarsh–Rose neuron model are applied for observing the dynamics revised by memristive computation. Nonlinearity hidden in a memristor makes a dynamic system prone to be chaos. Inherent dynamics in a dynamic system can be preserved in specific circumstances. Specifically, as an example, offset boosting in the original system is inherited in the derived memristive system, where the average value of the system variable is rescaled linearly by the offset booster. Additional feedback from memristive computation raises chaos, as a case, in the Hindmarsh–Rose neuron model the spiking behavior of membrane potential exhibits chaos with a relatively large parameter region of the memristor.

Introduction

Memristor is a new nonlinear component that brings great convivence for chaos generation [1–5] and dynamics control [6–10]. When a memristor is introduced, a dynamical system finds its way to exhibit more complicated evolvements. Whatever in a 3D [11–13] or 4D [14–16] or an even higher dimensional [17, 18] system, a memristor does endow abundant dynamics including hidden attractor [19, 20], bistability [21, 22], tristability [23], extreme multistability [24–27], and megamultistability [28–30]. Memristor, meminductor [31, 32], and memcapacitor [33, 34] are in fact representations of special computation, where the current output is critically associated with the past states and the current input. This is essentially a kind of time delay, which brings nonlinear factors and makes the system more prone to be chaos or even hyperchaos [35–37].

In this paper, a memristor-based computation is introduced in a variable boostable chaotic system and the Hindmarsh–Rose neuron model for observing the influence of memory from the memristive computation. As shown in Figure 1, chaos oscillation, and dynamics control are explored and discussed in a variable boostable system and neuron cells. In A 3D Memristive Chaotic System, the VB14 system is applied to host a memristor, where chaotic oscillation is preserved with the inherent property of offset boosting. The system and component parameter shows their separate power for preserving chaos and revising dynamics . In A Memristive Hindmarsh-Rose Neuron, the Hindmarsh–Rose neuron model is studied as an example to demonstrate the effect of memory. Memristive computation shows its disturbance for chaos production. Some discussion and future work are presented in the last section.

FIGURE 1

FIGURE 1. Memristive computation-oriented dynamics.

A 3D Memristive Chaotic System

Basic Analysis

A variable boostable chaotic system is a class of chaotic systems with an independent variable that can be controlled with a linearly rescaled average value. By introducing a constant, the offset of the variable can be boosted to any desired level. Thus, we can control the variable switch between a bipolar signal and a unipolar signal according to the constant. In this paper, VB14 is selected as the seed system for hosting a memristor,

$\{\begin{array}{l}\dot{x}=1-ayz,\\ \dot{y}=z^2-z,\\ \dot{z}=x-bz.\end{array}(1)$

when a = 3.55, b = 0.5, IC = (1, 0, 1), system (1) is chaotic with Lyapunov exponents (0.151, 0, −0.651) and Kaplan–Yorke dimension $D_{KY}$ of 2.2319. A memristor is introduced into the VB14 system, as shown in Eq. 2,

$\{\begin{array}{l}\dot{x}=1-a\left(-c+d\left|y\right|\right)z,\\ \dot{y}=z^2-yz,\\ \dot{z}=x-bz.\end{array}(2)$

where the flux-controlled memductance is described as,

$\{\begin{array}{l}{i}_M=W\left(y\right)z,\\ W\left(y\right)=-c+d\left|y\right|,\\ \dot{y}=z^2-yz.\end{array}(3)$

Here y is the internal variable of the memristor and can be regarded as the flux-controlled variable of the memristor. The memristor function curve and the corresponding hysteresis loop are plotted as shown in Figure 2. In the process memristor with the internal variable determined as, $\dot{y}=z^2-yz$ is selected for introducing a memristor-based computation. Here x, and z are system variables, a, and b, are the bifurcation parameters of the system (2); and c, and d are the internal parameters of the memristor. When a = 2.4, b = 0.5, c = 1.7, and d = 2.5, under initial conditions (1, 0, 1), system (2) has a chaotic attractor of Lyapunov exponents (0.18548, 0, −1.2907) and Kaplan–Yorke dimension of 2.1437, as shown in Figure 3.

FIGURE 2

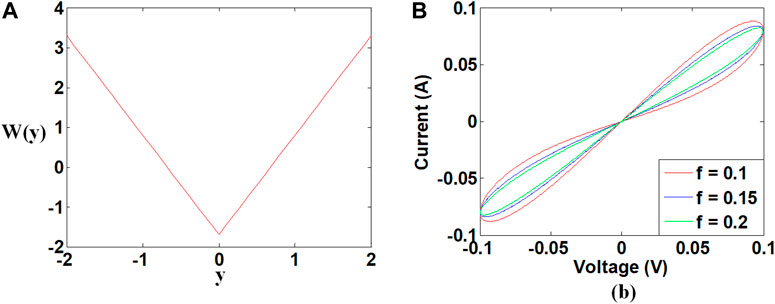
FIGURE 2. Memristor function and corresponding hysteresis loop. (A) memristor function, (B) hysteresis loop.

FIGURE 3

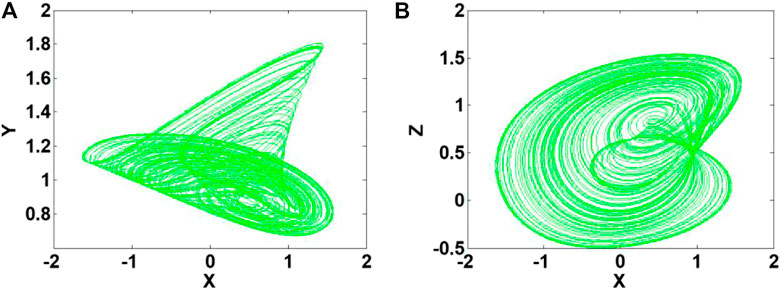
FIGURE 3. Strange attractor of system (2) with a = 2.4, b = 0.5, c = 1.7, d = 2.5 under initial conditions (1, 0, 1) (A) x-y plane, (B) x-z plane.

The hypervolume contraction of this system can be described by the following expression:

$\nabla V=\frac{\partial x}{\partial x}+\frac{\partial y}{\partial y}+\frac{\partial z}{\partial z}=-z-b(4)$

which is related to the values of the system variable z and parameter b. When system parameters are a = 2.4, b = 0.5, c = 1.7, and d = 2.5, the result of this equation $\nabla V$ is negative. Further examination revealed that the sum of Lyapunov exponents is also negative. So, system (1) is dissipative.

Let the left-hand side of the system (2) be equal to zero, the equilibria can be solved by the following equation:

$\{\begin{array}{l}1-a(-c+d\left|y\right|)z=0,\\ z^2-yz=0,\\ x-bz=0,\end{array}(5)$

system (2) has a non-zero equilibrium point S₀ = (0.43564387, 0.87128774, 0.87128774). Linearizing system (2) at the equilibrium point S₀, the Jacobian matrix can be obtained as,

$\text{J }=\left[\begin{array}{ccc}\text{0}& -ad\left|y\right|z& -a\left(-c+d\left|y\right|\right)\\ \text{0}& -z& -y+2z\\ 1& 0& -b\end{array}\right](6)$

The characteristic equation is derived as:

$\text{det}\left(\mathit{\lambda }\text{I}-\text{J}\right)=\left(a_1{\lambda }^3+a_2{\lambda }^2+a_3\lambda +a_4\right)=\text{0}(7)$

Therefore, $a_1=1$, $a_2=z+b$, $a_3=a\left(-c+d\left|y\right|\right)+bz$, $a_4=ad\left|y\right|z+a\left(-c+d\left|y\right|\right)$, when a = 2.4, b = 0.5, c = 1.7, d = 2.5, the eigenvalue of S₀ is: ${\lambda }_1=-1.9842081$, ${\lambda }_2=0.30646019-1.6448751i$, and ${\lambda }_3=0.30646019+1.6448751i$.

Bifurcation Observation

For system (2), the dynamic behavior of the system can be modified by changing the parameters. When b = 0.5, c = 1.7, d = 2.4 and the initial condition is (1, 0, 1), the bifurcation diagram and Lyapunov exponents of parameter a varies in [0.5, 3] are shown in Figures 4A,B. It can be seen from the figure that the system has a couple of periodic windows. When parameter a varies in the range of [0.5, 1.1], system (2) is periodic and exhibits a period-doubling process; then, the system enters a chaotic state around a = 1.1. After that system (2) remains in chaos in [1.1, 1.255], [1.4, 1.725], [1.8, 2.05], [2.1, 2.5], [2.55, 3] except a couple of interrupted period windows.

FIGURE 4

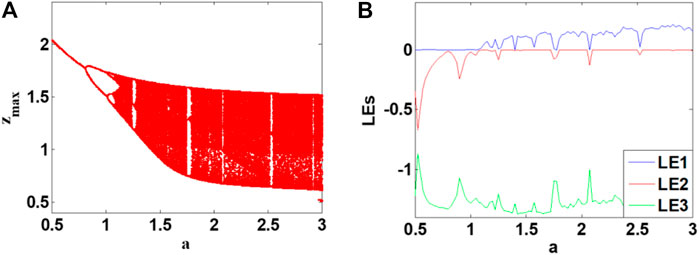
FIGURE 4. Bifurcation and Lyapunov exponents diagrams of oscillator (2) with b = 0.5, c = 1.7, d = 2.4 and the initial conditions is (1, 0, 1) when the parameter a is in [0.5, 3]. (A) bifurcation, (B) Lyapunov exponents.

When a = 2.4, c = 1.7, d = 2.5, the initial condition is (1, 0, 1) and b varies in (0, 1.5), the corresponding bifurcation and Lyapunov exponents are shown in Figure 5. From Lyapunov exponents and bifurcation, we observe that the system undergoes a typical inverse-period-doubling process from chaos. When b in [0, 0.385], [0.435, 0.735], and [0.785, 0.81], system (2) exhibits chaos. Some periodic windows such as [0.385, 0.435] are seen. When parameter b varies in [0.81, 1.5], system (2) gives cycle-4, cycle-2, and cycle-1 limit cycles.

FIGURE 5

FIGURE 5. Lyapunov exponents and bifurcation diagrams of system (2) with a = 2.4, c = 1.7, d = 2.5 and initial conditions (1, 0, 1) when the parameter b varies in [0, 1.5]. (A) bifurcation, (B) Lyapunov exponents.

To observe the memristive computation influence on system dynamics, here the coefficient d implying memristor resistance is used as a bifurcation parameter. When a = 2.4, b = 0.5, and c = 1.7, and initial condition (1, 0, 1), and d increases in the region of [0, 5], the bifurcation and Lyapunov exponents are shown in Figures 6A,B. When the internal parameter d of the memristor is in the range of [1.8, 2.01], the system shows periodic oscillation; similarly, when the internal parameter d of the memristor is in the range of [2.01, 2.71] and [2.71, 3.56], the system again turns to be chaos; when the internal parameter d of the memristor changes in the region of [3.56, 3.96], the system enters a chaotic state. A typical inverse periodic doubling bifurcation happens when d becomes larger.

FIGURE 6

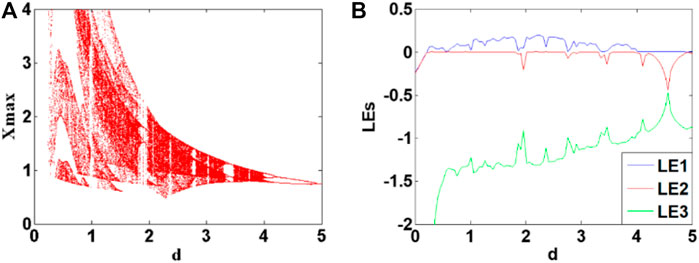
FIGURE 6. Lyapunov exponents and bifurcation diagrams of system (2) with a = 2.4, b = 0.5, c = 1.7 and initial condition (1, 0, 1) when the memristor parameter d varies in [0, 5]. (A) bifurcation, (B) Lyapunov exponents.

As shown in the latter, the newly introduced memristor does not break the property of offset boosting. Suppose if there is a constant e is introduced in the last dimension,

$\{\begin{array}{l}\dot{x}=1-a\left(-c+d\left|y\right|\right)z,\\ \dot{y}=z^2-yz,\\ \dot{z}=\left(x-e\right)-bz,\end{array}(8)$

Different constants of e revise the offset of the system variable x directly. As shown in Figure 7, three chaotic attractors with different offsets are displayed in cyan, green, and red. Here signal x(t) at e = 0 is bipolar signal, while signals at x(t) at e = $\pm 3$ are unipolar positive and negative signal. Offset controller e only rescales the average value of x without influencing system dynamics.

FIGURE 7

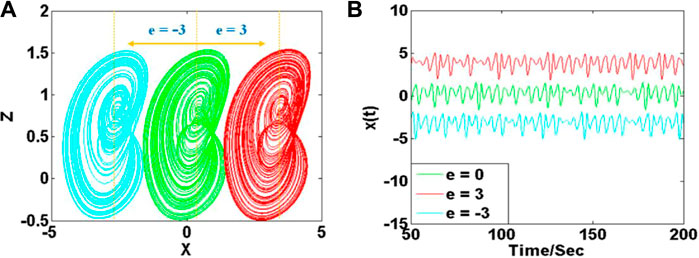
FIGURE 7. Offset boosted attractors of system (8) with a = 2.4, b = 0.5, c = 1.7,and d = 2.5: (A) attractors on plane of x-z, (B) signal x(t).

A Memristive Hindmarsh-Rose Neuron

The 2D HR neuro was simplified from the classical Hodgkin–Huxley model [25] by HR, which is expressed by the following expression,

$\{\begin{array}{l}\dot{x}=y-x^3+a{x}^2+I,\\ \dot{y}=1-b{x}^2-y.\end{array}(9)$

where a and b are positive constants, and I is the external current. In the system (9), x stands for membrane potential, and y stands for spiking variable, [38]. To better express the complex dynamical behaviors of the neuron electrical activities, here a new 3-D memristive HR neuron model is proposed [39]. The external current I in the 2-D HR neuron model (8) be replaced by a memristor, the new HR neuron model can be described as,

$\{\begin{array}{l}\dot{x}=y-x^3+a{x}^2-\left(-c+d\left|z\right|\right)x,\\ \dot{y}=1-b{x}^2-y,\\ \dot{z}=-x^2-xz.\end{array}(10)$

Let the left-hand side of the system (10) be equal to zero, the equilibria can be solved by the following equation:

$\{\begin{array}{l}y-x^3+a{x}^2-\left(-c+d\left|z\right|\right)x=0\\ 1-b{x}^2-y=0\\ -x^2-xz=0\end{array}(11)$

System (10) has a non-zero equilibrium point S = (0.58771263, $-$ 0.89973376, $-$ and 0.58771263). Linearizing system (10) at the equilibrium point S₀, the Jacobian matrix can be obtained as,

$J=\left[\begin{array}{ccc}3x^2+2ax-\left(-c+d\left|z\right|\right)& 1& -dxsgn\left(z\right)\\ -2bx& -1& 0\\ -2x-z& 0& -x\end{array}\right](12)$

The characteristic equation is derived as:

$\det \left(\lambda I-J\right)=\left(a_1{\lambda }^3+a_2{\lambda }^2+a_3\lambda +a_4\right)=0(13)$

where $a_1$, $a_2$, $a_3$, and $a_4$ are polynomials containing a, b, c, d, and variables x and z: $a_1=1$, $a_2=\left(-3x+1-2a\right)x-c+d\left|z\right|+1$, $a_3=-\left(x+1\right)\left(3x^2+2ax-c+d\left|z\right|\right)-dx\mathrm{sgn}\left(z\right)\left(2x+z\right)+\left(2b+1\right)x$, and $a_4=-x\left(3x^2+2ax+2bx-d\mathrm{sgn}\left(z\right)\left(2x+z\right)-c+d\left|z\right|\right)$. When a =2.8, b = 5.5, c = 1.7, and d = 2.5, the eigenvalues of S are:${\lambda }_1=0.683273$, and ${\lambda }_{\mathrm{2,3}}=0.107353\pm 0.597675i$, thus showing it is a saddle point.

The parameters in (10) are specified as follows: b = 5.5, c = 1.7, and d = 2.5, and the initial condition is (0, 0, 0). When a varies within the range of [2, 3.3], the bifurcation diagram of the membrane potential x and Lyapunov exponents are shown in Figures 8A,B. When the parameter a is increased in the region [2, 2.6], system (10) exhibits typical period-doubling bifurcation; when the range of parameter a varies in [2.6, 2.92], system (10) shows chaos; When parameter a is in the range of [2.92, 3.3], system (10) exhibits an inverse-period-doubling process. As shown in Figure 9, the neuronal electrical activity shows different modes by modifying the value of the system parameter a. Corresponding attractors are displayed in Figure 10.

FIGURE 8

FIGURE 8. Bifurcation and Lyapunov exponents of system (10) with b = 5.5, c = 1.7, d = 2.5 and initial condition (0, 0, 0) when parameter a varies in [2, 3.3]. (A) bifurcation, (B) Lyapunov exponents.

FIGURE 9

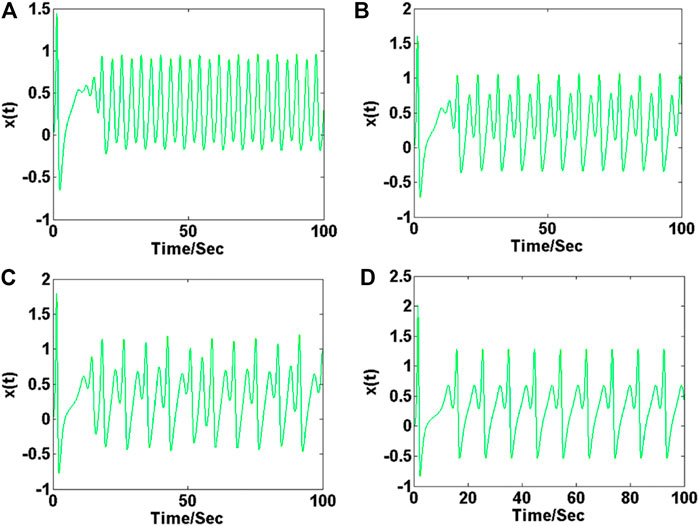
FIGURE 9. Time series of membrane potential under different parameters a of system (10) with b = 5.5, c = 1.7, d = 2.5 and initial condition (0, 0, 0): (A) a = 2.2, (B) a = 2.5, (C) a = 2.8, (D) a = 3.

FIGURE 10

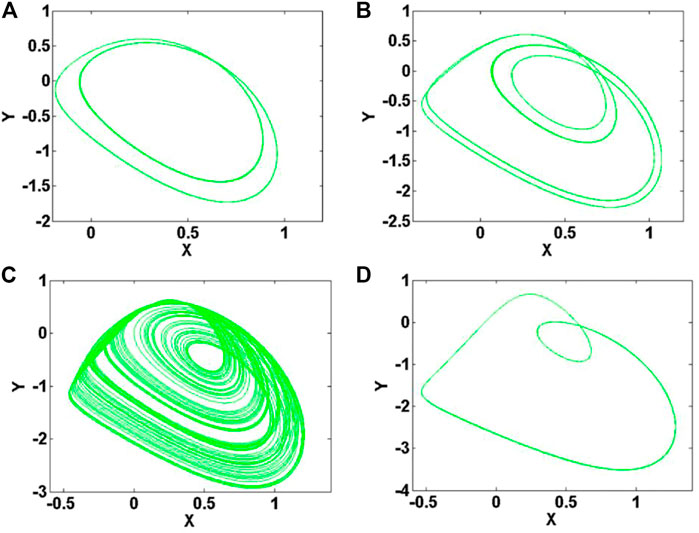
FIGURE 10. Dynamics of system (10) with b = 5.5, c = 1.7, d = 2.5 and initial condition (0, 0, 0): (A) a = 2.2, (B) a = 2.5, (C) a = 2.8, (D) a = 3.

When a = 2.8, c = 1.7, and d = 2.5, and the initial condition is (0, 0, 0), the bifurcation diagram of the maxima X of the membrane potential x and Lyapunov exponents of parameter b varies in the range of [2, 13] are shown in Figures 11A,B. When parameter b is increased in the region of [0, 5.25], the system (10) exhibits typical period-doubling bifurcation phenomenon; When parameter b varies in [5.25, 5.77], [6.68, 7.59], [8.5, 8.63], [8.89, 9.28], [10.84, 10.97], and [12.27, 12.4], system (4) exhibits chaos; When parameter b is in the range of [5.77, 6.68], [7.59, 8.5], [8.63 8.89], [9.28, 10.84], and [10.97, 12.27], system (10) gives periodic solution. When b increases in the region of [12.27, 13], system (10) moves from chaos to period again. As shown in Figure 12, the bursting state of neuronal electrical activity can be changed into different modes by modifying the value of the system parameter b. As shown in Figure 13, attractors correspond to the different bursting states of neuronal electrical activity.

FIGURE 11

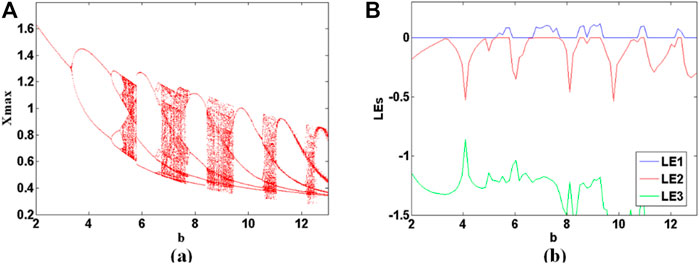
FIGURE 11. Bifurcation and Lyapunov exponents of system (10) with a = 2.8, c = 1.7, d = 2.5 and the initial conditions is (0, 0, 0) when the parameter b varies in [2, 13]. (A) bifurcation, (B) Lyapunov exponents.

FIGURE 12

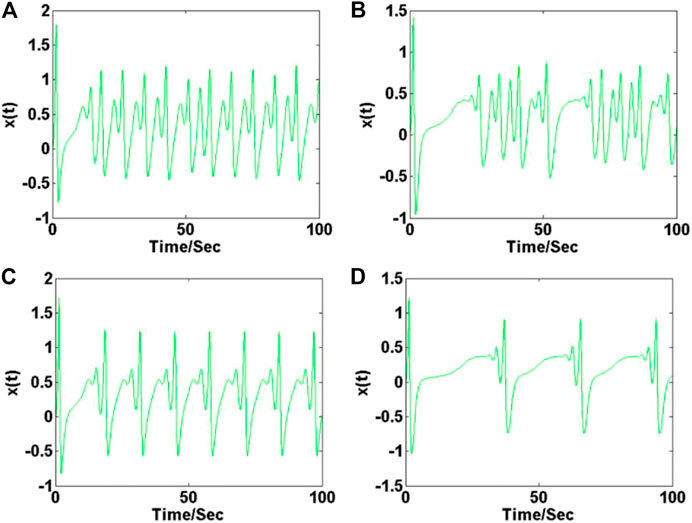
FIGURE 12. Time series of membrane potential of system (10) with a = 2.8, c = 1.7, d = 2.5 and initial conditions (0, 0, 0): (A) b = 5.5, (B) b = 6.2, (C) b = 9.2, (D) b = 11.5.

FIGURE 13

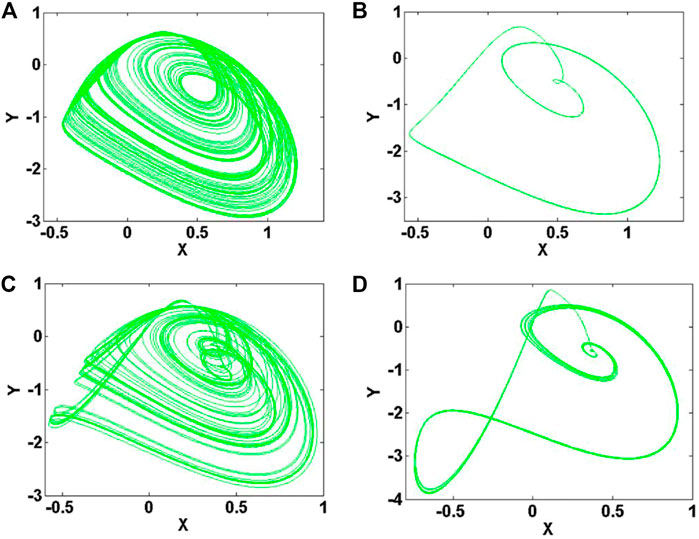
FIGURE 13. Dynamics of system (10) with a = 2.8, c = 1.7, d = 2.5 and initial condition (0, 0, 0): (A) b = 5.5, (B) b = 6.2, (C) b = 9.2, (D) b = 11.5.

Also to observe the memristive computation influence on system dynamics, here the coefficient d is used as a bifurcation parameter in the derived HR neuron model. When a = 2.4, b = 5.5, c = 1.7, and the initial condition is (0, 0, 0), the bifurcation diagram of the maxima X of the membrane potential x and Lyapunov exponents of parameter d varies in the range of [1, 4] are shown in Figures 14A,B. When the parameter d is increased in the region of [0, 2.24], The system exhibits typical period-doubling bifurcation phenomenon; When the range of the parameter d vary in [2.24, 2.75], the system (10) is chaotic, obviously, there are two typical period windows in this chaotic range; When parameter d is in the range of [2.75, 4], system (10) exhibits an inverse-period-doubling process. Interestingly, the function of the parameter d is similar to the system parameter a.

FIGURE 14

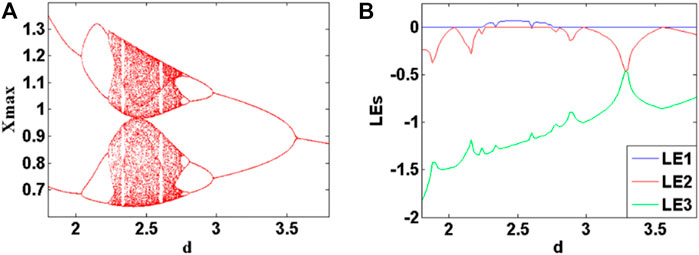
FIGURE 14. Lyapunov exponents and bifurcation of system (10) with a = 2.8, b = 5.5, c = 1.7 and the initial conditions are (0, 0, 0) when the memristor parameter d varies in [1.8, 3.8]. (A) bifurcation, (B) Lyapunov exponents.

As shown in the latter, the newly introduced memristor does not break the property of offset boosting. Suppose there is a constant e introduced in both of the first dimension and the second dimension,

$\{\begin{array}{l}\dot{x}=y-e-x^3+a{x}^2-\left(-c+d\left|z\right|\right)x,\\ \dot{y}=1-b{x}^2-\left(y-e\right),\\ \dot{z}=-x^2-xz.\end{array}(14)$

Different constants of e revise the offset of the system variable y directly. As shown in Figure 15, three chaotic attractors with different offsets are displayed in cyan, green, and red. Here signal x(t) at e = 0 is bipolar signal, while signals at x(t) at e = $\pm 3.5$ are unipolar positive and negative signal. Offset controller e only rescales the average value of y without influencing system dynamics.

FIGURE 15

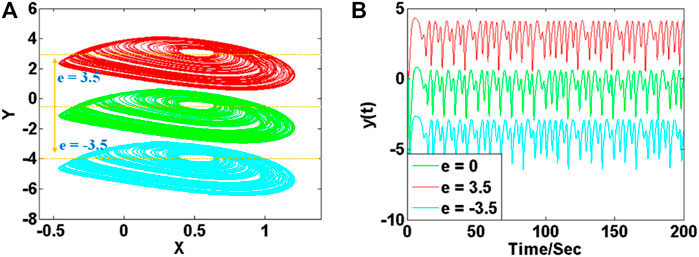
FIGURE 15. Offset boosted attractors of system (11) with a = 2.8, b = 5.5, c = 1.7, d = 2.5: (A) attractors on plane of x-y, (B) signal y(t).

Conclusion

Memristor and memristive computation have great merits for producing chaos and dynamics control due to the special nonlinearity. It shows that even a memristor function is a linear function, the memory effect from memristive computation still returns chaos under a specific bifurcation. In this paper, two systems are reformed to be memristive chaotic systems based on the same memristor function. Offset boosting is discussed in both systems. Memristive computation as a new type of computing shows great potential with chaos-based engineering and pattern recognition in artificial intelligence, which deserves further research and will yield great value in information engineering.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported financially by the National Natural Science Foundation of China (Grant no. 61871230), the Natural Science Foundation of Jiangsu Province (Grant no. BK20181410), and a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chua L. Memristor-The Missing Circuit Element. IEEE Trans Circuit Theor (1971) 18(5):507–19. doi:10.1109/TCT.1971.1083337

CrossRef Full Text | Google Scholar

Chua LO, Sung Mo Kang S. Memristive Devices and Systems. Proc IEEE (1976) 64(2):209–23. doi:10.1109/PROC.1976.10092

CrossRef Full Text | Google Scholar

Chua L, Komuro M, Matsumoto T. The Double Scroll Family. IEEE Trans Circuits Syst (1986) 33(11):1072–118. doi:10.1109/TCS.1986.1085869

CrossRef Full Text | Google Scholar

Chua LO, Komuro M, Matsumoto T. The Double Scroll Family. Part I: Rigorous Proof of Chaos IEEE Trans (1986) 33(11):1072–1118. doi:10.1109/TCS.1986.1085869

CrossRef Full Text | Google Scholar

Deng Q, Wang C, Yang L. Four-Wing Hidden Attractors with One Stable Equilibrium Point. Int J Bifurcation Chaos (2020) 30(6):2050086. doi:10.1142/S0218127420500868

CrossRef Full Text | Google Scholar

Wang R, Li C, Çiçek S, Rajagopal K, Zhang X. A Memristive Hyperjerk Chaotic System: Amplitude Control, FPGA Design, and Prediction with Artificial Neural Network. Complexity (2021) 2021(1):1–17. doi:10.1155/2021/6636813

CrossRef Full Text | Google Scholar

Lu T, Li C, Wang X, Tao C, Liu Z. A Memristive Chaotic System with Offset-Boostable Conditional Symmetry. Eur Phys J Spec Top (2020) 229(6):1059–69. doi:10.1140/epjst/e2020-900186-5

CrossRef Full Text | Google Scholar

Zhang X, Li C, Min F, Iu HH-C, Gao H. Broken Symmetry in a Memristive Chaotic Oscillator. IEEE Access (2020) 8(8):69222–9. Doidoi:10.1109/ACCESS.2020.298267110.1109/access.2020.2982671

CrossRef Full Text | Google Scholar

Gu Z, Li C, Iu HHC, Min F, Zhao Y. Constructing Hyperchaotic Attractors of Conditional Symmetry. Eur Phys J B (2019) 92(10):221. doi:10.1140/epjb/e2019-100165-9

CrossRef Full Text | Google Scholar

Wang C, Xia H, Zhou L. A Memristive Hyperchaotic Multiscroll Jerk System with Controllable Scroll Numbers. Int J Bifurcation Chaos (2017) 27(6):1750091. doi:10.1142/S0218127417500912

CrossRef Full Text | Google Scholar

Li C, Yang Y, Du J, Chen Z. A Simple Chaotic Circuit with Magnetic Flux-Controlled Memristor. Eur Phys J Spec Top (2021) 230:1723–36. doi:10.1140/epjs/s11734-021-00181-2

CrossRef Full Text | Google Scholar

Yu F, Zhang Z, Shen H, Huang Y, Cai S, Jin J, et al. Design and FPGA Implementation of a Pseudo-random Number Generator Based on a Hopfield Neural Network under Electromagnetic Radiation. Front Phys (2021) 9:690651. doi:10.3389/fphy.2021.690651

CrossRef Full Text | Google Scholar

Xin B, Peng W, Guerrini L. A Continuous Time Bertrand Duopoly Game with Fractional Delay and Conformable Derivative: Modeling, Discretization Process, Hopf Bifurcation, and Chaos. Front Phys (2019) 7:00084. doi:10.3389/fphy.2019.00084

CrossRef Full Text | Google Scholar

Xiu C, Zhou R, Liu Y. New Chaotic Memristive Cellular Neural Network and its Application in Secure Communication System. Chaos, Solitons & Fractals (2020) 141:110316. doi:10.1016/j.chaos.2020.110316

CrossRef Full Text | Google Scholar

Qiao X, Yi X, Sun Y. Hidden Dynamical Characteristics in Memristor-Based Hyperchaotic Lü System. J Univ Electron Sci Techn China (2018).

Google Scholar

He J-J, Lai B-C. A Novel 4D Chaotic System with Multistability: Dynamical Analysis, Circuit Implementation, Control Design. Mod Phys Lett B (2019) 33(21):1950240. doi:10.1142/S0217984919502403

CrossRef Full Text | Google Scholar

Ren X, Chen B, Xu Q, Wu H, Chen M. Parameter and Initial Offset Boosting Dynamics in Two-Memristor-Based Colpitts System. Eur Phys J Spec Top (2021) 230:1709–21. doi:10.1140/epjs/s11734-021-00118-9

CrossRef Full Text | Google Scholar

Vaidyanathan S, Sambas A, Azar AT. A 5-D Hyperchaotic Dynamo System with Multistability, its Dynamical Analysis, Active Backstepping Control, and Circuit simulationSystems. Backstepping Control of Nonlinear Dynamical(2021) 449–71. doi:10.1016/B978-0-12-817582-8.00025-8

CrossRef Full Text | Google Scholar

Lin H, Wang C, Tan Y. Hidden Extreme Multistability with Hyperchaos and Transient Chaos in a Hopfield Neural Network Affected by Electromagnetic Radiation. Nonlinear Dyn (2020) 99(4):2369–86. doi:10.1007/s11071-019-05408-5

CrossRef Full Text | Google Scholar

Prousalis DA, Volos CK, Bao B, Meletlidou E, Stouboulos IN, Kyprianidis IM. Extreme Multistability in a Hyperjerk Memristive System with Hidden Attractors. Chaotic Syst Synchronization (2019) 89–103. doi:10.1016/b978-0-12-815838-8.00006-6

CrossRef Full Text | Google Scholar

Li C, Sprott JC, Xing H. Crisis in Amplitude Control Hides in Multistability. Int J Bifurcation Chaos (2016) 26(14):1650233. doi:10.1142/S0218127416502333

CrossRef Full Text | Google Scholar

Li C, Sprott JC, Thio W. Bistability in a Hyperchaotic System with a Line Equilibrium. J Exp Theor Phys (2014) 118(3):494–500. doi:10.1134/S1063776114030121

CrossRef Full Text | Google Scholar

Li Y, Zeng Y, Zeng J. A Unique Jerk System with Abundant Dynamics: Symmetric or Asymmetric Bistability, Tristability, and Coexisting Bubbles. Braz J Phys (2020) 50(2):153–63. doi:10.1007/s13538-019-00731-z

CrossRef Full Text | Google Scholar

Yuan F, Deng Y, Li Y, Wang G. The Amplitude, Frequency and Parameter Space Boosting in a Memristor-Meminductor-Based Circuit. Nonlinear Dyn (2019) 96(1):389–405. doi:10.1007/s11071-019-04795-z

CrossRef Full Text | Google Scholar

Bao BC, Bao H, Wang N, Chen M, Xu Q. Hidden Extreme Multistability in Memristive Hyperchaotic System. Chaos, Solitons & Fractals (2017) 94:102–11. doi:10.1016/j.chaos.2016.11.016

CrossRef Full Text | Google Scholar

Zhang S, Zeng Y, Li Z, Zhou C. Hidden Extreme Multistability, Antimonotonicity and Offset Boosting Control in a Novel Fractional-Order Hyperchaotic System without Equilibrium. Int J Bifurcation Chaos (2018) 28(13):1850167. doi:10.1142/S0218127418501675

CrossRef Full Text | Google Scholar

Zhang Y, Liu Z, Wu H, Chen S, Bao B. Extreme Multistability in Memristive Hyper-Jerk System and Stability Mechanism Analysis Using Dimensionality Reduction Model. Eur Phys J Spec Top (2019) 228(10):1995–2009. doi:10.1140/epjst/e2019-800238-0

CrossRef Full Text | Google Scholar

Sprott JC, Jafari S, Khalaf AJM, Kapitaniak T. Megastability: Coexistence of a Countable Infinity of Nested Attractors in a Periodically-Forced Oscillator with Spatially-Periodic Damping. Eur Phys J Spec Top (2017) 226(9):1979–85. doi:10.1140/epjst/e2017-70037-1

CrossRef Full Text | Google Scholar

Singh JP, Jafari S, Khalaf AJM, Pham V-T, Roy BK. A Modified Chaotic Oscillator with Megastability and Variable Boosting and its Synchronisation Using Contraction Theory-Based Control Which Is Better Than Backstepping and Nonlinear Active Control. Pramana - J Phys (2020) 94(1):1–14. doi:10.1007/s12043-020-01993-y

CrossRef Full Text | Google Scholar

Singh JP, Koley J, Lochan K, Roy BK. Presence of Megastability and Infinitely Many Equilibria in a Periodically and Quasi-Periodically Excited Single-Link Manipulator. Int J Bifurcation Chaos (2021) 31(2):2130005. doi:10.1142/S0218127421300056

CrossRef Full Text | Google Scholar

Yuan F, Li Y. A Chaotic Circuit Constructed by a Memristor, a Memcapacitor and a Meminductor. Chaos (2019) 29(10):101101. doi:10.1063/1.5125673

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao Q, Wang C, Zhang X. A Universal Emulator for Memristor, Memcapacitor, and Meminductor and its Chaotic Circuit. Chaos (2019) 29(1):013141. doi:10.1063/1.5081076

PubMed Abstract | CrossRef Full Text | Google Scholar

Çam Taşkıran ZG, Sağbaş M, Ayten UE, Sedef H. A New Universal Mutator Circuit for Memcapacitor and Meminductor Elements. AEU - Int J Elect Commun (2020) 119:153180. doi:10.1016/j.aeue.2020.153180

CrossRef Full Text | Google Scholar

Akgul A. Chaotic Oscillator Based on Fractional Order Memcapacitor. J Circuit Syst Comp (2019) 28(14):1950239. doi:10.1142/S0218126619502396

CrossRef Full Text | Google Scholar

Kong S, Li C, He S, Çiçek SQ, Lai Q. A Memristive Map with Coexisting Chaos and Hyperchaos. Chin Phys. B (2021). doi:10.1088/1674-1056/abf4fb

CrossRef Full Text | Google Scholar

Peng Y, He S, Sun K. Chaos in the Discrete Memristor-Based System with Fractional-Order Difference. Results Phys (2021) 24:104106. doi:10.1016/j.rinp.2021.104106

CrossRef Full Text | Google Scholar

He S, Sun K, Peng Y, Wang L. Modeling of Discrete Fracmemristor and its Application. AIP Adv (2020) 10(1):015332. doi:10.1063/1.5134981

CrossRef Full Text | Google Scholar

Kaslik E. Analysis of Two- and Three-Dimensional Fractional-Order Hindmarsh-Rose Type Neuronal Models. Fract Calc Appl Anal (2017) 20(3):623–45. doi:10.1515/fca-2017-0033

CrossRef Full Text | Google Scholar

Bao H, Hu A, Liu W, Bao B. Hidden Bursting Firings and Bifurcation Mechanisms in Memristive Neuron Model with Threshold Electromagnetic Induction. IEEE Trans Neural Netw Learn Syst. (2020) 31:502–11. doi:10.1109/TNNLS.2019.2905137

PubMed Abstract | CrossRef Full Text | Google Scholar