Physical Intuition to Improve Electronic Properties of Thermoelectrics

Thermoelectrics convert heat to electricity and vice versa. They are of technological importance in cooling and energy harvesting. Their performances are defined by figure of merit, zT. Decades of studies have largely focused on the development of novel and advanced materials reaching higher performance in devices. To date, the lack of sufficiently high-performance thermoelectrics, especially among Earth-abundant and lightweight materials, is one of the reasons why there is no broad commercial application of thermoelectric devices yet. This challenge is due to the complex correlations of parameters that make up the zT. Theoretical estimation can reveal the optimal charge carrier concentration, which can provide a good idea of doping compositions. Depending on the material characteristics, decoupling these intercorrelated parameters could be viable. Broadly speaking, increasing carrier mobility, inducing a large fluctuation in density of states (DOS) at the Fermi level, and lowering the lattice thermal conductivity lead to better thermoelectric performance. In this mini review, we provide a broad picture of electronic property optimization for thermoelectric materials. This work will be a useful guide to quickly take readers to the forefront of thermoelectric research.

Introduction

In this era of rapid technological developments, more can be done to combat the climate change due to overconsumption of energy. As one of the potential alternative energy technologies, thermoelectric (TE) materials, which convert waste heat to electricity, are gaining increasing attention [1–8]. In general, a TE module is made of n- and p-type materials that are electrically connected in a series circuit, while the heat gradients applied are parallel to the device.

TE generators have been used for decades in space and automotive applications, especially high-temperature TEs [9–16], and recently in wearable electronic devices [17]. However, the efficiency of TE generators needs to be improved for commercialization. To date, the highest module efficiency achieved is ∼12% with Bi₂Te₃-based materials of at least zT ∼ 1.5 [18–22]. Figure 1A shows a progressive overview of research based on thermoelectric performance since the year 1960, as well as the main physical driving force behind the developments. In addition, low-dimensional TEs such as thin films and 2D materials are also popular [23]. Figure 1B illustrates the complexity of components that influences the dimensionless figure of merit, zT. The parameters that can be experimentally measured are highlighted as green in the figure, whereas experimentally measurable but only in single crystals is highlighted in yellow. It is evident that measuring fundamental properties such as elastic constant, dielectric constant, and band gaps are important to complement and accurately determine the other derived TE parameters. In addition, it is crucial to note that the viability for commercialization is dependent on thermoelectric performance for a range of working temperatures as well as processing methods. Hence, the application space is limited by the materials’ mechanical and chemical properties.

FIGURE 1

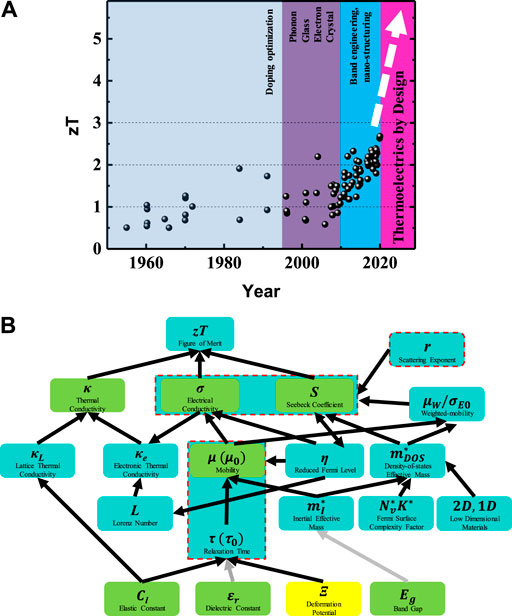
FIGURE 1. (A) Progressive overview of thermoelectric performance as a function to the timeline in years and correlations of zT components. (B) Tree diagram showing the complex web of interdependencies between electronic transport parameters that make up zT.

The overall TE device performance depends on two factors: materials performance and Carnot efficiency, which is temperature dependent. Materials wise, thermoelectric performance is typically expressed in terms of figure of merit zT, which is defined as zT = S²σT/κ, with S, σ, and κ denoting the Seebeck coefficient, electrical, and thermal conductivity, respectively. The overall power conversion efficiency depends on both zT and ∆T (temperature gradient) and can be expressed as follows:

$\eta = \frac{\Delta T}{T_h} \frac{\sqrt{1+Z{T}_{ave}}-1}{\sqrt{1+Z{T}_{ave}}+ T_c/T_h}(1)$

The first term of the equation, ∆T/T_h, represents the Carnot efficiency, which is the theoretical maximum efficiency limit in any energy conversion process. Mathematically, higher ∆T favors higher conversion efficiency and vice versa. The second term of the equation represents the relative efficiency of the TE, which is proportional to zT_ave (average zT over a temperature range). In addition, a more subtle interpretation from the above equation is the importance to keep the cold side temperature (T_c) low (i.e., through effective heat dissipation) in order to maximize the efficiency.

To date, the majority of efforts in thermoelectric materials research have been focused on maximizing the materials figure of merit zT. However, although it sounds simple, zT is not a trivial parameter to optimize or improve on. This is due to the complex interdependencies between the parameters that make up zT as summarized in Figure 1B. This is not considering the many interrelated parameters making up the lattice thermal conductivity, k_L. It is evident that these interdependencies and compromises exist even at the level of fundamental material properties. It has been a grand challenge with decades of research from the TE, physics, and chemistry communities to arrive at the current understanding.

In general, the strategies around enhancing thermoelectric performances can be categorized into two broad classes: Seebeck coefficient enhancement and mobility enhancement. Both aspects will be discussed in turn in the subsequent sections. More importantly, the discussion around these parameters will focus on the importance of taking grain boundaries resistance into account, which is an important topic that has been gaining prominence of late.

Seebeck Coefficient Enhancement

Based on postulates by Cutler and Mott [24], the value of S for degenerate semiconductors or metals can be written by the following formula [25]:

$S=\frac{{\pi }^2}{3}\frac{k_B}{e}\left(k_{B}T\right)\left[\frac{1}{n\left(E\right)}\frac{dn\left(E\right)}{dE}+\frac{1}{\mu \left(E\right)}\frac{d\mu \left(E\right)}{dE}\right](2)$

where S is the Seebeck coefficient, $k_B$ is Boltzmann’s constant, T is the temperature in Kelvin, $e$ is the electron mass, n is the charge carrier concentration, and μ is the charge carrier mobility. Enhanced S can be achieved through degenerate band convergence for Fermi level shifts towards the valence band maxima (VBM) or conduction band minima (CBM), or through enhancement of the density of states (DOS). Based on Eq. 2, S can be enhanced through the variation of both n(E) and μ(E) at E_F. The n and E_F have a significant influence on the energy-dependent electrical conductivity, σ. The n at energy E is equivalent to the g(E). See Figure 2 also. Variation of µ and n can be achieved by varying the effective mass of DOS (m′_dos) together with band engineering. In other words, the Seebeck coefficient depends on the symmetry breaking of both the DOS at the Fermi level and the energy-dependent mobility. In addition to these effects, phonon drag has also been widely reported to contribute to the Seebeck coefficient at low temperatures [26, 27]. It is worthy to mention the significant breakthroughs by Dresselhaus et al. in the field of TE to enhance zT with the modification of the electronic properties of some materials when prepared in the form of quantum-well superlattices or nanowires. This concept of quantum confinement offers additional degrees of freedom for enhancing the TE performance because of the strong dependence between electronic DOS and dimensionality [28, 29].

FIGURE 2

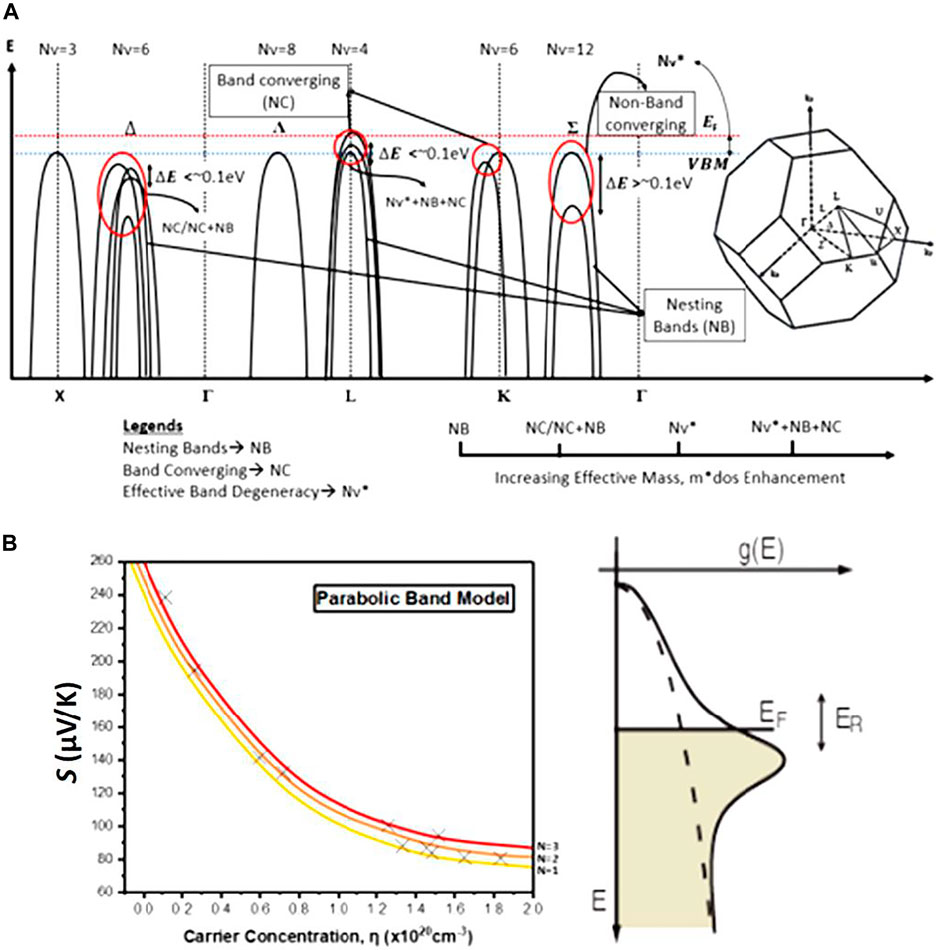
FIGURE 2. (A) An illustration of the band structure consisting of examples of converging, non-converging, and nesting bands, and the Brillouin zone of face-centered cubic (FCC) lattice. (B) An illustration of the Pisarenko plot based on single parabolic band (SPB) model calculations with a density of states (DOS) profile of 3D bulk material relative to energy.

To date, strategies to enhance the Seebeck coefficients at room temperature and above have been mainly via the first term of Eq. 2, dn(E)/dE (i.e., the slope of DOS vs. energy). This can be achieved via either band convergence or resonant doping. In addition, the second term of Eq. 2, dμ(E)/dE, is closely associated with energy filtering, which manifests in scattering exponent r. Lastly, size effects in low-dimensional materials have been known to provide such symmetry breaking in DOS, as well elucidated in a recent review [30].

Band Convergence

For effective transport, the DOS effective mass ($m_{DOS}^{\ast }$) must be asymmetric around the Fermi level. This means that symmetry breaking is desired (sharp peak in DOS) to achieve a high Seebeck coefficient.

The effective mass of the DOS, $m_{DOS}^{\ast }$, is expressed as

$m_{DOS}^{\ast }=m_{Band}^{\ast }{N}_V^{\frac{2}{3}}(3)$

where $m_{band}$ is the effective mass for the band and $N_V$ is the band degeneracy.

There are many ways of achieving band convergence [31, 32]. In p-type PbTe, the L and Σ band convergence happens at high temperatures due to the higher downward shift of L band compared with Σ band [33]. Such convergence is due to thermal expansion. On the other hand, with the addition of group 2 elements such as Mg or transition metal, Mn can also cause band convergence in PbTe due to the absence of s² lone pair in Mg/Mn, which replaces Pb [34, 35]. The absence of lone pairs in Mg/Mn weakens the quenching of lone pairs in PbTe, resulting in lower L band energy [36]. In addition, band convergence in PbTe and SnTe can be achieved by doping of Zn, Cd, Mg, Mn, or Ca, all of which are without s² lone pair [37–44]. A very useful reference for designing band convergence and resonant doping in binary chalcogenides can be found in Ref. [45]. To understand more about the role of lone pairs in the electronic band structure, Ref. [36] is a useful guide.

The face-centered cubic (FCC) lattice band structure consists of Γ, L, and K points in the reciprocal space representing the center, corners, and edges of the cubic lattice in real space, respectively. The illustration in Figure 2 summarizes the examples of nesting, converging, and non-converging bands.

FCC lattice has eight corners; thus, an electronic band on the L symmetry line in the band structure corresponds to eight energetically similar Fermi surfaces of the Brillouin zone as shown on the right side of Figure 2. These are degenerate bands, and the number or multiplicity of degenerate bands is defined by Nv. Further represented in Eq. 3, the higher the Nv, the larger the effective mass DOS. Hence, identifying the symmetry points with high Nv is crucial for enhancing Seebeck. The ideal band modulation doping is to have band converging and band nesting within the effective band degeneracy, Nv*, close to the valence band. See Figure 2.

In certain cases, band convergence can be achieved at structural phase-transition, just like in the case of GeTe. At low temperature, the s² lone pair is stereochemically expressed due to the light ligand field in GeTe compared with SnTe and PbTe. The stereochemical expression of the s² lone pair leads to rhombohedral structure, with Σ band as the VBM. However, at high temperatures, the cubic structure prevails, leading to L band as the VBM. Therefore, at the phase transition temperature, both L and Σ bands converge, leading to a high thermoelectric performance in GeTe. Consequently, manipulating phase transition temperature in GeTe becomes a versatile tool to control its peak performance at a particular temperature [22, 46–78].

Resonant Doping

In addition to band convergence, resonant doping and energy filtering are also popular in enhancing Seebeck. Resonant doping differs from the usual doping states such that the energy states of the resonant dopant lie within the valence band or conduction band, yet away from the VBM or the CBM. Resonant dopants normally have similar electronic configurations as the host atoms, and they are usually selected from the neighboring main group elements. Resonant doping is achieved when the dopant energy level coincides with the host energy level to form two extended states. These developed extended states have similar energy levels again with host energy states and resonate to form more energy states resulting in the increase in DOS. These new energy states introduce distortion to the existing DOS within the material. See Figure 2. When the dopant states lie near the band edge where the Fermi level is, the resonant level becomes beneficial in enhancing Seebeck. It is noteworthy that although fostering resonance levels can enhance the Seebeck, it can adversely affect the carrier mobility. Therefore, it is crucial to have a minimal doping level to achieve a resonance state (unlike band convergence, where the doping level can be much higher). Equation [4] postulates that increased DOS results in enhanced Seebeck. The Pisarenko plot in Figure 2 further illustrates this relationship between the Seebeck and DOS. One of the landmark papers on resonant doping was reported in 2008 by Heremans et al. on Tl-doped PbTe [79].

$S=\frac{8{\pi }^2{k}_B^{2}T}{3e{h}^2}{m}_{DOS}^{\ast }{\left(\frac{\pi }{3n}\right)}^{2/3}(4)$

Energy Filtering

On the other hand, the idea behind energy filtering lies in symmetry breaking of carrier energy. Due to the nature that carriers of lower and higher energy than Fermi level contribute oppositely to the total Seebeck coefficient, the presence of potential barriers to selectively block out lower energy carriers may be beneficial for the Seebeck coefficient while only sacrificing a little bit of electrical conductivity. Mathematically, energy filtering is described by dμ(E)/dE (see Eq. 2). A more rigorous mathematical treatment and derivation of energy filtering can be found in the literature [80]. Experimentally, such a large energy-dependent mobility, which gives rise to enhanced Seebeck coefficient, has been reported in the work by Xie et al. [81].

Enhancing Electrical Conductivity via Mobility

Electrical conductivity written as σ defines the capacity of a medium to transfer current in direct proportion to n and µ as shown below:

$\sigma =q\left({\text{μ}}_{n}n+{\text{μ}}_{p}p\right)(5)$

where $\sigma$ is the electrical conductivity, $q$ is the electronic charge, ${\text{μ}}_n$ and ${\text{μ}}_p$ refer to mobilities of electrons and holes, and n/p is the carrier concentration of each type.

From this equation, enhancing s requires that the values of n and µ are maintained at high levels. Usually, enhancing the value of n is achieved by the introduction of a dopant. In general, the optimal carrier concentration, n, ranges between 10¹⁹ and 10²¹ cm³ with considerable µ. The reduction of µ results from the enhanced scattering of ionized impurities. This calls for a midpoint between the two parameters n and µ. In order to achieve this midpoint, modulation doping is used for discretizing charge carriers from ionized dopants in a bid to reduce the scattering of ionized impurities to achieve high values of µ while enhancing the value of n in the thermoelectric material.

Owing to the variance in the value of E_f in the undoped and uniformly doped, the carriers found within the modulation-doped material overflow across the boundaries of the equitably doped region to the undoped region. This results in carriers eluding the scattering effect of ionized impurities, and therefore, µ is enhanced. The most recent application of modulation doping was in BiCuSeO where high values of PF and ZT were obtained, 5.4 μW·cm⁻¹·K⁻² and 0.99 at 873 K, respectively, compared with the lower values obtained from uniformly and highly doped BiCuSeO. Moreover, this method is known to enhance the carrier concentration, n, and reduce the carrier mobility, µ, due to intervalley scattering in PbTe quantum well. That said, as discussed in the previous section on band convergence, degenerate band convergence leads to an increase in effective mass, m*, which in this case outweighs the loss of carrier mobility. Hence, the overall zT is enhanced [82].

Just like enhancing Seebeck coefficients, there are a few reliable strategies to independently enhance carrier mobility without sacrificing the Seebeck coefficient (i.e., without changing carrier concentration or reduced Fermi level). These strategies can be broadly categorized into tuning inertial effective mass, tuning the deformation potential, tuning carrier scattering, and, in certain cases, even tuning dielectric constant, elastic constant, or band gaps.

In addition to the popular acoustic and ionized impurities scattering, grain boundary scattering, and alloy scattering are also prevalent, especially in polycrystalline materials. Physically, different scattering mechanisms mainly manifest in the temperature and energy (carrier concentration) dependency of carrier mobility. The temperature dependence of some common scattering mechanisms such as acoustic phonon (AP), ionized impurity (II), alloy (AL), and grain boundaries (GB) are as follows:

${\mu }_{AP}\propto T^{-3/2}{\eta }^{-1/2}(6)$

${\mu }_{II}\propto T^{3/2}{\eta }^{3/2}(7)$

${\mu }_{AL}\propto T^{-1/2}{\eta }^{-1/2}(8)$

${\mu }_{GB}\propto T^{-\frac{1}{2}}\exp \left(-C{T}^{-1}\right)(9)$

In fact, grain boundary scattering recently gained popularity among TE communities, driven by rigorous work from Kuo et al., who propose that in a system with mixed acoustic phonon and ionized impurities scattering, Matthiessen's rule does not adequately reconcile with the sharp transition in temperature dependence between these two scattering mechanisms [83]. This is later verified in NbFeSb system too [84]. The importance of taking grain boundaries into account can also affect the conclusion of other physical mechanisms, as illustrated in Figure 3. Figure 3A shows the lower peak power factor in polycrystalline materials where grain boundaries effects are considered (dashed lines) as compared with single crystals (solid line). Figure 3B shows the effect on weighted mobility vs. temperature, showing acoustic phonon-dominated behavior in single crystals (red curve) and gradually shifting to mixed scattering with increasing grain boundaries (dark green curve). Furthermore, overestimation of lattice thermal conductivity has also been reported when grain boundaries were not taken into account [85].

FIGURE 3

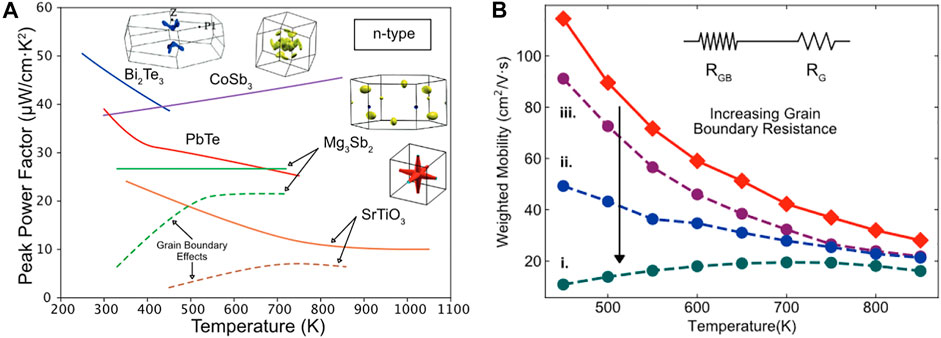
FIGURE 3. (A) The modelled peak power factor for different thermoelectric materials showing higher values when grain boundary resistance is not considered (solid lines) compared with when they are considered (dashed lines). (B) Influence of grain boundaries on weighted mobility vs. temperature trend. Smaller grain (more grain boundaries) lowers the low temperature weighted mobility. Figure reproduced with permission from [86]. Copyright Wiley 2019.

Summary and Outlook

In summary, although the existing physical understanding of the electronic properties of TEs is quite comprehensive, caution must still be taken when trying to draw conclusions from analyzing these properties. For instance, although it sounds trivial, the consideration of grain boundaries electrical resistance may lead to over/underestimation of lattice thermal conductivity and wrong conclusions about the predominant scattering mechanisms in a material. This is especially prevalent in polycrystalline materials, where grain boundaries are present in abundance.

Moving forward, this importance of grain boundaries can be a useful guide towards materials performance optimization especially in 3D-printed TEs, which has been gaining traction recently. By designing printing parameters to optimize the grain boundaries, there is much more performance that can be gained from 3D-printed TEs for power harvesting and cooling applications.

Author Contributions

WL wrote the paper. DZ helped with writing and literature review. SD helped with writing and literature review. XT helped with writing and literature review. CT helped with writing and literature review. JX helped with writing and literature review. AS supervised the writing and gave technical advice.

Funding

This research is supported by a funding from A*STAR “Brain-inspired Vision Sensors”: C210112022.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hamid Elsheikh M, Shnawah DA, Sabri MFM, Said SBM, Haji Hassan M, Ali Bashir MB, et al. A Review on Thermoelectric Renewable Energy: Principle Parameters that Affect Their Performance. Renew Sustain Energ Rev (2014) 30:337–55. doi:10.1016/j.rser.2013.10.027

CrossRef Full Text | Google Scholar

2. Ul Haq B, Ahmed R, AlFaify S, Butt FK, Shaari A, Laref A. Exploring Thermoelectric Materials for Renewable Energy Applications: The Case of Highly Mismatched Alloys Based on AlBi1-xSbx and InBi1-xSbx. Intermetallics (2018) 93:235–43. doi:10.1016/j.intermet.2017.09.017

CrossRef Full Text | Google Scholar

3. Suwardi A, Lim SH, Zheng Y, Wang X, Chien SW, Tan XY, et al. Effective Enhancement of Thermoelectric and Mechanical Properties of Germanium telluride via Rhenium-Doping. J Mater Chem C (2020) 8(47):16940–8. doi:10.1039/d0tc04903d

CrossRef Full Text | Google Scholar

4. Suwardi A, Bash D, Ng HK, Gomez JR, Repaka DVM, Kumar P, et al. Inertial Effective Mass as an Effective Descriptor for Thermoelectrics via Data-Driven Evaluation. J Mater Chem A (2019) 7(41):23762–9. doi:10.1039/c9ta05967a

CrossRef Full Text | Google Scholar

5. Tan LP, Sun T, Fan S, Ng LY, Suwardi A, Yan Q, et al. Facile Synthesis of Cu7Te4 Nanorods and the Enhanced Thermoelectric Properties of Cu7Te4-Bi0.4Sb1.6Te3 Nanocomposites. Nano Energy (2013) 2(1):4–11. doi:10.1016/j.nanoen.2012.07.004

CrossRef Full Text | Google Scholar

6. Zhu Q, Wang S, Wang X, Suwardi A, Chua MH, Soo XYD, et al. Bottom-Up Engineering Strategies for High-Performance Thermoelectric Materials. Nano-micro Lett (2021) 13(1):119. doi:10.1007/s40820-021-00637-z

CrossRef Full Text | Google Scholar

7. Zheng Y, Slade TJ, Hu L, Tan XY, Luo Y, Luo Z-Z, et al. Defect Engineering in Thermoelectric Materials: what Have We Learned?. Chem Soc Rev (2021) 50(16):9022–54. doi:10.1039/d1cs00347j

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhao Y, Zheng M, Wu J, Guan X, Suwardi A, Li Y, et al. Modification of thermal Transport in Few-Layer MoS2 by Atomic-Level Defect Engineering. Nanoscale (2021) 13(26):11561–7. doi:10.1039/d1nr01832a

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Yang J, Caillat T. Thermoelectric Materials for Space and Automotive Power Generation. MRS Bull (2006) 31(3):224–9. doi:10.1557/mrs2006.49

CrossRef Full Text | Google Scholar

10. LeBlanc S. Thermoelectric Generators: Linking Material Properties and Systems Engineering for Waste Heat Recovery Applications. Sustain Mater Tech (2014) 1-2:26–35. doi:10.1016/j.susmat.2014.11.002

CrossRef Full Text | Google Scholar

11. Qin F, Nikolaev SA, Suwardi A, Wood M, Zhu Y, Tan X, et al. Crystal Structure and Atomic Vacancy Optimized Thermoelectric Properties in Gadolinium Selenides. Chem Mater (2020) 32(23):10130–9. doi:10.1021/acs.chemmater.0c03581

CrossRef Full Text | Google Scholar

12. Jia N, Cao J, Tan XY, Zheng J, Chien SW, Yang L, et al. Suppressing Ge-Vacancies to Achieve High Single-Leg Efficiency in GeTe with an Ultra-high Room Temperature Power Factor. J Mater Chem A (2021) 9(41):23335–44. doi:10.1039/d1ta05866e

CrossRef Full Text | Google Scholar

13. Jia N, Cao J, Tan XY, Dong J, Liu H, Tan CKI, et al. Thermoelectric Materials and Transport Physics. Mater Today Phys (2021) 21:100519. doi:10.1016/j.mtphys.2021.100519

CrossRef Full Text | Google Scholar

14. Bourgès C, Srinivasan B, Fontaine B, Sauerschnig P, Minard A, Halet J-F, et al. Tailoring the Thermoelectric and Structural Properties of Cu-Sn Based Thiospinel Compounds [CuM1+xSn1−xS4 (M = Ti, V, Cr, Co)]. J Mater Chem C (2020) 8(46):16368–83. doi:10.1039/d0tc04393a

CrossRef Full Text | Google Scholar

15. Virtudazo RVR, Srinivasan B, Guo Q, Wu R, Takei T, Shimasaki Y, et al. Improvement in the Thermoelectric Properties of Porous Networked Al-Doped ZnO Nanostructured Materials Synthesized via an Alternative Interfacial Reaction and Low-Pressure SPS Processing. Inorg Chem Front (2020) 7(21):4118–32. doi:10.1039/d0qi00888e

CrossRef Full Text | Google Scholar

16. Srinivasan B, Cui S, Prestipino C, Gellé A, Boussard-Pledel C, Ababou-Girard S, et al. Possible Mechanism for Hole Conductivity in Cu-As-Te Thermoelectric Glasses: A XANES and EXAFS Study. J Phys Chem C (2017) 121(26):14045–50. doi:10.1021/acs.jpcc.7b04555

CrossRef Full Text | Google Scholar

17. Hong S, Gu Y, Seo JK, Wang J, Liu P, Meng YS, et al. Wearable Thermoelectrics for Personalized Thermoregulation. Sci Adv (2019) 5(5):eaaw0536. doi:10.1126/sciadv.aaw0536

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhang Q, Liao J, Tang Y, Gu M, Ming C, Qiu P, et al. Realizing a Thermoelectric Conversion Efficiency of 12% in Bismuth telluride/skutterudite Segmented Modules through Full-Parameter Optimization and Energy-Loss Minimized Integration. Energ Environ Sci (2017) 10(4):956–63.

Google Scholar

19. Recatala-Gomez J, Kumar P, Suwardi A, Abutaha A, Nandhakumar I, Hippalgaonkar K. Direct Measurement of the Thermoelectric Properties of Electrochemically Deposited Bi2Te3 Thin Films. Sci Rep (2020) 10(1):17922–10. doi:10.1038/s41598-020-74887-z

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hu L, Luo Y, Fang YW, Qin F, Cao X, Xie H, et al. High Thermoelectric Performance through Crystal Symmetry Enhancement in Triply Doped Diamondoid Compound Cu 2 SnSe 3. Adv Energ Mater. (2021) 2100661. doi:10.1002/aenm.202100661

CrossRef Full Text | Google Scholar

21. Hu L, Fang Y-W, Qin F, Cao X, Zhao X, Luo Y, et al. High Thermoelectric Performance Enabled by Convergence of Nested Conduction Bands in Pb7Bi4Se13 with Low thermal Conductivity. Nat Commun (2021) 12(1):4793. doi:10.1038/s41467-021-25119-z

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hong M, Zheng K, Lyv W, Li M, Qu X, Sun Q, et al. Computer-aided Design of High-Efficiency GeTe-Based Thermoelectric Devices. Energy Environ. Sci. (2020) 13(6):1856–64. doi:10.1039/d0ee01004a

CrossRef Full Text | Google Scholar

23. Dresselhaus MS, Chen G, Tang MY, Yang RG, Lee H, Wang DZ, et al. New Directions for Low-Dimensional Thermoelectric Materials. Adv Mater (2007) 19(8):1043–53. doi:10.1002/adma.200600527

CrossRef Full Text | Google Scholar

24. Cutler M, Mott NF. Observation of Anderson Localization in an Electron Gas. Phys Rev (1969) 181(3):1336–40. doi:10.1103/physrev.181.1336

CrossRef Full Text | Google Scholar

25. Wei S-H. Overcoming the Doping Bottleneck in Semiconductors. Comput Mater Sci (2004) 30(3):337–48. doi:10.1016/j.commatsci.2004.02.024

CrossRef Full Text | Google Scholar

26. Vavro J, Llaguno MC, Fischer JE, Ramesh S, Saini RK, Ericson LM, et al. Thermoelectric Power of P-Doped Single-wall Carbon Nanotubes and the Role of Phonon Drag. Phys Rev Lett (2003) 90(6):065503. doi:10.1103/PhysRevLett.90.065503

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhou J, Liao B, Qiu B, Huberman S, Esfarjani K, Dresselhaus MS, et al. Ab Initio optimization of Phonon Drag Effect for Lower-Temperature Thermoelectric Energy Conversion. Proc Natl Acad Sci USA (2015) 112(48):14777–82. doi:10.1073/pnas.1512328112

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hicks LD, Dresselhaus MS. Effect of Quantum-Well Structures on the Thermoelectric Figure of merit. Phys Rev B (1993) 47(19):12727–31. doi:10.1103/physrevb.47.12727

CrossRef Full Text | Google Scholar

29. Hicks LD, Dresselhaus MS. Thermoelectric Figure of merit of a One-Dimensional Conductor. Phys Rev B (1993) 47(24):16631–4. doi:10.1103/physrevb.47.16631

CrossRef Full Text | Google Scholar

30. Mao J, Liu Z, Ren Z. Size Effect in Thermoelectric Materials. Npj Quant Mater (2016) 1(1):16028. doi:10.1038/npjquantmats.2016.28

CrossRef Full Text | Google Scholar

31. Fu C, Zhu T, Pei Y, Xie H, Wang H, Snyder GJ, et al. High Band Degeneracy Contributes to High Thermoelectric Performance in P-type Half-Heusler Compounds. Adv Energ Mater. (2014) 4(18):1400600. doi:10.1002/aenm.201400600

CrossRef Full Text | Google Scholar

32. Srinivasan B, Fontaine B, Gucci F, Dorcet V, Saunders TG, Yu M, et al. Effect of the Processing Route on the Thermoelectric Performance of Nanostructured CuPb18SbTe20. Inorg Chem (2018) 57(20):12976–86. doi:10.1021/acs.inorgchem.8b02248

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Pei Y, Shi X, LaLonde A, Wang H, Chen L, Snyder GJ. Convergence of Electronic Bands for High Performance Bulk Thermoelectrics. Nature (2011) 473(7345):66–9. doi:10.1038/nature09996

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zhao LD, Wu HJ, Hao SQ, Wu CI, Zhou XY, Biswas K, et al. All-scale Hierarchical Thermoelectrics: MgTe in PbTe Facilitates Valence Band Convergence and Suppresses Bipolar thermal Transport for High Performance. Energ Environ. Sci. (2013) 6(11):3346–55. doi:10.1039/c3ee42187b

CrossRef Full Text | Google Scholar

35. Pei Y, Wang H, Gibbs ZM, LaLonde AD, Snyder GJ. Thermopower Enhancement in Pb1−xMnxTe Alloys and its Effect on Thermoelectric Efficiency. NPG Asia Mater (2012) 4(9):e28. doi:10.1038/am.2012.52

CrossRef Full Text | Google Scholar

36. Zeier WG, Zevalkink A, Gibbs ZM, Hautier G, Kanatzidis MG, Snyder GJ. Thinking like a Chemist: Intuition in Thermoelectric Materials. Angew Chem Int Ed (2016) 55(24):6826–41. doi:10.1002/anie.201508381

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Pei Y, LaLonde AD, Heinz NA, Shi X, Iwanaga S, Wang H, et al. Stabilizing the Optimal Carrier Concentration for High Thermoelectric Efficiency. Adv Mater (2011) 23(47):5674–8. doi:10.1002/adma.201103153

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Biswas K, He J, Wang G, Lo S-H, Uher C, Dravid VP, et al. High Thermoelectric Figure of merit in Nanostructured P-type PbTe-MTe (M = Ca, Ba). Energ Environ. Sci. (2011) 4(11):4675–84. doi:10.1039/c1ee02297k

CrossRef Full Text | Google Scholar

39. Pei Y, LaLonde AD, Heinz NA, Snyder GJ. High Thermoelectric Figure of Merit in PbTe Alloys Demonstrated in PbTe-CdTe. Adv Energ Mater. (2012) 2(6):670–5. doi:10.1002/aenm.201100770

CrossRef Full Text | Google Scholar

40. Al Rahal Al Orabi R, Mecholsky NA, Hwang J, Kim W, Rhyee J-S, Wee D, et al. Band Degeneracy, Low Thermal Conductivity, and High Thermoelectric Figure of Merit in SnTe-CaTe Alloys. Chem Mater (2016) 28(1):376–84. doi:10.1021/acs.chemmater.5b04365

CrossRef Full Text | Google Scholar

41. He J, Xu J, Liu G-Q, Shao H, Tan X, Liu Z, et al. Enhanced Thermopower in Rock-Salt SnTe-CdTe from Band Convergence. RSC Adv (2016) 6(38):32189–92. doi:10.1039/c6ra02658c

CrossRef Full Text | Google Scholar

42. Bhat DK, Shenoy US. Zn: a Versatile Resonant Dopant for SnTe Thermoelectrics. Mater Today Phys (2019) 11:100158. doi:10.1016/j.mtphys.2019.100158

CrossRef Full Text | Google Scholar

43. Srinivasan B, Gellé A, Gucci F, Boussard-Pledel C, Fontaine B, Gautier R, et al. Realizing a Stable High Thermoelectric zT ∼ 2 over a Broad Temperature Range in Ge1−x−yGaxSbyTe via Band Engineering and Hybrid Flash-SPS Processing. Inorg Chem Front (2019) 6(1):63–73. doi:10.1039/c8qi00703a

CrossRef Full Text | Google Scholar

44. Muchtar AR, Srinivasan B, Tonquesse SL, Singh S, Soelami N, Yuliarto B, et al. Physical Insights on the Lattice Softening Driven Mid‐Temperature Range Thermoelectrics of Ti/Zr‐Inserted SnTe-An Outlook beyond the Horizons of Conventional Phonon Scattering and Excavation of Heikes' Equation for Estimating Carrier Properties. Adv Energ Mater. (2021) 11:2101122. doi:10.1002/aenm.202101122

CrossRef Full Text | Google Scholar

45. Tan X, Wang H, Liu G, Noudem JG, Hu H, Xu J, et al. Designing Band Engineering for Thermoelectrics Starting from the Periodic Table of Elements. Mater Today Phys (2018) 7:35–44. doi:10.1016/j.mtphys.2018.10.004

CrossRef Full Text | Google Scholar

46. Suwardi A, Cao J, Hu L, Wei F, Wu J, Zhao Y, et al. Tailoring the Phase Transition Temperature to Achieve High-Performance Cubic GeTe-Based Thermoelectrics. J Mater Chem A (2020) 8(36):18880–90. doi:10.1039/d0ta06013e

CrossRef Full Text | Google Scholar

47. Jin Y, Xiao Y, Wang D, Huang Z, Qiu Y, Zhao L-D. Realizing High Thermoelectric Performance in GeTe through Optimizing Ge Vacancies and Manipulating Ge Precipitates. ACS Appl Energ Mater. (2019) 2(10):7594–601. doi:10.1021/acsaem.9b01585

CrossRef Full Text | Google Scholar

48. Liu WD, Wang DZ, Liu Q, Zhou W, Shao Z, Chen Z-G. High‐Performance GeTe‐Based Thermoelectrics: From Materials to Devices. Adv. Energy Mater. (2020) 10(19):2000367.

CrossRef Full Text | Google Scholar

49. Li P, Ding T, Li J, Zhang C, Dou Y, Li Y, et al. Positive Effect of Ge Vacancies on Facilitating Band Convergence and Suppressing Bipolar Transport in GeTe‐Based Alloys for High Thermoelectric Performance. Adv Funct Mater (2020) 30(15):1910059. doi:10.1002/adfm.201910059

CrossRef Full Text | Google Scholar

50. Suwardi A, Bash D, Ng HK, Gomez JR, Repaka DVM, Kumar P, et al. Inertial Effective Mass as an Effective Descriptor for Thermoelectrics via Data-Driven Evaluation. J Mater Chem A (2019) 7(41):23762–9. doi:10.1039/c9ta05967a

CrossRef Full Text | Google Scholar

51. Tsai YF, Wei PC, Chang L, Wang KK, Yang CC, Lai YC, et al. Compositional Fluctuations Locked by Athermal Transformation Yielding High Thermoelectric Performance in GeTe. Adv Mater (2021) 33(1):2005612. doi:10.1002/adma.202005612

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Xing T, Zhu C, Song Q, Huang H, Xiao J, Ren D, et al. Ultralow Lattice Thermal Conductivity and Superhigh Thermoelectric Figure‐of‐Merit in (Mg, Bi) Co‐Doped GeTe. Adv Mater (2021) 33(17):2008773. doi:10.1002/adma.202008773

CrossRef Full Text | Google Scholar

53. Cao J, Chien SW, Tan XY, Tan CKI, Zhu Q, Wu J, et al. Realizing zT Values of 2.0 in Cubic GeTe. ChemNanoMat (2021) 7(4):476–82. doi:10.1002/cnma.202100033

CrossRef Full Text | Google Scholar

54. Srinivasan B, Berthebaud D, Mori T. Is Lii a Potential Dopant Candidate to Enhance the Thermoelectric Performance in Sb-free Gete Systems? A Prelusive Study. Energies (2020) 13(3):643. doi:10.3390/en13030643

CrossRef Full Text | Google Scholar

55. Xing T, Song Q, Qiu P, Zhang Q, Gu M, Xia X, et al. High Efficiency GeTe-Based Materials and Modules for Thermoelectric Power Generation. Energ Environ. Sci. (2021) 14(2):995–1003. doi:10.1039/d0ee02791j

CrossRef Full Text | Google Scholar

56. Dong J, Sun F-H, Tang H, Pei J, Zhuang H-L, Hu H-H, et al. Medium-temperature Thermoelectric GeTe: Vacancy Suppression and Band Structure Engineering Leading to High Performance. Energ Environ. Sci. (2019) 12(4):1396–403. doi:10.1039/c9ee00317g

CrossRef Full Text | Google Scholar

57. Hong M, Zheng K, Lyv W, Li M, Qu X, Sun Q, et al. Computer-aided Design of High-Efficiency GeTe-Based Thermoelectric Devices. Energ Environ. Sci. (2020) 13(6):1856–64. doi:10.1039/d0ee01004a

CrossRef Full Text | Google Scholar

58. Li J, Zhang X, Chen Z, Lin S, Li W, Shen J, et al. Low-Symmetry Rhombohedral GeTe Thermoelectrics. Joule (2018) 2(5):976–87. doi:10.1016/j.joule.2018.02.016

CrossRef Full Text | Google Scholar

59. Perumal S, Samanta M, Ghosh T, Shenoy US, Bohra AK, Bhattacharya S, et al. Realization of High Thermoelectric Figure of Merit in GeTe by Complementary Co-doping of Bi and in. Joule (2019) 3(10):2565–80. doi:10.1016/j.joule.2019.08.017

CrossRef Full Text | Google Scholar

60. Zhang X, Bu Z, Lin S, Chen Z, Li W, Pei Y. GeTe Thermoelectrics. Joule (2020) 4(5):986–1003. doi:10.1016/j.joule.2020.03.004

CrossRef Full Text | Google Scholar

61. Bayikadi KS, Wu CT, Chen L-C, Chen K-H, Chou F-C, Sankar R. Synergistic Optimization of Thermoelectric Performance of Sb Doped GeTe with a Strained Domain and Domain Boundaries. J Mater Chem A (2020) 8(10):5332–41. doi:10.1039/d0ta00628a

CrossRef Full Text | Google Scholar

62. Feng Y, Li J, Li Y, Ding T, Zhang C, Hu L, et al. Band Convergence and Carrier-Density fine-tuning as the Electronic Origin of High-Average Thermoelectric Performance in Pb-Doped GeTe-Based Alloys. J Mater Chem A (2020) 8(22):11370–80. doi:10.1039/d0ta02758h

CrossRef Full Text | Google Scholar

63. Nshimyimana E, Hao S, Su X, Zhang C, Liu W, Yan Y, et al. Discordant Nature of Cd in GeTe Enhances Phonon Scattering and Improves Band Convergence for High Thermoelectric Performance. J Mater Chem A (2020) 8(3):1193–204. doi:10.1039/c9ta10436d

CrossRef Full Text | Google Scholar

64. Qiu Y, Jin Y, Wang D, Guan M, He W, Peng S, et al. Realizing High Thermoelectric Performance in GeTe through Decreasing the Phase Transition Temperature via Entropy Engineering. J Mater Chem A (2019) 7(46):26393–401. doi:10.1039/c9ta10963c

CrossRef Full Text | Google Scholar

65. Srinivasan B, Le Tonquesse S, Gellé A, Bourgès C, Monier L, Ohkubo I, et al. Screening of Transition (Y, Zr, Hf, V, Nb, Mo, and Ru) and Rare-Earth (La and Pr) Elements as Potential Effective Dopants for Thermoelectric GeTe - an Experimental and Theoretical Appraisal. J Mater Chem A (2020) 8(38):19805–21. doi:10.1039/d0ta06710e

CrossRef Full Text | Google Scholar

66. Wang L, Li J, Zhang C, Ding T, Xie Y, Li Y, et al. Discovery of Low-Temperature GeTe-Based Thermoelectric Alloys with High Performance Competing with Bi2Te3. J Mater Chem A (2020) 8(4):1660–7. doi:10.1039/c9ta11901a

CrossRef Full Text | Google Scholar

67. Samanta M, Ghosh T, Arora R, Waghmare UV, Biswas K. Realization of Both N- and P-type GeTe Thermoelectrics: Electronic Structure Modulation by AgBiSe2 Alloying. J Am Chem Soc (2019) 141(49):19505–12. doi:10.1021/jacs.9b11405

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Shuai J, Tan XJ, Guo Q, Xu JT, Gellé A, Gautier R, et al. Enhanced Thermoelectric Performance through crystal Field Engineering in Transition Metal-Doped GeTe. Mater Today Phys (2019) 9:100094. doi:10.1016/j.mtphys.2019.100094

CrossRef Full Text | Google Scholar

69. Li M, Hong M, Tang X, Sun Q, Lyu W-Y, Xu S-D, et al. Crystal Symmetry Induced Structure and Bonding Manipulation Boosting Thermoelectric Performance of GeTe. Nano Energy (2020) 73:104740. doi:10.1016/j.nanoen.2020.104740

CrossRef Full Text | Google Scholar

70. Xing T, Song Q, Qiu P, Zhang Q, Xia X, Liao J, et al. Superior Performance and High Service Stability for GeTe-Based Thermoelectric Compounds. Natl Sci Rev (2019) 6(5):944–54. doi:10.1093/nsr/nwz052

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Bu Z, Zhang X, Shan B, Tang J, Liu H, Chen Z, et al. Realizing a 14% Single-Leg Thermoelectric Efficiency in GeTe Alloys. Sci Adv (2021) 7(19):eabf2738. doi:10.1126/sciadv.abf2738

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Shuai J, Sun Y, Tan X, Mori T. Manipulating the Ge Vacancies and Ge Precipitates through Cr Doping for Realizing the High‐Performance GeTe Thermoelectric Material. Small (2020) 16(13):1906921. doi:10.1002/smll.201906921

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Suwardi A, Hu L, Wang X, Tan XY, Repaka DVM, Wong L-M, et al. Origin of High Thermoelectric Performance in Earth-Abundant Phosphide-Tetrahedrite. ACS Appl Mater Inter (2020) 12(8):9150–7. doi:10.1021/acsami.9b17269

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Yang F, Wu J, Suwardi A, Zhao Y, Liang B, Jiang J, et al. Gate‐Tunable Polar Optical Phonon to Piezoelectric Scattering in Few‐Layer Bi 2 O 2 Se for High‐Performance Thermoelectrics. Adv Mater (2021) 33(4):2004786. doi:10.1002/adma.202004786

CrossRef Full Text | Google Scholar

75. Suwardi A, Lim SH, Zheng Y, Wang X, Chien SW, Tan XY, et al. Effective Enhancement of Thermoelectric and Mechanical Properties of Germanium telluride via Rhenium-Doping. J Mater Chem C (2020) 8(47):16940–8. doi:10.1039/d0tc04903d

CrossRef Full Text | Google Scholar

76. Wang X, Suwardi A, Lim SL, Wei F, Xu J. Transparent Flexible Thin-Film P–N junction Thermoelectric Module. Npj Flexible Electron (2020) 4(1):1–9. doi:10.1038/s41528-020-00082-9

CrossRef Full Text | Google Scholar

77. Dinh KN, Sun Y, Pei Z, Yuan Z, Suwardi A, Huang Q, et al. Electronic Modulation of Nickel Disulfide toward Efficient Water Electrolysis. Small (2020) 16(17):1905885. doi:10.1002/smll.201905885

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Suwardi A, Prasad B, Lee S, Choi E-M, Lu P, Zhang W, et al. Turning Antiferromagnetic Sm0.34Sr0.66MnO3 into a 140 K Ferromagnet Using a Nanocomposite Strain Tuning Approach. Nanoscale (2016) 8(15):8083–90. doi:10.1039/c6nr01037g

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Heremans JP, Jovovic V, Toberer ES, Saramat A, Kurosaki K, Charoenphakdee A, et al. Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science (2008) 321(5888):554–7. doi:10.1126/science.1159725

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Narducci D, Selezneva E, Cerofolini G, Frabboni S, Ottaviani G. Impact of Energy Filtering and Carrier Localization on the Thermoelectric Properties of Granular Semiconductors. J Solid State Chem (2012) 193:19–25. doi:10.1016/j.jssc.2012.03.032

CrossRef Full Text | Google Scholar

81. Xie H, Su X, Bailey TP, Zhang C, Liu W, Uher C, et al. Anomalously Large Seebeck Coefficient of CuFeS2 Derives from Large Asymmetry in the Energy Dependence of Carrier Relaxation Time. Chem Mater (2020) 32(6):2639–46. doi:10.1021/acs.chemmater.0c00388

CrossRef Full Text | Google Scholar

82. Xiao Y, Zhao L-D. Charge and Phonon Transport in PbTe-Based Thermoelectric Materials. Npj Quant Mater (2018) 3(1):55. doi:10.1038/s41535-018-0127-y

CrossRef Full Text | Google Scholar

83. Kuo JJ, Kang SD, Imasato K, Tamaki H, Ohno S, Kanno T, et al. Grain Boundary Dominated Charge Transport in Mg3Sb2-Based Compounds. Energ Environ. Sci. (2018) 11(2):429–34. doi:10.1039/c7ee03326e

CrossRef Full Text | Google Scholar

84. Shen J, Fan L, Hu C, Zhu T, Xin J, Fu T, et al. Enhanced Thermoelectric Performance in the N-type NbFeSb Half-Heusler Compound with Heavy Element Ir Doping. Mater Today Phys (2019) 8:62–70. doi:10.1016/j.mtphys.2019.01.004

CrossRef Full Text | Google Scholar

85. Kuo JJ, Wood M, Slade TJ, Kanatzidis MG, Snyder GJ. Systematic Over-estimation of Lattice thermal Conductivity in Materials with Electrically-Resistive Grain Boundaries. Energ Environ. Sci. (2020) 13(4):1250–8. doi:10.1039/c9ee03921j

CrossRef Full Text | Google Scholar

86. Dylla MT, Kuo JJ, Witting I, Snyder GJ. Grain Boundary Engineering Nanostructured SrTiO 3 for Thermoelectric Applications. Adv Mater Inter (2019) 6(15):1900222. doi:10.1002/admi.201900222

CrossRef Full Text | Google Scholar