
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 12 January 2022
Sec. Biophysics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.750539
This article is part of the Research TopicStructure, Function and Dynamics of BiomembranesView all 10 articles
 Mohammad Arif Kamal1,2†
Mohammad Arif Kamal1,2† Josip Augustin Janeš3,4†
Josip Augustin Janeš3,4† Long Li4,5
Long Li4,5 Franck Thibaudau1
Franck Thibaudau1 Ana-Sunčana Smith3,4*
Ana-Sunčana Smith3,4* Kheya Sengupta1*
Kheya Sengupta1*Tremendous progress has been made recently in imaging the contacts between intra-cellular organelles, which are thought to be mediated by soluble tethers. However, they are still difficult to study in cellulo, and reconstituting them in vitro is a standing challenge. Here we take a mimetic approach to study Giant unilamellar vesicles (GUVs) and supported lipid bilayers (SLBs) interacting via single- (or double-) stranded DNA sequences of two different lengths. Like intra-cellular tethers which may reside in the cytosol when unbound, the DNA-tethers are soluble, but can insert into the membrane with the help of cholesterol moieties found at their extremities. Tether-exchange between the bulk “cytosol” and the GUV/SLB membrane leads to a novel statistical ensemble in which the entire system equilibrates together, rather than individual GUVs behaving as separate closed systems. As a consequence, adhesion between the GUV and the SLB is driven by collective entropic effects amplified by tether shape changes associated with membrane bridging. A direct experimental consequence is an unusual dependence on tether-concentration, which becomes an important control parameter at low concentrations, while tether length/flexibility are less important. The establishment of this fundamentally different interaction between two membranes suggests that in physiological conditions, the regulation of contact formation inside cells may be very different from the case of the much studied ligand-receptor mediated cell adhesion.
The correct organization of organelles, essential for the coherent functioning of eukaryotic cells, is maintained via specialized patches called organelle-contacts [1]. While early electron microscopy images revealed the existence of these patches, their dynamical nature, molecular machinery and function is only beginning to be explored [1–6]. These contacts not only provide structural scaffolding but also act as important sites of inter-organelle communication, exchanging proteins, small molecules, and lipids across the organelle membranes [7]. It is increasingly clear that these structurally-confined contacts between membranes are mediated by anchoring molecules, somewhat reminiscent of cell surface ligand-receptor binding that mediates cell adhesion. In analogy with adhesion receptors that are sometimes called “linkers”, the proteins that span the inter-organelle gap and physically keep two organelles together are termed “tethers”. Many, possibly all, organelles communicate by means of such inter-organellar tethering [1, 7]. In spite of recent progress, very little is known about the nature of the contact sites and the molecules that mediate their formation. Two broad groups of tethers have been identified, with very different length and flexibility [8]. Some of these tethers reside on the membrane, whereas some others are soluble cytosolic molecules that are recruited to the membranes dynamically. Many are expected to undergo major conformation changes upon tethering.
Purification of intra-cellular tethers remains extremely challenging, not least because very little is known about them. Attachment of trafficking endo- and exocytotic vesicles to the ER and Golgi are special cases of inter-organellar contacts, which has been better studied. The focus however, has been on fusion and fission of the membrane [8–11]. To avoid the bottleneck created by protein purification challenges, artificial proteins, macromolecules or even nucleic acids have been used to mimic tethers and anchors, lipid-grafted DNA tethers used as mimic of the SNARE complex being an early example [12, 13]. Simple synthesis and variability of design make DNA tethers particularly attractive artificial tethers. Besides the capacity to tune the binding by adjusting the length of the sequence used for sense/antisense recognition, their design allows for the systematic modifications of length and flexibility [12]. In addition to being used for tethering [12, 13], DNA constructs were also extensively used as glycocalyx-mimetic spacers [14–16]. More recently, they have been used as force sensors in hybrid cell-surface systems [17, 18]. DNA-tethers have in fact been used in a plethora of situations including building foam-like structures [19], self-assembly of soft Brownian objects [20], or for exploring thermal control of particle-assemblies [21].
While molecular details are definitely required to get a complete understanding of function, consideration of general thermodynamic and geometric arguments can already help us predict the possibilities of a system, without need of specific chemical details. In the past, such a generic approach has elucidated a number of physical determinants of membrane anchoring [22–25]. Particular success was achieved using the paradigm of adhesion between giant unilammelar vesicles (GUVs) and solid supported lipid bilayers (SLBs) [25, 26]. Early work focused on adhesion mediated by strong generic forces or strong and numerous bonds, which is controlled by the area and volume geometrical constraints [27], the vesicle typically spreading to its full extent, using up all extra membrane area that may have become available in the process of volume reduction during equilibration of osmotic pressures of inner and outer vesicle solutions, thus forming the largest possible contact zone [28]. In this limit of strong adhesion, entropic contributions can typically be ignored and a Young-Dupre like equation can be written with the caveat that unlike a droplet, the real contact-angle cannot be defined due to the finite bending modulus of the membrane. An effective contact angle may however be defined and used to measure the adhesion energy, taking into account the tension and the bending costs [27, 29–31]. A very convenient method, that uses the unique capability of RICM to reconstitute the membrane shape with nanometer precision close to the adhesive surface, was proposed which takes advantage of the separation of scales between the global and local deformation and thus allows for simultaneous calculation of tension and adhesion energy from the vesicle shape for relatively weakly adhering GUVs [32–34].
Expanding on this body of work, later contributions revealed more subtle effects like positional entropy of the binders [24], the presence of repelers [35], jamming related size effects [36], and relative tether lengths in a dual-binder system [37]. Two striking examples of such an approach, where prediction from model system was vindicated in a cellular system, include the predictions about the role of glycocalyx [34, 35, 38] that was later shown to be relevant for cancer cells [39], and the possible role of the plasma membrane in mechanotransduction [40], that is now accepted as a probable candidate in sensing by immune cells [41].
Here we use such a GUV/SLB adhesion paradigm to explore organelle contact formation. The fundamental difference is that in case of cell adhesion, the binders reside on the interacting membranes and the global concentration of binders on a given membrane is not expected to change in the time-scale of interest. In case of organelle binding however, the tethers may be soluble and may transfer from the cytosol to the membrane, thus fundamentally changing the physical paradigm in terms of the statistical ensemble that must be used to calculate the free energy. Experimentally, we take advantage of DNA technology to design mimics of inter-organellar tethers that generate contact between two synthetic membranes of a GUV/SLB system. We use single-stranded DNA (ss-DNA) or double-stranded DNA (ds-DNA) tethers, of two different lengths, to bridge the membranes and create stable contact patches. In each case, the DNA-tether can insert into a membrane, and can bind a self-similar DNA-tether via a sticky-end. The tethers dimerize via their sticky-ends, and may exist in three possible states - in solution (as monomers or dimers), in cis-configuration where both tethers are anchored on the same membrane forming a “U”-shape, and in trans-configuration where the tether bridges the SLB and the GUV forming an “I”-shape. The latter creates intermembrane contacts or adhesion. The combination of solubility and configuration change leads to a novel adhesion mechanism that is not based on the single-tether sense/antisense recognition affinity, but on the interplay between the soluble pool and the cis/trans configurations with different geometries.
1–stearoyl–2–oleoyl–sn–glycero–3–phosphocholine (SOPC), 1,2–distearoyl–sn–glycero–3–phospho ethanolamine–N–[amino (polyethylene glycol)–2000] (DSPE—PEG 2000), head-labeled 1,2–dioleoyl–sn–glycero–3–phosphoethanolamine–N–[7–nitro–2–1,3–benzoxadiazol–4–yl] (NBD–PE), chain-labeled 1-oleoyl-2-6-[(7-nitro-2-1,3-benzoxadiazol-4-yl)amino]hexanoyl-sn-glycero-3-phosphocholine (NBD-PC) and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (RhodamineB) were purchased from Avanti Polar Lipids (Alabaster, AL) and used without further purification. Dextrose (Glucose), BioXtra, ≥ 99.5% (GC) was purchased from Sigma Aldrich, France. The DNA-tethers were short custom-made single-stranded DNA-oligomers from Eurogentech, Belgium. The received lyophilized DNA was dissolved in PBS so as to make 100 μM stock solution and stored at -20C. Prior to use, a working solution of 1 μM was prepared in PBS. For ss-DNA experiments, appropriate amounts of this solution was introduced into the observation chamber containing the SLB immersed in PBS (480 μl), if necessary after further intermediate dilution. For ds-DNA experiments, the ss-DNA strand was first mixed with the complementary backbone strand in approximately 5% excess. The mixture was heated to 60 degC and held at that temperature for about 5 min before allowing the whole to cool down to room temperature. This solution was then introduced into the observation chamber as described above. 20 μL of the GUV solution was introduced into the chamber and the whole was allowed to equilibrate at room temperature for 2 hours before observation.
SLBs were prepared with a film balance (Nima, Coventry, UK) applying the Langmuir-Blodgett Langmuir-Schäfer technique [42]. The subphase was ultrapure water. SLBs consisted of pure SOPC in the proximal layer. The distal layer facing the buffer was formed by SOPC with 2 mol% DSPE-PEG 2000 and 1 mol% NBD-PC (or NBD-PE or RhodamineB). Transfer pressure was set to 20 mN/m. SLBs were constantly kept under water and used directly after preparation. GUVs were prepared using the well established electro-swelling method. Briefly, 10 μL of the lipid mixture (98 mol% SOPC and 2 mol% DSPE-PEG2000) dissolved in chloroform was spread on indium tin oxide coated glass slides (Sigma Aldrich, France). In order to ensure complete evaporation of chloroform the slides were desiccated under vacuum overnight. Two lipid-coated glass slides were mounted in a Teflon chamber filled with 230 mOsmL−1 glucose solution, at a distance of 1 mm. An alternating voltage of 2 V at 10 Hz was applied for 2 h s which resulted in GUVs with an average diameter of around 20–30 μm. For experiments, vesicles were immersed in PBS buffer of 270 mOsmL−1. The difference in osmolarity between the inside and outside solutions resulted in vesicles exhibiting the necessary excess area to build up a contact zone with the substrate. All osmolarities were measured before each experiment with an osmometer (Osmomat 030, Gonotec GmbH, Berlin, Germany). 20–40 μL of the vesicle solution was added into the experimental chamber filled with PBS buffer (volume 1 ml). Vesicles were allowed to sediment and achieve a steady adhesion state before the first measurement. The waiting time on an average was 30 min. Observation chambers were filled completely with PBS and covered with a glass slide to avoid osmolarity changes due to evaporation. For height determination using RICM, the refractive indices of the vesicle solution and the outer buffer were measured for each experiment with an Abbé Refractometer (Kruss, Germany).
For quantification of DNA absorption, images were acquired using a confocal microscope (Leica Microsystems, Germany) fitted with a ×63 oil immersion objective. For all other experiments, images were acquired using an inverted microscope, Zeiss Axiovert 200, equipped with a EM-CCD camera (Andor, Ireland), a filter cube with crossed polarizers and a ×63 Antiflex Plan-Neofluar oil objective (Carl Zeiss, Göttingen,Germany) having a numerical aperture of 1.25. In addition the objective had a built in lambda quarter plate. For reflection interference contrast microscopy (RICM), the green illumination was selected from the light emitted by a metal halogenide lamp (X-Cite, Exfo, Quebec, Canada) using an interference filter (546 ± 12 nm). The numerical aperture of illumination was set to approximately 0.5. Image sequences consisted of 50 consecutive frames with an individual exposure time of 100 ms for each observation set. The adhesion state of GUVs was probed using RICM. Map of membrane-substrate distances from the measured interference patterns were constructed [34]. Briefly, the entire image (the vesicle as well as the background) was first corrected for anomalies arising from an inhomogeneous illumination. Next, the average background intensity (Ibg) in the image was measured and the entire image was normalized with respect to Ibg. Finally, the normalized intensities were used to find the corresponding height by inverting the intensity height relation [34]. For all quantitative evaluation, images were analyzed using self-written routines in IgorPro (Wavemetrix, Portland, OR).
The experimental system is described in Figure 1. The GUV and SLB membrane are decorated with ss- or ds-DNA sequences which are designed as follows. ss-DNA sequences with number of base-pairs N = 28 (short) or N = 40 (long) are first constructed. Out of these N base pairs, 10 base pairs build a sticky end, and the reminder form the backbone attached to a cholesterol moiety via a flexible Tetra Ethylene Glycol (TEG) strand linked to a short single-stranded sequence. Two identical segments are allowed to recombine at the sticky ends to make a strand twice as long with a cholesterol at each end. Consequently we obtain two constructs which we denote as short and long ss-tethers, respectively. To create ds-DNA tethers, the short or long ss-DNA sequences are first incubated with appropriate backbone sequences of 12 or 24 base pairs such that they combine using sense/antisense recognition (Figure 1B).
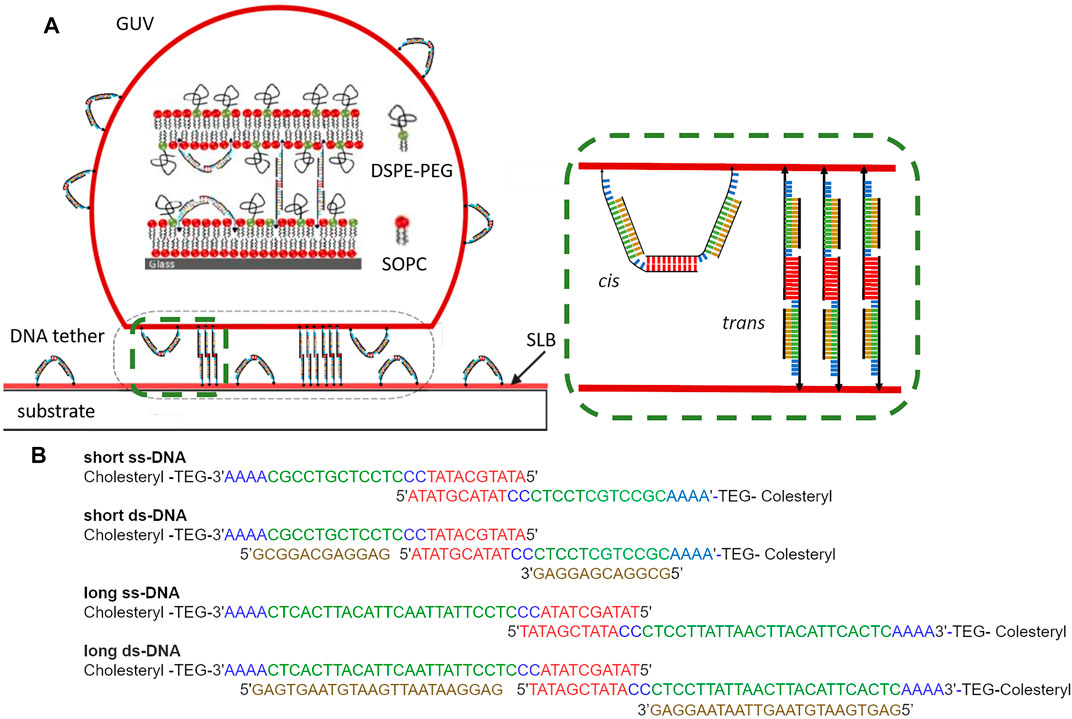
FIGURE 1. (A) Sketch of the GUV-SLB adhesion mediated by DNA tethers. DNA tethers can be either in cis (“U”-shaped) configuration, or in trans (“I”-shaped) configuration. GUV-SLB adhesion is mediated by trans tethers. Green dashed frame (zoom): ss-DNA sequences with 28 (short) or 40 (long) base-pairs, out of which 10 build a sticky end (red), and the reminder form the backbone (green) attached to a cholesterol moiety (black arrow-head) via a flexible TEG-tether linked to a short single-stranded sequence (blue). Two identical segments recombine at the sticky ends to make a tether twice as long with a cholesterol at each end. ds-DNA tethers are formed by incubation of ss-DNA sequences with backbone sequences (brown). (B) Explicit DNA sequence for all tether types.
The ss-DNA tether, with persistence length of about 1 nm, is expected to behave as a flexible spring. The ds-DNA tether, in its dimerized form, can be considered as a joined rod with three parts: the middle, corresponding to the hybridized sticky-end of 10 base-pairs, is 3 nm long and the two back-bones terminating in the TEG-tag are 4 or 8 nm respectively (calculated using 0.3 nm per base pair). Thus, ignoring the highly flexible TEG and single-stranded DNA parts, the length of the long and short tethers in dimerized and extended configuration (cholesterol excluded) is 11 and 19 nm respectively (Figure 1).
In solution, in presence of a lipid membrane, the DNA-tethers are expected to be inserted into the membrane by their cholesterol moiety. This absorption was quantified by adding fluorescently labeled tethers to a chamber containing a SLB. Adsorption affinity of the tethers was inferred from their SLB-surface densities ρ, as quantified using confocal fluorescent microscopy for different bulk concentrations c. The relation between density and affinity is given by the Langmuir adsorption isotherm
where KB is the Boltzmann constant, T the temperature, α a normalization constant 1 and ρmax the maximal surface density of tethers. The tether surface density ρ is obtained by comparing the fluorescence intensities of the molecules on the SLB with the intensities in the bulk solution (at known bulk concentration c). Fitting the measured data to the inverted eq. 1:
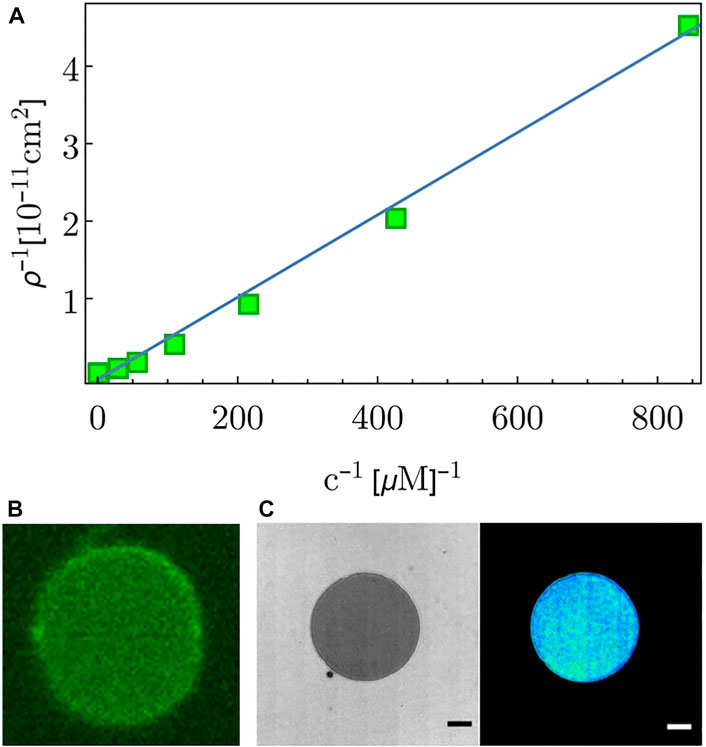
FIGURE 2. (A) Dots correspond to the measured adsorbed surface density ρ for different bulk concentrations c of ds-tethers. The line is a linear fit. (B) Fluorescence image of a free floating GUV, indicating DNA tether adsorption onto the GUV membrane. (C) RICM and reconstructed height images of a GUV adsorbed on the SLB. Scale-bar = 5 μm.
To understand how such soluble tethers may support contact formation, we adapt an existing statistical mechanical model in which the enthalpy of binding is balanced by total entropy of the system [30, 43]. We model the GUV and the SLB as two equivalent lattices with N lattice sites, of which Ncz < N are in a contact-zone, where tethers can mediate the formation of intimate contact - which will be called adhesion domain. We consider a fixed contact zone, and then the contact zone is relaxed in the second step through the calculation of the spreading pressure. The local bending elasticity of the membrane, as well as the inter-membrane distance, is locally integrated into the parameters of the model [24], but the energy of global shape-change is considered small compared to the free energy stored in the ensemble of linkers [30, 44]. As in the experimental system, the tethers in the contact-zone can be in one of the two states: 1) trans-state, occupying both a single GUV-lattice site and a single SLB-lattice site; or 2) in the cis-state, occupying ϵ GUV-lattice sites or ϵ SLB-lattice sites. The ‘shape factor’ ϵ accounts for the expected difference in the projected area of the cis- and the trans. Clearly, therefore, ϵ ≥ 1, or in other words, the projected area of the cis-state on the membrane-plane is assumed to be ϵ times larger than that of the trans state. The exact value of ϵ depends on the microstructure of the tethers: the size of the cholesterol-occupied membrane patch is not relevant. For example, if the tether is a highly flexible polymeric chain, its geometric size may be estimated by its radius of gyration, which is expected to be larger than the cholesterol-occupied membrane patch and may not be significantly affected by the transition from the cis to the trans-state, resulting in ϵ ∼ 1. On the other hand, if the tether is composed of interconnected rigid rods, as is the case of ds-DNA tethers, the cis to trans transition may significantly decrease its projected area making ϵ ≫ 1. Tethers adsorbed outside the contact zone are assumed to be in the cis-state (see footnote 2 and Figure 1A).
To keep track of tether numbers in each state, we introduce the following variables;
Here U is the total binding entalphy of all tethers and σ is their entropy of mixing, expressed in terms of kBT (kB being the Boltzmann constant). The last set of terms, proportional to μ(c), are associated with the free energy change for bringing the tether from the bulk onto the designated part of the GUV or SLB surface. Negative μ corresponds to energy cost for absorbing bulk tethers onto the GUV-SLB system, which is decreased by increasing the bulk concentration of tethers (and leading to less negative μ).
The enthalpy of the system is given by
where Eb and λEb are respectively the cis- and trans- adsorption energies, with λ being a dimensionless number. In the current system Eb = 12kBT (see footnote 2). It is anticipated that λ < 1, making the cis binding more likely than the adhesive trans state. The reason is the small but finite free energy cost of transitioning from the cis- to the trans-state, due to the relative restriction of the internal configurational space of tethers in the trans-state, as compared to the cis-state. Thus, transition from cis- to trans- actually costs free energy and makes the tether-binding fundamentally different from the typical ligand-receptor pairing [40, 43].
Total positional entropy is calculated by counting the possible configurations of tethers on the GUV and the SLB, giving:
Here we take into account the entropy of trans tethers (first term), and cis-tethers inside the contact zone on the vesicle (second term) and the SLB (third term), together with the entropy of cis-tethers on the vesicle (fourth) and the SLB (firth term) outside the contact zone. Here again, the shape-factor ϵ marks an importance difference compared to ligand-receptor binding [40, 43].
Equilibrium densities of cis-states and trans-states are calculated by minimizing eq. 2 with respect to the tether numbers on the SLB and the GUV in and out of the contact zone, under the constraint of the constant chemical potential
Solving the coupled Eq. 5 at equilibrium gives
We start with the case of identical adsorption affinities of cis- and trans-states (λ = 1), and we explore the role of the shape parameter ϵ (Figure 3A). If ϵ = 1 (cis- and trans-states have the same footprint on the membrane), NT/Ncz adopts a bell-shaped curve with a maximum at μ = − Eb. This implies that for high bulk concentrations (μ close to zero), the system strongly prefers cis-state over trans, inhibiting adhesion. Although such behavior is seemingly different from receptor-ligand bonding, where higher concentrations of tethers are expected to strengthen the adhesion, it is not unexpected since the enthalpy density per cis-tether is double that of a trans-tether - the two cholesterols of the cis-tether are inserted into the half of the membrane area of the trans-tether. The bell shaped curve is maintained until ϵ = 2, at which point the trans and the cis-tether contribute equally to the total free energy (λ = 1). Consequently, there are the same number of cis and trans tethers in the μ = 0 limit. In the regime ϵ > 2, the increasing tether concentration results in the monotonous increase of adhesion-promoting trans-tethers and therefore strengthening of adhesion. If the cost for making the trans bond increases (decreasing λ) the trans density rapidly decreases for all μ (Figure 3B). However, binding can still be achieved by increasing ϵ.
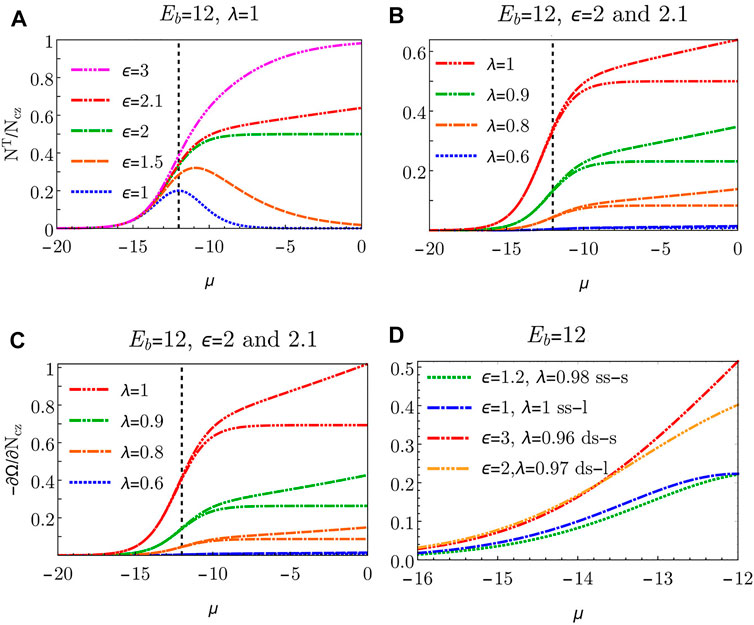
FIGURE 3. (A) Equilibrium density of trans-states as a function of the chemical potential μ for λ = 1 and several values of ϵ. (B) Equilibrium density of trans-states as a function of the chemical potential μ for ϵ = 2 and ϵ = 2.1 for several values of λ. (C) Spreading pressure ∂Ω/∂Ncz as a function of the chemical potential μ for ϵ = 2 and ϵ = 2.1 and several values of λ. Vertical dashed lines denote μ = − Eb = − 12. (D) Spreading pressure with the estimates of system parameters ϵ and λ that reproduce the qualitative behavior observed in experiments; short ss-DNA (…), long ss-DNA (-. -), short ds-DNA (- . -), long ds-DNA (-…-).
This leads to the striking conclusion that the difference in the projected areas between states alone can drive contact formation due to collective entropic considerations. Even more strikingly, this remains true even if the adsorption affinity of the non-adhesive cis-state is larger than that of the adhesion-promoting trans-state, or, in other words, the cis state is on the single-molecule level energetically more favourable. It is important to note that the shape-factor ϵ enters through entropic considerations in eq. 4. Its effect on contact-formation increases with bulk tether density because only in the crowded regime, where cis and trans states compete for adsorption area, do their projected area sizes become important. This can also clearly be seen in Figure 3, where the low tether concentration regime does not depend on ϵ. Adhesion is therefore driven purely by collective effects and not by individual tethers. This indeed may be particularly relevant to the DNA- tethers where λ is indeed expected to be somewhat smaller than one.
Finally, we inspect the tendency of the contact-zone growth by visualizing the change in the system’s energy Ω with the change of the contact zone size Ncz - captured by the so-called spreading pressure ∂Ω/∂Ncz (Figure 3C). The observed negative spreading pressure corresponds to the tendency of the contact zone to spread. A higher tendency for contact-zone spreading is highly correlated with a higher density of trans bonds (compare Figures 3B,C). We therefore expect trans-mediated adhesion to drive the spreading of the contact zone. However, unlike in the ligand-receptor binding, spreading tendency does not depend on the current size of the contact zone. The consequences of this size insensitivity would be very different response to forcefully induced de-adhesion.
To quantify tether-mediated membrane contact formation, we let GUVs interact with DNA-tether decorated SLBs. GUVs are introduced into a chamber containing an SLB already incubated with DNA-tethers. Due to the high adsorption affinity, tethers incorporate into the SLB as well as GUV membrane, probably both in cis (“U”) configuration (see footnote 2). GUV sedimentation is followed by formation of close contacts with the SLB visible as dark patches in RICM. The GUVs usually form an expanding contact zone, where the two membranes are closely apposed. In this zone, referred to as the adhesion domain, the two membranes are held together by DNA-tethers in trans (“I”) configurations (Figure 2C). In the absence of tethers, no formation of adhesion domains and no widening of the contact zone is observed. If tethers are present, in all cases we obtain a circular adhesion zone, leading us to infer that the adhesion proceeded through the formation of a radially growing adhesion patch [24]. This patch is formed by the transitioning of adsorbed cis tethers to the trans configuration through the re-insertion of one of the cholesterols into the apposing membrane. Alternatively, tethers can be adsorbed in trans configuration directly from the bulk solution. Both processes lead to adhesion (Figure 1A) and result in identical end-states that are indistinguishable in an equilibrium analysis.
Visual inspection of RICM images reveals that in the same sample, some vesicles simply hover close to the SLB (non-adhered), some adhere exhibiting many fringes (weak), some adhere with just a few fringes visible (intermediate) and few have no fringes at all (complete adhesion). Figure 4A illustrates the different adhesion states that are encountered. The defined visual categories can be attributed objectively by defining an “adhesion parameter” f, which is given by the ratio of the diameter of the adhesion patch and the diameter of the GUV. f for each category is: No Adhesion 0 < f < 0.15, Weak 0.15 < f < 0.5, Intermediate 0.5 < f < 0.75, Complete 0.75 < f < 1.
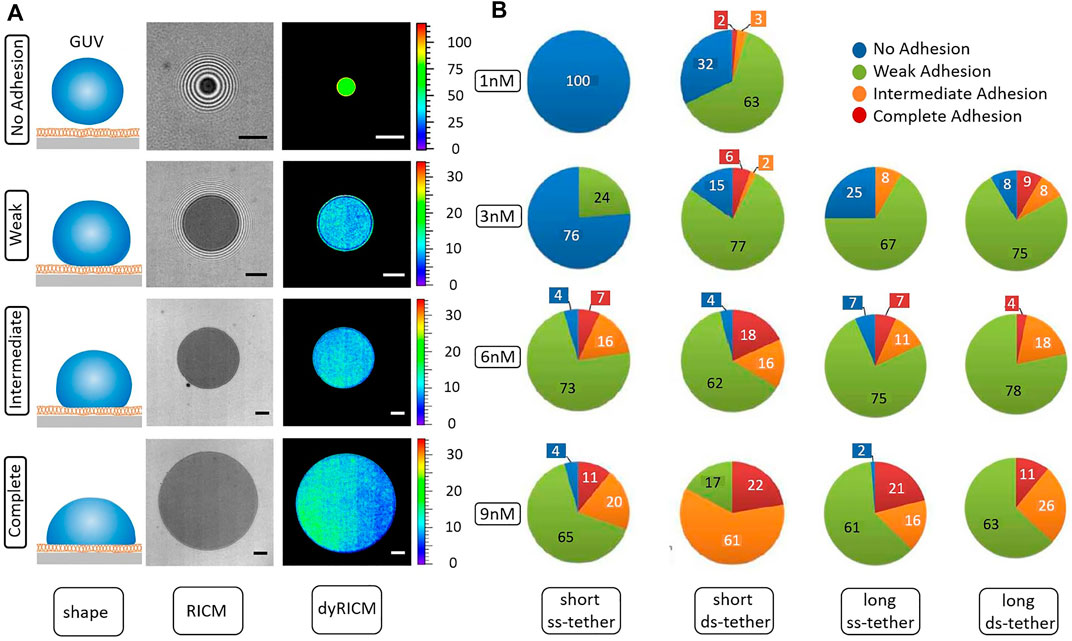
FIGURE 4. (A) Different adhesion states identified on the basis of the ratio between the adhesion disc diameter and vesicle diameter. Note that the Weak case, where the energy can be estimated, shows that all the vesicles deemed to be in this state have the same adhesion energy, about 0.02 μJ/m2, irrespective of the binder properties. The scale bar corresponds to 5 μm. (B) Comparison of the adhesion states between the ss-tethers and ds-tethers of two different lengths as a function of concentration. 1st (2nd) column shows ss (ds)-DNA tether of length 11 nm, while 3rd (4th) column shows ss- (ds-tether) of length 19 nm. Long ss-tethers, on average, have larger adhesion efficiency than short ss-tethers. On the other hand, short ds-tethers are on average more efficient than long ds-tethers.
Though we attributed names to the adhesion states based on morphology, only the so-called weak adhesion state can be quantified using the Bruinsma construction which uses the Young-Dupre law, with an ad-hoc line tension that takes into account the elastic cost of extra bending due to the adhesion induced deformation [45, 46], to infer adhesion energy density. We calculated the free energy in this state and find that all vesicles, irrespective of tether type and concentration, identified to be in the weak adhesion state have an adhesion energy ranging from about 0.002 to 0.1 μJ/m2 (with mean at 0.02, averaged over 65 GUVs over different conditions), and the final membrane tension of about 0.02–0.9 mN/m (with mean at 0.2, averaged over the same 65 GUVs). Importantly, for this given ‘f’ range, all the vesicles exhibit adhesion energy in the same range independently of the tether type, concentration or GUV size - implying that the classification according to f is consistent.
We characterize the extent of contact formation by counting the number of GUVs in each of these adhesion states (Figure 4B). Increasing the bulk concentration consistently increases the average contact zone size, independently of the tether type. Within the different tether types, ds-DNA clearly emerges as a more efficient binder than ss-DNA as seen at low concentrations.
It should be noted that while the distribution of different adhesion states (f) may arise from the inevitable tension polydispersity, the shifts in this distribution at population level, with varying experimental conditions, arises due to variations in adhesion energy, which can be expressed as a spreading pressure [24, 25, 31]. The polydispersity in spreading behaviour is much more pronounced in this system than in previously studied ligand-receptor mediated GUV/SLB adhesion, even though the GUVs are identically prepared and hence expected to have the same tension distribution.
Another difference compared to the traditionally studied ligand-receptor system is that there, addition of binders, in the form of competing soluble ligands, induces un-binding of the GUV [25]. Here addition of binders in solution results in their recruitment to the membrane which leads to higher adhesion. While such a mechanism could be devised for ligand-receptor system, that would be atypical.
In this system, the existence of stable adhesion, found both in experiments and in theory, is in itself non-trivial. In the well-studied ligand-receptor case, membrane adhesion is driven by the free energy gain due to establishment of an individual bond. In the current system, the cis configuration is, from the perspective of the free energy of a single binder, the preferred state, as compared to the membrane adhesion inducing trans configuration. This energetic preference can be estimated by assuming that the cholesterol insertion is mostly independent of the tether type, while the difference between the free energy of cis and trans configurations occurs due to the restriction of the internal structural degrees of freedom of the tethers upon transitioning from the cis to the trans state, quantified by the entropic cost of transition. The measure of the entropic cost λ can be estimated from the ratio of the expected tether volumes in cis and trans states, and is therefore related to the estimate of ϵ, with larger ϵ corresponding to smaller λ. Assuming Gaussian chains for the ss-DNA tethers (which do not significantly change their accessible conformation space on cis to trans transformation), and treating the ds-DNA tethers as two rods connected by a flexible joints (which do change their conformation space significantly), leads to estimates presented in Figure 3D. As expected, the estimated volume change is more significant for short tethers which are stretched more significantly compared to their long counterparts. This is quantified by larger ϵ and smaller λ for long tethers compared to their shorter counterparts. Furthermore, the entropic cost is larger for the rigid ds-DNA tethers as compared to the flexible ss-DNA tethers, quantified by larger ϵ and smaller λ for ds-DNA tether compared to ss-DNA tether. It is clear from (Figure 3D) that small changes in the choice of the parameters can make substantial changes in the spreading pressure. The range of μ is chosen to be consistent with the experimental range of concentrations, and the theoretical behaviour of the spreading pressure reproduces the experimentally observed monotonous growth of pressure with concentration. Moreover, our model predicts that the ds-short tethers are the most efficient for promoting adhesion, again in accordance with experimental observations. Hence, our model offers an underlying explanation for the experimentally observed trends.
Furthermore, our theory predicts and experiments confirm that titration of additional DNA tethers yields stronger adhesion. The dependence on the concentration of titrated tethers is clearly seen in experiments for all the different tethers where the tendency to adhesion increases with increasing bulk concentration of the tethers and then saturates when all available area is exhausted. This tendency is reflected in the monotonic increase and saturation seen in (Figure 3C) which plots the theoretical spreading pressure ∂Ω/∂Ncz (a measure of the tendency of an adhesion zone to increase in size) as a function of the chemical potential determined by the bulk concentration.
Another observation, namely the large spread in adhesion state for a given experimental condition, can also be understood in the light of the model which clearly shows that since the DNA-tethers freely exchange between the different membranes, individual GUVs do not equilibriate as isolated systems. Instead, the entire system equilibrates collectively. Thus, unlike in ligand-receptor mediated adhesion, the relevant parameter should not be the individual f values but rather the collective total area. Hence, the adhesion state of an individual GUV evolves not only according to their initial membrane tension but also under the influence of their interaction history. Thus, an equilibrium analysis of individual GUVs is not expected to be meaningful. Instead, the focus should be on the population-wide trends.
We also exploit the fact that RICM is almost the unique tool to measure the distance between two interacting membranes. As could be expected, the inter-membrane distance (h) increases with increasing tether length (Figure 5A). However, h is independent of the bulk concentration of tethers, suggesting that a relatively high density of trans tethers is obtained in all cases. This is furthermore confirmed by the values of membrane roughness (defined as the spatial variation in h), which also adopts values independent of the tether concentrations. h depends weakly on the tether stiffness (ss or ds), the gap being wider for ds-tethers. As expected, longer tethers support wider gaps.
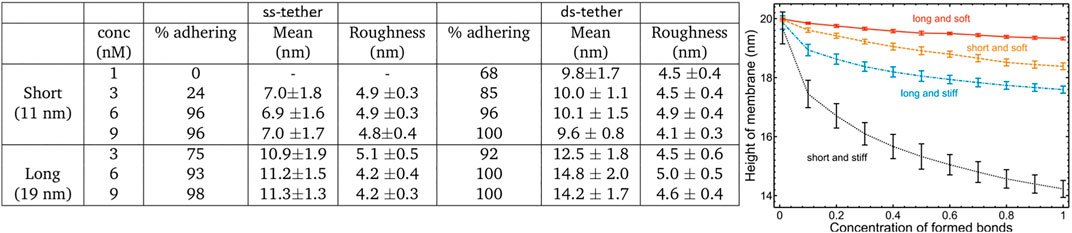
FIGURE 5. (A) Table showing experimental data: the percentage of adhered vesicles (all adhered states including weak adhesion), the mean height and the roughness for all the cases studied. About 70 vesicles were recorded in each case, the heights were calculated on adhered vesicles, roughness is calculated as the standard deviation of height within the adhesion zone of each vesicle, the errors reported are the standard deviation of the entire population for each case. (B) Theoretical average height of the membrane as a function of trans bond concentrations. Calculation was done according to the procedure described in [47], with the caveat that the role of the ligand-receptor bonds is now played by the trans tethers. In the adhered state, the inter-membrane distance and roughness are uniquely determined by the tether length and flexibility, in a manner that is universally applicable. Adhesion mediated by longer tethers has larger inter-membrane distance. Stiffness of the tether increases the sensitivity of the inter-membrane distance and roughness on tether length.
These findings are supported by theoretical calculations of the mean membrane height and roughness using the well-studied formalism for receptor-ligand cell adhesion [47]. Here, trans configurations are modeled as elastic springs pinning the membrane. By varying their density, length and stiffness we reproduce the qualitative behaviour observed in experiments (Figure 5B), as long as the rigidity of the tether is not very high. The roughness (represented by error bar) is calculated as the true variation in membrane height averaged over the surface area. The height and the roughness of the membrane both decrease with density and independently of tether type, and both saturate to a constant value when the surface coverage of tethers in trans configurations exceeds a threshold density. However, the density dependent changes in roughness are very weak, and with the experimental resolution of few nanometers, they are not likely to be observed. Interestingly, the membrane height is sensitive to both the rest length of the tether and its stiffness. For a given stiffness, h is of course larger for longer tethers. For a given length, the softer tethers tend to support wider gaps. Note that the gap between the two membranes is set by the bio-mechanical properties of the membranes and the linkers. For tethers that are shorter than the gap-size determined by non-specific interactions that emerge from fixing the membrane properties, softer tethers allow for larger extensions, yielding larger gaps. This effect is not unique for DNA tethers and would work in the same way for ligand-receptor constructs [24]. Comparing this result with experiments, we conclude that a jointed-rod configuration (ds-tethers) may in fact appear softer than a polymer-like configuration (ss-DNA tethers), due to the very flexible joint. Over all, the gap-width can be regulated by adjusting either the length or the overall effective stiffness of the tethers.
The system presented here introduces tethers that are soluble, rather than those that are permanently membrane bound. From a statistical physics point of view, this ensures that the chemical potential is maintained constant on all the surfaces and the bulk. In cellulo, this would correspond to a free exchange between the contact-forming membranes and the cytoplasm. This alone completely changes the overall physics of the system since now the entire system equilibrates together rather than each GUV finding its own equilibrium state. The direct consequence is a degeneracy and spread in GUV adhesion states, as seen in experiments (Figure 4). Individual GUVs may be fully adhered, or not at all, even if they are initially identical, since it is the overall population-level adhesion that matters.
Furthermore, if in addition, there is a conformation change upon formation of membrane bridges, the consequences are far-reaching. The geometric parameter associated with change in conformation gets coupled to the surface density of the tethers on both membranes. The cytosolic concentration of tethers then becomes a potent tool to regulate membrane-bridging and contact formation (Figure 3). This is even more important if the trans configuration is costlier than the cis configuration - that is to say, if individual bonds are, in fact, energetically unfavorable. In this case, there is no binding expected without the cooperative effect induced by the geometrical parameter. In the DNA-tether system presented here, the trans configuration may in fact be costlier, since it involves pulling and confining a polymer–the tether–to a given length corresponding to the inter-membrane separation. This mechanism can of course work only if the tethers are soluble and exchange via the cytosol.
In traditionally studied ligand-receptor systems, tether length and flexibility are expected to be important control parameters. Here ds- or ss-DNA was used to mimic soft or stiff tethers. These have indirect effect via shape and energy terms. For the choice of ss and ds DNA here, this indirect effect is not very strong, though it does ensure that the ds-DNA is a stronger binder than ss-DNA (Figure 5). In addition, there is a secondary direct effect analogous to the traditional case. Intriguingly, modelling shows that the double-stranded DNA behaves as though it was the softer system - due to the fact that there are hinges around which the rod-like ds-DNA fragments can freely rotate. This is a cautionary tale about how details of the molecular structure may dominate the mechanics. We have shown both experimentally and theoretically that length and flexibility become secondary parameters. Geometry and energy differences between cis and trans states, along with bulk concentration, are paramount control variables. Nevertheless, we show that tether length and flexibility can act as secondary parameters that determine the contact gap-size (intermembrane distance), which in turn determines size exclusion - that is to say, it determines which molecules, whether soluble or membrane bound, can enter the contact-site and which cannot.
While macroscopic contacts were studied here, in cellulo, the contacts may be much smaller. However, if the system is large enough for statistical physics to be applicable, equilibrium results should be size-invariant. However, there is a caveat that the edges of the adhesion should not cost energy. Here we have focused on the equilibrium case; while the treatment of the transient dynamics of the adhesion domains on a nanometer scale would require more detailed account, we can already observe that the exchange of the adhesion tethers between the membrane and the solution would introduce an additional source of new tethers, compared to the case where there is a fixed number of membrane-anchored tethers which are transported to the transient adhesion domain only via diffusion on the membrane. This could both increase the growth rate of the domain, but also destabilize already formed domains, emphasizing collective effects between the tethers.
Here we presented prediction and in vitro experimental verification of how this novel class of tethers may behave. The question arises whether this possible mechanism is exploited by nature. Even though identification of tethers and elucidating their dynamic structural parameters is very much in its infancy, there is at least one candidate - the Munc13 complex - which may have similar geometry [48]. The Munc13-Munc18 complex plays an important role in the capture of synaptic vesicles, forming a tripartite system close to the one described here. Even though the presence of three parts can be expected to modify the kinetics of contact formation, the essential steady-state/equilibrium features are already captured in our quantitative model.
In summary, in case of classical ligand-receptor mediated cell adhesion, the adhesion molecules are either already present on the cell membrane or are delivered to the membrane from the cytosol—there is usually no mechanism of exchange via the bulk phase, in this case the extra-cellular space between the membranes. In case of organelle contact formation, the tethers may reside in the intervening bulk phase—the intra-cellular cytosol. This possibility changes the statistical mechanics of the system. If, in addition, the tethers show strong geometrical transformation on binding to the membrane, additional consequences appear. Tethers that can be both soluble and membrane-inserted provides the cell with a powerful toolbox that can be exploited for controlling intra-cellular adhesion-like processes. The most intriguing aspect is the revelation of conformation as a key parameter in inducing stable contacts, purely due to thermodynamic reasons totally separate from conformation induced affinity changes of single molecules. In particular, the cooperative nature of the process dominates over the single-tether level properties, and leads to contact formation even if it is energetically forbidden at a single molecular level. We show here that combination of solubility and size mismatch between cis and trans conformations, leads to totally new ways of controlling membrane-membrane contact formation. Such knowledge will help structural biologists to propose molecular mechanisms that were hitherto not considered to be within the realm of possibility.
The original contributions presented in the study are included in the article/supplementary files, further inquiries can be directed to the corresponding authors.
KS and A-SS directed and supervised the project. FT was in charge of designing, characterising and supervising the use of the tethers. MK and KS developed the GUV-SLB system and performed the measurements and analysis. JJ. and A-SS provided theoretical modeling and applied it on experimental data. LL calculated the membrane height vs. concentration of trans states (Figure 5B). KS, A-SS, JJ, and MK wrote the manuscript with contributions from all authors.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank Laurent Limozin and Etienne Loiseau for fruitful discussions and careful reading of the manuscript. KS and A-SS thank the joint German Science Foundation and the French National Research Agency project SM 289/8-1, AOBJ: 652 939/ANR-18-CE92-0033(microCJ). JJ and A-SS thank European Research Council Starting Grant MembranesAct 337 283. JJ. was in part supported by Croatian Science Foundation project DOK-2018-01-9055. LL was further supported by the China Scholarship Council (CSC, File No. 201 806 185 038). MK and KS acknowledge AMIDEX grant AFFINITY.
1α = 75 M−1. The standard practice is to multiply the value of dissociation constant by a factor to cancel out the unit of the Langmuir equilibrium constant. This factor, equivalent to α−1, is 55.5 M, or equivalently 1,000 g/L, of water However, as discussed in Ref. [49], it is not strictly valid to consider a mole of water equivalent to 1 mol of solute in case of dissolved macromolecules. We have therefore used a volume equivalence instead which works out to α−1 = 1.3.10−2 M, or α = 75 M−1.
2The estimation above is used in later calculations and is valid for monomer absorption, as well as for absorption of dimers, provided that both cholesterols are inserted in the SLB. The latter is also the most likely configuration since the configuration with only one cholesterol inserted is possible but energetically unfavorable. We’ll ignore this state in later calculations - inclusion of this possibility is not expected to change the conclusions qualitatively.
1. Eisenberg-Bord M, Shai N, Schuldiner M, Bohnert M. A Tether Is a Tether Is a Tether: Tethering at Membrane Contact Sites. Dev Cel (2016) 39:395–409. doi:10.1016/j.devcel.2016.10.022
2. Olkkonen VM. Osbp-related Protein Family in Lipid Transport over Membrane Contact Sites. Lipid Insights (2015) 8s1:LPI.S31726. doi:10.4137/LPI.S31726
3. Saheki Y, De Camilli P. Endoplasmic Reticulum-Plasma Membrane Contact Sites. Annu Rev Biochem (2017) 86:659–84. doi:10.1146/annurev-biochem-061516-044932
4. Lees JA, Messa M, Sun EW, Wheeler H, Torta F, Wenk MR, et al. Lipid Transport by Tmem24 at Er-Plasma Membrane Contacts Regulates Pulsatile Insulin Secretion. Science (2017) 355:eaah6171. doi:10.1126/science.aah6171
5. Shai N, Yifrach E, van Roermund CWT, Cohen N, Bibi C, IJlst L, et al. Systematic Mapping of Contact Sites Reveals Tethers and a Function for the Peroxisome-Mitochondria Contact. Nat Commun (2018) 9:1761. doi:10.1038/s41467-018-03957-8
6. Naito T, Ercan B, Krshnan L, Triebl A, Koh DHZ, Wei F-Y, et al. Movement of Accessible Plasma Membrane Cholesterol by the Gramd1 Lipid Transfer Protein Complex. eLife (2019) 8:e51401. doi:10.7554/eLife.51401
7. Elbaz-Alon Y, Eisenberg-Bord M, Shinder V, Stiller SB, Shimoni E, Wiedemann N, et al. Lam6 Regulates the Extent of Contacts between Organelles. Cel Rep (2015) 12:7–14. doi:10.1016/j.celrep.2015.06.022
9. Tareste D, Roux A. Common Energetic and Mechanical Features of Membrane Fusion and Fission Machineries. Cham: Springer International Publishing (2018). p. 421–69. doi:10.1007/978-3-030-00630-3_16
10. Bassereau P, Jin R, Baumgart T, Deserno M, Dimova R, Frolov VA, et al. The 2018 Biomembrane Curvature and Remodeling Roadmap. J Phys D: Appl Phys (2018) 51:343001. doi:10.1088/1361-6463/aacb98
11. Simunovic M, Evergren E, Callan-Jones A, Bassereau P. Curving Cells inside and Out: Roles of Bar Domain Proteins in Membrane Shaping and its Cellular Implications. Annu Rev Cel Dev. Biol. (2019) 35:111–29. doi:10.1146/annurev-cellbio-100617-060558
12. Chan Y-HM, van Lengerich B, Boxer SG. Effects of Linker Sequences on Vesicle Fusion Mediated by Lipid-Anchored Dna Oligonucleotides. Proc Natl Acad Sci (2009) 106:979–84. doi:10.1073/pnas.0812356106
13. Xu W, Wang J, Rothman JE, Pincet F. Accelerating SNARE‐Mediated Membrane Fusion by DNA-Lipid Tethers. Angew Chem Int Ed (2015) 54:14388–92. doi:10.1002/anie.201506844
14. Moreira AG, Jeppesen C, Tanaka F, Marques CM. Irreversible vs. Reversible Bridging: When Is Kinetics Relevant for Adhesion? Europhys Lett (2003) 62:876–82. doi:10.1209/epl/i2003-00454-4
15. Hisette M-L, Haddad P, Gisler T, Marques CM, Schröder AP. Spreading of Bio-Adhesive Vesicles on DNA Carpets. Soft Matter (2008) 4:828–32. doi:10.1039/b715530a
16. Nam G, Hisette ML, Sun YL, Gisler T, Johner A, Thalmann F, et al. Scraping and Stapling of End-Grafted DNA Chains by a Bioadhesive Spreading Vesicle to Reveal Chain Internal Friction and Topological Complexity. Phys Rev Lett (2010) 105:88101. doi:10.1103/physrevlett.105.088101
17. Zhang Y, Ge C, Zhu C, Salaita K. Dna-based Digital Tension Probes Reveal Integrin Forces during Early Cell Adhesion. Nat Commun (2014) 5:5167. doi:10.1038/ncomms6167
18. Blakely BL, Dumelin CE, Trappmann B, McGregor LM, Choi CK, Anthony PC, et al. A Dna-Based Molecular Probe for Optically Reporting Cellular Traction Forces. Nat Methods (2014) 11:1229–32. doi:10.1038/nmeth.3145
19. Hadorn M, Eggenberger Hotz P. DNA-mediated Self-Assembly of Artificial Vesicles. PLoS One (2010) 5:e9886. doi:10.1371/journal.pone.0009886
20. Parolini L, Mognetti BM, Kotar J, Eiser E, Cicuta P, Di Michele L. Volume and Porosity thermal Regulation in Lipid Mesophases by Coupling mobile Ligands to Soft Membranes. Nat Commun (2015) 6:59481–594810. doi:10.1038/ncomms6948
21. Shimobayashi SF, Mognetti BM, Parolini L, Orsi D, Cicuta P, Di Michele L. Direct Measurement of DNA-Mediated Adhesion between Lipid Bilayers. Phys Chem Chem Phys (2015) 7:15615–15628. doi:10.1039/c5cp01340b
23. Sengupta K, Smith AS. Adhesion of Biological Membranes. Cham: Springer International Publishing (2018). p. 499–535. doi:10.1007/978-3-030-00630-3_18
24. Fenz SF, Bihr T, Schmidt D, Merkel R, Seifert U, Sengupta K, et al. Membrane Fluctuations Mediate Lateral Interaction between Cadherin Bonds. Nat Phys (2017) 13:906–13. doi:10.1038/nphys4138
25. Fenz SF, Sengupta K. Giant Vesicles as Cell Models. Integr Biol (2012) 4:982–95. doi:10.1039/c2ib00188h
26. Sackmann E, Smith AS. Physics of Cell Adhesion: Some Lessons from Cell-Mimetic Systems. Soft Matter (2014) 10:1644. doi:10.1039/c3sm51910d
27. Seifert U, Lipowsky R. Adhesion of Vesicles. Phys Rev A (1990) 42:4768–71. doi:10.1103/PhysRevA.42.4768
28. Smith A-S, Sackmann E. Progress in Mimetic Studies of Cell Adhesion and the Mechanosensing. ChemPhysChem (2009) 10:66–78. doi:10.1002/cphc.200800683
29. Bruinsma R. Adhesion and Rolling of Leukocytes: a Physical Model. Proc NATO Adv Inst Phys Biomater NATO ASI Ser (1995) 332:61–75.
30. Smith A-S, Seifert U. Effective Adhesion Strength of Specifically Bound Vesicles. Phys Rev E (2005) 71:1–11. doi:10.1103/PhysRevE.71.061902
31. Sengupta K, Limozin L. Adhesion of Soft Membranes Controlled by Tension and Interfacial Polymers. Phys Rev Lett (2010) 104:088101. doi:10.1103/PhysRevLett.104.088101
32. Bruinsma R, Goulian M, Pincus P. Self-assembly of Membrane Junctions. Biophysical J (1994) 67:746–50. doi:10.1016/s0006-3495(94)80535-1
33. Albersdörfer A, Feder T, Sackmann E, Albersdorfer A, Feder T, Sackmann E, et al. Adhesion-induced Domain Formation by Interplay of Long-Range Repulsion and Short-Range Attraction Force: A Model Membrane Study. Biophysical J (1997) 73:245–57. doi:10.1016/S0006-3495(97)78065-2
34. Limozin L, Sengupta K. Modulation of Vesicle Adhesion and Spreading Kinetics by Hyaluronan Cushions. Biophysical J (2007) 93:3300–13. doi:10.1529/biophysj.107.105544
35. Lorz BG, Smith A-S, Gege C, Sackmann E. Adhesion of Giant Vesicles Mediated by Weak Binding of Sialyl-LewisX to E-Selectin in the Presence of Repelling Poly(ethylene Glycol) Molecules. Langmuir (2007) 23:12293–300. doi:10.1021/la701824q
36. Fenz SF, Smith A-S, Merkel R, Sengupta K. Inter-membrane Adhesion Mediated by mobile Linkers: Effect of Receptor Shortage. Soft Matter (2011) 7:952–62. doi:10.1039/c0sm00550a
37. Schmid EM, Bakalar MH, Choudhuri K, Weichsel J, Ann HS, Geissler PL, et al. Size-dependent Protein Segregation at Membrane Interfaces. Nat Phys (2016) 12:704–11. doi:10.1038/nphys3678
38. Marx S, Schilling J, Sackmann E, Bruinsma R. Helfrich Repulsion and Dynamical Phase Separation of Multicomponent Lipid Bilayers. Phys Rev Lett (2002) 88:138102. doi:10.1103/PhysRevLett.88.138102
39. Paszek MJ, DuFort CC, Rossier O, Bainer R, Mouw JK, Godula K, et al. The Cancer Glycocalyx Mechanically Primes Integrin-Mediated Growth and Survival. Nature (2014) 511:319–25. doi:10.1038/nature13535
40. Smith A-S, Sengupta K, Goennenwein S, Seifert U, Sackmann E. Force-induced Growth of Adhesion Domains Is Controlled by Receptor Mobility. Proc Natl Acad Sci (2008) 105:6906–11. doi:10.1073/pnas.0801706105
41. Belardi B, Son S, Felce JH, Dustin ML, Fletcher DA. Cell-cell Interfaces as Specialized Compartments Directing Cell Function. Nat Rev Mol Cel Biol (2020) 21:750–64. doi:10.1038/s41580-020-00298-7
42. Fenz S, Merkel R, Sengupta K. Diffusion and Intermembrane Distance: Case Study of Avidin and E-Cadherin Mediated Adhesion. Langmuir. (2009) 25(2):1074–85. doi:10.1021/la803227s
43. Smith A-S, Seifert U. Vesicles as a Model for Controlled (De-)adhesion of Cells: a Thermodynamic Approach. Soft Matter (2007) 3:275–89. doi:10.1039/b611892e
44. Smith LA, Aranda-Espinoza H, Haun JB, Dembo M, Hammer DA. Neutrophil Traction Stresses Are Concentrated in the Uropod during Migration. Biophysical J (2007) 92:L58–L60. doi:10.1529/biophysj.106.102822
45. Nardi J, Bruinsma R, Sackmann E. Adhesion-induced Reorganization of Charged Fluid Membranes. Phys Rev E (1998) 58:6340–54. doi:10.1103/physreve.58.6340
46. Sackmann E, Bruinsma RF. Cell Adhesion as Wetting Transition? ChemPhysChem (2002) 3:262–9. doi:10.1002/1439-7641(20020315)3:3<262:aid-cphc262>3.0.co;2-u
47. Schmidt D, Bihr T, Seifert U, Smith AS. Coexistence of Dilute and Densely Packed Domains of Ligand-Receptor Bonds in Membrane Adhesion. Epl (2012) 99:38003. doi:10.1209/0295-5075/99/38003
48. Augustin I, Rosenmund C, Südhof TC, Brose N. Munc13-1 Is Essential for Fusion Competence of Glutamatergic Synaptic Vesicles. Nature (1999) 400:457–61. doi:10.1038/22768
Keywords: biomembranes, cell adhesion, DNA tethers, vesicles, biomimetic systems, GUV, organelle bridging, tethers
Citation: Kamal MA, Janeš JA, Li L, Thibaudau F, Smith A-S and Sengupta K (2022) Physics of Organelle Membrane Bridging via Cytosolic Tethers is Distinct From Cell Adhesion. Front. Phys. 9:750539. doi: 10.3389/fphy.2021.750539
Received: 30 July 2021; Accepted: 06 December 2021;
Published: 12 January 2022.
Edited by:
Jinglei Hu, Nanjing University, ChinaReviewed by:
Fan Song, Institute of Mechanics (CAS), ChinaCopyright © 2022 Kamal, Janeš, Li, Thibaudau, Smith and Sengupta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ana-Sunčana Smith, c21pdGhAcGh5c2lrLnVuaS1lcmxhbmdlbi5kZQ==; Kheya Sengupta, c2VuZ3VwdGFAY2luYW0udW5pdi1tcnMuZnI=
†These authors have contributed equally to this work and share first authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.