Formation of Magnetic Flux Rope During Solar Eruption. I. Evolution of Toroidal Flux and Reconnection Flux

Magnetic flux ropes (MFRs) constitute the core structure of coronal mass ejections (CMEs), but hot debates remain on whether the MFR forms before or during solar eruptions. Furthermore, how flare reconnection shapes the erupting MFR is still elusive in three dimensions. Here we studied a new MHD simulation of CME initiation by tether-cutting magnetic reconnection in a single magnetic arcade. The simulation follows the whole life, including the birth and subsequent evolution, of an MFR during eruption. In the early phase, the MFR is partially separated from its ambient field by a magnetic quasi-separatrix layer (QSL) that has a double-J shaped footprint on the bottom surface. With the ongoing of the reconnection, the arms of the two J-shaped footprints continually separate from each other, and the hooks of the J shaped footprints expand and eventually become closed almost at the eruption peak time, and thereafter the MFR is fully separated from the un-reconnected field by the QSL. We further studied the evolution of the toroidal flux in the MFR and compared it with that of the reconnected flux. Our simulation reproduced an evolution pattern of increase-to-decrease of the toroidal flux, which is reported recently in observations of variations in flare ribbons and transient coronal dimming. The increase of toroidal flux is owing to the flare reconnection in the early phase that transforms the sheared arcade to twisted field lines, while its decrease is a result of reconnection between field lines in the interior of the MFR in the later phase.

1 Introduction

Solar eruptions are spectacular manifestation of explosive release of magnetic energy in the Sun’s atmosphere, i.e., the solar corona, and therefore, unveiling the relevant magnetic field structures and their evolution holds a central position in the study of solar eruptions. Magnetic flux rope (MFR), a bundle of twisted magnetic field lines winding around a common axis with the same sign, is believed to be a fundamental structure in solar eruptions [1–3], especially in those which successfully produce coronal mass ejections (CMEs). By reconstruction of the cross section of ICME (i.e., CMEs that evolves into the inter-planetary space) from the in-situ data obtained by satellites passing through the ICME, it has been well established that typical ICMEs have structure of highly twisted MFR (e.g., [4,5]).

Although there is little doubt that MFR constitutes the core structure of CMEs, whether MFR exists in the solar corona before CME initiation is still in intense debates [6,7]. Currently, there are two different opinions; one is that MFR does not exist before solar eruption, and it is the latter that creates MFR through magnetic reconnection; the other is that MFR should exist prior to eruption and it is the ideal magnetohydrodynamic (MHD) instability of the MFR that initiates the eruption. The typical scenarios for the first opinion include the runaway tether-cutting reconnection model [8–10] and the magnetic breakout model [11–14]. In these models, the coronal magnetic field before eruption is strongly sheared and eruption is triggered by magnetic reconnection, internally within the sheared arcade (i.e., tether-cutting), or above it (i.e., breakout), while MFR is built up during the eruption through reconnection which transforms the sheared arcade into the rope. For the models assuming the pre-existence of MFR, such as the catastrophe model [15,16], the torus instability and kink instability models [17–21], an MFR is proposed to either emerge from below the photosphere (i.e., in the convective zone, where the turbulent convection can create thin, twisted magnetic tubes [22,23]), or forms slowly by reconnection in the lower atmosphere [24] through the so-called flux cancellation process [25]. Observations seem to indicate that both opinions are possible. For example, on one hand, Song et al [26] presented a good observation that an MFR can formed during a CME. On the other hand, an MFR characterized by a hot sigmoid structure may pre-exist before eruption, as manifested by precursor oscillation [27] or precursor external magnetic reconnection between the top of the MFR and ambient magnetic field [28].

Regardless of which model is relevant to the real case in the corona, it is commonly agreed that flare reconnection (i.e., the main reconnection that occurs below the erupting MFR) can shape substantially the on-the-fly MFR. In the purely two-dimensional (2D) standard flare model, a plasmoid (corresponding to the cross section of MFR in 3D) rises from the top of the flare current sheet, and reconnection in the current sheet continuously adds poloidal flux to the MFR, which thus grows and expands during the eruption. As a result, the observed double flare ribbons, which indicate the locations of the reconnecting field-line footpoints in the opposite magnetic polarities, are continuously separated with each other. However, in a fully 3D case, it is not that straightforward how the reconnection shapes the MFR. Numerical simulations of the simplest magnetic configuration (i.e., a bipolar magnetic field), aided with accurate analysis of magnetic topology evolution, have been developed to study how an MFR evolves with reconnection during eruption [20,29], and the findings are becoming known as the standard flare model in 3D [29–31], although it is still an over-simplified version of the realistic cases as demonstrated in recent data-constrained and data-driven simulations (e.g., [32–34]).

In the standard 3D model, the erupting MFR is separated from the ambient field by a quasi-separatrix layer (QSL [35]), and in more details, this QSL intersects with itself below the MFR, forming a hyperbolic flux tube (HFT, [36]), and the flare reconnection occurs mainly in the HFT. The footprints of this QSL at the bottom surface, i.e., the photosphere, forms two thin strips of J shape on each side of the main polarity inversion line (PIL), and the legs of the MFR are anchored within the hooked parts of the J-shaped strips. Thus, the observed flare ribbons usually exhibit double-J pattern, and the transient coronal holes [37], i.e., post-eruptive twin coronal dimmings, are naturally suggested to map the feet of erupting MFRs, along which mass leakage into interplanetary space could take place [38–40], and the boundaries of such twin coronal dimmings are outlined by the hooks of flare ribbons. With the ongoing of reconnection, the arms of the double-J ribbons separate, and their hooks gradually extends outwards. In such process, the flare reconnection, which occurs between the pre-reconnection sheared arcade (as shown in the classic cartoon of tether-cutting model, i.e., Figure 1 of [10]), should increase the toroidal (axial) flux by increasing the number of field lines within the MFR.

However, such a “standard” type of flare reconnection in 3D still cannot explain fully the observations of “standard” two-ribbon flares. A well-known, unexplained fact is that the feet of the erupting flux rope, as manifested by twin coronal dimmings and also by the hook ends of double-J flare ribbons, are found to be drifting progressively away from the main PIL during eruption [37], even though the photosphere can be regarded as motionless during the short time scale of eruption. To this end, Aulanier and Dudík [41] analyzed in more details the reconnection process in their simulation of flux rope eruption and showed that the flare reconnection actually occurs in three different types of events according to their different effect in building up the flux rope. The first one is named as aa-rf reconnection, which is the standard 3D flare reconnection that occurs between two arcades and results in a long field line joining the flux rope and a short one as a flare loop. The second one is the so-called rr-rf reconnection, which occurs within the flux rope by reconnecting two flux-rope field lines with each other and generates a new multi-turn flux-rope field line and a flare loop. The third one is ar-rf reconnection, in which an inclined arcade reconnects with the leg of a flux-rope field line, and it generates new flux-rope field line rooted far away from the PIL and a flare loop. Thus, it is the ar-rf reconnection that actually leads to gradual drifting of the MFR footpoints.

Observations show even more features not explained (or not mentioned) in the “advanced” standard model of [41]. For instance, using high-resolution observations, [42] found two closed-ring-shaped flare ribbons in the case of a buildup of highly twisted MFRs with the development of a flare reconnection. During the separation of the main flare ribbons, the flare rings expand significantly, starting from almost point-like brightening. Note that such closed circular shape flare ribbons have different nature from those formed by null-point topology which also produce circular ribbon due to reconnection in the null’s spine-fan separatrix [32]. It is predicted by theoretical models [35] that if the MFR grows to sufficiently twisted, the hooks of the double-J shaped footprints of the QSL can indeed close onto themselves, becoming two closed rings, although this is not reproduced by the numerical model of [20], possibly because their simulation run is stopped before the MFR grows to such a high degree of twist.

Very recently, a few papers reported that there is a systematic decrease of the toroidal flux of erupting MFR after its fast increase (e.g., [40,42,43]). In particular, Xing et al [40] developed a practical method for estimation of the toroidal flux of MFR during eruption by combining twin coronal dimmings and the hooks of flare ribbons. They found that the toroidal flux of the CME flux rope for all four studied events shows a two-phase evolution: a rapid increasing phase followed by a decreasing phase, and moreover, the evolution is well synchronous in time with that of the flare soft X-ray flux. The increase of MFR’s toroidal flux can be easily understood by the aa-rf reconnection while the subsequent decrease remains unclear. Although Xing et al [40] invoked the rr-rf reconnection as the mechanism responsible for such decrease, it is still unknown whether the increase-to-decrease evolution of toroidal flux can self-consistently be reproduced in any MHD simulation.

This series of papers are devoted to a comprehensive analysis of a new MHD simulation of eruption [44], focusing on the formation of MFR during eruption. That simulation demonstrated in fully 3D that solar eruption can be initiated from a single magnetic arcade without the formation of MFR before the triggering of eruption. This is different from the aforementioned simulations [20,41], in which the eruption is initiated by torus instability (which is a kind of ideal MHD instability [17]) of an MFR formed well before the eruption. With the new MHD simulation, one can follow whole life, i.e., the birth and subsequent evolution, of an MFR during the eruption. As the first paper of this series, here we show, for the first time, that both the closing of the hook ends of the QSLs at the MFR’s feet and the increase-to-decrease evolution of the toroidal magnetic flux can be self-consistently reproduced by the simulation, suggesting that they are genuine features of erupting MFRs. We further quantified the evolution of reconnection flux during the eruption, and found that the evolution of QSLs is rather complex within the MFR. In the second article of this series, we will illustrate the 3D configuration of the different types of magnetic reconnection in building up the MFR and disclose why the QSLs evolve in such a complex way, following the pioneering work by [41].

2 MHD Simulation and Analysis Method

Recently, Jiang et al [44] performed an ultra-high accuracy, fully 3D MHD simulation and demonstrated that solar eruptions can be initiated in a single sheared arcade with no additional special topology. Their simulation shows that, “through photospheric shearing motion alone, an electric current sheet forms in the highly sheared core field of the magnetic arcade during its quasi-static evolution. Once magnetic reconnection sets in, the whole arcade is expelled impulsively, forming a fast-expanding twisted flux rope with a highly turbulent reconnecting region underneath”. They further found that the high-speed reconnection jet plays the key role in driving the eruption. The simplicity and efficacy of this scenario, in the theoretical point of view, argue strongly for its fundamental importance in the initiation of solar eruptions. Since the model do not need a pre-existing MFR, the MFR itself comes into being after the eruption initiation.

Here we focus on the formation and evolution of MFR during the eruption by using a simulation run like the one in [44], but with a lower resolution than the original ones. Such simulation solves the full set of MHD equations and starts from a bipolar potential magnetic field and a hydrostatic plasma stratified by solar gravity with typical coronal temperature. Then shearing flows along the PIL, which are implemented by rotating the two magnetic polarities at the photosphere in the same count-clockwise direction, are applied on the bottom boundary to energize the coronal field until an eruption is triggered, and after then the surface flow is stopped. The whole computational box extends as (−32, −32, 0) < (x, y, z) < (32, 32, 64) with length unit of 11.5 Mm. We solve a full MHD equation with both solar gravity and plasma pressure included, but with the energy equation simplified as an isothermal process. The time unit of the model is τ = 105 s, and the shearing motion is applied by approximately 120τ before the onset of the eruption, during which a current sheet is gradually built up. Since no explicit resistivity is used in the MHD model, magnetic reconnection is triggered when the current sheet is sufficiently thin such that its width is close to the grid resolution. For more details of the simulation settings, the readers are referred to [44]. In that paper, the simulation is managed to be of very high resolutions with Lundquist number achieving ∼ 10⁵ for a length unit. Therefore, the secondary tearing instability (or plasmoid instability) is triggered in the current sheet and the magnetic topology becomes extremely complicated in small scales along with formation of the large-scale MFR. Such a complexity substantially complicates our analysis of the large-scale magnetic topology evolution associated with the erupting MFR, thus in this paper we used a lower-resolution run (corresponding to a Lundquist number of ∼ 10³). In the lower-resolution run, the basic evolution of the MFR during the eruption is not changed as compared to the high-resolution run, except that the small-scale structure will not arise, and thus the QSLs are computed in a cleaner pattern. Moreover, with the lower resolution, we can run the simulation longer and thus follow a longer evolution of MFR.

To help revealing the variation of the magnetic topology, we study the distribution and evolution of two parameters, the magnetic squashing degree and the magnetic twist number, which are commonly used for the study of 3D magnetic fields and their dynamics [2,29,30,45–47]. The magnetic squashing degree Q quantifies the gradient of magnetic field-line mapping with respect to their footpoints, and it is helpful for searching QSLs (and true separatries) of magnetic fields [36], which can have extremely large values of Q (e.g., ≥ 10⁵) and are preferential sites of magnetic reconnection. By locating the QSLs from the high values of Q we can see how the magnetic topology is evolved by the magnetic reconnection. Specifically, for a field line starting at one footpoint (x, y) and ending at the other footpoint (X, Y) where X and Y are both functions of x and y, the squashing degree Q associated with this field line is given by [36]

$Q=\frac{a^2+b^2+c^2+d^2}{|ad-bc|}(1)$

where

$a=\frac{\partial X}{\partial x},b=\frac{\partial X}{\partial y},c=\frac{\partial Y}{\partial x},d=\frac{\partial Y}{\partial y}.(2)$

The magnetic twist number T_w [48] is defined for a given (closed) field line by taking integration of T_w = ∫_LJ⋅B/B²dl/(4π) along the length L of the field line between two conjugated footpoints on the photosphere. Note that T_w is not identical to the classic winding number of field lines about a common axis, but an approximation of the number of turns that two infinitesimally close field lines wind about each other [47].

3 Results

3.1 Overview of the Eruption

Figure 1 (and Supplementary Movie S1) shows the magnetic field lines, current density, and energies evolution from slightly before the eruption onset to a time well after the eruption peak time (that is, the peak time of energy conversion rate, which is t = 6.5). As can be seen, our simulation demonstrates a typical coronal eruption leading to a CME, as seen in observations as well as many previous numerical simulations with different scenarios [49–51]. The core magnetic field changes from the pre-eruptive sheared arcades to a inverse S-shaped MFR structure that subsequently exhibits a huge growth in size. From the top view, the MFR axis shows a significant anti-clockwise rotation during the eruption. Figure 1C shows a dimensionless current density, defined as JΔ/B (where J is the current density, Δ is the grid resolution and B is the magnetic field strength), on the central cross section, i.e., the x = 0 slice of the 3D volume. One can see a picture of the 2D standard flare model: a plasmoid rises and leaves behind a cusp structure corresponding to the edge of post-flare loop, and connecting them is a long CS in which magnetic reconnection occurs continuously. This reconnection results in high-speed bi-directional (up and down) plasma jets due to the “slingshot” effect, and the upward jet flow continuously pushes outward the newly reconnected magnetic flux. Eventually, it produces a CME and drives an arc-shaped fast magnetosonic shock enclosing the erupting structure.

FIGURE 1

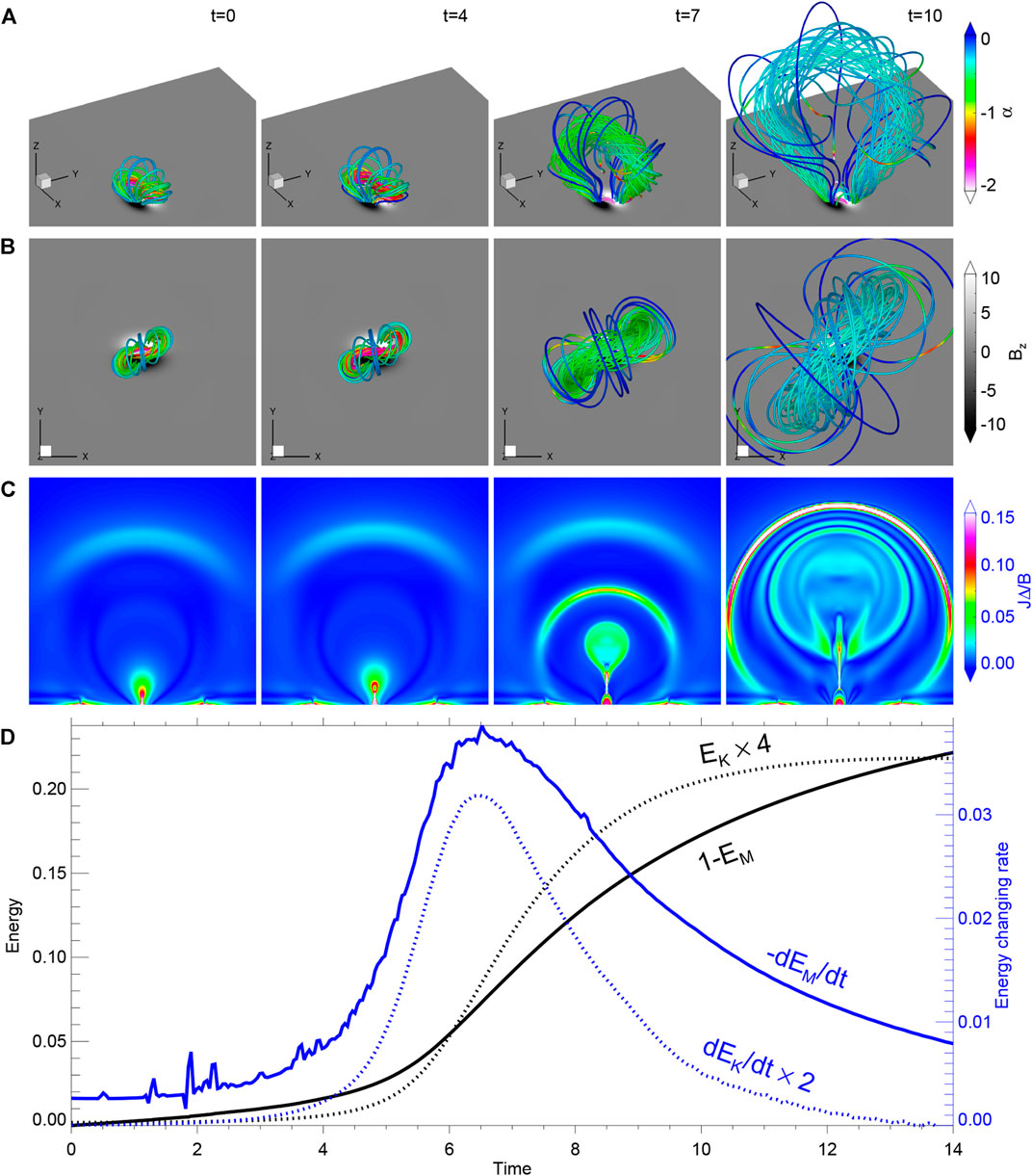
FIGURE 1. Structural evolution of the eruption. (A) 3D prospective view of magnetic field lines colored by the force-free factor. Here the field lines are traced at fixed footpoints on the bottom surface, and they represent the core structure of the pre-eruption field. (B) Top view of the structure shown in (a). (C) Evolution of the dimensionless current density JΔ/B on the central cross section (i.e., the x = 0 slice). (D) Evolution of magnetic and kinetic energies and their temporal changing rate. The energies are all normalized by the magnetic energy at t = 0 and the unit of time is 105 s. Also see Supplementary Movie S1 for a high-cadence evolution of the eruption process.

3.2 Evolution of Magnetic Squashing Factor and Twist Number

To analyze the evolution of magnetic topology, in particular the formation of MFR, during the simulated eruption, we calculate the magnetic squashing factor Q and magnetic twist number T_w at the bottom surface and at a vertical central cross section of the 3D volume. The results are shown in Figure 2 for a few snapshots and Supplementary Movie S2 for the whole evolution. At the bottom surface, initially there are two thin strips of high Q, i.e., QSLs (or more precisely, the footprints of QSLs), forming two J shapes on either side of the PIL. With onset of the eruption, the two J-shaped QSLs on the bottom surface begin to evolve rapidly (see Figure 2A and the high-cadence evolution in Supplementary Movie S2). In Figures 3A,B, we show the field lines traced from the bottom QSLs at two different times, and the 3D structure of the reconnection current sheet by an iso-surface of extremely strong current density. As can be seen, all the field lines pass through the reconnection current sheet, which demonstrates clearly that the field lines in the QSLs are undergoing reconnection. Consequently, the motion of the bottom QSLs corresponds to the apparent motion of footpoints of the field lines that were undergoing reconnection. Furthermore, from Figure 3, one can see that in the early phase the reconnection is a fully 3D manner with a strong guide field component (i.e., B_x) because joining in the reconnection is mainly the strongly sheared, low-lying flux. While in the later phase, as the sheared flux has been reconnected, the reconnection transfers into a quasi-2D manner, which consumes mainly the large-scale, overlying flux that is barely sheared.

FIGURE 2

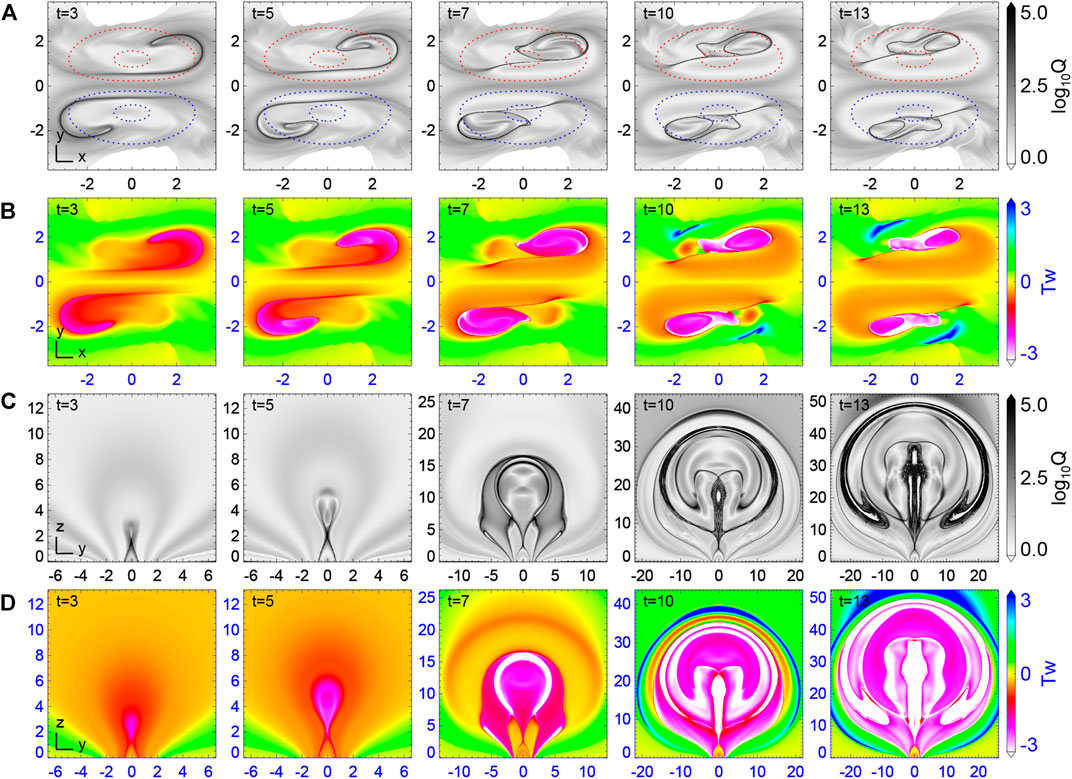
FIGURE 2. Magnetic topology evolution and formation of MFR during the eruption. (A) Magnetic squashing degree Q on the bottom surface. The dashed lines are contours of B_z = −5, −10 (blue) and 5, 10 (red). (B) Magnetic twist number T_w on the bottom surface. (C) and (D) show the two parameters Q and T_w on the central vertical cross section (i.e., x = 0 plane). Also see Supplementary Movie S2 for a high-cadence evolution.

FIGURE 3

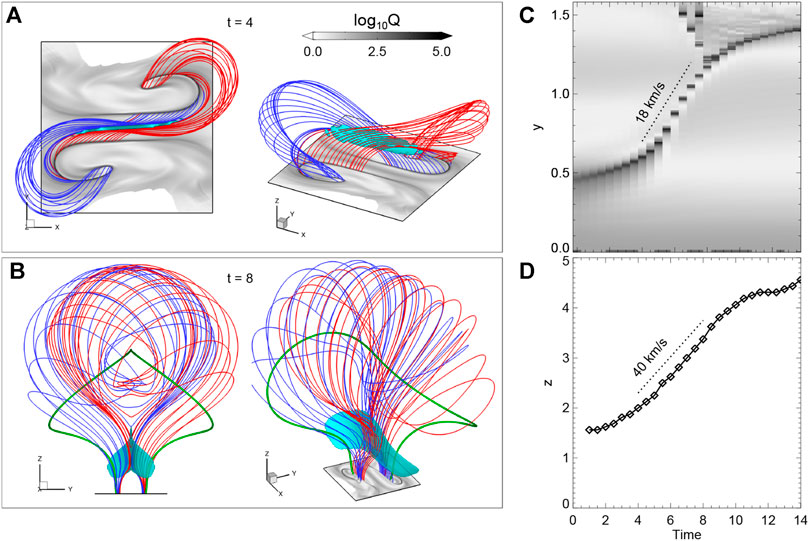
FIGURE 3. Details of reconnection. (A) Structure of the reconnecting field lines at t = 4. The field lines are colored in red and blue. The cyan object is the iso-surface of JΔ/B = 0.2, i.e., the reconnection CS. The magnetic field lines are traced from the QSLs shown on the bottom surface, and as can be seen, they all contact the CS as these field lines are undergoing reconnection. (B) Sample of reconnecting field lines at t = 8. The thick green lines represent the axis of the newly formed MFR. Note that the actual sizes of the bottom surfaces shown in (a) and (b) are identical. (C) A stacked time sequence of the bottom Q map in y-direction and centred at x = 0, which shows the separation motion of the two J-shaped QSLs shown in Figure 2A. The sloped, dashed line denotes the largest separation speed. (D) Time evolution of the height of X point of the hyperbolic flux tube, i.e., the apex of the cusp structure, shown in Figure 2C. The slopped, dashed line denotes the largest rising speed.

On the central cross section (Figure 2C), the QSLs intersect with each other, developing into an X shape, i.e., an HFT [36], and the intersection X point is essentially the reconnection site (in analogy to the null point in a 2D X-shaped reconnection configuration). As the eruption proceeds, more and more magnetic fluxes reconnect, and consequently, the two J-shaped QSLs on the bottom surface continuously separate with each other (see also Figure 3C, in which the separation speed is estimated). In the end of the simulation, they have swept to the center of each magnetic polarity (which is analogous to the umbra of sunspot). Meanwhile, the X point of the HFT rises upward progressively (see also Figure 3D, in which the rising speed is estimated) with the cusp region expanding below. Such two QSLs with their separation should be manifested as two separating flare ribbons in observations [33,46], while the rise of the X point corresponds to the apparent rising of the apex of post-flare arcades.

Figures 2B,D present the T_w distribution on the bottom surface and the central cross section, respectively. Starting from the hooks of the J-shaped QSLs, magnetic flux with high twist (as denoted by large absolute values of T_w) begins to form owing to the tether-cutting reconnection, which creates long field lines connecting the far ends of the two pre-reconnection sheared arcades. With the twisted flux accumulated through the continuation of reconnection, the areas occupied by the footpoints of the highly twisted field lines at the hooks expand. Consequently, the hook of each J-shaped QSL continuously extends inward until its end reaches the arm, forming a closed curve encircling the highly twisted flux (see the QSL at t = 7). Such a transition of QSLs reproduces the evolution of flare ribbons that gradually forms close rings at their ends [42]. With this, the MFR is fully separated with its surroundings by the QSLs. Consistently, as can be seen in the vertical cross section at t = 7, the QSL form a closed tear-drop shape connecting the HFT, within which the twisted flux of the MFR has twist number T_w mostly below −2.

The evolution speed of the QSLs is related to the rate of reconnection. As shown in Figure 3C, at the beginning of the eruption, the distance of the two QSLs is about 10 Mm, and it reaches ∼ 30 Mm at the end of the simulation. The separation speed first increases and then decreases, with its largest value of about 18 km s⁻¹ at the time of around t = 6.5, which is also the time the plasma acceleration reaches its maximum (see Figure 1). Meanwhile, the rising speed of the X point, i.e., the apex of the cusp structure reaches a maximum of about 40 km s⁻¹. Our simulated flare-ribbon distances, their separation speed as well as the rising speed of the cusp are all comparable to typical observed ones [52–55].

Nearly at the same time when the hook ends of the J-shaped QSLs close, there is even a new QSL forms within the closed QSLs (see t = 10 and t = 13 in Figure 2A). In the positive polarity, for example, this new QSL is bifurcated from the hook end and moves to the right. As a result, the region bounded by the closed QSL, i.e., the foot of the MFR, is divided into two regions separated by the newly formed QSL, and the region after swept by the new QSL shows even stronger magnetic twist than before. This indicates that there must be internal reconnection between different field lines of the MFR. Another noticeable change is the decrease of the area in the closed QSLs, i.e., the feet of the MFR, which is quantified below.

3.3 Evolution of MFR’s Toroidal Flux

The toroidal flux of the MFR, i.e., the content of the rope’s flux that connects the bottom surface, can be quantified by using the distributions of twist number T_w and squashing factor Q at the bottom surface. Before the full closing of the hook ends of the QSLs, the feet of the MFR are characterized by the high T_w areas, while after the closing of the hooked QSLs, they can be identified more accurately by the area within the closed QSLs, but the T_w is still a good indicator since the QSL-enclosed region has a distinctly strong twist number (compare T_w and Q in Figure 2). We thus directly use the distribution of T_w to locate the MFR’s feet in the whole evolution. However, it should be noted that the T_w provides only an approximation of the classic definition of the winding number around a common axis, and that there is no consensus on the definition of MFR based on either the winding number or the twist number T_w, although it is generally agreed that the winding of field lines in an MFR should be at least one turn. Therefore, we use two different thresholds for T_w to locate the MFR, and two values of the toroidal flux of the MFR are calculated by summing the magnetic flux with T_w exceeding the two thresholds, respectively. One is T_w ≤ −1, which is also used by Duan et al [2] for searching MFRs in coronal field extrapolations, and the other is T_w ≤ −1.5, which is properly chosen such that the MFR can be clearly differentiated from the background flux that has moderate twist number of T_w ∼ −1 but without reconnection during the eruption (thus remains non-flux-rope field lines during the eruption). We also compute the areas of the MFR foot using the two thresholds, as well as the average twist number of the toroidal flux. The results are present in Figures 4A,B, which clearly show that the toroidal flux (as computed by either thresholds) first increases, reaching its peak value fast, and then decrease slowly. Such an evolution pattern also applies to that of the MFR foot area. This increase-to-decrease pattern of toroidal flux reproduces the observed variations of magnetic flux in erupting MFR’s foot as identified by flare ribbons and transient coronal dimming [40]. On the other hand, the mean twist number shows a systematic increase to a value close to 3.5 at the end of simulation.

FIGURE 4

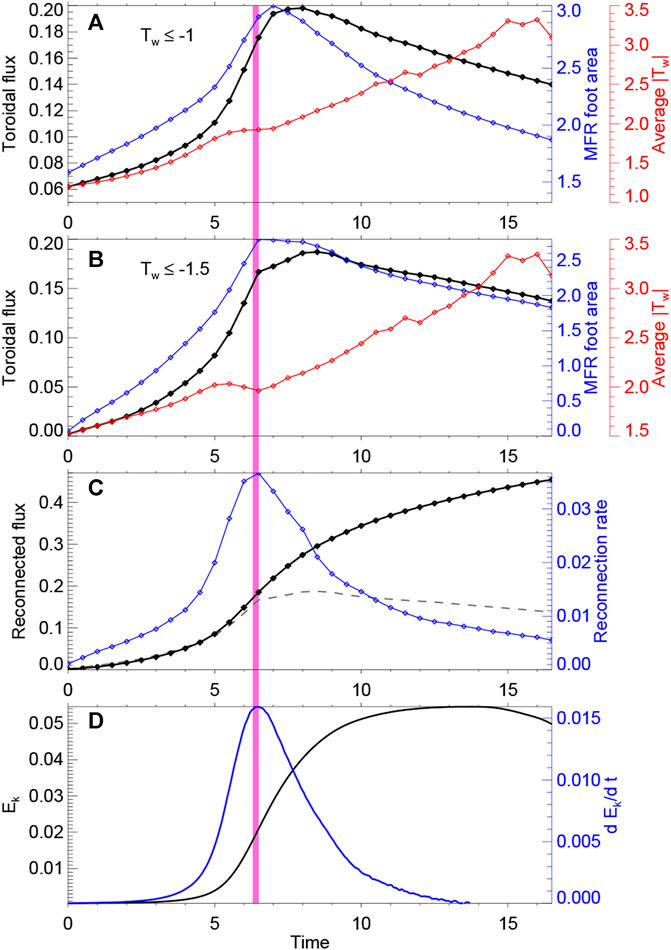
FIGURE 4. Temporal evolution of different parameters in the eruption. (A) Toroidal flux (black line), foot area (blue line) and average twist number (red line) of the MFR as calculated with T_w ≤ −1. They are defined as, respectively, ∫_SB_zds, area of S and ∫_SB_zT_wds/∫_SB_zds, in which S is the region of T_w ≤ −1 at the bottom surface. (B) Same as (A) but with T_w ≤ −1.5. (C) Magnetic reconnected flux and its increasing rate. The dashed line shows the toroidal flux with T_w ≤ −1.5. (D) Kinetic energy and its changing rate. The pink vertical bar denotes the peak time of the increasing rate of kinetic energy.

3.4 Evolution of Reconnection Flux

We further quantify how much of the magnetic flux is reconnected during the eruption. In principle, the total reconnected flux is simply the flux (by a factor of two) that is swept by the QSLs at the bottom surface in magnetic polarities of the same sign. This is analogous to counting the photospheric magnetic flux swept by flare ribbons to measure reconnection rate from direct observations [52,56]. However, this requires a very high time cadence of simulated data to capture the fast motion of the QSLs, such that the combination of all the QSLs at different times can seamlessly form the whole area that experiences reconnection. Furthermore, the geometry of QSLs is rather complex, and it is not straightforward to compute the areas swept by the QSLs. For instance, in Figure 5A, the QSLs at two consecutive times (t = 6 and 6.5) are over-plotted. As can be seen, there are clearly a margin between them, and this margin area is exactly the region swept by the QSL in the time increment (i.e., from t = 6 to 6.5). It is not easy to calculate the flux in this bounded area owing to its very irregular shape.

FIGURE 5

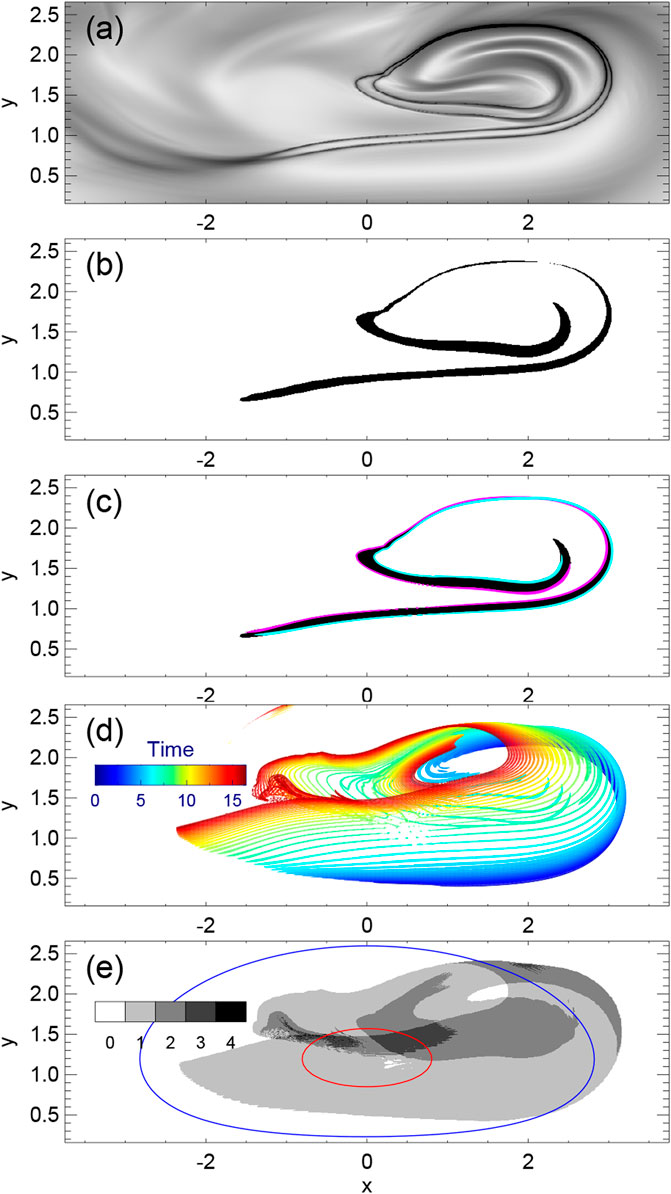
FIGURE 5. Areas swept by the QSLs at the bottom surface. (A) A overlaid image of Q at two consecutive times t = 8 and 8.5. (B) The reconnected region (shown in black) as calculated by using the slipping of the field line footpoints. (C) Same as (B) and overlaid with the QSLs at t = 8 (colored in cyan) and t = 8.5 (colored in pink). (D) Overlaid plot of the QSLs at all the different times from t = 0 to 16.5. The QSLs at different times are color coded by time. (E) All the regions swept by the QSL. Note that some regions are swept by the QSL with more than one time, and the swept times are denoted by gray color. Two contours of B_z, 10 (red) and 5 (blue), are overlaid for showing the location of the magnetic polarity.

Thus, we proposed an alternative way to calculate the reconnected flux by taking advantage of the fast-slipping motion of the footpoints of the reconnected field lines. In our simulation the bottom surface is fixed without any motion, thus for any field line without reconnection, it will be perfectly frozen with the plasma, and its two footpoints will not change with time. So, if tracing from a fixed footpoint of a field line to the other end, the conjugate footpoint will also be a fixed point at different times. If the field line undergoes reconnection, the conjugate footpoint will slip to a different location in the time step, and thus by the displacement one can easily find whether the field line reconnects or not during the time step. By this approach, the region between the two QSLs at the two consecutive times is clearly enhanced, as shown in Figures 5B,C, and then we can calculate the reconnected flux in the time step. In Figure 5D all the QSLs at different times (in one polarity) are overlaid, and in Figure 5E all the regions swept by the moving QSL are shown. We note that a large portion of the polarity is swept and therefore reconnects during the eruption, and an evident drift of the MFR foot can be seen. Interestingly, there are some regions that are swept by the QSL with more than one time, some even reaching 4 times, suggesting a rather complex internal reconnection in the erupting MFR.

The reconnection flux and its changing rate are shown in Figure 4C. The total reconnected flux increases monotonically, attaining nearly half of AR’s total flux content at the end of the simulation. The reconnection rate, i.e., the increasing rate of the reconnected flux, shows an evolution pattern (i.e., fast increase and then slow decrease) like the changing rate of the kinetic and magnetic energies (see also Figure 1), and all of them reach the peak at the same time. Such temporal correlation between reconnection rate (or flare emission) and CME acceleration has been well revealed in observation studies [57,58], stressing the central role and fundamental importance of magnetic reconnection in producing flare and CME [59].

It is interesting to compare evolution of the MFR’s toroidal flux and that of the reconnected flux. In Figure 4C, the dashed line shows the toroidal flux as present in Figure 4B. In the early stage, i.e., before the reconnection rate reaches its peak, the reconnected flux almost equals to the toroidal flux, meaning that the reconnection builds up the MFR by transferring the same amount of sheared arcade flux into the same amount of flux in the rope. However, after the peak time, although the reconnected flux continues to increase, the toroidal flux in the rope decreases, and this suggesting that there must be reconnection within the MFR, by the so-called rr-rf reconnection [41]. We note that, interestingly, the peak time of reconnection rate (at t = 6.5) also coincides with the time of the closing of the QSLs, and immediately afterward, the toroidal flux also reaches it maximum.

4 Summary

In this paper, we have studied the magnetic evolution of an MFR formed during the eruption in an MHD simulation. The MFR is generated absolutely by tether-cutting reconnection of the pre-eruption, strongly sheared arcade. In the early phase, the MFR is partially separated from its ambient field by a QSL that has a double-J shaped footprint on the bottom surface. With the ongoing of the reconnection, the arms (i.e., the straight parts) of the two J-shaped footprints continually separate from each other, which eventually pass through the centers of each polarity. Meanwhile, the hooks of the J shaped footprints expand and eventually become closed almost at the eruption peak time, and thereafter the MFR is fully separated with the un-reconnected field by a QSL. The reconnection substantially shapes the MFR by first increasing quickly and then decreasing gradually its total toroidal flux, which explains a recent observation of magnetic flux variation in erupting MFR’s foot. In the whole eruption, nearly half of the AR’s flux is reconnected, and the reconnection rate, as measured by the increasing rate of the reconnection flux, synchronizes well with the energy conversion rate (i.e., magnetic energy releasing rate and the kinetic energy increasing rate). In the early stage, i.e., before the reconnection rate reaches its peak, the reconnected flux almost equals to the toroidal flux in the MFR, whereas after the peak time the toroidal flux in the MFR decreases despite that the reconnected flux continues to increase. The increase of toroidal flux is owing to the flare reconnection in the early phase that transforms the sheared arcade to twisted field lines, while its decrease should be a result of reconnection between field lines in the interior of the MFR in the later phase, as first disclosed in [41].

Our simulation shows that the QSLs associated with the MFR in the later phase become more complex than expected, since there are new QSLs formed within the MFR, while the flux associated with these new QSLs becomes extremely highly twisted. This is due to a fast expansion of the MFR as well as its complex 3D nature, and thus at certain locations field lines reconnect with others in the MFR or themselves. Such reconnection may happen multiple times for field lines rooted at the same locations, even making some of field lines self-closed in the corona, which might be an important way for a CME flux to be totally detached from the Sun. The details of such complexity and the involved reconnection, and whether such complexity is hinted in observation, are to be elaborated in future works.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

CJ leads this work and all contribute to the study.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work is jointly supported by National Natural Science Foundation of China (NSFC 4217040250, 41822404, 41731067) and Shenzhen Technology Project JCYJ20180306171748011. The computational work was carried out on TianHe-1(A), National Supercomputer Center in Tianjin, China.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.746576/full#supplementary-material

References

1. Cheng X, Guo Y, Ding M. Origin and Structures of Solar Eruptions I: Magnetic Flux Rope. Sci China Earth Sci (2017) 60:1383–407. doi:10.1007/s11430-017-9074-6

CrossRef Full Text | Google Scholar

2. Duan A, Jiang C, He W, Feng X, Zou P, Cui J. A Study of Pre-flare Solar Coronal Magnetic Fields: Magnetic Flux Ropes. ApJ (2019) 884:73. doi:10.3847/1538-4357/ab3e33

CrossRef Full Text | Google Scholar

3. Liu R. Magnetic Flux Ropes in the Solar corona: Structure and Evolution toward Eruption. Res Astron Astrophys (2020) 20:165. doi:10.1088/1674-4527/20/10/165

CrossRef Full Text | Google Scholar

4. Wang Y, Zhuang B, Hu Q, Liu R, Shen C, Chi Y. On the Twists of Interplanetary Magnetic Flux Ropes Observed at 1 AU. J Geophys Res Space Phys (2016) 121:9316–39. doi:10.1002/2016ja023075

CrossRef Full Text | Google Scholar

5. Hu Q. The Grad-Shafranov Reconstruction in Twenty Years: 1996-2016. Sci China Earth Sci (2017) 60:1466–94. doi:10.1007/s11430-017-9067-2

CrossRef Full Text | Google Scholar

6. Chen PF. Coronal Mass Ejections: Models and Their Observational Basis. Living Rev Solar Phys (2011) 8:1. doi:10.12942/lrsp-2011-1

CrossRef Full Text | Google Scholar

7. Patsourakos S, Vourlidas A, Török T, Kliem B, Antiochos SK, Archontis V, et al. Decoding the Pre-eruptive Magnetic Field Configurations of Coronal Mass Ejections. Space Sci Rev (2020) 216:131. doi:10.1007/s11214-020-00757-9

CrossRef Full Text | Google Scholar

8. Moore RL, Labonte BJ. In: M Dryer, and E Tandberg-Hanssen, editors. IAU Symposium, Vol. 91, Solar and Interplanetary Dynamics (1980). p. 207–10.

9. Moore RL, Roumeliotis G. Lecture Notes in Physics. In: Z Svestka, and BV Jackson, editors. IAU Colloq. 133: Eruptive Solar Flares, 399. Berlin Springer Verlag& M. E. Machado (1992). p. 69.

Google Scholar

10. Moore RL, Sterling AC, Hudson HS, Lemen JR. Onset of the Magnetic Explosion in Solar Flares and Coronal Mass Ejections. ApJ (2001) 552:833–48. doi:10.1086/320559

CrossRef Full Text | Google Scholar

11. Antiochos SK, DeVore CR, Klimchuk JA. A Model for Solar Coronal Mass Ejections. ApJ (1999) 510:485–93. doi:10.1086/306563

CrossRef Full Text | Google Scholar

12. Aulanier G, DeLuca EE, Antiochos SK, McMullen RA, Golub L. The Topology and Evolution of the Bastille Day Flare. ApJ (2000) 540:1126–42. doi:10.1086/309376

CrossRef Full Text | Google Scholar

13. Lynch BJ, Antiochos SK, DeVore CR, Luhmann JG, Zurbuchen TH. Topological Evolution of a Fast Magnetic Breakout CME in Three Dimensions. ApJ (2008) 683:1192–206. doi:10.1086/589738

CrossRef Full Text | Google Scholar

14. Wyper PF, Antiochos SK, DeVore CR. A Universal Model for Solar Eruptions. Nature (2017) 544:452–5. doi:10.1038/nature22050

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Forbes TG, Isenberg PA. A Catastrophe Mechanism for Coronal Mass Ejections. ApJ (1991) 373:294. doi:10.1086/170051

CrossRef Full Text | Google Scholar

16. Lin J, Forbes TG, Isenberg PA. Prominence Eruptions and Coronal Mass Ejections Triggered by Newly Emerging Flux. J Geophys Res (2001) 106:25053–73. doi:10.1029/2001ja000046

CrossRef Full Text | Google Scholar

17. Kliem B, Török T. Torus Instability. Phys Rev Lett (2006) 96:255002. doi:10.1103/physrevlett.96.255002

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Török T, Kliem B. Confined and Ejective Eruptions of Kink-Unstable Flux Ropes. ApJ (2005) 630:L97–L100. doi:10.1086/462412

CrossRef Full Text | Google Scholar

19. Fan Y, Gibson SE. Onset of Coronal Mass Ejections Due to Loss of Confinement of Coronal Flux Ropes. ApJ (2007) 668:1232–45. doi:10.1086/521335

CrossRef Full Text | Google Scholar

20. Aulanier G, Török T, Démoulin P, DeLuca EE. Formation of Torus-Unstable Flux Ropes and Electric Currents in Erupting Sigmoids. ApJ (2010) 708:314–33. doi:10.1088/0004-637x/708/1/314

CrossRef Full Text | Google Scholar

21. Amari T, Canou A, Aly J-J, Delyon F, Alauzet F. Magnetic Cage and Rope as the Key for Solar Eruptions. Nature (2018) 554:211–5. doi:10.1038/nature24671

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Fan Y. The Emergence of a Twisted Ω-Tube into the Solar Atmosphere. ApJL (2001) 554:L111–L114. doi:10.1086/320935

CrossRef Full Text | Google Scholar

23. Cheung MCM, Isobe H. Flux Emergence (Theory). Living Rev Solar Phys (2014) 11. doi:10.12942/lrsp-2014-3

CrossRef Full Text | Google Scholar

24. Green LM, Kliem B, Wallace AJ. Photospheric Flux Cancellation and Associated Flux Rope Formation and Eruption. A&A (2011) 526:A2. doi:10.1051/0004-6361/201015146

CrossRef Full Text | Google Scholar

25. van Ballegooijen AA, Martens PCH. Formation and Eruption of Solar Prominences. ApJ (1989) 343:971. doi:10.1086/167766

CrossRef Full Text | Google Scholar

26. Song HQ, Zhang J, Chen Y, Cheng X. Direct Observations of Magnetic Flux Rope Formation during a Solar Coronal Mass Ejection. ApJ (2014) 792:L40. doi:10.1088/2041-8205/792/2/l40

CrossRef Full Text | Google Scholar

27. Zhou GP, Zhang J, Wang JX. Observations of Magnetic Flux-Rope Oscillation during the Precursor Phase of a Solar Eruption. ApJ (2016) 823:L19. doi:10.3847/2041-8205/823/1/l19

CrossRef Full Text | Google Scholar

28. Zhou GP, Tan CM, Su YN, Shen CL, Tan BL, Jin CL, et al. Multiple Magnetic Reconnections Driven by a Large-Scale Magnetic Flux Rope. ApJ (2019) 873:23. doi:10.3847/1538-4357/ab01cf

CrossRef Full Text | Google Scholar

29. Aulanier G, Janvier M, Schmieder B. The Standard Flare Model in Three Dimensions. A&A (2012) 543:A110. doi:10.1051/0004-6361/201219311

CrossRef Full Text | Google Scholar

30. Janvier M, Aulanier G, Pariat E, Démoulin P. The Standard Flare Model in Three Dimensions. A&A (2013) 555:A77. doi:10.1051/0004-6361/201321164

CrossRef Full Text | Google Scholar

31. Janvier M, Aulanier G, Bommier V, Schmieder B, Démoulin P, Pariat E. Electric Currents in Flare Ribbons: Observations and Three-Dimensional Standard Model. ApJ (2014) 788:60. doi:10.1088/0004-637x/788/1/60

CrossRef Full Text | Google Scholar

32. Jiang C, Feng X, Hu Q. Formation and Eruption of an Active Region Sigmoid. II. Magnetohydrodynamic Simulation of a Multistage Eruption. ApJ (2018) 866:96. doi:10.3847/1538-4357/aadd08

CrossRef Full Text | Google Scholar

33. Jiang C, Zou P, Feng X, Hu Q, Liu R, Vemareddy P, et al. Magnetohydrodynamic Simulation of the X9.3 Flare on 2017 September 6: Evolving Magnetic Topology. ApJ (2018) 869:13. doi:10.3847/1538-4357/aaeacc

CrossRef Full Text | Google Scholar

34. Zhong Z, Guo Y, Ding MD. The Role of Non-Axisymmetry of Magnetic Flux Rope in Constraining Solar Eruptions. Nat Commun (2021) 12:2734. doi:10.1038/s41467-021-24745-x

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Demoulin P, Henoux JC, Priest ER, Mandrini CH. Quasi-Separatrix Layers in Solar Flares. I. Method. A&A (1996) 308:643.

Google Scholar

36. Titov VS, Hornig G, Démoulin P. Theory of Magnetic Connectivity in the Solar Corona. J Geophys Res (2002) 107:1164. doi:10.1029/2001ja000278

CrossRef Full Text | Google Scholar

37. Kahler SW, Hudson HS. Origin and Development of Transient Coronal Holes. J Geophys Res (2001) 106:29239–47. doi:10.1029/2001ja000127

CrossRef Full Text | Google Scholar

38. Webb DF, Lepping RP, Burlaga LF, DeForest CE, Larson DE, Martin SF, et al. The Origin and Development of the May 1997 Magnetic Cloud. J Geophys Res (2000) 105:27251–9. doi:10.1029/2000ja000021

CrossRef Full Text | Google Scholar

39. Qiu J, Hu Q, Howard TA, Yurchyshyn VB. On the Magnetic Flux Budget in Low‐Corona Magnetic Reconnection and Interplanetary Coronal Mass Ejections. ApJ (2007) 659:758–72. doi:10.1086/512060

CrossRef Full Text | Google Scholar

40. Xing C, Cheng X, Ding M. Evolution of the Toroidal Flux of CME Flux Ropes during Eruption. The Innovation (2020) 1:100059. doi:10.1016/j.xinn.2020.100059

CrossRef Full Text | Google Scholar

41. Aulanier G, Dudík J. Drifting of the Line-Tied Footpoints of CME Flux-Ropes. A&A (2019) 621:A72. doi:10.1051/0004-6361/201834221

CrossRef Full Text | Google Scholar

42. Wang W, Liu R, Wang Y, Hu Q, Shen C, Jiang C, et al. Buildup of a Highly Twisted Magnetic Flux Rope during a Solar Eruption. Nat Commun (2017) 8:1330. doi:10.1038/s41467-017-01207-x

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Chen H, Yang J, Ji K, Duan Y. Observational Analysis on the Early Evolution of a CME Flux Rope: Preflare Reconnection and Flux Rope's Footpoint Drift. ApJ (2019) 887:118. doi:10.3847/1538-4357/ab527e

CrossRef Full Text | Google Scholar

44. Jiang C, Feng X, Liu R, Yan X, Hu Q, Moore RL, et al. A Fundamental Mechanism of Solar Eruption Initiation. Nat Astron (2021). doi:10.1038/s41550-021-01414-z

CrossRef Full Text | Google Scholar

45. Inoue S, Hayashi K, Shiota D, Magara T, Choe GS. Magnetic Structure Producing X- and M-Class Solar Flares in Solar Active Region 11158. ApJ (2013) 770:79. doi:10.1088/0004-637x/770/1/79

CrossRef Full Text | Google Scholar

46. Savcheva A, Pariat E, McKillop S, McCauley P, Hanson E, Su Y, et al. The Relation between Solar Eruption Topologies and Observed Flare Features. Ii. Dynamical Evolution. ApJ (2016) 817:43. doi:10.3847/0004-637x/817/1/43

CrossRef Full Text | Google Scholar

47. Liu R, Kliem B, Titov VS, Chen J, Wang Y, Wang H, et al. Structure, Stability, and Evolution of Magnetic Flux Ropes from the Perspective of Magnetic Twist. ApJ (2016) 818:148. doi:10.3847/0004-637x/818/2/148

CrossRef Full Text | Google Scholar

48. Berger MA, Prior C. The Writhe of Open and Closed Curves. J Phys A: Math Gen (2006) 39:8321–48. doi:10.1088/0305-4470/39/26/005

CrossRef Full Text | Google Scholar

49. Linker JA, Mikić Z, Lionello R, Riley P, Amari T, Odstrcil D. Flux Cancellation and Coronal Mass Ejections. Phys Plasmas (2003) 10:1971–8. doi:10.1063/1.1563668

CrossRef Full Text | Google Scholar

50. Amari T, Luciani JF, Aly JJ, Mikic Z, Linker J. Coronal Mass Ejection: Initiation, Magnetic Helicity, and Flux Ropes. I. Boundary Motion-Driven Evolution. ApJ (2003) 585:1073–86. doi:10.1086/345501

CrossRef Full Text | Google Scholar

51. Török T, Downs C, Linker JA, Lionello R, Titov VS, Mikić Z, et al. Sun-to-Earth MHD Simulation of the 2000 July 14 "Bastille Day" Eruption. ApJ (2018) 856:75. doi:10.3847/1538-4357/aab36d

CrossRef Full Text | Google Scholar

52. Wang H, Qiu J, Jing J, Zhang H. Study of Ribbon Separation of a Flare Associated with a Quiescent Filament Eruption. ApJ (2003) 593:564–70. doi:10.1086/376360

CrossRef Full Text | Google Scholar

53. Qiu J, Gary DE, Fleishman GD. Evaluating Mean Magnetic Field in Flare Loops. Sol Phys (2009) 255:107–18. doi:10.1007/s11207-009-9316-y

CrossRef Full Text | Google Scholar

54. Hinterreiter J, Veronig AM, Thalmann JK, Tschernitz J, Pötzi W. Statistical Properties of Ribbon Evolution and Reconnection Electric Fields in Eruptive and Confined Flares. Sol Phys (2018) 293:38. doi:10.1007/s11207-018-1253-1

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Yan XL, Wang JC, Pan GM, Kong DF, Xue ZK, Yang LH, et al. Successive X-Class Flares and Coronal Mass Ejections Driven by Shearing Motion and Sunspot Rotation in Active Region NOAA 12673. ApJ (2018) 856:79. doi:10.3847/1538-4357/aab153

CrossRef Full Text | Google Scholar

56. Qiu J, Lee J, Gary DE, Wang H. Motion of Flare Footpoint Emission and Inferred Electric Field in Reconnecting Current Sheets. ApJ (2002) 565:1335–47. doi:10.1086/324706

CrossRef Full Text | Google Scholar

57. Zhang J, Dere KP, Howard RA, Kundu MR, White SM. On the Temporal Relationship between Coronal Mass Ejections and Flares. ApJ (2001) 559:452–62. doi:10.1086/322405

CrossRef Full Text | Google Scholar

58. Qiu J, Wang H, Cheng CZ, Gary DE. Magnetic Reconnection and Mass Acceleration in Flare-Coronal Mass Ejection Events. ApJ (2004) 604:900–5. doi:10.1086/382122

CrossRef Full Text | Google Scholar

59. Zhu C, Qiu J, Liewer P, Vourlidas A, Spiegel M, Hu Q. How Does Magnetic Reconnection Drive the Early-Stage Evolution of Coronal Mass Ejections. ApJ (2020) 893:141. arXiv: 2003.11134. doi:10.3847/1538-4357/ab838a

CrossRef Full Text | Google Scholar