An Ownership Verification Mechanism Against Encrypted Forwarding Attacks in Data-Driven Social Computing

Data-driven deep learning has accelerated the spread of social computing applications. To develop a reliable social application, service providers need massive data on human behavior and interactions. As the data is highly relevant to users’ privacy, researchers have conducted extensive research on how to securely build a collaborative training model. Cryptography methods are an essential component of collaborative training which is used to protect privacy information in gradients. However, the encrypted gradient is semantically invisible, so it is difficult to detect malicious participants forwarding other’s gradient to profit unfairly. In this paper, we propose a data ownership verification mechanism based on Σ-protocol and Pedersen commitment, which can help prevent gradient stealing behavior. We deploy the Paillier algorithm on the encoded gradient to protect privacy information in collaborative training. In addition, we design a united commitment scheme to complete the verification process of commitments in batches, and reduce verification consumption for aggregators in large-scale social computing. The evaluation of the experiments demonstrates the effectiveness and efficiency of our proposed mechanism.

Introduction

Social computing, a field highly relevant to human behavior, has made considerable progress in recent years. With the proliferation of cell phones and IoT devices, information about humans, behaviors, and interactions is being recorded in unprecedented detail. Combined with deep learning models, the application of social computing can profoundly solve various industry challenges such as epidemic prediction [1, 2], social network service [3], and hot topic recommendations [4]. For example, data-driven epidemic propagation can help governments and hospitals prepare resources in advance [1]. Moreover, some well-designed pre-diagnosis models of COVID-19 may alleviate physician shortages [2].

As a data-driven technology, deep learning has a natural desire for data to be more accurate and higher-quality. Since user data in social computing is closely tied to privacy, providing the data directly would cause extremely serious privacy damage. Google [5] proposed the concept of federated learning in 2016, which is an innovation in collaborative training. Without directly obtaining local data from multiple parties, it can take full advantage of the value of the data by sharing gradients. However, transmitted gradients are subject to model inversion attacks, attribute inference attacks, membership inference attacks, etc. Thus, the privacy of users requires further protection.

To resolve the problem of privacy leakage in transmitted gradients, researchers have proposed a wide range of solutions that can be roughly divided into two categories: differential privacy [6] and cryptographic algorithms [7]. Differential privacy is a method of adding noise so that the attacker cannot determine the user’s exact gradient. However, the differential privacy-based method modifies the original data, resulting in a loss of model accuracy. Unlike differential privacy methods, cryptographic algorithms such as homomorphic encryption do not alter the value of the gradient. But instead, they prevent third parties and model aggregators from obtaining a single participant’s model parameters by encryption or concealment. Most cryptography-based parameter protection methods have a higher arithmetic overhead and many researchers are committed to optimizing their overhead.

Apart from performance issues, cryptography-based privacy-preserving methods will also introduce a derivative problem. Because of the semantic invisibility of encrypted data, data aggregators cannot judge whether a problem exists. The most obvious problem associated with data invisibility is that data tampering is difficult to detect, and some work has been done to try to resolve this. Li et al. [8] proposed to store verification tags on the blockchain and generate a Merkle tree as proof. The transaction information must be uploaded to the blockchain, which prevents malicious users from tampering during the training process. Weng et al. [9] proposed a blockchain-based auditing model called Deepchain that considers the malicious behavior of model aggregators.

However, another problem of semantic invisibility in encrypted data was left behind. Cryptography methods blur the user’s ownership of the real information corresponding to the ciphertext data during the transaction. Malicious users can steal historically encrypted gradients from publicly audited information or previous transactions, and upload them elsewhere to gain benefits, in what we call an encrypted forwarding attack. The attack will destroy the fairness of the entire system, and make fewer users willing to participate in collaborative training. Recently, researchers have proposed extracting user data features through the first few layers of deep neural networks, making them adaptable to multiple uncertain deep learning tasks [10, 11]. This will lead to a change in traditional collaborative training from focusing on a single defined task to completing multiple uncertain tasks, further expanding the reach of encrypted forwarding attacks.

In this paper, we aim to resolve the problem of encrypted forwarding attacks in collaborative training. To prevent users from submitting others’ encrypted gradients maliciously, users need to use Pedersen commitment to commit on the uploaded gradient. The model aggregator can verify the ownership of the encrypted gradient by determining whether the user has plaintext. Our main contributions are as follows:

• We propose a data ownership verification mechanism to counter encrypted forwarding attacks caused by cryptography-based privacy-preserving methods. We use an interactive Σ-protocol and Pedersen commitment algorithm to prove that the user has the plaintext corresponding to the encrypted gradients.

• We design a united commitment scheme to complete the verification process of commitments in batches, thereby reducing verification consumption for the aggregator.

• We verify the effectiveness of the model on a social face dataset CelebA and a digital recognition dataset MNIST, then provide a safety analysis. The experimental results demonstrate that the commitment scheme does not impose an additional burden on secure aggregation of social applications.

The rest of this paper is organized as follows. In Related Work, we introduce the existing work of cryptography-based privacy-preserving methods and derivative audits approaches of encrypted data. Preliminaries introduces the relevant background knowledge of the Σ-protocol, Pedersen commitment, and attack models. System Design elaborates the details of the ownership verification mechanism. In Security Analysis, we analyze the correctness and safety of our mechanism. Experimental Results evaluates and analyses the performance of Paillier algorithm and Pedersen commitment in our mechanism. Finally, we conclude our paper in Conclusion.

Related Work

Cryptography-Based Privacy-Preserving Methods in Collaborative Training

Privacy concern is one of the main problems in collaborative training. Although some collaborative training allows collaborative participants to only share model updates rather than raw training data, such as federated learning. There are still some privacy problems that are not completely solved [12–14]. Attackers may infer whether a sample exists in the training dataset or contain certain privacy attributes from the user gradient, called member inference attacks [15] and attribute inference attacks [16].

Secure aggregation [17] is a cryptography-based privacy-preserving method that prevents aggregators from gaining direct access to individual participants’ gradients and committing privacy attacks. Homomorphic encryption is a common security aggregation algorithm that allows users to operate on ciphertext and decrypt the results of operations, where the decryption result is the same as for operating on plaintext. Participants can first encrypt the gradient via homomorphic encryption. The parameter aggregator then aggregates all encrypted gradients and decrypts the aggregated result, thereby indirectly obtaining a global model update contributed by the participants. The existing homomorphic encryption methods are mainly based on full-homomorphic encryption [18] and semi-homomorphic encryption [19].

Fully homomorphic encryption is mainly based on ideal lattices theory [20]. It relies on a large number of polynomial-based power operations and modulo operations, which greatly increases the consumption of implementation. It is still difficult to apply directly in the existing work.

Paillier encryption [19] is a representative work of semi-homomorphism that is widely used because of its simple structure. Phong et al. [21] proposed the method combining asynchronous stochastic gradient descent and Paillier homomorphic encryption. They proved that the system could prevent the aggregator from learning the data privacy of the participants, and ensure the availability of the model training with the acceptable system overhead. Zhou et al. [22] applied a homomorphic encryption scheme to fog computing. They proposed a scheme that combines Paillier encryption and blindness technology, which can resist collusion attacks by multiple malicious entities.

In order to improve the efficiency of the homomorphic encryption system, Zhang et al. [23] proposed a federated learning model called BatchCrypt. They encoded batches of gradients and perform homomorphic encryption with less time, which greatly reduces the overhead of the whole system. LWE has more extensive applicability because of its full-homomorphism. Hao et al. [24] utilized and improved the BGV algorithm based on LWE, which achieves the secure aggregation of gradients to prevent privacy disclosure. It makes the scheme based on homomorphic encryption practical.

The above works complete the data privacy protection for the participants and make the system feasible, but another potential problem has appeared: it is difficult for the aggregator to determine whether a problem exists due to the semantic invisibility of the encrypted data.

Verification of Secure Aggregation

Semantic invisibility of encrypted data presents numerous challenges, including transmission errors, malicious tampering by intermediaries, and the exclusion of some user-generated gradients by dishonest aggregators.

The correctness audit of the transmission gradient becomes very difficult in the encrypted state. Weng et al. [9] provided an audit mechanism based on ∑-protocol [25] which generates proofs of correctness for each gradient. Guo et al. [26] proposed a Paillier-based zero-knowledge proof algorithm. The server and users can jointly calculate the statement of encrypted gradients to prove the correctness of gradients.

To ensure that the gradients provided by each participant are indeed aggregated correctly, Xu et al. [27] use a homomorphic hash technique combined with pseudorandom function to help users verify the correctness of aggregation. To extend the applicability of the algorithm, Guo et al. [28] proposed a commitment scheme based on linearly homomorphic hash to verify the integrity of aggregation. Before sending gradient to the server, the users need to generate and exchange the hash value of their gradient. The users can verify whether the gradient is tampered with by checking hash values.

Despite the foregoing, there is a serious problem that has not been addressed. Encrypted data may be accessed by multiple users as public data. Malicious users can forward them to other collaborative tasks with the same purpose for improper profit. There are even cases where multiple users claim ownership of ciphertext in the same task. This will undermine the willingness of honest users to engage in collaborative training and thus lead to a shortage of training data for social applications. In this paper, we propose an ownership verification mechanism based on the Patterson commitment that can prove that the user owns the plaintext of the data without providing the plaintext.

Preliminaries

In this section, we briefly recall the definition of Σ-protocol and Pedersen commitment, and introduce the attack models.

Σ-protocol

Σ-protocol [25] is a two-party interaction protocol in zero-knowledge proof field. It is used to prove that someone knows a secret without disclosing it. There are many classic examples such as Schnorr’s protocol [29], which is used for authentication.

Consider a binary relation $R$ and an element $\left(x,y\right)\in R$, and we have $f\left(x\right)=y$, where $x$ is called the pre-image of $y$ under a mapping $f$. In Σ-protocol, we think of $x$ as a witness and $y$ as the corresponding instance for $x$, where $x$ and $y$ are finite values.

Suppose that there are two parties, one of which is prover, and the other is verifier. Without exposing $x$, the prover wants to prove to the verifier that he knows the pre-image value $x$ of $y$ under the mapping $f$. As shown in Figure 1, they need to follow Σ-protocol with the steps below:

FIGURE 1

FIGURE 1. The general process of Σ-protocols.

Step 1: Prover computes a commitment $c$ with the value of, and sends it to verifier.

Step 2: Verifier returns a random value $e$ called challenge to prover.

Step 3: Prover sends a response $z$ to verifier. It is computed with $x$ and $e$.

Step 4: Verifier uses instance $y$ and the message $\left(c, e, z\right)$ generated in previous steps to compute the verification result.

Since the challenge $e$ is randomly selected, if the prover does not know the witness x, he cannot use challenge $e$ to compute a correct response $z$ in Step 3. When the verification passes, the verifier is convinced that the prover knows the witness $x$. The witness in our ownership verification mechanism can be a secret gradient used for social computing. A user can prove that it knows the secret gradient $x$ corresponding to the commitment$c$

Pedersen Commitment

Pedersen commitment [30] is a homomorphic commitment scheme, in which one computes a commitment bound to a chosen value. Pedersen commitment scheme can be used to prove that a committed value is not tampered with. According to its homomorphism, it is usually used to prove that the secret committed data satisfies certain binding relationships. The scheme consists of a commitment phase and a verification phase. In the beginning, A trusted third party selects a multiplicative group $G$ with the order of large prime $q$, then selects two prime elements $g$ and $h$ of group $G$, where no one knows the value $x$ to make $g=x\ast h$. After the committer and verifier agree on two elements $g$ and $h$, they follow the process as follows:

Commitment: To commit to secret value $v$, the committer chooses a random value $r$, computes commitment $\mathit{comm}\left(v,r\right)=v\ast g+r\ast h$ and sends it to verifier.

Verification: Committer sends $\left(v,r\right)$ to verifier. Verifier use $\left(v,r\right)$ to computes $com{m}^{\prime }\left(v,r\right)=v\ast g+r\ast h$ and checks whether it is equal to $comm(v,r)$. If the verification passed, it means that $v$ is not tampered with.

Pedersen commitment scheme is designed that the sum of two commitments can also be seen as a commitment. It can be represented by $comm\left(v_3,r_3\right)=com\left(v_1,r_1\right)+com\left(v_2,r_2\right)$, where $v_3=v_1+v_2$, $r_3=r_1+r_2$. It seems like someone use a random value $r_3$ to commit to $v_3$.

Pedersen commitment scheme has the following properties: 1) Perfectly hiding: the $r$ in the commitment computation is randomly chosen, so two commitments to one value will be different. No one can find a correlation between commitment and committed value. 2) Computationally binding: the commitments on different messages are different, which means that the malicious party cannot deny the value he committed. A more detailed introduction and proof can be seen in [30].

Different from Σ-protocol, the committed value in Pedersen commitment scheme needs to be revealed in the verification phase. It cannot be directly used to prove that the single encrypted gradient is not tampered with. In our scheme, we use the homomorphism of Pedersen commitment scheme to check whether the aggregated commitment is correctly corresponding to the aggregated gradient, further confirming the binding relationship between the commitment and encrypted gradient.

Threat Models

As we attempt to solve the problem of data silos in social computing through cooperative training, privacy protection and data ownership have become unavoidable difficulties. Cryptography-based secure aggregation methods can be a good solution to keep private information from being accessed by unauthorized users, but they also make it more difficult to verify data ownership. Two main roles are included in the current collaborative training:

Model Aggregator is a service provider that publishes the request for data training. It asks multiple users to provide trained gradients to conduct social computing.

Data Owners are users who have datasets and are willing to participate in collaborative training. They submit the trained models or gradients to the model aggregator for model updating.

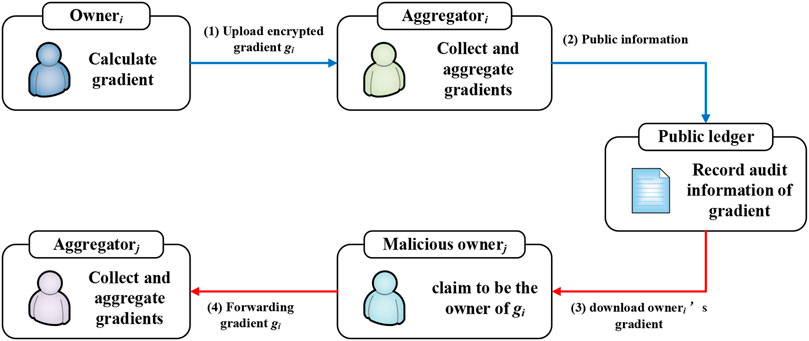
Once we use a cryptography-based secure aggregation algorithm that prevents model aggregators from obtaining plaintext data from a single data owner. It is difficult to distinguish whether the user who submits encrypted data is its real owner or not. As shown in Figure 2, attackers can download encrypted data from elsewhere or historically, and then participate in the current cooperative training for improper profit, which we call encrypted forwarding attacks. In addition, we present several threat scenarios for encrypted forwarding attacks.

FIGURE 2

FIGURE 2. Encrypted forwarding attacks in cooperative training.

Threat 1. Attackers can only obtain encrypted data and claim ownership of the encrypted data. Malicious users access encrypted data through public channels, such as the available audit information or publicly accessible blocks on the blockchain. The encrypted data is being downloaded by attackers and forwarded to similar tasks for unfair gain.

Threat 2. Attackers can obtain encrypted data as well as its verification information. As an intermediate forwarder, a malicious user receives not only the encrypted data but also the previous verification information. By masquerading as a data owner and participating in social computing, traditional mechanisms of ownership verification may be bypassed.

Security Goal: To prevent encrypted forwarding attacks by malicious attackers, we need an ownership verification mechanism for encrypted data. For privacy reasons, it can conclusively confirm ownership of data without directly obtaining the plaintext of user’s data. In addition, verification information must be real-time to prevent falsification by forwarding historical verification information.

System Design

In this section, we present the specific construction of our data ownership verification mechanism. Our mechanism prevents the leakage of user information to curious aggregators while resisting encrypted forwarding attacks by malicious users, as detailed in the threat model.

System Overview

We suppose that there exist many users who possess private training data in a community. They all agree on the structure and configuration of a common task model. When a user wants to update its model, it claims to be a model aggregator and requests collaborative training from other users. Other data owners will respond to the model aggregator. We denote the model aggregator as $ag$ and data owners as $o{w}_i$,$i\in \{1,\cdots ,N\}$

The aggregator $ag$ then collects gradients from these data owners to update its task model. The process of gradient collecting is shown in Figure 3.

FIGURE 3

FIGURE 3. The workflow of our system.

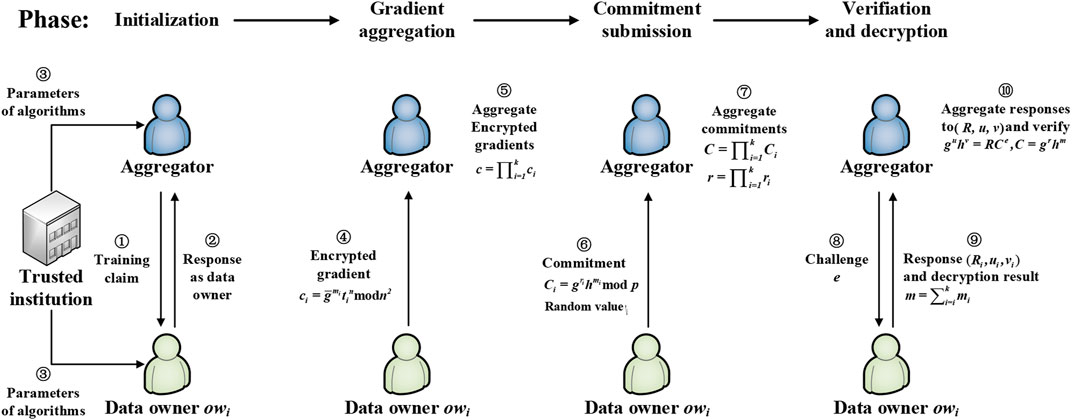
Phase 1. Initialization

A user claims to be an aggregator to all other users in the community. Others will respond to the claim and form a group with the aggregator by some means [31]. After that, a trusted institution executes the initialization of threshold Paillier algorithm and Pedersen commitment scheme for the group.

Phase 2. Gradient Aggregation

After each data owner $o{w}_i$ gets gradient $g_i$ through local training, it uses the threshold Paillier algorithm to encrypt it to cipher $c_i$, then uploads it to the aggregator $ag$. The aggregator $ag$ will aggregate the gradients.

Phase 3. Commitment Submission

Each data owner $o{w}_i$ who has uploaded gradient uses gradient $g_i$to compute a commitment $com{m}_i$ based on Pedersen commitment scheme and uploads it to the aggregator $ag$.

Phase 4. Verification and Decryption

The aggregator $ag$ conducts the verification of commitment with each data owner$o{w}_i$. If the verification passes, the aggregator $ag$ asks data owners to collaboratively decrypt the aggregated gradient. At last, the aggregator $ag$ confirms the ownership of gradients by checking commitments and gradients.

After the aggregator $ag$ and all data owners have finished the process as above, the aggregator will pay each data owner for the model update. We can think that they have finished a round of secure aggregation.

Gradient Aggregation Based on Paillier Algorithm

Initialization: After the aggregator and data owners form a group together, a trusted institution will execute the initialization process. Concretely, it confirms the scale of the group and initializes the $\left(l,N\right)$ threshold Paillier algorithm, where $N$ is the number of data owners and $l\in \left\{\frac{N}{3}+1, \mathrm{...}, N\right\}$ is the least number of data owners together to decrypt a cipher. The concrete process is shown in Algorithm 1.

The trusted institution publishes the public key $PK=\left(\overline{g},n,\theta \right)$. It also distributes shares of private key $S{K}_i$ and verification key $V{K}_i$ to each data owner $o{w}_i$, respectively.Encoding of gradient: The homomorphism of Paillier algorithm can be represented as ${\displaystyle \prod }_{i}Enc\left(m_i\right)=\mathit{Enc}\left({\displaystyle \sum _i{m}_i}\right)$, where $Enc\left(\right)$ denotes the encryption. The aggregator $ag$ can aggregate encrypted gradients $Enc\left(m_i\right)$ and decrypt it to obtain aggregated gradient ${\displaystyle \sum _i{m}_i}$. Suppose that a data owner $o{w}_i$ has the gradient $g_{\text{i}}=\left(g_{i1,}\cdots ,g_{ij},\cdots ,g_{in}\right)$ to upload. Each element $g_{ij}$ represents the gradient of the $j-th$ component of the model. First of all, each data owner $o{w}_i$ encodes the gradient. They divide each element $g_{ij}$ into several vectors $g_{ij}^{\left(\text{k}\right)}$ and encode them into a specific format which can be encrypted by Paillier algorithm. The data owner $o{w}_i$ encrypts the gradient by encrypting each vector $g_{ij}^{\left(\text{k}\right)}$. To explain the encryption of gradients briefly, we use $m_{\text{i}}$ to represent the gradient encrypted by Paillier algorithm.Encryption and aggregation: We assume that there is a group composed of $k$ data owners. Given the public parameter $PK=\left(\overline{g},n,\theta \right)$ and threshold $l$, each data owner$o{w}_i$ encrypts its gradient $g_{\text{i}}$ by computing $c_i={\overline{g}}^{m_i}{t}_i^n\mathrm{mod}{n}^2$, where $t_i$ is a random element chosen from $Z_n^{\ast }$. Then they together upload the cipher $c_i$ to the aggregator $ag$. The aggregator $ag$ will aggregate all the encrypted gradient $c_i$ by computing $c={\displaystyle \prod }_{i=1}^k{c}_i$ and return the aggregation result $c$ to each data owner $o{w}_i$ to request the decryption. To ensure that the aggregator $ag$ correctly aggregates all the encrypted gradient $c_i$, we introduce the commitment scheme in [28].Decryption and update: In the decryption phase, each data owner $o{w}_i$ provides his decryption share $d_i=c^{2\Delta s_i}\mathrm{mod}{n}^2$, where $s_i$ is its share of the private key. In addition, each data owner $o{w}_i$will also publish the proof $s_i={\log }_{v^{\Delta }}V{K}_i={\log }_{c^{4\Delta }}{\left(d_i\right)}^2$. If at least $l$ data owners are verified to provide correct decryption shares, the aggregator $ag$ can obtain the decryption result by computing $m=L\left({\displaystyle \prod }_{i\in S}{d}_i^{2u_i}\mathrm{mod}{n}^2\right)\times \frac{1}{4{\Delta }^2\theta }\mathrm{mod}n$, where $u_i=\Delta \times {\lambda }_{0,i}^S\in Z$, ${\lambda }_{x,i}^S={\displaystyle \prod }_{i\text{'}\in S\backslash \left\{i\right\}}\frac{x-i\text{'}}{i-i\text{'}}$ and $L\left(u\right)=\frac{u-1}{N}$. The proof of correctness can be seen in [32]. To request data owners to join in the decryption process, the aggregator $ag$ should pay for the gradients to them. According to the addictive homomorphism of Paillier algorithm, the decryption result $m$ is equal to ${\displaystyle \sum _{i=1}^k{m}_i}$. The aggregator $ag$ will use it to update the task model.

Ownership Verification

In the collaborative training based on homomorphic encryption such as Paillier encryption, the aggregator is set to obtain only the decrypted aggregation result but not any gradient from individual data owner. Only in this way, the privacy in gradients will not be directly obtained by the aggregator. If a malicious user obtains an encrypted gradient, he may forward the encrypted gradient to another aggregator to profit. To solve the forwarding problem, the aggregator is required to verify the ownership of each received encrypted gradient.

The verification mechanism is based on Σ-protocol and Pedersen commitment scheme. As for Pedersen commitment scheme, a trusted institution is required to select two prime elements $g,h\in G$, where G is a cyclic group and ${\log }_{g}h$ is unknown to others. The process of verification is shown in Algorithm 2:

Commitment submission: After data owner $o{w}_i$ has uploaded the encrypted gradient $c_i$ to the aggregator $ag$, it computes a commitment $comm\left(r_i,m_i\right):=C_i=g^{r_i}{h}^{m_i}$, where $r_i$ is a random value and $m_i$ is the gradient. Then it submits ($C_i$, $r_i$) to the aggregator $ag$.

Commitment verification: The aggregator $ag$ will compute the aggregated gradient $c={\displaystyle \prod }_{i=1}^k{c}_i$ and the aggregated commitments $C={\displaystyle \prod }_{i=1}^k{C}_i$, $r={\displaystyle \sum _{i=1}^k{r}_i}$. Then it sends a random challenge value $e$ back to each data owner. Each $data$ owner $o{w}_i$ needs to use the challenge value $e$ to compute a response $R_i=g^{k_i}{h}^{l_i}$, $u_i=k_i+e{r}_i\mathrm{mod}p$, $v_i=l_i+e{m}_i\mathrm{mod}p$. Then each data owner submits $\left(R_i,u_i,v_i\right)$ to the aggregator $ag$. After that, the aggregator $ag$ aggregates all $\left(R_i,u_i,v_i\right)$ to obtain $\left(R,u,v\right)$ by computing $R={\displaystyle \prod }_{i=1}^k{R}_i$, $u={\displaystyle \sum _{i=1}^k{u}_i}$, $v={\displaystyle \sum _{i=1}^k{v}_i}$. Then it verifies whether $g^u{h}^v=R{C}^e$ holds. If it passes, it means that each data owner $o{w}_i$ proves it knows the secret value $m_i$ bound to the commitments $C_i$.

Ownership verification: To verify the committed value is the correct gradient, the aggregator $ag$ requests owners to decrypt the gradient $c={\displaystyle \prod }_{i=1}^k{c}_i$, and obtains the aggregated gradient $m={\displaystyle \sum }_{i=1}^k{m}_i$. Then he checks whether $C=g^r{h}^m$. If it passes, it means that the secret value $m_i$ is indeed the gradient corresponding to cipher $c_i$. The aggregator $ag$ confirms that each data owner owns the plaintext of his gradient.In our scheme, the aggregator can reduce the consumption of verification through checking the aggregated commitments. If the verification failed, it means that some data owners cannot provide the correct plaintext of their gradients. The aggregation of gradients and commitments will be rescheduled. Concretely, the aggregator can divide the group into several subgroups, then repeat the gradient aggregation and commitment verification. The malicious data owner will be identified through a series of verifications.

Security Analysis

The Protection of Gradient

In order to maintain the correctness of gradient and prevent it from being obtained directly by others, we use the addictive threshold Paillier homomorphic encryption algorithm. Firstly, we discuss the feasibility of the threshold Paillier encryption algorithm for gradient protection in our scheme.

Lemma 1:${\epsilon }_g\left(x,y\right)\to g^x\ast y^n\mathrm{mod}{n}^2$ is bijective when the order of $g$ is a non-zero multiple of $n$, and it is also a homomorphic mapping that ${\epsilon }_g\left(x_1,y_1\right)\ast {\epsilon }_g\left(x_2,y_2\right)={\epsilon }_g\left(x_1+x_2,y_1+y_2\right)$.

Lemma 2: A number $x$ is said to be an nth residue modulo $n^2$ if there exists a number $y\in Z_{n^2}^{\text{*}}$ such that $z=y^n\mathrm{mod}{n}^2$, and it is hard to find the value of $z$.The proof of Lemma 1 and Lemma 2 can be seen in [19]. Lemma 1 indicates that the aggregated ciphertext of gradient can be decrypted to the aggregated gradient. The aggregator is able to acquire aggregated gradient without knowing individual gradients. From Lemma 2, we can conclude that the ciphertext of gradient is hard to be cracked.Each data owner in our threshold Paillier algorithm has the ability to decrypt a cipher only in groups, so whenever a data owner obtains an individual encrypted gradient, he can’t decrypt it unless others collude with him. The individual gradient can be well protected in our encryption scheme.The Σ-protocol can make one prove that he knows the secret without revealing it. Specifically, a prover can state a commitment and prove that he knows the secret in the commitment. In the process of our protocol, the data owner $o{w}_i$ states $C_i:=g^{r_i}{h}^{m_i}$, and then generates two random values $\left(k_{\text{i}},l_{\text{i}}\right)$ to hide the information in $\left(R_i,u_i,v_i\right)$ to prevent gradient $m_i$ from being exposed to others.

Lemma 3: Only when the generated random values $k_{\text{i}}$ and $l_{\text{i}}$ are different, no one can recover the secret value from the $\left(R_i,u_i,v_i\right)$, that is, a commitment will not disclose any information about the committed value.The concrete proofs can be seen in [33]. As long as the data owner ensures that the random values $k_{\text{i}}$ and $l_{\text{i}}$ are different, we can think that the gradient is protected in the commitment according to Lemma 3.

The Validity of Commitment

Lemma 4: Two commitments for two different messages are different, otherwise the relationship between $g$ and $h$ can be calculated, which is not in line with the discrete logarithm hypothesis.According to Lemma 4, we know each commitment is corresponding to a unique gradient. If a data owner submits a commitment, it means that it states the ownership of a gradient. We suppose that there exists a user who forwards another data owner’s encrypted gradient. As we stated in Threat Models, we consider two kinds of treat model.If an attacker only obtains encrypted gradient, it needs to state a commitment. Consider that it does not know the plaintext of gradient $g_i$, it may commit to a secret fake gradient $g_{fake}$ and upload the commitment $C_{fake}$. In the following steps, it needs to respond to the challenge $e$, which proves the binding relationship between fake gradient $g_{fake}$ and commitment $C_{fake}$. In other words, if the verification passes, the aggregator can think that the user has committed to the plaintext of gradient, which can be denoted as $g_i$. After that, the aggregator uses the decryption result to check whether the committed $g_{fake}$ is equal to the gradient $g_i$. If not, the user’s malicious behavior of forwarding will be discovered.If an attacker obtains encrypted data as well as its historical verification information, it needs to respond to the dynamic challenge $e$ in the verification process. Due to it even does not know the committed value in commitments, the verification will fail. In other words, the historical verification information is not reusable for an attacker.Despite each data owner may obtain encrypted gradient from the aggregator in the decryption phase, the forwarding attack still does not work because of our commitment scheme.

Experimental Results

In this section, we introduce the experiments in our scheme, including the performance evaluation of Paillier algorithm and Pedersen commitment scheme. We deploy an aggregator and multiple data owners to simulate the process of collaborative training.

We build the deep learning model with Python(version3.83), Numpy(version 1.18.5), Pytorch(1.6.0) on GPUs. We use CelebFaces Attributes Dataset (CelebA) to conduct smile recognition. The dataset includes 202,599 face images with 40 binary attributes. We randomly select 60,000 images and averagely assign them to the data owners. We also use the famous MNIST dataset to conduct handwritten digit recognition. We set the epoch of training as 3. The structure of the network is shown in Table 1.

TABLE 1

TABLE 1. The structure of model.

After each iteration of the training, we output the gradient and evaluate the performance of Paillier algorithm. We compress the gradient by setting the precision of each gradient at 3–5, and use the gradient to update the model. Concretely, the data owners train their local model and output the gradient in given precision. Then we aggregate these gradients o update the model. With the change of given precision, the accuracy of the model is shown in Figure 4.

FIGURE 4

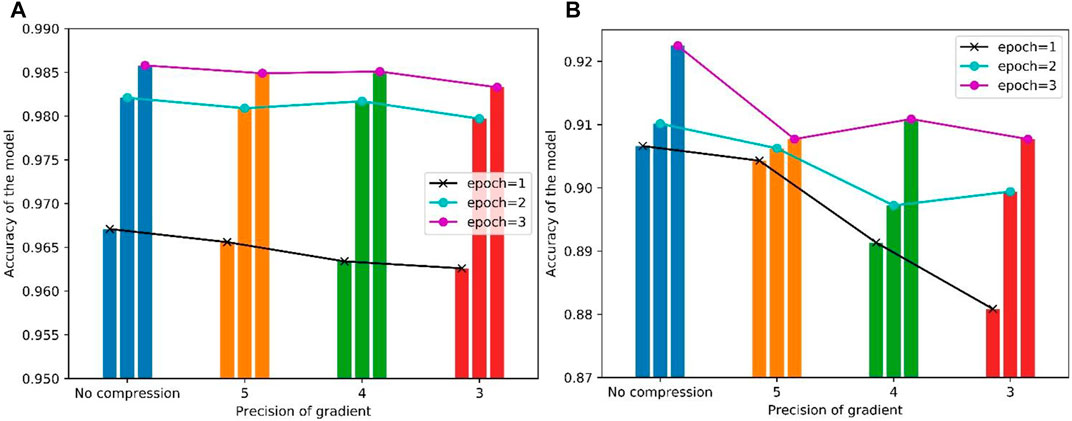
FIGURE 4. The accuracy with different precision of gradient. (A); On MNIST dataset (B) On CelebA dataset;

If we do not compress the gradient, the accuracy on CelebA dataset in each epoch is 90.66, 91.01, and 92.24%, respectively. The accuracy on MNIST dataset in each epoch is 96.71, 98.21, and 98.58%, respectively. When we control the precision of gradient at 5, 4, 3, the accuracy on CelebA dataset in the third epoch changes to 90.77, 91.08, and 90.41%, which is approximately 1.5% lower compared to the accuracy with no gradient compression. With gradient compression, the accuracy decline is not obvious on MNIST dataset, where the accuracy in the third epoch is 98.49, 98.51, and 98.33%. decreasing within 0.2%. The change of gradient precision has a more significant impact on large-scale training. When the precision decreases, the accuracy in different epochs is lower, which makes the training more difficult to converge. To ensure the quality and stability of training, we choose to set the precision at five in our subsequent experiment.

As for gradient encryption, we use the Paillier algorithm implemented in Python based on CPU. We use the Charm-crypto.¹ library to perform the encryption and decryption process of Paillier algorithm. Charm-crypto is a Python library for fast encryption on large numbers. We encode the gradient as a vector of integers that can be encrypted by Paillier algorithm. By controlling the precision of gradients, we get multiple vectors of the gradient in various lengths. Because the precision changes, the total number of parameters varies. We choose to evaluate the Paillier algorithm on a message with a length of ${10}^5$ digits. The evaluation of overhead is shown in Figure 5.

FIGURE 5

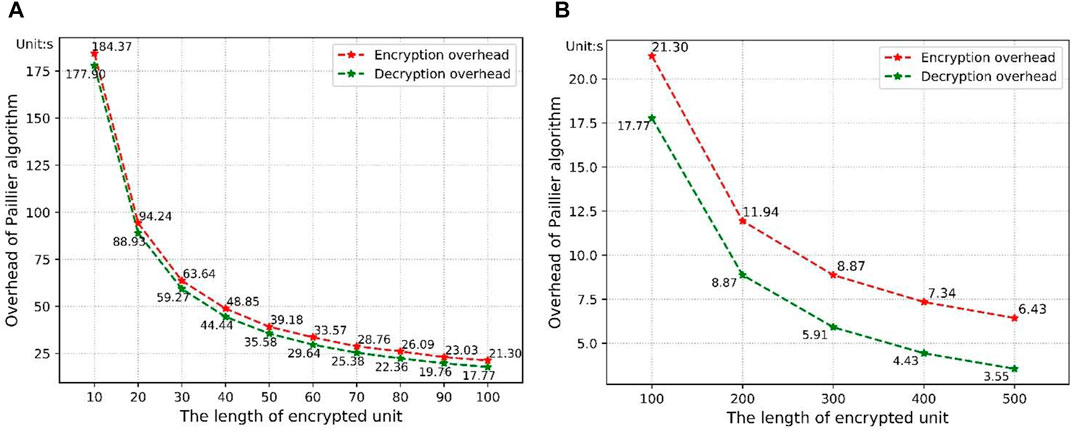
FIGURE 5. The overhead of Paillier algorithm. (A) encrypted unit $\in$[10,100]; (B) encrypted unit $\in$[100,500].

To maintain the correctness of decryption results after cipher aggregation, the length of the encrypted unit is limited by the number of ciphers and security parameters of the Paillier algorithm. On the premise that we maintain the correctness of decryption, we divide the message into multiple units to encrypt. When the length of an encrypted unit ranges from 10 to 100, as the length is doubled, the time consumption is almost halved. The length of the unit does not have a significant impact on unit encryption time. When the length ranges from 100 to 500, the unit encryption time obviously increases as the length increases, however, the total time consumption still decreases. It is better to choose a larger encryption unit if possible. Since training overhead is much higher than the gradient encryption in cooperative training, the overhead of Paillier algorithm above is acceptable.

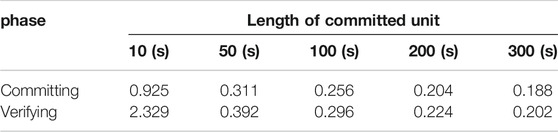
As for the Pedersen commitment scheme, we use cryptographic algorithms based on discrete logarithm to deploy it. We divide the message with a length of ${10}^5$ digits into multiple units again and evaluate the time consumption of the scheme. We first simulate the process of commitment and verification of a device. The overhead is shown in Table 2.

TABLE 2

TABLE 2. Overhead of Pedersen commitment scheme with one data owner.

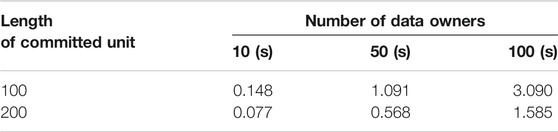
The time consumption of committing is much less than the time consumption of encryption and decryption. When the unit is larger, the total overhead of the commitment scheme is at a lower level. To evaluate the impact of the number of data owners on the commitment scheme, we set the number of data owners from 1 to 10, respectively. Each data owner needs to commit to a message with a length of ${10}^5$ digits. The experimental results can be seen in Figure 6. The total time of commitment aggregation increases because the number of devices increases. The time consumption of verification increases slightly as the number of devices increases, which almost does not influence the total time consumption of our commitment scheme.

FIGURE 6

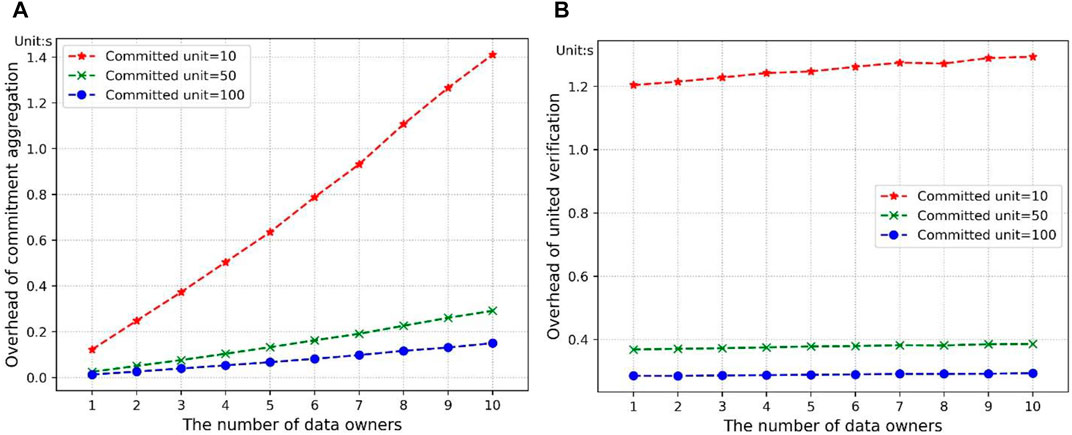
FIGURE 6. The overhead of Pedersen commitment scheme. (A) commitment aggregation; (B) commitment verification.

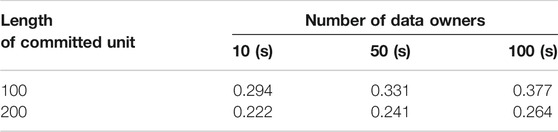
To better show the practicality of this commitment scheme in large-scale cooperative learning, we set the committed unit at 100, 200, respectively, and expand the number of devices to 50 and 100. The evaluation result can be seen in Tables 3, 4. The total time consumption is still much lower than the encryption and decryption. It means that the increase in data owners will not impose a clear burden on the commitment scheme. Our experimental results indicate that our commitment scheme is feasible in the cooperative training.

TABLE 3

TABLE 3. Overhead of large-scale commitment aggregation.

TABLE 4

TABLE 4. The Overhead of large-scale commitment verification.

Conclusion

In this paper, we propose an ownership verification mechanism against encrypted forwarding attacks in data-driven social computing. It can defend against the malicious gradient stealing and forwarding behavior in cryptography-based privacy-preserving methods. Based on the premise of maintaining gradient privacy, we present a protocol based on Σ-protocol and Pedersen commitment to achieve our security goal. Specifically, we design a united commitment algorithm to make participants cooperate to submit gradients and provide proof of data ownership. If any user submits other’s gradient, it will fail to provide correct proof to pass the verification process. The experiment results validate the security of our proposed mechanism and demonstrate the practicality of our solution.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: the Large-scale CelebFaces Attributes (CelebA) Dataset, http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html, and THE MNIST DATABASE of handwritten digits, http://yann.lecun.com/exdb/mnist/.

Author Contributions

ZS: Conceptualization and methodology, writing—original draft preparation; JW: formal analysis, validation, writing —original draft preparation; ZC: visualization; BW: project administration, supervision, and writing—review and editing; RL and YH: writing—review and editing.

Funding

This work was supported in part by the National Key R&D Program of China (No. 2018YFB2100400), in part by the National Natural Science Foundation of China (No. 62002077, 61872100), in part by the China Postdoctoral Science Foundation (No. 2020M682657), in part by Guangdong Basic and Applied Basic Research Foundation (No. 2020A1515110385), in part by Zhejiang Lab (No. 2020NF0AB01), in part by Guangzhou Science and Technology Plan Project (202102010440).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank reviewers for their critical reading and improvement of the manuscript.

Footnotes

¹The encryption library called Charm-crypto can be download in https://github.com/JHUISI/charm.

References

1. Zeroual A, Harrou F, Dairi A, Sun Y. Deep Learning Methods for Forecasting COVID-19 Time-Series Data: A Comparative Study. Chaos, Solitons & Fractals (2020) 140:110121. doi:10.1016/j.chaos.2020.110121

CrossRef Full Text | Google Scholar

2. Liang W, Yao J, Chen A, Lv Q, Zanin M, Liu J, et al. Early Triage of Critically Ill COVID-19 Patients Using Deep Learning. Nat Commun (2020) 11:3543–7. doi:10.1016/j.physrep.2007.04.00410.1038/s41467-020-17280-8

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Li F, Sun Z, Li A, Niu B, Li H, Cao G. Hideme: Privacy-Preserving Photo Sharing on Social Networks. In: IEEE INFOCOM 2019-IEEE Conference on Computer Communications; 2019, April 29-May 2; Paris, France (2019). doi:10.1109/INFOCOM.2019.8737466

CrossRef Full Text | Google Scholar

4. Han W, Tian Z, Huang Z, Li S, Jia Y. Topic Representation Model Based on Microblogging Behavior Analysis. World Wide Web (2020) 23:3083–97. doi:10.1007/s11280-020-00822-x

CrossRef Full Text | Google Scholar

5. Konečný J, McMahan HB, Ramage D, Richtárik P. Federated Optimization: Distributed Machine Learning for On-Device Intelligence. (2016) arXiv preprint arXiv:1610.02527.

Google Scholar

6. Abadi M, Chu A, Goodfellow I, McMahan HB, Mironov I, Talwar K, Zhang L. Deep Learning with Differential Privacy. In: Proceedings of the 2016 ACM SIGSAC conference on computer and communications security (2016). doi:10.1145/2976749.2978318

CrossRef Full Text | Google Scholar

7. Li T, Sahu AK, Talwalkar A, Smith V. Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal Process Mag (2020) 37:50–60. doi:10.1109/MSP.2020.2975749

CrossRef Full Text | Google Scholar

8. Li J, Wu J, Jiang G, Srikanthan T. Blockchain-based Public Auditing for Big Data in Cloud Storage. Inf Process Manage (2020) 57:102382. doi:10.1016/j.ipm.2020.102382

CrossRef Full Text | Google Scholar

9. Weng J, Weng J, Zhang J, Li M, Zhang Y, Luo W. Deepchain: Auditable and Privacy-Preserving Deep Learning with Blockchain-Based Incentive. IEEE Trans Dependable Secure Comput (2019) 1. doi:10.1109/TDSC.2019.2952332

CrossRef Full Text | Google Scholar

10. Li A, Duan Y, Yang H, Chen Y, Yang J. TIPRDC: Task-independent Privacy-Respecting Data Crowdsourcing Framework for Deep Learning with Anonymized Intermediate Representations. In: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2020, July 6-10; Virtual Event, CA, USA (2020). doi:10.1145/3394486.3403125

CrossRef Full Text | Google Scholar

11. Sun Z, Yin L, Li C, Zhang W, Li A, Tian Z. The QoS and Privacy Trade-Off of Adversarial Deep Learning: An Evolutionary Game Approach. Comput Security (2020) 96:101876. doi:10.1016/j.cose.2020.101876

CrossRef Full Text | Google Scholar

12. Aghasian E, Garg S, Gao L, Yu S, Montgomery J. Scoring Users' Privacy Disclosure across Multiple Online Social Networks. IEEE access (2017) 5:13118–30. doi:10.1109/ACCESS.2017.2720187

CrossRef Full Text | Google Scholar

13. Li S, Zhao D, Wu X, Tian Z, Li A, Wang Z. Functional Immunization of Networks Based on Message Passing. Appl Maths Comput (2020) 366:124728. doi:10.1016/j.amc.2019.124728

CrossRef Full Text | Google Scholar

14. Du J, Jiang C, Chen K-C, Ren Y, Poor HV. Community-structured Evolutionary Game for Privacy protection in Social Networks. IEEE Trans.Inform.Forensic Secur. (2018) 13:574–89. doi:10.1109/TIFS.2017.2758756

CrossRef Full Text | Google Scholar

15. Shokri R, Stronati M, Song C, Shmatikov V. Membership Inference Attacks against Machine Learning Models. In: IEEE Symposium on Security and Privacy; 2017, May 22-26; San Jose, CA, USA (2017). doi:10.1109/SP.2017.41

CrossRef Full Text | Google Scholar

16. Melis L, Song C, De Cristofaro E, Shmatikov V. Exploiting Unintended Feature Leakage in Collaborative Learning. In: IEEE Symposium on Security and Privacy. (2017); 2019, May 19-23; San Jose, CA, USA (2019). doi:10.1109/SP.2019.00029

CrossRef Full Text | Google Scholar

17. Yin L, Feng J, Lin S, Cao Z, Sun Z. A Blockchain-Based Collaborative Training Method for Multi-Party Data Sharing. Comput Commun (2021) 173:70–8. doi:10.1016/j.comcom.2021.03.027

CrossRef Full Text | Google Scholar

18. Brakerski Z, Vaikuntanathan V. Efficient Fully Homomorphic Encryption from (Standard) $\Mathsf{LWE}$. SIAM J Comput (2014) 43:831–71. doi:10.1137/120868669

CrossRef Full Text | Google Scholar

19. Paillier P. Public-key Cryptosystems Based on Composite Degree Residuosity Classes. In: International Conference on the Theory and Applications of Cryptographic Techniques; 1999, May 2-6; Prague, Czech Republic (1999). p. 223–38. doi:10.1007/3-540-48910-X_16

CrossRef Full Text | Google Scholar

20. Gentry C. Fully Homomorphic Encryption Using Ideal Lattices. In: Proceedings of the forty-first annual ACM symposium on Theory of computing; 2009, May 31-June 2; Bethesda, MD, USA (2009). doi:10.1145/1536414.1536440

CrossRef Full Text | Google Scholar

21. Phong LT, Aono Y, Hayashi T, Wang L, Moriai S. Privacy-Preserving Deep Learning via Additively Homomorphic Encryption. IEEE Trans.Inform.Forensic Secur. (2018) 13:1333–45. doi:10.1109/TIFS.2017.2787987

CrossRef Full Text | Google Scholar

22. Zhou C, Fu A, Yu S, Yang W, Wang H, Zhang Y. Privacy-preserving Federated Learning in Fog Computing. IEEE Internet Things J (2020) 7:10782–93. doi:10.1109/JIOT.2020.2987958

CrossRef Full Text | Google Scholar

23. Zhang CL, Li SY, Xia JZ, Wang W. Batchcrypt: Efficient Homomorphic Encryption for Cross-Silo Federated Learning. In: USENIX Annual Technical Conference. (2020); 2020, July 15-17; Boston, MA, USA (2020).

Google Scholar

24. Hao M, Li H, Luo X, Xu G, Yang H, Liu S. Efficient and Privacy-Enhanced Federated Learning for Industrial Artificial Intelligence. IEEE Trans Ind Inf (2020) 16:6532–42. doi:10.1109/TII.2019.2945367

CrossRef Full Text | Google Scholar

25. Damgård I. On Σ-protocols. Lecture Notes. University of Aarhus, Department for Computer Science (2002).

26. Guo JL, Liu ZY, Lam KY, Zhao J, Chen YQ, Xing CP. Secure Weighted Aggregation for Federated Learning. (2020) arXiv preprint arXiv:2010.08730.

Google Scholar

27. Xu G, Li H, Liu S, Yang K, Lin X. Verifynet: Secure and Verifiable Federated Learning. IEEE Trans.Inform.Forensic Secur. (2020) 15:911–26. doi:10.1109/TIFS.2019.2929409

CrossRef Full Text | Google Scholar

28. Guo X, Liu Z, Li J, Gao J, Hou B, Dong C, et al. VeriFL: Communication-Efficient and Fast Verifiable Aggregation for Federated Learning. IEEE Trans.Inform.Forensic Secur. (2021) 16:1736–51. doi:10.1109/TIFS.2020.3043139

CrossRef Full Text | Google Scholar

29. Schnorr CP. Efficient Signature Generation by Smart Cards. J Cryptology (1991) 4:161–74. doi:10.1007/BF00196725

CrossRef Full Text | Google Scholar

30. Pedersen TP. Non-interactive and Information-Theoretic Secure Verifiable Secret Sharing. In: Annual international cryptology conference; 1991, July 11-15; Santa Barbara, CA, USA (1991). p. 129–40. doi:10.1007/3-540-46766-1_9

CrossRef Full Text | Google Scholar

31. Li S, Jiang L, Wu X, Han W, Zhao D, Wang Z. A Weighted Network Community Detection Algorithm Based on Deep Learning. Appl Maths Comput (2021) 401:126012. doi:10.1016/j.amc.2021.126012

CrossRef Full Text | Google Scholar

32. Schoenmakers B, Veeningen M. Universally Verifiable Multiparty Computation from Threshold Homomorphic Cryptosystems. In: International Conference on Applied Cryptography and Network Security; 2015, June 2-5; New York, USA (2015). p. 3–22. doi:10.1007/978-3-319-28166-7_1

CrossRef Full Text | Google Scholar

33. Yu G. Simple Schnorr Signature with Pedersen Commitment as Key. IACR Cryptol Eprint Arch (2020).

Google Scholar