3D Mueller Matrix Reconstruction of the Optical Anisotropy Parameters of Myocardial Histopathology Tissue Samples

Diseases affecting myocardial tissues are currently a leading cause of death in developed nations. Fast and reliable techniques for analysing and understanding how tissues are affected by disease and respond to treatment are fundamental to combating the effects of heart disease. A 3D Mueller matrix method that reconstructs the linear and circular birefringence and dichroism parameters has been developed to image the biological structures in myocardial tissues. The required optical data is gathered using a Stokes polarimeter and then processed mathematically to recover the individual optical anisotropy parameters, expanding on existing 2D Mueller matrix implementations by combining with a digital holography approach. Changes in the different optical anisotropy parameters are rationalised with reference to the general tissue structure, such that the structures can be identified from the anisotropy distributions. The first to fourth order statistical moments characterising the distribution of the parameters of the optical anisotropy of the polycrystalline structure of the partially depolarising layer of tissues in different phase sections of their volumes are investigated and analysed. The third and fourth order statistical moments are found to be the most sensitive to changes in the phase and amplitude anisotropy. The possibility of forensic medical differentiation of death in cases of acute coronary insufficiency (ACI) and coronary heart disease (CHD) is considered as a diagnostic application. The optimal phase plane (${\theta }^{\ast }=0.7rad$) has been found, in which excellent differentiation accuracy is achieved ACI and CHD -$Ac\left(\Delta Z_4\left({\theta }^{\ast },{\Phi }_L,{\Delta }_L\right)\right)=93.05\%÷95.8\%$. A comparative analysis of the accuracy of the Mueller-matrix reconstruction of the parameters of the optical anisotropy of the myocardium in different phase planes ($\theta =0.9rad$ and $\theta =1.2rad$), as well as the 2D Mueller-matrix reconstruction method was carried out. This work demonstrates that a 3D Mueller matrix method can be used to effectively analyse the optical anisotropy parameters of myocardial tissues with potential for definitive diagnostics in forensic medicine.

Introduction

Myocardial tissues form the muscles in the heart and are hence critical to human life [1–3]; diseases affecting myocardial tissues are currently the leading cause of death in developed nations [4]. Myocardial tissue sections provide an excellent platform for wider understanding of cardiac function [5], and hence imaging methods that can be applied to myocardial tissues are of significant interest. As exemplified by the recent rapid spread of COVID-19, new threats with potential to affect the heart are continually emerging [6]. To keep up, fast and reliable techniques for analysing and understanding how tissues are affected by disease, and respond to treatment, are fundamental necessities. 3D imaging of structures within tissues can provide such insights. Computed tomography scanning, magnetic resonance imaging, and X-rays are widely used. However, 3D imaging techniques can be limited by relatively low sample throughput, and high cost [7–9]. Furthermore, as medical diagnostics move away from human analysis to more automated, AI-driven approaches, different techniques for looking at tissues become more viable. In particular, statistical analysis of tissue properties can give rapid results with high degrees of accuracy [10, 11]. One possibility of emerging interest is to look at the optical anisotropy of the tissue, from which one can then infer the tissue structure and other properties [12–15].

Optical anisotropy is a result of a material interacting differently with different polarisations of incident light, such that the different polarisations are absorbed, transmitted, reflected and refracted with different intensities [16]. There are four optical anisotropy properties that can be considered: linear birefringence, linear dichroism, circular birefringence, and circular dichroism. The birefringence and dichroism of a material can be determined by measuring changes in the polarisation of light passing through the material, by so-called polarimetry measurements [16–19]. Polarimetry is a relatively easy technique to implement - at its most simple, requiring only: a light source (laser), polarising filters (and quarter wave plate for circular birefringence and dichroism measurements), and a detector [20, 21]. To achieve greater sensitivity of measurements, one can employ interferometric techniques.

Looking at the optical anisotropy of myocardial tissues is promising for two reasons: firstly, the tissues contain spatially ordered protein fibrils which should demonstrate clear linear anisotropy; secondly, the tissues are partially depolarising. After polarimetric measurements of the four anisotropy properties, it is necessary to correlate the experimental data with the physical sample under investigation. Mueller Matrix Polarimetric (MMP) diagnostics are the tool of choice for this purpose, with many distinct directions being considered, including: the investigation of scattering matrices [1, 22–25]; Mueller matrix polarimetry [17, 26–29]; polar decomposition of Mueller matrices [30, 31]; and two-dimensional Mueller matrix mapping [18, 19, 32, 33]. A Mueller matrix is a 4 × 4 matrix representing the effect of a specific optical element on the polarisation of light. The multiplication of the initial Stokes vector of light passing through the element by the Mueller matrix of the element gives the Stokes vector of the output light. MMP methods and tools have evolved around two limiting approximations. The first is the search for relationships between the angular indicatrices (1D), the coordinate Mueller matrix distributions (2D), and the structure of diffuse (depolarising) layers [1, 24–27]. The second is the MMP of optically thin, non-depolarising layers [17, 28, 29] with subsequent reconstruction of the distributions of the phase and amplitude anisotropy parameters [10, 11, 34–41].

However, while such 2D methods maybe useful for imaging and characterising surfaces or materials which are isotropic in at least one direction, they are of limited use for more complex systems. It is generally desirable to understand variations across a structure fully in three dimensions. Hence, there is a need to expand MMP diagnostic techniques to three dimensions. Additionally, most biological objects are partially depolarising. They have spatially inhomogeneous, optically anisotropic structures. Therefore, it is necessary to further develop and generalise existing MMP techniques to consider such partially depolarising structures. The theoretical basis of this direction can be established from the synthesis of methods of differential Mueller matrix [12, 13, 42–45] and holographic mapping of phase-inhomogeneous layers [46, 47]. Here, we develop and experimentally demonstrate a technique for the 3D Mueller matrix reconstruction of the phase and amplitude anisotropy parameters. We first outline the method for Mueller matrix analysis in two dimensions, before demonstrating the further development to three dimensions. We then consider the functional possibility of 3D reconstruction of each of the four parameters of the optical anisotropy of a myocardial tissue layer. Finally, the approbation of the approach is carried out for definitive diagnosis of myocardium tissue death as a result of acute coronary insufficiency (ACI) and coronary heart disease (CHD).

Theory and Methods

2D Mueller Matrix Reconstruction

The 2D Mueller matrix reconstruction of the distributions of linear and circular birefringence and dichroism within biological layers has previously been considered in detail [48]. The matrix operator $D$ characterises the distribution of the mean values of the parameters of the phase ($\Phi$) and amplitude ($\Delta$) anisotropy. The second-order differential matrix $\tilde{D}$ determines the changes in the polarisation due to fluctuations of the linear and circular birefringence ($\tilde{\Phi }$) and dichroism ($\tilde{\Delta }$). The Mueller matrix resulting from the superposition of the first order (fully polarised part $D$) and second order (fully depolarised part $\tilde{D}$) differential matrices [42, 43] gives algorithms for the interrelation between the distributions of phase and amplitude anisotropy and Mueller matrix images. Here we confine ourselves to the consideration of the completely polarised component of the Mueller matrix - the coordinate distributions of the elements of the first-order differential matrix $d_{ik}\left(x,y\right)$. The matrix operator $D$ is defined as

$\begin{array}{c}\langle \Vert D\Vert \rangle =\Vert \begin{array}{cccc}0& {\mathit{\Delta }}_{\mathrm{0,90}}& {\mathit{\Delta }}_{\mathrm{45,135}}& {\mathit{\Delta }}_{\otimes ,\oplus }\\ {\mathit{\Delta }}_{\mathrm{0,90}}& 0& {\mathit{\Phi }}_{\otimes ,\oplus }& -{\mathit{\Phi }}_{\mathrm{45,135}}\\ {\mathit{\Delta }}_{\mathrm{45,135}}& -{\mathit{\Phi }}_{\otimes ,\oplus }& 0& {\mathit{\Phi }}_{\mathrm{0,90}}\\ {\mathit{\Delta }}_{\otimes ,\oplus }& {\mathit{\Phi }}_{\mathrm{45,135}}& -{\mathit{\Phi }}_{\mathrm{0,90}}& 0\end{array}\Vert \end{array}.(1)$

It contains six distinct, non-zero parameters:

• ${\mathit{\Delta }}_{\mathrm{0,90}} , {\mathit{\Delta }}_{\mathrm{45,135}}$ – the linear dichroism between the orthogonal components $0°-90°$ and $45°-135°$, respectively;

• ${\mathit{\Phi }}_{\mathrm{0,90}} , {\mathit{\Phi }}_{\mathrm{45,135}}$ – the linear birefringence between the orthogonal components $0°-90°$ and $45°-135°$, respectively;

• ${\mathit{\Delta }}_{\otimes ,\oplus }$ – the circular dichroism for between right- ($\otimes$) and left- ($\oplus$) circularly polarised components.

These phase and amplitude anisotropy parameters are in turn determined by the following identities:

$\begin{array}{c}\begin{array}{cc}{\varphi }_{\mathrm{0,90}}=\frac{2\pi }{\lambda }\Delta n_{\mathrm{0,90}}l;& \mathit{\Delta }{n}_{\mathrm{0,90}}=n_0-n_{90};\end{array}\end{array}(2)$

$\begin{array}{c}\begin{array}{cc}{\varphi }_{45;135}=\frac{2\pi }{\lambda }\Delta n_{45;135}l;& \mathit{\Delta }{n}_{45;135}=n_{45}-n_{135};\end{array}\end{array}(3)$

$\begin{array}{c}{\varphi }_{\otimes ,\oplus }\equiv {\varphi }_C=\frac{2\pi }{\lambda }\mathit{\Delta }{n}_{\otimes ,\oplus }l\begin{array}{cc};& \mathit{\Delta }{n}_{\otimes ,\oplus }=n_{\otimes }-n_{\oplus }\end{array};\end{array}(4)$

$\begin{array}{c}\begin{array}{cc}{\mathit{\Delta }}_{\mathrm{0,90}}=\frac{2\pi }{\lambda }\mathit{\Delta }{\tau }_{0;90}l;& \mathit{\Delta }{\tau }_{\mathrm{0,90}}={\tau }_0-{\tau }_{90};\end{array}\end{array}(5)$

$\begin{array}{c}\begin{array}{cc}{\mathit{\Delta }}_{45;135}=\frac{2\pi }{\lambda }\mathit{\Delta }{\tau }_{45;135}l;& \mathit{\Delta }{\tau }_{45;135}={\tau }_{45}-{\tau }_{135};\end{array}\end{array}(6)$

$\begin{array}{c}\begin{array}{cc}{\mathit{\Delta }}_{\otimes ;\oplus }\equiv {\mathit{\Delta }}_C=\frac{2\pi }{\lambda }\mathit{\Delta }{\tau }_{\otimes ;\oplus }l;& \mathit{\Delta }{\tau }_{\otimes ;\oplus }={\tau }_{\otimes }-{\tau }_{\oplus }\end{array}\end{array}(7)$

Here: $n_j$ and ${\tau }_j$ are the refractive indices and absorption coefficients for the j-polarised components (where j: $0°-90°$, $45°-135°$, and $\otimes -\oplus$) of the incident laser radiation; $\lambda$ is the wavelength of the laser radiation; and $l$ is the thickness of the sample under investigation. For a partially depolarising layer, the following inter-relations between the individual elements of the first-order differential matrix $d_{ik}$ and the individual elements of the Mueller matrix $F_{ik}$ exist:

$\begin{array}{c}\langle \Vert D\Vert \rangle =l^{-1}\{\begin{array}{c}\langle d_{12}\rangle =\langle d_{21}\rangle =ln\left(F_{12}{F}_{21}\right);\\ \langle d_{13}\rangle =\langle d_{31}\rangle =ln\left(F_{13}{F}_{31}\right);\\ \langle d_{14}\rangle =\langle d_{41}\rangle =ln\left(F_{14}{F}_{41}\right);\\ \langle d_{23}\rangle =\langle -d_{32}\rangle =ln\left(\frac{F_{23}}{F_{32}}\right);\\ \langle d_{24}\rangle =\langle -d_{42}\rangle =ln\left(\frac{F_{24}}{F_{42}}\right);\\ \langle d_{34}\rangle =\langle -d_{43}\rangle =ln\left(\frac{F_{34}}{F_{43}}\right).\end{array}\end{array}(8)$

By combining Eqs 2–7 with Eq. 8, we obtain algorithms determining the birefringence and dichroism from the elements of the Mueller matrix:

$\begin{array}{c}{\varphi }_{\left(0;90\right);\left(45;135\right);\left(\otimes ;\oplus \right)}=\{\begin{array}{c}{\delta }_{\mathrm{0,90}}=\frac{2\pi z}{\lambda }\Delta n_{\mathrm{0,90}}=ln\left(\frac{F_{24}}{F_{42}}\right);\\ {\delta }_{\mathrm{45,135}}=\frac{2\pi z}{\lambda }\Delta n_{\mathrm{45,135}}=ln\left(\frac{F_{34}}{F_{43}}\right);\\ {\varphi }_{\otimes ;\oplus }=\frac{2\pi z}{\lambda }\Delta n_{\otimes ,\oplus }=ln\left(\frac{F_{23}}{F_{32}}\right);\end{array}\end{array}(9)$

$\begin{array}{c}{\Delta }_{\left(0;90\right);\left(45;135\right);\left(\otimes ;\oplus \right)}=\{\begin{array}{c}{\tau }_{\mathrm{0,90}}=\frac{2\pi z}{\lambda }\Delta {\tau }_{\mathrm{0,90}}=ln\left(F_{12}{F}_{21}\right);\\ {\tau }_{\mathrm{45,135}}=\frac{2\pi z}{\lambda }\Delta {\tau }_{\mathrm{45,135}}=ln\left(F_{13}{F}_{31}\right);\\ {\chi }_{\otimes ;\oplus }=\frac{2\pi z}{\lambda }\Delta {\tau }_{\otimes ,\oplus }=ln\left(F_{14}{F}_{41}\right).\end{array}\end{array}(10)$

These analytical expressions are the basis of Mueller matrix reconstruction of mean values of the optical anisotropy parameters of the layer. Without reducing the completeness of the analysis [42], we can reduce the system to consider only the generalised parameters of linear birefringence $\left(\mathit{\Phi }\right)$ and linear dichroism $\left(\mathit{\Delta }\right)$:

$\begin{array}{c}{\mathit{\Phi }}_L=\sqrt{{\mathit{\Phi }}_{0;90}^2+{\mathit{\Phi }}_{45;135}^2};\end{array}(11)$

$\begin{array}{c}{\mathit{\Delta }}_L=\sqrt{{\mathit{\Delta }}_{0;90}^2+{\mathit{\Delta }}_{45;135}^2}.\end{array}(12)$

Also noting the identities Eq 4, 7, we now have a complete set of the four anisotropy parameters ${\mathit{\Delta }}_L$, ${\mathit{\Delta }}_C$, ${\mathit{\Phi }}_L$, and ${\mathit{\Phi }}_C$. We note that the 2D Mueller matrix reconstruction obtains the averaged distributions of linear and circular birefringence and dichroism over the entire thickness $l$ of the sample, without considering variations in the $z$ direction. However, a complete analysis requires equal consideration of all three dimensions. Therefore, it is important to obtain 3D Mueller matrix images (i.e., $F_{ik}\left(x,y,z\right)\to \left\{{\mathit{\Phi }}_L;{\mathit{\Phi }}_C;{\Delta }_L{\Delta }_C\right\}\left(x,y,z\right)$).

3D Expansion

The key principle for the determination of a three-dimensional layered series of distributions of Mueller matrix elements $F_{ik}\left(x,y,z\right)$ is the use of a reference laser radiation wave [48, 49]. The six distinct polarization states are obtained in both the illuminating (Zond) and reference (Ref) beams: {Zond–Ref} => 0°; 90°; 45°; 135°; $\otimes ; \oplus$ utilizing polarizer. The detection of partial interference patterns at the CCD camera (14, see Figure 1) through the polarizer-analyzer is defined with the orientation of the transmission plane at angles p = 0°; 90°. A two-dimensional discrete Fourier transform $DF\left(\upsilon ,\nu \right)$ is applied to each partial interference distribution/image. The $DF\left(\upsilon ,\nu \right)$ of a two-dimensional array $I_{P=0^0;{90}^0}\left(x,y\right)$ is a function of two discrete variables coordinates $\left(x,y\right)$ is defined as [23]:

$D{F}_{P=0^0;0^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(\upsilon ,\nu \right)=\frac{1}{A\times B}{\displaystyle \sum _{a=0}^{A-1}{\displaystyle \sum _{b=0}^{B-1}{I}_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(a,b\right)\exp \left[-i2\pi \left(\frac{a\times \upsilon }{A}+\frac{b\times \nu }{B}\right)\right]}},(13)$

where $I_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(a,b\right)=E_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(a,b\right)E_{P=0^0;{90}^0}^{\ast 0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(a,b\right)$ are the coordinate distributions of the intensity of the interference pattern filtered by the analyser with the orientation of its transmission axis at $\begin{array}{cc}P=0^0;& {90}^0\end{array}$; $E_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(a,b\right)$ are the orthogonal projections of the complex amplitudes; $\ast$ denotes the complex conjugation operation; $\left(\upsilon ,\nu \right)$ are the spatial frequencies in the x and y directions respectively; and $\left(A\times B\right)$ are the number of pixels of the CCD camera in the $a$ and $b$ directions respectively, such that $0\le a,\upsilon \le A$ and $0\le b,\nu \le B$. The results of this transformation contain three peaks, one central (main) peak and two secondary side peaks. Thereby, $DF\left(\upsilon ,\nu \right)$ works like a low-pass filter extracting complex representation of real field by removing carrier (interference fringes). Since the extracted part has limited size, it also serves like a low-pass filter for the object field. By extracting one of the secondary side peak and placing it into centre of a newly generated spectrum $D{F}_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(\upsilon ,\nu \right)$ can be created. Applying a two-dimensional inverse discrete Fourier transform ${\left(D{F}^{\ast }\right)}_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(\upsilon ,\nu \right)$ on the newly obtained spectrum $D{F}_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(\upsilon ,\nu \right)$, one gets:

${\left(D{F}^{\ast }\right)}_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(\upsilon ,\nu \right)=\frac{1}{A\times B}{\displaystyle \sum _{a=0}^{A-1}{\displaystyle \sum _{b=0}^{B-1}{I}_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(a,b\right)\exp \left[-i2\pi \left(\frac{a\times \upsilon }{A}+\frac{b\times \nu }{B}\right)\right]}},(14)$

where ${\left(D{F}^{\ast }\right)}_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(a,b\right)\equiv E_{P=0^0;{90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left(a,b\right)$.

FIGURE 1

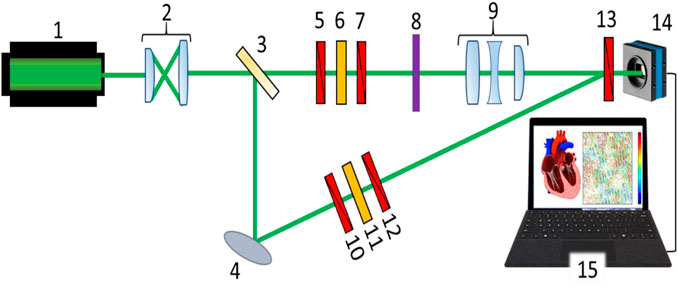
FIGURE 1. Schematic presentation of the 3D Mueller matrix-based polarimetry system: 1 – HeNe laser; 2 – collimator; 3 – beam splitter; 4 – rotary mirror; 5,7,10,12,13 – polarisation filters; 6 – quarter wave plate; 8 – sample under investigation; 9 – strain-free objective; 14 – CCD camera; and 15 – PC.

Therefore, a distribution of complex amplitudes:

$\{\begin{array}{l}{P}_{0^0}\to \left|E_{P=0^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\right|;\\ P_{{90}^0}\to \left|E_{P={90}^0}^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\right|\exp \left(i\left({\delta }_{{90}^0}-{\delta }_{0^0}\right)\right)\end{array}.(15)$

is obtained for each state of polarization {Zond–Ref} in different phase planes ${\theta }_i=\left({\delta }_{{90}^0}-{\delta }_{0^0}\right)$.

In single scattering approximation the phase of the fields of complex amplitudes Eq. 15 relates to physical depth $z_i$ in the volume of an optical anisotropy of biological layer

$z_i=\frac{\lambda }{2\pi \Delta n}{\theta }_i.(16)$

While in multiple scattering the physical or effective depth $z_i^{\ast }$ becomes proportional to the thickness of biological layer $z$

$z_i^{\ast }\sim {\rm K}z.(17)$

The corresponding parameters of Stokes vector and polarization parameters of the object field for each phase plane ${\theta }_i$ are defined as:

$\{\begin{array}{c}{S}_1^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left({\theta }_i,a,b\right)=\left({\left|E_0\right|}^2+{\left|E_{90}\right|}^2\right)\left({\theta }_i,a,b\right);\\ S_2^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left({\theta }_i,a,b\right)=\left({\left|E_0\right|}^2-{\left|E_{90}\right|}^2\right)\left({\theta }_i,a,b\right);\\ S_3^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left({\theta }_i,a,b\right)=2\mathrm{Re}\left|E_0{E}_{90}^{\ast }\right|\left({\theta }_i,a,b\right);\\ S_4^{0^0;{90}^0;{45}^0;{135}^0;\otimes ;\oplus }\left({\theta }_i,a,b\right)=2\mathrm{Im}\left|E_0{E}_{90}^{\ast }\right|\left({\theta }_i,a,b\right).\end{array}(18)$

Based on relations Eq 14, 15, 18, the elements of Mueller matrix $\left\{F\right\}$ are calculated using the following Stokes-based polarimetric relation:

$\begin{array}{l}\left\{F\right\}\left({\theta }_i,a,b\right)=\Vert \begin{array}{cccc}{F}_{11}& F_{12}& F_{13}& F_{14}\\ F_{21}& F_{22}& F_{23}& F_{24}\\ F_{31}& F_{23}& F_{24}& F_{34}\\ F_{41}& F_{24}& F_{34}& F_{44}\end{array}\Vert =\\ \begin{array}{c}=0.5\left(\Vert \begin{array}{cccc}\left(S_1^0+S_1^{90}\right);& \left(S_1^0-S_1^{90}\right);& \left(S_1^{45}-S_1^{135}\right);& \left(S_1^{\otimes }-S_1^{\oplus }\right);\\ \left(S_2^0+S_2^{90}\right);& \left(S_2^0-S_2^{90}\right);& \left(S_2^{45}-S_2^{135}\right);& \left(S_2^{\otimes }-S_2^{\oplus }\right);\\ \left(S_3^0+S_3^{90}\right);& \left(S_3^0-S_3^{90}\right);& \left(S_3^{45}-S_3^{135}\right);& \left(S_3^{\otimes }-S_3^{\oplus }\right);\\ \left(S_4^0+S_4^{90}\right);& \left(S_4^0-S_4^{90}\right);& \left(S_4^{45}-S_4^{135}\right);& \left(S_4^{\otimes }-S_4^{\oplus }\right)\end{array}\Vert \right)\left({\theta }_i,a,b\right).\end{array}\end{array}(19)$

Finally, the layer-by-layer distributions of the mean values of linear and circular birefringence and dichroism $W\left({\Phi }_{0;90},{\Phi }_{45;135},{\Phi }_{\otimes ;\oplus },{\Delta }_{0;90},{\Delta }_{45;135},{\Delta }_{\otimes ;\oplus }\right)$ is obtained by applying Eq 9, 10 to distributions Eq. 19:

${\Phi }_{0;90}\left({\theta }_i,a,b\right)=\ln \left(\frac{\left(S_3^{\otimes }-S_3^{\oplus }\right)}{\left(S_4^{45}-S_4^{135}\right)}\right)\left({\theta }_i,a,b\right),(20)$

${\Phi }_{45;135}\left({\theta }_i,a,b\right)=\ln \left(\frac{\left(S_2^{\otimes }-S_2^{\oplus }\right)}{\left(S_4^0-S_4^{90}\right)}\right)\left({\theta }_i,a,b\right),(21)$

${\Phi }_{\otimes ;\oplus }\left({\theta }_i,a,b\right)=\ln \left(\frac{\left(S_2^{45}-S_2^{135}\right)}{\left(S_3^0-S_3^{90}\right)}\right)\left({\theta }_i,a,b\right),(22)$

${\Delta }_{0;90}\left({\theta }_i,a,b\right)=\ln \left(\left(S_1^0-S_1^{90}\right)\left(S_2^0+S_2^{90}\right)\right)\left({\theta }_i,a,b\right),(23)$

${\Delta }_{45;135}\left({\theta }_i,a,b\right)=\ln \left(\left(S_1^{45}-S_1^{135}\right)\left(S_3^0+S_3^{90}\right)\right)\left({\theta }_i,a,b\right),(24)$

${\Delta }_{\otimes ;\oplus }\left({\theta }_i,a,b\right)=\ln \left(\left(S_1^{\otimes }-S_1^{\oplus }\right)\left(S_4^0+S_4^{90}\right)\right)\left({\theta }_i,a,b\right).(25)$

Thus, such a polarization-interference-based cultivation Eqs 13–15, 18, 19 of elements of the first-order differential matrix Eqs 1–10 provides layer-by-layer maps of linear and circular birefringence and dichroism of the myocardial fibrillary networks. This approach extends significantly the functionality of the 3D Mueller-matrix imaging technique for depolarization mapping of diffuse biological layers [48, 49], that presently utilized only diagonal elements of the resulting Mueller matrix Eq. 19.

Experimental Setup

Figure 1 shows the optical arrangement of the 3D Mueller matrix-based polarimetry system developed in-house. The parallel beam ($\mathrm{\oslash }=2\times {10}^3\mu m$) of the He-Ne laser ($\lambda =0.6328 \mu m$), formed by the collimator, and the beam splitter, is divided into two equally intense beams. These are denoted as the irradiating and reference beams, respectively. The irradiating beam is guided through the polarisation filters 5–7 to the sample 8.

A polarisation-inhomogeneous image of the object 8 is projected into the plane of the digital camera 14 (The Imaging Source DMK 41AU02.AS, monochrome 1/2 " CCD, Sony ICX205AL (progressive scan); resolution–1280 × 960; sensor area - 7600 × 6200 μm; sensitivity - 0.05 lx; dynamic range - 8 bit; signal-to-noise ratio - 9 bit) by the lens 9 (Nikon CFI Achromat P, focal distance - 30mm, numerical aperture - 0.1, magnification - ×4). The reference beam is guided, by the mirror 4, through the polarisation filters 10–12 into the plane of the polarisation-inhomogeneous image of the object 9. As a result, an interference pattern is formed which is recorded by the digital camera 14. The formation of the required polarisation states of the irradiating and reference beams is carried out using polarisation filters 5–7 and 10–12, each of which contains two linear polarisers (B + W Kaesemann XS-Pro Polariser MRC Nano) and a quarter-wave plate (Achromatic True Zero-Order Waveplate).

The layer-by-layer 3D Muller-matrix polarimetry system was calibrated using quarter and half wave-plates, demonstrating an accuracy of measuring the magnitude of the elements of Mueller matrix: $F_{i=1;2;3;j=1;2;3}$ ∼ 0.005, and $F_{i=1;2;3;4;j=4;}{F}_{i=4;j=1;2;3;4}$ - 0.01.

Assessment of Optical Anisotropy

The layer-by-layer assessment of optical anisotropy $W$ of myocardium histological sections is utilized by using first ($Z_1$) second ($Z_2$), third ($Z_3$) and fourth ($Z_4$) order statistical moments [14, 15]:

$\begin{array}{c}{Z}_1=\frac{1}{C}{\displaystyle \sum _{j=1}^{C}W{\left({\theta }_i,a,b\right)}_j;}\\ Z_2=\sqrt{\frac{1}{C}{\displaystyle \sum _{j=1}^C{\left(W^2\left({\theta }_i,a,b\right)\right)}_j;}}\\ Z_3=\frac{1}{Z_2^3}\frac{1}{C}{\displaystyle \sum _{j=1}^C{\left(W^3\left({\theta }_i,a,b\right)\right)}_j;}\\ Z_4=\frac{1}{Z_2^4}\frac{1}{C}{\displaystyle \sum _{j=1}^C{\left(W^4\left({\theta }_i,a,b\right)\right)}_j,}\end{array}(26)$

where $C=A\times B$ - number of pixels of the photosensitive area of the CCD camera.

Biological Samples

Three groups of myocardial histological sections were utilized in the study. Control group–Group 1 with the myocardial tissues that have no relation to myocardial diseases, whereas Group 2 and Group 3 with the structural malformations in myocardial tissues caused by ACI and CHD, respectively. All the groups consisted of equal number of histological sections:$k=36$ .The histological sections of the myocardium were prepared according to the standard technique on a microtome with quick freezing.

Figure 2 shows the original images of the histological sections of the myocardium from all three groups. The coordinate intensity distribution $I\left(a,b\right)$ was normalized according to the maximum value $I_{\max }$ in the image plane.

FIGURE 2

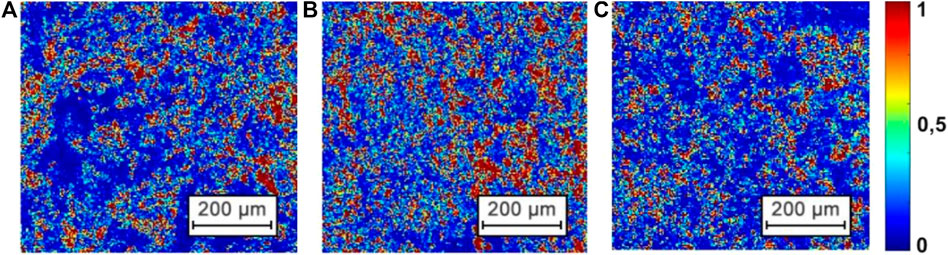
FIGURE 2. The examples of original CCD detected images of samples of histological sections of the myocardium from Group 1 (A), Group 2 (B), and Group 3 (C).

The obtained images (see Figure 2) show for all groups a fibrillar morphology structure consisting of a network of protein fibers, formed by optically active molecules of myosin and by optically isotropic molecules of actin [1].

Qualitative (visual) and quantitative (statistical) analysis of given microscopic images did not reveal significant differences between the three groups of myocardium histological samples. Table 1 presents the optical, geometrical and statistical parameters of the myocardium histological samples from each of the groups.

TABLE 1

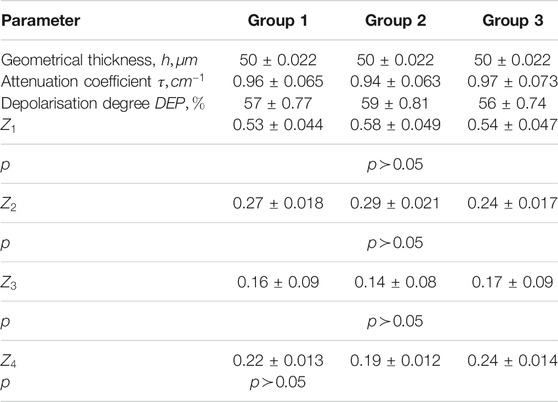
TABLE 1. Optical, geometrical and statistical parameters of the myocardium histological sections samples.

The attenuation (extinction) coefficient ($\tau ,c{m}^{-1}$) of the myocardium histological samples was assessed by standard photometry spectral approach [50], utilizing the integrating sphere [51]. The degree of depolarization ($DEP,\%$) was measured with standard Mueller-matrix polarimeter [14, 15]. In terms of statistical significance [52] the standard deviation (${\vartheta }^2\le 0.025$) corresponds to a confidence interval $p\prec 0.05$, which demonstrates the statistical reliability of the 3D Mueller-matrix mapping method. The quantitative differentiation of samples of histological sections of the myocardium of different groups by the method of statistical analysis of coordinate distributions $\frac{I\left(a,b\right)}{I_{\max }}$ turned out to be statistically unreliable $p\succ 0.05$.

The studies conducted in accordance with the principles of the Declaration of Helsinki, and in compliance with the International Conference on Harmonization-Good Clinical Practice and local regulatory requirements. Ethical approval was obtained from the Ethics Committee of the Bureau of Forensic Medicine of the Chernivtsi National University and the Bukovinian State Medical University (Chernivtsi, Ukraine), and written informed consent was obtained from all subjects prior to study initiation.

The spatial order of fibrillary network that formed polycrystalline structure of myocardium, is optically discernible as linear birefringences and dichroism, whereas the optical activity of molecular domains of myosin forms a circular birefringence and dichroism [1–6, 17, 25]. The most optically expressed such These phenomena are seeing more clearly at the low level of depolarization background that is formed due to multiple scattering of light within the sample of histological sections of myocardium.

Therefore, polarization-based layer-by-layer detection of optical anisotropy and its variations provides a new quantitative approach of the evaluation of myocardial samples morphological structure and its pathological changes.

Results and Discussion

A key feature of the morphological structure of myocardial tissue is the presence of a spatially ordered network of protein fibrils. These fibrils are formed by optically active molecules of myosin and isotropic actin proteins [1]. In terms of optics such a network has two types of anisotropy, namely the structural anisotropy leading to linear birefringence (${\Phi }_L$) and dichroism (${\Delta }_L$), and correspondingly to the circular birefringence (${\Phi }_C$) and dichroism (${\Delta }_C$) [25].

3D Mueller matrix-based polarimetry approach (see Figure 1) is utilized for preconstruction of the phase and amplitude anisotropy parameters to the functional diagnostic imaging of myocardial tissues in vitro. In particular functional capabilities of 3D Mueller-matrix layer-by-layer reconstruction of optical anisotropy parameters were investigated utilizing sample of myocardium histological section from Group 1. Figures 3, 4 show structural optical anisotropy obtained, respectively, for linear and circular birefringence and linear and circular dichroism for the different physical depths Eq. 16, and, correspondingly, Figures 5, 6 demonstrate structural optical anisotropy for the effective depths Eq. 17.

FIGURE 3

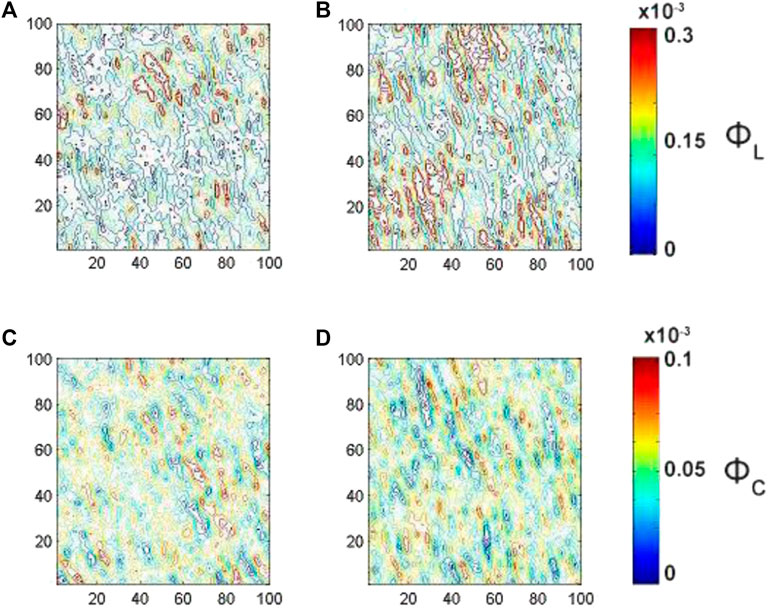
FIGURE 3. Embossed topographic maps of linear (A)${\Phi }_L\left({\theta }_1=0.4rad\iff z_1\approx 25\mu m\right)$ and (B)${\Phi }_L\left({\theta }_2=0.75rad\iff z_2\approx 50\mu m\right)$, and circular (C)${\Phi }_C\left({\theta }_1=0.4rad\iff z_1\approx 25\mu m\right)$ and (D)${\Phi }_C\left({\theta }_2=0.75rad\iff z_2\approx 50\mu m\right)$ birefringence of myocardial histological section.

FIGURE 4

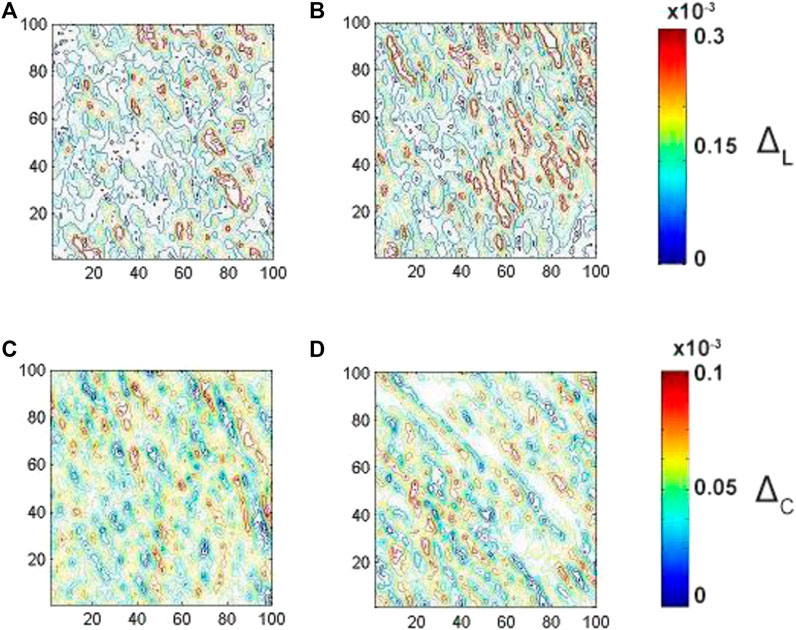
FIGURE 4. Embossed topographic maps of linear (A)${\Delta }_L\left({\theta }_1=0.4rad\iff z_1\approx 25\mu m\right)$ and (B)${\Delta }_L\left({\theta }_2=0.75rad\iff z_2\approx 50\mu m\right)$ and circular (C)${\Delta }_C\left({\theta }_1=0.4rad\iff z_1\approx 25\mu m\right)$ and (D)${\Delta }_C\left({\theta }_2=0.75rad\iff z_2\approx 50\mu m\right)$ dichroism of myocardial histological section.

FIGURE 5

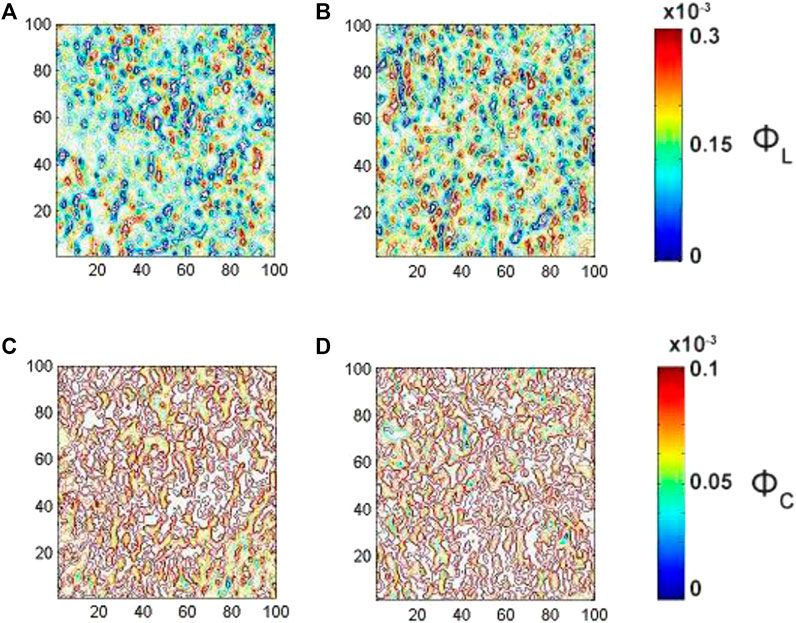
FIGURE 5. Embossed topographic maps of linear (A)${\Phi }_L\left({\theta }_3=1.5rad\iff z_3^{\ast }\approx 100\mu m\right)$ and (B)${\Phi }_L\left({\theta }_4=2.3rad\iff z_4^{\ast }\approx 150\mu m\right)$ and circular (C)${\Phi }_C\left({\theta }_3=1.5rad\iff z_3^{\ast }\approx 100\mu m\right)$ and (D)${\Phi }_C\left({\theta }_4=2.3rad\iff z_4^{\ast }\approx 150\mu m\right)$ birefringence of myocardial histological section.

FIGURE 6

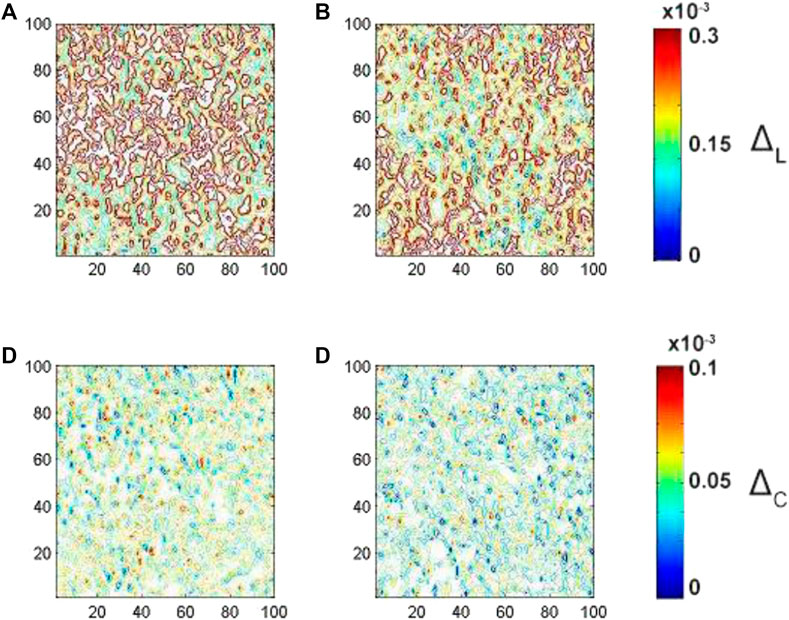
FIGURE 6. Embossed topographic maps of (A) linear ${\Delta }_L\left({\theta }_3=1.5rad\iff z_3^{\ast }\approx 100\mu m\right)$ and (B)${\Delta }_L\left({\theta }_4=2.3rad\iff z_4^{\ast }\approx 150\mu m\right)$ birefringence and circular (C)${\Delta }_C\left({\theta }_3=1.5rad\iff z_3^{\ast }\approx 100\mu m\right)$ and (D)${\Delta }_C\left({\theta }_4=2.3rad\iff z_4^{\ast }\approx 150\mu m\right)$ dichroism of myocardial histological section.

The next stage is devoted to demarcation of the samples of myocardium histological sections from Group 2 and Group 3 according the most effective phase plan Eq. 15 and the corresponding depth Eq 16, 17, guided with the following parameters: $\Delta n\approx 1.5\times {10}^{-3}$,$h=50\mu m$, $\lambda =0.63\mu m$.

A single pass of laser light through the histological section of the myocardium corresponds to the value θ(K = 1) ≈ 0.75 rad ⇔ z(K = 1) ≈ 50 µm double θ(K = 2) ≈ 1.5 rad ⇔ z(K = 2) ≈ 50 µm etc. In other words, the phase shifts correspond to the predominantly single scattering or low order of multiplicity of scattering. Whereas for $\theta \ge 1.5rad$ and over the multiple scattering prevails. Therefor the complex amplitudes phase scanning are considered for both single scattering: ${\theta }_1=0.4rad\iff z_1\approx 25\mu m;{\theta }_2=0.75rad\iff z_2\approx 50\mu m$(see Figures 3, 4) and multiple scattering: ${\theta }_3=1.5rad\iff z_3^{\ast }\approx 100\mu m;{\theta }_4=2.3rad\iff z_4^{\ast }\approx 150\mu m$(see Figures 5, 6).

The analysis of the embossed topographic maps of myocardial histological section with distinctive single scattering shows a peculiar spatial distribution of linear and circular birefringence (see Figure 3) and dichroism (see Figure 4) at the variety of physical depths (Z_i), defined by Eq. 16. The large-scale domains, the structure of which correlates with the size and directions of folding of protein fibrillar fibers, are seeing clearly both at the embossed topographic maps of circularly birefringence ${\Phi }_L$ in Figures 3A,B and dichroism ${\Delta }_L$ in Figures 4A,B. At the same time the small-scale domains that correspond to the coordinate positions of optically active molecular domains are observed at the embossed topographic maps of circularly birefringence ${\Phi }_C$ (see Figures 3C,D) and dichroism ${\Delta }_C$ (see Figures 4C,D). With the increase of physical depth (Z_i) the magnitude and spread of random values of the parameters of linear and circular birefringence are also growing progressively.

The analysis of the embossed topographic maps of myocardial histological section at multiple scattering shows the significantly lower alterations in the structure of the spatial distributions of linear and circular birefringence (see Figure 5) and dichroism (see Figure 6) at the variety of physical depths (Z_i*), defined by Eq. 17. The scale of domain structure of the embossed topographic maps of linear birefringence ${\Phi }_L$ (see Figures 5A,B) and dichroism ${\Delta }_L$ (see Figures 6A,B) notably decreases and no correlation with the size and directions of laying of protein fibrillar fibres is observed. The scale of the domain structure of the embossed topographic maps of circular birefringence ${\Phi }_C$ (see Figures 5C,D) and dichroism ${\Delta }_C$ (see Figures 6C,D) is reduced as well. An increase of effective depth (Z_i*) provides growth of magnitude and spread of random values of the parameters of linear and circular birefringence.

From a physical point of view, this can be related to the peculiarities of the morphological structure of the myocardial tissue. Each partial fibril has a long-range geometric order that determines the structural anisotropy ${\Phi }_L$ and ${\Delta }_L$ along the direction of optical axis and the phase shift between the linearly and orthogonally polarised components of the laser wave [17, 28, 29]. For small values of the phase plane (${\theta }_1=0.4rad\iff z_1\approx 25\mu m;{\theta }_2=0.75rad\iff z_2\approx 50\mu m$) within the volume of the histological section of the myocardium, single scattering events are dominant. Therefore, within the corresponding ${\varphi }_L\left({\theta }_i,x,y\right)$ and ${\Delta }_L\left({\theta }_i,x,y\right)$ distribution’s cross-sections, there is a direct relationship between the morphological structure of the myocardial fibrillar network and the parameters of linear anisotropy. An increase in the phase plane level ${\theta }_3=1.5rad\iff z_3^{\ast }\approx 100\mu m;{\theta }_4=2.3rad\iff z_4^{\ast }\approx 150\mu m$ is accompanied by an increase in the average multiplicity of light scattering. As a result, the parameters of linear birefringence and dichroism are averaged. Quantitatively, this process manifests itself in an increase in the magnitude of the mean ${\varphi }_L\left({\theta }_i,x,y\right)$ and the dispersion ${\Delta }_L\left({\theta }_i,x,y\right)$ of the distributions. The distributions of circular birefringence ${\varphi }_C\left({\theta }_i,x,y\right)$ and dichroism ${\Delta }_C\left({\theta }_i,x,y\right)$ of protein complexes of the histological section of the myocardium have a different structure. The layered maps of these parameters present small-scale island structures with weak coordinate fluctuations. Physically, this can be attributed to the fact that the level of anisotropy of this type is determined by the concentration of optically active molecules of myosin, which are equally distributed in different phase sections of the myocardial tissue.

Figure 7 shows the series of dependences of the statistical moments orders ($Z_{1;2;3;4}$), characterising the layer-by-layer distributions of the parameters of the anisotropy phase and amplitude of the partially depolarising layer of the myocardium tissue. To display the complete dynamics of changes in the value of statistical moments of the 3rd and 4th orders, which characterize the distributions $W\left({\theta }_i\right)$, the corresponding individual range of values was selected along the ordinate for each type of optical anisotropy. The values of the statistical moments of the 1st and 2nd orders are presented with a coefficient $\times 1000$.

FIGURE 7

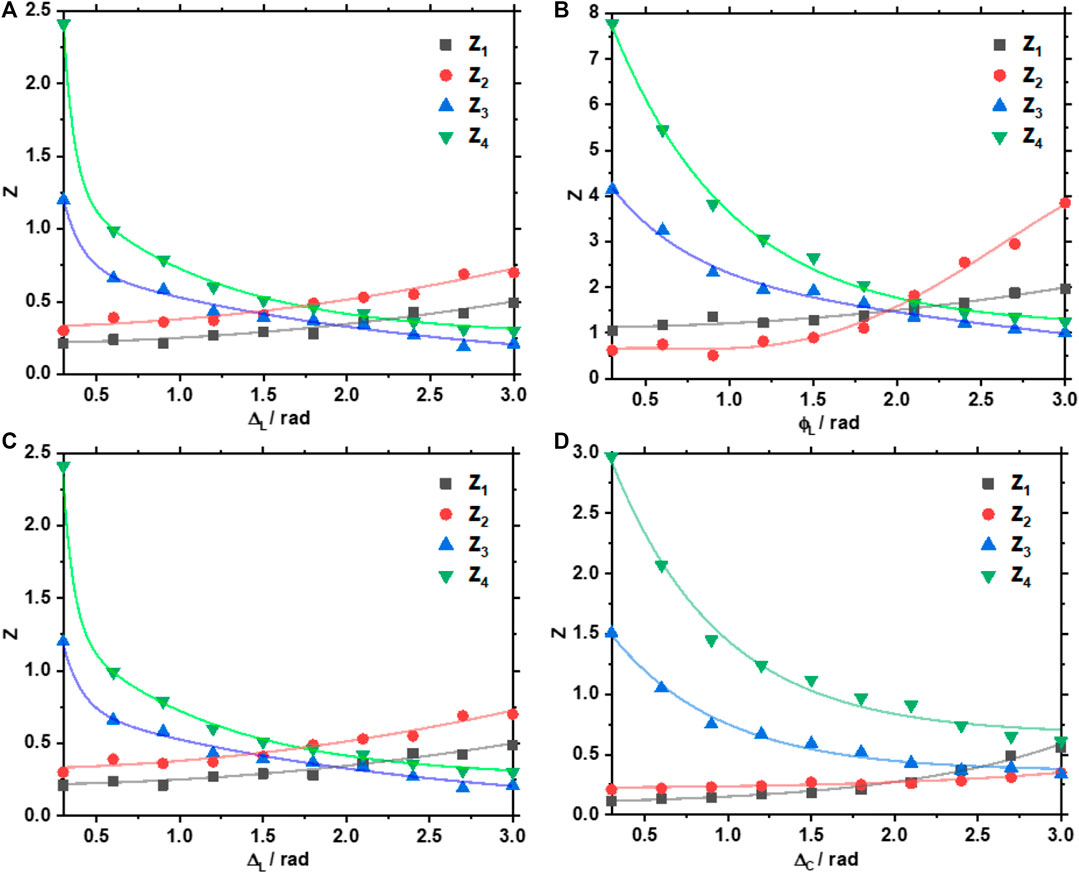
FIGURE 7. Phase dependences of the magnitude of the first to fourth statistical moments order characterising the distributions of (A)${\Phi }_L$(B)${\Delta }_L$, (C)${\Phi }_C$(D)${\Delta }_C$ of the partially depolarising ($\tau =1.02$) myocardium histological section.

Analysis of the obtained data revealed the following trends, which characterises the changes in the distributions of the parameters of the optical anisotropy of the myocardium layer:

${\theta }_i\uparrow \iff \{\begin{array}{c}{Z}_{1;2}\left({\theta }_i,{\mathit{\Phi }}_L,{\mathit{\Phi }}_C,{\mathit{\Delta }}_L,{\mathit{\Delta }}_C\right)\uparrow ;\\ Z_{3;4}\left({\theta }_i,{\mathit{\Phi }}_L,{\mathit{\Phi }}_C,{\mathit{\Delta }}_L,{\mathit{\Delta }}_C\right)\downarrow .\end{array}$

The observed regularities can be related to the fact that as the multiplicity of light scattering in the volume of the myocardium increases, in the limit of small ${\theta }_i$ the asymmetric ($Z_{3;4}\ge Z_{1;2}$) distributions ${\varphi }_L,{\varphi }_C,{\Delta }_L,{\Delta }_C\left(x,y\right)$, tend to normal ($Z_{1;2}\uparrow ;Z_{3;4}\to 0$) in accordance with the central limit theorem [50, 51]. The statistical moments of the third and fourth orders are the most sensitive to changes in the polarisation manifestations of phase and amplitude anisotropy. The range of changes for these two cases spans an order of magnitude.

Differentiation of ACI and CHD Myocardium Histological Samples

Finally, for the definitive diagnosis of ACI and CHD by the layer-by-layer Mueller-matrix approach described above the following protocol of reconstruction of myocardium optical anisotropy parameters has been developed. 1) As soon as the position of the phase plane most sensitive to pathological changes in the parameters of the optical anisotropy structure is determined ${\theta }^{\ast }$with the selected step of discrete phase “macro” scanning $\Delta {\theta }_i^{\max }=0.05\text{rad}$. 2) A series of layer-by-layer spatial distributions $W\left({\theta }_i,a,b\right)$ corresponding to each $\Delta {\theta }_i^{\max }=0.05\text{rad}$ are reconstructed, and statistical moments of the 1st–4th orders $Z_{i=1;2;;3;4}$, that characterizing $W\left({\theta }_i,a,b\right)$, are calculated. 3) The phase interval $\Delta {\theta }^{\ast }=\left({\theta }_{i+1}^{\max }÷{\theta }_i^{\max }\right)$ in frame of which the monotonic increase of difference between the values of each statistical moment $\Delta Z_k=Z_k\left({\theta }_{i+1}^{\max }\right)-Z_k\left({\theta }_i^{\max }\right)\le 0$ ceases, is determined. 4) Within the limits of $\Delta {\theta }^{\ast }$ a new series of values $\Delta Z_k=Z_k\left({\theta }_{i+1}^{\min }\right)-Z_k\left({\theta }_i^{\min }\right)$ is calculated with a discrete phase “micro” scanning step $\Delta {\theta }_i^{\min }=0.01\text{rad}$. 5) The optimal phase plane ${\theta }^{\ast }$ is determined - $\Delta Z_k\left({\theta }^{\ast }\right)=\max$. 6) The mean $\Delta {\overline{Z}}_{k=1;2;3;4}^{\ast }$ and standard deviations $\vartheta \left(\Delta Z_k^{\ast }\right)$ are defined within the representative samplings of myocardial histological sections from Group 2 and Group 3.

The sensitivity ($Se=\frac{q}{q+g}100\%$), specificity ($Sp=\frac{j}{j+s}100\%$) and balanced accuracy ($Ac=0.5\left(Se+Sp\right)$) of the approach is estimated [53]. Here, q and g are the number of correct and incorrect diagnoses within Group 3, and j and s are the same within Group 2.

The experimental results of 3D layer-by-layer Mueller-matrix reconstruction are presented as embossed topographic maps [48] of linear and circular birefringence (Figure 8) and dichroism (Figure 9) of ACI and CHD myocardial histological tissue samples.

FIGURE 8

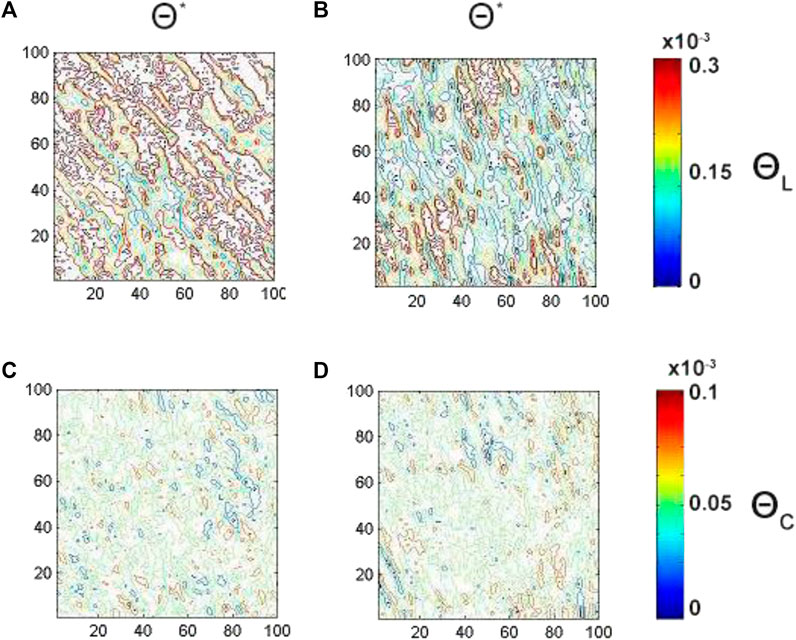
FIGURE 8. Embossed topographic maps of linear (A, B) and circular (C, D) birefringence of ACI (left column) and CHD (right column) myocardial histological sections. The determined optimal phase planes are ${\theta }^{\ast }\left({\varphi }_L,{\varphi }_C\right)=0.7\text{rad}$.

FIGURE 9

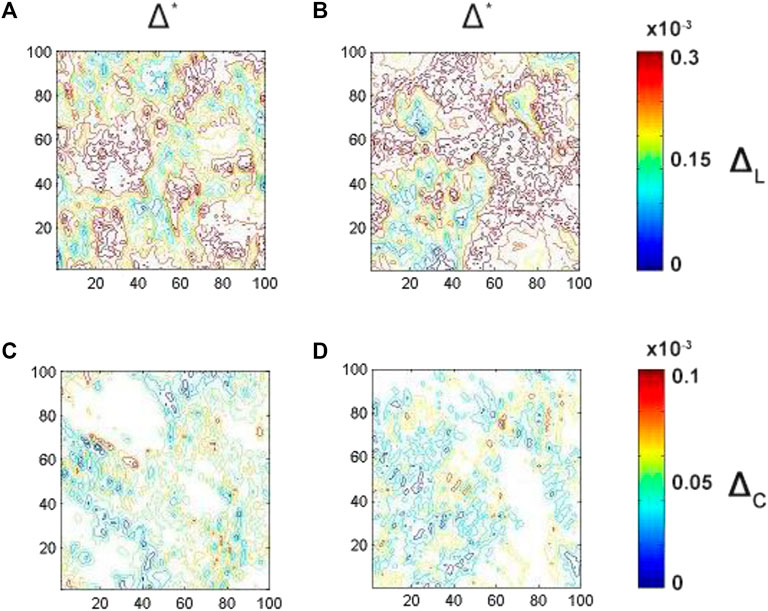
FIGURE 9. Embossed topographic maps of linear (A, B) and circular (C, D) dichroism of ACI (left column) and CHD (right column) myocardial histological sections. The determined optimal phase planes are ${\theta }^{\ast }\left({\Delta }_L,{\Delta }_C\right)=0.55\text{rad}$.

As one can see the average magnitude of linear birefringence and dichroism (see Figures 8A,B, 9A,B) is prevail up to 3 times compare to the magnitude of circular (see Figures 8C,D, 9C,D) birefringence and dichroism for both ACI and CHD myocardial histological samples. A decrease ($\downarrow$) in the level of structural anisotropy $\left({\varphi }_L,{\Delta }_L\right)$ of the CHD myocardium is associated with degenerative-dystrophic changes in the spatial-angular ordering of myosin fibrillary networks. While changes in concentrations of optically active molecules $\left({\varphi }_L,{\Delta }_L\right)$ of myosin seems to be insignificant. Thus, the values of intergroup difference can be assessed quantitatively by handling the embossed maps of optical anisotropy $\{\begin{array}{l}{\Phi }_L\left({\theta }_i,a,b\right);\\ {\Phi }_C\left({\theta }_i,a,b\right)\end{array}$ and $\{\begin{array}{l}{\Delta }_L\left({\theta }_i,a,b\right);\\ {\Delta }_C\left({\theta }_i,a,b\right)\end{array}$ of myocardial histological tissue samples from Group 2 and Group 3 utilizing higher order statistical moments $Z_k$(26). These values presented in Table 2.

TABLE 2

TABLE 2. Intergroup difference of high order statistical moments characterizing embossed maps of linear and circular birefringence and dichroism in optimal phase sections of myocardial histological samples. θ* = 0.7 rad.

4th order statistical moment ($\Delta Z_4$), defining kurtosis of distributions of anisotropy phase and amplitude $\{\begin{array}{l}{\Phi }_L\left({\theta }^{\ast },a,b\right);\\ {\Delta }_L\left({\theta }^{\ast },a,b\right)\end{array}$ for myocardial histological tissue samples, demonstrates the highest sensitivity (see Table 2). The sensitivity $Se$, specificity $Sp$ and balanced accuracy $Ac$ of practical use of 4th order statistical moment for ACI and CHD diagnosis are presented in Table 3.

TABLE 3

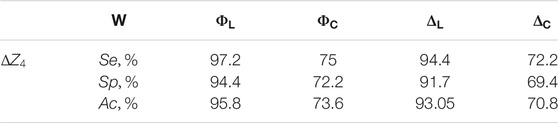
TABLE 3. Operational characteristics of diagnostic performance of myocardial histological sections by 3D Mueller-matrix reconstruction of optical anisotropy. ${\theta }^{\ast }=0.7rad$.

In comparison Table 4 presents the operational characteristics of diagnostic performance of the 3D Mueller-matrix reconstruction method of optical anisotropy of myocardial histological sections in other phase planes $\theta =0.9rad$ and $\theta =1.2rad$, as well as the 2D Mueller-matrix reconstruction approach.

TABLE 4

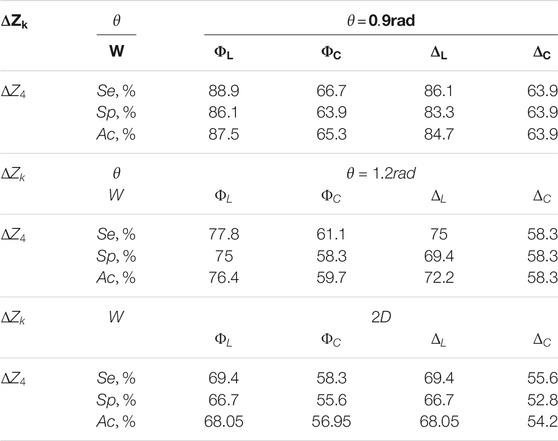
TABLE 4. Operational characteristics of the diagnostic performance of the 3D Mueller-matrix reconstruction method of optical anisotropy of myocardial histological sections.

The results show an excellent level of accuracy in differentiation of ACI and CHD: $Ac\left(\Delta Z_4\left({\theta }^{\ast },{\Phi }_L,{\Delta }_L\right)\right)=93.05\%÷95.8\%$ with linear birefringence ${\Phi }_L\left({\theta }^{\ast },a,b\right)$ and dichroism ${\Delta }_L\left({\theta }^{\ast },a,b\right)$ in the optimal phase plane ${\theta }^{\ast }=0.7rad$. Whereas, the accuracy of differentiation of ACI and CHD with circular birefringence ${\Phi }_C\left({\theta }^{\ast },a,b\right)$ and dichroism ${\Delta }_C\left({\theta }^{\ast },a,b\right)$ is significantly lower $Ac\left(\Delta Z_4\left({\theta }^{\ast },{\Phi }_C,{\Delta }_C\right)\right)=70.8\%÷73.6\%$ and does not exceed a satisfactory level. For other phase planes ($\theta =0.9rad$ and $\theta =1.2rad$) there is a clear tendency to decrease the efficiency of the approach to $Ac\left(\Delta Z_4\left(\theta =0.9rad,{\Phi }_L,{\Delta }_L\right)\right)=84.7\%÷87.5\%$ and satisfactory $Ac\left(\Delta Z_4\left(\theta =1.2rad,{\Phi }_L,{\Delta }_L\right)\right)=72.2\%÷76.4\%$ levels, respectively. The diagnostic performance of differentiating ACI and CHD cases by the traditional 2D Muller-matrix reconstruction method becomes much lower $Ac\left(\Delta Z_4\left(2D,{\Phi }_L,{\Delta }_L\right)\right)=68.05\%$ and does not exceed a satisfactory level.

Summary and Conclusions

A method for 3D Mueller matrix reconstruction of layer-by-layer distributions of the linear and circular birefringence and dichroism has been, for the first time to the best of our knowledge, introduced theoretically in line with the protocol of experimental measurements. The proposed approach has been tested for the case of partially depolarising layers of myocardial tissues. The dynamics of the change in the magnitude of the statistical moments of the first to fourth orders that characterise the distribution of the parameters of the optical anisotropy of the polycrystalline structure of the partially depolarising layer ($\tau =1.02; \text{Λ}=57\%$) of the myocardial tissue sample in different phase sections of its volume was successfully investigated and analysed. The third and fourth order statistical moments are the most sensitive to changes in the polarisation manifestations of the phase and amplitude anisotropy. The range of changes for these two cases spans an order of magnitude. This study paves the way for the wider use of 3D Mueller matrix approach to the analysis and morphological imaging of optically anisotropic structures. The 3rd and 4th order statistical moments (Z₃ and Z₄) are found to be the most sensitive to the changes in phase anisotropy of myocardium histological sections (in a range θ_i = 0.01–3 rad) both for linear ${\Phi }_L\left(Z_3\equiv 1.27÷0.31;Z_4\equiv 2.26÷0.39\right)$ and circular ${\Phi }_C\left(Z_3\equiv 4.13÷1.12;Z_4\equiv 7.86÷1.36\right)$ birefringence; linear ${\Delta }_L\left(Z_3\equiv 1.23÷0.28;Z_4\equiv 2.41÷0.37\right)$ and circular ${\Delta }_C\left(Z_3\equiv 1.49÷0.43;Z_4\equiv 2.99÷0.78\right)$ dichroism. The optimal phase plane (${\theta }^{\ast }=0.7rad$) has been found, for which an excellent ACI-CHD differentiation accuracy is achieved $Ac\left(\Delta Z_4\left({\theta }^{\ast },{\Phi }_L,{\Delta }_L\right)\right)=93.05\%÷95.8\%$. Current study demonstrates that a 3D Mueller matrix method can be used to effectively analyse the optical anisotropy parameters of myocardial tissues with a strong potential for definitive diagnosis in forensic medicine.

The developed approach has a high potential in various applications in optical histopathology and biopsy, including: early cancer detection, monitoring of stage of cancer aggressiveness by means of reconstruction of the polycrystalline structure of human fluids (blood, saliva, etc.); definitive diagnosis of histological sections of biopsy of benign and malignant tumours of human organs (prostate, uterus, breast), aseptic and septic conditions of human joints by means of reconstruction of the polycrystalline structure of the synovial fluid; and importantly in forensic pathology determining the time of death by means of temporary monitoring of necrotic changes in the polycrystalline structure of tissues and organ fluids of the deceased.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

Current research supported by the ATTRACT project funded by the EC under Grant Agreement 777222, Academy of Finland (grants 314639 and 325097), National Research Foundation of Ukraine (Project 2020.02/0061) and INFOTECH strategic funding, and with the support of a grant under the Decree of the Government of the Russian Federation No. 220 of 09 April 2010 (Agreement No. 075-15-2021-615 of 04 June 2021). This work was also financed by the Ministry of Science and Higher Education of the Russian Federation (Agreement no. 075-02-2021-1748).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tuchin VV. Tissue Optics and Photonics: Biological Tissue Structures. Jbpe (2015) 1:3–21. doi:10.18287/JBPE-2015-1-1-3

CrossRef Full Text | Google Scholar

2. Camici PG, Tschöpe C, Di Carli MF, Rimoldi O, Van Linthout S. Coronary Microvascular Dysfunction in Hypertrophy and Heart Failure. Cardiovasc Res (2020) 116:806–16. doi:10.1093/cvr/cvaa023

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Meli AC, de Tombe P. Scientists on the Spot: Myocardium and Myofilaments. Cardiovasc Res (2020) 116:e96–e97. doi:10.1093/cvr/cvz317

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lozano R, Naghavi M, Foreman K, Lim S, Shibuya K, Aboyans V, et al. Global and Regional Mortality from 235 Causes of Death for 20 Age Groups in 1990 and 2010: a Systematic Analysis for the Global Burden of Disease Study 2010. Lancet (2012) 380:2095–128. doi:10.1016/S0140-6736(12)61728-0

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Pitoulis FG, Watson SA, Perbellini F, Terracciano CM. Myocardial Slices Come to Age: an Intermediate Complexity In Vitro Cardiac Model for Translational Research. Cardiovasc Res (2020) 116:1275–87. doi:10.1093/cvr/cvz341

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Bermejo-Martin JF, Almansa R, Torres A, González-Rivera M, Kelvin DJ. COVID-19 as a Cardiovascular Disease: the Potential Role of Chronic Endothelial Dysfunction. Cardiovasc Res (2020) 116:e132–e133. doi:10.1093/cvr/cvaa140

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bykov A, Hautala T, Kinnunen M, Popov A, Karhula S, Saarakkala S, et al. Imaging of Subchondral Bone by Optical Coherence Tomography upon Optical Clearing of Articular Cartilage. J Biophoton (2016) 9(3):270–5. doi:10.1002/jbio.201500130

CrossRef Full Text | Google Scholar

8. Farahani N, Braun A, Jutt D, Huffman T, Reder N, Liu Z, et al. Three-dimensional Imaging and Scanning: Current and Future Applications for Pathology. J Pathol Inform (2017) 8:36. doi:10.4103/jpi.jpi_32_17

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Azaripour A, Lagerweij T, Scharfbillig C, Jadczak AE, Willershausen B, Van Noorden CJF. A Survey of Clearing Techniques for 3D Imaging of Tissues with Special Reference to Connective Tissue. Prog Histochem Cytochem (2016) 51:9–23. doi:10.1016/j.proghi.2016.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Borovkova M, Peyvasteh M, Dubolazov O, Ushenko Y, Ushenko V, Bykov A, et al. Complementary Analysis of Mueller-Matrix Images of Optically Anisotropic Highly Scattering Biological Tissues. J Eur Opt Soc-Rapid Publ (2018) 14:20. doi:10.1186/s41476-018-0085-9

CrossRef Full Text | Google Scholar

11. Das NK, Dey R, Chakraborty S, Panigrahi PK, Meglinski I, Ghosh N. Quantitative Assessment of Submicron Scale Anisotropy in Tissue Multifractality by Scattering Mueller Matrix in the Framework of Born Approximation. Opt Commun (2018) 413:172–8. doi:10.1016/j.optcom.2017.11.082

CrossRef Full Text | Google Scholar

12. Devlaminck V. Physical Model of Differential Mueller Matrix for Depolarizing Uniform media. J Opt Soc Am A (2013) 30:2196. doi:10.1364/JOSAA.30.002196

CrossRef Full Text | Google Scholar

13. Ossikovski R, Arteaga O. Statistical Meaning of the Differential Mueller Matrix of Depolarizing Homogeneous media. Opt Lett (2014) 39:4470. doi:10.1364/OL.39.004470

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Peyvasteh M, Dubolazov A, Popov A, Ushenko A, Ushenko Y, Meglinski I. Two-point Stokes Vector Diagnostic Approach for Characterization of Optically Anisotropic Biological Tissues. J Phys D Appl Phys (2020) 53(39):395401. doi:10.1088/1361-6463/ab9571

CrossRef Full Text | Google Scholar

15. Trifonyuk L, Sdobnov A, Baranowski W, Ushenko V, Olar O, Dubolazov A, et al. Differential Mueller Matrix Imaging of Partially Depolarizing Optically Anisotropic Biological Tissues. Lasers Med Sci (2020) 35(4):877–91. doi:10.1007/s10103-019-02878-2

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Rodger A, Norden B. Circular Dichroism and Linear Dichroism. Oxford: Oxford University Press (1997).

Google Scholar

17. Ushenko AG, Pishak VP. Laser Polarimetry of Biological Tissue: Principles and Applications. In: VVV̆ V Tuchin, editor. Handbook Of Coherent-Domain Optical Methods : Biomedical Diagnosis, Environmental Monitoring, and Materials Science. Springer. 2004, p. 93–138.

CrossRef Full Text | Google Scholar

18. Buscemi IC, Guyot S. Near Real-Time Polarimetric Imaging System. J Biomed Opt (2013) 18:1. doi:10.1117/1.JBO.18.11.116002

CrossRef Full Text | Google Scholar

19. Manhas S, Vizet J, Deby S, Vanel J-C, Boito P, Verdier M, et al. Demonstration of Full 4×4 Mueller Polarimetry through an Optical Fiber for Endoscopic Applications. Opt Express (2015) 23:3047. doi:10.1364/OE.23.003047

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Negara C, Li Z, Längle T, Beyerer J. Simplified Stokes Polarimeter Based on Division-Of-Amplitude. In: B Zagar, P Mazurek, M Rosenberger, and P-G Dittrich, editors. Photonics and Education in Measurement Science 2019 (2019) p. 44. doi:10.1117/12.2532399

CrossRef Full Text | Google Scholar

21. Lin Z, Rusch L, Chen Y, Shi W. Chip-scale, Full-Stokes Polarimeter. Opt Express (2019) 27:4867. doi:10.1364/oe.27.004867

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Mishchenko MI, Travis LD, Lacis AA. Scattering, Absorption, and Emission of Light by Small Particles. Cambridge University Press (2002).

Google Scholar

23. Swami MK, Patel HS, Gupta PK. Conversion of 3×3 Mueller Matrix to 4×4 Mueller Matrix for Non-depolarizing Samples. Opt Commun (2013) 286:18–22. doi:10.1016/j.optcom.2012.08.094

CrossRef Full Text | Google Scholar

24. Izotova VF, Maksimova IL, Nefedov IS, Romanov SV. Investigation of Mueller Matrices of Anisotropic Nonhomogeneous Layers in Application to an Optical Model of the Cornea. Appl Opt (1997) 36:164. doi:10.1364/AO.36.000164

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Tuchin VV. Tissue Optics and Photonics: Light-Tissue Interaction. Jbpe (2015) 1:98–134. doi:10.18287/JBPE-2015-1-2-98

CrossRef Full Text | Google Scholar

26. Manhas S, Swami MK, Buddhiwant P, Ghosh N, Gupta PK, Singh J. Mueller Matrix Approach for Determination of Optical Rotation in Chiral Turbid media in Backscattering Geometry. Opt Express (2006) 14:190. doi:10.1364/OPEX.14.000190

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Deng Y, Zeng S, Lu Q, Zhu D, Luo Q. Characterization of Backscattering Mueller Matrix Patterns of Highly Scattering media with Triple Scattering assumption. Opt Express (2007) 15:9672. doi:10.1364/OE.15.009672

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Angelsky O, Ushenko A, Ushenko Y, Pishak V, Peresunko A. Statistical, Correlation, and Topological Approaches in Diagnostics of the Structure and Physiological State of Birefringent Biological Tissues. In: VV Tuchin, editor. Handbook Of Photonics For Biomedical Science. Boca Raton: CRC Press (2010) p. 283–322. doi:10.1201/9781439806296-c10

CrossRef Full Text | Google Scholar

29. Ushenko YA, Boychuk TM, Bachynsky VT, Mincer OP. Diagnostics of Structure and Physiological State of Birefringent Biological Tissues: Statistical, Correlation and Topological Approaches. In: VV(V̆ V Tuchin, editor. Handbook Of Coherent-Domain Optical Methods. New York, NY: Springer New York (2013) p. 107–48. doi:10.1007/978-1-4614-5176-1_3

CrossRef Full Text | Google Scholar

30. Lu S-Y, Chipman RA. Interpretation of Mueller Matrices Based on Polar Decomposition. J Opt Soc Am A (1996) 13:1106. doi:10.1364/JOSAA.13.001106

CrossRef Full Text | Google Scholar

31. Guo Y, Zeng N, He H, Yun T, Du E, Liao R, et al. A Study on Forward Scattering Mueller Matrix Decomposition in Anisotropic Medium. Opt Express (2013) 21:18361. doi:10.1364/OE.21.018361

PubMed Abstract | CrossRef Full Text | Google Scholar

32. DeBoo B, Sasian J, Chipman R. Degree of Polarization Surfaces and Maps for Analysis of Depolarization. Opt Express (2004) 12:4941. doi:10.1364/OPEX.12.004941

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Pierangelo A, Manhas S, Benali A, Fallet C, Totobenazara J-L, Antonelli M-R, et al. Multispectral Mueller Polarimetric Imaging Detecting Residual Cancer and Cancer Regression after Neoadjuvant Treatment for Colorectal Carcinomas. J Biomed Opt (2013) 18:046014. doi:10.1117/1.JBO.18.4.046014

CrossRef Full Text | Google Scholar

34. Ushenko VA, Dubolazov AV, Pidkamin LY, Sakchnovsky MY, Bodnar AB, Ushenko YA, et al. Mapping of Polycrystalline Films of Biological Fluids Utilizing the Jones-matrix Formalism. Laser Phys (2018) 28(2):025602. doi:10.1088/1555-6611/aa8cd9

CrossRef Full Text | Google Scholar

35. Ushenko V, Sdobnov A, Syvokorovskaya A, Dubolazov A, Vanchulyak O, Ushenko A, et al. 3D Mueller-Matrix Diffusive Tomography of Polycrystalline Blood Films for Cancer Diagnosis. Photonics (2018) 5:54. doi:10.3390/photonics5040054

CrossRef Full Text | Google Scholar

36. Ushenko A, Sdobnov A, Dubolazov A, Grytsiuk M, Ushenko Y, Bykov A, et al. Stokes-Correlometry Analysis of Biological Tissues with Polycrystalline Structure. IEEE J Select Top Quan Electron (2019) 25(1):1–12. doi:10.1109/JSTQE.2018.2865443

CrossRef Full Text | Google Scholar

37. Borovkova M, Trifonyuk L, Ushenko V, Dubolazov O, Vanchulyak O, Bodnar G, et al. Mueller-matrix-based Polarization Imaging and Quantitative Assessment of Optically Anisotropic Polycrystalline Networks. PLOS One (2019) 14(5):e0214494. doi:10.1371/journal.pone.0214494

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Ushenko VA, Sdobnov AY, Mishalov WD, Dubolazov AV, Olar OV, Bachinskyi VT, et al. Biomedical Applications of Jones-matrix Tomography to Polycrystalline Films of Biological Fluids. J Innov Opt Health Sci (2019) 12(6):1950017. doi:10.1142/S1793545819500172

CrossRef Full Text | Google Scholar

39. Ushenko VA, Pavlyukovich ND, Trifonyuk L. Spatial-Frequency Azimuthally Stable Cartography of Biological Polycrystalline Networks. Int J Opt (2013) 2013:1–7. doi:10.1155/2013/683174

CrossRef Full Text | Google Scholar

40. Ushenko VA, Dubolazov OV, Karachevtsev AO. Two Wavelength Mueller Matrix Reconstruction of Blood Plasma Films Polycrystalline Structure in Diagnostics of Breast Cancer. Appl Opt (2014) 53:B128. doi:10.1364/AO.53.00B128

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Prysyazhnyuk VP, Ushenko YA, Dubolazov AV, Ushenko AG, Ushenko VA. Polarization-dependent Laser Autofluorescence of the Polycrystalline Networks of Blood Plasma Films in the Task of Liver Pathology Differentiation. Appl Opt (2016) 55:B126. doi:10.1364/AO.55.00B126

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Ortega-Quijano N, Arce-Diego JL. Depolarizing Differential Mueller Matrices. Opt Lett (2011) 36:2429. doi:10.1364/OL.36.002429

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ortega-Quijano N, Arce-Diego JL. Mueller Matrix Differential Decomposition. Opt Lett (2011) 36:1942. doi:10.1364/OL.36.001942

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Ossikovski R, Devlaminck V. General Criterion for the Physical Realizability of the Differential Mueller Matrix. Opt Lett (2014) 39:1216. doi:10.1364/OL.39.001216

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Devlaminck V, Ossikovski R. Uniqueness of the Differential Mueller Matrix of Uniform Homogeneous media. Opt Lett (2014) 39:3149. doi:10.1364/OL.39.003149

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Yasuno Y, Ju M-J, Hong Y-J, Makita S, Miura M. (2013), In Vivo Three-Dimensional Investigation of Tissue Birefringence by Jones Matrix Tomography, Conf Lasers Electro-Optics Pacific Rim, 30 June-4 July 2013, Kyoto, Japan, IEEE.

CrossRef Full Text | Google Scholar

47. Kobata T, Nomura T. Digital Holographic Three-Dimensional Mueller Matrix Imaging. Appl Opt (2015) 54:5591. doi:10.1364/AO.54.005591

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Ushenko VA, Hogan BT, Dubolazov A, Grechina AV, Boronikhina TV, Gorsky M, et al. Embossed Topographic Depolarisation Maps of Biological Tissues with Different Morphological Structures. Sci Rep (2021) 11:3871. doi:10.1038/s41598-021-83017-2

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Ushenko VA, Hogan BT, Dubolazov A, Piavchenko G, Kuznetsov SL, Ushenko AG, et al. 3D Mueller Matrix Mapping of Layered Distributions of Depolarisation Degree for Analysis of Prostate Adenoma and Carcinoma Diffuse Tissues. Sci Rep (2021) 11:5162. doi:10.1038/s41598-021-83986-4

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Cassidy LD. Basic Concepts of Statistical Analysis for Surgical Research. J Surg Res (2005) 128:199–206. doi:10.1016/j.jss.2005.07.005

CrossRef Full Text | Google Scholar

51. Davis CS. Statistical Methods for the Analysis of Repeated Measurements. New York, NY: Springer New York (2003) doi:10.1007/b97287

CrossRef Full Text | Google Scholar

52. Goodman JW. Statistical Properties of Laser Speckle Patterns. Berlin: Springer (1975).

Google Scholar

53. Robinson SP. Principles of Forensic Medicine. London: Greenwich Medical Media (1996).

Google Scholar