
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 30 September 2021
Sec. Quantum Engineering and Technology
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.735321
This article is part of the Research TopicQuantum Computing: Towards Practical ApplicationsView all 8 articles
 Qing Guo1,2
Qing Guo1,2 Ping-Xing Chen1,2*
Ping-Xing Chen1,2*The accurate calculation of molecular energy spectra, a very complicated work, is of importance in many applied fields. Relying on the VQE-UCC algorithm, it is very possible to calculate the molecular energy spectrum on a noisy intermediate scale quantum computer. However, due to the limitation of the number of qubits and coherent time in quantum computers, the complexity of VQE-UCC algorithm still needs to be reduced in the simulation of macromolecules. We develop a new VQE-UCC method to calculate the ground state of the molecule according to the symmetry of the system, the complexity of which is reduced. Using this method we get the ground and excite state of four kinds of molecules. The method and the results are of great significance for the promotion of quantum chemical simulations.
In this year, quantum computing has been widely concerned as a new paradigm of computing. Compared with classical computing, the computing power of quantum computing increases exponentially with the increase of the number of qubits. One of the most likely applications of quantum computers is to simulate quantum mechanical systems [1], which is made possible by the emergence of some algorithms [2, 3] and later quantum processors [4, 5]. Molecule is one of the common quantum systems in nature. Calculating the energy spectra of a molecular system is one of the main goals of quantum chemistry, so the algorithm of simulating quantum chemistry by the noisy intermediate scale quantum computer (NISQ) has been of interest. However, due to the limitation of the number of qubits and coherent time of NISQ, there is still difficulties for us to simulate for macromolecules.
There are many methods having been used to reduce the complexity of quantum chemistry simulation, such as hybrid quantum classical algorithm (HQC) [6]. One of the most important algorithm is the variational quantum eigensolver (VQE) algorithm [7]. The VQE algorithm is based on the Ritz variational principle. The preparation of the ansatz and the measurement of the expected value of the Hamiltonian are carried out on the quantum computer. Then the classical computer optimizes the iterative parameters of the next ansatz according to the principle of minimizing the expected value of the Hamiltonian. The VQE algorithm can be used to find the molecular ground state energy. Compared with pure quantum algorithm, the VQE algorithm uses shorter quantum circuits and has stronger fault tolerance, but needs more measurements and the assistance of classical processes.
The two main steps of implementing VQE algorithm on NISQ are the selection of initial states and to effectively prepare the ansatz. The initial state is generally prepared into Hatree-Fock state. Because the Hatree-Fock method does not take into account the dynamic interaction between electrons, it cannot obtain accurate electron energy. To prepare the ansatz, one mainly chooses the unitary coupled cluster method (UCC) [8, 9], coming from the classical single reference coupled cluster method (SRCC) [10, 11], which is more suitable for quantum computers. It divides the electron orbitals into two parts, the occupied orbitals and the unoccupied orbitals. Beginning with initial state (the Hatree-Fock state), a series of single excitation, double excitation and higher excitation operators which excite the electrons from the occupied orbitals to the unoccupied orbitals are applied to the initial state. After many rounds of operators, one may get the real ground state of the Hamiltonian. The details will be described in the second section. Some works have shown its accuracy. However, due to the limitation of the number of qubits and coherent time in quantum computers [12], it is still a great challenge for macromolecules to implement VQE-UCC algorithm on quantum computers.
In this paper, we propose a simpler UCC variant method, the singlet and pair UCC (SPUCC), based on the spin symmetry of molecules. In this mothed, the single excitation is classified and the double excitation only retains the pair excitation. The method can reduce the computational complexity while keeping the computational accuracy. Based on this method, we calculate the grounds of molecules with different structures and properties, and get good results as expected.
Now we will introduce all the steps of realizing quantum chemical simulation on a quantum computer.
Using the Born-Oppenheimer approximation (B-O approximation), the Hamiltonian of the molecule can be written as:
Where
In the second quantization, the wave function of the fermion is written as the fermion creation operator acting on the vacuum state. The creation operator and the annihilation operator can be identified as,
After the second quantization is introduced, the Hamiltonian in Eq. 1.1 can be written as,
where,
The wave function
In order to simulate quantum chemistry on a quantum computer, we use Jordan-Wigner (J-W) transformation [15] to map the contents of the above-mentioned second quantization to the quantum computer. In the J-W transformation, the creation and annihilation operator are designed as,
Where
In this way, the Hamiltonian in Eq. 1.3 is transformed into the continuous product of a series of Pauli operators,
The above-mentioned
The VQE algorithm uses the quantum computer to prepare quantum states and to get the expected value of Hamiltonian, which are difficult for the classical computer. The tedious process of parameter optimization is handed over to the classical computer. It is based on Rayleigh-Ritz variational principle,
It shows that for a parameterized quantum state
To get the ground state, we usually start from the Hatree-Fock state. Selecting parameterize
We feedback the measured
Then repeat the above steps to get
The UCC is an improved version of the classical CC method, and the parameterized system wave function is given by the CC method,
The
For the trade-off between efficiency and accuracy, we usually intercept double excitations. Because the Hamiltonian mainly involves the interaction between monomer and two electrons, and then it can be proved that higher-order excitations can be composed of a combination of single and double excitations, resulting in coupled cluster single and double excitation methods (CCSD) [16].
By UCC method, the trial ansatz state is
Since
However, for many molecules, some of its own characteristics are also important factors that can reduce the cost of quantum chemical simulation, such as the number of electrons and wave function symmetry of molecules. For a definite molecule, then the selected basis function can be reduced to a smaller subspace. So the excitation operator that keeps the spin symmetry plays an important role. Based on this idea, we divide the single excitation operator into two categories:
This classification is similar to the singlet unitary coupled cluster (UCCD0) method [17, 18],
Where the triplet-paired operator
It is mainly based on the fact that
This method only retains the exited channel which keep the symmetry begin and after excitation. The number of excitation operator terms involved is
However,
Similarly,
Conbinating Eqs. 5.6, 5.7 we have
So we can replace the operator
The number of excitation operators involved in this method is
by Taylor expansion. While in
Let us consider a molecule with 2 M orbitals and 2 m electrons. We need 2 M qubits to code quantum state. The HF state
For a single excitation,
According to the decomposition of the quantum circuit [19, 20], we need 10 single qubit gates and
For a double excitation, the unitary evolution operator can be expressed by Paul operators as follow,
where
Similarly, it needs 72 single qubit gates and
While in SPUCC, we use the spin symmetry, the single excitation is
We have studied four kinds of molecules
At the same time, we compare the time cost of the three molecules simulated by different methods on the classical computer, which we think can be used as a qualitative comparison of the complexity of the three methods. Because of the deviation of the pUCCD method, we do not evaluate its cost. For details, please see Table 1.
The data in the table is the time cost of different methods under this structure,
Molecule
Where,
The results show that the ground state of molecule
Molecule
The molecule
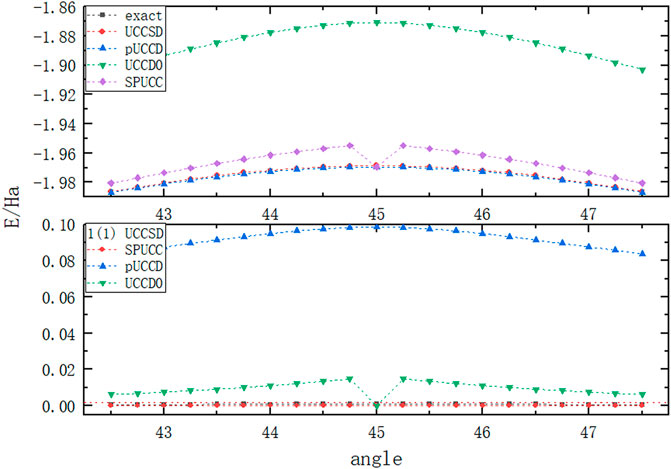
FIGURE 1. The picture above shows the variation of the energy of
It can be seen from Figure 1 that there is a large energy deviation between pUCCD and UCCD0, while SPUCC shows the same accuracy as UCCSD. At the same time, UCCD0 shows the same superiority as SPUCC when the circumferential angle is
At the same time, we are also interested in studying the fidelity. The results have been shown in Figure 2. We can find that SPUCC shows better accuracy than the usual VQE-UCC method.
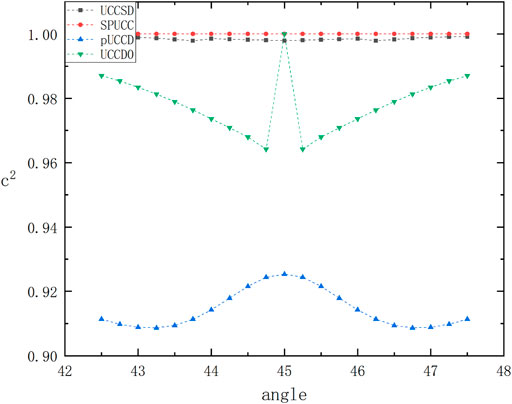
FIGURE 2. The graph above shows the variation of the overlapping integral square of the experimental state and the exact diagonalized wave function with the circumferential angle simulated by different methods, with a maximum of 1.
Molecule
Figure 3 shows that all methods show high accuracy in
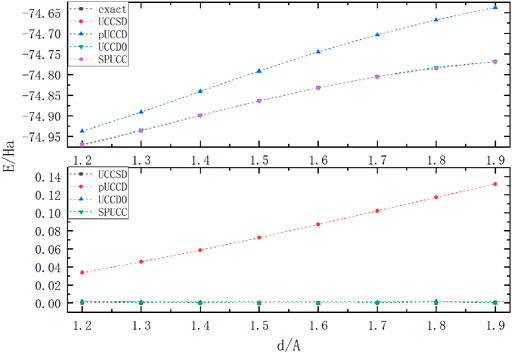
FIGURE 3. The graph above shows the energy of molecule
Because of the existence of three bonds with strong correlation, molecule
In Figure 4, excepting for the offset of pUCCD, all the other methods have good accuracy. SPUCC shows better results than UCCD0 on the graph, and its maximum error is about
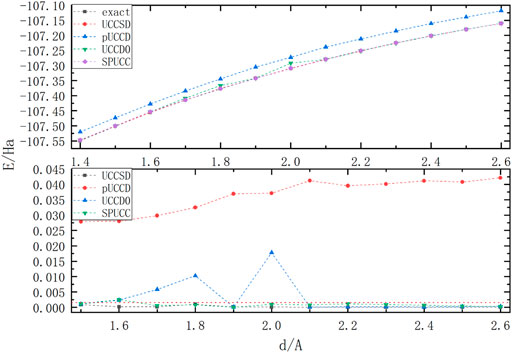
FIGURE 4. A graph in which the energy of a molecule
On the basis of the previous work, we have studied the different molecular spin states. For example, the ground state and the second excited state (singlet state) and the first excited state (triplet state) of molecule
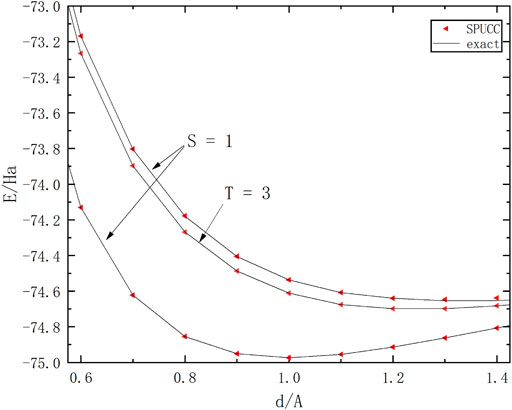
FIGURE 5. A graph in which the energy of a molecule
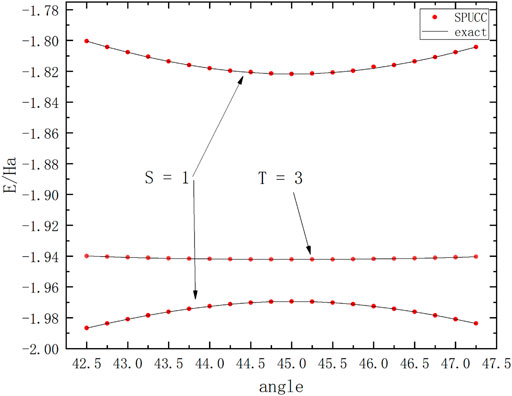
FIGURE 6. A graph in which the energy of a molecule
The VQE-UCC method is a practical quantum algorithm for calculating molecular energy spectra. It can reproduce the exact electronic structure properties of many molecular systems within the range of chemical accuracy. The main reason for the success of this algorithm is its variational property. However, limited by the current technology, the number of qubits and coherent time limit the scalability of the quantum chemistry simulation system. The complexity of UCCSD leads to the increase of quantum circuit depth, and our proposed UCC method variant SPUCC method reduces its complexity, correspondingly reduces the circuit depth of quantum simulation, and makes it more suitable for today’s NISQ. We calculate the energy changes of a series of molecules along the bond length. Our simulations show correct qualitative dissociation curves, which are basically within the range of chemical accuracy on the whole dissociation curve. At the same time, we also calculate their excited states across spin symmetry, which provides some experience for us to calculate the excited states of molecules in the future. In a word, we prove that the potential of the SPUCC method proposed in this paper can be equal to that of the current variants, and it can also deal with the strong correlation system very well. The combination of this method with the recent VQE method is expected to open up a new possibility for the use of ground-depth circuits in NISQ to solve the electronic structure problems of macromolecular systems.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
This work is supported by the National Basic Research Program of China under Grant No. 2016YFA0301903 and the National Natural Science Foundation of China under Grants No. 61632021, No. 11904402 and No. 12004430.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
2. Georgescu IM, Ashhab S, Nori F. Quantum Simulation. Rev Mod Phys (2014) 86(1):153–85. doi:10.1103/RevModPhys.86.153
3.Proceedings 35th Annual Symposium on Foundations of Computer Science. In: Paper presented at the Proceedings 35th Annual Symposium on Foundations of Computer Science; 20-22 Nov. 1994; Santa Fe, NM, USA. IEEE (1994). doi:10.1109/SFCS.1994.365747
4. Kelly J. “Engineering Superconducting Qubit Arrays for Quantum Supremacy,” in APS March Meeting 2018. American Physical Society (2018). https://ui.adsabs.harvard.edu/abs/2018APS.MARA33001K.
5. Murali P, Linke N, Martonosi M, Abhari A, Nguyen N, Huerta Alderete C. Full-Stack, Real-System Quantum Computer Studies: Architectural Comparisons and Design Insights. In: ISCA 19: The 46th Annual International Symposium on Computer Architecture; June 22 - 26, 2019; Phoenix AZ. Phoenix, AZ: Association for Computing Machinery (2019). p. 527–40. doi:10.1145/3307650.3322273
6. McClean JR, Romero J, Babbush R, Aspuru-Guzik A. The Theory of Variational Hybrid Quantum-Classical Algorithms. New J Phys (2016) 18(2):023023. doi:10.1088/1367-2630/18/2/023023
7. Peruzzo A, McClean J, Shadbolt P, Yung M-H, Zhou X-Q, Love PJ. A Variational Eigenvalue Solver on a Photonic Quantum Processor. Nat Commun (2014) 5:4213. doi:10.1038/ncomms5213
8. Hempel C, Maier C, Romero J, McClean J, Monz T, Shen H. Quantum Chemistry Calculations on a Trapped-Ion Quantum Simulator. Phys Rev X (2018) 8(3):031022. doi:10.1103/PhysRevX.8.031022
9. Shen Y, Zhang X, Zhang S, Zhang J-N, Yung M-H, Kim K. Quantum Implementation of the Unitary Coupled Cluster for Simulating Molecular Electronic Structure. Phys Rev A (2017) 95(2):020501. doi:10.1103/PhysRevA.95.020501
10. Čížek J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell‐Type Expansion Using Quantum‐Field Theoretical Methods. J Chem Phys (1966) 45(11):4256–66. doi:10.1063/1.1727484
11. Bartlett RJ, Musiał M. Coupled-cluster Theory in Quantum Chemistry. Rev Mod Phys (2007) 79:291–352. doi:10.1103/revmodphys.79.291
12. Preskill J. Quantum Computing in the NISQ Era and beyond. Quantum (2018) 2:79. doi:10.22331/q-2018-08-06-79
13. Jensen F. Atomic Orbital Basis Sets. Wires Comput Mol Sci (2013) 3:273–95. doi:10.1002/wcms.1123
14. Nagy B, Jensen F. Basis Sets in Quantum Chemistry in: Reviews in Computational Chemistry. Chapter 3. Hoboken, NJ: Wiley Online Library (2017). p. 93–149.
15. Whitfield JD, Biamonte J, Aspuru-Guzik A. Simulation of Electronic Structure Hamiltonians Using Quantum Computers. Mol Phys (2011) 109:735–50. doi:10.1080/00268976.2011.552441
16. Wecker D, Hastings MB, Troyer M. Progress towards Practical Quantum Variational Algorithms. Phys Rev A: Mol Opt Phys (2015) 92:042303. doi:10.1103/physreva.92.042303
17. Bulik IW, Henderson TM, Scuseria GE. Can Single-Reference Coupled Cluster Theory Describe Static Correlation? J Chem Theor Comput. (2015) 11(7):3171–9. doi:10.1021/acs.jctc.5b00422
18. Gomez JA, Henderson TM, Scuseria GE. Recoupling the Singlet- and Triplet-Pairing Channels in Single-Reference Coupled Cluster Theory. J Chem Phys (2016) 145(13):134103. doi:10.1063/1.4963870
19. Cao Y, Romero J, Olson JP, Degroote M, Johnson PD, Kieferová M. Quantum Chemistry in the Age of Quantum Computing. Chem Rev (2019) 119(19):10856–915. doi:10.1021/acs.chemrev.8b00803
20. Romero J, Babbush R, McClean JR, Hempel C, Love PJ, Aspuru-Guzik A. Strategies for Quantum Computing Molecular Energies Using the Unitary Coupled Cluster Ansatz. Quan Sci. Technol. (2018) 4(1):014008. doi:10.1088/2058-9565/aad3e4
21. Smith DGA, Burns LA, Simmonett AC, Parrish RM, Schieber MC, Galvelis R. Psi4 1.4: Open-Source Software for High-Throughput Quantum Chemistry. J Chem Phys (2020) 152:184108. doi:10.1063/5.0006002
22. McClean JR, Rubin NC, Sung KJ, Kivlichan ID, Bonet-Monroig X, Cao Y. OpenFermion: the Electronic Structure Package for Quantum Computers. Quan Sci. Technol. (2020) 5(3):034014. doi:10.1088/2058-9565/ab8ebc
23. Johansson JR, Nation PD, Nori F. QuTiP 2: A Python Framework for the Dynamics of Open Quantum Systems. Comp Phys Commun (2013) 184(4):1234–40. doi:10.1016/j.cpc.2012.11.019
24. Zhao L, Neuscamman E. Amplitude Determinant Coupled Cluster with Pairwise Doubles. J Chem Theor Comput. (2016) 12:5841–50. doi:10.1021/acs.jctc.6b00812
25. Higgott O, Wang DS, Brierley S. Variational Quantum Computation of Excited States. Quantum (2019) 3:156. doi:10.22331/q-2019-07-01-156
Keywords: quantum computation, variational quantum eigensolver, unitary coupled cluster, quantum chemical, quantum simulation
Citation: Guo Q and Chen P-X (2021) Optimization of VQE-UCC Algorithm Based on Spin State Symmetry. Front. Phys. 9:735321. doi: 10.3389/fphy.2021.735321
Received: 02 July 2021; Accepted: 10 September 2021;
Published: 30 September 2021.
Edited by:
Alexandre M Souza, Centro Brasileiro de Pesquisas Físicas, BrazilReviewed by:
Che-Ming Li, National Cheng Kung University, TaiwanCopyright © 2021 Guo and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ping-Xing Chen, cHhjaGVuQG51ZHQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.