Waves Generated by Electron Beam in a Crater-Shaped Flux Rope

Understanding the nature and characteristics of high-frequency waves inside a flux rope may be important as the wave-particle interaction is important for charged-particle energization and the ensuing dissipation process. We analyze waves generated by an electron beam in a crater-shaped magnetic flux rope observed by MMS spacecraft on the dawnside tailward magnetopause. In this MMS observation, a depression of magnetic field, or a crater, of ∼100 km is located at the center of the magnetic flux rope of ∼650 km. There exist parallel and perpendicular electrostatic wave modes inside the depression of the magnetic field at the center of the flux rope, and they are distinguished by their locations and frequencies. The parallel mode exists at the center of the magnetic depression and its power spectrum peaks below F_ce (electron cyclotron frequency). In contrast, the perpendicular mode exists in the outer region associated with the magnetic depression, and its power spectrum peaks near F_ce. The linear analysis of kinetic instability using a generalized dispersion solver shows that the parallel mode can be generated by the electron beam of 5,000 km/s. They can thermalize electrons ≲100 eV effectively. However, the generation mechanism of the perpendicular mode is not clear yet, which requires further study.

1 Introduction

Magnetic flux ropes are 3-D helical structures with coherently twisted magnetic field lines winding about a common axis. A typical flux rope features an enhancement of magnetic field intensity in the core region and a reversal of the normal component of the magnetic field line at the center. Such characteristics are employed for the identification of flux ropes. It is known that the generation of flux ropes is closely related to the magnetic reconnection process. Converging reconnection jets in the same plane coming from two distinct reconnection X-lines can form a flux rope [1, 2]. Alternatively, the instability of a single X-line may generate flux ropes as secondary islands [3, 4].

Previous studies have shown that flux ropes can play an important role in the energization of particles during magnetic reconnection. Several acceleration mechanisms associated with flux ropes have been suggested. The O-type acceleration explains electron acceleration by contracting flux ropes [3]. A newly reconnected magnetic field becomes contracted due to a tension force. The electrons trapped in the flux rope gain energy through multiple reflections at the converging boundaries (Fermi acceleration). The anti-reconnection, or equivalently, the secondary reconnection describes coalescence of multiple flux ropes [5]. If the central X-line is weaker than the other two adjacent X-lines in a configuration of three sequential magnetic islands, then two flux ropes may emerge by absorbing the central structure. Subsequently, they may further merge into a sinle large flux rope as a consequence of secondary reconnection between two the flux ropes. By employing a two-dimensional (2D) Particle-In-Cell (PIC) simulation, Oka et al. [5] showed that energization in the secondary reconnection region is the most important among other processes.

Recent in-situ observations have shown that various waves exist in the near vicinity of flux ropes. Flux ropes are made of complex and dynamic structures. Their formation is intimately involved with reconnection jets and gradients of density, temperature, and magnetic field intensity. Consequently, flux ropes contain a variety of free energy sources, which can generate waves. By analyzing data from Cluster spacecraft, Khotyaintsev et al. [6] identified solitary structures associated with the electric field. The observed solitary structures are interpreted as slow electron holes and weak double layers generated by Buneman instability at the center of the flux rope. Jiang et al. [7] studied whistler waves near two sequential flux ropes and compared properties of whistler waves inside and outside of the flux ropes. They report that the frequency range inside (0.5F_ce ∼ F_ce) is higher than outside (0.1F_ce ∼ F_ce), where F_ce is electron cyclotron frequency. Low-frequency waves such as lower-hybrid drift waves (LHDI) and kinetic Alfven waves (KAW) were also studied by Tang et al. [8, 9]. A variety of waves associated with the flux ropes were intensively studied by Øieroset et al. [10], showing an entire picture of wave distribution near the flux rope. Charged particles may efficiently interact with a number of different plasma waves and thus be energized. Moreover, the electrostatic perpendicular mode can modify larger-scale equilibrium or force-balance by changing electric current, temperature, and off-diagonal pressure tensors [11]. Consequently, understanding waves in flux ropes and magnetic reconnection is important, and may provide clues as to the underlying charged-particle acceleration processes.

In this paper, we investigate waves inside the magnetic field depression (crater) at the center of a crater-shaped flux rope on the May 5. 2017 event using observation data from the Magnetospheric Multiscale (MMS) mission [12]. The MMS Mission has provided multi-spacecraft measurements at separations varying from a few electron inertial lengths (d_e) to several ion inertial lengths (d_i). MMS enables investigations of multi-scale structures from electron- to ion-scale by its unprecedented high-resolution data. We use burst mode data from the fluxgate magnetometer [13], the electric field double probes [14, 15], and the fast plasma investigation [16] in this study.

2 Data Analysis and Results

The event on May 5. 2017 was analyzed in detail by Hwang et al. [17], but we will briefly describe the event for the sake of completeness. Note here that we present MMS1 data because the MMS4 EDP data, essential for the electric wave analysis, is not available at this event. All of the other three MMS1-3 spacecraft observed similar features of the flux rope and waves, and MMS1 shows the clearest features. Figure 1 presents an overview of the MMS observation of the event. Figures 1A–C show (a) magnetic field, (b) particle density (black: electron, blue: ion), and (c) ion velocity during 10-min time interval in GSM coordinates. All of the quantities show quasi-periodic fluctuations: positive B_x and B_y are accompanied by enhanced particle densities and reduced temperature, and vise versa. On the basis of several approaches, Hwang et al. [17] demonstrated that these large-scale fluctuations are nonlinearly developed Kelvin-Helmholtz waves (KHW). Specifically, they showed that the averaged quantities from the magnetosheath side and the magnetosphere side satisfy the threshold condition for the KHW, ${\left[\mathbf{k}\cdot \left({\mathbf{V}}_{sh}-{\mathbf{V}}_{sp}\right)\right]}^2>{\mu }_0^{-1}\left({\rho }_{sp}^{-1}+{\rho }_{sh}^{-1}\right)\left[{\left({\mathbf{B}}_{sp}\cdot \mathbf{k}\right)}^2+{\left({\mathbf{B}}_{sh}\cdot \mathbf{k}\right)}^2\right]$, where subscripts sp and sh stand for magnetopause and magnetosphere, respectively; V, B, and ρ, are flow velocity, magnetic field vector, and plasma density, respectively; k is the wave vector associated with KHW; and μ₀ denotes the vacuum permeability [18]. They further showed that normal directions of leading (vertical solid lines in 1) and trailing edges (vertical dashed lines) agreed with the PIC simulation results of KHW. In addition, they found that the shapes of fluctuations are attributed to nonlinearly developed KHWs or rolled-up Kelvin-Helmholtz vortices (KHVs). This interpretation is supported by the finding that the particle densities abruptly jump around trailing edges forming compressed layers while slowly decrease around leading edges forming thicker mixed layers, a feature consistent with KH dynamics.

FIGURE 1

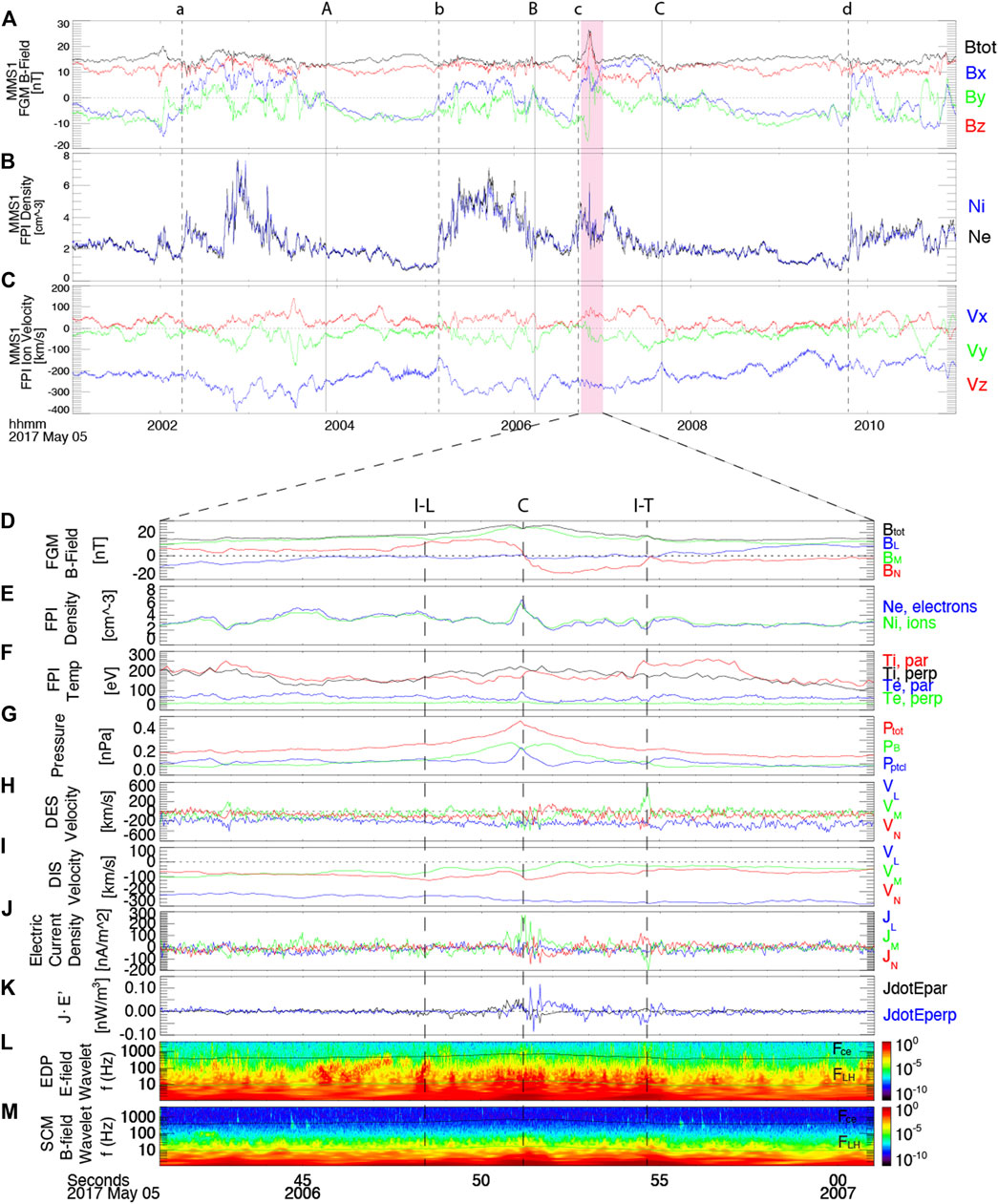
FIGURE 1. (A–C) Overview of MMS1 observation of May 5. 2017 event. (A) Magnetic field, (B) particle density, and (C) ion velocity in the GSM coordinate. Vertical dashed lines (A–D) correspond to trailing edges of nonlinear developed K-H waves, and solid vertical lines (A–C) correspond to leading edges. (D–M) Enlarged plots showing the crater flux rope in LMN coordinate. (D) Magnetic field, (E) density, (F) temperature, (G) pressure, (H) electron velocity, (I) ion velocity, (J) electric current density, (K) energy dissipation proxy J⋅E′, (L) electric field power spectrogram, and (M) magnetic field power spectrogram.

A peak in the magnetic field intensity near 20:06:51 UTC can be identified in relation to KHWs. Figures 1D–M are enlarged portion of the red-shaded region showing the details of this peak in LMN coordinates, which are calculated by the MVA method [19] using the magnetic field data ($\widehat{\mathbf{m}}$ is the axis of a flux rope, $\widehat{\mathbf{n}}$ is outward direction from the magnetopause, and $\widehat{\mathbf{l}}$ completes the orthonormal coordinates). We marked three vertical lines for inner-leading edge “I–L”, inner-trailing edge “I–T”, and core region “C” of the flux rope. In Figure 1D, B_N is reversed from positive to negative inside the enhancement of the total magnetic field B_TOT. It means that this peak is associated with a flux rope structure. We note that there is a depression of total magnetic strength at the center of the flux rope “C”. The magnetic pressure decreases at the depression “C” in Figure 1G. However, total pressure increases because plasma pressure increases due to the enhancement of plasma density and electron parallel temperature, as shown in Figures 1E,F. As a consequence, Hwang et al. [17] concluded that this is an M-shaped crater flux rope similar to a crater flux transfer event (FTE). Their sizes of the flux rope and the crater measured by the cross-sectional distances of the peak-to-peak B_n component are ∼650 km (∼ 4.3d_i, d_i: ion inertial length) and ∼100 km (∼ 0.7d_i), respectively (Δt ∼2.6 s, ∼0.4 s, and V_i,l ∼−250 km/s).

Figure 1J shows the electric current around this flux rope that is calculated from electron (Figure 1H) and ion bulk velocity (Figure 1I). It was found that these currents are related to the electron jet coming from magnetic reconnection under a strong guide field [17]. Ion bulk velocity is not changed significantly in the flux rope; thus, this current is carried by the electrons. The coincidence of nonzero J⋅E′ and wave activities near “I–T” and “C” shown in Figures 1L, M is a strong indication that the energy conversion might be mediated by waves inside the flux rope. The frequency of J ⋅E′ fluctuation is few Hz which is slightly lower than the lower-hybrid frequency. Thus, it might come from electric field associated with the enhanced lower-hybrid mode as mentioned by Hwang et al. [17].

Figure 2 is an enlarged plot showing the wave spectrum near the depression of magnetic field “C”. Figures 2A,B present magnetic field in LMN coordinate and electron density, respectively. Figure 2C is the parallel and perpendicular energy dissipation proxy J⋅E′. Figures 2D,E are pitch angle distributions of electrons in low and middle energy ranges, which show there are bi-direction (parallel and anti-parallel) beams near “C”. Figures 2F–H show power spectra of (f) parallel electric field, (g) perpendicular electric field, and (h) magnetic field. The parallel and perpendicular components of the electric field are decomposed using the instantaneous magnetic field. As shown in Figures 2F, G, we observe that there are two high-frequency wave modes in this region, one is a parallel mode in Figure 2F, and the other is a perpendicular mode in Figure 2F. Frequencies of both wave modes are close to the electron cyclotron frequency (F_ce) plotted by horizontal dashed lines in each figure. We conclude that both high-frequency modes near F_ce are electrostatic or quasi-electrostatic modes because there is no significant signal of the magnetic field near F_ce as shown in Figure 2H. Moreover, the ratio between amplitudes of electric and magnetic fluctuations E/cB is 5–10 for both modes.

FIGURE 2

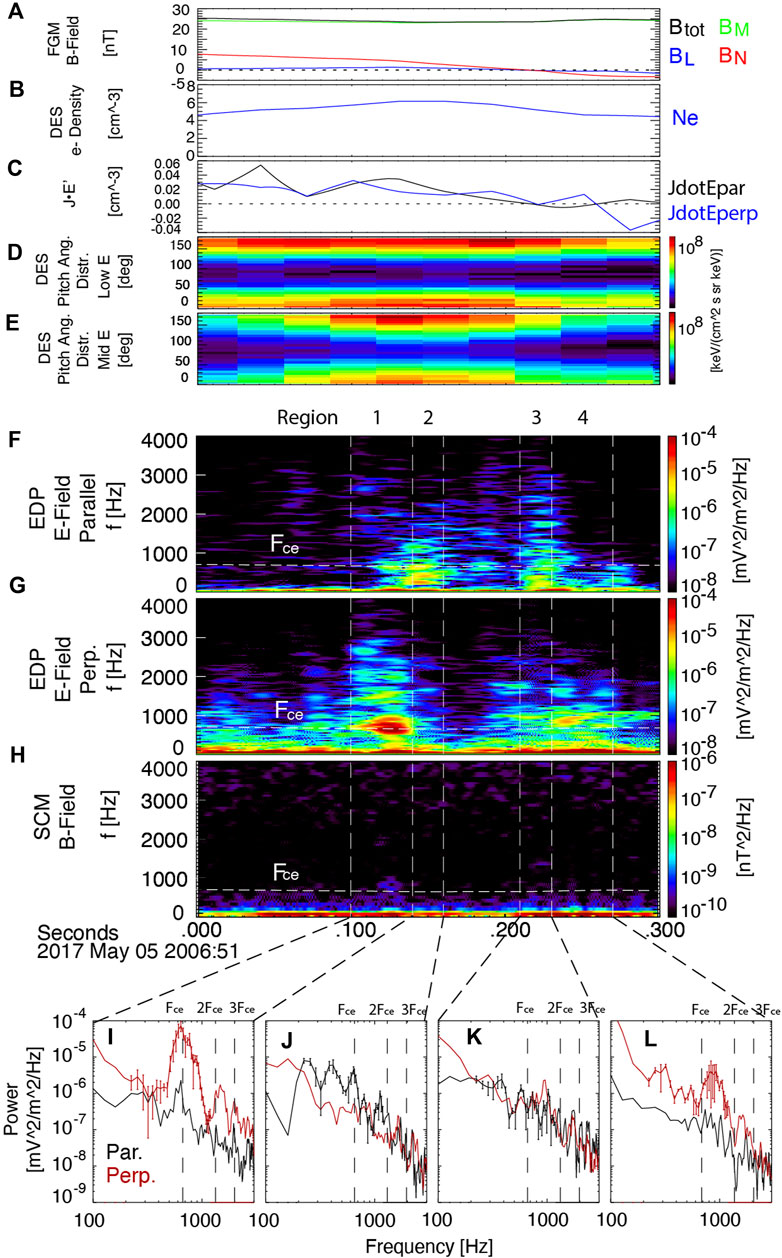
FIGURE 2. Wave data near the depression of magnetic field at the center of the flux rope. (A) Magnetic field in LMN coordinate, (B) electron density, (C) energy dissipation proxy J⋅E′, (D) electron pitch angle distribution of low energy range, and (E) mid energy range, (F) power spectrum of the parallel electric field, (G) perpendicular electric field, and (H) magnetic field. (I–L) Averaged power spectrum of electric field in time ranges of (I) 20:06:51.100–0.140, (J) 0.140–0.160, (K) 0.210–0.230, and (L) 0.230–0.270 showing the distribution of parallel and perpendicular modes. (Error bars: standard errors).

The two modes exist very close to each other but can be distinguished because they have different characteristics. Figures 2I–L present averaged power spectra of electric field in the time ranges of 1) 20:06:51.100–140, (j) 0.140–0.160, (k) 0.210–0.230, and (L) 0.230–0.270. These figures show that the two wave modes occur at different locations. We also checked the Lomb-Scargle periodogram [20, 21], and it shows similar peaks with power spectrogram of Figures 2I–L (not shown here). Therefore, we concluded that those peaks are significant. Black and red lines denote the power spectra for parallel and perpendicular electric fields, respectively. The enhancement of parallel mode, as displayed in Figures 2J, K, occurs in the inner region of the magnetic field depression, while the perpendicular mode (black) locates in the outer region, 1) and (L). Moreover, their frequencies are also different. The frequency of the parallel mode is lower than F_ce (vertical dashed lines), but the frequency of the perpendicular mode is almost the same as or is higher than F_ce. It is notewothy that the perpendicular mode features harmonics near the integer multiples of F_ce.

To understand the generation mechanism of waves, we carry out linear stability analysis based upon observed electron distribution functions. Figure 3 shows electron distributions and the associated linear stability characteristics. Figures 3A, B are the 2D reduced electron distribution obtained from MMS1 spacecraft at the center of the flux rope in velocity space of V_par vs. V_B×V for (a), and ${\text{V}}_{{\text{V}}_{perp}\times \text{B}}$ vs. V_B×V for (b). Figure 3A shows bi-direction electron beams along the magnetic field with a speed of about 5,000 km/s. We note that this electron beam does not exist outside of the magnetic field depression. Therefore, this beam would be a free energy source for waves excited inside the magnetic field depression region.

FIGURE 3

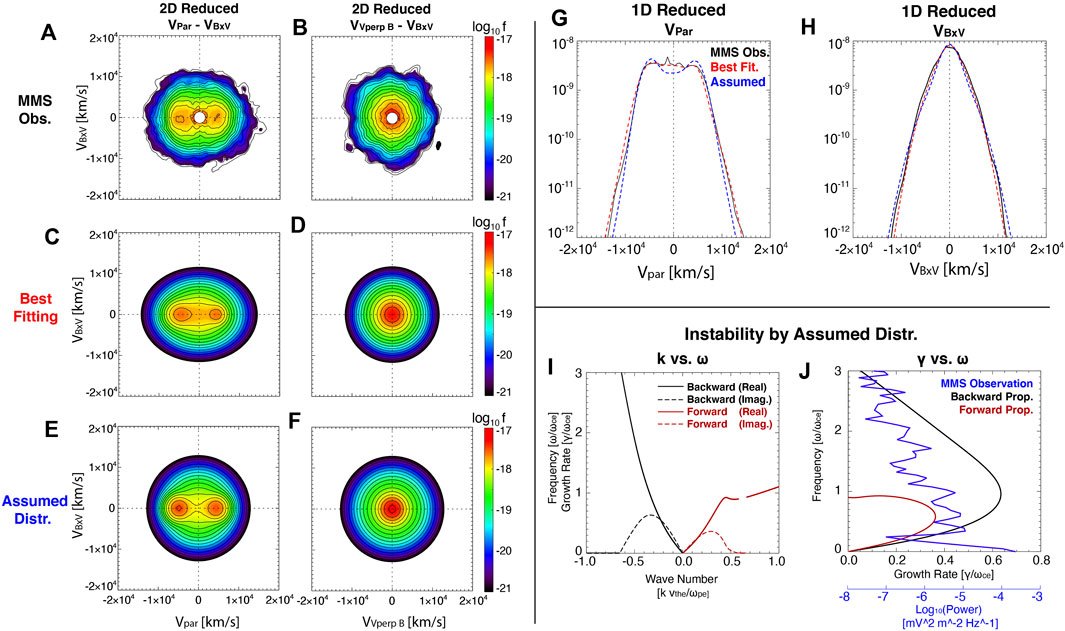
FIGURE 3. (Left) 2D reduced electron distribution of (A, B) MMS observation, (C, D) the best fitting, and (E, F) an assumed distribution for wave instability in V_par-V_B×V and ${\text{V}}_{{\text{V}}_{\text{perp}}\times \text{B}}$-V_B×V space. (Right Top) 1D reduced distribution in (G) V_par, and (H) V_B×V space: (black) MMS observation, (red) the best fitting, and (blue) the assumed distribution. (Right Bottom) Instability derived from the assumed distribution. (I) wave number k vs. frequency ω. (black) the backward-propagating mode, and (red) the forward-propagating mode. Solid lines and dashed lines are real and imaginary parts of solutions. (J) Comparison between (red) the forward-, (black) backward-propagating mode, and (blue) power spectrum in MMS observation.

In order to investigate the possible unstable mode, we model the observed electron distribution as a sum of Maxwellian distributions as shown in Figures 3C, D, where the 2D reduced distribution that produces the best fitting is shown. In addition, Figures 3G,H show 1D reduced distribution from MMS observation (black solid line) and the best fitting results (red dashed line). The best fitting model is given as follows: n₀ = 2.8 cm⁻³, v_th∥,0 = 5,400 km/s, v_th⊥,0 = 4,000 km/s, v_d∥,0 = 0.0 km/s, n₁ = 1.05 cm⁻³, v_th∥,1 = 2,500 km/s, v_th⊥,1 = 2,300 km/s, v_d∥,1 = −5,000 km/s, n₂ = 0.55 cm⁻³, v_th∥,2 = v_th⊥,2 = 1,800 km/s, v_d∥,2 = 4,500 km/s, where indices 0, 1, and 2 mean core electron, parallel beam in negative direction, and positive direction, respectively. v_th∥ and v_th⊥ are parallel and perpendicular thermal speeds, while v_d∥ is the beam speed in the parallel direction. In these figures, the fitting result agrees with MMS data remarkably. However, we found that there is no instability nor growing mode associated with this distribution. We note that electron distributions from all of the other MMS spacecraft are almost identical when they passed the crater. This can be interpreted either as the waves generated elsewhere and have simply propagated into the observation location, or alternatively, the waves might be generated at an earlier time so the thermalization of electrons has already been completed. In the case of latter, the observed distribution may represent the relaxed state rather than the true initial state that is subject to instability.

We model another electron distribution assuming plasma conditions when the beam is injected into the plasma. We use the parameters of plasma outside of the flux rope for core electrons. Considering the thermalized distribution after the wave generation and thermalization process to become similar to the MMS observation, we calculate the beam density and speeds as follows: n₀ = 1.8 cm⁻³, v_th∥,0 = v_th⊥,0 = 4,600 km/s, v_d = 0.0 km/s, n₁ = 1.4 cm⁻³, v_th∥,1 = v_th⊥,1 = 2,150 km/s, v_d∥,1 = −5,000.0 km/s, n₂ = 1.2 cm⁻³, v_th∥,2 = v_th⊥,2 = 2,150 km/s, v_d∥,2 = 4,500.0 km/s. The 2D and 1D reduced distributions of the assumed electron distribution are plotted in Figures 3E–H using the same format.

By making use of this assumed distribution, we carried out the linear kinetic instability analysis using BO code [22]. Figure 3I shows the solutions by way of plotting the wave number k versus frequency ω, where solid lines and dashed lines are real and imaginary parts, respectively. Wave number k is normalized by electron Debye length (λ_De = v_the/ω_pe) and frequency is normalized by electron cyclotron frequency ω_ce. We found that there are two growing modes: one is a backward-propagating mode along the negative (−) direction with respect to the ambient magnetic field plotted by black lines, and the other is a forward-propagating mode along the positive (+) direction plotted by red lines, which is consistent with their generation by bi-directional beams. Note that the backward-propagating mode grows faster than the forward-propagating mode. The maximum growth rate of the backward-propagating mode is twice that of the forward-propagating mode, and the frequency range of the backward-propagating mode is much broader than the forward-propagating mode.

We compare MMS observation and two growing modes in Figure 3J where x-axis is the wave power and the growth rate γ, while y-axis denotes the frequency. The blue line is the power spectrum of parallel electric field observed by MMS, and red and black lines are the growth rates of forward- and backward-propagating modes, respectively. In the y-axis, it is seen that the growth rate of forward mode is located below ω_ce and its peak is ∼ 0.6 ω_ce. The peak of the backward mode locates slightly higher than the forward mode near ∼ 0.9 ω_ce, and its range is much broader from 0 to 4 ω_ce. The shape of the MMS observation in Figure 3J is not exactly matched with the growth rates because MMS observed a highly nonlinear phase of waves as the fully thermalized electron distribution indicates. Even so, the broad frequency range of the observation agrees with the backward mode, and its peak seems to agree with the forward mode. Therefore, we think this MMS observation shows a mixed feature of both modes, and the observed waves were generated by electron beams in the crater. However, we cannot clearly distinguish forward- and backward-propagating modes in the MMS observation.

We note here that the frequency range of beam modes in this event is unusual and extremely low if we consider that beam mode waves are usually generated near or under 1 F_pe as a result of beam-plasma interaction. At the center of the flux rope, the electron plasma frequency F_pe is ∼ 22 kHz, and the electron cyclotron frequency F_ce is ∼ 640 Hz, thus, F_ce ≅ 2.9 × 10^–2 F_pe. This downshift of the frequency range of beam mode from 1 F_pe is caused by high beam density [23, 24]. The sum of densities of two beams is higher than that of the core electrons in the assumed electron distribution as shown in Figures 3E–G. The agreement of wave analysis appears to indicate that the assumed electron distribution well represents the situation when the beams are injected, and when the beam modes are generated. Despite the good agreement in the parallel direction, no instability in the perpendicular direction was found within the framework of uniform plasma dispersion relation solver. It is possible that agyrotropic crescent-shaped electron distribution or ring-shaped distribution might exist where the perpendicular waves are generated if we consider that the May 5, 2017 event is closely related to magnetic reconnection. The reconstruction of the nonlinear structure of this flux rope using the second-order Taylor expansion showed that the core-field topology of this flux rope indicates two interlinked flux tubes [17]. Thus, the crater “C” could be interpreted as a reconnecting current sheet between two interlinked flux tubes [25, 26] Such electron distributions are known to generate (electrostatic and perpendicular) electron Bernstein waves near integer harmonics of F_ce [24, 27]. However, all four MMS spacecraft didn’t observe agyrotropic or ring-shaped electron distribution. Therefore, we couldn’t clearly verify the generation mechanism of perpendicular mode at this stage. We will discuss this and other possibilities in more detail in the following section.

3 Discussion and Conclusion

In the present manuscript the issue of high-frequency waves measured inside the center of the magnetic field depression in a crater-shaped flux rope is discussed. Upon comparing MMS observation and linear dispersion relation, we found that the characteristics of wave dispersion relation are consistent with the beam mode generated by a counter-streaming electron populations. In particular, it is found that the frequencies of the beam mode are downshifted to the order of F_ce because of high beam density.

In this event, other waves are also observed, as mentioned in previous papers. In Figure 4A, we schematically plot location where such waves are observed. Electron cyclotron waves (ECW) are observed in Figures 1L, M. Although they appear intermittently during the entire event, it seems that they are more frequently observed outside of the inner edge (I–L and I–T) of the flux rope. Those sporadic ECW might be the same branch of waves with the perpendicular beam mode in our study, but they are related to the primary reconnection generating the flux rope. During the time interval of 20:06:45–47 in Figure 1L, wave signals in a frequency range of 0.1–0.9 F_ce are observed. It might be an oblique whistler wave generated in separatrix or outflow region of magnetic reconnection. Around the flux rope (20:06:48–55), low frequency waves are also observed in Figures 1L, M. Their frequency is lower than the lower-hybrid frequency. Thus, it might be a lower-hybrid drift wave (LHDW) generated by the density gradient of the flux rope.

FIGURE 4

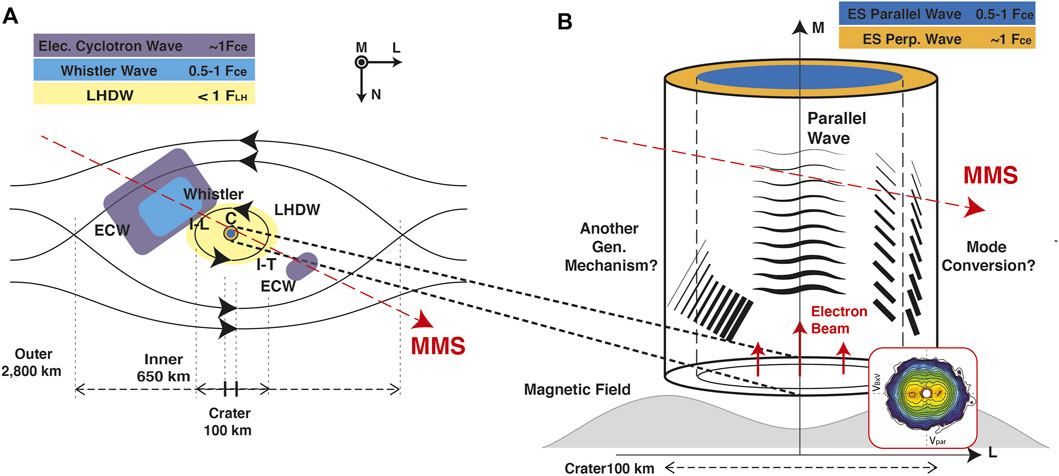
FIGURE 4. (A) Various waves observed in May 5. 2017 event. Waves observed in Figure 2 are plotted in a flux rope diagram. Red-dashed line shows the trajectory of MMS spacecraft. (B) Waves in the depression of magnetic field at the center of flux rope. Two possibilities of perpendicular wave generation are plotted together.

Figure 4B schematically depict the spatial location where high-frequency waves associated with the magnetic field depression are measured. The parallel wave is dominant in the central region, while the perpendicular wave is dominant in the outer region. However, we were not able to identify the generation mechanism of perpendicular waves based upon the uniform plasma theory of wave excitation. We have entertained, however, a possibility of a perpendicular beam, in the location of wave generation. Since the May 5. 2017 event is closely related to magnetic reconnection as investigated by Hwang et al. [17], it is possible that agyrotropic crescent-shaped electron distribution or ring-shaped distribution might exist, which in turn may excite the quasi perpendicular electrostatic electron Bernstein waves near integer harmonics of F_ce [24, 27]. Another possible scenario is a mode conversion from parallel waves at the edge of magnetic field depression. In the edge of magnetic field depression, the gradients of magnetic field and density are formed. Moreover, the direction of the magnetic field is drastically changed. Therefore, the parallel mode would not remain an eigenmode of the region. Hence, mode conversion to quasi-perpendicular mode may take place.

Speaking of the density and magnetic field gradient on the edge of the magnetic field depression region, we may entertain further possibilities as well. In the presence of density gradient, warm ions undergoing diamagnetic drift may lead to the electron cyclotron drift instability at the multiple harmonics of F_ce [28–30]. Another possibility is that, even in the absence of free energy source, for sufficiently energetic electrons, the spontaneous emission of electrostatic cyclotron harmonics may take place [31, 32]. As a matter of fact, the emission of multiple harmonic cyclotron emission is frequently observed in inner magnetosphere and other planetary magnetopheric environment during active and even quiet periods [33–35]. The analysis of quasi-perpendicular multiple cyclotron harmonic mode by the above-referenced alternative scenarios is, however, beyond the scope of the present paper.

The results of the present study may be summarized as follows. In a crater flux rope, beam-generated waves are observed by MMS spacecraft. At the center of the magnetic field depression, there exist parallel and perpendicular wave modes near the electron cyclotron frequency F_ce. The kinetic linear dispersion analysis shows that the bi-direction electron beam generates the parallel modes. Because the beam density is very high compared to the core electrons, the frequency of the parallel mode is quite low. The peak of the power spectrum locates in the frequency range of 0.6 ∼0.9 F_ce where F_ce ≅ 2.9 × 10^–2 F_pe. The generation mechanism of the perpendicular mode is not clear in the observation because MMS spacecraft passed far from where the waves were generated. A mode-conversion from the parallel mode at the outer edge of the magnetic field depression might generate the perpendicular mode, or other instability mechanisms might be operative near the wave generation location. Our study shows that the electron beam inside a flux rope can not only change the flux rope structure making the magnetic field depression but also thermalize electrons inside the magnetic field depression by wave activity.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://lasp.colorado.edu/mms/sdc/public/.

Author Contributions

All authors contributed conception and design of this study. KD and K-JH wrote the first draft of the manuscript. All authors contributed to scientific discussion, manuscripts revision and writing of the manuscript.

Funding

This study was supported, in part, by NASA Guest Investigator Grant 80NSSC18K1337. KD and K-JH. were partly supported by NASA 80NSSC18K0693. K-JH was supported, in part, by NSF AGS-1834451 and NASA 80NSSC18K1534 and 80NSSC18K0570. PY acknowledges NSF Grant AGS1842643 and NASA Grant NNH18ZDA001N-HSR to the University of Maryland and BK21 Plus grant to Kyung Hee University, Korea, from NRF.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge the use of Pleiades in NASA High-End Computing Program.

References

1. Hughes WJ, Sibeck DG. On the 3-dimensional Structure of Plasmoids. Geophys Res Lett (1987) 14:636–9. doi:10.1029/GL014i006p00636

CrossRef Full Text | Google Scholar

2. Eastwood JP. Observations of Multiple X-Line Structure in the Earth’s Magnetotail Current Sheet: A Cluster Case Study. Geophys Res Lett (2005) 32:L11105. doi:10.1029/2005GL022509

CrossRef Full Text | Google Scholar

3. Drake JF, Swisdak M, Che H, Shay MA. Electron Acceleration from Contracting Magnetic Islands during Reconnection. Nature (2006) 443:553–6. doi:10.1038/nature05116

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Daughton W, Scudder J, Karimabadi H. Fully Kinetic Simulations of Undriven Magnetic Reconnection with Open Boundary Conditions. Phys Plasmas (2006) 13:072101. doi:10.1063/1.2218817

CrossRef Full Text | Google Scholar

5. Oka M, Phan TD, Krucker S, Fujimoto M, Shinohara I. Electron Acceleration By Multi-Island Coalescence. Astrophysical J (2010) 714:915–26. doi:10.1088/0004-637X/714/1/915

CrossRef Full Text | Google Scholar

6. Khotyaintsev YV, Vaivads A, André M, Fujimoto M, Retinò A, Owen CJ. Observations of Slow Electron Holes at a Magnetic Reconnection Site. Phys Rev Lett (2010) 105:165002. doi:10.1103/PhysRevLett.105.165002

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Jiang K, Huang SY, Yuan ZG, Yu XD, Liu S, Deng D, et al. Observations of Whistler Waves in Two Sequential Flux Ropes at the Magnetopause. Astrophysics Space Sci (2019) 364. doi:10.1007/s10509-019-3647-4

CrossRef Full Text | Google Scholar

8. Tang B, Li W, Wang C, Dai L, Khotyaintsev Y, Lindqvist PA, et al. Magnetic Depression and Electron Transport in an Ion-Scale Flux Rope Associated with Kelvin-Helmholtz Waves. Ann Geophysicae (2018) 36:879–89. doi:10.5194/angeo-36-879-2018

CrossRef Full Text | Google Scholar

9. Tang BB, Li WY, Wang C, Dai L, Han JP. Effect of Kinetic Alfvén Waves on Electron Transport in an Ion-Scale Flux Rope. Chin Phys Lett (2018) 35. doi:10.1088/0256-307X/35/11/119401

CrossRef Full Text | Google Scholar

10. Øieroset M, Sundkvist D, Chaston CC, Phan TD, Mozer FS, McFadden JP, et al. Observations of Plasma Waves in the Colliding Jet Region of a Magnetic Flux Rope Flanked by Two Active X Lines at the Subsolar Magnetopause. J Geophys Res Space Phys (2014) 119:6256–72. doi:10.1002/2014JA020124

CrossRef Full Text | Google Scholar

11. Dokgo K, Hwang K, Burch JL, Yoon PH, Graham DB, Li W. The Effects of Upper-Hybrid Waves on Energy Dissipation in the Electron Diffusion Region. Geophys Res Lett (2020) 47:e2020GL089778. doi:10.1029/2020GL089778

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Burch JL, Moore TE, Torbert RB, Giles BL. Magnetospheric Multiscale Overview and Science Objectives. Space Sci Rev (2016) 199:5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

13. Russell CT, Anderson BJ, Baumjohann W, Bromund KR, Dearborn D, Fischer D, et al. The Magnetospheric Multiscale Magnetometers. Space Sci Rev (2016) 199:189–256. doi:10.1007/s11214-014-0057-3

CrossRef Full Text | Google Scholar

14. Ergun RE, Tucker S, Westfall J, Goodrich KA, Malaspina DM, Summers D, et al. The Axial Double Probe and Fields Signal Processing for the MMS Mission. Space Sci Rev (2016) 199:167–88. doi:10.1007/s11214-014-0115-x

CrossRef Full Text | Google Scholar

15. Lindqvist PA, Olsson G, Torbert RB, King B, Granoff M, Rau D, et al. The Spin-Plane Double Probe Electric Field Instrument for MMS. Space Sci Rev (2016) 199:137–65. doi:10.1007/s11214-014-0116-9

CrossRef Full Text | Google Scholar

16. Pollock C, Moore T, Jacques A, Burch J, Gliese U, Saito Y, et al. Fast Plasma Investigation for Magnetospheric Multiscale. Space Sci Rev (2016) 199:331–406. doi:10.1007/s11214-016-0245-4

CrossRef Full Text | Google Scholar

17. Hwang KJ, Dokgo K, Choi E, Burch JL, Sibeck DG, Giles BL, et al. Magnetic Reconnection inside a Flux Rope Induced by Kelvin-Helmholtz Vortices. J Geophys Res Space Phys (2020) 125. doi:10.1029/2019JA027665

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hasegawa A. Plasma Instabilities and Nonlinear Effects, Physics and Chemistry in Space, Vol. 8. Berlin, Heidelberg: Springer Berlin Heidelberg (1975) doi:10.1007/978-3-642-65980-5

CrossRef Full Text

19. Sonnerup BUO, Scheible M. Minimum and Maximum Variance Analysis. ISSI Scientific Rep (1998) 1:185–220.

Google Scholar

20. Lomb NR. Least-squares Frequency Analysis of Unequally Spaced Data. Astrophysics Space Sci (1976) 39:447–62. doi:10.1007/BF00648343

CrossRef Full Text | Google Scholar

21. Scargle JD. Studies in Astronomical Time Series Analysis. II - Statistical Aspects of Spectral Analysis of Unevenly Spaced Data. Astrophysical J (1982) 263:835. doi:10.1086/160554

CrossRef Full Text | Google Scholar

22. Xie HBO. A Unified Tool for Plasma Waves and Instabilities Analysis. Comput Phys Commun (2019) 244:343–71. doi:10.1016/j.cpc.2019.06.014

CrossRef Full Text | Google Scholar

23. Cairns IH. Electrostatic Wave Generation above and below the Plasma Frequency by Electron Beams. Phys Fluids B (1989) 1:204–13. doi:10.1063/1.859088

CrossRef Full Text | Google Scholar

24. Dokgo K, Hwang KJ, Burch JL, Yoon PH, Graham DB, Li W. High-Frequency Waves Driven by Agyrotropic Electrons Near the Electron Diffusion Region. Geophys Res Lett (2020) 47. doi:10.1029/2020GL087111

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kacem I, Jacquey C, Génot V, Lavraud B, Vernisse Y, Marchaudon A, et al. Magnetic Reconnection at a Thin Current Sheet Separating Two Interlaced Flux Tubes at the Earth’s Magnetopause. J Geophys Res Space Phys (2018) 123:1779–93. doi:10.1002/2017JA024537

CrossRef Full Text | Google Scholar

26. Øieroset M, Phan TD, Drake JF, Eastwood JP, Fuselier SA, Strangeway RJ, et al. Reconnection with Magnetic Flux Pileup at the Interface of Converging Jets at the Magnetopause. Geophys Res Lett (2019) 46:1937–46. doi:10.1029/2018GL080994

CrossRef Full Text | Google Scholar

27. Li WY, Graham DB, Khotyaintsev YV, Vaivads A, André M, Min K, et al. Electron Bernstein Waves Driven by Electron Crescents Near the Electron Diffusion Region. Nat Commun (2020) 11:141. doi:10.1038/s41467-019-13920-w

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Forslund DW, Morse RL, Nielson CW. Electron Cyclotron Drift Instability. Phys Rev Lett (1970) 25:1266–70. doi:10.1103/PhysRevLett.25.1266

CrossRef Full Text | Google Scholar

29. Wu CS, Fredricks RW. Cyclotron Drift Instability in the bow Shock. J Geophys Res (1972) 77:5585–9. doi:10.1029/JA077i028p05585

CrossRef Full Text | Google Scholar

30. Janhunen S, Smolyakov A, Sydorenko D, Jimenez M, Kaganovich I, Raitses Y. Evolution of the Electron Cyclotron Drift Instability in Two-Dimensions. Phys Plasmas (2018) 25:082308. doi:10.1063/1.5033896

CrossRef Full Text | Google Scholar

31. Sentman DD. Thermal Fluctuations and the Diffuse Electrostatic Emissions. J Geophys Res Space Phys (1982) 87:1455–72. doi:10.1029/JA087iA03p01455

CrossRef Full Text | Google Scholar

32. Yoon PH, Hwang J, Kim H, Seough J. Quasi Thermal Noise Spectroscopy for Van Allen Probes. J Geophys Res Space Phys (2019) 124:2811–8. doi:10.1029/2019JA026460

CrossRef Full Text | Google Scholar

33. Meyer-Vernet N, Hoang S, Moncuquet M. Bernstein Waves in the Io Plasma Torus: A Novel Kind of Electron Temperature Sensor. J Geophys Res (1993) 98:21163–76. doi:10.1029/93JA02587

CrossRef Full Text | Google Scholar

34. Moncuquet M, Lecacheux A, Meyer-Vernet N, Cecconi B, Kurth WS. Quasi thermal Noise Spectroscopy in the Inner Magnetosphere of Saturn with Cassini/RPWS: Electron Temperatures and Density. Geophys Res Lett (2005) 32:L20S02. doi:10.1029/2005GL022508

CrossRef Full Text | Google Scholar

35. Kurth WS, De Pascuale S, Faden JB, Kletzing CA, Hospodarsky GB, Thaller S, et al. Electron Densities Inferred from Plasma Wave Spectra Obtained by the Waves Instrument on Van Allen Probes. J Geophys Res Space Phys (2015) 120:904–14. doi:10.1002/2014JA020857

PubMed Abstract | CrossRef Full Text | Google Scholar