- 1Departamento de Física, Universidade Federal de São Carlos, São Carlos, Brazil
- 2Departamento de Física, Universidade Federal de Santa Catarina, Florianópolis, Brazil
- 3Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, Brazil
In this review article, we are interested in the detailed analysis of complexity aspects of both time and space that arises from the implementation of a quantum algorithm on a quantum based hardware. In particular, some steps of the implementation, as the preparation of an arbitrary superposition state and readout of the final state, in most of the cases can surpass the complexity aspects of the algorithm itself. We present the complexity involved in the full implementation of circuit-based quantum algorithms, from state preparation to the number of measurements needed to obtain good statistics from the final states of the quantum system, in order to assess the overall space and time costs of the processes.
1 Introduction
Quantum computing takes advantage of the unique properties of quantum mechanics, such as superposition and entanglement to carry out computational tasks in distinct ways than the classical computers do [1]. Since Richard Feynman’s idealization that a quantum architecture would be a proper way to simulate actual quantum systems that occur in nature in the early 1980’s [2], much attention has been given to the application of quantum systems for computational tasks. Among the greatest and most famous achievements of quantum information and quantum computation, one can cite superdense coding [3], the BB-84 algorithm for quantum public key distribution of cryptography systems [4], Shor’s integer factoring algorithm [5], Grover’s database search algorithm [6], alongside examples of no less importance or relevance. The advances have also reached important areas of mathematics and natural sciences in general, with quantum algorithms and circuit designing being developed to accomplish linear algebra tasks like eigen- [7, 8] and singular- value [9, 10] decompositions of matrices, finding solutions to linear systems of equations [11], solving linear [12–14] and nonlinear [15] differential equations, partial non-homogeneous linear differential equations [16], among other potential applications.
There have been recent progress in the current era of Noisy Intermediate Scale Quantum (NISQ) devices, such as problems that cannot be solved by any classical shallow circuits in reasonable time, but turns out to be possible by shallow quantum circuits [17], quantum supremacy using a superconducting quantum processor architecture achieved by Google team [18], and also quantum advantages over classical computation using boson sampling [19] and the simulation of quantum systems by means of quantum based architecture in D-Wave systems [20].
In general, the implementation of a quantum algorithm is based on many steps, that involve data pre-processing, preparation of input quantum states, the processing of the input information through quantum gates and operations applied to the system, measurement of the final state of the composite quantum system, and post-processing of the data collected by the measurement process. In the present work, we will not deal with the pre- and post-processing steps, which are usually done by classical means. In most quantum algorithms, the quantum advantage over classical computation lies in the processing or evolution step, which takes advantage of the dimension of the Hilbert space of quantum systems and quantum parallelism to manipulate very large amounts of data, a task for which the present classical computers usually require exponential scaling resources, such as memory and state-of-the-art processors in supercomputer units. However, the preparation and measurement processes present in some quantum algorithms, which are essential for their proper implementations, are often neglected in their presentations, because of the intrinsic difficulties of these tasks.
The main purpose of this work is to perform a detailed analysis of the computational complexity defined by the space and time costs of quantum algorithms, considering all steps, from state preparation to readout processes. This work considers a scenario in which the rapid development of quantum computing has attracted the attention of people with different background, not only restricted to physicists or computer scientists from academia, but curious, investors, bankers, and entrepreneurs, which are delighted with the quantum speedups at first sight. Although quantum computing provides amazing results compared to its classical counterpart, a suitable interpretation of the algorithmic costs demands a proper analysis, which includes the circuit width, represented by the number of qubits necessary to carry on the tasks, as well as the circuit depth, which takes into account the number of quantum operations that must be implemented on the system for the proper processing of the information encoded in the qubit system. We are also concerned with the processes of recovering the resulting information of the processing, which can be represented by observable statistics or quantum tomography, depending on the task aimed by the quantum algorithm.
This work is organized as follows. In section 2 the costs of state preparation using different schemes are covered. Section 3 covers matrix and quantum gate decomposition and their complexity bounds. Section 4 considers quantum state tomography, with emphasis on the required number of measurements and repetitions of the execution of a quantum algorithm to achieve a desired accuracy in the results. In section 5, the overall complexity aspects for implementation are given, from state preparation to readout process. Finally, section 6 contains the conclusion of the work.
2 Complexity of Quantum State Preparation
The need for preparation of quantum states as input for solving a given problem is a common task in many quantum algorithms implemented in the circuit model of Quantum Computation (QC) [1]. Such a preparation constitutes an important part in the process of implementation of a given algorithm for circuit gate-based quantum computing, as the final quantum state encoding the solution of the problem is directly linked to the input state through the evolution step. Thus, the complexity aspects of preparing the input state must be taken into account in a detailed resource analysis.
To describe the encoding of input states properly, we must split the entire quantum system that constitutes a quantum computer into two parts: the ancilla qubits, which are used, for instance, to encode relevant information and control logical operations, and the work system, that encodes the initial conditions of the problem to be solved, which is submitted to the evolution process defined by the quantum algorithm. For instance, consider the processes to encode the initial conditions for a linear differential equation [14] or for the HHL quantum linear problem [11] in the work system. The goal of state preparation is to initialize the system in a N-dimensional specific quantum superposition that is suitable to the problem to be solved on a quantum computer. This task is often accomplished by subroutines that, in quantum algorithms, are usually referred to as system encoding.
It is important to remark that there are different kinds of encoding, such as basis encoding and amplitude encoding: the former is often used when one needs to manipulate real numbers arithmetically, and the latter when one takes advantage of the large size of the Hilbert space to encode data as probability amplitudes [21]. As an example of basis encoding, let us see how a real number is encoded in a binary string. Suppose we must represent the real value vector
For amplitude encoding, the relevant information for computation is stored in the probability amplitudes of the quantum state. The process usually starts from the n-qubit state
with
The state initialization can follow the procedure described in detail in [26], which makes use of standard single- and controlledk-operations, which are operations controlled by k qubits, acting on a single target. This method requires
As an example of state preparation, the Divide-and-Conquer scheme [34] presents an algorithm for amplitude encoding in the form of a superposition like
in which the qubits of the work and ancilla systems are entangled. So, although the system is prepared in a superposition state, the results after observation of ancilla qubtis will be left the work system as a mixed density matrix, what, in the case of algorithms for solving systems of linear or differential equations, this could be a disadvantage. Nevertheless, the algorithm is useful for machine learning and statistical analysis, and other applications, such as data sorting [34]. The algorithm structure presents the idea of dividing a problem into subproblems of the same class. The idea for creating the quantum superposition is to divide the problem like the scheme presented in Figure 1. The algorithm is based on the circuit model for quantum computing, which are presented in detail in [34], and presents space and time costs that scales as O(N) and
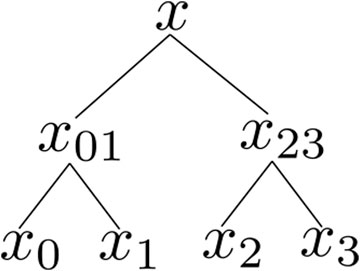
FIGURE 1. Schematic representation of the Divide-and-Conquer algorithm for loading a four-dimensional vector x into a quantum state. The task of preparing
The circuit for implementation of the Divide-and-Conquer algorithm for state preparation presents polylogarithmic depth and has a simplified structure, with the tasks divided into problems of the same class. It also presents the advantage of being based on the circuit model of computation, making its implementation simple as a subroutine for the main algorithm just by including the corresponding circuit in the state preparation step. However, this polylogarithmic depth comes at the cost of increasing the circuit width, as ancilla qubits are necessary to carry on its implementation. Thus, one can observe a trade-off between gate counts and number of qubits playing a significant role for this scheme.
Another state preparation scheme usually mentioned in quantum algorithms involves accessing a quantum database in which the quantum states are prepared in advance and can be quickly transferred to the working qubits. Below we describe this scheme in more detail, paying special attention to its complexity.
2.1 Quantum Database and Quantum Random Access Memory
Employing calls on Random Access Memory (RAM) devices is an approach that aims to accomplish the task of preparation of quantum states by querying a database that contains the information of interest. For the purpose of querying a memory device with relevant information about the input state, one must be able to construct a database which consists in a set of state vectors containing the information for quantum computation. For instance, suppose a set of m vectors S = {ψ1, ψ2, … , ψm}, each of them containing k components. The quantum equivalent of this database is the quantum associative memory representation [35] given by the uniform superposition of each state vector [21].
The cost for the creation of
There are other architectures for the implementation of quantum random access memory, such as the “Bucket Brigade” (BB) [36] and the Flip-Flop qRAM [37], which make use of different schemes to retrieve the content of a memory cell coherently. The BB architecture, for instance, is composed of a series of three-level quantum systems (qutrits), described by the states
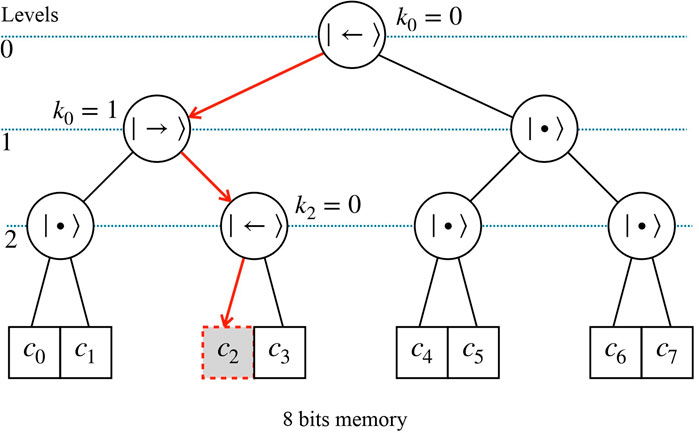
FIGURE 2. Schematic representation of the BB architecture for a eight states qRAM. To address the memory cells only 3 = log 2(8) are needed. The nodes of the tree are composed by qutrits, which are initially in the wait state. The bit string determines the path to be followed by the bus signal, in which 0 means left path and 1 right path. Depending on the bits of the given string, the states of the qutrits are left in
The Flip-Flop qRAM (FF-qRAM) [37] scheme has the advantage of being based on the circuit model for quantum computation, and thus can be implemented as a subroutine in the state preparation step of a quantum algorithm to generate a quantum database by just adding the circuit to the state preparation step. The circuit for one Flip-Flop iteration is shown in Figure 3. The operation executed by the complete circuit has the effect [37].
where
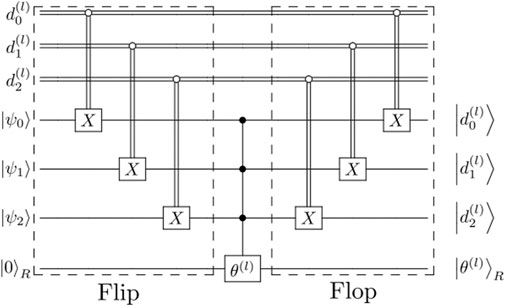
FIGURE 3. Quantum circuit corresponding to one Flip-Flop iteration of the FF-qRAM algorithm. The classically-controlled operations X are applied to the states
According to Ref. [37], the costs of space and time amounts to O(log 2(N)) qubits and O(m log 2(N)) multi-qubit operations for creating superpositions of basis states with specific probability amplitudes on a quantum database such as represented by Eq. 1. The information can also be read and updated through repeated iterations of the Flip-Flop scheme. It has the advantage of not depending on proper routing algorithms, as it happens with the conventional and BB qRAM architectures [36], and is based on the quantum circuit computation model, what makes possible the application of quantum error-correction routines [37, 39–41]. The major disadvantage of the FF-qRAM architecture is the requirement of multi-controlled qubit rotations, whose cost can surpass the entire complexity of implementation for the whole FF-qRAM circuit, as the decomposition of such an operation can increase considerably the depth of the corresponding quantum circuit (see Section 3), depending on the architecture of the hardware in which it must be implemented.
In Table 1, the space and time costs for the preparation schemes are summarized. The BB based architecture for qRAM presents polylogarithmic time costs, as well as the Divide-and-Conquer algorithm, but needs O(N) qutrits (represented in brackets), although only O(log 2(N)) of these qutrits are activated during the process, and a proper routing algorithm, together with the O(log 2(N)) address qubits for routing the bus signals to the corresponding the memory cells.
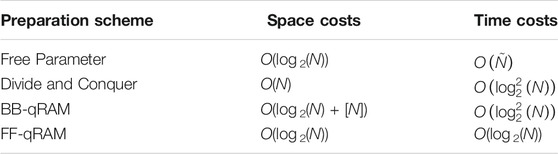
TABLE 1. Resource Analysis of space and time for schemes of preparation (Free Parameters, BB—Bucket Brigade, Divide and Conquer, FF—Flip-Flop). The quantities in brackets represent the quantity of qutrits needed for the considered architecture.
3 Gate Decomposition Complexity Bounds
Gate decomposition consists in the task of writing general operators that act upon a n-qubit system in the form of simpler gates that can be implemented in a quantum computer. For this purpose, different approaches and techniques have been developed, such as cosine-sine decomposition (CSD) [42], QR decomposition [43],2 the Khaneja-Glaser decomposition (KGD) [44] among other methods with no less relevance.
In general, an arbitrary n-qubit gate U is represented by a N × N matrix, with N2 degrees of freedom, that can be written as a product of O(N2) two-level unitary operations. To achieve such a decomposition, one can make use of a set of universal gates for computation, i.e., a set of one- and two-qubit operations from which any arbitrary operator U can be decomposed. For instance, it is known that the set of single-qubit and CNOT gates is universal [1]. With respect to the complexity regarding the implementation of U in terms of this universal set, the theoretical lower bound amounts to
Different approaches of circuit designing for gate decomposition are available in the literature. In particular, using the QR approach, the decomposition of U results in a quantum circuit with gate cost that amounts to
Although the lower bound of CNOT gates for implementing an arbitrary U has an exponential cost in terms of the number of qubits n, it is possible to reduce the depth of a CNOT based circuit by the realization of a space-depth trade-off. This technique consists in the use of additional ancilla qubits, thus increasing the width of the quantum circuit, to parallelize the CNOT operations that must be realized throughout the circuit to implement the generic n-qubit gate U. The ideia was first demonstrated in [48], where it is proved that making use of O(n2) ancilla qubits, a n-qubit CNOT circuit can be parallelized to O(log 2(n)) depth. It has been also already proved that each n-qubit CNOT circuit can be synthesized with
Thus, besides the exponential complexity of decomposing arbitrary n-qubit unitary operators, the space-depth trade-off presents an alternative in optimizing the circuit synthesis. Nevertheless, it is worth to consider that this parallel approach requires additional qubits to make the trade-off, having the immediate effect of increasing the circuit width of a quantum algorithm. It is also worth noting that different architectures for quantum computing may present different sets of basic gates in which the quantum operations must be decomposed, and also other different important aspects, such as connectivity, making the costs of decomposition and implementation of gates also dependent on the architecture of the quantum computer.
4 Complexity of Quantum State Tomography
Quantum state tomography (QST) is a procedure that aims for the complete reconstruction of an unknown density matrix ρ [1]. Often, for information encoded in amplitudes or phases of a quantum state, after executing a quantum algorithm, one is presented with a density matrix whose elements (ρij) codify the algorithm’s output [51]. Information encoded in the complex amplitudes of a quantum state is not directly accessible through trivial means [1]. Thus, QST could represent a fundamental step in the knowledge of obtaining the full solution of a given problem. This consideration is important for a proper comparison between quantum and classical algorithms in which the quantum solution is a superposition state while the classical solution is a vector where all coefficients are known [52]. At the same time quantum information can be stored in a Hilbert space whose dimension increases exponentially according to the number of qubits. To retrieve such information it is necessary to pay the price for that, which also requires exponential steps. Alternatively, some global properties of the solution could be obtained by means of the expectation values of some observables, i.e.,
There are many quantum algorithms whose output state has coherence in the computational basis. There are algorithms to solve partial differential equations [53–59], linear differential equations [12–14], nonlinear differential equations [60], linear system of equations (also named quantum linear problem) [61, 62]. In these examples, QST may be required depending on the level of detail expected to be known.
There is a variety of QST processes and schemes available to accomplish the characterization task, such as Simple Quantum State Tomography (SQST) [1], Ancilla Assisted Process Tomography3 (AAPT) [63], QST via Linear Regression Estimation [64], Compressed-Sensing QST [65], Principal Component Analysis [66], efficient process tomography [67] and permutationally invariant tomography schemes [68, 69], each of these with particular complexity aspects, being suitable for specific problems. Their different computational costs arise from taking advantage of particular characteristics of ρ.
In general, QST is based on the decomposition of the density matrix in a linear combination of basis operators. For a system of n qubits, the reconstruction of a density matrix ρ in such space requires 4n − 1 = N2 − 1 basis operators [1], which scales polynomially in the dimension O(N2). These exponential aspects of complexity are well known [70]. Besides the number of basis operators needed for characterization, it is important to remind that the reconstruction of ρ is based on expectation values of those basis operators. For instance, in the case of a single qubit, the set of 41 − 1 = 3 basis operators needed for the proper quantum statistics could be based on the Pauli matrices X, Y, and Z, such that
where
The overall costs of implementation 4 yielded from SQST is O(N4 log 2(N)), and the same relation holds for AAPT using Joint Separable Measurement (JSM) scheme. Both SQST and AAPT-JSM require only single body interactions [51], while the Mutually Unbiased Bases (MUB) and the generalized POVM AAPT-schemes require many-body interactions. The costs for MUB scale as
In practice, all of the costs rising from measurement schemes used for obtaining prior information about the systems under consideration will increase the overall cost of its implementation in quantum computing devices, which will be brought together in section 5. The cost of tomography schemes are brought together in Table 2.

TABLE 2. Resource Analysis for schemes of tomography of quantum states. The schemes presented consists of Standard Quantum State Tomography (SQST), Joint Separable Measurements (JSM), Mutual Unbiased Measurements (MUB), Positive Operator Valued Measurements (POVM), Quantum Principal Component Analysis (QPCA), Compressed-Sensing (CS) and the Permutationally Invariant Quantum Tomography (PI) scheme. Note that QPCA process can be used to reconstruct large eigenvalues of the Hilbert space, as well as the full density matrix (QPCA Full).
4.1 Pure State Tomography
There exist certain procedures where one is not interested in the full description of the resulting state ρ (e.g., some special cases of the algorithm in [14]). Instead, let us assume that the output of the algorithm is fully codified in the squares of the state’s amplitudes, i.e., if
where the first qubit is an auxiliary one,
Moreover, the probability of the system to be found in the state
where
We conclude that if p has a non-null minimum as a function of N, then the computational complexity of the tomography of all the pi is of order N. Otherwise, one needs to determine the asymptotic behavior of the success probability p as N grows (e.g. Ref. [14]).
5 Overall Complexity of Implementation
The overall complexity for implementation of a quantum algorithm accounts for all tasks that must be executed. It must take into account the total resource aspect, such as the number of work and ancilla qubits, represented by the width of the circuit, that could eventually include qRAM systems, as well as the usual gate cost aspect, brought together with the number of measurements. The last accounts for the number of copies times the number of measurements per copy done upon the final state in order to reconstruct its proper statistical averages and features.
Space costs: As discussed in section 2, the preparation of a generic superposition can be done by manipulating the work system, by the application of quantum gates that correspond to the transformations defined by the free parameters of the state. This results in a space cost which corresponds to the dimension of the work system alone. Assuming that such system has a Hilbert space dimension corresponding to a n-qubit space, it results in O(log 2(N)) qubits needed for its implementation. The Divide-and-Conquer scheme requires a circuit width which have a space cost of O(N) for implementation, but it is worth noting that it makes use of ancilla qubits that are left entangled with the work system. The discussed schemes for qRAM have similar aspects of qubit resources, but the presence of routing and O(N) qutrits (although this is not the number of activated qutrits during a memory call) in the BB architecture makes it less favorable for the implementation of gate-based algorithms for computation.
Gate or time costs: For the analysis of the corresponding overall gate complexity of an implementation, we need to consider also the amount of identical copies of ρ needed for its proper reconstruction, given a determined scheme for the task [51]. The overall cost of these schemes will appear as a multiplying factor in the full time cost analysis, since all the operations in the implementation of the quantum algorithm, from preparation to readout, should be done this corresponding number of times.
Preparation: The overall time cost of the preparation step depends on whether it is implemented by operating directly on the work system based on the free parameters of the state, or by queries made upon a previously prepared quantum RAM device 6. With preparation based on the free parameters, the amount of quantum operations has the upper bound of O(N) for preparing a N-dimensional quantum superposition. The Divide-and-Conquer quantum algorithm can create an entangled superposition between ancilla and work systems, with a
Evolution: We define the expression evolution to denote the process in which the previously prepared work system is evolved to its last configuration, which could represent, for instance, the solution of a system of linear equations [11], a system of coupled differential equations [14], among other examples of possible applications for quantum computation. The quantum algorithm is composed by a sequence of defined steps and operations, which transforms the initial state under linear operations, that can be controlled by ancilla qubits that compose the full system under consideration. The evolution process will be denoted here as a linear map, represented by ɛ, as in Ref. [49]. The gate and resource costs of a given algorithm depend on the tasks that may be executed through its implementation, so different quantum algorithms have distinct space and time costs. To represent generically the time cost of the processing step of the algorithm, we will define a function C(ɛ), of which one excludes the steps of preparation and measurement of the quantum states.
Readout: The readout aspect must bring the analysis of the number of gates per measurement necessary to characterize a N-dimensional quantum system. For both SQTP and AAPT-JSM, O(log 2(N)) single qubit operations must be implemented in order to reconstruct the density matrix. For AAPT-MUB based schemes, one needs
Overall Complexity: The overall gate cost for implementation of a quantum algorithm will now be classified according to each of the techniques discussed in the previous sections, including preparation and measurement schemes. The first multiplicative factors in each of the bounds presented stands for the number of experimental samples needed for each measurement scheme, which will be O(N4 log 2(N)) for both SQTP and JSM,

TABLE 3. Gate Complexity Analysis for various schemes of preparation (FP - Free Parameters, DC—Divide-and-Conquer, BB—Bucket Brigade, FF—Flip-Flop) and readout—Measurement procedures. The quantities in brackets are only taken into account if the system shows local interaction between qubits, in the case of the MUB sheme only. C(ɛ) stands only for the time cost of the evolution stage of the quantum algorithm, represented via the linear map ɛ.
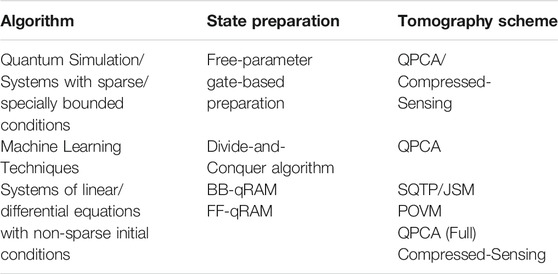
TABLE 4. Quantum algorithms and possible choices for input state preparation and tomography schemes.
6 Conclusion
We have presented a theoretic overview of the total complexity for the implementation of circuit-based quantum algorithms, involving the codification of the system parameters in the initial state of the work/register qubits, the evolution step towards the final state encoding the solution of the problem and the readout of this solution. A comparison between several schemes of preparation of input states as well as of tomography of final states was provided.
It is important to notice that algorithms that depend on the preparation of input states as superpositions of the basis states have at least
The evolution step can be represented by a linear map ε of the initial state to the final state. Its time cost, C(ε), is strongly dependent on the quantum algorithm, and usually shows an exponential speedup compared to the classical algorithm solving the same problem. The origin of such speedup comes from the nature of the Hilbert space, i.e., the ability of a given number of qubits to encode an exponential number of states. Concerning the readout of the solution encoded in the final state, we have done a generic analysis assuming a fairly uniform probability distribution over the basis states of the Hilbert space. In this case, if the desired result is encoded in a single amplitude of a given basis state, the number of required ensemble copies will scale as O(N) in the best scenario. This means a cost that is at least exponential in number of qubits. It is also important to mention that expectation values of observables which represent global features of the solution can be realized as a method to avoid the full tomography of the system [11]. Combining this fact with the classical shadows technique [75] for measurements, it is possible to diminish even more the overall quantum algorithmic complexity.
Therefore, for algorithms depending upon the preparation of a superposition state, for which the solution is encoded in the final superposition state of the work qubits, the overall complexity to obtain the solution will be at least O(N log 2(N)C(ε)), which can be significantly higher than C(ε). We point out that this complexity overview also depends on the architecture of the quantum hardware in which the algorithm should be implemented, and the availability of basic quantum gates for proper decomposition of all operations needed in the process of implementation.
Author Contributions
FC contributed mainly in the manuscritpt production. DA contributed in reviewing tomography schemes. VC reviewed and corrected the main text. ED reviewed and corrected the main text. AJ contributed with discussions and writing in probability of success of the algorithms and tomography. CV supervised the work, contributed to the manuscript and discussions.
Funding
São Paulo Research Foundation (FAPESP), Grant No. 2019/11999-5 Brazilian National Institute of Science and Technology for Quantum Information (INCT-IQ/CNPq) Grant No. 465469/2014-0. This work was supported by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES)—Finance Code 001, and through the CAPES/STINT project, grant No. 88881.304807/2018-01. CV is also grateful for the support by the São Paulo Research Foundation (FAPESP) Grant No. 2019/11999-5, and the National Council for Scientific and Technological Development (CNPq) Grant No. 307077/2018-7. This work is also part of the Brazilian National Institute of Science and Technology for Quantum Information (INCT-IQ/CNPq) Grant No. 465469/2014-0.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1A real number x ∈ [0, 2) can be represented in binary basis as
2QR decomposition consists in decomposing an operator in a product of matrices, Q and R, each of which have particular properties.
3Although Ref. [63] discusses quantum process tomography, a QST procedure is needed in order to complete the protocol in SQPT and AAPT schemes, and an insight about the complexity of quantum state tomography can be obtained.
4The overall complexity is defined as in [51], given by the number of copies of ρ times the number of gates per measurement.
5This exactly means that
6The complexity of preparing a quantum RAM device is beyond the scope of the present work.
References
1. Nielsen MA, Chuang I. Quantum computation and quantum information. Cambridge: Cambridge University Press (2002).
2. Feynman RP. Simulating physics with computers. Int J Theor Phys (1982) 21. doi:10.1007/bf02650179
3. Bennett CH, Wiesner SJ. Communication via one- and two-particle operators on einstein-podolsky-rosen states. Phys Rev Lett (1992) 69:2881–4. doi:10.1103/physrevlett.69.2881
4. Bennett CH, Brassard G. Quantum cryptography: Public key distribution and coin tossing (1984). arXiv preprint arXiv:2003.06557.
5. Shor PW. Algorithms for quantum computation: discrete logarithms and factoring. Ieee (1994). p. 124–34.
6. Grover LK. Quantum computers can search arbitrarily large databases by a single query. Phys Rev Lett (1997) 79:4709–12. doi:10.1103/physrevlett.79.4709
7. Abrams DS, Lloyd S. Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors. Phys Rev Lett (1999) 83:5162–5. doi:10.1103/physrevlett.83.5162
8. Zhou X-Q, Kalasuwan P, Ralph TC, O'Brien JL. Calculating unknown eigenvalues with a quantum algorithm. Nat Photon (2013) 7:223–8. doi:10.1038/nphoton.2012.360
9. Rebentrost P, Steffens A, Marvian I, Lloyd S. Quantum singular-value decomposition of nonsparse low-rank matrices. Phys Rev A (2018) 97:012327. doi:10.1103/physreva.97.012327
10. Gilyén A, Su Y, Low GH, Wiebe N. Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics. InProceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, 2019 Jun (2019). p. 193–204. doi:10.1145/3313276.3316366
11. Harrow AW, Hassidim A, Lloyd S. Quantum algorithm for linear systems of equations. Phys Rev Lett (2009) 103:150502. doi:10.1103/physrevlett.103.150502
12. Berry DW. High-order quantum algorithm for solving linear differential equations. J Phys A: Math Theor (2014) 47:105301. doi:10.1088/1751-8113/47/10/105301
13. Berry DW, Childs AM, Ostrander A, Wang G. Quantum algorithm for linear differential equations with exponentially improved dependence on precision. Commun Math Phys (2017) 356:1057–81. doi:10.1007/s00220-017-3002-y
14. Xin T, Wei S, Cui J, Xiao J, Arrazola In., Lamata L, et al. Quantum algorithm for solving linear differential equations: Theory and experiment. Phys Rev A (2020) 101:032307. doi:10.1103/physreva.101.032307
15. Leyton SK, Osborne TJ. A quantum algorithm to solve nonlinear differential equations (2008). arXiv:0812.4423 [quant-ph].
16. Arrazola JM, Kalajdzievski T, Weedbrook C, Lloyd S. Quantum algorithm for nonhomogeneous linear partial differential equations. Phys Rev A (2019) 100:032306. doi:10.1103/physreva.100.032306
17. Bravyi S, Gosset D, König R, Tomamichel M. Quantum advantage with noisy shallow circuits. Nat Phys (2020) 16:1040–5. doi:10.1038/s41567-020-0948-z
18. Arute F, Arya K, Babbush R, Bacon D, Bardin JC, Barends R, et al. supremacy using a programmable superconducting processor. Nature (2019) 574:505. doi:10.1038/s41586-019-1666-5
19. Zhong H-S, Wang H, Deng Y-H, Chen M-C, Peng L-C, Luo Y-H, et al. Quantum computational advantage using photons. Science (2020) 370:1460. doi:10.1126/science.abe8770
20. King AD, Raymond J, Lanting T, Isakov SV, Mohseni M, Poulin-Lamarre G, et al. Scaling advantage over path-integral monte carlo in quantum simulation of geometrically frustrated magnets. Nat Commun (2021) 12:1. doi:10.1038/s41467-021-20901-5
21. Leymann F, Barzen J. The bitter truth about gate-based quantum algorithms in the NISQ era. Quan Sci Tech (2020) 5:044007. doi:10.1088/2058-9565/abae7d
22. Cortese JA, Braje TM. Loading classical data into a quantum computer (2018). arXiv preprint arXiv:1803.01958.
23. Jiang S, Britt KA, McCaskey AJ, Humble TS, Kais S. Quantum annealing for prime factorization. Scientific Rep (2018) 8(17667):1. doi:10.1038/s41598-018-36058-z
24. Neven H, Denchev VS, Rose G, Macready WG. Training a binary classifier with the quantum adiabatic algorithm (2008). arXiv preprint arXiv:0811.0416.
25. Das A, Chakrabarti BK. Colloquium: Quantum annealing and analog quantum computation. Rev Mod Phys (2008) 80:1061. doi:10.1103/revmodphys.80.1061
26. Long G-L, Sun Y. Efficient scheme for initializing a quantum register with an arbitrary superposed state. Phys Rev A (2001) 64:014303. doi:10.1103/physreva.64.014303
27. Andrecut M, Ali M. Efficient algorithm for initializing amplitude distribution of a quantum register. Mod Phys Lett B (2001) 15:1259. doi:10.1142/s0217984901003093
28. Ward NJ, Kassal I, Aspuru-Guzik A. Preparation of many-body states for quantum simulation. J Chem Phys (2009) 130:194105. doi:10.1063/1.3115177
29. Girolami D. How difficult is it to prepare a quantum state?. Phys Rev Lett (2019) 122:010505. doi:10.1103/PhysRevLett.122.010505
30. Shende VV, Markov IL. Quantum circuits for incompletely specified two-qubit operators (2004). arXiv preprint quant-ph/0401162.
31. Halimeh JC, Zauner-Stauber V. Dynamical phase diagram of quantum spin chains with long-range interactions. Phys Rev B (2017) 96:134427. doi:10.1103/physrevb.96.134427
32. Barenco A, Bennett CH, Cleve R, DiVincenzo DP, Margolus N, Shor P, et al. Elementary gates for quantum computation. Phys Rev A (1995) 52:3457. doi:10.1103/physreva.52.3457
33. Soklakov AN, Schack R. Efficient state preparation for a register of quantum bits. Phys Rev A (2006) 73:012307. doi:10.1103/physreva.73.012307
34. Araujo IF, Park DK, Petruccione F, da Silva AJ. A divide-and-conquer algorithm for quantum state preparation. Scientific Rep (2021) 11:1. doi:10.1038/s41598-021-85474-1
35. Ventura D, Martinez T. Quantum associative memory. Inf Sci (2000) 124:273. doi:10.1016/s0020-0255(99)00101-2
36. Giovannetti V, Lloyd S, Maccone L. Architectures for a quantum random access memory. Phys Rev A (2008) 78:052310. doi:10.1103/PhysRevLett.100.160501
37. Park D, Petruccione F, Rhee J. Circuit-based quantum random access memory for classical data. Sci Rep (2019) 3949. doi:10.1038/s41598-019-40439-3
38. Giovannetti V, Lloyd S, Maccone L. Quantum random access memory. Phys Rev Lett (2008) 100:160501. doi:10.1103/physrevlett.100.160501
39. Paetznick A, Reichardt BW. Universal fault-tolerant quantum computation with only transversal gates and error correction. Phys Rev Lett (2013) 111:090505. doi:10.1103/PhysRevLett.111.090505
40. Anderson JT, Duclos-Cianci G, Poulin D. Fault-tolerant conversion between the steane and reed-muller quantum codes. Phys Rev Lett (2014) 113:080501. doi:10.1103/PhysRevLett.113.080501
41. Jochym-O’Connor T, Laflamme R. Using concatenated quantum codes for universal fault-tolerant quantum gates. Phys Rev Lett (2014) 112:010505.
42. Paige C, Wei M. History and generality of the CS decomposition. Linear Algebra its Appl (1994) 208-209:303–26. doi:10.1016/0024-3795(94)90446-4
44. Khaneja N, Glaser SJ. Cartan decomposition of su(2n) and control of spin systems. Chem Phys (2001) 267:11. doi:10.1016/s0301-0104(01)00318-4
45. Möttönen M, Vartiainen JJ, Bergholm V, Salomaa MM. Quantum circuits for general multiqubit gates. Phys Rev Lett (2004) 93:130502. doi:10.1103/physrevlett.93.130502
46. Vartiainen JJ, Möttönen M, Salomaa MM. Efficient decomposition of quantum gates. Phys Rev Lett (2004) 92:177902. doi:10.1103/physrevlett.92.177902
47. Press WH, Teukolsky SA, Flannery BP, Vetterling WT. Numerical recipes in fortran 77: volume 1, volume 1 of fortran numerical recipes: the art of scientific computing (1992).
48. Moore C, Nilsson M. Parallel quantum computation and quantum codes. SIAM J Comput (2001) 31:799. doi:10.1137/S0097539799355053
49. Patel KN, Markov IL, Hayes JP. Optimal synthesis of linear reversible circuits. Quan Inf. Comput. (2008) 8:282. doi:10.26421/qic8.3-4-4
50. Jiang J, Sun X, Teng S-H, Wu B, Wu K, Zhang J. Optimal space-depth trade-off of cnot circuits in quantum logic synthesis (2020). https://epubs.siam.org/doi/pdf/10.1137/1.9781611975994.13 (Accessed August 17, 2021).
51. Mohseni M, Rezakhani AT, Lidar DA. Quantum-process tomography: Resource analysis of different strategies. Phys Rev A (2008) 77:032322. doi:10.1103/physreva.77.032322
53. Ekert AK, Alves CM, Oi DKL, Horodecki M, Horodecki P, Kwek LC. Direct estimations of linear and nonlinear functionals of a quantum state. Phys Rev Lett (2002) 88:217901. doi:10.1103/physrevlett.88.217901
54. Clader BD, Jacobs BC, Sprouse CR. Preconditioned quantum linear system algorithm. Phys Rev Lett (2013) 110:250504. doi:10.1103/physrevlett.110.250504
55. Cao Y, Papageorgiou A, Petras I, Traub J, Kais S. Quantum algorithm and circuit design solving the poisson equation. New J Phys (2013) 15:013021. doi:10.1088/1367-2630/15/1/013021
56. Montanaro A, Pallister S Quantum algorithms and the finite element, method Phys Rev A. 93 (2016). p. 032324. doi:10.1103/physreva.93.032324
57. Costa PC, Jordan S, Ostrander A. Quantum algorithm for simulating the wave equation. Phys Rev A (2019) 99:012323. doi:10.1103/physreva.99.012323
58. Fillion-Gourdeau LEF. Simple digital quantum algorithm for symmetric first-order linear hyperbolic systems. Numer Algor (2019) 82. doi:10.1007/s11075-018-0639-3
59. Wang S, Wang Z, Li W, Fan L, Wei Z, Gu Y. Quantum fast poisson solver: the algorithm and complete and modular circuit design. Quan Inf Process (2020) 19:1. doi:10.1007/s11128-020-02669-7
60. Leyton SK, Osborne TJ. A quantum algorithm to solve nonlinear differential equations (2008). p. 4423. arXiv preprint arXiv:0812.
61. Childs AM, Kothari R, Somma RD. Quantum algorithm for systems of linear equations with exponentially improved dependence on precision. SIAM J Comput (2017) 46:1920. doi:10.1137/16m1087072
62. Subaşı Y, Somma RD, Orsucci D. Quantum algorithms for systems of linear equations inspired by adiabatic quantum computing. Phys Rev Lett (2019) 122:060504. doi:10.1103/PhysRevLett.122.060504
63. Altepeter JB, Branning D, Jeffrey E, Wei TC, Kwiat PG, Thew RT, et al. Ancilla-assisted quantum process tomography. Phys Rev Lett (2003) 90:193601. doi:10.1103/physrevlett.90.193601
64. Qi B, Hou Z, Li L, Dong D, Xiang G, Guo G. Quantum state tomography via linear regression estimation. Scientific Rep (2013) 3:1. doi:10.1038/srep03496
65. Gross D, Liu Y-K, Flammia ST, Becker S, Eisert J. Quantum state tomography via compressed sensing. Phys Rev Lett (2010) 105:150401. doi:10.1103/physrevlett.105.150401
66. Lloyd S, Mohseni M, Rebentrost P. Quantum principal component analysis. Nat Phys (2014) 10:631. doi:10.1038/nphys3029
67. Cramer M, Plenio MB, Flammia ST, Somma R, Gross D, Bartlett SD, et al. Efficient quantum state tomography. Nat Commun (2010) 1:1. doi:10.1038/ncomms1147
68. Tóth G, Wieczorek W, Gross D, Krischek R, Schwemmer C, Weinfurter H. Permutationally invariant quantum tomography. Phys Rev Lett (2010) 105:250403. doi:10.1103/physrevlett.105.250403
69. Schwemmer C, Tóth G, Niggebaum A, Moroder T, Gross D, Gühne O, et al. Experimental comparison of efficient tomography schemes for a six-qubit state. Phys Rev Lett (2014) 113:040503. doi:10.1103/PhysRevLett.113.040503
70. Aaronson S. The learnability of quantum states. Proc R Soc A: Math Phys Eng Sci (2007) 463:3089. doi:10.1098/rspa.2007.0113
71. Flammia ST, Gross D, Liu Y-K, Eisert J. Quantum tomography via compressed sensing: error bounds, sample complexity and efficient estimators. New J Phys (2012) 14:095022. doi:10.1088/1367-2630/14/9/095022
72. Hartmann S. Generalized dicke states. Quan Inf Comput (2016) 16:1333. doi:10.26421/qic16.15-16-5
73. Kitagawa M, Ueda M. Squeezed spin states. Phys Rev A (1993) 47:5138. doi:10.1103/physreva.47.5138
74. Suzuki Y, Uno S, Raymond R, Tanaka T, Onodera T, Yamamoto N. Amplitude estimation without phase estimation. Quan Inf Process (2020) 19. doi:10.1007/s11128-019-2565-2
Keywords: quantum algorithms, quantum computation, quantum computational complexity, quantum tomography, quantum state preparation, quantum circuit model
Citation: Cardoso FR, Akamatsu DY, Campo Junior VL, Duzzioni EI, Jaramillo A and Villas-Boas CJ (2021) Detailed Account of Complexity for Implementation of Circuit-Based Quantum Algorithms. Front. Phys. 9:731007. doi: 10.3389/fphy.2021.731007
Received: 25 June 2021; Accepted: 20 September 2021;
Published: 01 November 2021.
Edited by:
Deniz Türkpençe, Istanbul Technical University, TurkeyReviewed by:
Jie-Hong Jiang, National Taiwan University, TaiwanDongsheng Wang, Institute of Theoretical Physics (CAS), China
Copyright © 2021 Cardoso, Akamatsu, Campo Junior, Duzzioni, Jaramillo and Villas-Boas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fernando R. Cardoso, ZnJjQGRmLnVmc2Nhci5icg==
 Fernando R. Cardoso
Fernando R. Cardoso Daniel Yoshio Akamatsu1
Daniel Yoshio Akamatsu1 Eduardo I. Duzzioni
Eduardo I. Duzzioni Alfredo Jaramillo
Alfredo Jaramillo Celso J. Villas-Boas
Celso J. Villas-Boas