Magnetic Skyrmion Generation by Reflective Spin Wave Focusing

We propose a method to generate magnetic skyrmions by focusing spin waves totally reflected by a curved film edge. The edge contour is derived to be parabolic and frequency-independent based on the identical magnonic path length principle. We performed micromagnetic simulations to verify our theoretical design. Under proper conditions, the reflected spin waves first converge at the focal point with the enhanced intensity leading to the emergence of magnetic droplets, which are then converted to magnetic skyrmion accompanied by a change in the topological charge. We numerically obtain the phase diagram of skyrmion generation with respect to the amplitude and frequency of the driving field. Our finding would be helpful for the design of spintronic devices combining the advantage of skyrmionics and magnonics.

1 Introduction

Magnetic skyrmions are topologically protected spin textures with a high thermal stability [1, 2]. They normally emerge in chiral bulk magnets or magnetic thin films with broken inversion symmetry, which gives rise to the Dzyaloshinskii–Moriya interaction (DMI) [3, 4]. In contrast to skyrmions, magnons are low-energy excitations in magnetic systems and can be easily generated and destroyed because of their bosonic nature. Both skyrmions and magnons have been extensively investigated and applied in information transmission and procession, which gives birth to two emerging subfields of magnetism: skyrmionics [5–8] and magnonics [9–11].

The interaction between skyrmions and magnons has been widely studied in magnon–skyrmion scattering [12, 13], magnon-driven skyrmion motion [14, 15], skyrmion-based magnonic crystal [16, 17], and skyrmion-induced magnon frequency comb [18]. Recently, the conversion between skyrmions and magnons has been attracting much attention. For example, the spin wave emission is often observed during the annihilation and core switching of magnetic skyrmions [19, 20]. However, it is quite hard to convert magnons to skyrmions because the energy carried by spin waves is much lower than the barrier between the skyrmion and the uniform ferromagnetic state. To create skyrmions by spin waves, the spin wave energy should be accumulated to overcome the energy barrier, which has been realized by the combination of the geometry change and the DMI-induced effective magnetic field [21] and by spin wave focusing [22]. In previous studies, the spin wave focusing is achieved by constructing a spin wave lens, which can be designed by a curved interface [22–24], a local graded-index region [25, 26], and a metasurface [27, 28]. In these methods, the spin wave reflection at the interface would decrease the efficiency of spin wave focusing. In this regard, one should avoid the spin wave reflection as much as possible, intuitively.

However, it is known that the spin wave can transmit through an interface without reflection only in rare cases [29]. On the contrary, spin wave can be completely reflected under more loose conditions, such as at the magnetic–non-magnetic interface. One natural issue is how to accumulate all reflected spin waves. In this study, we design a curved film edge based on the principle of identical magnonic path length, which suggests that the parabolic film edge can focus all reflected spin waves independent of their frequencies. At the focal point, the spin wave intensity can be significantly enhanced and the focal point magnetization oscillates strongly and might even be locally reversed, which is considered as the precursor for the skyrmion formation.

2 Analytical Model

We consider a chiral ferromagnetic film with a curved boundary, which is magnetized along the $+\widehat{z}$ direction. The spin wave dynamics are governed by the Landau–Lifshitz–Gilbert (LLG) equation,

$\frac{\partial \mathbf{m}}{\partial t}=-\gamma {\mu }_0\mathbf{m}\times {\mathbf{H}}_{\text{eff}}+\alpha \mathbf{m}\times \frac{\partial \mathbf{m}}{\partial t},(1)$

where m = M/M_s is the unit magnetization vector with the saturated magnetization M_s, γ is the gyromagnetic ratio, μ₀ is the vacuum permeability, and α is the Gilbert damping constant. The effective field H_eff comprises the exchange field, the DM field, the anisotropy field, and the dipolar field. In the following discussion, the interfacial DMI is considered.

The film edge for total-reflection focusing can be designed based on the identical magnonic path length (MPL) principle [22]. We first consider a plane spin wave incident from the left source (x = −x_s), which is reflected by the film edge and converges into a focal point (−x_f, 0), as shown in Figure 1. The identical MPL principle yields the following:

$x+x_s+\sqrt{{(x+x_f)}^2+y^2}=x_s+x_f,(2)$

and the edge contour is described as

$y^2=-2px,(3)$

where p = 2x_f . One can see that the shape of the film edge is parabolic for the total-reflection focusing of the plane spin waves.

FIGURE 1

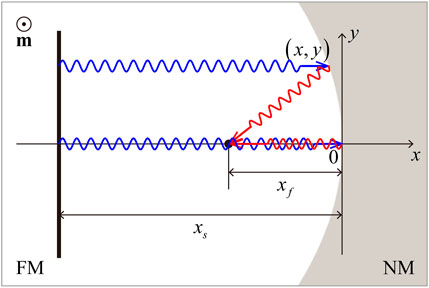
FIGURE 1. Schematic of the film edge for total-reflection focusing of spin waves. The static magnetization m is oriented along the + z direction. FM and NM denote the ferromagnetic and non-magnetic regions, respectively. The black bar located at x = −x_s is the spin wave source. A parallel incident spin wave (blue wavy lines with arrow) propagates towards the curved edge, and the reflected spin wave (red wavy lines with arrow) converges on the focal point at x = −x_f (black point).

3 Numerical Results and Discussions

To verify our theoretical design, we numerically solve the full LLG equation (Equation 1) using the micromagnetic simulation code MuMax3 [30]. Magnetic parameters of the adopted Co are as follows: M_s = 5.8 × 10⁵ A/m, A_ex = 15 pJ/m, D = 2.5 mJ/m², and K_u = 6 × 10⁵ J/m³. The cell size 2 × 2 × 1 nm³ is used to discretize the film in simulations. The Gilbert damping constant α = 10⁻³ is used to ensure a long-distance propagation of spin waves, and absorbing boundary conditions are adopted to avoid the spin wave reflection by the film edges except for the curved edge [31].

We first set the focal length as x_f = 400 nm in simulations and design a parabolic edge to focus the reflected spin waves. A sinusoidal monochromatic microwave field ${\mathbf{H}}_{\text{ext}}=h_0\sin (\omega t)\widehat{x}$ is applied in a narrow rectangular area (black bar in Figure 2A) to excite the incident plane spin waves. Numerical results for focusing spin waves with 60 GHz are shown in Figure 2A. Using the equation $I_{SW}=\frac{1}{T}{\int }_0^T(\delta m_x^2+\delta m_y^2)dt$, we calculate the spin wave intensity, as plotted in Figure 2B. The profiles of the spin wave intensity are also shown (black curve in Figure 2B). One can see that spin waves are reflected from the film edge and focused, leading to a significantly enhanced intensity around the focal point. However, it is found that the focal point obtained from the numerical simulation is shifted slightly along the +x direction from the theoretical position of the focal point (black point shown in Figure 2B). It may be attributed to two reasons: one is the ray optic approximation for analyzing the spin wave propagation, which requires the spin wave wavelength (about tens of nanometers) to be much smaller than the size of the film edge. The other is the spin canting at the curved edge (Figure 3D), which would influence the propagation of the reflected spin waves. Eq. 3 suggests that the shape of the parabolic edge for the total-reflection focusing is independent of the spin wave frequency. Figures 2C,D indeed confirm this result, which would promote the applications of the spin wave focusing in magnonic devices.

FIGURE 2

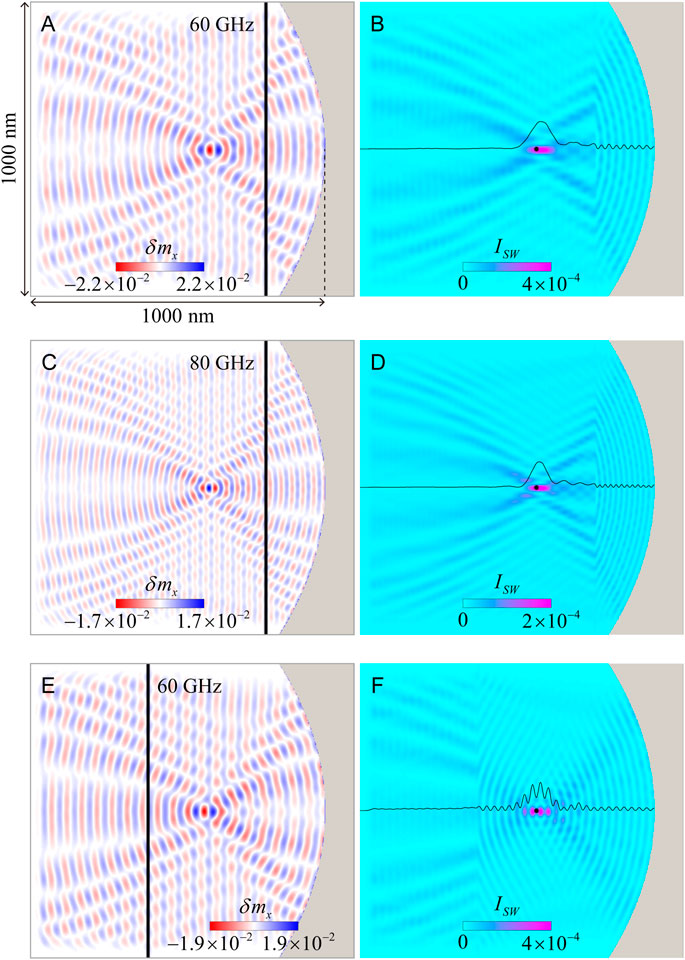
FIGURE 2. (A) Snapshot of the spin waves reflected from the parabolic edge. The spin wave frequency is ω/2π = 60 GHz. The black bar in (A) denotes the spin wave source located at x = −200 nm, which is excited by a microwave field with μ₀h₀ = 10 mT. (B) The spin wave intensity in (A). The black point represents the ideal position of the focal point. The black curve shows the profile of the spin wave intensity along the x axis at y = 0. (C) and (D) Snapshot of total-reflection focusing of spin waves and the corresponding intensity for ω/2π = 80 GHz. (E) and (F) Snapshot of spin waves and their intensity for the exciting source located at x = −600 nm.

FIGURE 3

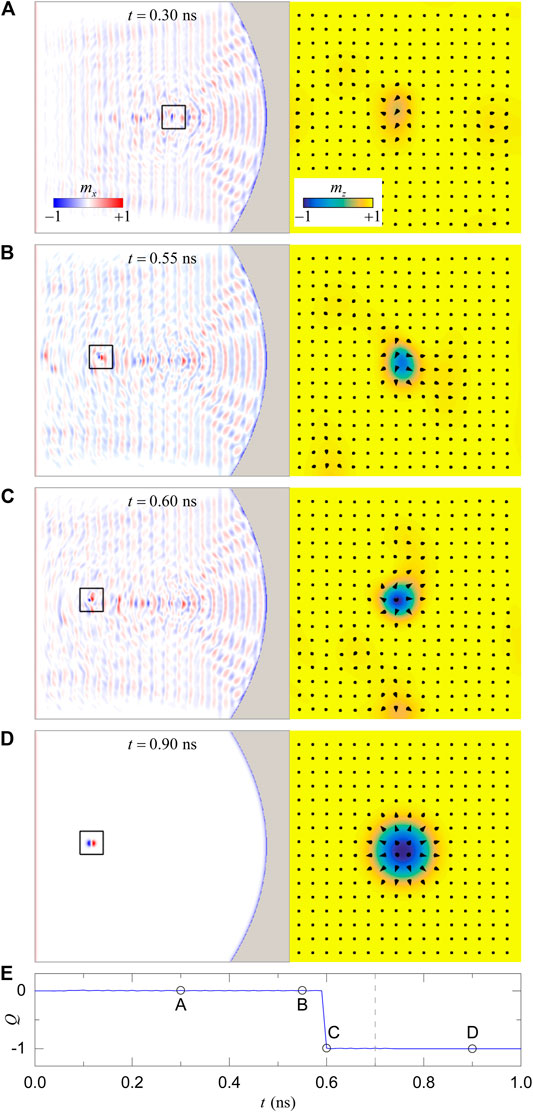
FIGURE 3. The creation process of the magnetic skyrmion induced by the total-reflection focusing. The exciting field with μ₀h₀ = 360 mT is applied in (A–C) and is turned off in (D). The z-component magnetization of the rectangular area in the left column is enlarged in the right column. (E) Temporal evolution of the topological number Q. The microwave field starts at t = 0 and ends at t = 0.7 ns, indicated by the gray dashed line.

A close inspection shows that there is a sharp kink of the spin wave intensity at the magnon source (Figures 2B,D,F). It results from the change in the coherence of spin waves through the magnon source. On the right side of the magnon source, the emitted spin waves and reflected spin waves are coherent, leading to a strong interference with a significant interference fringe. The phase of the reflected spin wave would change when it propagates through the magnon source. The coherence between the reflected and emitted spin waves on the left side is destroyed, which shows a slight fluctuation in the spin wave intensity. Different fluctuations in spin wave intensities on both sides of the magnon source induce a sharp kink. Therefore, the spin wave intensity at the focal point would fluctuate drastically when the magnon source is located at the left side of the focal point, as shown in Figures 2E,F. This severe fluctuation of the spin wave intensity would destroy the localized spin wave soliton (droplet) around the focal point, which hinders the generation of skyrmion. In what follows, we focus on the case of the magnon source locating at the right side of the focal point for generating skyrmion by spin wave focusing.

To generate magnetic skyrmions, we increase the amplitude of the microwave field to μ₀h₀ = 360 mT. The spin wave intensity around the focal point is enhanced significantly, which shows a strong magnetization oscillation, as plotted in Figure 3A. With the continuous excitation of spin waves, more energy is harvested, leading to the local switching of the magnetization and the formation of magnetic droplets, which can be easily driven by spin waves (Figure 3B). The magnetic droplet is a non-topological localized spin wave soliton [32, 33] and is unstable in a chiral ferromagnetic film because of high DMI energy. Under the disturbance of spin waves, the magnetic droplet is converted to a dynamical skyrmion at t = 0.6 ns, as shown in Figure 3C. Then, we turn off the microwave field at t = 0.7 ns and the system is relaxed toward an equilibrium state with a stable skyrmion state (Figure 3D). Moreover, it is noted that the skyrmion is not created exactly at the focal point. This is because the first nucleated droplet driven by spin waves moves faster than the skyrmion during which the transformation from the droplet to skyrmion happens. This would lead to the skyrmion nucleation site developing far away from the focal point.

The topological charge, which is given by

$Q=\frac{1}{4\pi }\iint \mathbf{m}\cdot \left(\frac{\partial \mathbf{m}}{\partial x}\times \frac{\partial \mathbf{m}}{\partial y}\right)dxdy,(4)$

can be used to characterize the topology of skyrmions in two-dimensional systems. However, the large spatial variations of m in the process of the skyrmion nucleation and annihilation reduce the accuracy of the finite difference approximation of Eq. 4 and result in non-integer values of Q [22]. To avoid this spurious deviation, we follow the definition of the topological charge given by Berg and Lüscher [34], which is expressed as

$Q=\frac{1}{4\pi }\sum _{⟨ijk⟩}{q}_{ijk},(5)$

with

$\tan \left(\frac{q_{ijk}}{2}\right)=\frac{{\mathbf{m}}_i\cdot ({\mathbf{m}}_j\times {\mathbf{m}}_k)}{1+{\mathbf{m}}_i\cdot {\mathbf{m}}_j+{\mathbf{m}}_i\cdot {\mathbf{m}}_k+{\mathbf{m}}_j\cdot {\mathbf{m}}_k},(6)$

where q_ijk is the local topological charge density of elementary-signed triangles, which is invariant under a cyclic permutation of the indices ijk. This lattice-based approach has been employed in quantifying the topological charge in micromagnetics recently [35–37]. Based on this scheme, we calculate the time evolution of the topological charge Q in the process of the skyrmion generation (Figure 3E), where nonphysical values of Q are excluded. An abrupt change in Q from 0 to −1 is observed at t = 0.6 ns, which confirms the skyrmion creation.

From the generation process of the skyrmion, one can see that the magnetic droplet is an indispensable intermediate between ferromagnetic and skyrmion states. Although the energy of the magnetic droplet is higher than the skyrmion, the skyrmion cannot be created directly from the ferromagnetic state. This is because the droplet is non-topological and can be transformed continuously from a ferromagnetic state. However, the continuous transformation from a ferromagnetic state to the skyrmion state is highly unlikely, which is due to the topological protection of the skyrmion. Compared to the droplet, a change in the topological charge is accompanied for the skyrmion creation, which requires more energy input from the external driving.

Figure 4A plots the nucleation time of the first skyrmion $t_{SW}^1$ induced by the total-reflection focusing of spin waves. It is found that the skyrmion creation at the field frequency with ω/2π = 70, 85, and 95 GHz needs a longer time and requires a higher amplitude of the exciting field. To find the reason for such a frequency dependence of the skyrmion generation, we plot the spin wave intensity at the focal point for different frequencies, as shown in Figure 4B. We find that these three frequencies correspond to the local minima of the spin wave intensity, which is due to the destructive interference between the reflected spin waves and emitted spin waves from the magnon source at the focal point. In addition, we also plot a phase diagram of skyrmion generation induced by the total-reflection focusing of spin waves within 10 ns (Figure 4C). As in the spin wave focusing for the transmitted waves [22], the generated skyrmion number N_Sk is not monotonically increased with the field amplitude h₀, owing to the skyrmion annihilation induced by the interaction between the magnetic droplet and skyrmion. It should be stressed that the generated skyrmion is not able to arrive at the magnon source and is destroyed at the duration time (10 ns) considered in our study, although it moves towards the magnon source driven by spin waves [12–14, 38]. This is because the velocity of the magnon-driven skyrmion motion is very slow (<10 m/s). It has been demonstrated that the number of the nucleated skyrmion depends on the duration time of the microwave field [22]. Thus, we can tune the duration time of the microwave field pulse to generate a single skyrmion (Figure 3).

FIGURE 4

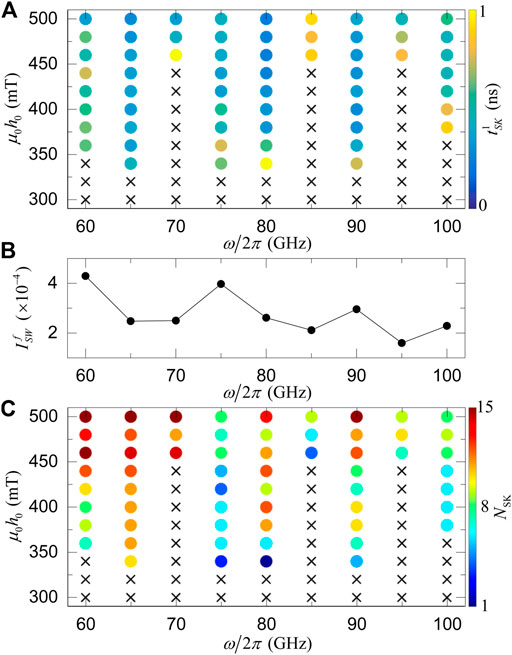
FIGURE 4. (A) The nucleation time of the first skyrmion $t_{\text{SK}}^1$ as a function of the field amplitude and frequency. The black crosses represent no skyrmion creation. (B) The frequency dependence of the spin wave intensity at the focal point under the microwave field with μ₀h₀ = 10 mT. (C) Phase diagram of skyrmion generation with respect to the amplitude and frequency of the exciting field with the duration time 10 ns.

The above micromagnetic simulations are all performed for the idealized edge, which is often not the case in practical applications, due to edge roughness. To make the roughness effect on the total-reflection focusing clear, we performed additional simulations with random roughness, which is close to the rough edge in real cases. For the roughness amplitude A_r = 6 nm, the reflected spin waves with 60 GHz can be well focused with a reduced intensity (≈81%), as shown in Figures 5A,B. With the increase in A_r, the focal point intensity of spin waves $I_{SW}^f$ decreases. For a large amplitude of roughness, the reflected spin waves are disordered and cannot be focused (black crosses in Figure 5C). We also investigate the frequency dependence of the roughness effect and find that the roughness influence becomes weak with the decrease in the spin wave frequency. This result suggests that our method is valid for spin waves with long wavelength (λ ≫ A_r), for which the roughness effect can be ignored.

FIGURE 5

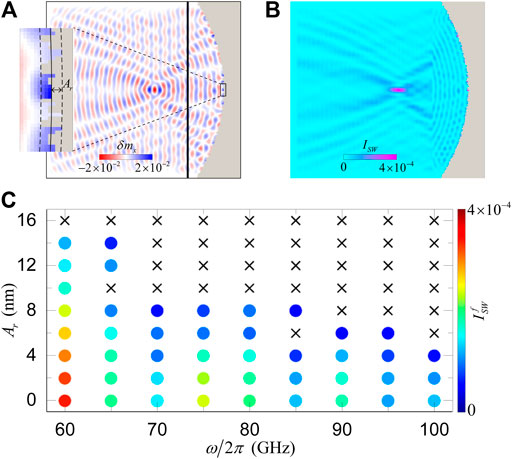
FIGURE 5. (A) Snapshot of spin waves reflected from the parabolic edge with a random roughness, which is depicted by the formula x = −y²/(4x_f) + A_rI_r, where A_r is the roughness amplitude and I_r is a random value in the interval (−1, 1). The black bar shows the exciting source of spin waves with μ₀h₀ = 10 mT and ω/2π = 60 GHz. The enlarged image of the rectangular area is shown on the left. The solid line in the inset denotes the ideal parabolic edge, and the dashed lines show the amplitude of the roughness (A_r = 6 nm). (B) The spin wave intensity in (A). (C) Phase diagram of the spin wave intensity at the focal point as a function of the roughness amplitude and the spin wave frequency. The black crosses represent no spin wave focusing, and the colored dots are the spin wave intensity.

The results in this study are obtained in magnetic metals, which usually have high perpendicular magnetic anisotropy and high damping. A large-amplitude microwave field is needed for the skyrmion creation, which is difficult to achieve in experiments. Fortunately, magnetic insulators with perpendicular anisotropy and ultra-low damping have been demonstrated to host skyrmions [39–41], which makes our method more applicable from the view of materials realizations. In a previous study, we proposed a method to generate skyrmion by focusing the transmitted spin waves, which is realized by constructing a spin wave lens with a curved interface [22]. The shape of the interface depends on the relative refraction index of spin waves, which is frequency-dependent. Thus, that method is only feasible for focusing spin waves with one certain frequency. For spin wave focusing with a different frequency, a new curved interface should be designed, which hinders the practical application of that method. We, therefore, believe that the total-reflection focusing in the present study provides a promising way to generate the skyrmion.

4 Conclusion

In summary, we theoretically investigated the skyrmion generation induced by the total-reflection focusing of spin waves. The shape of the film edge was derived based on the identical magnonic path length principle. Micromagnetic simulations were performed to confirm the focusing effect of spin waves reflected from the parabolic edge. By increasing the field amplitude, we observed the nucleation of magnetic droplet induced by the total-reflection focusing and the transformation to the skyrmion with a change in the topological charge. Our results provide a method to generate skyrmion by reflective focusing of spin waves, which is frequency-independent and would promote the development and application of spintronic devices combing magnons and skyrmions.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

ZW and PY conceived the idea and wrote the paper. ZW and XY finished the analytical deduction and performed all the simulations. MD, Z-XL, ZZ, and YC corrected the paper and discussed.

Funding

This work was supported by the National Natural Science Foundation of China (Grants No. 12074057 and No. 11704060). ZW acknowledges financial support from the China Postdoctoral Science Foundation (Grant No. 2019M653063). Z-XL acknowledges financial support from the China Postdoctoral Science Foundation (Grant No. 2019M663461) and the NSFC (Grant No. 11904048). ZZ acknowledges financial support from the China Postdoctoral Science Foundation (Grant No. 2020M673180).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank H. Yang and L. Song for helpful discussions.

References

1. Wild J, Meier TNG, Pöllath S, Kronseder M, Bauer A, Chacon A, et al. Entropy-limited Topological protection of Skyrmions. Sci Adv (2017) 3:e1701704. doi:10.1126/sciadv.1701704

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Desplat L, Suess D, Kim J-V, Stamps RL. Thermal Stability of Metastable Magnetic Skyrmions: Entropic Narrowing and Significance of Internal Eigenmodes. Phys Rev B (2018) 98:134407. doi:10.1103/PhysRevB.98.134407

CrossRef Full Text | Google Scholar

3. Dzyaloshinsky I. A Thermodynamic Theory of “Weak” Ferromagnetism of Antiferromagnetics. J Phys Chem Sol (1958) 4:241–55. doi:10.1016/0022-3697(58)90076-3

CrossRef Full Text | Google Scholar

4. Moriya T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys Rev (1960) 120:91–8. doi:10.1103/PhysRev.120.91

CrossRef Full Text | Google Scholar

5. Nagaosa N, Tokura Y. Topological Properties and Dynamics of Magnetic Skyrmions. Nat Nanotech (2013) 8:899–911. doi:10.1038/nnano.2013.243

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Fert A, Cros V, Sampaio J. Skyrmions on the Track. Nat Nanotech (2013) 8:152–6. doi:10.1038/nnano.2013.29

CrossRef Full Text | Google Scholar

7. Krause S, Wiesendanger R. Skyrmionics Gets Hot. Nat Mater (2016) 15:493–4. doi:10.1038/nmat4615

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhang X, Zhou Y, Mee Song K, Park T-E, Xia J, Ezawa M, et al. Skyrmion-electronics: Writing, Deleting, reading and Processing Magnetic Skyrmions toward Spintronic Applications. J Phys Condens Matter (2020) 32:143001. doi:10.1088/1361-648x/ab5488

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Serga AA, Chumak AV, Hillebrands B. YIG Magnonics. J Phys D: Appl Phys (2010) 43:264002. doi:10.1088/0022-3727/43/26/264002

CrossRef Full Text | Google Scholar

10. Lenk B, Ulrichs H, Garbs F, Münzenberg M. The Building Blocks of Magnonics. Phys Rep (2011) 507:107–36. doi:10.1016/j.physrep.2011.06.003

CrossRef Full Text | Google Scholar

11. Chumak AV, Vasyuchka VI, Serga AA, Hillebrands B. Magnon Spintronics. Nat Phys (2015) 11:453–61. doi:10.1038/nphys3347

CrossRef Full Text | Google Scholar

12. Iwasaki J, Beekman AJ, Nagaosa N. Theory of Magnon-Skyrmion Scattering in Chiral Magnets. Phys Rev B (2014) 89:064412. doi:10.1103/PhysRevB.89.064412

CrossRef Full Text | Google Scholar

13. Schütte C, Garst M. Magnon-skyrmion Scattering in Chiral Magnets. Phys Rev B (2014) 90:094423. doi:10.1103/PhysRevB.90.094423

CrossRef Full Text | Google Scholar

14. Zhang X, Müller J, Xia J, Garst M, Liu X, Zhou Y. Motion of Skyrmions in Nanowires Driven by Magnonic Momentum-Transfer Forces. New J Phys (2017) 19:065001. doi:10.1088/1367-2630/aa6b70

CrossRef Full Text | Google Scholar

15. Jiang Y, Yuan HY, Li Z-X, Wang Z, Zhang HW, Cao Y, et al. Twisted Magnon as a Magnetic Tweezer. Phys Rev Lett (2020) 124:217204. doi:10.1103/physrevlett.124.217204

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ma F, Zhou Y, Braun HB, Lew WS. Skyrmion-based Dynamic Magnonic crystal. Nano Lett (2015) 15:4029–36. doi:10.1021/acs.nanolett.5b00996

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Moon KW, Chun BS, Kim W, Hwang C. Control of Spin-Wave Refraction Using Arrays of Skyrmions. Phys Rev Appl (2016) 6:064027. doi:10.1103/physrevapplied.6.064027

CrossRef Full Text | Google Scholar

18. Wang Z, Yuan HY, Cao Y, Li Z-X, Duine RA, Yan P. Magnonic Frequency Comb through Nonlinear Magnon-Skyrmion Scattering. Phys Rev Lett (2021) 127:037202. doi:10.1103/PhysRevLett.127.037202

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Zhang X, Xia J, Zhou Y, Liu X, Zhang H, Ezawa M. Skyrmion Dynamics in a Frustrated Ferromagnetic Film and Current-Induced Helicity Locking-Unlocking Transition. Nat Commun (2017) 8:1717. doi:10.1038/s41467-017-01785-w

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zhang B, Wang W, Beg M, Fangohr H, Kuch W. Microwave-induced Dynamic Switching of Magnetic Skyrmion Cores in Nanodots. Appl Phys Lett (2015) 106:102401. doi:10.1063/1.4914496

CrossRef Full Text | Google Scholar

21. Liu Y, Yin G, Zang J, Shi J, Lake RK. Skyrmion Creation and Annihilation by Spin Waves. Appl Phys Lett (2015) 107:152411. doi:10.1063/1.4933407

CrossRef Full Text | Google Scholar

22. Wang Z, Li Z-X, Wang R, Liu B, Meng H, Cao Y, et al. Spin-wave Focusing Induced Skyrmion Generation. Appl Phys Lett (2020) 117:222406. doi:10.1063/5.0029401

CrossRef Full Text | Google Scholar

23. Toedt J-N, Mundkowski M, Heitmann D, Mendach S, Hansen W. Design and Construction of a Spin-Wave Lens. Sci Rep (2016) 6:33169. doi:10.1038/srep33169

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Bao W, Wang Z, Cao Y, Yan P. Off-axial Focusing of a Spin-Wave Lens in the Presence of Dzyaloshinskii-Moriya Interaction. Phys Rev B (2020) 102:014423. doi:10.1103/PhysRevB.102.014423

CrossRef Full Text | Google Scholar

25. Whitehead NJ, Horsley SAR, Philbin TG, Kruglyak VV. A Luneburg Lens for Spin Waves. Appl Phys Lett (2018) 113:212404. doi:10.1063/1.5049470

CrossRef Full Text | Google Scholar

26. Vogel M, Pirro P, Hillebrands B, von Freymann G. Optical Elements for Anisotropic Spin-Wave Propagation. Appl Phys Lett (2020) 116:262404. doi:10.1063/5.0018519

CrossRef Full Text | Google Scholar

27. Zelent M, Mailyan M, Vashistha V, Gruszecki P, Gorobets OY, Gorobets YI, et al. Spin Wave Collimation Using a Flat Metasurface. Nanoscale (2019) 11:9743–8. doi:10.1039/C8NR10484K

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gräfe J, Gruszecki P, Zelent M, Decker M, Keskinbora K, Noske M, et al. Direct Observation of Spin-Wave Focusing by a Fresnel Lens. Phys Rev B (2020) 102:024420. doi:10.1103/PhysRevB.102.024420

CrossRef Full Text | Google Scholar

29. Yan P, Wang XS, Wang XR. All-magnonic Spin-Transfer Torque and Domain wall Propagation. Phys Rev Lett (2011) 107:177207. doi:10.1103/physrevlett.107.177207

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Vansteenkiste A, Leliaert J, Dvornik M, Helsen M, Garcia-Sanchez F, Van Waeyenberge B. The Design and Verification of Mumax3. AIP Adv (2014) 4:107133. doi:10.1063/1.4899186

CrossRef Full Text | Google Scholar

31. Venkat G, Fangohr H, Prabhakar A. Absorbing Boundary Layers for Spin Wave Micromagnetics. J Magnetism Magn Mater (2018) 450:34–9. Perspectives on magnon spintronics. doi:10.1016/j.jmmm.2017.06.057

CrossRef Full Text | Google Scholar

32. Chaves-O'Flynn GD, Stein DL. Thermal Activation Barriers for Creation and Annihilation of Magnetic Droplet Solitons in the Presence of Spin Transfer Torque. Phys Rev B (2020) 101:184421. doi:10.1103/PhysRevB.101.184421

CrossRef Full Text | Google Scholar

33. Macià F, Kent AD. Magnetic Droplet Solitons. J Appl Phys (2020) 128:100901. doi:10.1063/5.0018251

CrossRef Full Text | Google Scholar

34. Berg B, Lüscher M. Definition and Statistical Distributions of a Topological Number in the Lattice O(3) σ-model. Nucl Phys B (1981) 190:412–24. doi:10.1016/0550-3213(81)90568-X

CrossRef Full Text | Google Scholar

35. Böttcher M, Heinze S, Egorov S, Sinova J, Dupé B. B-T Phase Diagram of Pd/Fe/Ir(111) Computed with Parallel Tempering Monte Carlo. New J Phys (2018) 20:103014. doi:10.1088/1367-2630/aae282

CrossRef Full Text | Google Scholar

36. Müller GP, Hoffmann M, Dißelkamp C, Schürhoff D, Mavros S, Sallermann M, et al. Spirit : Multifunctional Framework for Atomistic Spin Simulations. Phys Rev B (2019) 99:224414. doi:10.1103/PhysRevB.99.224414

CrossRef Full Text | Google Scholar

37. Kim J-V, Mulkers J. On Quantifying the Topological Charge in Micromagnetics Using a Lattice-Based Approach. IOP SciNotes (2020) 1:025211. doi:10.1088/2633-1357/abad0c

CrossRef Full Text | Google Scholar

38. Yu X, Kagawa F, Seki S, Kubota M, Masell J, Yasin F, et al. Real-space Observations of 60-nm Skyrmion Dynamics in an Insulating Magnet under Low Heat, Nat Commun (2021) 12:5079. PREPRINT (Version 1) available at Research Square doi:10.1038/s41467-021-25291-2

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Soumah L, Beaulieu N, Qassym L, Carrétéro C, Jacquet E, Lebourgeois R, et al. Ultra-low Damping Insulating Magnetic Thin Films Get Perpendicular. Nat Commun (2018) 9:3355. doi:10.1038/s41467-018-05732-1

PubMed Abstract | CrossRef Full Text | Google Scholar

40. You C-Y. Skyrmions in Magnetic Insulators Warm up. Nat Electron (2019) 2:176–7. doi:10.1038/s41928-019-0250-1

CrossRef Full Text | Google Scholar

41. Caretta L, Rosenberg E, Büttner F, Fakhrul T, Gargiani P, Valvidares M, et al. Interfacial Dzyaloshinskii-Moriya Interaction Arising from Rare-Earth Orbital Magnetism in Insulating Magnetic Oxides. Nat Commun (2020) 11:1090. doi:10.1038/s41467-020-14924-7

PubMed Abstract | CrossRef Full Text | Google Scholar