
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
PERSPECTIVE article
Front. Phys., 15 December 2021
Sec. Condensed Matter Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.725853
In this perspective, we discuss the current and future impact of artificial intelligence and machine learning for the purposes of better understanding phase transitions, particularly in correlated electron materials. We take as a model system the rare-earth nickelates, famous for their thermally-driven metal-insulator transition, and describe various complementary approaches in which machine learning can contribute to the scientific process. In particular, we focus on electron microscopy as a bottom-up approach and metascale statistical analyses of classes of metal-insulator transition materials as a bottom-down approach. Finally, we outline how this improved understanding will lead to better control of phase transitions and present as an example the implementation of rare-earth nickelates in resistive switching devices. These devices could see a future as part of a neuromorphic computing architecture, providing a more efficient platform for neural network analyses – a key area of machine learning.
Around the last decade, artificial intelligence (AI) has become the staple for teasing out insights from large sets of data in both a scientific context and from our everyday lives. AI defines a wide class of computer-based approaches to solve problems that normally require human intelligence [1]. AI, and especially the subfield of machine learning (ML), where the model is able to self-improve based on previous outputs, can reveal patterns in multidimensional data sets that would not have been appreciated otherwise. This can be used in many ways, from relatively benign recommendation systems [2] to potentially more insidious implementations in mass surveillance [3]. One thing that has become clear in this age of AI is that a model can only be as good as the input data. In physics, machine learning has proven itself particularly useful in the context of high-energy physics, and astrophysics, where large, centralized datasets exist. All this leads to the question of why ML is not more ubiquitous in condensed matter physics, the largest subfield of contemporary physics by activity [4].
The nature of the field is no doubt partially to blame for this: the average condensed matter physicist generates relatively little data when compared to their counterparts from other areas of physics. Physical conclusions tend to be drawn from multiple complementary measurements on a small set of samples or devices rather than one large dataset. Compounding this is that data is seldom centralised. Even within a close collaboration between different groups: synthesis parameters are rarely shared with the theoretical scientist, while details of the electronic structure calculation are not shared with the experimentalist. Computational results in the field of correlated materials are performed with a variety of codes and techniques, that do not always give the same results, making the consistent application of machine learning techniques to data generated by multiple groups more difficult.
Here we will discuss two AI-based approaches in condensed matter physics, one nanoscale and one metascale. By metascale we mean that – rather than looking at an individual material at a particular physical scale, new insight is brought into the field from AI or other forms of statistical analysis of multiple materials, at a variety of different possible scales. We attempt to address one of the most fundamental concepts in the subject: the metal-insulator phase transition (MIT). We discuss how ML can contribute to both a bottom-up and top-down understanding of phase transitions through electron microscopy techniques, and metascale analyses of MIT materials respectively. These two approaches, enhanced by ML, will improve understanding and control of the MIT. Then, we will show how the cycle of development can be completed by future implementation of phase transition systems into neuromorphic hardware that could significantly enhance the efficiency of artificial neural networks, used to model a wide variety of nonlinear processes from object recognition [5] to translation [6].
Most MIT materials are transition metal oxides [7] and, as a model system in which to study MITs, the rare earth nickelates are a shining example for multiple reasons. These include - when synthesised as epitaxial thin films - their high quality and adaptability in terms of multilayer and superlattice structures as well as their intrinsic physics [8].
The family of perovskite rare earth nickelates, RNiO3, where R can be most of the rare earths, has been widely studied for many decades already [8, 9]. At high temperature, the RNiO3 compounds are paramagnetic metals with a strong hybridisation between the Ni cation and the six oxygens in immediate coordination [10, 11]. Upon reducing temperature, the RNiO3 compounds enter an insulating state with an energy gap characterised by the O-Ni charge transfer energy, i.e., the material is in the charge-transfer regime. [12, 13]. Locally, the material undergoes a structural and electronic disproportionation while entering the insulating phase [14–16] stabilised by the electron-lattice coupling [17].
The transition induces a change of resistivity of several orders of magnitude and varies from occurring at cryogenic temperatures to occurring at hundreds of Kelvin. The large range of MIT temperatures is brought about through the substitution of the various rare earth cations, representing a largely steric effect on the electronic bandwidth, along with an associated change in the lattice stiffness to structural disproportionation [17–19].
The MIT can be controlled in bulk by parameters, such as pressure [20]. Due to the relative unavailability of large single crystals, much of the work on rare earth nickelates has taken place in the context of thin film heterostructures. The film geometry facilitates the control of the MIT by electric field [21] and light [22] and introduces new tuning parameters such as strain, substrate symmetry, and confinement and interfacial effects [19, 23–28].
In recent years, development of aberration-corrected scanning transmission electron microscopy (STEM) has allowed, sometimes subtle and often pico-scale, effects at heterointerfaces to be accessed.
STEM is a powerful technique that can image crystals and non-periodic structures directly in real space with sub-atomic resolution. Through monitoring unit cell by unit cell, this analysis is critical to understand the physical properties of materials and particularly those that emerge in epitaxial heterostructures. However, as a scanning technique, the acquired datasets are typically large (up to a few terabytes), noisy (especially from scanning distortions), redundant (most pixels contain similar information) and sometimes require complex interpretation. Therefore, in some cases it might be difficult to identify the most relevant information from a given dataset and to efficiently extract it, particularly when studying an unknown compound. In this respect, ML has unlocked the ability to rapidly and automatically extract physically relevant features from STEM images [29], for example defects and dopants in graphene lattices [30–36], allowing access to a treasure-trove of information on the atomic scale physics and chemistry of materials.
Furthermore, the possibility of coupling imaging detectors with spectrometers, such as energy dispersive x-ray (EDS) or electron energy loss (EELS), makes STEM even more complete. When combined, these detectors generate 3D datasets where each individual real space image pixel contains a spectrum of chemical and electronic information from the corresponding lattice position. However, in contrast to other spectroscopic techniques such as x-ray absorption spectroscopy, the output signal in EELS or EDS is significantly lower due the smaller volume of sample that is probed, which ultimately limits the energy resolution. In this aspect, ML algorithms have become an indispensable tool for boosting the signal-to-noise ratio of the acquired spectra and/or for isolating mixed spectral contributions. Among all the different approaches, principal component analysis (PCA) is one of the most routinely used methods for spectral noise reduction. This method consists of decomposing the initial dataset into a new set of orthogonal components which are then re-ordered as a function of their statistical variance. By discarding the low-variance components associated to the spectral noise, one can recover the original data containing only the most relevant information [37–40]. This method has recently enabled the spatial mapping of the electronic phases in rare-earth nickelate superlattices to almost atomic resolution, revealing how structural and electronic properties are coupled at the interfaces of these novel, artificially engineered materials [41]. Understanding the coupling length scales has been crucial for harnessing the phase transition in such devices [42]. However, the use of PCA is less convenient to effectively unmix overlapped spectral features since the resulting orthogonal components do not have a physical meaning. To this end, alternative methods have also been developed [43–53].
As a technique, STEM can be expected to become even more popular in laboratories across the globe thanks to the continuing advancement of the hardware. Among these advancements, the powerful functionalities of STEM can be further combined with high-stability TEM stages that enable measurement at fixed temperatures from approximately −200°C to 1,000°C and allow in-situ electrical biasing of the TEM specimen while preserving the atomic resolution [54, 55]. In addition, significant improvements in data collection are being made through the development of new generation cameras. In the case of EELS for instance, the signal-to-noise ratio of the acquired spectra has been remarkably enhanced thanks to the advent of direct electron detection cameras which, compared to conventional charge coupled device cameras, offer much better detector quantum efficiency and point-spread function [56, 57]. This will allow, for instance, the scanning dose rate to be significantly reduced, which is critical for beam sensitive materials, and even more subtle fine structure modulations associated to complex lattice, charge or spin orderings to be studied.
Another exciting recent advancement that will play a key role to investigate local structural and electronic modulations in the years to come is pixelated detectors [39, 58]. This new imaging mode, commonly referred to as 4D-STEM, provides a 4-dimensional dataset that is composed by a 2D image where all of its pixels contain an associated 2D electron diffractogram. These large and complex datasets reconstruct local electrostatic fields, charge densities or structural ordering of the imaged crystal. For instance, it has recently been used to reveal the presence of complex magnetic textures emerging in ferroelectric superlattices [59]. This type of technique presents an unprecedented opportunity to study the kind of structure-property relationships that underpin many phase transitions, as has been shown in scanning probe microscopy measurements [60].
Even though these latest advances will give access to a wealth of new information that will be key to better understand phase transitions, new processing tools based on AI or ML methods absolutely must be employed to truly leverage these ever-evolving techniques in a reliable and time-efficient way [61].
Combining these powerful new developments in STEM with the established ability of ML to find patterns in large and complex datasets will be key to both streamlining analysis and detecting correlations between datasets that are vital in addressing fundamental atomic-scale questions about phase transitions in rare earth nickelates and beyond.
Complementary to the information on the microscopic mechanisms of MITs that can be accessed by AI-assisted STEM-EELS, a global overview of a range of materials and techniques can yield extraordinary novel insights. This can be thought of as a secondary metascale analysis of the firsthand results.
Decades of research across the globe has generated a vast amount of data on MIT and MIT-adjacent materials using a variety of probes. However, a human can still only read through a relatively small number of articles provided by the literature search and the search itself may be biased. Such biases can arise via both the user, through the keywords that they choose to input, and the search system itself, which may prioritise whatever generates the most clicks or only suggest works that are very closely related to those of the scientist performing the search. As a result, direct literature search, while the most common approach, is a rather inefficient and unidimensional way for a scientist to improve their understanding of the relevant field.
To help somewhat, computational databases exist [62–66] that compile the outputs of first-principles calculations. However, importantly, and specific to MIT materials in particular, it is often difficult to know how reliable first-principles calculations are in predicting whether a material has an MIT or not due to correlation effects. Also, the fact that DFT is a ground state theory means that even if DFT correctly predicted the insulating ground state of a material, whether it becomes metallic at higher temperatures or not would remain unknown, given current theory. As a result, experimental validation is still required. Experimental databases [67–70] also exist but do not include accurate classifications based on transport for MIT materials: for example, Ca2RuO4 is listed as a non-metal on Springer Materials [71].
Natural language processing (NLP), a sub-discipline of ML that can analyse text data, offers a way to bypass these initial biases. First, in a very practical way, by scanning through a much wider part of the literature than humanly possible. Secondly, by identifying key new properties – or materials – associated with a particular class of materials from the literature, usually through a form of similarity score, increasing the range of knowledge available to the scientist [72]. A database, built with the assistance of NLP techniques, identifies around 60 experimentally-confirmed thermally-driven MIT compounds [73]. Expanding this dataset remains difficult: though NLP can assist in finding published work describing MIT materials that are relatively less studied [74, 75], the classification of each material is still done by a human through a deep analysis of each paper. Secondly, many materials may be misclassified either due to materials quality or to limited experimental data, for example the lack of high temperature transport. Further, this database currently only contains thermally-driven MIT materials and not those accessed by e.g., pressure. Even this relatively small dataset is too large and multidimensional for a conventional scientist to be able to discern patterns, making this type of analysis problem ideally suited for ML.
One of the main advantages of machine learning as a tool to understand datasets of MIT materials is that it can look at a wide variety of features at once, and may not have the same biases as a human. For instance, as all theoretical or computational materials studies are based on approximations to quantum effects, it is often tempting to assume that the aspects that are treated most accurately are the most important in driving the physics. Machine learning – as a model-agnostic tool – may be used to remove some of these biases and provide new insight into yet unexplored directions. This may also help overcome some of the limitations inherent in current theoretical studies of MIT materials and may not need the same amount of user input as, for instance, a first principles calculation [7]. ML approaches, for example, using classifiers trained on existing literature [7, 76] can be useful in quickly identifying which materials should be studied in more detail from large databases such as Materials Project [63].
In meeting these challenges some studies have made progress in identifying certain key features of MIT materials such as the rare-earth nickelates [7]. The most important is the transition metal-transition metal distance, which is essential in setting the electronic bandwidth, as well as in determining electronic interaction parameters such as the Hubbard U. The high importance of its interaction with other features, such as the Hubbard U, both highlights the ability of machine learning approaches to gain physical insight and confirms previous theories about the nature of the MIT in an unbiased way. The extraction of previously-underappreciated relevant features, such as Ewald energy, global instability index and average deviation of the atoms’ covalent radii, may provide new directions to understand and tune nickelates and other MIT materials.
Finally, machine learning methods may be used to analyse multiple structures within a particular materials class, and extract relevant information, as has been done in the case of the RNiO3 materials [77].
Even harnessing the power of ML to scrape together a comprehensive dataset and detect the patterns within, MIT materials pose additional challenges. First, the experimental dataset of MIT materials is quite scarce for ML purposes, albeit much larger than what most scientists are normally aware of. Second, this class of materials is very heterogeneous meaning that the materials can have many transition types and mechanisms and it is not clear a priori that a ML model would see them as similar. Furthermore, if each set of compounds is fundamentally different, the scarcity issue, as seen by a ML algorithm, increases in severity. This, however, also presents an opportunity: it may be possible to see similar underlying causes of the MIT, even for materials that seem dissimilar.
Machine learning can also be used to streamline functionality when a particular underlying function and its properties are completely unknown by minimising the number of sampling attempts required to find the global minimum of the function, through Bayesian optimisation (BO) [78]. BO is most useful in cases in which the evaluation of each data point (for example, the synthesis or detailed calculation of a material) is sufficiently expensive, that the computational cost of BO is negligible by comparison [79]. As such, it should prove to be a particularly useful tool in the discovery of new materials [80]. This method, in combination with dimensionality reduction techniques can furthermore be used in the field of MIT materials as well, for example by focusing on a particular materials family, as has been done on the lacunar spinel family [81].
Once a promising material has been identified, machine learning techniques can be used to accelerate its synthesis. BO techniques have already proven themselves useful in the field of oxide heterostructure growth, significantly lowering the number of samples needed for growth optimisation [82], and are clearly an underused tool in the relatively slow and expensive process of optimizing new materials’ growth via atomic-precision tools such as molecular beam epitaxy. In the direction of bulk material synthesis, NLP combined with neural networks may suggest new synthesizable materials for physical analysis [83]. NLP can then be used to prescribe techniques for the synthesis of new materials [84, 85]. BO and other machine learning tools may help optimise the process [86, 87].
Finally, symbolic regression is an aspect of machine learning that can be used to obtain the functional form of an underlying function. This may be useful to obtain physical insight into the phenomenology of materials of interest, such as in the case of relevant energy landscapes describing MIT and MIT-related materials [17, 88].
Machine learning is therefore a valuable ally in every step of the materials-by-design process, from accessing atomic-scale information of already-known MIT materials such as rare earth nickelates, to synthesis conditions and properties of known, and as-yet unstudied MIT materials to finally, discovery of completely new materials. With this new power, we can understand and control the MIT, which is essential for implementation in devices. Figure 1 summarises the continual feedback and reinforcement between fundamental physics and device implementation taking the rare earth nickelates as example materials where ML assists in the nanoscale and metascale analysis of materials.
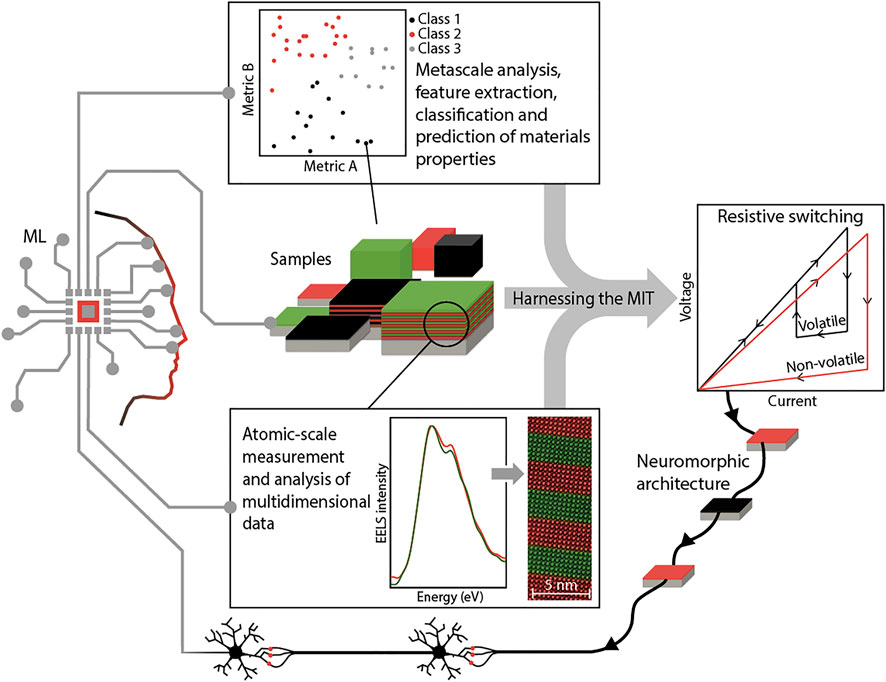
FIGURE 1. Summary of the influence of machine learning on atomic scale and metascale analysis of MIT materials. The EEL spectra and STEM image are adapted from reference 40. The clustering sketch shows that with a good choice of features (here called Metric A and Metric B) and enough data points extracted from firsthand results, correlations can be uncovered providing new understanding or guiding new materials discovery. Together, the MIT can be better-controlled and these materials can provide new neuromorphic computing architectures using resistive switching. These architectures are in turn expected to significantly contribute to deep-learning applications.
One exciting area currently being developed involves building up MIT material elements to support neural networks, a technique that mimics aspects of how the brain learns to find patterns and relationships in data, and which is a key part of the ML landscape that helped to glean so much insight into the materials in the first place.
The current approach to artificial intelligence is based on software running on conventional computers, not designed or optimised for such a task. Corporations such as Intel [89] or IBM [90] have embarked on ambitious projects that circumvent this limitation by implementing hardware-based elements that resemble the electrical characteristics of biological neural networks, an approach known as neuromorphic computing. But these efforts are based on traditional CMOS transistor technology [91], not developed for this purpose. This necessitates neuronal or synaptic elements to be comprised of dozens of components, compromising scalability and efficiency.
A solution to this problem is “neuromorphic materials” that have intrinsic properties that directly mimic neurons and synapses [92]. Several approaches have been proposed to this end, based on diverse phenomenology such as spin-torque transfer [93] or optically active materials [94]. But arguably the most advanced approach is based on resistive switching, a phenomenon in which the resistance of a material can be modified by applying an electric field [92]. There are two basic types of resistive switching: non-volatile and volatile. The origins of the two types are very different.
In non-volatile resistive switching, the material becomes conducting after a voltage is applied and the resistance after the voltage is removed does not recover its initial value. The system keeps a memory of the switching event, behaviour that resembles that of synapses. Non-volatile resistive switching is observed in almost every oxide, and in most cases it is caused by the drift of ions - especially oxygen - under strong electric fields [95], although an alternative mechanism based on electrostriction has also been reported for several Mott insulators such as Cr-doped V2O3 [96] or compounds of the AM4X8 family (A = Ga,Ge; M = V,Nb,Ta; X = S,Se) [97]. Non-volatile effects are well-documented in both binary transition metal oxides as well as rare earth nickelate devices [98–102], making them good candidates for implementing artificial synapses. Still, fundamental questions regarding the nature of non-volatile switching in the RNiO3 compounds, such as its bulk/interfacial character or the use of other mobile ion species, remain open.
Volatile resistive switching, on the other hand, has been far less studied. It is observed in many materials that have an MIT such as VO2, V2O3, and NbO2 [92] and the rare-earth nickelates NdNiO3 [103], SmNiO3 [104] and Sm0.6Nd0.4NiO3 [105]. Upon the application of a voltage, the system is driven from the insulating into the metallic state, returning to its insulating phase when the voltage goes back to zero, mimicking the behaviour of neurons [106]. The origin and mechanism of this electrically-induced transition are still under study [107, 108]. Most literature regarding the electrically-triggered MIT has been done in vanadium or niobium oxides, with very few works on the rare earth nickelates. Topics such as the triggering mechanism, filament formation or the emulation of neuronal spiking patterns [109–111], which are well documented for oxides such as VO2, have not been explored at all for RNiO3, offering a broad field of research opportunities.
Rare earth nickelates - as well as other oxides with an MIT - are thus a rather unique class of materials. They feature both non-volatile and volatile resistive switching, meaning that both synaptic and neuronal behaviour could be implemented in a single platform, opening the possibility of fully oxide-based scalable neural networks.
Much more needs to be learned about resistive switching in MIT materials such as rare earth nickelates before all-oxide neural networks can be achieved, from a fundamental perspective but also from a device development standpoint. Aiding in this endeavour is the knowledge-base currently being constructed from the picoscale upwards via advances in probes of condensed matter systems such as STEM and from the metascale downwards through compilations and analyses of databases. In both of these approaches machine learning is already playing a key role and will be even more invaluable as datasets expand and measurements push the cutting edge. Machine learning can, and should, play a role in the continued discovery, study and synthesis of new materials.
These big prospects and challenges are sure to maintain an active and exciting research panorama for many years to come.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
All authors contributed to manuscript revision, read, and approved the submitted version.
JF and BM acknowledge support by the Swiss National Science Foundation through Division II project 200020\_179155. JV thanks the Swiss National Science Foundation for an Ambizione Fellowship (#PZ00P2_185848). ABG was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001209. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The authors wish to thank Adrien Teurtrie and Jean-Marc Triscone for helpful feedback on the manuscript, James Rondinelli for discussion, and Xavier Ravinet for assistance with the figure.
1. Copeland B. Artificial Intelligence, Encyclopedia Britannica (2020). [Online]. Available: https://www.britannica.com/technology/artificial-intelligence (Accessed Jun 04, 2021).
2. Adomavicius G, Tuzhilin A. Toward the Next Generation of Recommender Systems: a Survey of the State-Of-The-Art and Possible Extensions. IEEE Trans Knowl Data Eng (2005) 17(6):734–49. doi:10.1109/tkde.2005.99
3. Verhelst HM, Stannat AW, Mecacci G. Machine Learning against Terrorism: How Big Data Collection and Analysis Influences the Privacy-Security Dilemma. Sci Eng Ethics (2020) 26(6):2975–84. doi:10.1007/s11948-020-00254-w
4.Aps. Division of Condensed Matter Physics (2019). Available at: https://engage.aps.org/dcmp/home (Accessed 04 Jun, 2021).
5. Liu L, Ouyang W, Wang X, Fieguth P, Chen J, Liu X, et al. Deep Learning for Generic Object Detection: A Survey. Int J Comput Vis (2020) 128(2):261–318. doi:10.1007/s11263-019-01247-4
6. Stahlberg F. Neural Machine Translation: A Review. jair (2020) 69:343–418. doi:10.1613/jair.1.12007
7. Georgescu AB, Ren P, Toland AR, Zhang S, Miller KD, Apley DW, et al. Database, Features, and Machine Learning Model to Identify Thermally Driven Metal-Insulator Transition Compounds. Chem Mater (2021) 33(14):5591–605. doi:10.1021/acs.chemmater.1c00905
8. Catalano S, Gibert M, Fowlie J, Íñiguez J, Triscone J-M, Kreisel J. Rare-earth nickelatesRNiO3: Thin Films and Heterostructures. Rep Prog Phys (2018) 81:046501. doi:10.1088/1361-6633/aaa37a
9. Medarde ML. Structural, Magnetic and Electronic Properties of Perovskites (R = Rare Earth). J Phys Condens Matter (1997) 9(8):1679–707. doi:10.1088/0953-8984/9/8/003
10. Mizokawa T, Khomskii DI, Sawatzky GA. Spin and Charge Ordering in Self-Doped Mott Insulators. Phys Rev B (2000) 61(17):11263–6. doi:10.1103/physrevb.61.11263
11. Bisogni V, Catalano S, Green RJ, Gibert M, Scherwitzl R, Huang Y, et al. Ground-state Oxygen Holes and the Metal-Insulator Transition in the Negative Charge-Transfer Rare-Earth Nickelates. Nat Commun (2016) 7:13017–8. doi:10.1038/ncomms13017
12. Mazin II, Khomskii DI, Lengsdorf R, Alonso JA, Marshall WG, Ibberson RM, et al. Charge Ordering as Alternative to Jahn-Teller Distortion. Phys Rev Lett (2007) 98(17):176406. doi:10.1103/physrevlett.98.176406
13. Johnston S, Mukherjee A, Elfimov I, Berciu M, Sawatzky GA. Charge Disproportionation without Charge Transfer in the Rare-Earth-Element Nickelates as a Possible Mechanism for the Metal-Insulator Transition. Phys Rev Lett (2014) 112(10):106404–5. doi:10.1103/PhysRevLett.112.106404
14. Alonso JA, García-Muñoz JL, Fernández-Díaz MT, Aranda MAG, Martínez-Lope MJ, Casais MT. Charge Disproportionation inRNiO3Perovskites: Simultaneous Metal-Insulator and Structural Transition inYNiO3. Phys Rev Lett (1999) 82(19):3871–4. doi:10.1103/physrevlett.82.3871
15. Staub U, Meijer GI, Fauth F, Allenspach R, Bednorz JG, Karpinski J, et al. Direct Observation of Charge Order in an Epitaxial NdNiO3 Film. Phys Rev Lett (2002) 88(12):126402. doi:10.1103/PhysRevLett.88.126402
16. Park H, Millis AJ, Marianetti CA. Site-selective Mott Transition in Rare-Earth-Element Nickelates. Phys Rev Lett (2012) 109(15):156402–5. doi:10.1103/PhysRevLett.109.156402
17. Georgescu AB, Millis AJ. Energy Landscape Analysis of Metal-Insulator Transitions: Theory and Application to Ca2RuO4, RNiO3 and Their Heterostructures. Available at: https://arxiv.org/abs/2105.02271 (2021).
18. Peil OE, Hampel A, Ederer C, Georges A. Mechanism and Control Parameters of the Coupled Structural and Metal-Insulator Transition in Nickelates. Phys Rev B (2019) 99(24):245127. doi:10.1103/physrevb.99.245127
19. Georgescu AB, Peil OE, Disa AS, Georges A, Millis AJ. Disentangling Lattice and Electronic Contributions to the Metal-Insulator Transition from Bulk vs. Layer Confined RNiO3. Proc Natl Acad Sci USA (2019) 116(29):14434–9. doi:10.1073/pnas.1818728116
20. Obradors X, Paulius LM, Maple MB, Torrance JB, Nazzal AI, Fontcuberta J, et al. Pressure Dependence of the Metal-Insulator Transition in the Charge-Transfer oxidesRNiO3(R=Pr,Nd,Nd0.7La0.3). Phys Rev B (1993) 47(18):12353–6. doi:10.1103/physrevb.47.12353
21. Scherwitzl R, Zubko P, Lezama IG, Ono S, Morpurgo AF, Catalan G, et al. Electric-field Control of the Metal-Insulator Transition in Ultrathin NdNiO3 Films. Adv Mater (2010) 22(48):5517–20. doi:10.1002/adma.201003241
22. Caviglia AD, Scherwitzl R, Popovich P, Hu W, Bromberger H, Singla R, et al. Ultrafast Strain Engineering in Complex Oxide Heterostructures. Phys Rev Lett (2012) 108(13):136801. doi:10.1103/PhysRevLett.108.136801
23. Tiwari A, Jin C, Narayan J. Strain-induced Tuning of Metal-Insulator Transition in NdNiO3. Appl Phys Lett (2002) 80(21):4039–41. doi:10.1063/1.1480475
24. Liu J, Kareev M, Gray B, Kim JW, Ryan P, Dabrowski B, et al. Strain-mediated Metal-Insulator Transition in Epitaxial Ultrathin Films of NdNiO3. Appl Phys Lett (2010) 96(23):1–4. doi:10.1063/1.3451462
25. Catalano S, Gibert M, Bisogni V, Peil OE, He F, Sutarto R, et al. Electronic Transitions in Strained SmNiO3 Thin Films. APL Mater (2014) 2(11). doi:10.1063/1.4902138
26. Hauser AJ, Mikheev E, Moreno NE, Hwang J, Zhang JY, Stemmer S. Correlation between Stoichiometry, Strain, and Metal-Insulator Transitions of NdNiO3 Films. Appl Phys Lett (2015) 106(9). doi:10.1063/1.4914002
27. Catalano S, Gibert M, Bisogni V, He F, Sutarto R, Viret M, et al. Tailoring the Electronic Transitions of NdNiO3 Films through (111)pc Oriented Interfaces. APL Mater (2015) 3(6). doi:10.1063/1.4919803
28. Liao Z, Gauquelin N, Green RJ, Müller-Caspary K, Lobato I, Li L, et al. Metal-insulator-transition engineering by modulation tilt-control in perovskite nickelates for room temperature optical switching. Proc Natl Acad Sci U S A (2018) 115(43):E10284. doi:10.1073/pnas.1816794115
29. Ge M, Su F, Zhao Z, Su D. Deep Learning Analysis on Microscopic Imaging in Materials Science. Mater Today Nano (2020) 11. doi:10.1016/j.mtnano.2020.100087
30. Ziatdinov M, Dyck O, Maksov A, Li X, Sang X, Xiao K, et al. Deep Learning of Atomically Resolved Scanning Transmission Electron Microscopy Images: Chemical Identification and Tracking Local Transformations. ACS Nano (2017) 11(12):12742–52. doi:10.1021/acsnano.7b07504
31. Ziatdinov M, Dyck O, Jesse S, Kalinin SV. Atomic Mechanisms for the Si Atom Dynamics in Graphene: Chemical Transformations at the Edge and in the Bulk. Adv Funct Mater (2019) 29(52):1–8. doi:10.1002/adfm.201904480
32. Ziatdinov M, Dyck O, Li X, Sumpter BG, Jesse S, Vasudevan RK, et al. Building and Exploring Libraries of Atomic Defects in Graphene: Scanning Transmission Electron and Scanning Tunneling Microscopy Study. Sci Adv (2019) 5(9):eaaw8989. doi:10.1126/sciadv.aaw8989
33. Maksov A, Dyck O, Wang K, Xiao K, Geohegan DB, Sumpter BG, et al. Deep Learning Analysis of Defect and Phase Evolution during Electron Beam-Induced Transformations in WS2. Npj Comput Mater (2019) 5(1):1–8. doi:10.1038/s41524-019-0152-9
34. Chakraborty M, Ziatdinov M, Dyck O, Jesse S, White AD, Kalinin SV. Reconstruction of the Interatomic Forces from Dynamic Scanning Transmission Electron Microscopy Data. J Appl Phys (2020) 127(22):224301. doi:10.1063/5.0009413
35. Ziatdinov M, Jesse S, Sumpter BG, Kalinin SV, Dyck O. Tracking Atomic Structure Evolution during Directed Electron Beam Induced Si-Atom Motion in Graphene via Deep Machine Learning. Nanotechnology (2020) 32(3):035703.
36. V Kalinin S, Dyck O, Jesse S, Ziatdinov M. Exploring Order Parameters and Dynamic Processes in Disordered Systems via Variational Autoencoders. Sci Adv (2021) 7(17):1–10. doi:10.1126/sciadv.abd5084
37. Trebbia P, Bonnet N. EELS Elemental Mapping with Unconventional Methods I. Theoretical Basis: Image Analysis with Multivariate Statistics and Entropy Concepts. Ultramicroscopy (1990) 34(3):165–78. doi:10.1016/0304-3991(90)90070-3
38. Bosman M, Watanabe M, Alexander DT, Keast VJ. Mapping Chemical and Bonding Information Using Multivariate Analysis of Electron Energy-Loss Spectrum Images. Ultramicroscopy (2006) 106(11):1024–32. doi:10.1016/j.ultramic.2006.04.016
39. Chen Z, Jiang Y, Shao Y-T, Holtz ME, Odstrčil M, Guizar-Sicairos M, et al. Electron Ptychography Achieves Atomic-Resolution Limits Set by Lattice Vibrations. Science (2021) 372(6544):826–31. doi:10.1126/science.abg2533
40. Vasudevan RK, Ziatdinov M, Sharma V, Oxley MP, Vlcek L, Morozovska AN, et al. Investigating Phase Transitions from Local Crystallographic Analysis Based on Statistical Learning of Atomic Environments in 2D MoS2-ReS2. Appl Phys Rev (2021) 8(1). doi:10.1063/5.0012761
41. Mundet B, Domínguez C, Fowlie J, Gibert M, Triscone J-M, Alexander DTL. Near-Atomic-Scale Mapping of Electronic Phases in Rare Earth Nickelate Superlattices. Nano Lett (2021) 21(6):2436–43. doi:10.1021/acs.nanolett.0c04538
42. Domínguez C, Georgescu AB, Mundet B, Zhang Y, Fowlie J, Mercy A, et al. Length Scales of Interfacial Coupling between Metal and Insulator Phases in Oxides. Nat Mater (2020) 19(11):1182–7. doi:10.1038/s41563-020-0757-x
43. Jutten C, Herault J. Blind Separation of Sources, Part I: An Adaptive Algorithm Based on Neuromimetic Architecture. Signal Process. (1991) 24(1):1–10. doi:10.1016/0165-1684(91)90079-x
44. Bonnet N, Nuzillard D. Independent Component Analysis: A New Possibility for Analysing Series of Electron Energy Loss Spectra. Ultramicroscopy (2005) 102(4):327–37. doi:10.1016/j.ultramic.2004.11.003
45. de la Peña F, Berger M-H, Hochepied J-F, Dynys F, Stephan O, Walls M. Mapping Titanium and Tin Oxide Phases Using EELS: An Application of Independent Component Analysis. Ultramicroscopy (2011) 111(2):169–76. doi:10.1016/j.ultramic.2010.10.001
46. Dobigeon N, Brun N. Spectral Mixture Analysis of EELS Spectrum-Images. Ultramicroscopy (2012) 120:25–34. doi:10.1016/j.ultramic.2012.05.006
47. Shiga M, Tatsumi K, Muto S, Tsuda K, Yamamoto Y, Mori T, et al. Sparse Modeling of EELS and EDX Spectral Imaging Data by Nonnegative Matrix Factorization. Ultramicroscopy (2016) 170:43–59. doi:10.1016/j.ultramic.2016.08.006
48. Spiegelberg J, Rusz J, Thersleff T, Pelckmans K. Analysis of Electron Energy Loss Spectroscopy Data Using Geometric Extraction Methods. Ultramicroscopy (20162017) 174:14–26. doi:10.1016/j.ultramic.2016.12.014
49. Spiegelberg J, Rusz J, Pelckmans K, 175. January (2017). p. 36–45. doi:10.1016/j.ultramic.2016.12.025Tensor Decompositions for the Analysis of Atomic Resolution Electron Energy Loss SpectraUltramicroscopy
50. Spiegelberg J, Rusz J, Leifer K, Thersleff T. The Usage of Data Compression for the Background Estimation of Electron Energy Loss Spectra. Ultramicroscopy (2017) 181:117–22. doi:10.1016/j.ultramic.2017.05.017
51. Torruella P, Estrader M, López-Ortega A, Baró MD, Varela M, Peiró F, et al. Clustering Analysis Strategies for Electron Energy Loss Spectroscopy (EELS). Ultramicroscopy (2018) 185:42–8. doi:10.1016/j.ultramic.2017.11.010
52. Chatzidakis M, Botton GA. Towards Calibration-Invariant Spectroscopy Using Deep Learning. Sci Rep (2019) 9(1):2126–10. doi:10.1038/s41598-019-38482-1
53. Cai RF, Chang MT, Lo SC, Chen CC. Novel Spectral Unmixing Approach for Electron Energy-Loss Spectroscopy. New J Phys (2020) 22(3):0–8. doi:10.1088/1367-2630/ab7a89
54. El Baggari I, Savitzky BH, Admasu AS, Kim J, Cheong S-W, Hovden R, et al. Nature and Evolution of Incommensurate Charge Order in Manganites Visualized with Cryogenic Scanning Transmission Electron Microscopy. Proc Natl Acad Sci USA (2018) 115(7):1445–50. doi:10.1073/pnas.1714901115
55. Yao L, Inkinen S, Van Dijken S. Direct Observation of Oxygen Vacancy-Driven Structural and Resistive Phase Transitions in La2/3Sr1/3MnO3. Nat Commun (2017) 8:14544–9. doi:10.1038/ncomms14544
56. Hart JL, Lang AC, Leff AC, Longo P, Trevor C, Twesten RD, et al. Direct Detection Electron Energy-Loss Spectroscopy: A Method to Push the Limits of Resolution and Sensitivity. Sci Rep (2017) 7(1):8243–14. doi:10.1038/s41598-017-07709-4
57. Cheng S, Pofelski A, Longo P, Twesten RD, Zhu Y, Botton GA, 212. January (2020). p. 112942. doi:10.1016/j.ultramic.2020.112942The Performance Evaluation of Direct Detection Electron Energy-Loss Spectroscopy at 200 kV and 80 kV Accelerating VoltagesUltramicroscopy
58. Ophus C. Four-Dimensional Scanning Transmission Electron Microscopy (4D-STEM): From Scanning Nanodiffraction to Ptychography and beyond. Microsc Microanal (2019) 25:563–82. doi:10.1017/s1431927619000497
59. Das S, Tang YL, Hong Z, Gonçalves MAP, McCarter MR, Klewe C, et al. Observation of Room-Temperature Polar Skyrmions. Nature (2019) 568(7752):368–72. doi:10.1038/s41586-019-1092-8
60. Kalinin SV, Kelley K, Vasudevan RK, Ziatdinov M. Toward Decoding the Relationship between Domain Structure and Functionality in Ferroelectrics via Hidden Latent Variables. ACS Appl Mater Inter (2021) 13(1):1693–703. doi:10.1021/acsami.0c15085
61. Spurgeon SR, Ophus C, Jones L, Petford-Long A, Kalinin SV, Olszta MJ, et al. Towards Data-Driven Next-Generation Transmission Electron Microscopy. Nat Mater (2021) 20(3):274–9. doi:10.1038/s41563-020-00833-z
62.NCCR Marvel (2021). Available at: https://nccr-marvel.ch/project (Accessed Jun 04, 2021).
63. Jain A, Ong SP, Hautier G, Chen W, Jain A, Richards WD, et al. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater (2013) 1(1). doi:10.1063/1.4812323
64. Kirklin S, Saal JE, Meredig B, Thompson A, Doak JW, Aykol M, et al. ,The Open Quantum Materials Database (OQMD): Assessing the Accuracy of DFT Formation Energies. Npj Comput Mater (2015) 1. doi:10.1038/npjcompumats.2015.10
65. Saal JE, Kirklin S, Aykol M, Meredig B, Wolverton C. Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD). Jom (2013) 65(11):1501–9. doi:10.1007/s11837-013-0755-4
66. Vergniory MG, Elcoro L, Felser C, Regnault N, Bernevig BA, Wang Z. A Complete Catalogue of High-Quality Topological Materials. Nature (2019) 566(7745):480–5. doi:10.1038/s41586-019-0954-4
67. Nist . National Institute of Standards and Technology, “NIST Inogranic Crystal Structure Database (2021). NIST Standard Reference Database Number 3.” [Online]. Available at: https://icsd.nist.gov/ (Accessed 04Jun, 2021).
68. Aroyo MI, Perez-Mato JM, Capillas C, Kroumova E, Ivantchev S, Madariaga G, et al. Bilbao Crystallographic Server: I. Databases and Crystallographic Computing Programs. Z für Krist. - Cryst. Mater. (2006) 221(1):15–27. doi:10.1524/zkri.2006.221.1.15
69. Aroyo MI, Kirov A, Capillas C, Perez-Mato JM, Wondratschek H. Bilbao Crystallographic Server. II. Representations of Crystallographic point Groups and Space Groups. Acta Cryst Sect A (2006) 62:115–28. doi:10.1107/s0108767305040286
70. Aroyo MI, Perez-Mato JM, Orobengoa D, Tasci E, De La Flor G, Kirov A. Crystallography Online: Bilbao Crystallographic Server. Bulg Chem Commun (2011) 43(2):183–97.
71.Springer Materials (2021). Available at: https://materials.springer.com/ (Accessed Jun 06, 2021).
72. Olivetti EA, Cole JM, Kim E, Kononova O, Ceder G, Han TY-J, et al. Data-driven Materials Research Enabled by Natural Language Processing and Information Extraction. Appl Phys Rev (2020) 7(4):041317. doi:10.1063/5.0021106
73. Georgescu AB, Ren P, Toland AR, Olivetti EA, Wagner N, Rondinelli JM. Thermally-Driven Metal-Insulator Transition Compound Classification Dataset. [Online]. Available at: https://mtd.mccormick.northwestern.edu/mit-classification-dataset/ (Accessed Jun 04, 2021).
74. Matsuhira K, Hinatsu Y, Sekine C, Togashi T, Maki H, Shirotani I, et al. Metal-Insulator Transition of Filled Skutterudite Compound SmRu4P12. J Phys Soc Jpn (2002) 71(Suppl. l):237–9. doi:10.1143/jpsjs.71s.237
75. Lee CH, Matsuhata H, Yamamoto A, Ohta T, Takazawa H, Ueno K, et al. Structural Phase Transition Accompanied by Metal-Insulator Transition in PrRu4 P12. J Phys Condens Matter (2001) 13(2), L45–L48. doi:10.1088/0953-8984/13/2/102
76. Mit . MIT Classifier (2021). Available at: https://tinyurl.com/mit-classifiers [Accessed Jun 06, 2021).
77. Wagner N, Puggioni D, Rondinelli JM. Learning from Correlations Based on Local Structure: Rare-Earth Nickelates Revisited. J Chem Inf Model (2018) 58(12):2491–501. doi:10.1021/acs.jcim.8b00411
78. Shahriari B, Swersky K, Wang Z, Adams RP, De Freitas N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc IEEE (2016) 104(1):148–75. doi:10.1109/jproc.2015.2494218
79. Greenhill S, Rana S, Gupta S, Vellanki P, Venkatesh S. Bayesian Optimization for Adaptive Experimental Design: A Review. IEEE Access (2020) 8:13937–48. doi:10.1109/access.2020.2966228
80. Frazier PI, Wang J. Bayesian Optimization for Materials Design. In: T Lookman, F. J Alexander, and K Rajan, editors. Information Science for Materials Discovery and Design, 225. Cham: Springer International Publishing (2016). p. 45–75. doi:10.1007/978-3-319-23871-5_3
81. Wang Y, Iyer A, Chen W, Rondinelli JM. Featureless Adaptive Optimization Accelerates Functional Electronic Materials Design. Appl Phys Rev (2020) 7(4). doi:10.1063/5.0018811
82. Wakabayashi YK, Otsuka T, Krockenberger Y, Sawada H, Taniyasu Y, Yamamoto H. Machine-learning-assisted Thin-Film Growth: Bayesian Optimization in Molecular Beam Epitaxy of SrRuO3 Thin Films. APL Mater (2019) 7(10). doi:10.1063/1.5123019
83. Kim E, Jensen Z, van Grootel A, Huang K, Staib M, Mysore S, et al. Inorganic Materials Synthesis Planning with Literature-Trained Neural Networks. J Chem Inf Model (2020) 60(3):1194–201. doi:10.1021/acs.jcim.9b00995
84. Kim E, Huang K, Saunders A, McCallum A, Ceder G, Olivetti E. Materials Synthesis Insights from Scientific Literature via Text Extraction and Machine Learning. Chem Mater (2017) 29(21):9436–44. doi:10.1021/acs.chemmater.7b03500
85. Mahbub R, Huang K, Jensen Z, Hood ZD, Rupp JLM, Olivetti EA. Text Mining for Processing Conditions of Solid-State Battery Electrolytes. Electrochemistry Commun (2020) 121:106860. doi:10.1016/j.elecom.2020.106860
86. Yunchao X, Zhang C, Deng H, Zheng B, Su J-W, Shutt K, et al. Accelerate Synthesis of Metal–Organic Frameworks by a Robotic Platform and Bayesian Optimization. ACS Appl Mater Inter (2021) 13(45):53485–91.
87. Nisbet ML, Pendleton IM, Nolis GM, Griffith KJ, Schrier J, Cabana J, et al. Machine-Learning-Assisted Synthesis of Polar Racemates. J Am Chem Soc (2020) 142(16):7555–66. doi:10.1021/jacs.0c01239
88. Wang Y, Wagner N, Rondinelli JM. Symbolic Regression in Materials Science. MRS Commun (2019) 9(3): 793–805. doi:10.1557/mrc.2019.85
89. Davies M, Srinivasa N, Lin T-H, Chinya G, Cao Y, Choday SH, et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro (2018) 38(1):82–99. doi:10.1109/mm.2018.112130359
90. Merolla PA, Arthur JV, Alvarez-Icaza R, Cassidy AS, Sawada J, Akopyan F, et al. A Million Spiking-Neuron Integrated Circuit with a Scalable Communication Network and Interface. Science (2014) 345(6197):668–73. doi:10.1126/science.1254642
91. Indiveri G, Linares-Barranco B, Hamilton TJ, Schaik Av, Etienne-Cummings R, Delbruck T, et al. Neuromorphic Silicon Neuron Circuits. Front Neurosci (2011) 5. doi:10.3389/fnins.2011.00118
92. del Valle J, Ramírez JG, Rozenberg MJ, Schuller IK. Challenges in Materials and Devices for Resistive-Switching-Based Neuromorphic Computing. J Appl Phys (2018) 124(21):211101. doi:10.1063/1.5047800
93. Romera M, Talatchian P, Tsunegi S, Abreu Araujo F, Cros V, Bortolotti P, et al. Vowel Recognition with Four Coupled Spin-Torque Nano-Oscillators. Nature (2018) 563(7730):230–4. doi:10.1038/s41586-018-0632-y
94. Feldmann J, Youngblood N, Wright CD, Bhaskaran H, Pernice WHP. All-optical Spiking Neurosynaptic Networks with Self-Learning Capabilities. Nature (2019) 569(7755):208–14. doi:10.1038/s41586-019-1157-8
95. Yang JJ, Strukov DB, Stewart DR. Memristive Devices for Computing. Nat Nanotech (2013) 8(1):13–24. doi:10.1038/nnano.2012.240
96. Babich D, Tranchant J, Adda C, Corraze B, Besland M. P, Warnicke P, et al. Lattice Contraction Induced by Resistive Switching in Chromium-Doped V2O3: A Hallmark of Mott Physics. Available at: https://arxiv.org/abs/2105.05093 (2020).
97. Cario L, Vaju C, Corraze B, Guiot V, Janod E. Electric-field-induced Resistive Switching in a Family of mott Insulators: Towards a New Class of RRAM Memories. Adv Mater (2010) 22(45):5193–7. doi:10.1002/adma.201002521
98. Shi J, Ha SD, Zhou Y, Schoofs F, Ramanathan S. A Correlated Nickelate Synaptic Transistor. Nat Commun (2013) 4(1):2676. doi:10.1038/ncomms3676
99. Shi J, Zhou Y, Ramanathan S. Colossal Resistance Switching and Band gap Modulation in a Perovskite Nickelate by Electron Doping. Nat Commun (2014) 5(1):4860. doi:10.1038/ncomms5860
100. Wang L, Zhang Q, Chang L, You L, He X, Jin K, et al. Electrochemically Driven Giant Resistive Switching in Perovskite Nickelates Heterostructures. Adv Electron Mater (2017) 3(10):1700321. doi:10.1002/aelm.201700321
101. Zhang H-T, Park TJ, Zaluzhnyy IA, Wang Q, Wadekar SN, Manna S, et al. Perovskite Neural Trees. Nat Commun (2020) 11(1):2245. doi:10.1038/s41467-020-16105-y
102. Gonzalez‐Rosillo JC, et al. Nanoscale Correlations between Metal–Insulator Transition and Resistive Switching Effect in Metallic Perovskite Oxides. Small (2020) 16(23).
103. del Valle J, et al. Dynamics of the Electrically Induced Insulator-To-Metal Transition in Rare-Earth Nickelates. Phys Rev B (2021) 104(16):1–7. doi:10.1103/physrevb.104.165141
104. Shukla N, Joshi T, Dasgupta S, Borisov P, Lederman D, Datta S. Electrically Induced Insulator to Metal Transition in Epitaxial SmNiO3 Thin Films. Appl Phys Lett (2014) 105(1):012108. doi:10.1063/1.4890329
105. Huang H, Luo Z, Yang Y, Yun Y, Yang M, Meng D, et al. DC Current Induced Metal-Insulator Transition in Epitaxial Sm0.6Nd0.4NiO3/LaAlO3thin Film. AIP Adv (2014) 4(5):057102. doi:10.1063/1.4874642
106. del Valle J, Salev P, Tesler F, Vargas NM, Kalcheim Y, Wang P, et al. Subthreshold Firing in Mott Nanodevices. Nature (2019) 569(7756):388–92. doi:10.1038/s41586-019-1159-6
107. Kalcheim Y, Camjayi A, del Valle J, Salev P, Rozenberg M, Schuller IK. Non-thermal Resistive Switching in Mott Insulator Nanowires. Nat Commun (2020) 11(1):2985. doi:10.1038/s41467-020-16752-1
108. Kumar S, Pickett MD, Strachan JP, Gibson G, Nishi Y, Williams RS. Local Temperature Redistribution and Structural Transition during Joule-Heating-Driven Conductance Switching in VO2. Adv Mater (2013) 25(42):6128–32. doi:10.1002/adma.201302046
109. Pickett MD, Medeiros-Ribeiro G, Williams RS. A Scalable Neuristor Built with Mott Memristors. Nat Mater (2013) 12(2):114–7. doi:10.1038/nmat3510
110. Yi W, Tsang KK, Lam SK, Bai X, Crowell JA, Flores EA. Biological Plausibility and Stochasticity in Scalable VO2 Active Memristor Neurons. Nat Commun (2018) 9(1):4661. doi:10.1038/s41467-018-07052-w
Keywords: machine learning, rare-earth nickelates, artificial intelligence, resistive switching, neuromorphic computing, metal-insulator transitions, scanning transmission elctron microscopy
Citation: Fowlie J, Georgescu AB, Mundet B, del Valle J and Tückmantel P (2021) Machines for Materials and Materials for Machines: Metal-Insulator Transitions and Artificial Intelligence. Front. Phys. 9:725853. doi: 10.3389/fphy.2021.725853
Received: 15 June 2021; Accepted: 29 November 2021;
Published: 15 December 2021.
Edited by:
Le Wang, Pacific Northwest National Laboratory (DOE), United StatesReviewed by:
Daniele Preziosi, UMR7504 Institut de physique et chimie des matériaux de Strasbourg, FranceCopyright © 2021 Fowlie, Georgescu, Mundet, del Valle and Tückmantel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jennifer Fowlie, amZvd2xpZUBzdGFuZm9yZC5jb20=
†Present address:Jennifer Fowlie,Department of Applied Physics, Stanford University, Stanford, California, United States
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.