- School of Optoelectronic Engineering and Instrumentation Science, Dalian University of Technology, Dalian, China
Cell migration through extracellular matrices is critical to many physiological processes, such as tissue development, immunological response and cancer metastasis. Previous models including persistent random walk (PRW) and Lévy walk only explain the migratory dynamics of some cell types in a homogeneous environment. Recently, it was discovered that the intracellular actin flow can robustly ensure a universal coupling between cell migratory speed and persistence for a variety of cell types migrating in the in vitro assays and live tissues. However, effects of the correlation between speed and persistence on the macroscopic cell migration dynamics and patterns in complex environments are largely unknown. In this study, we developed a Monte Carlo random walk simulation to investigate the motility, the search ability and the search efficiency of a cell moving in both homogeneous and porous environments. The cell is simplified as a dimensionless particle, moving according to PRW, Lévy walk, random walk with linear speed-persistence correlation (linear RWSP) and random walk with nonlinear speed-persistence correlation (nonlinear RWSP). The coarse-grained analysis showed that the nonlinear RWSP achieved the largest motility in both homogeneous and porous environments. When a particle searches for targets, the nonlinear coupling of speed and persistence improves the search ability (i.e. find more targets in a fixed time period), but sacrifices the search efficiency (i.e. find less targets per unit distance). Moreover, both the convex and concave pores restrict particle motion, especially for the nonlinear RWSP and Lévy walk. Overall, our results demonstrate that the nonlinear correlation of speed and persistence has the potential to enhance the motility and searching properties in complex environments, and could serve as a starting point for more detailed studies of active particles in biological, engineering and social science fields.
1 Introduction
Eukaryotic cell migration is a crucial process for the normal development and maintenance of organs and tissues. In a wide range of human diseases, such as tumor metastasis, immunological responses and wound healing, cell migration is activated and plays a key role [1–3]. For example, the migratory trajectories and patterns of malignant tumor cells influence the distribution of the secondary tumor, leading to the organotropism phenomenon [4]. Therefore, understanding the cell migration dynamics and patterns could provide valuable insights about the physiological functions and disease stages.
To access the migration dynamics, cell migrating trajectories in the in vitro matrices and live tissues are recorded using live-cell imaging or multi-photon microscopy [5,6]. Early works extracted cell speed
However, after recording and analyzing trajectories of more cell types, results suggested the PRW and Lévy walk are not general rules for cell migration. For example, Wu et al. [13] showed that the profiles of the moving speed and direction can be anisotropic and self-correlated for fibrosarcoma cells migrating in 2D and 3D collagen-based matrices. Based on a vast amount of migrating trajectories of many cells in various environments collected in the First World Cell Race [16], Maiuri et al. [17] for the first time proposed a universal governing mechanism of cell migration. Specifically, they observed that there is a general trend that faster cells migrate more straight than slower cells, because a large migratory speed leads to the increasing of actin flows and the asymmetry of the concentration profile of polarity cues. Thereby, the cell polarization is stabilized and cell persistence is consequently increased at a large migrating speed. As the actin flow represents a very conserved aspect of cell locomotion, the coupling between cell speed and persistence exists over most cell types migrating via both mesenchymal mode (strong cell-matrix adhesion and elongated cell morphology) and ameboid mode (minimal cell-matrix adhesion and rounded cell morphology). As of yet, the molecular mechanisms that regulate the retrograde actin flows and generate forces to drive the migration have been studied extensively [17–19]. However, effects of the universal coupling between speed and persistence on the macroscopic movement patterns and its functional advantages are still largely unknown.
Moreover, the in vivo extracellular microenvironment contains confining pores and channel-like tracks such as the interstitial space between muscle and nerve fibers and the vasculature in the organs [3,20]. These environmental topographies significantly alter cell motility and the optimal moving and searching strategies [14,21–23]. For example, Volpe et al. [24] studied the Lévy walks in the porous media through a Monte Carlo simulation. They found that the concave porous structure alters the optimal moving strategy toward less ballistic and more Brownian strategies. Wondergem et al. [25] measured the trajectories of cells migrating among asymmetrically placed micropillars, and showed that a directed topotactic drift can be generated by the pillar field. Schakenraad et al. [26] further used a PRW model with reflected obstacle boundaries to illustrate how the large-scale topotaxis emerges in the pillar field. Thus, we hypothesize that cells migrating with correlated speed and persistence is also influenced by the environmental topographies. And whether there is an optimal moving strategy among PRW, Lévy walk and random walks with correlated speed and persistence that achieves large cell motility in different environments needs to be further investigated.
To explore the cell locomotion behaviors in complex environmental topographies, in this study we developed a Monte Carlo random walk model to describe four types of migratory strategies, including the PRW, Lévy walk, random walk with linearly correlated speed and persistence (linear RWSP), and random walk with nonlinearly correlated speed and persistence (nonlinear RWSP). In particular, the cell is simplified as a dimensionless particle moving and performing a blind search in a homogeneous environment, in concave and convex porous environments, respectively. The particle motility, the ability and efficiency of searching for targets influenced by the environmental topographies are calculated. We showed that Lévy walk and nonlinear RWSP maintain the superdiffusive motion at long times, while PRW and linear RWSP lead to the normal diffusion
2 Methods
2.1 The Model
We developed a Monte Carlo based simulation pipeline to describe a cell, which is simplified as a dimensionless particle, moving in a 2D space according to the four strategies, PRW, Lévy walk, linear RWSP and nonlinear RWSP. The coarse grained model ignores the complicated intracellular dynamics, the driving force of the migration as well as the chemotaxis behavior. It only considers core governing physics of a random walker to reduce the computational cost, such that the macroscopic cell motility and patterns over a long time period can be studied based on the model.
Specifically, the 2D random motion of the particle can be described as
where
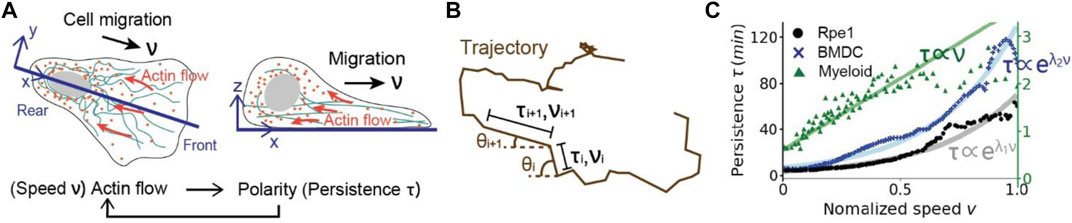
FIGURE 1. The correlation between migratory speed
The Monte Carlo simulation pipeline is shown in Figure 2. At the beginning of a straight motion, the particle speed, persistence and moving direction are chosen. In the following each time step
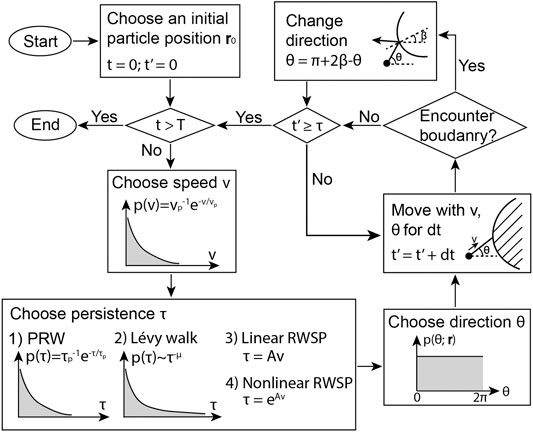
FIGURE 2. The pipeline of the Monte Carlo simulation of a particle performing PRW, Lévy walk, linear RWSP and nonlinear RWSP.
2.2 Quantification of the Dynamics
The cell migration dynamics is characterized by its motility, and its ability and efficiency to reach a targeting position or to find a target such as a pathogen. The motility is mainly described by the MSDs and the distributions over time. The MSDs are calculated as
Where
To quantify the ability and efficiency for a cell to reach targeting positions or to find targets, the average numbers of targets found in a fixed time period and per unit migratory distance are calculated. Specifically, targets with density
2.3 Simulation Method and Model Parameters
In the simulation, a
To generate a porous environment,
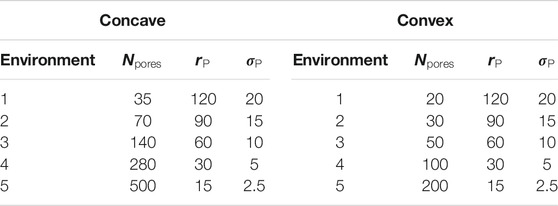
TABLE 1. Parameters of the circular pores of the concave and convex porous medium.
3 Results
3.1 Dynamics in a Homogeneous Environment
In a homogeneous environment, the directional preference is isotropic and the speed follows an exponentially decaying probability distribution. As expected, the power-law distribution of the persistence in the Lévy walk (
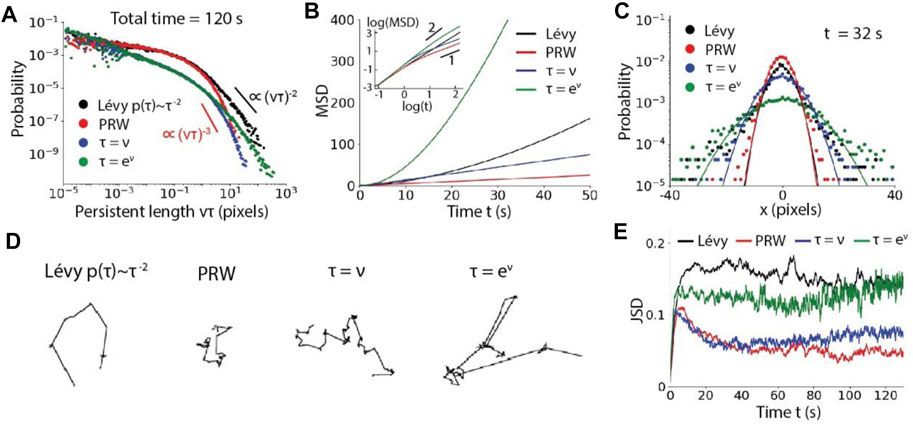
FIGURE 4. Particle motility influenced by the moving strategies in a homogeneous environment. (A), Distributions of persistent length
What is the best moving strategy for a cell to search for randomly located pathogens or to reach targeting tissue spots? It is long believed that Lévy walk reduces oversampling and is more efficient in finding targets than PRW when targets are sparse [33,34]. But whether the correlation between speed and persistence can further improve searching for targets is not known. Thus, we compared the ability and efficiency of searching for targets among PRW, Lévy walk, linear RWSP and nonlinear RWSP (Figure 5A). The search ability is represented by the average number of targets found by the particle in a fixed time period, denoted as
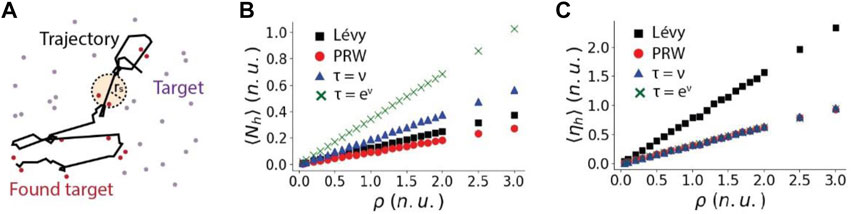
FIGURE 5. The search ability
As suggested by the experimental results in Figure 1C, the coefficient
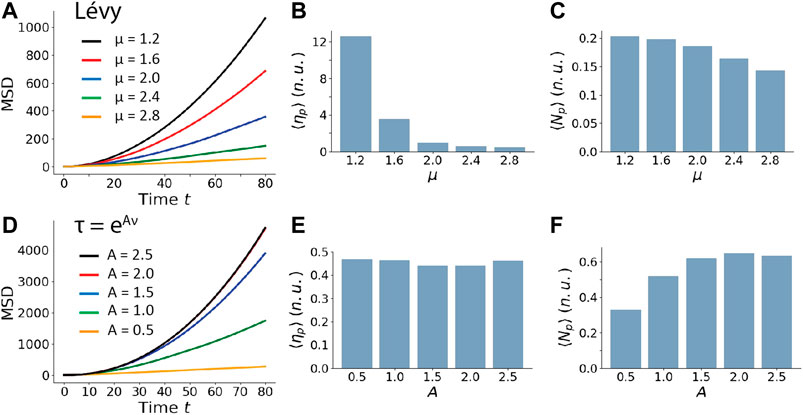
FIGURE 6. The influence of model parameters of Lévy walk and nonlinear RWSP on the particle motility, searching ability and efficiency in a homogeneous medium. For a particle performing the Lévy walk, (A), the MSD, (B), the search efficiency
3.2 Dynamics in a Concave Porous Environment
To understand how the complexity of the environment influences the motility, the search ability and the search efficiency of a particle moving with different strategies, we then consider a particle in a heterogeneous topography. Specifically, the 2D space is now a concave porous medium composed of uniformly distributed circular interconnected pores with mean radius

FIGURE 7. Particle mobility influenced by the moving strategies in a concave porous environment. (A), Example trajectories of Lévy walk, PRW, linear RWSP (
Next, we investigated the search ability and efficiency of a particle influenced by the concave porous topographies. Specifically, numbers of targets found by the particle in 150 s and per unit distance are calculated over different pore sizes and target densities. Figure 8A shows the representative trajectories of the particles in small-size, intermediate-size and large-size porous media. As expected, the confinement is significant when the pore size is small for the Lévy walk and nonlinear RWSP. Therefore, the searching ability
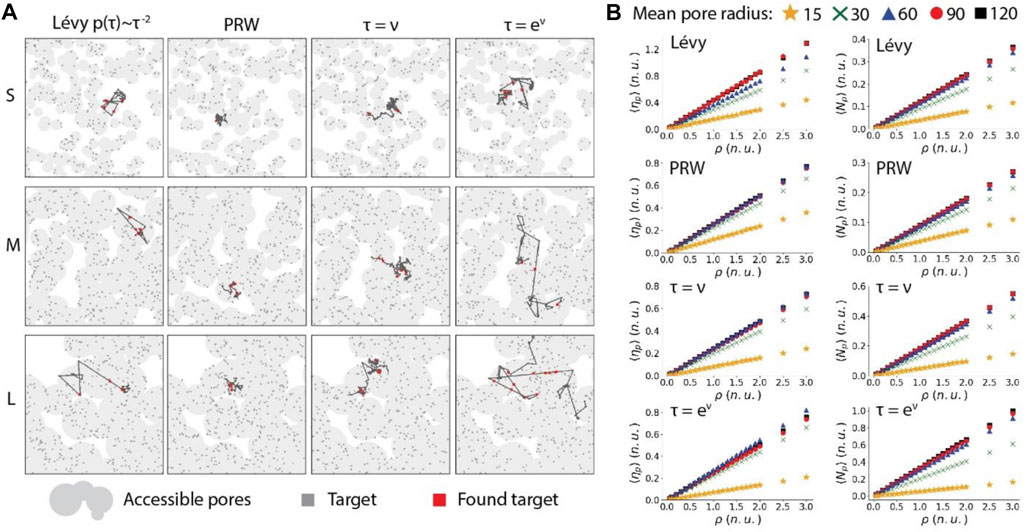
FIGURE 8. The search ability and efficiency of a particle influenced by different moving strategies in the concave porous environments. (A), Example trajectories of Lévy walk, PRW, linear RWSP
3.3 Dynamics in a convex porous environment
Lastly, we considered a porous medium with convex topographies. In the convex porous environment as shown in Figure 9A, a particle moves in the white space and is reflected by the gray circular obstacles, which are randomly and uniformly distributed in the space. The density of circular obstacles is
FIGURE 9. Particle motility influenced by the moving strategies in a convex porous environment. (A), Example trajectories of Lévy walk, PRW, linear RWSP and nonlinear RWSP reflected by the circular obstacles. (B), The distribution of the persistent length, whose tails are approximated by power laws with cutoff at large values. (C), MSD curves over time. The particle motion is superdiffusive at short times and subdiffusive at long times.
In the convex porous media, examples of a particle searching for targets with small, intermediate and large obstacle sizes are shown in Figure 10A. Because the particle is probable to be reflected back and forth within the narrow space between several obstacles, the area that the searcher can cover in a fixed time period is reduced (Figure 10A). The results show that the size of pores has a small influence on the searching ability of the particle, regardless of the moving strategies and the target densities (Figure 10B). Similar to the dynamics in the homogeneous and concave porous environments, the nonlinear and linear RWSP can find relatively larger numbers of targets than the Lévy walk and PRW. Interestingly, we found that the search efficiency is the largest when the circular obstacles have the largest mean radius of 120 pixels for all the four types of moving strategies (Figure 10B). For the other obstacle sizes (i.e. their mean radiuses range from 15 pixels to 90 pixels), the search efficiencies of the Lévy walk and the PRW are not influenced by the obstacle size. And the search efficiencies for the linear and nonlinear RWSP slightly decrease when the obstacle size increases (Figure 10B). The lowest search efficiency in the intermediate-size porous environment is caused by many narrow channel-like spaces that trap the particle inside. In general, influenced by the large-size obstacles, Lévy walk has the highest search efficiency. And among the intermediate-size and small-size obstacles, the search efficiencies of the nonlinear RWSP and Lévy walk are relatively large. In addition, both the search ability and efficiency increases linearly over the target densities (Figure 9B). Overall, in the convex topographies, the nonlinear RWSP also show advantageous properties among the four moving strategies.
FIGURE 10. The search efficiency of a particle influenced by the moving strategies in the convex porous environments. (A), Examples of a particle moving according to the Lévy walk, PRW, linear RWSP and nonlinear RWSP in the porous media and searching for targets. S represents small pore size (
4 Discussion
In this study, we developed a coarse-grained random walk model to study the dynamics of a cell, which is represented by a dimensionless particle, moving in the homogeneous and porous media with correlated speed and persistence. The motility (i.e. MSDs and distributions), the search ability (i.e. the number of targets found in a fixed time period) and the search efficiency (i.e. the number of targets found per unit distance) are calculated and compared among the four moving strategies, including the Lévy walk, PRW, linear RWSP and nonlinear RWSP. We show that when the speed and persistence are exponentially correlated (nonlinear RWSP), the motility of the particle is the largest in both homogeneous and porous environments. Compared with the Lévy walk which is believed to be an efficient searching method in many studies [28,33], our results demonstrate that the nonlinear RWSP has a larger search ability but sacrifices the search efficiency. Moreover, the concave and convex porous topographies modify the dynamics of the Lévy walk and nonlinear RWSP significantly by interrupting long straight movements and transiently trapping the particles within the narrow pores or channel-like spaces. Our model and analysis provide fundamental evidences and insights about how the correlation between cell speed and persistence improves the cell locomotion behaviors. Our model has the potential to be further used to understand the influence of disease-impaired speed and persistence on cell migration.
There were previous models that describe cell migration based on the changing of cell configuration or the protrusion force, resistance force and friction experienced by the cell [34–37]. For example, the cellular potts model considers the adhesion to the matrix and the resistance to the volume change, and predicts the migration by minimizing the energy of a particular cell configuration [34]. Yang et al. includes the protrusion force generated by the filament network, and modeled the chemotaxis behavior when the chemoacttractant stimulation changes the number of filaments and modifies the protrusion force [35]. To uncover more realistic migratory dynamics and improve the prediction power and accuracy, the effects of cell configuration and the mechanical forces acting on the cell can be further included in the proposed model.
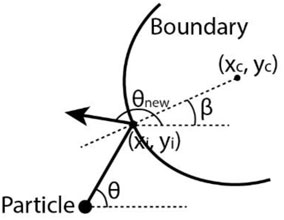
Several aspects in our model could influence the moving dynamics of the particle. First, in this work, reflective boundary conditions of the porous structures are implemented. Specifically, when the particle reaches the porous boundaries, it will immediately change the moving direction and move away from the boundary. This scenario is discovered in biological and artificial microswimmers such as Janus particles [38] and elementary robots [39]. The interactions between a cell and a wall or other repulsive sources can be more complicated. For example, a cell can migrate along the wall boundaries instead of migrating away [40]. Sometimes, the cell can penetrate the wall barriers. For example, the circulating tumor cells can actively attach to the vessel wall and extravasate to the surrounding matrix [41]. Therefore, other physiological-relevant boundary conditions need to be considered in the future studies, which could potentially influence the optimality of the random walks with nonlinearly correlated speed and persistence. Second, in reality, the moving and searching time is generally finite. Therefore, the particle is allowed to move in the environment for a finite simulation time in this study. However, it would be interesting to investigate particle motion in the environment in the limit of infinite times from a fundamental perspective. Other important statistics such as the survival probability and first passage time can be understood accordingly. Lastly, other moving strategies, such as the intermittent random walk and correlated random walk, have been observed in biological and ecological systems [42–44]. For example, in the intermittent random walk, a particle is assumed to randomly switch between Brownian diffusion and ballistic motion [42]. Furthermore, a particle can also perform a mixture of many types of motions, such as a mixture of Lévy walk, PRW and nonlinear RWSP. It would also be interesting to further investigate if the combination of several moving strategies is advantageous in complex environmental topographies.
The model and results are relevant for all random moving and searching problems at various length and time scales, such as the intracellular protein diffusion, bacteria spreading, animal foraging and human travelling. As suggested by our results that the correlation between speed and persistence could potentially improve the motility and searching properties, these results could inspire studies of the novel migratory statistics and rules in many other science and engineering fields.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary files, further inquiries can be directed to the corresponding author/s.
Author Contributions
KC: Conceptualization, Methodology, Software, Validation, Investigation, Formal analysis, Data curation, Writing – original draft, Writing – review & editing; K-RQ: Conceptualization, Methodology, Writing–review & editing, Supervision, Project administration, Funding acquisition, Resources, Investigation.
Funding
This research is supported by the Fundamental Research Funds for the Central Universities in China (DUT21RC(3)044 and DUT20YG113).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.719293/full#supplementary-material
References
1. Krummel MF, Bartumeus F, Gérard A “T Cell Migration, Search Strategies and Mechanisms”. Nat Rev Immunol 16, no. 3 (2016): 193, 201. doi:10.1038/nri.2015.16
2. Yamada KM, Sixt M. "Mechanisms of 3D Cell Migration." Nat Rev Mol Cel Biol 20, no. 12 (2019): 738–52. doi:10.1038/s41580-019-0172-9
3. Paul CD, Mistriotis P, Konstantopoulos K. "Cancer Cell Motility: Lessons from Migration in Confined Spaces." Nat Rev Cancer 17, no. 2 (2017): 131, 40. doi:10.1038/nrc.2016.123
4. Lo HC, Zhang XH-F. "EMT in Metastasis: Finding the Right Balance." Develop Cel 45, no. 6 (2018): 663–5. doi:10.1016/j.devcel.2018.05.033
5. Hackl MJ, Burford JL, Villanueva K, Lam L, Suszták K, Schermer B, et al. "Tracking the Fate of Glomerular Epithelial Cells In Vivo Using Serial Multiphoton Imaging in New Mouse Models with Fluorescent Lineage Tags." Nat Med 19, no. 12 (2013): 1661–6. doi:10.1038/nm.3405
6. Wu P-H, Giri A, Wirtz D. "Statistical Analysis of Cell Migration in 3D Using the Anisotropic Persistent Random Walk Model." Nat Protoc 10, no. 3 (2015): 517–27. doi:10.1038/nprot.2015.030
7. Gorelik R, Gautreau A. "Quantitative and Unbiased Analysis of Directional Persistence in Cell Migration." Nat Protoc 9, no. 8 (2014): 1931, 43. doi:10.1038/nprot.2014.131
8. Campos D, Méndez V, Llopis I. "Persistent Random Motion: Uncovering Cell Migration Dynamics." J Theor Biol 267, no. 4 (2010): 526–34. doi:10.1016/j.jtbi.2010.09.022
9. Selmeczi D, Li L, Pedersen LII, Nrrelykke SF, Hagedorn PH, Mosler S, et al. “Cell Motility as Random Motion: A Review”. Eur Phys J Spec Top 157, no. 1 (2008): 1–15. doi:10.1140/epjst/e2008-00626-x
10. Stokes CL, Lauffenburger DA, Williams SK. "Migration of Individual Microvessel Endothelial Cells: Stochastic Model and Parameter Measurement." J Cel Sci 99, no. 2 (1991): 419–30. doi:10.1242/jcs.99.2.419
11. Harris TH, Banigan EJ, Christian DA, Konradt C, Elia D, Tait W, et al. “Generalized Lévy Walks and the Role of Chemokines in Migration of Effector CD8+ T Cells.” Nature 486, no. 7404 (2012): 545-548. doi:10.1038/nature11098
12. Huda S, Weigelin B, Wolf K, Tretiakov KV, Polev K, Gary W, et al. "Lévy-like Movement Patterns of Metastatic Cancer Cells Revealed in Microfabricated Systems and Implicated In Vivo." Nat Commun 9, no. 1 (2018): 1–11. doi:10.1038/s41467-018-06563-w
13. Wu P-H, Giri A, Sun SX, Wirtz D. "Three-dimensional Cell Migration Does Not Follow a Random Walk." Proc Natl Acad Sci 111, no. 11 (2014): 3949–54. doi:10.1073/pnas.1318967111
14. Baumgart F, Schneider M, Schütz GJ. "How T Cells Do the “Search for the Needle in the Haystack." Front Phys 7 (2019): 11. doi:10.3389/fphy.2019.00011
15. Banigan EJ, Harris TH, Christian DA, Hunter CA, Liu AJ. "Heterogeneous CD8+ T Cell Migration in the Lymph Node in the Absence of Inflammation Revealed by Quantitative Migration Analysis." Plos Comput Biol 11, no. 2 (2015): doi:e1004058 doi:10.1371/journal.pcbi.1004058
16. Maiuri P, Terriac E, Paul-Gilloteaux P, Vignaud T, McNally K, Onuffer J, et al. "The First World Cell Race." Curr Biol 22, no. 17 (2012): R673–R675. doi:10.1016/j.cub.2012.07.052
17. Maiuri P, Rupprecht J-F, Wieser S, Ruprecht V, Bénichou O, Carpi N, et al. "Actin Flows Mediate a Universal Coupling between Cell Speed and Cell Persistence." Cell 161, no. 2 (2015): 374–86. doi:10.1016/j.cell.2015.01.056
18. Petrie RJ, Doyle AD, Yamada KM. "Random versus Directionally Persistent Cell Migration." Nat Rev Mol Cel Biol 10, no. 8 (2009): 538–49. doi:10.1038/nrm2729
19. Leithner A, Eichner A, Müller J, Reversat A, Brown M, Schwarz J, et al. "Diversified Actin Protrusions Promote Environmental Exploration but Are Dispensable for Locomotion of Leukocytes." Nat Cel Biol 18, no. 11 (2016): 1253–9. doi:10.1038/ncb3426
20. Charras G, Sahai E. "Physical Influences of the Extracellular Environment on Cell Migration." Nat Rev Mol Cel Biol 15, no. 12 (2014): 813–24. doi:10.1038/nrm3897
21. Park J, Kim D-H, Levchenko A. "Topotaxis: a New Mechanism of Directed Cell Migration in Topographic ECM Gradients." Biophysical J 114, no. 6 (2018): 1257–63. doi:10.1016/j.bpj.2017.11.3813
22. Reversat A, Gaertner F, Merrin J, Stopp J, Tasciyan S, Aguilera J, et al. "Cellular Locomotion Using Environmental Topography." Nature, 582 (2020): 582–585. doi:10.1038/s41586-020-2283-z
23. Lee H-pyo, Alisafaei F, Adebawale K, Chang J, Shenoy VB, Chaudhuri O. "The Nuclear Piston Activates Mechanosensitive Ion Channels to Generate Cell Migration Paths in Confining Microenvironments." Sci Adv 7, no. 2 (2021): doi:eabd4058 doi:10.1126/sciadv.abd4058
24. Volpe G, Volpe G. "The Topography of the Environment Alters the Optimal Search Strategy for Active Particles." Proc Natl Acad Sci USA 114, no. 43 (2017): 11350–5. doi:10.1073/pnas.1711371114
25. Joeri AJ W, Mytiliniou M, Falko CHde W, Reuvers TGA, Holcman D, Heinrich D. "Chemotaxis and Topotaxis Add Vectorially for Amoeboid Cell Migration." bioRxiv (2019): doi:735779 doi:10.1101/735779
26. Schakenraad K, Ravazzano L, Sarkar N, Joeri AJ W, Merks RMH, Giomi L. "Topotaxis of Active Brownian Particles." Phys Rev E 101, no. 3 (2020): doi:032602 doi:10.1103/physreve.101.032602
27. Masoliver J, Lindenberg K, Weiss GH, Weiss . "A Continuous-Time Generalization of the Persistent Random Walk." Physica A: Stat Mech its Appl 157, no. 2 (1989): 891–898. doi:10.1016/0378-4371(89)90071-x
28. Zaburdaev V, Denisov S, Klafter J. Lévy Walks. Rev Mod Phys 87, no. 2 (2015): 483, 530. doi:10.1103/revmodphys.87.483
29. Volpe G, Gigan S, Volpe G. "Simulation of the Active Brownian Motion of a Microswimmer." Am J Phys 82, no. 7 (2014): 659–664. doi:10.1119/1.4870398
30. Jacobs K. "Stochastic Processes for Physicists: Understanding Noisy Systems". Cambridge, UK, Cambridge University Press, 2010. doi:10.1017/cbo9780511815980
31. Oliveira FA, Ferreira R, Lapas LC, Vainstein MH. "Anomalous Diffusion: A Basic Mechanism for the Evolution of Inhomogeneous Systems." Front Phys 7 (2019): 18. doi:10.3389/fphy.2019.00018
32. Fuglede B, Topsoe F. "Jensen-Shannon Divergence and Hilbert Space Embedding." In Proceedings of the 2004 International Symposium onInformation Theory, 2004. Chicago, Illinois, USA, p. 31. IEEE.
33. Viswanathan GM, Buldyrev SV, Havlin S, Da Luz MGE, Raposo EP, Eugene Stanley H. "Optimizing the success of Random Searches." nature 401, no. 6756 (1999): 911-914. doi:10.1038/44831
34. Rens EG, Edelstein-Keshet. L "From Energy to Cellular Forces in the Cellular Potts Model: An Algorithmic Approach." PLoS Comput Biol 15, no. 12 (2019): doi:e1007459 doi:10.1371/journal.pcbi.1007459
35. Yang H, Gou X, Wang Y, Fahmy TM, Leung AY-H, Lu J, et al. "A Dynamic Model of Chemoattractant-Induced Cell Migration." Biophysical J 108, no. 7 (2015): 1645–51. doi:10.1016/j.bpj.2014.12.060
36. Niculescu I, Textor J, Rob J, De Boer . "Crawling and Gliding: a Computational Model for Shape-Driven Cell Migration." Plos Comput Biol 11, no. 10 (2015): e1004280. doi:10.1371/journal.pcbi.1004280
37. Kim M-C, Silberberg YR, Abeyaratne R, Kamm KRD, Asada HH. "Computational Modeling of Three-Dimensional ECM-Rigidity Sensing to Guide Directed Cell Migration." Proc Natl Acad Sci USA 115, no. 3 (2018): E390–E399. doi:10.1073/pnas.1717230115
38. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. "Active Particles in Complex and Crowded Environments." Rev Mod Phys 88, no. 4 (2016): doi:045006 doi:10.1103/revmodphys.88.045006
39. Dimidov C, Oriolo G, Trianni V. “Random Walks in Swarm Robotics: an experiment with Kilobots.” In International Conference on Swarm Intelligence, pp. 185–196. Springer, Padma Resort Legian, Indonesia, 2016. doi:10.1007/978-3-319-44427-7_16
40. Katanov D, Gompper G, Fedosov DA. Microvascular Blood Flow Resistance: Role of Red Blood Cell Migration and Dispersion." Microvasc Res 99 (2015): 57–66. doi:10.1016/j.mvr.2015.02.006
41. Tichet M, Prod’Homme V, Fenouille N, Ambrosetti D, Mallavialle A, Cerezo M, et al. "Tumour-derived SPARC Drives Vascular Permeability and Extravasation through Endothelial VCAM1 Signalling to Promote Metastasis." Nat Commun 6, no. 1 (2015): 1–15. doi:10.1038/ncomms7993
42. Mrass P, Rao Oruganti S, Fricke GM, Tafoya J, Byrum JR, Yang L, et al. "ROCK Regulates the Intermittent Mode of Interstitial T Cell Migration in Inflamed Lungs." Nat Commun 8, no. 1 (2017): 1–14. doi:10.1038/s41467-017-01032-2
43. Van H, Peter JM. "A Model for a Correlated Random Walk Based on the Ordered Extension of Pseudopodia." Plos Comput Biol 6, no. 8 (2010): e1000874. doi:10.1371/journal.pcbi.1000874
Keywords: random walks, cell migration, correlated speed and persistence, complex topographies, active particles
Citation: Chen K and Qin K-R (2021) Random Walks of a Cell With Correlated Speed and Persistence Influenced by the Extracellular Topography. Front. Phys. 9:719293. doi: 10.3389/fphy.2021.719293
Received: 02 June 2021; Accepted: 29 June 2021;
Published: 13 July 2021.
Edited by:
Claudia Tanja Mierke, Leipzig University, GermanyReviewed by:
Masato S. Abe, RIKEN Center for Advanced Intelligence Project (AIP), JapanLuis Diambra, National University of La Plata, Argentina
Copyright © 2021 Chen and Qin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kai-Rong Qin, a3JxaW5AZGx1dC5lZHUuY24=
 Kejie Chen
Kejie Chen Kai-Rong Qin
Kai-Rong Qin