Diffuse Josephson Radiation in Turbulence

The possibility of generating diffuse radiation in extended astronomical media by plasma turbulence is investigated under the assumption that the turbulence can be understood as an ensemble of small-scale magnetic filaments (narrow current sheets) forming a texture around a large number of magnetic depletions or voids. On astronomically microscopic scales, the dilute high temperature medium (plasma) is to be considered ideally conducting, forming a collection of Josephson junctions between two such adjacent quasi-superconductors. The oscillation frequency of those junctions depends on the part of the spectrum that contributes to the oscillation, causing weak radio backgrounds. Lowest Josephson frequencies/energies near zero may become sources of quasi-stationary magnetic fields.

1 Introduction

Diffuse radiation from extended astrophysical objects like clusters of galaxies is conventionally attributed to synchrotron radiation [1, 2] from a distribution of relativistic particles which have been accelerated by some diffusive Fermi-like acceleration mechanism [cf., e.g., the monography 3] in the assumed always present magnetohydrodynamic plasma turbulence, both well-established, commonly accepted and successfully applied processes which provide valuable information about the physical state of the radiation sources, in particular the energy of the radiating particles and the strength of the scattering magnetic fields.

Here, we propose a different mechanism, which in some cases may add to provide additional diagnostic information about turbulent emission sources. It is not based on the assumption of an energetic particle distribution but restricts to the presence of turbulence in extended objects such as turbulent supernova remnants, galaxies, clusters of galaxies, and possibly even the cosmological large-scale structure of the Universe, which exhibits a particular texture consisting of filamented matter and voids. The weak emission generated may in such large extended turbulent media sometimes add up to observable intensities.

In configuration space, turbulent media are not smooth on the mesoscopic and microscopic scales but consist of a very large number of vortices, which on the large scale appear to be homogeneous. Interaction on the small scales provides effects which could map into observations. A well-known example is magnetohydrodynamic instabilities (mirror modes, alfvénic structures, discontinuities, shock waves, etc.), which structure any extended turbulent plasmas. The medium subject to this kind of turbulence consists of magnetic vortices, small-scale current sheets, and magnetic depletions separated on the larger scale by very narrow magnetic walls and filaments, which, in well-developed turbulence, may form more or less irregular chains of magnetic voids.

Chains of this kind and irregular distributions of partially depleted voids in the turbulent medium, which on those scales is almost perfectly conducting, can if forming magnetic voids be interpreted as a network of Josephson junctions. These are not connected to form a large multi-junction array; rather, they can be considered as a multitude of single junctions distributed over the entire turbulent volume. Any interaction occurs only between nearest neighbors while rapidly decreasing with distance. Each individual junction then consists of just two neighboring magnetic depletions, which are connected via the narrow separating magnetic wall or filament, structures of which belong to the turbulent texture that is generated in the volume by the free energy source of the turbulence: active galactic nuclei (AGNs), supernova remnants (SNRs), or any other object/process responsible for feeding turbulence such as collisionless shocks [4] and their environments [5, 6], the interstellar medium [7], or stellar winds, as shown by the example of the solar wind [8–10].

2 Josephson Junctions

The physics of such junctions had been discovered and formulated 60 years ago [11, 12] and in quantum devices has become an extraordinarily important diagnostic tool for measuring tiny electric potential differences. For natural systems, it has been reviewed in recent work, focusing on meso-scale mirror mode turbulence [13] in near-Earth space. The scales will be vastly different, but it is reasonable to assume that turbulence basically forms structures occupying the range from the largest mechanically driven alfvénic scales down into the ion inertial scale range in interaction with their nearest neighbors, preferentially of similar scale, by exchanging tunneling currents [14–16] across the separating magnetic filamentary walls. Their magnetic effect is the classical skin depth which allows the magnetic field to penetrate a short distance into the matter.

In the semi-classical approximation, these currents are real electric currents indeed, flowing perpendicular to the separating magnetic fields. These currents are carried solely by electrons. They temporarily bridge the wall between the voids but are not allowed to penetrate the void over more than a microscopic skin depth λ_e = c/ω_e (with ${\omega }_e^2=e^2{N}_0/{ϵ}_0{m}_e$ being the squared plasma frequency, m_e being the electron mass, and N₀ being the ambient density), which implies that they become reflected and oscillate back and forth while being locally confined to the filaments. The oscillation frequency of the fluctuating currents is high, and the order of the Josephson frequency is as follows:

${\nu }_J\equiv \frac{{\omega }_J}{2\pi }=\frac{|q|}{2\pi \hslash }\langle \mathrm{\Delta }V\rangle \approx 2.5\times 10^5\langle \mathrm{\Delta }V\rangle \mathrm{G}\mathrm{H}\mathrm{z}(1)$

(with q = −e electron elementary charge) if only a weak electric potential difference ⟨ΔV⟩ (in volts) is applied to the junction [cf., e.g. [17, 18] or the above cited original publications]. Clearly, even for small electric potentials, this frequency is high, actually far above any cyclotron frequency ω_J ≫ ω_ce = eB/m_e in the ambient magnetic field B such that the electron magnetic moment μ_e = T_e/B is not conserved. This violates adiabaticity and permits tunneling. The source of the potential can either be found in the always present thermal fluctuation level of plasma turbulence [19, 20] or in the turbulent streaming itself as we will demonstrate below.

Plasmas are quasi-neutral, and any potential difference across the void-separating walls imposed by the turbulent flow will necessarily be rather small locally because the walls are narrow and the cross-potential drop is small. This holds, in particular, in weak magnetic fields where in the near Earth space and solar wind, for instance, the average flow-electric fields typically are of the order of ⟨δE⟩∼ few μV/m, becoming at most mV/m, which, for narrow junction boundaries of width, say, L_n ≲ 10 λ_e, may shift the Josephson frequency down to the (astronomically interesting) radio frequency range of or below ∼ 1 GHz.¹ Larger potentials, which are not necessarily expected to occur, are also broader, and therefore, probably less effective walls would shift the frequency up. Such strong electric fields are barely expected except locally in collisionless shock transitions or in relativistic streams and, presumably, become depleted over large distances.

Josephson currents are carried solely by the mobile electrons and quantum mechanically subject to the mentioned microscopic tunneling. It is of course clear that the strengths of the tunneling and the tunneling current depend on the width L_n of the wall because the electron wave function ψ(x) decays with distance. It will therefore be strongest for microscopically thin junction walls, which will put us into the high wave number range of the turbulence close to turbulent dissipation.

With Josephson frequency ω_J = 2πν_J, the amplitude of the oscillating current density is given by the following:

$j_n(t)=j_J\sin (\mathrm{\Delta }{\varphi }_0-{\omega }_{J}t),j_J=\frac{e\hslash N_0}{m_e{L}_n}|\psi {|}^2,(2)$

where $\mathrm{\Delta }{\varphi }_0={({\varphi }_2-{\varphi }_1)}_0$ is the original undisturbed phase difference between the interacting magnetic voids and |ψ|² = δN/N₀ is the semi-classical fractional density fluctuation δN in the interacting nearest neighbor voids normalized to the average density N₀. Usually, one expects that in the average, δN/N₀ ∼ O (0.1) in well-developed turbulence.

The oscillating current j_n(t) is a localized high frequency source (antenna), which necessarily will serve as a radiator of electromagnetic waves. Its oscillation frequency depends on the electric potential difference ΔV, which is applied to the junction. Hence, it maps even very small potential differences into radiation. One does not expect very strong radiation emitted from a single junction because the current amplitude is of the order of

$|j_n|\sim 10^{-23}|\delta N/N_0|N_0{L}_n^{-1}{\mathrm{A}\mathrm{m}}^{-2},$

which is inversely proportional to the width L_n of the junction. Radiation from a single current is weak. For an idea, chose the magnetosheath. Assuming a density of, say, N₀ ≈ 10³ m⁻³, a minimum width of the wall of L_n ≈ 10⁴ m, and a density contrast of |δN/N₀|∼ 10^–1, the single-junction current density amounts to not more than |j_n|∼ 10^–25 Am⁻², completely independent of the potential drop ΔV which enters through phase invariance only. This will contribute just to very weak radiation only. However in huge volumes, like those of extended objects in the Universe, the radiation of all the myriads of junctions present may possibly add up to a measurable intensity. In the following, we investigate this possibility.²

2.1 Thermal Josephson Frequency

Prior to attacking the radiation problem, we infer about the expected frequency range of Josephson oscillations. The current depends on the density contrast |j_n|∝|ψ|², while the frequency depends solely on the applied potential difference V. Hence, the frequency decouples from the radiation problem, which can be considered separately later. Since there are no obvious sources expected in the medium to contribute to the potential other than the mean thermal fluctuation level of plasma oscillations and plasma turbulence, the question is which potential differences can they cause? Clearly large and medium potential drops imply high photon energies and accordingly low radiation power.

Electrostatic thermal fluctuations cause an average rms potential of the order of

$\begin{array}{ccc}\hfill {⟨\mathrm{\Delta }V⟩}_{\mathit{th}}& \approx \hfill & {\ell }_D{\left(\frac{2T_e}{{ϵ}_0{\lambda }_D}\right)}^{\frac{1}{2}}\approx \hfill \\ \hfill 1.24{\ell }_D& \times \hfill & 10^{-4}\mathrm{V}\sqrt[4]{T_{e[\mathrm{k}\mathrm{e}\mathrm{V}]}{N}_{0[10^3{\mathrm{m}}^{-3}]}}.\hfill \end{array}(3)$

Here, the dominant length scale of thermal fluctuations is the Debye length ${\lambda }_D={(2T_e/m_e{\omega }_e^2)}^{\frac{1}{2}}$. The quantity ℓ_D = L_n/λ_D, a rather large number, is the mean cross-scale number of Debye lengths over which the potential is measured across the junction boundary (realistic values should be of the order of at least ℓ_D ∼ 10⁵ for a junction). Here, the electron temperature T_e ∼ keV and a density N₀ ∼ 10³ m⁻³ are used, with density usually taken for the intracluster gas, for instance, inferred basically from x-ray observations under the assumption of fully virialized motion. This thus holds for the high-energy component of matter which barely participates in the turbulence as one would expect that the latter involves the denser low-energy part which is less involved into the supposed virial equilibration.

Hence, even though we assumed a rather high temperature for the intracluster gas based on x-ray observations and the assumption of complete virialization, decreasing the frequency below ∼ 1 GHz into the domain of radio frequency observation requires unrealistically low temperatures (at least for a virialized x-ray cluster). Any radiation will be in the optical to x-ray range.³

It is therefore hardly believable that thermal fluctuations play any remarkable role in generating Josephson radiation, at least not in the radio wavelength, and it will be of very low power. Nevertheless, the possibility cannot be excluded that a finite thermal fluctuation level, which cannot be avoided, in particular, at the high assumed cluster temperatures inferred from x-ray observations, contributes to weak high frequency/high energy radiation.

3 Turbulent Josephson Spectrum

Returning to the problem of generation of potential drops, we consider the presence of well-developed turbulence. Extended astrophysical objects (stellar winds, SNR, clusters, and galaxies) are generally turbulent. The electric field is caused by the turbulent flow, in particular in the presence of an ideal conductivity, which on the micro-scales under consideration is always given in extended objects. This applies to almost all candidates (SNRs, the intra-cluster medium, etc.) on scales down from alfvénic to the ion-inertial range covering the interval λ_e < λ ≲ v_Aτ_A, where λ_e = c/ω_e ≫ λ_D is the electron skin depth, λ_i = c/ω_i is the ion skin depth, $v_A=B/\sqrt{{\mu }_0{N}_0{m}_i}$ is the Alfvén speed in the mean magnetic field B ≡⟨B⟩, and τ_A is the Alfvén time, a loosely defined quantity, only which corresponds to the injection range of mechanical energy into plasma turbulence. The turbulent electric field δE in the scale range > λ_i is obtained from

$\delta \mathbf{E}=⟨\mathbf{B}⟩\times \delta \mathbf{v}-⟨\mathbf{v}⟩\times \delta \mathbf{B}-\delta \mathbf{v}\times \delta \mathbf{B}+⟨\delta \mathbf{v}\times \delta \mathbf{B}⟩.(4)$

We are less interested in the macroscopic motion ⟨v⟩ of matter and for simplicity drop the second term in this expression. In fact, ⟨v⟩ is basically the macroscopic turbulent rotation speed in the mean magnetic field ⟨B⟩, and the turbulent velocities δv belong to smaller scale vortices which produce small-scale electric fields responsible for the potential drops across the junctions. The average macroscopic rotation speed |⟨v⟩| = ⟨v⟩_ϕ can become large in a larger radial range of a cluster, in particular, in its outer skirts where it, however, is about constant and will not contribute remarkably to the potential in a weakly turbulent magnetic field. Eq. 4 refers to the single fluid MHD model of turbulence [cf., e.g., 25] and should be refined to a two fluid or kinetic model when leaving the Alfvénic range, which for our perspective purposes is not required. This point will be discussed in passing below.⁴

3.1 Potentials

The nonlinear third term and its averaged fourth term in Eq. 4 are the correlations between the turbulent velocity and magnetic fields. This fourth term is driving the turbulent dynamo. To first order, we neglect it and the third term, assuming the product of the velocity and field fluctuation amplitudes |δv‖δB|, is of second order only, a point which must in a more extended treatment be re-evaluated but is not of principal importance here. Its inclusion would provide an interesting coupling between dynamo and Josephson effects, which if no resonance occurs is of second order and thus negligible.

The last condition suggests that the dominant turbulent electric field δE is perpendicular to the mean magnetic and turbulent velocity fields. To first order, it is only the mechanical turbulent flow δv that enters the Josephson effect. Since ⟨B⟩ in the wall of the junction is tangential to the junction, the direction of the electric field projects onto the normal n of the junction with angle α_k depending on the turbulent wave number k.

Turbulence is conventionally described by reference to the turbulent power spectrum S(k) taken under stationary conditions, with k being the modulus of the turbulent wave number in one dimension. Following the usual approach to turbulence, k is the projection of the wavenumber k of the turbulent fluctuations onto the direction of the electric field δE, the only direction of relevance to our problem which makes it locally unidimensional [cf., e.g., 25]. This dimension in our case is along the normal n of the junction across the wall between the two superconducting voids to which the turbulent electric field E is projected. The mean magnetic field ⟨B⟩ is confined to the junction wall and thus tangential to the voids forming a magnetic filament. As usual, we take this direction as coordinate z and the direction of the normal n across the junction as x. In cylindrical coordinates, integration over the angular dependence in the (y, z)-plane yields a factor 2π. With δE(x) = −∇δV(x), we then have⁵ the potential difference ΔV(k) = L_nn ⋅ δE(k) across the junction for its spectrum that

$\begin{array}{ccc}\hfill S_{E_n}(k)& =\hfill & 2\pi \langle {B\rangle }^2{S}_v(k){\cos }^2{\alpha }_k\hfill \end{array}(5)$

$\begin{array}{ccc}\hfill & \Downarrow \hfill & \hfill \\ \hfill S_V(k)& =\hfill & 2\pi L_n^2\langle {B\rangle }^2{S}_v(k){\cos }^2{\alpha }_k\hfill \end{array}(6)$

with $k_{\mathit{in}}\sim k_A<k<k_m\sim {\lambda }_i^{-1}$ and angle α_k, a function of turbulent wave number k, between electric field and direction of the normal. (Indices refer to the different turbulent fields.) Restriction to scales longer than λ_i warrants that for the present time, we remain in the alfvénic range only. In this scale range, it is known that the turbulent velocity spectrum S_v(k) is about Kolmogorov,⁶ and we have for the spectrum of the potential difference

$S_V(k)\approx C{⟨B⟩}^2{ϵ}^{\frac{2}{3}}{L}_n^2{k}^{-\frac{5}{3}}{\cos }^2{\alpha }_k,(7)$

where C ≈ 10.37 is Kolmogorov’s constant C_K ≈ 1.65 (modified by the factor 2π) as follows from numerical simulations [29–32] and [cf., e.g., 25] and ϵ is the stationary energy injection rate per unit mass and time. Due to our selection of terms in Eq. 4, only the velocity spectrum contributes. Inference about the contribution of the magnetic fluctuations through the neglected second convective term in Eq. 4 requires consideration of the spectrum of turbulent currents, which is second order and thus outside our purposes.

Our interest up till now is primarily in the determination of the scale range of relevance for generation of (possibly observable) radiation. Application to the Josephson frequency requires finding the power spectrum of the frequency. Since the frequency is a real quantity and there is no obvious damping⁷ of the Josephson oscillations on the radiation time scale, this is done by taking the Fourier transform of ${\nu }_J^2$, which gives directly

$\begin{array}{ccc}\hfill S_{\nu }(k)& =\hfill & \frac{e^2}{4{\pi }^2{\hslash }^2}{S}_V(k)\hfill \\ \hfill & =\hfill & \frac{e^2{L}_n^2}{4{\pi }^2{\hslash }^2}C{⟨B⟩}^2{ϵ}^{\frac{2}{3}}{k}^{-\frac{5}{3}}{\cos }^2{\alpha }_k.\hfill \end{array}(8)$

On taking the integral with respect to k, we find that in the average, it turns out that apparently the smallest wave numbers k_A (longest scales) contribute most to the frequency, that is, they are responsible for the highest frequencies, with an angular average $⟨{\cos }^2{\alpha }_k⟩=\frac{1}{2}$ yielding a spectral average of the turbulent Josephson frequency as follows:

$\begin{array}{ccc}\hfill ⟨{\nu }_J(k)⟩& \approx \hfill & \frac{e{L}_n⟨B⟩{ϵ}^{\frac{1}{3}}}{8\pi \hslash }{\left(3C\right)}^{\frac{1}{2}}{k}_A^{-\frac{1}{3}}\times \hfill \\ \hfill & \times \hfill & {\left[1-{\left(\frac{k_A}{k_m}\right)}^{\frac{2}{3}}\right]}^{\frac{1}{2}}|\cos {\alpha }_k|\hfill \\ \hfill & \approx \hfill & 3\times 10^4{L}_n{ϵ}^{\frac{2}{3}}⟨B⟩k_A^{-\frac{1}{3}}|\cos {\alpha }_k|\mathrm{G}\mathrm{H}\mathrm{z}.\hfill \end{array}(9)$

Here, $k_A^{-1}=v_A{\tau }_A\approx L_{J\Vert }$ is roughly the length of the junction, and we integrated over the angle α_k. (Note the dimension of [ϵ] = m²/s³.) All these quantities are to be taken locally in the generation region of radiation, the nearest neighbor interaction of the junctions. So the conclusion that the longest scales contribute most should be cautioned because only a fraction of the long scales maps to the junction walls. The effective scale responsible for contributing to the Josephson frequency is the product kL_n.

3.2 Wave Number Dependence

More interesting than the average frequency is the power spectrum of the Josephson frequency as a function of junction-projected scale k. It holds in the alfvénic range, that is, the long wavelength range k_A < k < k_m with frequency per root wavenumber as a function of the turbulent scale

$\begin{array}{ccc}\hfill \frac{{\nu }_J(k)}{\sqrt{k}}& =\hfill & \frac{\sqrt{C}}{2\pi }\frac{e}{\hslash }{L}_n\langle B\rangle {ϵ}^{\frac{1}{3}}{k}^{-\frac{5}{6}}|\cos {\alpha }_k|\hfill \\ \hfill & \approx \hfill & 10^6{L}_n\langle B\rangle {ϵ}^{\frac{1}{3}}{k}^{-\frac{5}{6}}|\cos {\alpha }_k|{\mathrm{G}\mathrm{H}\mathrm{z}\mathrm{m}}^{\frac{1}{2}}.\hfill \end{array}(10)$

Note the physical SI units in the second part of this equation and the following two estimates have been absorbed. This implies the unit [B] = m⁻² here. The magnetic field is measured in flux elements ℏ/e.

It is worth mentioning that L_nL_y⟨B⟩ is the flux contained in the wall carried by the magnetic filament separating the junction voids, if L_y is the dimension of the wall perpendicular to the main magnetic field. Multiplying with ${\mathrm{\Phi }}_0^{-1}=e/\pi \hslash$, the inverse elementary flux, gives the number N_Φ ≈ L_nL_y⟨B⟩ of flux elements the wall contains which participate in the Josephson oscillation. Its large number is the reason for the high Josephson frequency.

The Josephson frequency depends on the turbulent scale as ${\nu }_J(k)\propto k^{-\frac{1}{3}}$ GHz, weakly decaying toward the larger turbulent wave numbers. Smaller turbulent wave numbers k contribute to higher Josephson frequencies. Writing this in terms of the electron skin depth λ_e = c/ω_e gives

${\nu }_J(k)\approx 10^6{\lambda }_e^{\frac{1}{3}}{L}_n⟨B⟩{ϵ}^{\frac{1}{3}}{(k{\lambda }_e)}^{-\frac{1}{3}}|\cos {\alpha }_k|\mathrm{G}\mathrm{H}\mathrm{z}.(11)$

This expression depends on the projection angle α_k the turbulent electric fields make with the normal to the junction. Large angles α_k reduce the potential, thus lowering the Josephson frequency. The largest potentials and thus frequencies are obtained for α_k = 0. Turbulent flow velocities nearly parallel to the normal δv ≈ n contribute to the lowest frequencies because E is perpendicular to n for such flow directions. The direction of turbulent flow with respect to the junction (and magnetic field) thus modulates the Josephson frequency over a wide frequency range from ν_J ≈ 0 to its maximum, which is reached at k = k_A and ${\alpha }_{k_A}=0$.

It is convenient to introduce the ratio κ = k/k_A and write for $k_A\approx {\omega }_{ci}/v_A={\omega }_i/c\equiv {\lambda }_i^{-1}$, where ω_ci = e⟨B⟩/m_i is the ion cyclotron frequency. Then, $k_A{\lambda }_e\approx \sqrt{m_e/m_i}$. For protons, the above expression with ℓ_n = L_n/λ_e can be re-written more conveniently as follows:

$\begin{array}{ccc}\hfill {\nu }_J(\kappa )& =\hfill & {\nu }_{JA}|\sin {\beta }_k|{\kappa }^{-\frac{1}{3}},\hfill \end{array}(12)$

$\begin{array}{ccc}\hfill {\nu }_{JA}& \approx \hfill & 10^6{\ell }_n{\lambda }_e^{\frac{4}{3}}⟨B⟩{ϵ}^{\frac{1}{3}}\mathrm{G}\mathrm{H}\mathrm{z}.\hfill \end{array}(13)$

Here, α_k = π/2 − β_k has been replaced by its complementary angle β_k. Following the above discussion, small β_k ≪ π/2 are responsible for low Josephson frequencies. However, the frequency will remain high, which is seen when using the above given numbers. Josephson oscillations, once mapped into escaping radiation, should provide diffuse high-frequency/photon energy radiation backgrounds of extended turbulent objects independent of the presence of particles that have been accelerated to high energies.

The dependence of the Josephson frequency on the normalized wave number κ in Kolmogorov turbulence is shown in Figure 1 up to the wavenumber of dissipation κ_d, which corresponds to scales where particle inertial effects become important. The decay of frequency with increasing κ amounts to roughly 1.5 orders of magnitude only, however showing that large turbulent wave numbers near dissipation contribute most to the lowest frequencies.

FIGURE 1

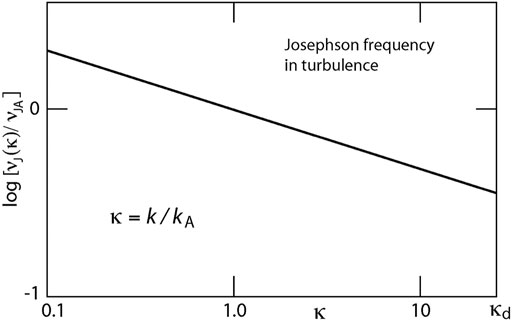
FIGURE 1. Dependence of the normalized Josephson frequency in Kolmogorov turbulence on the ratio κ ≡ k/k_A of turbulent wave numbers in the range 0.1k_A < k < k_d under the assumption that k_dλ_e ≈ 1 is the ultimate dissipation scale of turbulence, which is still far above the molecular scale, caused, for instance, by spontaneous collisionless reconnection in inertial scale turbulent current filaments, the most probable dissipation process in turbulence in collisionless plasma [cf., e.g., [33]].

The coefficient of the alfvénic frequency in the above expression corresponds to an oscillation energy of ≈ 4 eV, which directly maps into the frequency of radiation. The junction width will be l_n>10, while λ_e∼10⁴ m. Let us assume B∼1 nT somewhat larger than the magnetic field in the outskirts of clusters of galaxies. Then ν_J∼ 2 × 10⁻²∈^1/3 Hz, depending on the square of the mechanical turbulent velocity injected per second. Assume v/c∼10⁻⁵ corresponding to v∼10³ km/s. Then largest frequencies are ν_J∼ 2 × 10⁴ Hz for β_k = π/2, in the low frequency radio range. Depending on the angle, the Josephson frequency covers the range from zero frequency to this maximum. Frequencies below the local radiation cut off belong to quasi-stationary Josephson current-generated non-dynamo magnetic fields.

3.3 Ion Inertial Range

We briefly discuss the contribution of the ion-inertial wave number range λ_i > k⁻¹ > λ_e. Ions become non-magnetic there, and Eq. 4 is to be re-interpreted in the sense of electron-MHD [cf., e.g., 34, 35]. This leads to deviations from alfvénic magnetic turbulence with Alfvén waves turning into kinetic Alfvén waves of transverse scale k_⊥λ_i ∼ 1, parallel wave electric fields [36], and inclusion of shorter scale kλ_e < 1 whistler turbulence [35]. Parallel electric fields do not contribute to the Josephson frequency ν_J. A wealth of observations indicate that the turbulent magnetic spectra deviate from Kolmogorov in this range [cf., e.g., 37–43 and literature cited therein].⁸ As long as no bulk flow is included, any magnetic turbulence does not contribute to Josephson oscillations and radiation to first order. In view of application to the Josephson effect, this justifies extension of the active part of the turbulent spectrum down into the ion-inertial range at wave number k_d where dissipation sets on.⁹

There is, however, another contribution to the electric potential in this range which comes from the ion response to the turbulent induction electric field in the ion inertial range kλ_i > 1 and is responsible for deviations of the turbulent density spectrum from its original Kolmogorov shape [46]. This is of higher order and can be neglected.

Turbulent flow and currents in the ion inertial range are restricted to electrons. The relation between the turbulent electric and velocity fields includes Poisson’s equation. The divergence of the electric field δE is obtained from Eq. 4 being proportional to the turbulent density fluctuation δN. It causes a correction on the spectral density of the electric potential field,

$S_{V,N}(k)=\frac{e^2}{{ϵ}_0^2}{k}^{-2}{S}_N(k),(14)$

caused by S_N(k), the power spectral density of the turbulent density δN. The latter is proportional to the power spectrum S_v(k) of the turbulent velocity,

$S_N(k)\approx N_0^2\frac{v_A^2}{c^2}\frac{k^2}{{\omega }_i^2}{S}_v(k).(15)$

Note again that nothing is changed on the turbulent spectrum S_v(k) of the mechanical velocity which is imposed on the electromagnetic fluctuations. We therefore have

$S_{V,N}(k)\propto S_v(k).(16)$

The factor k² is compensated by the required factor in the Fourier transformed Poisson equation. (It might be noted that this expression could, in principle, be refined if taken into account an active response of the plasma through the inclusion of the inverse plasma response function D⁻¹ (ω, k), which would generate a more complicated dependence of the density power spectrum for comparison with observation.)

The effect is of second order in v_A/c and thus weak. Its contribution can to first order be suppressed. It just affects the density spectrum to let it respond to the electric field [for its reconstruction in real observations, see 46], which it experiences as a charge field. More important is that in this range, the turbulent velocity is determined by electron mobility. Electron-MHD takes care of it to some extent. The magnetic turbulence spectrum decays steeper than Kolmogorov [35]. Thus, to first order, neither magnetic effects (for principal reasons) nor density fluctuations are of interest in the turbulent Josephson effect.

4 Radiation

The single junction oscillates in the whole spectral range with Josephson frequency ν_J(k) as a function of wave number k or scale l ∼ k⁻¹. The oscillating Josephson current j_n(t) acts as a current source for the generation of escaping radiation. According to the above, the Josephson frequency and thus the radiation frequency are far above any plasma cut-off ω_J ≫ ω_e and thus can freely escape into space such that we do not need to consider any radiation transport or reabsorption as in all applications, the matter will locally be optically thin while of course over large spatial scales might be subject to scattering on the material background medium.

The total energy dW radiated into solid angle dΩ is defined as

$\frac{dW}{d\mathrm{\Omega }}=\frac{1}{2}{ϵ}_0{c}^3\int |\mathbf{A}(t){|}^{2}dt=\frac{1}{2}{ϵ}_0{c}^3\int |\mathbf{A}(\omega ){|}^{2}d\omega ,(17)$

where A is the radiated vector potential and ω is the radiation frequency. Since no single junction will be resolved in the volume, the expected radiation of all the junctions to which we refer below is diffuse for any remote observer, and one may integrate over the solid angle even for a single junction in order to obtain the radiation intensity per frequency interval,

$\frac{dI}{d\omega }\approx 4\pi {ϵ}_0{c}^3\sum _{\pm }|\mathbf{A}(\pm \omega ){|}^2\frac{\mathrm{J}}{\mathrm{H}\mathrm{z}}.(18)$

4.1 Vector Potential

It remains to determine the radiation vector potential as a function of frequency, solving the inhomogeneous wave equation with Josephson current as the source. The wave equation for the remaining component A_x is

$\begin{array}{ccc}\hfill \left[{\nabla }^2-\frac{{\partial }^2}{c^2\partial t^2}\right]\frac{A_x(\mathbf{x},t)}{{\mu }_0}& =\hfill & -j_x(\mathbf{x},t)\hfill \\ \hfill & \hfill & j_J\sin ({\omega }_{J}t)\delta ({\mathbf{x}-\mathbf{x}}_0)\hfill \end{array}(19)$

with Josephson current in direction $\mathbf{n}=\widehat{\mathbf{x}}$. Here, x₀ is the location of the junction in real space, and the spatial dependence of the Josephson frequency is suppressed. For any observer, the junction is a point source taken approximately as rectangular, neglecting any curvature effects. Also, the stationary phase difference Δϕ₀ is of no importance here as it drops out when calculating the radiation intensity. The magnetic field is in z-direction, and the radiation wave vector K varies in y, z. For an order of magnitude estimate, avoiding the complete Green’s function solution (which implies retaining just the dipolar term [1, 2], in which case the source current becomes a plane current with plane extended over short distance along the magnetic field in z and perpendicular in y), we seek for a particular solution of the wave equation. Fourier transformation with respect to time yields

$\begin{array}{ccc}\hfill & \hfill & \left[{\nabla }^2+\frac{{\omega }^2}{c^2}\right]A_x(\mathbf{x},\omega )=\hfill \\ \hfill & \hfill & i\pi {\mu }_0{j}_J\left[\delta (\omega +{\omega }_J)-\delta (\omega -{\omega }_J)\right]\delta ({\mathbf{x}-\mathbf{x}}_0).\hfill \end{array}(20)$

Note that the radiation wavelength at high frequencies is of course much shorter than any turbulence scale which justifies the neglect of the dependence on the turbulent scale x′ = (y, z). Physically, this implies that the energy loss by radiation is negligible against the turbulent energy. Fourier transforming yields

$\begin{array}{ccc}\hfill A_x(\mathbf{K},\omega )& =\hfill & -\frac{2{\pi }^{2}i{\mu }_0{j}_J{\mathrm{e}}^{-iK\mathbf{n}\cdot {\mathbf{x}}_0}}{K^2-{\omega }_J^2/c^2}\hfill \\ \hfill & \times \hfill & \left[\delta (\omega +{\omega }_J)-\delta (\omega -{\omega }_J)\right]\delta ({\mathbf{x}-\mathbf{x}}_0),\hfill \end{array}(21)$

with x₀ being the location of the junction in real space somewhere in the huge turbulent volume. The singularity in the denominator has to be treated accounting for the causality of outgoing radiation, which requires K = ±ω_J/c. Resolving the nominator yields

$\begin{array}{ccc}\hfill A_x(\mathbf{K},\omega )& =\hfill & -\frac{{\pi }^3{\mu }_{0}c{j}_J{\mathrm{e}}^{-iK\mathbf{n}\cdot {\mathbf{x}}_0}}{{\omega }_J}\left[\delta (\omega +{\omega }_J)-\delta (\omega -{\omega }_J)\right]\hfill \\ \hfill & \hfill & \hfill \\ \hfill & \times \hfill & \left[\delta (K+{\omega }_J/c)+\delta (K-{\omega }_J/c)\right]\delta ({\mathbf{x}-\mathbf{x}}_0).\hfill \end{array}(22)$

For a single turbulent junction, the amplitude becomes

$|A_x(\omega ){|}_{\omega ={\omega }_J}=4{\pi }^3{\mu }_0{c}^2{j}_J{\omega }_J^{-3}.(23)$

4.2 Intensity

The energy emitted per frequency ω = ω_J in radiation is

$\begin{array}{ccc}\hfill \frac{dI}{d\omega }{\left|\right.}_{{\omega }_J}& \approx \hfill & \frac{64{\pi }^7{c}^3}{{ϵ}_0{\omega }_J^6}{j}_J^2\hfill \\ \hfill & =\hfill & \frac{64{\pi }^5}{{\mu }_{0}c}{\left(\frac{{\lambda }_e}{L_n}\right)}^2{\left(\frac{{\omega }_e}{{\omega }_J}\right)}^6{\left(\frac{\langle \delta N\rangle }{N_0}\right)}^2{\mathrm{\Phi }}_0^2\hfill \\ \hfill & \approx \hfill & 2.1\times 10^{-28}{\ell }_n^{-2}{\left(\frac{{\omega }_e}{{\omega }_J}\right)}^6{\left(\frac{\langle \delta N\rangle }{N_0}\right)}^2\frac{\mathrm{J}}{\mathrm{H}\mathrm{z}}.\hfill \end{array}(24)$

We introduced the electron skin depth λ_e = c/ω_e, plasma frequency ${\omega }_e^2=e^2{N}_0/{ϵ}_0{m}_e$, flux quantum Φ₀ = πℏ/e, the ratio ℓ_n = L_n/λ_e, and the rms turbulent density fluctuation ⟨δN⟩. This depends sensitively on the Josephson frequency. For the large Josephson frequencies, the intensity of a single junction becomes very low. Inserting expression (12) with ω_e = 2πν_e, one obtains

$\begin{array}{ccc}\hfill \frac{dI}{d\omega }{\left|\right.}_{{\omega }_J}& \approx \hfill & 1.3\times 10^{-27}{\left(\frac{\kappa }{{\ell }_n}\right)}^2{\left(\frac{{\nu }_e}{{\nu }_{JA}}\right)}^6{\left(\frac{\langle \delta N\rangle }{N_0}\right)}^2\hfill \\ \hfill & \approx \hfill & \frac{6.6\times 10^{-57}{\kappa }^2}{{\ell }_n^8{\nu }_e^2{ϵ}^2\langle {B\rangle }^6|\sin {\beta }_k{|}^6}.\hfill \end{array}(25)$

Assuming ℓ_n ∼ O (10²) and ν_e ∼ 10⁴ Hz, and taking for the magnetic field ⟨B ⟩∼ 1 nT, produces for one single junction an emitted intensity per Hz of

$\frac{dI}{d\omega }{\left|\right.}_{\omega -{\omega }_J}\approx \frac{6.6\times 10^{-20}{\kappa }^2}{{\ell }_{n[10]}^8{\nu }_{e[10^4]}^2{⟨B⟩}_{[nT]}^6{ϵ}^2|\sin {\beta }_k{|}^6}\frac{\mathrm{J}}{\mathrm{H}\mathrm{z}},(26)$

which corresponds roughly to some 10^–8 eV/Hz. This expression is very sensitive to the strength of the ambient magnetic field. This value increases slightly with the participating wave number range κ and decays with the rate of energy injection into turbulence, which is basically unknown. The increase with κ is at most some factor 10² at the turbulent dissipation range. There is, however, a rather sensitive dependence on the angle β_k as we already discussed when dealing with the frequency. For small β_k implying lowest frequencies, the radiated intensity increases as the sixth power of β_k. This makes, for instance, for an angle β_k ∼ 0.1π/2 that the intensity increases by a factor of ∼ 10⁵. If the angle is β_k ∼ 0.01π/2, the intensity is increased by a factor ∼ 10¹¹. Figure 2 sketches the dependence of the emitted intensity as a function of β_k for two different spectral ranges κ.

FIGURE 2

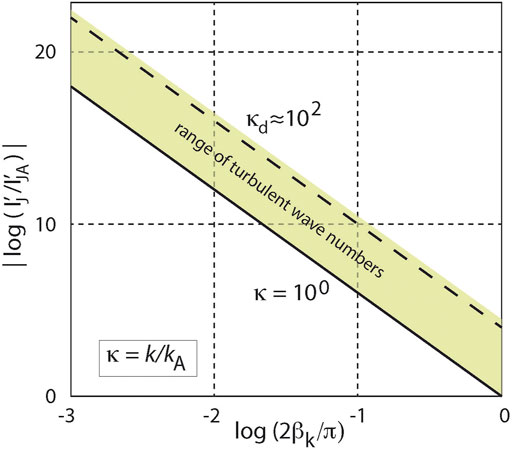
FIGURE 2. Dependence of the normalized intensity per frequency (dI/dω_J)/(dI/dω_JA) on the decrease in the angle $10^{-3}\le \frac{2}{\pi }{\beta }_k\le 1$ for two ratios κ ≡ k/k_A of turbulent wave numbers in the range 0.1k_A < k < k_d under the assumption that k_dλ_e ≈ 1 is the turbulent dissipation scale and turbulent energy injection is at or below the Alfvénic scale $k_A^{-1}$. The ultimate turbulent dissipation scale $k_d^{-1}$ is assumed to be two orders apart at κ ≈ 10². The interval between the two lines indicates the spectral width of the turbulence in its contribution to Josephson radiation (shown in green). The radiation intensity increases drastically with decreasing angle β_k, that is, with the obliqueness of the turbulent electric field with respect to the normal to the junction.

The largest spectral contribution comes from the large turbulent wavenumber range near dissipation, which also provides the lowest radiation frequencies. This suggests that the part of the spectrum of turbulence near dissipation wave numbers k_d contributes most to possibly observable radiation. Collisionless turbulence at those scales, still far away from any molecular interaction, is believed to dissipate its magnetic energy in the ion kλ_i ≳ 1 and electron kλ_e ≳ 1 inertial ranges by nonlinear plasma processes (see footnote 8), and one concludes that any observation of low-frequency Josephson radiation in the large-scale structure of the Universe is probably related to the direct signature of the wave number k_d above that collisionless turbulence enters its ultimate dissipation region.

4.3 Volume Filling Factor

Locating the oblique turbulent vortices into the large wave number turbulent range near dissipation then yields that the emitted intensity in radiation comes close to the eV-range in energy per Hz and per ϵ². Although this value remains rather low, in particular, for high energy injection rates and stronger ambient magnetic fields, it shows that the short wave number range of well-developed turbulence can indeed provide radiation at the Josephson frequency. However, one single junction will, in general, not generate any susceptible radiation which could be measured from remote, in particular not if the radiation source is at cosmological distance with radiation intensity decaying inversely proportional to some power of the cosmological red shift.

Observations never deal with one single junction which for any objects in the Universe is of microscopic size and thus undetectable. Any of the large turbulent volumes available in the Universe will however contain a large number of junctions distributed over the entire volume. A precise calculation requires knowledge of their spatial distribution function and the solution of the dipolar radiation pattern for each of the junction, which we so far avoided. Since the distribution is not known, a proxi to the sum over all contributions of junctions is provided by the estimate of the volume filling factor of the microscopic junctions and multiplying the radiation. The volume filling factor is defined as

$\xi =\sum _s{p}_{Js}{\mathcal{V}}_0/{⟨\mathrm{\Delta }\mathcal{V}⟩}_{Js},(27)$

where p_Js < 1 is the normalized probability of encountering a turbulent Josephson junction in the volume ${\mathcal{V}}_0$ and ${⟨\mathrm{\Delta }\mathcal{V}⟩}_{Js}$ is the average junction volume. This factor will be large, even for small probabilities. For a junction volume ${⟨\mathcal{V}⟩}_{Js}\sim 10^{16}{\mathrm{m}}^3$ and a spherical turbulence volume ${\mathcal{V}}_0\sim 3\times 10^{64}{\mathrm{m}}^3$ with probability not more than a mere p_Js ∼ 10^–10, the average filling factor is ⟨ξ⟩∼ 10³⁷, which increases the total average radiation intensity, replacing the numerical factor in the above expression by a factor ∼ 10¹⁰.

5 Conclusions

In this brief communication, we dealt with an unusual effect in classical high-temperature collisionless media as those encountered in extended astronomical objects such as SNRs and clusters of galaxies, which have evolved into a state of quasi-stationary turbulence in an extended range k_A ≲ k ≲ k_d of turbulent wave numbers k. On the junction scales, the matter is a dilute and collisionless, ideally conducting plasma. In its turbulent state, it consists of a texture of vortices of different scales, which at the assumed elevated temperatures are current vortices. They evolve into a texture of magnetic voids surrounded by magnetic filaments. Examples can be found in the large-scale structure of the Universe, which is known to exhibit a particular filamentary texture. We assume that this can be understood as a set of grossly independent Josephson junctions, each consisting of two adjacent voids and a separating magnetic wall, whose width is sufficiently narrow for permitting electron tunneling between the voids. Nearest neighbor interactions dominate. Josephson conditions suggest that these junctions, which are penetrated by smaller scale vortices, causing small cross-junction potential drops, emit radiation at Josephson frequency. The power emitted by one single junction is tiny, but filling the volume up with many such similar junctions adding up to possibly observable radiation intensity.

The main contribution to radiation intensity is provided by the smallest-scale vortices near dissipation in developed turbulence. The dissipation scale does not contribute, however, because it lacks any junctions. In general Josephson radiation is at low frequency. It will be observed only if the frequency exceeds the ambient plasma frequency cut off. This may be the case in dilute large astrophysical objects like the outskirts of galaxy clusters where huge volume filling factors raise its intensity. Part of its energy is then deposited into weak diffuse radiation in the radio range via the myriads of tiny junctions that form in the course of turbulence. The spectral range is, from the above estimates, of the order of one decade.

Josephson spectra extend down to zero frequency, which implies that Josephson currents are sources of stationary magnetic fields. They generate a magnetic texture independent of any dynamo action.

In all cases a mechanism is needed that produces a cross junction electric potential drop ΔV however weak. This is most probably provided by turbulence. For obtaining any measurable power in field or radiation, it requires a large volume providing large filling factors ξ.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work was part of a brief Visiting Scientist Programme at the International Space Science Institute, Bern. RT acknowledges the interest of the ISSI directorate as well as the generous hospitality of the ISSI staff, in particular, the assistance of the librarians Andrea Fischer and Irmela Schweitzer. We acknowledge valuable discussions with A. Balogh, R. Nakamura, and Z. Vörös. We also acknowledge the constructive suggestions of the referees.

Footnotes

¹When using numbers and dimensions from the magnetosheath or solar wind, we refer to [6, 8]; otherwise, when having in mind astrophysical applications in clusters of galaxies, the appropriate references are [21, 22].

²Quantum effects are ignored when L_n ≫ r₀ ∼ 10^{–10 m} exceeds the atomic radius r₀. L_n enters the Josephson current, while the gauge invariant quantum phase and ν_J remain unaffected. The Josephson effect thus exists always in any junction if ΔV ≠ 0 across the junction, even though L_n suppresses the current amplitude. Phase gauge invariance in such exceptional cases of spontaneous symmetry breaking or Berry’s phase [23, 24] causes observable effects. However, high temperatures would in addition obscure these quantum effects. The Josephson frequency is sufficiently far above any reasonable plasma oscillation frequency and thus spectrally immune against all collisionless temperatures in question. Very high temperatures would destruct any junction, inhibiting the Josephson effect. As long as walls and junctions exist (for example, in mirror modes in the magnetosheath at temperature T ∼ few 10 eV), the Josephson effect will be unavoidable though for small numbers of junctions being undetectable, unless a SQUID is used to monitor the Josephson frequency.

³Temperatures inferred from X ray observations are very high. It they are the true collisional plasma temperatures, no junction survives them, making our model obsolete.

⁴To preclude any misunderstanding, the present investigation does not contribute to turbulence theory. It merely makes use of turbulence as a model providing the potential drop in Josephson junctions. For economic reasons, it restricts itself to the well-established stationary spectral Kolmogorov model in wave number space [26], which, within wide margins, covers the basic physics in collisionless plasma turbulence. We do not refer to any of its moderate refinements, which in the past 80 years since its invention have been constructed in theory as well as from observations. The interested reader is referred to the cited selected literature [cf., e.g., 25, for review of older work].

⁵Strictly speaking, the potential of the induction electric field is V = −∮δE ⋅ ds, which yields δV/δs = −δE, and s projects onto the normal n to the narrow wall of the junction. That part then is the potential difference across the junction, which we write as the above product with n ⋅∇ = n ⋅ ∂/∂s.

⁶A Kolmogorov spectrum is sufficiently general for our purposes here. If restriction is made to mhd or anisotropic turbulence, reference to Iroshnikov-Kraichnan [27] or Goldreich-Shridar [28] turbulence, respectively, would be appropriate.

⁷Josephson oscillations are not damped by themselves. Their decay time is the physical decay time of the junctions, that is, the decay time of the turbulent magnetic vortices. In stationary turbulence, this plays no role because a decaying junction is replaced by some other newly formed one which might have a slightly different Josephson frequency. One thus expects that the bandwidth of the Josephson emissions will be determined mainly by the turbulent fluctuations of scales, which is implicitly taken care of in the assumption of the stationary Kolmogorov spectrum.

⁸Such deviations, if markedly affecting the velocity spectrum, modify the Josephson frequency spectrum on the ion scales. This requires a more precise theory and model of S_v(k) than Kolmogorov. (Some MMS electron observations seem to suggest that the electron spectrum S_e(k) parallels the turbulent spectrum of the electric field S_E(k), which is somewhat flatter than Kolmogorov [44, 45] in this range. Indeed, the currents are carried by electrons and the electric fields are due to current instabilities, mostly kinetic Alfvén waves on these scales. Thus, the relation between S_e(k) ∼ S_E(k) is reasonable. It does however not justify the conclusion that the mechanical turbulence S_v(k) ∼ S_e(k) follows the electrons.) Thus, for being cautious and conservative, we interpret the spectral cut-off k_d accordingly that, if the extension of Kolmogorov’s S_v(k) into the ion range is not warranted by observations, then k_dλ_i ∼ 1, and those wave numbers are understood as already belonging to the dissipative range. They then do contribute to neither Josephson frequency nor radiation.

⁹Briefly leaving our main route, we comment on two sorts of observations (a) in the ion inertial and (b) in the dissipative wave number ranges. (a) Occasionally, large electric field amplitudes have locally been measured [cf., e.g., 37]. Whatsoever the reason is for their generation (which for our purposes is of little interest but should be attributed to nonlinear, that is, higher order, effects such as electron holes or small-scale shocklets) and if the junction concept can be maintained (i.e., presence of magnetic vortices and voids separated by walls), such average potentials would shift ν_J up into the X ray domain although with presumably unobservable current (and radiation) intensity. Singular Josephson effects are unobservable. They could, however, be detected putting a SQUID on the spacecraft to catch the Josephson signal, measuring the electric field with high precision. (b) Observations in the dissipation region (by whatsoever process dissipation is caused) exhibit either exponential or algebraic spectral cut-offs in magnetic turbulence interpreted by different dissipation models of magnetic energy. This range corresponds to our high wavenumber cut-off k_d beyond which no junctions will evolve as the dissipation range is not anymore turbulent, cutting the Josephson frequency sharply at k_d; no other contribution to the turbulent Josephson effect is expected from larger wave numbers.

References

1. Jackson JD. Classical Electrodynamics. New York: John Wiley & Sons (1975).

2. Rybicki GB, Lightman AP. Radiative Processes in Astrophysics. New York: John Wiley & Sons (1979).

3. Schlickeiser R. Cosmic ray Astrophysics. Berlin: Springer (2002).

4. Balogh A, Treumann RA. Physics of Collisionless Shocks. New York: Springer Media (2013). doi:10.1007/978-1-4614-6099-2

CrossRef Full Text

5. Eastwood JP, Lucek EA, Mazelle C, Meziane K, Narita Y, Pickett J, et al. The Foreshock. Space Sci Rev (2005) 118:41–94. doi:10.1007/s11214-005-3824-3

CrossRef Full Text | Google Scholar

6. Lucek EA, Constantinescu D, Goldstein ML, Pickett J, Pinçon JL, Sahraoui F, et al. The Magnetosheath. Space Sci Rev (2005) 118:95–152. doi:10.1007/s11214-005-3825-2

CrossRef Full Text | Google Scholar

7. Haverkorn M, Spangler SR. Plasma Diagnostics of the Interstellar Medium with Radio Astronomy. Space Sci Rev (2013) 178:483–511. doi:10.1007/s11214-013-0014-6

CrossRef Full Text | Google Scholar

8. Goldstein1 ML, Eastwood JP, Treumann RA, Lucek EA, Pickett J, Décréau P. The Near-Earth Solar Wind. Space Sci Rev (2005) 118:7–39. doi:10.1007/s11214-005-3823-4

CrossRef Full Text | Google Scholar

9. Goldstein ML, Roberts DA, Matthaeus WH. Magnetohydrodynamic Turbulence in the Solar Wind. Annu Rev Astron Astrophys (1995) 33:283–325. doi:10.1146/annuref.aa.33.090195.00143510.1146/annurev.aa.33.090195.001435

CrossRef Full Text | Google Scholar

10. Khabarova OV. The Interplanetary Magnetic Field: Radial and Latitudinal Dependences. Astron Rep (2013) 57:844–59. doi:10.1134/S1063772913110024

CrossRef Full Text | Google Scholar

11. Josephson BD. Possible New Effects in Superconductive Tunnelling. Phys Lett (1962) 1:251–3. doi:10.1016/0031-9163(62)91369-0

CrossRef Full Text | Google Scholar

12. Josephson BD. Coupled Superconductors. Rev Mod Phys (1964) 36:216–20. doi:10.1103/RevModPhys.36.216

CrossRef Full Text | Google Scholar

13. Treumann RA, Baumjohann W. Mirror Mode Junctions as Sources of Radiation. Front Astron Space Sci (2021) 8:648744. doi:10.3389/fspas.2021.648744

CrossRef Full Text | Google Scholar

14. Josephson BD. Supercurrents through Barriers. Adv Phys (1965) 14(56):419–51. doi:10.1080/00018736500101091

CrossRef Full Text | Google Scholar

15. Bogoliubov NN. A New Method in the Theory of Superconductivity. I. Soviet Phys JETP (1958) 34(7):41–6.

Google Scholar

16. Valatin JG. Comments on the Theory of Superconductivity. Nuovo Cim (1958) 7:843–57. doi:10.1007/BF02745589

CrossRef Full Text | Google Scholar

17. Fetter AL, Walecka JD. Quantum Theory of many-particle Systems. In: International Series in Pure and Applied Physics, Vol. 601. San Francisco, USA: McGraw-Hill (1971).

Google Scholar

18. Ketterson JB, Song SN. Superconductivity, Chpt. 15. Cambridge, UK: Cambridge University Press (1999).

19. Krall NA, Trivelpiece AW. Principles of Plasma Physics. New York: McGraw-Hill (1973).

20. Baumjohann W, Treumann RA. Basic Space Plasma Physics. Singapore: Imperial College Press, London & World Scientific (1996).

21. Walker S, Simionescu A, Nagai D, Okabe N, Eckert D, Mroczkowski T, et al. The Physics of Galaxy Cluster Outskirts. Space Sci Rev (2019) 215:7. doi:10.1007/s11214-018-0572-8

CrossRef Full Text | Google Scholar

22. Simionescu A, ZuHone J, Zhuravleva I, Churazov E, Gaspari M, Nagai D, et al. Constraining Gas Motions in the Intra-cluster Medium. Space Sci Rev (2019) 215:24. doi:10.1007/s11214-019-0590-1

CrossRef Full Text | Google Scholar

23. Kato T. On the Adiabatic Theorem of Quantum Mechanics. J Phys Soc Jpn (1950) 5:435–9. doi:10.1143/JPSJ.5.435

CrossRef Full Text | Google Scholar

24. Berry MV. Quantal Phase Factors Accompanying Adiabatic Changes. Proc R Soc Lond A (1984) 392:45–57. doi:10.1098/rspa.1984.0023

CrossRef Full Text | Google Scholar

25. Biskamp D. Magnetohydrodynamic Turbulence. Cambridge, UK: Cambridge University Press (2003).

26. Kolmogorov AN. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. Proc R Soc Lond A (1991) 434:9–13. doi:10.1098/rspa.1991.0075

CrossRef Full Text | Google Scholar

27. Iroshnikov PS. Turbulence of a Conducting Fluid in a Strong Magnetic Field. Soviet Astron (1964) 7:566–71. Astronomicheskii Zhurnal 40, 702 (1963)). Available at: http://articles.adsabs.harvard.edu/pdf/1964SvA.....7..566I.

Google Scholar

28. Goldreich P, Sridhar S. Magnetohydrodynamic Turbulence Revisited. ApJ (1997) 485:680–8. doi:10.1086/304442

CrossRef Full Text | Google Scholar

29. Kaneda Y, Gotoh T. Lagrangian Velocity Autocorrelation in Isotropic Turbulence. Phys Fluids A: Fluid Dyn (1991) 3:1924–33. doi:10.1063/1.857922

CrossRef Full Text | Google Scholar

30. Kaneda Y. Lagrangian and Eulerian Time Correlations in Turbulence. Phys Fluids A: Fluid Dyn (1993) 5:2835–45. doi:10.1063/1.858747

CrossRef Full Text | Google Scholar

31. Fung JCH, Hunt JCR, Malik NA, Perkins RJ. Kinematic Simulation of Homogeneous Turbulence by Unsteady Random Fourier Modes. J Fluid Mech (1992) 236:281–318. doi:10.1017/S0022112092001423

CrossRef Full Text | Google Scholar

32. Gotoh T, Fukayama D. Pressure Spectrum in Homogeneous Turbulence. Phys Rev Lett (2001) 86:3775–8. doi:10.1103/PhysRevLett.86.3775

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Treumann RA, Baumjohann W. Spontaneous Magnetic Reconnection. Astron Astrophys Rev (2015) 23:4. doi:10.1007/s00159-015-0087-1

CrossRef Full Text | Google Scholar

34. Gordeev AV, Kingsep AS, Rudakov LI. Electron Magnetohydrodynamics. Phys Rep (1994) 243:215–315. doi:10.1016/0370(94)90097-310.1016/0370-1573(94)90097-3

CrossRef Full Text | Google Scholar

35. Lyutikov M. Electron Magnetohydrodynamics: Dynamics and Turbulence. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88:053103. doi:10.1103/PhysRevE.88.053103

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Lysak RL, Lotko W. On the Kinetic Dispersion Relation for Shear Alfvén Waves. J Geophys Res (1996) 101:5085–94. doi:10.1029/95JA03712

CrossRef Full Text | Google Scholar

37. Bale SD, Kellogg PJ, Mozer FS, Horbury TS, Rème H. Measurement of the Electric Fluctuation Spectrum of Magnetohydrodynamic Turbulence. Phys Rev Lett (2005) 94:215002. doi:10.1103/PhysRevLett.94.215002

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Alexandrova O, Saur J, Lacombe C, Mangeney A, Mitchell J, Schwartz SJ, et al. Universality of Solar-Wind Turbulent Spectrum from MHD to Electron Scales. Phys Rev Lett (2009) 103:165003. doi:10.1103/PhysRevLett.103.165003

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Alexandrova O, Krishna JV, Rossi C, Maksimovic M, Hellinger P, Shprits Y, et al. Kinetic Turbulence in Space Plasmas Observed in the Near-Earth and Near-Sun Solar Wind. arXiv [Epub ahead of print]. (2020).

Google Scholar

40. Alexandrova O, Krishna JV, Rossi C, Maksimovic M, Hellinger P, Shprits Y, et al. Spectrum of Kinetic Plasma Turbulence at 0.3-0.9 Astronomical Units from the Sun. Phys Rev E (2020) 103:063202. doi:10.1103/physreve.103.063202

CrossRef Full Text | Google Scholar

41. Matteini L, Alexandrova O, Chen CHK, Lacombe C. Electric and Magnetic Spectra from MHD to Electron Scales in the Magnetosheath. Mon Not R Astron Soc (2017) 466:945–51. doi:10.1093/mnras/stw3163

CrossRef Full Text | Google Scholar

42. Breuillard H, Matteini L, Argall MR, Sahraoui F, Andriopoulou M, Contel OL, et al. New Insights into the Nature of Turbulence in the Earth's Magnetosheath Using Magnetospheric MultiScale Mission Data. ApJ (2018) 859:127. doi:10.3847/1538-4357/aabae8

CrossRef Full Text | Google Scholar

43. Stawarz JE, Matteini L, Parashar TN, Franci L, Eastwood JP, Gonzalez CA, et al. Comparative Analysis of the Various Generalized Ohm's Law Terms in Magnetosheath Turbulence as Observed by Magnetospheric Multiscale. J Geophys Res Space Phys (2021) 126:e8447. doi:10.1029/2020JA028447

CrossRef Full Text | Google Scholar

44. Stawarz JE, Eriksson S, Wilder FD, Ergun RE, Schwartz SJ, Pouquet A, et al. Observations of Turbulence in a Kelvin-Helmholtz Event on 8 September 2015 by the Magnetospheric Multiscale mission. J Geophys Res Space Phys (2016) 121:021–11. doi:10.1002/2016JA023458

CrossRef Full Text | Google Scholar

45. Gershman DJ, F.-Viñas A, Dorelli JC, Goldstein ML, Shuster J, Avanov LA, et al. Energy Partitioning Constraints at Kinetic Scales in Low-Βturbulence. Phys Plasmas (2018) 25:022303. doi:10.1063/1.5009158

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Treumann RA, Baumjohann W, Narita Y. On the Ion-Inertial-Range Density-Power Spectra in Solar Wind Turbulence. Ann Geophys (2019) 37:183–99. arXiv:1811.09995. doi:10.5194/angeo-37-183-2019

CrossRef Full Text | Google Scholar