
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys., 13 January 2022
Sec. Radiation Detectors and Imaging
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.711317
This article is part of the Research TopicChallenges for Radiation Transport Modelling: Monte Carlo and BeyondView all 13 articles
The development of accurate physics models that enable track structure simulations of electrons in liquid water medium over a wide energy range, from the eV to the MeV scale, is a subject of continuous efforts due to its importance (among other things) in theoretical studies of radiation quality for application in radiotherapy and radiation protection. A few years ago, the Geant4-DNA very low-energy extension of the Geant4 Monte Carlo code had offered to users an improved set of physics models for discrete electron transport below 10 keV. In this work we present refinements to this model set and its extension to energies up to 1 MeV. Preliminary comparisons against the existing Geant4-DNA physics models with respect to total and differential ionization cross sections of electrons in liquid water are reported and discussed.
Theoretical studies of the effects of ionizing radiation in biological cells usually rely on Monte Carlo track-structure (MCTS) simulation codes [1]. The core input in these codes consists of a variety of discrete physics models that permit simulation of each and every interaction of radiation with the transport medium. Thus, MCTS codes may offer molecular resolution at the nanometer scale which is important for investigating radiation action at the cellular and sub-cellular level [2, 3]. This is in contrast to conventional macroscopic MC codes that are based on the condensed-history approach whereby interactions are grouped together and treated by multiple scattering models [4, 5]. In such MC simulations, the spatial resolution is usually at the micro-to milli-meter scale [6].
In medical physics applications, the transport medium is usually represented by liquid water which, to a good approximation, resembles soft tissue in terms of its radiation interaction properties. Although liquid water may be a poor approximation for other body tissues (like bone) or less accurate for specific biomolecules (like DNA), it is still the medium of choice since about 70–80% of the cellular material is composed of water [7]. For MCTS studies at the DNA level, many investigators have developed interaction cross sections specific to DNA bases or constituents to replace those of liquid water (e.g., [8–10]). These efforts rely on well-established atomic models that have been proved reliable for gas-phase molecular targets over a wide energy range and have the added value of being computationally tractable (e.g., [11]). DNA-specific cross sections in the condensed-phase have also been presented based on the dielectric approach [12–14].
MCTS codes are historically considered an important theoretical tool in understanding radiation quality aspects. This connection stems from the recognition that radiation quality originates from the spatial distribution of the discrete energy deposition events in the irradiated medium at the molecular scale [15]. Thus, MCTS codes have been widely used for RBE (relative biological effectiveness) studies in radiotherapy and radiation protection practice [16–21]. Since electrons form the main product of all types of ionizing radiation with significant contribution to absorbed dose and biological damage, the details of their interactions with matter consist a priority of every MCTS code [22]. Thus, discrete electron models of elastic and inelastic scattering is a prerequisite for MCTS simulations, and several such models have been developed [23–25]. Towards this goal, a major obstacle is handling electron interactions down to very low energies (eV scale) given that the physics of electron interactions becomes increasingly complicated [26]. This is especially true for condensed media (liquids and solids) due to long-range screening effects which represent a particularly difficult theoretical problem.
The Geant4 MC code, through its Geant4-DNA very low-energy extension, offers MCTS capabilities down to a few eV [27–30]. For the simulation of low energy electron interactions in liquid water, Geant4-DNA offers three sets of alternative discrete electron models that correspond to different sets of elastic and inelastic scattering cross sections [30]. These sets of models, formally called constructors, are the default “G4EmDNAPhysics_option2” constructor (which will be referred to as Opt2) [28], the “G4EmDNAPhysics_option4” constructor (which will be referred to as Opt4) [31] and the “G4EmDNAPhysics_option6” constructor (which will be referred to as Opt6) [32]. Ionization and excitation cross sections in both Opt2 and Opt4 are based on the dielectric theory of inelastic scattering [7, 25]. This is a key difference against Opt6 which employs analytical atomic models. A benefit of the dielectric approach is that condensed-phase effects are in-built into the methodology through the use of the dielectric response function (DRF) of the medium. The DRF of liquid water medium in both Opt2 and Opt4 is obtained from optical data models that allow, in the framework of the plane wave Born approximation (PWBA), to calculate with only moderate effort, inelastic cross-sections. Opt4 has proved to be more accurate than Opt2 at low electron energies due to the implementation of an improved parameterization algorithm [31]. However, contrary to Opt2 which extends up to 1 MeV, the upper energy of Opt4 is limited to 10 keV [33]. In the present work we report the relativistic extension of Opt4 (hereafter called Opt4Rel) up to 1 MeV along with an improved DRF parameterization that further reduces the sum-rule errors compared to the existing Opt4.
In both the existing (Opt2 and Opt4) and new (Opt4Rel) electron models of Geant4-DNA, the DRF is used to determine the energy-loss function (ELF) of liquid water through the standard expression for bulk media [34, 35]:
where E and q are the energy- and momentum-transfer, respectively, and
In both the existing (Opt2 and Opt4) and new (Opt4Rel) models, five excitation levels (A1B1, B1A1, Ryd A + B, Ryd C + D, db) and four outer shells (1b1, 3a1, 1b2, 2a1) are used and they are analytically represented by a sum of Drude-type functions. The details of the parameterization, however, differ among the models. Specifically, in Opt2 the imaginary part of DRF at the optical limit (q = 0) is represented by:
where
with
It is noteworthy that for each excitation level (k) or ionization shell (n) contribution to the ELF, the denominator of Eq. 5 represents the screening of the entire (outershell) electronic sub-system, i.e., represents the contribution of all k and n. The real part of the DRF,
where
To obtain the ELF for arbitrary values of q, analytic dispersion relations are introduced into the Drude coefficients [33]. These dispersion relations ensure that the ELF has the proper limiting behavior at q = 0 and q = ∞. The dispersion relations used in Geant4-DNA are common to all models (Opt2, Opt4, Opt4Rel).
An important aspect of the dielectric approach is that the fitting of ELF to the experimental data can be tested for internal consistency. In Geant4-DNA models, the following sum-rule constraints have been considered:
f sum-rule:
ELF sum-rule:
KK sum-rule:
where
In all dielectric models of Geant4-DNA (Opt2, Opt4, Opt4Rel), the ELF is used to describe the excitation and ionization of the outer-shell electrons (8 in number) of the water molecule which have condensed-phase properties, while the ionization of the innermost (K-shell) electrons is described by the BEAX model. Although the latter is of an atomic origin and disregards aggregation effects, it is generally considered a reasonable approximation for inner-shell electrons which are minimally perturbed by the phase of the medium.
In the framework of the PWBA, ELF is the only non-trivial material input to calculate inelastic cross sections due to the proportionality relation:
where Q is the free-recoil energy,
where α0 is the Bohr radius, N is the density of water molecules (=3.343 1022 molecules/cm3 in unit density water), T is the non-relativistic incident electron energy and
To calculate inelastic cross sections via Eq. 11, it is necessary to have defined the ELF for arbitrary values of q, i.e., within the limits imposed by Eq. 12. For ionizations, the non-relativistic quadratic (in q) dispersion relation is used and implemented within the Drude functions:
In the framework of the relativistic PWBA (RPWBA), the DICS is obtained as a sum of two terms:
where the subscripts “L” and “T” denote the longitudinal and transverse terms, respectively [38]. The longitudinal DICS reads:
where and β = υ/c with υ the incident electron velocity and c the speed of light, and the relativistic form of the free-recoil energy is
In Opt4Rel, the following relativistic dispersion relation is used:
The transverse DICS term is calculated from:
Note that only collisions with zero momentum transfer (q = 0 or Q = 0) contribute to Eq. 18 according to the small-angle approximation [38].
The low-energy corrections implemented in Opt2 and Opt4 are of two kinds, namely, corrections for exchange (EX) in electron-electron interactions and Coulomb (CB) corrections to account for deviations from first-order perturbation theory [39, 40]. As discussed elsewhere, the existing version of Opt4 includes a more consistent implementation of the low-energy (EX and CB) corrections terms [31, 33]. These improvements are also passed onto Opt4Rel. However, all low-energy (EX and CB) correction terms had to be re-evaluated in Opt4Rel using the new Drude coefficients that enter into the ELF.
The application of low-energy and relativistic corrections implemented in Opt4Rel increase the complexity of the calculations. Therefore, corrections are applied only within the energy regime that have a sizeable effect. In the present work, corrections to PWBA are applied only if they change the total electronic stopping power by at least 0.5–1%. Based on this criterion we distinguish between the following three regimes: 1) in the energy range 0.01–1 keV, we use the PWBA expression, Eq. 8, together with EX and CB corrections; 2) in the energy range 1–100 keV, we use the RPWBA expression, Eq. 10 (but setting the transverse term equal to zero), together with EX and CB corrections; and 3) in the energy range 100–1,000 keV, we use the complete RPWBA expression, Eq. 10.
In this section we report upon the internal consistency of the new ELF model implemented into Opt4Rel based on the estimated sum-rule errors. We also report results on the total and differential ionization cross section and compare the new Opt4Rel model against the default Opt2 and the existing (non-relativistic) Opt4 models. Since the excitation part of the ELF is similar between the new Opt4Rel and the existing (non-relativistic) Opt4, the difference in the corresponding cross section is negligible. Likewise, differences in the excitation cross sections between the new Opt4Rel and the default Opt2 can be inferred from earlier comparisons between Opt4 and Opt2 reported in previous publications [33].
In Figure 1 we compare the sum-rule errors of Opt2, Opt4, and Opt4Rel, which is defined as the deviation of Eqs 7–9 from unity. In all cases a reduction of the sum-rule error is achieved by Opt4Rel (compared to both Opt2 and Opt4), with the error in the f sum-rule being nearly zero, the error in the ELF sum-rule being below 1% and the error in the KK sum-rule being below 2%. The very small errors in the sum rules offer an extra degree of confidence about the internal consistency of our semi-empirical DRF and ELF of the liquid water medium.
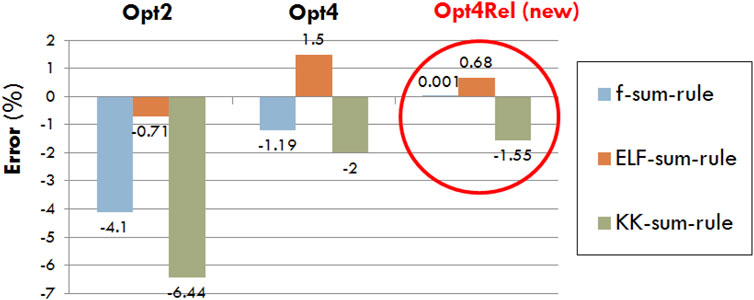
FIGURE 1. Percentage error in the f-, ELF-, and KK-sum-rules for the existing (Opt2 and Opt4) and new (Opt4Rel) Geant4-DNA physics models.
Figure 2 presents a comparison of the total ionization cross section of the default Opt2, the existing non-relativistic Opt4, and the new Opt4Rel models. The comparison between Opt2 and Opt4Rel extends from 10 eV up to 1 MeV (main panel) whereas the comparison against Opt4 (inset) is limited up to 10 keV since this model is not available beyond this energy. It may be seen from Figure 2 that differences between models are most evident at sub-keV energies. Specifically, compared to the default Opt2 model, the ionization cross section of the new Opt4Rel is slightly enhanced (by 5–10%) at high energies (>1 keV) whereas it is significantly lower (up to 50%) at sub-keV energies. These differences are mostly due to the different ELF parameterization that results from the implementation of the Emfietzoglou-Kyriakou algorithm in the new model. Compared to the existing Opt4, the new Opt4Rel is constantly higher (not visible) by about 5% above 32 eV due to the enhanced contribution of the 2a1 shell in the new model. Below the onset of the 2a1 shell, Opt4 and Opt4Rel are nearly identical. Note that Opt4Rel is still much lower than Opt2 at sub-keV energies, so the reported differences between Opt4 and Opt2 in low-energy electron transport should persist with Opt4Rel.
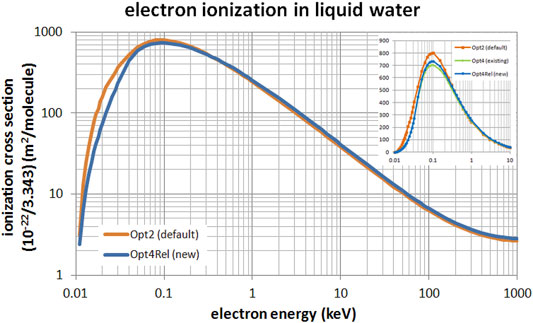
FIGURE 2. Total ionization cross section of electrons in liquid water in the energy range from 10 eV to 1 MeV. Comparison between the default Opt2 and new Opt4Rel Geant4-DNA physics models is shown. The inset focuses on the low-energy range (up to 10 keV) with the addition of the non-relativistic Opt4.
Figures 3, 4 present a comparison of the differential ionization cross section (DICS) between the models. In Figure 3 we compare the new Opt4Rel model against the default Opt2 model at 1 MeV electron energy. Sizeable difference is observed at both the region of the peak (around 20 eV) and at the onset of the 2a1 ionization shell (32 eV). These differences stem (mainly) from the different ELF parameterization in these two models as discussed also above. As the energy-transfer is increased well beyond the 2a1 binding energy (>32 eV) differences gradually diminish. In Figure 4 we compare the new Opt4Rel model against the existing non-relativistic Opt4 model at 1 keV electron energy. As expected, the difference between these two models is restricted around the onset of the 2a1 ionization shell, due to the different Drude coefficients being used for the contribution of this shell. Contrary to Figure 3, no difference around the peak region (20 eV) is observed in Figure 4, due to the similarities of the ELF models of Opt4 and of Opt4Rel in the sub-32 eV energy range. It must be emphasized that the observed differences between the models depicted in Figures 3, 4 persist at almost all electron energies because the DICS is (roughly) proportional to the ELF.
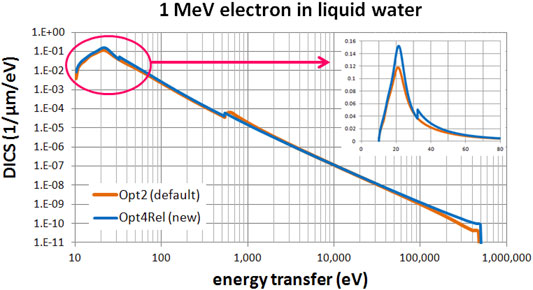
FIGURE 3. Differential ionization cross section (DICS) for 1 MeV electron in liquid water. Comparison between the default Opt2 and new Opt4Rel Geant4-DNA physics models. The inset focuses on the low energy-transfer part (up to 80 eV).
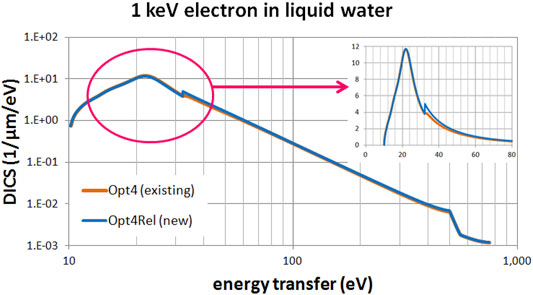
FIGURE 4. Differential ionization cross section (DICS) for 1 keV electron in liquid water. Comparison between the existing Opt4 and new Opt4Rel Geant4-DNA physics models. The inset focuses on the low energy-transfer part (up to 80 eV).
In conclusion, a relativistic extension and improvement of the inelastic model of Opt4 has been developed, offering improved electron transport capabilities from 10 eV up to 1 MeV. The new developments are based on the relativistic plane wave Born approximation and the ELF of the medium which is a slightly improved version of the existing (non-relativistic) Opt4. Work is in progress to further extend the new model up to 10 MeV. Once the complete relativistic extension is validated and benchmarked, the methodology can be extended to other condensed biologica media for which the needed DRF data are available.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
IK and DE have developed the physics models used in the study, performed simulations and written the manuscript. SI has performed benchmarking simulations. All authors contributed in reading, revising and approving the submitted version.
We would like to acknowledge financial support from the France-Greece “Projet International de Cooperation Scientifique (PICS)” #8235. IK and DE acknowledge financial support from European Space Agency (ESA Contract No. 4000126645/19/NL/BW).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Nikjoo H, Uehara S, Emfietzoglou D, Cucinotta FA. Track-structure Codes in Radiation Research. Radiat Measurements (2006) 41:1052–74. doi:10.1016/j.radmeas.2006.02.001
2. Friedland W, Dingfelder M, Kundrát P, Jacob P. Track Structures, DNA Targets and Radiation Effects in the Biophysical Monte Carlo Simulation Code PARTRAC. Mutat Research/Fundamental Mol Mech Mutagenesis (2011) 711:28–40. doi:10.1016/j.mrfmmm.2011.01.003
3. Nikjoo H, Taleei R, Liamsuwan T, Liljequist D, Emfietzoglou D. Perspectives in Radiation Biophysics: From Radiation Track Structure Simulation to Mechanistic Models of DNA Damage and Repair. Radiat Phys Chem (2016) 128:3–10. doi:10.1016/j.radphyschem.2016.05.005
4. Andreo P. Monte Carlo Techniques in Medical Radiation Physics. Phys Med Biol (1991) 36:861–920. doi:10.1088/0031-9155/36/7/001
5. Rogers DW. Fifty Years of Monte Carlo Simulations for Medical Physics. Phys Med Biol (2006) 51:R287–301. doi:10.1088/0031-9155/51/13/R17
6. Dingfelder M. Track Structure: Time Evolution from Physics to Chemistry. Radiat Prot Dosim (2006) 122:16–21. doi:10.1093/rpd/ncl494
7. Dingfelder M. Track-structure Simulations for Charged Particles. Health Phys (2012) 103:590–5. doi:10.1097/hp.0b013e3182621292
8. LaVerne JA, Pimblott SM. Electron Energy-Loss Distributions in Solid, Dry DNA. Radiat Res (1995) 141:208–15. doi:10.2307/3579049
9. Bug MU, Yong Baek W, Rabus H, Villagrasa C, Meylan S, Rosenfeld AB. An Electron-Impact Cross Section Data Set (10 eV-1 keV) of DNA Constituents Based on Consistent Experimental Data: A Requisite for Monte Carlo Simulations. Radiat Phys Chem (2017) 130:459–79. doi:10.1016/j.radphyschem.2016.09.027
10. Zein SA, Bordage MC, Francis Z, Macetti G, Genoni A, Cappello CD, et al. Electron Transport in DNA Bases: An Extension of the Geant4-DNA Monte Carlo Toolkit. Nucl Instrum Meth B (2012) 488:70–82. doi:10.1016/j.nimb.2020.11.021
11. Kim Y-K, Rudd ME. Binary-encounter-dipole Model for Electron-Impact Ionization. Phys Rev A (1994) 50:3954–67. doi:10.1103/physreva.50.3954
12. Abril I, Garcia-Molina R, Denton CD, Kyriakou I, Emfietzoglou D. Energy Loss of Hydrogen- and Helium-Ion Beams in DNA: Calculations Based on a Realistic Energy-Loss Function of the Target. Radiat Res (2011) 175:247–55. doi:10.1667/rr2142.1
13. Abril I, Garcia-Molina R, de Vera P, Kyriakou I, Emfietzoglou D. Inelastic Collisions of Energetic Protons in Biological media. Adv Quan Chem. (2013) 65:129–64. doi:10.1016/b978-0-12-396455-7.00006-6
14. Garcia-Molina R, Abril I, Kyriakou I, Emfietzoglou D. Inelastic Scattering and Energy Loss of swift Electron Beams in Biologically Relevant Materials. Surf Interf Anal. (2017) 49:11–7. doi:10.1002/sia.5947
16. Lindborg L, Hultqvist M, Carlsson Tedgren Å, Nikjoo H. Lineal Energy and Radiation Quality in Radiation Therapy: Model Calculations and Comparison with experiment. Phys Med Biol (2013) 58:3089–105. doi:10.1088/0031-9155/58/10/3089
17. Friedland W, Schmitt E, Kundrát P, Dingfelder M, Baiocco G, Barbieri S, et al. Comprehensive Track-Structure Based Evaluation of DNA Damage by Light Ions from Radiotherapy-Relevant Energies Down to Stopping. Sci Rep (2017) 7:45161. doi:10.1038/srep45161
18. Tang N, Bueno M, Meylan S, Perrot Y, Tran HN, Freneau A, et al. Assessment of Radio-Induced Damage in Endothelial Cells Irradiated with 40 kVp, 220 kVp, and 4 MV X-Rays by Means of Micro and Nanodosimetric Calculations. Ijms (2019) 20:6204. doi:10.3390/ijms20246204
19. Matsuya Y, Kai T, Yoshii Y, Yachi Y, Naijo S, Date H, et al. Modeling of Yield Estimation for DNA Strand Breaks Based on Monte Carlo Simulations of Electron Track Structure in Liquid Water. J Appl Phys (2019) 126:124701. doi:10.1063/1.5115519
20. Margis S, Magouni M, Kyriakou I, Georgakilas AG, Incerti S, Emfietzoglou D. Microdosimetric Calculations of the Direct DNA Damage Induced by Low Energy Electrons Using the Geant4-DNA Monte Carlo Code. Phys Med Biol (2020) 65:045007. doi:10.1088/1361-6560/ab6b47
21. Kyriakou I, Tremi I, Georgakilas AG, Emfietzoglou D. Microdosimetric Investigation of the Radiation Quality of Low-Medium Energy Electrons Using Geant4-DNA. Appl Radiat Isot (2021) 172:109654. doi:10.1016/j.apradiso.2021.109654
22. Emfietzoglou D, Nikjoo H. The Effect of Model Approximations on Single-Collision Distributions of Low-Energy Electrons in Liquid Water. Radiat Res (2005) 163:98–111. doi:10.1667/rr3281
23. Dingfelder M, Inokuti M. The Bethe Surface of Liquid Water. Radiat Environ Biophys (1999) 38:93–6. doi:10.1007/s004110050143
24. Emfietzoglou D, Papamichael G, Nikjoo H. Monte Carlo Electron Track Structure Calculations in Liquid Water Using a New Model Dielectric Response Function. Radiat Res (2017) 188:355–68. doi:10.1667/rr14705.1
25. Nikjoo H, Emfietzoglou D, Liamsuwan T, Taleei R, Liljequist D, Uehara S. Radiation Track, DNA Damage and Response-A Review. Rep Prog Phys (2016) 79:116601. doi:10.1088/0034-4885/79/11/116601
26. Emfietzoglou D, Kyriakou I, Garcia-Molina R, Abril I. Inelastic Mean Free Path of Low-Energy Electrons in Condensed media: beyond the Standard Models. Surf Interf Anal. (2017) 49:4–10. doi:10.1002/sia.5878
27. Incerti S, Baldacchino G, Bernal M, Capra R, Champion C, Francis Z, et al. The Geant4-DNA Project. Int J Model Simul Sci Comput (2010) 01:157–78. doi:10.1142/s1793962310000122
28. Incerti S, Ivanchenko A, Karamitros M, Mantero A, Moretto P, Tran HN, et al. Comparison ofGEANT4very Low Energy Cross Section Models with Experimental Data in Water. Med Phys (2010) 37:4692–708. doi:10.1118/1.3476457
29. Bernal MA, Bordage MC, Brown JMC, Davídková M, Delage E, El Bitar Z, et al. Track Structure Modeling in Liquid Water: A Review of the Geant4-DNA Very Low Energy Extension of the Geant4 Monte Carlo Simulation Toolkit. Physica Med (2015) 31:861–74. doi:10.1016/j.ejmp.2015.10.087
30. Incerti S, Kyriakou I, Bernal MA, Bordage MC, Francis Z, Guatelli S, et al. Geant4-DNA Example Applications for Track Structure Simulations in Liquid Water: A Report from the Geant4-DNA Project. Med Phys (2018) 45:722–39. doi:10.1002/mp.13048
31. Kyriakou I, Incerti S, Francis Z. Technical Note: Improvements in Geant 4 Energy-Loss Model and the Effect on Low-Energy Electron Transport in Liquid Water. Med Phys (2015) 42:3870–6. doi:10.1118/1.4921613
32. Bordage MC, Bordes J, Edel S, Terrissol M, Franceries X, Bardiès M, et al. Implementation of New Physics Models for Low Energy Electrons in Liquid Water in Geant4-DNA. Physica Med (2016) 32:1833–40. doi:10.1016/j.ejmp.2016.10.006
33. Kyriakou I, Šefl M, Nourry V, Incerti S. The Impact of New Geant4-DNA Cross Section Models on Electron Track Structure Simulations in Liquid Water. J Appl Phys (2016) 119:194902. doi:10.1063/1.4950808
34. Kyriakou I, Emfietzoglou D, Garcia-Molina R, Abril I, Kostarelos K. Simple Model of Bulk and Surface Excitation Effects to Inelastic Scattering in Low-Energy Electron Beam Irradiation of Multi-Walled Carbon Nanotubes. J Appl Phys (2011) 110:054304. doi:10.1063/1.3626460
35. Nikjoo H, Uehara S, Emfietzoglou D. Interaction of Radiation with Matter. Boca Raton, FL: CRC Press (2012). p. 348.
36. Heller JM, Hamm RN, Birkhoff RD, Painter LR. Collective Oscillation in Liquid Water. J Chem Phys (1974) 60:3483–6. doi:10.1063/1.1681563
37. Hayashi H, Watanabe N, Udagawa Y, Kao C-C. The Complete Optical Spectrum of Liquid Water Measured by Inelastic X-ray Scattering. Proc Natl Acad Sci (2000) 97:6264–6. doi:10.1073/pnas.110572097
38. Fernández-Varea JM, Llovet X, Salvat F. Cross Sections for Electron Interactions in Condensed Matter. Surf Interf Anal. (2005) 37:824–32. doi:10.1002/sia.2101
39. Emfietzoglou D, Kyriakou I, Garcia-Molina R, Abril I, Nikjoo H. Inelastic Cross Sections for Low-Energy Electrons in Liquid Water: Exchange and Correlation Effects. Radiat Res (2013) 180:499–513. doi:10.1667/rr13362.1
Keywords: Geant4-DNA, Monte Carlo, track structure, dielectric function, cross sections
Citation: Kyriakou I, Emfietzoglou D and Incerti S (2022) Status and Extension of the Geant4-DNA Dielectric Models for Application to Electron Transport. Front. Phys. 9:711317. doi: 10.3389/fphy.2021.711317
Received: 18 May 2021; Accepted: 07 December 2021;
Published: 13 January 2022.
Edited by:
Vasilis Vlachoudis, European Organization for Nuclear Research (CERN), SwitzerlandReviewed by:
Tuba Conka Yildiz, Türkisch-Deutsche Universität, TurkeyCopyright © 2022 Kyriakou, Emfietzoglou and Incerti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ioanna Kyriakou, aWt5cmlha0B1b2kuZ3I=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.