- 1Chernivtsi National University, Chernivtsi, Ukraine
- 2Rivne Regional Clinical Hopital, Rivne, Ukraine
- 3Institute of Traumathology and Orthopedics of NAMS, Kyiv, Ukraine
- 4Research Institute of Zhejiang University, Taizhou, China
The possibilities of the diagnostic use of the singular approach of the distributions of the number of characteristic values of the MMI is effective for differentiating the polarization properties of histological biopsy sections of benign and malignant tumours of the uterus and prostate. Within the framework of evidence-based medicine, the sensitivity, specificity and accuracy of the azimuthal-invariant express (∼15 min) method of Mueller-matrix mapping of polarization-singular states in the differential diagnosis of uterine myoma and adenocarcinoma, as well as adenocarcinoma of the prostate with varying degrees of differentiation have been determined.
Introduction
In biomedical optics, polarized light plays a decisive role in understanding and detecting the processes of conversion of electromagnetic waves by optically anisotropic structures of human biological tissues [1–20]. The most important analytical direction in the development of diagnostic techniques using polarization probing of biological layers is the Mueller-matrix formalism [10]. This approach provides the most complete information on the optical anisotropy of diagnostic objects. Several key strands of investigation have emerged, including: Mueller matrix polarimetry (MMP) [21–24] polar decomposition of Mueller matrices [25, 26]; and two [27–32] dimensional Mueller matrix mapping (MMM) using various approximations [19, 20, 33].
One of the main tasks of MMP is to detect and differentiate the type of oncological changes that occur in the tissues of human organs. Using MMM methods [14–16, 23–26], the possibility of differential diagnosis of histological sections of biopsy of benign and malignant tumours of the prostate, endometrium, cervix, breast, etc. has been demonstrated. However, the further successful development of MMP restrains a number of theoretical and experimental problems that have not been resolved to the end:
❖ Azimuthal dependence of the value of 12 out of 16 elements of the Mueller matrix, which worsens the accuracy of MMM methods in the process of serial measurements of histological preparations;
❖ Significant “computational” time required for processing large arrays of experimental data obtained by polar decomposition of Mueller matrices and two-dimensional MMM;
❖ Distorting effect of the depolarized background on the Mueller-matrix detection of optical anisotropy of tissue samples of human organs [34].
One of the options for a comprehensive solution to these MMP problems can be the synthesis of MMM methods of optically thin (non-depolarizing) biological preparations and the principles of polarization-singular analysis of their object fields [1–5, 7, 9]. The main idea of this approach is that for such layers there are direct relationships between the points of linear (“
At this point in time in biomedical optics, singular approaches were applied in so far, few publications [35–37]. Here, for the first time, the analytical conditions for the formation of singly (linear) and doubly degenerate (circular) polarization singularities of images of linearly birefringent biological tissues are determined. The distributions of the number of polarization singular states in the images of such biological tissues are experimentally investigated. It has been demonstrated that the statistical moments, which characterize the distributions of the number of singular points in the object field, are sensitive to changes in morphological structure of biological tissues of various physiological state.
However, this direction of biomedical diagnostics remains poorly researched and requires further extension of the ideology of the singularity of optical fields to methods and means of one of the most effective optical technologies–azimuthally invariant MMP of the polycrystalline component of pathologically altered tissues of various human organs.
Our work is aimed at:
❖Identification of analytical relationships between polarization-singular states of the object field of optically thin anisotropic layers of tissues of the uterus and prostate and characteristic values of their Mueller-matrix images;
❖Development of a new azimuthally invariant Mueller-matrix polarization-singular technique for serial and express (∼15 min) measurements for differential diagnosis of changes in optical anisotropy caused by tumours of uterus (malignant myoma and malignant adenocarcinoma) and prostate (adenocarcinoma with different malignant grades) tissues.
The relevance of such studies is associated with the widespread prevalence and high mortality caused by these cancers.
Prostate cancer is the second most common cancer globally in men, and in some countries is now the most diagnosed form of cancer [38, 39]. Early diagnosis, intervention, and management can give significantly improved patient outcomes [40]. It is necessary to differentiate between malignant (carcinoma) grades of tumour tissues [41]. A similar situation is realized for uterine cancer, which ranks fourth among women oncological diseases [42].
Brief Theory and Basic Relations
In a polarization-inhomogeneous field, the existence of lines or surfaces is possible, at each point of which an indefinite (singular) one of its parameters [1–5, 7, 9]:
1) points of circular polarization of the field (“C”-point), in which the polarization ellipse degenerates into a circle and, accordingly, the direction of the main axis (azimuth) of the polarization ellipse is uncertain;
2) points with linear polarization (“L”-point), which are degenerate in the direction of rotation of the electric vector.
The characteristic values of the fourth parameter
Here
At the same time, the analytical representation of the grid of polarization singularities of the object field of laser radiation does not carry direct information about the polycrystalline structure of the biological layer—the distributions of the directions of the optical axes
The fact is that the process of formation of a polarization-inhomogeneous field can be represented by a superposition of two main mechanisms:
❖ “object”-phase modulation [
❖ “diffractive”—secondary phase modulation [
Therefore, in each zone of laser radiation diffraction, the maps of polarization singularities [
Overcoming this problem can be the use of the Mueller-matrix formalism [10] in the description of the processes of the formation of the polarization-singular structure of the object field of an optically anisotropic biological layer. This approach provides unambiguous information on the relationships between the maps of polarization singularities and the parameters of the polycrystalline birefringent structure of fibrillar networks.
Within the framework of the model of birefringence of spatially structured fibrillar networks of the biological layer, developed in numerous studies [12–16, 18, 27–32], one can write the following expression for the Mueller matrix
where
Here
The Mueller-matrix formalism for describing the birefringent properties of biological tissues makes it possible to exhaustively describe the formation of polarization at the points (
Here
In expanded form, matrix Eq. 6 is rewritten as a system of four linear equations with coefficients
Taking into account relations Eqs 4–, expressions Eq. 3, which characterize the Stokes-polarimetric relationships Eqs 1, 2 of maps of polarization singularities and parameters of the polycrystalline birefringent structure of fibrillar networks, take the following form
Analysis of expressions Eq. 9 reveals two main dependences of formation
❖ “polarizing”
❖ “azimuth”
Hence (expressions Eqs 10, 11) there are significant limitations in the use of the Stokes-parametric approach in diagnostic serial measurements of maps of polarization singularities of a large number of biological preparations. Even in the situation of a constant polarization state (
To overcome this problem of Stokes polarimetry, we considered the diagnostic capabilities of the polarization-singular approach using the Mueller-matrix formalism.
Based on relations Eqs 3–5, it is possible to determine diagnostically important relationships between the characteristic values of the elements of the Mueller matrix of the conditions of formation

TABLE 1. Relationships between the characteristic values of the Mueller matrix elements and the singularity of polarization-inhomogeneous images of birefringent biological tissue.
The analysis of the ratios given in Table 1 revealed an azimuthal dependence of the formation of characteristic values
Measurement and Analysis of Experimental Data
In Figure 1 shows the optical scheme of Stokes polarimetry [14, 15] of the coordinate distributions of the Mueller-matrix invariant
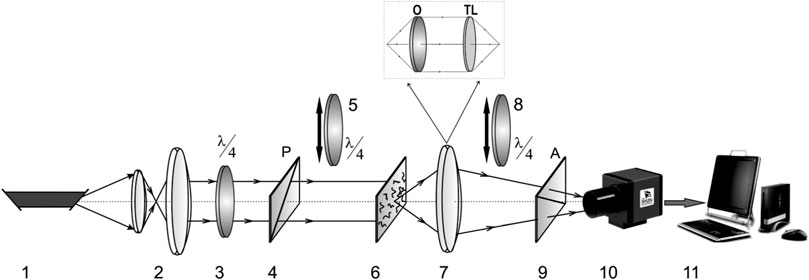
FIGURE 1. Optical scheme of laser Stokes-polarimeter of human organs histological sections. Here 1—He-Ne laser; 2—collimator; 3, 5, 8—quarter-wave plates; 4, 9—polarizer and analyzer respectively; 6—object of investigation; 7—optical system; 10—CCD camera; 11—PC.
The optical and metrological parameters of the Stokes-polarimeter are presented in detail in a series of publications [14, 15, 27–32]. Here we give a brief description of them, which is necessary for a better understanding of the further presentation of the experimental material.
Illumination of samples was performed by parallel (
The technique of experimental measurement of the set of characteristic elements of the Mueller-matrix invariant
1) Formation of the basic right-hand circularly polarized probing beam—the angle between the plane of polarization of the laser beam and the axis of the highest velocity of the quarter-wave plate—
2) Isolation by sequential polarization filtering of a set of partial plane and circularly polarized laser probes with the following parameters:
❖ azimuth of linear polarization
❖ azimuth of linear polarization
❖ introduction of a quarter-wave plate 5 into the optical path and rotation of the axis of its highest velocity by an angle
3) Projection by a polarizing microobjective 7 for each of the laser probes of the image of a histological section of a preparation of a uterine tumour into the plane of the photosensitive area of a digital camera 10.
4) Polarization selection of the right- and left-circularly polarized components of the object field at the points of the microscopic image by rotating the axis of the highest velocity of the quarter-wave plate 8 at angles
5) Calculations within each pixel of CCD camera 10 of the ensemble (
Here
Here
6) The accuracy of determining the value
7) By line-by-line scanning (
8) We calculated [14, 15, 42] the central statistical moments of the first–second orders, which characterize the average and dispersion of the distribution
Here
Characteristics of Research Objects
For the purpose of express (∼15 min) differential diagnosis of benign (myoma) and malignant (adenocarcinoma of varying degrees of differentiation), optically thin single-scattering histological sections of uterine tumours were made on a microtome with rapid freezing during the operation.
Three representative groups of histological biopsy sections of tumours were formed:
• Group 1 consisted of
• Group 2 consisted of
• Group 3 consisted of
The type of uterus tumour was determined by an independent assessment of stained histological samples (Figure 2).
❖ Fixation of prostate tissue with formalin (40% formaldehyde aqueous solution);
❖ Washing samples in running water for 24 h;
❖ Dehydration with alcohols with increasing concentration (70–100%) within 48 h;
❖ Fixing the material in a mixture of xylene-paraffin for 1–2 h at a temperature of
❖ Production of histological sections on a standard microtome;
❖ Staining of histological sections with hematoxylin-eosin (Figure 2 shows microscopic images in real colors);
❖ Microscopic examination of images of the obtained preparations with differentiation of their structure by grade and determination of the position of the prostate tumor sample according to the Gleason scale.
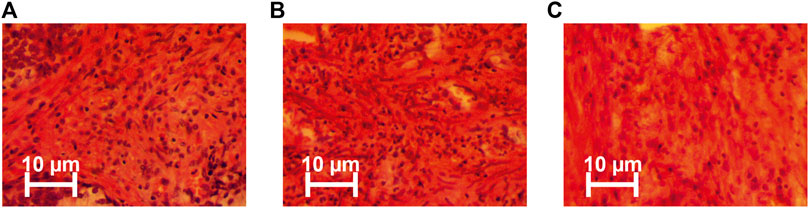
FIGURE 2. Representative microscopic images (magnification 50x) of: (A) myoma, (B) high differentiated adenocarcinoma, and (C) poorly differentiated uterus adenocarcinoma. The procedure for histological analysis included the following steps [43].
Table 2 presents the optical and geometric parameters of the samples of native histological sections of prostate tumour biopsies from each of the groups.
The geometric thickness (
The extinction coefficient (
The measurement of the integral degree of depolarization (
The experimental data presented in Table 2 indicate the adequacy of our model analysis of the phase modulation of laser radiation by birefringent fibrillar networks (relations Eqs 4–11, Table 1)—within the statistically reliable samplings of samples of all groups, the conditions of single scattering are realized (
To determine the statistical significance of a representative sampling of the number of samples by the cross-validation method [46], the standard deviation
Results
In the series in Figures 3–5 are presented:
❖Coordinate distributions of the value of the Mueller-matrix invariant
❖Maps of characteristic values
❖Maps of characteristic values
❖ Analysis of 2D mapping data (Figures 3–5) the values of the Mueller-matrix invariant
❖ The presence of characteristic values
❖sequential increase in the number of characteristic values
❖the opposite trend for maps
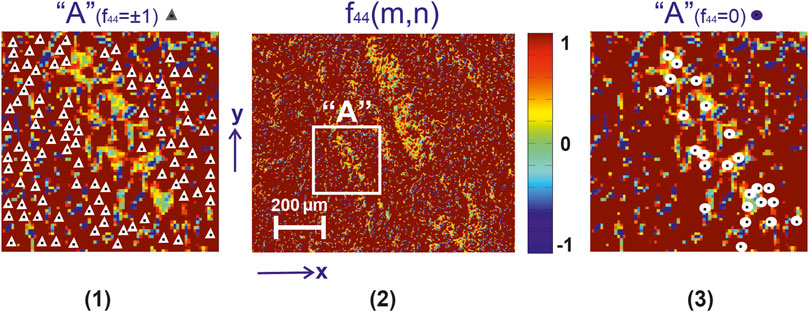
FIGURE 3. Mueller-matrix image [fragment (2)] of the azimuthal invariant
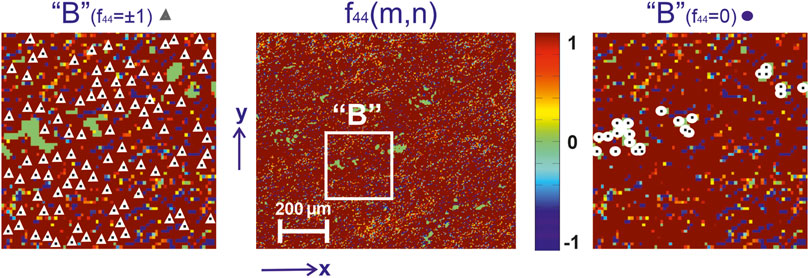
FIGURE 4. Mueller-matrix image [fragment (2)] of the azimuthal invariant
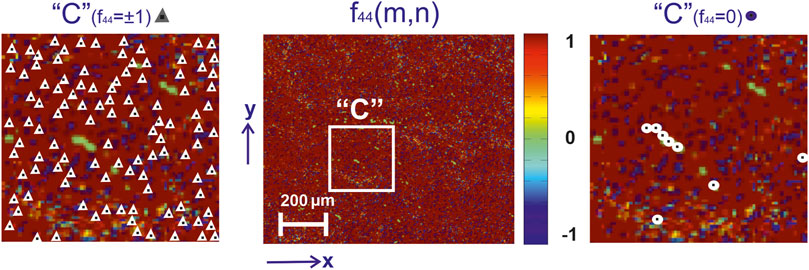
FIGURE 5. Mueller-matrix image (fragment (2)) of the azimuthal invariant
From a physical point of view, these results can be associated with the processes of necrotic destruction of birefringent fibrillar networks of the uterine tissue during the formation of benign neoplasms (myoma) of malignant adenocarcinomas with varying degrees of differentiation. As a result, the level of phase modulation (
These processes quantitatively illustrate the distributions
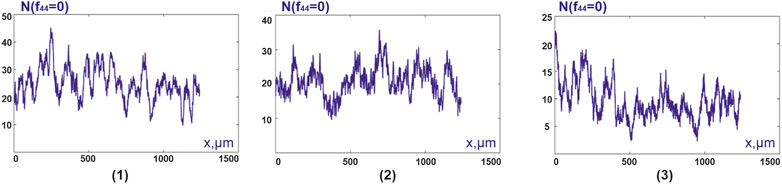
FIGURE 6. Distributions
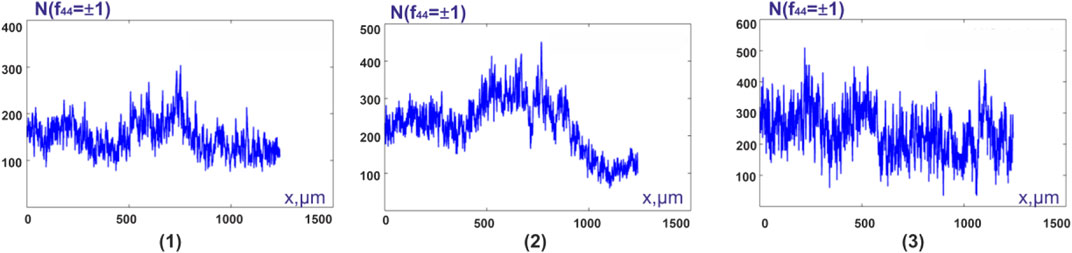
FIGURE 7. Distributions
The results of the statistical analysis of the distributions

TABLE 3. Statistical moments of the first and second orders, which characterize the distribution

TABLE 4. Statistical moments of the first and second orders, which characterize the distribution
Here are the mean (
From the data given in Table 3 it follows:
statistical moments of the first and second orders, which characterize the distributions
for the statistical moment of the first order, which characterizes the distribution
statistically significant in differential and intergroup diagnostics are the values for the statistical moment of the second order, which characterizes the distribution
From the data given in Table 4 it follows:
❖ for the statistical moments of the first and second orders, which characterize the average and dispersion of the distributions
❖ Intergroup diagnostics of samples of histological sections of biopsy of adenocarcinoma with a high and low degree of differentiation turned out to be statistically unreliable,—
Clinical Applications
With the aim of the possible clinical application of the data of Mueller-matrix mapping of polarization-singular distributions of characteristic values
To differentiate benign and malignant tumours, for each of the statistical moments
Similarly, to differentiate the grade of cancer, the sensitivity (
Tumours of the Uterus
The results of information analysis using statistical processing of the set of distributions of characteristic values
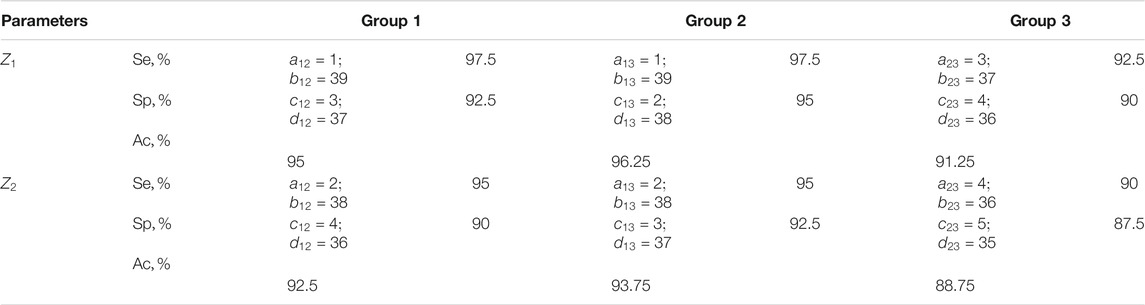
TABLE 5. Sensitivity, specificity, balanced accuracy of statistical analysis of distributions of characteristic values
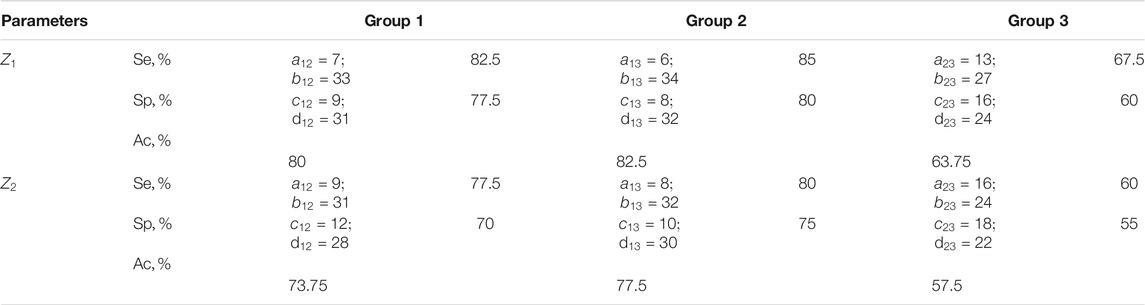
TABLE 6. Sensitivity, specificity, balanced accuracy of statistical analysis of distributions of characteristic values
The results shown in Tables 5, 6 indicate:
❖ a high (91.25–96.25%) efficiency of differential diagnosis of uterus tumours by Mueller matrix mapping of histological biopsy sections of myoma and adenocarcinoma with varying degrees of differentiation by statistical analysis of distributions of characteristic values
❖ low efficiency (80–82.5%) of statistical analysis of experimental data of polarization-singular Mueller-matrix differentiation of samples of benign and malignant tumours of the uterus;
❖ unsatisfactory accuracy (57.5–63.75%) of intergroup differentiation based on the data of statistical analysis of distributions of characteristic values
Tumours of the Prostate
Three Representative Groups of Histological Biopsy Sections of Tumours Were Formed:
• Group 1 consisted of
• Group 2 consisted of
• Group 3 consisted of
Table 7 presents the optical and geometric parameters of the samples of native histological sections of prostate tumour biopsies from each of the groups.
The results of information analysis using statistical processing of the set of distributions of characteristic values
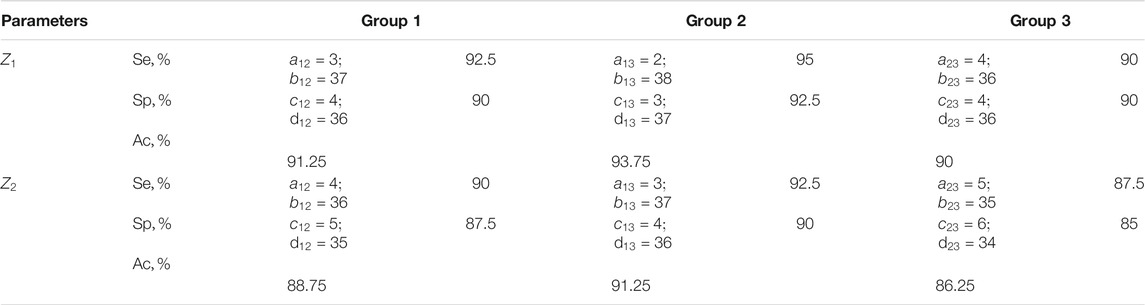
TABLE 8. Sensitivity, specificity, balanced accuracy of statistical analysis of distributions of characteristic values
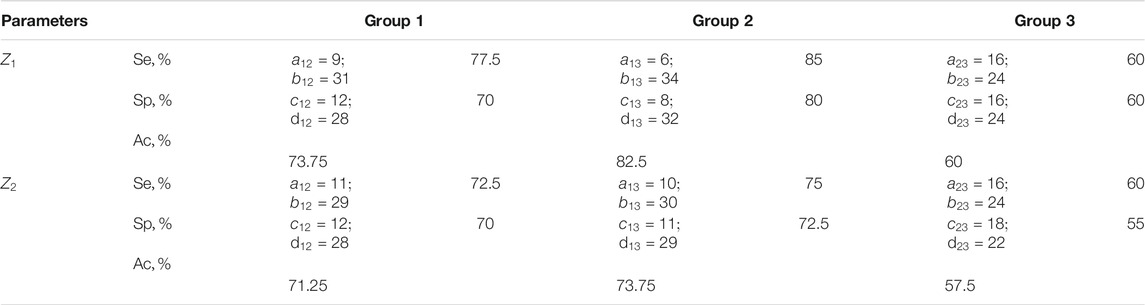
TABLE 9. Sensitivity, specificity, balanced accuracy of statistical analysis of distributions of characteristic values
The results shown in Table 8 indicate a high (90–93.75%) efficiency of differential diagnosis of prostate tumours by Mueller matrix mapping of histological sections of biopsy of adenocarcinoma with varying degrees of differentiation by means of a statistical analysis of distributions
The efficiency of differentiation of the degree of statistical analysis of the experimentally obtained distributions of characteristic values
Conclusions
1) For the first time, the Mueller-matrix approach to the described processes of the formation of polarization-singular states of microscopic images of optically thin histological sections of biopsy of benign and malignant tumours of the uterus and prostate was proposed.
2) The relationship between the characteristic values of the elements of the Mueller matrix and the types of singularity of polarization-inhomogeneous images of optically anisotropic biological preparations of fibroids (uterus) and adenocarcinomas with varying degrees of differentiation (uterus, prostate) has been established.
3) It was found that the statistical analysis of the distributions of the number of characteristic values of the Mueller-matrix invariant, which characterizes the mechanisms of formation
4) Within the framework of evidence-based medicine, the sensitivity, specificity and accuracy of the method of azimuthal-invariant mapping of the characteristic values of the Mueller-matrix invariant distributions have been established:
❖ A high (91.25–96.25%) efficiency of differential diagnosis of uterus tumours by Mueller matrix mapping of histological sections of biopsy of myoma and adenocarcinoma with varying degrees of differentiation by statistical analysis of distributions of characteristic values
❖ A high (90–93.75%) efficiency of differential diagnosis of prostate tumours by Mueller matrix mapping of histological biopsy sections of adenocarcinoma with varying degrees of differentiation by means of a statistical analysis of distributions
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by the Ethical approval was obtained from the Ethics Committee of the Bureau of Forensic Medicine of the Chernivtsi National University and the Bukovinian State Medical University (Chernivtsi, Ukraine), and written informed consent was obtained from all subjects prior to study initiation. The patients/participants provided their written informed consent to participate in this study.
Author Contributions
Manuscript preparation: AU, VU, and LT. Measurements, data processing: AS, IS, YU, YT, AD, VG and PG.
Funding
This work received funding from National Research Foundation of Ukraine, Project 2020.02/0061.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Freund I, Soskin MS, Mokhun AI. Elliptic Critical Points in Paraxial Optical fields. Opt Commun (2002) 208:223–53. doi:10.1016/s0030-4018(02)01585-7
2. Soskin MS, Denisenko V, Freund I. Optical Polarization Singularities and Elliptic Stationary Points. Opt Lett (2003) 28:1475–7. doi:10.1364/ol.28.001475
3. Dennis MR. Polarization Singularities in Paraxial Vector fields: Morphology and Statistics. Opt Commun (2002) 213:201–21. doi:10.1016/s0030-4018(02)02088-6
4. Nye JF. Lines of Circular Polarization in Electromagnetic Wave fields. Proc R Soc Lond A (1983) 389:279–90. doi:10.1098/rspa.1983.0109
5. Flossmann F, Schwarz UT, Maier M, Dennis MR. Polarization Singularities from Unfolding an Optical Vortex through a Birefringent crystal. Phys Rev Lett (2005) 95:253901. doi:10.1103/physrevlett.95.253901
6. Flossmann F, Schwarz UT, Maier M, Dennis MR. Stokes Parameters in the Unfolding of an Optical Vortex through a Birefringent crystal. Opt Express (2006) 14:11402–11. doi:10.1364/oe.14.011402
7. Аngelsky O, Besaha R, Mokhun A, Mokhun I, Sopin M, Soskin M. Vasnetsov M Singularities in Vectoral fields SPIE. Proc (1999) 3904:40–55. doi:10.1117/12.370443
8. Freund I, Mokhun AI, Soskin MS, Angelsky OV, Mokhun II. Stokes Singularity Relations. Opt Lett (2002) 27(7):545–7. doi:10.1364/ol.27.000545
9. Berry MV, Dennis MR. Polarization Singularities in Isotropic Random Vector Waves. Proc R Soc Lond A (2001) 457:141–55. doi:10.1098/rspa.2000.0660
10. Bickel WS, Bailey WM. Stokes Vectors, Mueller Matrices, and Polarized Scattered Light. Am J Phys (1985) 53:468–78. doi:10.1119/1.14202
11. Lu S-Y, Chipman RA. Interpretation of Mueller Matrices Based on Polar Decomposition. J Opt Soc Am A (1996) 13:1106–13. doi:10.1364/josaa.13.001106
12. Ghosh N, Wood M, Vitkin A. Polarized Light Assessment of Complex Turbid Media Such as Biological Tissues Using Mueller Matrix Decomposition. Science (2010) 9:253–82. doi:10.1201/9781439806296-c9
13. Gil JJ. Characteristic Properties of Mueller Matrices. J Opt Soc Am A (2000) 17:328–34. doi:10.1364/josaa.17.000328
14. Angelsky O, Ushenko A, Ushenko Y, Pishak V, Peresunko A. Correlation and Topological Approaches in Diagnostics of the Structure and Physiological State of Birefringent Biological Tissues. in: Handbook Of Photonics For Biomedical Science (2010). p. 283–322. doi:10.1201/9781439806296-c10
15. Ushenko YA, Boychuk TM, Bachynsky VT, Mincer OP. Diagnostics of Structure and Physiological State of Birefringent Biological Tissues: Statistical, Correlation and Topological Approaches Handbook Of Coherent-Domain Optical Methods (2013), New York, NY: Springer. p. 107–48. doi:10.1007/978-1-4614-5176-1_3
16. Ghosh N. Tissue Polarimetry: Concepts, Challenges, Applications, and Outlook. J Biomed Opt (2011) 16:110801. doi:10.1117/1.3652896
17. Jacques SL, Boas D, Pitris C. Ramanujam N Polarized Light Imaging of Biological Tissues Handbook Of Biomedical Optics. Boca Raton, London, New York: CRC Press (2011). 649–69.
18. Vitkin A, Ghosh N, Martino Ad.. Tissue Polarimetry in Photonics: Scientific Foundations, Technology And Applications. in: DL Andrews, editor, IV. Hoboken, New Jersey: John Wiley & Sons (2015). 239–321. doi:10.1002/9781119011804.ch7
19. Tuchin VV. Tissue Optics and Photonics: Light-Tissue Interaction. Jbpe (2015) 1:98–134. doi:10.18287/jbpe-2015-1-2-98
20. Tuchin VV. Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis. 3rd ed. Bellingham, WA: Society of Photo-Optical Instrumentation Engineers SPIE Press (2015). doi:10.1117/3.1003040
21. Swami MK, Patel HS, Gupta PK. Conversion of 3×3 Mueller Matrix to 4×4 Mueller Matrix for Non-depolarizing Samples. Opt Commun (2013) 286:18–22. doi:10.1016/j.optcom.2012.08.094
22. Izotova VF, Maksimova IL, Nefedov IS, Romanov SV. Investigation of Mueller Matrices of Anisotropic Nonhomogeneous Layers in Application to an Optical Model of the Cornea. Appl Opt (1997) 36:164. doi:10.1364/ao.36.000164
23. Manhas S, Swami MK, Buddhiwant P, Ghosh N, Gupta PK, Singh J. Mueller Matrix Approach for Determination of Optical Rotation in Chiral Turbid media in Backscattering Geometry. Opt Express (2006) 14:190. doi:10.1364/opex.14.000190
24. Deng Y, Zeng S, Lu Q, Zhu D, Luo Q. Characterization of Backscattering Mueller Matrix Patterns of Highly Scattering media with Triple Scattering assumption. Opt Express (2007) 15:9672. doi:10.1364/oe.15.009672
25. Lu S-Y, Chipman RA. Interpretation of Mueller Matrices Based on Polar Decomposition. J Opt Soc Am AA (1996) 13:1106. doi:10.1364/josaa.13.001106
26. Guo Y, Zeng N, He H, Yun T, Du E, Liao RA Study on Forward Scattering Mueller Matrix Decomposition in Anisotropic Medium. Opt Express (2013) 21:18361. doi:10.1364/oe.21.018361
27. Borovkova M, Peyvasteh M, Dubolazov O, Ushenko Y, Ushenko V, Bykov A, et al. Complementary Analysis of Mueller-Matrix Images of Optically Anisotropic Highly Scattering Biological Tissues. J Eur Opt Soc.-Rapid Publ (2018) 14(1):20. doi:10.1186/s41476-018-0085-9
28. Ushenko V, Sdobnov A, Syvokorovskaya A, Dubolazov A, Vanchulyak O, Ushenko A, et al. 3D Mueller-Matrix Diffusive Tomography of Polycrystalline Blood Films for Cancer Diagnosis. Photonics (2018) 5(4):54. doi:10.3390/photonics5040054
29. Ushenko A, Sdobnov A, Dubolazov A, Grytsiuk M, Ushenko Y, Bykov A. Meglinski I Stokes-Correlometry Analysis of Biological Tissues with Polycrystalline Structure. IEEE J Selected Top Quan Electro (2019) 25(1):8438957. doi:10.1109/jstqe.2018.2865443
30. Trifonyuk L, Baranowski W, Ushenko V, Olar O, Dubolazov A, Ushenko Y, et al. 2D-Mueller-matrix Tomography of Optically Anisotropic Polycrystalline Networks of Biological Tissues Histological Sections. Opto-electronics Rev (2018) 26(3):252–9. doi:10.1016/j.opelre.2018.07.001
31. Trifonyuk L, Sdobnov A, Baranowski W, Ushenko V, Olar O, Dubolazov A, et al. Differential Mueller Matrix Imaging of Partially Depolarizing Optically Anisotropic Biological Tissues. Lasers Med Sci (2020) 35(4):877–91. doi:10.1007/s10103-019-02878-2
32. Borovkova M, Trifonyuk L, Ushenko V, Dubolazov O, Vanchulyak O, Bodnar G, et al. Mueller-matrix-based Polarization Imaging and Quantitative Assessment of Optically Anisotropic Polycrystalline Networks. PLoS ONE (2019) 14(5):e0214494. doi:10.1371/journal.pone.0214494
33. Wang LV, Wu H-I. Biomedical Optics: Principles and Imaging. John Wiley & Sons (2009). doi:10.1002/9780470177013
34. Ushenko VA, Hogan BT, Dubolazov A, Grechina AV, Boronikhina TV, Gorsky M, et al. Embossed Topographic Depolarisation Maps of Biological Tissues with Different Morphological Structures. Sci Rep (2021) 11(1):3871. doi:10.1038/s41598-021-83017-2
35. Angelsky OV, Ushenko AG, Ushenko YA, Ushenko YG. Polarization Singularities of the Object Field of Skin Surface. J Phys D: Appl Phys (2006) 39:3547–58. doi:10.1088/0022-3727/39/16/005
36. Angelsky Ov Ushenko AG, Angelska AO. Ushenko YuA Correlation- and Singular-Optical Approaches in Diagnostics of Polarization Inhomogeneity of Coherent Optical fields from Biological Tissues Ukr. J Phys Opt (2007) 8(2):105–23. doi:10.3116/16091833/8/2/106/2007
37. Ushenko VO, Trifonyuk L, Ushenko YA, Dubolazov OV, Gorsky MP, Ushenko AG. Polarization Singularity Analysis of Mueller-Matrix Invariants of Optical Anisotropy of Biological Tissues Samples in Cancer Diagnostics. J Opt (2021) 23(6):064004. doi:10.1088/2040-8986/abf97a
38. Mohler J. Prostate Cancer J Natl Compr Cancer Netw (2010) 8:162–200. doi:10.6004/jnccn.2010.0010
40. Ilic D, Neuberger MM, Djulbegovic M, Dahm P. Screening for Prostate Cancer Cochrane Database Of Systematic Reviews (2013).
41. Albertsen PC, Hanley JA. 20-Year Outcomes Following Conservative Management of Clinically Localized Prostate Cancer. Jama (2005) 293:2095–101. doi:10.1001/jama.293.17.2095
42. Sung H, Ferlay J, Siegel RL, Laversanne M, Soerjomataram I, Jemal A, et al. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA A Cancer J Clin (2021) 71:209–49. doi:10.3322/caac.21660
43. Garcia-Lopez P, Garcia-Marin V, Freire MThe Histological Slides and Drawings of Cajal. Front Neuroanat (2010) 4:9. doi:10.3389/neuro.05.009.2010
44. Marchesini R, Bertoni A, Andreola S, Melloni E, Sichirollo AE. Extinction and Absorption Coefficients and Scattering Phase Functions of Human Tissues In Vitro. Appl Opt (1984) 28:2318–24. doi:10.1364/AO.28.002318
45. Edwards DK, Gier JT, Nelson KE, Roddick RD. Integrating Sphere for Imperfectly Diffuse Samples*. J Opt Soc Am (1961) 51:1279–88. doi:10.1364/josa.51.001279
46. Goodman JW. Statistical Properties of Laser Speckle Patterns. Berlin, Heidelberg: Springer (1975). p. 9–75. doi:10.1007/978-3-662-43205-1_2
Keywords: mueller matrix, singularity, polarization, S and C-state, optical anisotropy, birefringence, biological tissue, statistical moments
Citation: Dubolazov A, Ushenko V, Trifonyuk L, Stashkevich A, Soltys I, Ushenko Y, Tomka Y, Ushenko A, Gantyuk V and Gorodensky P (2021) Polarization-Singular Approach to Imaging Mueller-Matrix Polarimetry in the Differential Diagnosis of Histological Sections of Biopsy of Tumors of the Uterus and Prostate. Front. Phys. 9:711212. doi: 10.3389/fphy.2021.711212
Received: 18 May 2021; Accepted: 07 October 2021;
Published: 08 December 2021.
Edited by:
Steen Grüner Hanson, Technical University of Denmark, DenmarkReviewed by:
Sébastien Robert Mouchet, University of Exeter, United KingdomNirmal Mazumder, Manipal Academy of Higher Education, India
Copyright © 2021 Dubolazov, Ushenko, Trifonyuk, Stashkevich, Soltys, Ushenko, Tomka, Ushenko, Gantyuk and Gorodensky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. Dubolazov, YS5kdWJvbGF6b3ZAY2hudS5lZHUudWE=
 A. Dubolazov
A. Dubolazov V. Ushenko1
V. Ushenko1 Y. Ushenko
Y. Ushenko
