Decoherent Excitation of Transverse Free Currents in Dielectric Liquids via Inter-Molecular Interactions

We present a theoretical model for a class of optical scattering experiments in which short-duration, linearly-polarized electromagnetic pulses scatter off dielectric liquids. The pattern of scattering, particularly in the transverse direction, indicates that significant free currents are generated in the direction orthogonal to the polarization of the incident light. Modelling the target as a dense cluster of two-level systems, we show that transverse free currents are produced by short duration, electric-dipole interactions between proximate molecules, and result in scattering patterns similar to those observed in the experiments. Calculations provide a rationale for why these scattering patterns are not observed in the same molecules at lower densities or with lower field intensities. These features make this model a relevant alternative to proposed transverse optical magnetism theories.

1 Introduction

Optical or artificial magnetism is typically seen in specifically-engineered, nanofabricated metamaterials such as thin metallic strip pairs [1], split-ring resonators [2], and hyperbolic metamaterials [3]. As the name metamaterial implies, these devices are specifically engineered to have properties beyond those traditionally found in naturally-occuring materials, and typically contain nanostructures with precise geometries. Over the last decade, a series of experiments [4–7] have reported observing optical magnetism in dielectric liquids. These experiments have generated significant interest due to the prospect of observing magneto-optic interactions in naturally-occurring, non-magnetic materials [8]. These experiments, in which a dielectric liquid (such as water or carbon tetrachloride) is excited by a short-duration ($\approx 100-150$ fs), high-intensity ($\approx 1\times {10}^8-4\times {10}^8\text{W}/{\text{cm}}^2$) electromagnetic pulse, have shown that the scattered, free-emitted light in the propagation direction orthogonal to that of the incident light, has a significant intensity in the polarization direction orthogonal to the incident polarization. These results, suggestive of magnetic dipole radiation patterns, have led to the theory that intense optical fields induce magnetism in individual molecules, that lead to the generation of significant transverse free currents, which in turn generate the observed radiation patterns [9–12]. This “transverse optical magnetism” theory has encountered a number of criticisms, primarily centered around the need for a large relative magnetic permeability ${\mu }_r\approx c$ for agreement with experiments [9, 10, 13–16].

In this paper, we present an alternate theoretical model that can explain the experimental observations in Refs. [4–7] by including inter-molecular effects. In this model, strong, transverse free currents are produced through inter-molecular electric-dipole interactions without invoking magneto-optic effects in single molecules. Because the strength of inter-particle interactions decreases directly as the density of emitters decreases, this model can explain experiments in which scattering effects exhibit a strong density dependence. For example, it explains why these intensity patterns are not observed in scattering experiments that use low molecular density phases (such as the gas phase) [17].

2 Theoretical Model and Calculations

When a linearly-polarized electromagnetic pulse is incident on a dense ensemble of molecules, the light absorbed by an individual molecule creates a free current in the initial polarization direction. Upon spontaneous emission, this light is re-emitted in a well-known dipole pattern. In a dense medium, this light is reabsorbed by neighboring molecules located at different spatial positions. This subsequent absorption by neighboring molecules leads to a free current that is not necessarily in the same direction as the incident polarization direction. By exciting radiating dipoles perpendicular to the polarization of the incident field, the ensemble will emit photons in multiple polarization directions. This creates radiation patterns similar to those observed in the experiments.

In our calculations, we model the scattering of a strong, electromagnetic pulse by the target molecular liquid in the experiments by a single-particle model of a dense, driven ensemble of quantum dipoles (two-level systems) [18]. We assume that the incident electromagnetic pulse is near-resonant with a single optical transition in the molecule. Since the quantum dipoles are excited by the local electromagnetic field, the excitation direction of each dipole can be different from each other and from the initial polarization of the incident electromagnetic field. To model excitations in directions other than the incident polarization direction, the state of the ensemble is represented by the density matrix of a four-level quantum system with one ground energy level $\backslash ketg$ and three excited “directional” states $|e_x\rangle$, $|e_y\rangle$ and $|e_z\rangle$, an idea first proposed for a single atom in Ref. [19]. The three excited states $|e_x\rangle$, $|e_y\rangle$ and $|e_z\rangle$ represent the excited energy levels when an x, y or z-polarized photon is absorbed by the ensemble in the ground state. We assume that the polarization of the incident electromagnetic field is in the y-direction. The inter-molecular interactions are modelled by decoherences that arise from nearest-neighbor dipolar energy transfers [18, 20]. The ensemble density matrix representing a cluster of molecules is therefore a 4 × 4 matrix, and its evolution can be calculated quickly. This model requires no a priori assumptions about the specific quantum levels of the target molecules other than the applied field being near-resonant with a single transition, therefore the conclusions are generalized to a wide class of molecules.

The Hamiltonian of the ensemble of two-level molecules, after making the rotating wave approximation as in Ref. [18] is:

$H_{ens}=\left(\begin{array}{cccc}0& \frac{\hslash {\text{Ω}}_x}{2}& \frac{\hslash {\text{Ω}}_y}{2}& \frac{\hslash {\text{Ω}}_z}{2}\\ \frac{\hslash {\text{Ω}}_x^{\text{*}}}{2}& -\mathrm{△}& 0& 0\\ \frac{\hslash {\text{Ω}}_y^{\text{*}}}{2}& 0& -\mathrm{△}& 0\\ \frac{\hslash {\text{Ω}}_z^{\text{*}}}{2}& 0& 0& -\mathrm{△}\end{array}\right),(1)$

where $\mathrm{△}$ represents the detuning between the molecular transition frequency and the frequency of the incident light, and the Rabi frequency-like terms (${\text{Ω}}_i={\mu }_i{E}_i,i=x,y,z$) are proportional to the electric field amplitudes in each of the three Cartesian directions ($E_i$) and the transition dipole moment (${\mu }_i$). The incident electromagnetic pulse is polarized in the y-direction, and propagates along the x-direction. The electric field in the y-direction is dominated by the incident field, while the electric fields in the x and z directions represent the dipolar emission from a quantum emitter due to spontaneous emission, and are about an order of magnitude smaller than that of the incident field [18]. Note that we ignore the magnetic component of the electromagnetic field since it is much smaller than the electric field component, and the value of the relative magnetic permeability of the molecules is assumed to be 1.

In our four-level model, the spontaneous emission from the $|e_x\rangle$, $|e_y\rangle$, and $|e_z\rangle$ excited directional states to the ground state $|g\rangle$ have rates ${\gamma }_{xg}$, ${\gamma }_{yg}$ and ${\gamma }_{zg}$ respectively. These emission rates are determined using Fermi’s Golden Rule [20]. An individual molecule in the ensemble can spontaneously emit in all directions, and this radiation can excite a neighbouring molecule. These “inter-particle interactions” are modelled by adding in additional decoherence rates between all three excited states, represented by the set of all possible${\delta }_{ij}$’s ($i,j=x,y,z$) [18]. These rates represent the transfer of energy between molecules in which the energy emitted by one molecule transitioning to the ground state ($|i\rangle \to |g\rangle$) is absorbed and causes a nearby molecule in the ground state to transition to an excited state ($|g\rangle \to |j\rangle$). This model of the intermolecular energy transfer as a decoherence rate is inspired by models of the Forster-Resonance Energy Transfer (FRET) process commonly seen in biophysical systems [20]. These δ’s do not result in a loss of energy from the ensemble, therefore, they act like dephasing rates for the ensemble density matrix.

The magnitude of these dephasing rates associated with energy transfer between molecules (${\delta }_{ij}$) are calculated by modelling the radiation emitted by a molecule as electric dipole radiation that is absorbed by the nearest neighbors (separated by r) in a square lattice. The expressions are derived in [18] and are of the form:

$\frac{{\delta }_{ij}}{{\gamma }_0}=\frac{N_a\pi c^3}{4{\omega }^3}\left(3\left(\widehat{u_i}\cdot \widehat{r_i}\right)\left(\widehat{u_j}\cdot \widehat{r_i}\right)-\widehat{u_j}\cdot \widehat{u_i}\right)\left(\sqrt{{\overline{\rho }}_{ii}{\overline{\rho }}_{gg}}\sqrt{{\overline{\rho }}_{jj}{\overline{\rho }}_{gg}}\right),(2)$

where $N_a$ is the number density of the ensemble, ω is the natural frequency of the transition dipole, ${\gamma }_0={\gamma }_{ig}={\gamma }_{jg}$ is the spontaneous emission rate of the involved transitions and $\widehat{u_i}$ is the direction of the transition dipole moment.

The term $\sqrt{{\overline{\rho }}_{ii}{\overline{\rho }}_{gg}}\sqrt{{\overline{\rho }}_{jj}{\overline{\rho }}_{gg}}$, modifies the decoherence rate by estimating how many dipoles are undergoing transitions that experience the $|i\rangle \to |j\rangle$ energy transfer. Since ${\overline{\rho }}_{gg}$, ${\overline{\rho }}_{ii}$ and ${\overline{\rho }}_{jj}$ are functions of time, and depend on the intensity of the applied field, the dephasing rates exhibit an intensity-dependence. If the intensity of the applied field is significantly low, the ensemble state will simply oscillate around the ground state and these dephasing rates will remain close to zero.

A diagram of all the decoherence processes in the single-particle quantum model of the ensemble is provided in Figure 1. The Lindblad superoperator representing the spontaneous emission, and dephasing due to intermolecular energy transfer has the form:

$L\left(\overline{\rho }\right)={\displaystyle \sum }_{i=x,y,z}\frac{{\gamma }_{ig}}{2}\left({\sigma }_{ig}^{†}{\sigma }_{ig}\overline{\rho }+\overline{\rho }{\sigma }_{ig}^{†}{\sigma }_{ig}-2{\sigma }_{ig}\overline{\rho }{\sigma }_{ig}^{†}\right)(3)$

$+{\displaystyle \sum }_{i=x,y,z}{\displaystyle \sum }_{j=x,y,z}\frac{{\delta }_{ij}}{2}\left({\sigma }_{ij}^{†}{\sigma }_{ij}\overline{\rho }+\overline{\rho }{\sigma }_{ij}^{†}{\sigma }_{ij}-2{\sigma }_{ij}\overline{\rho }{\sigma }_{ij}^{†}\right),$

FIGURE 1

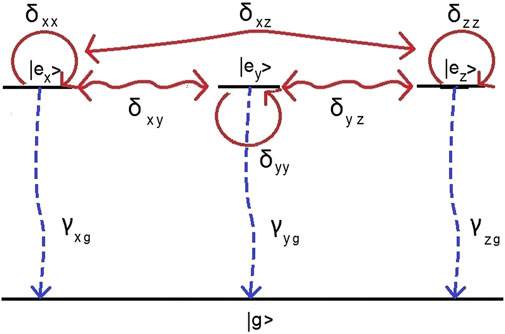
FIGURE 1. Decoherence structure in a single-particle approximation of a driven molecular ensemble. Inter-molecular energy transfer due to reabsorption of spontaneously emitted photons (${\gamma }_{ig}$’s in dashed/blue) are modelled as decoherent dephasing terms (${\delta }_{ij}$’s in solid/red) For details on how the decoherence rates are calculated, see Ref. [18].

with ${\sigma }_{ij}=|j\rangle \langle i|$.

The density matrix of the ensemble, $\overline{\rho }$, is evolved in time using the Lindblad-von Neumann equation:

$\dot{\overline{\rho }}=-\frac{i}{\hslash }[H_{ens},\overline{\rho }]-L\left(\overline{\rho }\right).(4)$

As shown in Ref. [18], the time-dependent behavior of the density matrix of an ensemble in a four-level basis, agrees very well with the numerically calculated, average time-dependent behavior of $\approx 4000$ two-level molecules calculated via a mean-field solution of Maxwell-Lindblad equations.

After calculating the time-dependent density matrix elements, we determine the Emission Ratio (R), the ratio of the intensity perpendicular the incident polarization (called $I_M$ as in the experimental papers) to the intensity parallel to the incident polarization ($I_E$). In comparison to the experiments, this ratio is calculated at a point along the transverse z-direction. The instantaneous intensities will be proportional to the ratio of the square of the modulus of the free currents (J_i)in the driving field polarization direction ($i=y$) and an orthogonal direction ($i=x$) [5], that is,

$\frac{I_M\left(t\right)}{I_E\left(t\right)}=\frac{{\left|J_x\left(t\right)\right|}^2}{{\left|J_y\left(t\right)\right|}^2}.(5)$

This ratio can be expressed in terms of the ensemble density matrix elements since $J_i={\dot{\mathrm{\mu }}}_i=Tr\left(\dot{\overline{\rho }}\underset{¯}{{\mu }_i}\right)=Tr\left(\dot{\overline{\rho }}\frac{\partial H}{\partial E_i}\right)$. The observed Emission Ratio is the ratio of the intensities integrated over time. Therefore,

$\overline{R}=\frac{{\displaystyle \int dt{\left|{\mu }_x\left({\dot{\overline{\rho }}}_{xg}+{\dot{\overline{\rho }}}_{gx}\right)\right|}^2}}{{\displaystyle \int dt{\left|{\mu }_y\left({\dot{\overline{\rho }}}_{yg}+{\dot{\overline{\rho }}}_{gy}\right)\right|}^2}},(6)$

which yields a simple relationship between calculated elements of the ensemble density matrix, and the measured Emission Ratio. We assume that the transition dipole moments are the same in each direction, ${\mu }_x={\mu }_y$, and as in Eq. 2, ${\overline{\rho }}_{ig}\approx \sqrt{{\overline{\rho }}_{ii}{\overline{\rho }}_{gg}}$. Note that the Emission Ratio scales with the dipole moment of the transition as ${\left(\frac{\mu }{{\mu }_0}\right)}^2$.

This model is sensitive to both the density of molecules in the ensemble as well as the intensity of the applied field. Under low intensities or low densities these inter-molecular effects are not significant. Over long time periods, these effects die out very quickly. However at high intensities, high densities and short time periods these effects can lead to significant excitation and free currents generated in orthogonal polarization directions [18]. This is similar to experiments in coherent atomic ensembles that have shown that inter-atomic interactions affect resonance frequencies and scattering polarizations, in a way that is dependent on both the density of emitters and the incident intensity [21].

3 Emission Ratios From a Dense Ensemble

We now calculate the Emission Ratio R generated in response to a strong incident pulse similar to the experiments in Refs. [5, 6]. A 100fs pulse with an intensity of $8\times {10}^8\text{W}/{\text{cm}}^2$ and a central wavelength of 775 nm excites an ensemble of molecules with a molecular number density $N_A$, assumed to have a value similar to that of water ($N_A=3.3\times {10}^{28}{m}^{-3}$). Our model makes the approximation that there is a single, optical transition that is resonantly excited by the pulse. We make the simplification that the pulse amplitude is a constant over its duration (i.e., it is a rectangular pulse). This simplification takes advantage of the pulse-area theorem used in quantum control frameworks, in which only the area under the pulse significantly affects excitation [22]. We also assume that all the molecules are initially in the ground state. The dipole moment of system was taken to be $\approx 1.8D=3.7\times {10}^{-11}em$, based on the net dipole of a single water molecule [23], however this value may actually be higher due to water being in a condensed phase [24].

Figure 2 shows the dependence of the emission ratio for water on the intensity of the applied 100fs pulse. The range of pulse intensities was chosen to match the overall range found in the experiments in Refs. [5, 6].

FIGURE 2

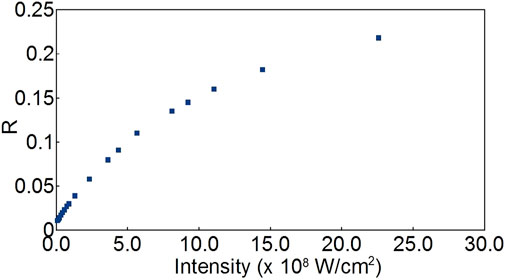
FIGURE 2. Emission Ratio of water as a function of increasing intensity of the applied 100fs pulse. As the intensity increases, the transition to the excited state of each molecule is driven more strongly, and the probability of inter-molecular energy transfer increases, thus increasing the Emission Ratio.

From this figure, it is seen that for the emission ratio to become significant for 100fs pulses, the average field intensity needs to be higher than $\approx {10}^7$ W/$c{m}^2$). This minimum intensity limit is seen in experiments [5]. The curve is similar to the measured experimental curves in that it shows a linear increase at low intensities [6]. At higher intensities, we predict the emission will reach a saturation value. We find that the calculated emission ratio for a dielectric liquid similar to water is fairly significant with a value of 0.15, close to the experimentally measured emission ratio of approximately 0.22 [6].

This quantitative difference is not surprising as our model treats the molecules as dipole emitters and looks at no other interactions between molecules. However, given the generality of our model and the fact that the Emission Ratio under this mechanism is similar in strength to what is measured, it suggests that this alternate pathway from transverse free currents and scattered intensities should represent a significant step in understanding short-pulse scattering experiments from dielectric liquids.

In addition to intensity-dependent effects, our model also predicts that there should be a strong dependence on the density of the medium. This dependence is an attractive feature of this alternate model as strong transverse free currents are typically not seen in gas-phase scattering experiments [17].

Using our simplified model, Figure 3 shows the predicted density dependence of the Emission Ratio of a general molecular ensemble with electric dipole transition moment around ${\mu }_0={10}^{-10}em$. As the density of the liquid increases (thus increasing the probability of intermolecular energy transfer), the emission ratio increases. Quantitative comparison to the experiments is made challenging since our model assumes that the molecules are infinitesimally small in size, whereas the size of molecules such as carbon tetra chloride or benzene is large, and the atoms in the molecules are actually much closer together than the number density suggests. Thus for larger molecules such as $CC{l}_4$, the Emission Ratio would reach saturation at lower intensities than predicted by the number density alone, which appears to be the case in experiments [6].

FIGURE 3

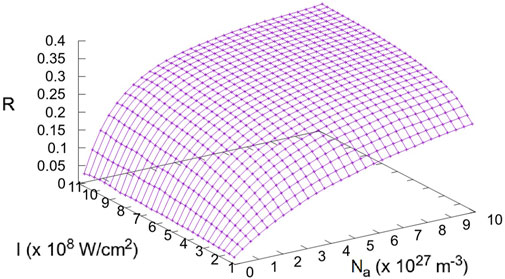
FIGURE 3. Density dependence of the Emission Ratio of an ensemble of molecules with electric dipole transition moment $\mu ={10}^{-10}em$ as a function of increasing number density in the ensemble. As the number density is increased, the probability of inter-molecular interactions increases, thus increasing the Emission Ratio.

Due to the presence of this density dependence, we suggest two possible experiments that could validate our model. The first involves performing the same experiments as described in Refs. [4–7] by using systems with varying molecular densities. If the transverse free currents are caused by inter-molecular electric interactions, the Emission Ratio should clearly increase as a function of density (whereas a single-molecule magneto-optic effect will not be effected by density). This may be accomplished by performing these short-pulse scattering experiments on the same liquids at different temperatures and pressures. The second suggested experiment is a measurement of the time-dependence of the scattered signal. Since out model involves absorption and re-emission between molecules, it is naturally time-dependent and thus the Emission Ratio should change as a function of time, and also be fairly sensitive to different pulse widths at the same intensity.

4 Conclusion

For optical scattering experiments in dense media, the interactions between molecules can have a significant effect on the observed scattering intensity patterns. We have proposed a theoretical model wherein significant transverse currents are generated in optical scattering experiments on dielectric liquids due to inter-molecular electric-dipole interactions. Using our model, we show that the strength of these inter-molecular interactions increase with both density and incident intensity. The calculated dependence of the transverse currents on the intensity of the incident electromagnetic pulse agrees with experimental results. The density dependence provides a direct explanation for why these effects do not appear in scattering experiments involving less-dense targets such as gases. We provide suggestions for future scattering experiments that can validate our model.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

CD performed the calculations, interpreted the results and co-wrote the manuscript. CR oversaw the project, advised CD, assisted in the analysis, and co-wrote the paper.

Funding

CD greatly acknowledges computing resources made available through the National Science Foundation under Grant No. 1624416. CR gratefully acknowledges support from the Discovery Grant program of the Natural Sciences and Engineering Research Council of Canada (funding reference number RGPIN-2019-06387).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Chettiar UK, Kildishev AV, Klar TA, Shalaev VM. Negative index Metamaterial Combining Magnetic Resonators with Metal Films. Opt Express (2006) 14:7872. doi:10.1364/oe.14.007872

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhou J, Koschny T, Kafesaki M, Economou EN, Pendry JB, Soukoulis CM. Saturation of the Magnetic Response of Split-Ring Resonators at Optical Frequencies. Phys Rev Lett (2005) 95:223902. doi:10.1103/physrevlett.95.223902

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Poddubny A, Iorsh I, Belov P, Kivshar Y. Hyperbolic Metamaterials. Nat Photon (2013) 7:948–57. doi:10.1038/nphoton.2013.243

CrossRef Full Text | Google Scholar

4. Oliveira SL, Rand SC. Intense Nonlinear Magnetic Dipole Radiation at Optical Frequencies: Molecular Scattering in a Dielectric Liquid. Phys Rev Lett (2007) 98. doi:10.1103/PhysRevLett.98.093901

CrossRef Full Text | Google Scholar

5. Rand SC, Fisher WM, Oliveira SL. Optically Induced Magnetization in Homogeneous, Undoped Dielectric media. J Opt Soc Am B (2008) 25:1106. doi:10.1364/josab.25.001106

CrossRef Full Text | Google Scholar

6. Fisher WM, Rand SC. Dependence of Optically Induced Magnetism on Molecular Electronic Structure. In: international Conference on Luminescence and Optical Spectroscopy of Condensed Matter (ICL’08); JUL 07-11, 2008, 129. Lyon, France: Univ Lumiere Lyon 2 (2009). p. 1407–9. doi:10.1016/j.jlumin.2009.02.036J Lumin

CrossRef Full Text | Google Scholar

7. Fisher AA, Dreyer EFC, Chakrabarty A, Rand SC. Optical Magnetization, Part I: Experiments on Radiant Optical Magnetization in Solids. Opt Express (2016) 24:26055. doi:10.1364/oe.24.026055

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Papadakis GT, Fleischman D, Davoyan A, Yeh P, Atwater HA. Optical Magnetism in Planar Metamaterial Heterostructures. Nat Commun (2018) 9:296. doi:10.1038/s41467-017-02589-8

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Rand SC. Quantum Theory of Coherent Transverse Optical Magnetism. J Opt Soc Am B (2009) 26:B120. doi:10.1364/josab.26.00b120

CrossRef Full Text | Google Scholar

10. Fisher WM, Rand SC. Light-induced Dynamics in the Lorentz Oscillator Model with Magnetic Forces. Phys Rev A (2010) 82:013802. doi:10.1103/physreva.82.013802

CrossRef Full Text | Google Scholar

11. Fisher AA, Cloos EF, Fisher WM, Rand SC. Dynamic Symmetry-Breaking in a Simple Quantum Model of Magneto-Electric Rectification, Optical Magnetization, and Harmonic Generation. Opt Express (2014) 22:2910. doi:10.1364/oe.22.002910

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Fisher AA, Dreyer EFC, Chakrabarty A, Rand SC. Optical Magnetization, Part II: Theory of Induced Optical Magnetism. Opt Express (2016) 24:26064. doi:10.1364/oe.24.026064

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Palffy-Muhoray P. Comment on "Intense Nonlinear Magnetic Dipole Radiation at Optical Frequencies: Molecular Scattering in a Dielectric Liquid". Phys Rev Lett (2007) 99:189401. doi:10.1103/physrevlett.99.189401

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Oliveira SL, Rand SC. Oliveira and Rand Reply:. Phys Rev Lett (2007) 99:189402. doi:10.1103/physrevlett.99.189402

CrossRef Full Text | Google Scholar

15. Sharma NL. Phys Rev Lett (2009) 102:119403.

PubMed Abstract

16. Oliveira SL, Rand SC. Oliveira and Rand Reply:. Phys Rev Lett (2009) 102:119404. doi:10.1103/physrevlett.102.119404

CrossRef Full Text | Google Scholar

17. Murphy WF. The Rayleigh Depolarization Ratio and Rotational Raman Spectrum of Water Vapor and the Polarizability Components for the Water Molecule. J Chem Phys (1977) 67:5877–82. doi:10.1063/1.434794

CrossRef Full Text | Google Scholar

18. DiLoreto CS, Rangan C. Single-particle Model of a Strongly Driven, Dense, Nanoscale Quantum Ensemble. Phys Rev A (2018) 97:013812. doi:10.1103/physreva.97.013812

CrossRef Full Text | Google Scholar

19. Fratalocchi A, Conti C, Ruocco G. Three-dimensional Ab Initio Investigation of Light-Matter Interaction in Mie Lasers. Phys Rev A (2008) 78:013806. doi:10.1103/physreva.78.013806

CrossRef Full Text | Google Scholar

20. Novotny L, Hecht B. “emph “Bibinfo Title Principles of Nano-Optics, 8. Cambridge University Press (2006).

21. Bromley SL, Zhu B, Bishof M, Zhang X, Bothwell T, Schachenmayer J, et al. Collective Atomic Scattering and Motional Effects in a Dense Coherent Medium. Nat Commun (2016) 7:11039. doi:10.1038/ncomms11039

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Tannor DJ. Introduction to Quantum Mechanics: A Time-dependent Perspective. Mill Valley, CA: University Science Books (2007).

23. Lovas FJ. Microwave Spectral Tables II. Triatomic Molecules. J Phys Chem Reference Data (1978) 7:1445–750. doi:10.1063/1.555588

CrossRef Full Text | Google Scholar

24. Gregory JK, Clary DC, Liu K, Brown MG, Saykally RJ. The Water Dipole Moment in Water Clusters. Science (1997) 275:814–7. doi:10.1126/science.275.5301.814

PubMed Abstract | CrossRef Full Text | Google Scholar