Effective Repulsion Between Oppositely Charged Particles in Symmetrical Multivalent Salt Solutions: Effect of Salt Valence

Salt ions play critical roles in the assembly of polyelectrolytes such as nucleic acids and colloids since ions can regulate the effective interactions between them. In this work, we investigated the effective interactions between oppositely charged particles in symmetrical (z:z) salt solutions by Monte Carlo simulations with salt valence z ranging from 1 to 4. We found that the effective interactions between oppositely charged particles are attractive for 1:1 and low multivalent salts, while they become apparently repulsive for high multivalent salts. Moreover, such effective repulsion becomes stronger as z increases from 2 to 3, while it becomes weaker when z increases from 3 to 4. Our analyses reveal that the overall effective interactions are attributed to the interplay between ion translational entropy and electrostatic energy, and the non-monotonic salt-valence dependence of the effective repulsions is caused by the rapid decrease of attractive electrostatic energy between two oppositely charged particles with their over-condensed counterions of opposite charges when z exceeds 3. Our further MC simulations show that the involvement of local-ranged counterion–co-ion repulsions can enhance the effective repulsions through weakening the attractive electrostatic energy, especially for higher salt valence.

Introduction

Salt ions can regulate the effective interactions among polyelectrolytes such as colloids [1–7], nucleic acids [8–22], and proteins [23–29], and consequently impact diverse physical phenomena including the structural assembly of polyelectrolytes [30], the stability of colloids [31, 32], and the collapse of nucleic acids [33–35]. Generally, a polyelectrolyte solution is often modeled through the Poisson–Boltzmann (PB) equation since the equation has a simple form and is rather successful in predicting the properties of polyelectrolytes in aqueous and monovalent salt solutions [36, 37]. However, for polyelectrolyte solution with multivalent ions, the PB theory can fail to make reliable predictions on some important physical properties due to the neglect of ion–ion correlations [38–41].

Effective interactions between polyelectrolytes in salt solutions have attracted rather attention and have been studied extensively in recent years [42–50]. The intrinsic repulsions between like-charged polyelectrolytes can be modulated into effective attractions by multivalent counterions, which is generally attributed to the bridging effect or the Coulomb depletion effect of condensed counterions [51–65]. For oppositely charged polyelectrolytes, the intrinsic attractive interaction can be mediated into apparent repulsions by nonsymmetrical 1:2 or 1:3 salt due to the respective under-neutralization and over-neutralization of the oppositely charged polyelectrolytes by their respective counterions [66–71]. Very recently, an unexpected apparent repulsion between oppositely charged spherical particles was observed at high symmetrical 2:2 salt [72], and such apparent repulsion is attributed to the weakening of attraction between two over-neutralized spherical particles by the release of condensed counterions when the two particles approach each other [72]. However, the effective interactions between oppositely and equally charged particles have not been explored for symmetrical salts with extensive valences.

In this work, the effective interactions between oppositely and equally charged particles in symmetrical z:z salt solutions have been investigated by extensive Monte Carlo (MC) simulations. Our simulations cover the wide ranges of salt valence, particle charge, and salt concentration. We found that the effective interactions between oppositely charged particles are attractive at 1:1 salt and at low multivalent salts, while the interactions become apparent repulsions at high multivalent salts. Interestingly, such effective repulsion appears to be non-monotonically dependent on salt valence z. Such non-monotonic salt-valence dependence of the effective repulsion is attributed to the interplay between ion translational entropy and electrostatic energy associated with counterion–co-ion Coulomb attractions. The mechanism is further illustrated by our MC simulations with artificially involving local-ranged counterion–co-ion repulsions.

Model System and Monte Carlo Simulations

The Model System

In this work, we employed a model system of two oppositely charged particles immersed in 1:1, 2:2, 3:3, and 4:4 salt solutions to investigate the effective interactions between them. In the model system, both charged particles and salt ions were represented by spheres with different radii, and the solvent was modeled as a continuous medium (see Figure 1). The interactions between charged particles and ions were simplified into Coulomb and hard-sphere repulsion interactions, and the interaction energy $u_{ij}$ between spheres i and j in the model system is given by [15, 41, 64]

$\begin{array}{c}{u}_{ij}=\{\begin{array}{cc}\frac{q_i{q}_j}{4\text{π}{\epsilon }_0\epsilon r_{ij}},& r_{ij}\ge a_i+a_j;\\ \infty , & r_{ij}<a_i+a_j.\end{array}\end{array}(1)$

Here, $a_i$ and $q_i$ represent the radius and charge of sphere i (particles or ions), respectively. $r_{ij}$ is the distance between the centers of two charged spheres i and j. ${\epsilon }_0$ is the permittivity of vacuum, and ε = 78 is the dielectric constant of the solvent. The potentials of mean force (PMFs) were calculated to describe the effective interactions between oppositely charged particles in symmetrical z:z salt solutions. Our systems cover the wide ranges of salt valence, salt concentration, and particle charge; z:z salts were taken as 1:1, 2:2, 3:3, and 4:4; salt concentrations ranged from 0.03 to 0.3 M; the charges on two particles were taken as +24 e/−24 e, +36 e/−36 e, +48 e/−48 e, and +60 e/−60 e, respectively; the diameters of charged particles and ions were taken as σ (=20 Å) and 0.3 σ, respectively.

FIGURE 1

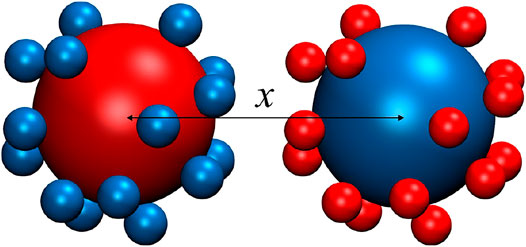
FIGURE 1. Schematic representation of the model system with two equally and oppositely charged particles in symmetrical multivalent (z:z) salt solutions, and x is the separation between the centers of two particles. Here |Z| is the absolute charge of particles in unit of e, and +z/−z are the valences of symmetrical salt ions.

Monte Carlo Simulations

For the model system, the MC simulations with the Metropolis algorithm have been employed to calculate the PMFs between oppositely charged particles in symmetrical salt solutions. The simulation cell was generally taken as a rectangular box, and to diminish the boundary effect, the box size was kept larger than the center-to-center separation x between oppositely charged particles by at least six Debye–Hückel lengths [62, 64]. Each MC simulation starts from an initial configuration with two particles constrained by a spring and randomly distributed ions, and the probability to accept a trial move of an ion or a particle is given by $\text{min}\left[1,-\Delta U/k_{B}T\right]$, where $\Delta U$ is the interaction energy change associated with the trial move of the ion or particle in the simulation cell. $k_B$ is the Boltzmann constant, and $T$ is the absolute temperature in kelvin. The process is repeated until the system reached equilibrium, where the separation between two oppositely charged particles becomes stable [62, 64].

Calculating Effective Potentials of Mean Forces Between Charged Particles

In this work, we employed the pseudo-spring method to calculate effective PMFs between oppositely charged particles [15, 41, 64], and a spring with spring constant k = 9 nN/Å was added to link the centers of the two particles in the MC simulations described above. Specifically, one particle remains frozen, while the other can move along x-axis with a constraint of the added spring with spring constant k. The effective force $F\left(x\right)$ between the two particles with a center-to-center separation x can be given by [15, 41, 64]:

$\begin{array}{c}F\left(x\right)=k\Delta x,\end{array}(2)$

where $\Delta x$ is the small deviation of spring length away from the original distance x at equilibrium. Therefore, the effective PMF $\Delta G\left(x\right)$ between the two particles can be calculated by the following integration [15, 41, 64]:

$\begin{array}{c}\Delta G\left(x\right)=G\left(x\right)-G\left(x_{\text{ref}}\right)={\displaystyle {\int }_x^{x_{\text{ref}}}F\left(x^{\prime }\right)\text{d}{x}^{\prime }},\end{array}(3)$

where $x_{ref}$ is the outer reference distance, which was practically taken as a large value, 45 Å.

Results and Discussion

In this section, we calculated the effective PMFs between equally and oppositely charged particles immersed in symmetrical z:z (1:1, 2:2, 3:3, and 4:4) salt solutions by MC simulations. We found that the effective interactions between oppositely charged particles are attractive at 1:1 salt and low multivalent salts, while the interactions can become apparently repulsive at high multivalent salts, and such apparent repulsion strength is non-monotonically dependent on salt valence z. Afterward, we analyzed the driving force for the effective repulsions and the mechanism for the non-monotonic salt-valence dependence of the effective repulsion. Finally, we performed further MC simulations with artificially involving local-ranged counterion–co-ion repulsions to illustrate the mechanism for the salt-valence dependence of the effective repulsion.

Effective Repulsion Between Oppositely Charged Particles at High 2:2, 3:3, and 4:4 Salts

As shown in Figures 2A–C, the effective ∆G(x) PMFs between oppositely charged particles in 1:1 salt solutions are always attractive, and the effective attractions become weakened with the increase of 1:1 salt concentration. For higher salt valence z, the effective PMFs between oppositely charged particles are still weakly attractive at low 2:2, 3:3, and 4:4 salts, although there are local maximums in the PMF profiles, and the attraction strengths are apparently weaker than those of 1:1 salt. With the increase of z:z salt concentration (e.g., >∼0.1 M), the effective repulsions between oppositely charged particles were observed at the separation of around one ion diameter for all multivalent z:z salts, and the separation where PMFs have maximum values would shift toward smaller separations for higher valence z. For example, for |Z| = 36 e, the maximum values of effective PMFs are ∼2 k_BT, ∼3 k_BT, and ∼1.5 k_BT at the separations of ∼27, ∼25, and 24 Å for 2:2, 3:3, and 4:4 salts, respectively, when salt concentration is 0.3 M, and such maximum values decrease gradually to (local) maximum ones of ∼ −0.2 k_BT, ∼0 k_BT, and −2 k_BT for 2:2, 3:3, and 4:4 salts when salt concentration is decreased to 0.03 M.

FIGURE 2

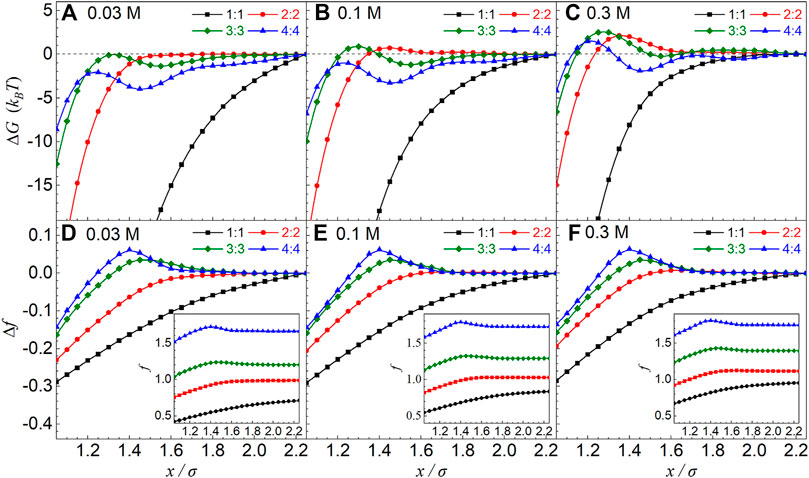
FIGURE 2. (A–C) Effective potentials of mean force ΔG(x) between equally and oppositely charged particles with |Z| = 36 e in symmetrical 1:1, 2:2, 3:3, and 4:4 salt solutions from the MC simulations. (D–F) The relative charge fraction Δf = f(x) − f(x_ref) of condensed counterions obtained from the MC simulations as a function of separation x between two oppositely charged particles. The insets are the charge fraction f(x). The salt concentrations and ion valences have been shown in the respective panels. The reference separation was taken as x_ref = 45 Å.

We also calculated the effective ∆G(x) PMFs between oppositely charged particles with different charges |Z| for all multivalent z:z salts. As shown in Figure 3, the increase of particle charge can visibly enhance the effective repulsion between oppositely charged particles. Specifically, when |Z| is increased from 24 e to 60 e, the maximum values of PMF profiles increase by ∼5 k_BT, ∼8 k_BT, and ∼9 k_BT for 2:2, 3:3 and 4:4 salts, respectively, when salt concentration is 0.3 M.

FIGURE 3

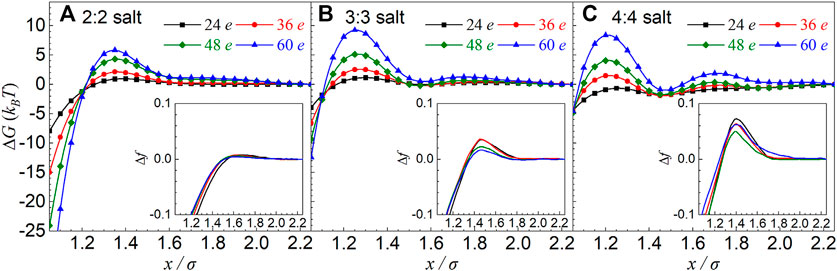
FIGURE 3. (A–C) Effective potentials of mean force ΔG(x) between equally and oppositely charged particles with different charge particles |Z| in symmetrical 2:2, 3:3, and 4:4 salt solutions from the MC simulations. The insets are the relative charge fraction Δf = f(x) − f(x_ref) of condensed counterions obtained from the MC simulations as a function of separation x between two particles. The salt concentrations are 0.3 M, and the particle charges and ion valences have been shown in the respective panels. The reference separation was taken as x_ref = 45 Å.

We summarized the (local) maximum values in effective PMFs between oppositely charged particles for different salt concentrations, salt valences, and particle charges. As shown in Figure 4, the effective repulsion becomes more apparent with the increase of z:z salt concentration and with the increase of particle charge. However, such effective repulsion is non-monotonically dependent on salt valence z; when z is increased from 2 to 3, the effective repulsion becomes stronger, while it becomes weaker when salt valence z increases from 3 to 4 (see also Figures 2–4). Such finding is interesting and will be discussed in detail in the following subsections.

FIGURE 4

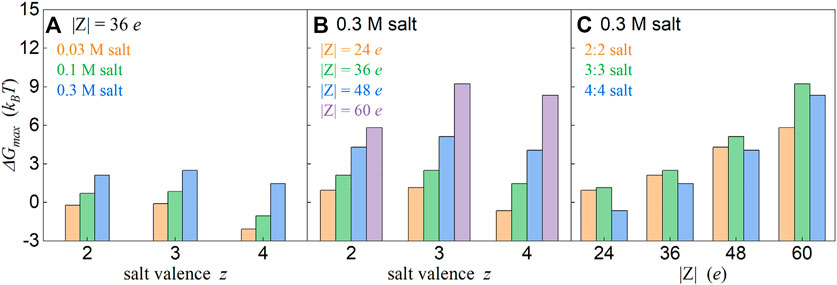
FIGURE 4. Relationship between the maximum values ΔG_max and ion valence z(A, B) and particle charge |Z| (C). ΔG_max denotes the (local) maximum values in the effective PMF profiles. The salt concentrations, particle charges, and ion valences have been shown in the respective panels. Here, the values for 1:1 salts were not shown since there is no effective (local) repulsion for 1:1 salt over the covered salt concentrations.

Condensed Counterions Around Charged Particles for High 2:2, 3:3, and 4:4 Salts

The ion-mediated effective interactions shown above are generally coupled to counterion condensation to the oppositely charged particles. Here, we calculated the charge fraction distribution Q(r) of the ions around respective charged particles by [41, 64, 72]:

$\begin{array}{c}Q\left(r\right)=-\frac{1}{Z}{\displaystyle {\int }_i^r{\displaystyle \sum _i{z}_i{c}_i\left(r\right)d^{3}r}.}\end{array}(4)$

Here, Z is the charge on the respective particles in unit of e, and r is the radial distance around a particle. $z_i$ and $c_i\left(\text{r}\right)$ are the ion valence and concentration at r, respectively. Following our previous work [72], the charge fraction f of the condensed counterions can be given by f = Q(r = R_c), and R_c is chosen as the radial distance where the charge fraction Q(r) exhibits a maximum value at high salt (see also Supplementary Figure 1).

As shown in Figures 2D–F and Supplementary Figure 2, at the reference separation, with the increase of salt valence z from 1 to 4, the charge fraction f of condensed counterions increases significantly from an under-neutralization value (f < 1) for 1:1 salt to over-neutralization values (f > 1) when z exceeds 2, and such over-neutralization becomes more pronounced for higher valence z, suggesting the under-condensation of monovalent counterions and over-condensation of multivalent counterions. For example, f ∼ 1.1, ∼ 1.4, and ∼ 1.8 at the reference separation for 2:2, 3:3, and 4:4 salts, respectively, when salt concentration is 0.3 M. As salt concentration is decreased, f decreases slightly due to the larger ion binding penalty at lower salt concentration and strong counterion–particle attraction, especially for higher valence z [73]. The over-neutralization of charged particles by multivalent counterions is understandable due to the very strong attraction between charged particles and multivalent counterions and the self-organization of condensed counterions to decrease the mutual Coulomb repulsions [35].

The dependence of f on the interparticle separation x would be of great interest and can be directly coupled to the driving force for the effective repulsion between oppositely charged particles in multivalent z:z salt solutions. Figures 2D–F and the insets of Figure 3 show the dependence of f on the interparticle separation x for extensive salt valences, salt concentrations, and particle charges. For 1:1 salt, f monotonically decreases with the decrease of separation x, suggesting the continuous release of condensed counterions when two oppositely charged particles approach each other [41]. However, when valence z increases from 2 to 4, f is almost maintained invariant at large separation x, and then increases with the decrease of x until x reaches around the separation for the maximum values of effective PMFs. Such increase in f with x appears apparently more pronounced for higher z.

Such increase of f with the decrease of x for z ≥ 2 is somewhat surprising although it is physically understandable. As shown in Supplementary Figures 1–3, two oppositely charged particles are both over-neutralized by multivalent counterions at large separation x, and the over-neutralization is more significant for higher z. Furthermore, co-ions would also condense in the shell adjacently around the over-condensed counterions, and such effect is more pronounced for higher z due to the stronger over-neutralization and stronger counterion–co-ion Coulombic attractions (see Supplementary Figures 1,3). Then when two over-neutralized (oppositely charged) particles approach each other, the condensed co-ions around “over-condensed” counterions for one particle would enter the condensed counterion shell of the other particle, which would favor the counterion condensation for the other (oppositely) charged particles since the co-ions for one particle are the counterions for the other one. As shown in Supplementary Figure 4, as x is decreased, the increased trend of f starts around the separation where the condensed co-ion shell around one particle begins to contact with the condensed counterion shell around the other oppositely charged particle, and ends around the separation where the condensed co-ion shell around one particle begins to contact with the surface of the other oppositely charged particle. This suggests that the condensed co-ions (around the over-condensed counterions) for a particle become the condensed counterions for another oppositely charged one when two particles approach. Such effect is naturally more pronounced for higher z due to the stronger counterion over-condensation and stronger counterion–co-ion Coulombic attractions. The increase in f is nearly independent on salt concentration due to strong counterion–particle attraction, especially for higher valence z. At small separation x (<one ion diameter), f decreases with the decrease of x due to the weakening of electrostatic field and the volume exclusion effect for counterions between oppositely charged particles.

Driving Force for Effective Repulsions Between Oppositely Charged Particles at High z:z Salts

To understand the effective repulsions between oppositely charged particles in z:z salt solutions, we split the effective ∆G(x) PMFs into the contribution of electrostatic energy ∆G_E(x) through $G_E\left(x\right)=\langle {\displaystyle {\sum }_{i<j}^N\frac{q_i{q}_j}{4\text{π}{\epsilon }_0\epsilon r_{ij}}}\rangle$ and that of ion translational entropy through ∆G_S(x) = ∆G(x) − ∆G_E(x) [72], where $\langle \cdot \cdot \cdot \rangle$ stands for the average over configuration ensemble in equilibrium and N is the number of charged spheres (particles and ions). As shown in Figure 5, it is very interesting that with the increase of salt valence z, ∆G_E(x) decreases from a repulsive one to an attractive one, while ∆G_S(x) increases from an attractive one to a repulsive one, in the separation range of the overall effective repulsions. Thus, the overall effective interactions for different z:z salts are attributed to the interplay of ∆G_E(x) and ∆G_S(x). For 1:1 salt, the very attractive ∆G_S(x) is overwhelming the repulsive ∆G_E(x), and consequently, the overall ∆G(x) is apparently attractive [74]. For 2:2 salt, the repulsive ∆G_E(x) is slightly stronger than a weakly attractive ∆G_S(x), causing an overall effective repulsion at high 2:2 salt [72]. However, for high 3:3 and 4:4 salts, ∆G_E(x) becomes attractive, while ∆G_S(x) becomes apparently more repulsive, causing the overall effective repulsions. Therefore, when z is increased from 2 to 4, the driving force for the overall effective repulsion between oppositely charged particles transits from the repulsive electrostatic energy to the repulsive contribution of ion translational entropy.

FIGURE 5

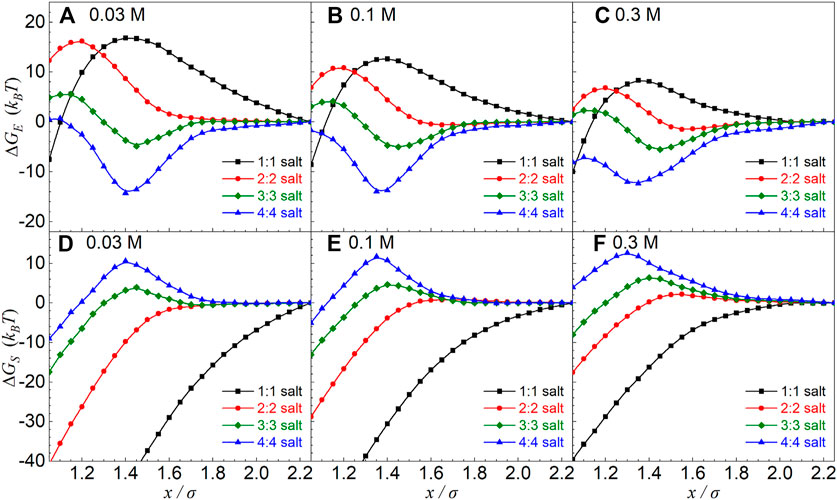
FIGURE 5. (A–C) Electrostatic energy ΔG_E and (D–F) entropic free-energy ΔG_S as functions of separation x in symmetrical z:z salt solutions from the MC simulations. The particle charge is |Z| = 36 e. The salt concentrations and ion valences have been shown in the respective panels. The reference separation was taken as x_ref = 45 Å.

The separation x-dependences of ∆G_S(x) and ∆G_E(x) shown above for different salt valence z values are interesting and understandable, which is directly coupled to the x-dependence of charge fraction f of condensed counterions (see Figures 2D–F–F,5). Furthermore, to explore the separation x-dependence of ∆G_E(x) for different z:z salts, as illustrated in Figures 6B–H, we also split the electrostatic energy ∆G_E(x) into three components: i) the interaction energy ∆G_a-b(x) between two particles with their respective condensed counterions; ii) the interaction energy ∆G_ion associated with diffusive ions including the interaction energy ∆G_ion-ion between diffusive ions and the interaction energy ∆G_ab-ion between condensed shells (a and b) and diffusive ions; and iii) the interaction energy ∆G_self within the condensed shells (a and b) including the interaction energy ∆G_c-c between condensed counterions and the interaction energy ∆G_p-c between charged particles and their respective condensed counterions.

FIGURE 6

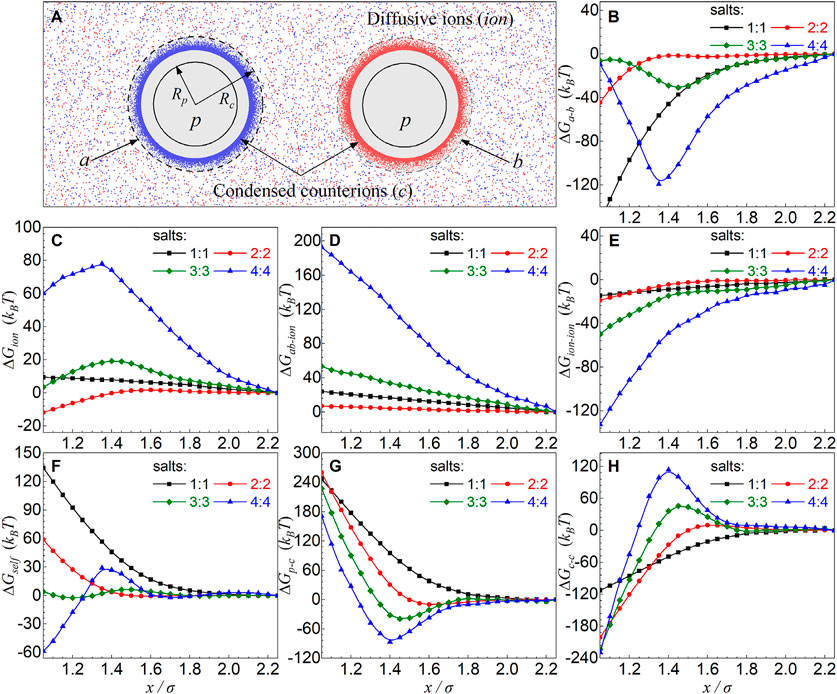
FIGURE 6. (A) An illustration for two oppositely charged particles in z:z salt solutions for analyzing in detail the different contributions to electrostatic energy: interaction energy ∆G_a-b between two oppositely charged particles with their respective condensed counterions denoted by “a” and “b” (the shaded regions), interaction energy associated with diffusive ions ∆G_ion including the interaction energy ∆G_ion-ion between diffusive ions and interaction energy ∆G_ab-ion between condensed shells (a and b) and diffusive ions, and the interaction energy ∆G_self within the condensed shells (a and b) including the interaction energy ∆G_c-c between condensed counterions and interaction energy ∆G_p-c between particles and their condensed counterions. Here, “c” denotes the condensed counterions and “ion” denotes the diffusive ions. (B–H) ∆G_a-b(B), ∆G_ion(C), ∆G_ab-ion(D), ∆G_ion-ion(E), ∆G_self(F), ∆G_p-c(G), and ∆G_c-c(H) as functions of the separation x between two oppositely charged particles in z:z salt solutions. The salt concentrations are 0.3 M, and the particle charge is |Z| = 36 e.

For 1:1 salt, the approaching of two oppositely charged particles with under-condensed counterions would cause the decrease in f due to the weakening of electric field between the particles, causing the increase of the translational entropy of counterions and the significant loss of electrostatic attraction between condensed counterions and particles, causing attractive ∆G_S(x) and repulsive ∆G_E(x) [74] (see Figures 2D–F–F, 6A,B,C,F. Such effect becomes more pronounced for lower 1:1 salt due to more release of ion translational entropy and more loss of electrostatic attraction between condensed counterions and charged particles with lower ion neutralization, causing more attractive ∆G_S(x) and more repulsive ∆G_E(x) (see Figures 5, 6F,G). Because of certain compensation between strongly attractive ∆G_a-b(x) and strongly repulsive ∆G_self, the repulsive ∆G_E(x) is relatively weaker than the attractive ∆G_S(x), causing the overall attractive PMFs for the covered 1:1 salts.

For 2:2 salt, two oppositely charged particles are only very slightly over-neutralized by condensed counterions, the increase in f with the decrease of x is very slight, and f will decrease for closer separation, causing very weakly repulsive ∆G_S(x) and repulsive ∆G_E(x) in the range of the overall effective repulsion. As shown in Figures 5, 6, such repulsive ∆G_E(x) is driven by the loss of the electrostatic attraction between charged particles and condensed counterions (see ∆G_self in Figures 6F–H). When z ≥ 3, due to the apparent increase of f with the decrease of separation x in the separation range of effective repulsions, ∆G_S(x) becomes apparently repulsive due to the significant decrease of translational entropy of condensed counterions, and ∆G_E(x) becomes visibly attractive due to the enhancement of electrostatic attraction ∆G_a-b(x) between two more strongly over-neutralized (oppositely) charged particles (with over-condensed counterions) (see Figure 6B). Such effect is more pronounced for z = 4, causing much more attractive ∆G_a-b(x) and ∆G_E(x), and consequently a weaker overall effective repulsion, as compared with z = 3. Here, we note that ∆G_a-b(x) mainly comes from the electrostatic attractions between “over-condensed” counterions belonging to two respective oppositely charged particles, that is, counterion–co-ion attractions, and consequently, such counterion–co-ion attractions should be responsible for the non-monotonic salt-valence dependence of the effective repulsion.

Therefore, when salt valence z is increased from 2 to 4, the driving force for the overall effective repulsion between oppositely charged particles transits from the repulsive electrostatic energy due to the release of condensed counterions and the consequent decrease of the condensed counterion–particle Columbic attraction, to the repulsive contribution of ion translational entropy due to the apparently more condensed counterions upon the approaching of particles at high 3:3 and 4:4 salts. The weaker effective repulsion for 4:4 salt than that for 3:3 salt is attributed to the apparently stronger attractive interaction between two oppositely charged particles with their respective “over-condensed” counterions which should be coupled to stronger counterion–co-ion attractions.

As described above and in the section of Introduction, the mechanism of the effective repulsion between oppositely charged particles for symmetrical salts is different from that for nonsymmetrical salts (e.g., 1:2 and 1:3 salts). In 1:2 and 1:3 salt solutions, two oppositely particles can electrostatically repel each other when they are under-neutralized and over-neutralized by their respective monovalent and multivalent counterions [75].

Involvement of Local-Ranged Counterion–Co-Ion Repulsion Apparently Enhances the Effective Repulsions

As discussed above, the apparent increase of f with the decrease of x for z > 2 is attributed to the Columbic attraction between “over-condensed” counterions for one particle and their co-ions which become the condensed counterions for the other particle, and the weaker overall effective repulsion for 4:4 salt than that for 3:3 salt is attributed to the stronger Columbic attractions between counterions and co-ions for 4:4 salt. Here, to further illustrate the non-monotonic salt-valence dependence of the effective repulsions, we performed the additional MC simulations through artificially involving local-ranged repulsions between counterions and co-ions to locally weaken counterion–co-ion Columbic attractions. In the MC simulations, we added a local-ranged repulsion potential to counteract the strong Columbic attraction between counterions and co-ions when they are very close to each other, and the u_ij interactions between counterion i and co-ion j are composed of hard-sphere repulsion, artificial local-ranged repulsion, and Coulomb interaction

$\begin{array}{c}{u}_{ij}=\{\begin{array}{cc}\frac{q_i{q}_j}{4\text{π}{\epsilon }_0\epsilon r_{ij}},& r_{ij}\ge a_i+a_j+\Delta ;\\ \infty ,& r_{ij}<a_i+a_j+\Delta .\end{array}\end{array}(5)$

Here, $a_i$ is the ion radius and $q_i$ represents the charge of ion i. $r_{ij}$ is the distance between the centers of counterion i and co-ion j. ∆ is the range of the added local-ranged repulsion between counterions and co-ions, and was taken as ∆ = 0.5 Å and ∆ = 2 Å in practice, respectively. The interactions other than those between counterions and co-ions are still given by Eq. 1.

As shown in Figures 7A,D, the involvement of local-ranged counterion–co-ion repulsions apparently enhances the effective repulsions between oppositely charged particles, and such effect is more pronounced for higher salt valence z and for larger ∆. It is also interesting that with the increase of z from 2 to 4, the effective repulsions become more apparent; that is, the salt-valence dependence of the effective repulsions becomes monotonic. Through calculating the charge fraction f of condensed counterions, we found that the involvement of local-ranged counterion–co-ion repulsion decreases f at large separation and weakens the increase in f (∆f) with the decrease of x, and such weakening effect for ∆f is more pronounced for higher salt valence z (see the insets of Figures 7A,D). Such decrease in ∆f comes from the decreased number of co-ions condensed adjacently around over-condensed counterions of a particle and the consequently decreased number of the co-ions entering the condensed counterion shell for the other particle (see Supplementary Figure 5). Similar to the analyses performed above, we split the overall effective ∆G(x) PMFs into the contributions from electrostatic energy ∆G_E(x) and ion translational entropy ∆G_S(x). As shown in Figures 7B,C,E,F, as we expected above, although the involvement of local-ranged counterion–co-ion repulsions causes less repulsive ∆G_S(x) due to the deceased ∆f, ∆G_E(x) becomes much less attractive and even becomes repulsive for ∆ = 2 Å, resulting in the stronger overall effective repulsions. Such effect is more pronounced for higher salt valence z due to the stronger weakening in counterion–co-ion attractions for higher z.

FIGURE 7

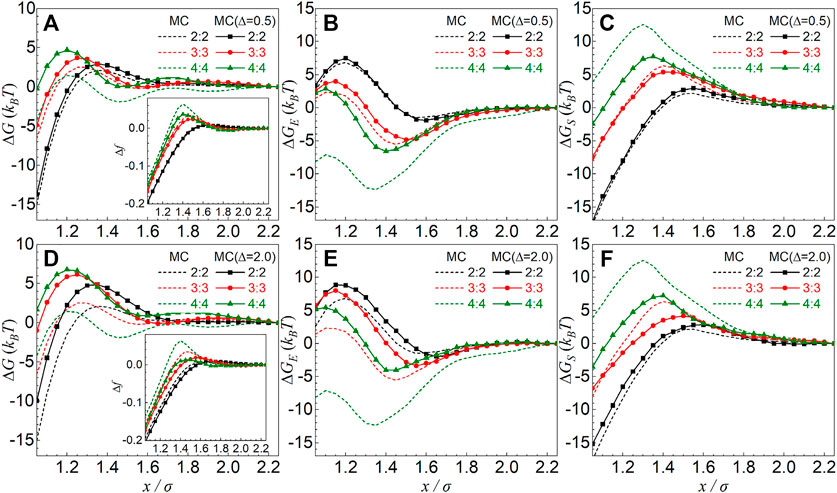
FIGURE 7. (A, D) Effective potentials of mean force ΔG(x) between equally and oppositely charged particles with |Z| = 36 e at 0.3 M symmetrical 2:2, 3:3, and 4:4 salts, from the MC simulations with involving local-ranged counterion–co-ion repulsions of ∆ = 0.5 Å (A) and ∆ = 2 Å (D) (see Eq. 5). The insets are the relative charge fraction Δf = f(x) − f(x_ref) of condensed counterions as a function of separation x between two particles. The dashed lines are the same as the lines in Figures 2C,F, 5C,F. (B, C) Electrostatic energy ΔG_E(x) (B) and entropic free-energy ΔG_S(x) (C) as functions of separation x, which are split from ΔG(x) in panel A. (E, F) Electrostatic energy ΔG_E(x) (E) and entropic free-energy ΔG_S(x) (F) as functions of separation x, which are split from ΔG(x) in panel D. The reference separation was taken as x_ref = 45 Å.

Therefore, our additional MC simulations further confirm our above analyses and indicate that the counterion–co-ion Coulombic attractions cause the non-monotonic salt-valence dependence of the effective repulsions for multivalent z:z salts.

Conclusion

In summary, in the present work, we investigated the effective interactions between equally and oppositely charged particles in symmetrical multivalent salt solutions by extensive MC simulations. Our simulations cover the extensive ranges of salt valence, salt concentration, and particle change. The major conclusions are listed as follows:

1. The effective interactions between oppositely charged particles are attractive for low multivalent salts and for 1:1 salt, while the interactions become apparent repulsions for high 2:2, 3:3, and 4:4 salts. Such apparent repulsion would become more pronounced for higher salt concentration and higher particle charge.

2. The driving force for the effective repulsion between oppositely charged particles transits from the repulsive electrostatic energy due to the release of condensed counterions and the consequent loss of counterion–particle Columbic attractions for high 2:2 salt, and to the repulsive entropic contribution of counterions due to the apparent increase of condensed counterions in the separation range of effective repulsion for high 3:3 and 4:4 salts.

3. The effective repulsion between oppositely charged particles becomes stronger for salt valence increases from 2 to 3, while it becomes weakened when salt valence exceeds 3 to 4. The non-monotonic salt-valence dependence of the effective repulsions is attributed to the interplay between the contributions of ion translational entropy and electrostatic energy. Specifically, the significantly stronger counterion–co-ion attractions are responsible for the weaker effective attraction for 4:4 salt than for 3:3 salt.

The effective repulsions between oppositely charged particles by symmetrical multivalent salts were predicted from the MC simulations, and are still required to be probed by experiments. For example, such effective repulsion can be probed by the atomic force microscopy which has been previously employed to probe the effective repulsion between oppositely charged particles by nonsymmetrical multivalent salts [76]. Moreover, the effective repulsions by high symmetrical multivalent salts were predicted for two oppositely charged spherical particles, while it is expected that such effective repulsions may also exist for two oppositely charged surfaces in symmetrical multivalent salt solutions, since the systems of two charged particles and of two charged surfaces are usually qualitatively similar [75, 77].

Our present work also involved some important simplifications. First, the model system with solvent and particles was modeled as uniform dielectric medium of high dielectric constant, and consequently, the dielectric boundary between particles and solvent was ignored [78–80]. Second, the charges of particles were placed at the centers of particle spheres, and the discreteness of charges on the particle surface was not involved in the work. Third, the solvent was implicitly modeled as a medium with high dielectric constant, and thus, the effect of solvent was naturally involved in electrostatic energy for analyzing the major driving force for the overall interactions [70]. Such simplifications may cause our model system deviating away from the realistic ones, and consequently, our obtained conclusions are more qualitative rather than quantitative. Although those simplifications were often used in previous modeling for ion–polyelectrolyte interactions, more realistic and accurate treatments are still required for more quantitative descriptions for realistic systems in the future works. Nevertheless, our findings and analyses can be very helpful for understanding the ion-mediated effective interactions between oppositely charged particles and the assembly of oppositely charged particles.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

Z-JT, YL, and CL designed the research. YL performed the calculations. Z-JT, YL, and CL analyzed the data. Z-J and YL wrote the manuscript. All authors discussed the results and reviewed the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (grant nos. 11774272 and 12075171). Parts of numerical calculations in this work were performed on the supercomputing system in the Supercomputing Center of Wuhan University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to Prof. Shi-Jie Chen (Univ. Missouri) and Prof. Xiangyun Qiu (George Washington Univ.) for valuable discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.696104/full#supplementary-material

References

1. Belloni L. Colloidal Interactions. J Phys Condens Matter (2000) 12:R549–R587. doi:10.1088/0953-8984/12/46/201

CrossRef Full Text | Google Scholar

2. Levin Y. Electrostatic Correlations: From Plasma to Biology. Rep Prog Phys (2002) 65:1577–632. doi:10.1088/0034-4885/65/11/201

CrossRef Full Text | Google Scholar

3. Guerrero-García GI, González-Tovar E, Olvera de la Cruz M. Entropic Effects in the Electric Double Layer of Model Colloids with Size-Asymmetric Monovalent Ions. J Chem Phys (2011) 135:054701. doi:10.1063/1.3622046

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ilyasov LO, Ogawa K, Panova IG, Yaroslavov AA, Adachi Y. Initial-stage Dynamics of Flocculation of Cationic Colloidal Particles Induced by Negatively Charged Polyelectrolytes, Polyelectrolyte Complexes, and Microgels Studied Using Standardized Colloid Mixing. Langmuir (2020) 36:8375–83. doi:10.1021/acs.langmuir.0c00619

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bakhshandeh A, Dos Santos AP, Levin Y. Interaction between Charge-Regulated Metal Nanoparticles in an Electrolyte Solution. J Phys Chem B (2020) 124:11762–70. doi:10.1021/acs.jpcb.0c09446

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Moazzami-Gudarzi M, Adam P, Smith AM, Trefalt G, Szilágyi I, Maroni P, et al. Interactions between Similar and Dissimilar Charged Interfaces in the Presence of Multivalent Anions. Phys Chem Chem Phys (2018) 20:9436–48. doi:10.1039/C8CP00679B

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Everts JC, Ravnik M. Complex Electric Double Layers in Charged Topological Colloids. Sci Rep (2018) 8:1–10. doi:10.1038/s41598-018-32550-8

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Tan Z-J, Chen S-J. Electrostatic Free Energy Landscapes for Nucleic Acid helix Assembly. Nucleic Acids Res (2006) 34:6629–39. doi:10.1093/nar/gkl810

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Qiu X, Khripin CY, Ke F, Howell SC, Zheng M. Electrostatically Driven Interactions between Hybrid DNA-Carbon Nanotubes. Phys Rev Lett (2013) 111:048301. doi:10.1103/PhysRevLett.111.048301

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Panteva MT, Giambaşu GM, York DM. Force Field for Mg2+, Mn2+, Zn2+, and Cd2+Ions that Have Balanced Interactions with Nucleic Acids. J Phys Chem B (2015) 119:15460–70. doi:10.1021/acs.jpcb.5b10423

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Cruz-León S, Schwierz N. Hofmeister Series for Metal-Cation-RNA Interactions: The Interplay of Binding Affinity and Exchange Kinetics. Langmuir (2020) 36:5979–89. doi:10.1021/acs.langmuir.0c00851

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Qiu X, Andresen K, Kwok LW, Lamb JS, Park HY, Pollack L. Inter-DNA Attraction Mediated by Divalent Counterions. Phys Rev Lett (2007) 99:038104. doi:10.1103/PhysRevLett.99.038104

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Tan Z-J, Chen S-J. Ion-mediated RNA Structural Collapse: Effect of Spatial Confinement. Biophysical J (2012) 103:827–36. doi:10.1016/j.bpj.2012.06.048

CrossRef Full Text | Google Scholar

14. Buyukdagli S. Like-charge Attraction and Opposite-Charge Decomplexation between Polymers and DNA Molecules. Phys Rev E (2017) 95:022502. doi:10.1103/PhysRevE.95.022502

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wu Y-Y, Zhang Z-L, Zhang J-S, Zhu X-L, Tan Z-J. Multivalent Ion-Mediated Nucleic Acid helix-helix Interactions: RNA versus DNA. Nucleic Acids Res (2015) 43:6156–65. doi:10.1093/nar/gkv570

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kushalkar MP, Liu B, Liu J. Promoting DNA Adsorption by Acids and Polyvalent Cations: Beyond Charge Screening. Langmuir (2020) 36:11183–95. doi:10.1021/acs.langmuir.0c02122

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chen S-J. RNA Folding: Conformational Statistics, Folding Kinetics, and Ion Electrostatics. Annu Rev Biophys (2008) 37:197–214. doi:10.1146/annurev.biophys.37.032807.125957

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Qiu X, Rau DC, Parsegian VA, Fang LT, Knobler CM, Gelbart WM. Salt-Dependent DNA-DNA Spacings in Intact BacteriophageλReflect Relative Importance of DNA Self-Repulsion and Bending Energies. Phys Rev Lett (2011) 106:028102. doi:10.1103/PhysRevLett.106.028102

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Cheatham TE. Simulation and Modeling of Nucleic Acid Structure, Dynamics and Interactions. Curr Opin Struct Biol (2004) 14:360–7. doi:10.1016/j.sbi.2004.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Srivastava A, Timsina R, Heo S, Dewage SW, Kirmizialtin S, Qiu X. Structure-guided DNA-DNA Attraction Mediated by Divalent Cations. Nucleic Acids Res (2020) 48:7018–26. doi:10.1093/nar/gkaa499

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Lipfert J, Doniach S, Das R, Herschlag D. Understanding Nucleic Acid-Ion Interactions. Annu Rev Biochem (2014) 83:813–41. doi:10.1146/annurev-biochem-060409-092720

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Nicasio-Collazo LA, Delgado-González A, Hernández-Lemus E, Castañeda-Priego R. Counterion Accumulation Effects on a Suspension of DNA Molecules: Equation of State and Pressure-Driven Denaturation. J Chem Phys (2017) 146:164902. doi:10.1063/1.4981208

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Lund M. Anisotropic Protein-Protein Interactions Due to Ion Binding. Colloids Surf B: Biointerfaces (2016) 137:17–21. doi:10.1016/j.colsurfb.2015.05.054

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Jordan E, Roosen-Runge F, Leibfarth S, Zhang F, Sztucki M, Hildebrandt A, et al. Competing Salt Effects on Phase Behavior of Protein Solutions: Tailoring of Protein Interaction by the Binding of Multivalent Ions and Charge Screening. J Phys Chem B (2014) 118:11365–74. doi:10.1021/jp5058622

PubMed Abstract | CrossRef Full Text | Google Scholar

25. de Souza JP, Bazant MZ. Continuum Theory of Electrostatic Correlations at Charged Surfaces. J Phys Chem C (2020) 124:11414–21. doi:10.1021/acs.jpcc.0c01261

CrossRef Full Text | Google Scholar

26. Wong GCL, Pollack L. Electrostatics of Strongly Charged Biological Polymers: Ion-Mediated Interactions and Self-Organization in Nucleic Acids and Proteins. Annu Rev Phys Chem (2010) 61:171–89. doi:10.1146/annurev.physchem.58.032806.104436

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wu JZ, Bratko D, Blanch HW, Prausnitz JM. Interaction between Oppositely Charged Micelles or Globular Proteins. Phys Rev E (2000) 62:5273–80. doi:10.1103/PhysRevE.62.5273

CrossRef Full Text | Google Scholar

28. Knipe PC, Thompson S, Hamilton AD. Ion-mediated Conformational Switches. Chem Sci (2015) 6:1630–9. doi:10.1039/C4SC03525A

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kalayan J, Henchman RH, Warwicker J. Model for Counterion Binding and Charge Reversal on Protein Surfaces. Mol Pharmaceutics (2019) 17:595–603. doi:10.1021/acs.molpharmaceut.9b01047

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Every AE, Russu IM. Influence of Magnesium Ions on Spontaneous Opening of DNA Base Pairs. J Phys Chem B (2008) 112:7689–95. doi:10.1021/jp8005876

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wennerström H, Vallina Estrada E, Danielsson J, Oliveberg M. Colloidal Stability of the Living Cell. Proc Natl Acad Sci USA (2020) 117:10113–21. doi:10.1073/pnas.1914599117

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Jing Y, Jadhao V, Zwanikken JW, Olvera de la Cruz M. Ionic Structure in Liquids Confined by Dielectric Interfaces. J Chem Phys (2015) 143:194508. doi:10.1063/1.4935704

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Hardwidge PR, Lee D-K, Prakash TP, Iglesias B, Den RB, Switzer C, et al. DNA Bending by Asymmetrically Tethered Cations: Influence of Tether Flexibility. Chem Biol (2001) 8:967–80. doi:10.1016/S1074-5521(01)00065-5

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Chakraborty K, Khatua P, Bandyopadhyay S. Exploring Ion Induced Folding of a Single-Stranded DNA Oligomer from Molecular Simulation Studies. Phys Chem Chem Phys (2016) 18:15899–910. doi:10.1039/C6CP00663A

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wang F-H, Wu Y-Y, Tan Z-J. Salt Contribution to the Flexibility of Single-Stranded Nucleic Acid of Finite Length. Biopolymers (2013) 99:370–81. doi:10.1002/bip.22189

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Carnie SL, Chan DYC, Stankovich J. Computation of Forces between Spherical Colloidal Particles: Nonlinear Poisson-Boltzmann Theory. J Colloid Interf Sci (1994) 165:116–28. doi:10.1006/jcis.1994.1212

CrossRef Full Text | Google Scholar

37. Dos Santos AP, Levin Y. Like-Charge Attraction between Metal Nanoparticles in a1∶1Electrolyte Solution. Phys Rev Lett (2019) 122:248005. doi:10.1103/PhysRevLett.122.248005

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Lee JW, Nilson RH, Templeton JA, Griffiths SK, Kung A, Wong BM. Comparison of Molecular Dynamics with Classical Density Functional and Poisson-Boltzmann Theories of the Electric Double Layer in Nanochannels. J Chem Theor Comput. (2012) 8:2012–22. doi:10.1021/ct3001156

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Gupta A, Govind Rajan A, Carter EA, Stone HA. Ionic Layering and Overcharging in Electrical Double Layers in a Poisson-Boltzmann Model. Phys Rev Lett (2020) 125:188004. doi:10.1103/PhysRevLett.125.188004

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Su M, Xu Z, Wang Y. Poisson-Boltzmann Theory with Non-linear Ion Correlations. J Phys Condens Matter (2019) 31:355101. doi:10.1088/1361-648X/ab24a9

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Zhang J-S, Zhang X, Zhang Z-L, Tan Z-J. Potential of Mean Force between Oppositely Charged Nanoparticles: A Comprehensive Comparison between Poisson-Boltzmann Theory and Monte Carlo Simulations. Sci Rep (2017) 7:14145. doi:10.1038/s41598-017-14636-x

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Tom AM, Rajesh R, Vemparala S. Aggregation of Flexible Polyelectrolytes: Phase Diagram and Dynamics. J Chem Phys (2017) 147:144903. doi:10.1063/1.4993684

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Xi K, Wang F-H, Xiong G, Zhang Z-L, Tan Z-J. Competitive Binding of Mg2+ and Na+ Ions to Nucleic Acids: From Helices to Tertiary Structures. Biophysical J (2018) 114:1776–90. doi:10.1016/j.bpj.2018.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Wang Z-Y, Ma Z. Examining the Contributions of Image-Charge Forces to Charge Reversal: Discrete versus Continuum Modeling of Surface Charges. J Chem Theor Comput. (2016) 12:2880–8. doi:10.1021/acs.jctc.6b00057

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Dishon M, Zohar O, Sivan U. From Repulsion to Attraction and Back to Repulsion: The Effect of NaCl, KCl, and CsCl on the Force between Silica Surfaces in Aqueous Solution. Langmuir (2009) 25:2831–6. doi:10.1021/la803022b

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Truzzolillo D, Bordi F, Sciortino F, Sennato S. Interaction between Like-Charged Polyelectrolyte-Colloid Complexes in Electrolyte Solutions: A Monte Carlo Simulation Study in the Debye-Hückel Approximation. J Chem Phys (2010) 133:024901. doi:10.1063/1.3459125

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Dahirel V, Jardat M, Dufrêche JF, Turq P. Ion-mediated Interactions between Charged and Neutral Nanoparticles. Phys Chem Chem Phys (2008) 10:5147–55. doi:10.1039/B806315J

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Tan Z-J, Chen S-J. Ion-mediated Nucleic Acid helix-helix Interactions. Biophysical J (2006) 91:518–36. doi:10.1529/biophysj.106.084285

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Sun L-Z, Chen S-J. Monte Carlo Tightly Bound Ion Model: Predicting Ion-Binding Properties of RNA with Ion Correlations and Fluctuations. J Chem Theor Comput. (2016) 12:3370–81. doi:10.1021/acs.jctc.6b00028

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Sun L-Z, Chen S-J. Predicting RNA-Metal Ion Binding with Ion Dehydration Effects. Biophysical J (2019) 116:184–95. doi:10.1016/j.bpj.2018.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Allahyarov E, D'Amico I, Löwen H. Attraction between Like-Charged Macroions by Coulomb Depletion. Phys Rev Lett (1998) 81:1334–7. doi:10.1103/PhysRevLett.81.1334

CrossRef Full Text | Google Scholar

52. May S, Iglič A, Reščič J, Maset S, Bohinc K. Bridging Like-Charged Macroions through Long Divalent Rodlike Ions. J Phys Chem B (2008) 112:1685–92. doi:10.1021/jp073355e

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Besteman K, Zevenbergen MAG, Lemay SG. Charge Inversion by Multivalent Ions: Dependence on Dielectric Constant and Surface-Charge Density. Phys Rev E (2005) 72:061501. doi:10.1103/PhysRevE.72.061501

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Finessi M, Sinha P, Szilágyi I, Popa I, Maroni P, Borkovec M. Charge Reversal of Sulfate Latex Particles by Adsorbed Linear Poly(ethylene Imine) Probed by Multiparticle Colloidal Probe Technique. J Phys Chem B (2011) 115:9098–105. doi:10.1021/jp203514r

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Qiu X, Parsegian VA, Rau DC. Divalent Counterion-Induced Condensation of Triple-Strand DNA. Proc Natl Acad Sci (2010) 107:21482–6. doi:10.1073/pnas.1003374107

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Zhang Z-L, Wu Y-Y, Xi K, Sang J-P, Tan Z-J. Divalent Ion-Mediated DNA-DNA Interactions: A Comparative Study of Triplex and Duplex. Biophysical J (2017) 113:517–28. doi:10.1016/j.bpj.2017.06.021

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Wu J, Bratko D, Prausnitz JM. Interaction between Like-Charged Colloidal Spheres in Electrolyte Solutions. Proc Natl Acad Sci (1998) 95:15169–72. doi:10.1073/pnas.95.26.15169

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Jiang L, Titmuss S, Klein J. Interactions of Hyaluronan Layers with Similarly Charged Surfaces: The Effect of Divalent Cations. Langmuir (2013) 29:12194–202. doi:10.1021/la401931y

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Labbez C, Jönsson B, Skarba M, Borkovec M. Ion−Ion Correlation and Charge Reversal at Titrating Solid Interfaces. Langmuir (2009) 25:7209–13. doi:10.1021/la900853e

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Butler JC, Angelini T, Tang JX, Wong GCL. Ion Multivalence and Like-Charge Polyelectrolyte Attraction. Phys Rev Lett (2003) 91:028301. doi:10.1103/PhysRevLett.91.028301

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Zheng Y, Lin C, Zhang J-S, Tan Z-J. Ion-mediated Interactions between Like-Charged Polyelectrolytes with Bending Flexibility. Sci Rep (2020) 10:21586. doi:10.1038/s41598-020-78684-6

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Lin C, Qiang X, Dong H-L, Huo J, Tan Z-J. Multivalent Ion-Mediated Attraction between Like-Charged Colloidal Particles: Nonmonotonic Dependence on the Particle Charge. ACS Omega (2021) 6:9876–86. doi:10.1021/acsomega.1c00613

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Jiménez-Ángeles F, Lozada-Cassou M. On the Regimes of Charge Reversal. J Chem Phys (2008) 128:174701. doi:10.1063/1.2911923

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Zhang X, Zhang J-S, Shi Y-Z, Zhu X-L, Tan Z-J. Potential of Mean Force between Like-Charged Nanoparticles: Many-body Effect. Sci Rep (2016) 6:23434. doi:10.1038/srep23434

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Lyklema J. Quest for Ion-Ion Correlations in Electric Double Layers and Overcharging Phenomena. Adv Colloid Interf Sci (2009) 147-148:205–13. doi:10.1016/j.cis.2008.12.002

CrossRef Full Text | Google Scholar

66. Taboada-Serrano P, Yiacoumi S, Tsouris C. Behavior of Mixtures of Symmetric and Asymmetric Electrolytes Near Discretely Charged Planar Surfaces: A Monte Carlo Study. J Chem Phys (2005) 123:054703. doi:10.1063/1.1992484

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Wang Z-y., Ma Y-q. Computational Evidence of Two Driving Mechanisms for Overcharging in an Electric Double Layer Near the point of Zero Charge. Phys Rev E (2012) 85:062501. doi:10.1103/PhysRevE.85.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Wang Z-y., Ma Y-q. Insights from Monte Carlo Simulations on Charge Inversion of Planar Electric Double Layers in Mixtures of Asymmetric Electrolytes. J Chem Phys (2010) 133:064704. doi:10.1063/1.3469795

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Martı́n-Molina A, Quesada-Pérez M, Galisteo-González F, Hidalgo-Álvarez R. Looking into Overcharging in Model Colloids through Electrophoresis: Asymmetric Electrolytes. J Chem Phys (2003) 118:4183–9. doi:10.1063/1.1540631

CrossRef Full Text | Google Scholar

70. Angelescu DG, Linse P. Monte Carlo Simulation of the Mean Force between Two Like-Charged Macroions with Simple 1:3 Salt Added. Langmuir (2003) 19:9661–8. doi:10.1021/la030153a

CrossRef Full Text | Google Scholar

71. Yan Q, de Pablo JJ. Phase Equilibria of Charge-, Size-, and Shape-Asymmetric Model Electrolytes. Phys Rev Lett (2002) 88:095504. doi:10.1103/PhysRevLett.88.095504

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Lin C, Zhang X, Qiang X, Zhang J-S, Tan Z-J. Apparent Repulsion between Equally and Oppositely Charged Spherical Polyelectrolytes in Symmetrical Salt Solutions. J Chem Phys (2019) 151:114902. doi:10.1063/1.5120756

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Tan Z-J, Chen S-J. Electrostatic Correlations and Fluctuations for Ion Binding to a Finite Length Polyelectrolyte. J Chem Phys (2005) 122:044903. doi:10.1063/1.1842059

CrossRef Full Text | Google Scholar

74. Fu J, Schlenoff JB. Driving Forces for Oppositely Charged Polyion Association in Aqueous Solutions: Enthalpic, Entropic, but Not Electrostatic. J Am Chem Soc (2016) 138:980–90. doi:10.1021/jacs.5b11878

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Trulsson M, Jönsson B, Åkesson T, Forsman J, Labbez C. Repulsion between Oppositely Charged Surfaces in Multivalent Electrolytes. Phys Rev Lett (2006) 97:068302. doi:10.1103/PhysRevLett.97.068302

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Besteman K, Zevenbergen MAG, Heering HA, Lemay SG. Direct Observation of Charge Inversion by Multivalent Ions as a Universal Electrostatic Phenomenon. Phys Rev Lett (2004) 93:170802. doi:10.1103/PhysRevLett.93.170802

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Trulsson M, Jönsson B, Åkesson T, Forsman J, Labbez C. Repulsion between Oppositely Charged Macromolecules or Particles. Langmuir (2007) 23:11562–9. doi:10.1021/la701222b

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Kanduč M, Naji A, Forsman J, Podgornik R. Dressed Counterions: Polyvalent and Monovalent Ions at Charged Dielectric Interfaces. Phys Rev E (2011) 84:011502. doi:10.1103/PhysRevE.84.011502

CrossRef Full Text | Google Scholar

79. Ghodrat M, Naji A, Komaie-Moghaddam H, Podgornik R. Strong Coupling Electrostatics for Randomly Charged Surfaces: Antifragility and Effective Interactions. Soft Matter (2015) 11:3441–59. doi:10.1039/C4SM02846E

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Adžić N, Podgornik R. Titratable Macroions in Multivalent Electrolyte Solutions: Strong Coupling Dressed Ion Approach. J Chem Phys (2016) 144:214901. doi:10.1063/1.4952980

PubMed Abstract | CrossRef Full Text | Google Scholar