Long-Lasting Orientation of Symmetric-Top Molecules Excited by Two-Color Femtosecond Pulses

Impulsive orientation of symmetric-top molecules excited by two-color femtosecond pulses is considered. In addition to the well-known transient orientation appearing immediately after the pulse and then reemerging periodically due to quantum revivals, we report the phenomenon of field-free long-lasting orientation. Long-lasting means that the time averaged orientation remains non-zero until destroyed by other physical effects, e.g., intermolecular collisions. The effect is caused by the combined action of the field-polarizability and field-hyperpolarizability interactions. The dependence of degree of long-lasting orientation on temperature and pulse parameters is considered. The effect can be measured by means of second (or higher-order) harmonic generation, and may be used to control the deflection of molecules traveling through inhomogeneous electrostatic fields.

1 Introduction

Over the years, diverse optical methods have been developed to align and orient molecules of varying complexity and many applications related to studies of molecular and photon-induced processes are based on the ability to control the absolute orientation of the molecules. For reviews, see [1–6].

There are several laser-based strategies for achieving molecular orientation in the gas phase, including using a combination of intense non-resonant laser and weak electrostatic fields [7–15], and using strong single-cycle terahertz (THz) pulses [16–23], alone or together with optical pulses [24–26]. In addition, laser and THz pulses with twisted polarization were shown to be effective for inducing enantioselective orientation of chiral molecules [27–33].

The techniques listed above rely on the laser-dipole and/or laser-polarizability interactions. Another route to molecular orientation stems from higher-order laser-molecule interactions, e.g., the laser field-hyperpolarizability interaction. Non-resonant phase-locked two-color laser pulses consisting of the fundamental wave (FW) and its second harmonic (SH) were used for inducing molecular orientation by interacting with the molecular hyperpolarizability [34–49].

Here, we investigate the orientation dynamics of symmetric-top molecules excited by single two-color femtosecond laser pulses. In addition to the well-known transient orientation appearing immediately as a response to the laser excitation, we predict the existence of long-lasting orientation. Long-lasting means that the time-averaged orientation remains non-zero, within the model, indefinitely or until destroyed by additional physical effects, e.g., by collisions. The long-lasting orientation induced by a two-color pulse has an intricate dependence on both the molecular polarizability and hyperpolarizability. Related effects have been recently observed in chiral molecules excited by one-color laser pulses with twisted polarization [30, 32] and investigated in non-linear molecules excited by THz pulses [23, 33].

The paper is organized as follows. In the next section, we describe our numerical approaches for simulating the laser-driven molecular rotational dynamics. In Section 3, we present the long-lasting orientation, which is the main result of this work. Section 4 is devoted to a qualitative analysis of the effect, and a derivation of the approximate classical formula for the degree of long-lasting orientation. Additional results are presented in Section 5.

2 Numerical Methods

In this work, the rotational dynamics of symmetric-top molecules is treated within the rigid rotor approximation. We performed both classical and quantum mechanical simulations of molecular rotation driven by two-color laser fields. This section outlines the theoretical approaches used in both cases.

2.1 Classical Simulation

In the classical limit, the rotational dynamics of a single rigid top is described by Euler’s equations [50]

$\mathbf{I}\dot{\mathbf{\Omega }}=\left(\mathbf{I\Omega }\right)\times \mathbf{\Omega }+\mathbf{T},(1)$

where $\mathbf{I}=\mathrm{diag}\left(I_a,I_b,I_c\right)$ is the moment of inertia tensor, $\mathbf{\Omega }=\left({\text{Ω}}_a,{\text{Ω}}_b,{\text{Ω}}_c\right)$ is the angular velocity, and $\mathbf{T}=\left(T_a,T_b,T_c\right)$ is the external torque resulting from the interaction between field-induced dipole moment and the electric field. All the quantities in Eq. 1 are expressed in the rotating molecular frame of reference, equipped with a basis set including the three principal axes of inertia, a, b, and c.

In the laboratory frame of reference, the electric field of a two-color laser pulse is defined by

$\mathbf{E}\left(t\right)={\epsilon }_1\left(t\right)\text{cos}\left(\omega t\right){\mathbf{e}}_Z+{\epsilon }_2\left(t\right)\text{cos}\left(2\omega t+\phi \right){\mathbf{e}}_{\text{SH}},(2)$

where the two terms correspond to the FW and its SH, respectively. ω is the carrier frequency of the FW field, φ is the relative phase of the second harmonic, ${\epsilon }_n\left(t\right)={\epsilon }_{n,0}\text{exp}[-2\text{\hspace{0.17em}ln}2{\left(t/{\sigma }_n\right)}^2],n=\mathrm{1,2},$ is the field’s envelope with ${\epsilon }_{n,0}$ as the peak amplitude, and ${\sigma }_n$ is the full width at half maximum (FWHM) of the laser pulse intensity profile. The polarization direction of the SH field is given by ${\mathbf{e}}_{\text{SH}}=\text{cos}\left({\varphi }_{\text{SH}}\right){\mathbf{e}}_Z+\text{sin}\left({\varphi }_{\text{SH}}\right){\mathbf{e}}_X$, where ${\varphi }_{\text{SH}}$ is its angle with respect to the Z axis, ${\mathbf{e}}_Z$ and ${\mathbf{e}}_X$ are the unit vectors along laboratory Z and X axes, respectively. The electric field in the molecular frame of reference can be expressed as

$\mathbf{E}\left(t\right)={\epsilon }_1\left(t\right)\text{\hspace{0.17em}cos}\left(\omega t\right){\mathbf{e}}_1+{\epsilon }_2\left(t\right)\text{\hspace{0.17em}cos}\left(2\omega t+\phi \right){\mathbf{e}}_2,(3)$

where ${\mathbf{e}}_1=Q{\mathbf{e}}_Z$ and ${\mathbf{e}}_2=Q{\mathbf{e}}_{\text{SH}}$ are the unit vectors expressed in the molecular frame of reference. Q is a $3\times 3$ time-dependent orthogonal matrix relating the laboratory and the molecular frames of reference. It is parametrized by a quaternion, q which has an equation of motion $\dot{q}=q\text{Ω}/2$, with $\text{Ω}=\left(0,\mathbf{\Omega }\right)$ being a pure quaternion [51, 52]. Considering laser-polarizability and laser-hyperpolarizabiltiy interactions, the torque induced by a two-color field has two contributions $\mathbf{T}={\mathbf{T}}^{\alpha }+{\mathbf{T}}^{\beta }$, where [53]

${\mathbf{T}}^{\alpha }=\overline{\left(\mathit{\alpha }\mathbf{E}\times \mathbf{E}\right)}=\frac{{\epsilon }_1^2}{2}\left(\mathit{\alpha }{\mathbf{e}}_1\right)\times {\mathbf{e}}_1+\frac{{\epsilon }_2^2}{2}\left(\mathit{\alpha }{\mathbf{e}}_2\right)\times {\mathbf{e}}_2,(4)$

${\mathbf{T}}_i^{\beta }=\frac{1}{2}{\overline{\left[\left(\mathbf{E}\mathit{\beta }\mathbf{E}\right)\times \mathbf{E}\right]}}_i={\displaystyle \sum }_{m,n,j,k}\frac{{\epsilon }_1^2{\epsilon }_2}{4}{\mathit{ϵ}}_{ijk}{\beta }_{mnj}{e}_{1m}{e}_{2n}{e}_{1k}+{\displaystyle \sum }_{m,n,j,k}\frac{{\epsilon }_1^2{\epsilon }_2}{8}{\mathit{ϵ}}_{ijk}{\beta }_{mnj}{e}_{1m}{e}_{1n}{e}_{2k}.(5)$

Here, the overline $\overline{(\cdots )}$ represents averaging over the optical cycle, $\mathit{\alpha }$ and $\mathit{\beta }$ are the polarizability and hyperpolarizability tensors, respectively. ${\mathit{ϵ}}_{ijk}$ is the Levi-Civita symbol, ${\beta }_{mnj}$ is a component of the hyperpolarizability tensor, $e_{1m}$ and $e_{2m}$ are the components of the FW and SH fields, respectively.

To simulate the behavior of an ensemble of non-interacting molecules, we use the Monte Carlo approach. For each molecule, the Euler’s equations [Eq. 1] with the torques in Eqs. 4, 5 are solved numerically using the standard fourth order Runge-Kutta algorithm. In the simulations we used ensembles consisting of $N\gg 1$ molecules. The initial uniform random quaternions, representing isotropically distributed molecules, were generated using the recipe from [54]. Initial angular velocities are distributed according to the Boltzmann distribution,

$f\left(\mathbf{\Omega }\right)\propto {\displaystyle \prod }_i\text{exp}\left(-\frac{I_i{\text{Ω}}_i^2}{2k_{B}T}\right),(6)$

where $i=a,b,c$, T is the temperature and $k_B$ is the Boltzmann constant.

2.2 Quantum Simulation

The Hamiltonian describing the rotational degrees of freedom of a molecule and the molecular polarizability and hyperpolarizability couplings to external time-dependent fields can be written as $H\left(t\right)=H_r+H_{\text{int}}\left(t\right)$, where $H_r$ is the field-free Hamiltonian [55], and $H_{\text{int}}\left(t\right)$ is the molecule-field interaction potential, with two contributions $H_{\text{int}}\left(t\right)=V_{\alpha }+V_{\beta }$, where [56]

$V_{\alpha }=-\frac{1}{2}{\displaystyle \sum }_{i,j}{\alpha }_{ij}{E}_i{E}_j,V_{\beta }=-\frac{1}{6}{\displaystyle \sum }_{i,j,k}{\beta }_{ijk}{E}_i{E}_j{E}_k.(7)$

Here $E_i$, ${\alpha }_{ij}$, and ${\beta }_{ijk}$ are the components of the field vector, polarizability tensor $\mathit{\alpha }$, and hyperpolarizability tensor $\mathit{\beta }$, respectively. Since the optical carrier frequency of the laser fields, ω [see Eq. 2], is several orders of magnitude larger than a typical rotational frequency of small molecules, the energy contribution due to the interaction with the molecular permanent dipole, $\mathit{\mu }$, $-\mathit{\mu }\cdot \mathbf{E}\left(t\right)$ is negligible.

We use the eigenstates of $H_r$, $|JKM\rangle$, describing the field-free motion of quantum symmetric-top [55], as the basis set in our numerical simulations. The three quantum numbers are J, K and M, where J is the total angular momentum, while K and M are its projections on the molecular a axis and the laboratory-fixed Z axis, respectively. The time-dependent Schrödinger equation $i\hslash {\partial }_t|\text{Ψ}\left(t\right)\rangle =H\left(t\right)|\text{Ψ}\left(t\right)\rangle$ is solved by numerical exponentiation of the Hamiltonian matrix (see Expokit [57]) with the initial state being one of the field-free eigenstates, $|\text{Ψ}(t=0)\rangle =|JKM\rangle$. The degree of molecular orientation is derived by calculating the induced polarization, the expectation value of the dipole projection. The polarization along each of the axes in the laboratory-fixed frame of reference is given by

$\langle {\mu }_i^{\left(J,K,M\right)}\rangle \left(t\right)=\langle \text{Ψ}\left(t\right)\left|\mathit{\mu }\cdot {\mathbf{e}}_i\right|\text{Ψ}\left(t\right)\rangle ,(8)$

where ${\mathbf{e}}_i$ represents one of the unit vectors ${\mathbf{e}}_X,{\mathbf{e}}_Y,{\mathbf{e}}_Z$. Thermal effects are accounted for by computing the incoherent average of the time-dependent polarizations obtained for the various initial states $|JKM\rangle$. The relative weight of each of the projections $\langle {\mu }_i^{\left(J,K,M\right)}\rangle \left(t\right)$ is defined by the Boltzmann distribution,

$\langle {\mu }_i\rangle \left(t\right)=\frac{1}{\mathrm{Ƶ}}{\displaystyle \sum }_{J,K,M}{\mathit{ϵ}}_K\exp \left[-\frac{{\epsilon }_{J,K,M}}{k_{B}T}\right]\langle {\mu }_i^{\left(J,K,M\right)}\rangle \left(t\right),(9)$

where $\mathrm{Ƶ}={\displaystyle {\sum }_{J,K,M}{\mathit{ϵ}}_K}\exp \left(-{\epsilon }_{J,K,M}/k_{B}T\right)$ is the partition function, and ${\epsilon }_{J,K,M}$ is the energy/eigenvalue corresponding to $|JKM\rangle$ state. For molecules with two or more identical atoms, an additional statistical factor ${\mathit{ϵ}}_K$ must be included in the distribution [58]. For the case of methyl fluoride (${\text{CH}}_3\text{F}$) molecule considered in this work, ${\mathit{ϵ}}_K$ is given by

${\mathit{ϵ}}_K=\frac{{\left(2I_H+1\right)}^3}{3}\left[1+\frac{2\text{cos}\left(2\pi K/3\right)}{{\left(2I_H+1\right)}^2}\right],(10)$

where $I_H=1/2$.

In our simulations, the basis set included all the states with $J\le 30$. For our sample molecule, ${\text{CH}}_3\text{F}$, at initial temperature of $T=5\text{K}$, this means that initial states with $J\le 8$ were included. Additional details about the numerical simulations, including the matrix elements of the interaction Hamiltonian $H_{\text{int}}$, can be found in Supplementary Appendix A.

3 Long-Lasting Orientation

We continue to consider the methyl fluoride (${\text{CH}}_3\text{F}$), as an example for a symmetric-top molecule. The molecule is excited by a two-color pulse in which the polarizations of the FW and SH are parallel and along Z axis [${\varphi }_{\text{SH}}=0$, see Eq. 2]. In addition, here we set the relative phase between them to be zero ($\phi =0$). Later on we discuss what changes when this phase changes. Table 1 summarizes the molecular properties of ${\text{CH}}_3\text{F}$. Moments of inertia, dipole moment, and polarizability tensor components are taken from NIST, where they were computed within the density functional theory (DFT, method CAM-B3LYP/aug-cc-pVTZ) [59]. The hyperpolarizability values are literature values taken from [60].

TABLE 1

TABLE 1. Molecular properties (in atomic units) of ${\text{CH}}_3\text{F}$: moments of inertia, nonzero elements of dipole moment, polarizability tensor, and hyperpolarizability tensor. All the quantities are represented in the reference frame of molecular principal axes of inertia.

Figure 1 shows the projection of the dipole moment along the laboratory Z axis, $\langle {\mu }_Z\rangle$, calculated classically and quantum mechanically (see Methods Section 2). In the classical case, the angle brackets $\langle \cdots \rangle$ denote ensemble average, that is the average of the dipole projections of $N={10}^8$ molecules, initially isotropically distributed in space and having random angular velocities [see Eq. 6]. In the quantum case, $\langle \cdots \rangle$ denotes incoherent average of initially populated rotational states [see Eq. 9]. Note that the averages $\langle {\mu }_X\rangle$ and $\langle {\mu }_Y\rangle$ are zero. Here, the initial temperature is $T=5\text{K}$, the peak intensities of the FW and SH fields are $I_{\text{FW}}=8\times {10}^{13}\text{W}/{\text{cm}}^2$ and $I_{\text{SH}}=3\times {10}^{13}\text{W}/{\text{cm}}^2$, respectively, and the duration (FWHM) of the pulses are ${\sigma }_1={\sigma }_2=120\text{fs}$ [see Eq. 2]. On the short time scale (first $\approx 2\text{ps}$), the classical and quantum results are in remarkable agreement, and show the expected immediate response to a kick by a two-color pulse. On the long time scale, the quantum mechanical simulation exhibits distinct quantum revivals of the orientation [61–65]. This transient orientation effect is well studied and was observed in the past [34–49].

FIGURE 1

FIGURE 1. Z-projection of the dipole moment, $\langle {\mu }_Z\rangle$ and the orientation factor, $\langle \text{cos}\left({\theta }_{\mu Z}\right)\rangle \equiv \langle {\mu }_Z\rangle /\mu$ as a function of time for ${\text{CH}}_3\text{F}$ molecule at initial rotational temperature $T=5\text{K}$. Here μ is the magnitude of the dipole moment and ${\theta }_{\mu Z}$ denotes the angle between the dipole moment and laboratory Z axis. The solid blue and dotted red lines represent the results of quantum and classical simulations, respectively. The solid green line is the time average defined by $\overline{\langle {\mu }_Z\rangle \left(t\right)}={\left(\text{Δ}t\right)}^{-1}{\displaystyle {\int }_{t-\text{Δ}t/2}^{t+\text{Δ}t/2}\text{d}{t}^{\prime }}\langle {\mu }_Z\rangle \left(t^{\prime }\right)$, where $\text{Δ}t=19.6\text{ps}$. The inset shows a magnified portion of the signals.

In the case of symmetric-top molecules considered here, we observe long-lasting (persistent) orientation, a previously unreported phenomenon in two-color orientation schemes. The inset in Figure 1 demonstrates that after the initial oscillations are washed out, the classical polarization/degree of orientation attains a constant, nonzero value. In the quantum case too, despite its being partially masked by the revivals, the sliding time average of the signal is approximately constant and it persists indefinitely within the adopted model. This long-lasting orientation is one of the main results of this work.

Several comments are in order. Additional physical effects can distort the long-term field-free picture of identical periodically appearing revivals seen in Figure 1. These include the centrifugal distortion and the radiation emission due to rapidly rotating molecular permanent dipole moment. Dephasing of the rotational states caused by the centrifugal distortion leads to the eventual decay of the revivals’ peaks [21, 22]. Nevertheless, the average dipole remains almost unchanged (see [23]). The radiative emission results in the gradual decrease of the rotational energy [21, 22]. However, for a rarefied molecular gas, the estimated relative energy loss during a single revival is very small. The proper description of the behavior on an even longer timescale (nanoseconds), requires the inclusion of collisions and fine structure effects [66, 67], which is beyond the scope of the current work. Furthermore, it should be noted that higher laser pulse intensities lead to higher degree of orientation, but when the intensity is high enough for molecular ionization, another effect kicks in, namely orientation mechanism due to selective molecular ionization of molecules with specific orientation [43, 44]. Considering this kind of orientation is also beyond the scope of this work.

4 Long-Lasting Orientation - A Qualitative Description

An explicit form of the interaction potential [Eq. 7] can be obtained by expressing the electric field vector in the rotating molecular frame of reference. For the sake of the current discussion, this can be done conveniently by using an orthogonal rotation matrix parameterized by the three Euler angles, $R\left(\varphi ,\theta ,\chi \right)$. We use the definition convention adopted in [55], according to which, ϕ and θ are the standard azimuth and polar angles defining the orientation of the molecular frame z axis, and χ is the additional rotation angle about z axis. The basis set in the rotating molecular frame of reference consists of the three principal axes of inertia, $a,b,c$. For molecules belonging to the $C_{3v}$ symmetry group (such as ${\text{CH}}_3\text{F}$), there are three non-zero polarizability components (two of them are equal), and 11 non-zero hyperpolarizability components (three of which are independent) [68]. For definiteness, we associate the axis of the three-fold rotational symmetry with the most polarizable molecular principal axis a (z axis in the rotating frame), having the smallest moment of inertia, $I_a$. In this case, the non-zero polarizability elements are ${\alpha }_{aa}>{\alpha }_{bb}={\alpha }_{cc}$, and the independent hyperpolarizability elements are ${\beta }_{aaa}$, ${\beta }_{abb}={\beta }_{acc}$, ${\beta }_{bbb}=-{\beta }_{bcc}$. The other non-zero hyperpolarizability elements are obtained by permuting the indices of the independent elements [68]. The parameters of the ${\text{CH}}_3\text{F}$ molecule are listed in Table 1.

We consider the case of a two-color pulse in which both the FW and SH are polarized along Z axis. The interaction potential is obtained by carrying out the summation in Eq. 7 (where all the quantities are expressed in the basis of principal axes of inertia) and we average over the optical cycle. The resulting potential has two contributions,

${\overline{V}}_{\alpha }\left(\theta \right)=-\frac{{\epsilon }_1^2\left(t\right)+{\epsilon }_2^2\left(t\right)}{4}\left({\alpha }_{aa}-{\alpha }_{bb}\right){\text{\hspace{0.17em}cos}}^2\left(\theta \right),(11)$

${\overline{V}}_{\beta }\left(\theta ,\chi \right)=-\frac{{\epsilon }_1^2\left(t\right){\epsilon }_2\left(t\right)}{8}\text{cos}\left(\phi \right){\text{\hspace{0.17em}sin}}^3\left(\theta \right)\text{\hspace{0.17em}cos}\left(3\chi \right){\beta }_{bcc}-\frac{{\epsilon }_1^2\left(t\right){\epsilon }_2\left(t\right)}{8}\text{cos}\left(\phi \right)\left[3{\text{\hspace{0.17em}sin}}^2\left(\theta \right)\text{\hspace{0.17em}cos}\left(\theta \right){\beta }_{abb}+{\text{cos}}^3\left(\theta \right){\beta }_{aaa}\right].(12)$

To facilitate the qualitative discussion in this section, we let ${\beta }_{bbb}={\beta }_{bcc}=0$. These elements of the hyperpolarizability tensor are the smallest (see Table 1), and their omission does not affect the qualitative features of the discussed phenomena. Thus, the hyperpolarizability interaction becomes

${\overline{V}}_{\beta }^{\mathrm{\star }}\left(\theta \right)=-\frac{{\epsilon }_1^2\left(t\right){\epsilon }_2\left(t\right)}{8}\text{cos}\left(\phi \right)\left[3{\text{sin}}^2\left(\theta \right)\text{cos}\left(\theta \right){\beta }_{abb}+{\text{cos}}^3\left(\theta \right){\beta }_{aaa}\right].(13)$

And $\overline{V}={\overline{V}}_{\alpha }+{\overline{V}}_{\beta }^{\mathrm{\star }}$ is a function of a single variable θ—the polar angle between the symmetry axis of the molecule (a axis) and the laboratory Z axis (axis of laser polarization).

The two parts of the interaction potential lead to two distinct effects. ${\overline{V}}_{\alpha }\left(\theta \right)$ is a symmetric function of θ (about $\theta =\pi /2$), and a kick by such a potential results in molecular alignment (for reviews, see [1–6]). The second part, ${\overline{V}}_{\beta }^{\mathrm{\star }}\left(\theta \right)$ is an asymmetric function of θ, causing molecular orientation. Transient orientation of linear molecules excited by two-color laser pulses has been observed [38–40, 42, 44] and is being studied theoretically [45–49]. Figure 2 shows the angular dependence of ${\overline{V}}_{\beta }^{\mathrm{\star }}\left(\theta \right)$, $\text{cos}\left(\phi \right)\left[3b{\text{sin}}^2\left(\theta \right)\text{cos}\left(\theta \right)+{\text{cos}}^3\left(\theta \right)\right]$, see Eq. 13. The orienting potential is proportional to $\text{cos}\left(\phi \right)$, such that the orientation is zero for $\phi =\pi /2$. Also, the relative phase can be used to control the orientation direction. To simplify the following expressions, we set $\phi =0$.

FIGURE 2

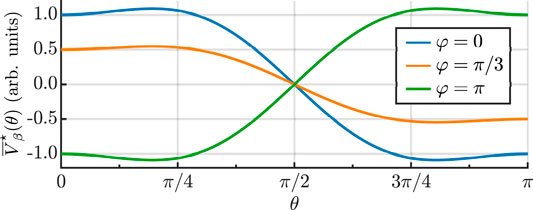
FIGURE 2. Angle dependence of the potential ${\overline{V}}_{\beta }^{\mathrm{\star }}\left(\theta \right)$, $\text{cos}\left(\phi \right)\left[3b{\text{sin}}^2\left(\theta \right)\text{cos}\left(\theta \right)+{\text{cos}}^3\left(\theta \right)\right]$, see Eq. 13, for different relative phases, φ. Here, $b={\beta }_{\mathit{a}\mathit{b}\mathit{b}}/{\beta }_{\mathit{a}\mathit{a}\mathit{a}}=2/3$.

4.1 Approximate Classical Formula

In the case of weak excitation, we can derive an approximate classical formula for the degree of long-lasting orientation. Since the long-lasting orientation manifests itself under field-free conditions, we begin by considering the free motion of a single classical symmetric top. The free motion of the unit vector $\mathbf{a}$, pointing along the rotational symmetry axis of the molecule, is given by a simple vectorial differential equation $\dot{\mathbf{a}}=\left(\mathbf{L}/I\right)\times \mathbf{a}$. Here, $\mathbf{L}$ is the conserved angular momentum vector, I is the moment of inertia along the orthogonal axes b and c$\left(I_a<I_b=I_c\equiv I\right)$. The solution of this equation is given by

$\mathbf{a}\left(t\right)=\mathbf{L}\frac{\mathbf{L}\cdot \mathbf{a}\left(0\right)}{L^2}+\left[\mathbf{a}\left(0\right)-\mathbf{L}\frac{\mathbf{L}\cdot \mathbf{a}\left(0\right)}{L^2}\right]\text{cos}\left(\frac{L}{I}t\right)+\frac{\mathbf{L}}{L}\times \mathbf{a}\left(0\right)\text{sin}\left(\frac{L}{I}t\right),(14)$

where L is the magnitude of angular momentum and $\mathbf{a}\left(0\right)$ is vector $\mathbf{a}$ at $t=0$. The above equation describes precession of $\mathbf{a}$ around $\mathbf{L}$ at a rate $L/I$ (see Figure 3). In the special case of a linear molecule, $L_a=\mathbf{L}\cdot \mathbf{a}\left(0\right)=0$, so that Eq. 14 reduces to

$\mathbf{a}\left(t\right)=\mathbf{a}\left(0\right)\text{cos}\left(\frac{L}{I}t\right)+\frac{\mathbf{L}}{L}\times \mathbf{a}\left(0\right)\text{sin}\left(\frac{L}{I}t\right).(15)$

Equation 15 describes a uniform rotation of $\mathbf{a}$ in a plane perpendicular to the angular momentum vector $\mathbf{L}$.

FIGURE 3

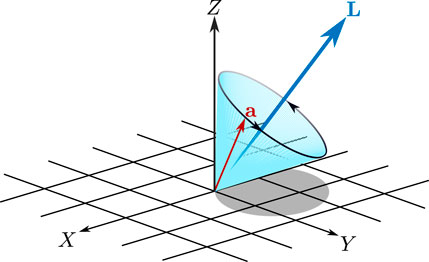
FIGURE 3. Illustration of precession of the vector $\mathbf{a}$ about the angular momentum vector $\mathbf{L}$. The tip of $\mathbf{a}$ describes a circle, while the arrow lies on the surface of a cone. The angular frequency of the precession is $L/I$, see Eq. 14.

The degree of long-lasting orientation (see the inset of Figure 1) can be obtained by considering the ensemble average projection of the molecular axis $\mathbf{a}$ on the laboratory Z axis, $a_Z={\mathbf{e}}_Z\cdot \mathbf{a}$, and then evaluating its time average

$\overline{\langle a_Z\rangle }=\underset{\tau \to \infty }{\text{lim}}\frac{1}{\tau }{\displaystyle {\int }_0^{\tau }\langle {\mathbf{e}}_Z\cdot \mathbf{a}\left(t\right)\rangle }dt,(16)$

where $t=0$ defines the end of the two-color pulse (when the free motion begins). Note that for ${\text{CH}}_3\text{F}$ the molecular dipole, $\mathit{\mu }$ points along $-\mathbf{a}$ (see Table 1). Next, we exchange the order of the ensemble and time averaging. The time average of $a_Z$ is obtained from Eq. 14 and it reads

$\overline{a_Z}=\frac{{\left(L_Z\right)}_f{\left(L_a\right)}_f}{L_f^2},(17)$

where $L_Z={\mathbf{e}}_Z\cdot \mathbf{L}$, $L_a=\mathbf{a}\cdot \mathbf{L}$, and subindex f denotes that all the quantities are taken after the pulse. With the potential in Eqs. 11, 13, both ϕ and χ are cyclic coordinates. Therefore, the canonically conjugate angular momenta $L_Z$ and $L_a$ are conserved. As a consequence, Eq. 17 becomes

$\overline{a_Z}=\frac{L_Z{L}_a}{L_f^2},(18)$

where $L_Z$ and $L_a$ are taken before the pulse. At this stage, we can conclude that the long-lasting orientation is strictly zero when the initial temperature is zero and/or in the limit of a linear rotor. In the first case, $L_Z=L_a=0$, while in the second case $L_a=0$, because $I_a=0$ for linear molecules.

For the ensemble averaging, it is advantageous to express all the quantities in the basis of principal axes of inertia. The magnitude of the angular momentum after the pulse, $L_f^2$, is given by

$L_f^2={\left(L_b+\delta L_b\right)}^2+{\left(L_c+\delta L_c\right)}^2+L_a^2,(19)$

where $L_a,L_b,L_c$ are the values before the pulse, while $\delta L_b$ and $\delta L_c$ are the changes in angular momentum components due to laser excitation. Explicit expressions for $\delta L_b$ and $\delta L_c$ can be obtained using the impulsive approximation. In this approximation, we assume that the duration of the two-color pulse is much shorter than the typical period of molecular rotation, such that the molecular orientation remains unchanged during the pulse. Using this approximation and the Euler-Lagrange equations, we derive the explicit expressions for $\delta L_b$ and $\delta L_c$ (the details are summarized in Supplementary Appendix B),

$\delta L_b=f\left(\theta \right)\text{sin}\left(\chi \right),(20)$

$\delta L_c=f\left(\theta \right)\text{cos}\left(\chi \right),(21)$

where

$f\left(\theta \right)=P_1\text{sin}\left(2\theta \right)+P_2\text{sin}\left(\theta \right)\left[\left(3\text{cos}\left(2\theta \right)+1\right){\beta }_{abb}-2{\text{cos}}^2\left(\theta \right){\beta }_{aaa}\right],(22)$

and

$P_1=\frac{\sigma }{4}\sqrt{\frac{\pi }{\text{ln}\left(16\right)}}\left({\epsilon }_{\mathrm{1,0}}^2+{\epsilon }_{\mathrm{2,0}}^2\right)\left({\alpha }_{bb}-{\alpha }_{aa}\right),(23)$

$P_2=\frac{3\sigma }{16}\sqrt{\frac{\pi }{\text{ln}\left(64\right)}}{\epsilon }_{\mathrm{1,0}}^2{\epsilon }_{\mathrm{2,0}}.(24)$

Here $\sigma ={\sigma }_1={\sigma }_2$, ${\epsilon }_{\mathrm{1,0}}$, and ${\epsilon }_{\mathrm{2,0}}$ are the peak amplitudes of the FW and SH, respectively. $L_Z$ is expressed in terms of the molecular frame components $L_{a,b,c}$ using the rotation matrix $R\left(\varphi ,\theta ,\chi \right)$, such that

$L_Z=-\text{sin}\left(\theta \right)\text{cos}\left(\chi \right)L_b+\text{sin}\left(\theta \right)\text{sin}\left(\chi \right)L_c+L_a\text{cos}\left(\theta \right).(25)$

Finally, we carry out the ensemble average

$\langle \overline{a_Z}\rangle =\frac{1}{\mathrm{Ƶ}}{\displaystyle {\int }_{\text{Ω}}{\displaystyle {\int }_{L^3}\frac{L_Z{L}_a}{L_f^2}}}\exp \left[-\frac{1}{2k_{B}T}\left(\frac{L_a^2}{I_a}+\frac{L_b^2}{I}+\frac{L_c^2}{I}\right)\right]\times \sin \theta d\theta d\chi d\varphi d{L}_{a}d{L}_{b}d{L}_c,(26)$

where $\mathrm{Ƶ}$ is the partition function. To simplify the integral, we assume that $\left|\delta L_b/L_b\right|,\left|\delta L_c/L_c\right|\ll 1$ [see Eqs. 19–21] and expand $1/L_f^2$ in powers of $f\left(\theta \right)$ [see Eq. 22]. Only terms proportional to even powers of $f\left(\theta \right)$ contribute to the integral. We consider the first non-vanishing term proportional to $f^2\left(\theta \right)$, such that [see Supplementary Equation S26]

$\langle \overline{a_Z}\rangle \approx \frac{{\tilde{I}}_L\left(w\right)}{4k_{B}TI}\sqrt{\frac{w}{\pi }}{{\displaystyle \int }}^{\text{}}{f}^2\left(\theta \right)\text{sin}\left(2\theta \right)d\theta ,(27)$

where $w=I/I_a$, and ${\tilde{I}}_L\left(w\right)$ is a monotonic function of $w>1$. In the limit of a linear molecule ($w\to \infty$), ${\tilde{I}}_L\left(w\right)\to 0$ [see Supplementary Equation S27 and Figure S1].

For the polarizability interaction alone, $f\left(\theta \right)=P_1\text{sin}\left(2\theta \right)$, and ${{\displaystyle \int }}^{\text{}}{f}^{2n}\left(\theta \right)\text{sin}\left(2\theta \right)d\theta =0$. For the hyperpolarizability interaction alone, $f\left(\theta \right)=P_2\text{sin}\left(\theta \right)\left[\left(3\text{cos}\left(2\theta \right)+1\right){\beta }_{abb}-2{\text{cos}}^2\left(\theta \right){\beta }_{aaa}\right]$ which is a symmetric function (about $\theta =\pi /2$), and therefore ${{\displaystyle \int }}^{\text{}}{f}^n\left(\theta \right)\text{sin}\left(2\theta \right)d\theta =0$ for all n. Only when both polarizability and hyperpolarizability interactions are included, $\langle \overline{a_Z}\rangle \ne 0$. In this case,

$\langle \overline{a_Z}\rangle \approx \frac{16{\tilde{I}}_L\left(w\right)}{105k_{B}TI}\sqrt{\frac{w}{\pi }}{P}_1{P}_2\left(2{\beta }_{abb}-3{\beta }_{aaa}\right),(28)$

where $P_1$ and $P_2$ are given by Eqs. 23, 24, and ${\tilde{I}}_L\left(w\right)$ is given by Supplementary Equation S27. The details of the derivation of Eq. 28 are summarized in Supplementary Appendix C.

According to Eq. 28, the degree of long-lasting orientation scales as ${\sigma }^2/T$. In Figure 4, we compare the temperature (panel A) and pulse duration (panel B) dependencies of the long-lasting orientation obtained using the approximate formula in Eq. 28 with the numerical results obtained by evaluating the formula in Eq. 18 using the Monte Carlo approach as described in the Methods Section 2 (using the impulsive approximation, see Supplementary Appendix B).

FIGURE 4

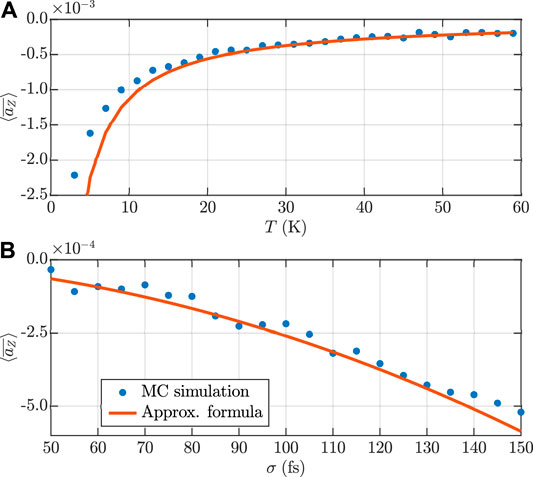
FIGURE 4. (A) Temperature and (B) pulse duration dependence of the degree of long-lasting orientation obtained using the approximate formula in Eq. 28 (red line) and numerically using the impulsive approximation (blue dots). Here $I_{\text{FW}}=2\times {10}^{13}\text{W}/{\text{cm}}^2$, $I_{\text{SH}}=0.75\times {10}^{13}\text{W}/{\text{cm}}^2$, and $\sigma =120\text{fs}$. Each point is an average of ${10}^8$ sample molecules. In B, the temperature is fixed to $T=30\text{K}$.

There is a good agreement between the numerical results and the results obtained using the approximate formula, especially at higher temperatures (higher initial angular momenta), where the assumption $\left|\delta L_b/L_b\right|,\left|\delta L_c/L_c\right|\ll 1$ is well satisfied. The pulse duration dependence shows the connection to the energy gained by the molecule from the laser pulse. In the limit of weak excitation (low pulse intensity and/or high temperature), the approximate formula also reveals the more involved dependence on the fields’ amplitudes, according to Eqs. 23, 24.

The hyperpolarizability part of the interaction potential, ${\overline{V}}_{\beta }^{\mathrm{\star }}\left(\theta \right)$ [see Eq. 13], is an asymmetric function of θ (about $\theta =\pi /2$, see Figure 2), similar to the orienting potential, which is proportional to $-\text{cos}\left(\theta \right)$, due to a single THz pulse interacting with the molecular dipole, $\mathit{\mu }$. As we show here and as it was shown in [23], excitation by such orienting potentials results in transient orientation followed by residual long-lasting orientation.

Despite the similarity, the mechanisms behind the long-lasting orientation induced by a femtosecond two-color and a picosecond THz pulse are not the same. It was shown in [23] that in the limit of vanishing THz pulse duration, the induced long-lasting orientation tends to zero. In other words, a δ-kick by a purely orienting potential doesn’t lead to long-lasting orientation. In contrast, here we show that a δ-kick by a combined, aligning and orienting, potentials results in a long-lasting orientation [see the discussion under Eq. 27, also see Figure 5].

FIGURE 5

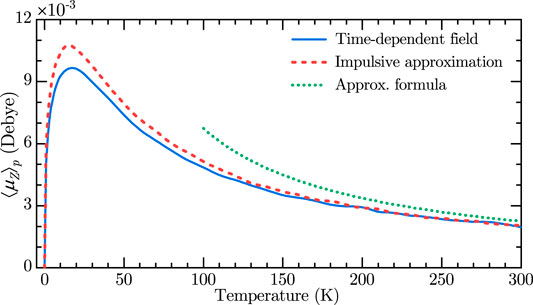
FIGURE 5. Classically calculated permanent values of Z-projection of the dipole moment. The field parameters are similar to Figure 1. Cases of fully time-dependent field (solid blue) and using impulsive approximation (dashed red) are compared. The dotted green line is obtained using the approximate formula in Eq. 28 with $\langle {\mu }_Z{\rangle }_p=-\mu \langle \overline{a_Z}\rangle$ (dipole moment points againts a axis, see Table 1).

5 Temperature and Polarization Dependence of the Long-Lasting Orientation

Figure 5 depicts the long-lasting orientation of the dipole moment as a function of temperature for the case of collinearly polarized two-color pulse. Due to the short pulse duration ($\sigma =120\text{fs}$), the results of the fully time-dependent simulation (solid blue line) are well reproduced using the impulsive approximation (dashed red line). The impulsive approximation is described in Supplementary Appendix B. As mentioned in Section 4, the long-lasting orientation vanishes at $T=0\text{K}$, (see Eq. 18). At high temperatures, the long-lasting orientation decreases as $\propto T^{-1}$. Therefore, there should be an optimal temperature for which the long-lasting orientation is maximal. As is shown in Figure 5, for the field parameters used here, the optimal temperature is $T\approx 20\text{K}$. In the derivation leading to the approximate formula in Eq. 28, we assumed ${\beta }_{bbb}={\beta }_{bcc}=0$. Nevertheless, the results obtained using Eq. 28 qualitatively agree with the numerical results at higher temperatures as well (dotted green line).

As an additional example, we consider the case of a cross-polarized two-color pulse in which the polarizations of the FW and SH are along Z and X axes, respectively. Figure 6 shows the dipole signal along the laboratory X axis. Note that the Y and Z-projections of the dipole moment, $\langle {\mu }_{Y,Z}\rangle$ are exactly zero. In this case, a similar transient dipole response along the polarization direction of SH can be seen. On the long time scale, it is followed by the long-lasting orientation. Notice that for the field parameters used here, the achieved degree of both transient and long-lasting orientation is higher in the case of cross-polarized FW and SH compared with Figure 1 (also see [46]).

FIGURE 6

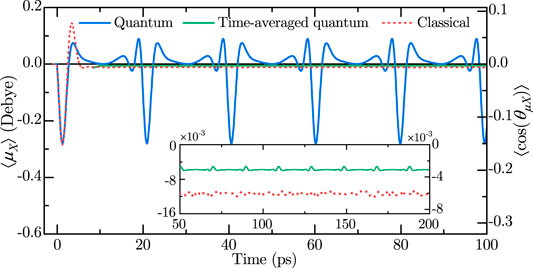
FIGURE 6. X-projection of the dipole moment, $\langle {\mu }_X\rangle$ and the orientation factor, $\langle \text{cos}\left({\theta }_{\mu X}\right)\rangle \equiv \langle {\mu }_X\rangle /\mu$ as a function of time. ${\theta }_{\mu X}$ denotes the angle between the dipole moment and laboratory X axis. The conditions used here are the same as in the case shown in Figure 1, except that the angle between the polarizations of FW and SH is ${\varphi }_{\text{SH}}=\pi /2$ [see Eq. 2].

6 Conclusion

We have theoretically demonstrated a new phenomenon of long-lasting (persistent) orientation of symmetric-top molecules excited by a single two-color femtosecond pulse. The residual orientation was shown to last indefinitely (within the adopted model), or until destroyed by other physical effects, e.g., intermolecular collisions. We derived an approximate classical expression revealing several qualitative features of the phenomenon, including the scaling with temperature, pulse duration, and other field and molecular parameters. The predictions of the formula are in full agreement with the results of numerical simulations in the limit of weak excitation. A quick check for different polarizations showed that in the case of cross-polarized FW and SH, the achieved degree of both transient and long-lasting orientation may be higher than in the case of parallel configuration. The magnitude of the long-lasting dipole signal shown in this work is about $10\times {10}^{-3}$ Debye, corresponding to a degree of molecular orientation of about 0.5%. This value is similar to typical experimental values observed by means of the Coulomb explosion technique, which is of the order of 0.1%, e.g., see [32, 44]. Further and careful optimization of the parameters of the two-color pulse may give rise to even higher degrees of long-lasting orientation. Moreover, it has been demonstrated before that the degree of molecular alignment/orientation can be enhanced when a sequence of several laser pulses is used instead of a single pulse [17, 69–74], and a similar approach may be beneficial for increasing the degree of the long-lasting orientation. The orientation may be measured with the help of second (or higher-order) harmonic generation [42]. In addition, the long-lasting orientation may be utilized in deflection experiments using inhomogeneous electrostatic fields [75–77], where the deflection angle of a molecular beam in a static electric field depends on the time-averaged directional cosine, $\overline{\langle \text{cos(}\theta )\rangle }$. Therefore, although small compared to the peak value of the transient orientation, the long-lasting orientation may have a significant, observable effect on the deflection angle.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All the authors participated in formulating the problem and initiating this study. LX and IT equally contributed to the calculations and numerical simulations. All the authors participated in analyzing the results and writing the manuscript. YP and IA supervised and guided the work.

Funding

We gratefully acknowledge support by the Israel Science Foundation (Grant No. 746/15). IA acknowledges support as the Patricia Elman Bildner Professorial Chair. This research was made possible in part by the historic generosity of the Harold Perlman Family.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.689635/full#supplementary-material

References

1. Stapelfeldt H, Seideman T. Colloquium: Aligning Molecules with strong Laser Pulses. Rev Mod Phys (2003) 75:543.

CrossRef Full Text | Google Scholar

2. Ohshima Y, Hasegawa H. Coherent Rotational Excitation by Intense Nonresonant Laser fields. Int Rev Phys Chem (2010) 29:619.

CrossRef Full Text | Google Scholar

3. Fleischer S, Khodorkovsky Y, Gershnabel E, Prior Y, Averbukh IS. Molecular Alignment Induced by Ultrashort Laser Pulses and its Impact on Molecular Motion. Isr J Chem (2012) 52:414.

CrossRef Full Text | Google Scholar

4. Lemeshko M, Krems RV, Doyle JM, Kais S. Manipulation of Molecules with Electromagnetic fields. Mol Phys (2013) 111:1648.

CrossRef Full Text | Google Scholar

5. Koch CP, Lemeshko M, Sugny D. Quantum Control of Molecular Rotation. Rev Mod Phys (2019) 91:035005.

CrossRef Full Text | Google Scholar

6. Lin K, Tutunnikov I, Ma J, Qiang J, Zhou L, Faucher O, et al. Spatiotemporal Rotational Dynamics of Laser-Driven Molecules. Adv Photon (2020) 2:024002.

CrossRef Full Text | Google Scholar

7. Friedrich B, Herschbach D. Enhanced Orientation of Polar Molecules by Combined Electrostatic and Nonresonant Induced Dipole Forces. J Chem Phys (1999) 111:6157.

CrossRef Full Text | Google Scholar

8. Sakai H, Minemoto S, Nanjo H, Tanji H, Suzuki T. Controlling the Orientation of Polar Molecules with Combined Electrostatic and Pulsed, Nonresonant Laser fields. Phys Rev Lett (2003) 90:083001.

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Goban A, Minemoto S, Sakai H. Laser-field-free Molecular Orientation. Phys Rev Lett (2008) 101:013001.

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Ghafur O, Rouzée A, Gijsbertsen A, Siu WK, Stolte S, Vrakking MJJ. Impulsive Orientation and Alignment of Quantum-State-Selected NO Molecules. Nat Phys (2009) 5:289.

CrossRef Full Text | Google Scholar

11. Holmegaard L, Nielsen JH, Nevo I, Stapelfeldt H, Filsinger F, Küpper J, et al. Laser-induced Alignment and Orientation of Quantum-State-Selected Large Molecules. Phys Rev Lett (2009) 102:023001.

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Mun JH, Takei D, Minemoto S, Sakai H. Laser-field-free Orientation of State-Selected Asymmetric Top Molecules. Phys Rev A (2014) 89:051402(R).

CrossRef Full Text | Google Scholar

13. Takei D, Mun JH, Minemoto S, Sakai H. Laser-field-free Three-Dimensional Molecular Orientation. Phys Rev A (2016) 94:013401.

CrossRef Full Text | Google Scholar

14. Omiste JJ, González-Férez R. Theoretical Description of the Mixed-Field Orientation of Asymmetric-Top Molecules: A Time-dependent Study. Phys Rev A (2016) 94:063408.

CrossRef Full Text | Google Scholar

15. Thesing LV, Küpper J, González-Férez R. Time-dependent Analysis of the Mixed-Field Orientation of Molecules without Rotational Symmetry. J Chem Phys (2017) 146:244304.

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Harde H, Keiding S, Grischkowsky D. THz Commensurate Echoes: Periodic Rephasing of Molecular Transitions in Free-Induction Decay. Phys Rev Lett (1991) 66:1834.

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Averbukh IS, Arvieu R. Angular Focusing, Squeezing, and Rainbow Formation in a Strongly Driven Quantum Rotor. Phys Rev Lett (2001) 87:163601.

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Machholm M, Henriksen NE. Field-free Orientation of Molecules. Phys Rev Lett (2001) 87:193001.

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Fleischer S, Zhou Y, Field RW, Nelson KA. Molecular Orientation and Alignment by Intense Single-Cycle THz Pulses. Phys Rev Lett (2011) 107:163603.

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kitano K, Ishii N, Kanda N, Matsumoto Y, Kanai T, Kuwata-Gonokami M, et al. Orientation of Jet-Cooled Polar Molecules with an Intense Single-Cycle THz Pulse. Phys Rev A (2013) 88:061405(R).

CrossRef Full Text | Google Scholar

21. Damari R, Kallush S, Fleischer S. Rotational Control of Asymmetric Molecules: Dipole- versus Polarizability-Driven Rotational Dynamics. Phys Rev Lett (2016) 117:103001.

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Babilotte P, Hamraoui K, Billard F, Hertz E, Lavorel B, Faucher O, et al. Observation of the Field-free Orientation of a Symmetric-Top Molecule by Terahertz Laser Pulses at High Temperature. Phys Rev A (2016) 94:043403.

CrossRef Full Text | Google Scholar

23. Xu L, Tutunnikov I, Gershnabel E, Prior Y, Averbukh IS. Long-lasting Molecular Orientation Induced by a Single Terahertz Pulse. Phys Rev Lett (2020) 125:013201.

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Daems D, Guérin S, Sugny D, Jauslin HR. Efficient and Long-Lived Field-free Orientation of Molecules by a Single Hybrid Short Pulse. Phys Rev Lett (2005) 94:153003.

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Gershnabel E, Averbukh IS, Gordon RJ. Orientation of Molecules via Laser-Induced Antialignment. Phys Rev A (2006) 73:061401(R).

CrossRef Full Text | Google Scholar

26. Egodapitiya KN, Li S, Jones RR. Terahertz-induced Field-free Orientation of Rotationally Excited Molecules. Phys Rev Lett (2014) 112:103002.

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yachmenev A, Yurchenko SN. Detecting Chirality in Molecules by Linearly Polarized Laser fields. Phys Rev Lett (2016) 117:033001.

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gershnabel E, Averbukh IS. Orienting Asymmetric Molecules by Laser fields with Twisted Polarization. Phys Rev Lett (2018) 120:083204.

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Tutunnikov I, Gershnabel E, Gold S, Averbukh IS. Selective Orientation of Chiral Molecules by Laser fields with Twisted Polarization. J Phys Chem Lett (2018) 9:1105.

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Milner AA, Fordyce JAM, MacPhail-Bartley I, Wasserman W, Milner V, Tutunnikov I, et al. Controlled Enantioselective Orientation of Chiral Molecules with an Optical Centrifuge. Phys Rev Lett (2019) 122:223201.

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Tutunnikov I, Floß J, Gershnabel E, Brumer P, Averbukh IS. Laser-induced Persistent Orientation of Chiral Molecules. Phys Rev A (2019) 100:043406.

CrossRef Full Text | Google Scholar

32. Tutunnikov I, Floß J, Gershnabel E, Brumer P, Averbukh IS, Milner AA, et al. Observation of Persistent Orientation of Chiral Molecules by a Laser Field with Twisted Polarization. Phys Rev A (2020) 101:021403(R).

CrossRef Full Text | Google Scholar

33. Tutunnikov I, Xu L, Field RW, Nelson KA, Prior Y, Averbukh IS. Enantioselective Orientation of Chiral Molecules Induced by Terahertz Pulses with Twisted Polarization. Phys Rev Res (2021) 3:013249.

CrossRef Full Text | Google Scholar

34. Vrakking MJJ, Stolte S. Coherent Control of Molecular Orientation. Chem Phys Lett (1997) 271:209.

CrossRef Full Text | Google Scholar

35. Dion C, Bandrauk AD, Atabek O, Keller A, Umeda H, Fujimura Y. Two-frequency IR Laser Orientation of Polar Molecules. Numerical Simulations for HCN. Chem Phys Lett (1999) 302:215.

CrossRef Full Text | Google Scholar

36. Kanai T, Sakai H. Numerical Simulations of Molecular Orientation Using strong, Nonresonant, Two-Color Laser fields. J Chem Phys (2001) 115:5492.

CrossRef Full Text | Google Scholar

37. Takemoto N, Yamanouchi K. Fixing Chiral Molecules in Space by Intense Two-Color Phase-Locked Laser fields. Chem Phys Lett (2008) 451:1.

CrossRef Full Text | Google Scholar

38. De S, Znakovskaya I, Ray D, Anis F, Johnson NG, Bocharova IA, et al. Field-Free Orientation of CO Molecules by Femtosecond Two-Color Laser Fields. Phys Rev Lett (2009) 103:153002.

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Oda K, Hita M, Minemoto S, Sakai H. All-optical Molecular Orientation. Phys Rev Lett (2010) 104:213901.

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wu J, Zeng H. Field-free Molecular Orientation Control by Two Ultrashort Dual-Color Laser Pulses. Phys Rev A (2010) 81:053401.

CrossRef Full Text | Google Scholar

41. Zhang S, Shi J, Zhang H, Jia T, Wang Z, Sun Z. Field-free Molecular Orientation by a Multicolor Laser Field. Phys Rev A (2011) 83:023416.

CrossRef Full Text | Google Scholar

42. Frumker E, Hebeisen CT, Kajumba N, Bertrand JB, Wörner HJ, Spanner M, et al. Oriented Rotational Wave-Packet Dynamics Studies via High Harmonic Generation. Phys Rev Lett (2012) 109:113901.

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Spanner M, Patchkovskii S, Frumker E, Corkum P. Mechanisms of Two-Color Laser-Induced Field-free Molecular Orientation. Phys Rev Lett (2012) 109:113001.

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Znakovskaya I, Spanner M, De S, Li H, Ray D, Corkum P, et al. Transition between Mechanisms of Laser-Induced Field-free Molecular Orientation. Phys Rev Lett (2014) 112:113005.

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Mun JH, Sakai H. Improving Molecular Orientation by Optimizing Relative Delay and Intensities of Two-Color Laser Pulses. Phys Rev A (2018) 98:013404.

CrossRef Full Text | Google Scholar

46. Mun JH, Sakai H, González-Férez R. Orientation of Linear Molecules in Two-Color Laser fields with Perpendicularly Crossed Polarizations. Phys Rev A (2019) 99:053424.

CrossRef Full Text | Google Scholar

47. Mun JH, Kim DE. Field-free Molecular Orientation by Delay- and Polarization-Optimized Two Fs Pulses. Sci Rep (2020) 10:18875.

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Mellado-Alcedo D, Quintero NR, González-Férez R. Linear Polar Molecule in a Two-Color Cw Laser Field: A Symmetry Analysis. Phys Rev A (2020) 102:023110.

CrossRef Full Text | Google Scholar

49. Wang S, Henriksen NE. Optimal Field-Free Molecular Orientation with Nonresonant Two-Color Adiabatic-Turn-On and Sudden-Turn-Off Laser Pulses. Phys Rev A (2020) 102:063120.

CrossRef Full Text | Google Scholar

50. Goldstein H, Poole C, Safko J. Classical Mechanics. San Francisco, CA: Addison-Wesley (2002).

51. Coutsias EA, Romero L. The Quaternions with an Application to Rigid Body Dynamics. Sandia Technical Report (2004) SAND2004-0153.

52. Kuipers JB. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality. Princeton, N.J.: Princeton University Press (1999).

53. Lin K, Tutunnikov I, Qiang J, Ma J, Song Q, Ji Q, et al. All-optical Field-free Three-Dimensional Orientation of Asymmetric-Top Molecules. Nat Commun (2018) 9:5134.

PubMed Abstract | CrossRef Full Text | Google Scholar

54. LaValle SM. Planning Algorithms. New York: Cambridge University Press (2006).

55. Zare RN. Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics. New York: Wiley (1988).

56. Buckingham AD. Advances in Chemical Physics. New York: John Wiley & Sons (2007). p. 107–42. Permanent and Induced Molecular Moments and Long-Range Intermolecular Forces.

CrossRef Full Text | Google Scholar

57. Sidje RB. Expokit: A Software Package for Computing Matrix Exponentials. ACM Trans Math Softw (1998) 24:130.

CrossRef Full Text | Google Scholar

58. McDowell RS. Rotational Partition Functions for Symmetric-top Molecules. J Chem Phys (1990) 93:2801.

CrossRef Full Text | Google Scholar

59. Johnson RD. NIST Computational Chemistry Comparison and Benchmark Database, Release 20. Tech. Rep (2019).

60. Chong DP. Theoretical Calculations of Dipole Moments, Polarizabilities, and Hyperpolarizabilities of HF, OCS, O₃, CH₃F, and CH₃Cl by Local Density Approximation. J Chin Chem Soc (1992) 39:375.

CrossRef Full Text | Google Scholar

61. Eberly JH, Narozhny NB, Sanchez-Mondragon JJ. Periodic Spontaneous Collapse and Revival in a Simple Quantum Model. Phys Rev Lett (1980) 44:1323.

CrossRef Full Text | Google Scholar

62. Parker J, Stroud CR Coherence and Decay of Rydberg Wave Packets. Phys Rev Lett (1986) 56:716.

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Averbukh IS, Perelman NF. Fractional Revivals: Universality in the Long-Term Evolution of Quantum Wave Packets beyond the Correspondence Principle Dynamics. Phys Lett A (1989) 139:449.

CrossRef Full Text | Google Scholar

64. Felker PM. Rotational Coherence Spectroscopy: Studies of the Geometries of Large Gas-phase Species by Picosecond Time-Domain Methods. J Phys Chem (1992) 96:7844.

CrossRef Full Text | Google Scholar

65. Robinett RW. Quantum Wave Packet Revivals. Phys Rep (2004) 392:1.

CrossRef Full Text | Google Scholar

66. Thomas EF, Søndergaard AA, Shepperson B, Henriksen NE, Stapelfeldt H. Hyperfine-structure-induced Depolarization of Impulsively Aligned I₂ Molecules. Phys Rev Lett (2018) 120:163202.

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Thesing LV, Yachmenev A, González-Férez R, Küpper J. The Effect of Nuclear-Quadrupole Coupling in the Laser-Induced Alignment of Molecules. J Phys Chem A (2020) 124:2225.

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Buckingham AD, Orr BJ. Molecular Hyperpolarisabilities. Q Rev Chem Soc (1967) 21:195.

CrossRef Full Text | Google Scholar

69. Leibscher M, Averbukh IS, Rabitz H. Molecular Alignment by Trains of Short Laser Pulses. Phys Rev Lett (2003) 90:213001.

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Leibscher M, Averbukh IS, Rabitz H. Enhanced Molecular Alignment by Short Laser Pulses. Phys Rev A (2004) 69:013402.

CrossRef Full Text | Google Scholar

71. Lee KF, Litvinyuk IV, Dooley PW, Spanner M, Villeneuve DM, Corkum PB. Two-pulse Alignment of Molecules. J Phys B: Mol Opt Phys (2004) 37:L43.

CrossRef Full Text | Google Scholar

72. Bisgaard CZ, Poulsen MD, Péronne E, Viftrup SS, Stapelfeldt H. Observation of Enhanced Field-free Molecular Alignment by Two Laser Pulses. Phys Rev Lett (2004) 92:173004.

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Pinkham D, Mooney KE, Jones RR. Optimizing Dynamic Alignment in Room Temperature CO. Phys Rev A (2007) 75:013422.

CrossRef Full Text | Google Scholar

74. Zhang S, Lu C, Jia T, Wang Z, Sun Z. Field-free Molecular Orientation Enhanced by Two Dual-Color Laser Subpulses. J Chem Phys (2011) 135:034301.

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Gershnabel E, Averbukh IS. Electric Deflection of Rotating Molecules. J Chem Phys (2011) 134:054304.

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Gershnabel E, Averbukh IS. Deflection of Rotating Symmetric Top Molecules by Inhomogeneous fields. J Chem Phys (2011) 135:084307.

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Küpper J, Filsinger F, Meijer G, Stapelfeldt H. Manipulating the Motion of Complex Molecules: Deflection, Focusing, and Deceleration of Molecular Beams for Quantum-State and Conformer Selection, in Methods in Physical Chemistry. John Wiley & Sons (2012). p. 1–28.

Google Scholar