Implementation of a Framelet-Based Spectral Reconstruction for Multi-Slice Spiral CT

Spectral CT utilizes spectral information of X-ray sources to reconstruct energy-resolved X-ray images and has wide medical applications. Compared with conventional energy-integrated CT scanners, however, spectral CT faces serious technical difficulties in hardware, and hence its clinical use has been expensive and limited. The goal of this paper is to present a software solution and an implementation of a framelet-based spectral reconstruction algorithm for multi-slice spiral scanning based on a conventional energy-integrated CT hardware platform. In the present work, we implement the framelet-based spectral reconstruction algorithm using compute unified device architecture (CUDA) with bowtie filtration. The platform CUDA enables fast execution of the program, while the bowtie filter reduces radiation exposure. We also adopt an order-subset technique to accelerate the convergence. The multi-slice spiral scanning geometry with these additional features will make the framelet-based spectral reconstruction algorithm more powerful for clinical applications. The method provides spectral information from just one scan with a standard energy-integrating detector and produces color CT images, spectral curves of the attenuation coefficient at every point inside the object, and photoelectric images, which are all valuable imaging tools in cancerous diagnosis. The proposed algorithm is tested with a Catphan phantom and real patient data sets for its performance. In experiments with the Catphan 504 phantom, the synthesized color image reveals changes in the level of colors and details and the yellow color in Teflon indicates a special spectral property which is invisible in regular CT reconstruction. In experiments with clinical images, the synthesized color images provide some extra details which are helpful for clinical diagnosis, for example, details about the renal pelvis and lumbar join. The numerical studies indicate that the proposed method provides spectral image information which can reveal fine structures in clinical images and that the algorithm is efficient regarding to the computational time. Thus, the proposed algorithm has a great potential in practical application.

1. Introduction

In conventional computed tomography (CT) reconstruction algorithms, X-rays are assumed to be monochromatic, thus the attenuation coefficients of objects are independent of the X-ray energy and determined by the material only. However, X-rays are polychromatic [1]. Low-energy photons are easier to be absorbed than high-energy photons. Ignoring the spectrum of X-rays in reconstruction causes beam-hardening artifacts [2, 3] which are not satisfactory for clinical diagnosis. On the other hand, using energy information in polychromatic X-rays could provide properties of the material being scanned, such as the density and atomic number.

Spectral CT, which uses multiple energies of X-rays, has attracted much attention from both clinical physicists and researchers since last decade when the technology became possible. Spectral imaging can provide energy-related attenuation characteristics of the composition of the material and quantitative tissue information to help diagnosis. Furthermore, the radiation dose is reduced since the detection and characterization of findings can be performed with spectral CT in a single exam. So spectral CT has its benefits in enhancing the accuracy of clinical diagnosis and efficiency of patient care. The basis of spectral CT is that a CT scan can be decomposed into a set of multiple basis materials if the projection data is measured at different energies [4]. This leads to the development of dual-energy CT and multi-spectral CT [5]. Dual-energy refers to the use of two X-ray energies in scanning. Multi-spectral CT is an extension of dual-energy CT. Currently dual-energy CT is the most common form of spectral CT used in clinical applications due to the limit of technology [6].

There are different technologies to utilize dual-energy CT but mainly in two categories. One is source-based, and the other one is detector-based. The first category utilizes X-ray beams with different energies by employing two X-ray tubes with different potentials or a single X-ray tube switching between low and high potentials [7, 8]. The switch occurs during the collection of projection data in a single scan or after a full projection scan in two scans. The second category utilizes energy-discriminative detectors in a single X-ray spectrum scan [9]. This involves dual-layer detectors with a different X-ray stopping power in each layer or a photon-counting detector. Each method of dual-energy CT has its respective advantages and disadvantages [10]. Some spectral CT iterative reconstruction algorithms are developed for the hardware technology methods [11–13].

In either source based or detector based methods, spectral CT needs more complicated equipment for data requisition and requires longer time for data requisition and image reconstruction than conventional CT. Besides, for a hospital, adding a new spectral CT scanner to its lab which has facilitated a conventional CT scanner involves practical issues in cost and space. Recently, a framelet-based iterative reconstruction algorithm is proposed to solve the spectral CT reconstruction problem from the aspect of software in the current CT hardware platform [14–18] by our group. The key technique is the sparse representation of X-ray attenuation coefficients in a framelet system. The method provides spectral information from just one scan with a standard energy-integrating detector and produces color CT images, spectral curves of the attenuation coefficient at every point inside the object, and photoelectric images, which are all valuable imaging tools in cancerous diagnosis.

In this paper, we extend the framelet-based spectral reconstruction algorithm from fan-beam geometry to multi-slice spiral scanning and implement the algorithm using compute unified device architecture (CUDA) with bowtie filtration. The platform CUDA allows fast execution of the program, while the bowtie filter reduces the radiation exposure by shaping an X-ray beam. Therefore, the multi-slice spiral scanning geometry with these additional features will make the framelet-based spectral reconstruction algorithm more powerful for clinical applications.

The rest of the paper is organized as follows. In section 2, we describe the methodology and the implementation of the framelet-based iterative reconstruction algorithm for multi-slice spiral scanning. In section 3, the results from extensive experiments on a Catphan phantom and real patient datasets are summarized. Discussions and conclusions are given in section 4.

2. Method

2.1. Methodology

In this section we extend the framelet-based spectral reconstruction algorithm from fan-beam geometry [14–18] to multi-slice spiral scanning with the bowtie filtering making it more practical in clinical applications.

Let μ(r, E) be the X-ray attenuation coefficient at point r ∈ Ω for energy level E, where Ω is the image domain. The attenuation coefficient can be approximated by [19].

$\begin{array}{ll}\mu (r,E)=\varphi (r)E^{-3}+\theta (r)f_{KN}(E),& (1)\end{array}$

where the photoelectric component ϕ(r) and the Compton scatter component θ(r) are independent of energy E, and the Klein-Nishina function f_KN (E) is given by

$\begin{array}{l}{f}_{KN}(E)=\frac{1+\epsilon }{{\epsilon }^2}\left(\frac{2(1+\epsilon )}{1+2\epsilon }-\frac{1}{\epsilon }ln(1+2\epsilon )\right)\\ +\frac{1}{2\epsilon }ln(1+2\epsilon )-\frac{1+3\epsilon }{{(1+2\epsilon )}^2},& (2)\end{array}$

with ε = E/511 keV.

We consider a polychromatic acquisition model in this paper. Let L be an X-ray beam and I₀(E) be the known spectrum of the X-ray tube. The intensity measured by a detector bin after the beam L passes through the image is

$\begin{array}{ll}I={\displaystyle {\int }_0^{\infty }}{I}_0(E)exp\left(-{\displaystyle {\int }_L}\mu (r,E)dr\right)dE.& (3)\end{array}$

In our previous work [14, 15], I₀(E) is constant for all X-ray beams. Here we assume I₀(E) varies with respect to positions of X-ray beams and take bowtie filtering into consideration. Then the x-ray spectrum distribution after passing the bowtie filtering is

$\begin{array}{ll}{I}_0(E,L)=I_0(E)exp(-{\mu }_{bowtie}(r,E)t(L)),& (4)\end{array}$

where μ_bowtie indicates the linear attenuation coefficient of the bowtie material (e.g., aluminum), and t(L) denotes the bowtie thickness along the X-ray path L.

Due to the relative position relationship of the X-ray tube, the bowtie filter, and the detector, the bowtie filter and the detector are fixed during a scan, and the distribution of filtered X-ray spectrum are also fixed on the detector. Let d_i,j be the detector bin at the position (i, j) which receives the X-ray beam L. Then Equation (4) can be rewritten as

$\begin{array}{ll}{I}_0(E,d_{i,j})=I_0(E)exp\left(-{\mu }_{bowtie}(r,E)t\left(d_{i,j}\right)\right).& (5)\end{array}$

Consequently, Equation (3) can be expressed as

$\begin{array}{ll}I={\displaystyle {\int }_0^{\infty }}{I}_0(E,d_{i,j})exp\left(-{\displaystyle {\int }_L}\mu (r,E)dr\right)dE.& (6)\end{array}$

In the discrete setting, we denote the photon energies by E_k, k = 1, 2, …, K, the observed measurements by y_i, i = 1, 2, …, M, and the linear attenuation coefficients by μ_jk, j = 1, 2, …, J, and k = 1, 2, …, K, where i, j, k are indexes of the detector, pixel, and energy, respectively. Then Equation (1) can be rewritten as

$\begin{array}{ll}{\mu }_{jk}={\varphi }_j\Phi (E_k)+{\theta }_j\Theta (E_k),& (7)\end{array}$

where $\Phi (E_k)=E_0^3/E_k^3$ for a reference energy E₀, and Θ(E_k) = f_KN (E_k)/f_KN (E₀). Note that ϕ_j and θ_j are unknowns, representing photoelectric and Compton scatter terms at energy E₀, respectively. Substituting Equation (7) into (6), we get an acquisition model

$\begin{array}{ll}{\widehat{y}}_i={\displaystyle \sum _{k=1}^K}{b}_{ik}exp\left(-{\displaystyle \sum _{j=1}^J}{l}_{ij}\left({\varphi }_j\Phi (E_k)+{\theta }_j\Theta (E_k)\right)\right),& (8)\end{array}$

where b_ik is the total intensity detected by detector at the ith projection and the kth energy. The measured data y_i approximately follow a Poisson distribution [20] with expectation ŷ_i, where the probability density function is

$\begin{array}{ll}p(y_i)=\frac{{\widehat{y}}_i^{y_i}}{y_i!}exp\left(-{\widehat{y}}_i\right).& (9)\end{array}$

The log-likelihood is given by

$\begin{array}{ll}L(\varphi ,\theta )={\displaystyle \sum _{i=1}^M}\left(y_{i}log\left({\widehat{y}}_i\right)-{\widehat{y}}_i\right).& (10)\end{array}$

The minimization problem becomes

$\begin{array}{ll}{\displaystyle \underset{\varphi ,\theta }{min}}-L(\varphi ,\theta ),\text{subject to image sparsity of }\varphi \text{ and }\theta .& (11)\end{array}$

For the sparsity constraint, we use the discrete framelet transform given by [14]

$\begin{array}{ll}D=\left[\begin{array}{c}{h}_0*\\ ⋮\\ h_s*\end{array}\right],& (12)\end{array}$

where h_i*, i = 0, 1, …, s, is the matrix form of the discrete convolution with kernel h_i. In this work, we apply the following filters in bivariate Harr wavelet framelet system:

$\begin{array}{l}{h}_0=\frac{1}{4}\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right],h_1=\frac{1}{4}\left[\begin{array}{cc}1& -1\\ 1& -1\end{array}\right],\\ h_2=\frac{1}{4}\left[\begin{array}{cc}1& 1\\ -1& -1\end{array}\right],h_3=\frac{1}{4}\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right].\end{array}$

To solve the optimization problem (11), the coefficients ϕ and θ should be non-negative and sparse in the framelet domain. Therefore, the iterative reconstruction can be split into the following three steps.

(1) Data fidelity:

$\begin{array}{ll}\{\begin{array}{c}{\varphi }_j^{n+\frac{1}{3}}={\varphi }_j^n-{\delta }_1\frac{\partial L}{\partial {\varphi }_j}({\varphi }^n,{\theta }^n){\left({\sum }_{h=1}^J\left(\frac{{\partial }^{2}L}{\partial {\varphi }_j\partial {\varphi }_h}+\frac{{\partial }^{2}L}{\partial {\varphi }_j\partial {\theta }_h}\right)({\varphi }^n,{\theta }^n)\right)}^{-1}\\ {\theta }_j^{n+\frac{1}{3}}={\theta }_j^n-{\delta }_2\frac{\partial L}{\partial {\theta }_j}({\varphi }^n,{\theta }^n){\left({\sum }_{h=1}^J\left(\frac{{\partial }^{2}L}{\partial {\theta }_j\partial {\varphi }_h}+\frac{{\partial }^{2}L}{\partial {\theta }_j\partial {\theta }_h}\right)({\varphi }^n,{\theta }^n)\right)}^{-1}.\end{array}& (13)\end{array}$

(2) Nonnegativity:

$\begin{array}{ll}\{\begin{array}{c}{\varphi }_j^{n+\frac{2}{3}}=max\left\{{\displaystyle {\varphi }_j^{n+\frac{1}{3}}},0\right\}\\ {\theta }_j^{n+\frac{2}{3}}=max\left\{{\displaystyle {\theta }_j^{n+\frac{1}{3}}},0\right\}.\end{array}& (14)\end{array}$

(3) Sparsity:

$\begin{array}{ll}\{\begin{array}{c}{\varphi }_j^{n+1}=W^T{T}_{{\lambda }_1}\left(W{\varphi }_j^{n+\frac{2}{3}}\right)\\ {\theta }_j^{n+1}=W^T{T}_{{\lambda }_2}\left(W{\theta }_j^{n+\frac{2}{3}}\right).\end{array}& (15)\end{array}$

where W denotes the tight frame analysis transform, and T_λ is a soft-thresholding operator, defined as $T_{\lambda }(x)=\frac{\left|x\right|-\lambda }{\left|x\right|}x$ if |x| > λ, otherwise T_λ(x) = 0.

2.2. Algorithm and Implementation

We implement our method for multi-slice spiral scanning using both Matlab and CUDA. CUDA is a software development platform enabling general purpose C-like programs on the NVIDIA graphics processing unit (GPU) [21]. Since the operations of forward and backward projections are time consuming, we use CUDA in GPU card to perform forward and backward projections. Matlab is user-friendly for fast development of new methods, so we conduct non-negativity and sparsity constraints on Matlab and sync the results from CUDA with the embedded “mex” functions in Matlab¹.

To accelerate the convergence, we adopt the ordered-subset (OS) technique [22]. We uniformly divide total projections into 16 subsets and update photoelectric and Compton scatter volumes on every subset's iteration. The reconstruction stops after a preset number of iterations, which is set to 10 in this study.

Our algorithm for spiral scanning spectral reconstruction is summarized as follows.

ALGORITHM 1

Algorithm 1: (Spectral CT reconstruction)

3. Results

In this section, the proposed algorithm is evaluated with a Catphan phantom and real patient data sets. Numerical experiments are conducted on an Xeon Gold 6242R @3.1 GHz/NVIDIA Quadro RTX 8000 workstation in Matlab R2017b & CUDA 9.0. The spiral CT scanning has 960 projections per rotation, and the pitch is 1. There are 16 rows of detectors and each row consists of 896 detector bins. Each reconstructed slice consists of 512×512 pixels. The slice thicknesses of reconstructed volumes are 5 mm for chest and abdomen, and 2.5 mm for head data in this work. We use the proposed algorithm to reconstruct the photoelectric coefficients ϕ and the Compton scatter coefficients θ. In the experiments presented in this paper, we choose step size δ₁ = 0.5 for ϕ, δ₂ = 1 for θ, and threshold parameters ${\lambda }_1=1.5\times 10^{-4}$ for ϕ, ${\lambda }_2=4.5\times 10^{-4}$ for θ.

3.1. Experiment With Catphan Phantom

Experiments are conducted with the Catphan 504 phantom designed for multi-slice spiral CT algorithm evaluation by the Phantom Laboratory². The image reconstructed at monochromatic 70 keV labeled with different materials and the color image overlaid by the attenuation coefficients at monochromatic 40, 50, and 100 keV are shown in Figure 1. From the synthesized color image, changes in the level of colors and details are visible. In specific, the yellow shown in Teflon indicates a special spectral property which is invisible in regular CT reconstruction. In addition, acrylic is more clear in the synthesized color image.

FIGURE 1

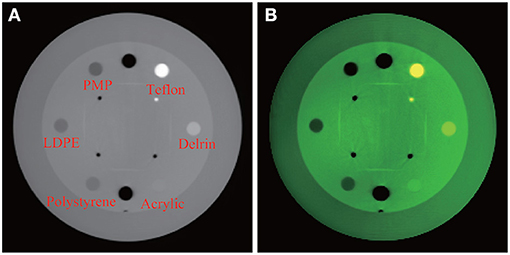
Figure 1. Experiment with Catphan 504. From left, (A) reconstructed image at monochromatic 70 keV with labels of various materials; (B) synthesized color image.

To evaluate the quantitative performance of the proposed method, we compute the mean values and standard deviations of CT numbers of specific materials in the reconstructed Catphan 504 phantom. Table 1 lists the mean CT numbers μ with their standard deviations σ computed at monochromatic 40, 50, and 100 keV, together with reference CT numbers provided by manufacturer's manual. It is remarkable that the standard deviations σ are relatively small in most of the cases, in the sense that the length of 95% confidence interval is much smaller than the corresponding CT number range given in the manual, except for LDPE. For example, the 95% confidence interval (μ − 2σ, μ + 2σ) for the CT number of polystyrene at 100 keV is (−72.2, −51.8). Its length of 20.4 is significantly smaller than 36, the length of the corresponding interval (−65, −29) in the manual. This is a manifestation of the accuracy of our spectral reconstruction algorithm.

TABLE 1

Table 1. CT numbers reconstructed for materials in Catphan 504 (Unit: HU).

Note that manufacturer's reference CT numbers are obtained from polychromatic X-ray systems. It is known that CT numbers depend largely on energy levels and spectra of X-ray sources [23]. Since the X-ray spectra used for Catphan reference CT numbers are not known, there are no direct ways to compare the CT numbers reconstructed by our algorithm and the manufacturer's reference CT numbers. What Table 1 shows, however, is a clear trend of dependence of CT numbers on X-ray energy levels. Except for Delrin, the 95% confidence intervals of our CT numbers overlap with the corresponding reference intervals at least at some energy levels.

3.2. Experiment With Clinical Images

Experiments are also conducted with clinical data. Conventional FBP reconstructed images of patients' head, chest, and abdomen images are obtained from a CT scanner XHCT-16 manufactured by Shinva Medical Instrument Limited Co. Then the images reconstructed and synthesized from the proposed algorithm are compared with the images reconstructed directly from the Shinva XHCT-16.

A brain image reconstructed directly by a Shinva XHCT-16 is shown in Figure 2A. The photoelectric, Compton scatter, and attenuation coefficients reconstructed by the proposed method at monochromatic 70 keV from the same data are shown in Figures 2B–D. The color image overlaid by the attenuation coefficients at monochromatic 40, 50, and 100 keV is shown in Figure 3. The following features are observed from Figures 2, 3. Firstly, the images in Figures 2B–D reconstructed by the proposed method provide more details about the brain tissue than the image Figure 2A from the Shinva XHCT-16. For example, there is no structure except noise displayed in the brain tissue ditches in Figure 2A, but some details are visible in the brain tissue ditches in Figures 2B–D. Secondly, the green color of the brain tissue and the yellow color of head bones in Figure 3 indicate different spectral properties of brain tissue, skull bone, and trabecular bone. In addition to the brain tissue, Figure 3 displays the inner layer of skull bone, the outer layer of skull bone, and the trabecular bone between them, while a conventional gray CT image can hardly show them simultaneously. Thirdly, the thin green layer inside the skull bone shows clearly the connection between meninges and the brain tissue ditches, which is not indicated in Figure 2A anywhere. The upper sagittal sinus connecting the central longitudinal fissure at the back of the brain tissue displays its internal structure and its connection with the meninges, which is not shown in Figure 2A. Finally, the gray ring between the skull bone and brain tissue in Figure 2A doesn't provide any structural information, in particular, it is wide and uniformly gray in the forehead region. It is remarked that the corresponding region in Figures 2B–D, 3 is informative and provides clear structural information.

FIGURE 2

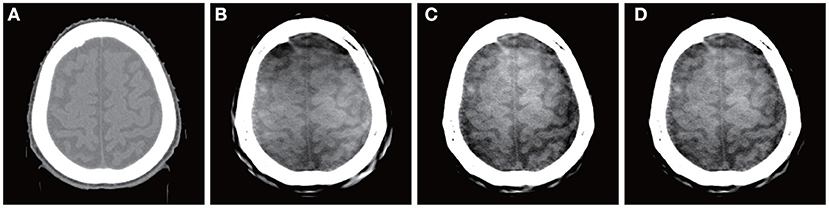
Figure 2. Brain images reconstructed by a Shinva XHCT-16 and the proposed method at monochromatic 70 keV from the same data. From left, (A) Shinva XHCT-16 with the display window [−150, 210] (Unit: HU); (B) reconstructed photoelectric component; (C) reconstructed Compton scatter component; (D) reconstructed attenuation coefficients.

FIGURE 3

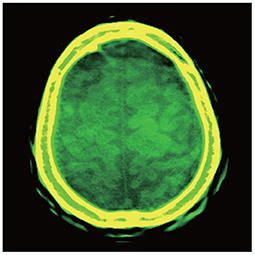
Figure 3. Color image overlaid by the attenuation coefficients at monochromatic 40, 50, and 100 keV, with the display window [−150, 210] (Unit: HU) of the components at each keV.

Figures 4, 5 show the images reconstructed by a Shinva XHCT-16 and the synthesized color images by the proposed method, for an abdomen image and a chest image, respectively. Compared with the images by the Shinva XHCT-16, the color images provide some extra details which are helpful for clinical diagnosis, for example, details about the renal pelvis and lumbar joint in Figure 4B and the rectangular region in Figure 5B.

FIGURE 4

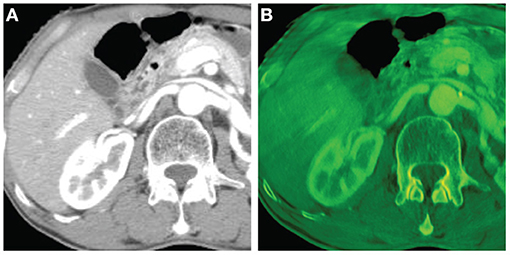
Figure 4. Abdomen images with the display window [−280, 320] (Unit: HU). From left, (A) image reconstructed by a Shinva XHCT-16; (B) synthesized color image with components at 40 keV, 50 keV, and 100 keV.

FIGURE 5

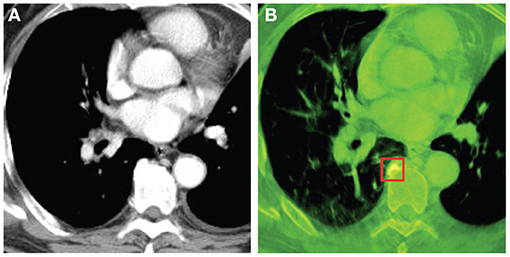
Figure 5. Chest images with the display window [−532, 166] (Unit: HU). From left, (A) image reconstructed by Shinva XHCT-16; (B) synthesized color image with components at 40 keV, 50 keV, and 100 keV.

In summary, the proposed reconstruction algorithm provides spectral image information which reveals tiny structures in clinical images and is helpful for clinical diagnosis.

3.3. Computation and Convergence Speed

In this section, we compare the computational time of the proposed algorithm with that of the fan beam spectral reconstruction algorithm [14]. Experiments with both algorithms are conducted on the Xeon Gold 6242R @3.1 GHz/NVIDIA Quadro RTX 8000 workstation in the same operating environment. Chest data are selected as an example. The reconstructed volume has 723 slices, and each slice is with three sizes of 1,024*1,024, 768*768, and 512*512 pixels, respectively. The total number of iterations is preset to 10 because it is observed that the algorithm converges rapidly before the 10th iteration but changes slightly and slowly after 10 iterations, as shown in Figure 6. The average running times of an iteration for a single slice with the previous fan beam algorithm are 1686.5, 936.1, and 393.7 s for the three image resolutions, respectively, while with our proposed algorithm, the average running times of an iteration for the whole volume are 1164.2, 714.1, and 375.3 s, respectively, for the three image resolutions. The results show that the proposed algorithm significantly reduces the computational time.

FIGURE 6

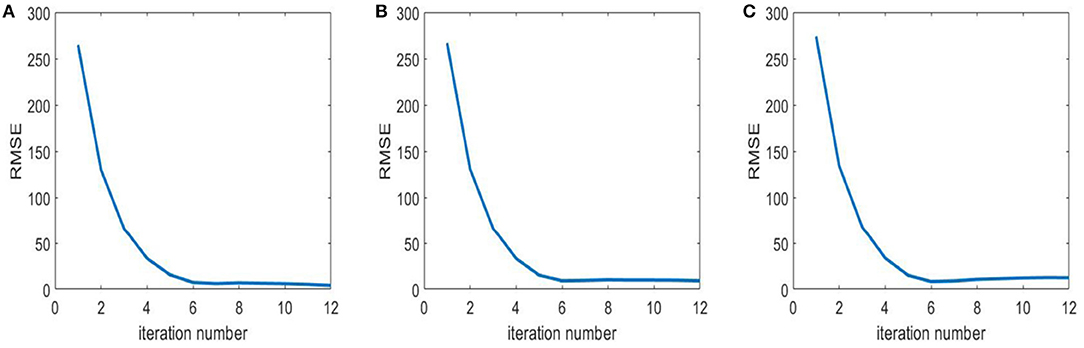
Figure 6. Root Mean Square Error (RMSE) of Teflon in Figure 1 to reveal the convergence rate of the proposed algorithm. From left, (A) RMSE of Teflon under 40 kev; (B) RMSE of Teflon under 50 kev; (C) RMSE of Teflon under 100 kev.

4. Discussions and Conclusions

4.1. Comparison With Existing Spectral Reconstruction Algorithms

In our previous method [14], the reconstruction process were all realized in the environment of MATLAB and running on the CPU without any acceleration technologies. Besides, it only reconstructs a central slice from the rebined fanbeam projections. In comparison, the method proposed in this paper reconstructs a whole volume from the spiral multi-slice projections and adopts GPU to significantly speed up the reconstruction, making our method a great potential in practical application.

In De Man et al. [24], the authors select a set of base substances including air, water, bone, and iron. Using the photoelectric coefficients ϕ and the Compton coefficients θ of these base substances, a piecewise-linear ϕ–θ curve is plotted. By assuming all other substances have their ϕ and θ coefficients lie on this ϕ–θ curve, they effectively reduce the number of unknowns from 2J to J after discretization as in Equation (7). De Man et al. [24] proposes an iterative maximum-likelihood algorithm (IMPACT) to reconstruct these J unknowns and a postreconstruction algorithm (IBHC) for beam-hardening correction.

As opposite to [24], the algorithm presented in this paper is a true spectral reconstruction in the sense of solving for all 2J unknowns. We do not have codes for IMPACT and IBHC to run on our datasets to make a direct comparison, but by looking at [24, Figures 5–9] and our Figures 1–5, our reconstructions appear better.

4.2. Limitations

State-of-the-art spectral CT platforms such as the detector-based IQon Elite Spectral CT by Philips³, dual-energy spectral CT Discovery 750 HD by GE⁴, and dual-source spectral CT SOMATOM Force by Siemens⁵ use sophisticated hardware technology and produce spectral CT images of high quality. The algorithm presented here is on the other hand a software solution to spectral CT. Since our algorithm is based on datasets obtained from conventional energy-integrated CT scanners, the amount of information in our scanned data is much less than those in footnotes 3, 4, and 5. This determines a priori that our image quality cannot be expected to reach the levels of footnotes 3, 4, and 5. Our algorithm, however, may provide a low-cost solution to spectral CT and hence promote more clinical usage.

4.3. Conclusion

In this paper, we implement a framelet-based spectral reconstruction for conventional multi-slice spiral CT using CUDA with bowtie filtration and the OS technique. The experiments demonstrate that the synthesized color image produced by the proposed algorithm can reveal fine structures in clinical images and that the algorithm is efficient regarding to the computational time. Thus, the proposed algorithm has a great potential in practical application. In the future, we will further investigate the proposed method in clinical settings and study the convergence of proposed algorithm in theory.

Data Availability Statement

The datasets presented in this article are not readily available because, proprietary data will not be released. Requests to access the datasets should be directed to yangbo-ye@uiowa.edu.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

The authors express their sincere thanks to Shandong University for Grant No. 10000086393120 (Precision Oncology) and to Xinhua Medical Instrument Co. Ltd. (Shinva) for a grant.

Conflict of Interest

Intellectual property related to International Patent Application No. PCT/US17/23851, including references [16–18], was licensed to Shandong Xinhua Medical Instrument Co. Ltd. who provided partial funding to this research.

Acknowledgments

The authors express their sincere thanks to Shandong University for facilities and support, to Xinhua Medical Instrument Co. Ltd. (Shinva) for cooperation and clinical and experimental data, and to Analogic Corporation for a permission to scanned data. Gratitude is also due to Zhien Qin, Charles Shaughnessy, and Zhendong Wang for their valuable help.

Footnotes

1. ^https://www.mathworks.com/help/parallel-computing/accessing-advanced-cuda-features-using-mex.html (2021).

2. ^https://www.phantomlab.com/ (2021).

3. ^https://www.usa.philips.com/healthcare/product/HC729332/iqon-elite-spectral-ct-ct-scanner (2021).

4. ^https://www.gehealthcare.com/-/jssmedia/c47da2e232d1498db841631ee28eb3d9.pdf (2021).

5. ^https://www.siemens-healthineers.com/en-us/computed-tomography/dual-source-ct/somatom-force (2021).

References

1. Brooks RA. Energy dependence of the Hounsfield number. In: Proceedings of the Annual Symposium on Computer Application in Medical Care Washington, DC (1977). p. 368–71.

Google Scholar

2. Brooks RA, Di Chiro G. Beam hardening in X-ray reconstructive tomography. Phys Med Biol. (1976) 21:390–8. doi: 10.1088/0031-9155/21/3/004

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Herman GT. Correction for beam hardening in computed tomography. Phys Med Biol. (1979) 24:81–106. doi: 10.1088/0031-9155/24/1/008

CrossRef Full Text | Google Scholar

4. Alvarez RE, Macovski A. Energy-selective reconstructions in X-ray computerized tomography. Phys Med Biol. (1976) 21:733–44. doi: 10.1088/0031-9155/21/5/002

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Garnett R. A comprehensive review of dual-energy and multi-spectral computed tomography. Clin Imaging. (2020) 67:160–9. doi: 10.1016/j.clinimag.2020.07.030

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Johnson T, Fink C, Schönberg SO, Reiser MF. Dual Energy CT in Clinical Practice. Berlin: Springer (2011).

Google Scholar

7. Macovski A, Alvarez RE, Chan JL, Stonestrom JP, Zatz LM. Energy dependent reconstruction in X-ray computerized tomography. Comput Biol Med. (1976) 6:325–34. doi: 10.1016/0010-4825(76)90069-x

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Flohr TG, Bruder H, Stierstorfer K, Petersilka M, Schmidt B, McCollough CH. Image reconstruction and image quality evaluation for a dual source CT scanner. Med Phys. (2008) 35:5882–97. doi: 10.1118/1.3020756

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Barnes GT, Sones RA, Tesic MM, Morgan DR, Sanders JN. Detector for dual-energy digital radiography. Radiology. (1985) 156:537–40. doi: 10.1148/radiology.156.2.4011921

CrossRef Full Text | Google Scholar

10. McCollough CH, Leng S, Yu L, Fletcher JG. Dual- and multi-energy CT: principles, technical approaches, and clinical applications. Radiology. (2015) 276:637–53. doi: 10.1148/radiol.2015142631

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yan CH, Whalen RT, Beaupré GS, Yen SY, Napel S. Reconstruction algorithm for polychromatic CT imaging: application to beam hardening correction. IEEE Trans Biomed Eng. (2009) 19:1–11. doi: 10.1109/42.832955

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Fessler JA, Elbakri IA, Sukovic P, Clinthorne NH. Maximum-likelihood dual-energy tomographic image reconstruction. In: Proceedings Volume 4684 Medical Imaging. Bellingham, WA (2002) p. 38–49.

Google Scholar

13. Zhao B, Ding H, Lu Y, Wang G, Zhao J, Molloi S. Dual-dictionary learning-based iterative image reconstruction for spectral computed tomography application. Phys Med Biol. (2012) 57:8217–29. doi: 10.1088/0031-9155/57/24/8217

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang Y, Wang G, Mao S, Cong W, Ji Z, Cai JF, et al. A framelet-based iterative maximum-likelihood reconstruction algorithm for spectral CT. Inverse Probl. (2016) 32:115021. doi: 10.1088/0266-5611/32/11/115021

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang Y, Wang G, Mao S, Cong W, Ji Z, Cai JF, et al. A spectral interior CT by a framelet-based reconstruction algorithm. J X-Ray Sci Technol. (2016) 24:771–85. doi: 10.3233/XST-160586

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Cong W, Ye Y, Wang G, Mao S, Wang Y. Devices, Systems and Methods Utilizing Framelet-Based Iterative Maximum-Likelihood Reconstruction Algorithms in Spectral CT. Alexandria, VA: The United States Patent and Trademark Office (USPTO), US Patent 10489942 (2019).

Google Scholar

17. Cong W, Ye Y, Wang G, Mao S, Wang Y. Devices, Systems and Methods Utilizing Framelet-Based Iterative Maximum-Likelihood Reconstruction Algorithms in Spectral CT. Beijing, China: The China National Intellectual Property Administration, China Patent Application: 201780019606.1 (2017).

Google Scholar

18. Cong W, Ye Y, Wang G, Mao S, Wang Y. Devices, Systems and Methods Utilizing Framelet-Based Iterative Maximum-Likelihood Reconstruction Algorithms in Spectral CT. Alexandria, VA: The United States Patent and Trademark Office (USPTO), US Notice of Allowance: US Patent Application: 16/597,250 (2020).

Google Scholar

19. Stonestrom JP, Alvarez RE, Macovski A. A framework for spectral artifact corrections in X-Ray CT. IEEE Trans Biomed Eng. (1981) 2:128–41. doi: 10.1109/TBME.1981.324786

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hsieh J. Adaptive streak artifact reduction in computed tomography resulting from excessive X-ray photon noise. Med Phy. (1998) 25:2139–47. doi: 10.1118/1.598410

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Jia X, Dong B, Lou Y, Jiang SB. GPU-based iterative cone-beam CT reconstruction using tight frame regularization. Phys Med Biol. (2011) 56:3787–807. doi: 10.1088/0031-9155/56/13/004

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Wang G, Jiang M. Ordered-subset simultaneous algebraic reconstruction techniques (OS-SART). J X-ray Sci Technol. (2004) 12:169–77.

Google Scholar

23. Chan MF, Yang J, Song Y, Burman C, Chan P, Li S. Evaluation of imaging performance of major image guidance systems. Biomed Imaging Interv J. (2011) 7:e11. doi: 10.2349/biij.7.2.e11

PubMed Abstract | CrossRef Full Text | Google Scholar

24. De Man B, Nuyts J, Dupont P, Marchal G, Suetens P. An iterative maximum-likelihood polychromatic algorithm for CT. IEEE Trans Med Imaging. (2001) 20:999–1008. doi: 10.1109/42.959297

PubMed Abstract | CrossRef Full Text | Google Scholar