Certain Properties of Domination in Product Vague Graphs With an Application in Medicine

The product vague graph (PVG) is one of the most significant issues in fuzzy graph theory, which has many applications in the medical sciences today. The PVG can manage the uncertainty, connected to the unpredictable and unspecified data of all real-world problems, in which fuzzy graphs (FGs) will not conceivably ensue into generating adequate results. The limitations of previous definitions in FGs have led us to present new definitions in PVGs. Domination is one of the highly remarkable areas in fuzzy graph theory that have many applications in medical and computer sciences. Therefore, in this study, we introduce distinctive concepts and properties related to domination in product vague graphs such as the edge dominating set, total dominating set, perfect dominating set, global dominating set, and edge independent set, with some examples. Finally, we propose an implementation of the concept of a dominating set in medicine that is related to the COVID-19 pandemic.

Mathematics Subject Classification: 05C99, 03E72

1 Introduction

Graph theory began its adventure from the well-known “Konigsberg bridge problem.” This problem is frequently believed to have been the beginning of graph theory. In 1739, Euler finally elucidated this problem using graphs. Even though graph theory is an extraordinarily old concept, its growing utilization in operations research, chemistry, genetics, electrical engineering, geography, and so forth has reserved its freshness. In graph theory, it is highly considered that the nodes, edges, weights, and so on are definite. To be exact, there may be no question concerning the existence of these objects. However, the real world sits on a plethora of uncertainties, indicating that in some situations, it is believed that the nodes, edges, and weights may be additional or may not be certain. For instance, the vehicle travel time or vehicle capacity on a road network may not be exactly identified or known. To embody such graphs, Rosenfeld [1] brought up the idea of the “fuzzy graph” in 1975. FG-models are advantageous mathematical tools for handling different domains of combinatorial problems embracing algebra, topology, optimization, computer science, social sciences, and physics (e.g., vulnerability of networks: fractional percolation on random graphs). The VS theory was defined by Gau and Buehrer [2]. Using Zadeh’s fuzzy relation [3], Kauffman [4] illustrated FGs. Mordeson et al. [5–7] evaluated some results in FGs. Pal et al. [8–10] investigated some remarks on bipolar fuzzy graphs and competition graphs. Akram et al. [11, 12] epitomized new definitions in FGs. Ramakrishna [13] described the VG concepts and examined the properties. Rashmanlou et al. [14] defined PVGs and studied new concepts such as the complete-PVG, complement of a PVG, and the edge regular PVG with several examples. Shao et al. [15–20] proposed new concepts in vague graph structures and vague incidence graphs such as the maximal product, residue product, irregular vague graphs, valid degree, isolated vertex, vague incidence irredundant set, Laplacian energy, adjacency matrix, and Laplacian matrix in VGs and investigated their properties with several examples. Also, they described several applications of these concepts in the medical sciences. Borzooei et al. [21–24] analyzed several concepts of VGs. Ore [25] defined “domination” for undirected graphs and studied its properties. Somasundaram [26] defined the DS and IDS in FGs. Nagoorgani et al. [27, 28] represented the fuzzy DS and IDS notions using strong arcs. Parvathi and Thamizhendhi [29] represented the domination number, independent set, independent domination number, and total domination number in intuitionistic fuzzy graphs [29]. Cockayne [30] and Hedetniemi [31, 32] introduced fundamentals of domination in graphs.

Fuzzy graph theory has a wide range of applications in various fields. Since indeterminate information is an essential real-life problem, mostly uncertain, modeling those problems based on fuzzy graphs (FGs) is highly demanding for an expert. A PVG is an indiscriminately comprehensive structure of an FG that offers higher precision, adaptability, and compatibility to a system when coordinated with systems running on FGs. PVGs are a very useful tool for examining many issues such as networking, social systems, geometry, biology, clustering, medical science, and traffic plans. Domination is one of the most important issues in graph theory and has found numerous applications in formulating and solving many problems in several domains of science and technology exemplified by computer networks, artificial intelligence, combinatorial analyses, etc. Domination of PVGs is an interesting and powerful concept and can play an important role in applications. Thus, in this study, we introduce different kinds of domination in PVGs, such as the EDS, TDS, PDS, GDS, and EIS, with some examples and also discuss the properties of each of them. Today, almost every country in the world is inflicted by a dangerous disease called Covid-19. Unfortunately, many people have lost their lives due to contracting this dangerous virus and the lack of necessary medical equipment for treatment. So, we have tried to identify a suitable hospital for a person infected with the coronavirus that has more appropriate medical facilities and equipment and is in the most favorable conditions in terms of distance and amount of traffic, so that time and money are saved, with the help of the DS in the VG. Some basic notations introduced in Table 1

TABLE 1

TABLE 1. Some basic notations.

2 Preliminaries

A (crisp) graph $G^{\text{*}}=\left(V,E\right)$ consists of two sets called the vertices (V) and the edge (E). The elements of V are called vertices and the elements of E are called edges. An FG has the form of $\zeta =\left(\sigma ,\phi \right)$, so that $\sigma :V\to \left[\mathrm{0,1}\right]$ and $\phi :V\times V\to \left[\mathrm{0,1}\right]$, as is defined as $\phi \left(xy\right)\le \sigma \left(x\right)\wedge \sigma \left(y\right)$, $\forall x,y\in V$, and φ is a symmetric fuzzy relation on σ and $\wedge$ denotes the minimum.

Definition 2.1: [2] A VS A is a pair$\left(t_M,f_M\right)$where$t_M$and$f_M$are considered as real-valued functions that can be described on$V\to \left[\mathrm{0,1}\right]$, such that$t_M\left(x\right)+f_M\left(x\right)\le 1$,$\forall x\in V$.

Definition 2.2: [13] A pair$\xi =\left(M,N\right)$is named as a VG on$G^{\text{*}}$, such that$M=\left(t_M,f_M\right)$is a VS on V and$N=\left(t_N,f_N\right)$is a VS on$E\subseteq V\times V$so that for all$xy\in E$, we have$t_N\left(xy\right)\le \text{min}\left(t_M\left(x\right),t_M\left(y\right)\right)$, and$f_N\left(xy\right)\ge \text{max}\left(f_M\left(x\right),f_M\left(y\right)\right)$.

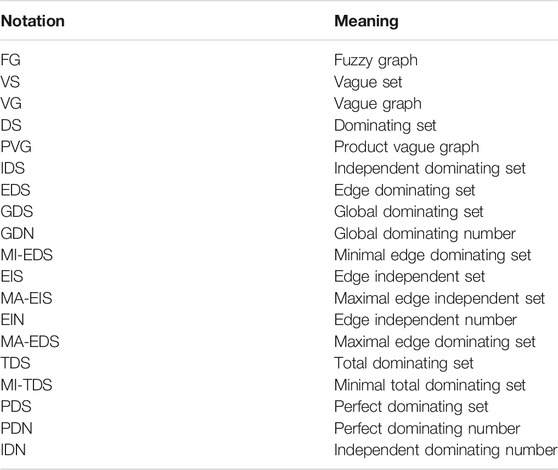
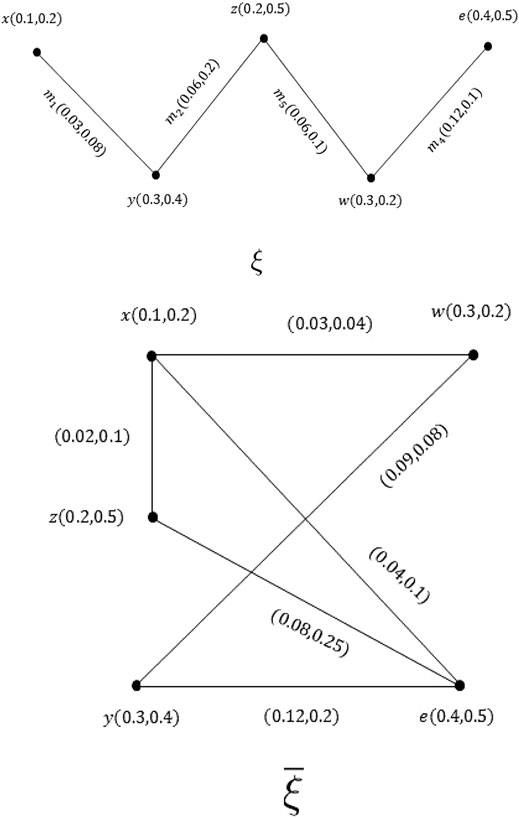
Example 2.3: Consider a VG ξ asFigure 1, so that$V=\left\{x,y,z\right\}$and$E=\left\{xy,xz,yz\right\}$. Clearly, ξ is a VG.

FIGURE 1

FIGURE 1. VG ξ.

Definition 2.4: [23] Let$\xi =\left(M,N\right)$be a VG. The cardinality, vertex cardinality, and edge cardinality of ξ are defined as follows:

(1) $\left|\xi \right|=|{\displaystyle \sum }_{x_i\in V}\frac{1+t_M\left(x_i\right)-f_M\left(x_i\right)}{2}+{\displaystyle \sum }_{x_i{y}_i\in E}\frac{1+t_N\left(x_i{y}_i\right)-f_N\left(x_i{y}_i\right)}{2}|.$

(2) $\left|V\right|={\displaystyle {\sum }_{x_i\in V}\frac{1+t_M\left(x_i\right)-f_M\left(x_i\right)}{2}}$,$\forall x_i\in V$.

(3) $\left|E\right|={\displaystyle {\sum }_{x_i{b}_i\in E}\frac{1+t_N\left(x_i{y}_i\right)-f_N\left(x_i{y}_i\right)}{2}}$,$\forall x_i{y}_i\in E$.

Definition 2.5: [24] Consider$\xi =\left(M,N\right)$as a VG. Provided that$x_i,x_j\in V$, the connectedness t-strength between$x_i$and$x_j$is termed as$t_N^{\infty }\left(x_i,x_j\right)=\text{sup}\{t_N^k\left(x_i,x_j\right)k=\mathrm{1,2},\cdots ,n\}$and the connectedness f-strength between$x_i$and$x_j$is termed as$f_N^{\infty }\left(x_i,x_j\right)=\text{inf}\{f_N^k\left(x_i,x_j\right)k=\mathrm{1,2},\cdots ,n\}$.

Definition 2.6: [22] An edge$xy$in a VG$\xi =\left(M,N\right)$will be a strong edge provided that$t_N\left(xy\right)\ge {\left(t_N\right)}^{\infty }\left(xy\right)$and$f_N\left(xy\right)\le {\left(f_N\right)}^{\infty }\left(xy\right)$.

Definition 2.7: [23] A VG$\xi =\left(M,N\right)$is called complete provided that$t_N\left(x_i{x}_j\right)=\text{min}\left\{t_M\left(x_i\right),t_M\left(x_j\right)\right\}$and$f_N\left(x_i{x}_j\right)=\text{max}\left\{f_M\left(x_i\right),f_M\left(x_j\right)\right\}$,$\forall x_i,x_j\in V$.A VG ξ is called strong provided that $t_N\left(x_i{x}_j\right)=\text{min}\left\{t_M\left(x_i\right),t_M\left(x_j\right)\right\}$ and $f_N\left(x_i{x}_j\right)=\text{max}\left\{f_M\left(x_i\right),f_M\left(x_j\right)\right\}$, $\forall x_i{x}_j\in E$.

Definition 2.8: [22] Consider ξ as a VG. Assuming$x,y\in V$, we state that x dominates y in ξ, provided that there is a strong edge between them.A subset $K\subseteq V$ will be named a DS in ξ provided that for every $x\in V-S$, there exists $y\in K$ so that x dominated y. A DS K of a VG ξ is referred to as an MI-DS, provided that no proper subset of K is a DS.

Definition 2.9: [14] Let$\xi =\left(M,N\right)$be a VG. If$t_N\left(xy\right)\le t_M\left(x\right)\times t_M\left(y\right)$and$f_N\left(xy\right)\ge f_M\left(x\right)\times f_M\left(y\right)$,$\forall x,y\in V$, then the VG ξ is called a PVG. Note that a PVG ξ is not necessarily a VG. A PVG ξ is called complete-PVG if$t_N\left(xy\right)=t_M\left(x\right)\times t_M\left(y\right)$and$f_N\left(xy\right)=f_M\left(x\right)\times f_M\left(y\right)$,$\forall x,y\in V$.The complement of a PVG $\xi =\left(M,N\right)$ is $\overline{\xi }=\left(\overline{M},\overline{N}\right)$, where $\overline{M}=M=\left(t_M,f_M\right)$ and $\overline{N}=\left(\overline{t_N},\overline{f_N}\right)$ so that $\overline{t_N}\left(xy\right)=t_M\left(x\right)\times t_M\left(y\right)-t_N\left(xy\right)$ and $\overline{f_N}\left(xy\right)=f_N\left(xy\right)-f_M\left(x\right)\times f_M\left(y\right)$.

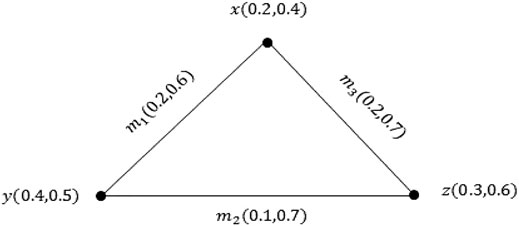
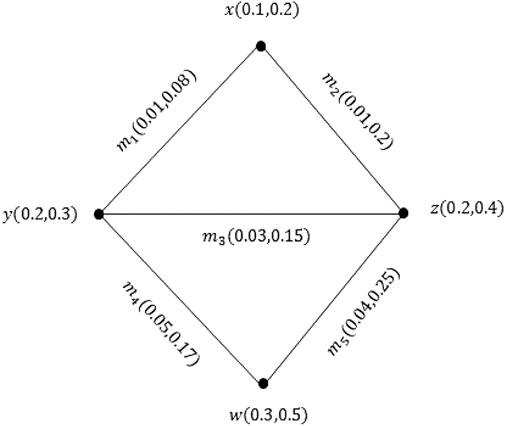
Example 2.10: Consider the PVG ξ asFigure 2.For the $xy$ edge, we have the following:

$0.01=t_N\left(xy\right)\le t_M\left(x\right)\times t_M\left(y\right)=0.02,$

$0.15=f_N\left(xy\right)\ge f_M\left(x\right)\times f_M\left(y\right)=\mathrm{0.01.}$

In the same way, we can show that both conditions of Definition 2.9 are true for other edges. So, ξ is a PVG.

FIGURE 2

FIGURE 2. product vague graph ξ.

Definition 2.11: [14] An edge$xy$in a PVG ξ is named an effective edge if$t_N\left(xy\right)=t_M\left(x\right)\times t_M\left(y\right)$and$f_N\left(xy\right)=f_M\left(x\right)\times f_M\left(y\right)$.

Definition 2.12: [14] If ξ is a PVG, then the vertex cardinality of$K\subseteq V$is described as follows:

$\left|K\right|=\left|{\displaystyle \sum }_{x\in K}\frac{1+t_M\left(x\right)-f_M\left(x\right)}{2}\right|.$

Definition 2.13: [14] Let$\xi =\left(M,N\right)$be a PVG; then the edge cardinality of$S\subseteq E$is defined as follows:

$\left|S\right|=\left|{\displaystyle \sum }_{xy\in S}\frac{1+t_N\left(xy\right)-f_N\left(xy\right)}{2}\right|.$

Definition 2.14: [14] Two edges$xy$and$zw$in a PVG ξ are named adjacent if they are neighbors. Also, they are independent if they are not adjacent.

Definition 2.15: [22] Let ξ be a PVG.$K\subseteq V\left(\xi \right)$is called a DS of ξ if$\forall$$x\in V-K$, and there exists a vertex$y\in K$so that the following occurs:

$t_N\left(xy\right)=t_M\left(x\right)\times t_M\left(y\right)and{f}_N\left(xy\right)=f_M\left(x\right)\times f_M\left(y\right).$

A DS K of a PVG ξ is said to be a minimal-DS if no proper subset of K is a DS.

Definition 2.16: [5] Let$\xi =\left(M,N\right)$be a PVG. Then we have$\text{deg}\left(x\right)=\left({\text{deg}}^t\left(x\right),{\text{deg}}^f\left(x\right)\right)=\left(M_1,M_2\right)$, where$M_1={\displaystyle {\sum }_{x\ne y}{t}_N\left(xy\right)}$and$M_2={\displaystyle {\sum }_{x\ne y}{f}_N\left(xy\right)}$, for$xy\in E$.Two vertices, $x_i$ and $x_j$, are said to be strong neighbors if $t_N\left(x_i{x}_j\right)=\text{min}\left\{t_M\left(x_i\right),t_M\left(x_j\right)\right\}$ and $f_N\left(x_i{x}_j\right)=\text{max}\left\{f_M\left(x_i\right),f_M\left(x_j\right)\right\}$.

Definition 2.17: [22] Two vertices,$x_i$and$x_j$, are said to be independent vertices if there is no strong arc among them.$K\subseteq V$is called an independent set if every two vertices of K are independent.

3 New Kinds of Domination in Product Vague Graphs

Definition 3.1: Let$\xi =\left(M,N\right)$be a PVG and$m_i$and$m_j$be two adjacent edges of ξ. We say that$m_i$dominates$m_j$if$m_i$is an effective edge in ξ.

Definition 3.2: $D\subseteq E$is named an EDS in ξ if for every$m_j\in E-D$, there is an$m_i\in E-D$, so that$m_i$dominates$m_j$.

Definition 3.3: An EDS D of a PVG ξ is named an MI-EDS if no proper subset of D is an EDS.

Definition 3.4: Minimum cardinality between all MI-EDSs is named an EDN of ξ and is denoted by$\gamma \prime \left(\xi \right)$.

Definition 3.5: The strong neighborhood of an edge$m_i$in a PVG ξ is defined as$N_s\left(m_i\right)=\{m_j\in E\left(\xi \right)| m_j is effective edge and neighbor to m_i in \xi \}$.

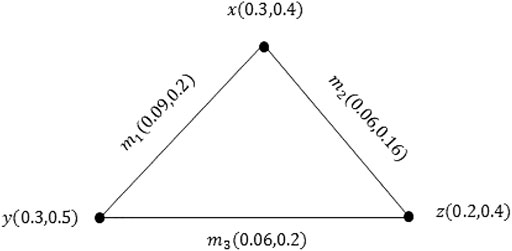
Example 3.6: Consider a PVG$\xi =\left(M,N\right)$on$V=\left\{x,y,z,w\right\}$, as shown inFigure 3.Here, $\left\{m_1,m_3\right\}$, $\left\{m_3,m_4\right\}$, $\left\{m_2,m_4\right\}$, and $\left\{m_1,m_2\right\}$ are EDSs and $\gamma \prime \left(\xi \right)=0.91$.

FIGURE 3

FIGURE 3. PVG ξ with effective edges.

Definition 3.7: Let$\xi =\left(M,N\right)$be a PVG. Two edges,$m_i$and$m_j$, are called edge independent, if$m_i\notin N_s\left(m_j\right)$and$m_j\notin N_s\left(m_i\right)$

Definition 3.8: Let$\xi =\left(M,N\right)$be a PVG. A subset S of E is called an EIS of ξ if any two edges in S are edge independent.

Definition 3.9: An EIS S of a PVG ξ is called an MA-EIS if for every edge$m\in E-S$, the set$S\cup \left\{m\right\}$is not independent. The minimum cardinality between all MA-EISs is called an EIN of ξ and is denoted by$\beta \prime \left(\xi \right)$.

Example 3.10: Consider the example of a PVG$\xi =\left(A,B\right)$as shown inFigure 4. Clearly,$\left\{m_1,m_5\right\}$and$\left\{m_2,m_4\right\}$are MA-EISs of ξ and$\beta \prime \left(\xi \right)=0.84$.

FIGURE 4

FIGURE 4. PVG ξ with MA-EISs.

Definition 3.11: If all the edges are effective edges in a PVG ξ, then it is called an effective-PVG.

Definition 3.12: Assume that$E\text{'}$is a subset of edge set E. Then, the node cover of$E\text{'}$is defined as the set of all nodes incident to every edge in$E\text{'}$.

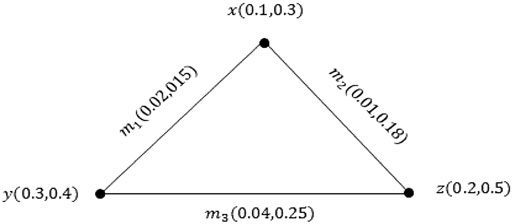
Example 3.13: Consider the PVG ξ as shown inFigure 5. Obviously, ξ is an effective-PVG.

FIGURE 5

FIGURE 5. Effective PVG ξ.

Theorem 3.14: Node cover of an EDS of a PVG ξ is a DS of ξ.

Proof: Let ξ be a PVG. Suppose that S is a node cover of an EDS K. We prove that S is a DS. Let $y\in V-S$, since K is an EDS; then there is a strong edge $m\in K$ such that m is incident to y. Since S is a node cover of K, there is an $x\in S$ so that x dominated y or x covers m. Hence, S is a DS of ξ.

Definition 3.15: An edge in a PVG ξ is called an isolated edge if it is not a neighbor to any effective edge in ξ.

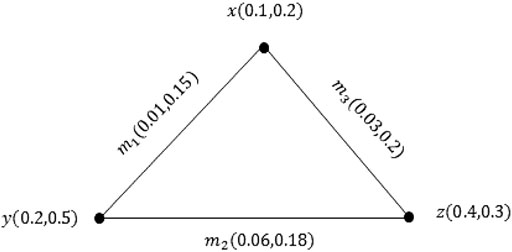
Example 3.16: Consider the PVG ξ as shown inFigure 6. It is obvious that$m_1$is an isolated edge.

FIGURE 6

FIGURE 6. PVG ξ with isolated edge.

Theorem 3.17: Let ξ be a PVG without isolated edges, and there exists no edge$m_i\in E$so that$N_s\left(m_i\right)\subseteq S$. If S is an MI-EDS, then$K-S$is an EDS where K is the set of all effective edges in ξ.

Proof: Let S be an MI-EDS of a PVG ξ. Suppose that $K-S$ is not an EDS. Then, there exists at least one edge $m_i\in S$ that is not dominated by $K-S$. Because ξ has no isolated edges and there is no edge $m_i\in E$ so that $N_s\left(m_i\right)\subseteq S$, $m_i$ neighbors at least one effective edge $m_j$ in K. Since $K-S$ is not an EDS of ξ, $m_j\notin K-S$. So $m_j\in S$. Hence, $m_j\in S$. Therefore, $S-\left\{m_i\right\}$ is an EDS that is a contradiction of the fact that S is an MI-EDS. Hence, each edge in $E-K$ is dominated by an edge in $K-S$. Thus, $K-S$ is an EDS.

Theorem 3.18: An EIS of a PVG ξ having only effective edges is an MA-EIS if and only if it is edge independent and an EDS.

Proof: Suppose that S is an EIS of a PVG ξ having only effective edges. Consider that S is an MA-EIS of ξ. Then, $\forall m_i\in E-S$, and the set $S\cup \left\{m_i\right\}$ is not an EIS, that is, for every $m_i\in E-S$, there is an edge $m_j$ so that $m_j\in N_s\left(m_i\right)$. Hence, S is an EDS of ξ. Conversely, suppose that S is both edge independent and an EDS of ξ. We have to prove that S is an MA-EIS having only effective edges. Because S is an EDS of ξ, it has only effective edges. Assume that S is not an MA-EIS. Then, there is an edge $m_i\notin S$ so that $S\cup \left\{m_i\right\}$ is an EIS, and there is no edge in S belonging to $N_s\left(m_i\right)$ and hence, $m_i$ is not dominated by S. So, S cannot be an EDS of ξ; that is a contradiction. Therefore, we conclude that for every edge $m\in E-S$, the set $S\cup \left\{m\right\}$ is not independent. Thus, S is an MA-EIS of ξ having only effective edges.

Theorem 3.19: Node cover of an MA-EIS of a PVG ξ having only effective edges is a DS of ξ.

Proof: Let S be an MA-EIS of a PVG ξ having only effective edges. Let $V\text{'}$ be the node cover of S. We know that each MA-EDS having only effective edges is a minimal DS of ξ. Then, $V\text{'}$ is a node cover of a PVG ξ. According to Theorem 3.14, the node cover of an EDS of a PVG ξ is a DS of ξ. Hence, $V\text{'}$ is a DS of ξ.

Definition 3.20: Consider$\xi =\left(M,N\right)$as a PVG on V without isolated nodes. A subset$S\subseteq V$is a TDS provided that for each node$y\in V$,$\exists$a node$x\in S$,$x\ne y$, so that x dominates y.

Definition 3.21: A TDS S of a PVG ξ is called an MI-TDS if no proper subset of S is a TDS. The minimum cardinality of an MI-TDS is named a lower-TDN of ξ and is shown by${\gamma }_t\left(\xi \right)$.

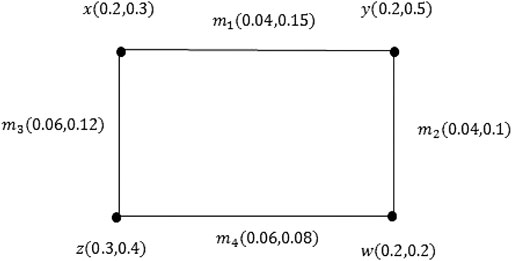
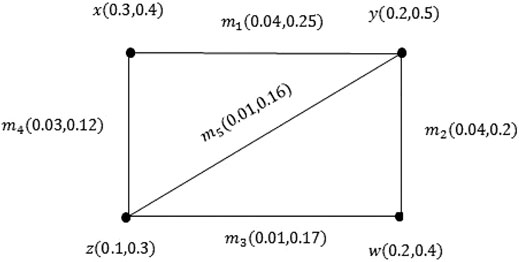
Example 3.22: InFigure 7,$\left\{x,y\right\}$,$\left\{x,w\right\}$,$\left\{y,z\right\}$, and$\left\{y,w\right\}$are TDSs and${\gamma }_t\left(\xi \right)=0.85$.

FIGURE 7

FIGURE 7. PVG ξ with TOSs.

Theorem 3.23: Let$\xi =\left(M,N\right)$be a PVG without isolated nodes and S is a minimal-DS of ξ; then$V-S$is a DS of ξ.

Proof: Let S be a minimal-DS and $s\in S$. Since ξ has no isolated nodes, there is a node $y\in N\left(s\right)$ so that y must be dominated by at least one node in $S-\left\{s\right\}$, that is, $S-\left\{s\right\}$ is a DS and $y\in V-S$. Thus, each node in S is dominated by at least one node in $V-S$, and so $V-S$ is a DS.

Definition 3.24: A DS S in a PVG ξ is called a PDS if for each node$y\in V-S$, there is exactly one node$x\in S$so that x dominates y.

Definition 3.25: A PDS S in a PVG ξ is said to be an MI-PDS if for every$y\in S$,$S-\left\{y\right\}$is not a PDS in ξ. The minimum cardinality among all MI-PDSs is called a PDN of ξ and is denoted by${\gamma }_p\left(\xi \right)$.

Example 3.26: InFigure 8,$\left\{x,y\right\}$,$\left\{x,w\right\}$,$\left\{y,z\right\}$, and$\left\{z,w\right\}$are MI-PDSs and${\gamma }_p\left(\xi \right)=0.75$.

FIGURE 8

FIGURE 8. PVG ξ with MI-PDSs.

Theorem 3.27: Every DS in a complete PVG ξ is a PDS.

Proof: Let S be a minimal-DS of a PVG ξ. Since ξ is complete, every edge in ξ is an effective edge and every node $y\in V-S$ is exactly neighboring one node $x\in S$. Hence, every DS in ξ is a PDS.

Theorem 3.28: A PDS S in a PVG ξ is an MI-PDS if and only if for each node$y\in S$, one of the following conditions is present:

(i) $N\left(y\right)\cap S=\varnothing$,

(ii) $\exists$a node$x\in V-S$so that$N\left(x\right)\cap S=\left\{b\right\}$.

Proof: Let S be an MI-PDS and $y\in S$. Then, $S=S-\left\{y\right\}$ is not a DS and hence $\exists$ a node $x\in V-S$ so that x is not dominated by an element of S. If $x=y$, we get $\left(i\right)$ and if $x\ne y$, we get $\left(ii\right)$. On the contrary, suppose that S is a PDS and for every vertex $x\in S$, one of the two conditions is met. We prove that S is an MI-PDS. Assume that S is not an MI-PDS. So, there exists a vertex $x\in S$ such that $S-x$ is a PDS. Thus, x is a perfect dominated by exactly one vertex in $S-x$. Therefore, condition (i) is not held. Also, if $S-x$ is a PDS, then every vertex in $V-S$ is dominated by exactly one vertex in $S-x$. So, condition (ii) is not held and this is a contradiction.

Theorem 3.29: Let$\xi =\left(M,N\right)$be a connected PVG and S be an MI-PDS of ξ. Then,$V-S$is a DS of ξ.

Proof: Let S be an MI-PDS of ξ, and $V-S$ is not a DS. Then, $\exists$ a node $y\in S$ so that y is not dominated by any node in $V-S$. Since ξ is connected, y is a strong neighbor of at least one node in $S-\left\{y\right\}$. Then, $S-\left\{y\right\}$ is a DS, which contradicts the minimality of S. Thus, for each node b in S, there is at least one node x in $V-S$ so that $t_N\left(xy\right)=t_M\left(x\right)\times t_M\left(y\right)$ and $f_N\left(xy\right)=f_M\left(x\right)\times f_M\left(y\right)$. Hence, $V-S$ is a DS.

Definition 3.30: A DS S of a PVG ξ is named a GDS if S is a DS of$\overline{\xi }$, too. The minimum cardinality between all GDSs is called a GDN, and is described by${\gamma }_g\left(\xi \right)$.

Example 3.31: Let ξ and$\overline{\xi }$be PVGs inFigure 9.It is obvious that $\left\{x,w\right\}$ and $\left\{y,e\right\}$ are GDSs and ${\gamma }_g\left(\xi \right)=0.9$.

FIGURE 9

FIGURE 9. ξ and $\overline{\xi }$.

Theorem 3.32: A DS S in a PVG ξ is called a GDS if and only if$\forall$$y\in V-S$,$\exists$a vertex$x\in S$such that x and y are not dominating each other.

Proof: Suppose that S is a GDS in a PVG ξ. Let x in S be dominated by y in $V-S$; then S is not a DS, contradicting S which is a DS of ξ. Conversely, let $\forall$$b\in V-S$, $\exists x\in S$ so that x and y will not be dominating each other; then S is a DS in both ξ and $\overline{\xi }$, which indicates that S is a GDS of ξ and so the result.

4 Application of Domination in Medical Sciences

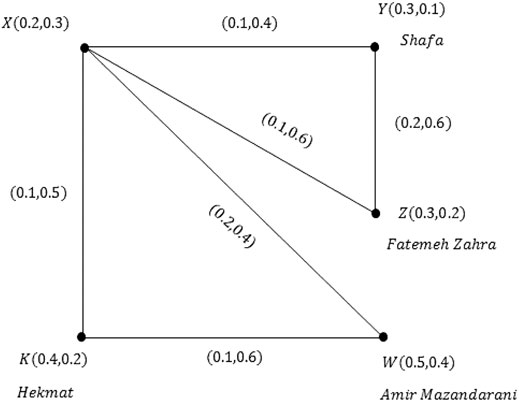
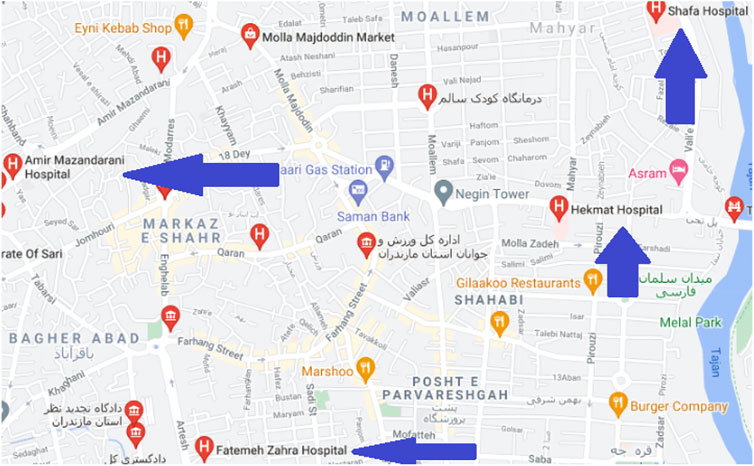
Today, almost every country in the world is affected by a dangerous disease called COVID-19, which is also commonly referred to as Corona. COVID-19 is an infectious disease caused by the coronavirus of acute respiratory syndrome. Its common symptoms are fever, cough, shortness of breath, and, most recently, infertility. Although the majority of cases of the disease cause mild symptoms, some cases progress to pneumonia and multiple sclerosis. The mortality rate is appraised at 2$2\text{\%}$–5%$5\text{\%}$ but varies with age and other health conditions. The pathogenicity of the virus touches the respiratory system and instigates symptoms similar to those of the common cold, which can be very precarious for a patient because the patient assumes that the condition is not very serious. Over time, the disease progresses and can easily derail the patient and lead to poor health. But the issue that can be very important is how to find out when a person is infected with this dangerous virus (with the help of medical diagnostic kits) and what medical facilities and equipment should be used to treat this patient. Considering that this virus has appeared in just one year, most countries are not equipped with the necessary facilities to treat it, and this point can be very critical and threatening for a patient. Accordingly, in this study, we have tried to locate a suitable hospital for a person infected with the coronavirus, which has more appropriate medical facilities and equipment and is in the most favorable condition in terms of distance and amount of traffic, so that the patient can regain his or her health faster and also save time and money. To do so, we consider four hospitals in Iran (Sari city) named Shafa, Fatemeh Zahra, Amir Mazandarani, and Hekmat, which are shown in the graph with the symbols Y, Z, W, and K. The patient’s home is located at point X. In this vague graph, one vertex illustrates the patient’s home and other vertices represent the hospitals in the city. The edges specify the accumulation of cars in the city. The location of hospitals is shown in Figure 11. Weight of nodes and edges defined in Table 2 and Table 3.

TABLE 2

TABLE 2. Weight of nodes in a VG ζ.

TABLE 3

TABLE 3. Weight of edges in a VG ζ.

The vertex $E\left(0.4,0.2\right)$ asserts that it involves 40%$40\text{\%}$ of the prerequisite amenities and services for curing the patient and unfortunately is short of 20%$20\text{\%}$ of the necessary tools. The edge $AC$ indicates that simply 10%$10\text{\%}$ of the patient’s transport route to the hospital is not obstructed by any traffic if taken by ambulance, and unfortunately, 60%$60\text{\%}$ of the route between these two points is congested with cars, especially during the rush hours. The DSs for Figure 10 will be as follows:

$S_1=\left\{X,Y\right\},$

$S_2=\left\{X,Z\right\},$

$S_3=\left\{X,W\right\},$

$S_4=\left\{X,K\right\},$

$S_5=\left\{X,Y,Z\right\},$

$S_6=\left\{X,Y,W\right\},$

$S_7=\left\{X,Y,K\right\},$

$S_8=\left\{Z,W,K\right\},$

$S_9=\left\{X,Y,Z,W\right\},$

$S_{10}=\left\{X,Y,Z,K\right\},$

$S_{11}=\left\{X,Z,W,K\right\},$

$S_{12}=\left\{Y,Z,W,K\right\},$

$S_{13}=\left\{X,Y,W,K\right\}.$

After calculating the cardinality of $S_1,\cdots ,S_{11}$, we have the following:

$\left|S_1\right|=1.05,$

$\left|S_2\right|=1,$

$\left|S_3\right|=1,$

$\left|S_4\right|=1.05,$

$\left|S_5\right|=1.6,$

$\left|S_6\right|=1.6,$

$\left|S_7\right|=1.65,$

$\left|S_8\right|=1.7,$

$\left|S_9\right|=2.15,$

$\left|S_{10}\right|=2.2,$

$\left|S_{11}\right|=2.15,$

$\left|S_{12}\right|=2.3,$

$\left|S_{13}\right|=\mathrm{2.2.}$

FIGURE 10

FIGURE 10. Vague graph ξ for medical sciences.

Clearly, $S_3$ holds the smallest proportions among other DSs, so it is concluded that it serves as the best selection since first, the free space for the ambulance from the patient’s home to the Amir Mazandarani hospital is higher; therefore, the patient cannot be taken to the desired location faster, leading to the saving of money and time. Second, considering the medical services in all the hospitals in the region, the Amir Mazandarani hospital is the most equipped and supplied. Therefore, we conclude that the government should, first, allocate more funds to hospitals and medical staff so that they can purchase respirators and diagnostic kits for coronary heart disease from rich countries and, second, cooperate with the roads and transportation organization to improve the road quality, especially the routes leading to hospitals.

5 Conclusion

Product vague graphs are used in many sciences today, including computers, artificial intelligence, fuzzy social networks, physics, chemistry, and biology. Since all the data in the problem can be considered on it, researchers use it to display the theories in their research work well. Domination is one of the most important issues in graph theory and has found many uses and functions in terms of formulating and solving many problems in different domains of technology and science exemplified by computer networks, artificial intelligence, combinatorial analyses, etc. Domination helps consider the best way to save time and money. Hence, in this study, we introduced different concepts and properties related to domination in product vague graphs, such as the edge dominating set, total dominating set, perfect dominating set, global dominating set, and edge independent set, and studied their properties by giving some examples. Finally, an application of domination in the field of medical sciences that is related to COVID-19 has been introduced. In our future work, we will introduce vague incidence graphs and study the concepts of the connected perfect dominating set, regular perfect dominating set, inverse perfect dominating set, and independent perfect dominating set on the vague incidence graph.

FIGURE 11

FIGURE 11. Location of hospitals in Sari city.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Key R&D Program of China (No. 2019YFA0706402) and the National Natural Science Foundation of China under Grant 61772376 and 62072129.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rosenfeld A. FUZZY GRAPHS††The Support of the Office of Computing Activities, National Science Foundation, under Grant GJ-32258X, Is Gratefully Acknowledged, as Is the Help of Shelly Rowe in Preparing This Paper. In: LA Zadeh, KS Fu, and M Shimura, editors. Fuzzy Sets and Their Applications. New York, NY, USA: Academic Press (1975). p. 77–95. doi:10.1016/b978-0-12-775260-0.50008-6

CrossRef Full Text | Google Scholar

2. Gau W-L, Buehrer DJ. Vague Sets. IEEE Trans Syst Man Cybern (1993) 23:610–4. doi:10.1109/21.229476

CrossRef Full Text | Google Scholar

3. Zadeh LA. The Concept of a Linguistic Variable and its Application to Approximate Reasoning-I. Inf Sci (1975) 8:199–249. doi:10.1016/0020-0255(75)90036-5

CrossRef Full Text | Google Scholar

4. Kaufmann A. Introduction a la Theorie des Sour-Ensembles Flous. Paris, France: Masson et Cie (1973).

5. Mordeson JN, Mathew S. Fuzzy End Nodes in Fuzzy Incidence Graphs. New Math Nat Comput (2017) 13(3):13–20. doi:10.1142/s1793005717500028

CrossRef Full Text | Google Scholar

6. Mordeson JN, Mathew S. Human Trafficking: Source, Transit, Destination, Designations. New Math Nat Comput (2017) 13(3):209–18. doi:10.1142/s1793005717400063

CrossRef Full Text | Google Scholar

7. Mordeson JN, Mathew S, Borzooei RA. Vulnerability and Government Response to Human Trafficking: Vague Fuzzy Incidence Graphs. New Math Nat Comput (2018) 14(2):203–19. doi:10.1142/s1793005718500138

CrossRef Full Text | Google Scholar

8. Samanta S, Pal M. Fuzzy K-Competition Graphs and P-Competition Fuzzy Graphs. Fuzzy Inf Eng (2013) 5:191–204. doi:10.1007/s12543-013-0140-6

CrossRef Full Text | Google Scholar

9. Samanta S, Akram M, Pal M. m-Step Fuzzy Competition Graphs. J Appl Math Comput (2014) 47(1-2):461–72. doi:10.1007/s12190-s12014-s10785-s10782

CrossRef Full Text | Google Scholar

10. Samanta S, Pal M. Irregular Bipolar Fuzzy Graphs. Int J Appl Fuzzy Sets (2012) 2:91–102.

Google Scholar

11. Akram M, Naz S. Energy of Pythagorean Fuzzy Graphs with Applications. Mathematics (2018) 6:136. doi:10.3390/math6080136

CrossRef Full Text | Google Scholar

12. Akram M, Sitara M. Certain Concepts in Intuitionistic Neutrosophic Graph Structures. Information (2017) 8:154. doi:10.3390/info8040154

CrossRef Full Text | Google Scholar

13. Ramakrishna N. Vague Graphs. Int J Comput Cogn (2009) 7:51–8.

Google Scholar

14. Rashmanlou H, Borzooei RA. Product Vague Graphs and its Applications. J Intell Fuzzy Syst (2016) 30:371–82. doi:10.3233/ifs-162089

CrossRef Full Text | Google Scholar

15. Kosari S, Rao Y, Jiang H, Liu X, Wu P, Shao Z. Vague Graph Structure with Application in Medical Diagnosis. Symmetry (2020) 12(10):1582. doi:10.3390/sym12101582

CrossRef Full Text | Google Scholar

16. Rao Y, Kosari S, Shao Z. Certain Properties of Vague Graphs with a Novel Application. Mathematics (2020) 8:1647. doi:10.3390/math8101647

CrossRef Full Text | Google Scholar

17. Rao Y, Kosari S, Shao Z, Cai R, Xinyue L. A Study on Domination in Vague Incidence Graph and its Application in Medical Sciences. Symmetry (2020) 12:1885. doi:10.3390/sym12111885

CrossRef Full Text | Google Scholar

18. Rao Y, Chen R, Wu P, Jiang H, Kosari S. A Survey on Domination in Vague Graphs with Application in Transferring Cancer Patients between Countries. Mathematics (2021) 9(11):1258. doi:10.3390/math9111258

CrossRef Full Text | Google Scholar

19. Shao Z, Kosari S, Rashmanlou H, Shoaib M. New Concepts in Intuitionistic Fuzzy Graph with Application in Water Supplier Systems. Mathematics (2020) 8:1241. doi:10.3390/math8081241

CrossRef Full Text | Google Scholar

20. Shao Z, Kosari S, Shoaib M, Rashmanlou H. Certain Concepts of Vague Graphs with Applications to Medical Diagnosis. Front Phys (2020) 8:357. doi:10.3389/fphy.2020.00357

CrossRef Full Text | Google Scholar

21. Borzooei RA, Rashmanlou H. Semi Global Domination Sets in Vague Graphs with Application. J Intell Fuzzy Syst (2015) 7:16–31. doi:10.3233/IFS-162110

CrossRef Full Text | Google Scholar

22. Borzooei R, Rashmanlou H. Domination in Vague Graphs and its Applications. Ifs (2015) 29:1933–40. doi:10.3233/ifs-151671

CrossRef Full Text | Google Scholar

23. Borzooei RA, Rashmanlou H. Degree of Vertices in Vague Graphs. J Appl Math Inform (2015) 33:545–57. doi:10.14317/jami.2015.545

CrossRef Full Text | Google Scholar

24. Borzooei RA, Rashmanlou H, Samanta S, Pal M. Regularity of Vague Graphs. Ifs (2016) 30:3681–9. doi:10.3233/ifs-162114

CrossRef Full Text | Google Scholar

25. Ore O. Theory of Graphs, Vol. 38. Providence: American Mathematical Society Publications (1962).

26. Somasundaram A, Somasundaram S. Domination in Fuzzy Graphs - I. Pattern Recognition Lett (1998) 19(9):787–91. doi:10.1016/s0167-8655(98)00064-6

CrossRef Full Text | Google Scholar

27. Nagoorgani A, Mohamed SY, Hussain RJ. Point Set Domination of Intuitionistic Fuzzy Graphs. Int J Fuzzy Math Archive (2015) 7(1):43–9.

Google Scholar

28. Nagoorgani A, Chandrasekaran VT. Domination in Fuzzy Graphs. Adv Fuzzy Sets Syst (2006) I(1):17–26. doi:10.1016/S0167-8655(98)00064-6

CrossRef Full Text | Google Scholar

29. Parvathi R, Thamizhendhi G. Domination in Intuitionistic Fuzzy Graph. Proc 14th Int Conf Intuiyionistic Fuzzy Graphs, Notes Intuitionistic Fuzzy Sets (2010) 16(2):39–49. doi:10.1007/S12190-015-0952-0

CrossRef Full Text | Google Scholar

30. Cockayne EJ, Favaron O, Payan C, Thomason AG. Contributions to the Theory of Domination, independence and Irredundance in Graphs. Discrete Math (1981) 33(3):249–58. doi:10.1016/0012-365x(81)90268-5

CrossRef Full Text | Google Scholar

31. Haynes TW, Hedetniemi S, Slater P. Fundamentals of Domination in Graphs. Boca Raton: CRC Press (2013).

32. Zadeh LA. Fuzzy Sets. Inf Control (1965) 8:338–53. doi:10.1016/s0019-9958(65)90241-x

CrossRef Full Text | Google Scholar