Manipulation of Multielectron Dynamics of Molecules by Fourier-Synthesized Intense Laser Pulses: Effective Potential Analysis of CO

We present a theoretical investigation as to how multielectron dynamics of CO are manipulated by Fourier-synthesized intense laser pulses. The pulses used are assumed to be comprised of harmonics up to the fourth order. The multiconfiguration time-dependent (TD) Hartree-Fock (MCTDHF) method, where the multielectron wavefunction $\Psi \left(t\right)$ is expressed as a linear combination of various electron configurations, is employed to simulate the dynamics of CO interacting with Fourier-synthesized pulses. The multielectron nature such as electron correlation is quantified by using our effective potential approach. To begin with, the time-dependent natural orbitals $\left\{{\varphi }_j(\mathit{r},t)\right\}$ which diagonalize the first order reduced density matrix are obtained from $\Psi \left(t\right)$, where r is the one-electron coordinate. The effective potentials ${\mathit{\upsilon }}_j^{\text{eff}}(\mathit{r},t)$ that determine the dynamics of ${\varphi }_j(\mathit{r},t)$ are then derived from the equations of motion for $\left\{{\varphi }_j(\mathit{r},t)\right\}$. ${\mathit{\upsilon }}_j^{\text{eff}}(\mathit{r},t)$ consists of the one-body part ${\mathit{\upsilon }}_1\left(t\right)$ including the interaction with the laser electric field $\mathit{\epsilon }\left(t\right)$ and the two-body part ${\mathit{\upsilon }}_{2,j}\left(t\right)$ originating from electron-electron interaction. In this way, the role of electron correlation can be quantified by comparing ${\mathit{\upsilon }}_j^{\text{eff}}(\mathit{r},t)$ with those obtained by the TDHF method, where $\Psi \left(t\right)$ is approximated by a single Slater determinant. We found a very similar profile in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$ of the 5σ highest occupied molecular orbital for both near-infrared one-color (ω) and directionally asymmetric ω+2ω two-color pulses; when $\mathit{\epsilon }\left(t\right)$ points from the nucleus C to O, a hump appears in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$ only 2 bohrs outward from C. The hump formation, which originates from the field-induced change in υ_2,5σ(t) (especially, due to electron correlation), is responsible for preferential electron ejection from the C atom side (experimentally observed anisotropic ionization). A coherent superposition of ω and 2ω fields with an appropriate relative phase thus works as a one-color pulse of which either positive or negative peaks are filtered out. More sophisticated manipulation is possible by adding higher harmonics to a synthesized field. We show that the 5σ orbital can be squeezed toward the inside of the potential valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$, which encloses the molecule at a radius of ∼7 bohrs (semicircle in the region of z <0), by adjusting the phases of a ω+2ω+3ω+4ω field. The hump and valley formation in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$ are closely correlated with domains of increasing and decreasing electron density, respectively.

Introduction

Coherence is the succinct but vital word in modern science that features a wave of definite phase such as a laser field. The coherence of light [1] can be engraved in matter. Interaction of a coherent laser field with matter induces unique phenomena such as molecular alignment [2, 3] and high-order harmonic generation (HHG) of emission by intense near-infrared laser pulses [4]. Molecules can be aligned by intense near-infrared (IR) laser fields along a given space-fixed axis or plane, depending on the choice of light polarization through the anisotropic interaction of the electric field vector of intense laser radiation with the induced dipole moment. For a polarizable molecule, the major principal axis of the polarizability tensor is forced parallel to the polarization direction of a linearly polarized laser field. The mechanism of HHG is associated with the dynamics of an electron in field-dressed continuum states: Electrons freed by tunnel ionization (TI) [5–7] are pulled away from, pulled back near to, and recollided with parent ions within one optical cycle (the well-known three-step model [8]), while synchronized with the oscillating field. High energy photons even up to the soft x-ray range are emitted upon radiative recombination of an electron in field-driven quiver motion with the parent ion. In HHG, electronic continuum states in atoms or molecules are coherently excited with certain phases (described by a linear superposition of states), which leads to quantum interference between different electron trajectories (such as short and long trajectories) in the applied laser field [9, 10]. The HHG intensity is provided by the Fourier components of the induced dipole moment associated with individual trajectories. Coherent electronic motion in an ensemble of atoms or molecules, characterized by a definite dipole phase, is prerequisite for coherent emission of soft x-rays.

Phase coherence is the key concept in the optical control of quantum systems with high accuracy. Constructive and destructive interference between the wave packets created by a phase-locked pump-probe sequence can be controlled by varying the delay between the two pulses with interferometric precision [11, 12]. Various schemes for the control of optical phases have been devised to manipulate the wave functions or dynamics of quantum systems directly through the coherent nature of a laser field. This extensively growing research area is called coherent (or quantum) control [13–15]. Among various coherent control scenarios is utilization of a two-color phase-controlled laser field consisting of fundamental light and its harmonic light, which has been theoretically explored by Brumer and Shapiro [14]. For laser fields of moderate light intensity (below ∼10¹² W/cm²), the population of a target state $|f\rangle$ can be controlled through quantum interference between two photo-induced transitions to $|f\rangle$, which is achieved by adjusting the relative phase between fundamental and harmonic fields [14]. In contrast, for the high intensity regime (above ∼10¹² W/cm²), phase-controlled two-color fields can steer the motion of charges or dipoles with large amplitude. Such intense fields are used to induce asymmetric dynamics such as selective C-O bond breaking of ionized CO₂ [16, 17] and also to control the nonlinear coherent motion in TI [18–27] or HHG [28–31] of atoms and molecules.

An ultimate extension of this kind of methodology is Fourier synthesis of arbitrary light waveforms constructed of a fundamental frequency of light and its harmonics [32]. Sophisticated Fourier syntheses of laser fields have been reported [33–36]. Light wave engineering based on Fourier synthesis enables precise manipulation of electron motion beyond the case of single-frequency excitation; e.g., trajectory control of the HHG electrons in atoms and molecules by intense laser fields with various waveforms has been investigated theoretically [37] and achieved experimentally [38, 39]. Directionally asymmetric molecular TI induced by Fourier-synthesized four-color laser fields, consisting of fundamental, second-, third-, and fourth-harmonic light, can make possible orientation-selective molecular TI [40–43].

For a few-cycle single-frequency (one-color) pulse, carrier-envelope phase (CEP), i.e., the phase between the carrier wave and envelope peak of the pulse, also plays a significant role in electron dynamics such as TI and HHG. CEP stabilization has been achieved by the active feedback control which uses the combination of an f-to-2f interferometer to detect CEP drifts and a stereo-ATI (Above Threshold Ionization) phasemeter [44] to determine the value of CEP [45–48]. Few-cycle intense laser pulses with a stable CEP enable one to steer the electronic motion of atoms and molecules with an ultimate precision. Consequently, the HHG spectrum exhibits unique features depending on the CEP [49, 50].

Intense laser fields of light intensity above I≈10¹²–10¹³ Wcm⁻² initiate large amplitude electronic motion in atoms, molecules, etc., which triggers various physical or chemical phenomena in a wide range of timescale. Such systems can then be excited to high-lying electronic states or ionized in a nonperturbative manner. A typical phenomenon is TI, which is the source of the HHG upon recombination with the parent ion, as mentioned above. TI occurs mainly in the sub-femotosecond or attosecond (1 as = 10^–18 s) region, owing to a highly nonlinear optical response, when the electric field of the laser reaches its maximum values. A number of experimental and theoretical studies have been devoted to profoundly understanding the intense-field induced electron dynamics in atoms [51], molecules [52], solids [53], and biological systems [54].

Different types of theoretical approaches beyond perturbation theory have been developed to deal with nonperturbative electronic dynamics of molecules. Epoch-making is the one proposed by Keldysh [55], in which the intense-field ionization rate or probability of an atom is formulated as an electronic transition from the ground state to continuum states of an electron liberated in a driving laser electric field (Volkov states) [56]. In this approach, the detailed atomic energy structure, such as information on excited states or electron correlation, is not taken into account and the Coulomb interaction of the released electron in the laser field with the remaining ion core is neglected. In the Perelemov-Popov-Terent'ev (PPT) approach [57], the long-range Coulomb interaction is incorporated into the Keldysh approach as the first-order correction in the quasi-classical action of the electron. These types of approaches can be integrated into S-matrix theory in which the transition amplitude of a quantum process is formulated by the projection of the total wave function of the system onto the final state. Several versions of the S-matrix approach have been developed which are together known as the Keldysh-Faisal-Reiss (KFR) theory or Strong Field Approximation (SFA) [58, 59].

Ionization induced by intense fields is characterized by the Keldysh parameter $\gamma =\left(\omega /f_{\max }\right){\left(2I_{\text{P}}\right)}^{1/2}$ [55] (in atomic units), where $\omega$ is the angular frequency of the applied laser electric field $\mathit{\epsilon }\left(t\right)$, $f_{\max }$ is the maximum of the envelop $f\left(t\right)$ of $\mathit{\epsilon }\left(t\right)$ and $I_{\text{P}}$ is the ionization potential of the system. As $f\left(t\right)$ becomes larger and/or its optical period $2\pi /\omega$ becomes longer (i.e., $\gamma <1$), an electron penetrates (or goes beyond) the “quasistatic” distorted barrier for ionization before the sign of the laser field reverses. The opposite case of $\gamma >1$ is the multiphoton regime. In the case of $\gamma <1$, the Ammosov–Delone–Krainov (ADK) model [60], which is the quasistatic limit $\gamma \to 0$ of the PPT approach, is most commonly used for atoms. A molecular version of the ADK model is developed by Lin et al. (called MO-ADK theory) [61].

In the above theoretical approaches, only one atomic or molecular orbital is considered as the main ionizing orbital and is allowed to interact with the applied field [61–63]. This is the so-called single active electron (SAE) approximation, where the time-dependent (TD) Schrödinger equation to be solved for the least-bound one-electron is constructed by modelling an “effective potential” after the interaction with the remaining electrons, the nuclei, and the applied fields. In [64, 65], model effective potentials for the ionizing orbital of a CO molecule were constructed by semiempirically formulating the dynamic multielectron polarization effects induced by the applied field [66–68]. The TD version of the Hartree-Fock (HF) method, which is a first-principles approach, can be used to describe the time evolution of a multielectron system (beyond the above SAE approximation). In this TDHF, the multielectron wave function $\Psi \left(t\right)$ at time t is however approximated by a single Slater determinant and the atomic or molecular orbitals involved therein evolve in time under the mean field approximation for electron-electron interaction; electron correlation (correlated electron motion) is thus not taken into account, as in the case of the HF method.

Correlated multielectron dynamics such as simultaneous double ionization of atoms and molecules is currently one of the primary targets in the research field of attosecond science [50, 52, 69, 70]. Among related subjects are correlated intramolecular electron dynamics [71, 72] and channel interference in HHG [73]. To describe such dynamics properly, one has to go beyond the computationally inexpensive SAE approximation or TDHF method. The multiconfiguration time-dependent Hartree-Fock (MCTDHF) method [74–83] has been developed in the past two decades as a legitimate method for including electron correlation in dynamics. In the MCTDHF, the multielectron wave function $\Psi \left(t\right)$ is expanded in terms of Slater determinants corresponding to various electron configurations, as in the case of time-independent quantum chemistry; both the orbitals and the coefficients of Slater determinants are optimized in compliance with TD variational schemes such as the Dirac-Frenkel variational principle [84, 85]. As the number of Slater determinants used increases, the quantitative accuracy is systematically improved.

As the level of the theory employed is higher, numerical results obtained become more detailed and reliable; accordingly, what is acquired to unveil the intrinsic physics underlying behind the numerical results becomes more complicated. The TD orbitals in the MCTDHF method evolves under the effects of electron correlation, but it is hard to extract the information of electron correlation from the time evolution of each orbital. For example, the temporal change in MCTDHF orbitals cannot be linearly decomposed into the change due to the one-body interaction (interaction of an electron with nuclei and external fields) and that due to the two-body interaction.

In our previous papers [86–90], a novel approach, i.e., a single orbital picture was established under the framework of the MCTDHF. We adopted the representation of TD natural spin-orbitals (SOs) $\left\{{\varphi }_j\left(t\right)\right\}$ (see, for the natural SO, [91]), which diagonalizes the first-order reduced density matrix of electrons constructed from the MCTDHF multielectron wave function $\Psi \left(t\right)$. The orbital-dependent effective potentials $\left\{{\mathit{\upsilon }}_j^{\text{eff}}\left(t\right)\right\}$ that govern the time evolution of $\left\{{\varphi }_j\left(t\right)\right\}$ under the influence of electron correlation were then derived as a function of the spatial coordinate of an electron, r [88–90]. The obtained effective potential ${\mathit{\upsilon }}_j^{\text{eff}}(\mathit{r},t)$ for ${\varphi }_j\left(t\right)$ can be partitioned into ${\mathit{\upsilon }}_j^{\text{eff}}\left(t\right)=$${\mathit{\upsilon }}_1\left(t\right)+{\mathit{\upsilon }}_{2,j}\left(t\right)$, where ${\mathit{\upsilon }}_1\left(t\right)$ is the one-body interaction and ${\mathit{\upsilon }}_{2,j}\left(t\right)$ originates from the two-body interaction between electrons. We have investigated the mechanisms of the directional anisotropy in intense-field induced ionization of heteronuclear diatomic molecules CO [88–90] and LiH [90] by scrutinizing the temporal change in their effective potentials. The results of CO effective potentials are summarized in the second last paragraph of this section.

Directional anisotropy in the intense-field induced ionization of CO has been extensively investigated [20, 21, 26, 92] by using space-asymmetric ω+2ω two-color fields. The emission direction of C⁺ or O⁺ from CO in two-color field ionization experiments indicates that ionization is enhanced when the laser electric field $\mathit{\epsilon }\left(t\right)$ points from C to O [20, 21, 26, 92] (ionization from the C atom side). Intense-field ionization of CO mainly proceeds from the highest occupied molecular orbital (HOMO). It has been suggested, e.g., in the SAE approximation or single active orbital treatment [20, 21, 26, 61] that for CO the large-amplitude lobe of the HOMO around C is the origin of the preferential TI from C.

The direction of anisotropic ionization does not always agree with the prediction based solely on the shape of the HOMO. For OCS, the HOMO has a large amplitude around the C-S axis but ionization in a circularly polarized field is enhanced when the electric field turns to the direction from O to S [93]. This anisotropy is attributed to the linear Stark effect for polar molecules which increases (or reduces) the ionization potential of HOMO when $\mathit{\epsilon }\left(t\right)$ is parallel (or antiparallel) to the HOMO permanent dipole moment. In the linearly polarized ω+2ω two-color experiment reported by Ohmura et al. [27], the preferential direction was however from the S atom side (opposite to the case for circularly polarized pulses [93]). The linear Stark effect on intense-field-induced ionization has yet to be fully elucidated [94–100].

The results obtained by the conventional MO-ADK theory [61] are in agreement with the experimental result that the ionization rate of the HOMO of CO takes the maximum when $\mathit{\epsilon }\left(t\right)$ points from C to O. The Stark-shift-corrected MO-ADK theory, on the contrary, indicates the opposite trend [21], which directly reflects the tendency that the linear Stark effect increases the ionization potential of CO when $\mathit{\epsilon }\left(t\right)$ points from C to O and is therefore apt to reduce the HOMO ionization rate from the C atom side. The prediction by the Stark-shift-corrected molecular SFA [21] is in accord with the experimental observation. The diversity of theoretical predictions requires further investigation of the anisotropic ionization of CO.

Among other relevant factors to be considered for intense field ionization are the combined contribution from multiple orbitals [101, 102], field-induced multielectron correlation effects [87], and dynamic electron polarization [64, 99]. Although the emission direction of C⁺ or O⁺ from CO in the two-color ionization experiments [20, 21, 26] suggests that the main channel of the TI in CO is the 5σ HOMO, next lower lying orbitals such as 1π HOMO-1 and 4σ HOMO-2 can contribute to the ionization yield [88, 101]. These factors also affect the HHG process. The effects of dynamic electron polarization on HHG have also been discussed in [103, 104].

In previous studies [88–90], we calculated the effective potentials for natural orbitals of CO in an intense near-IR field (λ = 760 nm, I = 10¹⁴ Wcm⁻²) from the MCTDHF wave function and investigated the mechanism of anisotropic ionization of CO. The analysis of the 5σ HOMO effective potential ${\upsilon }_{5\sigma }^{\mathrm{eff}}\left(t\right)={\upsilon }_1\left(t\right)+{\upsilon }_{\mathrm{2,5}\sigma }\left(t\right)$ obtained indicates that when $\mathit{\epsilon }\left(t\right)$ points to the direction from C to O, TI from the C atom side is enhanced and a thin hump barrier then emerges in ${\mathit{\upsilon }}_1\left(0\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\mathit{\sigma }}\left(t\right)$. A hump formed in ${\upsilon }_{5\sigma }^{\mathrm{eff}}\left(t\right)$, of which the location is only 2 bohrs away outside from the nucleus C, originates from the interaction between the electron leaving the ion core and the electrons swarming to the region of hump formation (ionization exit). We attributed the origin of the anisotropic TI in CO to this thin hump barrier, through which an ionizing electron penetrates. This kind of hump structure due to electron correlation is general and cannot be described by the TDHF. We simulated the dynamics of LiH interacting with an intense pulse of λ = 1,520 nm, which also indicates that a hump structure emerges in the 2σ HOMO effective potential and brings about anisotropic ionization.

We have so far shown how useful the effective potential approach is to unveil the intrinsic nature of multielectron dynamics [88–90]. In this paper, we examine the role of electron-electron interaction or electron correlation in CO interacting with Fourier-synthesized intense laser pulses by monitoring the temporal change in effective potentials, though the effective potential itself comes from a single-electron picture. The structure of this paper is as follows. The MCTDHF method for the calculation of multielectron dynamics is outlined in Methodology for Effective Potential, together with a brief derivation of the effective potentials for time-dependent natural orbitals. The results and discussion on the ionization and multielectron dynamics of CO in one-color to four-color phase-controlled fields are presented in Results and Discussion. Finally, conclusions about the manipulation of multielectron dynamics of CO by Fourier-synthesized pulses are given in Conclusion.

Methodology for Effective Potential

In this section, we outline the MCTDHF method developed for the simulation of multielectron dynamics of atoms and molecules. In our approach, the multielectron wave function $\Psi \left(t\right)$ of a target system is obtained by numerically solving the equations of motion (EOMs) for time-dependent SOs and configuration interaction (CI) expansion coefficients in the MCTDHF method. We then convert the set of SOs in $\Psi \left(t\right)$ to an appropriate set of natural orbitals. The effective potential for each natural orbital is derived from the EOMs for natural orbitals; in this way, the role of multielectron dynamics or electron correlation can be quantified in a single orbital picture.

Outline of the Multiconfiguration Time-Dependent Hartree-Fock Method

The dynamics of an N_e-electron system is governed by the TD Schrödinger equation for the wave function $\Psi \left(t\right)$

$i\hslash \frac{\partial \Psi \left(t\right)}{\partial t}=\widehat{H}\left(t\right)\Psi \left(t\right)(1)$

where $\widehat{H}\left(t\right)$ is the total electronic Hamiltonian including the interaction with the applied radiation field $\mathit{\epsilon }\left(t\right)$. We solve Eq. 1 by using the MCTDHF method where $\Psi \left(t\right)$ is approximated as a liner combination of different electron configurations $\left\{{\Phi }_I\left(t\right)\right\}$ (represented by Slater determinants or configuration state functions) [74–83]:

$\Psi \left(t\right)={\displaystyle \sum _{I=1}^M{C}_I\left(t\right){\Phi }_I\left(t\right)}(2)$

where $C_I\left(t\right)$ are the CI coefficients for ${\Phi }_I\left(t\right)$ and M is the total number of ${\Phi }_I\left(t\right)$. Each electron configuration is constructed of $N_{\text{e}}$ spin-orbitals (SOs) $\left\{{\psi }_k\left(t\right)\right\}$; ${\psi }_k\left(t\right)$ is the product of a one-electron spatial orbital and a one-electron spin eigenfunction for the kth single-orbital state $|k\left(t\right)\rangle$. One may write ${\psi }_k\left(t\right)$ as ${\psi }_k\left(t\right)=\langle \mathit{x}|k\left(t\right)\rangle$, where $\mathit{x}$ consists of the spatial coordinate r and the spin coordinate μ of an electron. In the present study, the spin state of $\Psi \left(t\right)$ is assumed to be a singlet. The SOs used in the expansion of $\Psi \left(t\right)$ are here referred to as occupied orbitals. The number of the occupied orbitals, denoted by $N_{\text{o}}$, satisfies the relation $N_{\text{o}}\ge N_{\text{e}}$ in general; $N_{\text{o}}=N_{\text{e}}$ for TDHF.

The working EOMs for $\left\{{\psi }_k\left(t\right)\right\}$ and $\left\{C_I\left(t\right)\right\}$ have been derived by means of the Dirac-Frenkel TD variational principle [84, 85]:

$\langle \delta \Psi \left(t\right)|\left[\widehat{H}\left(t\right)-i\hslash \frac{\partial }{\partial t}\right]|\Psi \left(t\right)\rangle =0(3)$

where $\delta \Psi \left(t\right)$ represents possible variations of $\left\{{\psi }_k\left(t\right)\right\}$ and $\left\{C_I\left(t\right)\right\}$ in the wave function (2). The EOMs for $\left\{{\psi }_k\left(t\right)\right\}$ are derived by inserting $\langle \delta \Psi \left(t\right)|=\langle \partial \Psi \left(t\right)/\partial {\psi }_k|\delta {\psi }_k$ into Eq. 3, whereas the EOMs for CI-coefficients are derived by instead using $\langle \delta \Psi \left(t\right)|=\langle \partial \Psi \left(t\right)/\partial C_I|\delta C_I$. Once the EOMs for $\left\{{\psi }_k\left(t\right)\right\}$ and $\left\{C_I\left(t\right)\right\}$ are solved, various quantities such as the first-order reduced density matrix (1RDM) $\rho (\mathit{x},{\mathit{x}}^{\prime },t)$ can be calculated from $\left\{{\psi }_j\left(t\right)\right\}$ and $\left\{C_I\left(t\right)\right\}$.

$\rho (\mathit{x},{\mathit{x}}^{\prime },t)={\displaystyle \sum _{ij}^{N_{\text{O}}}{\mathit{A}}_{ij}\left(t\right){\psi }_i^{\ast }(\mathit{x},t){\psi }_j({\mathit{x}}^{\prime },t)}(4)$

where the (i, j) matrix element of the 1RDM, ${\mathit{A}}_{ij}\left(t\right)$, is expressed by using the annihilation operator ${\widehat{a}}_j\left(t\right)$ and creation operator ${\widehat{a}}_j^{†}\left(t\right)$ for an electron in each ${\psi }_j\left(t\right)$

${\mathit{A}}_{ij}\left(t\right)=\langle \Psi \left(t\right)|{\widehat{a}}_i^{†}\left(t\right){\widehat{a}}_j\left(t\right)|\Psi \left(t\right)\rangle (5)$

Up to this point, ${\mathit{A}}_{ij}\left(t\right)\ne 0$ in general ($\left\{{\psi }_k\left(t\right)\right\}$ are not natural orbitals). The expectation value $\mathit{u}\left(t\right)$ of any one-body operator $\widehat{\mathit{u}}$, such as the dipole moment operator $\widehat{\mathit{d}}$, is given by

$\mathit{u}\left(t\right)={\displaystyle \sum _{ij}^{N_{\text{O}}}{\mathit{A}}_{ij}\left(t\right)\langle {\psi }_i\left(t\right)|\widehat{\mathit{u}}|{\psi }_j\left(t\right)\rangle }(6)$

We now show briefly how to derive the effective potential for each SO. To begin with, we present in this paragraph the EOM for ${\psi }_k\left(t\right)$ derived in [88]:

$i\hslash \frac{\partial |{\psi }_k\left(t\right)\rangle }{\partial t}=\left[\widehat{h}\left(t\right)-\widehat{g}\left(t\right)\right]|{\psi }_k\left(t\right)\rangle +\widehat{Q}\left(t\right)\left[\widehat{g}\left(t\right)|{\psi }_k\left(t\right)\rangle +{\displaystyle \sum _{ij}^{N_{\text{O}}}{A}^{-1}{\left(t\right)}_{ki}{\widehat{V}}_{ij}(\mathit{r},t)|{\psi }_j\left(t\right)\rangle }\right](7)$

where $\widehat{h}\left(t\right)$ is the one-body Hamiltonian including the electric dipole interaction $\mathit{r}\cdot \mathit{\epsilon }\left(t\right)$, $\widehat{Q}\left(t\right)=1-{\displaystyle {\sum }_k^{N_{\text{O}}}|{\psi }_k\left(t\right)\rangle \langle {\psi }_k\left(t\right)|}$ is the projector onto the complement to the current orbital space $\left\{{\psi }_k\left(t\right)\right\}$, ${\widehat{V}}_{ij}(\mathit{r},t)$ represents the orbital coupling between i and j mediated by other orbitals [76] (which depends on $\left\{C_I\left(t\right)\right\}$), and $\widehat{g}\left(t\right)$ is to be determined so that the orthonormalization condition $\langle {\psi }_j\left(t\right)|{\psi }_k\left(t\right)\rangle ={\delta }_{jk}$ is maintained. Since Eq. 7 leads to the following relation

$i\hslash \langle {\psi }_j\left(t\right)|\frac{\partial }{\partial t}|{\psi }_k\left(t\right)\rangle =\langle {\psi }_j\left(t\right)|\left[\widehat{h}\left(t\right)-\widehat{g}\left(t\right)\right]|{\psi }_k\left(t\right)\rangle (8)$

the time propagation of $\left\{{\psi }_k\left(t\right)\right\}$ is unitary if $\widehat{g}\left(t\right)$ is a Hermitian operator like $\widehat{g}\left(t\right)={\displaystyle {\sum }_{mn}^{N_{\text{O}}}|{\psi }_m\left(t\right)\rangle g_{mn}\left(t\right)\langle {\psi }_n\left(t\right)|}$ with $g_{mn}\left(t\right)=g_{nm}^{\ast }\left(t\right)$. The EOM for $C_I\left(t\right)$, coupled with Eq. (7), contains $\left\{C_I\left(t\right)\right\}$, $\left\{g_{km}\left(t\right)\right\}$ and the matrix elements of electron-electron interaction among SOs [75–77]. We choose $\widehat{g}\left(t\right)=\widehat{h}\left(t\right)$ to ensure that solving the EOMs for $\left\{{\psi }_j\left(t\right)\right\}$ and $\left\{C_I\left(t\right)\right\}$ is numerically stable; then, because of $\langle {\psi }_i\left(t\right)|\partial {\psi }_j\left(t\right)/\partial t\rangle =0$ (for $i=j$ and $i\ne j$), the orthonormalization condition $\langle {\psi }_i\left(t\right)|{\psi }_j\left(t\right)\rangle ={\delta }_{ij}$ holds in the time-propagation of $|{\psi }_j\left(t\right)\rangle$.

How to Derive the Effective Potentials for Natural Orbitals

In the case of $\widehat{g}\left(t\right)=\widehat{h}\left(t\right)$, the off-diagonal elements of the 1RDM are in general nonzero, i.e., $A_{ij}\left(t\right)\ne 0$ for $i\ne j$. Diagonalization of the rhs of Eq. 4 is equivalent to find a unitary transformation which converts $\left\{{\psi }_j\left(t\right)\right\}$ to an orbital set $\left\{{\varphi }_j\left(t\right)\right\}$ that satisfies $A_{ij}\left(t\right)=0$ for $i\ne j$. These orbitals $\left\{{\varphi }_j\left(t\right)\right\}$ are called natural orbitals [91]. The diagonal element, $n_j\left(t\right)=A_{jj}\left(t\right)$, is the occupation number of ${\varphi }_j\left(t\right)$. For $\left\{{\varphi }_j\left(t\right)\right\}$, Eq. 6 becomes the sum of the diagonal ones ${\mathit{u}}_j\left(t\right)=\langle {\varphi }_j\left(t\right)|\widehat{\mathit{u}}|{\varphi }_j\left(t\right)\rangle$ as $\mathit{u}\left(t\right)={\displaystyle {\sum }_j^{N_{\text{O}}}{n}_j\left(t\right){\mathit{u}}_j\left(t\right)}$ [86, 87].

The elements $\left\{{\mathit{A}}_{km}\left(t\right)\right\}$ of Eq. 5 can be expressed by using CI-coefficients. We have derived the EOM for ${\mathit{A}}_{km}\left(t\right)$ in the natural orbital representation [88–90]:

$\frac{\text{d}{\mathit{A}}_{km}\left(t\right)}{\text{d}t}=-\frac{i}{\hslash }\left\{W_{mk}\left(t\right)-W_{km}^{\ast }\left(t\right)+g_{mk}\left(t\right)\left[n_k\left(t\right)-n_m\left(t\right)\right]\right\}(9)$

where $W_{km}\left(t\right)$ is given in atomic units by [105, 106]

$W_{km}\left(t\right)={\displaystyle \sum _{pqr}{\displaystyle \int \text{d}{\mathit{x}}_1\text{d}{\mathit{x}}_2{\varphi }_k^{\ast }\left({\mathit{x}}_1\right){\varphi }_q\left({\mathit{x}}_1\right){\left|{\mathit{r}}_1-{\mathit{r}}_2\right|}^{-1}{\varphi }_r^{\ast }\left({\mathit{x}}_2\right){\varphi }_p\left({\mathit{x}}_2\right)\langle \Psi \left(t\right)|{\widehat{a}}_m^{†}\left(t\right){\widehat{a}}_r^{†}\left(t\right){\widehat{a}}_p\left(t\right){\widehat{a}}_q\left(t\right)|\Psi \left(t\right)\rangle }}(10)$

We start with the natural orbitals at $t=t_0$, i.e., ${\psi }_j\left(t_0\right)={\varphi }_j\left(t_0\right)$, which are obtained from the MCTDHF wave function $\Psi \left(t\right)$ at $t=t_0$. To satisfy $A_{km}\left(t\right)=0$ at $t\ge t_0$ for $k\ne m$, we have to set $g_{mk}\left(t\right)$ for $m\ne k$ in Eq. 9 as

$g_{mk}\left(t\right)=\frac{W_{mk}\left(t\right)-W_{km}^{\ast }\left(t\right)}{n_m\left(t\right)-n_k\left(t\right)}(11)$

The constraint that $A_{km}\left(t\right)=0$ for $k\ne m$ does not fix the values of the diagonal elements $g_{kk}\left(t\right)$. The phases of $\left\{C_I\left(t\right)\right\}$ and the global phases of $\left\{{\varphi }_j\left(t\right)\right\}$ are consistently determined through Eq. 7 and EOMs for $\left\{C_I\left(t\right)\right\}$. For simplicity, we set the diagonal elements to be $g_{kk}\left(t\right)=0$.

By substituting Eq. 11 and $g_{kk}\left(t\right)=0$ into Eq. 7, we reach the EOMs for natural SOs [88]

$i\hslash \frac{\partial {\varphi }_k(\mathit{r},t)}{\partial t}=\left[\widehat{t}+{\mathit{\upsilon }}_k^{\text{eff}}(\mathit{r},t)\right]{\varphi }_k(\mathit{r},t)(12)$

where $\widehat{t}$ is the kinetic energy operator of an electron. Here, the one-body orbital-dependent effective potential ${\mathit{\upsilon }}_k^{\text{eff}}(\mathit{r},t)$, which determines the time evolution of ${\varphi }_k\left(t\right)$ under multielectron interaction, is comprised of the one-body term ${\mathit{\upsilon }}_1(\mathit{r},t)$ including the electric dipole interaction $\mathit{r}\cdot \mathit{\epsilon }\left(t\right)$ and the two-body interaction term υ_2,k(r,t):

${\mathit{\upsilon }}_k^{\text{eff}}\left(\mathit{r}\mathrm{,}t\right)={\mathit{\upsilon }}_1\left(\mathit{r}\mathrm{,}t\right)+{\displaystyle \sum _j^{N_{\text{O}}}\frac{\langle \mathit{r}|{\widehat{U}}_{kj}\left(t\right)|{\varphi }_j\left(t\right)\rangle }{{\varphi }_k\left(\mathit{r}\mathrm{,}t\right)}}={\mathit{\upsilon }}_1\left(\mathit{r}\mathrm{,}t\right)+\mathbf{ }{\mathit{\upsilon }}_{2,k}\left(\mathit{r}\mathrm{,}t\right)(13)$

where $\widehat{U}$_kj(t) is the coupling between ϕ_k(t) and ${\varphi }_j\left(t\right)$

${\widehat{U}}_{kj}\left(t\right)=\left(1-{\delta }_{kj}\right)\frac{W_{jk}\left(t\right)-W_{kj}^{\ast }\left(t\right)}{n_k\left(t\right)-n_j\left(t\right)}+Q\left(t\right)\frac{{\widehat{V}}_{kj}\left(t\right)}{n_k\left(t\right)}(14)$

We designate the expectation value of $\widehat{t}+{\mathit{\upsilon }}_k^{\text{eff}}\left(\mathit{r},t\right)$ over ${\varphi }_k\left(t\right)$ as a real-valued effective orbital energy $E_k\left(t\right)$. ${\upsilon }_k^{\text{eff}}(\mathit{r},t)$ is proved to be a Hermitian [88]. In practice, we calculate the “instantaneous” (orthonormal) natural orbitals $\left\{{\varphi }_j\left(t\right)\right\}$ at time t from $\left\{{\psi }_j\left(t\right)\right\}$ and $\left\{C_I\left(t\right)\right\}$ obtained under the condition of $\widehat{g}\left(t\right)=\widehat{h}\left(t\right)$. ${\mathit{\upsilon }}_k^{\text{eff}}(\mathit{r},t)$ can be plotted as a function of r by inserting $\left\{{\varphi }_j\left(t\right)\right\}$ and the corresponding $\left\{C_I\left(t\right)\right\}$ (different from those for $\widehat{g}\left(t\right)=\widehat{h}\left(t\right)$) into Eq. 13. Multielectron dynamics can be examined by plotting the temporal change in ${\mathit{\upsilon }}_1(\mathit{r},t)$ and that in ${\mathit{\upsilon }}_{2,k}(\mathit{r},t)$ separately. Electron correlation in dynamics can be quantified by the difference in ${\mathit{\upsilon }}_k^{\text{eff}}(\mathit{r},t)$ between TDHF and MCTDHF.

Results and Discussion

In addition to a one-color (ω) two-cycle pulse with different carrier-envelope phases [88–90], we theoretically investigated the response of CO to intense multicolor pulses; two-color (ω+2ω), three-color (ω+2ω+3ω), and four color (ω+2ω+3ω+4ω) pulses with different relative phases. We present the numerical results of ionization dynamics of a CO molecule interacting with the above four types of pulses to extract how laser field coherence affects multielectron dynamics from the spatial profiles of TD effective potentials of the 5σ HOMO natural orbital.

Applied Pulses

The C-O axis is assumed to be parallel to the polarization direction of the applied electric field $\mathit{\epsilon }\left(t\right)$. The frequency ω is chosen to be the fundamental of a Ti:Sapphire laser: here, $\hslash \omega =0.06E_{\text{h}}=$ 1.64 eV (wavelength λ = 760 nm), where E_h is the Hartree. The electric field of the one-color pulse, ${\mathit{\epsilon }}_1\left(t\right)$, is assumed to have the form:

${\mathit{\epsilon }}_1\left(t\right)=f\left(t\right)\cos \left(\omega t+{\phi }_1\right)(15)$

where ${\phi }_1$ is the CEP and $f\left(t\right)$ is the envelope function (The definition of ${\phi }_1$ is shifted by π, compared to that in [88–90]). For all pulses presented in this paper, we use the same shape for $f\left(t\right)$

$f\left(t\right)=F{\sin }^2\left(\pi t/2T_{\text{c}}\right)\text{for}0\le t\le 2T_{\text{c}}(16)$

and otherwise $f\left(t\right)=0$. Here $F$ is the maximum of $f\left(t\right)$ and $T_{\text{c}}=2\pi /\omega =$ 2.53 fs is the optical period for the fundamental. The pulse length is 5.06 fs for all pulses. If $f\left(t\right)=$ 0.0534 E_h/(ea₀) = 2.74 × 10¹⁰ Vm⁻¹, where e is the elementary charge and a₀ is the Bohr radius, the corresponding light intensity is $I=$ 1.0×10¹⁴ W cm⁻². We use the following general form for multi-color pulses:

$\epsilon \left(t\right)=f\left(t\right)\left[\cos \left(\omega t+{\phi }_1\right)+a_2\cos \left(2\omega t+{\phi }_2\right)+a_3\cos \left(3\omega t+{\phi }_3\right)+a_4\cos \left(4\omega t+{\phi }_4\right)\right](17)$

These four phases ${\phi }_1$,${\phi }_2$,${\phi }_3$, and ${\phi }_4$ are chosen so that the main profile of $\mathit{\epsilon }\left(t\right)$ is built in the middle of the pulse (Experimentally available is a pulse train of $\mathit{\epsilon }\left(t\right)$). ${\mathit{\epsilon }}_1\left(t\right)$ is given by setting $a_2=a_3=a_4=0$ in $\mathit{\epsilon }\left(t\right)$. $F$ in $f\left(t\right)$ is defined as

$F=F_T/\left(1+a_2+a_3+a_4\right)(18)$

where $F_T$ is determined so that the maximum peak $F_p$ of the electric field $\left|\mathit{\epsilon }\left(t\right)\right|$ is the same as $F_p=$ 0.0378 E_h/(ea₀) = 1.94×10¹⁰ Vm⁻¹ throughout this paper, unless otherwise noted. This field of $F_p$, which corresponds to I = 5.0×10¹³ Wcm⁻² in the case of one-color pulses, is weaker than in previous studies [88–90].

TD-CASSCF Calculation

In One-Color Pulses, Two-Color Pulses, Three-Color Pulses, Four-Color Pulses, we discuss the characteristic features of the ionization of CO for one- and multi-color pulses. The effects of electron correlation is in detail examined on the basis of the TD effective potentials for the 5σ natural orbitals obtained in the MCTDHF framework. We trace the temporal change in effective potentials to investigate how distinctly electron correlation influences the electronic dynamics.

In the numerical simulations for CO in one-color pulses of λ = 760 nm [88–90], we considered 10 spatial orbitals 1σ, 2σ, 3σ, 4σ, 2×1π, 5σ HOMO, 2×2π LUMO (lowest unoccupied molecular orbital) and 6σ. There is a limit to the number of molecular orbitals (MOs) that we can handle in practical applications of the MCTDHF. The most commonly used scheme is the complete active space (CAS) method, where the orbitals used in the Slater determinants (or configuration state functions) are divided into inactive (core) and active orbitals. The two inactive spin-orbitals (SOs) with the same spatial function are singly occupied respectively in all electron configurations; all possible electron configurations are generated by distributing the other electrons among the active orbitals. This type of expansion scheme is called the time-dependent complete-active-space self-consistent-field (TD-CASSCF) method [107, 108]. Various wave-function-based multiconfigurational TD approaches to the dynamics of indistinguishable particles are compiled in a recent review [109]. We adopted the following TD-CASSCF scheme in the present study; the lower lying core SOs up to 4σ were treated to be occupied by one electron and the shapes of the orbitals are allowed to vary according to the EOMs derived for the core SOs. The high lying 6 SOs, i.e., 2×1π, 5σ, 2×2π, 6σ, were treated as active orbitals that constitute the CAS to accommodate 14−8=6 electrons (the expansion length M = 400).

Since the molecular axis is parallel to the polarization direction, cylindrical symmetry is maintained; then, the cylindrical coordinates z and ρ are convenient for the numerical grid point representation of spatial orbitals; z is chosen parallel to the molecular axis. The nuclei C is placed at $z=$ −1.066 a₀ and O is placed at $z=$1.066 a₀ (ρ = 0). The C-O difference is equal to the equilibrium internuclear distance $R_{\text{e}}=$ 2.132 a₀. The parameters necessary to describe MOs such as grid intervals are given in [88]. To estimate the ionization probability, we simply set an absorbing boundary that eliminate outgoing ionizing currents from propagating molecular orbitals. The details are explained in [87, 88].

One-Color Pulses

The temporal change in induced dipole moments characterizes the overall electronic dynamics of a molecule. Shown in Figure 1A are the one-color pulse ${\mathit{\epsilon }}_1\left(t\right)$ (i.e., Eq. 15) with ${\phi }_1=0.5\pi$ and the induced dipole moment of the 5σ HOMO natural orbital ${\varphi }_{5\sigma }\left(t\right)$, denoted by $d_{5\sigma }\left(t\right)$. $F_T$ in Eq. 18 is chosen to be 0.04374 E_h/(ea₀) so that the maximum peak is the target value of $F_p=$ 0.0378 E_h/(ea₀) (of which the value is used in all figures except Figure 2D). Up to around the end of the first optical cycle, the electronic response is quasi-adiabatic with respect to temporal change in ${\epsilon }_1\left(t\right)$: the change in $d_{5\sigma }\left(t\right)$ is nearly proportional to ${\mathit{\epsilon }}_1\left(t\right)$. This quasi-adiabatic feature is related to the fact that the energies of the excited singlet states of CO are higher than 8.5 eV [110]. The total induced dipole moment is nearly proportional to $d_{5\sigma }\left(t\right)$. In the adiabatic regime, the induced dipole moment is represented by a function of the applied filed ${\epsilon }_1\left(t\right)$ (not necessarily a linear function of $\epsilon \left(t\right)$). In the second optical cycle, electrons go back and forth during a half cycle to some extent (continuum states are also involved); the response becomes nonadiabatic and more complex as the interaction proceeds.

FIGURE 1

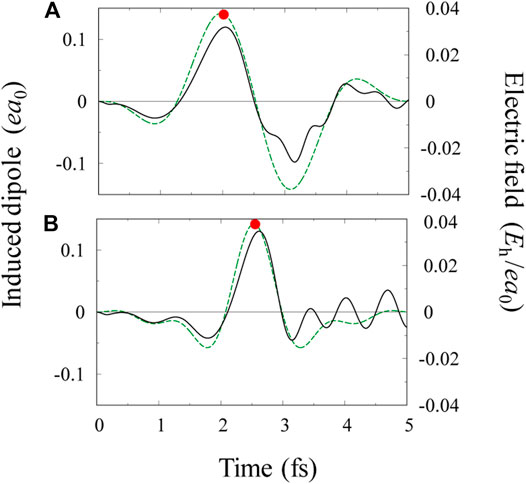
FIGURE 1. (A) Electric field profile ${\epsilon }_1\left(t\right)$ of the applied two-cycle pulse (15) of $\omega =0.06E_{\mathrm{h}}/\hslash$ with CEP of ${\phi }_1=0.5\pi$; (B) the asymmetric ω+2ω two-color field with ${\phi }_1={\phi }_2=0$ and $a_2=2/3$ (both are denoted by green broken lines). ${\epsilon }_2\left(t\right)$ is defined by Eq. 17. The value of $F_T$ in Eq. 18 is chosen to be 0.0437E_h/(ea₀) for ${\epsilon }_1\left(t\right)$ and 0.0378E_h/ea₀ for ${\epsilon }_2\left(t\right)$. The induced dipole moment $d_{5\sigma }\left(t\right)$ of the 5σ natural orbital of CO, obtained by TD-CASSCF, is superimposed in each panel (black solid lines).

FIGURE 2

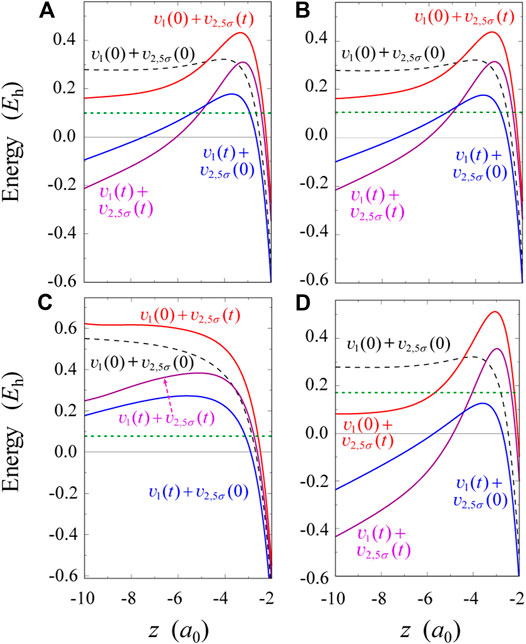
FIGURE 2. Four kinds of 5σ effective potentials plotted parallel to the z-axis at the fixed value of ρ = 0.755a₀: (A) potentials obtained by TD-CASSCF at t = t₁ ≈ 2 fs under the interaction with ${\epsilon }_1\left(t\right)$ in Figure 1A; (B) TD-CASSCF potentials at t ≈2.53 fs for ${\epsilon }_2\left(t\right)$ in Figure 1B; (C) TDHF potentials at t = t₁ ≈ 2 fs for ${\epsilon }_1\left(t\right)$, i.e., the same pulse as in Figure 1A; (D) TD-CASSCF potentials at t = t₁ ≈ 2 fs for the pulse (15) with a higher strength of $F_T$ = 0.06 E_h/(ea₀). ${\mathit{\upsilon }}_1\left(t\right)$ and ${\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ are respectively the one-body part and two-body part in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$. In each panel, the black broken, blue, red, and purple lines denote ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(0\right)$, ${\mathit{\upsilon }}_1\left(t\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(0\right)$, ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$, and ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)={\mathit{\upsilon }}_1\left(t\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$, repectively. For reference, the level of the effective orbital energy $E_{5\sigma }\left(t\right)$ is given by a green horizontal dotted line. The time point t at which the effective potentials are calculated is indicated by a red filled circle in each panel in Figure 1.

We have numerically confirmed that ionization exclusively occurs from the 5σ orbital when the electric field points from C to O, i.e., ${\epsilon }_1\left(t\right)>0$, for instance, at $t\approx$2 fs in Figure 1A. At ${\epsilon }_1\left(t\right)>0$, the electric field then exerts a force on electrons toward the direction from O to C. The calculated ionization rate around the second peak of ${\epsilon }_1\left(t\right)$ at $t\approx$2 fs is roughly a few times larger for ${\phi }_1=0.5\pi$ than for the phase reversed case of ${\phi }_1=-0.5\pi$ (The ionization from 5σ was significantly suppressed when ${\epsilon }_1\left(t\right)<0$.). This tendency, already found in the case of $F_T$∼0.06 E_h/(ea₀) [88], is in agreement with the experimentally observed anisotropy [26]. A criterion as to whether the ionization is adiabatic or not is given by the Keldysh parameter γ. For the pulse ${\epsilon }_1\left(t\right)$, γ∼1.6. It has been reported that TI remains as the dominant mechanism up to γ ∼3 for few-cycle laser pulses [111]. The ionization process for ${\epsilon }_1\left(t\right)$ is thus categorized as TI.

The origin of anisotropic ionization of CO in near-IR fields has been argued mostly in connection with the fact that the 5σ HOMO natural orbital has a large lobe around the C atom. In what follows, we examine what role electron correlation plays in the anisotropic ionization process. We investigate the mechanism of anisotropic near-IR induced ionization of CO by tracing the TD effective potentials of natural orbitals, defined by Eq. 13, which are changing every moment. More generally, the (correlated) multielectron nature intrinsic in intense-field-induced phenomena can be extracted from the analysis of the temporal change in the effective potential of each natural orbital.

Figure 2 display different types of 5σ HOMO effective potentials ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)=$${\mathit{\upsilon }}_1\left(t\right)+{\mathit{\upsilon }}_{2,5\sigma }\left(t\right)$ for four cases, which are one-dimensional cuts parallel to the z-axis. The value of ρ is fixed at ρ = 0.755a₀, around which the electron density integrated over z takes a maximum. For the pulse in Figure 1A with ${\phi }_1=0.5\pi$, the effective potentials at $\mathit{t}\approx {\mathit{t}}_1=$ 2 fs obtained by TD-CASSCF are shown in Figure 2A and those obtained by TDHF (M = 1) are shown in Figure 2C. The electric field ${\mathit{\epsilon }}_1\left(t\right)$ at $\mathit{t}\approx {\mathit{t}}_1$ points from C to O for the case of ${\phi }_1=0.5\pi$ (i.e., $\epsilon \left(t_1\right)>0$). The one-body part ${\mathit{\upsilon }}_1\left(t\right)$ changes according to the dipole interaction, i.e., ${\mathit{\upsilon }}_1\left(t\right)={\mathit{\upsilon }}_1\left(0\right)+z{\mathit{\epsilon }}_1\left(t\right)$; ${\mathit{\upsilon }}_1\left(t_1\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(0\right)$ in Figures 2A,C therefore exhibit the same linear slant in the asymptotic region of large $\left|z\right|$. On the other hand, the change in ${\mathit{\upsilon }}_{2,5\sigma }\left(t\right)$ is distinctly different between the two methods. The effective potential of ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ obtained by TD-CASSCF has a hump around z = −3a₀ and crosses ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(0\right)$ at z ≈ −5a₀; ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ asymptotically approaches ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(0\right)$ as z goes negative. As a result, the total one ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t_1\right)={\mathit{\upsilon }}_1\left(t_1\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ in Figure 2A has also a hump (extra thin barrier) around z = −3a₀ in comparison with ${\mathit{\upsilon }}_1\left(t_1\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(0\right)$.

When the sign of ${\epsilon }_1\left(t\right)$ is reversed in the next half cycle at $t\approx t_2=$ 3 fs, the two-body part ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_2\right)$ monotonically increases up to z ≈11a₀ (${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t_2\right)$ is even slightly higher than ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(0\right)$ up to z ≈ 11a₀, albeit the presence of the applied electric field of $\epsilon {}_1\left(t_2\right)<0$). A tunnel barrier in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t_2\right)$ is thus formed in the region of z > 10a₀, far away from the nuclei. Long propagation is required for an electron to reach the barrier located at z ≈ 10a₀. We found that these features are responsible for the suppression of TI when ${\epsilon }_1\left(t\right)<0$ [88–90]. The fact that the tunnel barrier is far distant from the O atom when the electric field points from O to C can be also clearly demonstrated by the TD-CASSCF effective potential ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t_1\right)$ for the opposite case of ${\phi }_1=-0.5\pi$. For this choice of ${\phi }_1$, ${\epsilon }_1\left(t_1\right)<0$; the upward slope in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t_1\right)$ shifts downward around z ≈ 13a₀. Another example for the opposite CEP is shown in Figure 5 in [90] (where the field strength is about one and a half times of the present one). The temporal change in the spatial profile of ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ is consistent with the experimentally observed anisotropic TI of CO.

To quantify the role of electron correlation, we compare the effective potentials in Figure 2A with TDHF ones shown in Figure 2C. In Figure 2C, ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ increases gradually with decreasing z and is higher than ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(0\right)$ by a constant of ∼0.1E_h. Accordingly, ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t_1\right)$ is nearly parallel to ${\mathit{\upsilon }}_1\left(t_1\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(0\right)$. The tunnel barrier in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t_1\right)$ is higher and wider in Figure 2C than in Figure 2A. As expected from the tunnel barriers in Figures 2A,C the ionization probability obtained by TDHF was less than 1/30 of the TD-CASSCF value (∼0.0008 for the whole pulse of ${\epsilon }_1\left(t\right)$ with ${\phi }_1=0.5\pi$). More importantly, hump formation in ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ is not observed in Figure 2C. Hump formation is hence ascribed to the effects of multielectron interaction beyond the mean field approximation, i.e., the electron correlation originating from the interaction with the applied field. To grasp the appearance of the hump more comprehensively, we present 5σ effective potentials for a higher field strength of $F_T$=0.06 E_h/(ea₀) in Figure 2D [88–90]. Comparison in ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ between Figures 2A,D shows that the hump grows and the peak position in ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ slightly shifts toward the nucleus C with increasing field strength (${\epsilon }_1\left(t_1\right)>0$). The resulting thin barrier formed around z = −3a₀ in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t_1\right)$, which is not reproduced by TDHF, clearly indicates preferential ionization from the C atom side. The hump formation in ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ reflects the process that an electron penetrates through the potential barrier due to a field-induced local rise of electron density, of which area may be called an ionization exit.

In Four-Color Pulses, we provide a more concrete picture to understand the root of hump formation in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ and the mechanism of anisotropic ionization of CO.

Two-Color Pulses

The one-color field ${\epsilon }_1\left(t\right)$ is directionally symmetric: the absolute value of ${\epsilon }_1\left(t\right)$ is the same for its positive and negative extremes. The TOF fragment analyses of ω +2ω experiments for CO [20, 21, 26] have indicated that the ionization rate takes the maximum when the field points from C to O and takes the minimum when the field is reversed. To reveal more explicitly the correlation in anisotropy between the ionization of CO and the applied field, we here employ two-color fields that provide asymmetric fields. Figure 1B is an example of an asymmetric two-color field ${\epsilon }_2\left(t\right)$. The parameters in Eq. 17 are chosen for ${\epsilon }_2\left(t\right)$ as $a_2=2/3$, ${\phi }_1={\phi }_2=0$, and $F_T=F_p=$ 0.0378 E/ea₀ ($a_3=a_4=0$). The sign of the electric field ${\epsilon }_2\left(t\right)$ is reversed by setting ${\phi }_1={\phi }_2=\pi$. Similar parameter sets of ${\phi }_1$,${\phi }_2$, $a_2$ and $E_T$ are experimentally feasible as demonstrated in [20, 21, 26].

The largest peak in ${\epsilon }_2\left(t\right)$ of Figure 1B appears in the positive side. The central peak at t ≈ 2.53 fs is overwhelmingly high and the effects of the other peaks are expected to be minute. The induced dipole moment of the 5σ orbital, calculated by TD-CASSCF, is also plotted in Figure 1B, indicating that the orbital responds to the two-color field mainly near the central peak. The TD-CASSCF effective potential ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ at t ≈ 2.5 fs is shown in Figure 2B, which quantitatively agrees with that in the one-color case of Figure 2A. The positive peak of ${\epsilon }_2\left(t\right)$ in Figure 1B has therefore almost the same effect on ionization as the positive peak of ${\epsilon }_1\left(t\right)$ in Figure 1A does. The ionization probabilities for the pulses in Figures 1A,B are nearly the same as ∼0.0008. This results again suggests that the ionization probability induced by the negative peak is much smaller than that by the positive peak, under the assumption that the effects of individual peaks in ${\epsilon }_1\left(t\right)$ on TI are separable from each other. What ionization dynamics the positive or negative peak of a one-color pulse brings about can be separately examined by employing two-color pulses that are per se directionally asymmetric like ${\epsilon }_2\left(t\right)$. The ionization probability for the sign-reversed pulse, i.e., $-{\epsilon }_2\left(t\right)$, is about one-third as small as that for ${\epsilon }_2\left(t\right)$. This approach has already been realized experimentally, as mentioned above.

Three-Color Pulses

Multicolor fields can be used to manipulate the modulation between the peaks of the electric field. In this subsection, we present $d_{5\sigma }\left(t\right)$ and ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ for three-color pulses with relative amplitudes $a_2=2/3$ and $a_3=1/3$. Two three-color pulses and corresponding $d_{5\sigma }\left(t\right)$ are shown in Figures 3A,B. The relative phases and the intensity parameter $F_T$ in Eq. 18 are as follows: (A)${\phi }_2=-\pi /2$ and $F_T=0.0541$E_h/(ea₀); (B)${\phi }_2=\pi /2$, and $F_T=$ 0.0611E_h/(ea₀). For both cases, ${\phi }_1=-\pi /2$ and ${\phi }_3=\pi /2$. In the case of (A), the time difference between the negative maximum at t = 2.05 fs and positive maximum at t = 3.02 fs is 0.97 fs. This may be converted to an optical period as 2 × 0.97=1.94 fs, which is a little shorter than the period of a one-color field and longer than that of a two-color field, i.e., $2\pi /\left(2\omega \right)=$ 1.27 fs. For the case of (B), an additional wiggle intervenes between the negative maximum at t = 1.81 fs and positive maximum at t = 3.26 fs. The time difference between the two peaks corresponds to the optical period of 2 × 1.45=2.90 fs, which is slightly longer than the one-color period of T_c = 2.53 fs. The period of the wiggle around t = T_c is ∼0.8 fs, which corresponds to the period of a 3ω field, i.e., $2\pi /\left(3\omega \right)=0.84$ fs.

FIGURE 3

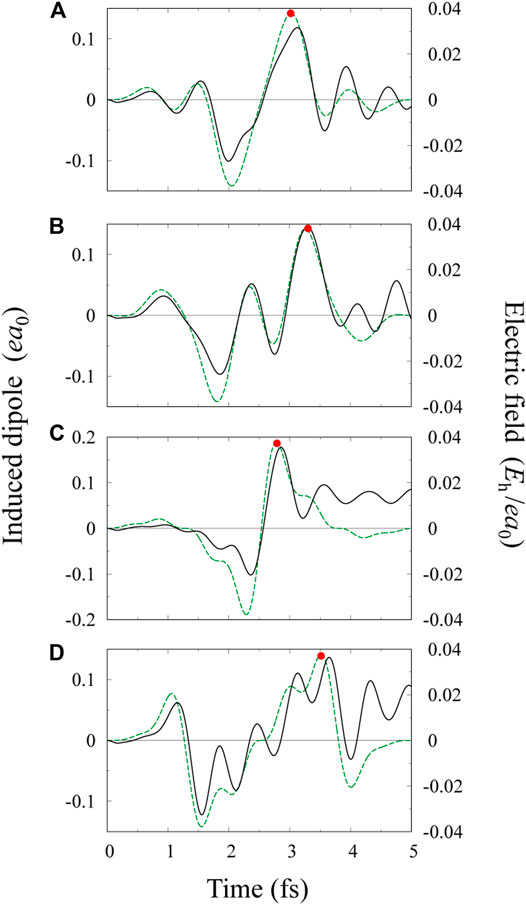
FIGURE 3. Electric field profiles for multi-color pulses (green broken lines): (A, B) three-color pulses with relative intensities $a_2=2/3$ and $a_3=1/3$; (C, D) four-color pulses with relative intensities $a_2=1/2$, $a_3=1/3$, and $a_4=1/4$. The relative pahses and the intensity parameter $F_T$ in Eq. 18 are given as follows: (A)${\phi }_1={\phi }_2=-\pi /2$,${\phi }_3=\pi /2$, and $E_T=0.0541$E_h/(ea₀); (B)${\phi }_1=-\pi /2$, ${\phi }_2={\phi }_3=\pi /2$, and $F_T=$ 0.0611E_h/(ea₀); (C)${\phi }_1={\phi }_2={\phi }_3={\phi }_4=-\pi /2$ and $F_T=$ 0.0528E_h/(ea₀); (D)${\phi }_1={\phi }_3=-\pi /2$, ${\phi }_2={\phi }_4=\pi /2$, and $F_T=$ 0.0778E_h/(ea₀). The induced dipole mements $d_{5\sigma }\left(t\right)$ of the 5σ natural orbital for each pulse, denoted by a black solid line, is obtained by TD-CASSCF.

The induced dipole moment $d_{5\sigma }\left(t\right)$ in Figure 3A shows a quasiadiabatic response and the maximum value is as large as in Figure 1A. Corresponding effective potentials of the 5σ HOMO at t ≈ 3.0 fs, shown in Figure 4A, are almost the same as in Figure 2A. These similarities to the case of the one-color pulse in Figure 1A may be attributed to the fact that the period between the main negative and positive peaks, i.e., 1.94 fs, is close to the period of one-color field, i.e., T_c = 2.53 fs. As a matter of fact, the ionization probability for the pulse in Figure 3A is nearly the same as that for ${\epsilon }_1\left(t\right)$ in Figure 1A. Although a wiggle intervenes between the main negative and positive peaks in the electric field in Figure 3B, the corresponding induced dipole moment $d_{5\sigma }\left(t\right)$ also behaves nearly adiabatic, especially around t = 3.3 fs,. The present calculation for CO indicates that the response to three-color pulses is still more or less adiabatic. The peaks in $d_{5\sigma }\left(t\right)$ nearly coincide temporally with the peaks of the applied three-color field. The adiabatic character of three-color pulses is consistent with the recently reported experimental results for CO using femtosecond ω +2ω +3ω laser fields [43], where the phase-dependent behavior of ionization was explained by the phase-dependence and directional anisotropy of the instantaneous maxima of applied three-color fields. The maximum value of $d_{5\sigma }\left(t\right)$ in Figure 3B is slightly larger than that in Figure 3A and the hump in ${\mathit{\upsilon }}_1\left(0\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ at t ≈3.3 fs in Figure 4B becomes more prominent, compared to Figure 2A or Figure 4A. The wiggle in the applied field of Figure 3B, which appears around t = 2.53 fs with a short period of ∼0.8 fs (≈the period of the 3ω field), exerts influence on the effective potential ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ at a later time t ≈ 3.3 fs, though the wiggle is relatively small and the overall response is almost adiabatic. The ionization barrier of ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ in Figure 4B is thus largely different from that of ${\mathit{\upsilon }}_1\left(t\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(0\right)$. The ionization probability for the pulse in Figure 3B is larger than that for Figure 3A. The former is ∼0.0013 and the latter is ∼0.0008.

FIGURE 4

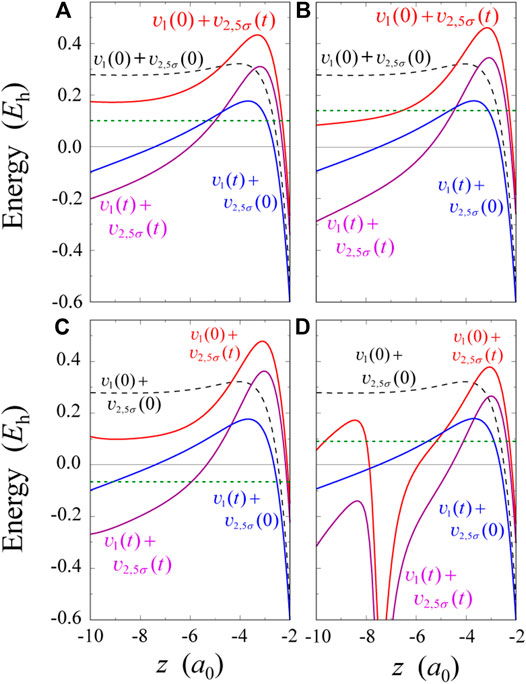
FIGURE 4. Four kinds of 5σ effective potentials plotted parallel to the z-axis at the fixed value of ρ = 0.755a₀. The pulses used in four panels (A–D) correspond to those in Figure 3(A–D), respectively. ${\mathit{\upsilon }}_1\left(t\right)$ and ${\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ are respectively the one-body part and two-body part in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$. The definitions of effective potentials are designated in each panel. The effective potentials in these panels are all calculated by TD-CASSCF. The green horizontal dotted line denotes the effective orbital energy $E_{5\sigma }\left(t\right)$. The time point at which the effective potentials are calculated is indicated by a red filled circle in each panel in Figure 3.

Four-Color Pulses

The effects of sawtooth wave forms on multielectron dynamics can be investigated by using four-color fields. The relative amplitudes are fixed as $a_2=1/2$, $a_3=1/3$, and $a_4=1/4$ in this subsection. We show the responses to two four-color pulses in Figures 3C,D: (C)${\phi }_2={\phi }_4=-\pi /2$ and $E_T=$ 0.0528E_h/(ea₀); (D) ${\phi }_2={\phi }_4=\pi /2$ and $E_T=$ 0.0778E_h/(ea₀). For both cases, ${\phi }_1={\phi }_3=-\pi /2$. These sets lead to $E_p=0.0378$E_h/(ea₀). In the case of Figure 3C, the time difference between the negative maximum at t = 2.29 fs and positive maximum at t = 2.78 fs is 0.49 fs. This may be converted to an optical period as 2×0.49 = 0.98 fs, which is shorter than the optical period of a two-color field and longer than that of a three-color field ($2\pi /\left(3\omega \right)=$ 0.84 fs). The electric field increases steeply and almost linearly from the negative maximum to the positive maximum. For the case of Figure 3D, an additional undulation intervenes between the negative maximum at t = 1.55 fs and positive maximum at t = 3.52 fs. The time difference between the two main peaks corresponds to the optical period of 3.94 fs, which is one and a half times as long as the one-color period of T_c = 2.53 fs. The period of the sawtooth-like undulation between the two peaks is 0.56 fs, which is close to the period of a 4ω field, i.e., $2\pi /\left(4\omega \right)=0.63$ fs.

The induced dipole moment $d_{5\sigma }\left(t\right)$ in Figure 3C behaves rather nonadiabatically even in the initial region up to t = 2 fs, though the appled field $\epsilon \left(t\right)$ as a whole seems a single cycle pulse with two dominant peaks at t = 2.29 fs and t = 2.78 fs. In fact, $d_{5\sigma }\left(t\right)$ in Figure 3C sensitively reflects how much high frequency components (in the present case, up to the fourth harmonic) are included in $\epsilon \left(t\right)$. Notice that the induced dipole moment $d_{5\sigma }\left(t\right)$ rises steeply from t ≈ 2.3 fs to t ≈ 2.8 fs, while the abolute value of $d_{5\sigma }\left(t\right)$ prior to the midpoint of the pulse (t = 2.53 fs) is relatively small. The maximum value of $d_{5\sigma }\left(t\right)$ at t ≈ 2.8 fs is as large as 0.18 ea₀, much larger than in the other cases of the same F_p. In Figure 3D, $d_{5\sigma }\left(t\right)$ increases with undulation from t = 1.55 fs to t = 3.52 fs, while reflecting the modulation in the applied pulse $\epsilon \left(t\right)$. The resulting undulation amplitude in $d_{5\sigma }\left(t\right)$ is much larger than that in $\epsilon \left(t\right)$, which indicates that the electron motion in ${\varphi }_{5\sigma }\left(t\right)$ is sensitive to the presence of high frequency componets in $\epsilon \left(t\right)$ even when the change in $\epsilon \left(t\right)$ is moderate. Peaks in $d_{5\sigma }\left(t\right)$ are delayed from the corresponding peaks in $\epsilon \left(t\right)$, which is a proof of nonadiabatic character.

Four types of 5σ effective potentials at t ≈ 2.8 fs for the pulse in Figure 3C are shown in Figure 4C. The difference between ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ and ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(0\right)$ in Figure 4C is striking in comparison with the cases of Figures 2A,B: A hump is more clearly observed around z = −3a₀ in ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ at t ≈2 .8 fs. The induced dipole moment of ${\varphi }_{5\sigma }\left(t\right)$ responds to the steep rise in $\epsilon \left(t\right)$ in the time span from t = 2.3 fs to t = 2.8 fs, and increases to a large maximum value (∼0.18 ea₀) as shown in Figure 3C; concurrently, the other electrons also enter or appraoch the ionization exit. This is the reason why the hump become more distinct in Figure 4C, which is attributed to the electron correlation (stronger electron-electron interaction) induced by the coherent four-color pulse in Figure 3C. A more concrete evidence will be presnted below.

In the present treatment, the effective potential of CO is a two-dimensional (2D) function, i.e., a function of z and ρ. We have already examined TD-CASSCF effective potentials in 2D representation for a one-color pulse [90]. In Figure 5A, we present a 2D contour plot of ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ at t ≈ 2.8 fs for the four-color pulse in Figure 3C. On the whole, the hump height in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ drops from (z, ρ) = (−3a₀, 0) with increasing $\rho$; i.e., the hump is formed around the molecular axis. The ridgeline of the hump slides down along a curve line from (z, ρ) = (−3a₀, 0) toward (−2a₀, 2a₀), which is schematically illustrated in Figure 5A by a dotted line.

FIGURE 5

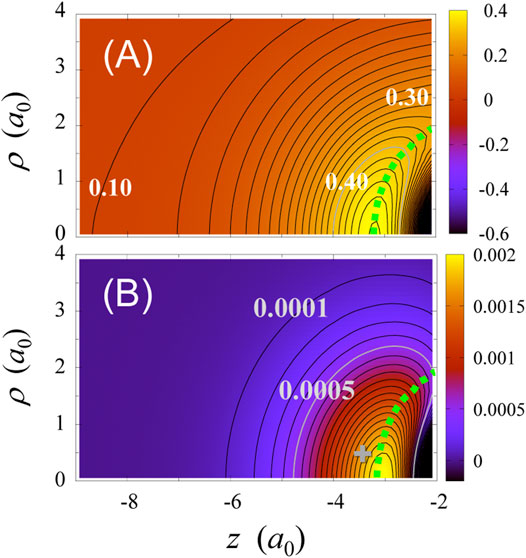
FIGURE 5. TD-CASSCF results for the pulse in Figure 3C: (A) 2D contour plot of ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ at t ≈ 2.8 fs; (B) Contour plot of the difference in total electron density between t ≈ 2.8 and t = 0. The contour lines in (A) are drawn at height intervals of 0.02E_h. The numbers near contour lines indicate the heights (in units of E_h). The contour lines in (B) are drawn at intervals of $0.0001a_0^{-3}$. The symbol “+” designates that the electron density increases in the region. The hump ridgeline in ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ is schematically illustrated in (A) by a light green dotted line, which is also drawn on the contour plot (B) as a dotted line.

The change in field-induced electron-electron interaction is definitely affected by the spatial change in total electron density $P(z,\rho ;t)$ or by the induced dipole moment. We present in Figure 5B a 2D plot of the difference $P(z,\rho ;t)-P(z,\rho ;0)$ at t ≈ 2.8 fs for the pulse in Figure 3C. A positive peak emerges around $(z,\rho )=$ (−3a₀, 0). Electrons mostly move along the C-O axis in the case where it is parallel to the polarization direction of the applied field. This buildup zone in the electron density $P(z,\rho ;t)-P(z,\rho ;0)$ overlaps with the hump in Figure 5A, as indicated by the hump ridgeline superimposed on Figure 5B. The hump formation is hence ascribed to the interactions between electrons swarming to the buildup zone or between orbitals, which cannot be described by the TDHF level of theory. In conclusion, the hump in ${\mathit{\upsilon }}_1\left(0\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ results from the penetration of an electron into the potential barrier formed by a field-induced local rise of electron density. When $\epsilon \left(t\right)<0$, $P(z,\rho ;t)-P(z,\rho ;0)$ exhibits no distinct peaks in the region en route to ionization.

The hump ridge elevates as the field strength $\epsilon \left(t\right)(>0)$ increases, which sharply incises the protruding lobe of the 5σ natural orbital ${\varphi }_{5\sigma }\left(t\right)$ around the C atom (See the light green dotted line in Figure 6A). This mechanism accelerates the ionization from ${\varphi }_{5\sigma }\left(t\right)$ in the area outside the hump ridge. The area of the newly emerging hump is regarded as a TI exit in the presence of electron correlation or a crowd of electrons. We have confirmed that the hump height from the asymptotic value of ${\mathit{\upsilon }}_1\left(0\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t_1\right)$ at $z=-\infty$ is nearly proportional to the induced dipole moment of ${\varphi }_{5\sigma }\left(t\right)$ associated with the spatial change in electron density [90]. For TDHF, the buildup zone in electron density spreads vaguely in comparison with the TD-CASSCF case, in agreement with the fact that no hump appears in Figure 2C.

FIGURE 6

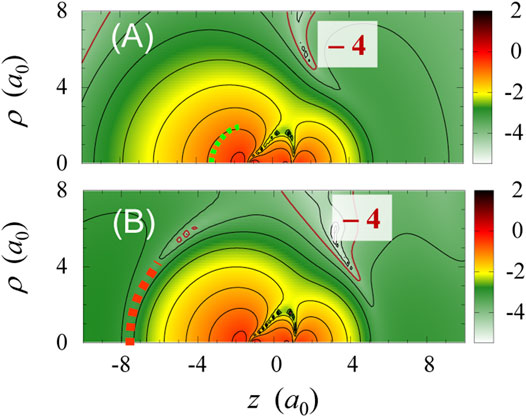
FIGURE 6. 2D contour plots of ${\varphi }_{5\sigma }\left(t\right)$ for four-color fields: (A) ${\log }_{10}\left|{\varphi }_{5\sigma }\left(t\right)\right|$ at t ≈ 2.8 fs for the pulse in Figure 3C; (B) ${\log }_{10}\left|{\varphi }_{5\sigma }\left(t\right)\right|$ at t ≈ 3.5 fs for the pulse in Figure 3D. The brown line represents the height of $\left|{\varphi }_{5\sigma }\left(t\right)\right|={10}^{-4}{a}_0^{-3/2}$. The contour interval on the logarithmic scale is 0.5. The light green dotted line in (A) denotes the hump ridgeline in Figure 5A. The red dotted line in (B) denotes the valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ for Figure 4D, along which a groove runs in the contour map of ${\log }_{10}\left|{\varphi }_{5\sigma }\left(t\right)\right|$.

For the pulse of Figure 3D, effective potentials at t ≈ 3.5 fs are shown in Figure 4D. The potential ${\mathit{\upsilon }}_1\left(0\right)\mathit{+}{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ at t ≈ 3.5 fs exhibits a very unique feature, i.e., a deep dent around z = −7.5a₀. The dents connected in the (z, ρ) space form a deep valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$, which significantly distorts the profile of ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$. The time span where $\epsilon \left(t\right)$ > 0 in the latter half of the pulse (t > 2.53 fs) is as long as 1.3 fs and the ionization barrier of ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ is then largely shifted down. Considering these facts and following a primitive picture of TI, we expected that the ionization probability for the pulse in Figure 3D is rather large. However, it is only slightly larger than that for Figure 3C; the ratio is ca. 0.008:0.006 (Overall, the ionization probabilities for the four-color pulses are about one order of magnitude larger than in the pulses comprised of harmonics up to the third order.). The ionization probaility for Figure 3D includes the additional contribution from the positive field area around t = 1 fs. We add that the effective potential ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ at t ≈ 3.5 fs obtained by TDHF levels off in the range from z = − 4a₀ to z = −7a₀ (as high as 0.4 E_h) and exhibits only a shallow valley at z ≈ −8a₀ (The depth is ∼0.1E_h). The TDHF ionization probabilities for Figures 3C,D were one order of magnitude smaller than the TD-CASSCF values.

An interpretation based on the present single-electron picture is that the valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ of Figure 4D serves to block the electron current from the bound region (by reflection). This interpretation can be evidenced by the 2D contour plot of $\left|{\varphi }_{5\sigma }\left(t\right)\right|$. Figure 6A represents ${\log }_{10}\left|{\varphi }_{5\sigma }\left(t\right)\right|$ at t ≈ 2.8 fs for the pulse in Figure 3C; Figure 6B represents ${\log }_{10}\left|{\varphi }_{5\sigma }\left(t\right)\right|$ at t ≈ 3.5 fs for the pulse in Figure 3D. Figure 6A simply shows a typical feature of TI that electron density leaks out from the bound region toward the negative z direction (for $\epsilon \left(t\right)$ > 0). On the other hand, Figure 6B shows that the bound component of ${\varphi }_{5\sigma }\left(t\right)$ is encircled by the valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$, which is indicated by the red dotted line. The four-color pulse $\epsilon \left(t\right)$ in Figure 3D behaves as if it squeezes ${\varphi }_{5\sigma }\left(t\right)$ toward the inside of the valley, i.e., toward the center of the molecule, though at this moment the field $\epsilon \left(t\right)$ pushes an electron toward the negative z direction. We found that the difference $P(z,\rho ;t)-P(z,\rho ;0)$ at t ≈3.5 fs becomes slightly negative in the area along the valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$ and it rises around the hump near (z, ρ) = (−3a₀,0) in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$, of which rise is more prominent than in the other cases with the same F_p. The valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}\left(t\right)$, associated with a diminution in electron density, is regarded as a signature of strong electron correlation induced by the four-color pulse. This type of coherent control of ${\varphi }_{5\sigma }\left(t\right)$ works in forvor of ionization suppression. Since ${\varphi }_{5\sigma }\left(t\right)$ in Figure 6B is spatially squeezed, $d_{5\sigma }\left(t\right)$ at t ≈ 3.5 fs in Figure 3D is smaller than $d_{5\sigma }\left(t\right)$ at t ≈ 2.8 fs in Figure 3C. The former is ∼0.13ea₀ and the latter is ∼0.18ea₀. The “squeezed” ${\varphi }_{5\sigma }\left(t\right)$ orbital might be associated with the formation of a localized excited or resonance state as discussed in the next subsection.

On the Information out of High-Order Harmonic Generation Spectra

We here discuss the connection of the present results of TI with HHG. The HHG spectra of asymmetric molecules, which reflect the presence and motion of the charges in applied fields, can be utilized to investigate the mechanism of coherent control and to assess the degree of controllability. The ionization potential for a polar molecule in an intense field is a time-dependent one, as denoted by $I_{\text{p}}\left(t\right)$, which is due to the Stark-shift of the ground state; for HeH²⁺, $I_{\text{p}}\left(t\right)$ is approximately given by $I_{\text{p}}\left(t\right)\approx I_0+R\mathit{\epsilon }\left(t\right)/2$ [112–114], where $I_0$ is the field-free ionization potential and R is the internuclear distance. The Stark-shifted ionization potential leads to a cutoff energy in HHG that is higher than the widely accepted prediction by the three-step model, i.e. $E_{\text{cutoff}}^{\left(0\right)}=I_0+3.17f_{\max }^2/4{\omega }^2$ [8], for the one-color applied field with a frequency ω, where $f_{\max }$ is the maximum field envelope. Etches and Madsen [115] have shown theoretically for a polar molecule CO that HHG components are generated beyond the predicted value of $E_{\text{cutoff}}^{\left(0\right)}$. The cutoff energy experimentally measured can serve as an index to quantify how the Fourier-synthesized fields manipulate the electronic wave function.

Another feature inherent in the HHG spectra of asymmetric molecules was pointed out by Bandrauk et al. [113, 114], who theoretically investigated the role of excited states in HHG for HeH²⁺. They found that a transient localized state (Stark-shifted or field-dressed first excited state of HeH²⁺) is resonantly populated prior to ionization by laser induced electron transfer from the He²⁺ side to the H⁺ side. This field-dressed excited state is able to get back directly to the ground state with emission. A resulting new HHG channel, regarded as the quasi two-step pathway, gives birth to an intense resonance peak (<$E_{\text{cutoff}}^{\left(0\right)}$) near the field-dressed energy gap between the transient excited state and the ground state. In the case where the resonance state has long lifetime, the ionization via the resonance state is expected to be delayed, which for short laser pulses, redshifts the HHG spectrum in the plateau region [113]. This type of resonance channel is also investigated in [116]. A four-step model was thus proposed for the HHG of asymmetric molecules [113, 114], in which the representative transient state is incorporated into the three-step model as an additional step in the HHG. The extension of the cutoff energy mentioned in the above paragraph can also be interpreted by the following four-step pathway in the four-step model: i) An electron is pumped from the ground state to the localized long lifetime excited state (field-induced electron transfer from the He²⁺ side to the H⁺ side), ii) then, part of the population is transferred to field-dressed continuum states, iii) the freed electron is accelerated in the laser field, and iv) recombination with the ground state (the neighboring He²⁺) [114]. The cutoff extension is attributed to the difference in electric field potential between (ii) the ionization site (H⁺) and (iv) recombination site (He²⁺). The four-step pathway interferes in HHG with the quasi two-step pathway. It has been theoretically demonstrated that distinct vestiges of the interference between the two pathways appear in the HHG spectrum if the amplitudes of the two pathways are comparable with each other [114].

Intermediate states prepared by tailored multi-color fields, such as represented by a “squeezed” orbital in Figure 6B, may work as such transient excited states leading to resonance HHG. A realistic attempt to confirm the existence of such resonance states and to assess the controllability of the wave function is to examine how the HHG spectrum (regarding the cutoff energy, individual peak positions and intensities, etc.) changes by varying the relative phases among multi-color fields. In line with this, it is necessary to quantify how long the intermediate states (orbitals) prepared live. We would like to take on the applications of the effective potential approach to the setup of new experimental schemes and to the search of possible results, as discussed in [90].

Conclusion

We presented the results of theoretical investigation of the multielectron dynamics of CO in intense laser fields and discussed various manipulation schemes by Fourier-synthesized coherent fields comprised of harmonics up to the fourth order. The multielectron wavefunction $\Psi \left(t\right)$ to describe the electron dynamics are obtained by using the MCTDHF method, where $\Psi \left(t\right)$ is expanded in terms of various electron configurations or Slater determinants $\left\{{\Phi }_I\left(t\right)\right\}$. In the MCTDHF, both the CI coefficients $\left\{C_I\left(t\right)\right\}$ and molecular orbitals $\left\{{\psi }_j(\mathit{r},t)\right\}$ in $\left\{{\Phi }_I\left(t\right)\right\}$ obey the coupled EOMs derived from the Dirac-Frenkel TD variational principle, where r is a one-electron coordinate. In actual numerical simulations for the dynamics of CO interacting with Fourier-synthesized pulses, we employed the TD-CASSCF scheme where the orbital space in the Slater determinants is split into inactive (core) and active orbitals. The peak of the applied field is fixed at $F_p=$ 0.0378 E_h/(ea₀) = 1.94×10¹⁰ Vm⁻¹ throughout this paper except that in Figure 2D, of which the light intensity corresponds to I = 5.0×10¹³ Wcm⁻² in the case of one-color pulses.

We then quantified the multielectron nature such as electron correlation by using our effective potential approach: the time-dependent natural orbitals $\left\{{\varphi }_j(\mathit{r},t)\right\}$, which diagonalize the first order reduced density matrix, are obtained from $\left\{{\psi }_j(\mathit{r},t)\right\}$; next, the EOMs for $\left\{{\varphi }_j(\mathit{r},t)\right\}$ are derived, which define the effective single-electron potentials ${\mathit{\upsilon }}_j^{\text{eff}}(\mathit{r},t)$ that determine the dynamics of ${\varphi }_j(\mathit{r},t)$ under the influence of electron-electron interaction. The effective potentials $\left\{{\mathit{\upsilon }}_j^{\text{eff}}\left(t\right)\right\}$ consist of two terms: ${\mathit{\upsilon }}_j^{\text{eff}}\left(t\right)={\mathit{\upsilon }}_1\left(t\right)+{\mathit{\upsilon }}_{2,j}\left(t\right)$, where ${\mathit{\upsilon }}_1\left(t\right)$ is the one-body interaction including that with the applied laser field $\mathit{\epsilon }\mathrm{(}t\mathrm{)}$ and ${\mathit{\upsilon }}_{2,j}\left(t\right)$ represents an effective two-body electron-electron interaction for a single electron. The TD effective potentials as functions of a one-electron spatial coordinate r are thus obtained from the natural orbitals $\left\{{\varphi }_j(\mathit{r},t)\right\}$ and CI expansion coefficients $\left\{C_I\left(t\right)\right\}$ of the calculated $\Psi \left(t\right).$ In this approach, the role of electron correlation can be quantitatively analyzed by comparing ${\mathit{\upsilon }}_j^{\text{eff}}(\mathit{r},t)$ with those obtained by the TDHF method.

Two-body interaction ${\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$ can dramatically change the shape of the tunnel barrier in the 5σ ΗΟΜΟ effective potential ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$, whereas the one-body potential ${\mathit{\upsilon }}_1\left(t\right)$ is simply slanted by the electric dipole interaction. For near-IR one-color pulses, as the field strength increases when $\mathit{\epsilon }\left(t\right)$ points from C to O ($\epsilon \left(t\right)>0$), a hump is formed ∼2 a₀ away outside from C (z < 0) in ${\mathit{\upsilon }}_1\left(0\right)+{\mathit{\upsilon }}_{\mathrm{2,5}\sigma }\left(t\right)$. Around this region, the lobe of ${\varphi }_{5\sigma }\left(t\right)$ spreads out extensively. Electron density is then transferred from the interior to the exterior region outside the hump ridge (which is considered the border between the interior and exterior regions), and ionization proceeds together with a bound component already distributed in the exterior region. The experimentally observed anisotropic ionization in CO is ascribed to the hump formation, which brings about preferential electron ejection from the C atom side. Hump formation originates from the field-induced change in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$ mainly due to electron correlation. Upon the reversal of the sign of $\epsilon \left(t\right)$, ionization is relatively suppressed, because the tunnel barrier is then located far away (>13a₀) from the O atom. This is the mechanism we proposed for the anisotropic ionization of CO [88–90].

We found that ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$ for an optimized asymmetric ω+2ω two-color pulse exhibits a very similar profile as in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$ for one-color pulses. A coherent superposition of ω and 2ω fields with an appropriate relative phase works as if either positive or negative peaks are filtered out from a one-color pulse. The induced dipole moments $d_{5\sigma }\left(t\right)$ for three-color pulses behave almost adiabatic. The peaks in $d_{5\sigma }\left(t\right)$ nearly coincide temporally with the peaks of the applied three-color field. This suggests that the main ionization mechanism in three-color fields is still TI. More sophisticated manipulation can be realized by adding higher harmonics to a synthesized field. The controllability of electron dynamics is higher in four-color fields than in three-color fields. By adjusting the relative phases of a ω+2ω+3ω+4ω field, one can create, in addition to a hump, a deep potential valley in the negative z region of ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$ which encloses the molecule at a radius of ∼7 a₀. The 5σ orbital of CO is then squeezed toward the inside of the potential valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$. It is of much interest to reveal what is the origin of this “squeezed” orbital. We would like to point out again that a hump and valley in ${\mathit{\upsilon }}_{5\sigma }^{\text{eff}}(\mathit{r},t)$ are closely correlated with domains of increasing and decreasing electron density, respectively. As a first step to establish robust control schemes for multielectron dynamics by Fourier-synthesized coherent laser fields, we are planning to extract the information of two-body parts $\text{{}{\mathit{\upsilon }}_{2,\mathit{j}}\left(\mathit{t}\right)\}$ from phase-dependent quantities (functions of relative phases among harmonics), e.g., HHG spectra as well as the yields and release-direction propensities of fragment ions and electrons.

The final point to be discussed here concerns the future extension of the present effective potential approach to chemical reactions. The strong coupling between intense fields and valence electrons dramatically distorts the potential hypersurfaces which determine the motion of the nuclei and brings about decisive changes in reaction pathways [17, 117, 118]. Kübel et al. [118] ionized H₂ by a few-cycle visible pulse and prepared a wave packet on the σ_g state of ${\text{H}}_2^{+}$. The behavior of ${\text{H}}_2^{+}$ was controlled by a mid-infrared pulse with a delay that couples the σ_g state with the σ_u state by one-, three-, and five-photon absorption. They analyzed a strongly modulated angular distribution of protons by using two-color Floquet theory and proved the existence of complex light-induced (field-dressed) potential surfaces that multiphoton couplings afford. These potentials can be shaped by the amplitude, phase, and duration of the applied fields, which allows for manipulating the dissociation or reaction dynamics of small molecules.

A feasible extension along with this line is to include the nuclear coordinates $\left\{Q_k\right\}$ as adiabatic parameters into the present approach, i.e., to define or calculate “adiabatic” natural orbitals $\left\{{\varphi }_j\left(\mathit{r},\left\{Q_k\right\},t\right)\right\}$. The effective potential for ${\varphi }_j\left(\mathit{r},\left\{Q_k\right\},t\right)$ are then expressed as ${\mathit{\upsilon }}_j^{\text{eff}}\left(\mathit{r},\left\{Q_k\right\},t\right)$, which might connect more tightly the two pictures of molecular orbital and molecular dynamics. Another conceivable approach is to use a more fundamental method, namely, the extended MCTDHF method where the nuclear coordinates in the total wave function $\Psi \left(\left\{{\mathit{r}}_j\right\},\left\{Q_k\right\},t\right)$ are dealt with as quantum mechanical variables (e.g., each nucleus is expressed by a single-particle function, like in the treatment of electrons as molecular orbitals) [89, 109, 119–121]. The molecular orbitals used in the extended MCTDHF are functions of a one-electron coordinate alone (i.e., $\left\{{\psi }_j\left(\mathit{r},t\right)\right\}$); $\left\{Q_k\right\}$ are not involved, unlike in the conventional Born-Hung expansion [122]. An effective potential for each nucleus could in principle be derived from the non-Born-Oppenheimer wave function $\Psi \left(\left\{{\mathit{r}}_j\right\},\left\{Q_k\right\},t\right)$, which would provide a single nucleus picture in the presence of correlated nuclear motion. The extended MCTDHF method also offers a novel concept of potential surfaces (extended-MCTDHF potentials). So far, the effective potential curves of the ground and excited states defined in this method are obtained for a 1D model H₂ [89, 120, 121] and the time-dependent system of 3D H₂⁺ [123]. The memory size used in this method is shown to be about two orders of magnitude smaller than in the Born-Hung expansion method when the same accuracy is required for the lowest vibronic energy. It is intriguing, especially for polyatomic molecules, to construct multiphoton field-dressed potentials based on Floquet theory from extended-MCTDHF potentials.

The various effective potential approaches abovementioned would help reveal the entire picture of the quantum electronic and nuclear dynamics of molecules and help contribute to further development of coherent control of chemical reactions. Challenges are widespread ahead of the frontier of the research on Coherent Phenomena in Molecular Physics.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

SO: Computation, preparation of figures. HO: conceptual proposal based on experimental feasibility, preparation of manuscript. TK: development of theoretical framework. HK: project coordination, preparation of manuscript. All authors developed the concept of the control of multielectron dynamics by multicolor fields and contributed to the article and approved the submitted version.

Funding

This work was supported in part by JSPS KAKENHI Grant Number JP16H04091.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank Prof. S. Koseki for providing us results of the electronic structure calculation of CO.

References

1. Glauber RJ. Quantum Theory of Optical Coherence: Selected Papers and Lectures. Weinheim, Germany: Wiley VCH (2007). doi:10.1002/9783527610075.ch16

CrossRef Full Text

2. Friedrich B, Herschbach DR. Alignment and Trapping of Molecules in Intense Laser Fields. Phys Rev Lett (1995) 74:4623. doi:10.1103/PhysRevLett.74.4623−6

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Stapelfeldt H, Seideman T. Colloquium: Aligning Molecules with Strong Laser Pulses. Rev Mod Phys (2003) 75: 543–57. doi:10.1103/RevModPhys.75.543

CrossRef Full Text | Google Scholar

4. Agostini P, Fabre F, Mainfray G, Petite G, Rahman NK. Free-free Transitions Following Six-Photon Ionization of Xenon Atoms. Phys Rev Lett (1979) 42: 1127–30. doi:10.1103/PhysRevLett.42.1127

CrossRef Full Text | Google Scholar

5. Chin SL, Yergeau F, Lavigne P. Tunnel Ionisation of Xe in an Ultra-intense CO₂ Laser Field (10¹⁴ Wcm⁻²) with Multiple Charge Creation. J Phys B: Atom Mol Phys (1985) 18:L213–5. doi:10.1088/0022-3700/18/8/001

CrossRef Full Text | Google Scholar

6. Augst S, Meyerhofer DD, Strickland D, Chint SL. Laser Ionization of Noble Gases by Coulomb-Barrier Suppression. J Opt Soc Am B (1991) 8:858. doi:10.1364/josab.8.000858

CrossRef Full Text | Google Scholar

7. DeWitt MJ, Levis RJ. Observing the Transition from a Multiphoton-Dominated to a Field-Mediated Ionization Process for Polyatomic Molecules in Intense Laser Fields. Phys Rev Lett (1998) 81:5101–4. doi:10.1103/PhysRevLett.81.5101

CrossRef Full Text | Google Scholar

8. Corkum PB. Plasma Perspective on Strong Field Multiphoton Ionization. Phys Rev Lett (1993) 71:1994. 10.1103/PhysRevLett.71.1994

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Lewenstein M, Salières P, L’Huillier A. Phase of the Atomic Polarization in High-Order Harmonic Generation. Phys Rev A (1995) 52: 4747–54. doi:10.1103/PhysRevA.52.4747

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Becker W, Grasbon F, Kopold R, Milošević DB, Paulus GG, Walther H. Above-threshold Ionization: From Classical Features to Quantum Effects. Adv At Mol Opt Phys (2002) 48: 35–98. doi:10.1016/S1049-250X(02)80006-4

CrossRef Full Text | Google Scholar

11. Scherer NF, Carlson RJ, Matro A, Du M, Ruggiero AJ, Romero‐Rochin V, et al. Fluorescence‐detected Wave Packet Interferometry: Time Resolved Molecular Spectroscopy with Sequences of Femtosecond Phase‐Locked Pulses. J Chem Phys (1991) 95: 1487–511. doi:10.1063/1.461064

CrossRef Full Text | Google Scholar

12. Katsuki H, Chiba H, Girard B, Meier C, Ohmori K. Visualizing Picometric Quantum Ripples of Ultrafast Wave-Packet Interference. Science (2006) 311: 1589–92. doi:10.1126/science.1121240

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Rice SA, Zhao M. Optical Control of Molecular Dynamics. New York: Wiley (2000). doi:10.1021/ja015259b

CrossRef Full Text

14. Shapiro M, Brumer P. Principles of the Quantum Control of Molecular Processes. 2nd ed. New York: Wiley (2011). doi:10.1002/9783527639700

CrossRef Full Text

15. Gordon RJ, Zhu L, Seideman T. Coherent Control of Chemical Reactions. Acc Chem Res (1999) 32:1007–16. doi:10.1021/ar970119l

CrossRef Full Text | Google Scholar

16. Endo T, Fujise H, Kawachi Y, Ishihara A, Matsuda A, Fushitani M, et al. Selective Bond Breaking of CO₂ in Phase-Locked Two-Color Intense Laser Fields: Laser Field Intensity Dependence. Phys Chem Chem Phys (2017) 19: 3550–6. doi:10.1039/c6cp07471e

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Sato Y, Kono H, Koseki S, Fujimura Y. Description of Molecular Dynamics in Intense Laser Fields by the Time-Dependent Adiabatic State Approach: Application to Simultaneous Two-Bond Dissociation of CO₂ and its Control. J Am Chem Soc (2003) 125:8019–31. doi:10.1021/ja0344819

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Schafer KJ, Kulander KC. Phase-dependent Effects in Multiphoton Ionization Induced by a Laser Field and its Second Harmonic. Phys Rev A (1992) 45: 8026–33. doi:10.1103/PhysRevA.45.8026

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Schumacher DW, Weihe F, Muller HG, Bucksbaum PH. Phase Dependence of Intense Field Ionization: A Study Using Two Colors. Phys Rev Lett (1994) 73: 1344–7. doi:10.1103/PhysRevLett.73.1344

PubMed Abstract | CrossRef Full Text | Google Scholar

20. De S, Znakovskaya I, Ray D, Anis F, Johnson NG, Bocharova IA, et al. Field-free Orientation of CO Molecules by Femtosecond Two-Color Laser Fields. Phys Rev Lett (2009) 103:153002. doi:10.1103/PhysRevLett.103.153002

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Li H, Ray D, De S, Znakovskaya I, Cao W, Laurent G, et al. Orientation Dependence of the Ionization of CO and NO in an Intense Femtosecond Two-Color Laser Field. Phys Rev A (2011) 84:043429. doi:10.1103/PhysRevA.84.043429

CrossRef Full Text | Google Scholar

22. Kaziannis S, Kotsina N, Kosmidis C. Interaction of Toluene with Two-Color Asymmetric Laser Fields: Controlling the Directional Emission of Molecular Hydrogen Fragments. J Chem Phys (2014) 141:104319. doi:10.1063/1.4895097

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ohmura H, Saito N, Tachiya M. Selective Ionization of Oriented Nonpolar Molecules with Asymmetric Structure by Phase-Controlled Two-Color Laser Fields. Phys Rev Lett (2006) 96:173001. doi:10.1103/PhysRevLett.96.173001

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ohmura H, Tachiya M. Robust Quantum Control of Molecular Tunneling Ionization in the Space Domain by Phase-Controlled Laser Fields. Phys Rev A (2008) 77:023408. doi:10.1103/physreva.77.023408

CrossRef Full Text

25. Ohmura H, Saito N, Nonaka H, Ichimura S. Dissociative Ionization of a Large Molecule Studied by Intense Phase-Controlled Laser Fields. Phys Rev A (2008) 77:053405. doi:10.1103/PhysRevA.77.053405

CrossRef Full Text | Google Scholar

26. Ohmura H, Saito N, Morishita T. Quantum Control of Molecular Tunneling Ionization in the Spatiotemporal Domain. Phys Rev A (2011) 83:063407. doi:10.1103/PhysRevA.83.063407

CrossRef Full Text | Google Scholar

27. Ohmura H, Saito N, Morishita T. Molecular Tunneling Ionization of the Carbonyl Sulfide Molecule by Double-Frequency Phase-Controlled Laser Fields. Phys Rev A (2014) 89:013405. doi:10.1103/PhysRevA.89.013405

CrossRef Full Text | Google Scholar

28. Kitzler M, Lezius M. Spatial Control of Recollision Wave Packets with Attosecond Precision. Phys Rev Lett (2005) 95:253001. doi:10.1103/PhysRevLett.95.253001

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kim IJ, Kim CM, Kim HT, Lee GH, Lee YS, Park JY, et al. Highly Efficient High-Harmonic Generation in an Orthogonally Polarized Two-Color Laser Field. Phys Rev Lett (2005) 94:243901. doi:10.1103/PhysRevLett.94.243901

CrossRef Full Text | Google Scholar

30. Mashiko H, Gilbertson S, Li C, Khan SD, Shakya MM, Moon E, et al. Double Optical Gating of High-Order Harmonic Generation with Carrier-Envelope Phase Stabilized Lasers. Phys Rev Lett (2008) 100:103906. doi:10.1103/PhysRevLett.100.103906

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Brugnera L, Hoffmann DJ, Siegel T, Frank F, Zaïr A, Tisch JWG, et al. Trajectory Selection in High Harmonic Generation by Controlling the Phase between Orthogonal Two-Color Fields. Phys Rev Lett (2011) 107:153902. doi:10.1103/PhysRevLett.107.153902

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Hänsch TW. A Proposed Sub-femtosecond Pulse Synthesizer Using Separate Phase-Locked Laser Oscillators. Opt Commum (1990) 80:71. doi:10.1016/0030-4018(90)90509-R

CrossRef Full Text | Google Scholar

33. Shverdin MY, Walker DR, Yavuz DD, Yin GY, Harris SE. Generation of a Single-Cycle Optical Pulse. Phys Rev Lett (2005) 94:033904. doi:10.1103/PhysRevLett.94.033904

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Yoshitomi D, Kobayashi Y, Torizuka K. Characterization of Fourier-Synthesized Optical Waveforms from Optically Phase-Locked Femtosecond Multicolor Pulses. Opt Lett (2008) 33:2925. doi:10.1364/OL.33.002925

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Chan H-S, Hsieh Z-M, Liang W-H, Kung AH, Lee C-K, Lai C-J, et al. Synthesis and Measurement of Ultrafast Waveforms from Five Discrete Optical Harmonics. Science (2011) 331:1165–8. doi:10.1126/science.1198397

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yoshii K, Kiran Anthony J, Katsuragawa M. The Simplest Route to Generating a Train of Attosecond Pulses. Light Sci Appl (2013) 2:e58. doi:10.1038/lsa.2013.14

CrossRef Full Text | Google Scholar

37. Chipperfield LE, Robinson JS, Tisch JWG, Marangos JP. Ideal Waveform to Generate the Maximum Possible Electron Recollision Energy for Any Given Oscillation Period. Phys Rev Lett (2009) 102:063003. doi:10.1103/PhysRevLett.102.063003

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Wei P, Miao J, Zeng Z, Li C, Ge X, Li R, et al. Selective Enhancement of a Single Harmonic Emission in a Driving Laser Field with Subcycle Waveform Control. Phys Rev Lett (2013) 110:233903. doi:10.1103/PhysRevLett.110.233903

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Haessler S, Balčiunas T, Fan G, Andriukaitis G, Pugžlys A, Baltuška A, et al. Optimization of Quantum Trajectories Driven by Strong-Field Waveforms. Phys Rev X (2014) 4:021028. doi:10.1103/PhysRevX.4.021028

CrossRef Full Text | Google Scholar

40. Ohmura H, Saito N. Quantum Control of a Molecular Ionization Process by Using Fourier-Synthesized Laser Fields. Phys Rev A (2015) 92:053408. doi:10.1103/PhysRevA.92.053408

CrossRef Full Text | Google Scholar

41. Yoshida T, Saito N, Ohmura H. Robust Generation of Fourier-Synthesized Laser Fields and Their Estimation of the Optical Phase by Using Quantum Control of Molecular Tunneling Ionization. J Phys B: Mol Opt Phys (2018) 51:065601. doi:10.1088/1361-6455/aaac20

CrossRef Full Text | Google Scholar

42. Ohmura H, Yoshida T, Saito N. Four-mode Multi-Selection in the Dual Phase Control of a Molecular Ionization Induced by Fourier-Synthesized Laser Fields. Appl Phys Lett (2019) 114:054101. doi:10.1063/1.5082578

CrossRef Full Text | Google Scholar

43. Ohmura H, Saito N. Sub-Optical-Cycle Attosecond Control of Molecular Ionization by Using Fourier-Synthesized Laser Fields. Phys Rev A (2020) 101:043419. doi:10.1103/PhysRevA.101.043419

CrossRef Full Text | Google Scholar

44. Paulus GG, Lindner F, Walther H, Baltuška A, Goulielmakis E, Lezius M, et al. Measurement of the Phase of Few-Cycle Laser Pulses. Phys Rev Lett (2003) 91:253004. doi:10.1103/PhysRevLett.91.253004

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Apolonski A, Poppe A, Tempea G, Spielmann C, Udem T, Holzwarth R, et al. Controlling the Phase Evolution of Few-Cycle Light Pulses. Phys Rev Lett (2000) 85:740–3. doi:10.1103/PhysRevLett.85.740

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Jones DJ, Diddams SA, Ranka JK, Stentz A, Windeler RS, Hall JL, et al. Carrier-Envelope Phase Control of Femtosecond Mode-Locked Lasers and Direct Optical Frequency Synthesis. Science (2000) 288:635–9. doi:10.1126/science.288.5466.635

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Baltuska A, Fuji T, Kobayashi T. Controlling the Carrier-Envelope Phase of Ultrashort Light Pulses with Optical Parametric Amplifiers. Phys Rev Lett (2002) 88:133901. doi:10.1103/PhysRevLett.88.13390110.1103

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Kakehata M, Takada H, Kobayashi Y, Torizuka K, Takamiya H, Nishijima K, et al. Carrier-Envelope-Phase Stabilized Chirped-Pulse Amplification System Scalable to Higher Pulse Energies. Opt Express (2004) 12:2070–80. doi:10.1364/OPEX.12.002070

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Baltuška A, Udem T, Uiberacker M, Hentschel M, Goulielmakis E, Gohle C, et al. Attosecond Control of Electronic Processes by Intense Light Fields. Nature (2003) 421:611–5. doi:10.1038/nature01414

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Krausz F, Ivanov M. Attosecond Physics. Rev Mod Phys (2009) 81: 163–234. doi:10.1103/RevModPhys.81.163

CrossRef Full Text | Google Scholar

51. Joachain CJ, Kylstra NJ, Potvliege RM. Atoms in Intense Laser Fields. Cambridge: Cambridge University Press (2011). doi:10.1017/CBO9780511993459

CrossRef Full Text

52. Nisoli M, Decleva P, Calegari F, Palacios A, Martín F. Attosecond Electron Dynamics in Molecules. Chem Rev (2017) 117: 10760–825. doi:10.1021/acs.chemrev.7b00226

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Schiffrin A, Paasch-Colberg T, Karpowicz N, Apalkov V, Gerster D, Mühlbrandt S, et al. Optical-Field-Induced Current in Dielectrics. Nature (2013) 493: 70–4. doi:10.1038/nature11567

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Vasa P, Mathur D. Ultrafast Biophotonics. Cham, Switzerland: Springer (2016). doi:10.1007/978-3-319-39614-9

CrossRef Full Text

55. Keldysh LV. Ionization in the Field of a Strong Electromagnetic Wave. Sov Phys JETP (1964) 20: 1307–14.

Google Scholar

56. Wolkov DM. Über eine Klasse von Lösungen der Diracschen Gleichung. Z Phys (1935) 94: 250–60. doi:10.1007/BF01331022

CrossRef Full Text | Google Scholar

57. Perelemov AM, Popov VS, Terent'ev MV. Ionization of Atoms in an Alternating Electric Filed. Soviet Phys JETP (1966) 23: 924–34.

Google Scholar

58. Faisal FHM. Multiple Absorption of Laser Photons by Atoms. J Phys B: Mol Phys (1973) 6:L89–L92. doi:10.1088/0022-3700/6/4/011

CrossRef Full Text | Google Scholar

59. Reiss HR. Effect of an Intense Electromagnetic Field on a Weakly Bound System. Phys Rev A (1980) 22: 1786–813. doi:10.1103/PhysRevA.22.1786

CrossRef Full Text | Google Scholar

60. Ammosov MV, Delone NB, Krainov VP. Tunnel Ionization of Complex Atoms and of Atomic Ions in an Alternating Electromagnetic Field. Soviet Phys JETP (1986) 64: 1191–4.

Google Scholar

61. Tong XM, Zhao Z, Lin CD. Theory of Molecular Tunneling Ionization. Phys Rev A (2002) 66:033402. doi:10.1103/PhysRevA.66.033402

CrossRef Full Text | Google Scholar

62. Abu-samha M, Madsen LB. Single-Active-Electron Potentials for Molecules in Intense Laser Fields. Phys Rev A (2010) 81:033416. doi:10.1103/PhysRevA.81.033416

CrossRef Full Text | Google Scholar

63. Awasthi M, Saenz A. Breakdown of the Single-Active-Electron Approximation for One-Photon Ionization of the B¹Σ_u⁺ State of H₂ Exposed to Intense Laser Fields. Phys Rev A (2010) 81:063406. doi:10.1103/PhysRevA.81.063406

CrossRef Full Text | Google Scholar

64. Zhang B, Yuan J, Zhao Z. Dynamic Core Polarization in Strong-Field Ionization of CO Molecules. Phys Rev Lett (2013) 111:163001. doi:10.1103/PhysRevLett.111.163001

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Abu-samha M, Madsen LB. Multielectron Effects in Strong-Field Ionization of the Oriented OCS Molecule. Phys Rev A (2020) 102:013433. doi:10.1103/PhysRevA.102.063111

CrossRef Full Text | Google Scholar

66. Zhao Z, Brabec T. Tunnel Ionization in Complex Systems. J Mod Opt (2007) 54: 981–97. doi:10.1080/09500340601043413

CrossRef Full Text | Google Scholar

67. Hoang V-H, Zhao S-F, Le V-H, Le A-T. Influence of Permanent Dipole and Dynamic Core-Electron Polarization on Tunneling Ionization of Polar Molecules. Phys Rev A (2017) 95:023407. doi:10.1103/physreva.95.023407

CrossRef Full Text

68. Kang H-P, Xu S-P, Wang Y-L, Yu S-G, Zhao X-Y, Hao X-L, et al. Polarization Effects in Above-Threshold Ionization with a Mid-infrared Strong Laser Field. J Phys B: Mol Opt Phys (2018) 51:105601. doi:10.1088/1361-6455/aabce0

CrossRef Full Text | Google Scholar

69. Kling MF, Vrakking MJJ. Attosecond Electron Dynamics. Annu Rev Phys Chem (2008) 59: 463–92. doi:10.1146/annurev.physchem.59.032607.093532

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Vrakking MJJ, Lepine F. Attosecond Molecular Dynamics. London: Royal Society of Chemistry (2018). doi:10.1039/9781788012669

CrossRef Full Text

71. Harumiya K, Kawata I, Kono H, Fujimura Y. Exact Two-Electron Wave Packet Dynamics of H₂ in an Intense Laser Field: Formation of Localized Ionic States H⁺H⁻. J Chem Phys (2000) 113: 8953–60. doi:10.1063/1.1319348

CrossRef Full Text | Google Scholar

72. Harumiya K, Kono H, Fujimura Y, Kawata I, Bandrauk AD. Intense Laser-Field Ionization of H₂ Enhanced by Two-Electron Dynamics. Phys Rev A (2002) 66:043403. doi:10.1103/PhysRevA.66.043403

CrossRef Full Text | Google Scholar

73. Smirnova O, Mairesse Y, Patchkovskii S, Dudovich N, Villeneuve D, Corkum P, et al. High Harmonic Interferometry of Multi-Electron Dynamics in Molecules. Nature (2009) 460: 972–7. doi:10.1038/nature08253

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Zanghellini J, Kitzler M, Fabian C, Brabec SA. An MCTDHF Approach to Multielectron Dynamics in Laser Fields. Laser Phys (2003) 13: 1064–8.

Google Scholar

75. Kato T, Kono H. Time-Dependent Multiconfiguration Theory for Electronic Dynamics of Molecules in an Intense Laser Field. Chem Phys Lett (2004) 392: 533–40. doi:10.1016/j.cplett.2004.05.106

CrossRef Full Text | Google Scholar

76. Kato T, Kono H. Time-Dependent Multiconfiguration Theory for Electronic Dynamics of Molecules in Intense Laser Fields: A Description in Terms of Numerical Orbital Functions. J Chem Phys (2008) 128:184102. doi:10.1063/1.2912066

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Nest M, Klamroth T. Correlated Many-electron Dynamics: Application to Inelastic Electron Scattering at a Metal Film. Phys Rev A (2005) 72:012710. doi:10.1103/PhysRevA.72.012710

CrossRef Full Text | Google Scholar

78. Jordan G, Caillat J, Ede C, Scrinzi A. Strong Field Ionization of Linear Molecules: a Correlated Three-Dimensional Calculation. J Phys B: Mol Opt Phys (2006) 39:S341–S347. doi:10.1088/0953-4075/39/13/S07

CrossRef Full Text | Google Scholar

79. Nest M, Padmanaban R, Saalfrank P. Time-Dependent Approach to Electronically Excited States of Molecules with the Multiconfiguration Time-Dependent Hartree-Fock Method. J Chem Phys (2007) 126:214106. doi:10.1063/1.2743007

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Sukiasyan S, McDonald C, Destefani C, Ivanov MY, Brabec T. Multielectron Correlation in High-Harmonic Generation: A 2D Model Analysis. Phys Rev Lett (2009) 102:223002. doi:10.1103/PhysRevLett.102.223002

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Nguyen-Dang T-T, Peters M, Wang S-M, Dion F. Toward Ab-Initio Simulations of Multiple Ionization Processes in Intense Laser Field. Chem Phys (2009) 366: 71–84. doi:10.1016/j.chemphys.2009.09.007

CrossRef Full Text | Google Scholar

82. Redkin P, Ganeev R. Simulation of Resonant High-Order Harmonic Generation in a Three-Dimensional Fullerenelike System by Means of a Multiconfigurational Time-Dependent Hartree-Fock Approach. Phys Rev A (2010) 81:063825.

CrossRef Full Text | Google Scholar

83. Hochstuhl D, Bauch S, Bonitz M. Multiconfigurational Time-Dependent Hartree-Fock Calculations for Photoionization of One-Dimensional Helium. J Phys Conf Ser (2010) 220(10):012019. doi:10.1088/1742-6596/220/1/012019

CrossRef Full Text | Google Scholar

84. Dirac PAM. The Principles of Quantum Mechanics, International Series of Monographs on Physics. 4th ed. 27. Oxford: Oxford Science (1958).

Google Scholar

85. Frenkel J. Wave Mechanics, Advanced General Theory. Oxford: Claredon Press (1934).

86. Kato T, Kono H. Time-Dependent Multiconfiguration Theory for Ultrafast Electronic Dynamics of Molecules in an Intense Laser Field: Electron Correlation and Energy Redistribution Among Natural Orbitals. Chem Phys (2009) 366: 46–53. doi:10.1016/j.chemphys.2009.09.017

CrossRef Full Text | Google Scholar

87. Ohmura S, Kono H, Oyamada T, Kato T, Nakai K, Koseki S. Characterization of Multielectron Dynamics in Molecules: A Multiconfiguration Time-Dependent Hartree-Fock Picture. J Chem Phys (2014) 141:114105. doi:10.1063/1.4894505

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Ohmura S, Kato T, Oyamada T, Koseki S, Ohmura H, Kono H. A Single-Electron Picture Based on the Multiconfiguration Time-Dependent Hartree-Fock Method: Application to the Anisotropic Ionization and Subsequent High-Harmonic Generation of the CO Molecule. J Phys B: Mol Opt Phys (2018) 51:034001. doi:10.1088/1361-6455/aa9e45

CrossRef Full Text | Google Scholar

89. Kato T, Yamanouchi K, Kono H. Attosecond Molecular Dynamics. London: Royal Society of Chemistry (2018). p. 139–81. doi:10.1039/9781788012669

CrossRef Full Text

90. Ohmura S, Kato T, Ohmura H, Koseki S, Kono H. Analysis of the Multielectron Dynamics in Intense Laser-Induced Ionization of CO by the Time-Dependent Effective Potentials for Natural Orbitals. J Phys B: Mol Opt Phys (2020) 53:184001. doi:10.1088/1361-6455/ab9f0e

CrossRef Full Text | Google Scholar

91. Löwdin P-O. Quantum Theory of Many-particle Systems. I. Physical Interpretations by Means of Density Matrices, Natural Spin-Orbitals, and Convergence Problems in the Method of Configurational Interaction. Phys Rev (1955) 97: 1474–89. doi:10.1103/PhysRev.97.1474

CrossRef Full Text | Google Scholar

92. Kraus PM, Baykusheva D, Wörner HJ. Two-pulse Orientation Dynamics and High-Harmonic Spectroscopy of Strongly-Oriented Molecules. J Phys B: Mol Opt Phys (2014) 47:124030. doi:10.1088/0953-4075/47/12/124030

CrossRef Full Text | Google Scholar

93. Holmegaard L, Hansen JL, Kalhøj L, Louise Kragh S, Stapelfeldt H, Filsinger F, et al. Photoelectron Angular Distributions from Strong-Field Ionization of Oriented Molecules. Nat Phys. (2010) 6: 428–32. doi:10.1038/nphys1666

CrossRef Full Text | Google Scholar

94. Majety VP, Scrinzi A. Static Field Ionization Rates for Multi-Electron Atoms and Small Molecules. J Phys B: Mol Opt Phys (2015) 48:245603. doi:10.1088/0953-4075/48/24/245603

CrossRef Full Text | Google Scholar

95. SakemiMinemoto YS, Minemoto S, Sakai H. Orientation Dependence in Multichannel Dissociative Ionization of OCS Molecules. Phys Rev A (2017) 96:011401. doi:10.1103/PhysRevA.96.011401

CrossRef Full Text | Google Scholar

96. Johansen R, Bay KG, Christensen L, Thøgersen J, Dimitrovski D, Madsen LB, et al. Alignment-dependent Strong-Field Ionization Yields of Carbonyl Sulfide Molecules Induced by Mid-infrared Laser Pulses. J Phys B: Mol Opt Phys (2016) 49:205601. doi:10.1088/0953-4075/49/20/2056010.1088/0953-4075/49/20/205601

CrossRef Full Text | Google Scholar

97. Sándor P, Sissay A, Mauger F, Abanador PM, Gorman TT, Scarborough TD, et al. Angle Dependence of Strong-Field Single and Double Ionization of Carbonyl Sulfide. Phys Rev A (2018) 98:043425. doi:10.1103/PhysRevA.98.043425

CrossRef Full Text | Google Scholar

98. Madsen LB, Jensen F, Tolstikhin OI, Morishita T. Structure Factors for Tunneling Ionization Rates of Molecules. Phys Rev A (2013) 87:013406. doi:10.1103/PhysRevA.87.013406

CrossRef Full Text | Google Scholar

99. Śpiewanowski MD, Madsen LB. Alignment- and Orientation-dependent Strong-Field Ionization of Molecules: Field-Induced Orbital Distortion Effects. Phys Rev A (2015) 91:043406. doi:10.1103/PhysRevA.91.043406

CrossRef Full Text | Google Scholar

100. Dimitrovski D, Martiny CPJ, Madsen LB. Strong-field Ionization of Polar Molecules: Stark-Shift-Corrected Strong-Field Approximation. Phys Rev A (2010) 82:053404. doi:10.1103/PhysRevA.82.053404

CrossRef Full Text | Google Scholar

101. Wu J, Schmidt LPH, Kunitski M, Meckel M, Voss S, Sann H, et al. Multiorbital Tunneling Ionization of the CO Molecule. Phys Rev Lett (2012) 108:183001. doi:10.1103/PhysRevLett.108.183001

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Akagi H, Otobe T, Itakura R. Deformation of an Inner Valence Molecular Orbital in Ethanol by an Intense Laser Field. Sci Adv (2019) 5:eaaw1885. doi:10.1126/sciadv.aaw1885

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Le C-T, Hoang V-H, Tran L-P, Le V-H. Effect of the Dynamic Core-Electron Polarization of CO Molecules on High-Order Harmonic Generation. Phys Rev A (2018) 97:043405. doi:10.1103/PhysRevA.97.043405

CrossRef Full Text | Google Scholar

104. Zhang B, Yuan J, Zhao Z. Dynamic Orbitals in High-Order Harmonic Generation from CO Molecules. Phys Rev A (2014) 90:035402. doi:10.1103/PhysRevA.90.035402

CrossRef Full Text | Google Scholar

105. Pernal K, Gritsenko O, Baerends EJ. Time-Dependent Density-Matrix-Functional Theory. Phys Rev A (2007) 75:012506. doi:10.1103/PhysRevA.75.012506

CrossRef Full Text | Google Scholar

106. Benavides-Rivero CL, Marques MAL. On the Time Evolution of Fermionic Occupation Numbers. J Chem Phys (2019) 151:044112. doi:10.1063/1.5109009

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Sato T, Ishikawa KL. Time-Dependent Complete-Active-Space Self-Consistent-Field Method for Multielectron Dynamics in Intense Laser Fields. Phys Rev A (2013) 88:023402. doi:10.1103/PhysRevA.88.023402

CrossRef Full Text | Google Scholar

108. Miyagi H, Madsen LB. Time-Dependent Restricted-Active-Space Self-Consistent-Field Theory for Laser-Driven Many-electron Dynamics. Phys Rev A (2013) 87:062511. doi:10.1103/PhysRevA.87.062511

CrossRef Full Text | Google Scholar

109. Lode AUJ, Lévêque C, Madsen LB. Colloquium: Multiconfigurational Time-Dependent Hartree Approaches for Indistinguishable Particles. Rev Mod Phys (2020) 92:011001. doi:10.1103/RevModPhys.92.011001

CrossRef Full Text | Google Scholar

110. Nielsen ES, Jo/rgensen P, Oddershede J. Transition Moments and Dynamic Polarizabilities in a Second Order Polarization Propagator Approach. J Chem Phys (1980) 73: 6238–46. doi:10.1063/1.440119

CrossRef Full Text | Google Scholar

111. Uiberacker M, Uphues T, Schultze M, Verhoef AJ, Yakovlev V, Kling MF, et al. Attosecond Real-Time Observation of Electron Tunnelling in Atoms. Nature (2007) 446: 627–32. doi:10.1038/nature05648

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Kamta GL, Bandrauk ADAD. Phase Dependence of Enhanced Ionization in Asymmetric Molecules. Phys Rev Lett (2005) 94:203003. doi:10.1103/PhysRevLett.94.203003

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Bian X-B, Bandrauk AD. Nonadiabatic Molecular High-Order Harmonic Generation from Polar Molecules: Spectral Redshift. Phys Rev A (2011) 83(R):041403. doi:10.1103/PhysRevA.83.041403

CrossRef Full Text | Google Scholar

114. Bian X-B, Bandrauk AD. Multichannel Molecular High-Order Harmonic Generation from Asymmetric Diatomic Molecules. Phys Rev Lett (2010) 105:093903. doi:10.1103/PhysRevLett.105.093903

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Etches A, Madsen LB. Extending the Strong-Field Approximation of High-Order Harmonic Generation to Polar Molecules: Gating Mechanisms and Extension of the Harmonic Cutoff. J Phys B: Mol Opt Phys (2010) 43:155602. doi:10.1088/0953-4075/43/15/155602

CrossRef Full Text | Google Scholar

116. Strelkov V. Role of Autoionizing State in Resonant High-Order Harmonic Generation and Attosecond Pulse Production. Phys Rev Lett (2010) 104:123901. doi:10.1103/PhysRevLett.104.123901

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Kono H, Sato Y, Kanno M, Nakai K, Kato T. Theoretical Investigations of the Electronic and Nuclear Dynamics of Molecules in Intense Laser Fields: Quantum Mechanical Wave Packet Approaches. Bcsj (2006) 79:196–227. doi:10.1246/bcsj.79.196

CrossRef Full Text | Google Scholar

118. Kübel M, Spanner M, Dube Z, Naumov AY, Chelkowski S, Bandrauk AD, et al. Probing Multiphoton Light-Induced Molecular Potentials. Nat Commun (2020) 11:2596. doi:10.1038/s41467-020-16422-2

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Kato T, Yamanouchi K. Time-Dependent Multiconfiguration Theory for Describing Molecular Dynamics in Diatomic-like Molecules. J Chem Phys (2009) 131:164118. doi:10.1063/1.3249967

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Ide Y, Kato T, Yamanouchi K. Non-Born-Oppenheimer Molecular Wave Functions of H2 by Extended Multi-Configuration Time-Dependent Hartree-Fock Method. Chem Phys Lett (2014) 595-596:180–4. doi:10.1016/j.cplett.2014.01.055

CrossRef Full Text | Google Scholar

121. Kato T, Ide Y, Yamanouchi K. Molecular Wave Function and Effective Adiabatic Potentials Calculated by Extended Multi-Configuration Time-Dependent Hartree-Fock Method. AIP Conf Proceed (2015) 1702:090024. doi:10.1063/1.4938832

CrossRef Full Text | Google Scholar

122. Azumi T, Matsuzaki K. What Does the Term “Vibronic Coupling” Mean? Photochem Photobiol (1977) 25:315–26. doi:10.1111/j.1751-1097.1977.tb06918.x

CrossRef Full Text | Google Scholar

123. Lötstedt E, Kato T, Yamanouchi K. Time-Dependent Multiconfiguration Method Applied to Laser-Driven H₂⁺. Phys Rev A (2019) 99:013404. doi:10.1103/PhysRevA.99.013404

CrossRef Full Text | Google Scholar