- Ultrafast Dynamics Group, Institut für Physik, Carl von Ossietzky Universität Oldenburg, Oldenburg, Germany
In this review, we report on recent progress in the generation and application of multichromatic polarization-tailored pulse sequences for the coherent control of multiphoton ionization (MPI) dynamics and present unpublished experimental results that complement our previous findings. Specifically, we utilize single-color, bichromatic, and trichromatic polarization-controlled pulse sequences generated by spectral amplitude, phase and polarization modulation of a carrier-envelope phase (CEP)-stable white light supercontinuum for MPI. The analysis of the number of ionization pathways and the number of distinct final free electron states shows that both increase significantly, but scale differently with the number of absorbed photons and the number of pulses in the sequence. In our experiments, ultrafast polarization shaping is combined with high-resolution photoelectron tomography to generate, control, and reconstruct three-dimensional photoelectron momentum distributions from atomic and molecular MPI. We discuss the use of polarization-controlled single-color and bichromatic pulse sequences in perturbative and non-perturbative coherent control of coupled electron-nuclear dynamics in molecules, atomic spin-orbit wave packet dynamics and the directional photoemission from atoms and chiral molecules. We compare the coherent control of CEP-insensitive intraband multipath interference in the MPI with a fixed number of photons with CEP-sensitive interband multipath interference in the ionization with a different number of photons. The generation and control of free electron vortices with even-numbered rotational symmetry by MPI with single-color pulse sequences is contrasted with the bichromatic control of CEP-sensitive electron vortices with odd-numbered rotational symmetry. To illustrate the potential of multichromatic pulse sequences for coherent control, we present a trichromatic scheme for shaper-based quantum state holography.
1 Introduction
The basic principles of coherent control have been established more than 30 years ago [1–6]. Today many applications of coherent control have been demonstrated in various areas of physics and chemistry including multiphoton excitation [7–10] and ionization (MPI) of atoms [11, 12] and small molecules [13–15], electronic transitions in condensed matter [16], controlled molecular dissociation [17], spectroscopy [18, 19] and laser chemistry [20, 21]. Even in emerging fields such as high harmonic generation (HHG) [22, 23], material processing [24, 25], nonlinear microscopy [19], photoassociation [26], nanomaterial research [27] and quantum information [28] coherent control has proven its usefulness. A very effective method to control the dynamics of quantum systems is by specific manipulation of constructive and destructive quantum interferences [29] using ultrashort tailored laser pulses. Advanced techniques for generating tailored ultrashort laser pulses on the one hand and for highly differential detection on the other hand, have been key to experimental advances in coherent control. Since the implementation of the first single layer 128 pixel pulse shaping devices [30–40], remarkable advances have been achieved towards high precision pulse shaping using 640 pixel devices [41–50] and polarization shapers [51, 52], vector-field synthesizers [53–58] and supercontinuum pulse shaping [59–66]. Recently, we have introduced a scheme for polarization shaping of carrier-envelope phase (CEP)-stable over-octave-spanning white light supercontinua (WLS) to generate polarization-tailored bichromatic fields [65]. The latter work resulted in the experimental demonstration of a new class of cycloidal pulse shapes, such as counterrotating circularly polarized (CRCP) and corotating circularly polarized (COCP) cycloidal fields. In general, polarization-tailored multicolor femtosecond laser fields have opened up new perspectives in numerous applications ranging from HHG [67–72, 74, 75] over the coherent control of ultrafast electron dynamics in atoms and molecules [73, 76–78] to the manipulation of coherent excitations in nanostructures [79, 80].
The use of advanced polarization-shaped pulses for the generation of free electron wave packets by MPI has necessitated 3D detection to characterize the full 3D photoelectron momentum distribution (PMD). While time-of-flight techniques enabled the kinetic energy-resolved detection of photoelectrons from ultrafast MPI dynamics [81, 82], their angular distribution became available through the use of velocity map imaging (VMI) techniques [83–85]. Currently, the most sophisticated detection method is based on COLTRIMS [86, 87]. Cylindrically symmetric PMDs can be retrieved from the measured 2D projections using the Abel-inversion technique [88]. In order to image non-cylindrically symmetric PMDs, we have introduced a VMI-based photoelectron tomography technique [89]. By now, photoelectron tomography has become an established method with versatile applications including 3D imaging of PMDs from atomic strong-field ionization [90], the reconstruction of molecular PMDs in the laboratory [91] and molecular [92] frame, the retrieval of circularly polarized XUV fields from HHG [93] or the reconstruction of PMDs from strong-field photodetachment of negatively charged ions [94]. Applications of photoelectron tomography have ranged from the generation and characterization of designer electron wave packets [95, 96] and multiphoton photoelectron circular dichroism (PECD) measurements [97] to the extraction of transition matrix elements from tomographic data [98]. More recently, we have used photoelectron tomography to study free electron angular momentum wave packets [99], spin-orbit [100] and Rydberg wave packet dynamics [101] and photoelectron vortices with even [102–104] and odd [73] rotational symmetries. An overview of our recent photoelectron tomography studies of coherent control of atomic MPI can be found in [105, 106].
In this contribution, we review the application of shaper-generated multichromatic polarization-controlled fields for coherent control of atomic and molecular MPI. We study the quantum dynamics of atomic and molecular model systems induced by absorption of
2 Theory
The MPI of atoms and molecules has been studied extensively both experimentally and theoretically. The fundamentals are documented in a vast body of literature, see for example [107–112]. In this section, we present the notation to describe multichromatic pulse sequences (Section 2.1) and summarize the theoretical concepts based on either non-perturbative description of the atomic and molecular neutral dynamics perturbatively coupled to the continuum (Section 2.2) or fully perturbative intraband and interband interference in MPI. The theoretical description is specifically adapted to reproduce the experimental results and discuss the relevant control aspects.
2.1 Ultrashort Polarization-Controlled Multichromatic Pulse Sequences
We start by describing the electric field of a pulse sequence consisting of
The coefficients
For example,
The total field is obtained by superposition of all
The physical field is given by Re[E(t)]. Schematic representations of single-color (
2.2 Simulation of Multiphoton Ionization
Many theoretical concepts and numerical methods are available to describe and simulate the quantum dynamics of atoms and molecules induced by the interaction with ultrashort laser pulses [4, 6, 114]. In the past two decades, we have used different methods to model ultrafast dynamics driven by shaped femtosecond pulses to model our experiments and interpret our observations. In parallel with our experimental studies, we have presented the corresponding theoretical descriptions and numerical simulations of the multilevel coherent control of atomic [115, 116] and molecular [117, 118] excitation. We have devised a resonant strong-field control mechanism based on the manipulation of dressed state populations and energies [119] and, in this context, developed a formalism to model photoelectron spectra from resonance-enhanced multiphoton ionization (REMPI) accounting for non-perturbative population dynamics and AC Stark shifts [118, 120]. In [48, 103], we provided a description for the calculation of sculpted 3D free electron wave packets from MPI, including the energy and angular distribution. Recently, we employed ab initio methods to numerically solve the time-dependent Schrödinger equation (TDSE) for a 2D model atom interacting with a polarization-tailored bichromatic femtosecond laser pulse sequence [121]. The model was applied to reproduce and analyze our experimental results reported in [73, 103] taking into account phase fluctuations in the CEP and the Gouy phase.
2.2.1 Non-Perturbative Neutral Dynamics Coupled to the Continuum
Resonant strong-field control of MPI dynamics is based on the non-perturbative manipulation of resonant bound state dynamics and the simultaneous perturbative mapping of those dynamics into the ionization continuum by absorption of additional photons. To model this type of non-perturbative REMPI processes we adapt the concept from Meier et al. [122] and divide the calculation into two steps. In the first step, we calculate the non-perturbative neutral dynamics of the time-dependent amplitudes ci(t) by solving the corresponding TDSE numerically for a multistate quantum system, including all relevant bound states. This procedure yields the time-dependent bound state populations |ci(t)|2. In the second step, we compute the photoelectron kinetic energy spectrum using time-dependent perturbation theory by inserting the amplitudes determined in the first step. This strategy is illustrated in Figure 1A for a generic atomic system and in (B) for the potassium molecule.
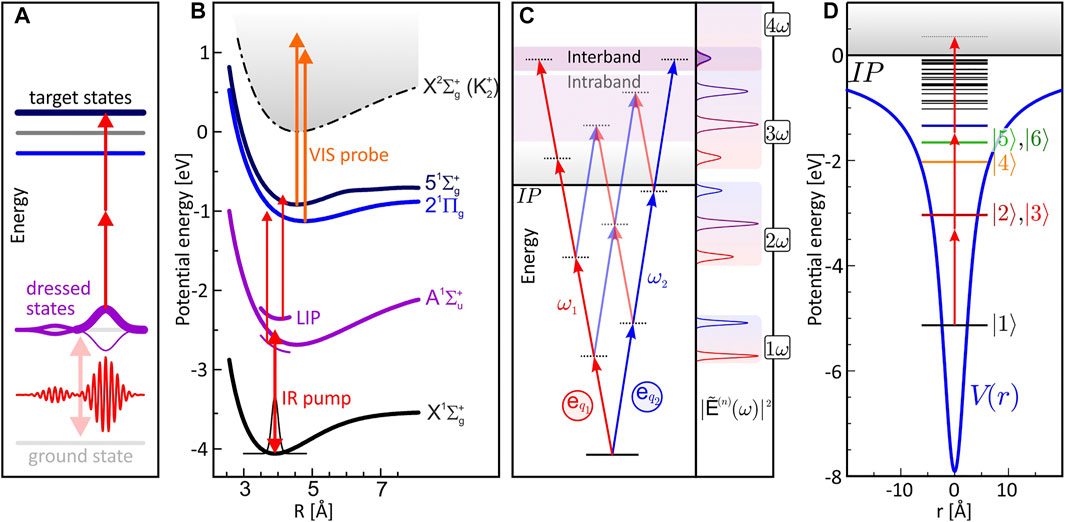
FIGURE 1. Generic ionization schemes: (A) and (B) Non-perturbative neutral dynamics perturbatively coupled to the continuum [119]. (A) Generic scheme for the selective population of dressed states [119]. (B) Light-induced potentials of potassium dimers for ultrafast switching via the selective population of dressed states. (C) Scheme for perturbative control of intraband [73] and interband [105] MPI with polarization-shaped pulses along with multiphoton spectra. (D) Model potential for ab initio simulations of MPI with cycloidal laser pulses [121].
2.2.1.1 Atomic Multiphoton Ionization
To simulate our experiments, we have modeled atomic systems by multilevel schemes involving two [120, 123–125], three [48, 116] or more [115] bound states. As an example, we consider a two-level atom, consisting of a ground state |1⟩ and an excited state |2⟩ separated in energy by ℏω21 = ℏω2−ℏω1 and coupled by the transition dipole moment μ21. The non-perturbative dynamics of the atom interacting with an intense near-resnant femtosecond laser pulse
Herein, δ = ω0−ω21 is the detuning of the laser with respect to the atomic resonance. The TDSE in Eq. 5 is solved numerically on a discrete temporal grid using short-time propagator methods [4]. This procedure yields the time evolution of the state vector
The notation was adapted from Dudovich et al. [128]. The multiphoton transition dipole moment
2.2.1.2 Molecular Multiphoton Ionization
Molecular systems are modeled in the framework of the Born-Oppenheimer approximation by a set of N bound electronic states |ϕn⟩ characterized by the adiabatic potential energy curves Vn(R). For simplicity, we restrict ourselves to the diatomic case, where the nuclear coordinate R denotes the internuclear separation of the atoms and describes the vibration of the molecule. In the electronic basis, the TDSE for the state vector
The time-dependent probability amplitudes ψn(R, t) of the electronic states describe the nuclear wave packets in the electronic potentials Vn(R). Making use of the dipole approximation, the Born-Oppenheimer Hamiltonian is given by [132]
with the reduced mass mr of the molecule. Explicit expressions of the Hamiltonian matrix are provided in [118, 132]. The diagonal matrix
To calculate the photoelectron contribution from a bound electronic state Vn(R), produced by perturbative one-photon ionization with a probe pulse
If ΔVn(R) is non-monotonous within the ionization window, i.e. ΔVn′(R) vanishes locally, we decompose the wave packet into a set of Gaussian functions which are locally mapped into Gaussian-shaped photoelectron distributions with a narrow, but finite spectral width in the order of the experimental energy resolution. The second approach is based on a perturbative quantum mechanical treatment of the ionization process. Consider a transition from the bound vibrational eigenstate ν to an ionic vibrational eigenstate ν′ with the transition frequency ων′ν = ων′−ων. For a fixed spectral component ω of the probe pulse spectrum
The quantum mechanical description was used to reproduce and analyze the experimental results in [132, 137]. Using intense PLP single-color multipulse sequences followed by an ionizing probe pulse with a different color, we were able to demonstrate the resonant non-pertubative control scheme described above experimentally [131, 132, 137].
2.2.2 Perturbative Intraband and Interband Interference in Multiphoton Ionization
In this section we consider perturbative atomic MPI with a pulse train consisting of
the order of the MPI process is
which is written down explicitly for a tricromatic field (
Taking the Fourier transform of the temporal multiphoton field
Taking into consideration the selection rules for absorption of RCP (Δm = −1) and LCP (Δm = + 1) photons and ignoring for simplicity Δl = −1, the dipole moments
where we sum over all indices
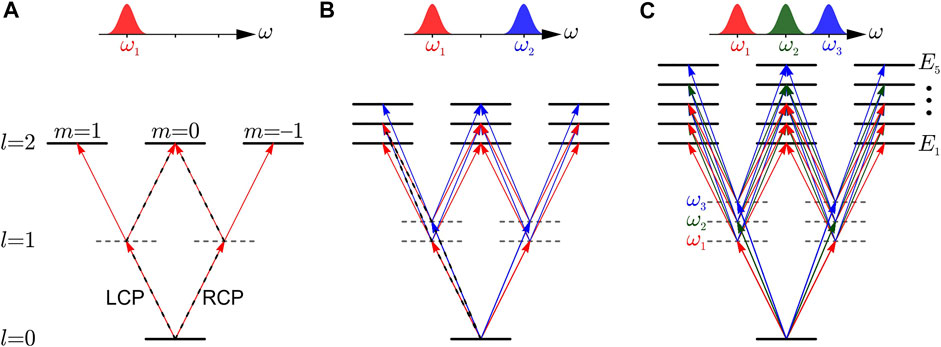
FIGURE 2. Pathways for intraband MPI with
Control of multiphoton processes by multichromatic pulse sequences is based on the interference of multiple pathways leading to the same final state. As we increase the number of pulses, both the number of available quantum pathways and the number of final states increase significantly, opening up more versatile options for control. Figure 2 illustrates the pathways for absorption of
some of which may be degenerate. For each absorption of a photon, there are
An overview of the numbers of angular momentum states

TABLE 1. Overview of the total number of possible pathways for ionization with a given number of photons
In addition to the above discussed intraband interferences characterized by absorption of
If both pathways address overlapping final continuum states, i.e. the energy gained by absorption of
2.2.3 2D Ab Initio Simulation of Atomic Multiphoton Ionization in Cycloidal Laser Fields
Another efficient method to simulate atomic photoionization dynamics by polarization-shaped ultrashort laser fields is based on solving of the TDSE numerically for a 2D model system aligned in the laser polarization plane. In [121], we employed the 2D model potential shown in Figure 1D
with the error function erf and a soft-core parameter a, and solved the TDSE for the time-dependent Hamiltonian
on a 2D grid using the Fourier-based split-operator method [134]. Specifically, atomic MPI with cycloidal, i.e. COCP and CRCP, femtosecond laser pulse sequences was investigated. Employing single-color pulse sequences, we were able to reproduce selected recent experimental results on the generation of photoelectron vortices [102, 103] and to analyze the transient vortex formation dynamics in different physical pictures, including the bound state population dynamics, the time evolution of the free electron wave function and its asymptotic topological charge. Employing cycloidal bichromatic fields, we reproduced the experimental results on the generation of free electron wave packets with odd rotational symmetries [73]. We analyzed the final state wave function with respect to the relative orientation between field and PMD and extracted the azimuthal probability density current to validate the physical discussions in the experimental studies [73, 105, 106]. Furthermore, the simulations allowed us to examine the influence of experimental CEP and Gouy phase fluctuations on the measured PMD. Eventually, we applied the technique to investigate photoelectron vortices theoretically in so far unexplored intensity regimes.
3 Experiment
In this section, we introduce our experimental scheme for the coherent control of ultrafast MPI dynamics in atoms and molecules using polarization-tailored single-color or multichromatic fields. In the experimental studies, we combine advanced supercontinuum pulse shaping techniques with the highly differential detection of photoelectrons using a VMI spectrometer. The experimental setup is portrayed in Figure 3. CEP-stable polarization-shaped laser pulse sequences are generated using a phase-stabilized white light polarization shaper in 4f geometry. Photoelectron wave packets, released by the interaction of the shaped pulses with the atomic or molecular sample in the VMI spectrometer, are observed with energy and angular resolution. By rotating the pulses about the laser beam axis using a wave plate, the VMI spectrometer is turned into a photoelectron tomography apparatus, allowing us to retrieve the full 3D PMD. In the following, we give an overview of white light polarization shaping in Section 3.1 and photoelectron tomography in Section 3.2. For a more detailed description of both techniques, we refer to [106].
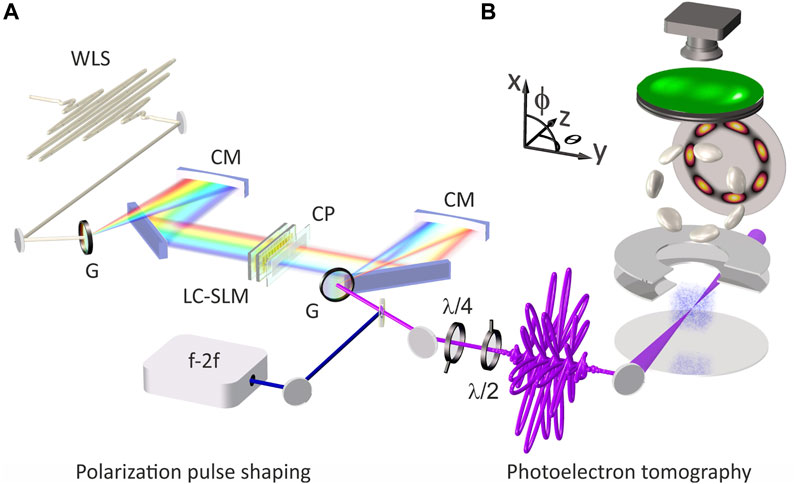
FIGURE 3. Experimental setup for multichromatic coherent control of MPI utilizing a white light polarization pulse shaper (A) and a photoelectron VMI spectrometer (B). Multichromatic amplitude, phase and polarization tailoring of an input WLS is implemented by a specifically adapted polarization shaper in folded 4f geometry. The WLS input beam is spectrally dispersed at the input grating (G), collimated at the cylindrical mirror (CM) and spectrally modulated in the Fourier plane by a dual-layer LC-SLM and a custom composite polarizer (CP). Active CEP-stabilization is realized by an f-2f interferometer feeding the control loop of the laser system. A superachromatic λ/4 wave plate at the output allows to generate circularly polarized pulse sequences. Using an additional λ/2 wave plate, the shaped laser pulse is rotated about the beam axis, which is the basis for VMI-based photoelectron tomography. The VMI spectrometer on the right consists of an electrostatic lens system projecting the PMD onto an microchannel plate detector attached to a phosphor screen. Images of the resulting 2D projections are recorded with a charge-coupled device camera. Exemplarily, a CRCP (3ω:4ω) output pulse is depicted in magenta along with the tomographically reconstructed 3D PMD created by MPI of potassium atoms.
3.1 Supercontinuum Polarization Pulse Shaping
Various experimental schemes for the generation of multicolor laser fields have been reported, including 4f pulse shapers adapted to an octave-spanning WLS [61, 64] and extensions to optical waveform synthesizers [139, 140] as well as four-wave mixing schemes [141] and molecular modulation [142–144]. Our method to generate multichromatic polarization-tailored pulse sequences is based on 4f-polarization pulse shaping of a white light supercontinuum. The primary light source of our experiments is an actively CEP-stabilized multipass chirped pulse amplifier system (Femtolasers Rainbow 500, CEP 4 module, Femtopower HR 3 kHz) providing 20 fs infrared pulses centered at 790 nm with an energy of 1.0 mJ. These pulses are used to seed a neon-filled hollow-core fiber (absolute pressure ∼ 2.0 bar) generating an over-octave spanning WLS which is amplitude- and phase-modulated in the spectral domain using a home-built 4f polarization pulse shaper [48, 50, 51, 145]. While traditional 4f pulse shaping allows for either independent amplitude and phase modulation or phase and polarization shaping [51, 145], recently we introduced a pulse shaping scheme specifically adapted for the independent shaping of amplitude, phase and polarization of bichromatic fields [65, 106, 146]. The bichromatic white light polarization shaper is shown on the lefthand side of Figure 3. Bichromatic amplitude profiles are sculptured from the WLS via combined amplitude and phase modulation using a traditional polarization shaping setup consisting of a 640 pixel dual-layer liquid crystal spatial light modulator (LC-SLM) in the Fourier plane of a folded 4f setup with holographic transmission gratings at the in- and output. A customized composite polarizer mounted directly behind the LC-SLM enables independent polarization control of both spectral bands (colors). Along the spectral axis, the polarizer is divided into two parts, each of which can be chosen in s- or p-configuration, resulting in the generation of either bichromatic PLP (both colors s- or p-polarized) or OLP (one color s-, the other one p-polarized) fields. The bichromatic pulse shaping approach allows us to control the center frequency ratio, spectral bandwidths and amplitude profiles of both spectral bands and, moreover, independently permits the application of arbitrary phase modulation functions. By use of a superachromatic quarter wave plate (λ/4) at the shaper output, we generate circularly polarized single-color or bichromatic pulse sequences. An additional half wave plate (λ/2) is used to rotate the polarization-shaped laser pulses about the propagation axis, which is the basis for the photoelectron tomography technique discussed in Section 3.2. To ensure the CEP-stability of the shaped pulses, we use the shaper to generate an additional (ω: 2ω) field which is split off the main beam by a dichroic mirror and sent to an f-2f interferometer. The interferometer feeds the active control loop of the amplifier, which stabilizes the CEP of the shaped pulses before they are focused into the VMI spectrometer. The root mean squared CEP stability after the shaper was measured over 11 h and is better than 215 mrad [101]. Finally, dispersion control and pulse characterization are implemented in situ, i.e. in the interaction region of the VMI spectrometer, by using the shaper for adaptive optimization of the highly nonlinear MPI of xenon atoms and to perform shaper-based cross-correlation measurements [146].
3.2 Photoelectron Tomography
In order to study the full 3D PMD caused by the interaction of atoms and molecules with polarization-tailored ultrashort laser pulses, we employ the VMI technique [83, 103] for the energy- and angle-resolved measurement of photoelectron wave packets. The VMI spectrometer is shown on the righthand side of Figure 3. The tailored laser pulses are focused via a broadband silver mirror with a focal length of 250 mm into the interaction region of the VMI spectrometer. The background pressure is typically in the order of 5 × 10−7 mbar. All experiments were carried out in the gas phase. Alkali atomic samples are supplied by dispenser sources (working pressure: ∼10−7 mbar), whereas rare gases or molecular samples are injected using an effusive gas-inlet (working pressure: ∼10−6 mbar). An electrostatic lens setup consisting of a repeller, an extractor and an Einzellens, projects the 3D PMD created by MPI of the sample by the incident laser pulses onto a chevron-type microchannel plate detector stacked with a phosphor screen. The resulting 2D image of the projected PMD is recorded by a charge-coupled device camera. PMDs created by MPI with either linearly or circularly polarized laser pulses are, in general, cylindrically symmetric and can therefore be reconstructed from a single 2D image via Abel inversion, e.g. using the pBASEX algorithm [88]. In contrast, PMDs created by polarization-shaped pulses typically exhibit no such symmetry. For the retrieval of 3D PMDs with arbitrary shape, we developed a tomographic reconstruction technique [89] based on the rotation of the laser pulse—and hence the PMD—using a superachromatic λ/2 wave plate. After acquiring numerous 2D projections of the PMD under various rotation angles, we retrieve the 3D PMD by application of tomographic techniques such as the Fourier slice algorithm [89, 147, 148] or the backprojection algorithm [90, 147, 149]. An advantage of the Fourier slice method is that the angular discretization inherent to the measurement appears only in the Fourier domain representation, whereas the retrieved real-space PMD is angularly smooth. For a typical tomographic measurement, we use about 45 different orientations of the λ/2 wave plate ranging from −90° to 86°. Energy calibration of the reconstructed 3D PMD is performed by taking 151 azimuthal 2D slices through the 3D data cube and convert the radial momentum distributions into corresponding energy distributions. We estimate an energy-resolution of better than 80 meV for photoelectrons with a kinetic energy of about 1 eV. Thus, our VMI-based photoelectron tomography technique is well suited to retrieve the highly structured 3D PMDs generally created by MPI with multichromatic polarization-shaped laser pulse sequences. Similar tomographic techniques have been applied, e.g., for the imaging of molecular orbitals [148], the discrimination of chiral molecules via the multiphoton PECD [150] and the time-resolved imaging of ultrafast laser-matter interactions inside transparent media [149].
4 Results and Discussion
In this section, we discuss our experimental results on photoelectron tomography of 3D PMDs obtained by atomic and molecular MPI using multichromatic polarization-controlled pulse sequences. We present our findings in the order of the type of pulse sequence: We start with experiments on MPI with single-color pulse sequences in Section 4.1 and focus on various coherent control scenarios by bichromatic pulse sequences in Section 4.2. New results on trichromatic pulse sequences are presented in Section 4.3.
4.1 Single-Color Pulse Sequences
Single-color pulses consist of a single connected spectral band with bandwidth Δω centered around a carrier frequency ω1. A set of single-color pulse sequences for different polarizations is depicted in Figure 4. These pulses are the starting point of our discussion.
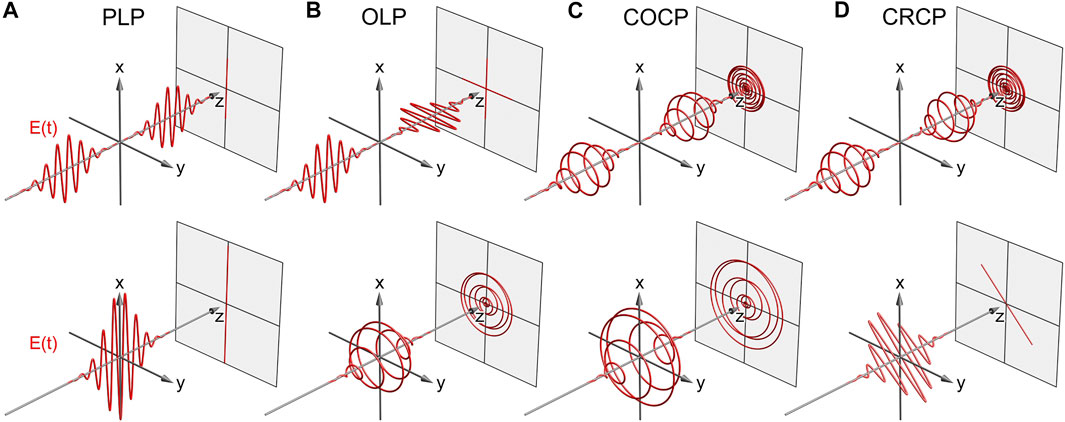
FIGURE 4. Single-color pulse sequences. The projection in z-direction visualizes the time-dependent electric field vector at the position of the atom or molecule. (A) PLP, (B) OLP, (C) COCP and (D) CRCP single-color pulse sequences. Upper figures: Sequence with separated pulses τ > 2Δt, lower figures: Coinciding pulses at τ = 0.
4.1.1 Single-Color Linearly Polarized Pulse Sequences
Single-color PLP pulse sequences with variable time-delay τ, as shown in Figure 4A, are the standard tool in pump-probe experiments [151]. Even in the overlapping region τ ≈ 0, such pulses remain linearly polarized. In contrast, OLP pulse sequences, as shown in Figure 4B, additionally address the spatiotemporal aspect of the light-matter interaction due to their time-dependent polarization. Their application ranges from the phase-control of currents in semiconductors [152] to the steering of molecular rotation [153, 154]. Crossed polarizations demand a vectorial description of the field and thus provide access to the angular properties of the interaction energy
4.1.1.1 Perturbative Multiphoton Ionization
In [11], Wollenhaupt et al. have used phase-locked pairs of linearly polarized single-color pulses to study the interference of ultrashort free electron wave packets generated by perturbative MPI of potassium atoms. By variation of the time delay in the PLP sequence, the interference pattern in the photoelectron kinetic energy spectrum from one-photon ionization of the excited 5p state was controlled. The observation of interferences in the photoelectron spectrum demonstrated that the coherence properties of the ultrashort laser pulses were transferred to the electrons. Using OLP sequences, i.e. crossed polarizations, no such interference fringes have been found in the threshold electrons. However, the quantum interferences reappeared at twice the modulation frequency in the above-threshold ionization (ATI).
To rationalize the experimental findings reported in [11], we apply the general formalism discussed in Section 2.2.2 to describe one- and two-photon ionization of a pre-excited atom with single-color PLP and OLP pulse sequences and analyze the full 3D PMD. Figure 5A shows a schematic energy level diagram of potassium atoms for the excitation of the 5p state and subsequent photoionization at the threshold (THR) and the ATI. The description in the spherical basis provides a consistent picture for excitation and ionization with both PLP and OLP sequences. Simulated PMDs at the ionization threshold and the ATI are depicted in Figure 5B. The left column shows the PMDs from ionization with either a single pulse or a PLP pulse sequence whose polarizations are parallel (p) to the initial blue excitation pulse. Ionization with a single orthogonal (o) polarized pulse or an OLP pulse sequence are depicted in the right column. To calculate the modulation of the interference in the photoelectron spectra, we first consider the wave function in the excited 5p state prepared by the initial, linearly polarized blue (405 nm) laser pulse. In the spherical basis, the p state is a superposition of the two ψ1,±1 states
Taking into account the transition dipole moments determined by the Wigner 3-j symbols, the absorption of another parallel or orthogonal polarized photon from the 5p state yields the wave functions for the photoelectrons at the ionization threshold
By calculating the electron density ρ(ɛ, θ, ϕ) = |Ψ(ɛ, θ, ϕ)|2, we see that ionization with a parallel polarized field yields the expected d-type electron density
characterized by the interference structures in the electron density
yielding the fully cosinusoidally modulated spectrum in agreement with the experimental results [11]. In contrast, in the OLP case, the superposition of two different wave functions
results in the highly patterned electron density
In the next step, we apply the same procedure to analyze the PMDs at the ATI. To this end, we write down the corresponding wave functions and densities and calculate the photoelectron spectra to rationalize the experimental findings in the ATI spectrum. Absorption of another parallel (orthogonal) linearly polarized photon from the threshold states given by Eq. 22 yields the wave functions in the ATI
The corresponding densities
Again, in the PLP case, the PMDs given by
Using the above method to calculate the PMDs from two-photon ionization with an OLP sequence, given by
In contrast to the unmodulated photoelectron spectra from ionization with OLP pulses at the threshold (Eq. 26), the spectra in the ATI are indeed modulated—albeit more weakly—in the OLP case in agreement with the experimental work.
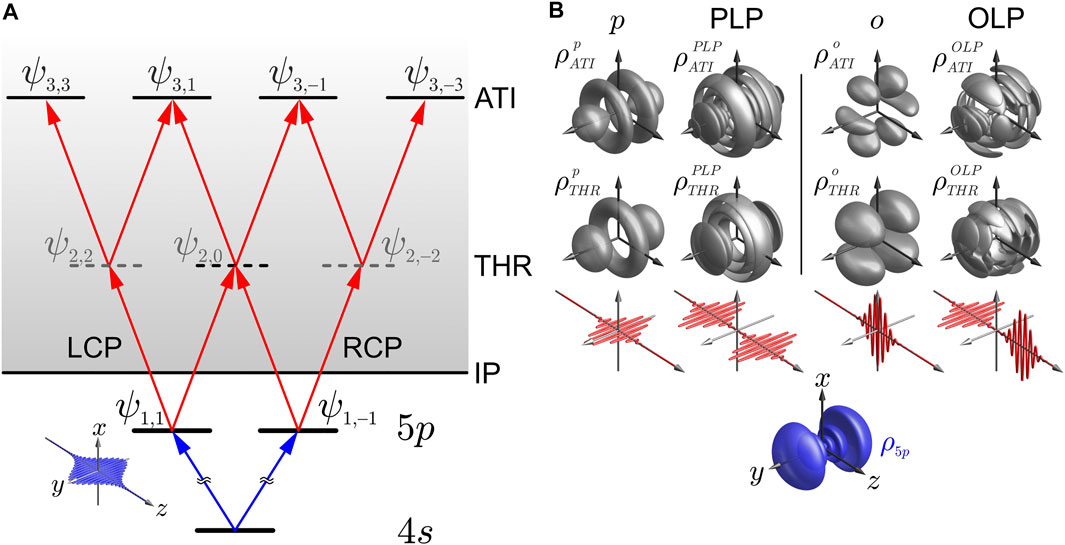
FIGURE 5. One- and two-photon ionization of potassium atoms with an infrared PLP or OLP pulse sequence after preparation of the atom in the excited 5p state by a blue prepulse. (A) Energy level diagram for excitation and ionization in the spherical basis. (B) Simulated electron densities of the excited 5p state (bottom) and the emitted photoelectron at the threshold (middle row) and ATI (top row). Left side of each column: Single pulse ionization at the threshold and the ATI for parallel
In another polarization-sensitive pump-probe experiment, single-color PLP and OLP pulse sequences have been used to control the perturbative MPI of potassium molecules [52]. It was demonstrated that the ionization efficiency is higher for OLP pulses than for PLP pulses. This result was rationalized by the orthogonality of transition dipole moments encountered along the major MPI pathways in the potassium dimer. The experiment, which included the first demonstration of control of molecular dynamics via ultrafast polarization shaping, showed that tailored polarization-shaped pulses are better suited than the corresponding linearly polarized fields to manipulate the spatiotemporal evolution of molecular wave functions.
4.1.1.2 Non-perturbative Resonance-Enhanced Multiphoton Ionization
The basic concept behind the non-perturbative control of REMPI processes is depicted in Figure 1A. The scheme is based on the selective population of dressed states (SPODS), recently reviewed in [119], by a sequence of PLP single-color femtosecond laser pulses. A relatively weak prepulse with a pulse area of π/2 [5] with respect to the resonant transition—typically between the ground and first excited state—is followed by an intense main pulse. Initially, the prepulse excites an electronic wave packet of maximum coherence, i.e., an efficient charge oscillation described by a time-dependent induced dipole moment
Resonant non-perturbative control via SPODS was first reported on 1 + 2 REMPI of potassium atoms [123]. Using interferometric double pulse sequences, we demonstrated efficient ultrafast switching between different ionization target channels by controlling the dressed state populations of the resonant 4s−4p transition via the relative optical phase. The interpretation of the scheme in a dressed state picture, was presented in [124]. On the same system, we also implemented SPODS with PLP single-color multipulse trains generated by sinusoidal spectral phase modulation [120]. In that work, dressed state control by all sine-parameters was demonstrated.
Subsequently, we applied SPODS to the non-perturbative control of coupled electron-nuclear dynamics in molecules. In the molecular case, the charge dynamics induced by the prepulse is altered due to the coupling between electronic and nuclear degrees of freedom. For example, the amplitude of the dipole oscillation depends on the overlap of vibrational wave packets launched in the resonant electronic states. Also, as the vibrational wave packets propagate, the electronic resonance frequency varies changing the eigenfrequency of the dipole and introducing an additional phase drift which the main pulse needs to adapt to. Our proof-of-principle studies were performed on the potassium dimer serving as a molecular prototype system. The corresponding excitation scheme is depicted in Figure 1B. The prepulse resonantly couples the
4.1.2 Free Electron Vortices With Circularly Polarized Pulse Sequences
In this section we consider the creation of free electron wave packets by REMPI of potassium atoms with single-color circularly polarized pulse sequences (Figures 4C,D). First, in Section 4.1.2.1, we discuss the formation of a FEV by perturbative MPI at the ionization threshold with c6 rotational symmetry and in the ATI with c8 rotational symmetry. In addition, we study the evolution of the c6 FEV into an angular momentum eigenstate as the time-delay in the sequence vanishes. Then, non-perturbative REMPI resulting in a FEV with c4 rotational symmetry is examined in Section 4.1.2.2. We show, how the wave function of the latter FEV is reconstructed using a holographic method.
4.1.2.1 Perturbative Resonance-Enhanced Multiphoton Ionization
Recently, the generation of FEVs by photoionization with two time-delayed CRCP attosecond laser pulses has been theoretically predicted and termed “an unusual kind of Ramsey interference” [155]. FEVs with
Note that, in the single-color case l1 = l2. Motivated by the helical interference structures in the electron density, Starace and coworkers [155] coined the term “electron vortex” for this type of PMD. In general, this notion of an electron vortex is not identical with a vortex state defined by its non-vanishing azimuthal probability density current
where
produces a vortex-shaped electron density distribution. In the same work, it was shown that changing from MPI with a time-delayed single-color CRCP sequence to the corresponding single-color COCP sequence (Figure 4C) results in the wave function
corresponding to a toroidal PMD with spectral interference fringes in the radial (energy) direction spaced by h/τ. Subsequently, Pengel et al. [103] reported on the formation of FEVs from polarization-shaped supercontinua and on the generation of an eight-armed FEV in the ATI with the wave function
The c8 rotationally symmetric FEV in the ATI is shown in Figure 6C. The time-dependent electric field of single-color CRCP sequences shown in Figure 4D reveals that, as the time delay vanishes, the sequence evolves into a linearly polarized field whose orientation is determined by the relative phase between the LCP and RCP components. In Figure 6D we present results from tomographic reconstruction of the PMDs as τ → 0. The initial c6 rotationally symmetric FEV (τ = 20 fs) evolves into a distorted vortex (14 fs) with more and more pronounced lobes in the vicinity of the x-axis at 10 fs and eventually turns into the rotated angular momentum state
where the amplitudes have been taken from Eq. 27. This result can be checked by decomposition of the rotated state into the unrotated basis
where
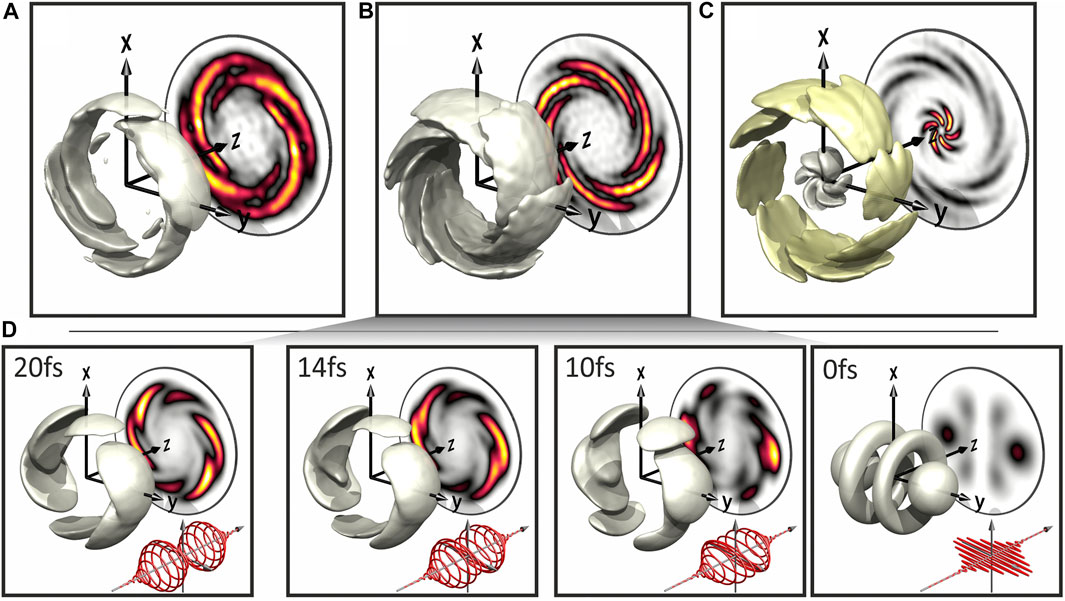
FIGURE 6. Tomographically reconstructed Archimedean spiral-shaped FEVs with c4, c6 and c8 rotational symmetry from 1 + 2 REMPI of potassium atoms using single-color CRCP pulses along with their projection in the z-direction [103]. (A) Non-perturbative REMPI with a sequence of two π pulses creates a FEV with four arms. (B) Perturbative REMPI gives rise to a six-armed FEV. (C) Absorption of an additional photon in the continuum results in an eight-armed FEV in the ATI. (D) Evolution of the c6 FEV as the time delay decreases from τ = 20 fs to τ = 0 fs.
4.1.2.2 Non-Perturbative Resonance-Enhanced Multiphoton Ionization
So far, we discussed c6 and c8 rotationally symmetric FEVs generated by perturbative three- and four-photon ionization, respectively, with the intermediate resonant 4p state being only weakly populated and not contributing significantly to the vortex formation. In contrast, it was demonstrated that FEVs with c4 rotational symmetry can be generated by non-perturbative REMPI [102]. By using CRCP pulse sequences with a pulse area of π [5], the 4s state was fully depleted and the 4p state fully populated. Hence, ionization with the second pulse started from the excited 4p state resulting in a wave function characterized by the superposition of angular momentum states with different values of |m|
The tomographic reconstruction of the corresponding PMD depicted in Figure 6A shows a FEV with four arms. Using the same REMPI scheme, Pengel et al. [103] demonstrated a holographic method for direct measurement of the wave function of the non-perturbative c4 vortex by measuring a π shift in the azimuthal interferences in the polar direction of the vortex due to the polar nodal line of the ψ3,1 angular momentum state.
4.2 Bichromatic Pulse Sequences
In this section, we discuss a number of applications of bichromatic polarization-shaped pulse sequences for femtosecond spectroscopy and coherent control of ultrafast quantum dynamics [105, 106]. Bichromatic fields are characterized by two spectral bands with individual bandwidths of Δω1 and Δω2 centered around two different carrier frequencies ω1 and ω2, as detailed in [99]. The spectral band with the lower (higher) carrier frequency is typically referred to as red (blue) component. Our shaper-based approach for the generation of bichromatic fields offers independent control over the amplitude, phase and polarization profile of the field [65, 146]. Shaper-generated polarization-tailored bichromatic fields are therefore very versatile, not only regarding their use in bichromatic coherent control schemes but also in terms of their application in time-resolved studies of ultrafast dynamics. For example, employing a linear spectral phase function (ω−ωi) ⋅ τ allows us to introduce a variable time delay τ between the two colors to generate bichromatic pulse sequences for polarization-sensitive two-color pump-probe experiments [177]. Several examples of polarization-controlled bichromatic pulse sequences, with both colors being fully separated in time, are depicted in the top row of Figure 7, including the prototypical PLP, OLP, COCP and CRCP fields. The bottom row illustrates the same sequences for τ = 0. In contrast to the single-color case, temporally overlapping bichromatic fields occur in a plethora of shapes and symmetries, depending on the frequency ratio, polarization, amplitude and relative phase of the two colors. For example, in the OLP case shown in Figure 7B, the bichromatic polarization profile exhibits a Lissajous-type shape, while in the COCP and CRCP cases, shown in (C) and (D), the polarization profiles are cycloidally shaped. The applications of polarization-tailored bichromatic fields are as versatile as their shapes. For example, PLP bichromatic fields were applied to control plasmon-enhanced photoemission from silver clusters [178] and strong-field photoemission from gold nanotips [79]. OLP bichromatic fields with commensurable frequencies, characterized by Lissajous-type polarization profiles which exhibit a time-varying optical chirality, have been used to investigate sub-cycle variations in the PECD of chiral molecules [179, 180]. Commensurable CRCP bichromatic fields exhibit unique propeller shapes with distinct rotational symmetry. Currently, such fields play a prominent role in HHG [67, 68, 70–72, 181, 182], strong-field ionization [158, 183–186], and were employed for the time-resolved probing of molecular chirality [187]. In the perturbative regime, coherent control of bichromatic MPI is governed by the manipulation of intra- and interband interferences [105] (Section 2.2.2). In the following, we discuss examples for the bichromatic control of MPI in atoms (Section 4.2.1) and molecules (Section 4.2.2).
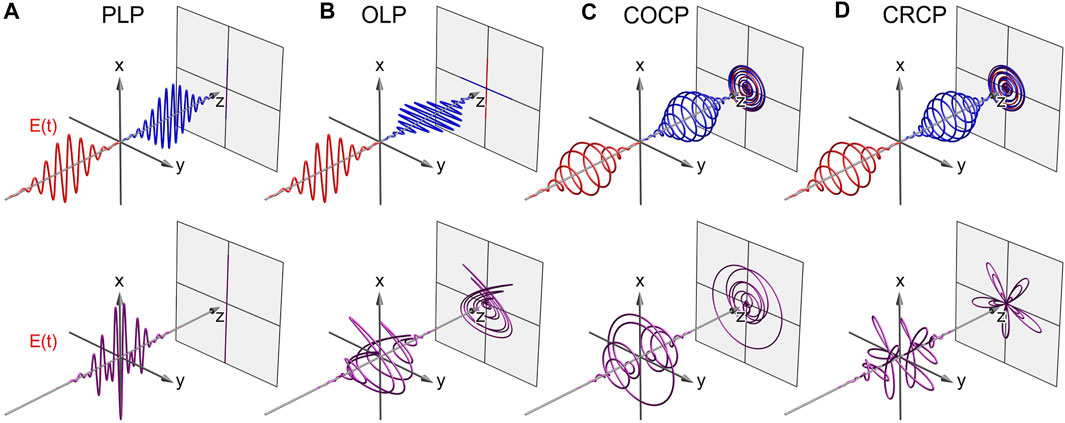
FIGURE 7. Bichromatic pulse sequences. The projection in z-direction visualized the time-dependent electric field vector at the position of the atom or molecule. (A) PLP, (B) OLP, (C) COCP and (D) CRCP bichromatic pulse sequences. Upper figures: Sequence with separated pulses τ > 2Δt, lower figures: Coinciding pulses at τ = 0.
4.2.1 Atomic Multiphoton Ionization
Atomic model systems interacting with multichromatic pulse sequences are ideally suited to elucidate the physical mechanisms underlying the coherent control. In this section, we study two mechanisms of coherent control of multipath interference in the atomic MPI by polarization-tailored bichromatic fields. We compare the CEP-insensitive intraband MPI with
4.2.1.1 Linearly Polarized Bichromatic Pulse Sequences
The two prototypes of linearly polarized bichromatic pulse sequences, PLP and OLP fields, are illustrated in Figures 7A,B, respectively. To illustrate the difference between interband and intraband interferences in optical phase-control, we discuss below the results from bichromatic MPI of alkali atoms using CEP-stable commensurable PLP (3ω:4ω) fields [73] on the one hand and incommensurable OLP bichromatic fields [99, 100] on the other hand. We start by investigating phase-sensitive interband interferences arising from the superposition of continuum states with opposite parity [73, 188]. MPI of sodium atoms with a PLP (3ω:4ω) field creates an f-type photoelectron wave packet (ψ3,0) via 3-photon ionization by the blue pulse (ω2) and a g-type wave packet (ψ4,0) via 4-photon ionization in the continuum by the red pulse (ω1). Both wave packets overlap at a kinetic energy of ɛ = 4ℏω1 = 3ℏω2 resulting in interband interferences. Because the difference between the number of photons absorbed by each partial wave is odd, the resulting photoelectron wave function is a superposition of two states with opposite parity
As illustrated in Figure 8A, this wave function exhibits a directional asymmetry along the laser polarization axis (y-axis), which is sensitive to the CEP. To study the CEP-dependence of the asymmetry, we measured 2D projections of the PMD for φce = 0 and φce = π. The recorded projections were Abel-inverted using the pBASEX algorithm [88]. The retrieved 2D sections of the PMD through the (x, y) polarization plane are shown in the left and middle frames of Figure 8A. The sections display a pronounced left/right asymmetry which is inverted by switching the CEP from 0 to π. To quantify the asymmetry, we derived the asymmetry contrast [105, 189] directly from the measured projections. The result shown in the right frame of Figure 8A reveals a CEP-induced directional asymmetry of up to ±28%. A similar scheme for the control of directional photoemission from xenon atoms by bichromatic MPI with phase-modulated PLP (7ω:8ω) fields was recently reported in [189, 190]. In that contribution, the bichromatic pulses were specifically tailored to induce phase-controlled 7- vs. 8-photon interband interference in the 5P3/2 ionization continuum of xenon. An alternative strategy to steer the directionality of ultrafast electronic processes in atoms [188, 189, 191, 192], molecules [193–195] or solids [196–201] is based on the use of CEP-stable few-cycle femtosecond laser pulses. In this case, however, the interpretation of the interference mechanism is generally complicated by the multitude of MPI pathways connecting the ground state to a specific energy target state. Using shaper-generated commensurable bichromatic fields tailored to the MPI process, has enabled us to excite specific asymmetric target states in the continuum by two-path interband interference, fully controllable via the CEP and the relative phase of the two colors. In contrast to the few-cycle approach, we were thus able to localize phase-controlled asymmetries in a preselected photoelectron energy window [189]. To demonstrate the concept of intraband interference, we employed temporally overlapping (τ < Δt) OLP bichromatic fields with incommensurable frequencies for 3-photon ionization of potassium atoms. While both the blue and the red component produce individual single-color signals centered at ɛ0 = 3ℏω1−ℏωIP and ɛ3 = 3ℏω2−ℏωIP, third-order intrapulse frequency mixing leads to two additional contributions centered at ɛ1 = 2ℏω1 + ℏω2 − ℏωIP and ɛ2 = ℏω1 + 2ℏω2 − ℏωIP, which are energetically disentangled from the single-color signals (cf. Eq. 15) [99, 100]. The measured and tomographically reconstructed 3D PMD is shown in the main frame of Figure 8B. The different above mentioned contributions are color-coded. Since each of the frequency mixing pathways is composed of three photons—albeit with different combinations of red and blue photons—the accumulated optical phase in each target state is identical, rendering the resulting intraband interference of all target states CEP-insensitive. Each of the photoelectron angular distributions within a given energy interval is determined by a specific coherent superposition of angular momentum states as described in Eq. 15. For example, the two single-color signals are described by rotated f-type wave packets perpendicularly to one another along the respective laser polarization axis, i.e. the x- and y-axis for the OLP pulse shown in Figure 7B. The two inner partial wave packets in the energy interval around ɛ1 (magenta) and ɛ2 (purple) resulting from intraband interference read
analogously to Eq. 27, where the upper and lower signs in the sum correspond to ɛ1 and ɛ2, respectively. Both reconstructed partial wave packets are shown separately in Figure 8C. They are also aligned perpendicularly with respect to one another and exhibit a pseudo c6 rotational symmetry. Using (ω:2ω) bichromatic OLP fields, we recently demonstrated the generation of a c4 rotationally symmetric PMD in the 2-photon ionization of potassium atoms [105] similar to the dx,y state shown in Figure 5B. Again, the mechanism was based on the cancellation of specific quantum pathways by intraband interference. Due to the energetic disentanglement of the different photoelectron contributions from intraband interference, this scheme is suitable for pump-probe experiments featuring background-free detection of ultrafast dynamics. For example, employing shaper-generated linearly polarized bichromatic pump-probe pulse sequences, we investigated Rydberg [177] and spin-orbit [100] wave packet dynamics. The full potential of polarization-shaped bichromatic fields to generate and manipulate angular momentum superposition states via frequency mixing has been studied in [99]. Very recently, we introduced a shaper-based quantum state holography (SQuaSH) method by combining intra- and interband interferences using commensurable CEP-stable bichromatic fields for phase-sensitive pump-probe measurements [101].
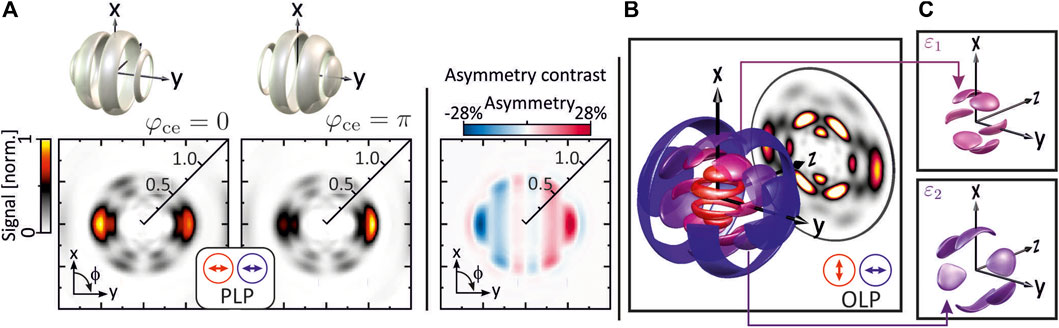
FIGURE 8. Measured PMDs from bichromatic MPI of sodium and potassium atoms. (A) Retrieved (x, y)-sections from the photoemission of sodium atoms using CEP-stable (3ω:4ω) PLP fields. The left and middle frames show the Abel-inverted sections for φce = 0 and φce = π, respectively. The top insets show the corresponding generic 3D PMDs of the wave packets. The calculated asymmetry contrast, depicted in the right frame, shows pronounced asymmetries in the laser polarization plane originating from CEP-sensitive interband interference. (B) Measured and tomographically reconstructed 3D PMD from three-photon ionization of potassium atoms using bichromatic fields with incommensurable frequencies. The PMD shows four energetically separated shells originating from single-color and frequency mixing contributions, equidistantly centered around energies ɛi (i = 0, 1, 2, 3). (C) The partial wave packets from the intermediate energy channels ɛ1 and ɛ2, exhibit pseudo c6 rotational symmetry resulting from intraband interference.
4.2.1.2 Circularly Polarized Bichromatic Pulse Sequences
Circularly polarized bichromatic fields, with their cycloidal polarization profiles (Figures 7C,D), offer fascinating possibilities for the generation and control of electronic angular momentum wave packets with unusual physical properties, whether in the neutral system as in the case of spin-orbit wave packets (SOWPs) or in the ionization continuum as in the case of free electron wave packets. Similar to the linearly polarized case discussed in Section 4.2.1.1, the mechanism to control the spectrum, the symmetry and the rotation of the PMD is based on the manipulation of intraband and interband interference by the polarization state of the sequence (CRCP or COCP) and the optical phases. We illustrate the basic concepts with two examples. In the first example, we use bichromatic CRCP pulse sequences with incommensurable frequencies for MPI of potassium atoms and make use of the energetic disentanglement of the angular momentum states in the continuum. This ionization scheme is utilized for background-free observation of SOWP dynamics in the bound state. The second example deals with the creation and coherent control of FEVs with unusual rotational symmetry by interband interference in the MPI of sodium atoms with CEP-stable commensurable cycloidal bichromatic pulse sequences.
Recently, we demonstrated intraband frequency mixing by shaper-generated CRCP bichromatic fields in the three-photon ionization of potassium [99]. Using temporally overlapping (τ < Δt) sequences of two colors with incommensurable frequencies, we showed that in the CRCP case, frequency mixing results in a complete energetic disentanglement of the different angular momentum target states in the ionization continuum. The reconstructed 3D PMD is depicted in Figure 9A. The two single-color contributions in the inner- (red) and outermost (blue) energy channels correspond to the torus-shaped partial waves ψ3,±3. The two frequency mixing contributions in the intermediate energy channels ɛ1 and ɛ2 correspond to the partial waves
displayed in the insets. This result shows that in the CRCP case, bichromatic frequency mixing provides a unique mapping between the number of absorbed red and blue photons and the different continuum target states, enabling the selective excitation of individual angular momentum states which otherwise (e.g. in the single-color case) overlap inseparably in the energy spectrum (Eq. 36). As pointed out in Section 4.2.1.1, if the two colors are spectrally disjoint, the frequency mixing signals are insensitive to the optical phases implying that frequency mixing signals are inherently robust with respect to phase fluctuations of the CEP, the relative phase between the colors or the Gouy-phase. Moreover, the process of frequency mixing is very efficient due to the large number of pathways leading to the same final state (see Figure 2). These properties, i.e. efficiency, robustness and the disentanglement of target states, make frequency mixing a well-suited test-bed for bichromatic pump-probe studies. The potential of shaper-based bichromatic pump-probe spectroscopy was recently demonstrated on the examples of time- and angular-resolved measurement [177] and holographic observation [101] of ultrafast Rydberg dynamics and the time-resolved 3D imaging of ultrafast SOWP dynamics in potassium atoms [100].
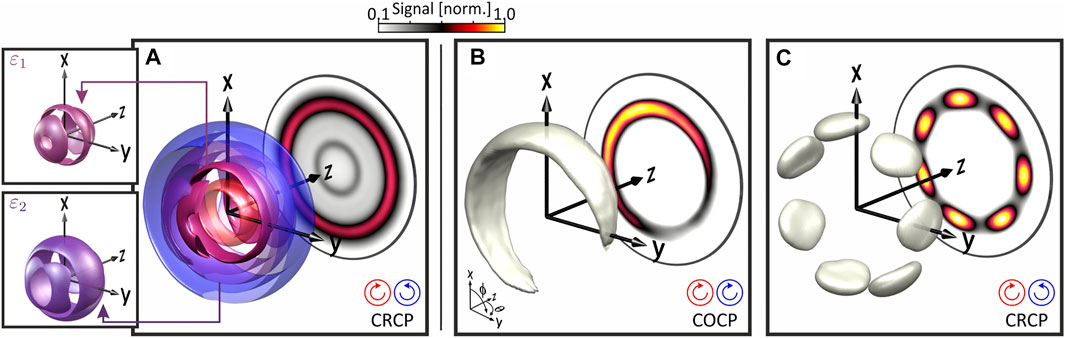
FIGURE 9. Tomographically reconstructed 3D PMDs of free electron wave packets created by MPI of potassium and sodium atoms with circularly polarized bichromatic pulses. (A) Intraband interferences and single-color contributions from MPI of potassium using CRCP bichromatic fields with incommensurable frequencies. (B) FEV with c1 rotational symmetry from interband interference in the MPI of sodium using CEP-stable COCP (3ω:4ω) bichromatic fields. (C) FEV with c7 rotational symmetry created by MPI of sodium using CRCP (3ω:4ω) fields.
In the latter experiment, the LCP blue pulse (pump) was tuned on resonance with the two 4p fine structure states 4p1/2 and 4p3/2. These states are separated energetically by Δɛ = 7 meV which corresponds to a SOWP oscillation period of T = h/Δɛ = 580 fs. The bandwidth of the pump was chosen sufficiently large to excite both states coherently and, thus, launch the SOWP in the neutral system. After a variable time delay τ, introduced experimentally by linear spectral phase modulation via the shaper, the RCP red pulse (probe) ionized the atom from the 4p states in a two-photon process, mapping the SOWP into the ionization continuum as depicted in Figure 10A. More specifically, the electron dynamics in the neutral atom were mapped into the ɛ1-channel, where—due to the energetic disentanglement from other contributions—the time evolution of the SOWP could be observed without any interfering background. By tomographic reconstruction of the PMD as a function of time delay τ, we obtained 3D images of the spatiotemporal SOWP dynamics. The images are shown in Figure 10B. Initially, at τ = 0, the partial wave from the ɛ1-channel displays ψ3,−1 symmetry. This symmetry maps the torus-shaped ψ1,1 state (4p (m = 1)) in the neutral system, which is consistent with the impulsive excitation of the 4p state by the circularly polarized pump pulse. At half-period τ ≈ T/2, the symmetry of the photoelectron angular distribution in the ɛ1-channel evolves into that of a ψ3,−2 state, mapping the dumbbell-shaped ψ1,0 state [4p (m = 0)]. The time evolution of the SOWP between these two states is driven by the spin-orbit interaction which, in a semi-classical picture, is interpreted as the precession of the coupled spin and orbital angular momenta around the total angular momentum. After a full period T, the distribution in the ɛ1-channel returns to ψ3,−1 symmetry indicating the completion of the first SOWP oscillation cycle. These findings, along with additional results obtained for OLP bichromatic pump-probe sequences [99, 100], showcase the capabilities of bichromatic pump-probe spectroscopy, based on shaper-generated polarization-shaped tailored bichromatic pulse sequences in combination with photoelectron tomography, for the background-free 3D imaging of ultrafast spatiotemporal quantum dynamics.
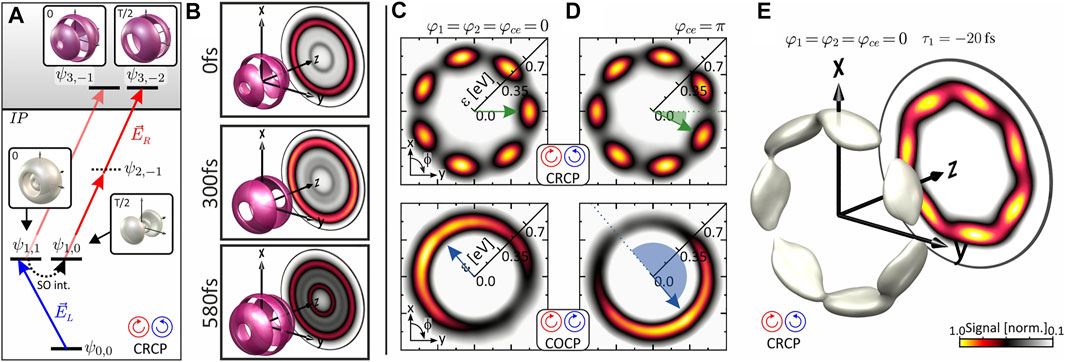
FIGURE 10. Applications of intra- and interband interference in the MPI of potassium and sodium atoms using circularly polarized bichromatic pulse sequences. (A) Excitation scheme for the time-resolved 3D imaging of ultrafast SOWP dynamics in potassium using shaper-generated bichromatic pump-probe pulse sequences. (B) Reconstructed 3D PMDs for different stages of the SOWP cycle, revealing the orbital realignment dynamics in the excited 4p state due to the spin-orbit interaction. (C) and (D) Coherent control of the azimuthal rotation of the c1 and c7 rotationally symmetric FEVs from Figures 9B,C, respectively. (E) Reconstructed 3D PMD of a seven-arm Archimedean spiral-shaped FEV created by MPI of sodium using a time-delayed (τ1 = −20 fs) CRCP (3ω:4ω) bichromatic pulse sequence.
Next, we discuss the application of circularly polarized bichromatic pulse sequences with commensurable frequencies for the coherent control of interband
Here, the upper and lower sign correspond to CRCP and COCP pulses, respectively, and gcd denotes the greatest common divisor. For the sake of clarity, we discuss below the case of
with
The phase term Δφ = 4φ1 − 3φ2 + φce describes the optically induced relative phase between both partial waves. The phase term ɛτ1/ℏ accounts for an additional energy-dependent propagation phase accumulated if the red pulse is time-delayed by τ1 relative to the blue pulse. The FEV described by Ψ1, created by COCP ionization, exhibits a single azimuthal lobe reminiscent of a crescent, while the FEV with the wave function Ψ7, created by CRCP ionization, displays seven lobes in the polarization plane. The corresponding tomographically reconstructed 3D PMDs, measured at the parameters Δφ = 0 and τ1 = 0, are shown in Figures 9B,C, respectively. To demonstrate the rotational control of both FEVs, we varied the CEP from φce = 0 to φce = π, analogously to the directional control discussed in Section 4.2.1.1 (Figure 8). The resulting rotation of the PMD is depicted in Figures 10C,D, indicated by the green and blue angle segments, respectively. While the c1 FEV is rotated by αCOCP = π, the c7 FEV is rotated by an angle of
4.2.2 Molecular Multiphoton Ionization
Two-color femtosecond pump-probe experiments are ideally suited to study ultrafast dynamics in molecules driven by femtosecond laser pulses [151]. In the following Section 4.2.2.1 and Section 4.2.2.2, we discuss the application of this concept to the observation of non-Born-Oppenheimer dynamics in sodium dimers and the mapping of non-perturbative control of concerted electron-nuclear dynamics in potassium dimers. In Section 4.2.2.3, we present new results demonstrating axial and lateral asymmetries in the photoemission from chiral molecules induced by MPI with CEP-stable circularly polarized few-cycle pulses from a WLS.
4.2.2.1 Non-adiabatic Molecular Dynamics
In [202], we used a PLP two-color pump-probe sequence to study the effect of adiabatic (non-Born-Oppenheimer) dynamics in the
4.2.2.2 Non-perturbative Electron-Nuclear Dynamics
In the experiments reported in [132, 137], we applied a two-color pump-probe scheme to demonstrate efficient ultrafast switching between bound electronic target states in the potassium dimer, based on a detailed understanding of the underlying strong-field control mechanism. Intense femtosecond pulse sequences, shaped with attosecond precision [50], were used to switch the neutral excitation selectively between the 21Πg and the
4.2.2.3 Asymmetries in the Photoemission From Chiral Molecules
Polarization-shaped bichromatic fields are particularly suitable to chiral applications. Recent examples comprise the control of optical chirality [206], fundamental investigations on the PECD of chiral molecules [179, 180] and time-resolved studies of molecular chirality [187, 207]. Motivated by our experimental findings on the CEP-control of lateral asymmetries in the atomic MPI of sodium atoms by (3ω: 4ω) [73] and xenon atoms by (7ω: 8ω) [189] bichromatic PLP pulses (cf. Section 4.2.1.1), we investigated asymmetries in the PMD from MPI of the chiral fenchone molecule using CEP-stable few-cycle pulses. The manipulation of lateral asymmetries in chiral molecules is particularly interesting because these molecules also exhibit a pronounced axial, i.e., forward/backward asymmetry in the photoelectron emission due to the PECD [208]. Recent measurements of the PECD of (-)-fenchone molecules from MPI with circularly polarized 400 nm pulses, depicted in Figure 11A, reproduce our previous results [97, 150]. Displayed is the antisymmetric part of the PMD with respect to the polarization plane, showing the well-known asymmetries of up to ±12%. Using a CEP-stable circularly polarized bandwidth-limited white light pulse centered at 800 nm, we observed CEP-sensitive lateral, i.e., left/right asymmetries in the photoelectron emission of (-)-fenchone. In Figure 11B we plot the difference between the PMDs measured with a CEP of φce = 0 and φce = π. This representation yields the antisymmetric part of the spectrum with respect to the propagation direction (z-direction), revealing pronounced lateral asymmetries of up to ±15%. The CEP-dependence of this asymmetry is shown in Figure 11C in the form of an energy-resolved asymmetry map obtained by integrating the spectra over the angular coordinate in one half-plane. These results demonstrate that MPI of chiral molecules with circularly polarized few-cycle pulses can be used to control the axial asymmetry via the PECD and, moreover, the lateral asymmetry via the CEP. Very recently, fully 3D polarization-tailored laser fields, generated by superposition of two polarization-controlled multichromatic laser pulses propagating non-collinearly in different directions, have been proposed as novel tools for the investigation of chiral light-matter interactions [209–212]. These so-called superchiral light fields [213] promise an unprecedented enantio-sensitivity which makes them highly attractive for chiral discrimination applications.
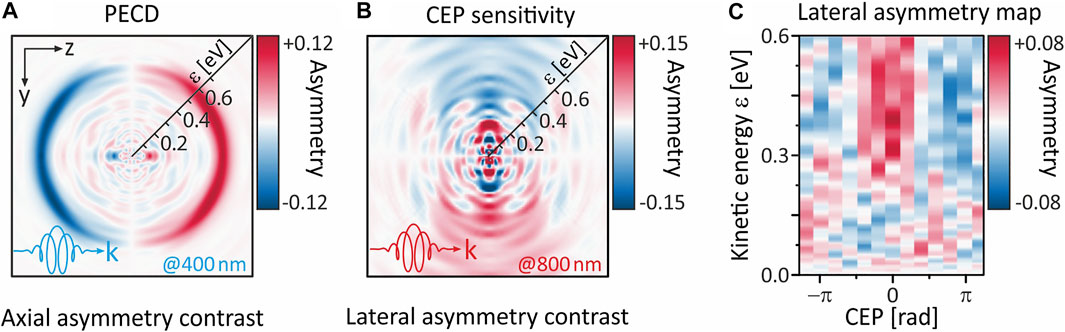
FIGURE 11. PECD and lateral photoelectron asymmetries in the MPI of (-)-fenchone molecules using circularly polarized femtosecond laser pulses. (A) PECD observed at 400 nm. (B) Previously unpublished results on lateral asymmetries in the photoelectron emission using LCP few-cycle pulses with a duration of Δt ≈ 5 fs centred at λ0 = 800 nm. (C) CEP-dependence of the lateral asymmetry displayed as an energy-resolved asymmetry map.
4.3 Multichromatic Pulse Sequences
A natural extension of bichromatic white-light polarization pulse shaping (cf. Section 3.1) is to generate multichromatic polarization-controlled pulse sequences. As a first step towards more complex pulses, we consider a trichromatic application. Trichromatic fields offer enhanced possibilities for ultrafast applications such as multicolor spectroscopy [214], strong-field physics [215, 216], the generation of terahertz radiation [217, 218] and HHG [219]. Further examples of trichromatic pulse sequences are illustrated in Figure 12. Each sequence consists of a temporally overlapping polarization-tailored bichromatic pulse which is either preceded by a circularly polarized [(A) and (B)] or followed by a linearly polarized [(C) and (D)] single pulse of a third color. The use of an additional color allows us to combine the bichromatic mechanism of intraband interference, e.g. for the background-free observation of ultrafast dynamics, with phase-sensitive interband interferences for the coherent control of the underlying multiphoton processes. For example, an auxiliary pulse can be used to provide a separate reference wave packet for an experimental implementation of wave packet holography. This extension opens up a manifold of coherent control scenarios ranging from multichromatic SQuaSH via the creation and manipulation of multiple FEVs to multichannel quantum-phase clocks [101, 220]. However, trichromatic MPI is not only an extension of bichromatic MPI but also changes the physical picture, since the number of available pathways and the number of target states scales differently with the number of pulses, as discussed in Section 2.2.2. So far, we have distinguished between intraband and interband interference in bichromatic MPI scenarios. Phase-sensitive interband interference was characterized by interfering pathways involving the absorption of a different number of photons per color, i.e.
involving two distinct pathways, e.g., with three pairwise different numbers of photons
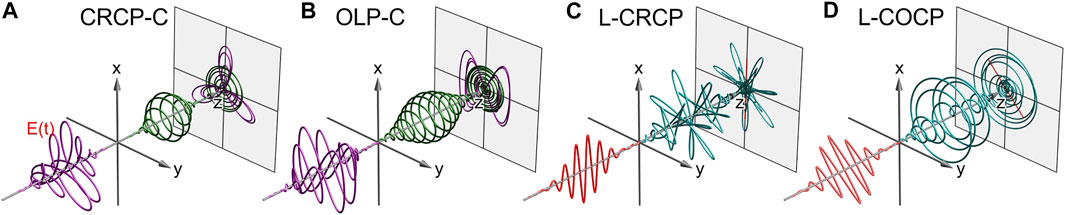
FIGURE 12. Trichromatic pulse sequences. The projection in z-direction visualizes the time-dependent electric field vector at the position of the atom or molecule. (A) Circularly polarized single pulse followed by a CRCP pulse sequence, (B) Circularly polarized single pulse followed by an OLP pulse sequence, (C) CRCP pulse sequence followed by a linearly polarized (s) single pulse and (D) COCP pulse sequence followed by a linearly polarized single pulse tilted by 45°. In all figures the single pulse is separated by a delay τ > 2Δt from the coinciding pulse sequences.
As shown in the excitation scheme in Figure 13A a photoelectron wave packet is created by resonant two-photon excitation of the 3d state by the red pump and subsequent one-photon ionization by the blue probe pulse. This wave packet interferes with the reference wave packet originating from off-resonant 3-photon ionization of the ground state by the green reference pulse to generate a phase-sensitive photoelectron hologram. We expect the hologram to be sensitive to the relative phases between the pump, the probe and the reference, but, because the same number of photons are absorbed in each pathway, the interference pattern should not depend on the CEP. To investigate this scheme experimentally, we apply spectral amplitude modulation of the WLS (cf. Figure 13B) to generate a tailored PLP trichromatic pulse sequence composed of a λpu = 928 nm pump pulse (red band), followed by a λpr = 722 nm probe (blue band) and λref = 848 nm reference pulse (green band). The time delays between the pulses are introduced via additional linear spectral phase modulation of the pump and probe band with τpu = −215 fs and τpr = −15 fs relative to the reference pulse. The wave function of the resulting photoelectron hologram reads
where cpu, cpr and cref denote the complex valued amplitudes including delay-dependent phases and φpu, φpr and φref the relative optical phases corresponding to the pump-the probe- and the reference pulse, respectively. A tomographically reconstructed 3D PMD is depicted in Figure 13C. To evaluate the phase-dependence of the hologram, we measure the modulation of the integral cross-section in the SQuaSH channel of the photoelectron spectrum by variation of the relative optical phase φref ∈ [−π, π]. To this end, the measured PMDs are energy-calibrated [221] and integrated over the angular coordinates to yield the photoelectron spectra. In Figures 13D,E the resulting energy-resolved photoelectron spectra I (ɛ; φref) with ɛ ∈ [0.01, 0.1] eV are plotted as a function of the relative phase of the reference pulse. The insets in the top frame show the measured projections for constructive (φref = −1.64 rad) and destructive interference (−0.77 rad). In agreement with Eq. 46, the interference signal shows a
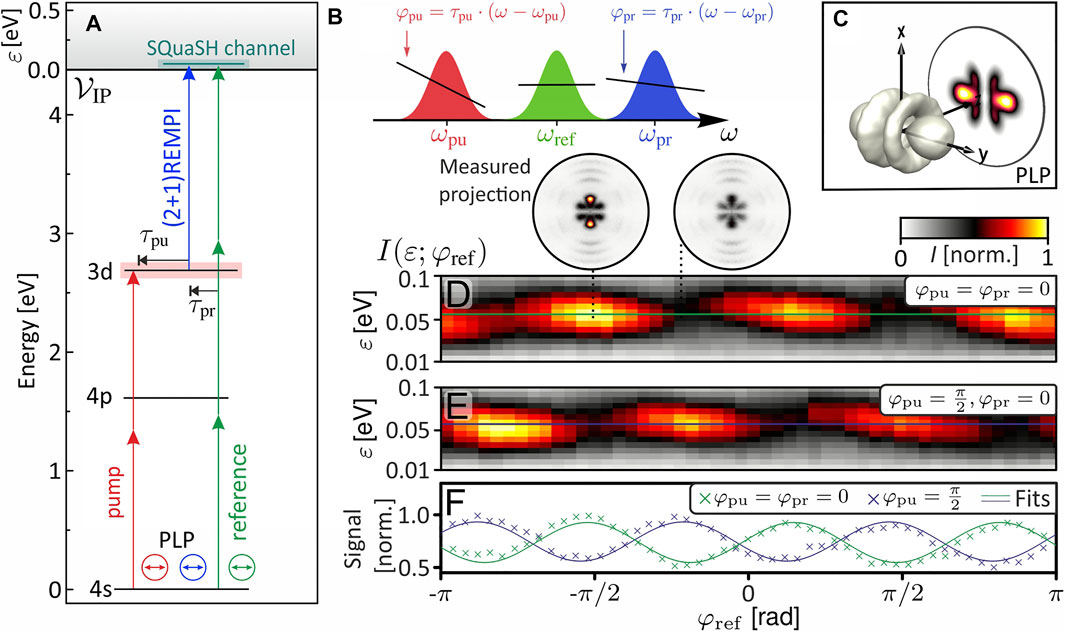
FIGURE 13. SQuaSH on potassium atoms using PLP trichromatic pulse sequences. (A) Excitation scheme for the two-photon excitation (pump) and time-delayed one-photon ionization (probe) of the potassium 3d state. Interference of the resulting free electron wave packet with a reference wave packet created by three-photon ionization of the ground state by the reference pulse provides a phase-sensitive photoelectron hologram in the continuum. (B) The triple pulse sequence is generated by trichromatic WLS shaping applying linear spectral phases to introduce the time delays of pump and probe relative to the reference pulse. (C) Tomographically reconstructed 3D PMD from SQuaSH with PLP trichromatic pulses. (D) Angularly integrated photoelectron spectra I (ɛ; φref) versus the applied optical phase φref of the reference pulse for φpu = 0 showing a pronounced
5 Summary and Outlook
In this review, we have reported on coherent control of MPI dynamics of atomic and molecular model systems using fully coherent polarization-tailored single-color, bichromatic and trichromatic pulse sequences. Building on previous experiments with single-color pulse sequences, we have shown that the advanced polarization shaping of CEP-stable supercontinua enables the generation of unprecedented bichromatic laser fields such as propeller-shaped CRCP pulses or Lissajous-like OLP pulses. Even more flexibility is achieved in trichromatic polarization shaping by the many possible combinations of linearly or circularly polarized pulses, resulting in an increasing number of final states and interfering pathways. These new pulse shapes enable the targeted use of CEP-insensitive intraband and CEP-sensitive interband multipath interference for quantum control. The experimental results on atomic and molecular MPI by multichromatic pulse sequences reviewed here, serve to illustrate the new options for coherent control. We have summarized the theoretical methods used to reproduce and analyze our experimental results and presented a powerful experimental technique combining supercontinuum polarization shaping and VMI-based high-resolution photoelectron tomography to reconstruct the full 3D PMD. The presented applications of single-color pulse sequences included perturbative and non-perturbative control of atomic and molecular MPI. We have analyzed the 3D PMD from a previous experiment on the interference of free electron wave packets created by PLP sequences and reported on free electron vortices with even-numbered rotational symmetry originating from MPI with single-color CRCP sequences. We have reviewed results on bichromatic coherent control by intraband and interband multipath interference on various examples including control of the directional photoemission in the MPI of atoms and chiral molecules by PLP and COCP fields, the use of COCP and CRCP cycloidal fields to generate and manipulate free electron vortices with odd-numbered rotational symmetry, and spin-orbit wave packets controlled by PLP pulses. Finally, we have introduced trichromatic shaper-based quantum state holography using a trichromatic PLP pulse sequence by adding a reference pulse to a bichromatic pump-probe sequence. As an example for the new options of trichromatic pulse shaping, we have devised an MPI scheme based on a polarization-tailored trichromatic CRCP pulse sequence which results in a CEP-insensitive c6 rotationally symmetric inner vortex surrounded by a CEP-sensitive crescent-shaped wave-packet (Figure 14). Extensions of our shaping scheme towards the generation of independently polarization-controlled multichromatic multipulse sequences are currently explored in our labs.
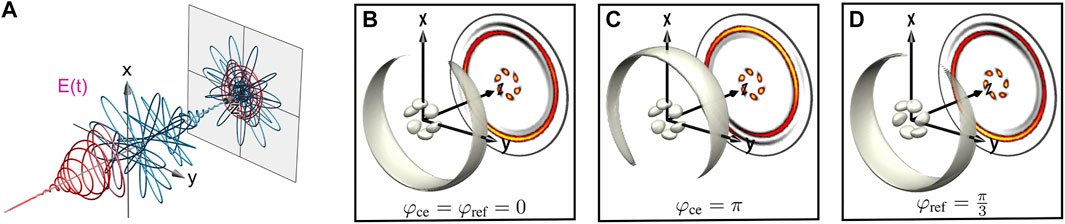
FIGURE 14. (A) Trichromatic pulse sequence consisting of a circularly polarized single pulse temporally overlapping with a CRCP pulse sequence. While the pump-probe pulse sequence is given by a (3ω:4ω) bichromatic field, the additional green component exhibits a frequency ratio of 5:6 with respect to the probe field. (B–D) show the resulting PMDs displaying a CEP-insensitive 6-armed inner vortex surrounded by a CEP-sensitive 1-armed outer vortex, for selected values of the CEP and the relative optical phase φref.
Shaper-based multi-color 2D spectroscopy using fully coherent multichromatic CEP-stable pulse sequences is another emerging application of our technique. Taking advantage of the shaper’s capability to additionally introduce higher order spectral phase modulation, the trichromatic scheme can be further developed into a powerful tool for coherent control spectroscopy by using sequences of tailored pulses, thus generalizing the concept of 2D spectroscopy. In addition, the tunability of the shaper-generated polarization-controlled multi-color fields makes them attractive for applications in quantum information [222], quantum metrology [109, 110, 223] and ultrafast nanotechnology [79, 178, 214, 224, 225]. In all the experiments reported above, the tailored polarization profile was confined to the (x, y)-plane perpendicular to the propagation direction of the pulse. Building on recent theoretical proposals [209–212, 226], we envision the next challenge in experimental coherent control to be the generation and tailoring of full 3D light fields by superimposing two polarization-shaped laser pulses propagating non-collinearly in different directions.
Author Contributions
KE and MW developed the topic and idea, collected the data, and prepared the original manuscript. MW coordinated this review and managed the project. KE, LE, TB, and MW contributed to the conception and development of the narrative. KE, TB, and MW were responsible for data analysis and simulations. LE contributed to the drafting of the manuscript and prepared the illustrations. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG) via the priority program SPP1840 QUTIF. Open access publication fees are granted by the University Oldenburg Open-Access publication fond supported by the DFG program Wissenschaftliche Literaturversorgungs-und Informationssysteme.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Dominik Pengel and Stefanie Kerbstadt for providing previously unpublished data on the FEVs in Figure 6 and the asymmetries in the PMDs of chiral molecules in Figure 11.
References
1. Shapiro M, Brumer P. Laser Control of Product Quantum State Populations in Unimolecular Reactions. J Chem Phys (1986) 84:4103–4. doi:10.1063/1.450074
2. Tannor DJ, Kosloff R, Rice SA. Coherent Pulse Sequence Induced Control of Selectivity of Reactions: Exact Quantum Mechanical Calculations. J Chem Phys (1986) 85:5805–20. doi:10.1063/1.451542
4. Tannor D. Introduction to Quantum Mechanics: A Time-dependent Perspective. Sausalito: University Science Books (2007). p. 662.
5. Shore BW. Manipulating Quantum Structures Using Laser Pulses. Cambridge University Press (2011). p. 1–600.
6. Shapiro M, Brumer P. Quantum Control of Molecular Processes. 2 edn.. New York: Wiley (2012). p. 562.
7. Meshulach D, Silberberg Y. Coherent Quantum Control of Two-Photon Transitions by a Femtosecond Laser Pulse. Nature (1998) 396:239–42. doi:10.1038/24329
8. Dudovich N, Dayan B, Gallagher Faeder SM, Silberberg Y. Transform-limited Pulses Are Not Optimal for Resonant Multiphoton Transitions. Phys Rev Lett (2001) 86:47–50. doi:10.1103/physrevlett.86.47
9. Dudovich N, Oron D, Silberberg Y. Quantum Control of the Angular Momentum Distribution in Multiphoton Absorption Processes. Phys Rev Lett (2004) 92:103003. doi:10.1103/physrevlett.92.103003
10. Präkelt A, Wollenhaupt M, Sarpe-Tudoran C, Baumert T. Phase Control of a Two-Photon Transition with Shaped Femtosecond Laser-Pulse Sequences. Phys Rev A (2004) 70:063407–10. doi:10.1103/physreva.70.063407
11. Wollenhaupt M, Assion A, Liese D, Sarpe-Tudoran C, Baumert T, Zamith S, et al. Interferences of Ultrashort Free Electron Wave Packets. Phys Rev Lett (2002) 89:173001. doi:10.1103/physrevlett.89.173001
12. Lee S, Lee HG, Cho J, Lim J, Park CY, Ahn J. Coherent Control of Multiphoton-Ionization Passage of Excited-State Rubidium Atoms. Phys Rev A (2012) 86:045402. doi:10.1103/physreva.86.045402
13. Baumert T, Grosser M, Thalweiser R, Gerber G. Femtosecond Time‐Resolved Molecular Multiphoton Ionization: The Na2 system. Phys Rev Lett (1991) 67:3753–6. doi:10.1103/physrevlett.67.3753
14. Park SM, Lu SP, Gordon RJ. Coherent Laser Control of the Resonance‐enhanced Multiphoton Ionization of HCl. J Chem Phys (1991) 94:8622–4. doi:10.1063/1.460047
15. Gordon RJ, Hu Z, Seideman T, Singha S, Sukharev M, Zhao Y. Coherent Phase Control of Internal Conversion in Pyrazine. J Chem Phys (2015) 142:144311. doi:10.1063/1.4916642
16. Singha S, Hu Z, Gordon RJ. Closed Loop Coherent Control of Electronic Transitions in Gallium Arsenide. J Phys Chem A (2011) 115:6093–101. doi:10.1021/jp110869f
17. Assion A, Baumert T, Bergt M, Brixner T, Kiefer B, Seyfried V, et al. Control of Chemical Reactions by Feedback-Optimized Phase-Shaped Femtosecond Laser Pulses. Science (1998) 282:919–22. doi:10.1126/science.282.5390.919
18. Meshulach D, Silberberg Y. Coherent Quantum Control of Multiphoton Transitions by Shaped Ultrashort Optical Pulses. Phys Rev A (1999) 60:1287–92. doi:10.1103/physreva.60.1287
19. Silberberg Y. Quantum Coherent Control for Nonlinear Spectroscopy and Microscopy. Annu Rev Phys Chem (2009) 60:277–92. doi:10.1146/annurev.physchem.040808.090427
20. Dantus M, Lozovoy VV. Experimental Coherent Laser Control of Physicochemical Processes. Chem Rev (2004) 104:1813–60. doi:10.1021/cr020668r
21. Gordon RJ, Rice SA. Active Control of the Dynamics of Atoms and Molecules. Annu Rev Phys Chem (1997) 48:601–41. doi:10.1146/annurev.physchem.48.1.601
22. Bartels R, Backus S, Zeek E, Misoguti L, Vdovin G, Christov IP, et al. Shaped-pulse Optimization of Coherent Emission of High-Harmonic Soft X-Rays. Nature (2000) 406:164–6. doi:10.1038/35018029
23. Pfeifer T, Walter D, Winterfeldt C, Spielmann C, Gerber G. Controlling the Spectral Shape of Coherent Soft X-Rays. Appl Phys B (2005) 80:277–80. doi:10.1007/s00340-005-1754-0
24. Englert L, Rethfeld B, Haag L, Wollenhaupt M, Sarpe-Tudoran C, Baumert T. Control of Ionization Processes in High Band gap Materials via Tailored Femtosecond Pulses. Opt Express (2007) 15:17855–62. doi:10.1364/oe.15.017855
25. Stoian R, Wollenhaupt M, Baumert T, Hertel IV. Temporal Pulse Tailoring in Ultrafast Laser Manufacturing Technologies. In: K Sugioka, M Meunier, and A Piqué, editors. Laser Precision Micro Fabrication, 135. Berlin Heidelberg: Springer Series in Material Science (2010). p. 121–44. doi:10.1007/978-3-642-10523-4_5
26. Salzmann W, Mullins T, Eng J, Albert M, Wester R, Weidemüller M, et al. Coherent Transients in the Femtosecond Photoassociation of Ultracold Molecules. Phys Rev Lett (2008) 100:233003––4. doi:10.1103/physrevlett.100.233003
27. Sukharev M, Seideman T, Gordon RJ, Salomon A, Prior Y. Ultrafast Energy Transfer between Molecular Assemblies and Surface Plasmons in the strong Coupling Regime. ACS Nano (2014) 8:807–17. doi:10.1021/nn4054528
28. Glaser SJ, Boscain U, Calarco T, Koch CP, Köckenberger W, Kosloff R, et al. Training Schrödinger's Cat: Quantum Optimal Control. Eur Phys J D (2015) 69:279. doi:10.1140/epjd/e2015-60464-1
29. Rabitz H, de Vivie-Riedle R, Motzkus M, Kompa K. Whither the Future of Controlling Quantum Phenomena?. Science (2000) 288:824–8. doi:10.1126/science.288.5467.824
30. Weiner AM, Heritage JP, Kirschner EM. High-resolution Femtosecond Pulse Shaping. J Opt Soc Am B (1988) 5:1563–72. doi:10.1364/josab.5.001563
31. Meshulach D, Yelin D, Silberberg Y. Adaptive Ultrashort Pulse Compression and Shaping. Opt Commun (1997) 138:345–8. doi:10.1016/s0030-4018(97)00090-4
32. Baumert T, Brixner T, Seyfried V, Strehle M, Gerber G. Femtosecond Pulse Shaping by an Evolutionary Algorithm with Feedback. Appl Phys B: Lasers Opt (1997) 65:779–82. doi:10.1007/s003400050346
33. Yelin D, Meshulach D, Silberberg Y. Adaptive Femtosecond Pulse Compression. Opt Lett (1997) 22:1793–5. doi:10.1364/ol.22.001793
34. Weiner AM. Femtosecond Pulse Shaping Using Spatial Light Modulators. Rev Sci Instrum (2000) 71:1929–60. doi:10.1063/1.1150614
35. Vajda Š, Bartelt A, Kaposta E-C, Leisner T, Lupulescu C, Minemoto S, et al. Feedback Optimization of Shaped Femtosecond Laser Pulses for Controlling the Wavepacket Dynamics and Reactivity of Mixed Alkaline Clusters. Chem Phys (2001) 267:231–9. doi:10.1016/s0301-0104(01)00275-0
36. Herek JL, Wohlleben W, Cogdell RJ, Zeidler D, Motzkus M. Quantum Control of Energy Flow in Light Harvesting. Nature (2002) 417:533–5. doi:10.1038/417533a
37. Goswami D. Optical Pulse Shaping Approaches to Coherent Control. Phys Rep (2003) 374:385–481. doi:10.1016/s0370-1573(02)00480-5
38. Steinmeyer Gn.. A Review of Ultrafast Optics and Optoelectronics. J Opt A: Pure Appl Opt (2003) 5:R1–R15. doi:10.1088/1464-4258/5/1/201
39. Präkelt A, Wollenhaupt M, Assion A, Horn C, Sarpe-Tudoran C, Winter M, et al. Compact, Robust, and Flexible Setup for Femtosecond Pulse Shaping. Rev Scientific Instr (2003) 74:4950–3. doi:10.1063/1.1611998
40. Renard M, Chaux R, Lavorel B, Faucher O. Pulse Trains Produced by Phase-Modulation of Ultrashort Optical Pulses: Tailoring and Characterization. Opt Express (2004) 12:473–82. doi:10.1364/opex.12.000473
41. Stobrawa G, Hacker M, Feurer T, Zeidler D, Motzkus M, Reichel F. A New High-Resolution Femtosecond Pulse Shaper. Appl Phys B (2001) 72:627–30. doi:10.1007/s003400100576
42. Dudovich N, Oron D, Silberberg Y. Single-pulse Coherent Anti-stokes Raman Spectroscopy in the Fingerprint Spectral Region. J Chem Phys (2003) 118:9208–15. doi:10.1063/1.1568072
43. Monmayrant A, Chatel B. New Phase and Amplitude High Resolution Pulse Shaper. Rev Scientific Instr (2004) 75:2668–71. doi:10.1063/1.1771492
44. Wohlleben W, Degert J, Monmayrant A, Chatel B, Motzkus M, Girard B. Coherent Transients as a Highly Sensitive Probe for Femtosecond Pulse Shapers. Appl Phys B (2004) 79:435–9. doi:10.1007/s00340-004-1555-x
45. von Vacano B, Buckup T, Motzkus M. Shaper-assisted Collinear Spider: Fast and Simple Broadband Pulse Compression in Nonlinear Microscopy. J Opt Soc Am B (2007) 24:1091–100. doi:10.1364/josab.24.001091
46. Zäh F, Halder M, Feurer T. Amplitude and Phase Modulation of Time-Energy Entangled Two-Photon States. Opt Express (2008) 16:16452–8. doi:10.1364/oe.16.016452
47. Suchowski H, Natan A, Bruner BD, Silberberg Y. Spatio-temporal Coherent Control of Atomic Systems: Weak to strong Field Transition and Breaking of Symmetry in 2d Maps. J Phys B: Mol Opt Phys (2008) 41:074008. doi:10.1088/0953-4075/41/7/074008
48. Wollenhaupt M, Krug M, Köhler J, Bayer T, Sarpe-Tudoran C, Baumert T. Photoelectron Angular Distributions from strong-field Coherent Electronic Excitation. Appl Phys B (2009) 95:245–59. doi:10.1007/s00340-009-3431-1
49. Monmayrant A, Weber S, Chatel B. A Newcomer's Guide to Ultrashort Pulse Shaping and Characterization. J Phys B: Mol Opt Phys (2010) 43:103001––34. doi:10.1088/0953-4075/43/10/103001
50. Köhler J, Wollenhaupt M, Bayer T, Sarpe C, Baumert T. Zeptosecond Precision Pulse Shaping. Opt Express (2011) 19:11638–53. doi:10.1364/oe.19.011638
51. Brixner T, Gerber G. Femtosecond Polarization Pulse Shaping. Opt Lett (2001) 26:557–9. doi:10.1364/ol.26.000557
52. Brixner T, Krampert G, Pfeifer T, Selle R, Gerber G, Wollenhaupt M, et al. Quantum Control by Ultrafast Polarization Shaping. Phys Rev Lett (2004) 92:208301. doi:10.1103/physrevlett.92.208301
53. Polachek L, Oron D, Silberberg Y. Full Control of the Spectral Polarization of Ultrashort Pulses. Opt Lett (2006) 31:631–3. doi:10.1364/ol.31.000631
54. Plewicki M, Weise F, Weber SM, Lindinger A. Phase, Amplitude, and Polarization Shaping with a Pulse Shaper in a Mach-Zehnder Interferometer. Appl Opt (2006) 45:8354–9. doi:10.1364/ao.45.008354
55. Ninck M, Galler A, Feurer T, Brixner T. Programmable Common-Path Vector Field Synthesizer for Femtosecond Pulses. Opt Lett (2007) 32:3379–81. doi:10.1364/ol.32.003379
56. Kupka D, Schlup P, Bartels RA. Simplified Ultrafast Pulse Shaper for Tailored Polarization States Using a Birefringent Prism. Rev Scientific Instr (2009) 80:053110. doi:10.1063/1.3130046
57. Weise F, Lindinger A. Full Control over the Electric Field Using Four Liquid crystal Arrays. Opt Lett (2009) 34:1258–12560. doi:10.1364/ol.34.001258
58. Schwarz C, Hüter O, Brixner T. Full Vector-Field Control of Ultrashort Laser Pulses Utilizing a Single Dual-Layer Spatial Light Modulator in a Common-Path Setup. J Opt Soc Am B (2015) 32:933–45. doi:10.1364/josab.32.000933
59. Zeidler D, Witte T, Proch D, Motzkus M. Optical Parametric Amplification of a Shaped white-light Continuum. Opt Lett (2001) 26:1921–3. doi:10.1364/ol.26.001921
60. Binhammer T, Rittweger E, Ell R, Kärtner FX, Morgner U. Prism-based Pulse Shaper for Octave Spanning Spectra. IEEE J Quan Electron. (2005) 41:1552–7. doi:10.1109/jqe.2005.858781
61. Xu B, Coello Y, Lozovoy VV, Harris DA, Dantus M. Pulse Shaping of Octave Spanning Femtosecond Laser Pulses. Opt Express (2006) 14:10939–44. doi:10.1364/oe.14.010939
62. Rausch S, Binhammer T, Harth A, Krtner FX, Morgner U. Few-cycle Femtosecond Field Synthesizer. Opt Express (2008) 16:17410–9. doi:10.1364/oe.16.017410
63. Demmler S, Rothhardt J, Heidt AM, Hartung A, Rohwer EG, Bartelt H, et al. Generation of High Quality, 13 Cycle Pulses by Active Phase Control of an Octave Spanning Supercontinuum. Opt Express (2011) 19:20151–8. doi:10.1364/oe.19.020151
64. Hagemann F, Gause O, Wöste L, Siebert T. Supercontinuum Pulse Shaping in the Few-Cycle Regime. Opt Express (2013) 21:5536–49. doi:10.1364/oe.21.005536
65. Kerbstadt S, Timmer D, Englert L, Bayer T, Wollenhaupt M. Ultrashort Polarization-Tailored Bichromatic fields from a CEP-Stable white Light Supercontinuum. Opt Express (2017) 25:12518. doi:10.1364/oe.25.012518
66. Patas A, Matthews M, Hermelin S, Gateau J, Kasparian J, Wolf JP, et al. Modifications of Filament Spectra by Shaped Octave-Spanning Laser Pulses. Phys Rev A (2018) 98:033804. doi:10.1103/physreva.98.033804
67. Long S, Becker W, McIver JK. Model Calculations of Polarization-dependent Two-Color High-Harmonic Generation. Phys Rev A (1995) 52:2262–78. doi:10.1103/physreva.52.2262
68. Zuo T, Bandrauk AD. High-order Harmonic Generation in Intense Laser and Magnetic fields. J Nonlinear Optic Phys Mat (1995) 04:533–46. doi:10.1142/s0218863595000227
69. Milosevic DB, Becker W, Kopold R. Generation of Circularly Polarized High-Order Harmonics by Two-Color Coplanar Field Mixing. Phys Rev A (2000) 61:063403. doi:10.1103/PhysRevA.61.063403
70. Fleischer A, Kfir O, Diskin T, Sidorenko P, Cohen O. Spin Angular Momentum and Tunable Polarization in High-Harmonic Generation. Nat Photon (2014) 8:543–9. doi:10.1038/nphoton.2014.108
71. Ivanov M, Pisanty E. Taking Control of Polarization. Nat Photon (2014) 8:501–3. doi:10.1038/nphoton.2014.141
72. Kfir O, Grychtol P, Turgut E, Knut R, Zusin D, Popmintchev D, et al. Generation of Bright Phase-Matched Circularly-Polarized Extreme Ultraviolet High Harmonics. Nat Photon (2015) 9:99–105. doi:10.1038/nphoton.2014.293
73. Kerbstadt S, Eickhoff K, Bayer T, Wollenhaupt M. Odd Electron Wave Packets from Cycloidal Ultrashort Laser fields. Nat Commun (2019) 10:658. doi:10.1038/s41467-019-08601-7
74. Song X, Yang S, Zuo R, Meier T, Yang W. Enhanced High-Order Harmonic Generation in Semiconductors by Excitation with Multicolor Pulses. Phys Rev A (2020) 101:033410. doi:10.1103/physreva.101.033410
75. Ansari IN, Hofmann C, Medišauskas L, Lewenstein M, Ciappina MF, Dixit G. Controlling Polarization of Attosecond Pulses with Plasmonic-Enhanced Bichromatic Counter-rotating Circularly Polarized fields. Phys Rev A (2021) 103:013104. doi:10.1103/physreva.103.013104
76. Astapenko VA. Radiative Processes in a Bichromatic Laser Field with Multiple Frequencies. Quan Electron. (2006) 36:1131–47. doi:10.1070/qe2006v036n12abeh013231
77. Solanpää J, Räsänen E. Control of Rydberg-State Population with Realistic Femtosecond Laser Pulses. Phys Rev A (2018) 98:053422. doi:10.1103/physreva.98.053422
78. Ohmura H, Saito N. Quantum Control of a Molecular Ionization Process by Using Fourier-Synthesized Laser fields. Phys Rev A (2015) 92:053408. doi:10.1103/physreva.92.053408
79. Dienstbier P, Paschen T, Hommelhoff P. Coherent Control at Gold Needle Tips Approaching the strong-field Regime. Nanophotonics (2021). doi:10.1515/nanoph-2021-0242
80. Mohammadzadeh A, Miri M. Resonance Fluorescence of a Hybrid Semiconductor-Quantum-Dot-Metal-Nanoparticle System Driven by a Bichromatic Field. Phys Rev B (2019) 99:115440. doi:10.1103/physrevb.99.115440
81. Baumert T, Buehler B, Grosser M, Thalweiser R, Weiss V, Wiedenmann E, et al. Femtosecond Time-Resolved Wave Packet Motion in Molecular Multiphoton Ionization and Fragmentation. J Phys Chem (1991) 95:8103–10. doi:10.1021/j100174a019
82. Meier C, Engel V. Electron Kinetic Energy Distributions from Multiphoton Ionization of Na2 with Femtosecond Laser Pulses. Chem Phys Lett (1993) 212:691–6. doi:10.1016/0009-2614(93)85506-j
83. Eppink ATJB, Parker DH. Velocity Map Imaging of Ions and Electrons Using Electrostatic Lenses: Application in Photoelectron and Photofragment Ion Imaging of Molecular Oxygen. Rev Scientific Instr (1997) 68:3477–84. doi:10.1063/1.1148310
85. Schomas D, Rendler N, Krull J, Richter R, Mudrich M. A Compact Design for Velocity-Map Imaging of Energetic Electrons and Ions. J Chem Phys (2017) 147:013942. doi:10.1063/1.4984076
86. Ullrich J, Moshammer R, Dorn A, D rner R, Schmidt LPH, Schmidt-B cking H. Recoil-ion and Electron Momentum Spectroscopy: Reaction-Microscopes. Rep Prog Phys (2003) 66:1463–545. doi:10.1088/0034-4885/66/9/203
87. Dörner R, Mergel V, Jagutzki O, Spielberger L, Ullrich J, Moshammer R, et al. Cold Target Recoil Ion Momentum Spectroscopy: a 'momentum Microscope' to View Atomic Collision Dynamics. Phys Rep (2000) 330:95–192. doi:10.1016/s0370-1573(99)00109-x
88. Garcia GA, Nahon L, Powis I. Two-dimensional Charged Particle Image Inversion Using a Polar Basis Function Expansion. Rev Scientific Instr (2004) 75:4989–96. doi:10.1063/1.1807578
89. Wollenhaupt M, Krug M, Köhler J, Bayer T, Sarpe-Tudoran C, Baumert T. Three-dimensional Tomographic Reconstruction of Ultrashort Free Electron Wave Packets. Appl Phys B (2009) 95:647–51. doi:10.1007/s00340-009-3513-0
90. Smeenk C, Arissian L, Staudte A, Villeneuve DM, Corkum PB. Momentum Space Tomographic Imaging of Photoelectrons. J Phys B: Mol Opt Phys (2009) 42:185402. doi:10.1088/0953-4075/42/18/185402
91. Hockett P, Staniforth M, Reid KL. Photoelectron Angular Distributions from Rotationally State-Selected NH3(B1E′′): Dependence on Ion Rotational State and Polarization Geometry. Mol Phys (2010) 108:1045–54. doi:10.1080/00268971003639266
92. Maurer J, Dimitrovski D, Christensen L, Madsen LB, Stapelfeldt H. Molecular-frame 3d Photoelectron Momentum Distributions by Tomographic Reconstruction. Phys Rev Lett (2012) 109:123001. doi:10.1103/physrevlett.109.123001
93. Chen C, Tao Z, Hernández-García C, Matyba P, Carr A, Knut R, et al. Tomographic Reconstruction of Circularly Polarized High-Harmonic fields: 3d Attosecond Metrology. Sci Adv (2016) 2:e1501333. doi:10.1126/sciadv.1501333
94. Eklund M, Hultgren H, Kiyan I, Helm H, Hanstorp D. Tomography of Photoelectron Distributions Produced through strong-field Photodetachment of Ag−. Phys Rev A (2020) 102:023114. doi:10.1103/physreva.102.023114
95. Wollenhaupt M, Lux C, Krug M, Baumert T. Tomographic Reconstruction of Designer Free-Electron Wave Packets. ChemPhysChem (2013) 14:1341–9. doi:10.1002/cphc.201200968
97. Lux C, Wollenhaupt M, Sarpe C, Baumert T. Photoelectron Circular Dichroism of Bicyclic Ketones from Multiphoton Ionization with Femtosecond Laser Pulses. Chemphyschem (2015) 16:115–37. doi:10.1002/cphc.201402643
98. Hockett P, Wollenhaupt M, Lux C, Baumert T. Complete Photoionization Experiments via Ultrafast Coherent Control with Polarization Multiplexing. Phys Rev Lett (2014) 112:223001. doi:10.1103/physrevlett.112.223001
99. Kerbstadt S, Pengel D, Johannmeyer D, Englert L, Bayer T, Wollenhaupt M. Control of Photoelectron Momentum Distributions by Bichromatic Polarization-Shaped Laser fields. New J Phys (2017) 19:103017. doi:10.1088/1367-2630/aa83a4
100. Bayer T, Gräfing D, Kerbstadt S, Pengel D, Eickhoff K, Englert L, et al. Time-resolved 3d Imaging of Ultrafast Spin-Orbit Wave Packet Dynamics. New J Phys (2019) 21:033001. doi:10.1088/1367-2630/aafb87
101. Eickhoff K, Kerbstadt S, Bayer T, Wollenhaupt M. Dynamic Quantum State Holography. Phys Rev A (2020) 101:013430. doi:10.1103/physreva.101.013430
102. Pengel D, Kerbstadt S, Johannmeyer D, Englert L, Bayer T, Wollenhaupt M. Electron Vortices in Femtosecond Multiphoton Ionization. Phys Rev Lett (2017) 118:053003. doi:10.1103/PhysRevLett.118.053003
103. Pengel D, Kerbstadt S, Englert L, Bayer T, Wollenhaupt M. Control of Three-Dimensional Electron Vortices from Femtosecond Multiphoton Ionization. Phys Rev A (2017) 96:043426. doi:10.1103/physreva.96.043426
104. Pengel D, Kerbstadt S, Bayer T, Wollenhaupt M. Femtosekunden-Laserpulse Erzeugen Elektronenwirbel. Phys Unserer Zeit (2017) 48:162–3. doi:10.1002/piuz.201770404
105. Kerbstadt S, Eickhoff K, Bayer T, Wollenhaupt M. Control of Free Electron Wave Packets by Polarization-Tailored Ultrashort Bichromatic Laser fields. Adv Phys X (2019) 4:1672583. doi:10.1080/23746149.2019.1672583
106. Kerbstadt S, Eickhoff K, Bayer T, Wollenhaupt M. Bichromatic Control of Free Electron Wave Packets. Springer (2020). p. 43–76. doi:10.1007/978-3-030-47098-2_3
108. Berkowitz J. Photoabsorption, Photoionization, and Photoelectron Spectroscopy. Academic Press (2012).
109. Hockett P. Quantum Metrology with Photoelectrons: Volume I: Foundations. San Rafael, CA, United States: Morgan & Claypool Publishers (2018).
110. Hockett P. Quantum Metrology with Photoelectrons: Volume II: Applications and Advances. San Rafael, CA, United States: Morgan & Claypool Publishers (2018).
113. Wollenhaupt M, Assion A, Baumert T. Springer Handbook of Lasers and Optics, Vol. 2. Springer (2012).
114. Bauer D. Computational strong-field Quantum Dynamics. In: Intense Light-Matter Interactions, 1. Berlin, Germany: De Gruyter (2017). doi:10.1515/9783110417265
115. Krug M, Bayer T, Wollenhaupt M, Sarpe-Tudoran C, Baumert T, Ivanov SS, et al. Coherent strong-field Control of Multiple States by a Single Chirped Femtosecond Laser Pulse. New J Phys (2009) 11:105051. doi:10.1088/1367-2630/11/10/105051
116. Wollenhaupt M, Bayer T, Vitanov NV, Baumert T. Three-state Selective Population of Dressed States via Generalized Spectral Phase-step Modulation. Phys Rev A (2010) 81:053422. doi:10.1103/physreva.81.053422
117. Wollenhaupt M, Liese D, Präkelt A, Sarpe-Tudoran C, Baumert T. Quantum Control by Ultrafast Dressed States Tailoring. Chem Phys Lett (2006) 419:184–90. doi:10.1016/j.cplett.2005.11.079
118. Wollenhaupt M, Baumert T. Ultrafast strong Field Quantum Control on K2 Dimers. J Photochem Photobiol A: Chem (2006) 180:248–55. doi:10.1016/j.jphotochem.2006.03.010
119. Bayer T, Wollenhaupt M, Braun H, Baumert T. Ultrafast and Efficient Control of Coherent Electron Dynamics via Spods. Adv Chem Phys (2016) 159:235–82. doi:10.1002/9781119096276.ch6
120. Wollenhaupt M, Präkelt A, Sarpe-Tudoran C, Liese D, Bayer T, Baumert T. Femtosecond strong-field Quantum Control with Sinusoidally Phase-Modulated Pulses. Phys Rev A (2006) 73:063409. doi:10.1103/physreva.73.063409
121. Bayer T, Philipp C, Eickhoff K, Wollenhaupt M. Atomic Photoionization Dynamics in Ultrashort Cycloidal Laser fields. Phy Rev A (2020) 102:013104. doi:10.1103/physreva.102.013104
122. Meier C, Engel V. Interference Structure in the Photoelectron Spectra Obtained from Multiphoton Ionization of Na2 with a Strong Femtosecond Laser Pulse. Phys Rev Lett (1994) 73:3207–10. doi:10.1103/physrevlett.73.3207
123. Wollenhaupt M, Assion A, Bazhan O, Horn C, Liese D, Sarpe-Tudoran C, et al. Control of Interferences in an Autler-Townes Doublet: Symmetry of Control Parameters. Phys Rev A (2003) 68:015401. doi:10.1103/physreva.68.015401
124. Wollenhaupt M, Präkelt A, Sarpe-Tudoran C, Liese D, Baumert T. Strong Field Quantum Control by Selective Population of Dressed States. J Opt B: Quan Semiclass. Opt. (2005) 7:S270–S276. doi:10.1088/1464-4266/7/10/010
125. Wollenhaupt M, Präkelt A, Sarpe-Tudoran C, Liese D, Baumert T. Quantum Control by Selective Population of Dressed States Using Intense Chirped Femtosecond Laser Pulses. Appl Phys B (2006) 82:183–8. doi:10.1007/s00340-005-2066-0
126. Torosov BT, Shore BW, Vitanov NV. Coherent Control Techniques for Two-State Quantum Systems: A Comparative Study. Phys Rev A (2021) 103:033110. doi:10.1103/physreva.103.033110
127. Bayer T, Wollenhaupt M, Sarpe-Tudoran C, Baumert T. Robust Photon Locking. Phys Rev Lett (2009) 102:023004. doi:10.1103/PhysRevLett.102.023004
128. Dudovich N, Polack T, Pe'er A, Silberberg Y. Simple Route to strong-field Coherent Control. Phys Rev Lett (2005) 94:083002–4. doi:10.1103/PhysRevLett.94.083002
129. Wollenhaupt M, Präkelt A, Sarpe-Tudoran C, Liese D, Baumert T. Quantum Control and Quantum Control Landscapes Using Intense Shaped Femtosecond Pulses. J Mod Opt (2005) 52:2187–95. doi:10.1080/09500340500275884
130. Bayer T, Wollenhaupt M, Baumert T. Strong-field Control Landscapes of Coherent Electronic Excitation. J Phys B: Mol Opt Phys (2008) 41:074007–13. doi:10.1088/0953-4075/41/7/074007
131. Thallmair S, Siemering R, Kölle P, Kling M, Wollenhaupt M, Baumert T, et al. The Interplay of Nuclear and Electronic Motion in the Control of Molecular Processes: A Theoretical Perspective. Springer (2014). p. 213–48. doi:10.1007/978-3-642-45290-1_8
132. Braun H, Bayer T, Sarpe C, Siemering R, de Vivie-Riedle R, Baumert T, et al. Coupled Electron-Nuclear Wavepacket Dynamics in Potassium Dimers. J Phys B: Mol Opt Phys (2014) 47:124015. doi:10.1088/0953-4075/47/12/124015
133. Petersen J, Mitrić R. Electronic Coherence within the Semiclassical Field-Induced Surface Hopping Method: strong Field Quantum Control in K2. Phys Chem Chem Phys (2012) 14:8299–306. doi:10.1039/c2cp40747g
134. Feit MD, Fleck JA, Steiger A. Solution of the Schrödinger Equation by a Spectral Method. J Comput Phys (1982) 47:412–33. doi:10.1016/0021-9991(82)90091-2
135. Mulliken RS. Role of Kinetic Energy in the Franck-condon Principle. J Chem Phys (1971) 55:309–14. doi:10.1063/1.1675522
136. Assion A, Geisler M, Helbing J, Seyfried V, Baumert T. Femtosecond Pump-Probe Photoelectron Spectroscopy: Mapping of Vibrational Wave-Packet Motion. Phys Rev A (1996) 54:R4605–4608. doi:10.1103/physreva.54.r4605
137. Bayer T, Braun H, Sarpe C, Siemering R, von den Hoff P, de Vivie-Riedle R, et al. Charge Oscillation Controlled Molecular Excitation. Phys Rev Lett (2013) 110:123003. doi:10.1103/physrevlett.110.123003
138. Eickhoff K, Feld LC, Köhnke D, Englert L, Bayer T, Wollenhaupt M. Coherent Control Mechanisms in Bichromatic Multiphoton Ionization. J Phys B (2021). doi:10.1088/1361-6455/ac11a0
139. Burger C, Frisch WF, Kardaś TM, Trubetskov M, Pervak V, Moshammer R, et al. Compact and Flexible Harmonic Generator and Three-Color Synthesizer for Femtosecond Coherent Control and Time-Resolved Studies. Opt Express (2017) 25:31130–9. doi:10.1364/oe.25.031130
140. Wirth A, Hassan MT, Grguras I, Gagnon J, Moulet A, Luu TT, et al. Synthesized Light Transients. Science (2011) 334:195–200. doi:10.1126/science.1210268
141. Liu J, Kobayashi T. Generation of uJ-Level Multicolored Femtosecond Laser Pulses Using Cascaded Four-Wave Mixing. Opt Express (2009) 17:4984–90. doi:10.1364/oe.17.004984
142. Harris SE, Sokolov AV. Subfemtosecond Pulse Generation by Molecular Modulation. Phys Rev Lett (1998) 81:2894–7. doi:10.1103/physrevlett.81.2894
143. Sokolov AV, Shverdin MY, Walker DR, Yavuz § DD, Burzo AM, Yin GY, et al. Generation and Control of Femtosecond Pulses by Molecular Modulation. J Mod Opt (2005) 52:285–304. doi:10.1080/09500340410001731020
144. Chan H-S, Hsieh Z-M, Liang W-H, Kung AH, Lee C-K, Lai C-J, et al. Synthesis and Measurement of Ultrafast Waveforms from Five Discrete Optical Harmonics. Science (2011) 331:1165–8. doi:10.1126/science.1198397
145. Weiner AM. Ultrafast Optical Pulse Shaping: A Tutorial Review. Opt Commun (2011) 284:3669–92. doi:10.1016/j.optcom.2011.03.084
146. Kerbstadt S, Englert L, Bayer T, Wollenhaupt M. Ultrashort Polarization-Tailored Bichromatic fields. J Mod Opt (2017) 64:1010–25. doi:10.1080/09500340.2016.1271151
147. Kak AC, Slaney M. Principles of Computerized Tomographic Imaging. New York: IEEE Press (1988). p. 1–339.
148. Itatani J, Levesque J, Zeidler D, Niikura H, Pépin H, Kieffer JC, et al. Tomographic Imaging of Molecular Orbitals. Nature (2004) 432:867–71. doi:10.1038/nature03183
149. Bergner K, Flamm D, Jenne M, Kumkar M, Tünnermann A, Nolte S. Time-resolved Tomography of Ultrafast Laser-Matter Interaction. Opt Express (2018) 26:2873–83. doi:10.1364/oe.26.002873
150. Lux C, Wollenhaupt M, Bolze T, Liang Q, Köhler J, Sarpe C, et al. Circular Dichroism in the Photoelectron Angular Distributions of Camphor and Fenchone from Multiphoton Ionization with Femtosecond Laser Pulses. Angew Chem Int Ed (2012) 51:5001–5. doi:10.1002/anie.201109035
151. Zewail AH. Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond. J Phys Chem A (2000) 104:5660–94. doi:10.1021/jp001460h
152. Paasch-Colberg T, Kruchinin SY, Sağlam Ö, Kapser S, Cabrini S, Muehlbrandt S, et al. Sub-cycle Optical Control of Current in a Semiconductor: from the Multiphoton to the Tunneling Regime. Optica (2016) 3:1358–61. doi:10.1364/optica.3.001358
153. Karras G, Ndong M, Hertz E, Sugny D, Billard F, Lavorel B, et al. Polarization Shaping for Unidirectional Rotational Motion of Molecules. Phys Rev Lett (2015) 114:103001. doi:10.1103/physrevlett.114.103001
154. Lin K, Tutunnikov I, Ma J, Qiang J, Zhou L, Faucher O, et al. Spatiotemporal Rotational Dynamics of Laser-Driven Molecules. Adv Photon (2020) 2:024002. doi:10.1117/1.ap.2.2.024002
155. Ngoko Djiokap JM, Hu SX, Madsen LB, Manakov NL, Meremianin AV, Starace AF. Electron Vortices in Photoionization by Circularly Polarized Attosecond Pulses. Phys Rev Lett (2015) 115:113004. doi:10.1103/physrevlett.115.113004
156. Eickhoff K, Rathje C, Köhnke D, Kerbstadt S, Englert L, Bayer T, et al. Orbital Angular Momentum Superposition States in Transmission Electron Microscopy and Bichromatic Multiphoton Ionization. New J Phys (2020) 22:103045. doi:10.1088/1367-2630/abbe54
157. Ngoko Djiokap JM, Meremianin AV, Manakov NL, Hu SX, Madsen LB, Starace AF. Multistart Spiral Electron Vortices in Ionization by Circularly Polarized Uv Pulses. Phys Rev A (2016) 94:013408. doi:10.1103/physreva.94.013408
158. Yuan KJ, Chelkowski S, Bandrauk AD. Photoelectron Momentum Distributions of Molecules in Bichromatic Circularly Polarized Attosecond UV Laser fields. Phys Rev A (2016) 93:053425. doi:10.1103/physreva.93.053425
159. Ngoko Djiokap JM, Meremianin AV, Manakov NL, Hu SX, Madsen LB, Starace AF. Kinematical Vortices in Double Photoionization of Helium by Attosecond Pulses. Phys Rev A (2017) 96:013405. doi:10.1103/physreva.96.013405
160. Yuan K-J, Lu H, Bandrauk AD. Photoionization of Triatomic Molecular Ions
161. Meng Li ML, Guizhong Zhang GZ, Tianqi Zhao TZ, Xin Ding XD, Jianquan Yao JY. Electron Vortices in Photoionization by a Pair of Elliptically Polarized Attosecond Pulses. Chin Opt Lett (2017) 15:120202. doi:10.3788/col201715.120202
162. Djiokap JMN, Starace AF. Doubly-excited State Effects on Two-Photon Double Ionization of Helium by Time-Delayed, Oppositely Circularly-Polarized Attosecond Pulses. J Opt (2017) 19:124003. doi:10.1088/2040-8986/aa8fc0
163. Li ZL, Li YJ, Xie BS. Momentum Vortices on Pairs Production by Two Counter-rotating fields. Phys Rev D (2017) 96:076010. doi:10.1103/physrevd.96.076010
164. Li M, Zhang G, Kong X, Wang T, Ding X, Yao J. Dynamic Stark Induced Vortex Momentum of Hydrogen in Circular fields. Opt Express (2018) 26:878–86. doi:10.1364/oe.26.000878
165. Li M, Zhang G, Ding X, Yao J. Symmetric Electron Vortices of Hydrogen Ionized by Orthogonal Elliptical fields. IEEE Photon J. (2018) 10:1–9. doi:10.1109/jphot.2018.2854237
166. Li ZL, Xie BS, Li YJ. Vortices in Multiphoton Pair Production by Two-Color Rotating Laser fields. J Phys B: Mol Opt Phys (2018) 52:025601. doi:10.1088/1361-6455/aaf3f9
167. Li M, Zhang G-z., Ding X, Yao J-q.. Carrier Envelope Phase Description for an Isolated Attosecond Pulse by Momentum Vortices. Chin Phys. Lett. (2019) 36:063201. doi:10.1088/0256-307x/36/6/063201
168. Djiokap JMN, Meremianin AV, Manakov NL, Madsen LB, Hu SX, Starace AF. Dynamical Electron Vortices in Attosecond Double Photoionization of H2. Phys Rev A (2018) 98:063407. doi:10.1103/physreva.98.063407
169. Li M, Zhang G, Ding X, Yao J. Ac Stark Effect on Vortex Spectra Generated by Circularly Polarized Pulses. IEEE Photon J. (2019) 11:1–11. doi:10.1109/jphot.2019.2916106
170. Armstrong GSJ, Clarke DDA, Benda J, Wragg J, Brown AC, van der Hart HW. Modeling Tomographic Measurements of Photoelectron Vortices in Counter-rotating Circularly Polarized Laser Pulses. Phys Rev A (2019) 100:063416. doi:10.1103/physreva.100.063416
171. Chen Z, He PL, He F. Spiral Nuclear Momentum Distribution for the Dissociation of
172. Chen Z, He F. Interference of Nuclear Wave Packets Carrying Different Angular Momenta in the Dissociation of
173. He Y, Zhang G, Tang J, Ding X, Yao J. Optical-stark Induced Distortions in Vortex Momentum Distributions of P-Orbital Electrons of Neon Atoms. IEEE Photon J. (2020) 12:1–9. doi:10.1109/jphot.2020.3037714
174. Geng L, Cajiao VF, Kamiński JZ, Peng LY, Krajewska K. Vortex Structures in Photodetachment by Few-Cycle Circularly Polarized Pulses. Phys Rev A (2020) 102:043117. doi:10.1103/physreva.102.043117
175. Varshalovich DA, Moskalev AN, Khersonskii VK. Quantum Theory of Angular Momentum. Singapore: World Scientific Publishing Co. Pte. Ltd. (1988).
176. Zare RN. Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics. Incorporated: Dover Publications (2007).
177. Kerbstadt S, Gabrisch L, Eickhoff K, Bayer T, Wollenhaupt M. Imaging Multiple Rydberg Wave Packets from Shaper-Generated Two-Color Femtosecond Pump-Probe Sequences. Phys Rev A (2019) 99:013406. doi:10.1103/physreva.99.013406
178. Passig J, Zherebtsov S, Irsig R, Arbeiter M, Peltz C, Göde S, et al. Nanoplasmonic Electron Acceleration by Attosecond-Controlled Forward Rescattering in Silver Clusters. Nat Commun (2017) 8:1181. doi:10.1038/s41467-017-01286-w
179. Demekhin PV, Artemyev AN, Kastner A, Baumert T. Photoelectron Circular Dichroism with Two Overlapping Laser Pulses of Carrier Frequencies ω and 2ω Linearly Polarized in Two Mutually Orthogonal Directions. Phys Rev Lett (2018) 121:253201. doi:10.1103/physrevlett.121.253201
180. Rozen S, Comby A, Bloch E, Beauvarlet S, Descamps D, Fabre B, et al. Controlling Subcycle Optical Chirality in the Photoionization of Chiral Molecules. Phys Rev X (2019) 9:031004. doi:10.1103/physrevx.9.031004
181. Eichmann H, Egbert A, Nolte S, Momma C, Wellegehausen B, Becker W, et al. Polarization-dependent High-Order Two-Color Mixing. Phys Rev A (1995) 51:R3414–R3417. doi:10.1103/physreva.51.r3414
182. Fan T, Grychtol P, Knut R, Hernández-García C, Hickstein DD, Zusin D, et al. Bright Circularly Polarized Soft X-ray High Harmonics for X-ray Magnetic Circular Dichroism. Proc Natl Acad Sci USA (2015) 112:14206–11. doi:10.1073/pnas.1519666112
183. Eckart S, Richter M, Kunitski M, Hartung A, Rist J, Henrichs K, et al. Nonsequential Double Ionization by Counterrotating Circularly Polarized Two-Color Laser fields. Phys Rev Lett (2016) 117:133202. doi:10.1103/physrevlett.117.133202
184. Mancuso CA, Hickstein DD, Grychtol P, Knut R, Kfir O, Tong XM, et al. Strong-field Ionization with Two-Color Circularly Polarized Laser fields. Phys Rev A (2015) 91:031402R. doi:10.1103/physreva.91.031402
185. Mancuso CA, Hickstein DD, Dorney KM, Ellis JL, Hasovic E, Knut R, et al. Controlling Electron-Ion Rescattering in Two-Color Circularly Polarized Femtosecond Laser fields. Phys Rev A (2016) 93:053406. doi:10.1103/physreva.93.053406
186. Miloševic DB. Atomic and Molecular Processes in a strong Bicircular Laser Field. Atoms (2018) 6:61. doi:10.3390/atoms6040061
187. Baykusheva D, Zindel D, Svoboda V, Bommeli E, Ochsner M, Tehlar A, et al. Real-time Probing of Chirality during a Chemical Reaction. Proc Natl Acad Sci USA (2019) 116:23923–9. doi:10.1073/pnas.1907189116
188. Abel MJ, Pfeifer T, Jullien A, Nagel PM, Bell MJ, Neumark DM, et al. Carrier-envelope Phase-dependent Quantum Interferences in Multiphoton Ionization. J Phys B: Mol Opt Phys (2009) 42:075601. doi:10.1088/0953-4075/42/7/075601
189. Kerbstadt S, Pengel D, Englert L, Bayer T, Wollenhaupt M. Carrier-envelope-phase Control of Asymmetries in the Multiphoton Ionization of Xenon Atoms by Ultrashort Bichromatic fields. Phys Rev A (2018) 97:063402. doi:10.1103/physreva.97.063402
190. Kerbstadt S, Pengel D, Bayer T, Wollenhaupt M. CEP Control of Multiphoton Ionization Using Shaper-Generated Variable Frequency Ratio Bichromatic fields. EPJ Web Conf (2019) 205:07003. doi:10.1051/epjconf/201920507003
191. Paulus GG, Grasbon F, Walther H, Villoresi P, Nisoli M, Stagira S, et al. Absolute-phase Phenomena in Photoionization with Few-Cycle Laser Pulses. Nature (2001) 414:182–4. doi:10.1038/35102520
192. Kling MF, Rauschenberger J, Verhoef AJ, Hasović E, Uphues T, Milošević DB, et al. Imaging of Carrier-Envelope Phase Effects in Above-Threshold Ionization with Intense Few-Cycle Laser fields. New J Phys (2008) 10:025024–17. doi:10.1088/1367-2630/10/2/025024
193. Kling MF, Siedschlag C, Verhoef AJ, Khan JI, Schultze M, Uphues T, et al. Control of Electron Localization in Molecular Dissociation. Science (2006) 312:246–8. doi:10.1126/science.1126259
194. Sansone G, Kelkensberg F, Pérez-Torres JF, Morales F, Kling MF, Siu W, et al. Electron Localization Following Attosecond Molecular Photoionization. Nature (2010) 465:763–6. doi:10.1038/nature09084
195. Alnaser AS, Litvinyuk IV. Subfemtosecond Directional Control of Chemical Processes in Molecules. J Phys B: Mol Opt Phys (2017) 50:032002. doi:10.1088/1361-6455/50/3/032002
196. Krüger M, Schenk M, Hommelhoff P. Attosecond Control of Electrons Emitted from a Nanoscale Metal Tip. Nature (2011) 475:78–81. doi:10.1038/nature10196
197. Schiffrin A, Paasch-Colberg T, Karpowicz N, Apalkov V, Gerster D, Mühlbrandt S, et al. Optical-field-induced Current in Dielectrics. Nature (2013) 493:70–4. doi:10.1038/nature11567
198. Piglosiewicz B, Schmidt S, Park DJ, Vogelsang J, Gross P, Manzoni C, et al. Carrier-envelope Phase Effects on the strong-field Photoemission of Electrons from Metallic Nanostructures. Nat Photon (2014) 8:38–43. doi:10.1038/nphoton.2013.344
199. Süßmann F, Seiffert L, Zherebtsov S, Mondes V, Stierle J, Arbeiter M, et al. Field Propagation-Induced Directionality of Carrier-Envelope Phase-Controlled Photoemission from Nanospheres. Nat Commun (2015) 6:7944. doi:10.1038/ncomms8944
200. Ciappina MF, Pérez-Hernández JA, Landsman AS, Okell WA, Zherebtsov S, Förg B, et al. Attosecond Physics at the Nanoscale. Rep Prog Phys (2017) 80:054401. doi:10.1088/1361-6633/aa574e
201. Higuchi T, Heide C, Ullmann K, Weber HB, Hommelhoff P. Light-field-driven Currents in Graphene. Nature (2017) 550:224–8. doi:10.1038/nature23900
202. Wollenhaupt M, Assion A, Graefe O, Liese D, Sarpe-Tudoran C, Winter M, Baumert T. Changes of the Electronic Structure along the Internuclear Coordinate Studied by Ultrafast Photoelectron Spectroscopy: the 21
203. Valance A, Tuan QN. The Molecular Electronic Structure of the Lowest
204. Arasaki Y, Takatsuka K, Wang K, McKoy V. Femtosecond Energy- and Angle-Resolved Photoelectron Spectra. Chem Phys Lett (1999) 302:363–74. doi:10.1016/s0009-2614(99)00153-0
205. Arasaki Y, Takatsuka K, Wang K, McKoy V. Femtosecond Energy- and Angle-Resolved Photoelectron Spectroscopy. J Chem Phys (2000) 112:8871–84. doi:10.1063/1.481534
206. Neufeld O, Cohen O. Optical Chirality in Nonlinear Optics: Application to High Harmonic Generation. Phys Rev Lett (2018) 120:133206. doi:10.1103/physrevlett.120.133206
207. Beaulieu S, Comby A, Clergerie A, Caillat J, Descamps D, Dudovich N, et al. Attosecond-resolved Photoionization of Chiral Molecules. Science (2017) 358:1288–94. doi:10.1126/science.aao5624
208. Powis I. Photoelectron Circular Dichroism, Vol. 1. Wiley (2012). p. 407–31. doi:10.1002/9781118120187.ch15
209. Ordonez AF, Smirnova O. Generalized Perspective on Chiral Measurements without Magnetic Interactions. Phys Rev A (2018) 98:063428. doi:10.1103/physreva.98.063428
210. Ayuso D, Neufeld O, Ordonez AF, Decleva P, Lerner G, Cohen O, et al. Synthetic Chiral Light for Efficient Control of Chiral Light-Matter Interaction. Nat Photon (2019) 13:866–71. doi:10.1038/s41566-019-0531-2
211. Neufeld O, Ayuso D, Decleva P, Ivanov MY, Smirnova O, Cohen O. Ultrasensitive Chiral Spectroscopy by Dynamical Symmetry Breaking in High Harmonic Generation. Phys Rev X (2019) 9:031002. doi:10.1103/physrevx.9.031002
212. Neufeld O, Tzur ME, Cohen O. Degree of Chirality of Electromagnetic fields and Maximally Chiral Light. Phys Rev A (2020) 101:053831. doi:10.1103/physreva.101.053831
213. Tang Y, Cohen AE. Enhanced Enantioselectivity in Excitation of Chiral Molecules by Superchiral Light. Science (2011) 332:333–6. doi:10.1126/science.1202817
214. Traum C, Henzler P, Lohner S, Becker H, Nabben D, Gumbsheimer P, et al. Multicolor Femtosecond Pump-Probe System with Single-Electron Sensitivity at Low Temperatures and High Magnetic fields. Rev Scientific Instr (2019) 90:123003. doi:10.1063/1.5126157
215. Luu TT, Garg M, Kruchinin SY, Moulet A, Hassan MT, Goulielmakis E. Extreme Ultraviolet High-Harmonic Spectroscopy of Solids. Nature (2015) 521:498–502. doi:10.1038/nature14456
216. Ohmura H, Saito N. Sub-optical-cycle Attosecond Control of Molecular Ionization by Using Fourier-Synthesized Laser fields. Phys Rev A (2020) 101:043419. doi:10.1103/physreva.101.043419
217. Zhang L, Wang G-L, Zhao S-F, Zhou X-X. Controlling of strong Tunable Thz Emission with Optimal Incommensurate Multi-Color Laser Field. Phys Plasmas (2017) 24:023116. doi:10.1063/1.4976549
218. Liu S, Fan Z, Lu C, Gui J, Luo C, Wang S, et al. Coherent Control of Boosted Terahertz Radiation from Air Plasma Pumped by a Femtosecond Three-Color Sawtooth Field. Phys Rev A (2020) 102:063522. doi:10.1103/physreva.102.063522
219. Yuan KJ, Bandrauk AD. Controlling Circularly Polarized High-Order Harmonic Generation in Molecules by Intense Tricircular Laser Pulses. Phys Rev A (2019) 100:033420. doi:10.1103/physreva.100.033420
220. Pfeiffer AN, Cirelli C, Smolarski M, Keller U. Recent Attoclock Measurements of strong Field Ionization. Chem Phys (2013) 414:84–91. doi:10.1016/j.chemphys.2012.02.005
221. Wituschek A, von Vangerow J, Grzesiak J, Stienkemeier F, Mudrich M. A Simple Photoionization Scheme for Characterizing Electron and Ion Spectrometers. Rev Scientific Instr (2016) 87:083105. doi:10.1063/1.4960401
222. Bruss D, Leuchs G. Quantum Information, 2 Volume Set: From Foundations to Quantum Technology Applications. John Wiley & Sons (2019).
223. Nawrocki W. Introduction to Quantum Metrology: Quantum Standards and Instrumentation. Heidelberg: Springer (2015).
224. Spektor G, Kilbane D, Mahro AK, Frank B, Ristok S, Gal L, et al. Revealing the Subfemtosecond Dynamics of Orbital Angular Momentum in Nanoplasmonic Vortices. Science (2017) 355:1187–91. doi:10.1126/science.aaj1699
225. Henzler P, Traum C, Holtkemper M, Nabben D, Erbe M, Reiter DE, et al. Femtosecond Transfer and Manipulation of Persistent Hot-trion Coherence in a Single Cdse/znse Quantum Dot. Phys Rev Lett (2021) 126:067402. doi:10.1103/PhysRevLett.126.067402
Keywords: coherent control, bichromatic polarization shaping, multiphoton ionization, photoelectron tomography, chiral molecules
Citation: Eickhoff K, Englert L, Bayer T and Wollenhaupt M (2021) Multichromatic Polarization-Controlled Pulse Sequences for Coherent Control of Multiphoton Ionization. Front. Phys. 9:675258. doi: 10.3389/fphy.2021.675258
Received: 02 March 2021; Accepted: 23 July 2021;
Published: 20 August 2021.
Edited by:
Robert Gordon, University of Illinois at Chicago, United StatesReviewed by:
Jianming Wen, Kennesaw State University, United StatesDavid Ayuso, Imperial College London, United Kingdom
Nicolas Douguet, Kennesaw State University, United States
Copyright © 2021 Eickhoff , Englert , Bayer and Wollenhaupt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Matthias Wollenhaupt, bWF0dGhpYXMud29sbGVuaGF1cHRAdW5pLW9sZGVuYnVyZy5kZQ==
 Kevin Eickhoff
Kevin Eickhoff  Lars Englert
Lars Englert  Tim Bayer
Tim Bayer  Matthias Wollenhaupt
Matthias Wollenhaupt