Chemomechanical Simulation of Microtubule Dynamics With Explicit Lateral Bond Dynamics

We introduce and parameterize a chemomechanical model of microtubule dynamics on the dimer level, which is based on the allosteric tubulin model and includes attachment, detachment and hydrolysis of tubulin dimers as well as stretching of lateral bonds, bending at longitudinal junctions, and the possibility of lateral bond rupture and formation. The model is computationally efficient such that we reach sufficiently long simulation times to observe repeated catastrophe and rescue events at realistic tubulin concentrations and hydrolysis rates, which allows us to deduce catastrophe and rescue rates. The chemomechanical model also allows us to gain insight into microscopic features of the GTP-tubulin cap structure and microscopic structural features triggering microtubule catastrophes and rescues. Dilution simulations show qualitative agreement with experiments. We also explore the consequences of a possible feedback of mechanical forces onto the hydrolysis process and the GTP-tubulin cap structure.

1. Introduction

Microtubule (MT) dynamics is essential for many cellular processes, such as the positioning and separation of chromosomes in mitosis [1], or maintenance of cell polarity and cell shape [2]. An important feature, which enables MTs to exert pulling and pushing forces in these cellular processes, is their dynamic instability, which is the stochastic switching of MTs between states of growth by polymerization and states of fast shrinkage by depolymerization [3].

Switching from growth into shrinkage happens in catastrophe events, whose mechanism and triggers are not completely understood on the molecular level, but they are associated with a loss of the GTP-cap by hydrolysis within the MT [4, 5] (see references [6, 7] for reviews). Hydrolysis is strongly coupled to mechanics of the MT, as is clearly seen in the curling of MT protofilaments into a “ram's horn” conformation after the catastrophe and during the shrinking phase [8]. The loss of the stabilizing GTP-cap triggers a release of binding energy and stored mechanical energy in the tubular MT structure. Therefore, shrinkage following a catastrophe is more than simple depolymerization of the MT; it is rather a rupture or crack propagation process between protofilaments, which releases chemical and mechanical energy while it propagates toward the minus end. The energy released during shrinking has biological functions and can be employed to exert pulling forces onto kinetochores during separation of MTs in mitosis [9].

The curling of hydrolyzed protofilaments into a ram's horn structure shows that GDP-tubulin dimers have a bent conformation [8, 10–12]. Tubulin dimers assembled within the MT body are in a straight conformation, on the other hand [13]. Hydrolysis of tubulin dimers embedded in a straight MT causes mechanical strains in the tubular structure because the surrounding MT lattice prevents these GDP-tubulin dimers from assuming their preferred bent conformation. This mechanical strain is released in a catastrophe via the rupture of lateral bonds.

There are different models explaining how the mechanical strain is increased by hydrolysis or how lateral bonds are weakened by hydrolysis such that the strained MT becomes more prone for catastrophes. The first cryo-electron microscopy (EM) studies showed blunt tips for growing MTs but curved tips for shrinking MTs [8] suggesting that GTP-protofilaments are straight while GDP-protofilaments are curved. Later evidence from cryo-EM showed that GTP-protofilaments are also curved, but significantly less than GDP-protofilaments [10]. The allosteric model is based on the assumption that hydrolysis of a tubulin dimer changes the dimer conformation from a rather straight GTP-conformation to a bent GDP-conformation. Hydrolysis of tubulin dimers embedded in a straight MT causes mechanical strain in the tubular structure because the surrounding MT lattice prevents these GDP-tubulin dimers from assuming their preferred bent conformation. This model was employed in almost all previous MT simulation models that consider MT mechanics [14–19]. The lattice model, on the other hand, is based on evidence from X-ray and cryo-EM structures [20–23] and simulations [24, 25] that also GTP-tubulin dimers assume a bent conformation and that hydrolysis rather affects the lateral and longitudinal dimer interaction energies. It is supported by recent experimental observations that both growing and shrinking MTs have bent protofilament ends [26]. Reference [26] also presents first simulation results with a lattice model. But there is also recent evidence from molecular dynamics (MD) simulation pointing in a different direction and supporting an intermediate model, where hydrolysis affects interactions but also lowers GDP-tubulin flexibility [27]. If hydrolysis weakens lateral interaction energies, hydrolysis makes the MT structure more prone for a catastrophe. While in the allosteric model, the mechanical strain in the structure is increased by hydrolysis, in the lattice model, the mechanical strain that the MT structure can tolerate is reduced by hydrolysis. In both models, the result is an increased propensity for lateral bonds to rupture. Therefore, chemomechanical MT models with explicit bond rupture are a necessity to reproduce catastrophes. We build on existing modeling approaches based on the allosteric model [14–19] and include lateral bond rupture as explicit stochastic events with force-dependent rates, which can give important clues about how catastrophes are triggered in the MT structure.

The influence of tubulin dimer hydrolysis onto the mechanics of the MT lattice suggests that, vice versa, mechanical forces and torques acting on tubulin dimers via strains in the tubular structure could also affect hydrolysis rates, an effect which has been explored only in reference [17] previously. Although this interplay is plausible from a mechanochemistry point of view, experimental verification on the dimer level is extremely difficult and not possible yet, but we can employ chemomechanical MT models to explore and suggest possible implications for the dynamic instability.

The coupling between chemical events—namely polymerization events, dimer hydrolysis, bond rupture—and mechanical forces because of conformational changes due to these chemical events, is a characteristic of MTs and requires chemomechanical MT models on the dimer level in order to develop a microscopic understanding of their dynamic instability including catastrophe and rescue events [28]. In this respect, chemomechanical models go beyond a phenomenological description of MT dynamics in a four-parameter model based on growth and shrinking velocities and phenomenological catastrophe and rescue rates [29]. The challenge for microscopic chemomechanical models is to include all chemical events as stochastic processes, to perform conformational relaxation governed by MT mechanics following each chemical event, and, eventually, to also include the feedback of mechanical forces within the MT onto reaction rates of the chemical events.

We present a stochastic chemomechanical MT model on the dimer level. Our model includes (i) a mechanical model of the MT containing lateral elastic bonds between tubulin monomers in neighboring protofilaments and a harmonic bending energy between tubulin monomers with a non-zero equilibrium angle after hydrolysis (allosteric model), (ii) stochastic addition and removal of tubulin dimers, (iii) explicit stochastic lateral bond rupture and bond formation; the bond rupture rate is coupled to the mechanical stress state of the bond and thus via elastic interactions within the MT lattice also to the other bonds, (iv) stochastic hydrolysis of dimers with a rate that can also couple to the mechanical bending stress in the dimer. The stochastic kinetics (ii)–(iv) is handled by a Gillespie algorithm and after each stochastic event, a mechanical energy minimization mimicking the relaxational dynamics of the structure is applied to the MT.

In order to parameterize our model, we will focus on the simplified scenarios of a growing MT consisting of GTP-tubulin only and a shrinking MT consisting of GDP-tubulin only. In both cases, we can neglect hydrolysis (iv); in the growing GTP-MT, we can also neglect mechanics, which is generated by hydrolysis. In the presence of mechanics and hydrolysis, repeated catastrophe and rescue events are obtained and will be described and analyzed. One problem in chemomechanical MT models is the computational effort associated with the mechanical relaxation. We investigate in detail, which level of computational effort is necessary in our model to obtain a sufficient mechanical relaxation following each chemical event, on the one hand, and which simplifications can be taken to assure a finite simulation time for growing MTs, on the other hand. This will allow us to simulate arbitrarily long growing MTs at fixed computational speed.

Our chemomechanical model has to be compared to previous modeling approaches, which include the mechanics of the MT [14–19]:

• References [15, 16] employ the allosteric model for dimer bending and include stochastic addition and removal of dimers. Hydrolysis is random. Mechanical energy minimization is performed only locally on randomly selected dimers. Lateral bond rupture is not implemented as explicit stochastic process but only included using a threshold energy criterion.

• The models in references [14, 19] focus on mechanics and do not include dimer addition and removal. They are also based on the allosteric model but consider fixed hydrolysis states. In reference [14], the lateral bond energy landscape is harmonic around a minimum but includes an energy barrier and a dissociated, i.e., ruptured state. Global energy minimization gives the final state of the static structure.

• In reference [18], the stochastic kinetics is added to a mechanical model similar to Molodtsov et al. [14]. Here, the mechanical relaxation and lateral bond rupture is performed using Brownian dynamics (which include thermal fluctuations) with small time steps (equivalent to 2 × 10⁷ minimization steps), which is only applied to 300 tubulin dimers at the plus end. Stochastic addition of dimers and removal by rupture of lateral and longitudinal bonds is included. The rupture of lateral bonds happens by activation over the bond energy barrier, the longitudinal rupture by a threshold criterion. Hydrolysis is random and stochastic with a rate that is independent of mechanics.

• Reference [17] is also based on the allosteric model. Lateral bond rupture is possible using a threshold criterion. Mechanical energy minimization was performed globally. There is no addition or removal of dimers, but hydrolysis is included. In a first attempt to include a coupling of the hydrolysis rate to mechanical forces, the hydrolysis kinetics remained deterministic, however, with the most probable hydrolysis event determined by mechanical forces. In the present paper, we will add addition and removal of dimers and a fully stochastic hydrolysis kinetics.

Our chemomechanical model has also to be compared to previous purely chemical modeling approaches on the dimer level but without explicit mechanical model [30–34]. These models include attachment and detachment of tubulin dimers; some of these models [32–34] also include lateral bond rupture and are thus able to produce crack-like catastrophe events. Crack-like catastrophe events are, however, triggered by adjusting chemical rupture rates rather than including MT mechanics. The model by Margolin et al. [33] has successfully reproduced features of the experimentally observed MT dynamic instability [35] but relies on a heuristic tuning of simulation parameters.

2. Materials and Methods

2.1. Microtubule Structure and Energy

Our MT model is formulated on the dimer level. The base units of the model are alpha- and beta-tubulin monomers. In our model, we represent each monomer as cylinder with radius r_t = 2 nm and height ℓ_t = 4 nm (see Table 1). Alpha- and beta-tubulin monomers form unbreakable tubulin dimers, which are arranged head-to-tail into protofilaments. Thirteen protofilaments form a 13_3 MT, i.e., a MT with a helical shift of three tubulin monomer lengths per turn.

TABLE 1

Table 1. Geometric parameters of our MT model.

For the remainder of this paper, we will use triples (p, d, t) to address specific tubulin monomers within the MT with p ∈ {1, 2, …, 13} as the protofilament number, d ∈ {1, 2, …, d(p)} as the tubulin layer [with d = 1 denoting the minus end and d = d(p) denoting the plus end of the protofilament p], and t ∈ {1, 2} denoting the tubulin monomer within the dimer with t = 1 for the alpha- and t = 2 for the beta-tubulin monomers. For simplicity, we assume periodicity in p (i.e., p = 0 ≡ 13 and p = 14 ≡ 1) and combined periodicity in d and t [i.e., (p, d, 3) ≡ (p, d + 1, 1) and (p, d, 0) ≡ (p, d − 1, 2)]. We will also generally refer to the lateral neighbors of tubulin monomer (p, d, t) using (p ± 1, d, t) even though at the seam, lateral neighbors differ in all three indices.

The MT is straight and oriented along the z-axis with the positive z-direction pointing to the plus end. Vectors $\overrightarrow{m}(p,d,t)$ and $\overrightarrow{p}(p,d,t)$ point to the to the lower (minus end) and upper (plus end) circular base of the tubulin monomer (p, d, t). The direction vector

$\begin{array}{ll}\overrightarrow{d}(p,d,t)=\overrightarrow{p}(p,d,t)-\overrightarrow{m}(p,d,t)={\ell }_{\text{t}}\left(\begin{array}{c}cos\varphi (p)sin\theta (p,d,t)\\ -sin\varphi (p)sin\theta (p,d,t)\\ cos\theta (p,d,t)\end{array}\right)& (1)\end{array}$

with length ℓ_t = 4 nm points from $\overrightarrow{m}(p,d,t)$ to $\overrightarrow{p}(p,d,t)$ and is specified using spherical coordinates, i.e., azimuthal and polar angles (see Figure 1A). The polar angle θ(p, d, t) is the only degree of freedom of each monomer, because we assume that monomers can only be displaced in radial direction, i.e., all azimuthal angles are fixed to ϕ(p) = 2π(p−1)/13. As both alpha- and beta-tubulin have their polar angles as a degree of freedom, the model supports intra- and inter-dimer curling [36].

FIGURE 1

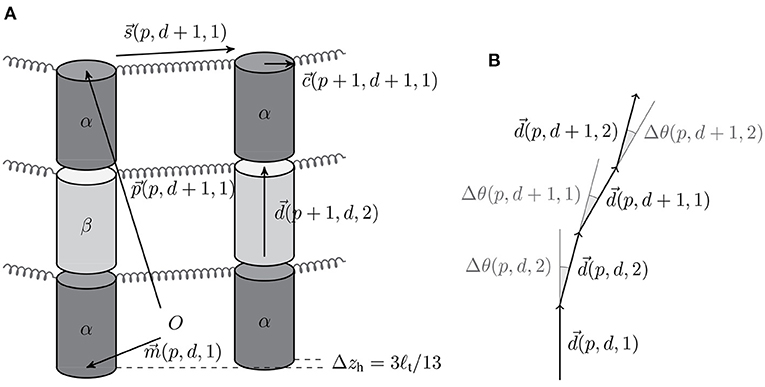
Figure 1. (A) Schematic illustration of the different vectors with the origin O (The vertical gaps between tubulin cylinders are for illustration purposes only). (B) Bending angles between the tubulin monomer direction vectors.

At the minus end of the MT each protofilament p starts with an alpha-tubulin arranged in a circle with mean MT radius R_MT = 10.5 nm and with an offset z(p, 1, 1) = 3ℓ_t(p − 1)/13 in z-direction, such that the seam is between the 13th and the 1st protofilament. The protofilament length that will be used to calculate the growth and shrinkage velocities is the maximum z-coordinate ℓ_max(p) of all tubulin monomers within the protofilament (see Supplementary Material for more details). The MT length is given by the average

$\begin{array}{ll}{\ell }_{\text{MT}}=\frac{1}{13}{\displaystyle \sum _{p=1}^{13}}{\ell }_{\text{max}}(p).& (2)\end{array}$

Every tubulin monomer has four interaction points: two in longitudinal direction and two in lateral direction. The longitudinal bond between alpha- and beta-tubulin monomers of the same dimer is considered unbreakable but the orientation of this junction can change via the beta-tubulin's polar angle θ(p, d, 2). In contrast, the longitudinal bond between adjacent tubulin monomers of different dimers can break and is modeled via the bond energy $\Delta G_{\text{long}}^{0*}$ (where the “0” refers to it being a standard energy [37] and the asterisk to the fact that it also includes the entropic cost of “immobilization” [30]). The lateral interaction points are located at the edge of the upper base (see Figure 1A). If there is a lateral bond between tubulin monomer (p, d, t) and its neighbor in the (p + 1)-th protofilament, the bond is modeled as a harmonic spring with base energy $\Delta G_{\text{lat}}^0$:

$\begin{array}{ll}{E}_{\text{lat}}(p,d,t)=\Delta G_{\text{lat}}^0+\frac{1}{2}{k}_{\text{lat}}{(|\overrightarrow{s}(p,d,t)|-s_0)}^2& (3)\end{array}$

with the spring constant k_lat of the bond and the vector $\overrightarrow{s}(p,d,t)$ connecting the lateral interaction points; s₀ ≃ 1.47 nm is the rest length of the spring (see [17] and also consider the helical shift between two neighboring tubulin monomers of 3ℓ_t/13). Lateral bonds at the seam are assumed to have identical mechanical properties as other lateral bonds based on evidence that they do not constitute a weaker bond [22, 38]. Additionally, there is a lateral repulsion term between neighboring tubulin monomers (regardless of whether they are bonded or not) to ensure a cylindrical form [17]:

$\begin{array}{ll}{E}_{\text{rep}}(p,d,t)=k_{\text{rep}}{\left(|\overrightarrow{p}(p,d,t)-\overrightarrow{p}(p+1,d,t)|-2r_{\text{t}}\right)}^{-12}.& (4)\end{array}$

The bending of monomer junctions is described by a harmonic potential with bending constant κ:

$\begin{array}{ll}{E}_{\text{bend}}(p,d,t)=\frac{1}{2}\kappa {\left(\Delta \theta (p,d,t)-\Delta {\theta }_0(p,d,t)\right)}^2.& (5)\end{array}$

The bending angle Δθ(p, d, t) = θ(p, d, t) − θ(p, d, t − 1) (see Figure 1B) is calculated with the neighboring monomer in the minus direction [using the periodicity convention in d and t, (p, d, 0) ≡ (p, d − 1, 2)], and Δθ₀(p, d, t) is its equilibrium value. For hydrolyzed beta-tubulin monomers and for alpha-tubulin monomers on top of a hydrolyzed beta-tubulin (and for the first alpha-tubulin monomers of each protofilament if the beta-tubulin in the same dimer is hydrolyzed), we use a rest angle Δθ₀(p, d, t) = 11° in order to reproduce the experimentally measured radius of curvature of 21 nm corresponding to an angle of 22° per dimer for a GDP-protofilament curling into the ram's horn configuration [10, 39]. Otherwise (for an unhydrolyzed beta-tubulin monomer or an alpha-tubulin monomer on top of an unhydrolyzed beta-tubulin monomer), we assume a straight equilibrium configuration with Δθ₀(p, d, t) = 0°. This choice of rest angles implements the allosteric model, where GTP-hydrolysis leads to bending of tubulin dimers.

Our mechanical MT model is defined by the total energy

$\begin{array}{l}{E}_{\text{MT}}={\displaystyle \sum _{p=1}^{13}{\displaystyle \sum _{d=1}^{d(p)}(\Delta G_{\text{long}}^{0*}+{\displaystyle \sum _{t=1}^2[E_{\text{lat}}(p,d,t)+E_{\text{rep}}(p,d,t)}}}\\ +E_{\text{bend}}(p,d,t)]),& (6)\end{array}$

where E_lat(p, d, t) only contributes if there is a lateral bond between tubulin monomers (p, d, t) and (p + 1, d, t) and E_rep(p, d, t) only contributes if tubulin monomer (p, d, t) has a lateral partner (p + 1, d, t).

There are four free parameters in our mechanical MT model (see Table 2): the longitudinal bond energy $\Delta G_{\text{long}}^{0*}$, the lateral bond energy $\Delta G_{\text{lat}}^0$, the lateral spring constant k_lat, and the bending constant κ. For the repulsion constant k_rep, we use the same value $k_{\text{rep}}=10^{-6}ra{d}^{2}m{m}^{12}\kappa$ that has been found previously to ensure the overall cylindrical shape of the MT and only contributes a small portion to the MT energy [17].

TABLE 2

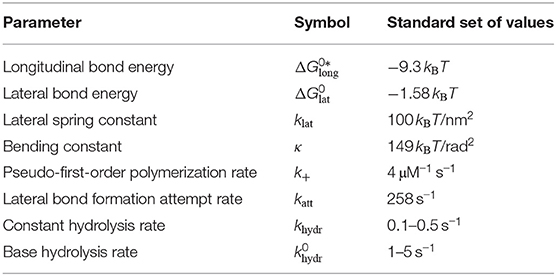
Table 2. Free parameters of our MT model and the “standard set” of their values that we will focus on in the rest of the paper.

In the simulation model, we do not use this mechanical energy to calculate forces for a microscopic dynamics, such as Brownian dynamics on the dimer level (as opposed to [18]). We rather assume that mechanical relaxation dynamics is fast compared to chemical changes in the MT due to tubulin attachment and detachment, bond rupture and formation, or hydrolysis. The slowest mechanical process is relaxation of bending modes of protofilaments governed by small restoring bending moments. The basic time scale for this process can be estimated as $\tau ~\eta {{\ell }_{\text{t}}}^3/\kappa$ [40], where η ~ 10⁻³ Pa s is the viscosity of water. This gives τ ~ 10⁻¹⁰ s, which is orders of magnitude smaller than typical time scales of seconds for chemical events. Therefore, even longer protofilaments relax fast compared to chemical changes. There is additional evidence from Brownian dynamics that bending mode relaxation is also much faster than immobilization in cryo-EM [41]. Therefore, we perform a quasi-instantaneous energy minimization of (6) between these chemical simulation steps. This is the computationally more efficient strategy to achieve mechanical relaxation. The rates of all chemical simulation events themselves determine the dynamics of the MT and are handled by a Gillespie algorithm as explained in more detail below.

2.2. Chemical Simulation Events

To simulate the dynamics of MTs, we include attachment of individual GTP-tubulin dimers and detachment of (laterally unbonded) tubulin dimers or whole (laterally unbonded) protofilament segments at the plus end, as well as lateral bond rupture and formation, and hydrolysis of tubulin dimers as stochastic chemical events into the simulation; Figure 2A summarizes the different possible events and the associated rates.

FIGURE 2

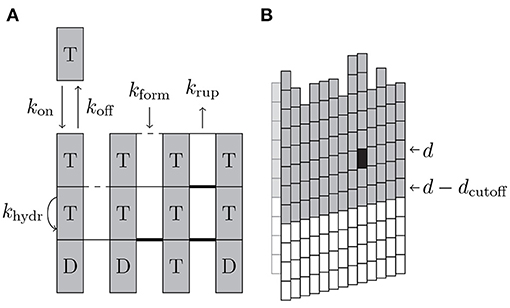
Figure 2. (A) Schematic illustration of the different simulation events with their rates. Dashed lateral bonds can be formed with rate k_form, thin solid lateral bonds can rupture with rate k_rup, and thick bond cannot rupture. “T” and “D” correspond to the hydrolysis state of beta-tubulin of the dimers. (B) If the black tubulin dimer in layer d is affected by an event and d_cutoff = 2 was used, all of the gray (and the black) tubulin dimers are used for energy minimization.

2.2.1. Attachment and Detachment

At the plus end of each protofilament, a GTP-tubulin dimer can attach with an on-rate

$\begin{array}{ll}{k}_{\text{on}}=k_{+}{c}_{\text{tub}}& (7)\end{array}$

where k₊ is the pseudo-first-order polymerization rate and c_tub is the concentration of free GTP-tubulin dimers. The on-rate is assumed to be independent of the hydrolysis state of the protofilament end.

For depolymerization, we assume that a tubulin dimer at the plus end can only detach if it has no lateral bonds. We also allow for detachment of whole protofilament segments starting from an interior dimer [d < d(p)] if the whole segment has no lateral bonds. Laterally unbounded dimers or segments can detach with a rate

$\begin{array}{ll}{k}_{\text{off}}=k_{+}{c}_{0}exp\left(\Delta G_{\text{long}}^{0*}\right)& (8)\end{array}$

as given by Kramers theory with the longitudinal standard bond energy $\Delta G_{\text{long}}^{0*}$ (including the entropic cost of “immobilization”) and the standard concentration c₀ = 1 M [37].

This approach differs from other models [15, 30, 42], where tubulin dimers can detach regardless of whether they have lateral bonds or not. In such models, if a tubulin dimer still has lateral bonds, its detachment rate decreases exponentially with the additional lateral bond energies. In our model, we rather include lateral bond rupture and formation as separate stochastic events into the simulation (similarly to the purely chemical models in [32–34]); bond rupture can then be followed by detachment of laterally unbounded dimers or protofilament segments. Bond rupture enables dimer detachment and is necessary prior to a catastrophe; vice versa, bond reformation is necessary for a rescue event. Therefore, it is essential to also include the process of bond formation into the model. Moreover, it has been observed in MD simulations in Kononova et al. [43] that lateral tubulin bonds can easily reform. The restriction that only laterally unbonded dimers can detach also causes an indirect increase of the effective off-rate if the last dimers of a protofilament are hydrolyzed because this tends to create stretched bonds, which rupture more easily.

2.2.2. Zipper-Like Lateral Bond Rupture and Bond Formation

We assume that bond rupture between protofilaments starts from the plus end and proceeds by a rupture front monomer by monomer toward the minus end; likewise, bonds can be reformed only monomer by monomer toward the plus end in a zipper-like fashion. As a result, we always have a rupture front between two neighboring protofilaments such that all monomers on top of the front toward the plus end are ruptured and all monomers below toward the minus end are intact. If tubulin monomer (p, d, t − 1) has a lateral bond with its neighbor in protofilament p+1 but the tubulin monomer on top of it, (p, d, t), has no lateral bond with this neighbor, the rupture front can recede toward the plus end, and tubulin monomer (p, d, t) can form a bond with rate

$\begin{array}{ll}{k}_{\text{form}}=k_{\text{att}}& (9)\end{array}$

with the attempt rate k_att. Vice versa, if the bond at (p, d, t) is intact and bond (p, d, t + 1) is broken, the rupture front can advance toward the minus end by rupturing this bond with a rate

$\begin{array}{ll}{k}_{\text{rup}}=k_{\text{att}}exp\left(\Delta G_{\text{lat}}^0+\Delta G_{\text{mech}}\right)& (10)\end{array}$

which contains the chemical lateral bond energy $\Delta G_{\text{lat}}^0$ and a mechanical energy ΔG_mech, which accounts for the weakening of the lateral bond due to mechanical strain in the bond and enters according to Bell theory [44, 45]. In our model, ΔG_mech is due to the stretching of the Hookean springs representing the lateral bonds so that ΔG_mech = F_latℓ_rup, where $F_{\text{lat}}=-\partial E_{\text{lat}}/\partial \left|\overrightarrow{s}(p,d,t)\right|$ is the force currently acting on the lateral bond and ℓ_rup is the characteristic bond rupture length. We define ℓ_rup as the length increase of the lateral bond from its rest length s₀ at which the stretching energy of the spring cancels the bond energy:

$\begin{array}{ll}{\ell }_{\text{rup}}=\sqrt{\frac{-2\Delta G_{\text{lat}}^0}{k_{\text{lat}}}}.& (11)\end{array}$

2.2.3. Hydrolysis Without and With Mechanical Feedback

Lastly, GTP in beta-tubulin monomers can hydrolyze into GDP via a random (or scalar) hydrolysis rule meaning that almost every GTP-tubulin dimer in the MT can hydrolyze with a fixed rate k_hydr regardless of the hydrolysis state of its longitudinal neighbor (which would be a vectorial hydrolysis rule). The “almost” in the previous sentence refers to the finding that the polymerization of the tubulin dimer (p, d) and thus the formation of a longitudinal bond between beta-tubulin (p, d − 1, 2) and alpha-tubulin (p, d, 1) catalyzes the hydrolysis reaction in beta-tubulin (p, d − 1, 2) [13]. As a consequence, only GTP-tubulin dimers that ever had another tubulin dimer on top of them can be hydrolyzed in our model.

We also consider the possibility that hydrolysis is mechanochemically coupled to the bending strain [17]. Then, the hydrolysis rate

$\begin{array}{ll}{k}_{\text{hydr}}(p,d)=k_{\text{hydr}}^{0}exp\left(-\Delta E_{\text{hydr}}(p,d)\right)& (12)\end{array}$

is modulated with a dimer-specific change ΔE_hydr(p, d) in the energy barrier height of the hydrolysis reaction, which depends on the bending state of dimer (p, d). Because this bending state also depends via lateral bonds on the bending states in all neighboring dimers, and because the bending state of all neighboring dimers strongly depends on their hydrolysis state, the hydrolysis dynamics becomes effectively non-random but depends on the hydrolysis state of the neighbors.

The basis for our assumption of a tubulin dimer-specific mechanochemical hydrolysis rate is to view the equilibrium bending angle Δθ₀ of a dimer as the reaction coordinate for hydrolysis which can be described by an energy profile F_hydr(Δθ₀). F_hydr(Δθ₀) has two local minima corresponding to the straight conformation with Δθ₀ = 0° and the curved conformation with Δθ₀ = 11° and a rate-limiting energy barrier of unknown height $\Delta F_{\text{hydr}}^{\text{barrier}}$ in between. We propose that hydrolysis of a tubulin dimer is eased if its actual bending angle Δθ is closer to the equilibrium angle Δθ₀ = 11° in the hydrolyzed state. We model this dependency by adding a dimer-specific bending energy contribution E_hydr(Δθ₀) to F_hydr(Δθ₀), which changes the energy barrier height from $\Delta F_{\text{hydr}}^{\text{barrier}}$ to $\Delta F_{\text{hydr}}^{\text{barrier}}+\Delta E_{\text{hydr}}(p,d)$ (see Figure 3). $\Delta F_{\text{hydr}}^{\text{barrier}}$ can be absorbed into the constant rate $k_{\text{hydr}}^0$ so that only ΔE_hydr(p, d) remains in the Arrhenius factor in (12).

FIGURE 3

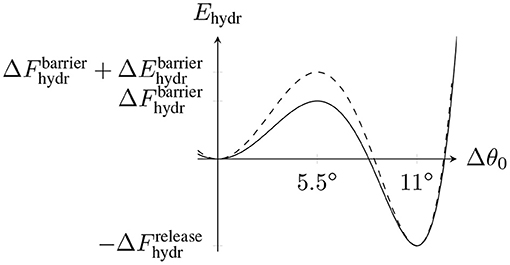
Figure 3. Schematic hydrolysis energy landscape with two local minima corresponding to the straight conformation (Δθ₀ = 0°) and the bent conformation (Δθ₀ = 11°) and an energy barrier $\Delta F_{\text{hydr}}^{\text{barrier}}$ at Δθ₀ = 5.5° between them. $\Delta F_{\text{hydr}}^{\text{release}}$ is the energy released by hydrolysis. The dashed line represents the modified energy landscape due to the dimer-dependent contribution E_hydr(Δθ₀).

To calculate the change in the energy barrier height ΔE_hydr(p, d), we now consider the total MT energy in (6) as a function of the hydrolysis reaction coordinate Δθ₀ while keeping all polar angles {θ(p, d, t)} fixed. We simply assume that the energy barrier is centered between the minima at $\Delta {\theta }_0^{\text{barrier}}=$ 5.5° resulting in

$\begin{array}{ll}\Delta E_{\text{hydr}}=E_{\text{MT}}(\Delta {\theta }_0=5.5°)-E_{\text{MT}}(\Delta {\theta }_0=0°).& (13)\end{array}$

Because hydrolysis of tubulin dimer (p, d) affects the rest bending angles of beta-tubulin monomer (p, d, 2) and alpha-tubulin monomer (p, d + 1, 1) and the rest bending angles only affect the bending energies (5), we finally obtain

$\begin{array}{l}\Delta E_{\text{hydr}}(p,d)=\frac{1}{2}\kappa [{(\Delta \theta (p,d,2)-5.5°)}^2-\Delta {\theta }^2(p,d,2)\\ +{(\Delta \theta (p,d+1,1)-5.5°)}^2-\Delta {\theta }^2(p,d+1,1)]\\ =\frac{1}{2}\kappa [-(\Delta \theta (p,d,2)+\Delta \theta (p,d+1,1))·11°\\ +2·{(5.5°)}^2]& (14)\end{array}$

so that only a local bending energy change has to be calculated. As a result, tubulin monomers in the MT lattice with larger bending angles Δθ(p, d, t) tend to hydrolyze preferentially. For the terminal tubulin dimer of a protofilament (p, d(p)), the d + 1-term in (14) is missing because tubulin monomer (p, d(p) + 1, 1) does not exist. This results in an overall smaller energy barrier and, thus, a higher hydrolysis rate of the terminal tubulin dimer.

We also see that the base hydrolysis rate $k_{\text{hydr}}^0$ in (12) is not the hydrolysis rate for a perfectly straight MT [Δθ(p, d, t)= 0° for all tubulin monomers] because there is still the constant contribution κ(5.5°)² to the energy barrier in (14) that reduces the hydrolysis rate. As these terms are proportional to the bending constant κ, we cannot simply absorb them into the constant factor $k_{\text{hydr}}^0$.

We note that for almost all GTP-tubulin dimers in the GDP-body of the MT, we will typically find negative bending angles; these dimers bend inward in order to allow the longitudinal GDP-dimer neighbors to further bend outwards. For such negative bending angles the hydrolysis rate is reduced according to (14).

In addition to the previous four free parameters from the MT energy, the simulation events add three additional free parameters: the pseudo-first-order polymerization rate k₊, the attempt rate k_att, and the hydrolysis rate k_hydr (or $k_{\text{hydr}}^0$). In total, there are now seven free parameters, which are listed in Table 2.

2.3. Simulation and Parameter Determination

The actual MT simulation (implemented in C++) works as follows:

1. Initially, a MT with N_GDP GDP-tubulin dimers followed by N_GTP GTP-tubulin dimers per protofilament is constructed with θ(p, d, t)= 0° for all (p, d, t).

2. Using the tubulin monomers' polar angles {θ(p, d, t)}, the MT's actual initial configuration is determined by minimizing its mechanical energy. Details on the minimization procedure will be discussed in the next section.

3. For all of the events described in the previous section, a list of possible events is determined and based on their rates k_i, a “tentative” event time t_i is calculated using Gillespie's first reaction method [46]:

$\begin{array}{ll}{t}_i=\frac{1}{k_i}ln\frac{1}{r}& (15)\end{array}$

where r is a uniformly distributed random number from 0 to 1. The event i with the shortest event time t_i is executed and the simulation time is increased by t_i.

4. Assuming fast mechanical relaxation the MT's energy is minimized after any event.

5. The simulation terminates if a protofilament is shorter than two tubulin dimers.¹ Otherwise we go back to the third step to determine the next event.

There is a general agreement between different experiments [3, 47–52] that the MT growth velocity v_gro increases linearly with the tubulin dimer concentration c_tub and that the shrinkage velocity v_shr is independent of c_tub. We will use the results by Walker et al. [47], which were measured for c_tub ∈ [7.7, 15.5 μM],

$\begin{array}{ll}{v}_{\text{gro}}(c_{\text{tub}})=(0.33\pm 0.01)\frac{\mu m}{min\mu M}{c}_{\text{tub}}-(1.59\pm 0.50)\frac{\mu m}{min},& (16)\end{array}$

$\begin{array}{ll}{v}_{\text{shr}}=(-27\pm 1)\frac{\mu m}{min},& (17)\end{array}$

and lead to an individual critical concentration c_tub,c ≃ 5 μM (below which v_gro < 0).

To determine the values of the model parameters, we use a “divide and conquer” approach [15, 30]. First, we consider MT growth, where mechanics are assumed not to play a significant role as protofilaments are not curling outward so that ΔG_mech = 0. Thus, we use a GTP-only MT (N_GDP = 0) and set k_lat = 0 and κ = 0 so that the only free parameters left are k₊, $\Delta G_{\text{long}}^{0*}$, $\Delta G_{\text{lat}}^0$, and k_att. The goal of these simulations is to reproduce the measured growth velocity in (16) as function of the free tubulin dimer concentration c_tub. Secondly, we consider MT shrinkage, where mechanics are now assumed to play a significant role, i.e., k_lat > 0 and κ > 0. For a shrinking MT, we use N_GTP = 0, N_GDP > 0, and the parameter values already determined by the growth simulations to reproduce the shrinkage velocity in (17). In both cases, hydrolysis is ignored. A schematic overview of the entire parameter determination procedure can be found in Figure S7 in the Supplementary Material.

Comparing the number of free parameters and the amount of experimental data, we can already predict that we will not be able to determine one set of fixed parameter values but only restrict some parameter values to specific values if other parameter values are set to (arbitrarily but reasonably) chosen values. We will discuss this issue in more detail in the conclusion.

2.4. Energy Minimization

In previous three-dimensional models, different energy minimization approaches have been used. VanBuren et al. [15] used a local minimization approach in which they randomly selected individual tubulin dimers and then only locally minimized with respect to the parameters of this dimer. On average, each tubulin dimer was visited three times for minimization. Zakharov et al. [18] employed a completely different approach by explicitly modeling the stochastic motion of tubulin monomers in space using Brownian dynamics (applied to the first 300 tubulin dimers at the plus end). They solve Langevin equations every 2 × 10⁻¹⁰ s while using × 10⁻³ s as the time step for the events in their simulation resulting in ${O}(10^7)$ dynamics steps between actual events. Using a parallel implementation run on a supercomputer, their simulation took more than a day to simulate 1 s of MT dynamics. There are drawbacks for both approaches: a local energy minimization scheme might not come close enough to a mechanically relaxed configuration, whereas a full Brownian dynamics simulation is computationally very costly. In this paper, we employ a systematic mechanical energy minimization between each stochastic chemical simulation event. We try to achieve a better mechanical energy relaxation than VanBuren et al. [15] with significantly less computational steps than Zakharov et al. [18].

In our simulation, we use the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm, a quasi-Newton method, provided by the GNU Scientific Library (GSL) [53] to minimize the total mechanical MT energy in (6) as a function of the polar angles {θ(p, d, t)}. If each protofilament in the simulated MT contains N_GDP + N_GTP tubulin dimers, there are a total of 26(N_GDP + N_GTP) polar angles and thus the same number of minimization parameters. In realistic simulations, MTs can stay in the growing phase for a very long time resulting in an unbounded increase in the number of minimization parameters drastically slowing down the simulation. In essence, the average time for one minimization step increases with the MT length in this scenario making long-running simulations impossible.

To overcome this limitation, we will explore two possibilities to avoid having a MT length-dependent number of minimization parameters:

1. restricting the number of minimization steps per energy minimization to a small value but still considering all minimization parameters (this approach is similar to the strategy in [15]),

2. restricting the number of minimization parameters by only considering the tip of the MT but not restricting the number of minimization steps.

While the first strategy is easy to understand and implement, the second needs further specifications in terms of how we define the tip of the MT here. If a certain event is executed that affects tubulin dimer (p, d), we include all layers starting from min(0, d − d_cutoff) in the mechanical energy minimization because mechanical interactions within the MT have a certain range; d_cutoff is a cutoff layer distance (see Figure 2B).

Below, we will compare these approaches of restricted minimization with respect to accuracy and speed and find that we obtain accurate energy minimization at a high simulation speed by using the second approach and restricting the number of minimization parameters with d_cutoff = 10. We can compare with the approaches of Zakharov et al. [18] and VanBuren et al. [15] in terms of the average number of minimization steps between chemical events.

Zakharov et al. [18] use ${O}(10^7)$ Brownian dynamics steps between events and restrict the number of simulation parameters to 300 tubulin dimers at the plus end. With d_cutoff = 10 we minimize on average with respect to a comparable number of 150 tubulin dimers at the plus end. To compare the efficiency, we consider a single quasi-Newton minimization step in our simulation to be equivalent to one time step of their Brownian dynamics (if we ignore the random thermal fluctuations in their Langevin equations, they are basically using a gradient descent method). We compare our event time t_i divided by the number of minimization steps after the execution of that event to their Brownian dynamics time step of 2 × 10¹⁰ s. For shrinking MTs, one minimization step takes ${O}$(10⁻⁵ s) after polymerization events, ${O}$(10⁻⁴ s) after depolymerization events, and ${O}$(10⁻⁷ s) after lateral bond events; all of these time steps are orders of magnitude larger than 2 × 10⁻¹⁰ s and, thus, the simulation proceeds orders of magnitude faster, while we still achieve an accurate energy minimization. As a comparison with the 1 s of MT dynamics simulated in more than a day in a parallel computation in reference [18], we generally do not require more than a few hours for 1 min of MT dynamics (for a constant hydrolysis rate) using just a single CPU core.

VanBuren et al. [15] apply a local minimization procedure and restrict minimization to, on average, three minimizations with respect to the parameters of each dimer. Because one step of their algorithm minimizes with respect to the parameters of a single tubulin dimer, a comparison to our quasi-Newton minimization steps which minimize the MT energy with respect to the parameters of, on average, ${O}(150)$ tubulin dimers is not straightforward. In addition, VanBuren et al.'s model also contains longitudinal springs so that outward bending of single tubulin dimers as a consequence of local minimization can be compensated by stretching the next longitudinal spring. As our model does not contain such longitudinal springs, bending one tubulin dimer causes the whole protofilament part above the tubulin dimer to also bend outwards creating an effectively non-local, far-reaching interaction. Consequently, we are not able to also implement a local minimization procedure for comparison. To make a qualitative comparison between the two approaches, we assume that one minimization step of our BFGS algorithm, which acts on average on 300 parameters, i.e., 150 tubulin dimers, corresponds to 100 single tubulin dimer minimizations in the model of reference [15] as they consider three parameters per tubulin dimer. Between chemical events, we perform on average 150 BFGS minimization steps, which corresponds to 1.5 × 10⁴ single tubulin dimer minimizations in reference [15]. Therefore, we apply the equivalent of 15, 000/150 = 100 single tubulin minimizations to each of the 150 tubulin dimers close to the plus tip on average as compared to three single tubulin dimer minimizations in the simulation model of reference [15]. Accordingly, we should achieve a more accurate mechanical energy relaxation.

We also compared our chosen minimization method, the BFGS algorithm, against the other multidimensional minimization algorithms using derivatives provided by GSL [53], including the conjugate gradient method, and found the BFGS algorithm to perform better. In particular, to fully minimize the initial configuration of a MT with N_GDP = 20 and N_GTP = 0, BFGS only required about a third of the time compared to the next best algorithm, a conjugate gradient method.

3. Results

3.1. GTP-Microtubule Growth and Model Parameterization

MT growth mainly depends on the four parameters k₊, $\Delta G_{\text{long}}^{0*}$, $\Delta G_{\text{lat}}^0$, and k_att, because the growing MT tip mainly consists of straight GTP-tubulin dimers. Therefore, we consider growth of a GTP-only MT (N_GDP = 0) in the absence of hydrolysis and set k_lat = 0 and κ = 0 so that the only free parameters left are k₊, $\Delta G_{\text{long}}^{0*}$, $\Delta G_{\text{lat}}^0$, and k_att. For k₊ = 2 μM⁻¹ s⁻¹ and k₊ = 4 μM⁻¹ s⁻¹, we scanned the parameter space $(\Delta G_{\text{long}}^{0*},\Delta G_{\text{lat}}^0,k_{\text{att}})$ in steps $\Delta \Delta G_{\text{long}}^{0*}=$ 0.2 k_BT to find parameter values that reproduce the experimental growth velocity data of Walker et al. in (16). The growth velocity v_gro for each simulation was determined by fitting ℓ_MT(t_sim) with a linear function. Experiments on MT growth show a linear dependence v_gro(c_tub) = a_groc_tub + b_gro characterized by two parameters a_gro and b_gro from (16). If simulations reproduce a linear dependence of v_gro as a function of c_tub, we can determine two of the three model parameters $(\Delta G_{\text{long}}^{0*},\Delta G_{\text{lat}}^0,k_{\text{att}})$ by fitting to the experimental data (16) for a_gro and b_gro, i.e., two experimental constraints fix two model parameters as a function of the third parameter. This will allow us to parameterize a one-dimensional sub-manifold (a line) within the three-dimensional parameter space $(\Delta G_{\text{long}}^{0*},\Delta G_{\text{lat}}^0,k_{\text{att}})$ where our model agrees with experimental growth data. This procedure is conceptually analogous to the approach of VanBuren et al. [30], but we work in a higher-dimensional (three-dimensional) space of model parameters.

As a result, we obtain a line in the three-dimensional parameter space, which we parameterize by $\Delta G_{\text{long}}^{0*}$, i.e., for a given value of $\Delta G_{\text{long}}^{0*}$, a value of $\Delta G_{\text{lat}}^0$ (see Figure 4A) and a value of k_att (see Figure 4B) is determined by the experimental growth data.

FIGURE 4

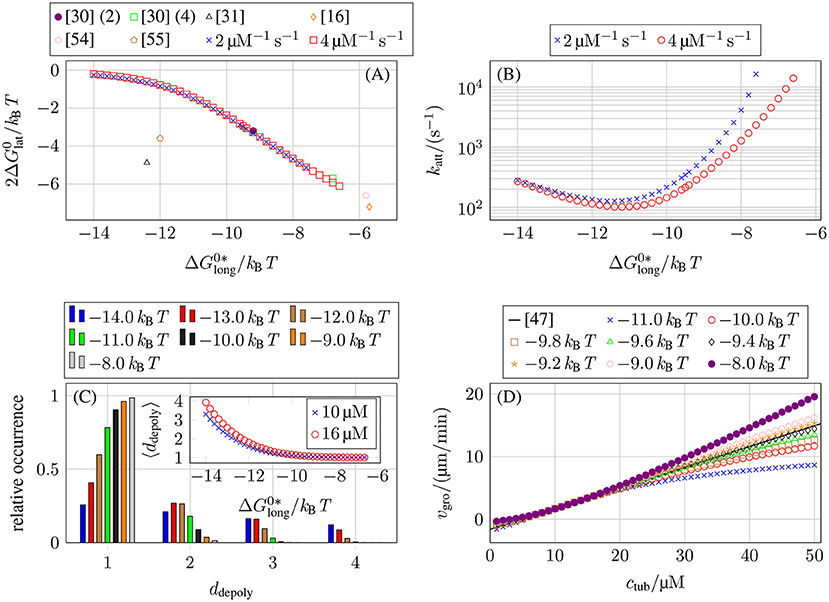
Figure 4. (A) Lateral bond energy $\Delta G_{\text{lat}}^0$ as a function of the longitudinal bond energy $\Delta G_{\text{long}}^{0*}$ from matching the concentration-dependent growth velocity data from Walker et al. [47], see (16). To compare our lateral bond energies (per tubulin monomer) to other publications (lateral bond energy per tubulin dimer), the y-axis shows $2\Delta G_{\text{lat}}^0$. (The numbers behind reference [30] refer to their value of k₊.) (B) Lateral bond attempt rate k_att as a function of the longitudinal bond energy $\Delta G_{\text{long}}^{0*}$ for our two values of k₊ from matching the concentration-dependent growth velocity data from Walker et al. [47], see (16). (C) Relative occurrence of different d_depoly values for MT growth with k₊ = 4 μM⁻¹ s⁻¹ and c_tub = 10 μM. The inset shows the average d_depoly as a function of $\Delta G_{\text{long}}^{0*}$ for k₊ = 4 μM⁻¹ s⁻¹ and c_tub = 10 μM and also for c_tub = 16 μM. (D) MT growth velocity v_gro as a function of a larger interval of free tubulin dimer concentration values c_tub for k₊ = 4 μM⁻¹ s⁻¹ and different longitudinal bond energies $\Delta G_{\text{long}}^{0*}$. We also plot (16) from the growth velocity data from Walker et al. [47] over the larger concentration interval.

Afterwards, we will fix a particular value of $\Delta G_{\text{long}}^{0*}$ by the additional requirement that the simulation should exhibit an as linear as possible concentration dependence of the growth velocity v_gro over a certain range of tubulin concentrations c_tub (see Figure 4D) such that we arrive at parameter sets $(\Delta G_{\text{long}}^{0*},\Delta G_{\text{lat}}^0,k_{\text{att}})$ for k₊ = 2 μM⁻¹ s⁻¹ and k₊ = 4 μM⁻¹ s⁻¹ (see Table 3).

TABLE 3

Table 3. Growth parameter values that generate the most linear dependence v_gro(c_tub).

The results in Figure 4A show that the values of $\Delta G_{\text{long}}^{0*}$ and $\Delta G_{\text{lat}}^0$ depend only weakly on our chosen k₊ values. Figure 4A also shows that our data matches results obtained in [30] (this data was later re-used in [15, 16, 54]) but also differs from other results [31, 55], which were all obtained by the same approach of fitting growth velocity data from Walker et al. [47] (or their own growth data in [55]). Kononova et al. [43] obtained bond energies from MD simulations of nano-indentation experiments; the values from Kononova et al. [43] are much larger for both types of bonds ($\Delta G_{\text{long}}^{0*}~2\Delta G_{\text{lat}}^0~25k_{B}T$) and, thus, not shown in Figure 4A.

Qualitatively, the measured dependencies of $\Delta G_{\text{lat}}^0$ and k_att on $\Delta G_{\text{long}}^{0*}$ can be understood as follows: the weaker longitudinal bonds are, the more likely it is that a tubulin dimer will depolymerize. To get the same growth velocity, this decrease in “longitudinal stability” has to be compensated by an increase in “lateral stability” by stronger lateral bonds (making it less likely that lateral bonds break and, thus, enabling depolymerization) or faster formation of lateral bonds (to stabilize newly polymerized tubulin dimers). Figure 4C shows the number of tubulin dimers d_depoly that detach at once during depolymerization events. For increasingly stronger longitudinal bonds and, thus, weaker lateral bonds, multi-dimer depolymerization becomes more relevant. The data in the inset in Figure 4C is also compatible with results in reference [33] obtained with a purely chemical model.

Until now, we only considered free tubulin dimer concentrations c_tub ∈ [7, 16 μM] to use similar values as Walker et al. [47], but there have also been other measurements with a larger range of c_tub values [3, 48, 51, 52]. In general, it is assumed that the growth velocity v_gro increases linearly with c_tub for the whole MT just as the polymerization rate in (7) increases linearly with c_tub for individual protofilaments. Theoretically, it has been shown that, for multistranded polymers, lateral interactions give rise to a non-linear relation between growth velocity on monomer concentration [56]. For MT growth, a non-linear dependence on tubulin concentration was found in reference [31] using a two-dimensional model based on reference [30]. Over a larger range of c_tub values, our simulations also exhibit a non-linear relation between v_gro and c_tub depending on the value of $\Delta G_{\text{long}}^{0*}$, as shown in Figure 4D. Data for different values of $\Delta G_{\text{long}}^{0*}$ (and correspondingly adjusted values of $\Delta G_{\text{lat}}^0$ and k_att, see Figures 4A,B) and the same value of k₊ that was previously overlapping in the interval c_tub ∈ [7, 16 μM] start to differentiate in a larger concentration interval. While possible non-linear relations have been predicted theoretically, the available experimental data show a linear v_gro(c_tub) dependence over a large range of c_tub values [3, 48, 51, 52]. Therefore, we determined the remaining free parameter value of $\Delta G_{\text{long}}^{0*}$ for the two k₊ values from the condition that the concentration dependence of v_gro is as linear as possible up to 50 μM. To determine these values of $\Delta G_{\text{long}}^{0*}$, we ignored concentrations c_tub below the individual critical concentration (for which v_gro < 0) which violate our fundamental assumption of a growing MT.

In summary, we find a triple $(\Delta G_{\text{long}}^{0*},\Delta G_{\text{lat}}^0,k_{\text{att}})$ that fits the growth velocity data from Walker et al. [47] and that gives a linear concentration dependence over a wide tubulin concentration range for two representative values of k₊. Table 3 lists these parameter triples for k₊ = 2 μM⁻¹ s⁻¹ and k₊ = 4 μM⁻¹ s⁻¹. For a given k₊, these results fix four of the seven model parameters in Table 2 using experimental data on MT growth. To address the parameters κ and k_lat, we now turn to MT shrinkage.

3.2. GDP-Microtubule Shrinkage and Model Parameterization

As opposed to MT growth, MT shrinkage also depends on the bending constant κ and spring constant k_lat as protofilament curling and bond rupture become relevant processes for a shrinking MT. We consider a shrinking MT that initially only consists of GDP-tubulin dimers (N_GTP = 0, N_GDP > 0) with parameter values k₊, $\Delta G_{\text{long}}^{0*}$, $\Delta G_{\text{lat}}^0$, and k_att as already determined by the growth simulations and in the absence of hydrolysis (a shrinking, initially GDP-only MT acquires some GTP-dimers by attachment but remains GDP-dominated). To investigate shrinkage, MTs with N_GDP = 20 and N_GTP = 0 were used. For each parameter set, 20 simulations were run to get an average shrinkage velocity v_shr. Experimental data on shrinking MTs show a shrinkage speed v_shr that is independent of the tubulin dimer concentration. For each value of k₊, we should be able to determine one of the two parameters (κ, k_lat) as a function of the other parameter by fitting such that the experimental value of the shrinkage velocity is reproduced in simulations (for parameters $\Delta G_{\text{long}}^{0*}$, $\Delta G_{\text{lat}}^0$, and k_att fixed by the growth velocity data). We use the experimental shrinkage velocity of Walker et al., see (17), for this fitting procedure.

Figures 5A,B show the values of k_lat and κ for k₊ = 2 μM⁻¹ s⁻¹ and k₊ = 4 μM⁻¹ s⁻¹ and different values of $\Delta G_{\text{long}}^{0*}$ that reproduce the experimentally measured shrinkage velocity in (17). All data points for each $\Delta G_{\text{long}}^{0*}$ fall on square root functions

$\begin{array}{ll}\kappa (k_{\text{lat}})=a_{\text{shr}}\sqrt{k_{\text{lat}}}+b_{\text{shr}}.& (18)\end{array}$

This functional dependence can be understood qualitatively by considering the mechanical contribution to the bond rupture rate (10), exp(F_latℓ_rup), which, on average, should have the same value for all mechanical parameter combinations to produce the same shrinkage velocity. As the characteristic bond rupture length in (11) depends on k_lat as ${\ell }_{\text{rup}}~{\sqrt{k_{\text{lat}}}}^{-1}$, the average lateral bond force at rupture should depend on k_lat like $F_{\text{rup}}~k_{\text{lat}}{\ell }_{\text{rup}}~\sqrt{k_{\text{lat}}}$. The lateral bond force F_lat is a consequence of the lateral bonds stretching as the tubulin monomers curl outward to decrease the bending force F_bend = κ(Δθ(p, d, t) − Δθ₀(p, d, t)), which leads to F_rup ~ F_bend ~ κ resulting in $\kappa ~\sqrt{k_{\text{lat}}}$ in accordance with Figures 5A,B.

FIGURE 5

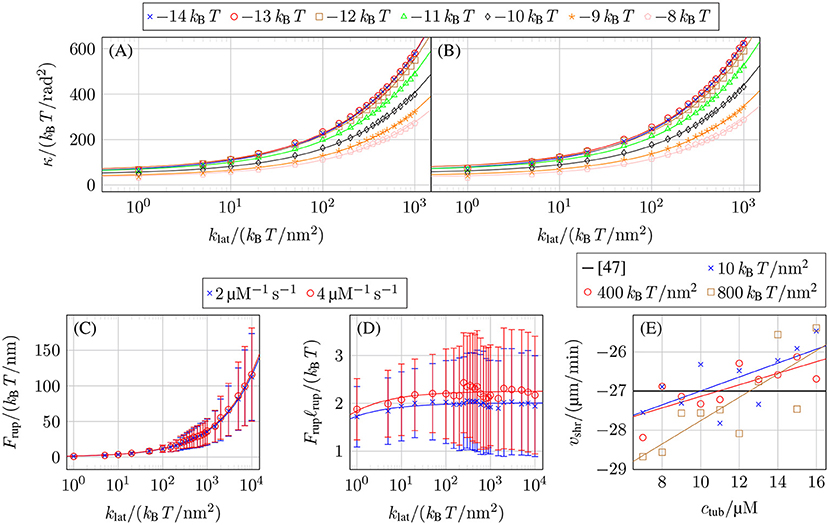
Figure 5. Mechanical parameter values reproducing the experimentally measured shrinkage velocity in (17) for (A) k₊ = 2 μM⁻¹ s⁻¹ and (B) k₊ = 4 μM⁻¹ s⁻¹ and different values of $\Delta G_{\text{long}}^{0*}$. (C) Force on lateral bonds at rupture F_rup as a function of k_lat for k₊ = 2 μM⁻¹ s⁻¹ with $\Delta G_{\text{long}}^{0*}=$ −9.5 k_BT and k₊ = 4 μM⁻¹ s⁻¹ with $\Delta G_{\text{long}}^{0*}=$ −9.0 k_BT, both at c_tub = 10 μM. (D) Rupture energy F_rupℓ_rup of lateral bonds as a function of k_lat for the same parameters as in (C). (E) Shrinkage velocity v_shr as a function of the free tubulin dimer concentration c_tub for k₊ = 4 μM⁻¹ s⁻¹, $\Delta G_{\text{long}}^{0*}=$ −9.3 k_BT, and different values of k_lat and linear fits v_shr(c_tub).

Figure 5C confirms that the average force on lateral bonds at rupture 〈F_rup〉 has the functional dependence $\langle F_{\text{rup}}\rangle ~\sqrt{k_{\text{lat}}}$ predicted by our above qualitative argument (〈F_rup〉 and error bars σ_Frup were determined by fitting normal distributions to the histogram of the lateral bond rupture forces collected for 20 shrinkage simulations per parameter set with N_GDP = 20). Also, the resulting mechanical contribution F_rupℓ_rup for the exponential function of the lateral bond rupture rate in Figure 5D is approximately constant as expected from our above argument.

As the experimentally measured shrinkage velocity v_shr does not depend on the free tubulin dimer concentration c_tub, we used constants to fit our v_shr(c_tub) data. In reality, however, our data shows a linear dependence between v_shr and c_tub as shown in Figure 5E corresponding to a slowing down of depolymerization. This is caused by an increased probability for intermediate addition of tubulin dimers and lateral bond formation between them; these lateral bonds require additional time to rupture. While this dependency of v_shr on c_tub will have a small influence on the concrete value of the shrinkage velocity, we expect it to not have any qualitative effect on the overall MT dynamics. At higher tubulin concentrations, where the decrease of |v_shr(c_tub)| would become significant, the catastrophe rates decrease dramatically so that shrinking will rarely occur.

Comparing our results from Figures 5A,B to other results is not always directly possible due to different modeling approaches but most find that k_lat ≪ 1.000 k_BT /nm² and κ ≪ 1.000 k_BT /rad² [15, 57, 58], with some exceptions [43, 59]. Previously, we used MD simulation data from Grafmüller et al. [60] to calculate the bending constant κ [17]. Compared to reference [17], we have to adjust the calculation to consider both inter-dimer and intra-dimer bending resulting in κ ≃ 50 k_BT /rad². MD simulation in Kononova et al. [43], on the other hand, give a persistence length of individual protofilaments of L_p ≃ 6 μM, which corresponds to a significantly larger value of κ ≃ 1.500 k_BT /rad² for the bending constant. This discrepancy cannot be resolved at present. We use κ= 149 k_BT /rad² in the following together with the corresponding value of k_lat = 100 k_BT /nm² according to Figure 5B which are values close to the ones used by VanBuren et al. [15].

3.3. Restricted Energy Minimization for Efficient Simulation

Until now, energy minimization was not restricted by either a maximum number of minimization steps or by only considering a subset of tubulin dimers at the MT tip so that we will consider this unrestricted minimization as the “gold standard” to which we will compare the two restricted energy minimization approaches described in section 2.4. We use the shrinkage velocity v_shr as the observable by which we judge the relevant cutoff values in the two approaches.

For restricting the number of quasi-Newton minimization steps, Figure 6A shows that an acceptable maximum number of minimization steps reproducing v_shr = −27 μm/min depends on the chosen mechanical parameters as the higher their values are, the greater the energy and its gradient. A maximum number of minimization steps of around 100 should be an appropriate value according to the results shown in Figure 6A. The results in Figure 6A also show that reducing the number of minimization steps by a factor of 10 can lead to deviating growth velocities. Therefore, the improved energy relaxation that we obtain in comparison to reference [15] by applying the equivalent of one order of magnitude more minimization steps should be relevant.

FIGURE 6

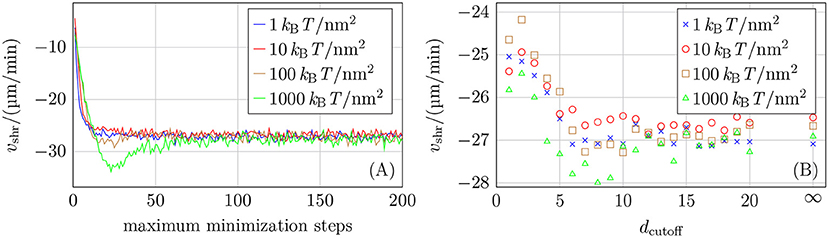
Figure 6. (A) Shrinkage velocity v_shr as a function of the maximum number of minimization steps. (B) Shrinkage velocity v_shr as a function of the layer cutoff distance d_cutoff (where d_cutoff = ∞ means that no cutoff was used). Twenty simulations for each parameter set were run for both plots and both used k₊ = 4 μM⁻¹ s⁻¹, $\Delta G_{\text{long}}^{0*}=$ −9.3 k_BT, c_tub = 10 μM, N_GDP = 20, and different values of k_lat.

If minimization is restricted to a subset of minimization parameters at the tip of the simulated MT, this subset is defined by the cutoff distance d_cutoff. To have a maximum improvement in simulation speed, d_cutoff should be as small as possible. It is evident from the data shown in Figure 6B that values d_cutoff < 5 have a detectable influence on the shrinkage velocity. We also ran some simulations with N_GDP = 50 and also for k₊ = 2 μM⁻¹ s⁻¹ (see Figure S8 in the Supplementary Material) and based on all data, we choose d_cutoff = 10 as a conservative value for the cutoff distance.

In summary, we are more confident in the second approach to only minimize the MT tip where actual conformational changes happen, because for this subset, the restricted energy is fully minimized. Additionally, the first approach still has the issue of slowing down with an increasing number of minimization parameters as all minimization parameters are considered. The second approach ensures that the number of minimization parameters does not scale with the MT length but remains bounded, which assures that we can simulate arbitrarily long growing MTs at a fixed minimal computational speed. In the first approach, the quality of the minimization will probably also decline because the number of minimization parameters increases while the number of minimization steps is kept constant. Lastly, the first approach, in contrast to the second approach, does not guarantee that the upper, i.e., the dynamic part of the MT is properly minimized.

We also note that in the presence of mechanical feedback onto hydrolysis, simulations take longer because minimizations after hydrolysis events need to consider more tubulin dimers if the hydrolyzed tubulin dimer is relatively deep in the MT lattice (see Supplementary Material for more details).

3.4. Full Simulations Exhibit Repeated Catastrophe and Rescue Events

Based on the previous section on energy minimization, we use d_cutoff = 10 for full simulations in which the initial MTs have both a GDP-body and a GTP-cap, thus N_GDP > 0 and N_GTP > 0. We now aim for realistic MT dynamics with repeated phases of growth and shrinkage in the same simulation and catastrophe and rescue events in between. First, we only consider strictly random hydrolysis with a hydrolysis rate k_hydr that is independent of tubulin dimers' position or mechanical forces and which is another unknown free parameter in our model. Hydrolysis coupled to mechanics via (12) will be considered later.

It poses a computational challenge for chemomechanical MT models to reach time scales of MT dynamics where repeated catastrophe events occur at realistic hydrolysis rates k_hydr and tubulin dimer concentrations c_tub. In reference [18], where mechanics was implemented via full Brownian dynamics, only short times scales could be reached (although the Brownian dynamics was applied to only 300 tubulin dimers at the plus end). Therefore, they increased the hydrolysis rate from their “normal” value of 0.5 s⁻¹ (based on the 2 s delay between polymerization and phosphate release measured by [61], which is also used by [62]) into a range of 3–11 s⁻¹ in order to trigger catastrophe events within computationally accessible time scales. They found a linear scaling of catastrophe rate with k_hydr and employed a linear extrapolation to obtain catastrophe rates for realistic hydrolysis rates (see their Figure 3A). In our simulations, we observe that increasing k_hydr beyond a certain (c_tub-dependent) value leads to immediate MT shrinkage because the initial cap quickly hydrolyzes; this can be interpreted as an instantaneous catastrophe. In such cases (like in Figure 7 for c_tub = 7 μM and k_hydr = 0.5 s⁻¹), there is no real growth phase based on which a catastrophe frequency could be determined. For these hydrolysis rates, the individual critical concentration c_tub,c (where v_gro = 0 is reached) has apparently increased above the given tubulin concentration.

FIGURE 7

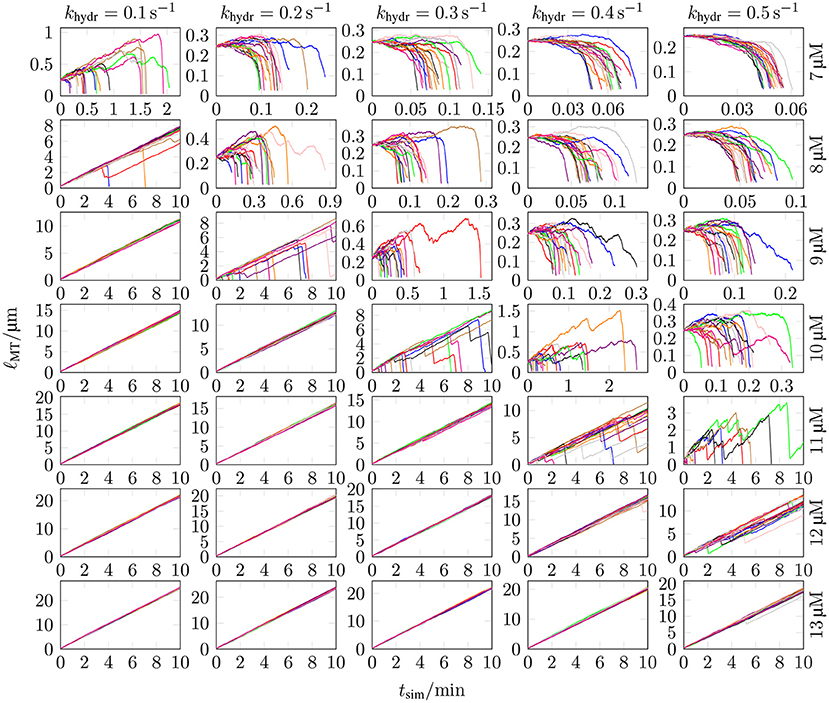
Figure 7. The MT length ℓ_MT was measured as a function of the simulation time t_sim for 20 different simulations with k₊ = 4 μM⁻¹ s⁻¹, $\Delta G_{\text{long}}^{0*}=$ −9.3 k_BT, k_lat = 100 k_BT /nm², seven different values of c_tub, and five different values of k_hydr. MT growth trajectories for three additional c_tub values can be found in Figure S9 in the Supplementary Material.

The experimental data on the hydrolysis rate is limited, so that many publications determine the hydrolysis rate themselves by matching simulation results with experimental data [16, 30–33, 63–65]. There are, however, more direct measurements in Melki et al. [61]. In most models and also in measurements from Melki et al. [61], the (random) hydrolysis rate is in the range of 0.1–0.5 s⁻¹ (reference [30] use a relatively high value of 0.95 s⁻¹). We explore exactly this range of hydrolysis rates, see Figure 7.

Figure 7 shows MT growth curves (length vs. time) over simulation times up to t_sim = 10 min for several representative tubulin concentrations and realistic hydrolysis rates. MT growth trajectories as in Figure 7 for other k_lat values can be found in Figures S10–13 in the Supplementary Material. Simulations in Figure 7 were started with N_GTP = 10 and N_GDP = 20, but results are largely independent of the initial ratio N_GTP/N_GDP (see, e.g., Figure S11 in the Supplementary Material).

Our chemomechanical MT model is computationally efficient such that we can determine catastrophe and rescue rates as inverse average growth and shrinking times between repeated catastrophe and rescue events. In the Supplementary Material, we explain the algorithm that we used to identify catastrophe and rescue events and, thus, growth and shrinking times from MT simulation trajectories in detail. The results are shown in Figure 8. In comparison to typical experimental data [47, 67], the decrease of the catastrophe rate with tubulin concentration seems too steep. Current phenomenological models for the MT catastrophe rate as a function of tubulin concentration can be found in Flyvbjerg et al. [68] and Zelinski and Kierfeld [69], experimental data in Walker et al. [47] and Janson et al. [66]; the decrease of the catastrophe rate with GTP-tubulin concentration c_tub appears steeper in the simulation for all hydrolysis rates k_hydr = 0.1–0.5 s⁻¹.

FIGURE 8

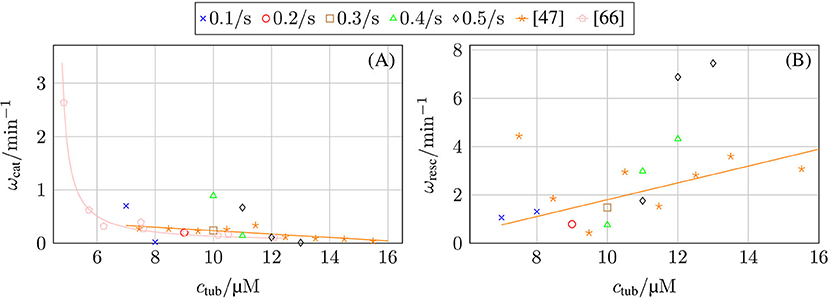
Figure 8. (A) Catastrophe rate ω_cat and (B) rescue rate ω_res as a function of GTP-tubulin concentration c_tub and in comparison with experimental data from Walker et al. [47] and Janson et al. [66].

In the following, we will discuss two aspects of MT growth and catastrophes in more detail, namely the dependence of growth velocity on hydrolysis rate and the detailed dynamics within single catastrophe events, which become accessible within a computational model and are impossible to address experimentally.

3.5. Growth Velocity Reduces Linearly With Hydrolysis Rate Because of Cap Structure

So far, we parameterized the model by fitting the growth velocity of GTP-only MTs, i.e., in the absence of hydrolysis to the experimentally measured velocity in (16). Hydrolysis reduces this growth velocity by increasing the probability of GDP-dimers at the plus end. This increases the rate of bond rupture because hydrolyzed dimers tend to create stretched bonds which rupture more easily (there is no direct increase of the off-rate for hydrolyzed GDP-dimers in our model). As only laterally unbounded dimers can detach, hydrolyzed GDP-dimers at the plus end have an effectively higher detachment rate.

The last row of Figure 7 indicates and Figure 9B shows explicitly that increasing the hydrolysis rate decreases the growth velocity linearly although the growth reduction mechanism is indirect via the increased probability of bond rupture for hydrolyzed GDP-dimers. Our model parameterization was such that we obtain the experimentally measured growth velocities by Walker et al. [47] at k_hydr = 0 s⁻¹ in Figure 9B. Nevertheless, Figure 9A shows that there is still a linear relation between the free tubulin dimer concentration c_tub and the growth velocity v_gro so that it is possible to re-adjust parameters to reproduce the growth velocity in the presence of hydrolysis, once a particular hydrolysis rate can be reliably selected.

FIGURE 9

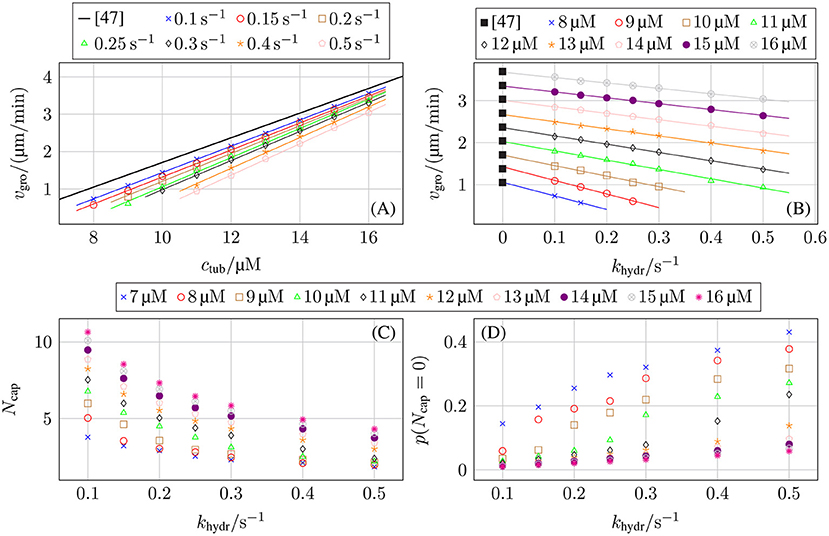
Figure 9. Growth velocity v_gro as a function of (A) the free tubulin dimer concentration c_tub for different hydrolysis rates k_hydr and as a function of (B) the hydrolysis rate k_hydr for different free tubulin dimer concentrations c_tub in comparison to the experimental data from Walker et al. [47]. (C) Average GTP-tubulin cap length 〈N_cap〉 of protofilaments and (D) fraction of protofilaments without a GTP-cap as a function of the hydrolysis rate k_hydr. The standard set of parameters from Table 2 was used.

Because both the dependence on tubulin concentration in Figure 9A remains linear and the reduction by the hydrolysis rate in Figure 9B is linear, we also expect that the individual critical concentration (where v_gro = 0 is reached) increases linearly with the hydrolysis rate beyond the value c_tub,c ≃ 5 μM of Walker et al. [47]. Figure 7 clearly shows that increasing k_hydr actually increases the individual critical concentration c_tub,c.²

The mechanism of growth velocity reduction by hydrolysis can be further elucidated by comparing the average GTP-tubulin cap length 〈N_cap〉 of protofilaments (see Figure 9C), and the fraction of protofilaments without a GTP-cap (see Figure 9D): The higher the hydrolysis rate is, the smaller the GTP-cap and the higher the fraction of cap-less protofilaments is.³ The increase in GDP-tubulin dimers depolymerizing from the protofilament tips for higher hydrolysis rates is due to an increase in the probability of uncapped protofilaments with the hydrolysis rate as shown in Figure 9D. In reference [70], dependencies $\langle N_{\text{cap}}\rangle \propto \sqrt{c_{\text{tub}}/k_{\text{hydr}}}$ and p(N_cap = 0) ∝ k_hydr/c_tub have been predicted, which are in agreement with Figures 9C,D.

3.6. Detailed Dynamics Within Single Catastrophe and Rescue Events

The chemomechanical model reproduces realistic MT dynamics including catastrophe and rescue events. Figure 10 shows typical MT growth paths featuring two catastrophe events and a rescue event in subfigure (C). Moreover, we observe “dips” in the growth path where a short phase of shrinking appears, which are similar to “stutter” events that have been observed in reference [35]. Videos of these two simulations with two- and three-dimensional representations of the MT structure can be found in the Supplementary Material.

FIGURE 10

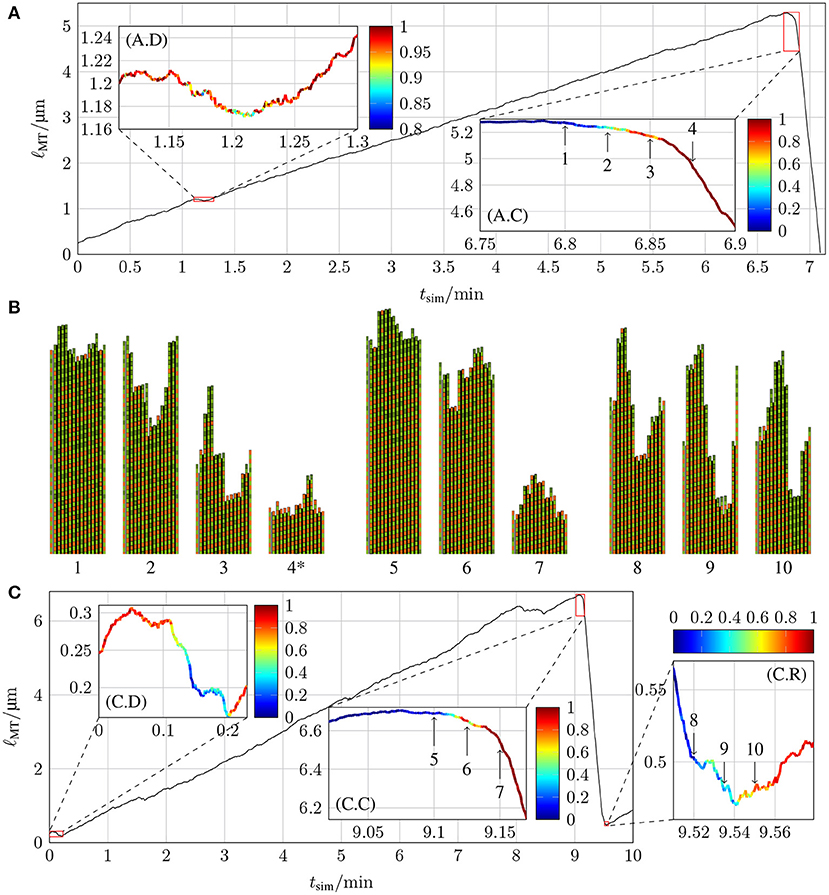
Figure 10. Lengths of two MTs as a function of simulation time t_sim with k₊ = 4 μM⁻¹ s⁻¹, $\Delta G_{\text{long}}^{0*}=$ −9.3 k_BT, k_lat = 100 k_BT /nm², and (A) c_tub = 8 μM and k_hydr = 0.1 s⁻¹ and (C) c_tub = 9 μM and k_hydr = 0.2 s⁻¹. The insets highlight parts of the trajectories of interest for the dynamics and color-code the probability of the ℓ_MT(t_sim) curve to stay quantitatively the same at the relevant point in time if new simulations are started with the relevant configuration as the initial configuration (for more details, refer to the text). (B) shows the two-dimensional representations of certain MT tip configurations that are marked by arrows in the insets of (A,C) (configuration 4^* has been shifted toward the MT tip by 24 tubulin dimer lengths). The first protofilament is the periodic image of p = 13 and the last protofilament is the periodic image of p = 1. Lateral bonds are represented by the thick black line between protofilaments.

Using our computational model, we can systematically identify the point in a MT growth path, where a catastrophe becomes structurally unavoidable. This allows us to search for typical catastrophe-triggering features in MT growth. To analyze how probable it is at specific points in the simulation of MT dynamics that the MT continues a certain growth path, we chose two simulations with at least one significant event (meaning a catastrophe, rescue, or a “dip”/“stutter”) and took configurations around such events as starting points for new simulations (similar to [33]). In these new simulations, MTs were allowed to grow (or shrink) for a maximum of 60 s, a sufficient amount of time to check if the new simulations show dynamics similar to the original simulation around the significant event.

The MT growth trajectory shown in Figure 10A has two significant events: a dip at t_sim = 1.2 min and a catastrophe at t_sim = 6.85 min; the trajectory in Figure 10C contains three significant events: a dip at the very beginning, a catastrophe at t_sim = 9.15 min, and a rescue at t_sim = 9.54 min. To determine whether newly run simulations with starting points from the initial simulation qualitatively follow the original simulation, we need criteria to identify dips, catastrophes, or rescue events. The exact criteria for these events in Figures 10A,C are stated in the Supplementary Material. In short, in order to identify whether a new simulation reproduces a catastrophe, we check after a time of 10–15 s whether the MT is sufficiently short that a catastrophe must have happened; for a dip, we check whether the MT continued to grow without entering a catastrophe; for a rescue, we check that the MT did not completely vanish because it continued to shrink. For each initial configuration, we ran 20 new simulations and calculated the fraction of simulations that fulfilled these criteria. These fractions are the probabilities for the original growth path at different points in time, and they are shown color-coded in all the insets in Figure 10.

Both catastrophes and the rescue show that the transition from a high probability to stay in the current dynamic state to a high probability to switch into the other dynamic state occurs within a few seconds. In Figures 10A,C, we first observe that catastrophes become practically unavoidable [red color code in (A.C) and (C.C)] after a phase of relatively slow shrinking by 50–100 nm; similar “transitional catastrophe” behavior has been observed in reference [35]. A dip, on the other hand, can only evade a catastrophe [yellow to red color code in (A.D) and (C.D)] if the MT length shrinks by significantly < 50 nm.

Because hydrolysis followed by straining and rupture of the lateral bonds is required before a laterally unbonded dimer can detach, MT shrinking by 50 nm suggests that roughly 6 dimer layers must hydrolyze in a row to trigger a catastrophe. This is, however, not sufficient to remove the entire GTP-cap. The GTP-cap length averaged over all protofilaments is still >1 when the catastrophe becomes unavoidable (at points 3 in Figure 10A and 6 in Figure 10C, see also Figure S1 in the Supplementary Material). As the corresponding MT snapshot insets 3 and 6 reveal, the reason for this discrepancy is the average over all protofilaments: it appears that typically only a “nucleus” of three neighboring protofilaments shrinks by more than 6 dimers, such that its GTP-cap is removed and its ends reach into the GDP-body of the MT, when a catastrophe is triggered. The MT snapshots in Figure 10B also suggest that rescue events require formation of a GTP-cap on almost all 13 protofilaments (with an average cap length ~ 4) such that nuclei of three neighboring uncapped GDP-protofilaments are avoided. Further investigation of more catastrophe events will be necessary to definitely deduce catastrophe- and rescue-triggering structural MT features.

3.7. Hydrolysis Coupled to Mechanics Changes the Cap Structure

We also test how a mechanical feedback onto the hydrolysis rate as introduced in (12) and (14) changes the cap structure and dynamic behavior. In the presence of this mechanical feedback, tubulin dimers in the MT lattice with larger bending angles tend to hydrolyze preferentially.

Overall, we find a linear relation between $k_{\text{hydr}}^0$ and the average hydrolysis rate 〈k_hydr〉 (see Figure 11A) with $k_{\text{hydr}}^0\gg \langle k_{\text{hydr}}\rangle$. When comparing MT growth with hydrolysis coupled to mechanics with average hydrolysis rate 〈k_hydr〉 to MT growth with constant hydrolysis rate k_hydr (for example in Figures 11D–F), we use Figure 11A to choose the base hydrolysis rate $k_{\text{hydr}}^0$ such that 〈k_hydr〉 ≈ k_hydr.

FIGURE 11

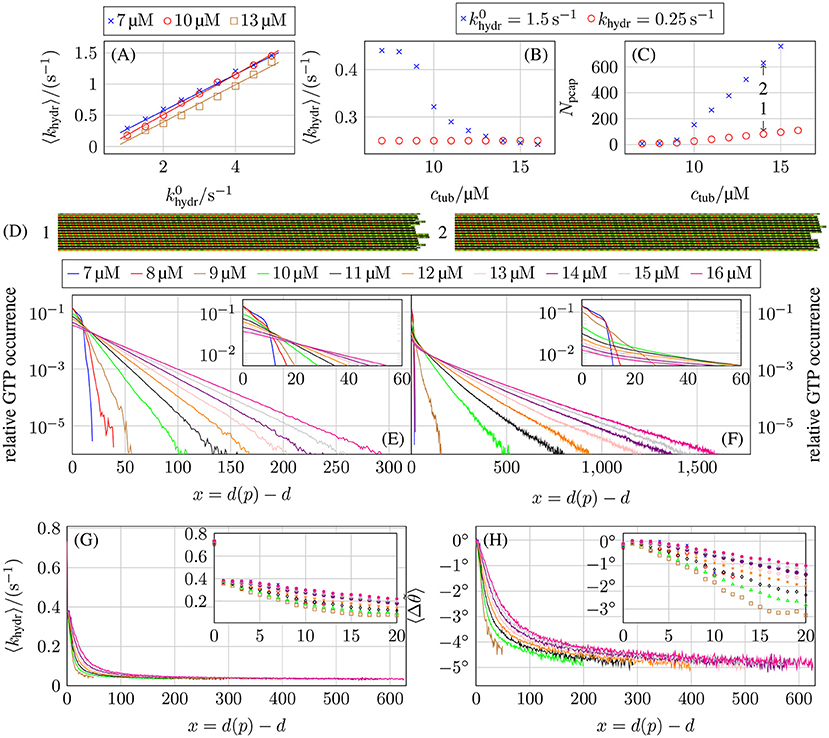
Figure 11. (A) Average actual hydrolysis rate 〈k_hydr〉 as a function of the constant base hydrolysis rate $k_{\text{hydr}}^0$. Comparison of (B) the average actual hydrolysis rate 〈k_hydr〉 and (C) the porous cap length N_pcap as a function of the free tubulin dimer concentration c_tub for hydrolysis coupled to mechanics with $k_{\text{hydr}}^0=$ 1.5 s⁻¹ and a constant hydrolysis rate of k_hydr = 0.25 s⁻¹. (D) Shows the two-dimensional representations of two MT tip configurations that are marked by arrows in (C) at t_sim = 5 min. The top and bottom protofilaments are periodic images of p = 13 and p = 1, respectively. Relative occurrence of GTP-tubulin dimers as a function of the dimer-based distance from the protofilament tip d(p) − d for (E) a constant hydrolysis rate of k_hydr = 0.25 s⁻¹ and (F) hydrolysis being coupled to mechanics and $k_{\text{hydr}}^0=$ 1.5 s⁻¹. (G) Average hydrolysis rate as a function of distance d(p) − d from the tip and (H) the associated average bending angle $\langle \Delta \tilde{\theta }\rangle$ for hydrolysis coupled to mechanics and $k_{\text{hydr}}^0=$ 1.5 s⁻¹. All plots are for k₊ = 4 μM⁻¹ s⁻¹, $\Delta G_{\text{long}}^{0*}=$ −9.3 k_BT, and k_lat = 100 k_BT /nm².

Figure 11B shows the average hydrolysis rate 〈k_hydr〉 as a function of the free tubulin dimer concentration c_tub for $k_{\text{hydr}}^0=$ 1.5 s⁻¹. Here, we observe a pronounced non-linear concentration dependence with a decrease around the individual critical tubulin concentration c_tub ≃ 10 μM. At the same concentration, also the porous cap length N_pcap (see Figure 11C), which is defined as the difference between the number of tubulin dimers in a protofilament and the value of d of the first GTP-tubulin dimer counted from the minus end, starts to increase. As a result, the porous cap length for hydrolysis coupled to mechanics is much longer compared to a constant hydrolysis rate, even if the average effective hydrolysis rate is roughly the same. In the following, we argue that the reason for this increase in porous cap length is a decrease of the hydrolysis rate for GTP-dimers away from the tip. Mechanical feedback gives rise to preferential hydrolysis at the tip, i.e., the average hydrolysis rate 〈k_hydr(x)〉 (over all actually executed hydrolysis events) is larger for small layer distances x ≡ d(p) − d from the tip, as can be seen in Figure 11G. This is in line with previous results in reference [17] from a much simpler version of our model with a deterministic hydrolysis kinetics and without dimer attachment and detachment.

According to (14), GTP-tubulin dimers with larger bending angles tend to hydrolyze preferentially. If a straight GTP-dimer is bent inward (Δθ < 0°), its hydrolysis rate is reduced according to (14); if it is bent outwards (Δθ > 0°) the rate is increased. From the hydrolysis rates shown in Figure 11G, it is possible to calculate the average bending angles using (12) and (14),

$\begin{array}{ll}\langle \Delta \tilde{\theta }(p,d)\rangle =\frac{1}{11°}\left[\frac{1+{\delta }_{d,d(p)}}{\kappa }ln\left(\frac{k_{\text{hydr}}(p,d)}{k_{\text{hydr}}^0}\right)+{(5.5°)}^2\right].& (19)\end{array}$

The results for these bending angles as a function of the distance x from the top are shown in Figure 11H. Surprisingly, almost all GTP-tubulin dimers are bent inwards (Δθ < 0°) on average prior to hydrolysis apart from dimers close to the tip. We will interpret these results in the following.

An isolated GTP-dimer within the GDP-body can alleviate the bending stress of GDP-dimers by bending inward (Δθ < 0°), which allows longitudinally neighboring GDP-dimers to bend outwards (such that Δθ > 0°) resulting in an overall decrease of the MT energy (see Figures S14, S15 in the Supplementary Material). Therefore, isolated GTP-dimers deep in the GDP-body hydrolyze with a reduced asymptotic rate 〈_khydr〉∞ ≪ k_hydr.

We also find that, for several consecutive GTP-dimers in the same protofilament, GTP-dimers curl inward directly at the GDP/GTP interface resulting in a reduced hydrolysis rate (see Figure S15), while GTP-dimers in the center of a GTP-island are straight so that they have a higher hydrolysis rate than at the GDP/GTP interfaces. Effectively, this hydrolysis rate distribution within a GTP-island results in a “anti-vectorial” hydrolysis mechanism with which GTP-islands are hydrolyzed from the interior in contrast to vectorial hydrolysis where hydrolysis happens at the GTP/GDP interfaces.

Also for GTP-dimers in layers closer to the MT tip, other longitudinally close-by GTP-dimers cooperate in alleviating bending stresses; then inward bending is still preferred, but the inward bending angle becomes smaller. This decrease in inward bending corresponds to an increase of the average hydrolysis rates 〈k_hydr(x)〉 for GTP-dimers in these layers compared to GTP-dimers buried deeper in the MT body (see Figures 11G,H). For terminal tubulin dimers (x = 0), we observe a hydrolysis rate 〈k_hydr(x)〉 higher than k_hydr (while it is equal or lower than k_hydr for all other layers x > 0). Hydrolysis in the first layer is enhanced because there are no tubulin dimers on top, such that hydrolysis has to overcome a smaller energy barrier as pointed out previously [the d + 1-term in (14) is missing corresponding to the δ_{d, d(p)}-contribution in (19)].

As a result of the hydrolysis bias toward the tip, the spatial GTP-tubulin dimer distribution also differs. For concentrations where the MTs are growing only on time scales of several minutes (c_tub ≥ 11 μM) for the chosen parameters, a constant hydrolysis rate leads to the expected exponential distribution of GTP-dimers shown in Figure 11E as observed in in vivo experiments [71]. Using an effective one-dimensional (or single protofilament) model similar to Padinhateeri et al. [63] to calculate the probability of tubulin dimers being GTP-tubulin dimers as a function of the polymerization rate k_on, effective depolymerization rate ${\tilde{k}}_{\text{off}}$, and hydrolysis rate k_hydr matches the simulation results for concentrations at which the MTs can be considered in a steady state of growth (see section 4 in the Supplementary Material). We use an effective depolymerization rate ${\tilde{k}}_{\text{off}}$ instead of k_off, because we map onto the depolymerization process of a one-dimensional model so that ${\tilde{k}}_{\text{off}}$ includes all effects from lateral bond formation and rupture and the actual depolymerization process in the full model.

If hydrolysis is coupled to mechanics, the spatial distribution is only exponential in its tail, has larger values at the MT tip, and GTP-tubulin dimers can be found much deeper in the GDP-body (see Figure 11F). These results reflect that the average hydrolysis rate 〈k_hydr(x)〉 is decreasing toward the GDP-body and reaches a small limiting value 〈_khydr〉∞ ≪ k_hydr for distances x = d(p) − d > 500 away from the tip, which governs the exponential tail (see Figure 11G). This can be rationalized by considering the probability p_GTP(x) to find a GTP-dimer at distance x from the tip in a single protofilament and continuum approximation. The balance between attachment/detachment and hydrolysis leads to

$\begin{array}{ll}0=-(k_{\text{on}}-{\tilde{k}}_{\text{off}})\frac{\text{d}{p}_{\text{GTP}}}{\text{d}x}-\langle k_{\text{hydr}}(x)\rangle p_{\text{GTP}}(x)& (20)\end{array}$

in the stationary state, which results in a sharp initial decrease of p_GTP(x) because 〈k_hydr(0)〉 is large at the tip but a much slower asymptotic exponential decrease when 〈k_hydr(x)〉 ≈ 〈_khydr〉∞ ≪ k_hydr, which explains the main features in Figure 11F. In section 4 in the Supplementary Material, we show that (20) describes simulations with a constant hydrolysis and with hydrolysis coupled to mechanics equally well. With p_GTP(x), we can define an “average cap length” as ${\stackrel{-}{\ell }}_{\text{cap}}={\int }_0^{\infty }\text{d}x{p}_{\text{GTP}}(x)x$. This average cap length ${\stackrel{-}{\ell }}_{\text{cap}}$ is longer if hydrolysis is coupled to mechanics compared to a constant hydrolysis rate because p_GTP(x) is much greater for larger x (see Figures 11E,F). As ${\stackrel{-}{\ell }}_{\text{cap}}<N_{\text{pcap}}$, this increase in average cap length also explains the increased porous cap length if hydrolysis is coupled to mechanics.

The relative increase of hydrolyzed GDP-dimers at the tip could make MTs more prone for catastrophes and give rise to an increased catastrophe rate and, eventually, a more realistic concentration dependence of catastrophe rates. Figure 12, however, shows that this is not the case. Instead, the same steep dependence on the (base) hydrolysis rate as in Figure 7 persists.

FIGURE 12

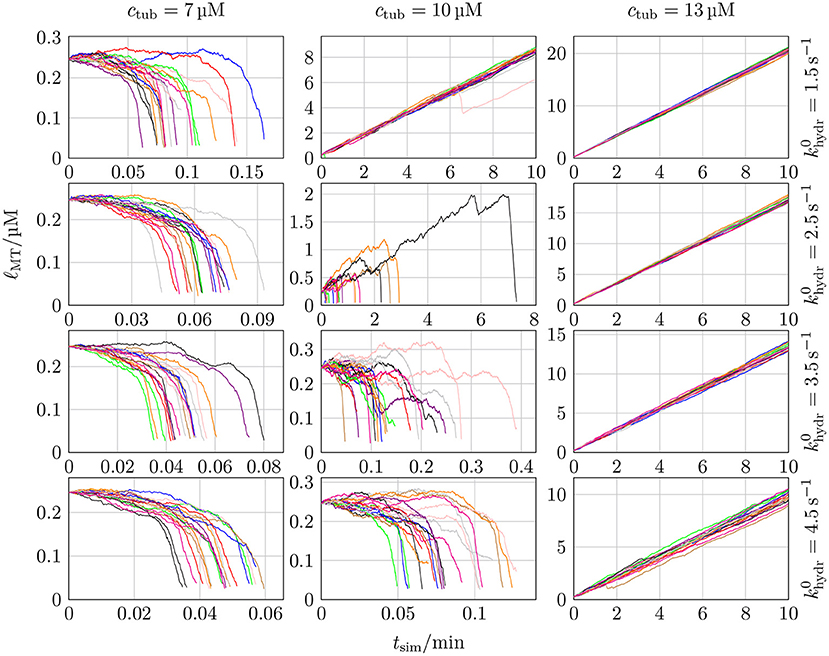
Figure 12. MT length ℓ_MT as a function of the simulation time t_sim for 20 different simulations with k₊ = 4 μM⁻¹ s⁻¹, $\Delta G_{\text{long}}^{0*}=$ −9.3 k_BT, k_lat = 100 k_BT/nm², three different values of c_tub, and four different values of $k_{\text{hydr}}^0$.

In comparison to the MT growth trajectories with a constant hydrolysis rate shown in Figures 10, 13 shows an example of a MT simulation in which the hydrolysis rate is coupled to mechanics. To calculate the probabilities shown in the insets, the same criteria as for Figure 10A were used. At first sight, these trajectories look similar to the corresponding trajectories for a constant hydrolysis rate (Figure 10A). There is, however, a significantly increased roughness of the trajectory during the growth phase, which could be interpreted as increased occurrence of “dips” or “stutter” events. A high probability of stutter events has also been observed in reference [35], which supports the existence of a mechanochemical coupling in hydrolysis. The catastrophe-triggering configuration of a “nucleus” of several neighboring protofilaments shrinking by more than 6 dimers is also similar as snapshots 4 and 5 in Figure 13B show.

FIGURE 13

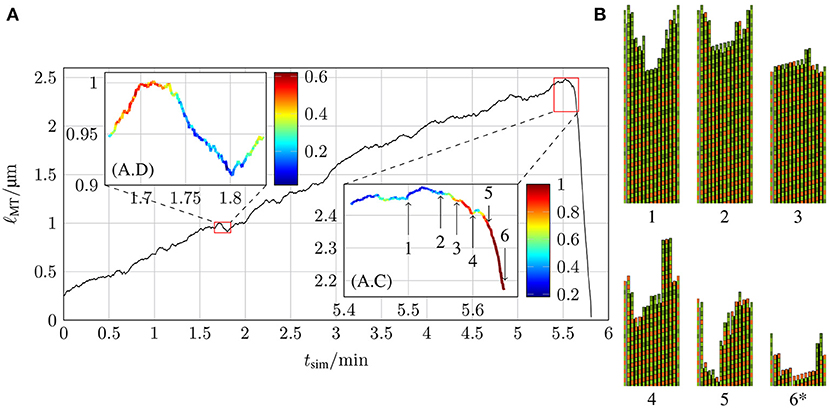
Figure 13. (A) Length of a MT ℓ_MT as a function of the simulation time t_sim with k₊ = 4 μM⁻¹ s⁻¹, $\Delta G_{\text{long}}^{0*}=$ −9.3 k_BT, k_lat = 100 k_BT /nm², c_tub = 9 μM and $k_{\text{hydr}}^0=$ 1.5 s⁻¹ with hydrolysis being coupled to mechanics and (B) the two-dimensional representations of certain MT tip configurations that are marked by arrows in the inset (A.C) (configuration 6^* has been shifted toward the MT tip by 21 tubulin dimer lengths).

3.8. Dilution Experiments

In dilution experiments, the free tubulin dimer concentration c_tub is reduced to c_dil ≪ c_tub at a certain point in time [5, 72, 73]. If the diluted concentration is sufficiently small or zero, the GTP-cap stops growing by polymerization (and depolymerizes) but continues to hydrolyze; after a characteristic delay time Δt_delay, the GTP-cap has vanished, a catastrophe is initiated, and the MT shrinks. Thus, dilution experiments and their comparison to corresponding dilution simulations can give information on the hydrolysis rate. Simulation results for the delay time are shown in Figure 14. In the Supplementary Material, we explain the algorithm that we used to determine the delay time Δt_delay from MT simulation trajectories in detail.

FIGURE 14

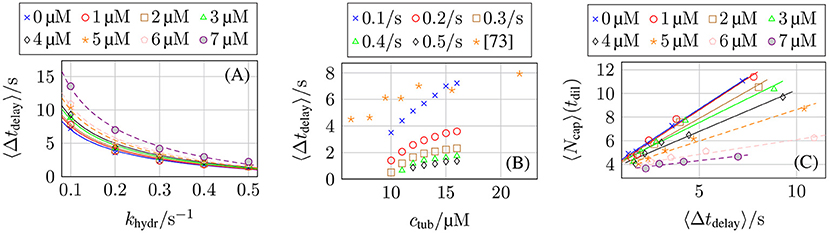
Figure 14. Average post-dilution delay time 〈Δt_delay〉 as a function of (A) the hydrolysis rate k_hydr for c_tub = 16 μM and different post-dilution GTP-tubulin dimer concentrations c_dil and (B) the pre-dilution GTP-tubulin dimer concentration c_tub for c_dil = 0 μM and different hydrolysis rates k_hydr. The averaged data from Duellberg et al. [73] specified the pre-dilution growth velocity, which was converted to c_tub for this plot. (C) Average GTP-cap length 〈N_cap〉 at the time of dilution t_dil as a function of the delay time 〈Δt_delay〉 for c_tub = 16 μM and different values of c_dil.

We expect the delay time to be proportional to the GTP-cap length, Δt_delay∝〈N_cap〉, as corroborated by Figure 14C and $\langle N_{\text{cap}}\rangle \propto \sqrt{c_{\text{tub}}/k_{\text{hydr}}}$ according to section 3.5 (see Figures 9C,D) [70]. This results in $\Delta t_{\text{delay}}\propto \sqrt{c_{\text{tub}}/k_{\text{hydr}}}$, which is in qualitative agreement with our simulation data in Figures 14A,B. The comparison with the experimental dilution data from reference [73] in Figure 14B shows that delay times for a hydrolysis rate k_hydr = 0.1 s⁻¹ come close to the experimental data but appear to depend too steeply on c_tub.

4. Discussion

We introduced, parameterized, and analyzed a chemomechanical model for MT dynamics in which, in addition to polymerization (attachment of dimers), depolymerization (detachment of dimers), and hydrolysis of dimers, the rupture of lateral bonds between monomers in neighboring protofilaments is explicitly modeled and coupled to the mechanics of the MT. The basis for this coupling is the allosteric model according to which a hydrolyzed dimer acquires a more bent configuration, which builds up mechanical stress in the MT tubular structure via lateral bonds between dimers.

As many model parameters as possible have been determined from the experimentally measured MT growth and shrinkage velocities measured by Walker et al. [47]. To determine the values of the model parameters, we use a “divide and conquer” approach [15, 30]. We used simulations of growing GTP-only MTs to parameterize longitudinal and lateral bond energies $\Delta G_{\text{long}}^{0*}$ and $\Delta G_{\text{lat}}^0$ and the attempt rate k_att for lateral bond formation. By requiring a linear concentration dependence of growth velocity, we can fix all three parameter values for a given value of k₊. We used simulations of shrinking GDP-only MTs to parameterize the bending constant κ and the spring constant k_lat of the lateral bonds. Here, we can only fix one of the two parameters. Moreover, the hydrolysis rate k_hydr is still a free parameter, for which we use values in the range 0.1–0.5 s⁻¹ known from experiments [61].

The general philosophy of a divide-and-conquer approach is the successive fixation of simulation parameters by using first GTP-only growth, then GDP-only shrinkage and, eventually, catastrophe frequencies or dilution to fix the hydrolysis rate. This successive fixation is, however, problematic, as the corresponding experimental data is influenced by all simulation parameters in general. The problem becomes apparent when considering the hydrolysis rate: changes in the hydrolysis rate also affect the growth rate over a wide concentration range because hydrolyzed dimers have an effectively higher detachment rate, see Figure 9B. Strictly speaking, all simulation parameters in Table 2 must be determined at once by fitting several experimental results simultaneously instead of the successive fixation in the divide-and-conquer approach or to apply the divide-and-conquer approach iteratively several times until a self-consistent parameter set is found. A simultaneous fixation of all parameters has been performed, for example, in reference [31] on a chemical model without bond rupture and, thus, with only four parameters (on-rate, bond energies, and hydrolysis rate). Future work on our model should include at least a re-adjustment of the parameters once a hydrolysis rate is selected such that the growth velocity of Walker et al. [47] is reproduced in the presence of hydrolysis. If mechanical feedback onto hydrolysis is included, the model has to be re-parameterized again, in principle.

Our simulation model handles all chemical events, i.e., dimer attachment and detachment, bond rupture and formation, and hydrolysis using a Gillespie algorithm. After each chemical event, we relax the resulting MT structure mechanically by energy minimization based on the assumption that the microscopic mechanical dynamics is much faster than the chemical steps. Therefore, mechanical energy minimization is the computationally most demanding step in the simulation. This is a common problem in all dimer-based chemomechanical MT models [15, 16, 18]. We address this problem by restricting the mechanical energy minimization to bounded number MT degrees of freedom near the plus end. We showed that restricting energy minimization to a depth of d_cutoff = 10 additional layers into the MT (in minus end direction) from the point of the last chemical event is an accurate and efficient choice. Computational efficiency of this procedure is better than performing a dedicated microscopic Brownian dynamics simulation [18] and better than random local energy minimization [15, 16] (for the same accuracy in energy minimization). The restricted energy minimization strategy also ensures that the number of minimization parameters does not scale with the MT length but remains bounded, which assures that we can simulate arbitrarily long growing MTs at a fixed minimal computational speed using our approach.

Simulations do not require more than a few hours for 1 min of MT dynamics (for a constant hydrolysis rate) using just a single CPU core. Therefore, we can reach time scales of several minutes of MT dynamics which is the time scale for repeated catastrophe events for concentrations above the individual critical concentration, where the dynamic instability can occur. We performed a first systematic analysis of catastrophe and rescue rates in Figure 8, which indicates that the decrease of the catastrophe rate with tubulin concentration is too steep compared to experimental data [47, 66]. It is also much steeper than simulation results of reference [18] but these results for the catastrophe rate relied on linear extrapolation from unrealistically high hydrolysis rates (3–11 s⁻¹) down to realistic values (0.1–0.5 s⁻¹). In the future, our computational model can also be used to measure the dependence of catastrophe rates on MT lifetime [67].

Within our model, we could also study single catastrophe and rescue events in detail (see Figure 10). The growth paths appear very similar to experimentally observed catastrophe and rescue events. Catastrophes typically feature an initial “transitional” phase of slow shrinking by 50–100 nm as also observed in reference [35]. Moreover, we observe “dips” in the growth paths resembling the “stutter” events from reference [35].

The most interesting results of chemomechanical models are possible statements about the typical catastrophe-triggering configurations. In this respect, our simulations indicate that a catastrophe could be triggered by a “nucleus” of three neighboring protofilaments shrinking by more than 6 dimers, such that its GTP-cap is removed and its ends reach into the GDP-body of the MT. To rescue a shrinking MT the GTP-cap has to be re-established on almost all 13 protofilaments such that nuclei of three neighboring uncapped GDP-protofilaments are avoided. This shows that mechanical correlations in the dynamics of protofilaments are important in triggering catastrophe events. This is an aspect which is absent in the calculation of catastrophe frequencies based on simplified purely chemical models, such as in reference [68], where protofilaments are regarded as effectively independent and uncorrelated.

Our model can achieve qualitative agreement with experimental data on dilution experiments (see Figure 14C) from reference [73] for relatively low hydrolysis rates of k_hydr = 0.1 s⁻¹, which is an indication that the catastrophe mechanism is correctly captured by our chemomechanical model. This also constrains the hydrolysis rate, which is still a free parameter in our model, to lower values around k_hydr = 0.1 s⁻¹.

Finally, we explored the consequences of a mechanochemical coupling in the hydrolysis of tubulin dimers. Because hydrolysis gives rise to bending of the GTP-dimers, we argue that mechanical forces on a dimer that increase its bending angle should also lead to higher hydrolysis rates, see (12) and (14). In the presence of mechanical feedback, hydrolysis gets a bias toward the MT plus end which, in turn, also causes an increase in porous cap length. At the same average hydrolysis rate, hydrolysis in the immediate tip of the GTP-cap is more likely while it is less likely in the remaining part of the cap such that GTP-tubulin dimers can be found much deeper in the GDP-body (see Figure 11). Individual catastrophe and rescue events (see Figure 13) look qualitatively similar in the presence of mechanical feedback but the probability of “dips” or “stutter” events is increased in agreement with reference [35]. The coupling of hydrolysis to mechanics does not increase catastrophe rates significantly such that the steep decrease of the catastrophe rate with tubulin concentration persists.

The main problem of our model appears to be the steep decrease of catastrophe rate with tubulin concentration, which could hint to a failure of basic assumptions. One possibility is that a direct effect of the hydrolysis state of the dimer onto the off-rate (as also suggested by atomistic simulations [74]) is relevant and not included in the model. Another possibility is a failure of allosteric models in general. The steep decline of catastrophe rates with the tubulin concentration gives a hint that MTs are structurally too stable for GTP-rich caps. This might provide evidence for a shortcoming of the underlying allosteric model, which inserts GTP-dimers in a straight configuration that is more prone to form stable lateral bonds than a curved configuration. An alternative are so-called lattice models [20, 21], according to which dimers are always bent but hydrolysis affects lateral and longitudinal dimer interaction energies. A systematic comparison of allosteric and lattice models toward the resulting concentration dependence of catastrophe rates within the framework provided here could help decide which class of models is more appropriate.

So far, almost all chemomechanical modeling approaches were based on the allosteric model [14–19] but recent experimental advancements in the analysis of the structure of MT tips [26] demonstrated that both growing and shrinking MTs have bent protofilament ends supporting similar earlier results [75–78]. Additionally, calculations using MT structures with different nucleotide content in the beta-tubulin [23] and all-atom MD simulations of GTP- and GDP-only MTs [24, 25] revealed that hydrolysis weakens lateral bonds and strengthens longitudinal bonds. Both aspects support the lattice model for the influence of hydrolysis on MT mechanics. There is, however, also evidence from MD simulations for intermediate models, where hydrolysis affects interactions and also leads to a much lower GDP-tubulin flexibility [27]. Independent of these findings, our study based on the allosteric model is valuable for the following reasons: (i) In both the allosteric and the lattice model, catastrophes are cascades of lateral bond rupture and in both models, the bent shape of GDP-dimers is the dominating cause of mechanical strain in the MT structure. In the allosteric model, bending and mechanical strain is directly generated by the hydrolysis of GTP-dimers, whereas in the lattice model, the tubulin dimers are always bent but hydrolysis weakens lateral bonds. In both models, the result is an increased lateral bond rupture rate of mechanically strained bonds after hydrolysis. Therefore, an explicit modeling approach for lateral bond rupture as a stochastic process under force generated by the bending of GDP-dimers will also be important in all future chemomechanical models based on the lattice model. So far explicit stochastic models of lateral bond rupture have only been included into two-dimensional models lacking explicit mechanics [32–34] or with heavy computational cost by explicitly simulating the Brownian dynamics of dimers and bonds [18]. (ii) The importance of lateral bond rupture becomes particularly clear for shrinking MTs or MTs entering a catastrophe. In these phases of the dynamic instability, GDP-tubulin dimers are significantly more relevant than GTP-tubulin dimers. As GDP-dimers are bent in both models and this bending gives rise to lateral bond stretching, we believe that both types of models will display a very similar behavior in these phases. The only difference in this scenario is that in the lattice model, the lateral bond energy $\Delta G_{\text{lat}}^0$ in the rupture rate (10) will depend on the nucleotide type of the bonded tubulin monomers, which also makes k_rup an explicit function of the nucleotide state. Because the nucleotide state is predominantly GDP during shrinkage, the results for properly parameterized models will be very similar. (iii) We also introduced a computationally efficient scheme to relax the mechanical energy between chemical events, which can also be employed in future chemomechanical lattice models. Within the allosteric model, we achieve a better mechanical energy relaxation than previous models [15] with significantly less computational steps than a full Brownian dynamics simulation requires [18]. (iv) The idea of a feedback of mechanical forces onto the hydrolysis rate can also be applied in future chemomechanical lattice models: if hydrolysis leads to a weakening of lateral bonds, one could expect mechanical strains that favor weakening of lateral bonds also to favor hydrolysis.

In the future, our model could be extended to also include regulating TIP+ proteins [79] for which different mechanisms of how they influence MTs could be implemented. Comparing the results of such simulations with experimental data could help to develop a mechanistic picture of the action of these proteins. Another future extension is MT polymerization under force [80, 81]. So far, polymerization under force has been investigated using chemical models [56, 82–85]; the influence of an external force on the microscopic level, in particular the detailed dynamics of catastrophe events and the catastrophe-triggering configurations is unknown.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MS performed the simulations and theoretical analysis, evaluated the data, wrote, and revised the manuscript. JK conceived the research, wrote, and revised the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

We acknowledge funding from the German Research Foundation (DFG, www.dfg.de) through Grant number KI 662/9-1. The authors gratefully acknowledge computing time provided on the Linux HPC cluster at Technical University Dortmund (LiDO3), partially funded in the course of the Large-Scale Equipment Initiative by the German Research Foundation (DFG) as project 271512359.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.673875/full#supplementary-material

Footnotes

1. ^To calculate shrinkage velocities of shrinkage simulations via a simple linear fit, it has proven to be easier to stop simulations if a protofilament still contains one tubulin dimer instead of zero tubulin dimers as the last tubulin dimer requires more time to depolymerize creating a “tail” in the length-vs.-time plot. This time increase is due to lateral springs being stretched less because there is no additional tubulin dimer below the terminal tubulin dimer that would exert an additional bending moment. In practice, for determining parameters and when running full simulations, this first layer at the minus end is irrelevant and could be regarded as a “seed” on which the MT grows.

2. ^The individual critical concentration can be read off from Figure 7 as the concentration below which immediate MT shrinkage sets in.

3. ^As the cap lengths shown in Figure 9C are averaged over the whole duration of the simulations, these cap lengths also average over growth and shrinkage phases. As cap lengths are shorter during shrinkage than growth, the cap lengths in Figure 9C can be regarded as a lower limit on the average cap length during MT growth.

References

1. McIntosh JR, Grishchuk EL, West RR. Chromosome-microtubule interactions during mitosis. Annu Rev Cell Dev Biol. (2002) 18:193–219. doi: 10.1146/annurev.cellbio.18.032002.132412

CrossRef Full Text | Google Scholar

2. Siegrist SE, Doe CQ. Microtubule-induced cortical cell polarity. Genes Dev. (2007) 21:483–96. doi: 10.1101/gad.1511207

CrossRef Full Text | Google Scholar

3. Mitchison T, Kirschner M. Dynamic instability of microtubule growth. Nature. (1984) 312:237–42. doi: 10.1038/312237a0

CrossRef Full Text | Google Scholar

4. Carlier MF, Hill TL, Chen Yd. Interference of GTP hydrolysis in the mechanism of microtubule assembly: an experimental study. Proc Natl Acad Sci USA. (1984) 81:771–5. doi: 10.1073/pnas.81.3.771

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Walker RA, Pryer NK, Salmon ED. Dilution of individual microtubules observed in real time in vitro: evidence that cap size is small and independent of elongation rate. J Cell Biol. (1991) 114:73–81. doi: 10.1083/jcb.114.1.73

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Howard J, Hyman AA. Growth, fluctuation and switching at microtubule plus ends. Nat Rev Mol Cell Biol. (2009) 10:569–74. doi: 10.1038/nrm2713

PubMed Abstract | CrossRef Full Text | Google Scholar

7. van Haren J, Wittmann T. Microtubule plus end dynamics-do we know how microtubules grow? Bioessays. (2019) 41:1800194. doi: 10.1002/bies.201800194

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Mandelkow EM, Mandelkow E, Milligan RA. Microtubule dynamics and microtubule caps: a time-resolved cryo-electron microscopy study. J Cell Biol. (1991) 114:977–91. doi: 10.1083/jcb.114.5.977

PubMed Abstract | CrossRef Full Text | Google Scholar

9. McIntosh JR, Volkov V, Ataullakhanov FI, Grishchuk EL. Tubulin depolymerization may be an ancient biological motor. J Cell Sci. (2010) 123:3425–34. doi: 10.1242/jcs.067611

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Müller-Reichert T, Chrétien D, Severin F, Hyman AA. Structural changes at microtubule ends accompanying GTP hydrolysis: Information from a slowly hydrolyzable analogue of GTP, guanylyl (α,β) methylenediphosphonate. Proc Natl Acad Sci USA. (1998) 95:3661–6. doi: 10.1073/pnas.95.7.3661

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Downing KH, Eva N. Tubulin and microtubule structure. Curr Opin Cell Biol. (1998) 10:16–22. doi: 10.1016/S0955-0674(98)80082-3

CrossRef Full Text | Google Scholar

12. Nogales E, Wang HW. Structural mechanisms underlying nucleotide-dependent self-assembly of tubulin and its relatives. Curr Opin Struct Biol. (2006) 16:221–9. doi: 10.1016/j.sbi.2006.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Nogales E, Whittaker M, Milligan RA, Downing KH. High-resolution model of the microtubule. Cell. (1999) 96:79–88. doi: 10.1016/S0092-8674(00)80961-7

CrossRef Full Text | Google Scholar

14. Molodtsov MI, Ermakova EA, Shnol EE, Grishchuk EL, McIntosh JR, Ataullakhanov FI. A molecular-mechanical model of the microtubule. Biophys J. (2005) 88:3167–79. doi: 10.1529/biophysj.104.051789

CrossRef Full Text | Google Scholar

15. VanBuren V, Cassimeris L, Odde DJ. Mechanochemical model of microtubule structure and self-assembly kinetics. Biophys J. (2005) 89:2911–26. doi: 10.1529/biophysj.105.060913

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Coombes C, Yamamoto A, Kenzie M, Odde D, Gardner M. Evolving tip structures can explain age-dependent microtubule catastrophe. Curr Biol. (2013) 23:1342–8. doi: 10.1016/j.cub.2013.05.059

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Müller N, Kierfeld J. Effects of microtubule mechanics on hydrolysis and catastrophes. Phys Biol. (2014) 11:046001. doi: 10.1088/1478-3975/11/4/046001

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zakharov P, Gudimchuk N, Voevodin V, Tikhonravov A, Ataullakhanov F, Grishchuk E. Molecular and mechanical causes of microtubule catastrophe and aging. Biophys J. (2015) 109:2574–91. doi: 10.1016/j.bpj.2015.10.048

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Jain I, Inamdar MM, Padinhateeri R. Statistical mechanics provides novel insights into microtubule stability and mechanism of shrinkage. PLoS Comput Biol. (2015) 11:e1004099. doi: 10.1371/journal.pcbi.1004099

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Buey RM, Díaz JF, Andreu JM. The nucleotide switch of tubulin and microtubule assembly: a polymerization-driven structural change. Biochemistry. (2006) 45:5933–8. doi: 10.1021/bi060334m

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rice LM, Montabana EA, Agard DA. The lattice as allosteric effector: structural studies of αβ- and γ-tubulin clarify the role of GTP in microtubule assembly. Proc Natl Acad Sci USA. (2008) 105:5378–83. doi: 10.1073/pnas.0801155105

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Alushin GM, Lander GC, Kellogg EH, Zhang R, Baker D, Nogales E. High-resolution microtubule structures reveal the structural transitions in αβ-tubulin upon GTP hydrolysis. Cell. (2014) 157:1117–29. doi: 10.1016/j.cell.2014.03.053

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Manka SW, Moores CA. The role of tubulin–tubulin lattice contacts in the mechanism of microtubule dynamic instability. Nat Struct Mol Biol. (2018) 25:607–15. doi: 10.1038/s41594-018-0087-8

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ayoub AT, Klobukowski M, Tuszynski JA. Detailed per-residue energetic analysis explains the driving force for microtubule disassembly. PLoS Comput Biol. (2015) 11:e1004313. doi: 10.1371/journal.pcbi.1004313

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Fedorov VA, Orekhov PS, Kholina EG, Zhmurov AA, Ataullakhanov FI, Kovalenko IB, et al. Mechanical properties of tubulin intra- and inter-dimer interfaces and their implications for microtubule dynamic instability. PLoS Comput Biol. (2019) 15:e1007327. doi: 10.1371/journal.pcbi.1007327

PubMed Abstract | CrossRef Full Text | Google Scholar

26. McIntosh JR, O'Toole E, Morgan G, Austin J, Ulyanov E, Ataullakhanov F, et al. Microtubules grow by the addition of bent guanosine triphosphate tubulin to the tips of curved protofilaments. J Cell Biol. (2018) 217:2691–708. doi: 10.1083/jcb.201802138

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Igaev M, Grubmüller H. Microtubule assembly governed by tubulin allosteric gain in flexibility and lattice induced fit. Elife. (2018) 7:e34353. doi: 10.7554/eLife.34353.041

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zakharov PN, Arzhanik VK, Ulyanov EV, Gudimchuk NB, Ataullakhanov FI. Microtubules: dynamically unstable stochastic phase-switching polymers. Phys Uspekhi. (2016) 59:773–86. doi: 10.3367/UFNe.2016.04.037779

CrossRef Full Text | Google Scholar

29. Dogterom M, Leibler S. Physical aspects of the growth and regulation of microtubule structures. Phys Rev Lett. (1993) 70:1347–50. doi: 10.1103/PhysRevLett.70.1347

PubMed Abstract | CrossRef Full Text | Google Scholar

30. VanBuren V, Odde DJ, Cassimeris L. Estimates of lateral and longitudinal bond energies within the microtubule lattice. Proc Natl Acad Sci USA. (2002) 99:6035–40. doi: 10.1073/pnas.092504999

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Piette BMAG, Liu J, Peeters K, Smertenko A, Hawkins T, Deeks M, et al. A thermodynamic model of microtubule assembly and disassembly. PLoS ONE. (2009) 4:e6378. doi: 10.1371/journal.pone.0006378

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Margolin G, Goodson HV, Alber MS. Mean-field study of the role of lateral cracks in microtubule dynamics. Phys Rev E. (2011) 83:041905. doi: 10.1103/PhysRevE.83.041905

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Margolin G, Gregoretti IV, Cickovski TM, Li C, Shi W, Alber MS, et al. The mechanisms of microtubule catastrophe and rescue: implications from analysis of a dimer-scale computational model. Mol Biol Cell. (2012) 23:642–56. doi: 10.1091/mbc.e11-08-0688

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Li C, Li J, Goodson HV, Alber MS. Microtubule dynamic instability: the role of cracks between protofilaments. Soft Matter. (2014) 10:2069–80. doi: 10.1039/C3SM52892H

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Mahserejian SM, Scripture JP, Mauro AJ, Lawrence EJ, Jonasson EM, Murray KS, et al. Stutter: a transient dynamic instability phase that is strongly associated with catastrophe. bioRxiv. (2019). doi: 10.1101/2019.12.16.878603

CrossRef Full Text | Google Scholar

36. Wang HW, Nogales E. Nucleotide-dependent bending flexibility of tubulin regulates microtubule assembly. Nature. (2005) 435:911–5. doi: 10.1038/nature03606

PubMed Abstract | CrossRef Full Text | Google Scholar

37. VanBuren V, Odde DJ, Cassimeris L., Errata for VanBuren, et al., Estimates of lateral and longitudinal bond energies within the microtubule lattice, PNAS 2002 99:6035–6040. Proc Natl Acad Sci USA. (2004) 101:14989. doi: 10.1073/pnas.0406393101

CrossRef Full Text | Google Scholar

38. Harris BJ, Ross JL, Hawkins TL. Microtubule seams are not mechanically weak defects. Phys Rev E. (2018) 97:062408. doi: 10.1103/PhysRevE.97.062408

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Elie-Caille C, Severin F, Helenius J, Howard J, Muller DJ, Hyman AA. Straight GDP-tubulin protofilaments form in the presence of taxol. Curr Biol. (2007) 17:1765–70. doi: 10.1016/j.cub.2007.08.063

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Kroy K, Frey E. Dynamic scattering from solutions of semiflexible polymers. Phys Rev E. (1997) 55:3092–101. doi: 10.1103/PhysRevE.55.3092

CrossRef Full Text | Google Scholar

41. Ulyanov EV, Vinogradov DS, McIntosh JR, Gudimchuk NB. Brownian dynamics simulation of protofilament relaxation during rapid freezing. PLoS ONE. (2021) 16:e0247022. doi: 10.1371/journal.pone.0247022

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Gardner M, Charlebois B, Jánosi I, Howard J, Hunt A, Odde D. Rapid microtubule self-assembly kinetics. Cell. (2011) 146:582–92. doi: 10.1016/j.cell.2011.06.053

CrossRef Full Text | Google Scholar

43. Kononova O, Kholodov Y, Theisen KE, Marx KA, Dima RI, Ataullakhanov FI, et al. Tubulin bond energies and microtubule biomechanics determined from nanoindentation in silico. J Am Chem Soc. (2014) 136:17036–45. doi: 10.1021/ja506385p

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Bell GI. Models for the specific adhesion of cells to cells. Science. (1978) 200:618–27. doi: 10.1126/science.347575

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Evans E, Ritchie K. Dynamic strength of molecular adhesion bonds. Biophys J. (1997) 72:1541–55. doi: 10.1016/S0006-3495(97)78802-7

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys. (1976) 22:403–34. doi: 10.1016/0021-9991(76)90041-3

CrossRef Full Text | Google Scholar

47. Walker RA, O'Brien ET, Pryer NK, Soboeiro MF, Voter WA, Erickson HP, et al. Dynamic instability of individual microtubules analyzed by video light microscopy: rate constants and transition frequencies. J Cell Biol. (1988) 107:1437–48. doi: 10.1083/jcb.107.4.1437

PubMed Abstract | CrossRef Full Text | Google Scholar

48. O'Brien ET, Salmon ED, Walker RA, Erickson HP. Effects of magnesium on the dynamic instability of individual microtubules. Biochemistry. (1990) 29:6648–56. doi: 10.1021/bi00480a014

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Drechsel DN, Hyman AA, Cobb MH, Kirschner MW. Modulation of the dynamic instability of tubulin assembly by the microtubule-associated protein tau. Mol Biol Cell. (1992) 3:1141–54. doi: 10.1091/mbc.3.10.1141

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Trinczek B, Marx A, Mandelkow EM, Murphy DB, Mandelkow E. Dynamics of microtubules from erythrocyte marginal bands. Mol Biol Cell. (1993) 4:323–35. doi: 10.1091/mbc.4.3.323

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Chrétien D, Fuller SD, Karsenti E. Structure of growing microtubule ends: two-dimensional sheets close into tubes at variable rates. J Cell Biol. (1995) 129:1311–28. doi: 10.1083/jcb.129.5.1311

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Pedigo S, Williams RC Jr. Concentration dependence of variability in growth rates of microtubules. Biophys J. (2002) 83:1809–19. doi: 10.1016/S0006-3495(02)73946-5

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Galassi M, Davies J, Theiler J, Gough B, Jungman G, Alken P, et al. GNU Scientific Library Reference Manual. Available online at: https://www.gnu.org/software/gsl/

Google Scholar

54. Ayaz P, Munyoki S, Geyer EA, Piedra FA, Vu ES, Bromberg R, et al. A tethered delivery mechanism explains the catalytic action of a microtubule polymerase. eLife. (2014) 3:e03069. doi: 10.7554/eLife.03069.014

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Mickolajczyk KJ, Geyer EA, Kim T, Rice LM, Hancock WO. Direct observation of individual tubulin dimers binding to growing microtubules. Proc Natl Acad Sci USA. (2019) 116:7314–22. doi: 10.1073/pnas.1815823116

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Stukalin EB, Kolomeisky AB. Simple growth models of rigid multifilament biopolymers. J Chem Phys. (2004) 121:1097–104. doi: 10.1063/1.1759316

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Sim H, Sept D. Properties of microtubules with isotropic and anisotropic mechanics. Cell Mol Bioeng. (2013) 6:361–8. doi: 10.1007/s12195-013-0302-y

CrossRef Full Text | Google Scholar

58. Driver JW, Geyer EA, Bailey ME, Rice LM, Asbury CL. Direct measurement of conformational strain energy in protofilaments curling outward from disassembling microtubule tips. eLife. (2017) 6:e28433. doi: 10.7554/eLife.28433.023

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Deriu MA, Enemark S, Soncini M, Montevecchi FM, Redaelli A. Tubulin: from atomistic structure to supramolecular mechanical properties. J Mater Sci. (2007) 42:8864–72. doi: 10.1007/s10853-007-1784-6

CrossRef Full Text | Google Scholar

60. Grafmüller A, Voth G. Intrinsic bending of microtubule protofilaments. Structure. (2011) 19:409–17. doi: 10.1016/j.str.2010.12.020

CrossRef Full Text | Google Scholar

61. Melki R, Fievez S, Carlier MF. Continuous monitoring of P_i release following nucleotide hydrolysis in actin or tubulin assembly using 2-amino-6-mer-capto-7-methylpurine ribonucleoside and purine-nucleoside phosphorylase as an enzyme-linked assay. Biochemistry. (1996) 35:12038–45. doi: 10.1021/bi961325o

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Aparna JS, Padinhateeri R, Das D. Signatures of a macroscopic switching transition for a dynamic microtubule. Sci Rep. (2017) 7:45747. doi: 10.1038/srep45747

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Padinhateeri R, Kolomeisky A, Lacoste D. Random hydrolysis controls the dynamic instability of microtubules. Biophys J. (2012) 102:1274–83. doi: 10.1016/j.bpj.2011.12.059

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Bowne-Anderson H, Zanic M, Kauer M, Howard J. Microtubule dynamic instability: a new model with coupled GTP hydrolysis and multistep catastrophe. Bioessays. (2013) 35:452–61. doi: 10.1002/bies.201200131

PubMed Abstract | CrossRef Full Text

65. Piedra FA, Kim T, Garza ES, Geyer EA, Burns A, Ye X, et al. GDP-to-GTP exchange on the microtubule end can contribute to the frequency of catastrophe. Mol Biol Cell. (2016) 27:3515–25. doi: 10.1091/mbc.e16-03-0199

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Janson ME, de Dood ME, Dogterom M. Dynamic instability of microtubules is regulated by force. J Cell Biol. (2003) 161:1029–34. doi: 10.1083/jcb.200301147

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Gardner M, Zanic M, Gell C, Bormuth V, Howard J. Depolymerizing kinesins Kip3 and MCAK shape cellular microtubule architecture by differential control of catastrophe. Cell. (2011) 147:1092–103. doi: 10.1016/j.cell.2011.10.037

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Flyvbjerg H, Holy TE, Leibler S. Microtubule dynamics: caps, catastrophes, and coupled hydrolysis. Phys Rev E. (1996) 54:5538–60. doi: 10.1103/PhysRevE.54.5538

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Zelinski B, Kierfeld J. Cooperative dynamics of microtubule ensembles: polymerization forces and rescue-induced oscillations. Phys Rev E. (2013) 87:012703. doi: 10.1103/PhysRevE.87.012703

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Li X, Lipowsky R, Kierfeld J. Coupling of actin hydrolysis and polymerization: reduced description with two nucleotide states. Europhys Lett. (2011) 89:38010. doi: 10.1209/0295-5075/89/38010

CrossRef Full Text | Google Scholar

71. Seetapun D, Castle B, McIntyre A, Tran P, Odde D. Estimating the microtubule GTP cap size in vivo. Curr Biol. (2012) 22:1681–7. doi: 10.1016/j.cub.2012.06.068

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Voter WA, O'Brien ET, Erickson HP. Dilution-induced disassembly of microtubules: relation to dynamic instability and the GTP cap. Cell Motil Cytoskeleton. (1991) 18:55–62. doi: 10.1002/cm.970180106

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Duellberg C, Cade NI, Holmes D, Surrey T. The size of the EB cap determines instantaneous microtubule stability. eLife. (2016) 5:e13470. doi: 10.7554/eLife.13470.023

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Grafmüller A, Noya EG, Voth GA. Nucleotide-dependent lateral and longitudinal interactions in microtubules. J Mol Biol. (2013) 425:2232–46. doi: 10.1016/j.jmb.2013.03.029

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Höög JL, Huisman SM, Sebö-Lemke Z, Sandblad L, McIntosh JR, Antony C, et al. Electron tomography reveals a flared morphology on growing microtubule ends. J Cell Sci. (2011) 124:693–8. doi: 10.1242/jcs.072967

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Kukulski W, Schorb M, Welsch S, Picco A, Kaksonen M, Briggs JAG. Correlated fluorescence and 3D electron microscopy with high sensitivity and spatial precision. J Cell Biol. (2011) 192:111–9. doi: 10.1083/jcb.201009037

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Nawrotek A, Knossow M, Gigant B. The determinants that govern microtubule assembly from the atomic structure of GTP-tubulin. J Mol Biol. (2011) 412:35–42. doi: 10.1016/j.jmb.2011.07.029

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Pecqueur L, Duellberg C, Dreier B, Jiang Q, Wang C, Plückthun A, et al. A designed ankyrin repeat protein selected to bind to tubulin caps the microtubule plus end. Proc Natl Acad Sci USA. (2012) 109:12011–16. doi: 10.1073/pnas.1204129109

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Akhmanova A, Steinmetz MO. Tracking the ends: a dynamic protein network controls the fate of microtubule tips. Nat Rev Mol Cell Biol. (2008) 9:309–22. doi: 10.1038/nrm2369

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Dogterom M, Yurke B. Measurement of the force-velocity relation for growing microtubules. Science. (1997) 278:856–60. doi: 10.1126/science.278.5339.856

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Dogterom M, Kerssemakers JWJ, Romet-Lemonne G, Janson ME. Force generation by dynamic microtubules. Curr Opin Cell Biol. (2005) 17:67–74. doi: 10.1016/j.ceb.2004.12.011

CrossRef Full Text | Google Scholar

82. van Doorn GS, Tănase C, Mulder BM, Dogterom M. On the stall force for growing microtubules. Eur Biophys J. (2000) 29:2–6. doi: 10.1007/s002490050245

CrossRef Full Text | Google Scholar

83. Kolomeisky AB, Fisher ME. Force-velocity relation for growing microtubules. Biophys J. (2001) 80:149–54. doi: 10.1016/S0006-3495(01)76002-X

CrossRef Full Text | Google Scholar

84. Ranjith P, Lacoste D, Mallick K, Joanny JF. Nonequilibrium self-assembly of a filament coupled to ATP/GTP hydrolysis. Biophys J. (2009) 96:2146–59. doi: 10.1016/j.bpj.2008.12.3920

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Krawczyk J, Kierfeld J. Stall force of polymerizing microtubules and filament bundles. Europhys Lett. (2011) 93:28006. doi: 10.1209/0295-5075/93/28006

CrossRef Full Text | Google Scholar