
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys., 28 May 2021
Sec. Space Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.672836
A correction has been applied to this article in:
Corrigendum: Olbert’s Kappa Fermi and Bose Distributions
The quantum version of Olbert’s kappa distribution applicable to fermions is obtained. Its construction is straightforward but requires recognition of the differences in the nature of states separated by Fermi momenta. Its complement, the bosonic version of the kappa distribution is also given, as is the procedure of how to construct a hypothetical kappa-anyon distribution. At very low temperature the degenerate kappa Fermi distribution yields a kappa-modified version of the ordinary degenerate Fermi energy and momentum. We provide the Olbert-generalized expressions of the Olbert-Fermi partition function and entropy which may serve determining all relevant statistical mechanical quantities. Possible applications are envisaged to condensed matter physics, possibly quantum plasmas, and dense astrophysical objects like the interior state of terrestrial planets, neutron stars, magnetars where quantum effects come into play and dominate the microscopic scale but may have macroscopic consequences.
The classical (nonrelativistic) kappa distribution was introduced by Stan Olbert in 1966 [1] and first applied in the PhD thesis of Binsack [2].1 Its first refereed version [3], applied to electron fluxes in Earth’s plasma sheet (acknowledging Olbert), is usually taken as its origin [for an account of its history, see Chapter 1 in Ref. 4]. In the honor of Olbert, we call it “Olbert’s kappa distribution,” while for simplicity shall speak of kappa distributions below.
The kappa distribution occurred almost permanently when dealing with particle distributions in high-temperature plasmas encountered in space [4–10]. It was also inferred from cosmic ray [11] spectra [12], extended into the relativistic domain, in the solar wind [13–17], near shocks [18–20], and in the heliosphere in general [21]. Various applications to statistical probabilities in correlated systems have been reviewed as well [see Refs. 22, 23, for collections]. It thus seems to represent a general distribution function in physical systems which in theory have been identified as obeying some kind of internal correlations. Conventionally, their evolution under nonstationary conditions, in particular in application to particle acceleration, is attributed to a Fokker–Planck description which naturally generates tails on the distribution function via momentum space diffusion. More basic theories have also been developed based on nonequilibrium statistical mechanics where they arise as stationary states far from thermal equilibrium [24–28]. In the asymptotic limit, nonlinear plasma theories [29–31] provide classical distributions of this kind. To some extent, kappa distributions are relatives of Tsallis’ nonextensive distributions in Tsallis’ thermostatistics [32] as in both formulations, the entropy turns out not to be simply extensive. Tsallis’ theory calls it nonextensive. Recently, the analytical form of the classical (nonquantum) kappa entropy has been constructed [33], which shows that it is super-extensive while being different from its thermo-statistical cousin, indicating that the fields of application in physics and statistics presumably refer to different domains.
The appearance of nonequilibrium distributions is physically no surprise. In classical physics, they arise as nonstationary distributions in quasi-linear (Fokker–Planck) theory where they can be made stationary by balancing particle injection and losses from the volume under consideration [11]. What, however, is unusual is that so far the attempts failed to construct a quantum equivalent of the classical kappa distribution. Formally, it seems very simple to obtain it from the partition function, but the distributions found [26, 34] were rather inconvenient versions of the classical Olbertian and no real quantum distributions as they did not allow for the presence of particles with energy below Fermi energy.2 As an explanation, it was concluded that quantum theory at low temperatures suppresses correlations of the Fokker–Planck kind, which cause the evolution of non-Gaussian tails on the distribution. However, such a conclusion is rather unsatisfactory because there is no obvious way to demonstrate that correlations are indeed excluded by quantum effects. Motivation for constructing a kappa quantum distribution can thus be found in the wish to correct this mismatch in order to complete and generalize the Olbertian statistical mechanical theory by extending it into the quantum domain. In the Discussion section, we also provide some hints on possible applications. An application to nonideal gases which the former version was given [38, 38] should, for consistency, probably be adapted to the correct kappa Fermi version of the distribution obtained below. One would expect that it improves the interpretation of the experimentally obtained results. Here, we identify the crucial step that was missed in those attempts and subsequently provide the correct kappa quantum distributions. We first restrict to the Fermi-Olbertian as this one is more important in view of the wide range of quantum problems to that it may possibly be applied to some particularly suited problems.
There are several ways of deriving the classical kappa distribution. Consider an ideal gas of indistinguishable particles. The simplest is to start from the classical either micro-canonical or canonical Gibbs partition function [27], which is just the sum of all micro-canonical probabilities, and replacing the Boltzmann factor with the Olbert factor:
Here,
One easily shows that this choice with
This same procedure fails in the quantum case in application to the Fermi or Bose distributions. One can, however, give it a different start when, for simplicity, referring to the slightly more lucid canonical so-called thermodynamic Gibbs potential [37, 38] defined as the form
where
This is the prescription for constructing the wanted distribution. However, simply substituting the Olbert factor for the Boltzmann factor in the above expression turns out to be wrong. Sometimes, a very small move is necessary to progress a bit. Before proceeding, the potential must be inverted by resolving the logarithm:
which yields a form that contains exponentials on both sides of the equation, and thus the substitution has to be done for both exponentials. Moreover, inspecting the exponential on the right one realizes that at
which with
Application of the Pauli principle in order to specify to the quantum exclusions which the Fermi distribution takes care of then produces
which must be differentiated with respect to μ keeping β and
for the average occupation number of states. It applies to both nonrelativistic as well as relativistic
For a gas of particles with momenta p, the above discrete Olbert κ Fermi distribution becomes a continuous function of particle energy
which for practical purposes when integrating over momentum and configuration space has to be properly normalized to the total number of particles in the volume, as indicated above, using the transition from summation over discrete states to continuous integration over space and momentum
The kappa Fermi distribution obtained in this way maintains the quantum properties of the gas which become most important at low temperature. For large
Asking for the shape of the kappa Fermi distribution at finite temperature, one excludes large
Figure 1 shows a schematic of the shape of the kappa Fermi distribution for the two cases of zero
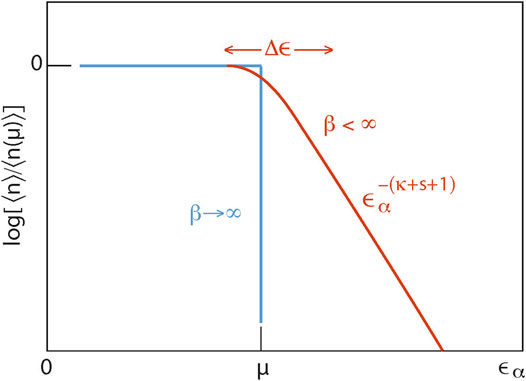
FIGURE 1. Schematic of Olbert’s kappa Fermi distribution as function of energy
In order to find a representation of the Olbert-Fermi thermodynamic Gibbs potential of an ideal gas, one must invert the above distribution and insert it into the expression for
which may serve to calculate the properties of the ideal Olbert-Fermi gas. The first part gives
which gives for the (dimensionless) entropy of state α the expression
One would like to have a representation of the entropy solely in terms of the mean occupation number
which replaces the well-known logarithmic form [38] of the Fermi entropy. The total entropy
Knowing the kappa Fermi distribution, the corresponding partition function can be written down. We here give it the canonical version which of course is identical with the above normalization condition with unspecified particle number
As usual, it can be used to evaluate all thermodynamically interesting quantities.
For completeness, we note in passing that the same procedure allows obtaining the complementary Olbert-Bose potential summing up the right-hand side of Eq. 13 for
which has to be differentiated with respect to μ holding
which must be normalized to the total particle number. Clearly, the chemical potential
Again, the Olbert-Bose partition function is the sum of all the un-normalized Olbert κ Bose distributions in states α
One may, in addition, note that the thermodynamic Gibbs potential is an energy. It thus remains additive, (extensive) independent of any other properties of the gas. Hence, on the way of fractionally adding the Olbert-Fermi and Bose potentials
The most interesting is the degenerate electron gas with temperature
This yields the expressions for
and
The mean energy
In this brief communication, we generalized, based on physical arguments, the classical kappa distribution to fermions and bosons, the quantum Fermi and Bose cases. We also noted how this can be extended to mixed fermion-boson anyon states. The distributions, Gibbs potentials, and partition functions can be used to derive all relevant thermodynamic and statistical mechanical quantities for quantum and classical systems. In principle, this completes and rounds up the task of a generalized Olbertian statistical mechanics which turns out in all cases to be the analytical generalization of Boltzmann-Gibbs statistical mechanics into the Lorentzian and quantum domains. It results in well-defined distributions, Gibbs potentials, partition functions, and entropies. If required, it can, under appropriate conditions, serve as the thermodynamic theory for both classical and quantum systems. As such, it does apply to any system, not being restricted to plasmas. In fact, plasmas may not be the most interesting of such systems. It seems that the main field of application could be envisaged in some kinds of solid state physics, condensed matter physics, suitable astrophysical object, and possibly also, if relevant, high-energy physics. It should be noted that even under quantum conditions, the thermodynamic definition of temperature is maintained, which is a satisfactory physical fact.
For finite temperatures, the kappa Fermi distribution yields a substantial modification which, however, in the degenerate case of near-zero temperature, that is, environmental temperature much below Fermi temperature
We should, however, note at this occasion that the above investigation of the finite temperature behavior of the kappa Fermi distribution with increase of the gap around Fermi energy might be of interest in superconductivity theory. It still awaits an extension of the BCS theory [44] to the application of the Olbert-Fermi statistical mechanics.
For completeness, the complementary Olbert-Bose thermodynamic potential and distribution have also been given. The thermodynamic potential may serve to obtain the Olbert-Bose entropy, and equation of state. In this case, there is no indication of any presence of a Bose-Einstein condensation such that one would conclude that internal quantum correlations hidden in a finite value of κ destroy the formation of a bosonic quantum condensate at zero physical temperature.
Classical Olbertian statistical mechanics, as by now known (for reference the reader is referred to the literature cited in the introduction) applies to high-temperature collisionless plasmas as encountered in dilute near-Earth space, the heliosphere, and probably also environments of stars and planetary systems. Kappa distributions of particles have in the past been inferred in a multitude of space plasmas. In dilute high temperature plasma, similar to ordinary quantum physics, quantum effects are wiped out. Application of Fermi and Bose Olbertians and the corresponding Olbertian physics there becomes clearly obsolete. Quantum plasmas, on the other hand, may provide a promising field of application but require the transition from the currently practiced fluid approach based on the Madelung–Bohm theory to an appropriate statistical mechanics. Quantum plasmas are dense enough in this case, have very high Fermi temperature which by far exceeds the physical temperature
In similar sense system closer-by and of large interest are terrestrial planetary interiors, for instance, Earth’s outer core. Its temperature is some 3500 K, corresponding to an energy of
This research was driven by curiosity, not by any applicational needs. It just presents a generalization of known classical statistical mechanics into the quantum domain. It may await application to the above indicated fields.
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was part of a brief Visiting Scientist Programme at the International Space Science Institute, Bern. RT acknowledges the interest of the ISSI directorate as well as the generous hospitality of the ISSI staff, in particular the assistance of the librarians Andrea Fischer and Irmela Schweitzer, and the Systems Administrator Saliba F. Saliba. We acknowledge valuable discussions with M. Leubner, R. Nakamura, and Z. Vörös.
1We thank C. Tsallis for kindly bringing this reference to our attention and G. Livadiotis for the access to the thesis.
2It was brought to our attention by the Associate Editor, G. Livadiotis, that in the framework of Tsallis’ nonextensive statistics, Fermi and Bose distributions had been derived already [cf. e.g., 35–37]. Since they arise from different propositions, they differ from Olbert’s kappa quantum distributions.
1. Olbert S. Summary of Experimental Results from M.I.T. Detector on IMP-1. In: Physics of the Magnetosphere, Proceedings of a Conference at Boston College, June 19-28, 1967 (RDL Carovillano, JF McClayAstrophysics and Space Science Library 40. Dordrecht: Reidel Publ. (1968). p. 641.
2. Binsack JH. Plasma Studies with the Imp-2 Satellite. Boston: PhD-Thesis, MIT (1966). p. 200. April 2, 2021.https://core.ac.uk/download/pdf/18321836.pdf.
3. Vasyliunas VM. A Survey of Low-Energy Electrons in the Evening Sector of the Magnetosphere with OGO 1 and OGO 3. J Geophys Res (1968) 73:2839–84. doi:10.1029/JA073i009p02839
4. Livadiotis G. In: G Livadiotis, editor. Kappa Distributions, Theory and Applications in Plasmas. Amsterdam, NL: Elsevier (2017).
5. Christon SP, Mitchell DG, Williams DJ, Frank LA, Huang CY, Eastman TE. Energy spectra of plasma sheet ions and electrons from 50 eV/e to 1 MeV during plasma temperature transitions. J Geophys Res (1988) 93:2562–72. doi:10.1029/JA093iA04p02562
6. Christon SP, Williams DJ, Mitchell DG, Frank LA, Huang CY. Spectral Characteristicds of Plasma Sheet Ion and Electron Populations during Undisturbed Geomagnetic Conditions. J Geophys Res (1989) 94:13409–24. doi:10.1029/JA094iA19p13409
7. Christon SP, Williams DJ, Mitchell DG, Huang CY, Frank LA. Spectral Characteristicds of Plasma Sheet Ion and Electron Populations during Disturbed Geomagnetic Conditions. J Geophys Res (1991) 96:1–22. doi:10.1029/90JA01633
8. Espinoza CM, Stepanova M, Moya PS, Antonova EE, Valdivia JA. Ion and Electron Distribution Functions along the Plasma Sheet. Geophys Res Lett (2018) 45:6362–70. doi:10.1029/2018GL078631
9. Kirpichev IP, Antonova EE. Dependencies of Kappa Parameter on the Core Energy of Kappa Distributions and Plasma Parameter in the Case of the Magnetosphere of the Earth. Astrophysical J (2020) 891:ID 35. doi:10.3847/1538-4365/abdec9
10. Eyelade AV, Stepanova M, Espinoza CM, Moya PS. On the Relation between Kappa Distribution Functions and the Plasma Beta Parameter in the Earth’s Magnetosphere: THEMIS Observations. Astrophysical JournalSupplement Ser (2021) 253:ID 34. doi:10.3847/1538-4357/ab700f
11. Schlickeiser R. Cosmic Ray Astrophysics. Berlin: Astronomy & Astrophysics Library, Springer (2002).
12. Treumann RA, Baumjohann W. The Differential Cosmic ray Energy Flux in the Light of an Ultrarelativistic Generalized Lorentzian Thermodynamics. Astrophysics Space Sci (2018) 363:37. doi:10.1007/s10509-018-3255-8
13. Goldstein ML, Eastwood JP, Treumann RA, Lucek EA, Pickett J, Décréau P. The Near-Earth Solar Wind. Space Sci Rev (2005) 118:7–39. doi:10.1007/s11214-005-3823-4
14. Pierrard V, Lazar M, Poedts S, Štervák Š, Maksimovic M, Trávníček PM. The Electron Temperature and Anisotropy in the Solar Wind. Comparison of the Core and Halo Populations. Solar Phys (2016) 291:2165–79. doi:10.1209/0295-5075/120/50002
15. Lazar M, Pierrard V, Poedts S, Fichtner H. Characteristics of Solar Wind Suprathermal Halo Electrons. Astron Astrophys (2020) 642:ID A130. doi:10.1051/0004-6361/2020038830
16. Yoon PH, Lazar M, Scherer K, Fichtner H, Schlickeiser R. Modified Kappa-Distribution of Solar Wind Electrons and Steady-State Langmuir Turbulence. Astrophysical J (2018) 868:111131. doi:10.3847/1538-4357/aaeb94
17. Livadiotis G, Desai MI, Wilson LB. Generation of kappa distributions in solar wind at 1 au. Astrophysical J (2018) 853:ID 142. doi:10.3847/1538-4357/aaa713
18. Eastwood JP, Lucek EA, Mazelle C, Meziane K, Narita Y, Pickett J, et al. The Foreshock. Space Sci Rev (2005) 118:41–94. doi:10.1007/s11214-005-3824-3
19. Lucek EA, Constantinescu D, Goldstein ML, Pickett J, Pinçon JL, Sahraoui F, et al. The Magnetosheath. Space Sci Rev (2005) 118:95–152. doi:10.1007/s11214-005-3825-2
20. Balogh A, Treumann RA. Physics of Collisionless Shocks. New York: Springer Media (2013). doi:10.1007/978-1-4614-6099-2
21. Fichtner H, Kleimann J, Yoon PH, Scherer K, Oughton S, Engelbrecht NE. On the Generation of Compressible Mirror-Mode Fluctuations in the Inner Heliosheath. Astrophysical J (2020) 901:76. doi:10.3847/1538-4357/abaf52
22. Livadiotis G, McComas DJ. Understanding Kappa Distributions: A Toolbox for Space Science and Astrophysics. Space Sci Rev (2013) 175:183–214. doi:10.1007/s11214-013-9982-9
23. Scherer K, Husidic E, Lazar M, Fichtner H. The κ-cookbook: a Novel Generalizing Approach to Unify κ-like Distributions for Plasma Particle Modelling. Monthly Notices R Astronomical Soc (2020) 497:1738–56. doi:10.1093/mnras/staa1969
24. Treumann RA. Kinetic Theoretical Foundation of Lorentzian Statistical Mechanics. Physica Scripta (1999) 59:19–26. doi:10.1238/Physica.Regular.059a00019
25. Treumann RA, Jaroschek CH, Scholer M. Stationary Plasma States Far from Equilibrium. Phys Plasmas (2004) 11:1317–25. doi:10.1063/1.1667498
26. Treumann RA, Jaroschek CH. Gibbsian Theory of Power Law Distributions. Phys Rev Lett (2008) 100:155005. doi:10.1103/PhysRevLett.100.155005
27. Livadiotis G. Kappa Distributions: Thermodynamic Origin and Generation in Space Plasmas. J Phys Conf Ser (2018) 1100:ID 012017. doi:10.1088/1742-6596/1100/1/012017
28. Livadiotis G. Kappa Distributions. Stat Phys Thermodynamics Space Astrophysical PlasmasUniverse (2018) 4:ID 144. doi:10.3390/universe4120144
29. Hasegawa A, Mima K, Duong-van M. Plasma Distribution Function in a Superthermal Radiation Field. Phys Rev Lett (1985) 54:2608–10. doi:10.1103/PhysRevLett.54.2608
30. Yoon PH, Rhee T, Ryu CM. Self-consistent Generation of Superthermal Electrons by Beam-Plasma Interaction. Phys Rev Lett (2005) 95:215003. doi:10.1103/PhysRevLett.95.215003
31. Yoon PH, Rhee T, Ryu CM. Self-consistent Generation of Electron κ Distribution: 1. Theory. J Geophys Res (2006) 111:A09106. doi:10.1029/2006JA011681
32. Tsallis C. Possible Generalization of Boltzmann-Gibbs Statistics. J Stat Phys (1988) 52:479–87. doi:10.1007/BF01016429
33. Treumann RA, Baumjohann W. Lorentzian Entropies and Olbert’s κ-distribution. Front Phys (2020) 8:221. doi:10.3389/fphy.2020.00221
34. Treumann RA, Baumjohann W. Beyond Gibbs-Boltzmann-Shannon: General Entropies – the Gibbs-Lorentzian Example. Front Phys (2014) 2:49. doi:10.3389/fphys.2014.00049
35. Aragão-Rêgo HH, Soares DJ, Lucena LS, da Silva LR, Lenzi EK, et al. Bose-Einstein and Fermi-Dirac Distributions in Nonextensive Tsallis Statistics: an Exact Study. Phys A: Stat Mech its Appl (2003) 317:199–208. doi:10.1016/50378-4371(02)01330-4
36. Christianto V, Smarandache F. A Note on Unified Statistics Including Fermi-Dirac, Bose-Einstein, and Tsallis Statistics, and Plausible Extension to Anisotropic Effect. Prog Phys (2007) 2:61–4. Available at: https://www.ptep-online.com/2007/PP-09-12.PDF.
37. Obregón O, Ortega-Cruz M. Generalizes Entropies Depending Only on the Probability and Their Quantum Statistics. Proceedings (2018) 2:169–75. doi:10.3390/ecea-4-05020
38. Domenech-Garret JL, Tierno SP, Conde L. Non-equilibrium Thermionic Electron Emission for Metals at High Temperatures. J Appl Phys (2015) 118:074904. doi:10.1063/1.49929150
39. Domenech-Garret JL. Transmission through potential barriers with a generalizsed Fermi-Dirac curren. J. Statis. Mech. Theory Exp. 2020:053102. doi:10.1088/172-5468/ab7af1
40. Scherer K, Fichtner H, Lazar M. Regularized κ-distributions with Non-diverging Moments. Europhysics Lett EPL (2017) 120:50002. doi:10.1209/0295-5075/120/50002
41. Lazar M, Scherer K, Fichtner H, Pierrard V. Toward a Realistic Macroscopic Parametrization of Space Plasmas with Regularized κ-distribution. Astron Astrophysics (2020) 643:A20. doi:10.1051/0004-6361/201936861
43. Landau LD, Lifshitz EM. Statistical Physics Part 1. In: Course of Theoretical Physics, 5. Oxford UK: Pergamon Press (1980).
Keywords: Kappa distribution, Fermi- and Bose distributions, solid state and condensed matter, quantum distributions, degenerate matter, entropy
Citation: Treumann RA and Baumjohann W (2021) Olbert’s Kappa Fermi and Bose Distributions. Front. Phys. 9:672836. doi: 10.3389/fphy.2021.672836
Received: 26 February 2021; Accepted: 07 May 2021;
Published: 28 May 2021.
Edited by:
George Livadiotis, Southwest Research Institute (SwRI), United StatesReviewed by:
Peter Haesung Yoon, University of Maryland, United StatesCopyright © 2021 Treumann and Baumjohann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wolfgang Baumjohann, V29sZmdhbmcuQmF1bWpvaGFubkBvZWF3LmFjLmF0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.